Numerical Study on Convective Heat Transfer of Liquid Metal Gallium in Turbine Guide Vane
Abstract
1. Introduction
2. One-Dimensional Thermal Conductivity Calculation
3. Three-Dimensional Steady-State Numerical Computation
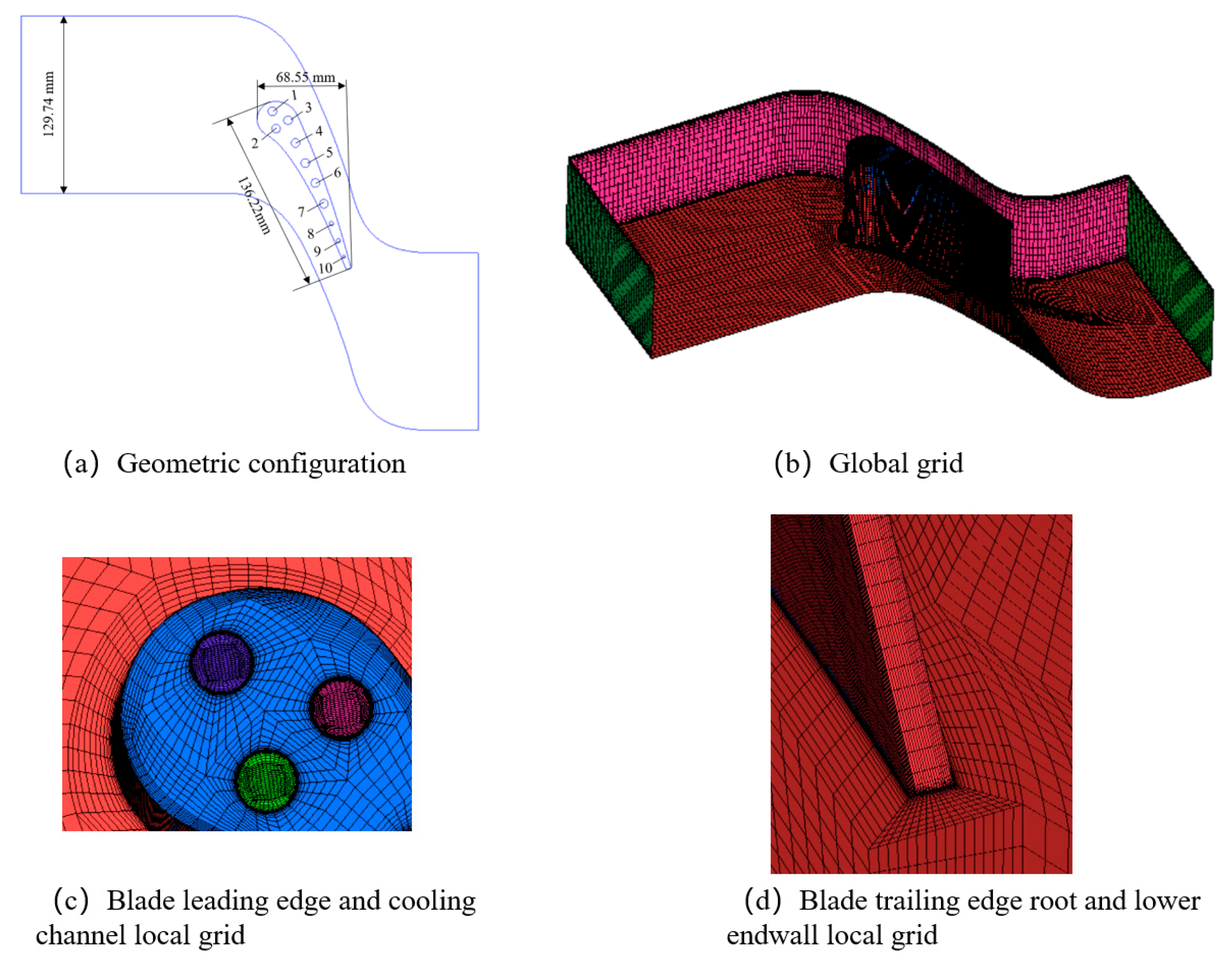
3.1. Geometric Configuration
3.2. Governing Equations
3.3. Physical Parameters and Boundary Settings
3.3.1. Dominant Physical Property
3.3.2. Solid Physical Property
3.3.3. Boundary Setting
4. Calculation Result and Analysis
4.1. Grid-Independent Verification
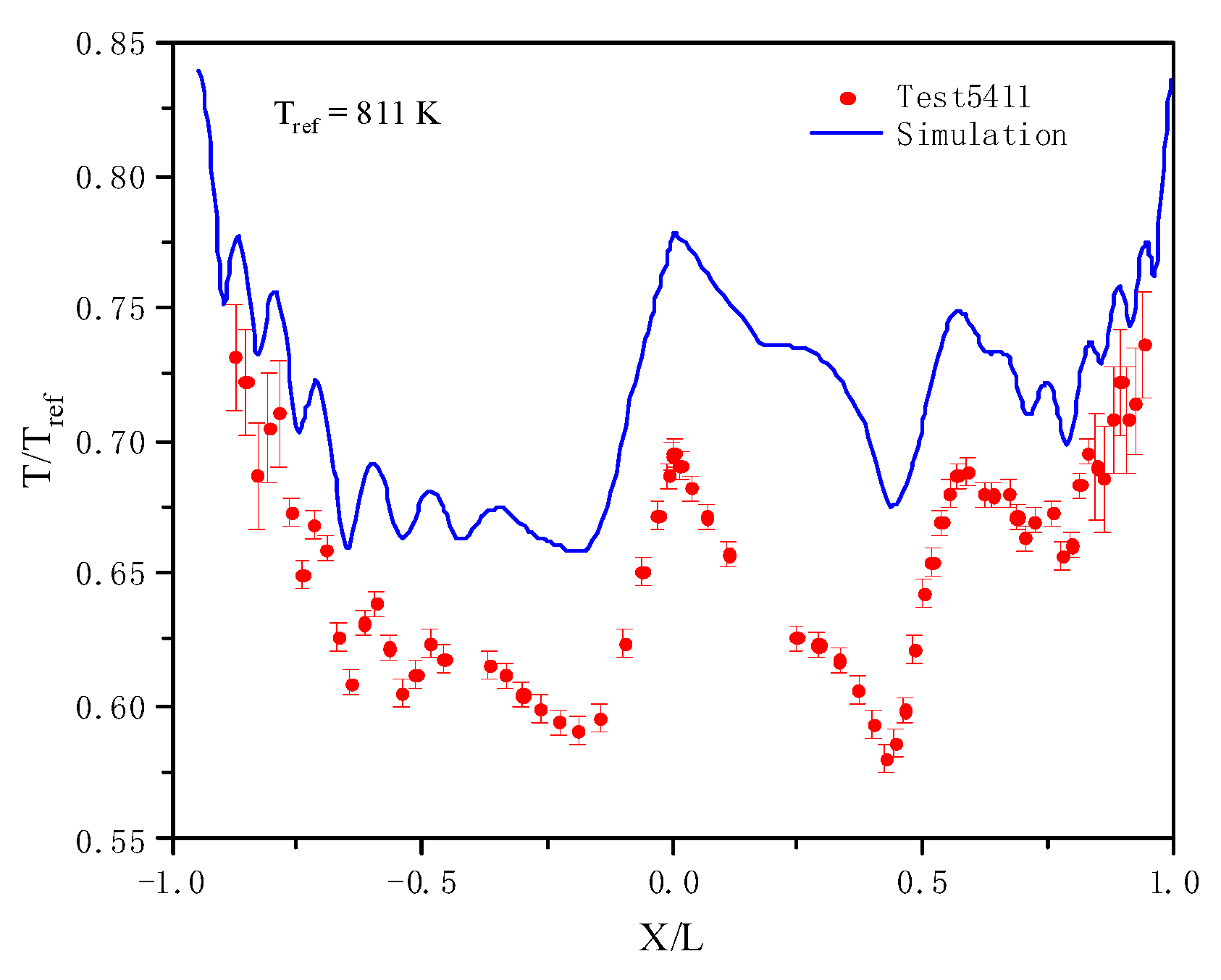
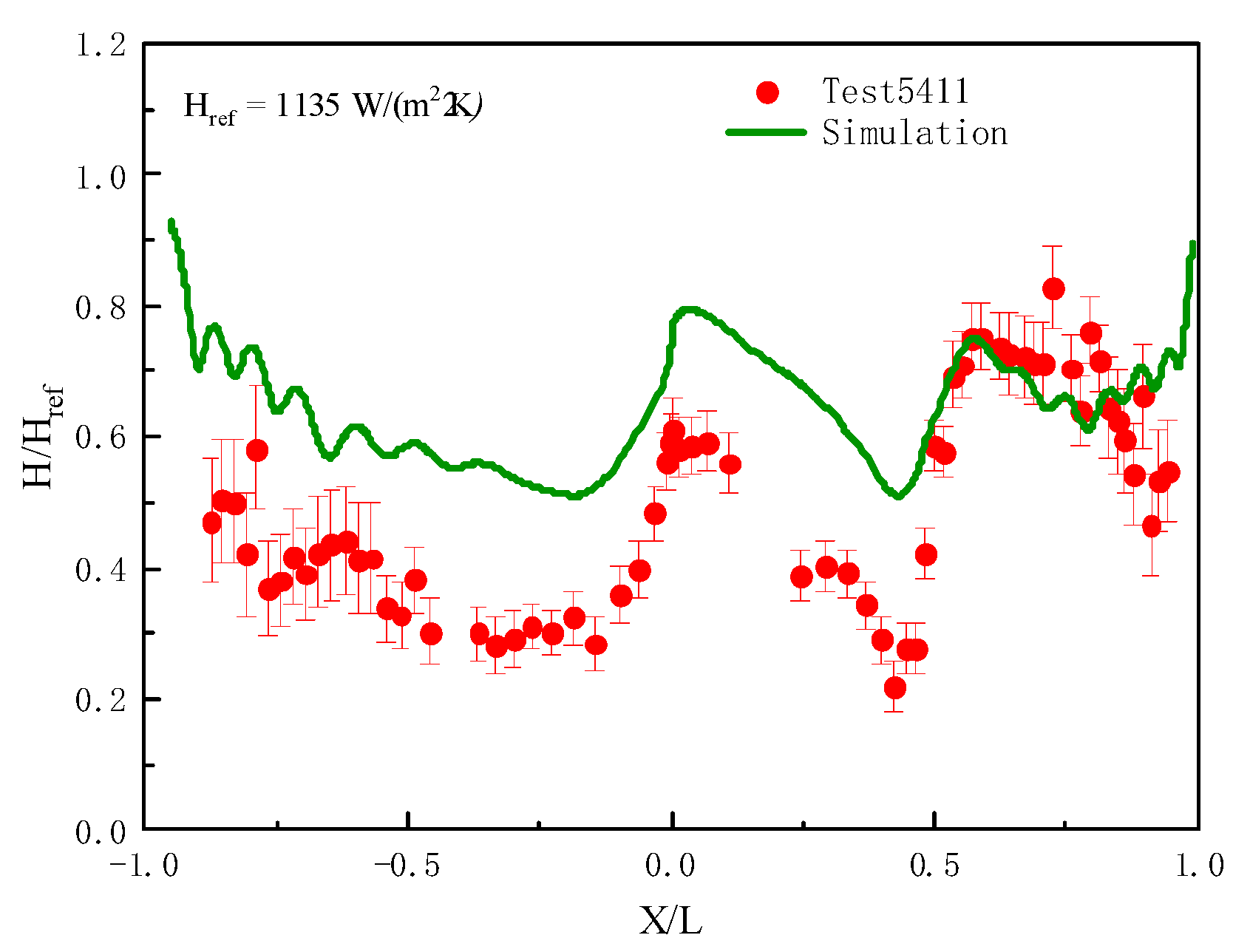
4.2. Experimental Verification
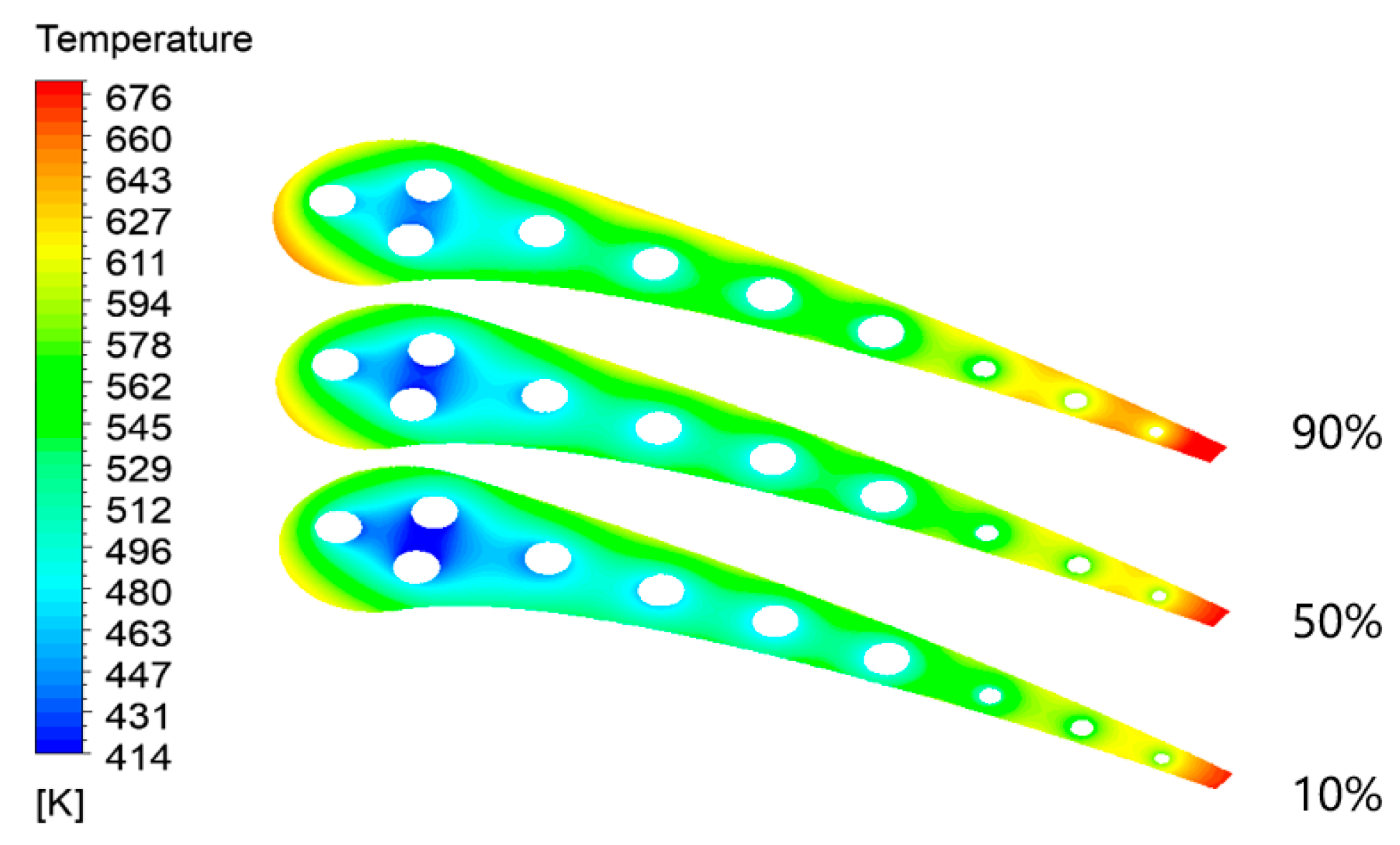
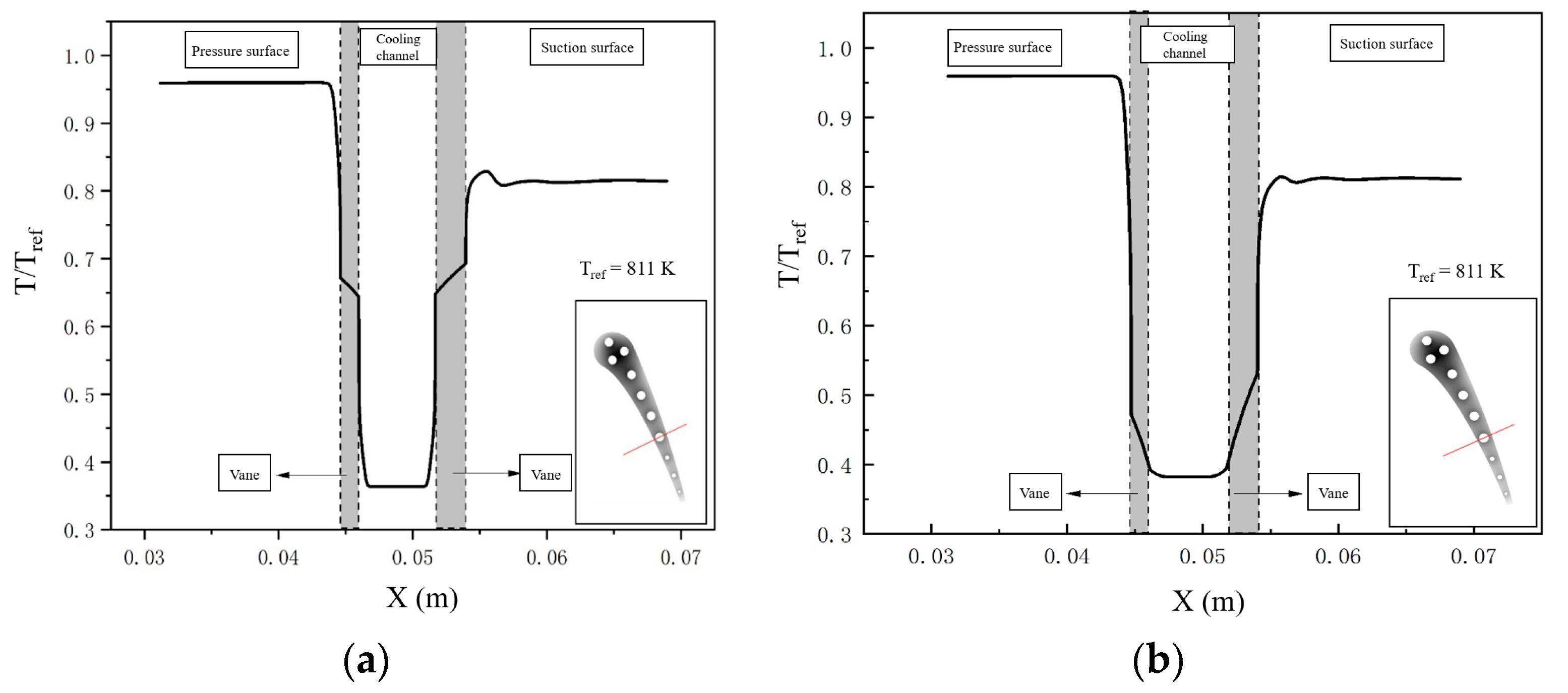
4.3. Air Cooling
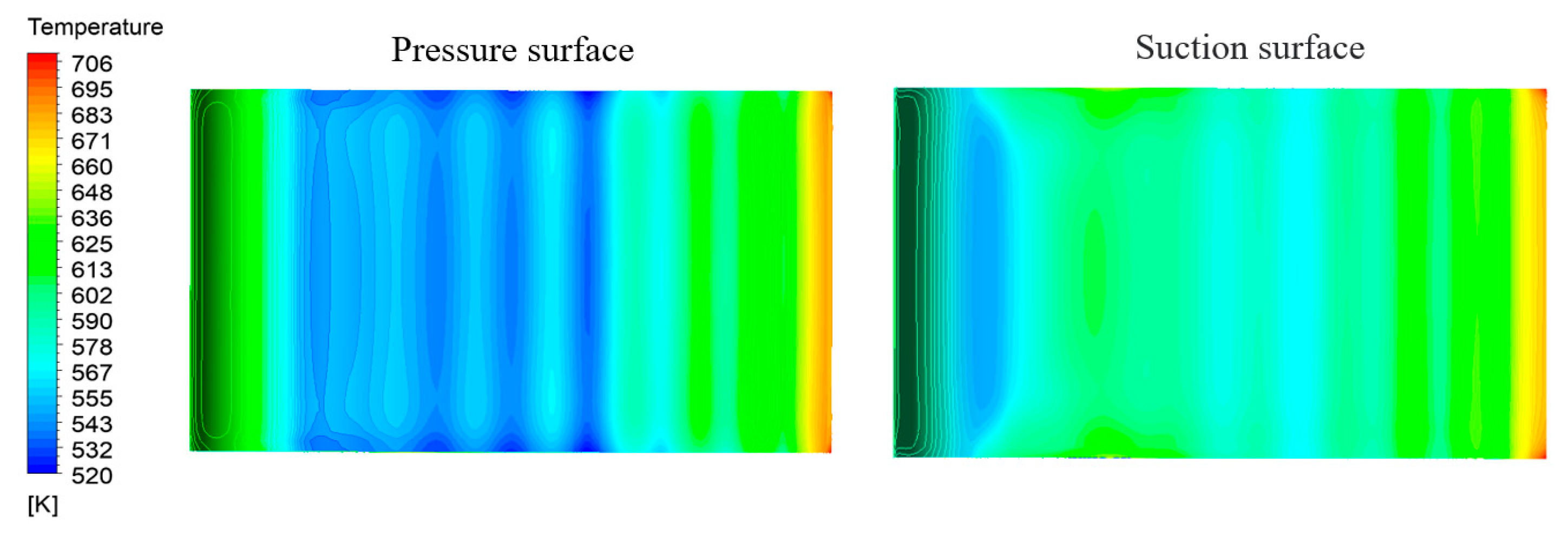
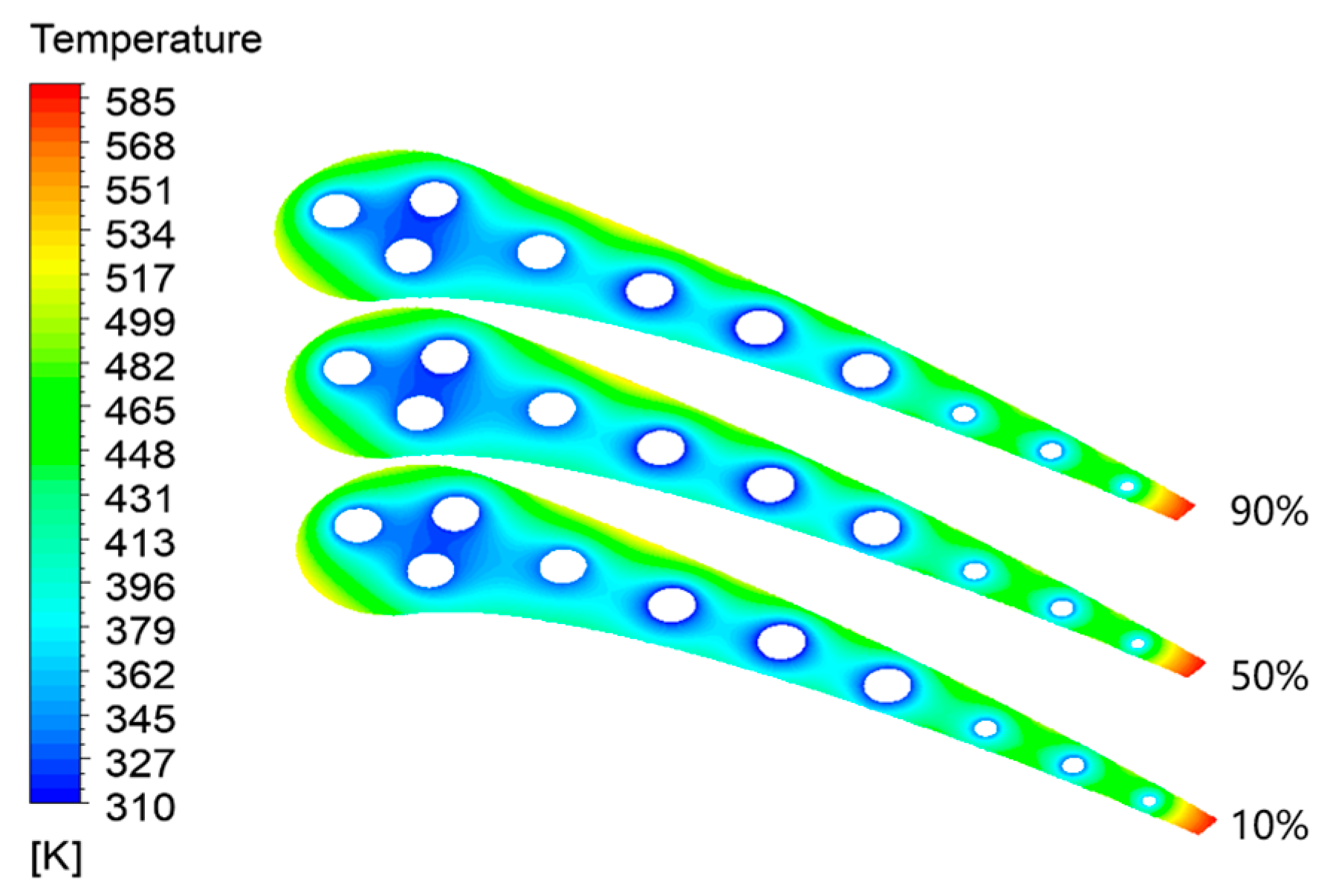
4.4. Liquid Metal Cooling
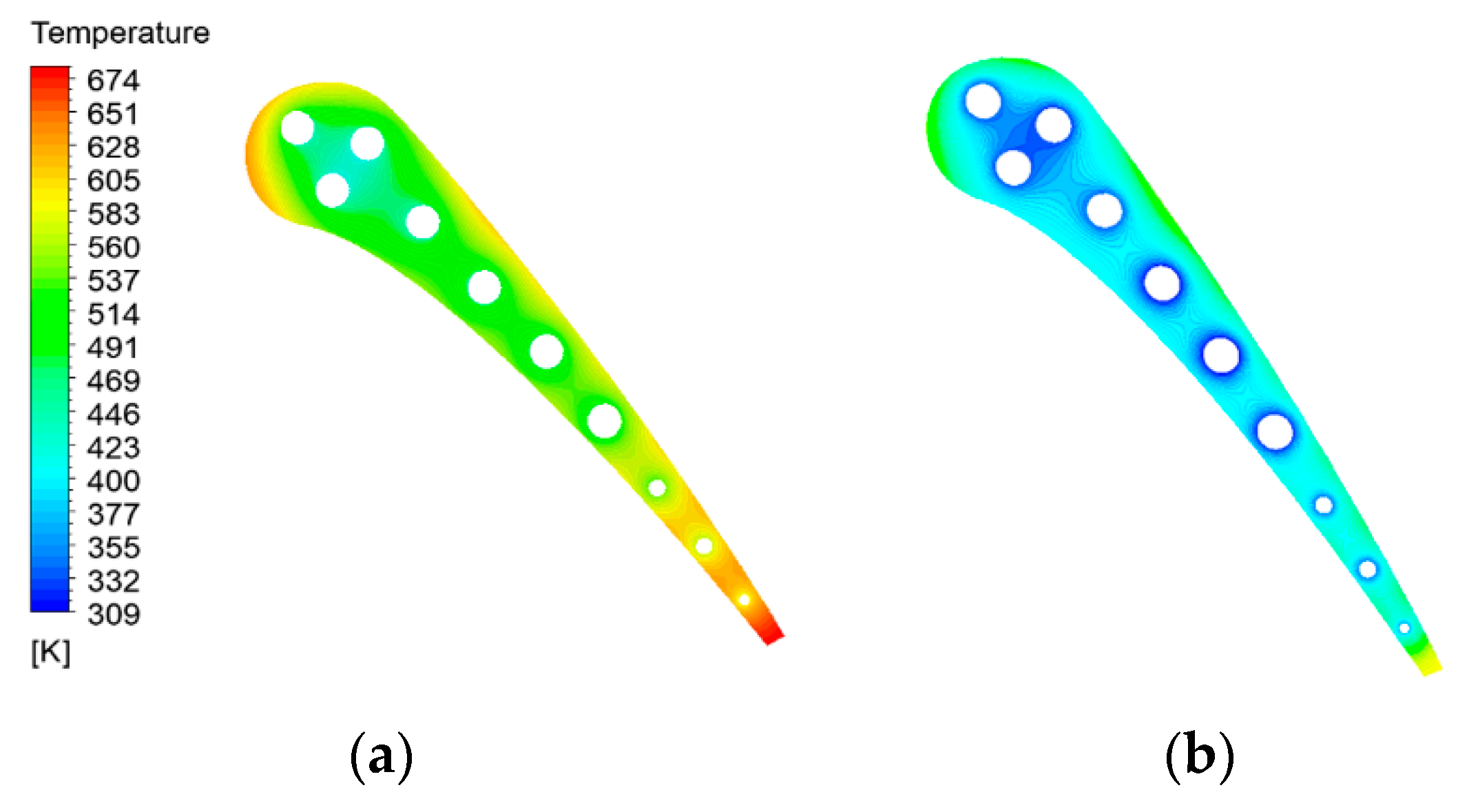
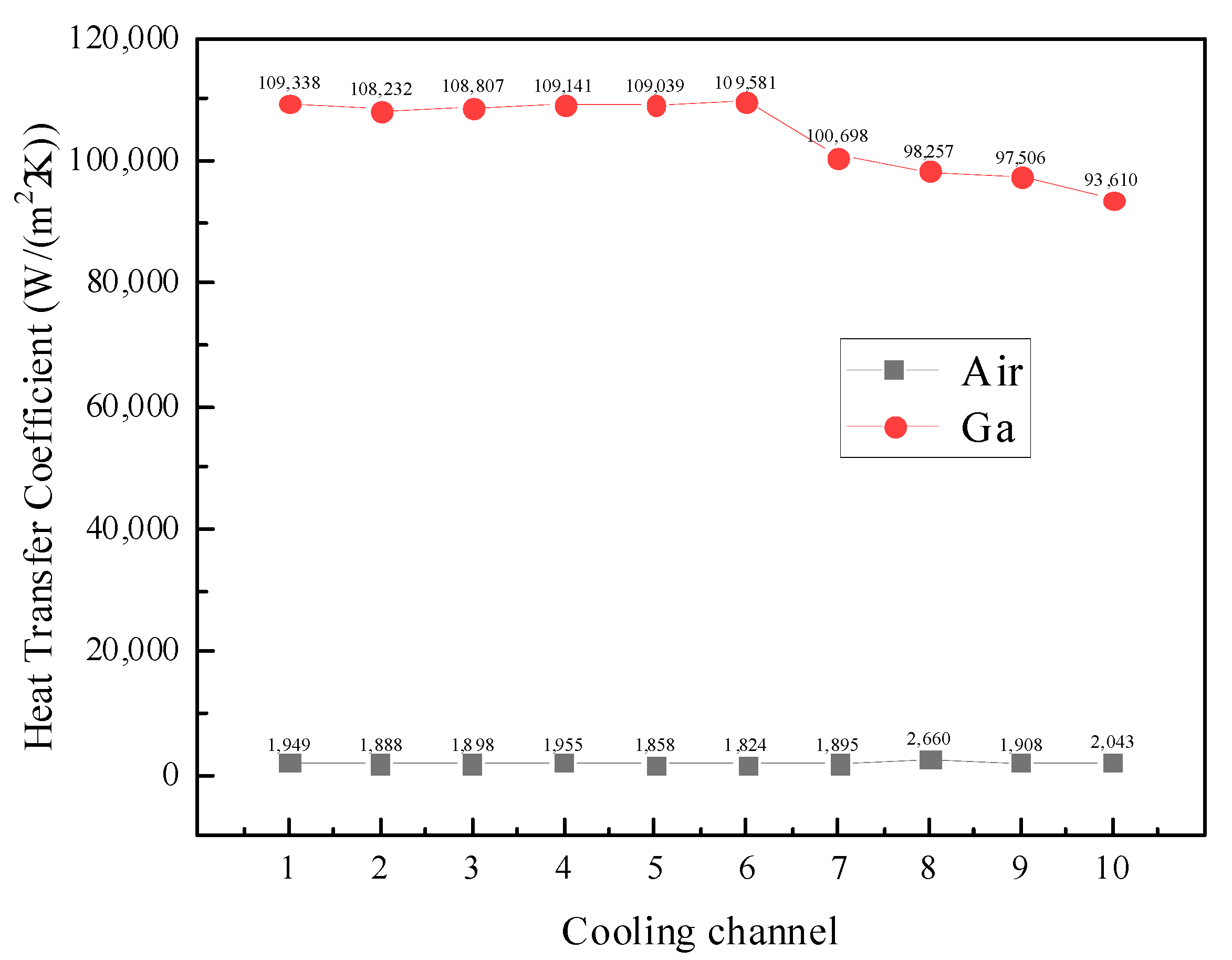
4.4.1. Comparative Analysis of Heat Transfer Effect
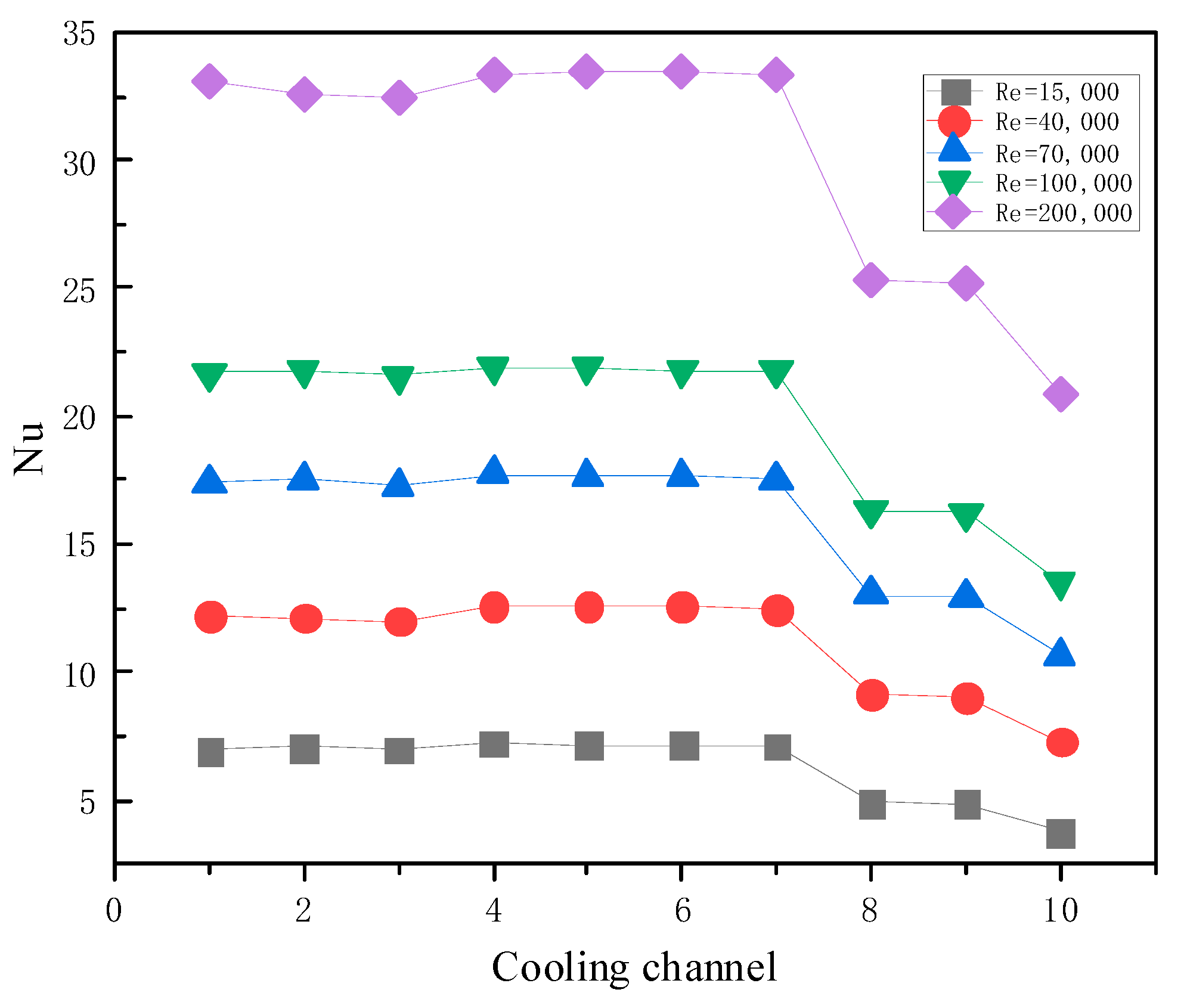
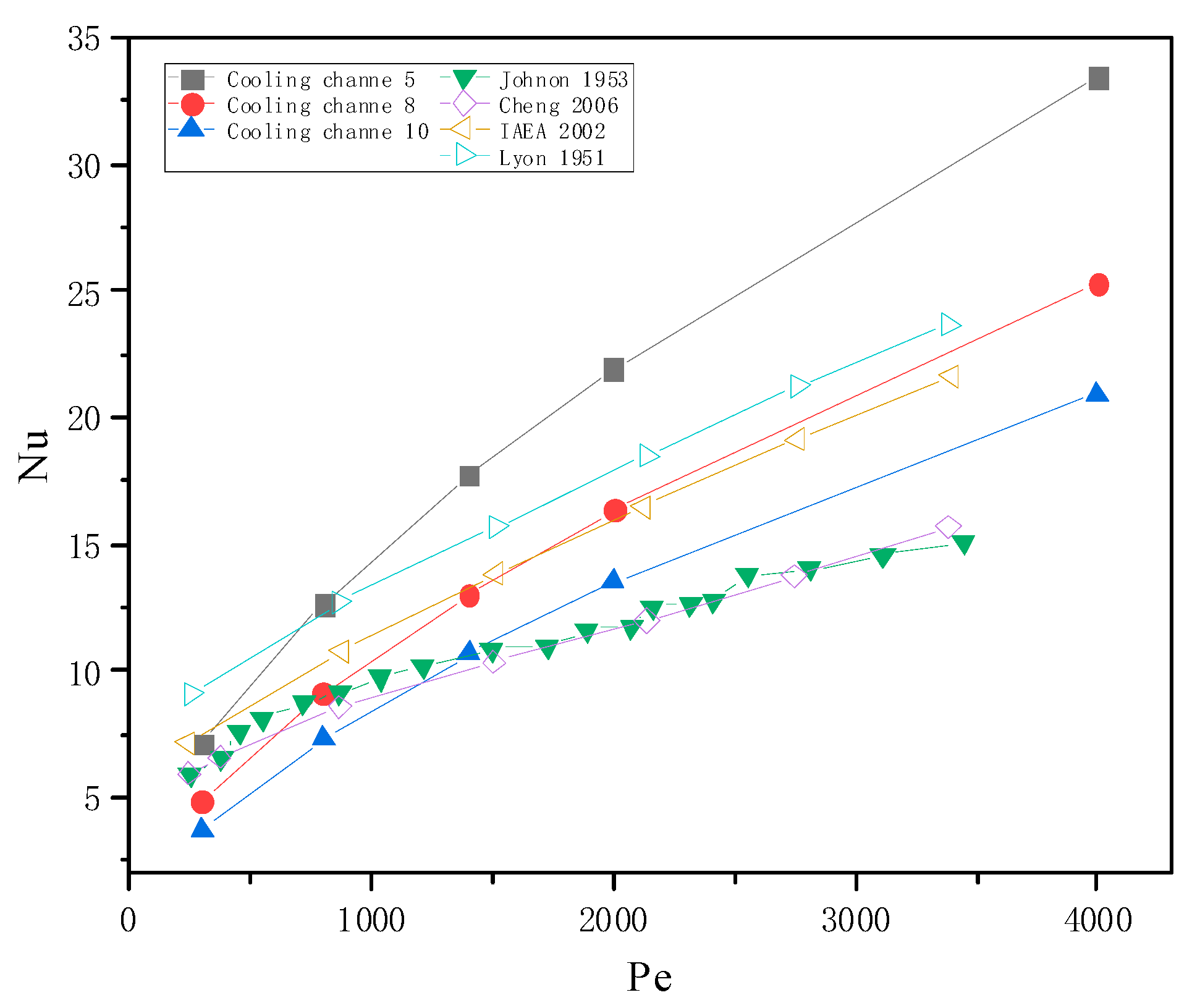
4.4.2. Influence of Cooling Channel Inlet Reynolds
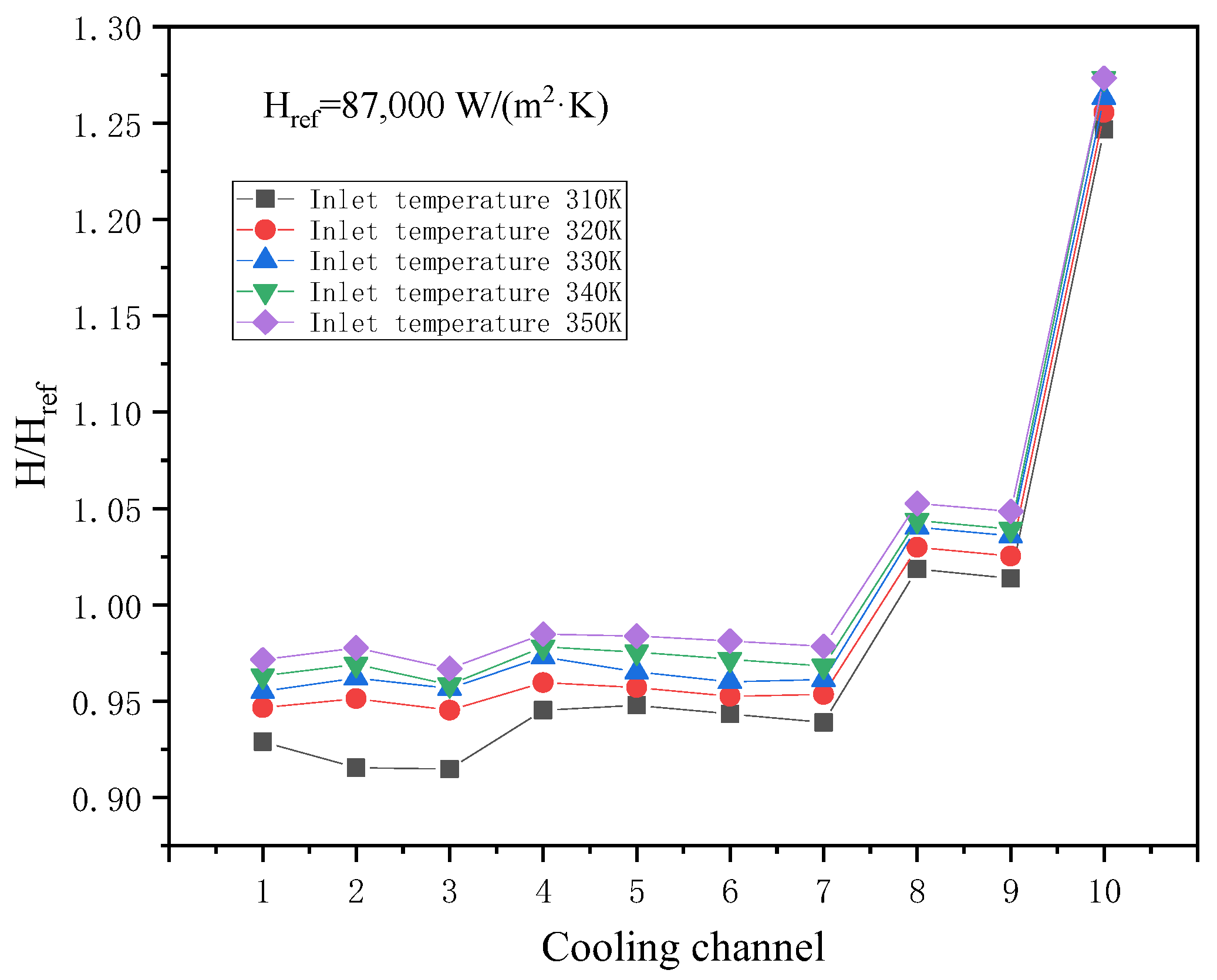
4.4.3. Influence of Cooling Channel Inlet Temperature
5. Conclusions
- (1)
- Compared with conventional air cooling, liquid metal Ga has obvious clear advantages, such as a lower temperature gradient and lower thermal stress, no matter the temperature gradient of each part of the middle-diameter vane section or the temperature distribution on the outer wall of the vane.
- (2)
- The heat transfer coefficient of liquid metal is much higher than that of air by tens of thousands of magnitude, which is the fundamental reason why liquid metal cooling is better than air cooling.
- (3)
- The larger the Re at the entrance of the cooling channel, the larger the average Nusselt number on the wall of the cooling channel; that is, the better the enhanced heat transfer effect of liquid metal gallium. The Peclet number is also an important index for heat transfer quality.
- (4)
- With an increase in Ga inlet temperature, the average heat transfer coefficient of the cooling channel wall presents a weak rise. The enhanced heat transfer quality factor can reveal the essence.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| h | heat transfer coefficient (W/(m2∙K)) |
| Re | Reynolds number |
| Nu | Nusselt number |
| Pr | Prandtl number |
| p | pressure (Pa) |
| Cp | specific heat capacity (J/(kg·K)) |
| H | average heat transfer coefficient (W/(m2∙K)) |
| d | pipe diameter (mm) |
| M | enhanced heat transfer quality factor |
| T | Kelvin temperature (K) |
| q | heat flux |
| A | heat transfer area (m2) |
| u | velocity in x direction (m/s) |
| v | velocity in y direction (m/s) |
| w | velocity in z direction (m/s) |
| x | Cartesian coordinate (m) |
| y | Cartesian coordinate (m) |
| z | Cartesian coordinate (m) |
| Greek symbols | |
| λ | heat conductivity coefficient (W/(m∙K)) |
| δ | thickness (mm) |
| η | dynamic viscosity (Pa·s) |
| ρ | density (kg/m3) |
| λf | thermal conductivity (W/(m·K)) |
| Subscripts | |
| g | high-temperature gas |
| c | cooling medium |
| w | wall |
| ref | qualitative |
| lm | liquid metal |
References
- Han, J.-C.; Dutta, S.; Ekkad, S. Gas Turbine Heat Transfer and Cooling Technology; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Boyce Meherwan, P. Gas Turbine Engineering Handbook; Elsevier: Amsterdam, The Netherlands, 2012; pp. 693–719. [Google Scholar]
- Bunker, R. Innovative gas turbine cooling techniques. In WIT Transactions on State-of-the-Art in Science and Engineering; WIT Press: Southampton, UK, 2008; Volume 42, pp. 199–229. [Google Scholar]
- Kumar, S.; Amano, R.S. An Investigation in the Numerical Approach to Solve the Heat Transfer Phenomenon in Gas Turbine. J. Energy Resour. Technol. 2021, 143, 080805. [Google Scholar] [CrossRef]
- Han, J.C. Heat Transfer and Friction Characteristics in Rectangular Channels With Rib Turbulators. J. Heat Transf. 1988, 110, 321–328. [Google Scholar] [CrossRef]
- Han, J.C. Heat Transfer and Friction in Channels With Two Opposite Rib-Roughened Walls. J. Heat Transf. 1984, 106, 774–781. [Google Scholar] [CrossRef]
- Elfert, M.; Schroll, M.; Förster, W. PIV Measurement of Secondary Flow in a Rotating Two-Pass Cooling System with an Improved Sequencer Technique. J. Turbomach. 2011, 134, 031001. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, J.; Wu, X.; Lu, H. A Simplified Approach to Design Transverse Ribs Which Array Alternately in Rectangular Channel. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, Glasgow, UK, 14–18 June 2010; pp. 197–203. [Google Scholar]
- Salameh, T.; Sunden, B. Effects of Ribs on Internal Blade-Tip Cooling. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition, 2011, Vancouver, BC, Canada, 6–10 June 2011; pp. 1033–1041. [Google Scholar]
- Gao, Z.; Narzary, D.P.; Han, J.-C. Film cooling on a gas turbine blade pressure side or suction side with axial shaped holes. Int. J. Heat Mass Transf. 2008, 51, 2139–2152. [Google Scholar] [CrossRef]
- Walters, D.K.; Leylek, J.H. A Detailed Analysis of Film–Cooling Physics: Part I—Streamwise Injection with Cylindrical Holes. In Proceedings of the ASME 1997 International Gas Turbine and Aeroengine Congress and Exhibition, Orlando, FL, USA, 2–5 June 1997. [Google Scholar]
- McGovern, K.T.; Leylek, J.H. A Detailed Analysis of Film Cooling Physics: Part II—Compound–Angle Injection with Cylindrical Holes. In Proceedings of the ASME 1997 International Gas Turbine and Aeroengine Congress and Exhibition, Orlando, FL, USA, 2–5 June 1997. [Google Scholar]
- Hyams, D.G.; Leylek, J.H. A Detailed Analysis of Film Cooling Physics: Part III—Streamwise Injection with Shaped Holes. In Proceedings of the ASME 1997 International Gas Turbine and Aeroengine Congress and Exhibition, Orlando, FL, USA, 2–5 June 1997. [Google Scholar]
- Kim, Y.J.; Kim, S.M. Influence of shaped injection holes on turbine blade leading edge film cooling. Int. J. Heat Mass Transf. 2004, 47, 245–256. [Google Scholar] [CrossRef]
- Cho, H.H.; Rhee, D.H.; Kim, B.G. Enhancement of Film Cooling Performance Using a Shaped Film Cooling Hole with Compound Angle Injection. JSME Int. J. Ser. B Fluids Therm. Eng. 2001, 44, 99–110. [Google Scholar] [CrossRef]
- Gritsch, M.; Colban, W.; Schär, H.; Döbbeling, K. Effect of Hole Geometry on the Thermal Performance of Fan-Shaped Film Cooling Holes. J. Turbomach. 2005, 127, 718–725. [Google Scholar] [CrossRef]
- Kim, S.-M.; Lee, K.-D.; Kim, K.-Y. A comparative analysis of various shaped film-cooling holes. Heat Mass Transf. 2012, 48, 1929–1939. [Google Scholar] [CrossRef]
- Kusterer, K.; Elyas, A.; Bohn, D.; Sugimoto, T.; Tanaka, R.; Kazari, M. The NEKOMIMI Cooling Technology: Cooling Holes With Ears for High-Efficient Film Cooling. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 6–10 June 2011; pp. 303–313. [Google Scholar]
- Lee, K.-D.; Kim, K.-Y. Shape optimization of a fan-shaped hole to enhance film-cooling effectiveness. Int. J. Heat Mass Transf. 2010, 53, 2996–3005. [Google Scholar] [CrossRef]
- Lee, K.-D.; Kim, K.-Y. Surrogate based optimization of a laidback fan-shaped hole for film-cooling. Int. J. Heat Fluid Flow 2011, 32, 226–238. [Google Scholar] [CrossRef]
- Bo, G.Y.; Ren, L.; Xu, X.; Du, Y.; Dou, S.X. Recent progress on liquid metals and their applications. Adv. Phys.-X 2018, 3, 411–441. [Google Scholar] [CrossRef]
- Deng, Y.; Jiang, Y.; Liu, J. Low-melting-point liquid metal convective heat transfer: A review. Appl. Therm. Eng. 2021, 193, 117021. [Google Scholar] [CrossRef]
- Liu, J. Advanced Liquid Metal Cooling for Chip, Device and System. In Advanced Liquid Metal Cooling for Chip, Device and System; World Scientific Publishers: Singapore, 2020. [Google Scholar]
- Liu, G.L.; Liu, J. Convective Cooling of Compact Electronic Devices via Liquid Metals with Low Melting Points. J. Heat Transf. 2021, 143, 050801. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, Y.-X.; Lv, Y.-G.; Li, T. Liquid Metal Based Miniaturized Chip-Cooling Device Driven by Electromagnetic Pump. In Proceedings of the ASME 2005 International Mechanical Engineering Congress and Exposition, Orlando, FL, USA, 5–11 November 2005; pp. 501–510. [Google Scholar]
- Ma, K.Q.; Liu, J. Heat-driven liquid metal cooling device for the thermal management of a computer chip. J. Phys. D Appl. Phys. 2007, 40, 4722–4729. [Google Scholar] [CrossRef]
- Deng, Y.-G.; Liu, J.; Zhou, Y.-X. Study on Liquid Metal Cooling of Photovoltaic Cell. In Inaugural US-EU-China Thermophysics Conference-Renewable Energy 2009 (UECTC 2009 Proceedings); Tao, Y., Ma, C., Eds.; ASME Press: New York, NY, USA, 2009; Volume 1. [Google Scholar]
- Pacio, J.; Singer, C.; Wetzel, T.; Uhlig, R. Thermodynamic evaluation of liquid metals as heat transfer fluids in concentrated solar power plants. Appl. Therm. Eng. 2013, 60, 295–302. [Google Scholar] [CrossRef]
- Frazer, D.; Stergar, E.; Cionea, C.; Hosemann, P. Liquid Metal as a Heat Transport Fluid for Thermal Solar Power Applications. Energy Procedia 2014, 49, 627–636. [Google Scholar] [CrossRef]
- Fritsch, A.; Flesch, J.; Geza, V.; Singer, C.; Uhlig, R.; Hoffschmidt, B. Conceptual Study of Central Receiver Systems with Liquid Metals as Efficient Heat Transfer Fluids. Energy Procedia 2015, 69, 644–653. [Google Scholar] [CrossRef]
- Deng, Y.; Liu, J. A liquid metal cooling system for the thermal management of high power LEDs. Int. Commun. Heat Mass Transf. 2010, 37, 788–791. [Google Scholar] [CrossRef]
- Peng, H.; Guo, W.; Li, M.; Feng, S. Melting behavior and heat transfer performance of gallium for spacecraft thermal energy storage application. Energy 2021, 228, 120575. [Google Scholar] [CrossRef]
- Cheng, K.; Xu, J.; Dang, C.; Qin, J.; Jing, W. Performance evaluation of fuel indirect cooling based thermal management system using liquid metal for hydrocarbon-fueled scramjet. Energy 2022, 260, 125068. [Google Scholar] [CrossRef]
- Zhang, X.-D.; Yang, X.-H.; Zhou, Y.-X.; Rao, W.; Gao, J.-Y.; Ding, Y.-J.; Shu, Q.-Q.; Liu, J. Experimental investigation of galinstan based minichannel cooling for high heat flux and large heat power thermal management. Energy Convers. Manag. 2019, 185, 248–258. [Google Scholar] [CrossRef]
- Al Omari, S.A.B.; Haik, Y.; Abu Jdayil, B. Flow characteristics of gallium in a meso-scale channel under the influence of magnetic fields. Int. Commun. Heat Mass Transf. 2010, 37, 1127–1134. [Google Scholar] [CrossRef]
- Al Omari, S. Characteristics of the flow and heat transfer of gallium in a mini-scale channel under the effect of magnetic field. J. Enhanc. Heat Transf. 2011, 18, 537–546. [Google Scholar] [CrossRef]
- Kang, S.; Ha, K.-S.; Kim, H.T.; Kim, J.H.; Bang, I.C. An experimental study on natural convection heat transfer of liquid gallium in a rectangular loop. Int. J. Heat Mass Transf. 2013, 66, 192–199. [Google Scholar] [CrossRef]
- Omari, S.A.B.A.; Elnajjar, E. An Experimental Study on Enhancing Cooling Rates of Low Thermal Conductivity Fluids Using Liquid Metals. Fluid Dyn. Mater. Process. 2013, 9, 91–109. [Google Scholar]
- Manservisi, S.; Menghini, F. A CFD four parameter heat transfer turbulence model for engineering applications in heavy liquid metals. Int. J. Heat Mass Transf. 2014, 69, 312–326. [Google Scholar] [CrossRef]
- Sharma, D.; Singh, P.P.; Garg, H. Comparative Study of Rectangular and Trapezoidal Microchannels Using Water and Liquid Metal. Procedia Eng. 2013, 51, 791–796. [Google Scholar] [CrossRef]
- Tawk, M.; Avenas, Y.; Kedous-Lebouc, A.; Petit, M. Numerical and Experimental Investigations of the Thermal Management of Power Electronics With Liquid Metal Mini-Channel Coolers. IEEE Trans. Ind. Appl. 2013, 49, 1421–1429. [Google Scholar] [CrossRef]
- Zhang, X.-D.; Gao, J.-Y.; Liu, J. Comparative Study of Heat Transfer in a Mini/Micro Pipe with Water and Liquid Metal As Fluid. In Proceedings of the ASME 2020 Heat Transfer Summer Conference collocated with the ASME 2020 Fluids Engineering Division Summer Meeting and the ASME 2020 18th International Conference on Nanochannels, Microchannels, and Minichannels, Virtual, Online, 13–15 July 2020. [Google Scholar]
- Wu, T.; Wang, L.; Tang, Y.; Yin, C.; Li, X. Flow and Heat Transfer Performances of Liquid Metal Based Microchannel Heat Sinks under High Temperature Conditions. Micromachines 2022, 13, 95. [Google Scholar] [CrossRef] [PubMed]
- Hojna, A.; Di Gabriele, F.; Klecka, J. Character of Liquid Metal Embrittlement of the Steel T91 in Contact with Lead-Bismuth Eutectic. In Proceedings of the 2014 22nd International Conference on Nuclear Engineering, Prague, Czech Republic, 7–11 July 2014. [Google Scholar]
- Cui, Y.; Ding, Y.; Xu, S.; Wang, Y.; Rao, W.; Liu, J. Study on Heat Transfer and Corrosion Resistance of Anodized Aluminum Alloy in Gallium-Based Liquid Metal. J. Electron. Packag. 2019, 141, 011001. [Google Scholar] [CrossRef]
- Miner, A.; Ghoshal, U. Cooling of high-power-density microdevices using liquid metal coolants. Appl. Phys. Lett. 2004, 85, 506–508. [Google Scholar] [CrossRef]
- Pacio, J.; Marocco, L.; Wetzel, T. Review of data and correlations for turbulent forced convective heat transfer of liquid metals in pipes. Heat Mass Transf. 2015, 51, 153–164. [Google Scholar] [CrossRef]
- Hylton, L.; Mihelc, M.; Turner, E.; Nealy, D.; York, R. Analytical and Experimental Evaluation of the Heat Transfer Distribution over the Surfaces of Turbine Vanes; NASA: Washington, DC, USA, 1983. [Google Scholar]
- Menter, F.; Kuntz, M.; Langtry, R.B. Ten years of industrial experience with the SST turbulence model. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Dong, P.; Wang, Q.; Guo, Z.; Huang, H.; Feng, G. Conjugate Calculation of Gas Turbine Vanes Cooled with Leading Edge Films. Chin. J. Aeronaut. 2009, 22, 145–152. [Google Scholar] [CrossRef]
- Bagabir, A.; Drikakis, D. Mach number effects on shock-bubble interaction. Shock Waves 2001, 11, 209–218. [Google Scholar] [CrossRef]
- Larsson, J.; Bermejo-Moreno, I.; Lele, S. Reynolds- and Mach-number effects in canonical shock-turbulence interaction. J. Fluid Mech. 2013, 717, 293–321. [Google Scholar] [CrossRef]
- Johnson, H.A.; Hartnett, J.P.; Clabaugh, W.J. Heat Transfer to Molten Lead-Bismuth Eutectic in Turbulent Pipe Flow. J. Heat Transf. 1953, 75, 1191–1198. [Google Scholar] [CrossRef]
- Cheng, X.; Tak, N.-I. Investigation on turbulent heat transfer to lead–bismuth eutectic flows in circular tubes for nuclear applications. Nucl. Eng. Des. 2006, 236, 385–393. [Google Scholar] [CrossRef]
- Lyon, R.N. Liquid metal heat transfer coefficients. Chem. Eng. Prog. 1951, 47, 269. [Google Scholar]
- International Atomic Energy Agency. Comparative Assessment of Thermophysical and Thermohydraulic Characteristics of Lead, Lead-Bismuth and Sodium Coolants for Fast Reactors; International Atomic Energy Agency: Vienna, Austria, 2002. [Google Scholar]


| Hot Gas | Turbine Guide Vane | Cooling Medium | ||||
|---|---|---|---|---|---|---|
| Coating | Metal Material | |||||
| 2400 K | 8000 W/(m2∙K) | 0.5 W/(m∙K) | 0.125 mm | 26 W/(m∙K) | 3.55 mm | 700 K |
| Cooling Medium | Heat Transfer Coefficient | Metal Material Temperature /K |
|---|---|---|
| Air | 2000 | 1769 |
| Gallium | 98,400 | 1174 |
| Inlet Conditions | Total Inlet Pressure/Pa | 337,097 |
|---|---|---|
| Total Inlet Temperature/K | 2400 | |
| Outlet conditions | Outlet static pressure/Pa | 175,713 |
| Cooling Channel | Diameter/mm | Inlet Mass Flow Rate/kg/s | Tin/K | Pout/MPa |
|---|---|---|---|---|
| 1 | 6.3 | 0.0246 | 326 | 0.3533 |
| 2 | 6.3 | 0.0237 | 316 | 0.3497 |
| 3 | 6.3 | 0.0238 | 322 | 0.3571 |
| 4 | 6.3 | 0.0247 | 328 | 0.3647 |
| 5 | 6.3 | 0.0233 | 308 | 0.3200 |
| 6 | 6.3 | 0.0228 | 305 | 0.3428 |
| 7 | 6.3 | 0.0238 | 313 | 0.3587 |
| 8 | 3.1 | 0.00775 | 335 | 0.7030 |
| 9 | 3.1 | 0.00511 | 330 | 0.5370 |
| 10 | 1.98 | 0.00334 | 354 | 1.0199 |
| Grid Number/Ten Thousand | 90 | 100 | 118 | 200 | 400 |
|---|---|---|---|---|---|
| Mainstream outlet average temperature/K | 677.0 | 677.1 | 676.6 | 677.3 | 676.5 |
| Working Condition | Condition 1 | Condition 2 | Condition 3 | Condition 4 | Condition 5 |
|---|---|---|---|---|---|
| Cooling channel inlet Reynolds number Re | 15,000 | 40,000 | 70,000 | 100,000 | 200,000 |
| Cooling Channel Pipe Diameter/(mm) | 6.3 | 3.1 | 1.98 |
|---|---|---|---|
| Cooling channel inlet velocity/(m/s) | 3.3 | 4 | 6 |
| Working Condition | Condition 1 | Condition 2 | Condition 3 | Condition 4 | Condition 5 |
|---|---|---|---|---|---|
| Inlet temperature/K | 310 | 320 | 330 | 340 | 350 |
| Temperature/K | 310 | 320 | 330 | 340 | 350 |
|---|---|---|---|---|---|
| 3.73 | 3.84 | 3.94 | 4.05 | 4.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Wu, Z.; Luo, X.; Liu, W. Numerical Study on Convective Heat Transfer of Liquid Metal Gallium in Turbine Guide Vane. Aerospace 2023, 10, 548. https://doi.org/10.3390/aerospace10060548
Zhang Z, Wu Z, Luo X, Liu W. Numerical Study on Convective Heat Transfer of Liquid Metal Gallium in Turbine Guide Vane. Aerospace. 2023; 10(6):548. https://doi.org/10.3390/aerospace10060548
Chicago/Turabian StyleZhang, Zhe, Zeyu Wu, Xiang Luo, and Weitong Liu. 2023. "Numerical Study on Convective Heat Transfer of Liquid Metal Gallium in Turbine Guide Vane" Aerospace 10, no. 6: 548. https://doi.org/10.3390/aerospace10060548
APA StyleZhang, Z., Wu, Z., Luo, X., & Liu, W. (2023). Numerical Study on Convective Heat Transfer of Liquid Metal Gallium in Turbine Guide Vane. Aerospace, 10(6), 548. https://doi.org/10.3390/aerospace10060548






