Closed-Loop Control of Transonic Buffet Using Active Shock Control Bump
Abstract
1. Introduction
2. Problem Definition
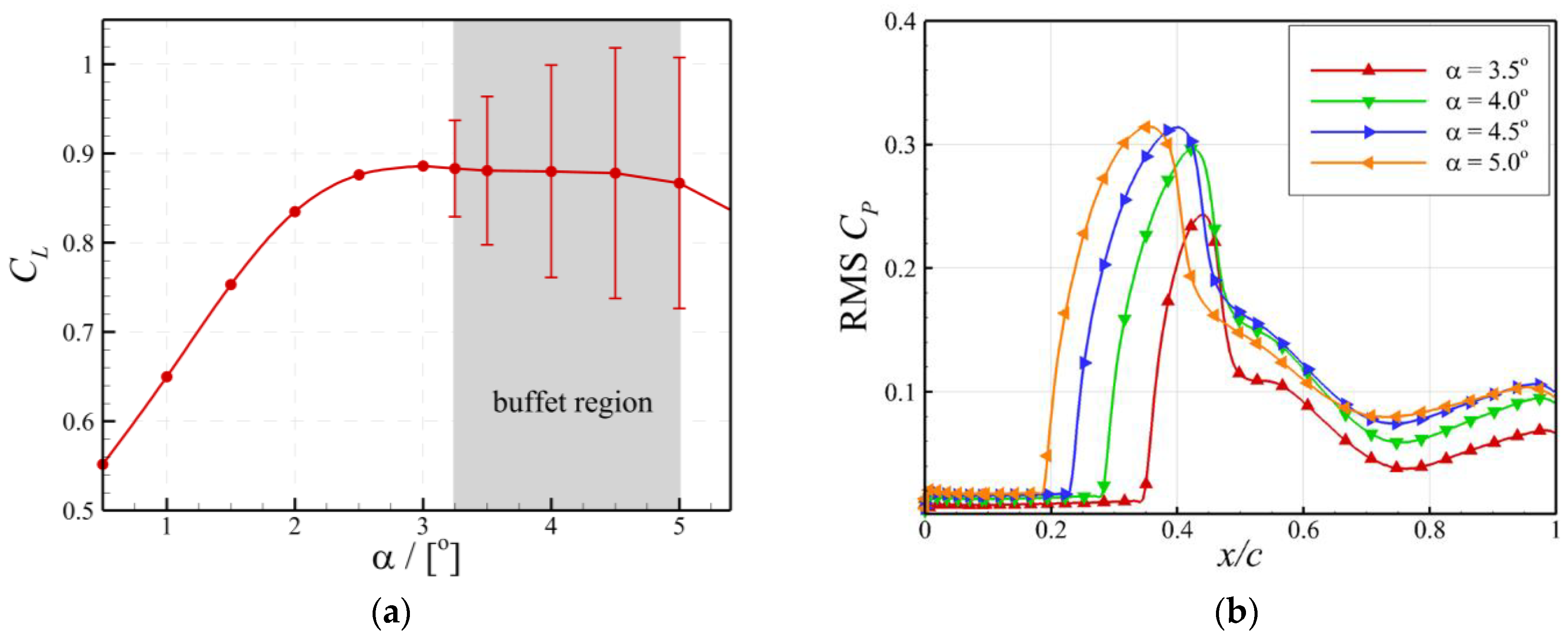
2.1. Baseline Airfoil
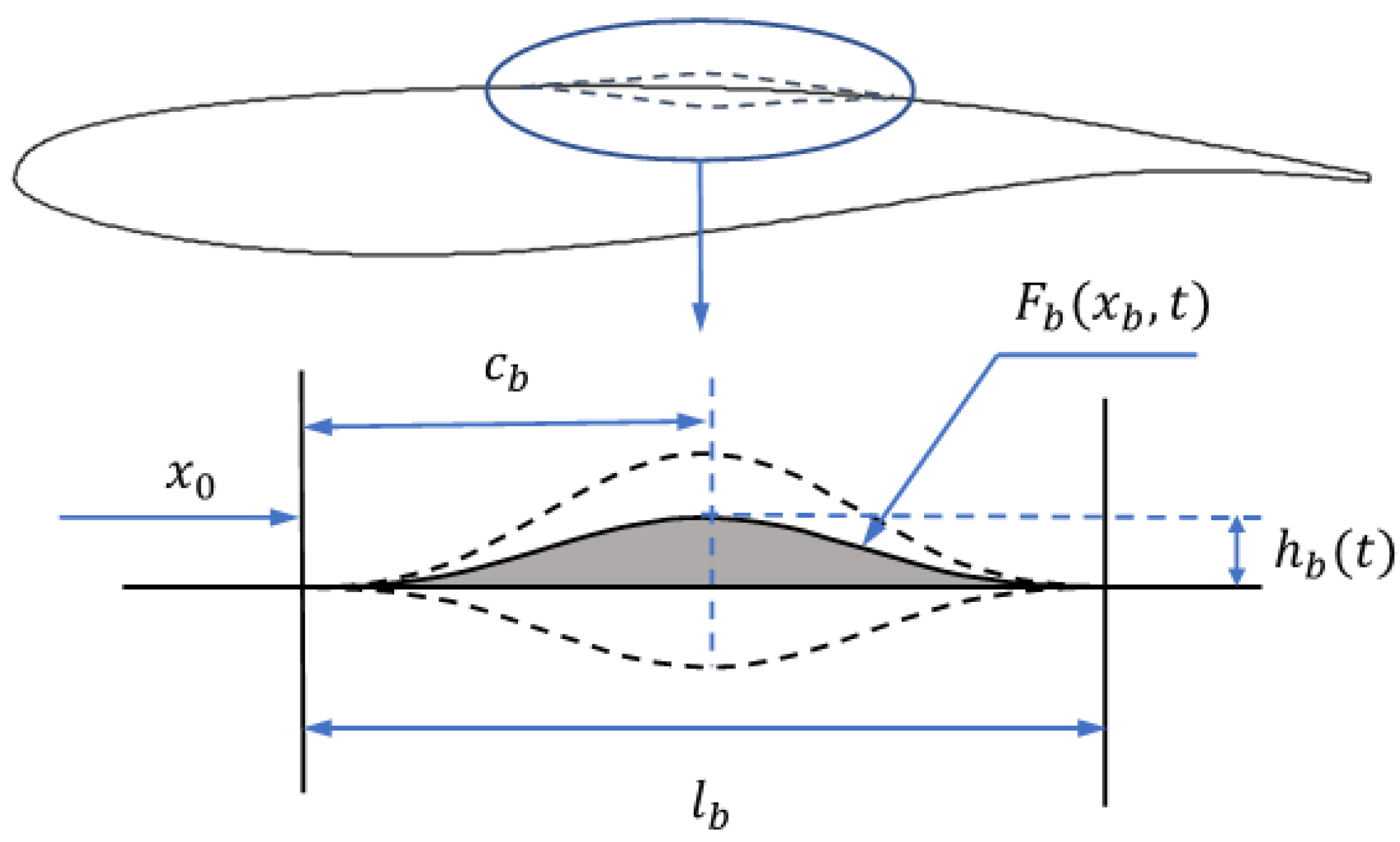
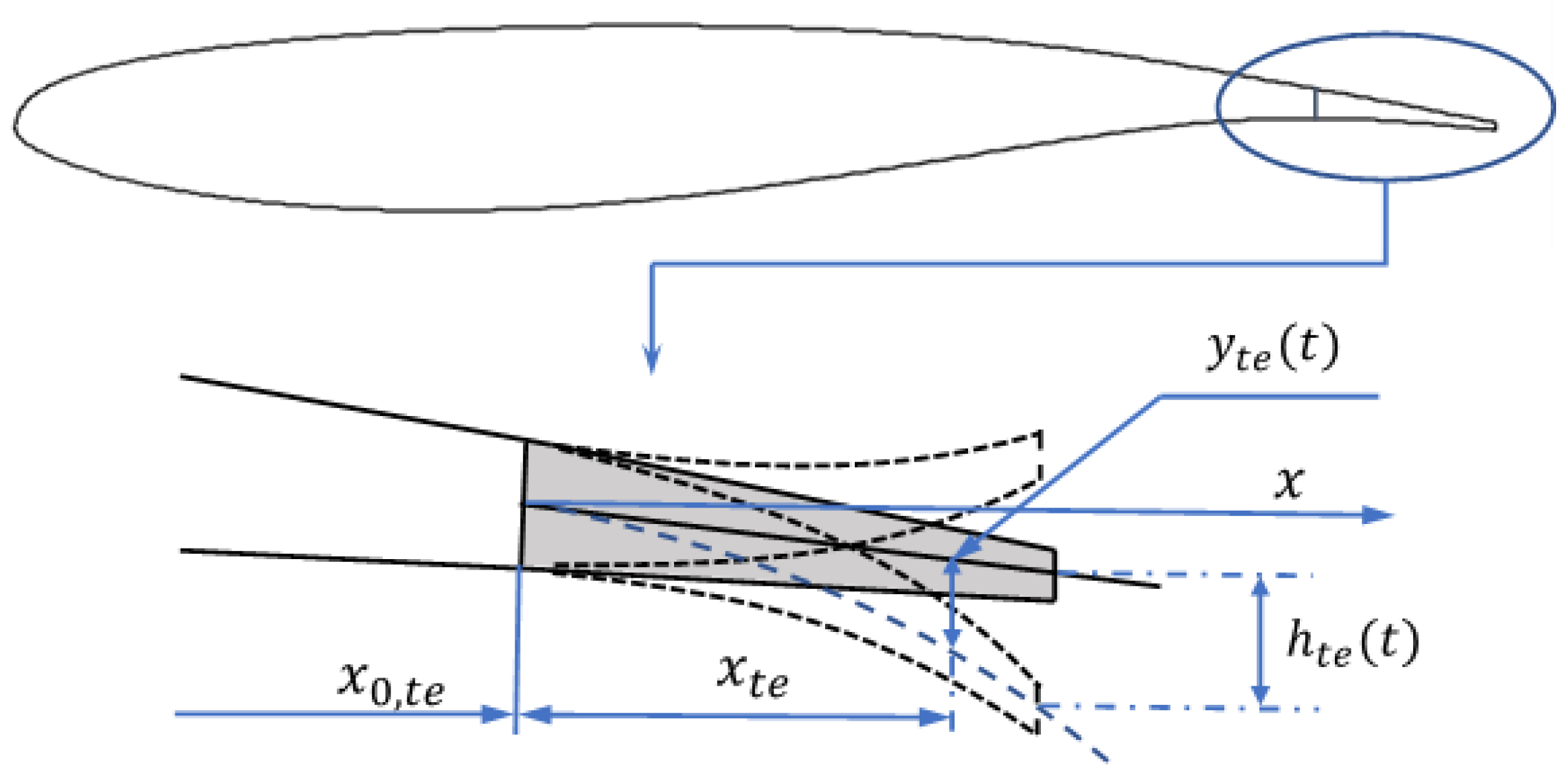
2.2. Definition of Active Control Devices
2.3. Closed-Loop Control Law for Buffet Alleviation
3. Numerical Methods
3.1. Flow Solver
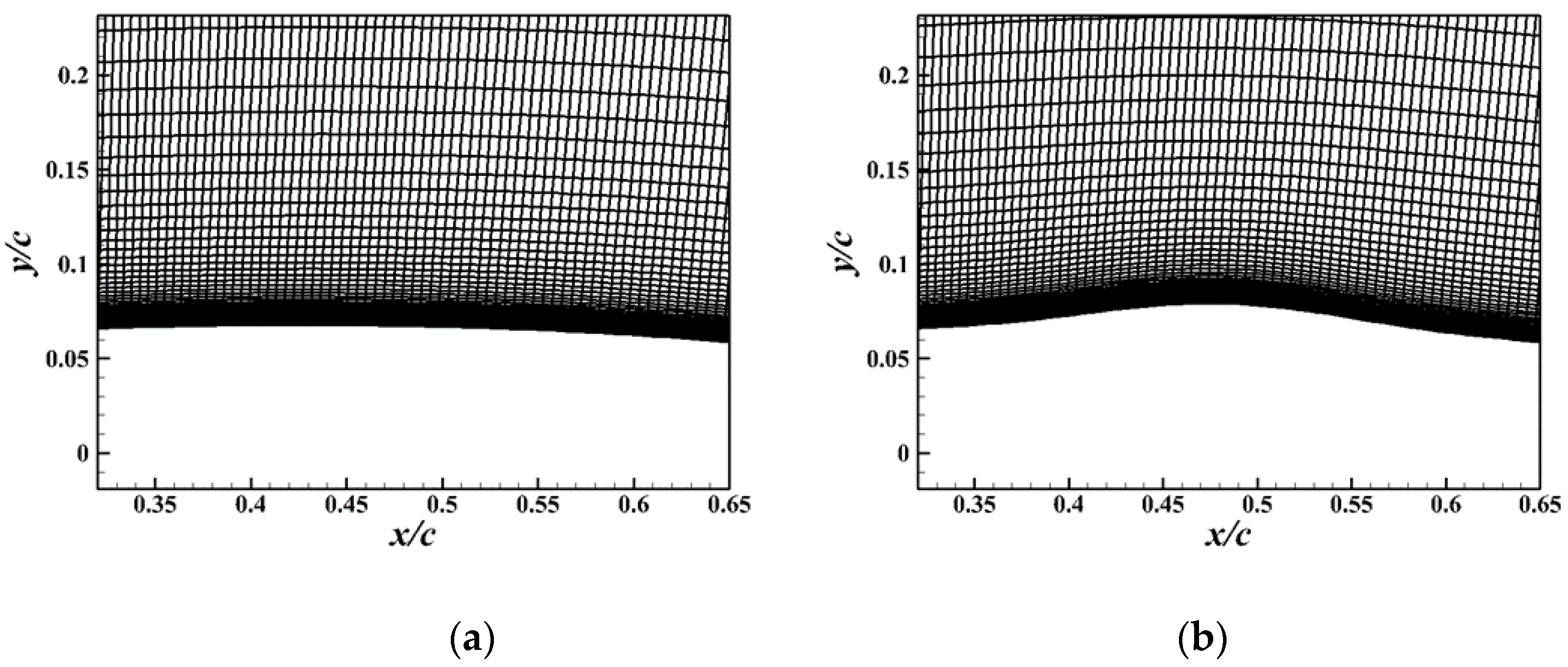
3.2. Grid Convergence Study
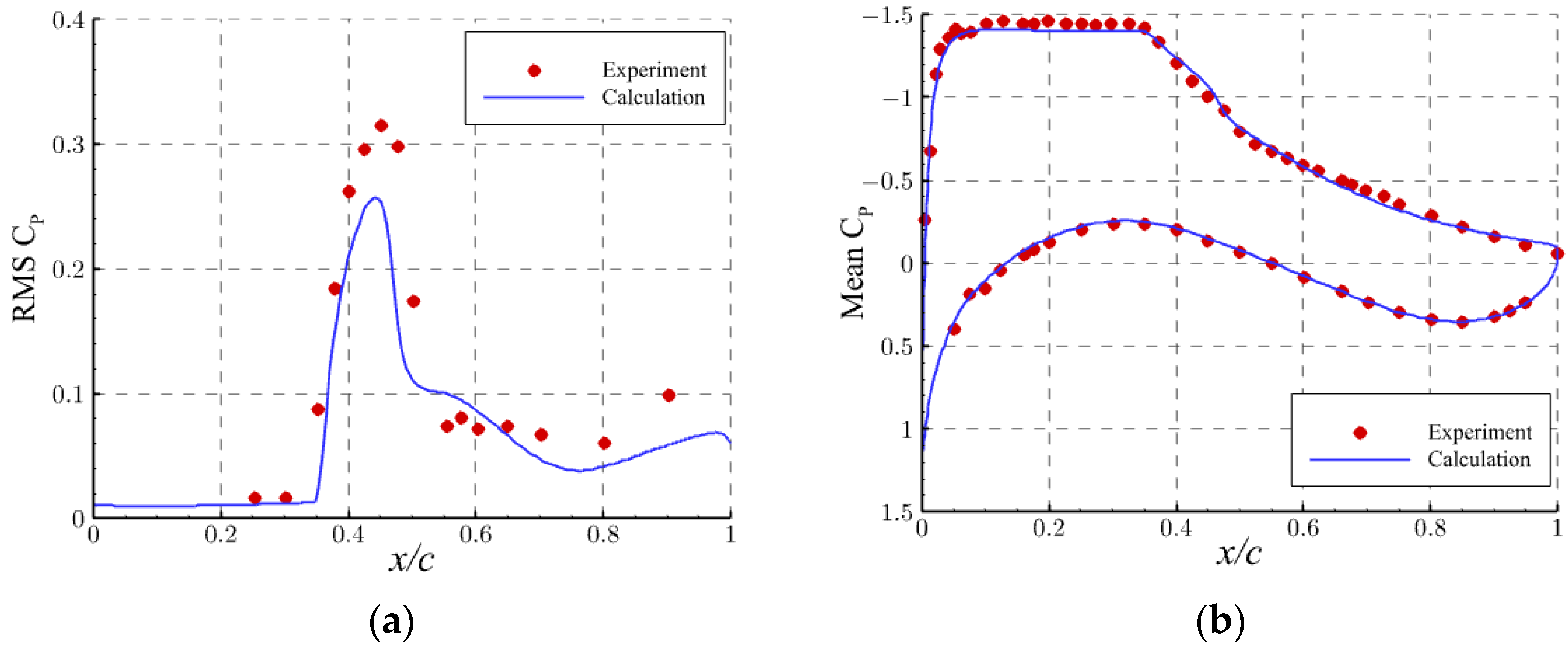
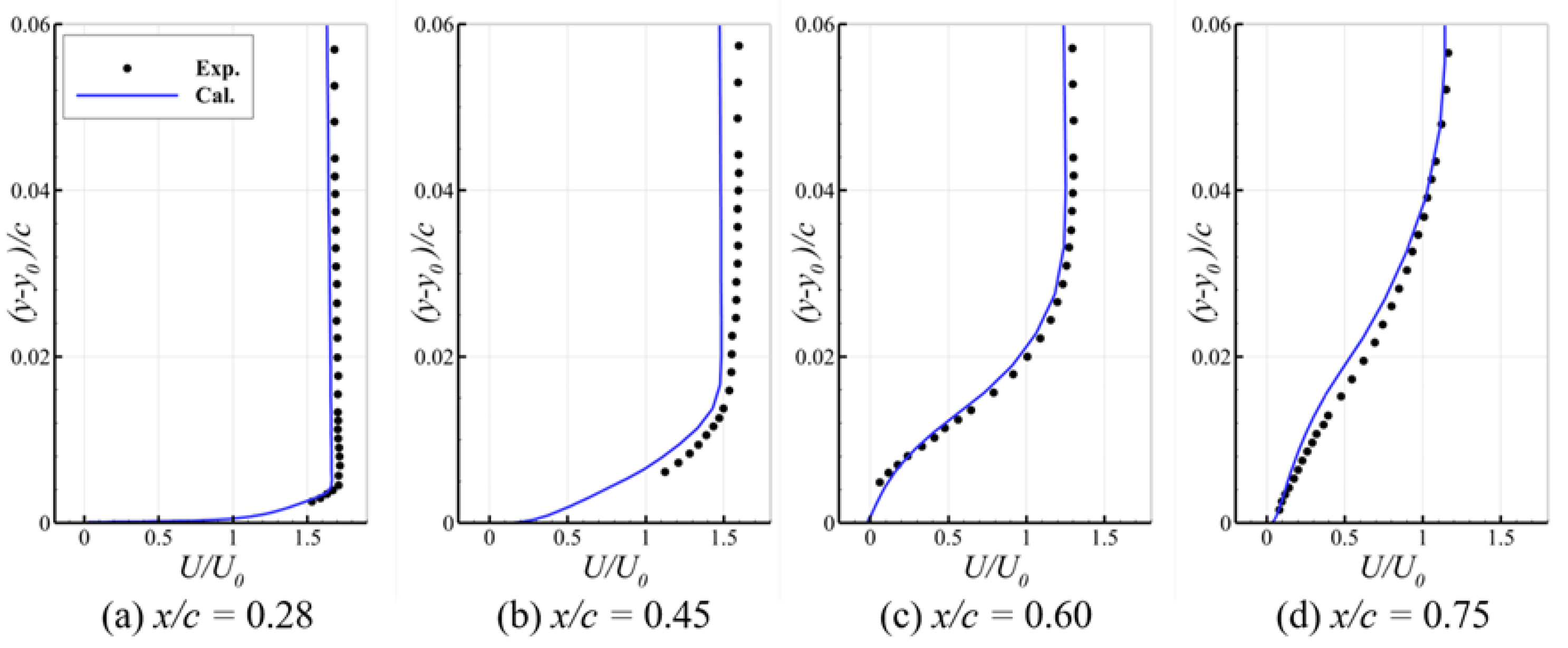
3.3. Validation
4. Results and Discussions
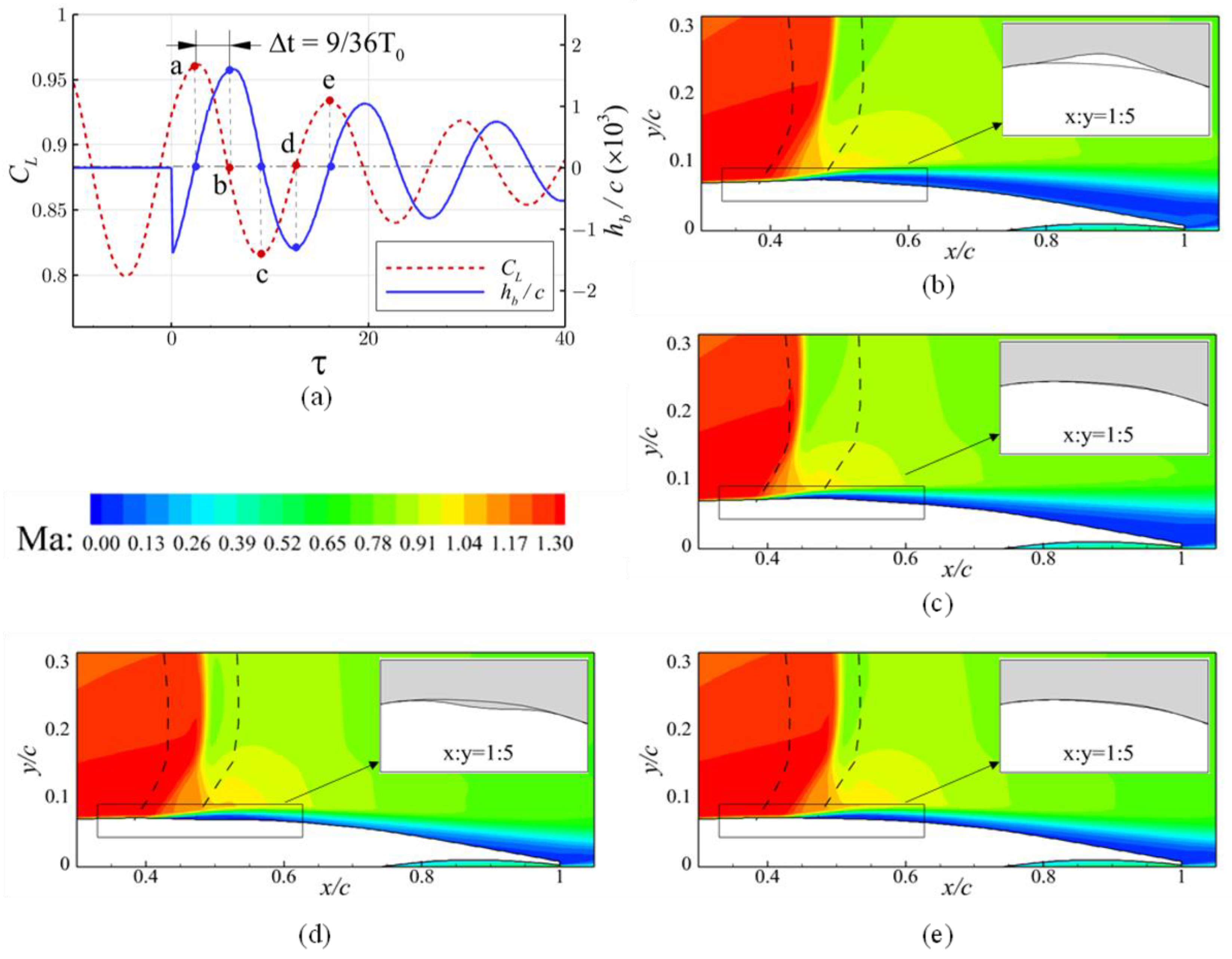
4.1. The Design of the Active SCB
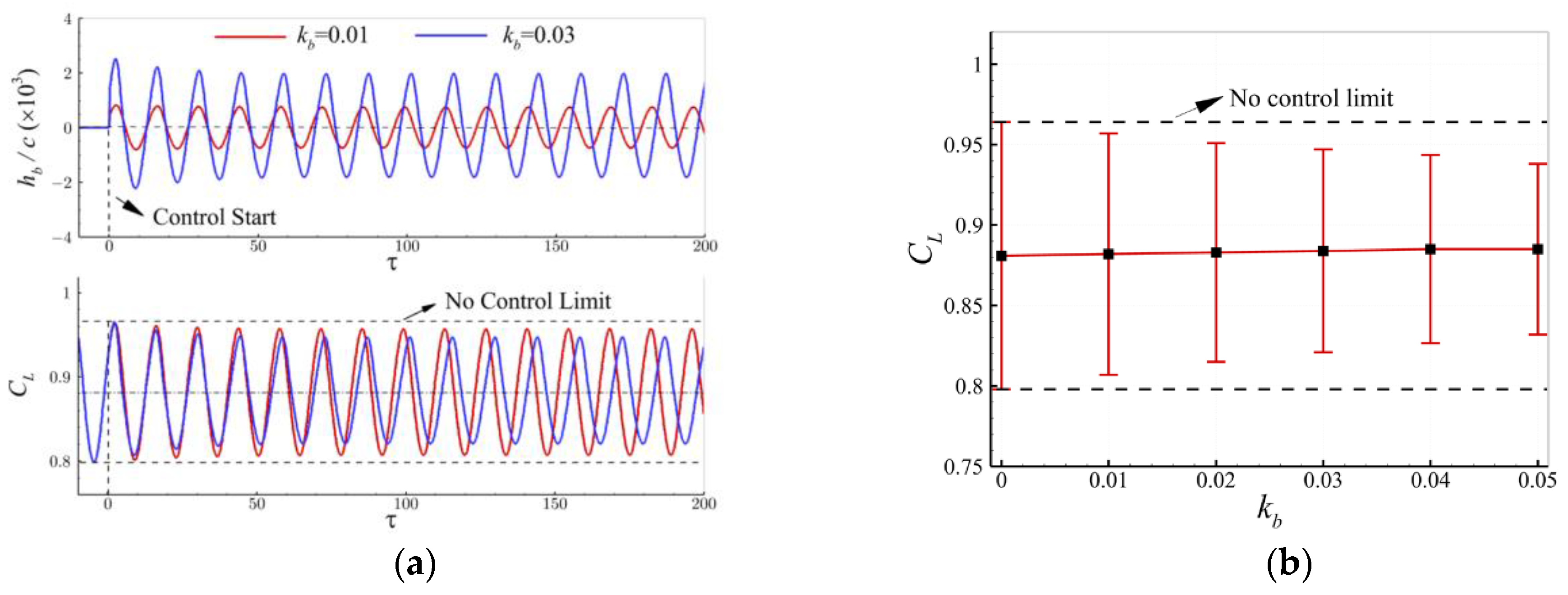
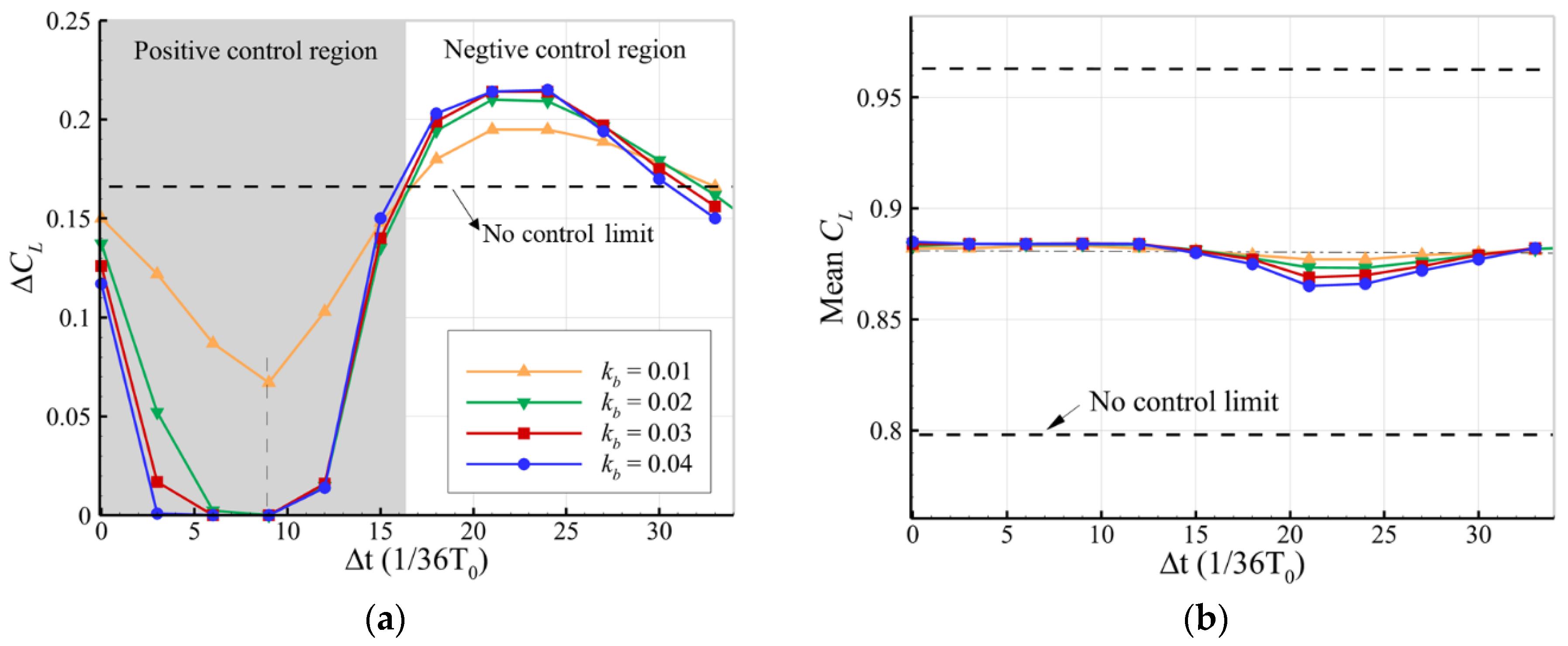
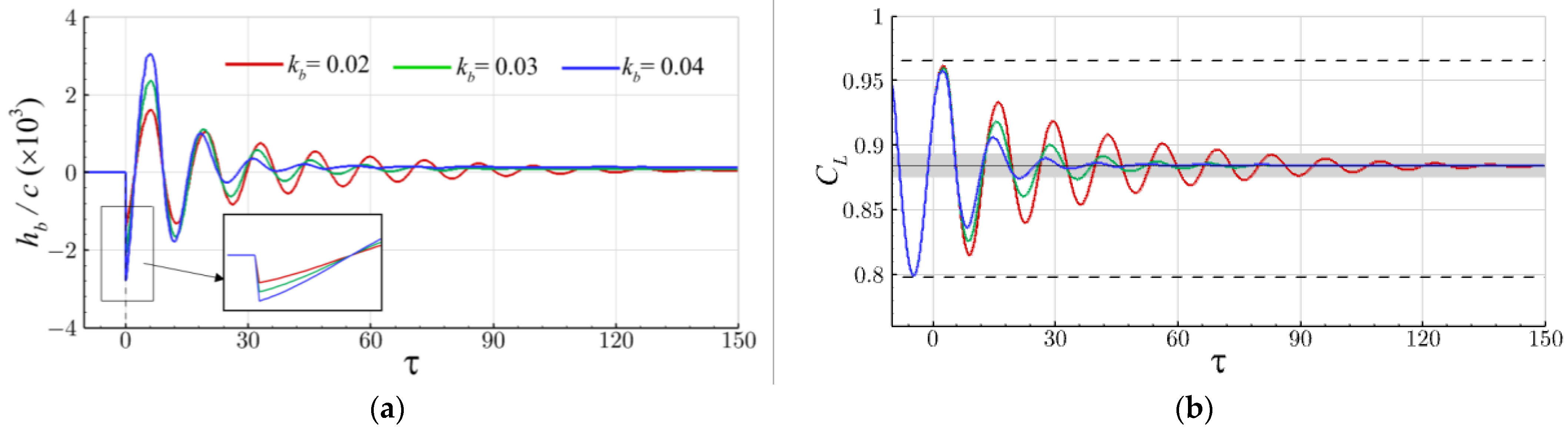
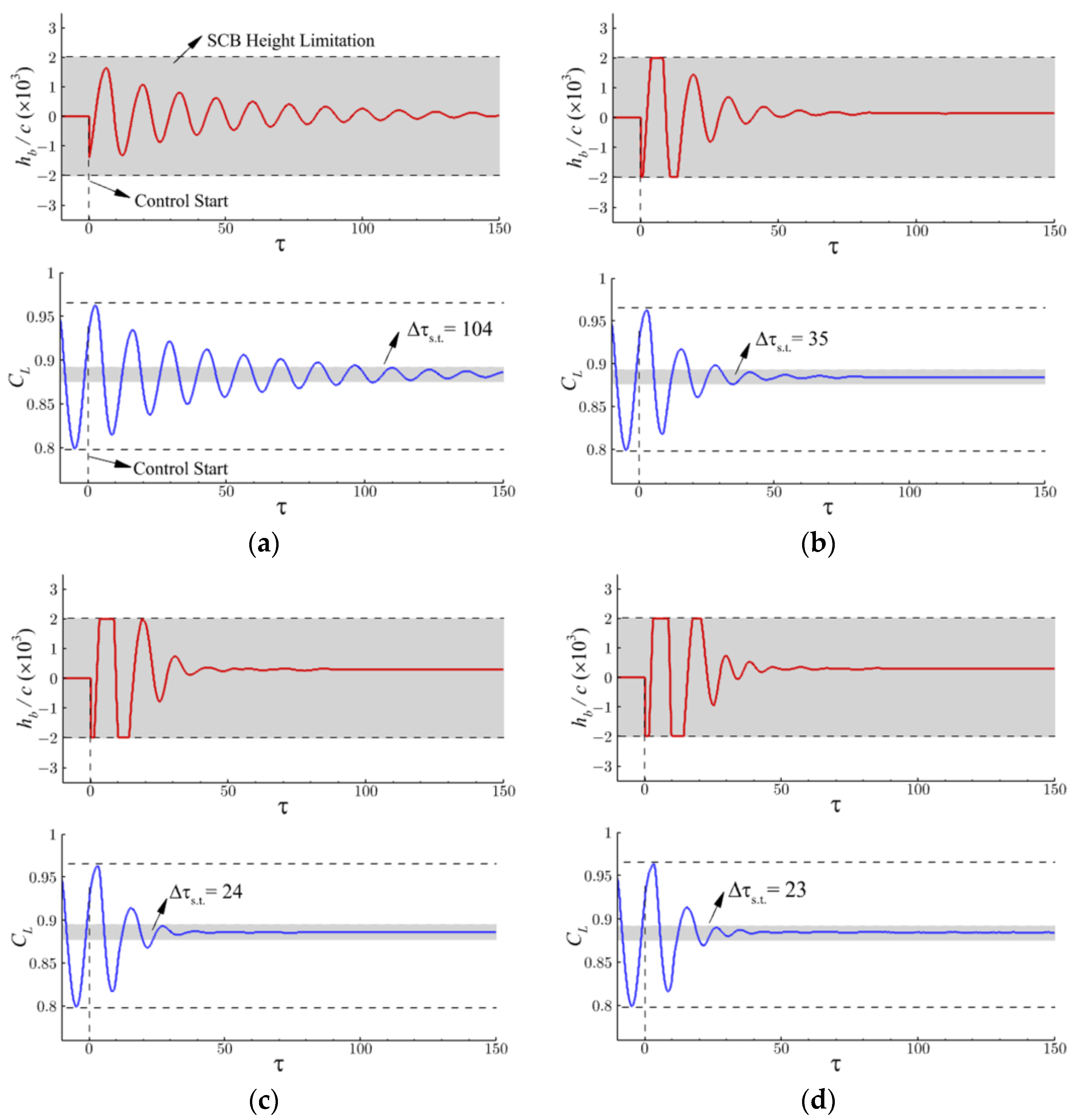
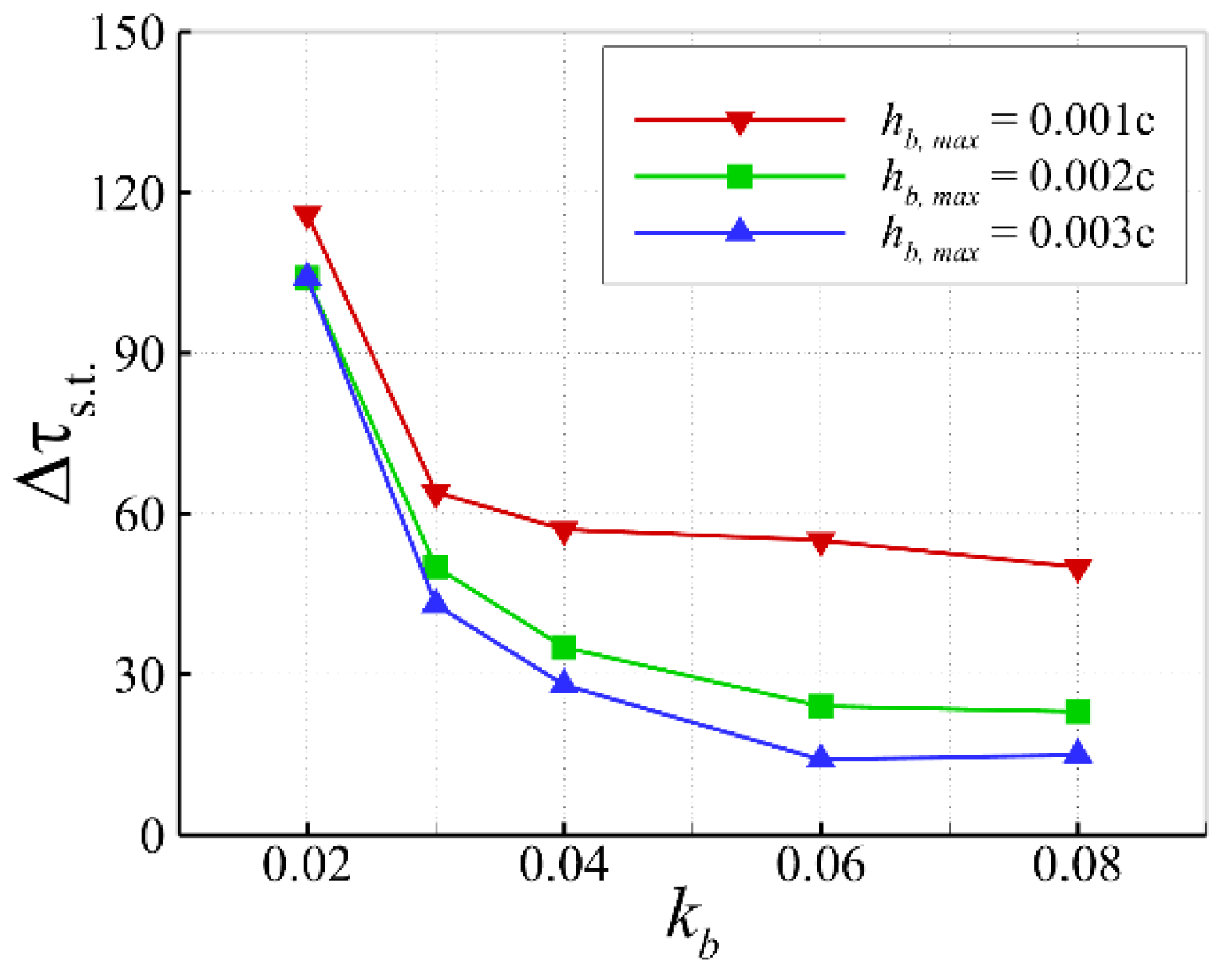
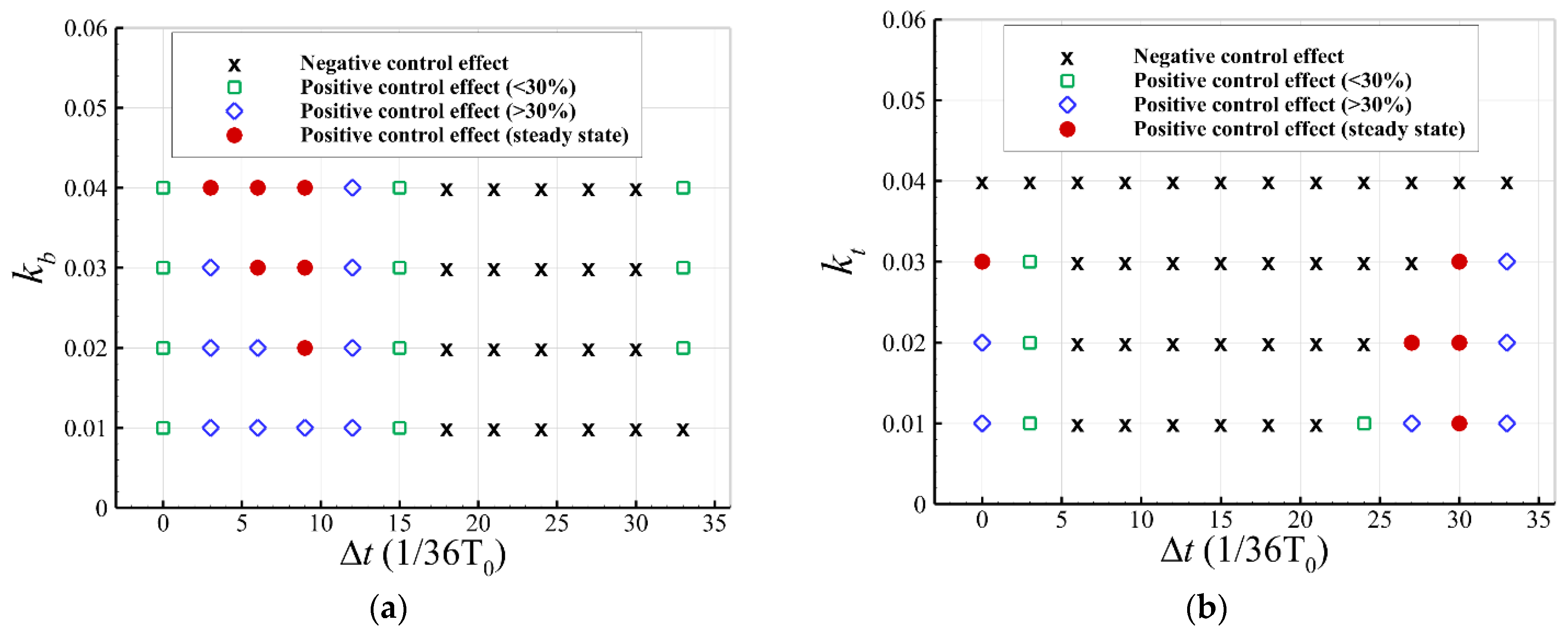
4.2. The Effects of Parameters of the Control Law on Buffet Alleviation
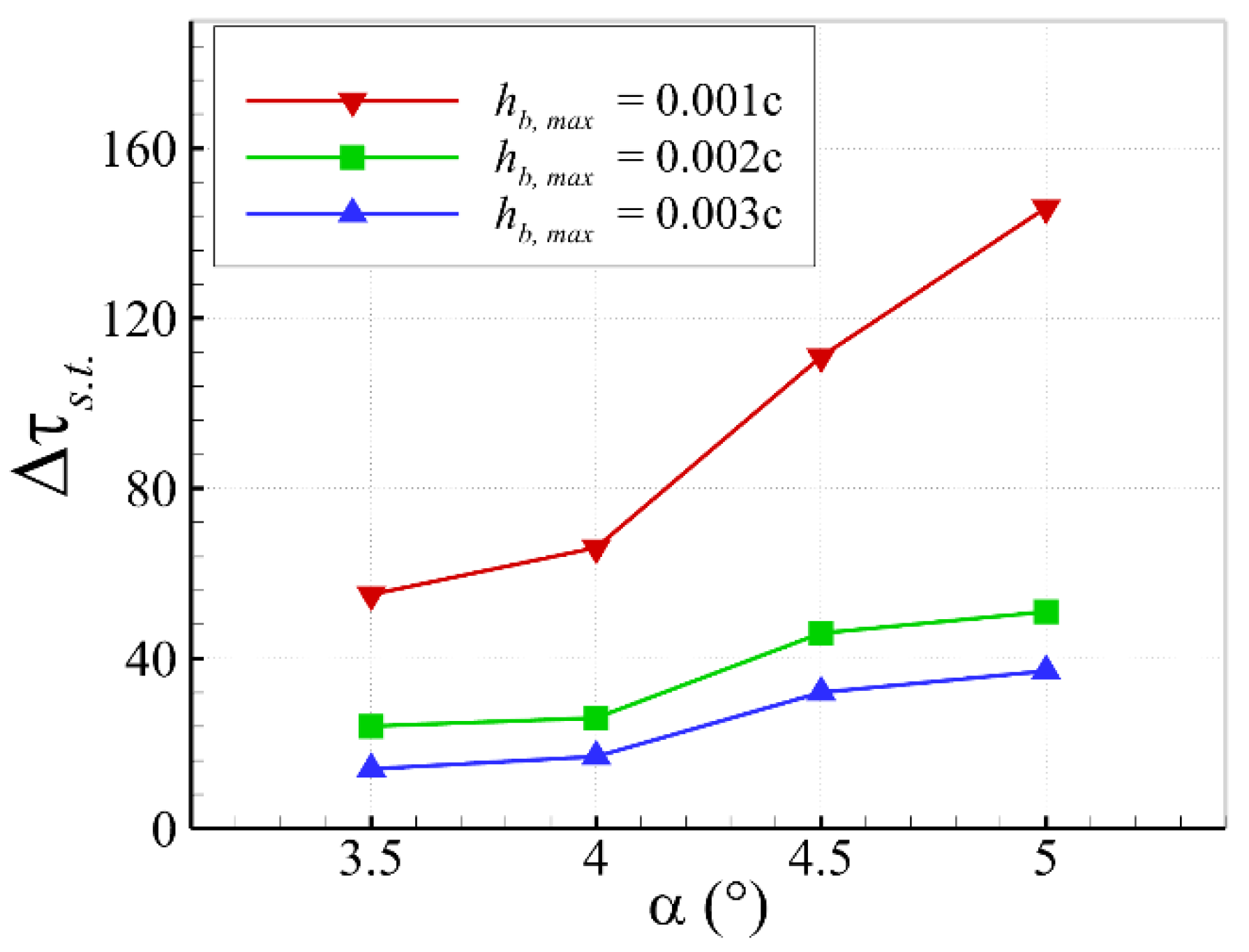
4.3. Buffet Control Constrained by Maximum Bump Height
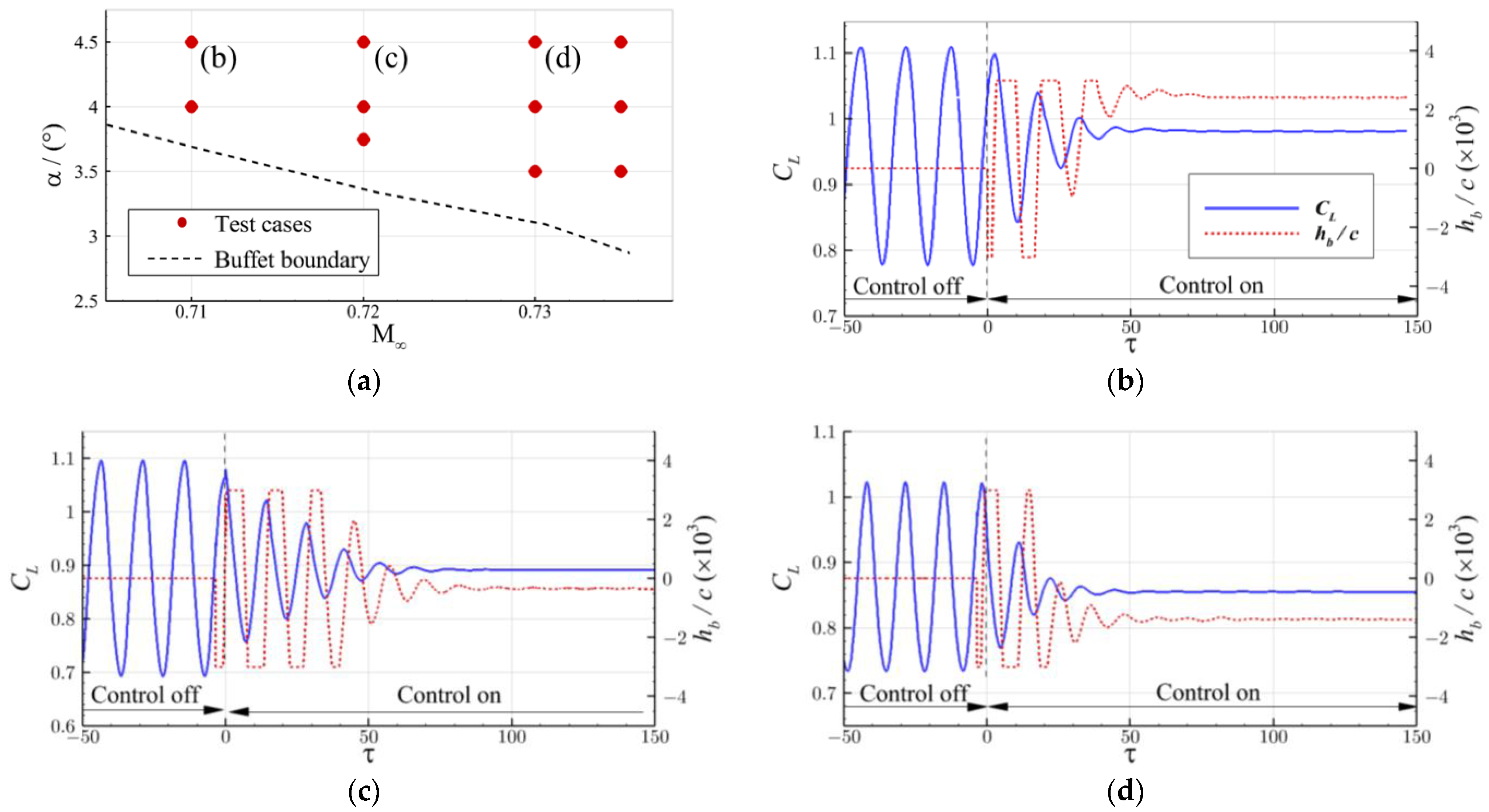
4.4. Buffet Control over a Range of Flow Conditions
4.5. Comparison of Active Closed-Loop Buffet Control Using SCB and TEF
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| c | Airfoil chord length |
| Lift coefficient | |
| Drag coefficient | |
| Pressure coefficient | |
| x-component of skin friction coefficient | |
| fsb | Shock buffet frequency |
| hb | Bump height |
| hte | Displacement of the trailing edge |
| k | Gain of the closed-loop control |
| lb | Bump length |
| M∞ | Freestream Mach number |
| p | Static pressure |
| Dynamic pressure | |
| Rec | Chord-based Reynolds number |
| Shock buffet period | |
| α | Freestream angle of attack |
| β | Flap deflection angle |
| τ | Non-dimensional time |
| Non-dimensional settling time of buffet suppression | |
| Delay time of the closed-loop control | |
| PSD | Power spectral density |
| Mean Cp | Mean pressure coefficient |
| RMS Cp | Root mean square |
References
- Li, R.; Deng, K.; Zhang, Y.; Chen, H. Pressure Distribution Guided Supercritical Wing Optimization. Chin. J. Aeronaut. 2018, 31, 1842–1854. [Google Scholar] [CrossRef]
- Lee, B.H.K. Self-Sustained Shock Oscillations on Airfoils at Transonic Speeds. Prog. Aerosp. Sci. 2001, 37, 147–196. [Google Scholar] [CrossRef]
- Jacquin, L.; Molton, P.; Deck, S.; Maury, B.; Soulevant, D. Experimental Study of Shock Oscillation over a Transonic Supercritical Profile. AIAA J. 2009, 47, 1985–1994. [Google Scholar] [CrossRef]
- Deck, S. Numerical Simulation of Transonic Buffet over a Supercritical Airfoil. AIAA J. 2005, 43, 1556–1566. [Google Scholar] [CrossRef]
- Grossi, F.; Braza, M.; Hoarau, Y. Prediction of Transonic Buffet by Delayed Detached-Eddy Simulation. AIAA J. 2014, 52, 2300–2312. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, P.; Li, R.; Chen, H. Unsteady Simulation of Transonic Buffet of a Supercritical Airfoil with Shock Control Bump. Aerospace 2021, 8, 203. [Google Scholar] [CrossRef]
- Huang, J.; Xiao, Z.; Liu, J.; Fu, S. Simulation of Shock Wave Buffet and Its Suppression on an OAT15A Supercritical Airfoil by IDDES. Sci. China Phys. Mech. Astron. 2012, 55, 260–271. [Google Scholar] [CrossRef]
- Levy, L.L., Jr. Experimental and Computational Steady and Unsteady Transonic Flows about a Thick Airfoil. AIAA J. 1978, 16, 564–572. [Google Scholar] [CrossRef]
- Iovnovich, M.; Raveh, D.E. Reynolds-Averaged Navier-Stokes Study of the Shock-Buffet Instability Mechanism. AIAA J. 2012, 50, 880–890. [Google Scholar] [CrossRef]
- Giannelis, N.F.; Levinski, O.; Vio, G.A. Influence of Mach Number and Angle of Attack on the Two-Dimensional Transonic Buffet Phenomenon. Aerosp. Sci. Technol. 2018, 78, 89–101. [Google Scholar] [CrossRef]
- Giannelis, N.F.; Levinski, O.; Vio, G.A. Origins of a Typical Shock Buffet Motions on a Supercritical Aerofoil. Aerosp. Sci. Technol. 2020, 107, 106304. [Google Scholar] [CrossRef]
- Smith, A.N.; Babinsky, H.; Fulker, J.L.; Ashill, P.R. Normal Shock Wave-Turbulent Boundary-Layer Interactions in the Presence of Streamwise Slots and Grooves. Aeronaut. J. 2002, 106, 493–500. [Google Scholar] [CrossRef]
- Holden, H.A.; Babinsky, H. Separated Shock-Boundary-Layer Interaction Control Using Streamwise Slots. J. Aircr. 2005, 42, 166–171. [Google Scholar] [CrossRef]
- Eastwood, J.P.; Jarrett, J.P. Toward Designing with Three-Dimensional Bumps for Lift/Drag Improvement and Buffet Alleviation. AIAA J. 2012, 50, 2882–2898. [Google Scholar] [CrossRef]
- Holden, H.; Babinsky, H. Effect of Microvortex Generators on Seperated Normal Shock/Boundary Layer Interactions. J. Aircr. 2007, 44, 170–174. [Google Scholar] [CrossRef]
- Rybalko, M.; Babinsky, H.; Loth, E. Vortex Generators for a Normal Shock/Boundary Layer Interaction with a Downstream Diffuser. J. Propuls. Power 2012, 28, 71–82. [Google Scholar] [CrossRef]
- Caruana, D.; Mignosi, A.; Robitaillié, C.; Corrège, M. Separated Flow and Buffeting Control. Flow Turbul. Combust. 2003, 71, 221–245. [Google Scholar] [CrossRef]
- Caruana, D.; Mignosi, A.; Corrège, M.; Le Pourhiet, A.; Rodde, A.M. Buffet and Buffeting Control in Transonic Flow. Aerosp. Sci. Technol. 2005, 9, 605–616. [Google Scholar] [CrossRef]
- Dandois, J.; Lepage, A.; Dor, J.-B.; Molton, P.; Ternoy, F.; Geeraert, A.; Brunet, V.; Coustols, É. Open and Closed-Loop Control of Transonic Buffet on 3D Turbulent Wings Using Fluidic Devices. Comptes Rendus Mec. 2014, 342, 425–436. [Google Scholar] [CrossRef]
- Gao, C.; Zhang, W.; Ye, Z. Numerical Study on Closed-Loop Control of Transonic Buffet Suppression by Trailing Edge Flap. Comput. Fluids 2016, 132, 32–45. [Google Scholar] [CrossRef]
- Ren, K.; Chen, Y.; Gao, C.; Zhang, W. Adaptive Control of Transonic Buffet Flows over an Airfoil. Phys. Fluids 2020, 32, 096106. [Google Scholar] [CrossRef]
- Birkemeyer, J.; Rosemann, H.; Stanewsky, E. Shock Control on a Swept Wing. Aerosp. Sci. Technol. 2000, 4, 147–156. [Google Scholar] [CrossRef]
- Qin, N.; Zhu, Y.; Shaw, S.T. Numerical Study of Active Shock Control for Transonic Aerodynamics. Int. J. Numer. Methods Heat Fluid Flow 2004, 14, 444–466. [Google Scholar] [CrossRef]
- Qin, N.; Wong, W.; Le Moigne, A. Three-Dimensional Contour Bumps for Transonic Wing Drag Reduction. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2008, 222, 619–629. [Google Scholar] [CrossRef]
- Mayer, R.; Lutz, T.; Krämer, E. Numerical Study on the Ability of Shock Control Bumps for Buffet Control. AIAA J. 2018, 56, 1978–1987. [Google Scholar] [CrossRef]
- Mayer, R.; Lutz, T.; Krämer, E.; Dandois, J. Control of Transonic Buffet by Shock Control Bumps on Wing-Body Configuration. J. Aircr. 2019, 56, 556–568. [Google Scholar] [CrossRef]
- Tian, Y.; Gao, S.; Liu, P.; Wang, J. Transonic Buffet Control Research with Two Types of Shock Control Bump Based on RAE2822 Airfoil. Chin. J. Aeronaut. 2017, 30, 1681–1696. [Google Scholar] [CrossRef]
- Geoghegan, J.A.; Giannelis, N.F.; Vio, G.A. A Numerical Study on Transonic Shock Buffet Alleviation through Oscillating Shock Control Bumps. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8 January 2018. [Google Scholar]
- Geoghegan, J.A.; Giannelis, N.F.; Vio, G.A. A Numerical Investigation of the Geometric Parametrisation of Shock Control Bumps for Transonic Shock Oscillation Control. Fluids 2020, 5, 46. [Google Scholar] [CrossRef]
- Geoghegan, J.A.; Giannelis, N.F.; Vio, G.A. Parametric Study of Active Shock Control Bumps for Transonic Shock Buffet Alleviation. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6 January 2020. [Google Scholar]
- Zhang, S.; Deng, F.; Qin, N. Cooperation of Trailing-Edge Flap and Shock Control Bump for Robust Buffet Control and Drag Reduction. Aerospace 2022, 9, 657. [Google Scholar] [CrossRef]
- Ren, K.; Gao, C.; Zhou, F.; Zhang, W. Transonic Buffet Active Control with Local Smart Skin. Actuators 2022, 11, 155. [Google Scholar] [CrossRef]
- Moigne, A.L.; Qin, N. Variable-Fidelity Aerodynamic Optimization for Turbulent Flows Using a Discrete Adjoint Formulation. AIAA J. 2004, 42, 1281–1292. [Google Scholar] [CrossRef]
- Sclafani, A.J.; DeHaan, M.A.; Vassberg, J.C.; Rumsey, C.L.; Pulliam, T.H. Drag Prediction for the Common Research Model Using CFL3D and OVERFLOW. J. Aircr. 2014, 51, 1101–1117. [Google Scholar] [CrossRef]
- CFL3D. Available online: https://nasa.github.io/CFL3D/ (accessed on 1 February 2023).
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Giannelis, N.F.; Vio, G.A. Influence of Turbulence Modelling Approach on Shock Buffet Computations at Deep Buffet Conditions. In Proceedings of the AIAA AVIATION 2021 FORUM, Virtual, 2 August 2021. [Google Scholar]
- Szubert, D.; Asproulias, I.; Grossi, F.; Duvigneau, R.; Hoarau, Y.; Braza, M. Numerical Study of the Turbulent Transonic Interaction and Transition Location Effect Involving Optimisation around a Supercritical Aerofoil. Eur. J. Mech.-B Fluids 2016, 55, 380–393. [Google Scholar] [CrossRef]
- Liu, K.; Wang, R.; Wang, X.; Wang, X. Anti-Saturation Adaptive Finite-Time Neural Network Based Fault-Tolerant Tracking Control for a Quadrotor UAV with External Disturbances. Aerosp. Sci. Technol. 2021, 115, 106790. [Google Scholar] [CrossRef]
- Liu, K.; Wang, R.; Zheng, S.; Dong, S.; Sun, G. Fixed-Time Disturbance Observer-Based Robust Fault-Tolerant Tracking Control for Uncertain Quadrotor UAV Subject to Input Delay. Nonlinear Dyn. 2022, 107, 2363–2390. [Google Scholar] [CrossRef]




| Grid | Airfoil Nodes | First Layer | Cell Count | |
|---|---|---|---|---|
| G1 | 417 | 1.5 × 10−6 | 0.75 | 55,000 |
| G2 | 517 | 1.2 × 10−6 | 0.70 | 83,000 |
| G3 | 647 | 1.0 × 10−6 | 0.50 | 106,000 |
| Grid | Mean | (Hz) | |
|---|---|---|---|
| G1 | 0.050 | 0.896 | 76 |
| G2 | 0.166 | 0.881 | 75 |
| G3 | 0.159 | 0.882 | 75 |
| Experiment [3] | 0.220 | - | 69 |
| Control Type | |||
|---|---|---|---|
| Baseline (Mean) | 0.881 | 0.0398 | - |
| Active trailing edge flap | 0.881 | 0.0390 | 93 |
| Active bump | 0.881 | 0.0389 | 37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, F.; Zhang, S.; Qin, N. Closed-Loop Control of Transonic Buffet Using Active Shock Control Bump. Aerospace 2023, 10, 537. https://doi.org/10.3390/aerospace10060537
Deng F, Zhang S, Qin N. Closed-Loop Control of Transonic Buffet Using Active Shock Control Bump. Aerospace. 2023; 10(6):537. https://doi.org/10.3390/aerospace10060537
Chicago/Turabian StyleDeng, Feng, Shenghua Zhang, and Ning Qin. 2023. "Closed-Loop Control of Transonic Buffet Using Active Shock Control Bump" Aerospace 10, no. 6: 537. https://doi.org/10.3390/aerospace10060537
APA StyleDeng, F., Zhang, S., & Qin, N. (2023). Closed-Loop Control of Transonic Buffet Using Active Shock Control Bump. Aerospace, 10(6), 537. https://doi.org/10.3390/aerospace10060537








