Aerodynamic Analysis of an Orthogonal Octorotor UAV Considering Horizontal Wind Disturbance

Abstract

In this paper, the aerodynamic performance of an orthogonal octorotor UAV considering horizontal wind disturbances is investigated with numerical simulations and experiments. To obtian the effect of horizontal wind on the flight efficiency of the orthogonal octorotor UAV, the power consumption and thrust with different wind speeds (0–4 m/s) and rotational speeds (1500–2300 RPM) are measured in a low-speed wind tunnel. Also, the velocity distribution of downwash flow, blade tip vortex distribution, streamline distribution and rotor blade tip pressure distribution of the orthogonal octorotor UAV were simulated by the computational fluid dynamics (CFD). The test results show that the thrust is increased at lower wind speed compared with 0 m/s. Specifically, it increased by 8.1% at 2 m/s and 8.8% at 4 m/s, respectively. It is interesting to note that the increased power consumption caused by the interference of horizontal wind at a higher rotor speed leads to a decrease in power loading (PL). Additionally, the thrust increased with a higher PL at low speed, where the PL achieved the maximum for the wind of 2.5 m/s and obtained a better aerodynamic performance. Compared with traditional octorotor UAVs and eight equivalent isolated rotors, the orthogonal octorotor UAV has also been proven to obtain good wind resistance. Simulation results show that the increase in wind speed and rotor speed will make the flow field more complex and the airflow interference between rotors more intense, which leads to changes in rotor thrust and power consumption.

1. Introduction

Unmanned Aerial Vehicles (UAVs) can be remotely controlled in a complex or narrow space with a wide range of applications to obtain high-resolution images or data [1,2,3,4]. In order to improve the capacity of UAVs with more devices, one of the most common methods is to increase their thrust by increasing the number of rotors on the UAV. However, as the number of rotors increases, the downwash flow between adjacent rotors may interfere with each other and lead to changes in the power consumption of the UAV [5]. In addition, wind interference will intensify the airflow interference between the rotors, resulting in difficulty for attitude control [6]. To figure out the effect of wind disturbances on the hovering efficiency of UAVs, a theoretical analysis is developed based on previous work on UAVs with specific rotor dynamics.

At present, most research on UAVs mainly focuses on control strategies. Russell C R et al. [7] performed wind tunnel tests to measure the power consumption and lift of UAVs with different attitudes, rotational speeds and wind speeds. Amiri M et al. [8] conducted experimental studies on a three-bladed wind turbine in a subsonic open-jet type wind tunnel. The experimental results show that increasing the blade aspect ratio can greatly improve the aerodynamic performance of the rotor. Frankenberg F V et al. [9] proposed a novel UAV that can maintain a pitch angle of 15 deg with translational motion and can be controlled to stay on an inclined plane of no more than 30 deg. Gautam, D et al. [10] proposed a smart self-tuning fuzzy PID controller based on the EKF algorithm to control the attitude and position of a quadrotor flying in an obstacle-filled environment for path planning.

Currently, a few studies have performed the analysis of aerodynamic interference between rotors. Balasubramanian Esakki et al. [11] studied the lift of a quadrotor UAV with different wind speeds by the CFD method, showing that the aerodynamic performance is optimal when the wind speed is 8 m/s with an angle of attack of 5 deg. Lei Y et al. [12] studied the flight efficiency of coaxial tri-rotor UAV with horizontal wind interference by experimental and numerical simulations. The results show that rotor interference and wind disturbance are advantageous to obtaining stable power consumption. Hwang J Y et al. [13] investigated the flow field and the aerodynamic interaction between the rotor and fuselage in forward flight for two configurations of quadrotor UAVs. Chasapogiannis et al. [14] verified the aerodynamic performance of the rotor system composed of seven rotors with the same good as seven isolated rotors by flow field analysis. For a new UAV configuration, this paper studies the aerodynamic performance of an orthogonal octorotor UAV considering horizontal wind interference.

The outline of this paper is as follows: Section 2 performs a theoretical analysis of the wind effect on the orthogonal octorotor UAV. Section 3 analyzes the flow field of the orthogonal octorotor UAV by numerical simulations. Section 4 measures the power consumption and thrust of the orthogonal octorotor UAV by wind tunnel tests. Conclusions are given in Section 5.

2. Theoretical Model

Figure 1 is a sketch of the orthogonal octorotor UAV, which consists of four main rotors (rotors 2, 3, 6, and 7) and 4 auxiliary rotors (rotors 1, 4, 5, and 8). The main rotors rotate counterclockwise, and the auxiliary rotors rotate clockwise. Due to the perpendicularity between the rotation axes of the main rotors and the auxiliary rotors, there is strong aerodynamic interference between the rotors. When the horizontal wind is considered, the aerodynamic interference between the rotors becomes more intense. Therefore, it is necessary to analyze the horizontal wind effect on the orthogonal octorotor UAV to obtain the optimal aerodynamic performance of the UAV.

Multi-rotor aircraft are generally immersed in wind varying from 0 to 5 m/s in the flight domain [15]. Normally, the angle of attack for the different rotor speeds is manipulated by the controller to keep the UAV stable when the wind speed is higher than 5 m/s. When the wind disturbance is introduced, it is compensated by the control strategies. However, wind from a horizontal direction will change the local airflow on the rotor tip with direct impact and lead to thrust variation. Figure 2 shows the horizontal wind interference model for the orthogonal octorotor UAV. Compared with the hovering state in Figure 2a, it is noted that the downwash of the rotor deviates toward the direction of the horizontal wind. The rear rotor is immersed in the vortex wake of the front rotor, and thus the horizontal wind will accelerate the interference between adjacent rotors.

2.1. Wind Effect on the Orthogonal Octorotor UAV

Figure 3a,b shows the wind disturbance model of rotors 1 and 4 of the orthogonal octorotor UAV, where rotor 1 is subject to a free airflow interference parallel to the positive direction of the z-axis, and rotor 4 is subject to a free airflow interference parallel to the negative direction of the z-axis. When there is no airflow interference in the z-axis direction, the angle of attack on the rotor surface is α (the angle between the induced velocity and the chord line). When there is airflow interference in the z-axis direction, the airflow will change the magnitude and direction of the relative airflow velocity on the rotor surface, where the angle of attack changes from $\alpha$ to ${\alpha }_1$ [16]. The total induced airflow velocity $V_s$ can be expressed as:

$$V_s = V_{\infty } + V$$

(1)

where $V_{\infty }$ is the freestream velocity. $V=\Omega R$ is the induced velocity of the rotor, $\Omega$ is the rotational speed of the rotor, and R is the radius of the rotor.

From Figure 3, it can be seen that the angle of attack ${\alpha }_1>\alpha$ when the wind is from the positive direction of the z-axis, and the angle of attack ${\alpha }_1<\alpha$ when the wind from the negative direction of the z-axis. The relation of the thrust coefficient ${\mathrm{C}}_{\mathrm{T}}$ and the angle of attack $\alpha$ can be expressed as:

$$\frac{{\mathrm{C}}_{\mathrm{T}}}{\alpha }=\delta$$

(2)

where $\delta$ is a constant measured by the wind tunnel experiment. From Equation (2), we can see that a large angle of attack resulted in higher thrust generated by the rotor. Therefore, the thrust generated by rotor 1 may decrease, and the thrust generated by rotor 4 may increase at the same time.

Figure 4 shows the airflow disturbance model parallel to the rotor disc. When the rotor rotates to an angle of $\theta$ with the horizontal wind, the total induced airflow velocity $V_s$ at r of the rotor is:

$$V_s=V_{\infty }\sin \theta +V$$

(3)

It is noted that the induced airflow velocity of the rotor varies periodically due to the effect of the horizontal wind, which changes the airflow above the rotor.

2.2. Force Analysis

The horizontal wind combined with the rotor interference from adjacent rotors caused changes in the thrust of the rotors. Figure 5 shows the downwash flow model of a rotor disk in the horizontal wind, where the downwash velocity $V_m$ of the mth rotor can be expressed as [17]:

$$V_m=k_{im}{V}_{im}+{\displaystyle \sum }_{n\ne m}{k}_{mn}{V}_{in}$$

(4)

where $k_{im}$ is the corrected value of rotor-induced velocity loss, $V_{im}$ is the induced velocity of the mth rotor without horizontal wind disturbance, $k_{mn}$ is the influence factor of the nth rotor on the mth rotor thrust, and $V_{in}$ is the induced velocity of the nth rotor without horizontal wind disturbance.

Thus the total downwash flow induction velocity $V_h$ is [18]:

$$V_h=\sqrt{{\left(V_{\infty }\cos \beta +V_p\right)}^2+{\left(V_{\infty }\sin \beta \right)}^2}$$

(5)

where $\beta$ is the angle between the downwash velocity of the rotor and the freestream.

The thrust of the mth rotor can be expressed as:

$$T_m=2\rho A{V}_h{V}_{\infty }$$

(6)

where $\rho$ and A are the air density and rotor blade disc area, respectively.

In this paper, PL (power loading) is introduced to evaluate the hovering efficiency of orthogonal octorotor UAVs. PL can be expressed as:

$$\mathrm{PL} =\frac{{\mathrm{C}}_{\mathrm{T}}}{{\Omega R\mathrm{C}}_{\mathrm{P}}}$$

(7)

${\mathrm{C}}_{\mathrm{T}}$ and ${\mathrm{C}}_{\mathrm{P}}$ are the thrust coefficient and power coefficient, which can be expressed as:

$${\mathrm{C}}_{\mathrm{T}}=\frac{T}{\rho A{\omega }^2{R}^2},{ \mathrm{C}}_{\mathrm{P}}=\frac{P}{\rho A{\omega }^3{R}^3}$$

(8)

It is obvious that the hovering efficiency of the orthogonal octorotor UAV mainly depends on its thrust and power consumption. The orthogonal octorotor UAV obtains the optimal aerodynamic performance either with higher thrust or less power.

3. Numerical Simulations

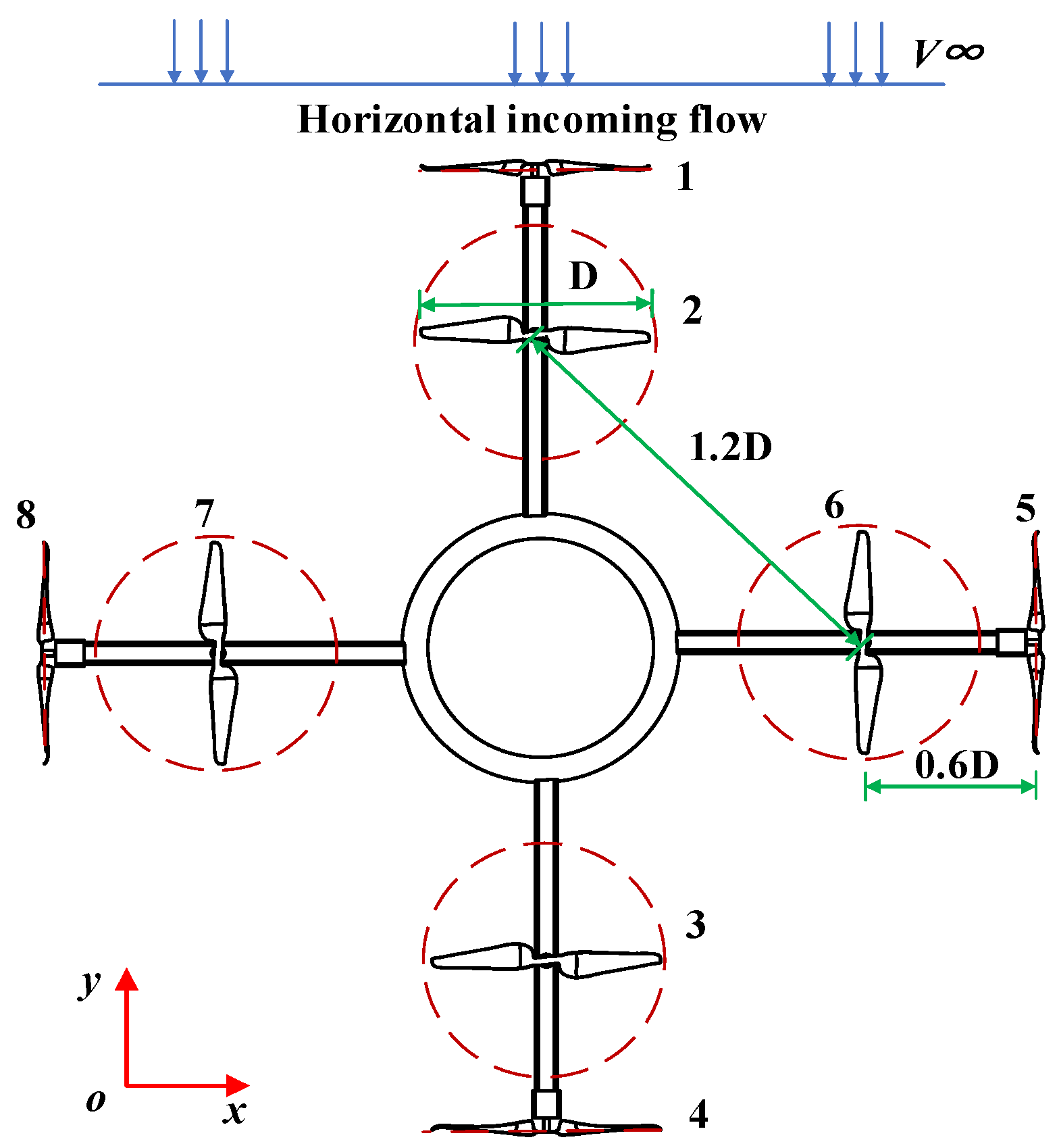
3.1. Simulation Setup

The numerical simulation of the orthogonal octorotor UAV is achieved by the computational fluid dynamics (CFD) method to obtain the flow field characteristics with different horizontal wind disturbances. As shown in Figure 6, the computational domain is divided into eight rotational regions and one stationary region. The velocity inlet and pressure outlet of the computational domain are set to simulate the wind velocity at different speeds. The dimensions of the computational domain are 3500 mm (length) × 2500 mm (width) × 3500 mm (height). The sliding mesh is applied for the entire flow field, and the mesh is refined at the interface between the stationary and rotating domains to obtain higher accuracy. The mesh size of the rotor surface was set to 0.1 mm with a mesh growth rate of 1.1. Also, the y+ value in the first cell is calculated between 5 and 60. The total number of mesh cells is 23.6 million, with a formal grid independence study showing that the results are already reaching the grid independence state. The turbulence model is set as the SST k-omega, and the momentum equations with turbulent viscosity are used in the transient calculation with a second-order upwind discretization scheme.

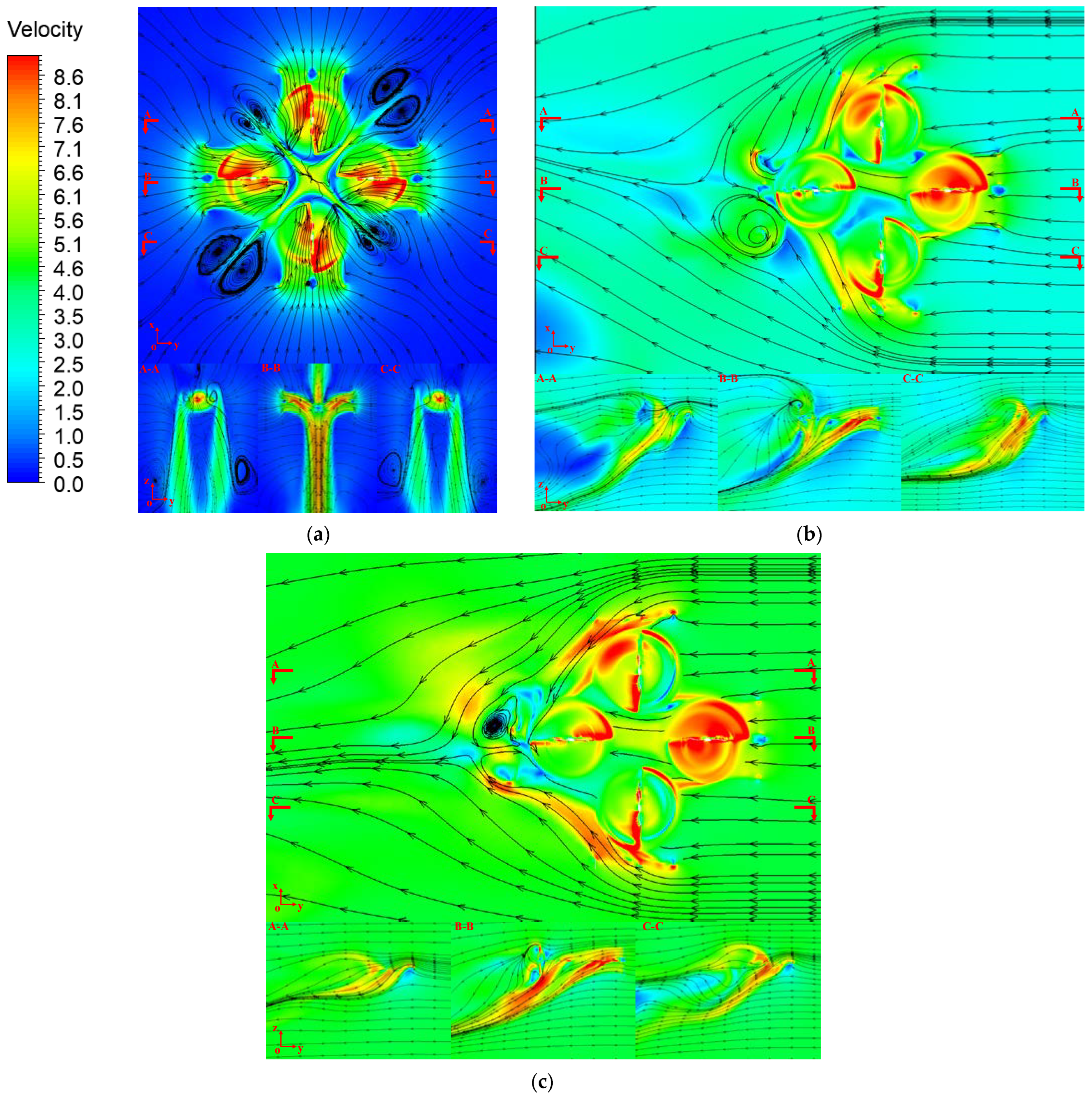
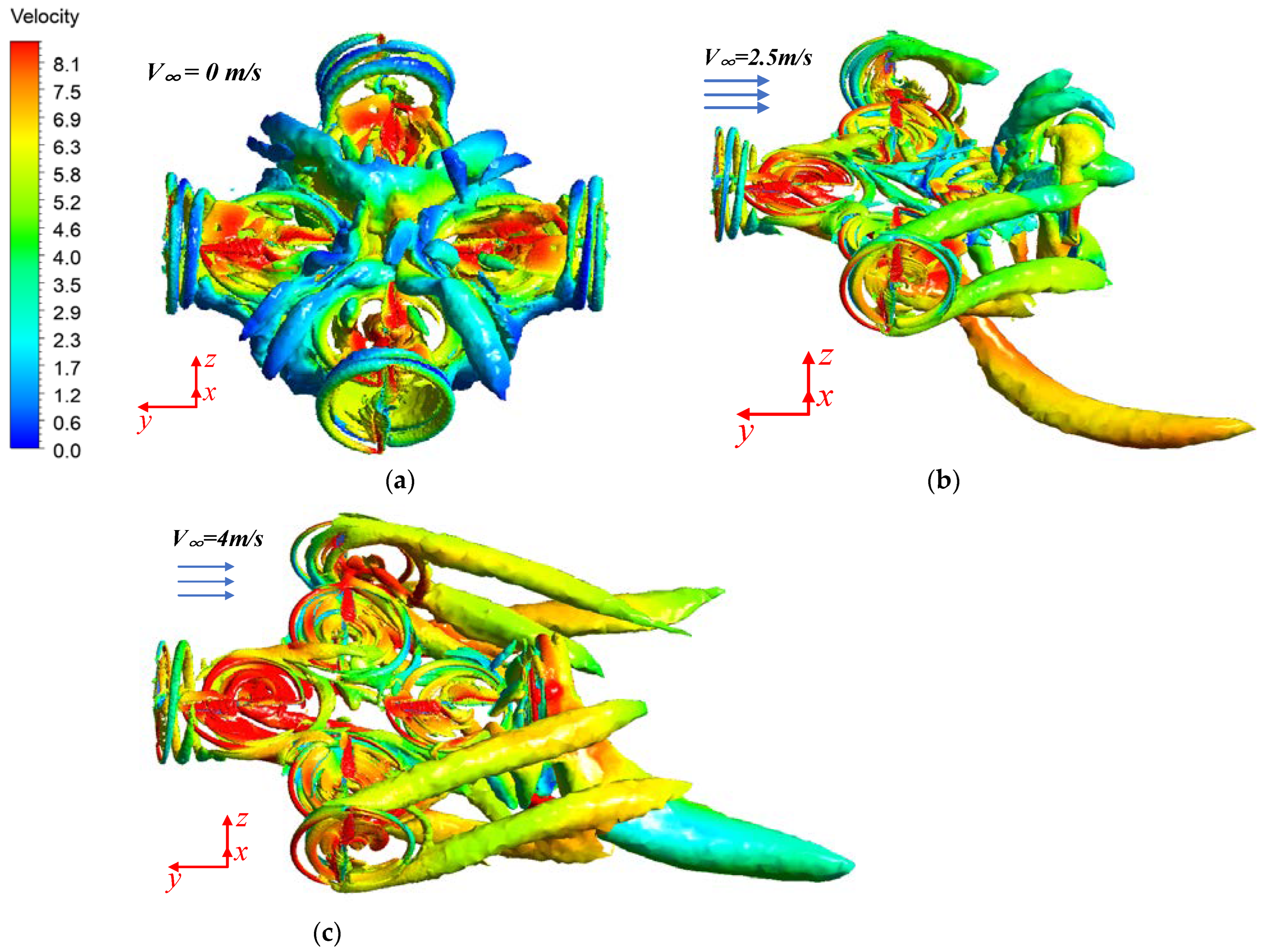
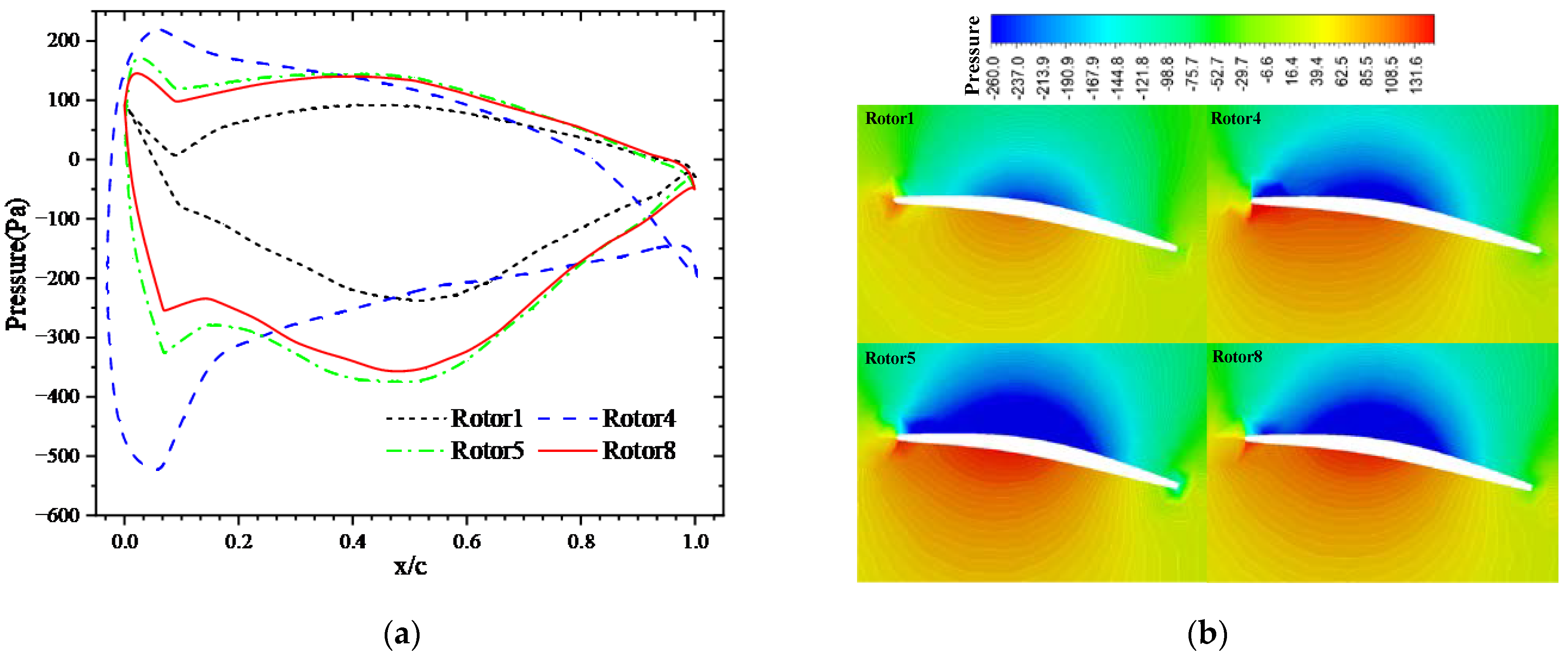
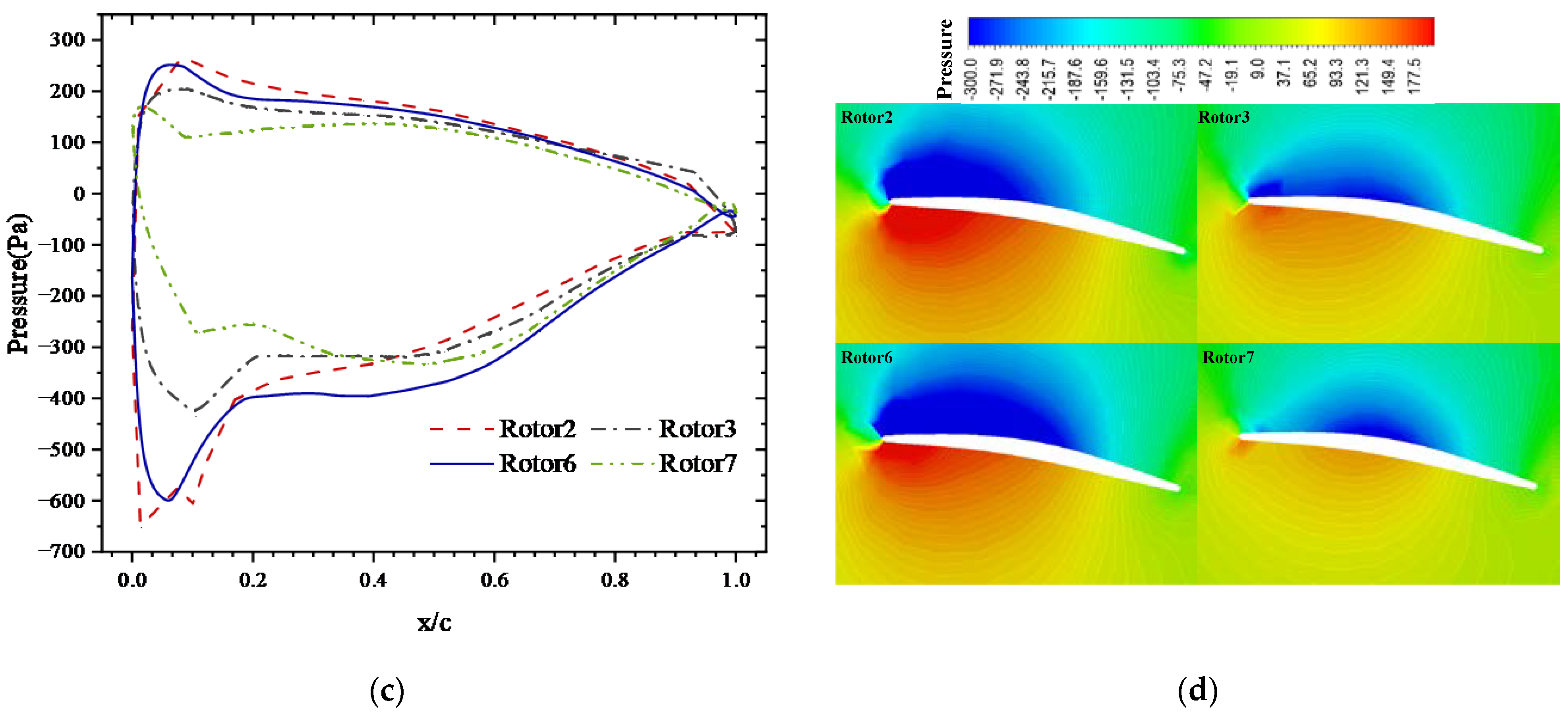
3.2. Simulation Results of the Orthogonal Octorotor UAV

Figure 7 shows the velocity distribution with different wind speeds. When the horizontal wind speed is 0 m/s, the induced velocity distribution of the rotor blades is symmetric along the geometric center of the orthogonal octorotor UAV, and disturbance of the airflow between adjacent rotor blades is weak. The induced velocity of the rotor disk increases with the wind speed, where the horizontal wind accelerates the rotor interference. Specifically, the velocity of the inflow and downwash flow increases at the same time, which may be the main reason for the increase of both rotor thrust and power consumption when the wind speed is introduced. Cross section B-B in Figure 7 shows that the horizontal wind disturbance aggravates the airflow disturbance between the rotor blades of the orthogonal octorotor UAV and changes the direction of the downwash flow with different wind speeds. Cross sections A-A and C-C show that the horizontal wind disturbance causes asymmetry in the downwash flow between rotor 6 and rotor 7, which may result in thrust variation.

Figure 8 shows the streamline distribution of the downwash flow of the orthogonal octorotor UAV. When there is no horizontal wind, the downwash flow is mainly concentrated below the rotor disk with an upward movement due to the auxiliary acceleration airflow. When the wind speed increases, the downwash flow is shifted along with the direction of wind speed. Also, the larger the wind speed is, the larger the shifting trend of the downwash flow is. It can be seen from the flow diagram that the inlet flow of the orthogonal octorotor UAV also increases with the wind speed. Furthermore, the coupling between the downwash flow and the wind disturbance and the downwash flow is inclined to be twisted with each other. Therefore, the increase in power consumption and thrust of the orthogonal octorotor UAV may be observed in this case.

Figure 9 shows the velocity vortices with different wind speeds. When there is no horizontal wind, the airflow between adjacent rotors is interacted with each other and is more concentrated in this case. As the horizontal wind is introduced, the rear rotor is completely immersed in the vortex of the front rotor, which leads to a more complicated disturbance for the rear rotor. It is interesting to note that higher wind speeds may cause greater thrust in the end, which can improve the hovering performance of the orthogonal octorotor UAV. However, the mutual interference between the rotors will also increase the power consumption, but this remains to be validated by experiments.

Figure 10 shows the pressure variation of the rotor tip and the 75% of the rotor chord length at 1700 RPM with the wind speed of $V_{\infty }$= 2.5 m/s. The thrust of the UAV is related to the pressure difference between the upper and lower surfaces of the rotor. The greater the pressure difference between the rotor surfaces, the greater the thrust of the rotor. As can be seen in Figure 10, the different pressure differences in each rotor may result in different thrusts in each rotor.

4. Experimental Analysis

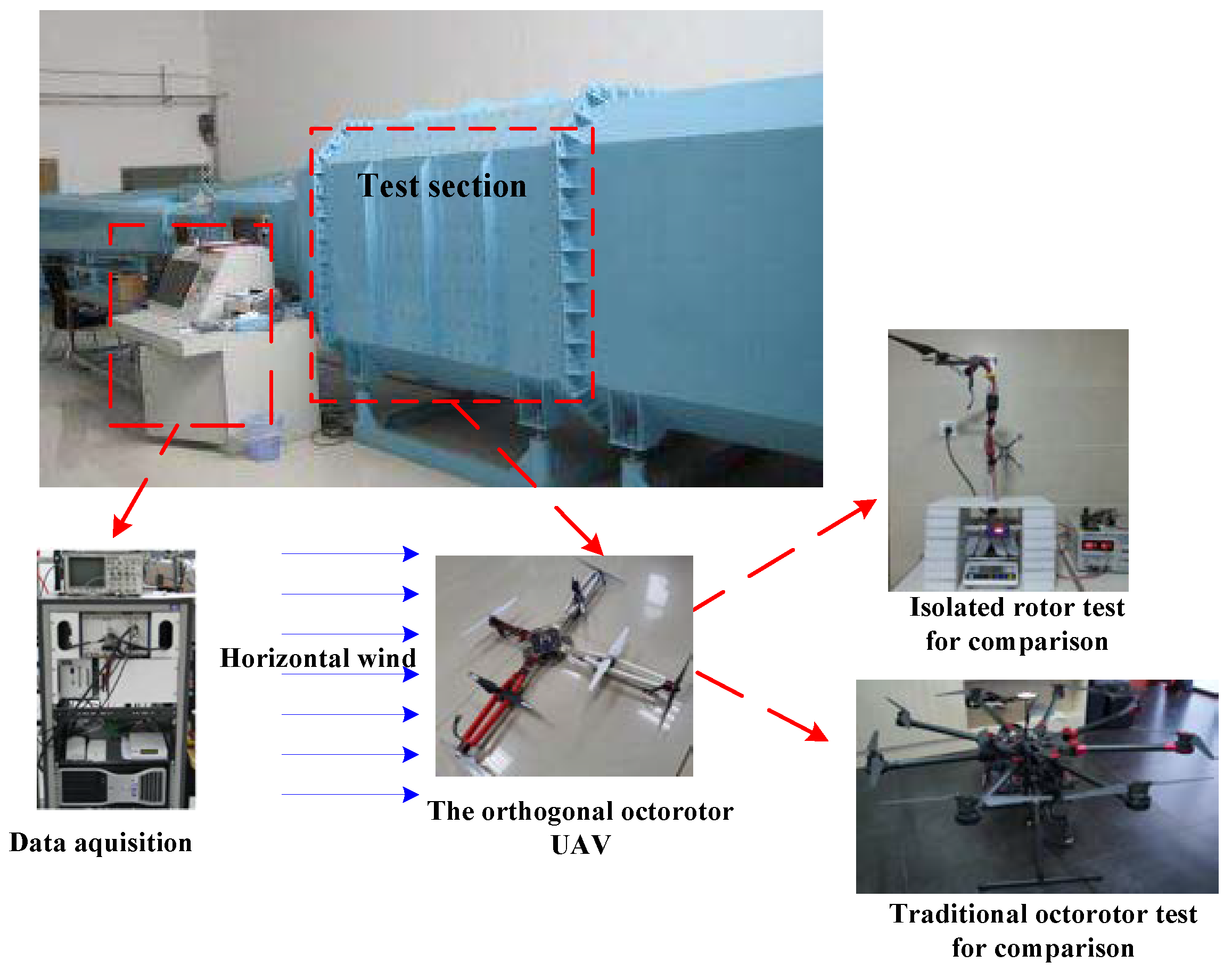
4.1. Experimental Setup

To validate the numerical simulations, it is important to perform wind tunnel tests on the orthogonal octorotor UAV to simulate the horizontal wind effect [19,20]. Figure 11 shows the sketch of the wind tunnel test for the orthogonal octorotor UAV. An open low-speed wind tunnel with a measurement area of 3 m (length) × 3 m (width) × 2.5 m (height) is applied to simulate the effect of the horizontal wind. It consists of four parts: contraction section (to reduce turbulence and vortices for airflow), test section (an area for orthogonal octorotor UAV tests), diffuser section (to maintain the stability and uniformity of flow), and power supply (to provide the power and control signals needed for wind tunnel experiments). Considering that the wind speed of the UAV is generally less than 5 m/s, the averaged wind speeds of 2.5 m/s of the light breeze and 4 m/s of the gentle breeze are measured through wind tunnel tests in comparison with $V_{\infty }=0 \mathrm{m}/\mathrm{s}$ to study the hovering efficiency of the orthogonal octorotor UAV. For the experimental setup, one of the highlights is that the structure is simple without redundant devices. The main sources of error in the experiments are the standard deviations of the rotational speed and the mean voltages from the thrust sensors. Typical values of the standard deviations of the thrust are about 1% of the mean values.

To avoid collisions between the rotors, the distance between the main rotors is 1.2 D, and the space between the main and auxiliary rotors is 0.6 D. The rotor speed is ranged from 1500 to 2300 RPM. The orthogonal octorotor UAV is driven by a brushless DC motor (SUNNYSKU X4112S), and the rotor speed is adjusted by PWM (Pulse Width Modulation). The rotational speed and thrust are measured by a tachometer (model TDT-2234C, accuracy: 6 ± (0.05% + 1 D) and a thrust sensor (model CZL605, accuracy: 0.02% F.S.), respectively. The current and voltage values of the rotor were recorded by DC power supply (model: RS Pro IPS-3202, accuracy: ±0.1 mV, ±0.1 µA). Then, the power consumption of the rotor was calculated by processing the obtained data.

Table 1. Experimental parameters.

Parameters	Value Range
Rotor diameter D (mm)	400
Number of blades	2
Material of blades	Carbon Fiber
Rotor speed (RPM)	1500–2300

shows the experimental parameters.

4.2. Experimental Results and Discussion

Figure 12 shows the thrust variation of the orthogonal octorotor UAV with the wind effect. It can be seen that the horizontal wind disturbance causes an increase in thrust of the orthogonal octorotor UAV, where the thrust increases by 8.1% at 2.5 m/s and 8.8% at 4 m/s for 1700 RPM. In this case, the increase in wind speed promotes the increase of thrust of the orthogonal octorotor UAV. Specifically, the thrust is much higher at 4 m/s than that at 2 m/s when the rotational speed is lower than 2100 RPM. This phenomenon is also observed through the vorticity contour. For a lower rotor speed, the intensity of the vortex increases significantly with the increase of the wind speed, thus leading to an increase in thrust. For the rotor speed at 2100 RPM, the vortex intensity at different wind speeds is not significant, and it can be seen that the effect of wind speed on UAV thrust decreases as the rotor speed is higher than 2100 RPM.

Figure 13 shows the power variation of the UAV. For a certain rotor speed, the power consumption of orthogonal octorotor UAV increased with the wind speed. On the contrary, the power consumption of the orthogonal octorotor UAV gradually decreases when the rotor speed is lower than 1700 RPM or higher than 2100 RPM. However, the power consumption of the orthogonal octorotor UAV gradually increases for the rotor speed ranging from 1700 to 2100 RPM. Compared with the simulation results, it is clear that the horizontal wind weakens the aerodynamic turbulence between the rotors at lower rotor speeds, thereby reducing power consumption in the end. For the high rotor speed, coupling between the downwash airflow of the UAV and the horizontal wind leads to severe downwash turbulence and increased power consumption. It also can be observed from the streamline distribution where the horizontal wind impacted directly on the auxiliary propeller disc and accelerated the side effects on the main rotor. Thus, the stronger the interaction between the rotors came from the greater the wind speed, which leads to increased power consumption. Additionally, the thrust increased to the maximum at 1700 RPM while the power consumption reached the minimum at the same time.

Figure 14 shows the variation of PL of the orthogonal octorotor UAV. It can be seen that the orthogonal octorotor UAV has a larger power loading when the horizontal wind speed is 2.5 m/s with the rotor speed is less than 2100 RPM. The reason for this might be that the wind effect weakened the airflow interference between the rotors at lower rotor speeds. Therefore, the thrust of the orthogonal octorotor UAV increases with stable power consumption. The downwash flow of the orthogonal octorotor UAV and the horizontal wind is coupled and twisted with each other leading to an increase in power consumption with a wind speed of 4 m/s. On the contrary, the thrust increment is relatively low, so the power loading at 4 m/s is lower than other wind speeds. From Figure 14, it can be seen that the smaller the rotor speed of the orthogonal octorotor UAV, the larger the power loading it has. Thus, for the orthogonal octorotor UAV, it will obtain a larger power loading in the horizontal wind with lower rotor speed.

Figure 15 shows the comparison of thrust and power variation of orthogonal octorotor UAV (with horizontal wind disturbance at 0 m/s, 2.5 m/s, 4 m/s), traditional octocopter UAV, and eight isolated rotors with different rotor speeds. As shown in Figure 15a, there is a significant increase in thrust for the orthogonal octorotor UAV compared to the octorotor UAV and the isolated rotors without interference. With the increase of rotor speed, the thrust increment of the orthogonal octorotor UAV gradually decreases. From Figure 15b, it can be seen that the airflow coupling between adjacent rotors will reduce the power consumption of the UAV when the rotational speed is low. Compared with the streamline distribution in Figure 13, it showed that the inflow velocity of the UAV would increase with the rotational speed, which will cause the internal airflow of the UAV to become more complex and, at last, result in increased power consumption. The power consumption of the orthogonal octorotor UAV is higher than that of the octorotor UAV due to downwash flow interference from the auxiliary rotors of the orthogonal octorotor UAV.

Figure 16 shows the PL variation of the different types of UAVs compared to the orthogonal octorotor UAV. It can be seen that the orthogonal octorotor UAV has a larger PL value than the traditional octorotor UAV and the eight isolated rotors when the rotor speed is less than 2100 RPM, especially for lower rotor speeds less than 1700 RPM. The larger rotational speed of the orthogonal octorotor UAV will lead to extreme airflow interference with the adjacent rotors and increase power consumption in the end. In this case, the higher PL value of the orthogonal octorotor UAV is obtained at low rotational speeds with improved aerodynamic performance.

5. Conclusions

This paper investigates the aerodynamic performance of an orthogonal octorotor UAV with the effect of horizontal wind varied from 0 m/s to 5 m/s and different rotational speeds ranging from 1500 to 2300 RPM by numerical simulations and low-speed wind tunnel tests. The conclusions are as follows:

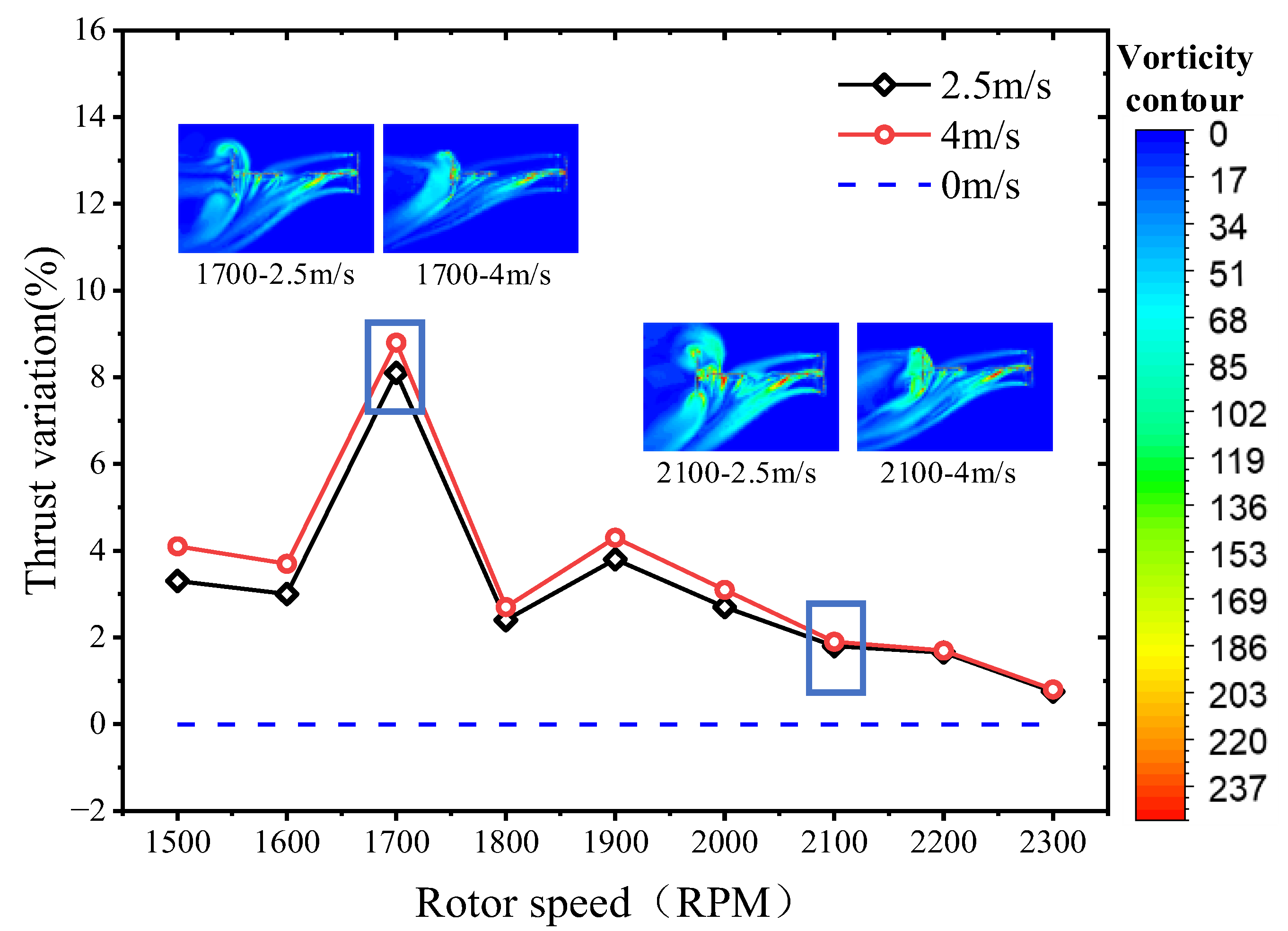
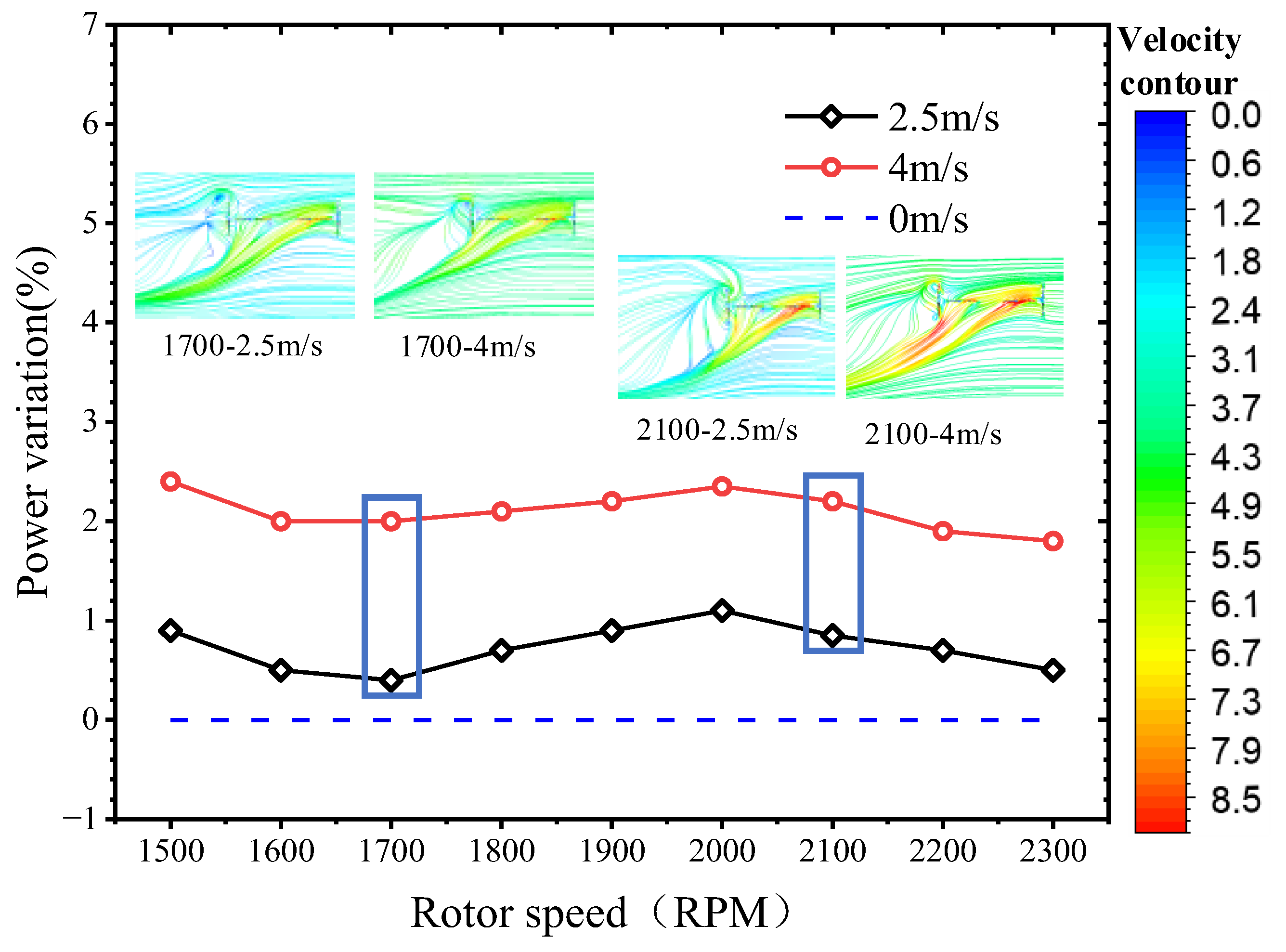
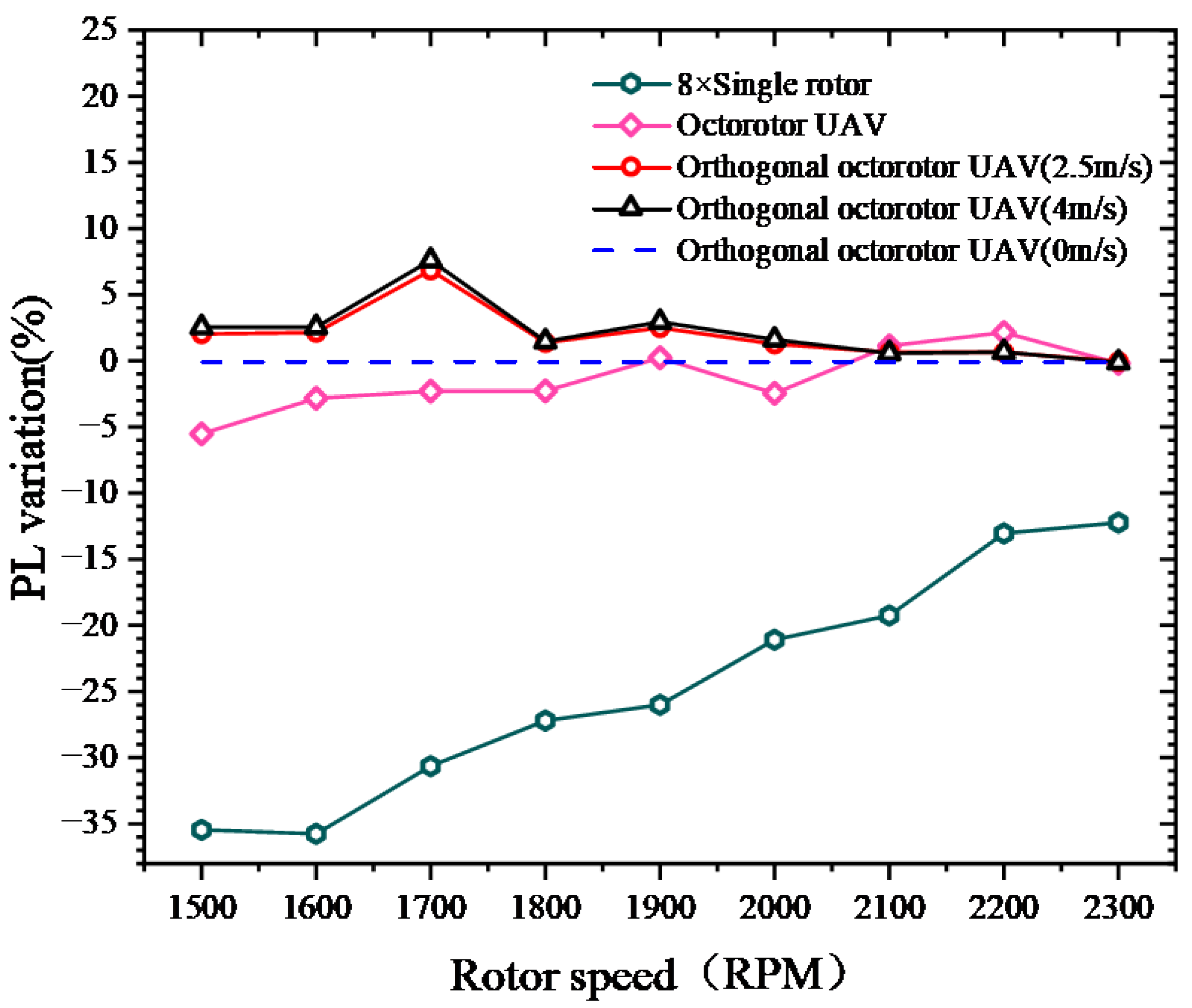
• The orthogonal octorotor UAV with the horizontal wind effect will obtain better aerodynamic performance for a lower rotor speed where the thrust is increased with stable power consumption, which means that the orthogonal octorotor UAV retains good wind resistance. Specifically, the thrust increases by 8.1% at 2.5 m/s and 8.8% at 4 m/s compared with no wind disturbance when the rotor speed is less than 1900 RPM. Also, simulation results showed that the airflow coupling between the rotor blades became extremely aggressive; thus, the power consumption increases significantly with the increasing thrust at higher rotor speed, and ultimately the aerodynamic performance decreases with the wind speed;
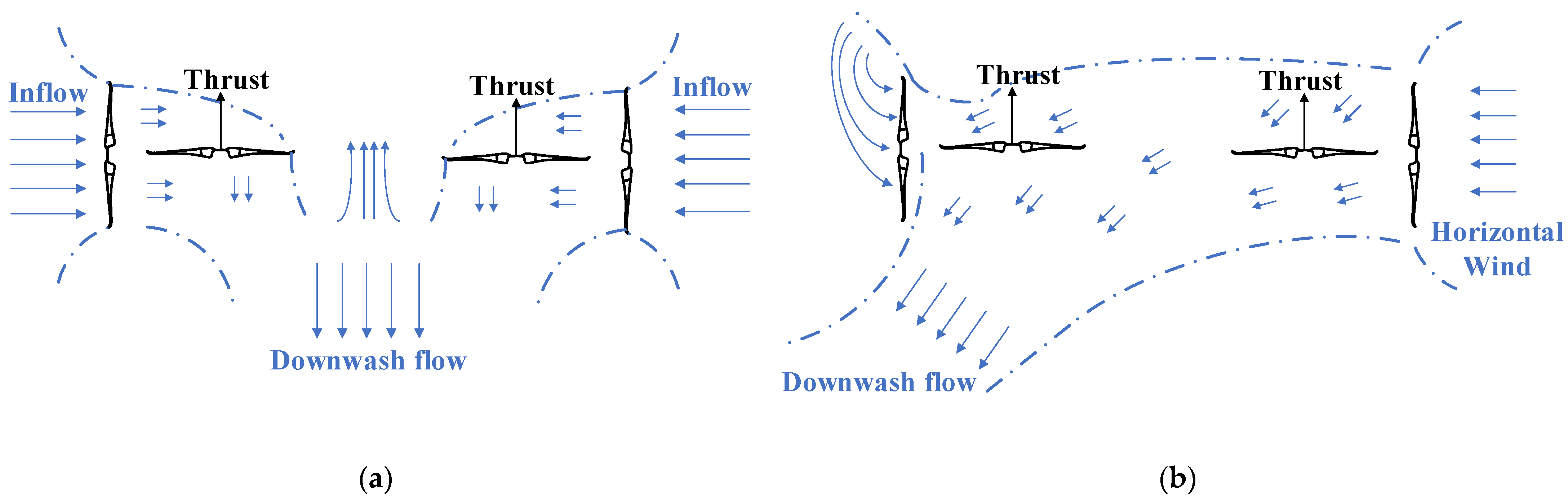
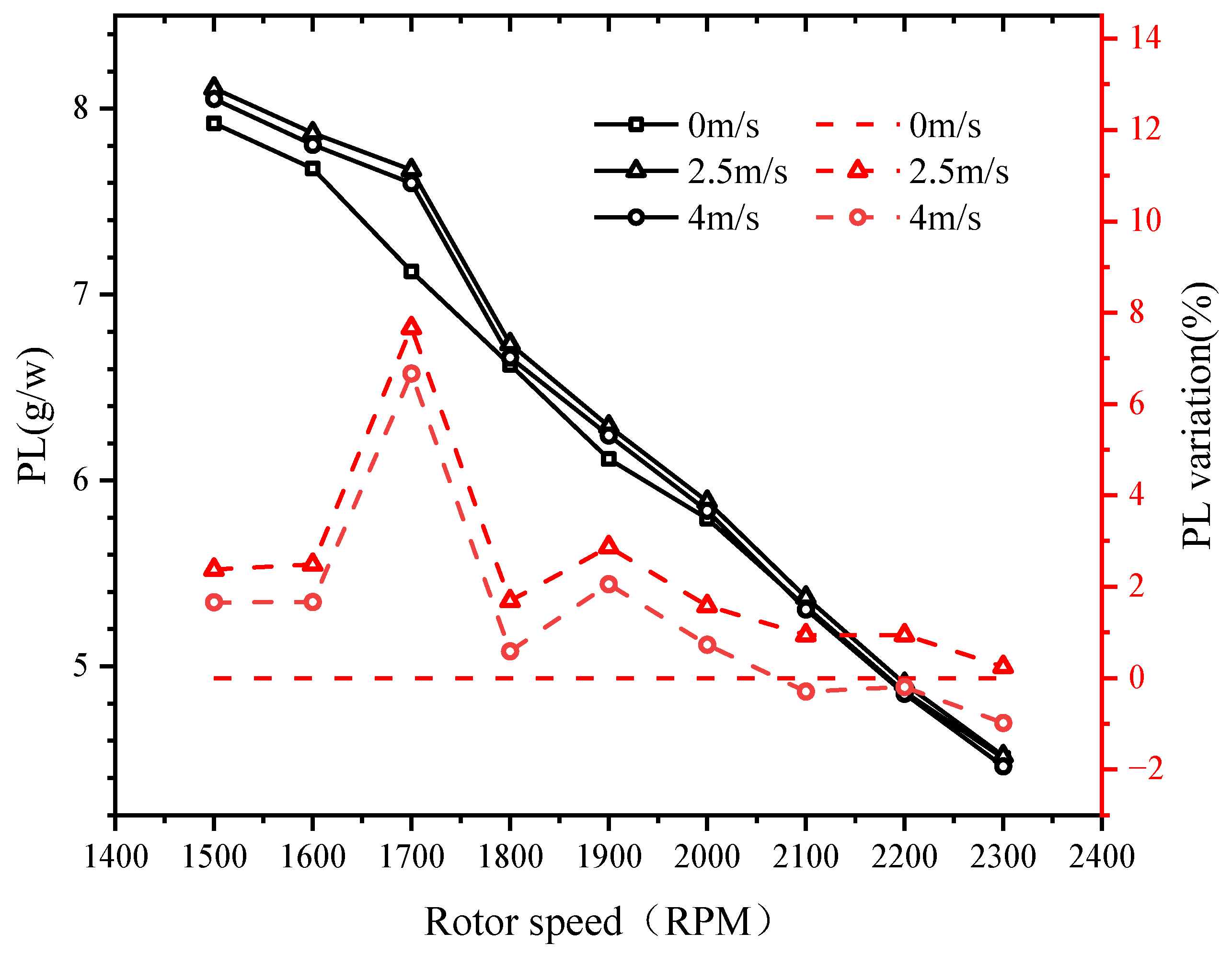
• The PL of the orthogonal octorotor UAV reached the maximum at 2.5 m/s, which indicated that the orthogonal octorotor UAV has the perfect wind resistance to operate in a wind domain where the wind effect became advantageous to offset the rotor interference. With the increasing wind speed, the downwash of the rotor will be shifted with the horizontal wind, which causes the rear rotor to be totally immersed in the wake of the front rotor and leads to extreme interference and decreased power loading;
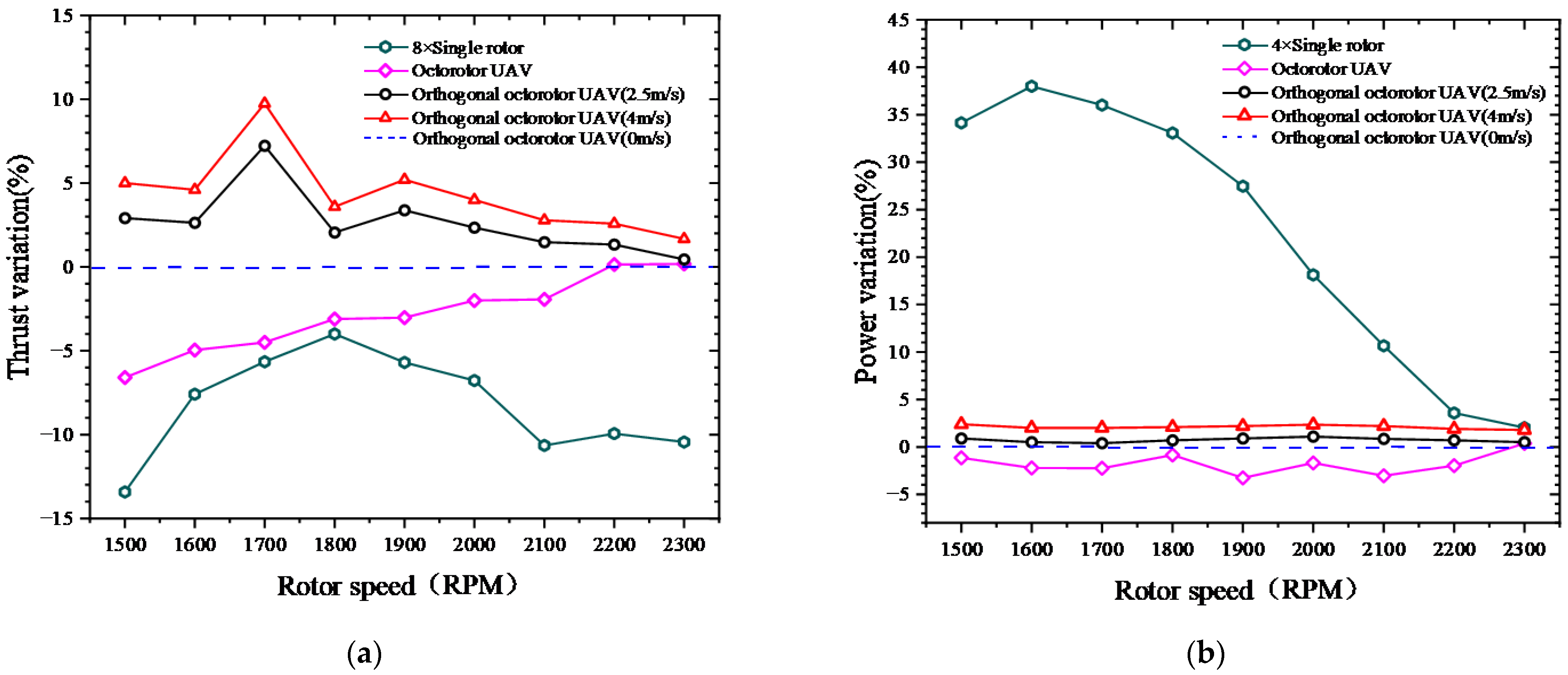
• Compared with the traditional octorotor UAV and eight isolated rotors without rotor interference, the orthogonal octorotor UAV showed a better aerodynamic performance both in hovering without wind effect and better wind resistance with a high PL in the horizontal wind. Moreover, the orthogonal octorotor UAV operated in the horizontal wind is inclined to reduce the rotor speed to avoid large power increments. Further study will examine vertical wind’s effect on orthogonal octorotor UAVs and involve more field flight tests.