Abstract
This paper is concerned with the idea of a significant improvement of state-of-the-art short-range rockets by means of using rocket artillery systems. Such a system consists of a rocket launcher aircraft (RLA) and a drone-launched short range rocket (DLSRR). An RLA is a reusable first stage of a military rocket. A DLSRR is the expendable second stage, which flies to the target. RLA-DLSRR systems have not yet been built, but they have been described in previous works by the author. State-of-the-art rocket systems are completely expendable and, hence, extremely expensive. No rocket artillery system with a reusable first stage has been built so far. Civilian spaceships with reusable first stages have been successful since 2015. In an electrically pumped rocket engine, the fuel and oxidizer are pumped into a combustion chamber by an electric-motor-driven pump. The electric motor is powered by a battery bank. Electrically pumped rocket engines would further decrease the cost of RLA-DLSRR systems. These engines are less expensive and more reliable then conventional rocket engines. In the present paper, it is shown that commercially available lithium polymer battery banks, as well as high specific power electric motors, provide sufficient power for the rocket engines needed for RLA-DLSRR systems. In the example given, it is calculated that an ERLA–DLSRR system with a liftoff mass of 15 tons can deliver a 210 kg payload to a range of up to 567 km with an impact velocity of up to 2415 m/s.
1. Introduction
The present work is concerned with the discussion and supporting calculations of the concept of a system composed of a vertical rocket launcher aircraft (RLA) and drone-launched short range rockets (DLSRRs). The concept has been suggested and discussed by the author in two previous works [1,2]. First, the RLA raises one or more DLSRR to a high altitude and fires them with high initial velocity. Second, the RLA returns to its base ready for refuelling and another sortie [1]. Third, the DLSRRs continue their mission to the target. An RLA-DLSRR system can also be seen as a military rocket with a reusable first stage. The RLAs and DLSRRs discussed in [1,2] use conventional rocket engines. In the present work, the rocket engines are different, i.e., they are such that the fuel is pumped into the combustion chamber by an electric motor. The motor is driven by a battery bank.
It is worth mentioning that state-of-the-art short range ballistic missiles are capable of precise strikes at ranges of 100 km to 1000 km [1]. These missiles are relatively common. The USA has 3700 ATACMS missiles, and each one can precisely deliver a 230 kg payload to 300 km or a 560 kg payload to 165 km [3]. China has over a thousand ballistic missiles with ranges of 300 km to 1000 km [4] (p. 31).
State-of-the-art short range ballistic missiles are very costly. Namely, the cost of delivering a payload to the target using ATACMS is $2700 per kg for a target at a distance of 165 km and $6500 per kg for a target at a distance of 300 km [2,3]. The cost of delivering a payload to a target at a distance of 500 km using a liquid propellant Dong-Feng 15 rocket is $6700 per kg.
The cost of a rocket launch can be significantly reduced for the case of rockets with reusable first stages. On 21 December 2015, Space X landed the first stage of a Falcon 9 spacecraft on the launching pad. Since then the cost of payload orbital delivery fell by a factor of five [5]. Military rockets with reusable first stages have not been introduced in practice yet, but they have been considered by the author in previous works [1,2].
An ERLA is an RLA which uses electrically pumped rockets for both the ascent and landing. The ascent is accomplished by the main rocket engine, while the landing is accomplished by several small rocket engines. Future ERLAs containing more powerful and energetic batteries will land using propellers driven by electric engines. DLSRRs powered by electrically pumped rockets are not given a special designation. The performance of these DLSRRs is discussed in this work. It is worth mentioning that the present work can be viewed as a sequel to the work discussing vertical rocket launcher aircraft [1] and another work discussing drone-launched short range rockets [2].
The use of an electric-pump-fed cycle does not improve the performance of the rocket engine. In fact, this cycle may produce a lower combustion chamber pressure and exhaust velocity than state-of-the-art cycles. Nevertheless, an electric-pump-fed cycle significantly reduces the cost of a rocket engine. Moreover, electrically pumped rocket engines should have a high reliability and flexible thrust adjustment [6]. Cost reduction is certainly important for the discardable rocket engines on DLSRRs. High reliability is crucial for an ERLA liftoff engine, which should be reusable hundreds of times. Flexible thrust adjustment is very important for ERLA landing engines.
Electrically pumped rockets are not new. The Rutherford rocket engine, which uses electric fuel and oxidizer pumps, has already been built and used [6]. Rutherford engines power a small space rocket with a reusable first stage called an Electron. Each space rocket uses nine Rutherford engines on the first stage and one Rutherford engine on the second stage. As of February 2023, 33 Electron rockets have been launched [7].
In recent years, there has been significant interest in the use of battery power for civilian vehicles. Much of this interest is related to electric vertical take-off and landing (EVTOL) [8,9,10]. In the presented work, the possibility of using battery power for military vehicles has been explored.
In this work, it is shown that both ERLAs and DLSRRs can use electric-pump-fed cycles and still achieve high performance. State-of-the-art batteries and electric motors can be used to sustain a pressure of 17 atm to 30 atm in DLSRR combustion chambers and 30 atm to 60 atm in ERLA combustion chambers. An ERLA can ascend using the main electrically pumped rocket engine and land using several small electrically pumped rocket engines. An example of an ERLA–DLSRR system demonstrates the feasibility of the concept. An ERLA with a liftoff mass of 15 tons raises a 1.05 ton DLSRR to an altitude of 35 km and releases it with an upward velocity of 867 m/s. The ERLA lands at 5 min 8 s after liftoff and is then ready to be recharged and reused. The DLSRR uses its own engines to accelerate upward and forward. It sends a 210 kg payload to a target that is 362 km from the initial ERLA liftoff point. The payload contains several projectiles, which can impact the target at a velocity up to 2016 m/s.
The current work consists of six sections. In Section 2, the concept of an electric-pump-driven liquid propellant rocket engine is described. In Section 2.1, a general description of the aforementioned engines is presented. In Section 2.2, the electric power consumption of the engines is calculated. In Section 2.3, the combustion chamber pressure is found.
In Section 3, the state-of-the-art technology for electrically pumped rocket engines is described. In Section 3.1, there is a list of some of the available lithium polymer batteries. In Section 3.2, there is a list some of the available electric motors. In Section 3.3, some of the available liquid rocket propellants are presented.
Section 4 is devoted to the description of an ERLA landing. Namely, in Section 4.1, it is shown that landing by rotors is almost impossible with state-of-the-art technology. In Section 4.2, it is shown that landing by small rockets is possible.
In Section 5, an example of an ERLA–DLSRR system is presented. In Section 5.1, the ERLA, DLSRR, and warheads are described and illustrated. In Section 5.2, the ERLA parameters are presented. In Section 5.3, the ERLA performance is calculated. In Section 5.4, the DLSRR parameters are presented. In Section 5.5, the DLSRR performance is calculated. Section 6 comprises the conclusion.
2. Electrically Pumped Liquid Propellant Rocket Engine
2.1. Engine Description
The general discussion on liquid propellant engines can be found in Section 4.2 regarding the work on RLAs [1]:
In a liquid propellant rocket engine, both the fuel and oxidizer are fed into the combustion chamber. Both liquids come into the chamber through hundreds of spray nozzles in order to ensure rapid mixing. Inside the combustion chamber, fuel reacts with the oxidizer to produce combustion with temperatures between 1500 °C and 3500 °C. Engines with higher combustion temperatures generally produce higher specific impulses, yet high combustion temperatures also causes rapid erosion of the combustion chamber. Combustion products are expended through a nozzle-producing jet stream in one direction and thrust in the opposite direction.
In state-of-the-art rocket engines, the fuel and oxidizer are driven into a combustion chamber by pumps, which consume large amounts of mechanical power. Generally, these pumps are driven by engines consuming a small fraction of the rocket fuel and oxidizer. These engines are prone to many failures [11]. Turbopump-driving engines are also very expensive. Indeed, they can account for more than 50% of the rocket launch cost.
ERLA and DLSRR engines are different from conventional liquid rocket engines in two respects. First, the pump that feeds the propellant and oxidizer into the combustion chamber is powered by an electric motor. Second, the combustion chamber pressure is considerably lower than that in most conventional engines. As mentioned in Equation (14) below, the combustion chamber pressure ranges from 17 atm to 30 atm for DLSRRs and from 30 atm to 60 atm for ERLAs.
2.2. Thrust-Specific Electric Power Consumption
In this subsection, it is demonstrated that the power requirement for the electric pump engine is directly proportional to the engine thrust and combustion chamber pressure. The required electric power is expressed as a function of the rocket mass and engine firing time.
Based on the physics of the process, it can be easily seen that the compressor shaft power can be given by the following formula:
where and are the fuel and oxidizer volumetric flow rates, respectively; and are the fuel and oxidizer mass flow rates, respectively; and are the fuel and oxidizer densities respectively; and are the fuel and oxidizer inlet pressures, respectively; and are the fuel and oxidizer outlet pressures, respectively; and and are the fuel and oxidizer pump efficiencies, respectively. If power to the shaft is supplied by a brushless electric motor, then the electric power consumption is
where and are the motor and inverter efficiencies, respectively.
The thrust of the rocket engine can be given by
where is the exhaust velocity. Thrust-specific electric power, which is the electric power per unit thrust, is given by
In the sequel, it is convenient to define the following quantities:
In this case, is the combustion chamber pressure. By substituting (5) into Formula (4), we obtain
Therein, the power coefficient is given by
which is a dimensionless constant that is dependent on the rocket parameters. Expressing the thrust-specific electric power in terms of the power coefficient yields
The rocket thrust can be expressed in terms of the rocket mass as
where is the rocket mass, is the flight-time-averaged exhaust velocity, is the propellant mass fraction of the rocket at liftoff, and is the rocket firing time. Using Formulas (3) and (8) for the of Formula (9) allows us to arrive at the following approximation for the mass-specific electric power:
Notice that the exhaust velocity changes little over the ERLA or DLSRR flight; hence, the last approximation given in Equation (10) is valid.
Brushless DC electric motors typically have and [12]. The only electrically pumped rocket engine produced so far is the Rutherford engine. This engine has the following parameters [6]:
The power constant can be lowered by increasing the efficiencies of the electric motor and inverter, as well as the fuel and oxidizer pumps. Since pumps and electric motors are mature technologies, it is unlikely that their efficiencies can be increased substantially at a reasonable cost. Another way of slightly decreasing the power constant is by using a dense oxidizer such as 95% hydrogen peroxide.
2.3. Combustion Chamber Pressure
The high electric power requirement for an ERLA or DLSRR engine creates several problems. First, it would necessitate a high mass fraction of the battery bank and electrically pumped engine. Second, it would increase the overall engine cost, which is problematic for the discardable engines of the DLSRR. Hence, mass-specific electric power must be limited. The limit of electric power available for compressors is estimated below. From that limit, the estimation of the maximal combustion chamber pressure follows immediately.
A high combustion chamber pressure () brings several advantages to the rocket engine. First, it allows the combustion chamber to be smaller by lowering both its mass and cost. Second, a high increases the exhaust velocity—especially for ERLAs, which have to start from sea level.
An evaluation of the of (10) yields:
As discussed above, decreasing the below four may be impractical. It is likely that discardable DLSRR engines will have less efficient engines and compressors with a .
In the DLSRRs considered, e.g., in [2], the propellant mass fraction is about 0.5, and the rocket firing times are from 0.7 min to 1.3 min. For RLAs, the propellant mass fraction is about 0.6, and the rocket firing times are from 1 min to 2 min. Heavier RLAs have higher propellant mass fractions and longer rocket firing times [1]. Hence, for most RLAs and DLSRRs, the following estimates hold:
Increasing the rocket firing times incurs an extra cost of higher velocity loss due to gravity.
Finally, the estimation of the combustion chamber pressure for ERLAs and DLSRRs is presented. Given the data of Section 3.2 below, the specific power of a battery–motor system should be about 2.5 kW/kg for a DLSRR and 1.25 kW/kg for an ERLA. Finding the optimal mass fractions for battery–motor systems for every type of DLSRR and ERLA remains an open engineering problem. Under the assumption that a battery–motor system makes up 5% of the liftoff rocket mass for a DLSRR and 10% of the liftoff rocket mass for an ERLA, it can really be seen that the overall mass-specific electric power for DLSRRs and ERLAs should be W/kg. By substituting (13) and the data for and into (12), we obtain the chamber pressure
3. State-of-the-Art Technology for Electrically Pumped Rocket Engines
3.1. Available Batteries
In order to evaluate the batteries for the storage of electric energy, it is convenient to recall several concepts describing them. The specific energy is the energy, that can be obtained by discharging a battery per unit of battery mass. Some lithium ion batteries can store up to 180 Wh/kg [13]. The specific power is the rate at which a battery can supply electric power. When a battery is discharged quickly, it supplies a high specific power, but it supplies a lower specific energy than when it is discharged slowly. By 2016, very high power LiPo batteries had a specific power of up to 6 kW/kg for a specific energy of 60 Wh/kg [13]. The discharge efficiency is the fraction of a battery’s specific energy, which can be obtained by discharging a battery at a given power. The discharge efficiency is a decreasing function of a battery’s specific power. If a battery is discharged over a long time, almost all of its maximum possible specific energy is harvested; hence, its discharge efficiency is close to . If a battery is short-circuited, then all of its energy is converted into internal heat; hence, its discharge efficiency is 0. The C rating is the measure of how fast a battery can be discharged. The discharge time is one hour divided by the C rating; thus, a battery with a C rating of 120 should be able to discharge within 30 s.
Below is a description of some lithium polymer (LiPo) batteries, which can be used by ERLAs and DLSRRs. LiPo batteries have a relatively low specific energy but a very high specific power. The data for some of these batteries is presented in Table 1.

Table 1.
Commercially available LiPo batteries.
From what is shown in Table 1, it would appear that Rampage has the worst specifications and the highest cost. Nevertheless, most battery packs provide lower C ratings than their manufacturers claim, which means that true battery parameters cannot be obtained without additional testing.
LiPo batteries with a specific power of 2.4 kW/kg and a specific energy of 118 Wh/kg have been available as early as 2007 [20]. According to Chargery [21], the model PHHE3300-5S LiPo battery has a specific energy of 100 Wh/kg at a specific power of 6 kW/kg. The Melasta [22] model SLPB8534126-65C can discharge all of its energy in one minute and has an 80% discharge efficiency.
Finding the best type of battery for every type of ERLA and DLSRR remains an open engineering problem. Many types of batteries would have to be tested to determine their specific power and specific energy. Moreover, economic factors, such as battery cost and a possible discount for bulk purchase, must be considered. These parameters would have to be weighed against the cost of these batteries.
Analysing the above data yields the following assumptions about the parameters for the batteries to be used in ERLAs and DLSRRs. Namely, a DLSRR battery will have to provide relatively high power for about 1 min, and, thus, a DLSRR battery should have a specific power of 6 kW/kg and a specific energy of 100 Wh/kg. An ERLA battery will have to provide electric power to the rocket engine’s compressor for 1 min to 1.5 min during liftoff. Such a battery will also have to provide power for about half a minute during landing while retaining some extra energy for a safety margin. Thus, an ERLA battery should have a specific power of 3 kW/kg and a specific energy of 120 Wh/kg.
3.2. Available Electric Motors
Both the DLSRR and ERLA will need an electric motor in order to pump fuel into rocket combustion chambers. Each ERLA will also need several smaller electric motors to power its propellers during landing. All of the aforementioned motors must have a high specific power. The specifications of EMRAX motors are presented in Table 2 below. The peak power can be sustained for several minutes [23].

Table 2.
EMRAX electric motors.
These electric motors can sustain a specific power of at least 8 kW/kg for two minutes. Recall that DLSRR batteries have a specific power of 6 kW/kg. The combination of a battery pack and an electric motor has to have extra mass in the form of wiring, invertors, and structural materials. The estimation of the specific power of a DLSRR battery–motor system can be calculated as follows:
where 9 kW/kg is a generous allowance for extra weight such as wiring, etc.
Recall that ERLA batteries have a specific power of 3 kW/kg. An electric-motor-powered ERLA rocket pump has a specific power of 8 kW/kg. Unlike a DLSRR, an ERLA has another set of electric motors. These engines are used to pump propellant into the combustion chambers of the landing rockets. The specific power of this engine set is also 8 kW/kg. Hence, the combined specific power of all the electric motors is only 4 kW/kg. Once again, the combination of a battery pack and an electric motor has to have extra mass in the form of wiring, invertors, and structural materials. The estimation of the specific power of an ERLA battery–motor system can be calculated as follows:
where 5 kW/kg is a generous allowance for extra weight such as wiring, etc.
3.3. Available Liquid Propellants
The performance of several liquid bipropellants for RLA and DLSRR rockets are described in this sub-section. Heavy RLAs are likely to use cryogenic propellants. Out of several fuels considered in the author’s previous work, propane gave the best performance with liquid oxygen [1]. Kerosene is the most commonly used fuel with a liquid oxygen oxidizer. Hypergolic propellants ignite as soon as the propellant spray and fuel spray are combined. Concentrated hydrogen peroxide is hypergolic with several ethanolamine mixtures [1]. The mixture denoted as EEC gives the best performance with 95% hydrogen peroxide. EEC is a mixture of 61% monoethanolamine, 30% ethanol, and 9% hydrated copper nitrate. On contact, EEC ignites with a delay of only [24]. A 50 N thruster using EEC and 90% hydrogen peroxide has been tested [25].
The performance of several cryogenic liquid fuel–oxidizer combinations is tabulated in Table 3 below. The first column is fuel. The second column lists the oxidizer. LOX denotes liquid oxygen. HP95 denotes 95% hydrogen peroxide. The third column is the oxidizer-to-fuel mass ratio. The forth column is the temperature at the rocket throat. The temperature of the flame where the oxidizer and fuel contact is higher. The fifth column is the exhaust velocity at sea level for a chamber pressure of 30 atm and an expansion ratio of six. The sixth column is the exhaust velocity in a vacuum for a chamber pressure of 30 atm and an expansion ratio of six. The seventh column is the exhaust velocity at sea level for a chamber pressure of 70 atm and an expansion ratio of 12. The eighth column is the exhaust velocity in a vacuum for a chamber pressure of 70 atm and an expansion ratio of 12.

Table 3.
Performance of several bipropellants.
The values in the last three columns are deduced from the values calculated by the Rocket Propulsion Analysis (RPA) program [26]. First, the RPA calculates the ideal exhaust velocity. Then, the RLA estimates the combustion and nozzle efficiencies. Finally, the RLA estimates the real exhaust velocity. These velocities are tabulated in Table 3 below.
Other cryogenic and hypergolic combinations should be tested in order to find the optimal combinations for every type of rocket. For example, triethylaluminum is an energetic fuel tht is hypergolic with many oxidizers.
As mentioned in the author’s previous work [1], the prices of fuel and oxidizer chemicals during the 2010s were relatively low. The prices listed below are from the 2010s, particularly from 2019. Ethanolamine cost about $1.80 per kg [27]. The 95% pure hydrogen peroxide cost $2.00 per kg [1]. Triethylaluminum had a wholesale price of $5.00 per kg [28].
4. Erla Landing
The first generation of ERLAs perform landing by using several small rocket engines with the landing propellant being taken from a separate tank. ERLA landing engines use electric motors to pump propellant into combustion chambers. The motors use electricity from the same battery bank, which has powered the main engine’s pumps during ascent.
Later generations of ERLAs may use electrically powered propellers for landing. This will be a possibility when both batteries and electric motors increase their specific power. In this section, it will be demonstrated that state-of-the-art technology will require ERLAs to have unreasonably large propellers in order to land.
4.1. Rotor Landing
The goal of this subsecton is to demonstrate that propeller or rotor landing is almost impossible with the present state-of-the-art technology. Future ERLAs may be able to land with rotors due to the availability of electric motors with a higher specific power, as well as batteries with a higher specific energy.
During rotor powered landing, an ERLA has to hover and fly under the power of vertical propellers driven by electric motors. The motors would be powered by electric charge left in the batteries after ascent. Even though most landings should take about 20 s, the batteries should have enough charge to sustain the flight for at least half a minute. Multi-use machinery must have a safety factor under any circumstances and especially under circumstances of combat, which may be unforeseeable.
Recall that, for an ERLA, the battery–motor system makes up 10% of takeoff mass. During ascent, an ERLA burns its rocket propellant. As soon as the rocket engine is turned off, the ERLA releases its payload, which consists of one or more DLSRRs. ERLA landing mass is, at most, 30% of its liftoff mass; hence, the battery–motor system now makes up 33% of the vehicle mass. According to Formula (16), the specific power of the battery–motor system is 1.25 kW/kg. The combined efficiency of brushless DC electric motors and invertors is generally 75% [12]. Hence, the specific power available for an ERLA during landing (denoted by ) is
where denotes the mass fraction of the battery–motor system within the landing ERLA, and is the efficiency of the electric system. For a theoretically ideal rotorcraft, the minimum lifting power is [9]:
where is the air density, and is the area of all the lifting rotors. For standard air density, expression (18) can be expressed as
where is the ideal specific power of the rotorcraft, and is called the disk loading. For actual rotorcraft, the hover power is 2.3 to 4.9 times higher than the value given by Equation (19). For most rotorcraft, the hover power is no higher then 3.3 times the ideal. For systems with axillary propellers, such as tilt rotors, tilt wings, and vertical propellers, the hover power is 4.9 times the ideal [29]. Hence, the specific power needed by an ERLA during landing can be approximated by
In calculating , each pair of counter-rotating rotors can be counted as two rotors of the same radius [30].
The power supplied by the ERLA engines given in (17) must exceed the power used by the ERLA given in (20). Hence, is bounded above as
This would require an ERLA to have relatively large propellers, which would increase aerodynamic drag during ascent. With the current state of technology, powering an ERLA landing using propellers would be impossible.
4.2. Rocket Landing
In order for the ERLA to land, its landing rockets should be able to sustain its hovering for at least half a minute, which is possible with state-of-the-art technology.
The formula for calculating the ERLA hovering time under landing rocket power is presented in Equation (22) below. The mass fraction of the landing propellant in an ascending ERLA should be 7% to 7.5%. As an ERLA burns up liftoff fuel and fires a DLSRR, it sheds at least 60% of its mass. A returning ERLA has a landing propellant fraction of at least 18%.
The typical specific impulse for landing rockets is 210 s. A landing fuel fraction of would give an ERLA a landing or hovering time of:
This is a more than sufficient landing time.
5. Example of an ERLA–DLSRR System
In this section, an example of an ERLA–DLSRR combination is presented. The parameters of such vehicles are described, and their performances are calculated.
5.1. ERLA, DLSRR, and Warhead Description
An ERLA is illustrated in Figure 1 below.

Figure 1.
Internal structure for a typical ERLA.
As the ERLA is ascending, the DLSRR acts as its aerodynamic nose. After the DLSRR is fired, the ERLA reaches the apogee and descends nose down. Although only two landing engines are shown in Figure 1, the ERLA has six landing engines. These engines point down during ascent in order to lower air resistance. During descent, the landing engines turn 180 °—thus, they continue pointing down.
A DLSRR is illustrated in Figure 2 below.
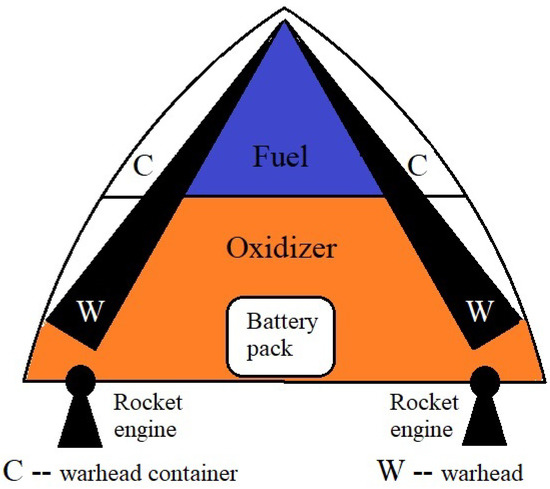
Figure 2.
DLSRR cross-section showing the main elements.
A DLSRR is relatively compact. It has the shape of an ogive cone. On the outside, it is covered by a heat shield. DLSRR heat shields are described in detail in Section 6.2.1 of [2]. The heat shield contains an Inconel sheet on the outside and a mineral wool on the inside. Most of the space inside the DLSRR is occupied by fuel and oxidizer tanks. A battery pack, guidance, and two or three warhead compartments are also inside the DLSRR. Each warhead compartment contains a relatively slim and long guided warhead.
As the DLSRR turns at an angle toward the airflow, both the air resistance and aerodynamic heating increase. Nevertheless, these factors do not present a significant problem, as the DLSRR enters autonomous flight at a relatively high altitude.
Two examples of warheads are illustrated in Figure 3 below. Both examples are taken from [2].
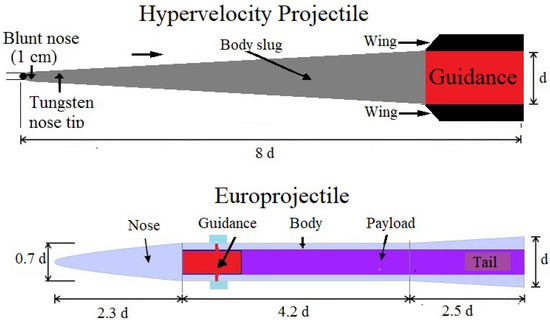
Figure 3.
The main elements of hypervelocity projectile and Europrojectile.
A hypervelocity projectile has a volume of
A Europrejectile has a volume of [2] (p. 15). Warhead (projectile) masses are proportional to the product of their volume and density. Tungsten seems to be the best material for warheads, as it is both dense and heat-resistant.
5.2. ERLA Parameters
An ERLA is shaped like a rocket with a diameter m, a height m, and a liftoff mass tons. An ERLA has a relatively high diameter-to-height ratio. This would add to the sturdiness of the construction and make landing easier. An ERLA has one main engine and six small landing engines. ERLA liftoff mass distribution is presented in Table 4 below:

Table 4.
Sample ERLA mass distribution.
The ERLA main engine uses EEC fuel and HP95 oxidizer. The oxidizer-to-fuel ratio is 2.6, and the combustion chamber temperature is 1810 °C. The combustion chamber pressure is 30 atm, and the expansion ratio is 6. The exhaust velocity is 2000 m/s at sea level and 2290 m/s in a vacuum. The liftoff rocket engine thrust is N or 27.8 tons at sea level and N or 32.3 tons in a vacuum.
5.3. ERLA Performance
The SciLab program ERLA.sce was used to calculate the position and velocity of an ERLA during flight. An ERLA is assumed to fly along a vertical line. The user has to input the RLA’s mass, diameter, drag coefficient, propellant mass fraction, sea level exhaust velocity, vacuum exhaust velocity, and propellant burning time. The ERLA drag coefficient was calculated using RASAero software [31]. The program ERLA.sce is a SciLab translation of a MatLab program VFirstStage.m, which the author has used in [1] (p. 29).
The ascent propellant mass fraction of 0.56 from Table 4, the exhaust velocities mentioned above, as well as the aerodynamic parameters of the ERLA were input into the program ERLA.sce, and the program was run. The program returns the vertical position and velocity of the ERLA at every time interval from liftoff to landing. The liftoff time was set to 0. DLSRRs were set to fire very soon after the main engine was turned off. The DLSRR firing altitude and initial velocity were computed by ERLA.sce. The apogee time and altitude were computed by the program as well. The landing engines were set to turn on when the ERLA descended to an altitude of about 4 km. The landing time of 20 s was assumed.
The flight schedule of an ERLA described in Table 4 is presented below:
−00:05 Main rocket engine starts.
00:00 Vertical liftoff using the main rocket engine.
01:00 Main rocket engine turns off. Altitude: 23 km; velocity: 1000 m/s up.
01:13 DLSRRs fired. Altitude: 35 km; velocity: 867 m/s up.
02:40 Flight apogee. Altitude: 73.1 km.
04:20 ERLA reaches the altitude of 25 km. Velocity: 930 m/s down.
04:48 Landing engines turned on. Altitude: 4.2 km; velocity: 415 m/s down.
05:08 ERLA landing.
The main measures of the ERLA performance are the DLSRR release altitude and velocity. A high release altitude simplifies the problems of air resistance and aerodynamic heating of the DLSRRs. A high release velocity enables DLSRRs to have a longer range and higher projectile impact velocity. As follows from the aforementioned schedule, the ERLA described in this work has a DLSRR release altitude of 35 km and a DLSRR release velocity of 867 m/s in the vertical direction.
5.4. DLSRR Parameters
As mentioned previously, the DLSRR has a mass of 1050 kg. The DLSRR is shaped like an ogive cone. During the ERLA ascent, the DLSRR acts as the rocket nose. The DLSRR liftoff mass distribution is presented in Table 5 below:

Table 5.
Sample DLSRR mass distribution.
The DLSRR uses the same fuel–oxidizer combination as the ERLA. The exhaust velocity is 2290 m/s. The combined thrust of the DLSRR rocket chambers is N or 1.61 tons in a vacuum.
Recall that the ERLA only provides the DLSRR with the vertical velocity component. In order to move forward, the DLSRR engines vector thrust not in the direction of flight, but at a deflection angle of the flight direction. Using the program Rocket.sce described below, we obtained optimal results with an °. This was the angle used in calculation.
5.5. DLSRR and Warhead Performance
The author has written the SciLab program Rocket.sce, which was used to calculate the position and velocity of an DLSRR during flight. Just as for the ERLA, the user has to input the DLSRR’s mass, diameter, drag coefficient, propellant mass fraction, sea level exhaust velocity, vacuum exhaust velocity, and propellant burning time. The DLSRR drag coefficient was calculated using RASAero software [31]. In addition, the user has to input the initial velocity and release altitude of the DLSRR, as well as the deflection angle. The program Rocket.sce is a slightly modified version of the program ERLA.sce. The modification accounts for nonzero initial velocity and altitude. It also accounts for the deflection of the rocket engine thrust.
The ascent propellant mass fraction of 0.56 from Table 5, the vacuum exhaust velocity, as well as the aerodynamic parameters of the DLSRR were input into the program Rocket.sce, and the program was run. The program returns the vertical position and velocity of the DLSRR at every time interval from liftoff to landing. The DLSRR firing time was 1 min 33 s—which was obtained from the previous subsection. The DLSRR apogee time, altitude, as well as forward position and velocity were computed by Rocket.sce. This was the time set for the DLSRR payload to be released. The payload impact time and forward position were calculated by Rocket.sce.
A DLSRR probable flight schedule is shown below:
01:13 DLSRRs fired. Altitude: 35 km; velocity: 867 m/s up.
02:43 Rocket burnout. Altitude: 122 km; velocity: 1500 m/s.
4:26 Flight apogee. Altitude: 174 km; velocity: 1114 m/s forward; horizontal location: 152 km forward.
4:26 Warheads (or warhead) are released. From here they continue a ballistic descent toward the target.
7:36 Impact.
The range was 362 km. The impact velocity depends on the type of warheads (or warhead). Theoretically, the maximal impact velocity is 2157 m/s for a projectile experiencing zero air resistance. For actual projectiles, the impact velocity is lowered by air resistance. The difference between the theoretical maximum impact velocity and an actual impact velocity is called the aerodynamic drag loss.
The impact velocity of a projectile was calculated by a SciLab program Impact.sce. The user inputs the projectile altitude and forward velocity at the flight apogee. The user also inputs the data for the projectile—mass, diameter, and drag coefficient. The projectile drag coefficient was calculated using RASAero software [31].
A hypervelocity projectile (HPV) shown in Figure 3 was constructed. It had a caliber of cm and a weight of 11.4 kg. It was assumed to be mostly composed of tungsten [2] (p. 5). If an HPV is among the warheads, then the impact velocity would be 1654 m/s, and, hence, the aerodynamic drag loss would be 503 m/s.
A version of an HPV with a 11.75 cm caliber has a length of 96.3 cm and a weight of 38.5 kg. The impact velocity would be 1820 m/s, and, hence, the aerodynamic drag loss would be 335 m/s. A DLSRR with a 210 kg payload can accommodate five such HPVs and a 17.5 kg packaging container.
A Europrojectile with a 10 cm caliber and a density of 11 g/cm3 is 90 cm long and weighs 39.0 kg. The impact velocity would be 2016 m/s, and, hence, the aerodynamic drag loss would be 141 m/s. A DLSRR with a 210 kg payload can accommodate five such Europrojectiles and a 15 kg packaging container.
6. Conclusions
In this work, it has been demonstrated that electrically pumped rocket engines can be used both for rocket launcher aircraft and drone-launched short range rockets. These engines have several important advantages over state-of-the-art rocket engines. Electrically pumped rocket engines have a relatively low cost, high reliability, and flexible thrust adjustment. Low cost is of primary importance to discardable DLSRRs. High reliability is of primary importance to ERLA liftoff engines, and flexible thrust adjustment is of primary importance to ERLA landing engines.
Electrically pumped rocket engines do have one disadvantage relative to state-of-the-art rocket engines. These engines have a slightly lower exhaust velocity than conventional rocket engines, which is caused by the relatively low combustion chamber pressure. Nevertheless, the advantages of electrically pumped rocket engines outweigh all the disadvantages.
The electric power consumption by the pump is directly proportional to the engine thrust and to the combustion chamber pressure. Thus, the maximum pressure within the rocket combustion chamber is limited by the available battery and motor power. Batteries with a specific power of 6.0 kW/kg and a specific energy of 100 Wh/kg are commercially available. Electric motors capable of sustaining a specific power of 8 kW/kg for up to two minutes are commercially available. Such motors and batteries can sustain a combustion chamber pressure given by (14):
The combination of EEC fuel and HP95 oxidizer was discussed in the paper. EEC is a mixture of 61% monoethanolamine, 30% ethanol, and 9% hydrated copper nitrate. HP95 consists of 95% hydrogen peroxide and 5% water. The combination is hypergolic, i.e., the fuel and oxidizer ignite on contact. An optimal combination for every type of ERLA and DLSRR remains to be determined by theoretical and experimental work.
It has been shown that an ERLA can land using several small electrically pumped rockets. Future generations of ERLAs equipped with advanced batteries and motors could land using electrically driven rotors. For state-of-the-art technology, rotor landing would require unreasonably large rotors.
Finally, an example of an ERLA–DLSRR system with a liftoff mass of 15 tons was presented. It ascends vertically and releases a DLSRR at an altitude of 35 km and an upward velocity of 867 m/s. The DLSRR has an initial mass of 1050 kg. DSLLR’s engines supply a horizontal component to its velocity. The DSLLR releases 210 kg of payload at the flight apogee with an altitude of 174 km and a forward velocity of 1114 m/s. The strike range can be up to 362 km. The impact velocity ranges from 1654 m/s to 2016 m/s depending on the warhead type.
This work is one of the first feasibility studies of military rockets with reusable first stage. The next step would consist of a detailed engineering design of such rockets. Then, a prototype of a military rocket with a reusable first stage can be built.
Funding
This research received no external funding.
Data Availability Statement
The author has used only publicly available data.
Conflicts of Interest
The author declares no conflict of interest.
Notations
| Latin Notations | |
| lifting area of all rotors | |
| d | warhead (projectile) caliber |
| ERLA rocket diameter | |
| landing fuel fraction for ERLA after it ascends and fires DLSRRs | |
| propellant mass fraction of the rocket at liftoff | |
| rocket engine thrust | |
| ERLA rocket height | |
| ERLA rocket liftoff mass | |
| fuel mass flow rate of combustion chamber | |
| oxidizer mass flow rate of combustion chamber | |
| rotorcraft mass | |
| liftoff rocket mass | |
| combustion chamber pressure | |
| fuel inlet pressure | |
| oxidizer inlet pressure | |
| oxidizer outlet pressure | |
| oxidizer outlet pressure | |
| ideal power of rotorcraft rotors | |
| electric power consumption by pump motor | |
| power of rotors lifting an electric rocket launcher aircraft | |
| power supplied to the compressor shaft | |
| specific power available for ERLA during landing | |
| specific power of an ideal rotorcraft | |
| specific power needed by ERLA during landing | |
| thrust-specific electric power | |
| fuel inlet pressure ratio | |
| oxidizer-to-fuel mass ratio | |
| oxidizer inlet pressure ratio | |
| rocket firing time | |
| Europrojectile volume | |
| exhaust velocity | |
| flight-time-averaged exhaust velocity | |
| fuel volumetric flow rate of combustion chamber | |
| hypervelocity projectile volume | |
| oxidizer volumetric flow rate of combustion chamber | |
| Greek Notations | |
| angle by which DLSRR engine thrust direction | |
| is ahead of DLSRR flight direction | |
| inverter efficiency | |
| fuel pump efficiency | |
| motor efficiency | |
| oxidizer pump efficiency | |
| power coefficient | |
| water density of 1000 | |
| air density | |
| fuel density | |
| oxidizer density | |
| rotorcraft disk loading |
References
- Shubov, M.V. The Concept and Theoretical Performance of Vertical Rocket Launcher Aircraft. Am. J. Aerosp. Eng. 2021, 8, 27–44. Available online: https://article.sciencepublishinggroup.com/pdf/10.11648.j.ajae.20210801.14.pdf (accessed on 29 May 2023).
- Shubov, M.V. Drone Launched Short Range Rockets. Aerospace 2020, 7, 76. [Google Scholar] [CrossRef]
- Parker, S.; Pang, A. The M270 Multiple Rocket Launcher; Capstone Press: Mankato, MN, USA, 2008. [Google Scholar]
- US Department of Defense (DoD). In Annual Report to Congress: Military and Security Developments Involving the People’s Republic of China; Office of the Secretary of Defense: Washington, DC, USA, 2017.
- Woodward, D. Space Launch Vehicle Design. Master’s Dissertation, Department of Mechanical and Aerospace Engineering University of Texas, Arlington, TX, USA, 2017. [Google Scholar]
- He, Y.; Liu, Y.; Ni, Z.; Wu, Y.; Yang, J. Concept and key technology analysis of electric pump-fed liquid propellant rocket engine. IOP Conf. Ser. Earth Environ. Sci. 2021, 781, 042016. [Google Scholar]
- Rocket Lab. Electron Dedicated Access to Space for Small Satellites. Available online: https://www.rocketlabusa.com/launch/electron/ (accessed on 27 March 2023).
- Cohen, A.; Fernando, C.; Goyal, R.; Reiche, C. Advanced Air Mobility: Demand Analysis and Market Potential of the Airport Shuttle and Air Taxi Markets. Sustainability 2021, 13, 7421. [Google Scholar] [CrossRef]
- Bacchini, A.; Cestino, E. Electric VTOL Configurations Comparison. Aerospace 2019, 6, 26. [Google Scholar] [CrossRef]
- Sripad, S.; Viswanathan, V. The Promise of Energy-Efficient Battery-Powered Urban Aircraft. Proc. Natl. Acad. Sci. USA 2021, 118, e2111164118. [Google Scholar] [CrossRef] [PubMed]
- Dillow, C. Rocket Lab Aims to Put Small Satellites in Space for Less. Fortune. Available online: https://fortune.com/2015/04/17/rocket-lab-satellites-space/ (accessed on 17 April 2015).
- Rachov, P.; Tacca, H.; Lentini, D. Electric Feed Systems for Liquid Propellant Rocket Engines, Buenos Aires, December 6th, 2010. Available online: https://www.aacademica.org/hernan.emilio.tacca/9.pdf (accessed on 29 May 2023).
- Deeken, J.C.; Hahn, R.H.S.; Waxenegger-Wilfing, G. Studies on Electric Pump-Fed Liquid Rocket Engines for Micro-Launcher. In Proceedings of the Space Propulsion 2018 Conference, Seville, Spain, 14–18 May 2018. [Google Scholar]
- Socokin Power Direct, Amazon.com. Available online: https://www.amazon.com/stores/SocokinPowerDirect/page/27F6AE8E-048F-4E1D-A25F-204C37503826 (accessed on 27 March 2023).
- Tindling Store, Amazon.com. Available online: https://www.amazon.com/stores/TINDLING/page/55A72056-7F9F-4801-B018-7B8C878EEEA2 (accessed on 27 March 2023).
- Zeee Power Direct, Amazon.com. 2022. Available online: https://www.amazon.com/stores/ZeeePowerDirect/page/3FBF2C81-B132-4D9A-8110-B46EACED54FD (accessed on 27 March 2023).
- Yowoo Power Store, Amazon.com. 2022. Available online: https://www.amazon.com/stores/Yowoopower/page/E5281F98-FD65-4825-9863-B7A40F4C8A1D (accessed on 27 March 2023).
- Turnigy, Amazon.com. 2022. Available online: https://www.amazon.com/s?k=Turnigy (accessed on 27 March 2023).
- Thunder Power. Available online: https://www.thunderpowerrc.com/ (accessed on 27 March 2023).
- Stux, A.; Swider-Lyons, K. Survey of Commercial Small Lithium Polymer Batteries; Technical Report NRL/MR/6110-07-9073; Naval Research Laboratory: Washington, DC, USA, 2007. [Google Scholar]
- Chargery. Available online: http://www.chargery.com/ (accessed on 27 March 2023).
- Melasta Battery Co., Ltd. 2022. Available online: https://www.melasta.com/ (accessed on 27 March 2023).
- Emrax Electric Motors/Generators. Available online: https://emrax.com/e-motors/ (accessed on 27 March 2023).
- Maschio, L.J.; Marques, R.I.; Meyer, W.M.; Pereira, L.G.F.; Vieira, R. A DOE study on the hypergolicity of hydrogen peroxide with a rocket liquid fuel based on monoethanolamine and ethanol. Int. J. Energetic Mater. Chem. Propuls. 2018, 17, 137–145. [Google Scholar]
- Araújo, E.; Gouvea, L.; Maschio, L.J.; Pereira, L.G.; Vieira, R. Assessing the Performance of a Green Liquid Fuel Hypergolic with Hydrogen Peroxide in a 50 N Bipropellant Thruster. Int. J. Energetic Mater. Chem. Propuls. 2021, 20, 21–30. [Google Scholar]
- Ponomarenko, I.A. Rocket Propulsion Analysis; V 1.2.6, Lite Edition 2011; Cologne, Germany, 2011; Available online: http://www.propulsion-analysis.com (accessed on 27 March 2023).
- Finch, H. Price and Market Trends: Europe Ethanolamines Stable to Firm. ECA. 2016. Available online: https://www.icis.com/explore/resources/news/2016/09/09/10032659/price-and-market-trends-europe-ethanolamines-stable-to-firm/ (accessed on 27 March 2023).
- Triethyl Aluminum Price Trend and Forecast. ChemAnalyst. 2021. Available online: https://www.chemanalyst.com/Pricing-data/triethylaluminium-teal-1189 (accessed on 27 March 2023).
- Jiang, Y.; Zhang, B. Numerical Assessment of a High Disk Loading Annular Lift Fan Aircraft. J. Am. Helicopter Soc. 2018, 63, 1–12. [Google Scholar] [CrossRef]
- Coleman, C.P. A Survey of Theoretical and Experimental Coaxial Rotor Aerodynamic Research; NASA Technical Paper 3675; National Aeronautics and Space Administration: Washington, DC, USA, 1997.
- Rogers, C.E.; Cooper, D. Rocket Aerodynamic Analysis and Flight Simulation Software V 1.0.1.; Rogers Aeroscience: Lancaster, CA, USA, 2016; Available online: http://www.rasaero.com/ (accessed on 27 March 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).