A Hybrid of NARX and Moving Average Structures for Exhaust Gas Temperature Prediction of Gas Turbine Engines
Abstract
1. Introduction
- An improved LSTM network, i.e., FAE-LSTM, is developed to construct the NARX structure for the long-term prediction of EGT.
- A novel hybrid prediction model is developed by combining the NARX and moving average structures, for the first time in the literature, for EGT prediction of gas turbine engines.
- A real flight process dataset is used to evaluate the proposed method, which improves the high practical value of the proposed method.
2. Methodology
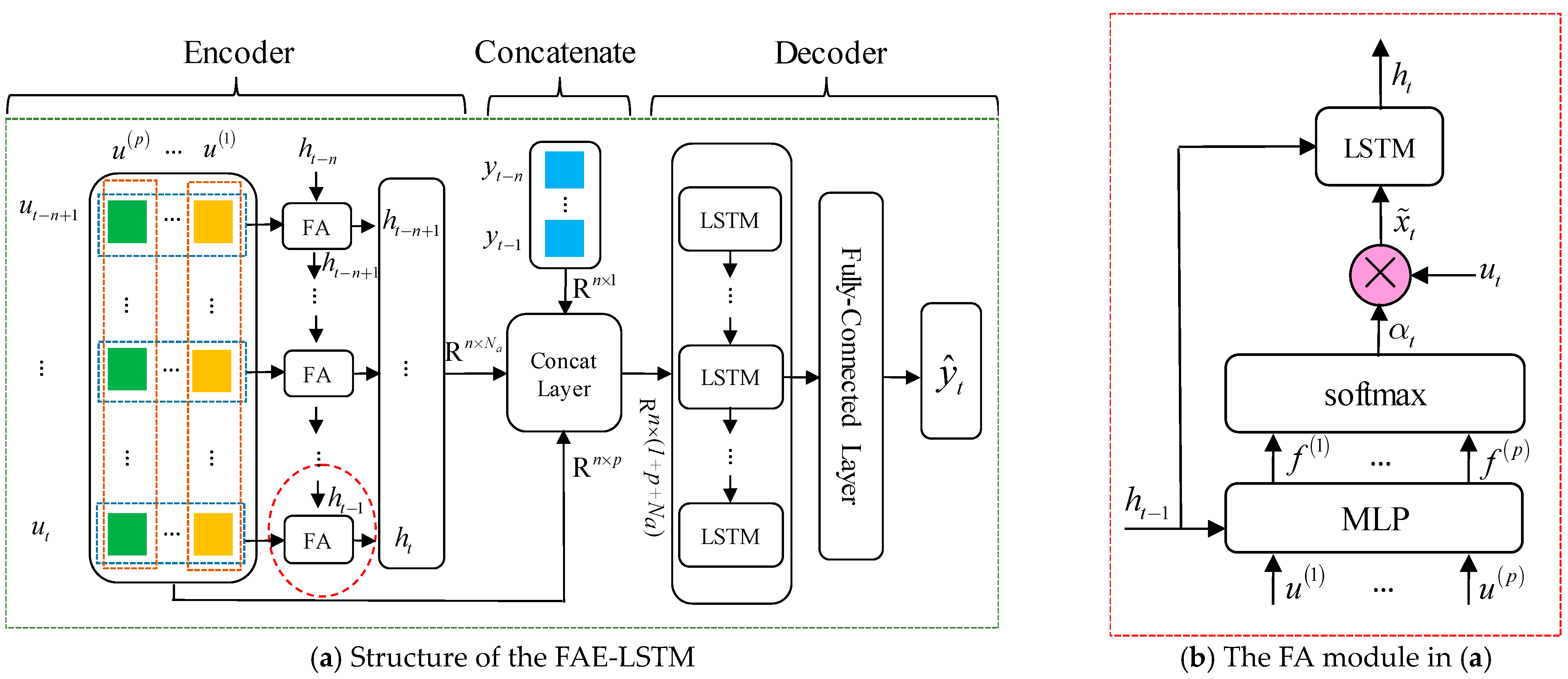
2.1. The Feature Attention-Enhanced-LSTM-Based NARX Structure
2.2. Vanilla LSTM-Based Moving Average Model
2.3. Improved Hybrid Model for EGT Prediction
3. Experiment Settings
3.1. The Flight Dataset
3.2. Network Settings
3.3. Evaluation Metrics
4. Results and Analysis
4.1. Comparision Results
4.2. Analysis of the Network Structure of the Single FAE-LSTM Model
4.3. Impact of the Input Features on the FAE-LSTM Performance
- Baseline,
- Baseline+ 1 additional sensor,
- Baseline+ 2 additional sensors,
- Baseline+ 3 additional sensors.
5. Conclusions
- (1)
- N1 and Wf substantially improve the prediction performance among the measurement input features, while N2 yields only a marginal performance improvement.
- (2)
- Among all the single models, our FAE-LSTM performs best, which demonstrates that the feature attention module and the concatenate layer of our FAE-LSTM can improve the long-term prediction performance effectively. In addition, the FAE-LSTM is not sensitive to the input sequence length and the number of neuron cells.
- (3)
- Compared to the single model, the proposed hybrid can reduce the RMSE and MAE by at least 13.23% and 18.47%, respectively. The hybrid model has the best performance in all flight phases.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| ALT | Flight altitude(ft) |
| ANN | Artificial neural network |
| AR | Autoregressive |
| ARIMA | Autoregressive integrated moving average |
| ARMA | Autoregressive moving average |
| DA-RNN | Dual attention-based recurrent neural networks |
| DSTP-RNN | Dual-stage two-level attention cycle network |
| EGT | Exhaust gas temperature(°R) |
| EKF | Extended Kalman filter |
| FAE-LSTM | Feature attention-enhanced LSTM network |
| FDI | Fault detection and isolation |
| LSTM | Long short-term memory |
| MA | Moving average |
| MAE | Mean absolute error |
| MN | Mach Number |
| MPR | Multiple polynomial regression |
| N1 | Fan speed(rpm) |
| N2 | Core speed(rpm) |
| NARX | Nonlinear autoregressive with exogenous inputs |
| NARX-NN | NARX neural network |
| PCC | Pearson’s linear correlation coefficient |
| T0 | Ambient temperature(°R) |
| Greek | |
| α | The attention weight |
| σ | Standard deviation |
| Latin | |
| b | Biases of the networks |
| c | Cell state of RNN networks |
| f() | Model function |
| f | Forget gate in LSTM cell |
| g | Candidate gate in LSTM cell |
| h | Hidden state of RNN networks |
| i | Input gate in LSTM cell |
| o | Output gate in LSTM cell |
| u | Output signal of Models |
| W,V | Weights of the neural networks |
| y | Output signal of Models |
| z | Encoder output |
| Superscript | |
| Train | Training data |
| (k) | The k-th feature |
| Test | Testing data |
| Subscript | |
| t | Time step index |
| f | Forget gate in LSTM cell |
| g | Candidate gate in LSTM cell |
| i | Input gate in LSTM cell |
| o | Output gate in LSTM cell |
| z | Encoder output |
References
- Chao, M.A.; Kulkarni, C.; Goebel, K.; Fink, O. Fusing physics-based and deep learning models for prognostics. Reliab. Eng. Syst. Saf. 2022, 217, 107961. [Google Scholar] [CrossRef]
- Alleyne, A.; Hedrick, J.K. Nonlinear adaptive control of active suspensions. IEEE Trans. Control Syst. Technol. 1995, 3, 94–101. [Google Scholar] [CrossRef]
- Volponi, A.J. Gas turbine engine health management: Past, present, and future trends. J. Eng. Gas Turbines Power 2014, 136, 051201. [Google Scholar] [CrossRef]
- Fentaye, A.D.; Gilani, S.I.U.H.; Baheta, A.T. Gas turbine gas path diagnostics: A review. MATEC Web Conf. EDP Sci. 2016, 74, 00005. [Google Scholar] [CrossRef]
- Rezaeianjouybari, B.; Shang, Y. Deep learning for prognostics and health management: State of the art, challenges, and opportunities. Measurement 2020, 163, 107929. [Google Scholar] [CrossRef]
- Fentaye, A.D.; Baheta, A.T.; Gilani, S.I.; Kyprianidis, K.G. A review on gas turbine gas-path diagnostics: State-of-the-art methods, challenges and opportunities. Aerospace 2019, 6, 83. [Google Scholar] [CrossRef]
- Volponi, A.; Simon, D.L. Enhanced Self-Tuning On-Board Real-Time Model (eSTORM) for Aircraft Engine Performance Health Tracking; Glenn Research Center: Cleveland, OH, USA, 2008.
- Naderi, E.; Meskin, N.; Khorasani, K. Nonlinear fault diagnosis of jet engines by using a multiple model-based approach. J. Eng. Gas Turbines Power 2012, 134, 011602. [Google Scholar] [CrossRef]
- Shang, L.; Liu, G. Sensor and actuator fault detection and isolation for a high performance aircraft engine bleed air temperature control system. IEEE Trans. Control Syst. Technol. 2011, 19, 1260–1268. [Google Scholar] [CrossRef]
- Daroogheh, N.; Meskin, N.; Khorasani, K. A dual particle filter-based fault diagnosis scheme for nonlinear systems. IEEE Trans. Control Syst. Technol. 2017, 26, 1317–1334. [Google Scholar] [CrossRef]
- Ahsan, S.; Lemma, T.A.; Muhammad, M. Prognosis of gas turbine remaining useful life using particle filter approach. Mater. Werkst. 2019, 50, 336–345. [Google Scholar] [CrossRef]
- Tayarani-Bathaie, S.S.; Khorasani, K. Fault detection and isolation of gas turbine engines using a bank of neural networks. J. Process Control 2015, 36, 22–41. [Google Scholar] [CrossRef]
- Shahnazari, H. Fault diagnosis of nonlinear systems using recurrent neural networks. Chem. Eng. Res. Des. 2020, 153, 233–245. [Google Scholar] [CrossRef]
- Bai, M.; Liu, J.; Chai, J.; Zhao, X.; Yu, D. Anomaly detection of gas turbines based on normal pattern extraction. Appl. Therm. Eng. 2020, 166, 114664. [Google Scholar] [CrossRef]
- Ibrahem, I.M.A.; Akhrif, O.; Moustapha, H.; Staniszewski, M. An Ensemble of Recurrent Neural Networks for Real Time Performance Modeling of Three-Spool Aero-Derivative Gas Turbine Engine. J. Eng. Gas Turbines Power 2021, 143, 101004. [Google Scholar] [CrossRef]
- Zhang, H.; Dong, K. Prediction of Aero-Engine Exhaust Gas Temperature Based on Autoregressive Integrated Moving Average Model. In Proceedings of the 2017 2nd International Conference on Automation, Mechanical Control and Computational Engineering (AMCCE 2017), Beijing, China, 25–26 March 2017; Atlantis Press: Dordrecht, The Netherlands, 2017; pp. 477–480. [Google Scholar]
- Koleini, I.; Roudbari, A.; Marefat, V. EGT prediction of a micro gas turbine using statistical and artificial intelligence approach. IEEE Aerosp. Electron. Syst. Mag. 2018, 33, 4–13. [Google Scholar] [CrossRef]
- Zhou, W. Aero-engine exhaust gas temperature prediction based on adaptive disturbance quantum-behaved particle swarm optimization. Adv. Mech. Eng. 2022, 14, 16878132221119044. [Google Scholar] [CrossRef]
- Ullah, S.; Li, S.G.; Khan, K.; Khan, S.; Khan, I.; Eldin, S.M. An Investigation of Exhaust Gas Temperature of Aircraft Engine using LSTM. IEEE Access 2023, 11, 5168–5177. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Qin, Y.; Song, D.; Chen, H.; Cheng, W.; Jiang, G.; Cottrell, G. A dual-stage attention-based recurrent neural network for time series prediction. In Proceedings of the 26th International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017; pp. 2627–2633. [Google Scholar]
- Liu, Y.; Gong, C.; Yang, L.; Chen, Y. DSTP-RNN: A dual-stage two-phase attention-based recurrent neural network for long-term and multivariate time series prediction. Expert Syst. Appl. 2020, 143, 113082. [Google Scholar] [CrossRef]
- Pham, H.T.; Yang, B.S. A hybrid of nonlinear autoregressive model with exogenous input and autoregressive moving average model for long-term machine state forecasting. Expert Syst. Appl. 2010, 37, 3310–3317. [Google Scholar] [CrossRef]
- Cho, W.; Kim, S.; Na, M.; Na, I. Forecasting of tomato yields using attention-based LSTM network and ARMA model. Electronics 2021, 10, 1576. [Google Scholar] [CrossRef]
- Banihabib, M.E.; Ahmadian, A.; Jamali, F.S. Hybrid DARIMA-NARX model for forecasting long-term daily inflow to Dez reservoir using the North Atlantic Oscillation (NAO) and rainfall data. GeoResJ 2017, 13, 9–16. [Google Scholar] [CrossRef]
- Kaytez, F. A hybrid approach based on autoregressive integrated moving average and least-square support vector machine for long-term forecasting of net electricity consumption. Energy 2020, 197, 117200. [Google Scholar] [CrossRef]
- Chen, S.; Billings, S.A.; Grant, P.M. Non-linear system identification using neural networks. Int. J. Control 1990, 51, 1191–1214. [Google Scholar] [CrossRef]
- Kumpati, S.N.; Kannan, P. Identification and control of dynamical systems using neural networks. IEEE Trans. Neural Netw. 1990, 1, 4–27. [Google Scholar]
- Kirchgässner, G.; Wolters, J.; Hassler, U. Introduction to Modern Time Series Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Li, Y.G.; Nilkitsaranont, P. Gas turbine performance prognostic for condition-based maintenance. Appl. Energy 2009, 86, 2152–2161. [Google Scholar] [CrossRef]
- Atasoy, V.E.; Suzer, A.E.; Ekici, S. A comparative analysis of exhaust gas temperature based on machine learning models for aviation applications. J. Energy Resour. Technol. 2022, 144, 082101. [Google Scholar] [CrossRef]
- Obilor, E.I.; Amadi, E.C. Test for significance of Pearson’s correlation coefficient. Int. J. Innov. Math. Stat. Energy Policies 2018, 6, 11–23. [Google Scholar]
- Simon, D.L.; Rinehart, A.W. Sensor selection for aircraft engine performance estimation and gas path fault diagnostics. J. Eng. Gas Turbines Power 2016, 138, 071201. [Google Scholar] [CrossRef]

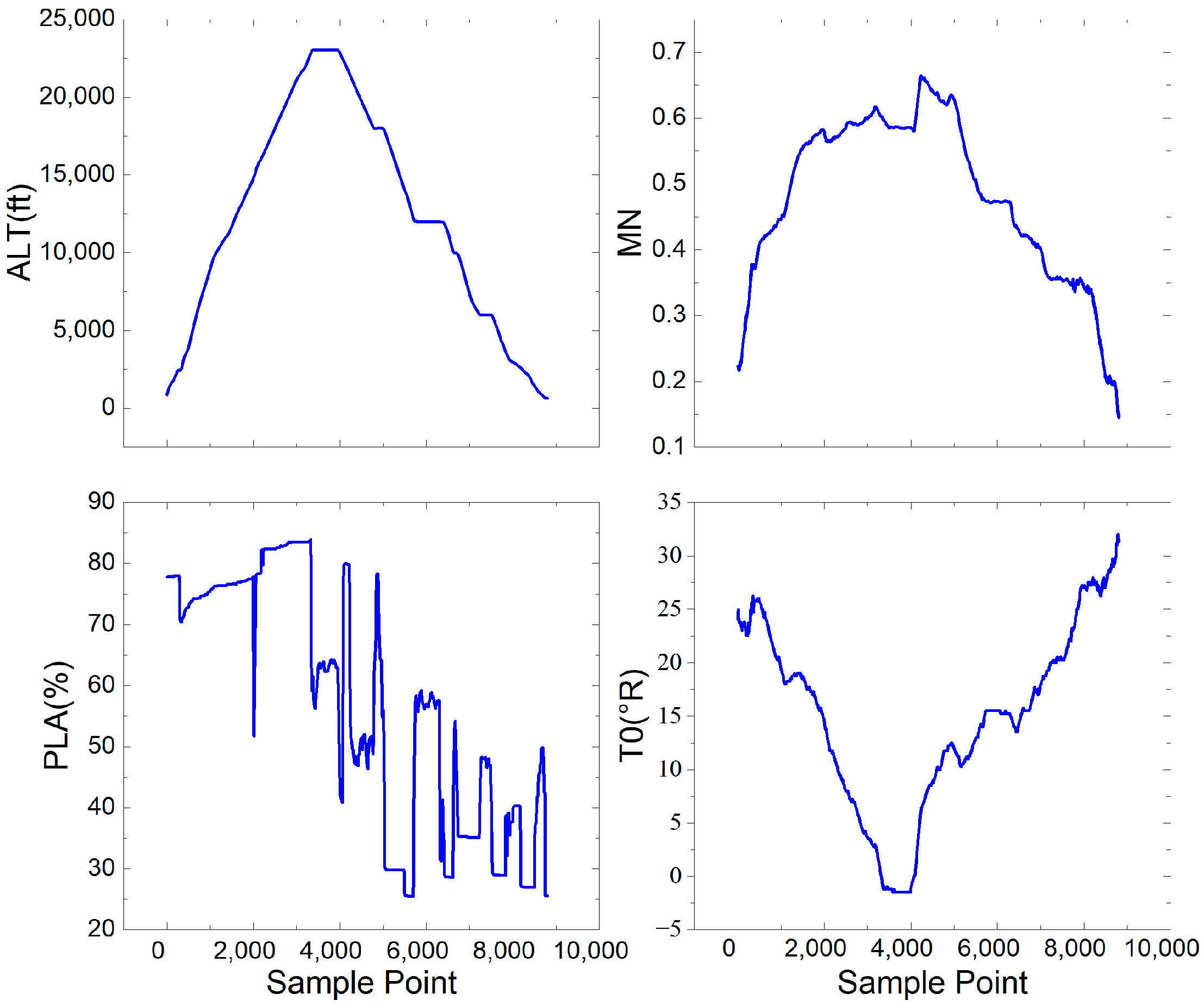





| # | Symbol | Description | Unit |
|---|---|---|---|
| 1 | ALT | Flight altitude | Ft |
| 2 | MN | Mach Number | - |
| 3 | PLA | Power lever angle | % |
| 4 | T0 | Ambient temperature | °R |
| 5 | Wf | Fuel flow | pps |
| 6 | N1 | Fan speed | rpm |
| 7 | N2 | Core speed | rpm |
| 8 | EGT | Exhaust gas temperature | °R |
| Dataset | No. of Cycles | No. of Samples |
|---|---|---|
| Training | 40 | 299,144 |
| Testing | 6 | 41,036 |
| Models | RMSE | MAE |
|---|---|---|
| NARX-NN [15] | 0.0709 | 0.0621 |
| LSTM [19] | 0.0451 | 0.0364 |
| DA-RNN [22] | 0.0516 | 0.0296 |
| DSTP-RNN [21] | 0.0469 | 0.0408 |
| FAE-LSTM | 0.0378 | 0.0287 |
| Our hybrid model | 0.0328 | 0.0234 |
| Models | RMSE | MAE |
|---|---|---|
| Without FA | 0.0513 ± 0.021 | 0.0388 ± 0.013 |
| Without concatenate layer | 0.0464 ± 0.023 | 0.0312 ± 0.019 |
| FAE-LSTM | 0.0457 ± 0.012 | 0.0292 ± 0.018 |
| Inputs | RMSE |
|---|---|
| [ALT, MN, T0, PLA] | 0.224 ± 0.143 |
| [ALT, MN, T0, PLA, Wf] | 0.174 ± 0.137 |
| [ALT, MN, T0, PLA, N1] | 0.174 ± 0.137 |
| [ALT, MN, T0, PLA, N2] | 0.214 ± 0.059 |
| [ALT, MN, T0, PLA, Wf, N1] | 0.047 ± 0.008 |
| [ALT, MN, T0, PLA, Wf, N2] | 0.180 ± 0.124 |
| [ALT, MN, T0, PLA, N1, N2] | 0.091 ± 0.019 |
| [ALT, MN, T0, PLA, Wf, N1, N2] | 0.046 ± 0.012 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, S.; Wu, Y.; Zheng, H.; Gou, L. A Hybrid of NARX and Moving Average Structures for Exhaust Gas Temperature Prediction of Gas Turbine Engines. Aerospace 2023, 10, 496. https://doi.org/10.3390/aerospace10060496
Ma S, Wu Y, Zheng H, Gou L. A Hybrid of NARX and Moving Average Structures for Exhaust Gas Temperature Prediction of Gas Turbine Engines. Aerospace. 2023; 10(6):496. https://doi.org/10.3390/aerospace10060496
Chicago/Turabian StyleMa, Shuai, Yafeng Wu, Hua Zheng, and Linfeng Gou. 2023. "A Hybrid of NARX and Moving Average Structures for Exhaust Gas Temperature Prediction of Gas Turbine Engines" Aerospace 10, no. 6: 496. https://doi.org/10.3390/aerospace10060496
APA StyleMa, S., Wu, Y., Zheng, H., & Gou, L. (2023). A Hybrid of NARX and Moving Average Structures for Exhaust Gas Temperature Prediction of Gas Turbine Engines. Aerospace, 10(6), 496. https://doi.org/10.3390/aerospace10060496






