Assessment of the Vortex Feature-Based Vorticity Confinement Method Applied to Rotor Aerodynamics and Aeroacoustics

Abstract

The accurate prediction of helicopter rotor aerodynamics and aeroacoustics using Computational Fluid Dynamics (CFD) techniques still remains a challenge, as the over-dissipation of numerical schemes results in a higher diffusive rate of rotor wake and vortices than what can be expected from the fluid governing equations. To alleviate this issue, a vortex feature-based vorticity confinement (FVC2-L2) method that combines the locally normalized ${\lambda }_2$ vortex detection method with the standard second vorticity confinement (VC2) scheme is presented to counterbalance the truncation error introduced by the numerical discretization of the convective term while avoiding the over-confinement inside the boundary layer. The FVC2-L2 scheme is adopted for helicopter rotor aerodynamic and aeroacoustic predictions through its implementation in the multi-block structured grid CFD solver ROSITA and coupling with the aeroacoustic code ROCAAP based on the permeable surface Ffowcs Williams–Hawkings (PS-FWH) equation. This approach is assessed in helicopter rotor flows via three databases. Firstly, the well-documented HART-II rotor in the baseline condition is used to evaluate the capability of the presented VC scheme in blade–vortex interaction (BVI) phenomena prediction. Subsequently, the UH-1H non-lifting hovering rotor and the AH-1/OLS low-speed descending flight rotor are adopted for assessment of such a method in aeroacoustics. The benefits of the FVC2-L2 scheme in terms of aerodynamics prediction, wake preservation, and noise signal prediction are well demonstrated by comparison with the experimental data and the results obtained without VC schemes. Particularly, the FVC2-L2 scheme mainly improves the highly unsteady airloads prediction, and results in an improvement of BVI noise prediction by more than 5 dB with respect to the case without VC schemes for AH-1/OLS rotor case. Additionally, some shortcomings of the approach are noticed in engineering applications. On the basis of a simplified convective vortex, some provisional guidelines on the required ${\epsilon }_o$ value in terms of number of cells per vortex diameter are provided: an ${\epsilon }_o$ value ranging from 0.01 to 0.04 for grids which may represent the vortex core diameter with 6 to 12 cells.

1. Introduction

The rotor vortical wake is among the most complex fluid dynamic structures in the helicopter unsteady flow field and strongly affects the flight performances of the helicopter. For instance, the shed blade tip vortices in the rotor wake may intersect with the following rotor blade causing the blade–vortex interaction (BVI) phenomenon, which significantly affects the blade airloads and results in the obtrusive noise levels. The rotor-induced wake that interacts with the surrounding obstacles can typically degrade the helicopter performance and creates a hazardous environment. The interference of the main/tail rotor/fuselage negatively influences the aerodynamics of the vehicle. For these reasons, accurate modeling of the rotor vortical flow is essential for helicopter rotor aerodynamics and aeroacoustics prediction.

Over the last three decades, Computational Fluid Dynamics (CFD) simulations have gained popularity due to their capability of resolving most phenomena of interest. However, an inherent issue of these simulations is that the vortex features are prematurely deformed and dissipated due to the dissipative nature of numerical schemes, this makes the employment of such techniques in helicopter rotor flows unsatisfactory. In recent years, four major classes of numerical methods, including scale-resolving simulation (SRS) [1,2,3], high-order spatial discretization schemes [4,5,6,7], vorticity confinement (VC) method [8,9,10,11], and grid refinement techniques [12,13,14] have emerged to help improve the capability of preserving vortices in CFD simulations. Nevertheless, some of them are often prohibitive for industrial applications due to the substantial computational time and resources. For example, the SRS approaches are capable of providing a more detailed description of vortices but require a large grid system to exploit the full potential of this technique. Even if the high-order schemes are able to alleviate the over-dissipation of the vortical structure with appropriate grid densities, the computation of high-order derivatives or the construction of complex stencils may result in additional computational costs. In terms of grid refinement techniques, Automatic Mesh Refinement (AMR), the most representative method for grid refinement, is also computationally expensive because of the additional mesh points created in the refined region. In contrast, the VC method presents potential advantages in the computational efficiency of preserving vortices as the grid system could be maintained at a moderate level. As a result, increasing numbers of research have focused on such an approach.

Vorticity confinement is a concept that allows preventing a vortex from being inorderly diffused by adding an ad hoc anti-diffusion term into the standard Euler/Navier–Stokes equations. It has proved effective in simulating vortex-dominated flows, especially for cases without satisfactory mesh sizes. Currently, two formulations of the VC method have been developed and briefly referred to as VC1 [15] and VC2 [16].

In the first vorticity confinement (VC1) scheme, the VC term is derived from the first derivative of velocity. It transports vorticity in the direction of increasing vorticity magnitude gradient, counteracting the spreading effect due to the numerical dissipation. Over the past decades, the VC1 formulation became attractive in the simulation of vortex-dominated flows due to its algorithmical simplicity and efficiency, especially for helicopter rotor flows. For instance, Steinhoff et al. [17] first applied the VC1 to hovering HELIX I rotor flows and received a promising result. Biava and Vigevano [8] investigated the variation of confinement parameters on thrust coefficient for ONERA 7A four-bladed rotor flows in both hover and forward flight. Even though the VC1 scheme is widely adopted, it suffers from two disadvantages. The first is related to a difficulty in the theoretical analysis of its properties, the singularity of VC1 term at the vortex center. The second concerns the conservation of the governing equations while using the VC1 term.

In order to correct the drawback of the VC1 scheme, the second vorticity confinement (VC2) formulation was later introduced [16]. The VC2 formulation is derived from the second derivative of velocity with no singularity at the vortex core, which allows more detailed analytical investigations on its properties [18,19] and with an exact conservative expression, which makes it easy to extend to higher-order schemes [20,21,22]. In recent years, the capabilities of VC2 formulation and its higher-order schemes on vorticity preservation and computational efficiency have been demonstrated by some studies [9,10,23] carried out in helicopter rotor flows.

Initially, the VC1 method was developed for incompressible flows. After several attempts [24,25], Hu et al. [26] presented a more stable VC correction for compressible simulations by interpreting Steinhoff’s VC1 formulation as a body force source term and adding to both the momentum and energy equations. However, additional studies [18,27] found that far better results could be obtained when the VC term was removed from the energy conservation equation. For this reason, Costes [18] suggested that the contributions of the VC term would only be treated as purely numerical corrections to the momentum conservation equation rather than physical source terms. On this basis, the compressible VC1 and VC2 schemes were successfully applied to a wide range of cases.

Besides the compressible extensions of the VC schemes, another primary challenge is the determination of the confinement parameter $\epsilon$, which controls the magnitude of the negative diffusion in the vorticity confinement, since a mistake in the choice of $\epsilon$ would result in the non-physical solutions and affect the stability of numerical simulation. To maintain dimensional consistency with the momentum terms, three scaled confinement parameters were derived by Lohner et al. [28] through dimensional analysis to ensure that they had the dimensions of velocity. Robinson [29] proposed a scaling expression based on helicity by extending Lohner’s work. Butsuntorn and Jameson [30] further extended the helicity formulation of Robinson by including a non-dimensional scaling parameter based on the local mesh size. In most studies, the $\epsilon$ value comes from a trial-and-error procedure, which is less efficient. Several attempts have been put forward to remove the empiricism of confinement parameter selection. Costes and Kowani [18,31] derived a dynamic confinement parameter related to the local vorticity. Hahn and Iaccarino [32] introduced a new adaptive VC parameter related to the difference between central and upwind discretization of the convection terms. More recently, Povitsky A et al. [33] employed the TVD (Total Variation Diminishing) limiters to reduce the sensitivity of confinement parameter values. Nonetheless, this problem is still not completely solved due to the non-conservation of the VC2 scheme introduced by the $\epsilon$ value varying in space.

In spite of the number of research employing VC to balance the excessive diffusion of vortical flows, there still remains a fundamental problem. In the standard VC method, the non-zero vorticity magnitude is adopted for detecting vortex features by default. However, it is not appropriate to use vorticity magnitude for vortex detection, particularly at the boundary and shear layer regions where there is no vortex but the vorticity magnitude is not equal to zero. It will cause over-confinement and spurious vortical structures in the results. To eliminate this issue, some studies [10,34,35] combined the standard VC method with the advanced vortex feature detection techniques, resulting in the vortex feature-based VC (FVC1 or FVC2) approach. 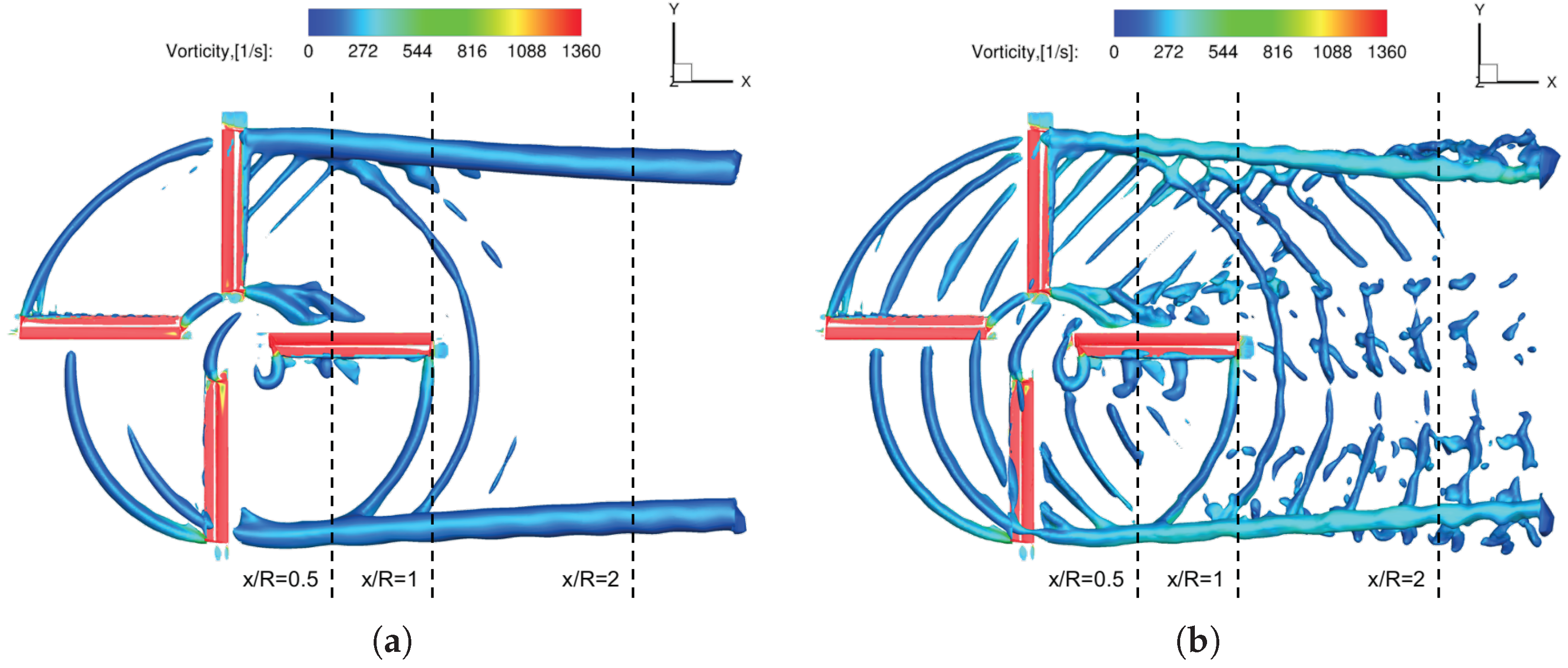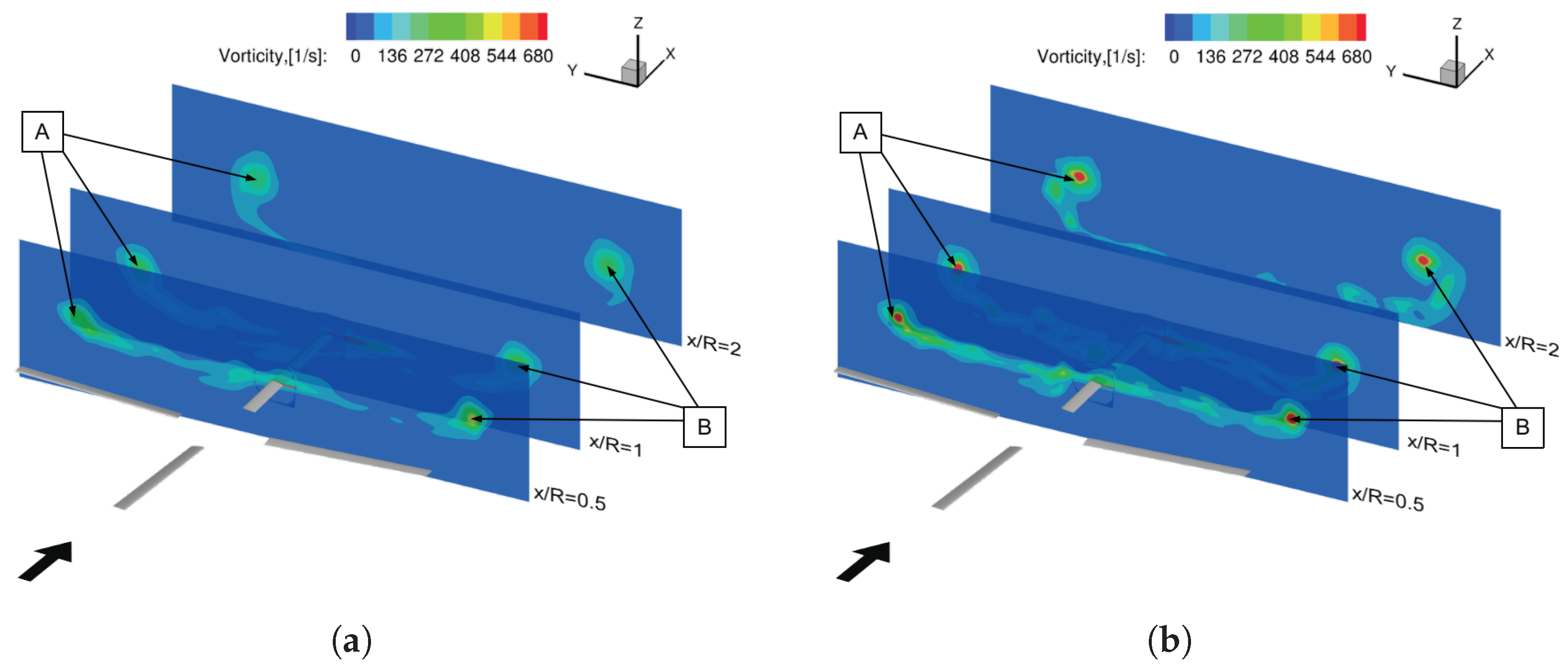In our previous work [11], the benefits of such treatment for 3D vortex-dominated flows in terms of computational stability, aerodynamic prediction, vorticity preservation, and computational efficiency, were explicitly demonstrated by comparing the standard VC2 scheme with two FVC2 formulations combining different vortex feature detection techniques (Q and ${\lambda }_2$). Moreover, the ${\lambda }_2$-based VC2 (FVC2-L2) scheme expressed a higher resolution of the vortical structure, more robust computational procedure, more accurate aerodynamic loads, and almost the same computational time cost if compared to the Q-based VC2 (FVC2-Q) scheme. Nevertheless, the better-performing FVC2-L2 scheme still needs to be further evaluated for helicopter rotor aerodynamic and aeroacoustic predictions, especially for the BVI phenomenon.

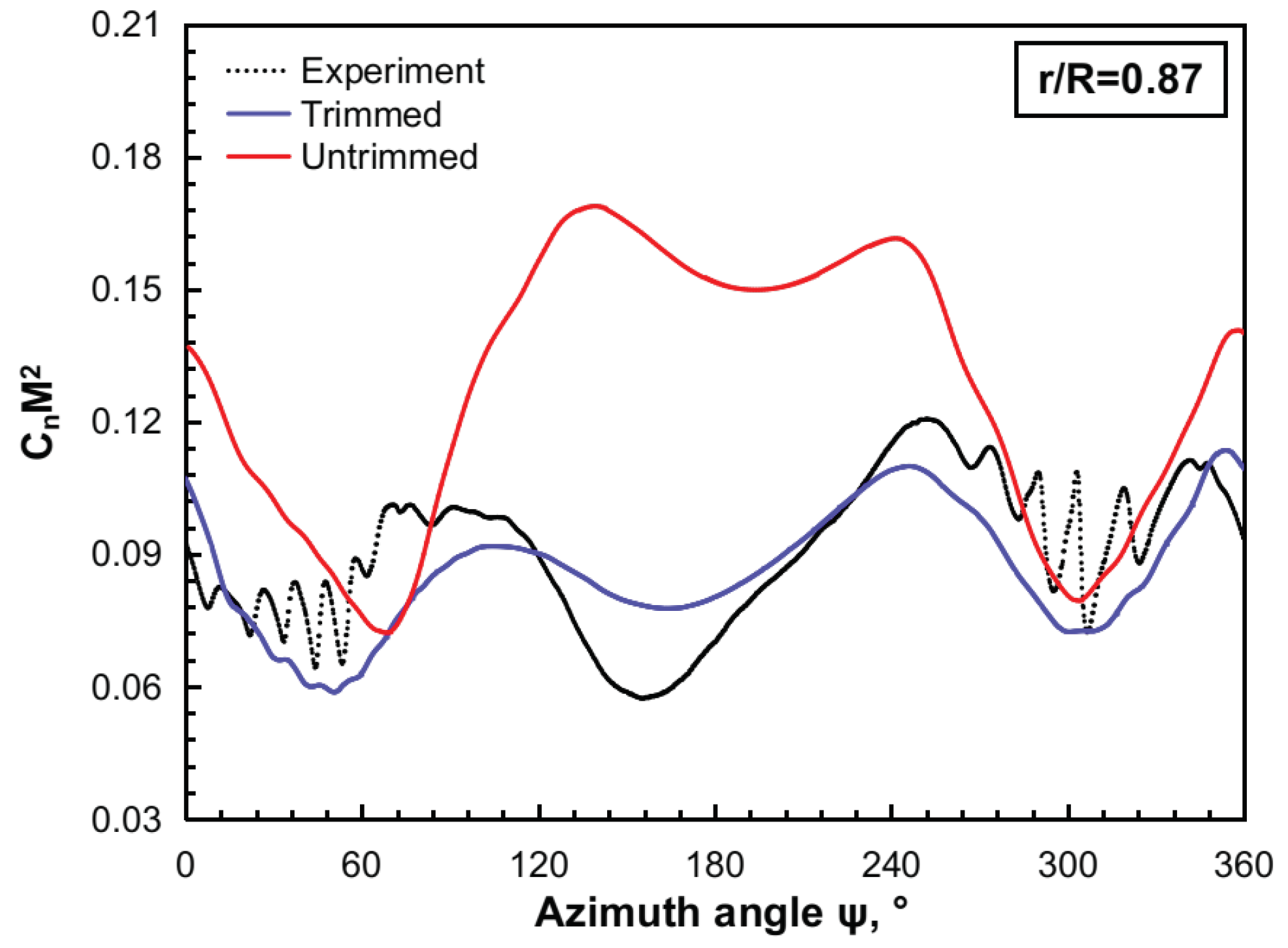
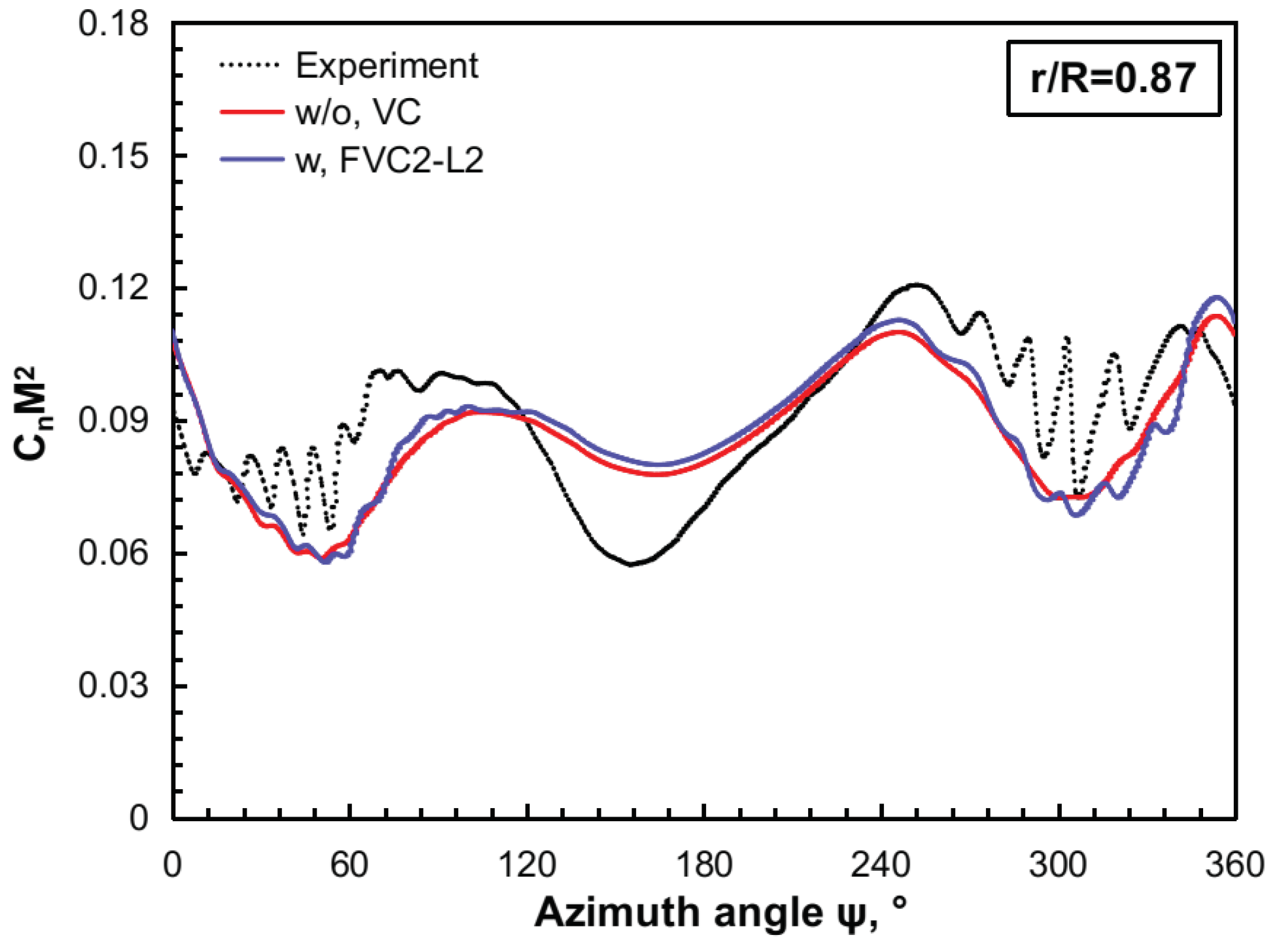
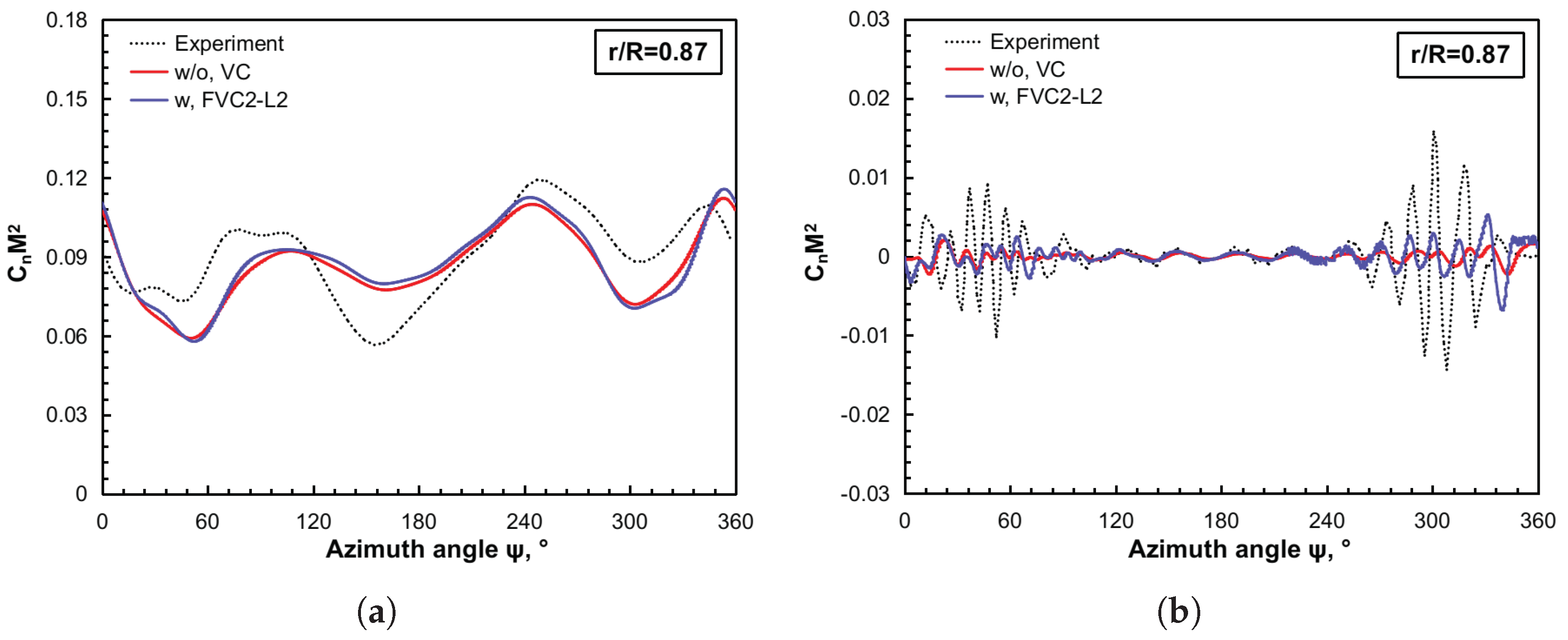
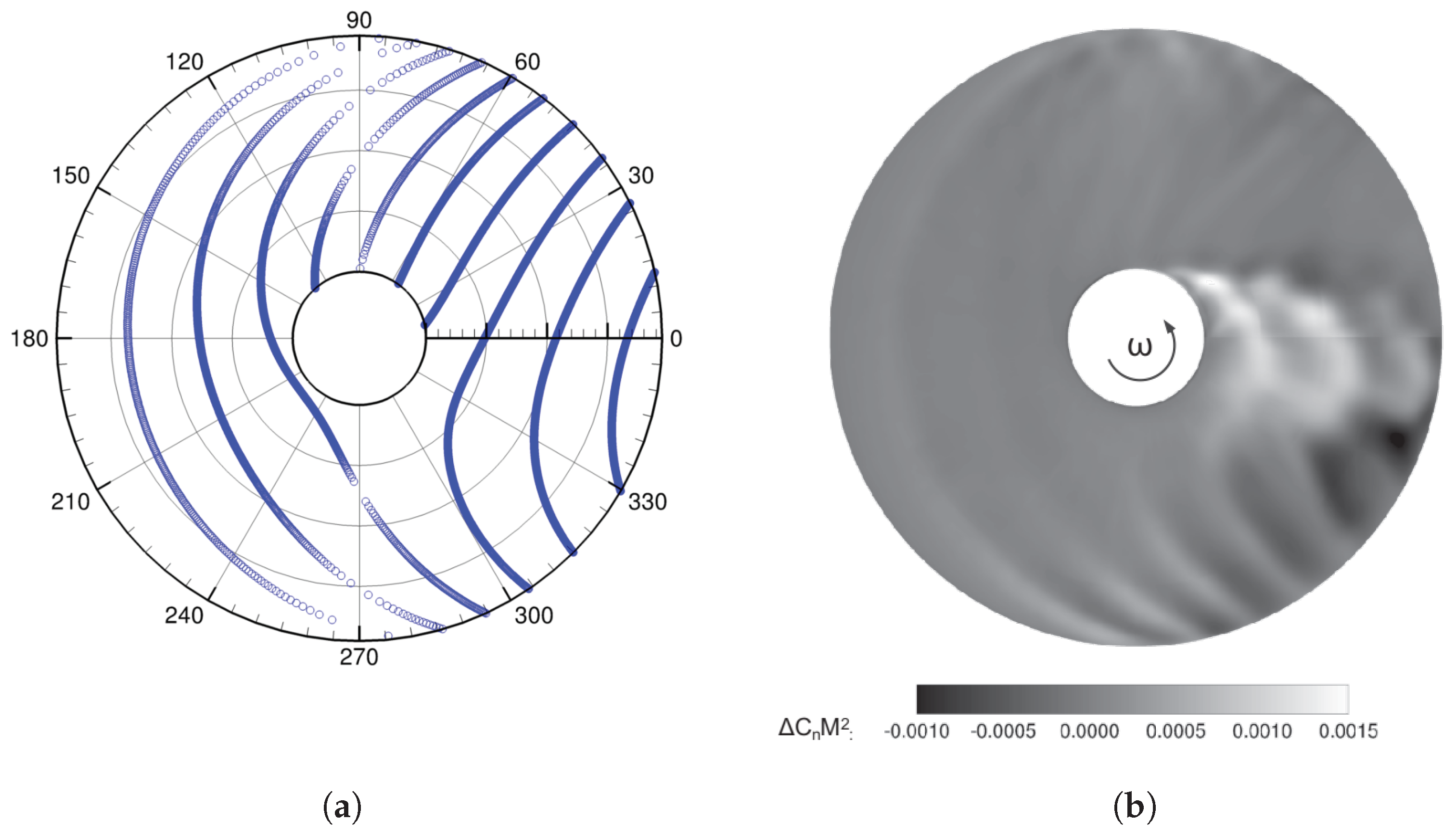
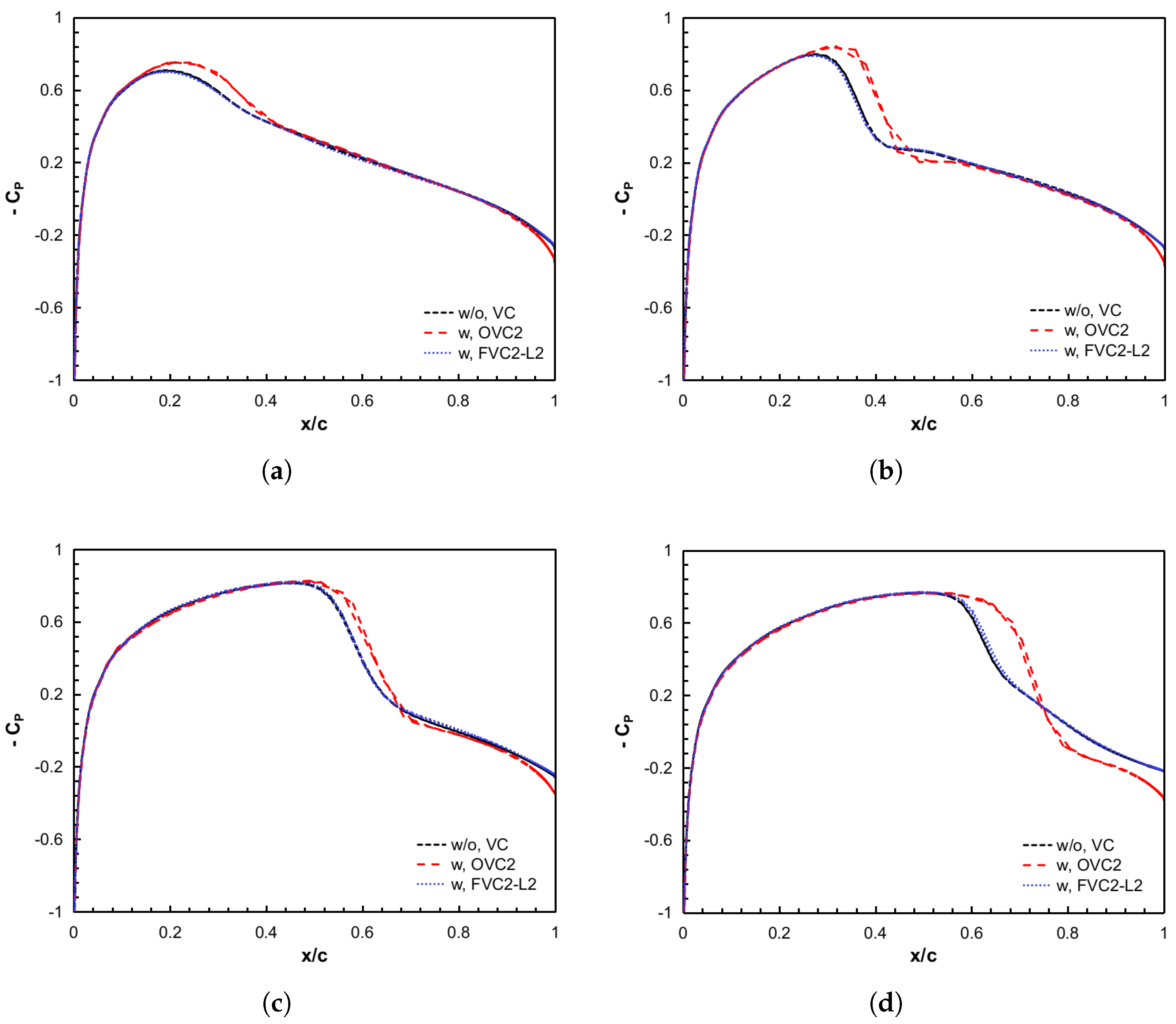
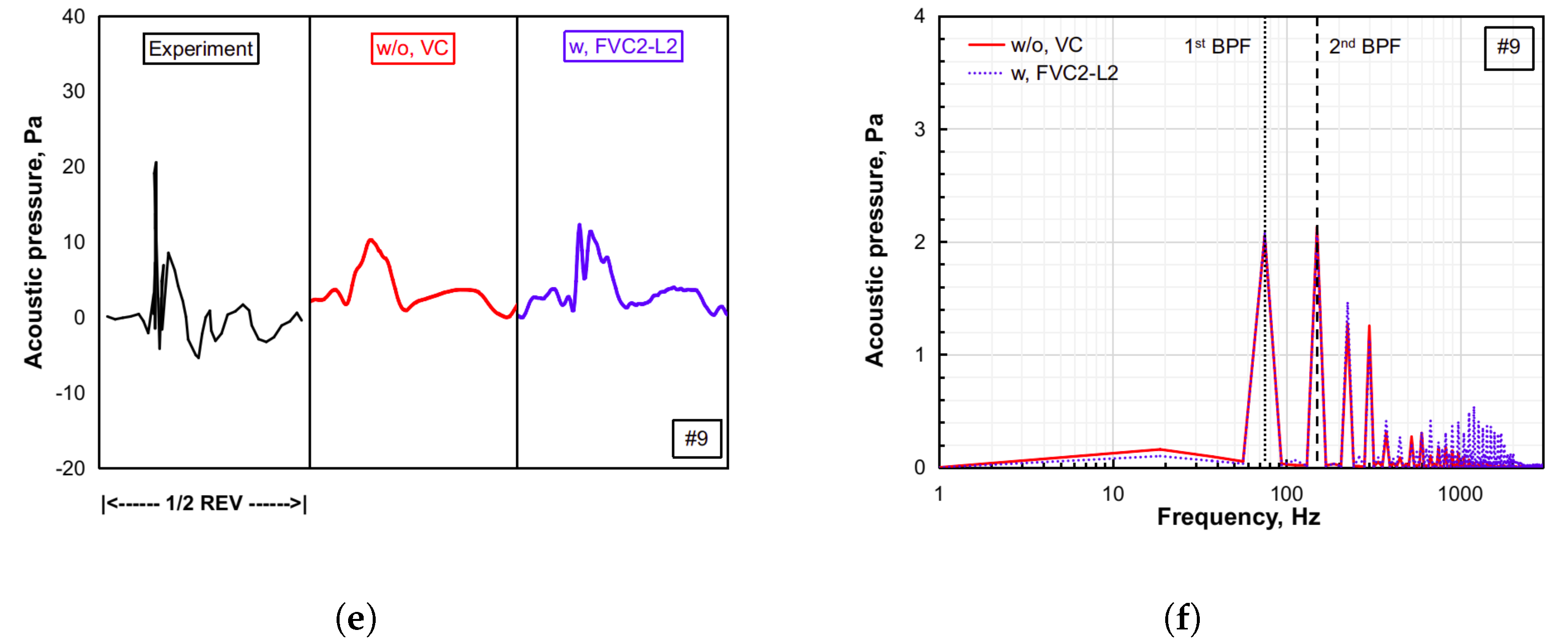
The main objective of this study is to evaluate the capabilities of the FVC2-L2 scheme to predict unsteady airloads, rotor wake development, and rotor noise radiation, particularly under BVI conditions. In addition, it is worth mentioning that the application of the ${\lambda }_2$-based VC2 formulation to the study of helicopter rotor aerodynamics and aeroacoustics constitutes a further original contribution of this paper. 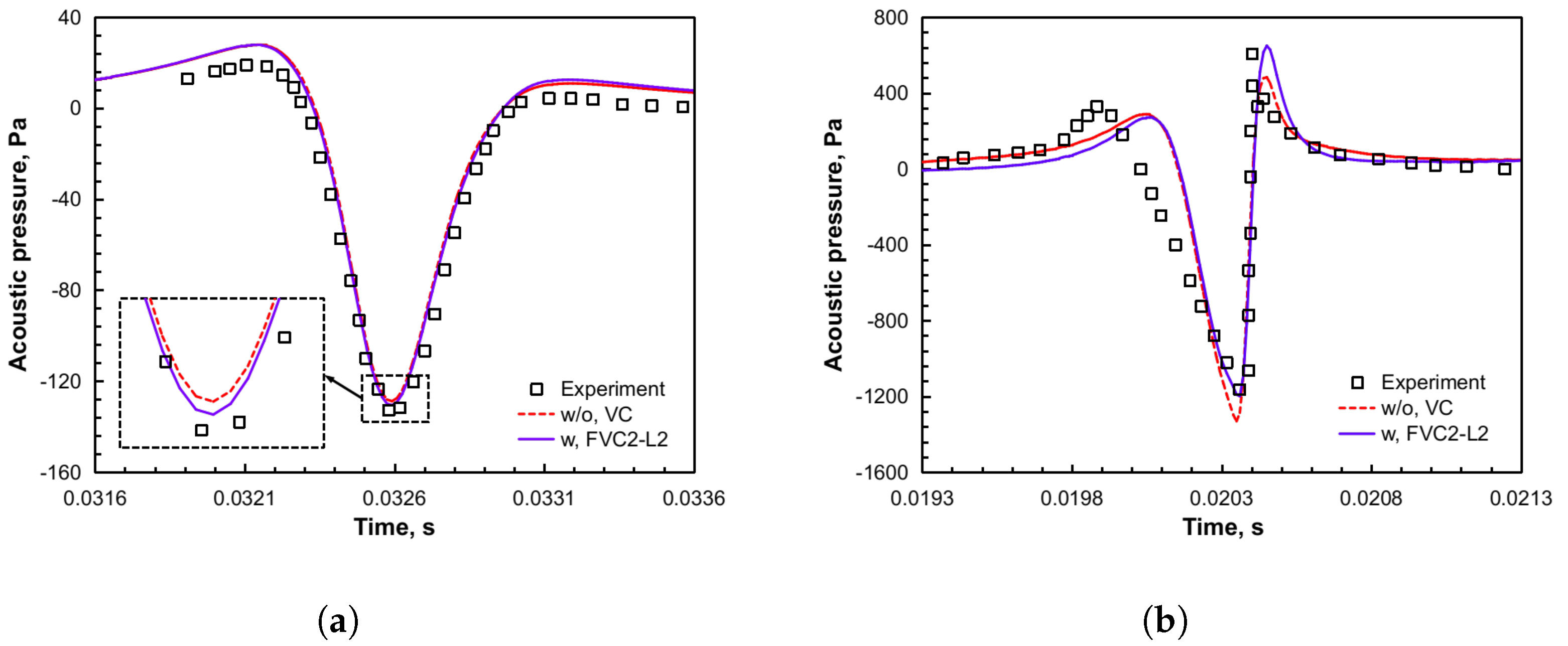Firstly, the HART-II baseline configuration was simulated to resolve the BVI phenomenon by using ROSITA, a multi-block, structured grid CFD solver that implements the FVC2-L2 scheme [11], and an in-house developed multi-dimensional delta trim procedure. Afterward, together with the permeable surface Ffowcs Williams–Hawkings (PS-FWH) equation, the influence of the FVC2-L2 scheme in rotor noise predictions was assessed via two benchmark test examples.

The remainder of this paper is structured as follows. In Section 2, the numerical implementations of the CFD approach and the FVC2-L2 scheme are introduced. Moreover, the in-house developed trimming method and aeroacoustic solver are mentioned. Section 3 discusses the application of the FVC2-L2 scheme in the HART-II rotor baseline configuration and the acoustic analysis of the non-lifting UH-1H hovering rotor and the AH-1/OLS low-speed descending flight rotor with the use of the FVC2-L2 scheme. Finally, the main conclusions are summarized in Section 4.

2. Computational Methods

2.1. Computational Fluid Dynamics Method (ROSITA Solver)

The in-house parallelized multi-block, structured grid, CFD code ROSITA (Rotorcraft Software ITAly) [36] is applied for the prediction of helicopter rotor aerodynamics. ROSITA solves the Reynolds-Averaged Navier–Stokes (RANS) equations in integral form with the one-equation Spalart–Allmaras (SA) turbulence model. The finite-volume formulation of governing equations could be written as

$$\frac{\partial }{\partial t}{\oint }_{V_{ijk}}\mathit{W}dV+{\int }_{S_{ijk}}({\mathit{f}}_{\mathit{c}}-{\mathit{f}}_{\mathit{d}})·\mathit{n}dS={\oint }_{V_{ijk}}{\mathit{f}}_{\mathit{s}}dV$$

(1)

where V is the cell volume with cell surface S and the outward normal unit vector n. $\mathbf{W}={[\rho ,\rho u,\rho v,\rho w,\rho e^t]}^T$ denotes the vector of conservative variables inside the flow domain, ${\mathit{f}}_{\mathit{c}}$ and ${\mathit{f}}_{\mathit{d}}$ are the convective flux tensor and diffusive flux tensor, respectively. ${\mathit{f}}_{\mathit{s}}$ represents the source term due to the movement of the relative reference frame.

The convective fluxes are evaluated by Roe’s scheme [37], the 2nd-order MUSCL (Monotone Upstream-centered Schemes for Conservation Laws) approach with a modified version of Van Albada limiter [38] is employed to provide second-order accuracy in space; the diffusive fluxes are calculated by a standard 2nd-order central difference scheme; the components of stress tensor are discretized by the application of the Gauss theorem. For unsteady simulation, the time advancement is carried out with an implicit dual-time method [39]. The moving Chimera technique based on the modified Chesshire and Henshaw algorithm [40] is used to facilitate the blade motion in the simulation. The Oct-tree and alternating digital tree data structure are adopted to speed up the tagging process.

2.2. Vortex Feature-Based Vorticity Confinement Scheme

In this work, the VC2 scheme, which has better numerical properties in conservation and regularity at the vortex center, is used to preserve vorticity in helicopter rotor flows. The implementation of the VC2 scheme relies on the experience of our past studies [8,11], that is, considering the vorticity confinement term as a body force source term ${\mathit{f}}_{\mathit{b}}$ on the momentum equation alone. This approach is preferred since the treatment that removes the vorticity confinement term from the energy conservation equation could obtain far better results [18]. The body force term ${\mathit{f}}_{\mathit{b}}$ is expressed as

$$\begin{array}{cc}\hfill \tilde{\omega }& =\mid \mathsf{\omega }\mid +\delta \hfill \\ \hfill \mathit{w}& \hfill =\frac{\mathsf{\omega }}{\tilde{\omega }}{\left[\frac{{\displaystyle \sum _{n=1}^N}{\left({\tilde{\omega }}_n\right)}^{-1}}{N}\right]}^{-1}\hfill \\ \hfill {\mathit{f}}_{\mathit{b}}& =\nabla \times \epsilon \mathit{w}\hfill \end{array}$$

(2)

In the preceding, $\mathit{w}$ represents the product of the locally normalized vorticity vector multiplied by the harmonic mean of vorticity magnitude. $\left|\mathsf{\omega }\right|$ denotes the vorticity magnitude. $\delta$ is a small positive constant to prevent division by 0 in $\mathit{w}$. The harmonic mean is computed over a localized stencil of seven cells (N = 7) for a uniform hexahedral mesh, which involves the center and six neighboring cells. $\epsilon$ is the confinement parameter which is a positive coefficient. Particularly, the value of $\epsilon$, is subject to an upper limit, which is highly influenced by various factors such as numerical schemes, grid resolution, and flow characteristics. If the value of $\epsilon$ exceeds this limit, it can lead to problems with stability, convergence, and produce over-confined or non-physical results. Therefore, when determining the value of $\epsilon$, it is important to consider the upper limit that ensures simulation stability and convergence and prevents over-confinement or non-physical results. This limit is referred to as the reference confinement parameter, ${\epsilon }_o$. In this work, the ${\epsilon }_o$ values come from past experiences and a trial-and-error procedure.

In numerical flow simulations, vorticity can be generated not only by physical means but also by artificial viscosity. This can result in the creation of artificial vorticity in the flow field. If the confinement term is applied to regions containing such artificial vorticity, it can produce spurious vortical structures that do not have physical significance. In this study, in order to restrict the application of VC2 in specified regions, such as the boundary layer, the advanced vortex feature detection techniques are incorporated with the standard VC2 scheme, resulting in a series of FVC2 schemes. In these schemes, the VC2 scheme is automatically activated in the area where the value of a threshold function $f_{threshold}$ overtakes a predefined cut-off value $f_0$. The FVC2-Q and FVC2-L2 schemes have been used in 3D flows that are dominated by vortices. Recent studies have shown that the FVC2-L2 scheme performs better than the FVC2-Q scheme in terms of computational stability, aerodynamic prediction, and vorticity preservation [11]. Based on this finding, the threshold function of the non-dimensional ${\lambda }_2$ criterion can be expressed as follows:

$$f_{threshold}=-\frac{{\lambda }_2}{{\Vert S\Vert }_F^2}$$

(3)

where ${\Vert ·\Vert }_F$ stands for the Frobenius norm; ${\lambda }_2$ is the second largest eigenvalue of the symmetric tensor $S^2+{\mathsf{\Omega }}^2$. S and $\mathsf{\Omega }$ denote the symmetric and asymmetric part of the vorticity gradient tensor, respectively, and have the following expression

$$\begin{array}{c}\hfill S=\frac{1}{2}\left[\nabla \mathit{u}+{\left(\nabla \mathit{u}\right)}^T\right];\mathsf{\Omega }=\frac{1}{2}\left[\nabla \mathit{u}-{\left(\nabla \mathit{u}\right)}^T\right]\end{array}$$

(4)

For all computations in this paper, the dimensional cut-off value is set to $f_0$ = 0.5, which is the same as used in our previous work [11].

2.3. Rotor Trim

An in-house developed multi-dimensional delta trim method is used for the trimming process of a helicopter rotor in forwarding flight. In this study, the rotor blades are assumed to move ’rigidly’, and the trim settings are the collective (${\theta }_0$), lateral (${\theta }_{1c}$), and longitudinal (${\theta }_{1s}$) cyclic pitch angles. Within the framework of trimming, the blade element theory (BET) and ROSITA codes are loosely coupled to obtain the trim settings of the rotor blades via a Newton–Raphson iterator. In an iterative fashion, this approach completely substitutes the CFD computed airloads with BET solutions in the Jacobian matrix computation, resulting in a high-efficiency trimming procedure. In particular, the combination of multiple levels of the grid and temporal resolutions is adopted to speed up the trimming process. The trimming procedure begins with the coarse simulation in which the coarse grid and temporal resolutions are used to calculate the low-precision trimmed control settings. Subsequently, the accurate trimmed control angles of the fine grid with satisfactory temporal resolution can be determined at the final simulation stage by using the trimmed settings computed at the previous stage as input.

2.4. Permeable Surface Ffowcs Williams–Hawkings Equation (ROCAAP Solver)

The acoustic prediction is performed by direct post-processing of the CFD solution using the acoustic code ROCAAP (ROtorcraft Code for AeroAcoustic Prediction) [41] based on the PS-FWH equation with Retarded-Time and Emission-Surface integral formulations. The self-defined cylindrical permeable control surface that encloses the blade surface is automatically extracted from the CFD solutions by using an algorithm presented in [41], where the Oct-tree search algorithm and a modified Chesshire and Henshaw algorithm [40] are used to detect the donor cells in the grid system and to interpolate the conservative flow variables on the control surface.

The integral form of Retarded-Time formulation which proved to be efficient for predicting the subsonic rotor noise is given below:

$$\begin{array}{cc}\hfill 4\pi p^{{}^{\prime }}(\mathbf{x},t)& =\frac{\partial }{\partial t}{\int }_S{\left[\frac{{\rho }_0{u}_n+(\rho -{\rho }_0)(u_n-v_n)}{r|1-M_r|}\right]}_{ret}dS\hfill \\ \hfill & \hfill +\frac{1}{c_0}\frac{\partial }{\partial t}{\int }_S{\left[\frac{P_{nr}+\rho u_r(u_n-v_n)}{r|1-M_r|}\right]}_{ret}dS+{\int }_S{\left[\frac{P_{nr}+\rho u_r(u_n-v_n)}{r^2|1-M_r|}\right]}_{ret}dS\hfill \end{array}$$

(5)

where $p^{{}^{\prime }}=p-p_0$ is the acoustic pressure; $p_0$, ${\rho }_0$ and $c_0$ are the pressure, density, and sound speed of the undisturbed air, respectively; the observer space-time variable is represented by $(\mathbf{x},t)$; r is the distance between the observer and source; $u_n=u_j{n}_j$ is the fluid velocity components outward normal to the permeable surface S; $v_n=v_j{n}_j$ is the projection of the surface velocity components along the outward normal to the surface S; the Doppler factor is $|1-M_r|$, $M_r=\mathbf{M}·\mathbf{r}$; S stands for the self-defined cylindrical permeable surface at same emission time. In particular, if the integration control surface coincides with the solid (impermeable) surface ($u_n=v_n$), the first term and the latter two terms on the right-hand side represent exactly the thickness and the loading contributions, respectively.

When the source is moving in transonic and supersonic regimes, the Retarded-Time formulation becomes unusable due to the singularity of the Doppler term. On the contrary, the Emission-Surface formulation is capable of avoiding the integral singularity effect by introducing a much less restrictive condition in the Doppler factor. Hence, the integral form of Emission-Surface formulation can be written as

$$\begin{array}{cc}\hfill 4\pi p^{{}^{\prime }}(\mathbf{x},t)& =\frac{\partial }{\partial t}{\int }_{\mathsf{\Sigma }}{\left[\frac{{\rho }_0{u}_n+(\rho -{\rho }_0)(u_n-v_n)}{r\mathsf{\Lambda }}\right]}_{ret}d\mathsf{\Sigma }\hfill \\ \hfill & \hfill +\frac{1}{c_0}\frac{\partial }{\partial t}{\int }_{\mathsf{\Sigma }}{\left[\frac{P_{nr}+\rho u_r(u_n-v_n)}{r\mathsf{\Lambda }}\right]}_{ret}d\mathsf{\Sigma }+{\int }_{\mathsf{\Sigma }}{\left[\frac{P_{nr}+\rho u_r(u_n-v_n)}{r^2\mathsf{\Lambda }}\right]}_{ret}d\mathsf{\Sigma }\hfill \end{array}$$

(6)

where, the Doppler term is $\mathsf{\Lambda }=\sqrt{1-2M_{n}cos\theta +M_n^2}$, $M_n=\mathbf{M}·\mathbf{n}$ and $\theta =arccos(\mathbf{n}·\mathbf{r})$; the emission surface is denoted by $\mathsf{\Sigma }$, a collection of source points in permeable control surface S whose emitting signals reach the observer simultaneously. In ROCAAP, the Marching-Cube algorithm is applied to construct the $\mathsf{\Sigma }$ surface. The details of its implementation can be found in [41].

3. Results and Discussion

3.1. Flow Application—HART-II Rotor in Descending Flight

Within the framework of the second Higher Harmonic Control Acoustic Rotor Test (HART-II), a highly instrumented 40% Mach scaled Bo-105 rotor test was conducted in the open 8 m × 6 m test section of the German-Dutch Wind tunnel (DNW) [42]. The aim of the HART-II program was to study the rotor wake and its development within the entire rotor disk. The equipped Bo-105 main rotor is a four-bladed hingeless rotor with a rotor radius of 2.0 m. The blades have a linear twist of $-8^{\circ }$ from root to tip. The profile of the blades uses a modified NACA23012 airfoil with a chord length of 0.121 m.

The baseline (BL) case of the HART-II experiment is employed as it is a descending flight dominated by BVI phenomena. The details of the operation condition are reported in

Table 1. Operation condition of the HART-II rotor BL configuration [42].

Advanced Ratio, $\mathit{\mu }$	Shift Angle, ${\mathit{\alpha }}_{\mathit{s}}$	Rotational Speed, $\mathit{\omega }$
0.15	4.5${}^{\circ }$	109 rad/s

.

The grid discretization is achieved using a multi-block overset grid system with Chimera technology. The grid system includes a far-field background grid (FG), a near-field background grid (NG), and four identical body-fitted blade grids (BG), as depicted in Figure 1. The far-field background grid is created to represent the flow domain far from the rotor. A uniform Cartesian grid is built as the near-field background grid to model the flow region close to the blades, as well as to capture the rotor wake. The body-fitted grid is created with a C-H topology type with a non-slip boundary condition on the blade surface. The wall distance of the first layer of blade surfaces is set to $1\times {10}^{-5}c$ so that the $y^{+}$ value is less than 1.

The multi-block structured grid system for the HART-II rotor has a total of 12.6 million cells with 0.9 million cells for the far-field background grid, 6.7 million cells for the near-field background grid, and 1.2 million cells for each of the body-fitted blade grid. More detailed grid information is reported in

Table 2. Details of the far-field and near-field grids (minimum spacing is outlined in terms of airfoil section chord c).

Mesh	${\mathit{N}}_{\mathit{tot}}$	${\mathit{N}}_{\mathit{X}}$	${\mathit{N}}_{\mathit{Y}}$	${\mathit{N}}_{\mathit{Z}}$	$\mathsf{\Delta }\mathit{X}$	$\mathsf{\Delta }\mathit{Y}$	$\mathsf{\Delta }\mathit{Z}$
FG	925,552	102	102	88	0.2	0.2	0.2
NG	6,732,000	374	250	72	0.165	0.165	0.165

. Meanwhile, a coarse grid system with 7.5 million cells is created for the trim process, where the far-field background grid of 0.6 million cells and the near-field background grid of 2.0 million cells.

3.1.1. Trim Convergence

The variations of CFD trim control angles and aerodynamic loads (continuous lines with symbols) against the experimental target values (dotted lines) with the trim cycles are shown in Figure 2a,b, respectively. It is observed that the trimmed lateral (${\theta }_{1c}$) and longitudinal (${\theta }_{1s}$) pitch cyclic angles show good agreement with the experimental data [42], but the collective pitch angle (${\theta }_0$) is underpredicted. This may be related to the blade elasticity that is not taken into account. As the trim process is managed by the BET code, the trim results are post-processed and calculated by the CFD code at each trim cycle. It should be mentioned that the BET trimmed values exactly match the trim target values at the end of trimming. Figure 3 shows the trimmed behavior of CFD computations on Mach-scaled, sectional normal force $C_n{M}^2$ obtained at $87\%$ radial station ($r/R$ = 0.87) with respect to the measurements reported in [42] and the untrimmed results computed using the experimental trim angles. As expected, the general shape of the trimmed solution is correlated much better with the experimental data than the untrimmed results, although some details of the measurements [42] are still not well reproduced due to the coarseness of the employed grid system and the neglected blade elasticity [43]. Overall, the trimmed control settings provide a satisfactory result for the simulation of the HART-II rotor in BL condition and thus can be used for further investigations.

3.1.2. Influence of Vorticity Confinement on Aerodynamics Prediction

Subsequently, the simulation using the FVC2-L2 with ${\epsilon }_o$ = 0.04 was conducted with the same trimmed control angles obtained in the previous section. When applying the vorticity confinement, the trimmed computation without confinement was carried out for four revolutions first, and then two more revolutions with the FVC2-L2 schemes were performed.

The $C_n{M}^2$ variations at $87\%$ rotor radius over one revolution are plotted in Figure 4 where the results predicted with and without VC schemes are compared against the measurements [42]. Analyzing the azimuthal ranges affected by the FVC2-L2 scheme, a slightly closer matching between the computed $C_n{M}^2$ variations with and without confinement may be found in the region ${120}^{\circ }<\mathsf{\Psi }<{240}^{\circ }$, and a improvement in the prediction of load oscillations due to BVI is achieved at the advancing ($0^{\circ }<\mathsf{\Psi }<{120}^{\circ }$) and retreating (${240}^{\circ }<\mathsf{\Psi }<{360}^{\circ }$) blade side for the FVC2-L2 solution when compared to the solution without confinement, although the high-frequency BVI fluctuations are still not adequately captured due to the coarseness of employed grid system.

Figure 5 presents the low- and high-frequency components of the $C_n{M}^2$ distributions at $87\%$ rotor radius decomposed by the low- and high-pass filters, respectively. The low frequency of $C_n{M}^2$ mainly represents the effect of aerodynamic modeling induced by the blade motion, whereas the high frequency of $C_n{M}^2$ is closely related to the BVI airloads. Therefore, the low-frequency content could be used to examine the correctness of aerodynamic modeling effects due to the blade movement. The high-frequency component could be applied to assess the adequacy of the VC scheme to predict the BVI-related phenomenon. From Figure 5a, the low-frequency content of $C_n{M}^2$ shows a negligible change between the non-VC and FVC2-L2 results. In contrast, an evident improvement of amplitude and phase of the $C_n{M}^2$ fluctuations is observed on the retreating side for the FVC2-L2 results compared to the solution without VC schemes in Figure 5b. Regarding the advancing side, the improvements of the $C_n{M}^2$ oscillations in the FVC2-L2 computation are relatively low compared to those in the non-VC solution. The possible reason is that the vortices interacting on the advancing blade side dissipate faster than those on the retreating side due to the wake age being older than that on the retreating side. Although the full amplitude of the high-frequency peaks is not reached, the simulation results with the FVC2-L2 scheme are encouraging and clearly show the potential of the FVC2-L2 scheme in capturing the BVI phenomenon.

The ability of the presented VC scheme in BVI capturing could also be interpreted as the difference of the normal force $C_n{M}^2$ between the FVC2-L2 results and the non-VC results on the rotor disk, as shown in Figure 6b. From this plot, the predicted BVI effects can be readily found in the first and fourth quadrants of the rotor disk and the positions are correlated well with the analytical solutions (Figure 6a).

3.1.3. Effect of Vorticity Confinement on Vorticity Preservation

Figure 7 shows the instantaneous 3D vortex system of the HART-II rotor BL case by using the Q-criterion (Q = 0.03). These images qualitatively illustrate the effectiveness of the present VC scheme. It is clear that a lower dissipation vortical structure with coherent characters over a large number of wake spirals in all four quadrants of the rotor disk is observed for the solution with the FVC2-L2 scheme. This represents an important feature for accurately predicting the BVI phenomenon. In addition, Figure 8 presents the detailed view of the vorticity contour at three streamwise slices ($x/R$ = 0.5, 1 and 2) from the center of the rotor in downstream direction. Solution with the FVC2-L2 scheme shows more concentrated vorticity at two side tip vortex pairs (A and B in Figure 8) than the non-VC results, which highlight the capability of the employed VC scheme in preserving the rotor vortical flow structures.

3.2. Acoustic Analysis—UH-1H Rotor in Hovering Flight

This section deals with the effect of the FVC2-L2 scheme on noise prediction for a helicopter rotor operated at non-lifting condition (i.e., ${\theta }_0=0^{\circ }$), where no tip vortices are shed from the blade tip. A 1/7-scaled model of the two-bladed UH-1H main rotor with the available experimental dataset documented by Boxwell et al. [44] is employed. The model rotor has two straight, untwisted blades with a NACA0012 airfoil section. The rotor radius is 1.045 m and the blade airfoil chord is 0.07623 m. Two test conditions with the blade tip Mach number $M_T$ equals 0.85 and 0.95 are considered. The noise prediction is conducted with the observer located at 3.09 radii away from the rotor hub, laying in the rotor disc plane.

Fu et al. [41] performed a grid dependency analysis using the presented CFD/PS-FWH workflow. A range of blade grid discretization from coarse to fine was created, and mesh convergence was verified by monitoring the blade chord-wise pressure distributions at a medium resolution. In the present study, the same medium-resolution grids within the same workflow are adopted to obtain the input data for noise prediction, instead of repeating the grid dependency analysis.

Figure 9 shows the blade chordwise $C_P$ profiles at two sectional positions ($r/R$ = 0.89 and 0.96) computed by using the FVC2-L2 scheme. The results of the non-VC scheme and the standard VC2 (OVC2) scheme are undertaken for comparison. The reference values ${\epsilon }_o$ = 0.01 and 0.06 are applied for the case with the OVC2 scheme and the FVC2-L2 scheme, respectively. It is observed that there are significant differences between the results simulated by the OVC2 scheme and the non-VC scheme on the $C_P$ profiles due to the over-confinement inside the boundary layer. In contrast, the FVC2-L2 simulation with the ${\lambda }_2$-criterion introduced inside the boundary layer gives almost identical $C_P$ distributions compared to the non-VC results. It implies that the robustness of the ROSITA solver on rotor blade aerodynamics prediction is maintained when the FVC2-L2 scheme is adopted.

The predicted acoustic time-domain signals at $M_T$ = 0.85 and 0.95 are compared with the measured data [45] in Figure 10, where the acoustic data predicted by the OVC2 simulation are not taken into account, due to its notable discrepancies in the $C_P$ profiles compared to the non-VC and FVC2-L2 solutions. Since $M_T$, for two test conditions is operated in a transonic regime, the noise predictions are conducted by using the Emission-Surface formulation of the PS-FWH equation, which has a much less restrictive nature in the Doppler factor, instead of using the Retarded-Time formulation. It is shown that the predicted results are in good agreement with the experimental data in terms of the peak values and wave shapes. In addition, simulations using the FVC2-L2 scheme predict the negative and positive peaks of noise signals more precisely than in the non-VC case. It is demonstrated that the FVC2-L2 scheme is able to improve the accuracy of the acoustic prediction to a certain extent, even if no tip vortices are shed from the blade tip.

3.3. Acoustic Analysis—AH-1/OLS Rotor in Forwarding Flight

This section concerns the acoustic prediction of the AH-1/OLS rotor in low-speed descent flight dominated by the BVI phenomenon. The rotor is composed of two rectangular blades with a linear twist of $-8.2^{\circ }$. The blade section is the BTH-540 airfoil with a 0.1039 m chord length. The rotor radius R is 0.958 m with a root cut-off distance of $0.182R$. The experimental test of this rotor was performed in the DNW within the framework of the Operational Load Survey (OLS) model rotor aerodynamic/aeroacoustic test [46]. The test condition employed in this section corresponds to the 10,014 test points with an advancing ratio of $\mu$ = 0.164, the rotational angular velocity of $\omega$ = 235.7 rad/s, the shaft angle of ${\alpha }_s$ = 0${}^{\circ }$, and a time-averaged target thrust coefficient of $C_T$ = 0.0054.

A moving embedded grid system was designed for the present study to simulate the motion of rotor blades in forwarding flight. It consisted of a far-field background grid (FG), a near-field background grid (NG), a wake grid (WG), and two identical body-fitted blade grids (BG), as illustrated in Figure 11. The far-field grid was generated to represent the flow domain far from the rotor, where outer boundaries were located 2R (above), 4R (below), and 5R (radial) away from the blade hub. The near-field grid was created to model the flow region close to the blades. The wake grid was built to capture the rotor wake. The body-fitted grid was modeled with a C-H topology with a non-slip boundary condition on the blade surface. The wall distance of the first layer of body surfaces was set to $1\times {10}^{-5}c$ so that the $y^{+}$ value was less than 1.

Two Chimera grid systems with the same geometry and topology, increasing the mesh size from 6.9 to 9.5 million, are created for the CFD simulation, in which the coarse grid is built up for trimming. The fine grid system uses the same blade grid of 292 (chordwise) × 132 (spanwise) × 60 (normal) as the coarse grid system but has finer background and wake grids. In detail, the finer grid system has 2.6 million grid cells for the far-field background grid, 1.0 million cells for the near-field background grid, and 1.1 million cells for the wake grid. The background and wake grid details are outlined in

Table 3. Details of the background grids (t: circumferential, r: radial, z: normal, Minimum spacing is outlined in terms of airfoil section chord c).

Mesh	${\mathit{N}}_{\mathit{tot}}$	${\mathit{N}}_{\mathit{t}}$	${\mathit{N}}_{\mathit{r}}$	${\mathit{N}}_{\mathit{z}}$	$\mathsf{\Delta }\mathit{t}$	$\mathsf{\Delta }\mathit{r}$	$\mathsf{\Delta }\mathit{z}$
FG	2,585,088	288	63	66	0.11	0.25	0.25
NG	1,020,600	360	72	30	0.09	0.2	0.2

and

Table 4. Details of the wake grids (minimum spacing is outlined in terms of airfoil section chord c).

Mesh	${\mathit{N}}_{\mathit{tot}}$	${\mathit{N}}_{\mathit{X}}$	${\mathit{N}}_{\mathit{Y}}$	${\mathit{N}}_{\mathit{Z}}$	$\mathsf{\Delta }\mathit{X}$	$\mathsf{\Delta }\mathit{Y}$	$\mathsf{\Delta }\mathit{Z}$
WG	1,113,600	174	160	40	0.2	0.2	0.2

, respectively. On the contrary, the coarse grid system has 1.5 million cells for the far-field background grid, 0.3 million cells for the near-field background grid, and 0.3 million cells for the wake grid.

3.3.1. Rotor Trim

In

Table 5. Trimmed control angles for the AH-1/OLS rotor operated in 10,014 test point [46].

	Collective Pitch, ${\mathit{\theta }}_0$	Lateral Cyclic Pitch, ${\mathit{\theta }}_{1\mathit{c}}$	Longitudinal Cyclic Pitch, ${\mathit{\theta }}_{1\mathit{s}}$
Strawn et al. [47]	6.14${}^{\circ }$	0.9${}^{\circ }$	−1.39${}^{\circ }$
Present study	5.72${}^{\circ }$	1.63${}^{\circ }$	−1.40${}^{\circ }$

, the trimmed control angles predicted using the presented multi-dimensional delta trim method are outlined. Figure 12 presents the $C_P$ distributions over the radial position of $r/R$ = 0.955 at 0${}^{\circ }$, 90${}^{\circ }$, 135${}^{\circ }$, and 180${}^{\circ }$ azimuths, where the untrimmed control settings refer to values obtained from Ref. [47]. The trimmed results agree well with the experimental data. Furthermore, an evident improvement for the $C_P$ predictions is observed for the results with the trimmed control angles, particularly for the data on the leading edge of the blade upper surface.

3.3.2. Influence of Vorticity Confinement on Aerodynamic Prediction

Subsequently, the ROSITA solver is run for four revolutions with the trimmed control angles and a small temporal resolution of 0.25${}^{\circ }$ azimuth increment (1440 steps per rotor revolution) to capture the highly unsteady airloads, and then two more revolutions with the FVC2-L2 schemes (${\epsilon }_o$ = 0.04) are performed to assess the ability of vorticity confinement to limit vortices dissipation.

The variation of $C_n{M}^2$ at two rotor radius stations ($r/R$ = 0.75 and 0.91) over one revolution are given in Figure 13. An evident improvement compared to the non-VC results is achieved using the FVC2-L2 scheme. For the FVC2-L2 computation, a clear amplification of the BVI fluctuations is observed on the retreating blade side. some BVI airloads are also captured on the advancing side, although it features a small interaction. The difference of the normal force $C_n{M}^2$ between the solution of the FVC2-L2 scheme and the non-VC scheme is plotted on the rotor disk to visualize the BVI effects, as shown in Figure 14b. With this plotting style, the improvements of the BVI airloads prediction for the FVC2-L2 solution can readily be identified in four quadrants of the rotor disk. In addition, the BVI positions are correlated well with the analytical positions (Figure 14a).

3.3.3. Effect of Vorticity Confinement on Vorticity Preservation

The instantaneous rotor wake system of the AH-1/OLS rotor, captured from the non-VC and the FVC2-L2 scheme cases, is depicted using the Q-criterion (Q = 0.02) in Figure 15. As can be seen, the non-VC and the FVC2-L2 cases express substantial differences in the wake resolution. The result with the FVC2-L2 scheme provides a more sophisticated tip vortex structure than those without VC schemes. For example, the case with vorticity confinement could preserve the trajectory of the wake more than two radii downstream, but the non-VC case only maintains the wake system to less than one and a half radii downstream. Furthermore, the same postprocessing as used in Figure 8 can be performed using slice cuts at three downstream positions ($x/R$ = 0.5, 1 and 2) to illustrate the difference of vorticity magnitude in the preserved tip vortex centers for the non-VC and the FVC2-L2 solutions, as shown in Figure 16. The FVC2-L2 case presents a higher extreme of vorticity magnitude than the case without confinement. These results reveal the low dissipation feature and high rotor wake resolution of the FVC2-L2 scheme, demonstrating its benefit for capturing the rotor vortical flows and analyzing the BVI phenomena.

3.3.4. Effect of Vorticity Confinement on Acoustic Prediction

Three microphone locations (Mic $\#3$, $\#7$, and $\#9$) in the AH-1/OLS acoustic test are employed in this case. They are installed ${30}^{\circ }$ below the rotor disk, 3.44 radii away from the rotor hub, for BVI noise measurement, the azimuths are ${180}^{\circ }$, ${150}^{\circ }$, and ${210}^{\circ }$, respectively. The coordinates for each microphone position are reported in

Table 6. Coordinates of microphones in the AH-1/OLS acoustic test [46].

Microphone	X, m	Y, m	Z, m	Noise Type
#3	−2.854	0.0	−1.648	BVI noise
#7	−2.472	1.427	−1.648
#9	−2.472	−1.427	−1.648

.

The time- and frequency-domain acoustic signals of rotor noise at three microphone positions are presented in Figure 17, where the frequency spectrum was computed by Fast Fourier Transformation (FFT) to understand the source contributions of the vorticity confinement on the predicted acoustic signatures. In this study, the $M_T$ for the 10,014 test point is less than 0.8, the noise predictions are conducted by using the Retarded-Time formulation due to its higher computational efficiency than the Emission-Surface formulation. From the time-domain signals, it is observed that a notable improvement in the predicted pulse amplitude is observed in the results with the FVC2-L2 scheme, the high-frequency fluctuation features are well resolved for all three observer positions. Furthermore, by introducing the FVC2-L2 scheme, the predicted noise signals correlate well with the experimental data, although there are some underestimated pulse peak pressures. It implies that the FVC2-L2 scheme is capable of improving the ability to capture the BVI noise. From the frequency spectrum plots, the FVC2-L2 scheme results in a significant increase in high-harmonic noise but a negligible change in low-frequency noise compared to the non-VC case. These differences are quantitatively presented in

Table 7. Comparisons of sound pressure level (SPL) for the non-VC and the FVC2-L2 results with noise signals filtered in <6th BPF and 6th–40th BPF range.

VC Scheme	Noise Filtered in (<6th BPF), dB			Noise Filtered in (6th–40th BPF), dB
	MIC #3	MIC #7	MIC #9	MIC #3	MIC #7	MIC #9
—	107.882	107.546	106.523	97.275	94.315	85.716
FVC2-L2	108.066	107.797	106.572	102.58	101.914	94.698

, where low-frequency noise is computed by low-pass filtering the predicted noise signals at 6th blade pass frequency (BPF), high-frequency noise, which represents the BVI noise, is calculated by band-pass filtering the noise signals in the frequency range between the 6th and 40th BPF. It is observed that the low-frequency noise levels of the non-VC and the FVC2-L2 cases are very similar, but the differences of high-frequency noise levels are more than 5 dB. Since high-frequency noise is related to highly unsteady sources and low-frequency noise relies on steady and periodic sources, one can further confirm that the use of the FVC2-L2 scheme mainly improves the prediction of highly unsteady airloads, the BVI effects, for instance.

3.4. Discussion on the Selection of Reference Confinement Parameter ${\epsilon }_o$

Although the FVC2-L2 scheme is capable of achieving promising results when applied to rotorcraft flows, some shortcomings/limitations of the approach may be noticed. In engineering applications, a trial and error procedure to select ${\epsilon }_o$, avoiding over-confinement and/or instability, is needed; furthermore, the lack of a-priori knowledge of the vortex spatial dimension make it impossible to quantify the mesh size required to properly capture the vortex. This makes it difficult to recommand an optimal grid size/${\epsilon }_o$ combination. Nonethless, an indication on the required ${\epsilon }_o$ value in terms of number of cells per vortex diameter may be obtained from the analysis of simplified vortex flows, considering for instance an isolated, two-dimensional vortex convected in uniform flow.

In this work, the two-dimensional Scully vortex model was considered, with a circulation $\mathsf{\Gamma }$ = 0.2536, core radius $r_0$ = 0.162, and convective Mach number $M_{\infty }$ = 0.626. The employed computational meshes are uniformly distributed with $\mathsf{\Delta }X$ = $\mathsf{\Delta }Y$ = 0.05/0.025, corresponding to 6 and 12 grid cells per vortex diameter. Figure 18 shows the time evolution of the overall vorticity of the convected Scully vortex, for different grid resolutions and different $\epsilon$ values. An over-confinement is observed at high $\epsilon$ values, $\epsilon$ = 0.08 for the coarse grid and $\epsilon$ = 0.02, 0.04 for the fine grid. On the contrary, the values $\epsilon$ = 0.04 for coarse grid and $\epsilon$ = 0.01 for the fine grid preserve the initial vorticity for a long time and can be selected as the ${\epsilon }_o$ value. One can notice that a grid refinement lowers the value of the reference $\epsilon$ value.

On the basis of the simple test, some provisional guidelines for a practical case can be provided: use ${\epsilon }_o$ in the range 0.01–0.04 and verify if the calculation does not become unstable and/or over-confinement.

4. Conclusions

In this paper, a vortex feature-based VC2 (FVC2-L2) scheme that combines the standard VC2 method with the locally normalized ${\lambda }_2$-criterion is presented and its benefits in helicopter rotor aerodynamic and aeroacoustic predictions are demonstrated. This VC2 approach allows for alleviating the diffusion introduced by the numerical discretization of the fluid governing equations in the region where concentrated vorticity is dominated while avoiding the over-confinement within the boundary layer. Applying the method to three practical helicopter rotor cases shows that the FVC2-L2 scheme not only well resolves the internal structure of rotor vortical flows and effectively improves the prediction of high-frequency BVI airloads as well as the noise generated by BVI effects, but also maintains the accuracy of low-frequency airloads and acoustic prediction. For example, in the case of AH-1/OLS rotor case, the FVC2-L2 scheme results in an improvement of BVI noise prediction by more than 5 dB at three microphone positions with respect to the non-VC results. In addition, the noise predicted using the FVC2-L2 scheme correlated better with the measurements than those calculated without VC, even if no vortices were shed from the blade tip.

The limitation of the FVC2-L2 approach stems in the selection of the confinement coefficient $\epsilon$, since the reference $\epsilon$ value depends on the mesh under-resolution. A qualitative guideline, derived from the analysis of the simplified convected vortex case, indicates an ${\epsilon }_o$ value ranging from 0.01 to 0.04 for grids which may represent the vortex core diameter with 6 to 12 cells.