Droplet Collection Efficiency Regularity of NACA0012 Airfoil Based on the Eulerian Method
Abstract
1. Introduction
2. Methods and Numerical Models
2.1. Assumptions
- (1)
- The distribution of water droplets is uniform, and they are simplified as spheres with medium volume. The average size remains unchanged without breaking during the motion process.
- (2)
- There is no heat or mass transfer between the droplets and air. The influence of droplets on the air phase is ignored, and the physical parameters of the water droplets will not change.
- (3)
- The effects of droplet collision, splash, and rebound are ignored, and only the resistance of the air to droplets is considered. In addition, the resistance is steady.
- (4)
- Gas viscosity does not affect the droplets.
2.2. Governing Equation for Airflow
2.3. Equation for Droplet Motion and Impact
2.4. Boundary Condition
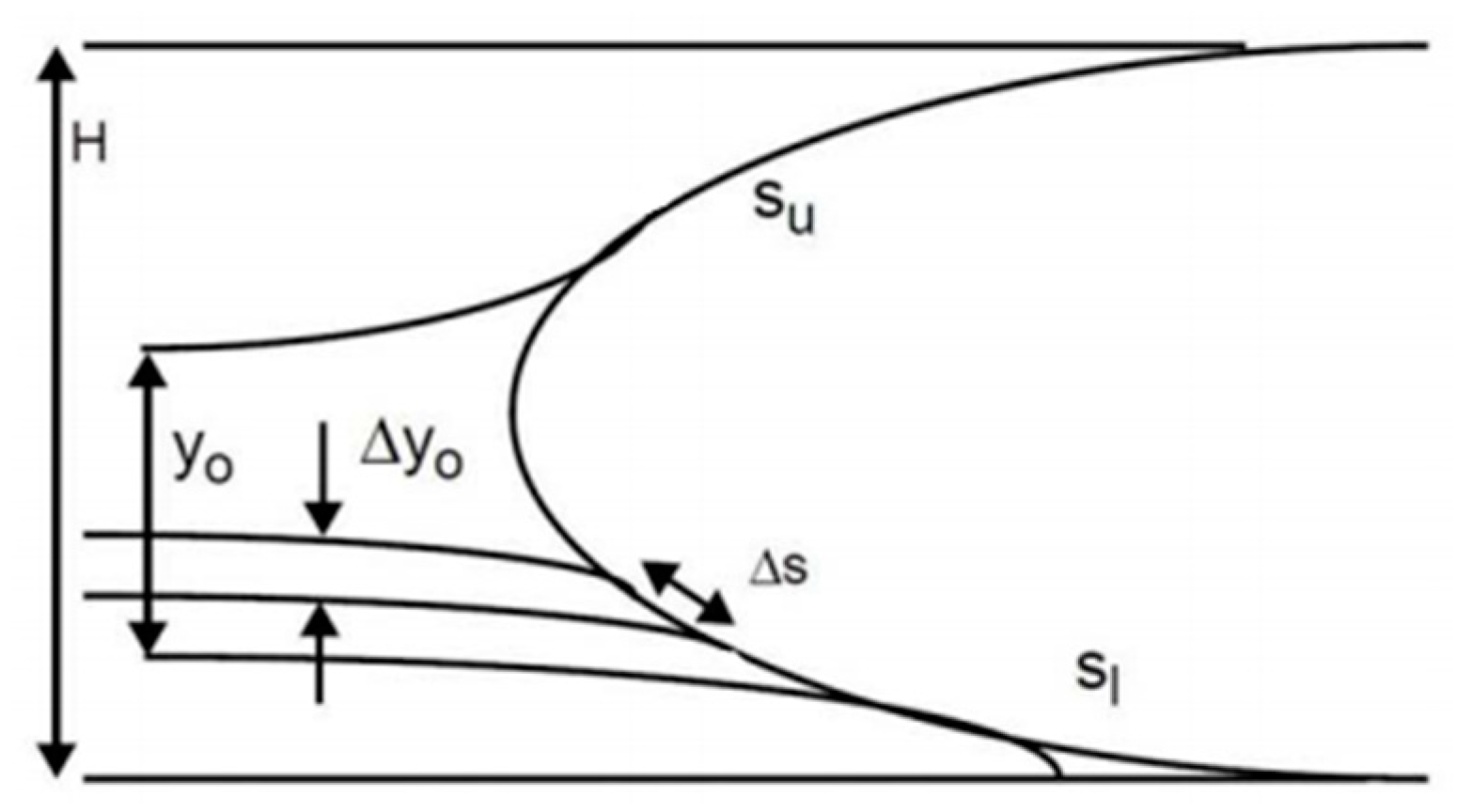
2.5. Collection Efficiency Definition
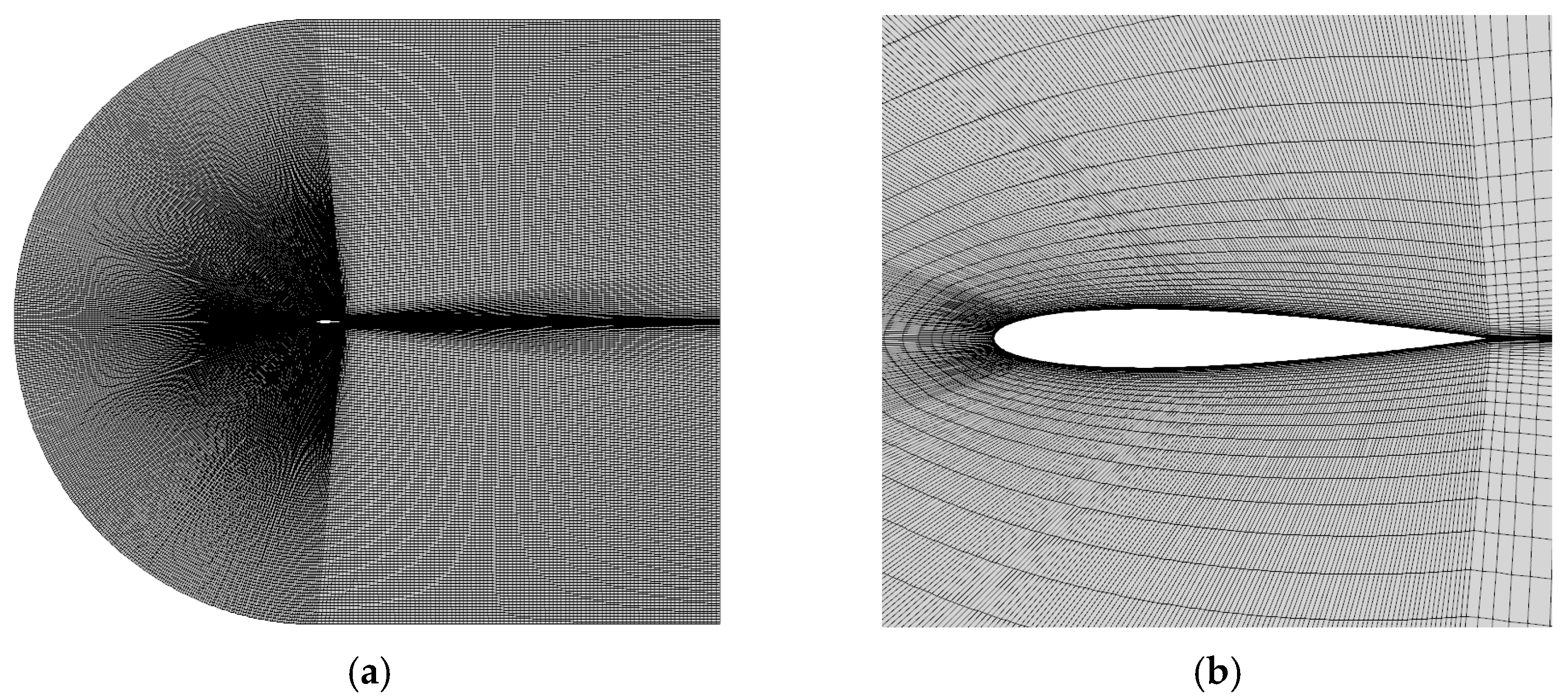
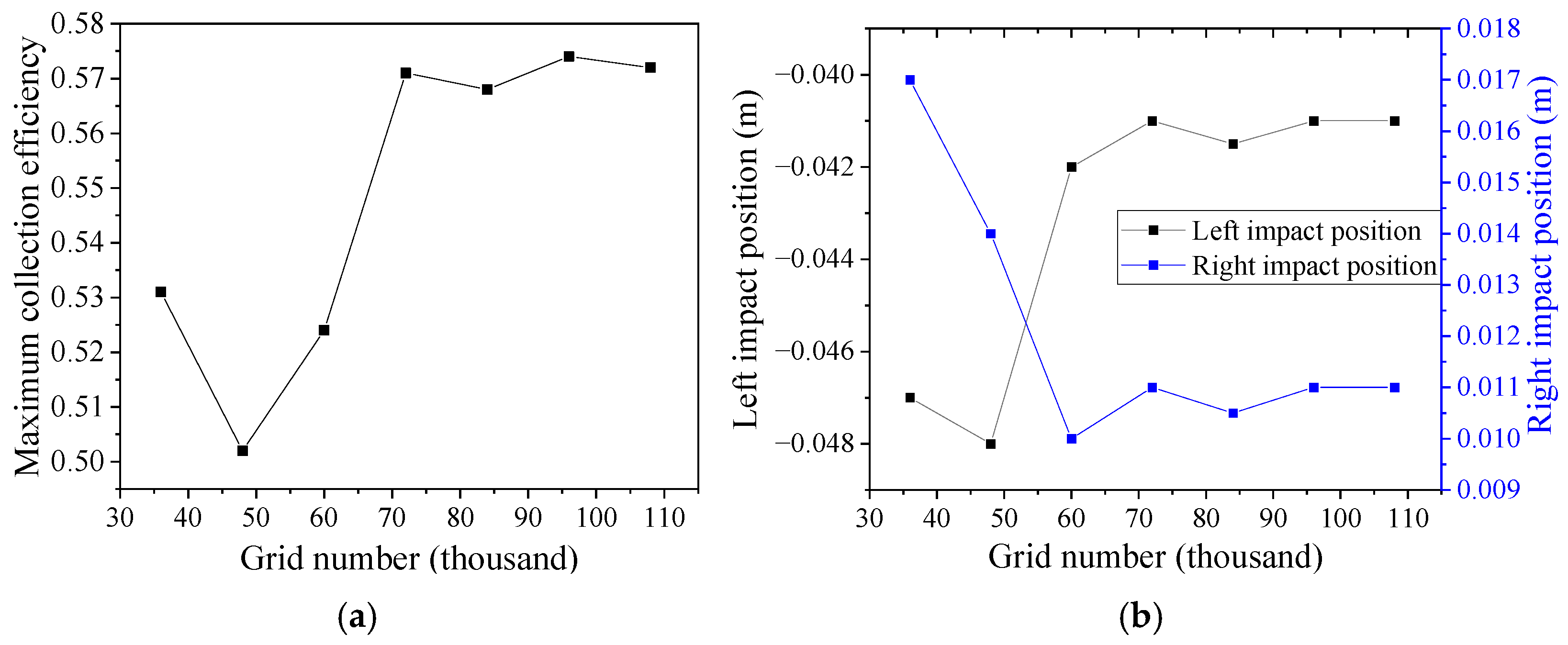
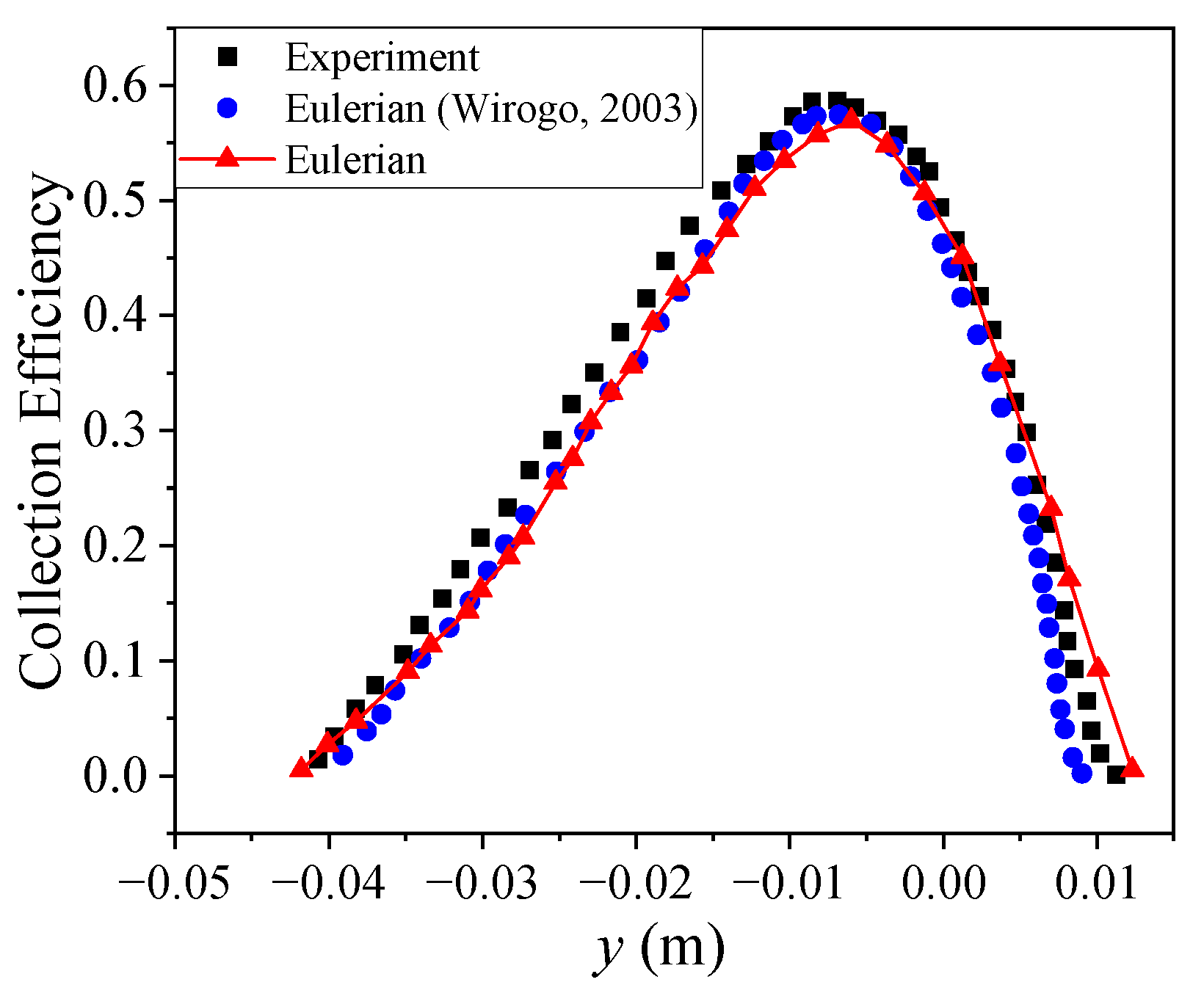
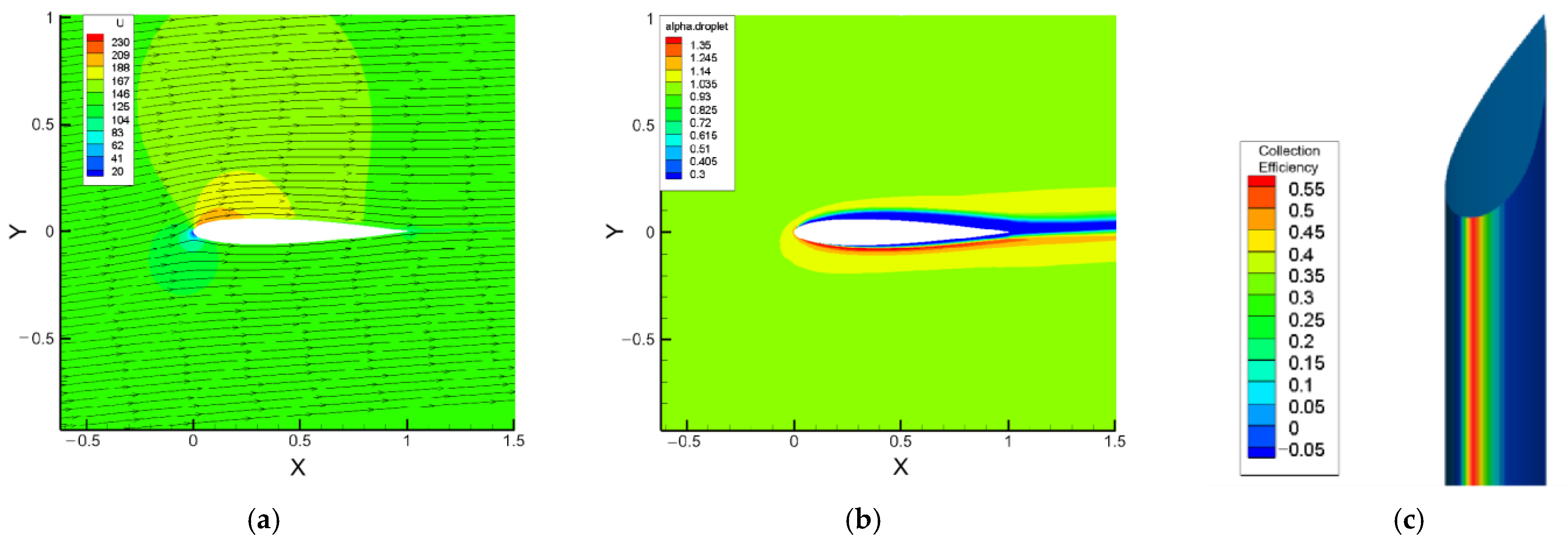
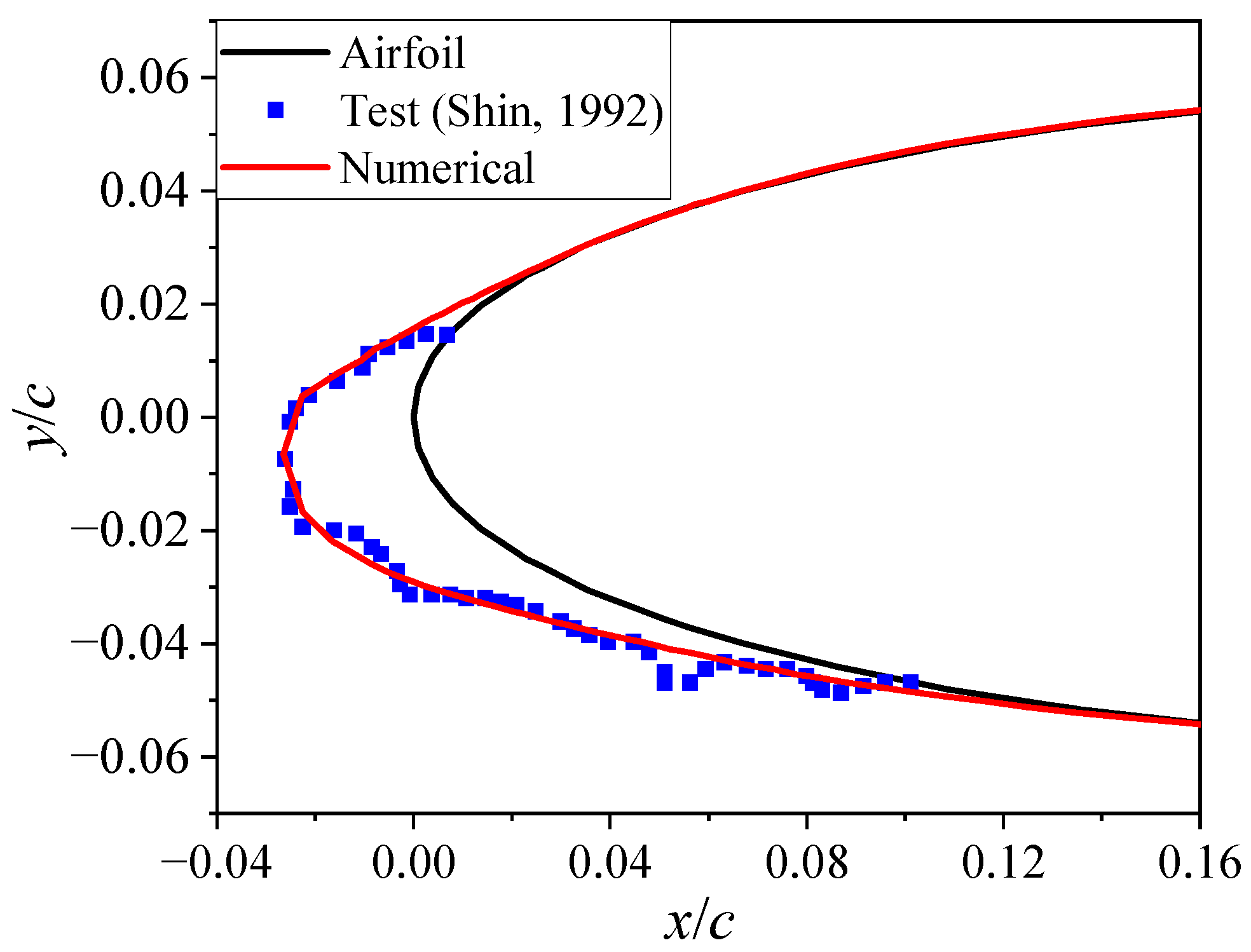
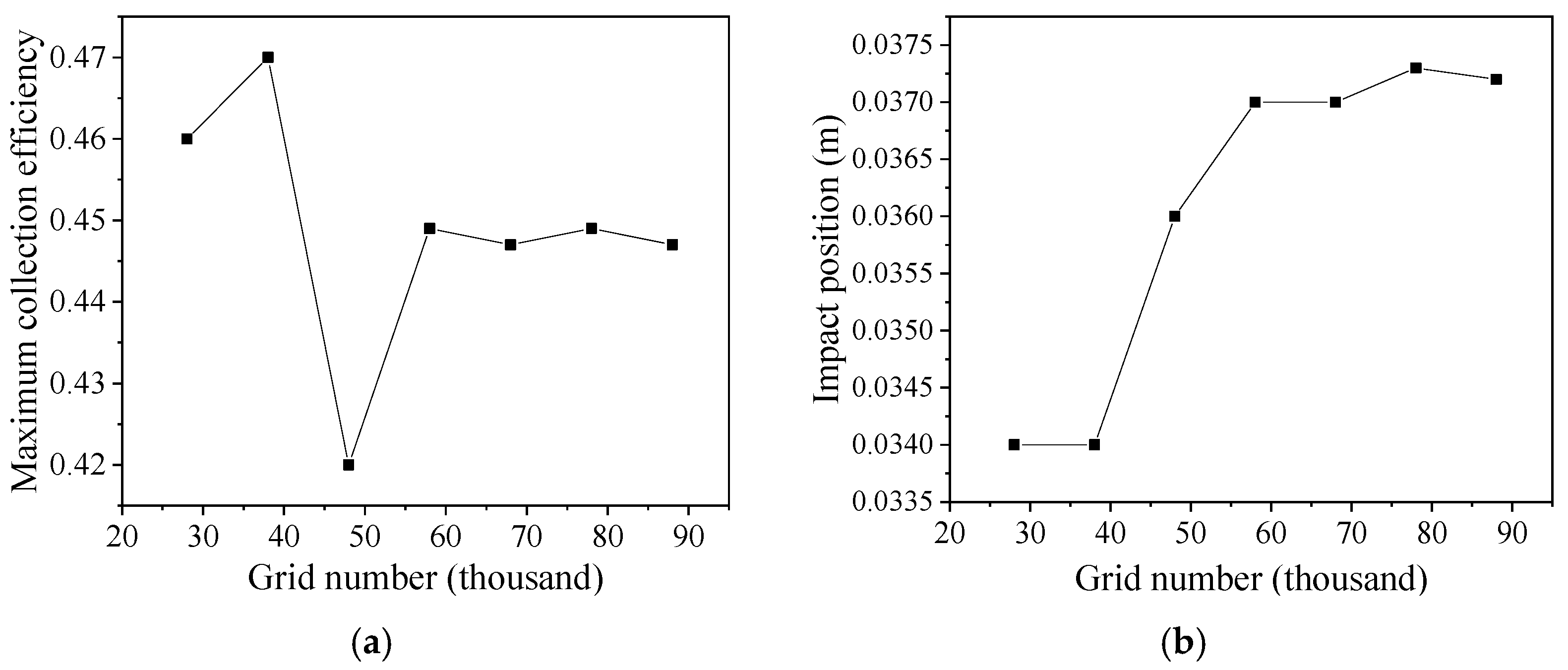
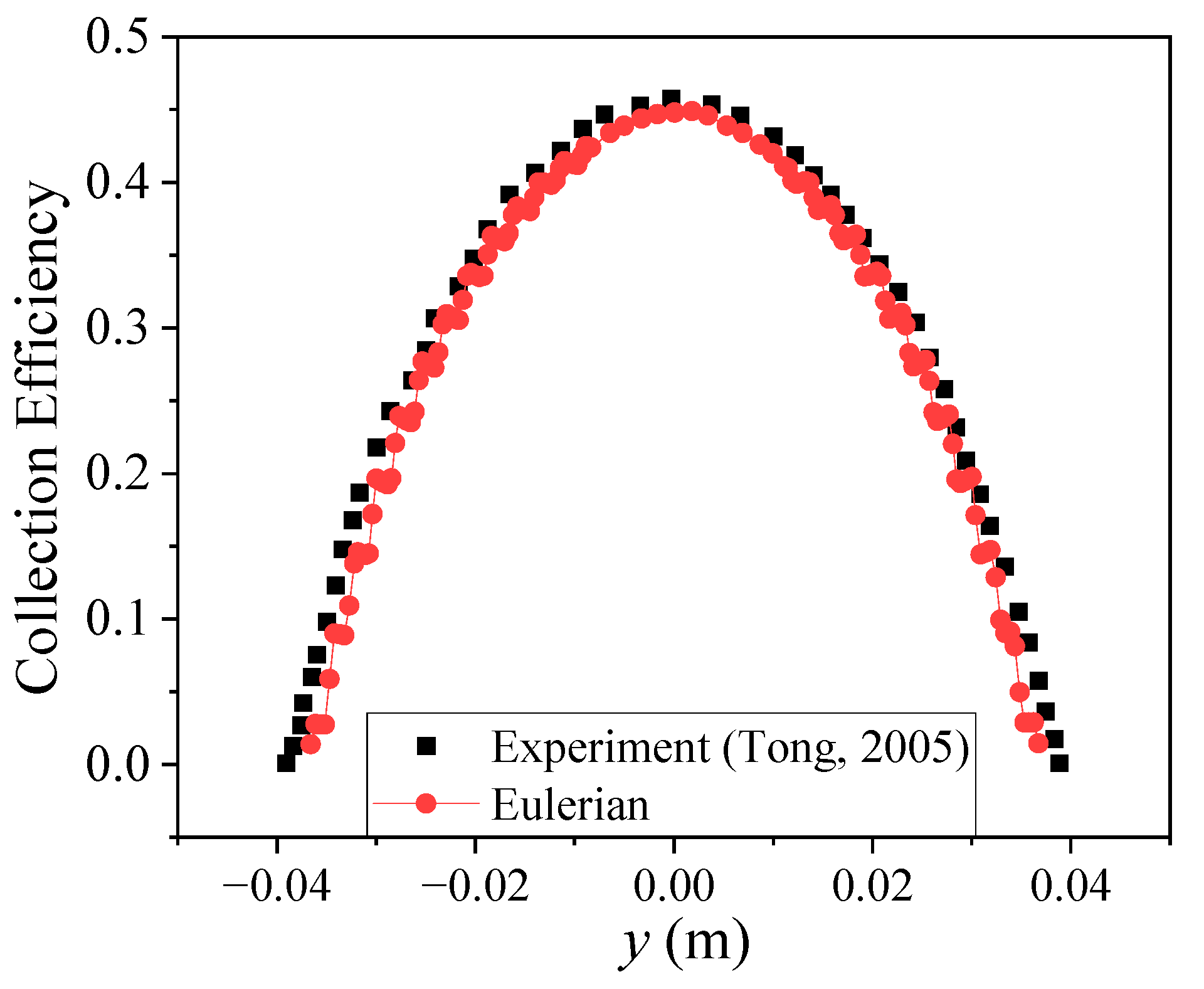
3. Results and Verification of the Eulerian Method
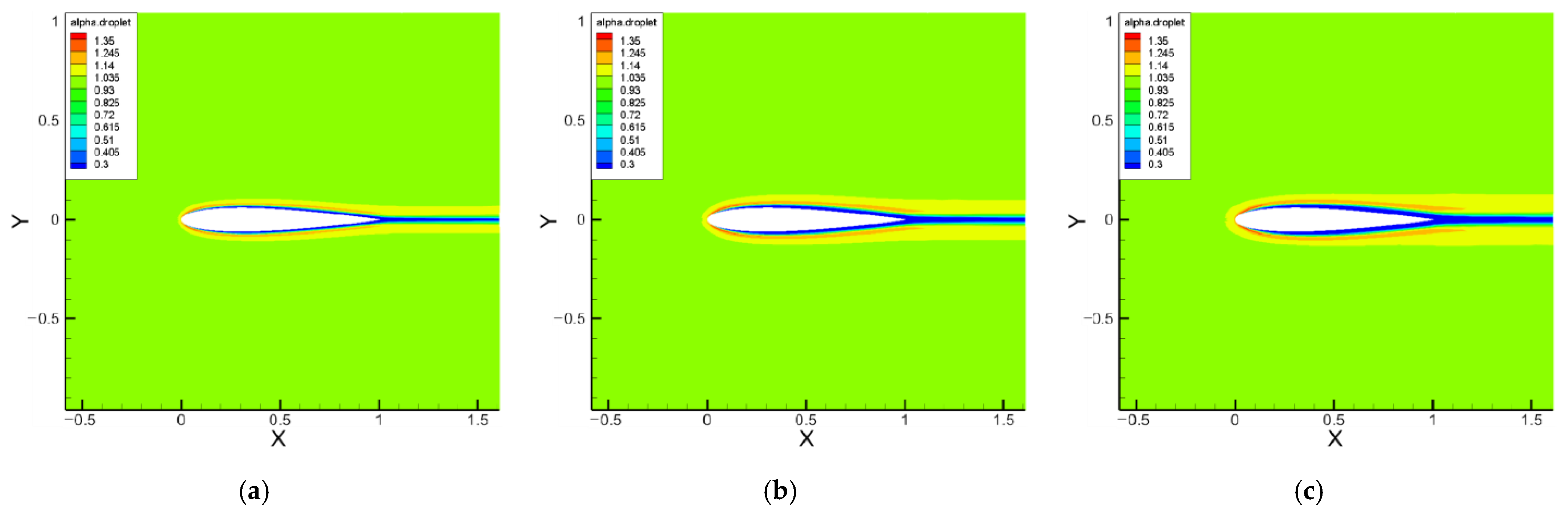
3.1. NACA 0012 Airfoil
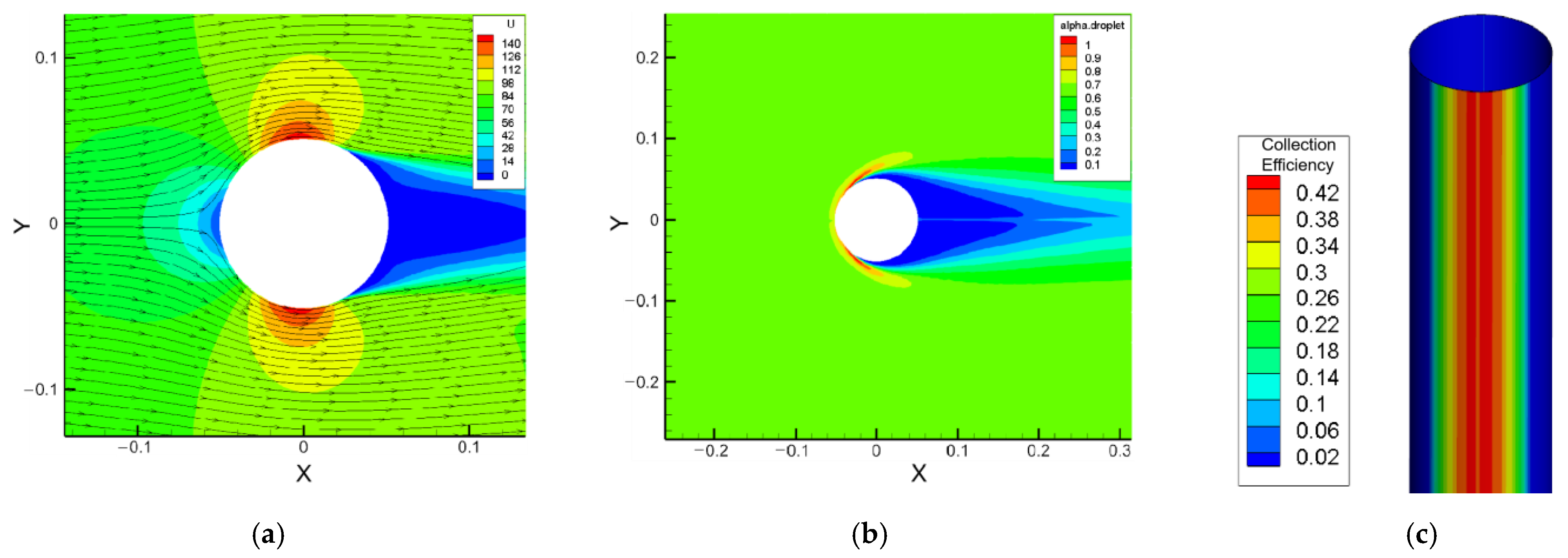
3.2. Cylinder
4. Distribution Characteristics of Collection Efficiency
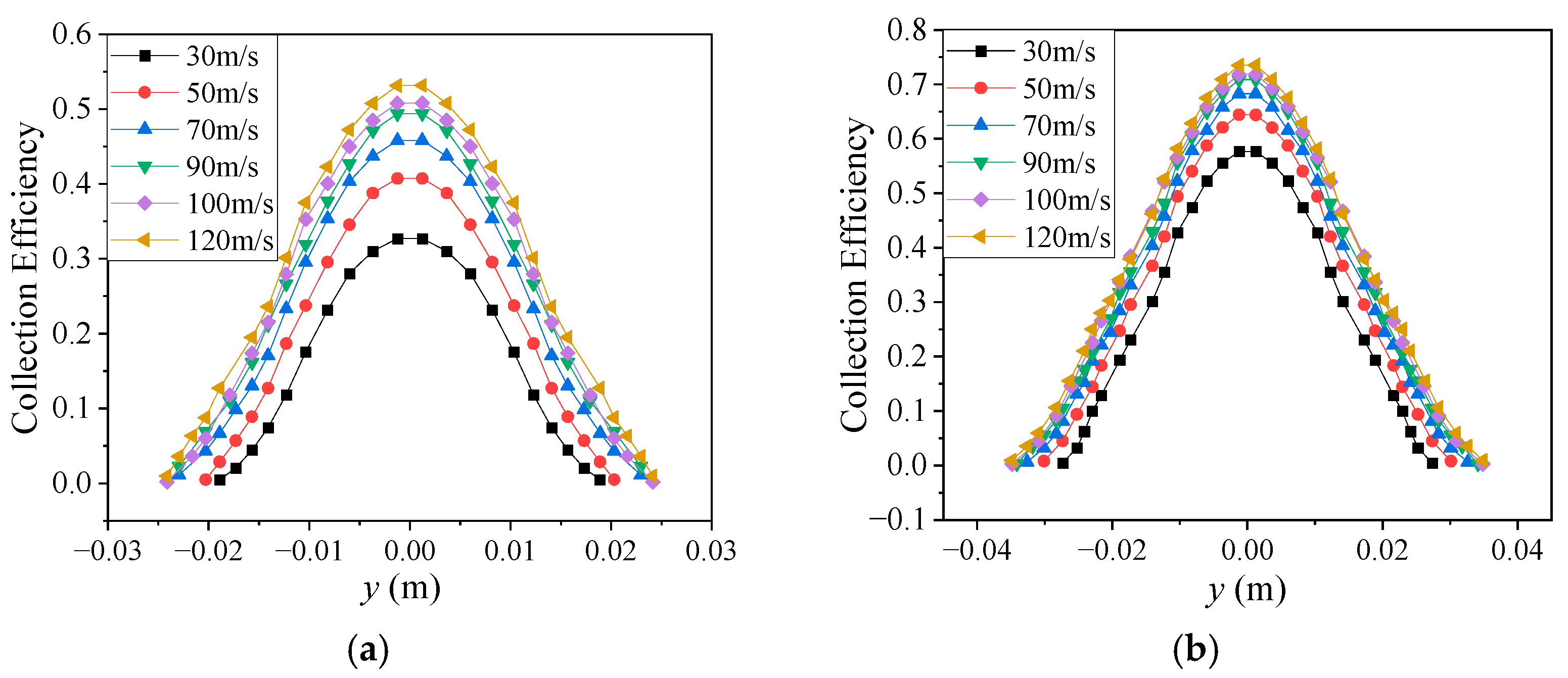
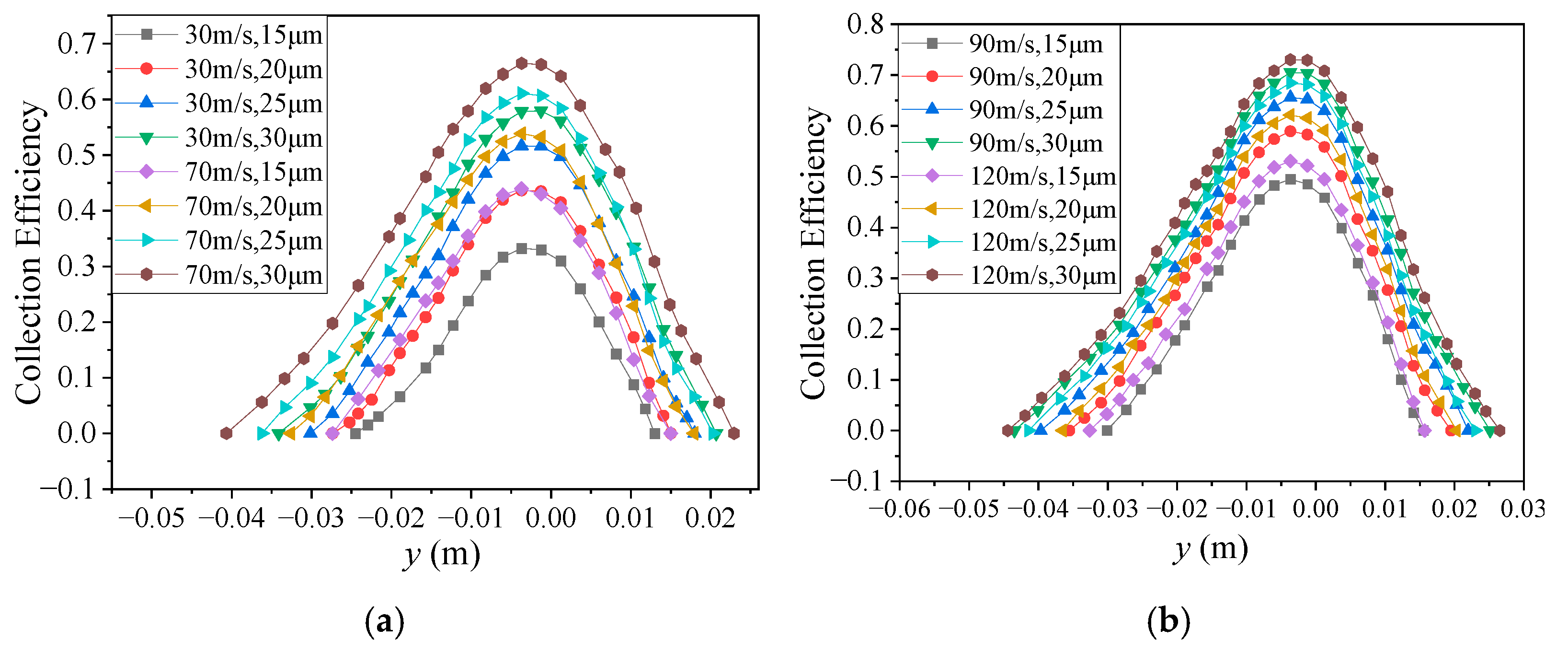
4.1. Influence of Different Inflow Parameters
4.1.1. LWC
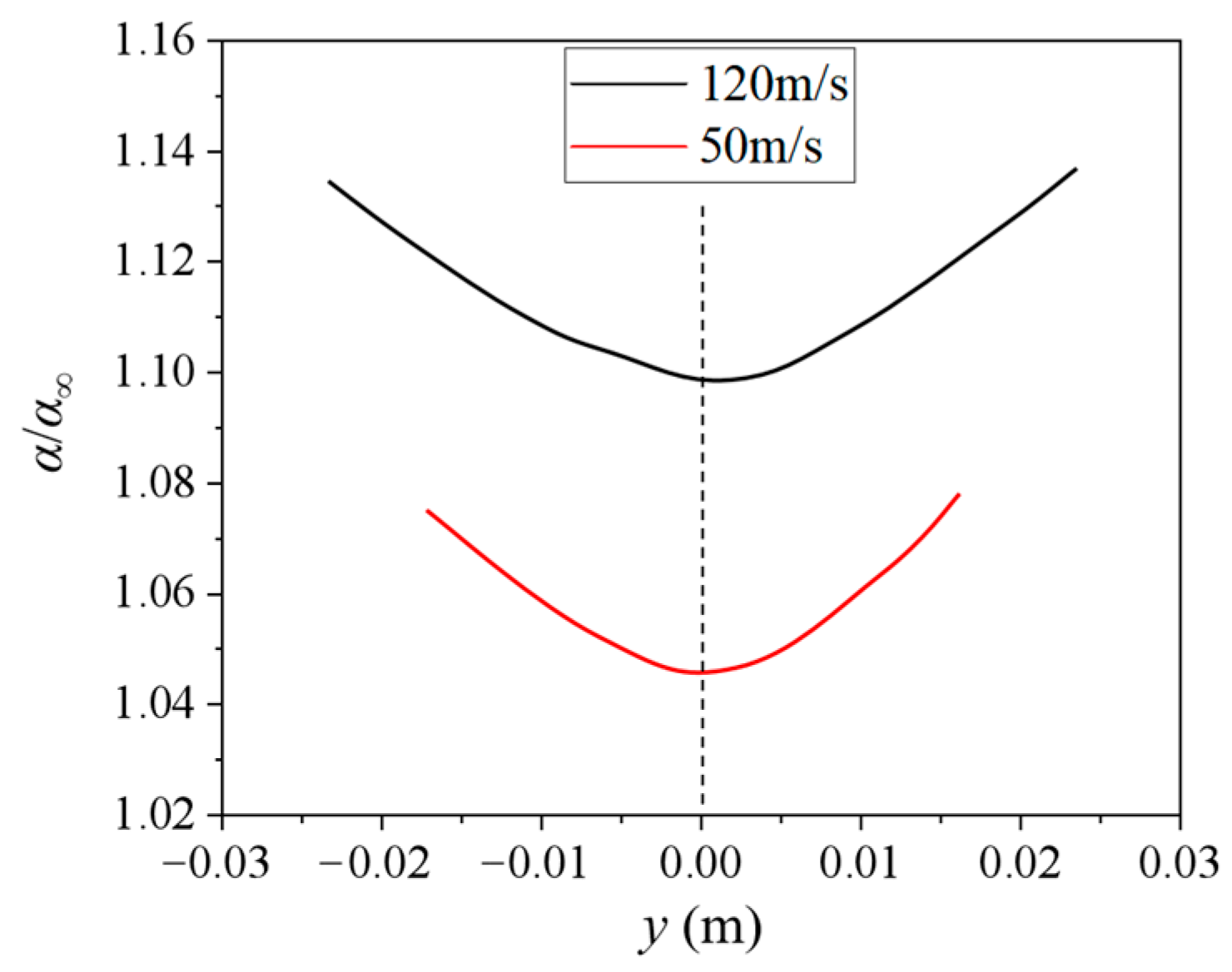
4.1.2. Incoming Velocity
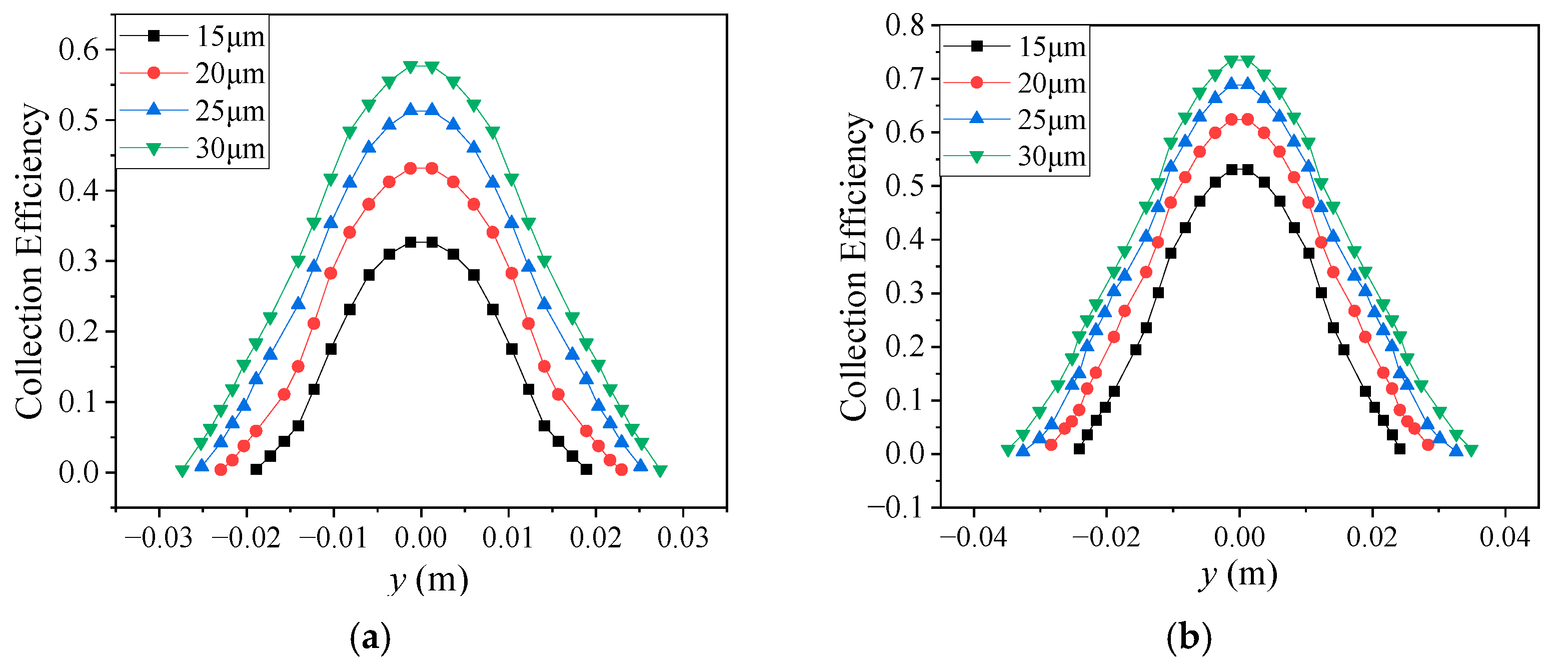
4.1.3. Droplet Diameter
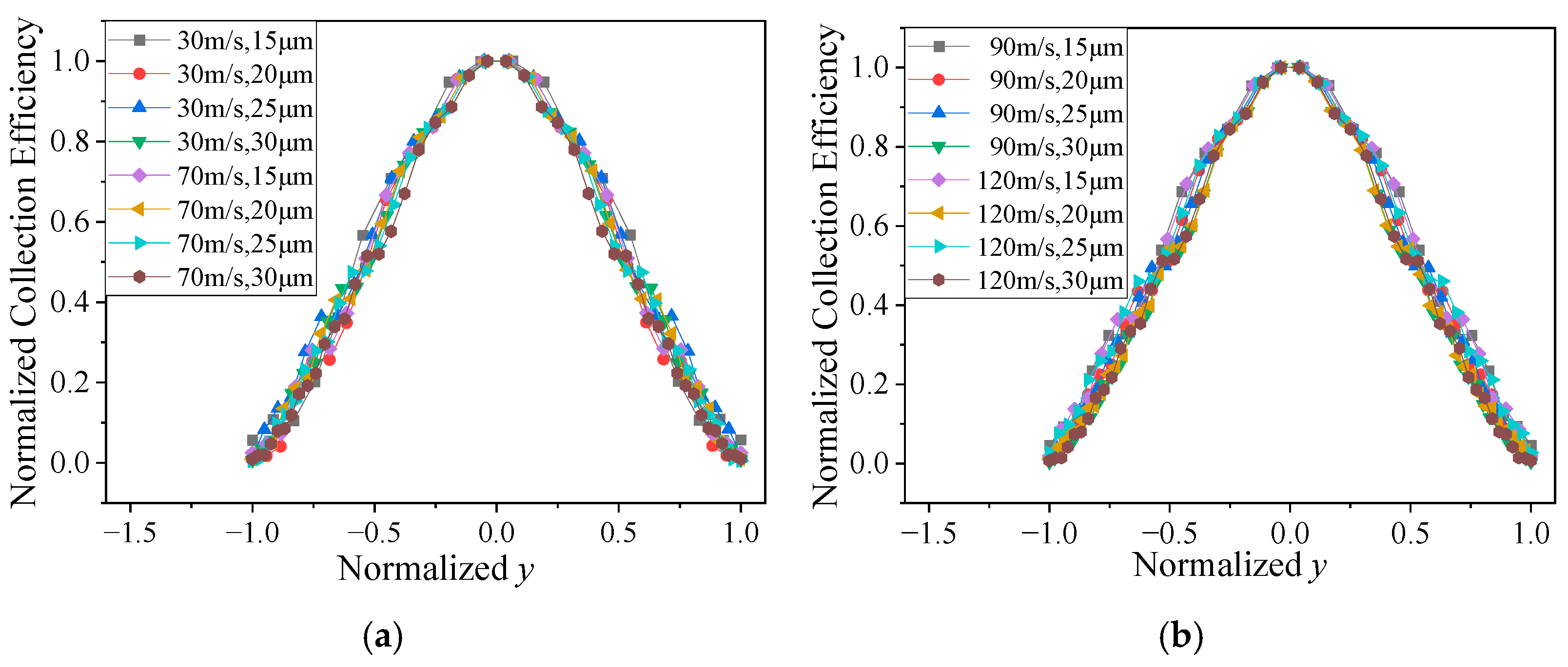
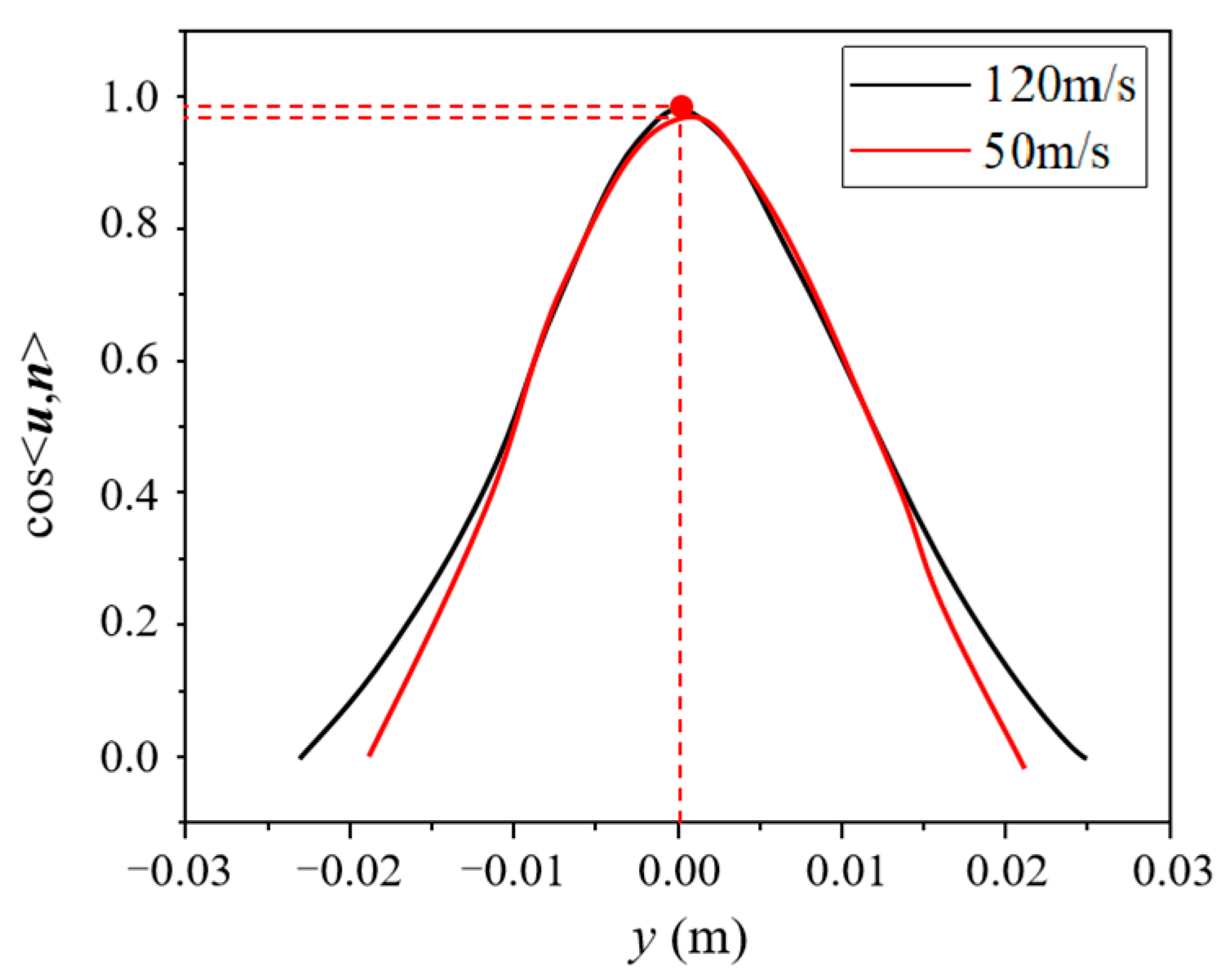
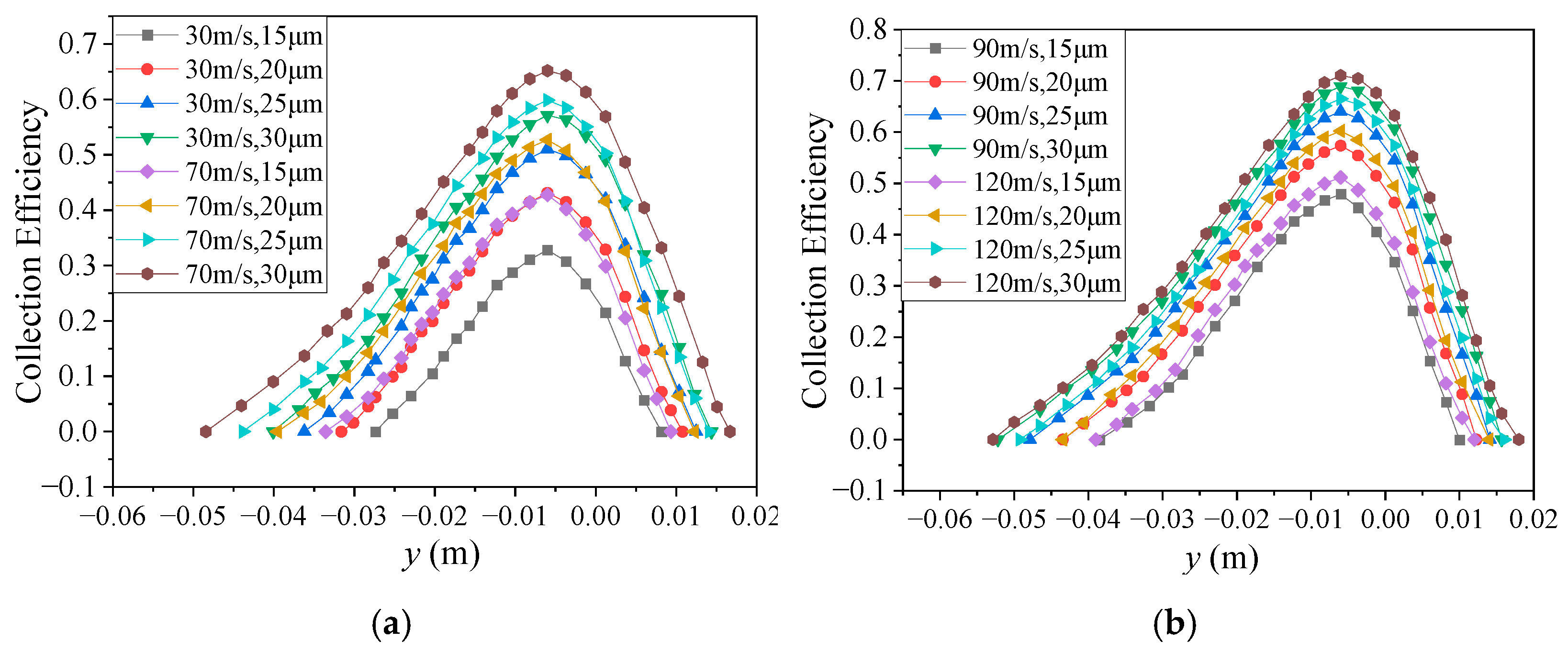
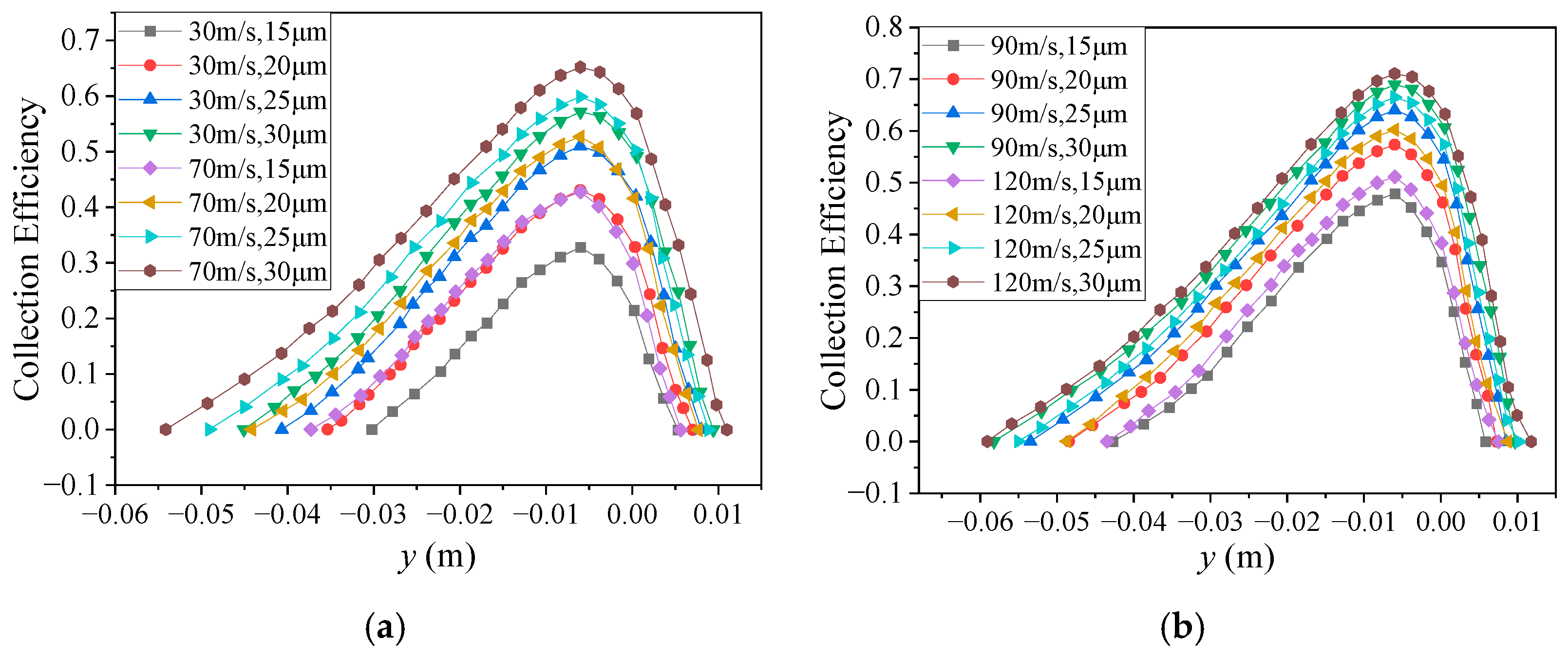
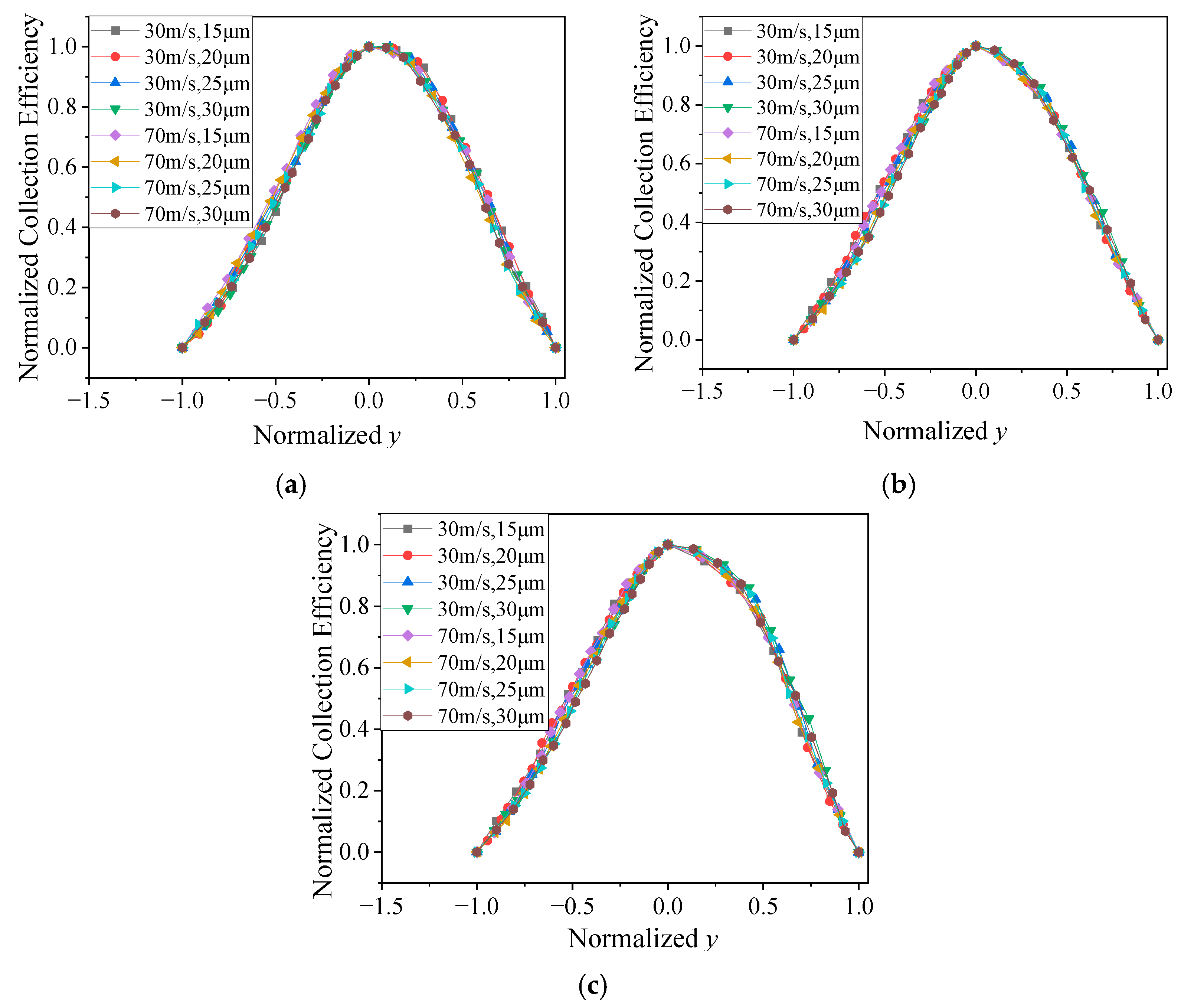
4.2. Regularity in the Collection Efficiency Distribution
4.3. The Effect of Angle of Attack
5. Conclusions
- (1)
- The LWC did not affect the DCE, while the incoming flow velocity and droplet size had remarkable effects on the DCE and the maximum position for the NACA0012 airfoil.
- (2)
- The DCE distribution under different conditions had a highly similar form, which could be normalized to the same distribution using the peak value βmax of DCE and maximum collection position ymax.
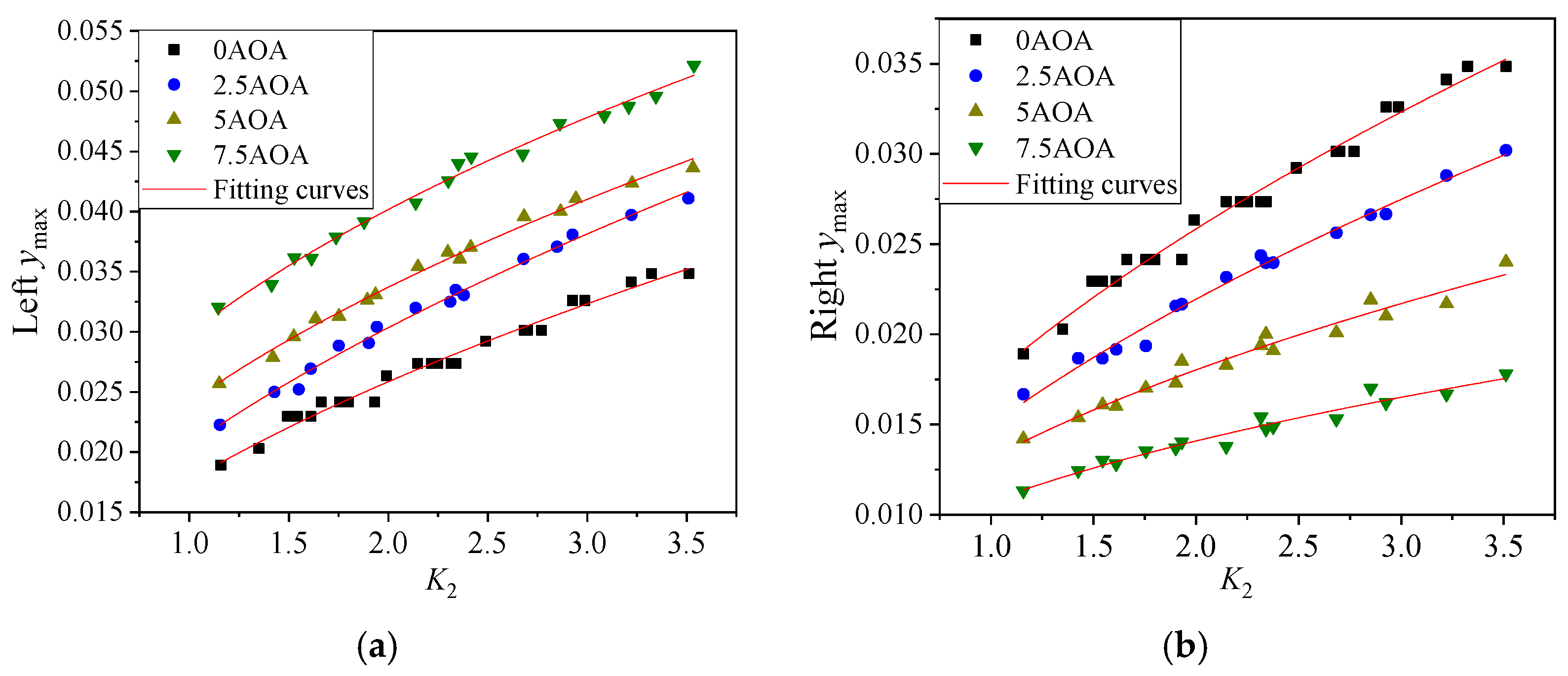
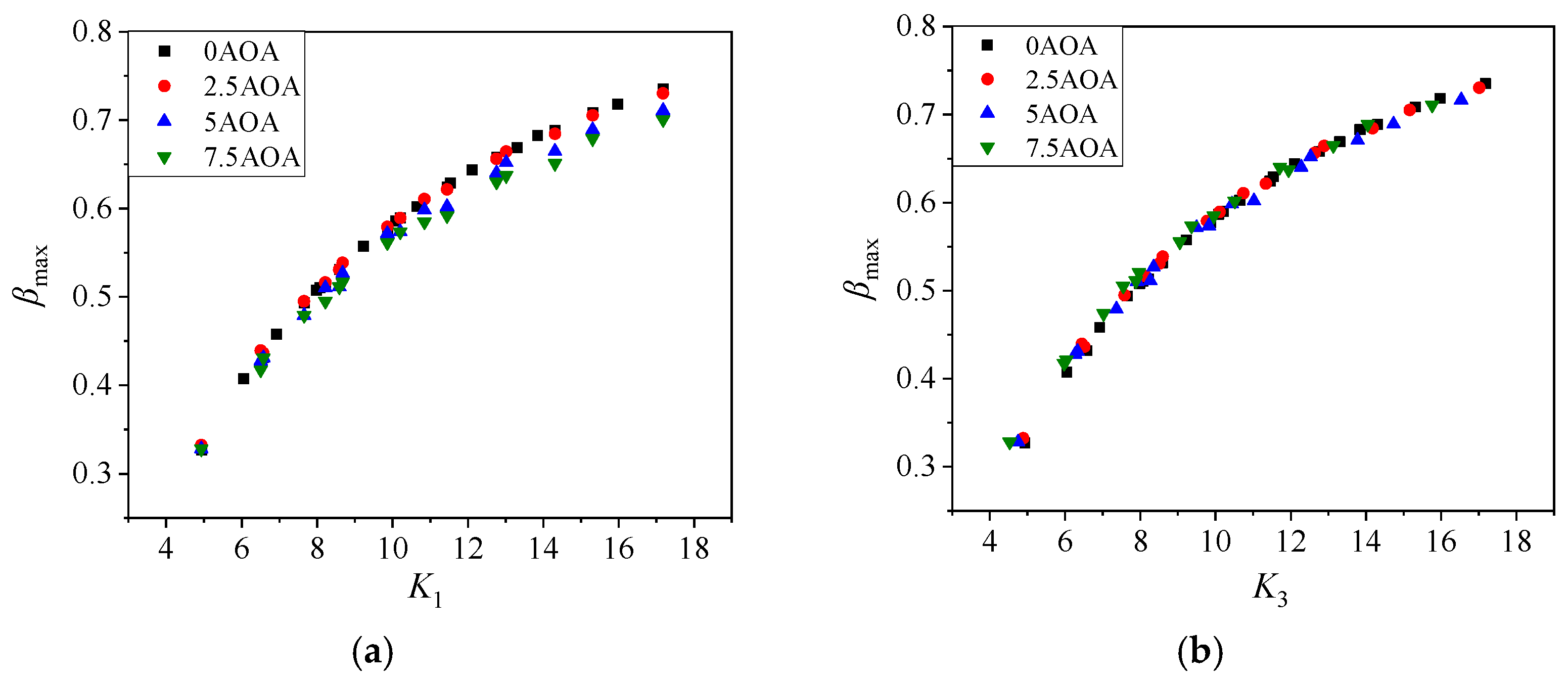
- (3)
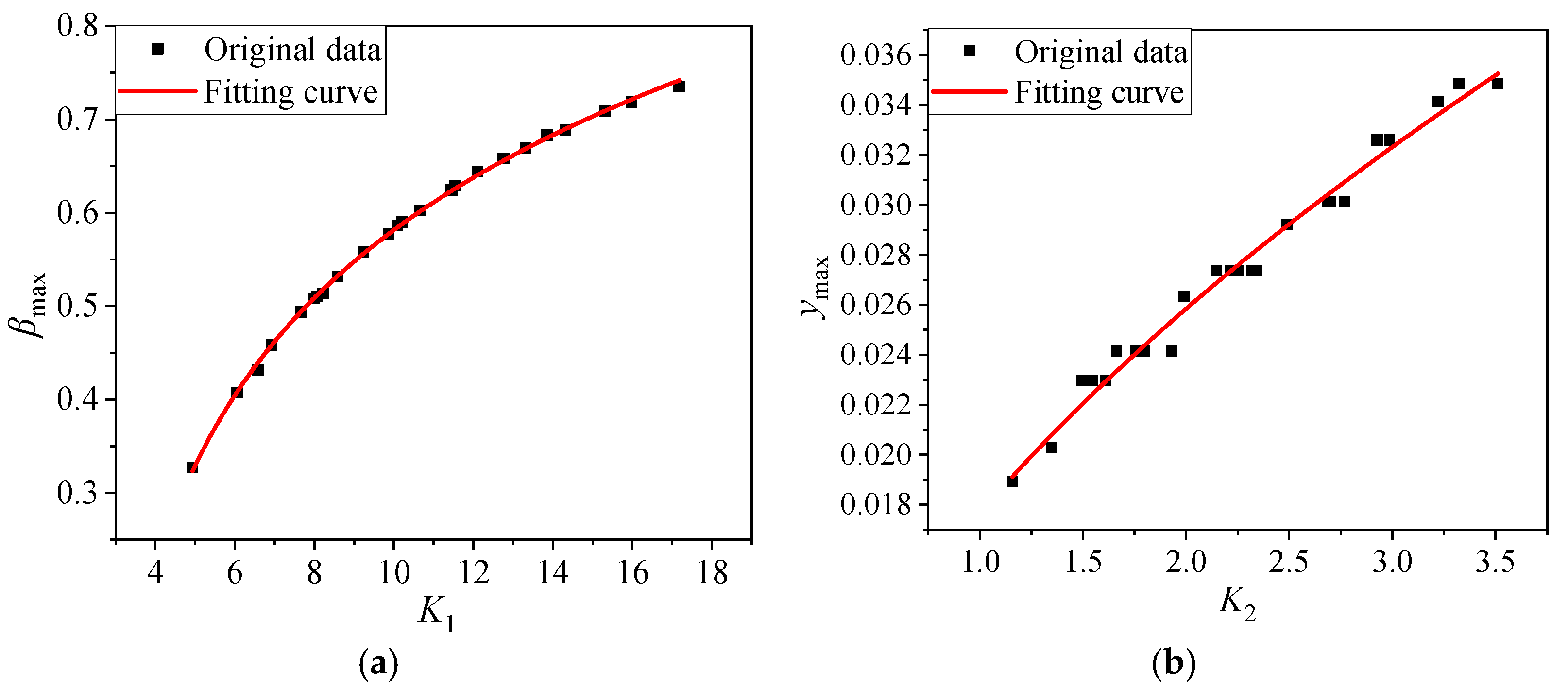
- Intermediate parameters K1 and K2 were used to establish the relationship between incoming flow parameters and the DCE distribution. This regularity was well-fitted using a simple function, which predicted DCE from the droplet and incoming flow parameters.
- (4)
- The shape of an airfoil plays the most important role in the DCE distribution. So, the normal vector of the airfoil surface should be considered first when DCE characteristics are analyzed.
- (5)
- This study provides ideas for predicting the DCE for different models in engineering. Finding the unified normalized curve and establishing the relationship between incoming flow and normalized parameters are meaningful in practice.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Morelli, M.; Zhou, B.Y.; Guardone, A. Simulation and analysis of oscillating airfoil ice shapes via a fully unsteady collection efficiency approach. In Proceedings of the 75th Annual Vertical Flight Society Forum and Technology Display (FORUM 75): The Future of Vertical Flight, Philadelphia, PA, USA, 13–16 May 2019. [Google Scholar]
- Cao, Y.; Huang, J.; Yin, J. Numerical simulation of three-dimensional ice accretion on an aircraft wing. Int. J. Heat Mass Transf. 2016, 92, 34–54. [Google Scholar] [CrossRef]
- You, T.; Sun, Y.; Zhang, Y.; Chen, J.; Zhang, P.; Yang, M. Accelerated frequent closed sequential pattern mining for uncertain data. Expert Syst. Appl. 2022, 204, 117254. [Google Scholar] [CrossRef]
- Liu, T.; Qu, K.; Cai, J.; Pan, S. A three-dimensional aircraft ice accretion model based on the numerical solution of the unsteady Stefan problem. Aerosp. Sci. Technol. 2019, 93, 105328. [Google Scholar] [CrossRef]
- McClain, S.T.; Vargas, M.M.; Tsao, J.C.; Broeren, A.P. Influence of airfoil angle of attack on ice accretion roughness. In Proceedings of the AIAA Aviation 2020 Forum, Virtual Event, 15–19 June 2020. [Google Scholar]
- Krishnakumar, M.; Lingadurai, K.; Mukesh, R.; Princeraj, L.; Naveen, V.; Kavya, M. Performance analysis of NACA2411 ice accreted original and optimized airfoils. In Proceedings of the International Conference on Material, Manufacturing and Machining, Tamilnadu, India, 8–9 March 2019. [Google Scholar]
- Bartkus, T.P.; Struk, P.M.; Tsao, J.C. Evaluation of a thermodynamic ice-crystal icing model using experimental ice accretion data. In Proceedings of the Atmospheric and Space Environments Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Li, S.; Paoli, R. Modeling of ice accretion over aircraft wings using a compressible OpenFOAM solver. Int. J. Aerospace. Eng. 2019, 2019, 4864927. [Google Scholar] [CrossRef]
- Nilamdeen, S.; Rao, V.S.; Switchenko, D.; Selvanayagam, J.; Ozcer, I.; Baruzzi, G.S. Numerical Simulation of Ice Crystal Accretion Inside an Engine Core Stator; SAE Technical Paper 2019-01-2017; SAE International: New York, NY, USA, 2019. [Google Scholar]
- Hamed, A.; Das, K.; Basu, D. Numerical simulations of ice droplet trajectories and collection efficiency on aero-engine rotating machinery. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. [Google Scholar]
- Hu, L.; Zhu, X.; Chen, J.; Shen, X.; Du, Z. Numerical simulation of rime ice on NREL Phase VI blade. J. Wind Eng. Ind. Aerod. 2018, 178, 57–68. [Google Scholar] [CrossRef]
- Ibrahim, G.M.; Pope, K.; Muzychka, Y.S. Effects of blade design on ice accretion for horizontal axis wind turbines. J. Wind Eng. Ind. Aerod. 2018, 173, 39–52. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, H. An experimental investigation on the unsteady heat transfer process over an ice accreting airfoil surface. Int. J. Heat Mass Transfer 2018, 122, 707–718. [Google Scholar] [CrossRef]
- McClain, S.T.; Vargas, M.; Tsao, J.C.; Broeren, A. Influence of freestream temperature on ice accretion roughness. SAE Int. J. Adv. Curr. Prac. Mobility 2020, 2, 227–237. [Google Scholar]
- Shin, J.; Bond, T.H. Experimental and Computational Ice Shapes and Resulting Drag Increase for a NACA0012 Airfoil. In Proceedings of the Fifth Symposium on Numerical and Physical Aspects of Aerodynamic Flows, Long Beach, CA, USA, 13–16 January 1992. NASA-TM-105743. [Google Scholar]
- Ruff, G.A.; Berkowitz, B.M. Users Manual for the NASA Lewis Ice Accretion Prediction Code (LEWICE); NASA-CR-185129; NASA: Washington, DC, USA, 1990.
- Wright, W.B. Users Manual for the Improved NASA Lewis Ice Accretion Code LEWICE 1.6; NASA-CR-198355; NASA: Washington, DC, USA, 1995.
- Hedde, T.; Guffond, D. Improvement of the ONERA 3D icing code, comparison with 3D experimental shapes. In Proceedings of the 31st Aerospace Sciences Meeting, Reno, NV, USA, 11–14 January 1993. [Google Scholar]
- Bourgault, Y.; Habashi, W.G.; Dompierre, J.; Baruzzi, G.S. A finite element method study of Eulerian droplets impingement models. Int. J. Numer. Methods Fluids 1999, 29, 429–449. [Google Scholar] [CrossRef]
- Bourgault, Y.; Boutanios, Z.; Habashi, W.G. Three-dimensional Eulerian approach to droplet impingement simulation using FENSAP-ICE, Part 1: Model, algorithm, and validation. J. Aircr. 2000, 37, 95–103. [Google Scholar] [CrossRef]
- Wirogo, S.; Srirambhatla, S. An Eulerian method to calculate the collection efficiency on two and three dimensional bodies. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003. [Google Scholar]
- Tong, X.; Luke, E. Eulerian simulations of icing collection efficiency using a singularity diffusion model. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. [Google Scholar]
- Iuliano, E.; Brandi, V.; Mingione, G.; Nicola, C.; Tognaccini, R. Water impingement prediction on multi-element airfoils by means of Eulerian and Lagrangian approach with viscous and inviscid air flow. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. [Google Scholar]
- Yoon, T.; Yee, K. Correction of local collection efficiency based on roughness element concept for glaze ice simulation. J. Mech. 2020, 36, 607–622. [Google Scholar] [CrossRef]
- Li, Z.; Tong, X.; Sun, J.; Jiang, F.; Yang, G.; Xiao, J. Methods and criterion for adaptive ICE accretion simulation: Mesh boundary merge and reconstruction. Int. J. Appl. Mech. 2020, 12, 2050105. [Google Scholar] [CrossRef]
- Takahashi, T.; Fukudome, K.; Mamori, H.; Fukushima, N.; Yamamoto, M. Effect of characteristic phenomena and temperature on super-cooled large droplet icing on NACA0012 airfoil and axial fan blade. Aerospace 2020, 7, 92. [Google Scholar] [CrossRef]
- Wen, C.Y. Mechanics of fluidization. Fluid Part. Technol. Chem. Eng. Prog. Symp. Ser. 1966, 62, 100–111. [Google Scholar]
- Gidaspow, D. Hydrodynamics of fiuidizatlon and heat transfer: Supercomputer modeling. Appl. Mech. Rev. 1986, 39, 1–23. [Google Scholar] [CrossRef]
- Papadakis, M.; Wong, S.C.; Rachman, A.; Huang, K.E.; Vu, G.T.; Bidwell, C.S. Large and Small Droplet Impingement Data on Airfoils and Two Simulated Ice Shapes; NASA/TM-2007-213959; NASA: Washington, DC, USA, 2007.
- Messinger, B.L. Equilibrium temperature of an unheated icing surface as a function of air speed. J. Aeronaut. Sci. 1953, 20, 29–42. [Google Scholar] [CrossRef]
- da Silva, G.A.L.; Arima, M.N.; Branco, N.N.; de Mattos, P.M. Proposed wall function models for heat transfer around a cylinder with rough surface in cross flow. In Proceedings of the SAE 2011 International Conference on Aircraft and Engine Icing and Ground Deicing, Chicago, IL, USA, 13–19 June 2011. [Google Scholar]

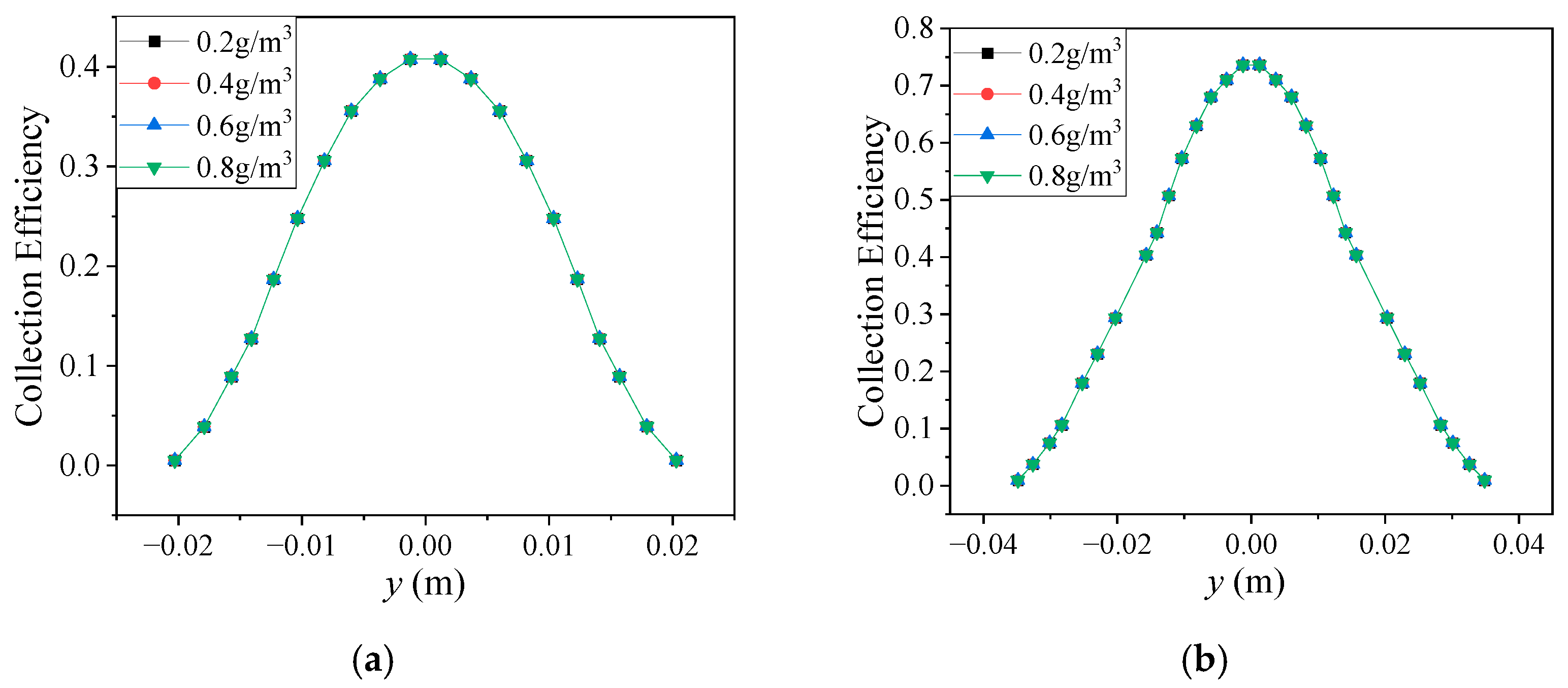



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Xu, Q.; Wu, F.; Xia, Q.; Xu, Q.; Li, S. Droplet Collection Efficiency Regularity of NACA0012 Airfoil Based on the Eulerian Method. Aerospace 2023, 10, 412. https://doi.org/10.3390/aerospace10050412
Wu J, Xu Q, Wu F, Xia Q, Xu Q, Li S. Droplet Collection Efficiency Regularity of NACA0012 Airfoil Based on the Eulerian Method. Aerospace. 2023; 10(5):412. https://doi.org/10.3390/aerospace10050412
Chicago/Turabian StyleWu, Jie, Quanyong Xu, Feng Wu, Quanzhong Xia, Qiannan Xu, and Shufeng Li. 2023. "Droplet Collection Efficiency Regularity of NACA0012 Airfoil Based on the Eulerian Method" Aerospace 10, no. 5: 412. https://doi.org/10.3390/aerospace10050412
APA StyleWu, J., Xu, Q., Wu, F., Xia, Q., Xu, Q., & Li, S. (2023). Droplet Collection Efficiency Regularity of NACA0012 Airfoil Based on the Eulerian Method. Aerospace, 10(5), 412. https://doi.org/10.3390/aerospace10050412




