Development of a High-Performance Low-Weight Hydraulic Damper for Active Vibration Control of the Main Rotor on Helicopters—Part 1: Design and Mathematical Model
Abstract
1. Introduction
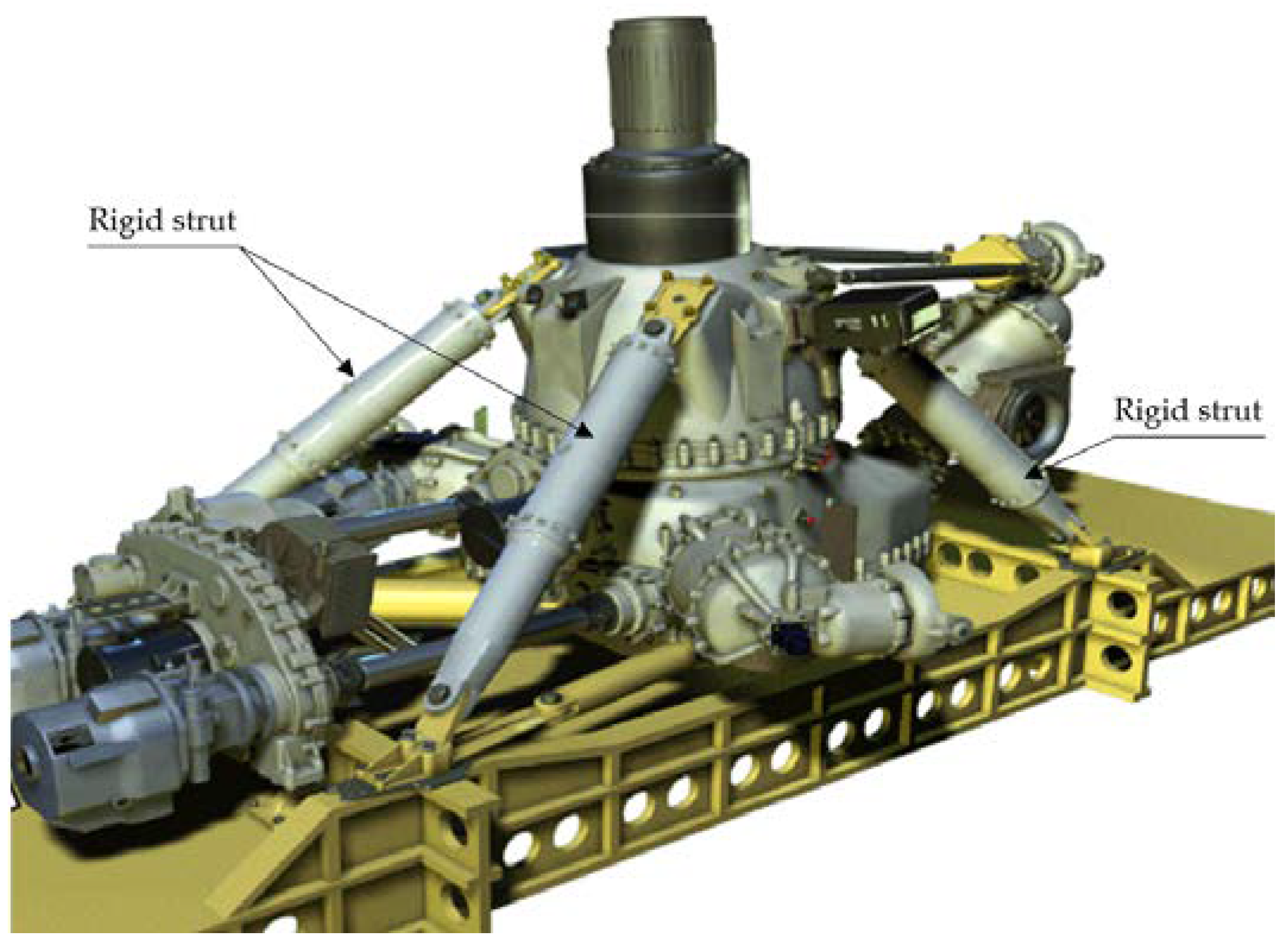
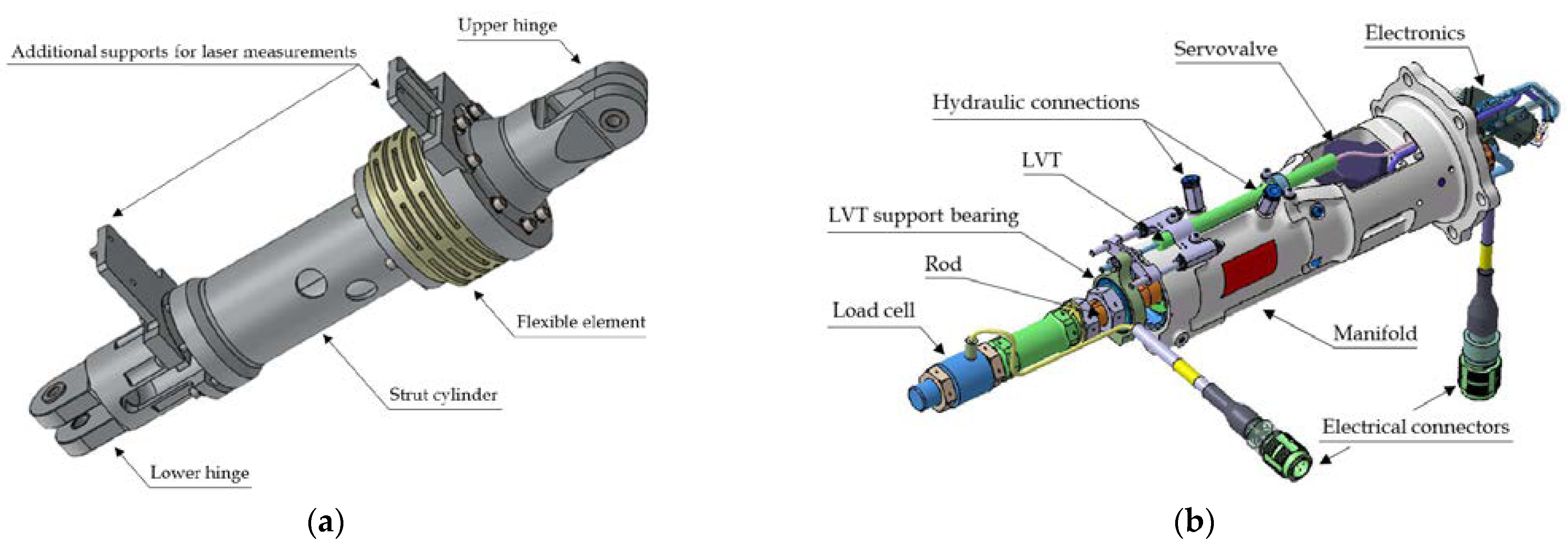
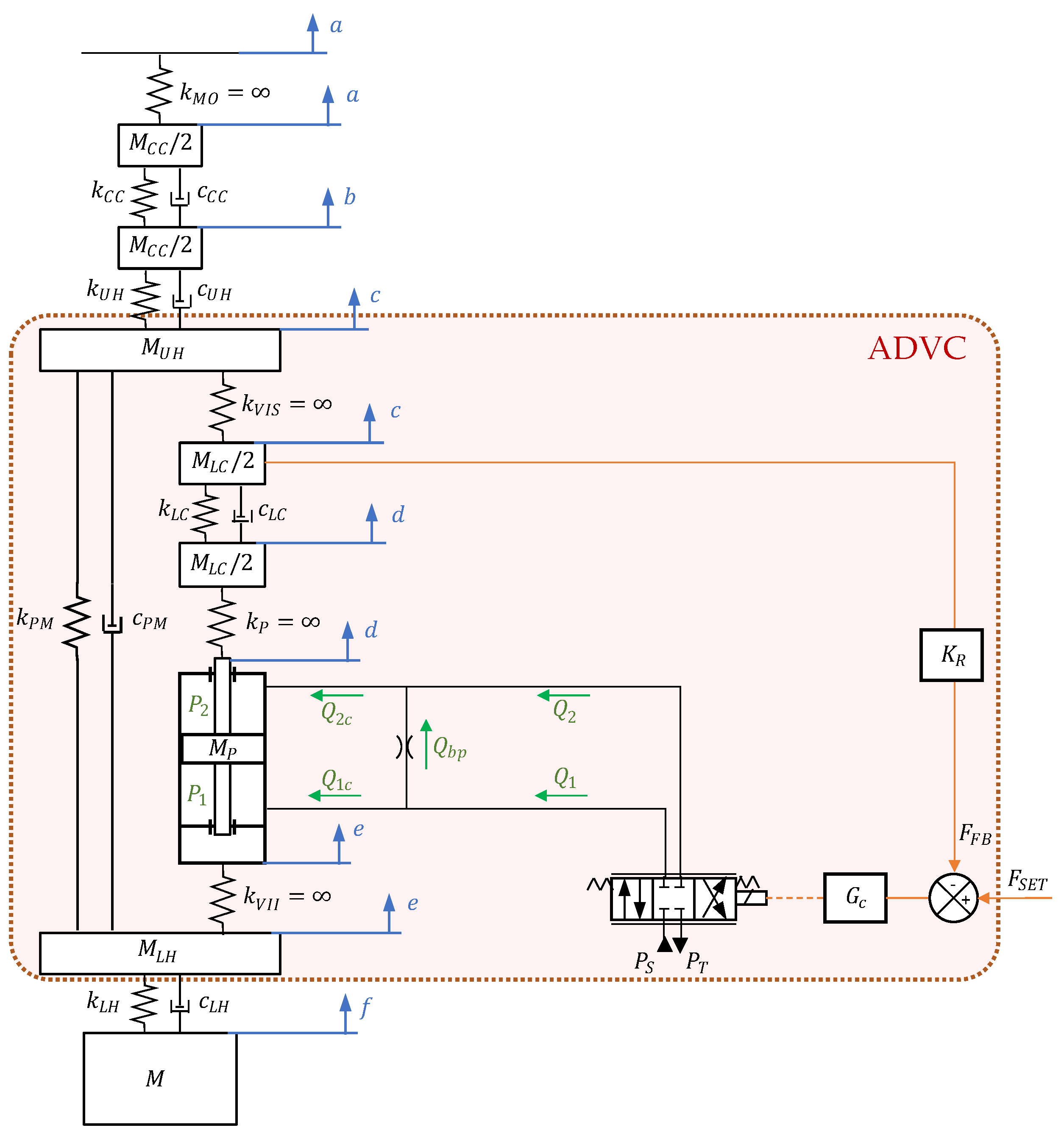
2. Active Damper Architecture
3. Technical and Performance Specifications
4. Mathematical Model
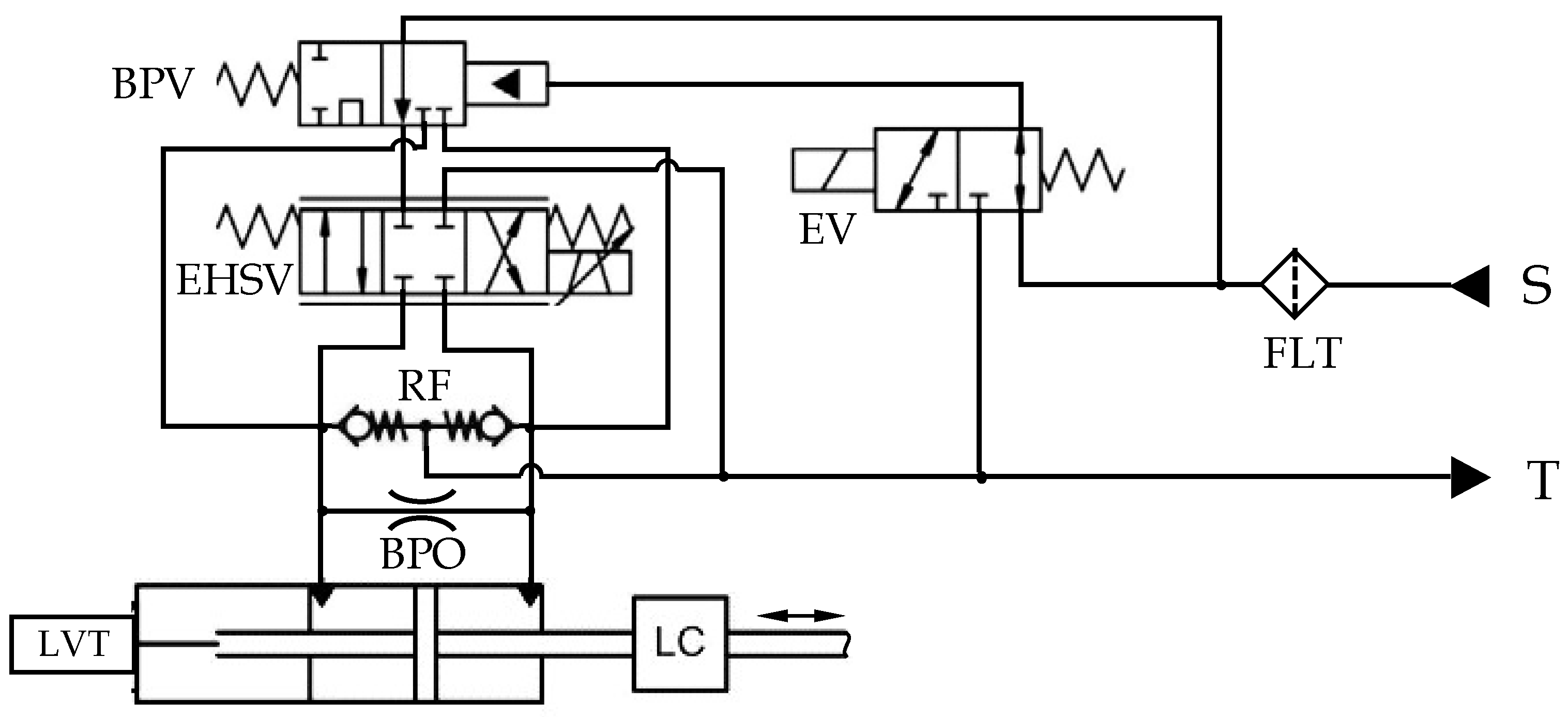
4.1. Electrohydraulic Servovalve (EHSV)
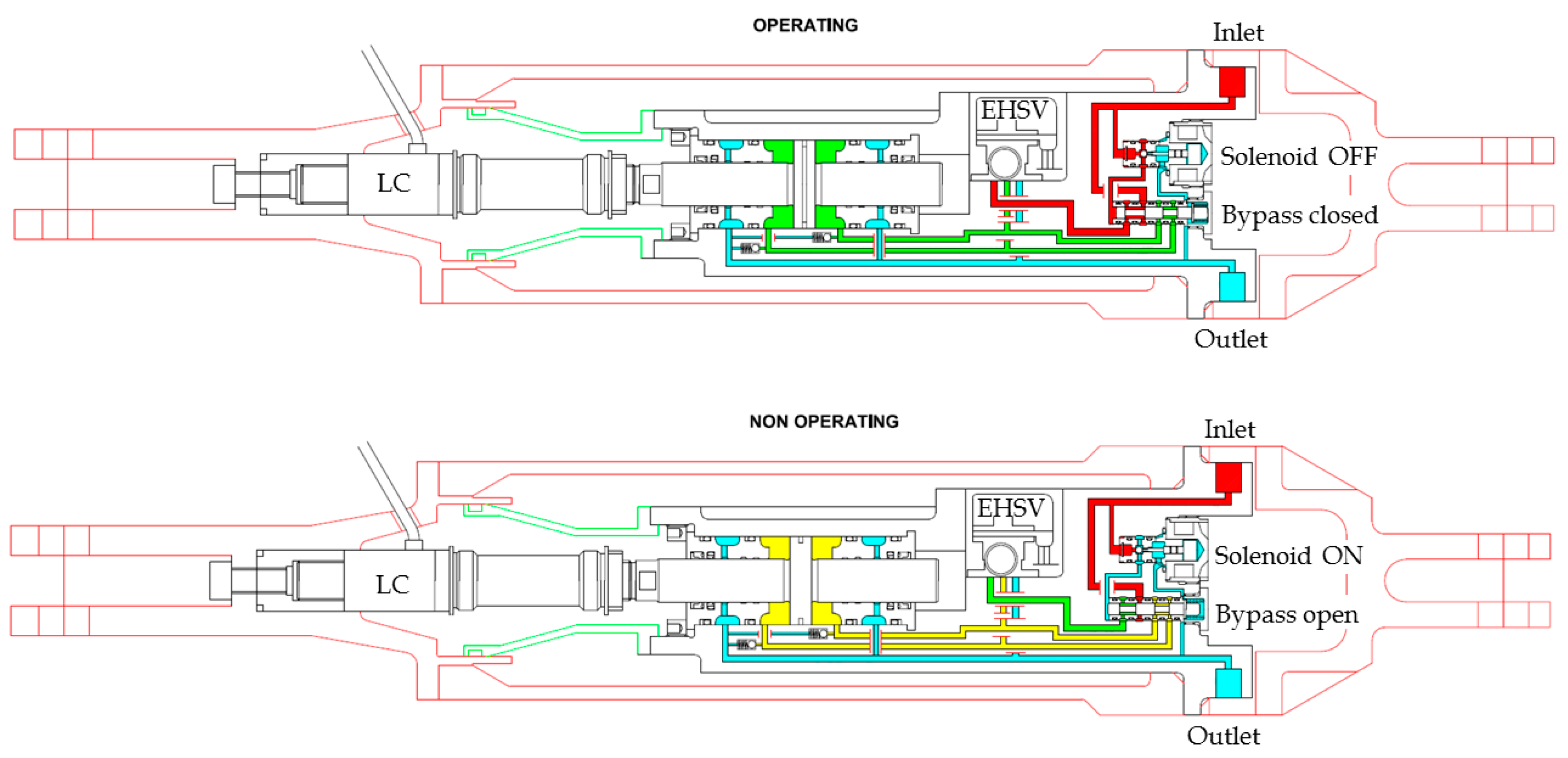
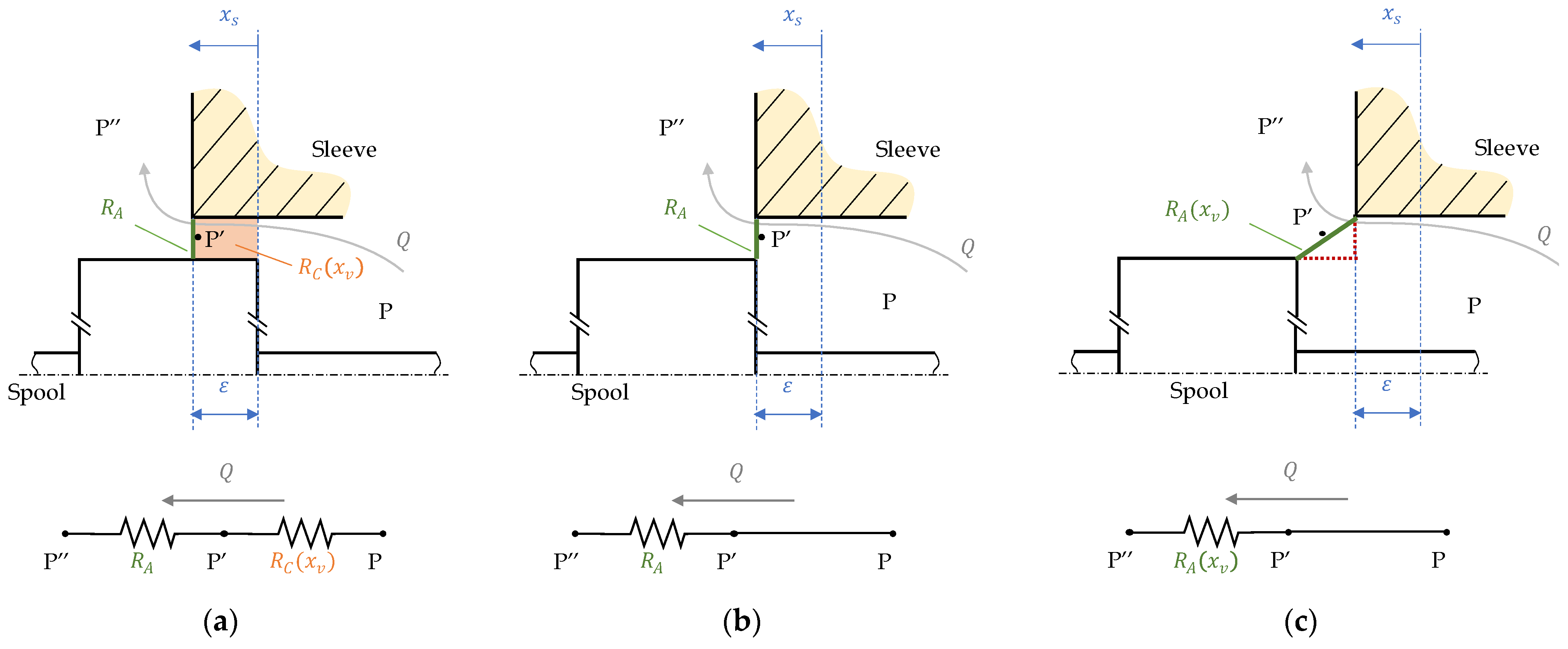
4.2. Bypass Orifice
4.3. Actuator
4.4. Electronic Control Unit
5. Results and Preliminary Design Validation
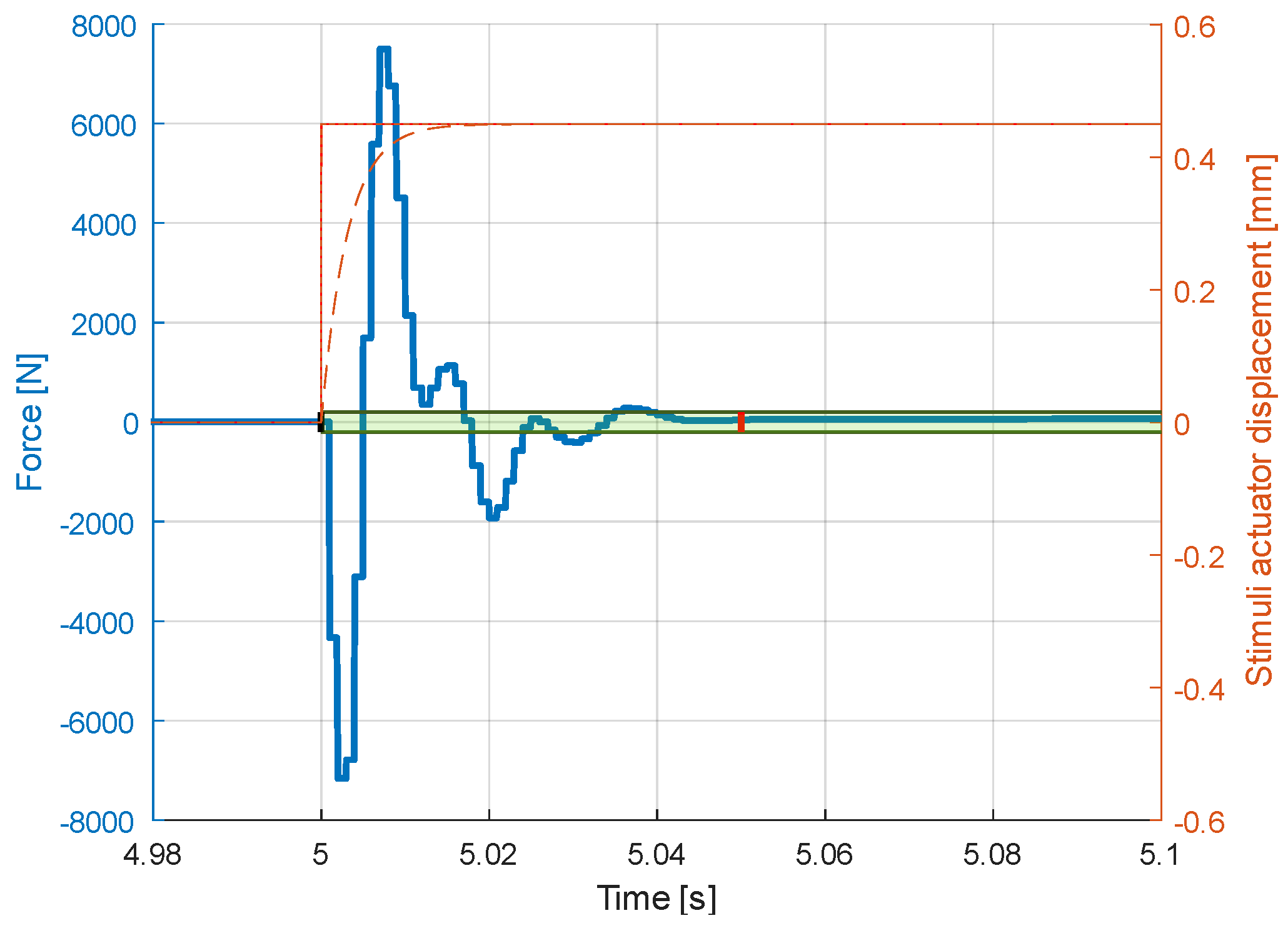
5.1. Stall Load Test
5.2. Compliant Structure’s Stiffness Test
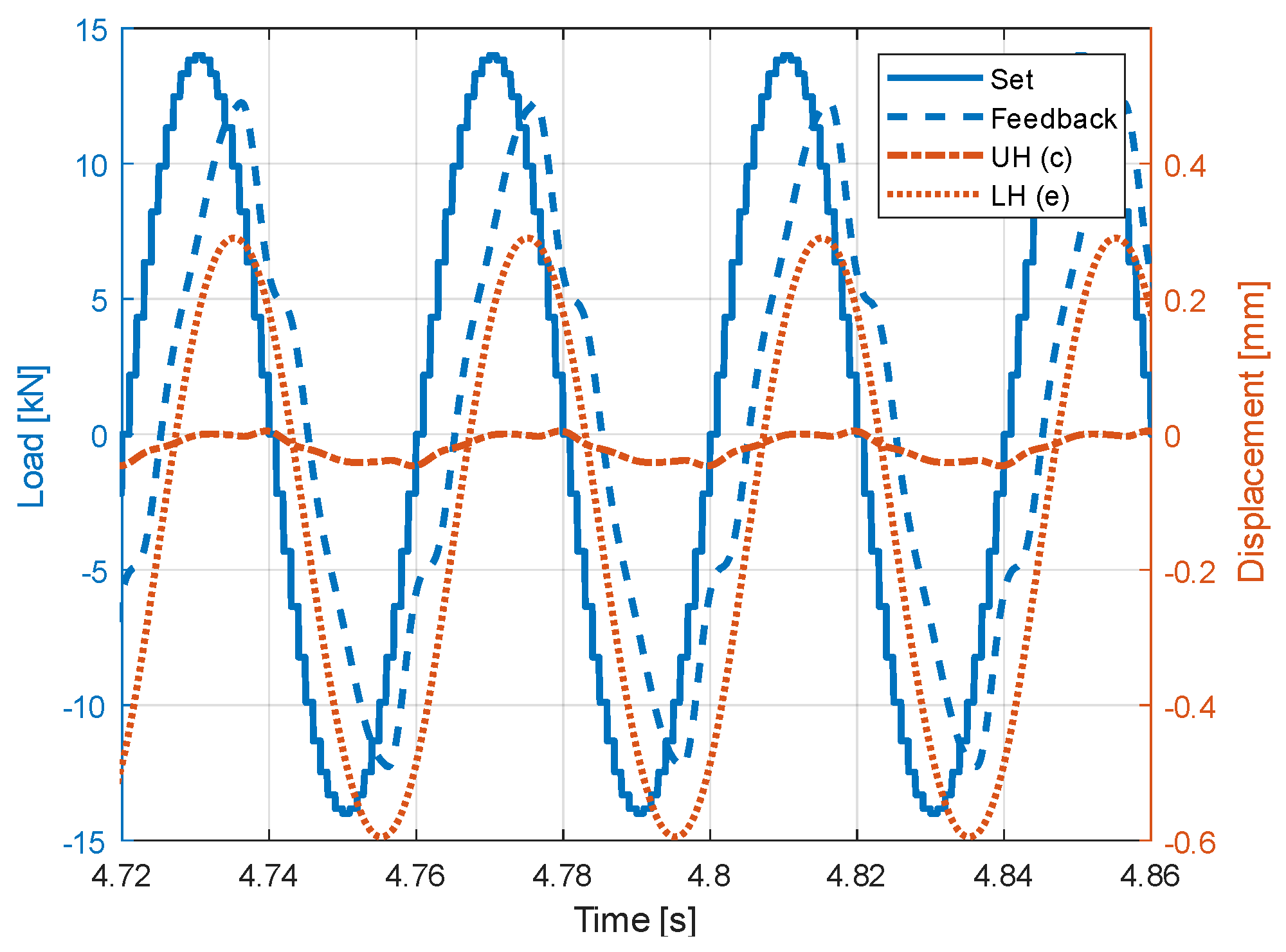
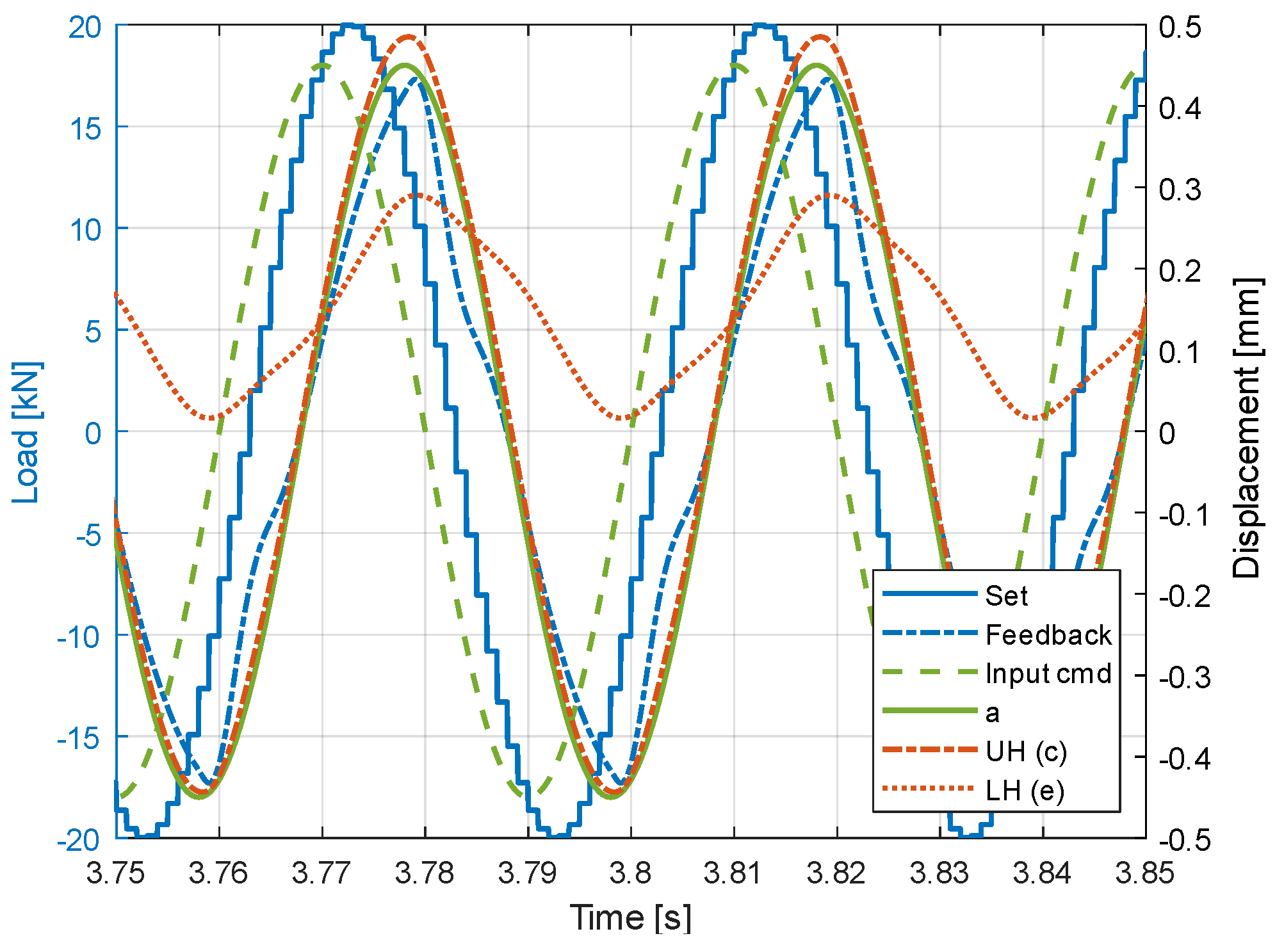
5.3. Actuator Controllability
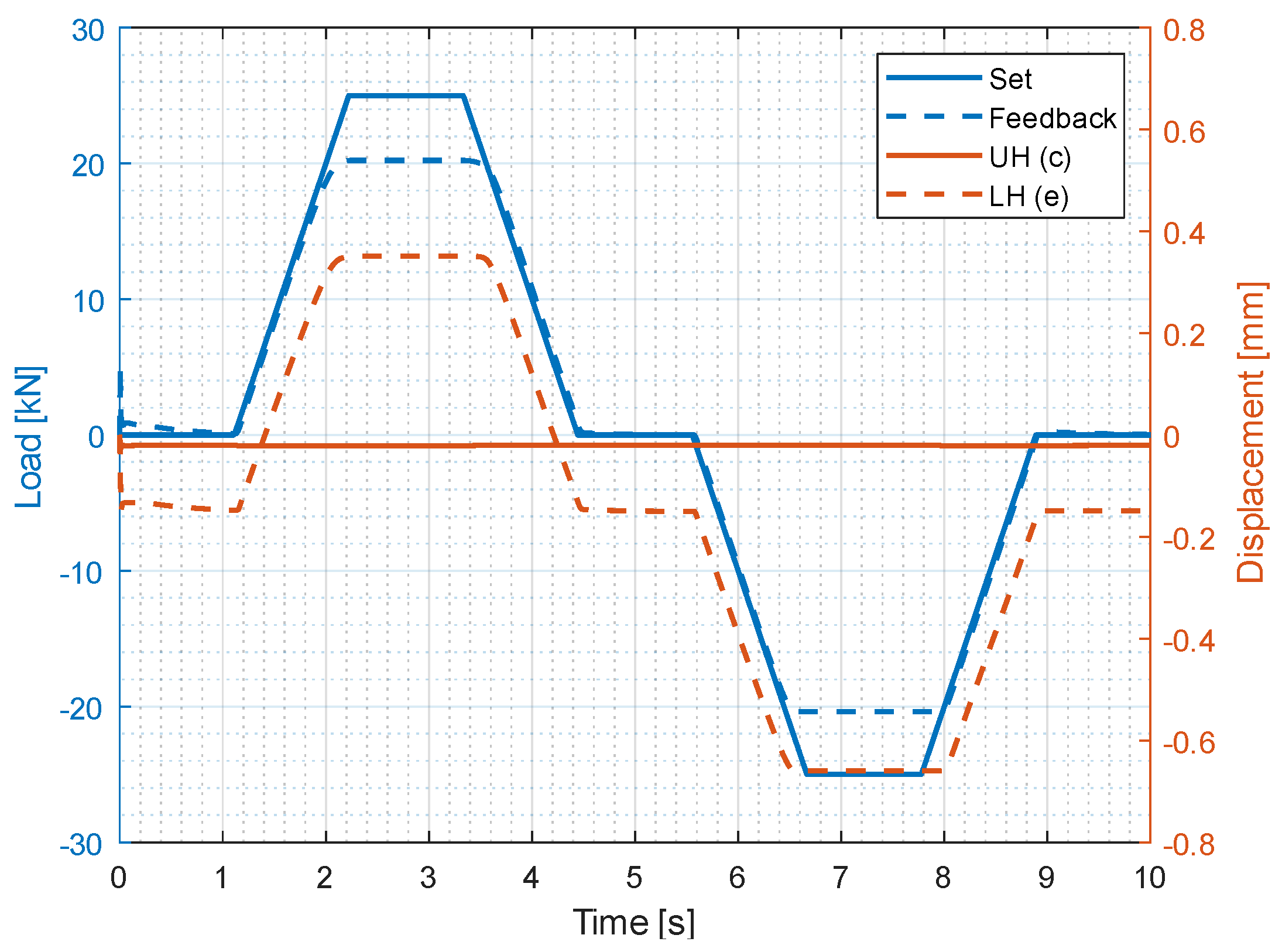
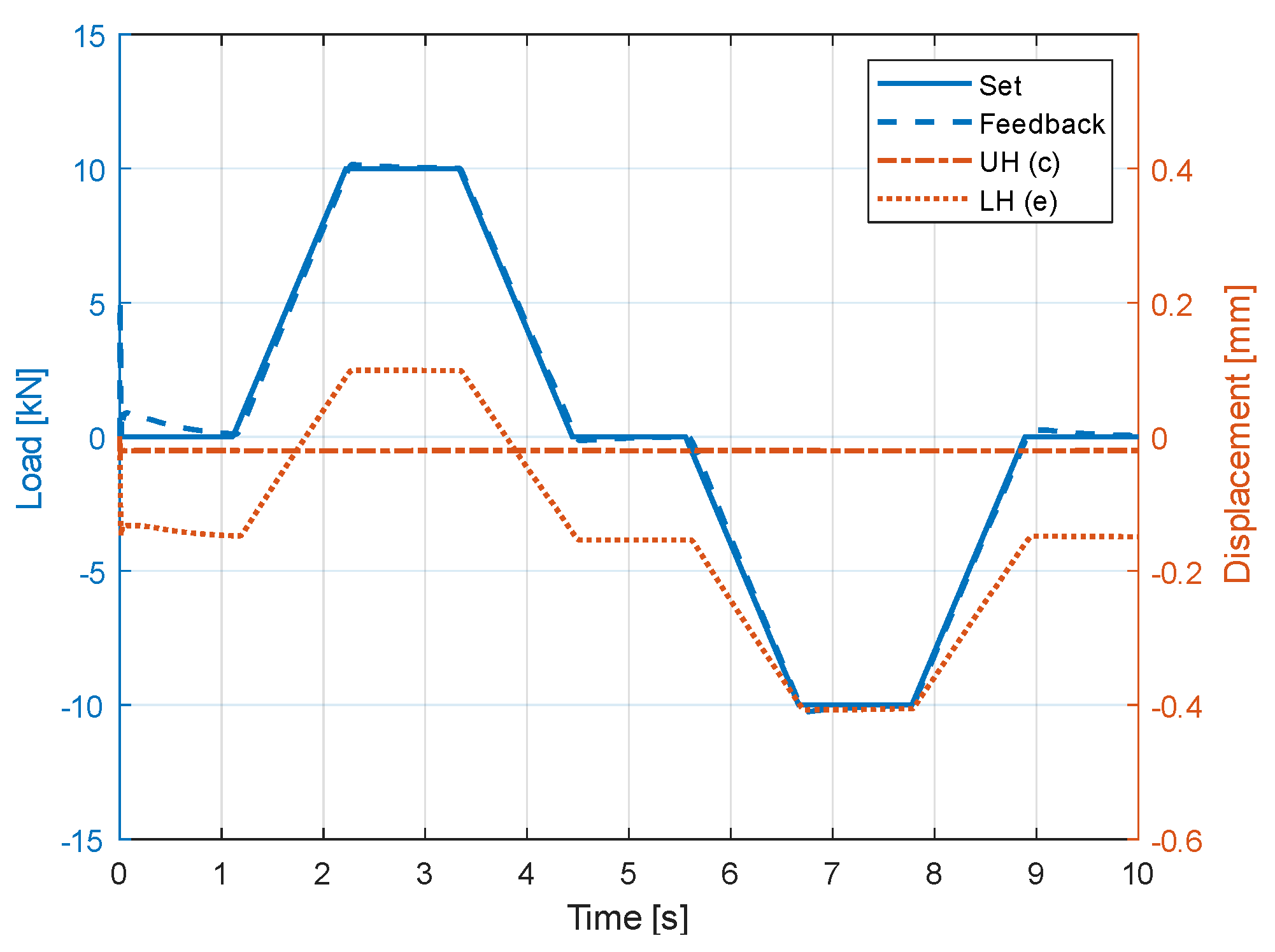
5.4. Frequency Response of the System with the Hung Mass
5.5. Displacement Transmissibility
5.6. Response to a Step Disturbance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Krysinski, T.; Malburet, F. Mechanical Vibrations—Active and Passive Control, 2nd ed.; ISTE Ltd.: London, UK, 2021; ISBN 9781905209293. [Google Scholar]
- Tamer, A.; Muscarello, V.; Masarati, P.; Quaranta, G. Evaluation of Vibration Reduction Devices for Helicopter Ride Quality Improvement. Aerosp. Sci. Technol. 2019, 95, 105456. [Google Scholar] [CrossRef]
- Delcor, L.; Parizet, E.; Ganivet-Ouzeneau, J.; Caillet, J. Model of Sound and Vibration Discomfort in Helicopter Cabins. Appl. Acoust. 2022, 195, 108847. [Google Scholar] [CrossRef]
- Harrer, K.L.; Yniguez, D.; Majar, M.; Ellenbecker, D.; Estrada, N.; Geiger, M. Whole Body Vibration Exposure for MH-60S Pilots. In Proceedings of the Forty Third Annual SAFE Association Symposium, Salt Lake City, UT, USA, 13–16 May 2005. [Google Scholar]
- Paul, W.F.; Mard, K.C. Vibration Damped Helicopter Rotor. U.S. Patent 3540809, 17 November 1970. [Google Scholar]
- Wachs, M.A. The Main Rotor Bifilar Absorber and Its Effect on Helicopter Reliability/Maintainability. SAE Tech. Pap. 1973, 82, 2972–2981. [Google Scholar] [CrossRef]
- Frahm, H. Device for Damping Vibrations of Bodies. U.S. Patent 989958, 18 April 1911. [Google Scholar]
- Welsh, W.A. Helicopter Vibration Reduction. In Morphing Wing Technologies: Large Commercial Aircraft and Civil Helicopters; Elsevier Ltd.: Stratford, CT, USA, 2018; pp. 865–892. ISBN 9780081009642. [Google Scholar]
- Ferris, D.L.; Smith, G.A. Helicopter Rotor Lead-Lag Damper. U.S. Patent 4105365, 8 August 1978. [Google Scholar]
- Lee, C.M.; Goverdovskiy, V.N.; Sotenko, A.V. Helicopter Vibration Isolation: Design Approach and Test Results. J. Sound Vib. 2016, 366, 15–26. [Google Scholar] [CrossRef]
- Jolly, M.R.; Rossetti, D.J.; Norris, M.A.; Miller, L.R. Hybrid Active-Passive Noise and Vibration Control System for Aircraft. U.S. Patent 5845236, 1 December 1996. [Google Scholar]
- Flannelly, W.G. Dynamic Antiresonant Vibration Isolator. U.S. Patent 3322379, 30 May 1967. [Google Scholar]
- Braun, D. Development of Antiresonance Force Isolators for Helicopter Vibration Reduction. J. Am. Helicopter Soc. 1982, 27, 37–44. [Google Scholar] [CrossRef]
- Riedel, K. Vibration Analysis and Testing of Bell 429 Helicopter. In Proceedings of the American Helicopter 66th Annual Forum, Phoenix, AZ, USA, 11–13 May 2010; American Helicopter Society International: Phoenix, AZ, USA, 2010. [Google Scholar]
- Hege, P.; Genoux, G. The Sarib Vibration Absorber. In Proceedings of the Ninth European Rotorcraft and Powered Lift Aircraft Forum, Stresa, Italy, 13–15 September 1983. [Google Scholar]
- Cresap, W.L.; Myers, A.W.; Viswanathan, S.P. Pylon Mounting System for Reducing Helicopter Vibration. U.S. Patent 4362281, 7 December 1982. [Google Scholar]
- Griffin, M.D.; Hendricks, M.W. Helicopter Transmission Mount System. U.S. Patent 9254914, 9 February 2015. [Google Scholar]
- Wang, F.; Lu, Y.; Lee, H.P.; Ma, X. Vibration and Noise Attenuation Performance of Compounded Periodic Struts for Helicopter Gearbox System. J. Sound Vib. 2019, 458, 407–425. [Google Scholar] [CrossRef]
- Pearson, J.T.; Goodall, R.M.; Lyndon, I. Active Control of Helicopter Vibration. Comput. Control Eng. J. 1994, 5, 277–284. [Google Scholar] [CrossRef]
- Lyu, W.L. Method for Eliminating Aerodynamic Lift Vibration of Rigid Rotor Helicopters Based on the Novel Sine-Trim Model. Aerosp. Sci. Technol. 2020, 98, 105655. [Google Scholar] [CrossRef]
- Mura, R.; Lovera, M. Baseline Vibration Attenuation in Helicopters: Robust MIMO-HHC Control; IFAC: New York, NY, USA, 2014; Volume 19, ISBN 9783902823625. [Google Scholar]
- Yang, R.; Gao, Y.; Wang, H.; Ni, X. Reducing Helicopter Vibration Loads by Individual Blade Control with Genetic Algorithm. Machines 2022, 10, 479. [Google Scholar] [CrossRef]
- Millott, T.; Friedmann, P. Vibration Reduction in Helicopter Rotors Using an Actively Controlled Partial Span Trailing Edge Flap Located on the Blade. Nasa Contractor Report, 1 June 1994; Volume 4611, 19940031916. [Google Scholar]
- Zhou, Z.X.; Huang, X.C.; Tian, J.J.; Hua, H.X.; Tang, M.; Wang, C. Numerical and Experimental Analysis on the Helicopter Rotor Dynamic Load Controlled by the Actively Trailing Edge Flap. Smart Mater. Struct. 2022, 31, 035023. [Google Scholar] [CrossRef]
- Viswamurthy, S.R.; Ganguli, R. Performance Sensitivity of Helicopter Global and Local Optimal Harmonic Vibration Controller. Comput. Math. Appl. 2008, 56, 2468–2480. [Google Scholar] [CrossRef]
- Gianfranceschi, M.; Jacazio, G.; Wang, J. High Bandwidth Electromechanical Actuator for Swashplateless Blade Control System. In Proceedings of the 6th International Conference on Recent Advances in Aerospace Actuation Systems and Components, Toulouse, France, 2–3 April 2014. [Google Scholar]
- Wang, J.; Wang, H.; Wu, C. Development of Swashplateless Helicopter Blade Pitch Control System Using the Limited Angle Direct-Drive Motor (LADDM). Chinese J. Aeronaut. 2015, 28, 1416–1425. [Google Scholar] [CrossRef]
- Kakaley, D.E.; Jolly, M.R.; Buckner, G.D. An Offset Hub Active Vibration Control System for Mitigating Helicopter Vibrations during Power Loss: Simulation and Experimental Demonstration. Aerosp. Sci. Technol. 2018, 77, 610–625. [Google Scholar] [CrossRef]
- Kim, D.H.; Kwak, D.I.; Song, Q. Demonstration of Active Vibration Control System on a Korean Utility Helicopter. Int. J. Aeronaut. Sp. Sci. 2019, 20, 249–259. [Google Scholar] [CrossRef]
- Swanson, D.; Black, P.; Girondin, V.; Bachmeyer, P.; Jolly, M. Active Vibration Control Using Circular Force Generators. In Proceedings of the 41st European Rotorcraft Forum 2015, ERF 2015, Munich, Germany, 1–4 September 2015; Volume 1, pp. 627–637. [Google Scholar]
- Lang, K.; Xia, P.; Shang, L. New Algorithm and Experiments for Helicopter Active Control of Structural Response. J. Aircr. 2022, 59, 1152–1161. [Google Scholar] [CrossRef]
- Duc, D.H.; Mura, R.; Piroddi, L.; Lovera, M.; Luca Ghiringhelli, G. Robust Harmonic Control: An Application to Structural Vibration Reduction in Helicopters. IFAC-PapersOnLine 2015, 28, 263–268. [Google Scholar] [CrossRef]
- Konstanzer, P.; Enenkl, B.; Aubourg, P.A.; Cranga, P. Recent Advances in Eurocopter’s Passive and Active Vibration Control. Annu. Forum Proc. AHS Int. 2008, 1, 854–871. [Google Scholar]
- Shivashankar, P.; Gopalakrishnan, S. Review on the Use of Piezoelectric Materials for Active Vibration, Noise, and Flow Control. Smart Mater. Struct. 2020, 29, 053001. [Google Scholar] [CrossRef]
- Lang, K.; Xia, P. Hybrid Active Vibration Control of Helicopter Fuselage Driven by Piezoelectric Stack Actuators. J. Aircr. 2019, 56, 719–729. [Google Scholar] [CrossRef]
- Meng, D.; Xia, P.; Lang, K.; Smith, E.C.; Rahn, C.D. Neural Network Based Hysteresis Compensation of Piezoelectric Stack Actuator Driven Active Control of Helicopter Vibration. Sens. Actuators A Phys. 2020, 302, 111809. [Google Scholar] [CrossRef]
- Arcara, P.; Bittanti, S.; Lovera, M. Periodic Control of Helicopter Rotors for Attenuation of Vibrations in Forward Flight. IEEE Trans. Control. Syst. Technol. 2000, 8, 883–894. [Google Scholar] [CrossRef]
- Qin, Y.; Lu, Y.; Ma, J.; Yue, H. Active Vibration Control of Helicopter Maneuvering Flight Using Feedforward-Robust Hybrid Control Based on Reference Signal Reconstruction. Shock Vib. 2021, 2021, 3153531. [Google Scholar] [CrossRef]
- King, S.P.; Hughes, C.I. Method and Apparatus for Reducing Vibration of a Helicopter Fuselage. U.S. Patent No. 4819182, 4 April 1989. [Google Scholar]
- Staple, A.E.; Wells, D.M. The Development and Testing of an Active Control of Structural Response System for the EH101 Helicopter. In Proceedings of the 16th European Rotorcraft Forum, London, UK, 1 January 1990. [Google Scholar]
- Mcguire, D.; Miller, L.R.; Jolly, M.R.; Badre-Alam, A. Helicopter Reduced Vibration Isolator Axial Support Strut. U.S. Patent No. 8113321, 14 February 2007. [Google Scholar]
- De Martin, A.; Jacazio, G.; Dellacasa, A.; Sorli, M. High-Fidelity Model of Electro-Hydraulic Actuators for Primary Flight Control Systems. In Proceedings of the Bath/ASME Symposium on Fluid Power and Motion Control, Bath, UK, 12 September 2018; ASME: Bath, UK, 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Ritter, O.; Wende, G.; Gentile, R.; Marino, F.; Bertolino, A.C.; Raviola, A. Intelligent Diagnostics for Aircraft Hydraulic Equipment. In Proceedings of the 4th European Conference of the Prognostics and Health Management Society, Utrecht, The Nederlands, 3–6 July 2018. [Google Scholar]
- Merrit, H.E. Hydraulic Control Systems; John Wiley & Sons, Inc.: New York, NY, USA; London, UK; Sydney, Australia, 1967; ISBN 0471596175. [Google Scholar]
- Jelali, M.; Kroll, A. Hydraulic Servo-Systems: Modeling, Identification and Control; Springer-Verlag London Limited: London, UK, 2003; ISBN 978-1-4471-0099-7. [Google Scholar]
- Van Schothorst, G. Modelling of Long-Stroke Hydraulic Servo-Systems; Mechanical Maritime and Materials Engineering: Delft, The Nederlands, 1997; ISBN 9037001610. [Google Scholar]
- Idelchik, I.E. Handbook of Hydraulic Resistance; Begell House Inc.: Moscow, Russia, 2007; ISBN 9781567002515. [Google Scholar]
- Bertolino, A.C.; Gentile, R.; Jacazio, G.; Marino, F.; Sorli, M. EHSA Primary Flight Controls Seals Wear Degradation Model. In Proceedings of the IMECE2018, Pittsburgh, PA, USA, 9–15 November 2018; ASME, Ed.; ASME: Pittsburgh, PA, USA, 2018; pp. 1–12. [Google Scholar]
- Andersson, S.; Söderberg, A.; Björklund, S. Friction Models for Sliding Dry, Boundary and Mixed Lubricated Contacts. Tribol. Int. 2007, 40, 580–587. [Google Scholar] [CrossRef]
- Bertolino, A.C.; De Martin, A.; Jacazio, G.; Sorli, M. A Case Study on the Detection and Prognosis of Internal Leakages in Electro-Hydraulic Flight Control Actuators. Actuators 2021, 10, 215. [Google Scholar] [CrossRef]


| Description | Value | |
|---|---|---|
| Hydraulic Power Supply | ||
| Hydraulic Fluid | MIL-PRF-83282 | |
| Supply Pressure | 202 210 bar | |
| Return Pressure | 5 7 bar | |
| Proof Pressure, Supply/Return | 310 bar/155 bar | |
| Burst Pressure, Supply/Return | 515 bar/310 bar | |
| Specification Actuator Flow Demand | Up to 5.7 L/min @ 195 bar | |
| Servovalve Rated Flow | 12 L/min @ 207 bar | |
| Electrical Power Supply | ||
| Rated Voltage of Solenoid | 28 VDC ( VDC) | |
| Rated Current of Servovalve | 10 mA Parallel | |
| Solenoid Current Absorption | 0.7 A max @ 28 VDC | |
| Functional and Performance Values | ||
| Stroke, Nominal/Maximum | mm/ mm | |
| Nominal Operating Frequency | Hz | |
| Stall Load, Nominal | kN | |
| Internal Actuator Dry Weight | 5 kg | |
| Total Dry Weight of ADVC | 15.9 kg | |
| Force (N) | Deflection (mm) | Stiffness (kN/mm) | |
|---|---|---|---|
| Compression | 10,109 | 0.253 | 39.986 |
| Extension | 10,039 | 0.253 | 39.714 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bertolino, A.C.; Gaidano, M.; Smorto, S.; Porro, P.G.; Sorli, M. Development of a High-Performance Low-Weight Hydraulic Damper for Active Vibration Control of the Main Rotor on Helicopters—Part 1: Design and Mathematical Model. Aerospace 2023, 10, 391. https://doi.org/10.3390/aerospace10050391
Bertolino AC, Gaidano M, Smorto S, Porro PG, Sorli M. Development of a High-Performance Low-Weight Hydraulic Damper for Active Vibration Control of the Main Rotor on Helicopters—Part 1: Design and Mathematical Model. Aerospace. 2023; 10(5):391. https://doi.org/10.3390/aerospace10050391
Chicago/Turabian StyleBertolino, Antonio Carlo, Matteo Gaidano, Stefano Smorto, Paolo Giovanni Porro, and Massimo Sorli. 2023. "Development of a High-Performance Low-Weight Hydraulic Damper for Active Vibration Control of the Main Rotor on Helicopters—Part 1: Design and Mathematical Model" Aerospace 10, no. 5: 391. https://doi.org/10.3390/aerospace10050391
APA StyleBertolino, A. C., Gaidano, M., Smorto, S., Porro, P. G., & Sorli, M. (2023). Development of a High-Performance Low-Weight Hydraulic Damper for Active Vibration Control of the Main Rotor on Helicopters—Part 1: Design and Mathematical Model. Aerospace, 10(5), 391. https://doi.org/10.3390/aerospace10050391








