Sensitivity Analysis of a Hybrid MCDM Model for Sustainability Assessment—An Example from the Aviation Industry
Abstract
1. Introduction
| Work | MCDM Used | Sensitivity Analysis |
|---|---|---|
| Hsu and Liou (2013) [13] | SWM, DEMATEL, ANP | - |
| Sánchez-Lozano et al. (2015) [14] | AHP and TOPSIS | - |
| Garg (2016) [15] | AHP, TOPSIS | Weights variation |
| Bae et al. (2017) [16] | AHP and TOPSIS | - |
| Görener et al. (2017) [17] | AHP, TOPSIS | - |
| Barak and Dahooei (2018) [18] | SWM, TOPSIS, VIKOR | - |
| Sun et al. (2018) [19] | TOPSIS, VIKOR | - |
| Mahtani, 2018 [20] | AHP | Weights variation |
2. Methodology
2.1. Basic Considerations
2.2. Sustainability-Related Metrics
2.3. Structure of the Hybrid MCDM Tool and Sensitivity Analysis
2.3.1. Factors’ Weights Determination
2.3.2. Assessment of the Tool Sensitivity to the Applied Normalization Technique
2.3.3. Assessment of the Tool to Criteria Weights and Data Variation
3. Results and Discussion
3.1. Circular Economy Indicator Calculation
3.2. Environmental and Economic Impact Indicators Calculation
3.3. Sensitivity Analysis Results
3.3.1. Normalization Method Sensitivity Results
3.3.2. Sensitivity to Weights and Data Variation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| AHP | Analytic Hierarchy Process |
| BWM | Best-Worst Method |
| CE | Circular Economy |
| CEI | Circular Economy Indicator |
| CFRP | Carbon Fiber Reinforced Plastics |
| ELECTRE | Elimination and Choice Translating Reality |
| EoL | End of Life |
| FBP | Fluidized Bed Process |
| GHG | Greenhouse Gases |
| LCA | Life Cycle Assessment |
| LCC | Life Cycle Costing |
| MCDM | Multi-Criteria Decision-Making |
| PAN fibers | Polyacrylonitrile fibers |
| SAW | Simple Additive Weighting |
| TOPSIS | Technique for Order of Preference by Similarity to Ideal Solution |
| TRL | Technology Readiness Level |
| VIKOR | VIseKriterijumska Optimizacija I Kompromisno Resenje |
| WSM | Weighted Sum Model |
References
- European Commission. Flightpath 2050, Europe’s Vision for Aviation; Report of the High Level Group on Aviation Research, Directorate-General for Research and Innovation, Directorate General for Mobility and Transport; European Commission: Brussels, Belgium, 2011; p. 28. [Google Scholar]
- Communication from the Commission to the European Parliament, the European Council, the Council, the European Economic and Social Committee and the Committee of the Regions the European Green Deal com/2019/640 final. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=COM%3A2019%3A640%3AFIN (accessed on 5 April 2022).
- Graver, B.; Rutherford, D.; Zheng, S. CO2 Emissions from Commercial Aviation: 2013, 2018, and 2019; Report of the ICCT (The International Council on Clean Transportation); ICCT: Binangonan, Philippines, 2020. [Google Scholar]
- Gnadt, A.R.; Speth, R.L.; Sabnis, J.S.; Barrett, S.R.H. Technical and environmental assessment of all-electric 180-passenger commercial aircraft. Prog. Aerosp. Sci. 2019, 105, 1–30. [Google Scholar] [CrossRef]
- Léonard, P.; Nylander, J. Sustainability assessment of composites in aero-engine components. In Proceedings of the Design Society: DESIGN Conference; Cambridge University Press: Cambridge, UK, 2020; pp. 1989–1998. [Google Scholar]
- Meng, F.; Cui, Y.; Pickering, S.; McKechnie, J. From aviation to aviation: Environmental and financial viability of closed-loop recycling of carbon fibre composite. Compos. Part B Eng. 2020, 200, 108362. [Google Scholar] [CrossRef]
- Markatos, D.N.; Katsiropoulos, C.; Tserpes, K.; Pantelakis, S. A holistic End-of-Life (EοL) Index for the quantitative impact assessment of CFRP waste recycling techniques. Manuf. Rev. 2021, 8, 18. [Google Scholar]
- Zhang, J.; Chevali, V.S.; Wang, H.; Wang, C.H. Current status of carbon fibre and carbon fibre composites recycling. Compos. B. Eng. 2020, 193, 108053. [Google Scholar] [CrossRef]
- Pimenta, S.; Pinho, S.T. Recycling carbon fibre reinforced polymers for structural applications: Technology review and market outlook. Waste Manag. 2011, 31, 378–392. [Google Scholar] [CrossRef]
- Carbon fibers/Aerospace. Available online: https://www.compositesworld.com/articles/recycled-carbon-fibre-proves-its-potential-for-aircraft-interiors (accessed on 9 January 2023).
- Tapper, R.J.; Longana, M.L.; Norton, A.; Potter, K.D.; Hamerton, I. An evaluation of life cycle assessment and its application to the closed-loop recycling of carbon fibre reinforced polymers. Compos. Part B Eng. 2020, 184, 107665. [Google Scholar] [CrossRef]
- Slavica Dožić, S. Multi-criteria decision making methods: Application in the aviation industry. J. Air Transp. Manag. 2019, 79, 101683. [Google Scholar] [CrossRef]
- Hsu, C.-C.; Liou, J.J.H. An outsourcing provider decision model for the airline industry. J. Air Transp. Manag. 2013, 28, 40–46. [Google Scholar] [CrossRef]
- Sánchez-Lozano, J.M.; Serna, J.; Dolón-Payán, A.; Sánchez-Lozano, J.M.; Serna, J.; Dolón-Payán, A. Evaluating military training aircrafts through the combination of multi-criteria decision making processes with fuzzy logic. A case study in the Spanish Air Force Academy. Aerosp. Sci. Technol. 2015, 42, 58–65. [Google Scholar] [CrossRef]
- Garg, C.P. A robust hybrid decision model for evaluation and selection of the strategic alliance partner in the airline industry. J. Air Transp. Manag. 2016, 52, 55–66. [Google Scholar] [CrossRef]
- Bae, B.-Y.; Kim, S.; Lee, J.-W.; Nguyen, N.V.; Chung, B.-C. Process of establishing design requirements and selecting alternative configurations for conceptual design of a VLA. Chin. J. Aeronaut. 2017, 30, 738–751. [Google Scholar] [CrossRef]
- Görener, A.; Ayvaz, B.; Kusakci, A.O.; Altinokc, E. A hybrid type-2 fuzzy based supplier performance evaluation methodology: The Turkish Airlines technic case. Appl. Soft. Comput. 2017, 56, 436–445. [Google Scholar] [CrossRef]
- Barak, S.; Dahooei, J.H. A novel hybrid fuzzy DEA-Fuzzy MADM method for airlines safety evaluation. J. Air Transp. Manag. 2018, 73, 134–149. [Google Scholar] [CrossRef]
- Sun, G.; Guan, X.; Yi, X.; Zhou, Z. An innovative TOPSIS approach based on hesitant fuzzy correlation coefficient and its applications. Appl. Soft. Comput. 2018, 68, 249–267. [Google Scholar] [CrossRef]
- Mahtani, U.S.; Garg, C.P. An analysis of key factors of financial distress in airline companies in India using fuzzy AHP framework. Transport. Res. Part A 2018, 117, 87–102. [Google Scholar] [CrossRef]
- Athawale, V.M.; Chakraborty, S. Material selection using multi-criteria decision-making methods: A comparative study. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2012, 226, 266–285. [Google Scholar] [CrossRef]
- Markatos, D.N.; Pantelakis, S.G. Assessment of the Impact of Material Selection on Aviation Sustainability, from a Circular Economy Perspective. Aerospace 2022, 9, 52. [Google Scholar] [CrossRef]
- Deng, Y. Life Cycle Assessment of Biobased Fibre-Reinforced Polymer Composites. Ph.D. Thesis, KU Leuven, Science, Engineering & Technology, Leuven, Belgium, 2014. [Google Scholar]
- Patton, R.; Li, F. Causes of Weight Reduction Effects of Material Substitution on Constant Stiffness Components; SAE Technical: Warrendale, PA, USA, 2002. [Google Scholar]
- Li, F.; Patton, R.; Moghal, K. The relationship between weight reduction and force distribution for thin wall structures. Thin-Walled Struct. 2005, 43, 591–616. [Google Scholar] [CrossRef]
- Meng, F.; Olivetti, E.A.; Zhao, Y.; Chang, J.C.; Pickering, S.J.; McKechnie, J. Comparing life cycle energy and global warming potential of carbon fibre composite recycling technologies and waste management options. ACS Sustain. Chem. Eng. 2018, 6, 9854–9865. [Google Scholar] [CrossRef]
- Suzuki, T.; Jun Takahashi, J. Prediction of energy intensity of carbon fibre reinforced plastics for mass-produced passenger cars. In Proceedings of the Ninth Japan International SAMPE Symposium, Tokyo, Japan, 29 November–2 December 2005. [Google Scholar]
- Ghosh, T.; Kim, H.C.; De Kleine, R.; Wallington, T.J.; Bakshi, B.R. Life cycle energy and greenhouse gas emissions implications of using carbon fibre reinforced polymers in automotive components: Front subframe case study. Sustain. Mater. Technol. 2021, 28, e00263. [Google Scholar]
- Dér, A.; Dilger, N.; Kaluza, A.; Creighton, C.; Kara, S.; Varley, R.; Herrmann, C.; Thiede, S. Modelling and analysis of the energy intensity in polyacrylonitrile (PAN) precursor and carbon fibre manufacturing. J. Clean. Prod. 2021, 303, 127105. [Google Scholar] [CrossRef]
- Meng, F.; McKechnie, J.; Pickering, S.J. An assessment of financial viability of recycled carbon fibre in automotive applications. Compos. Part A Appl. Sci. 2018, 109, 207–220. [Google Scholar] [CrossRef]
- Karuppannan Gopalraj, S.; Kärki, T. A study to investigate the mechanical properties of recycled carbon fibre/glass fibre-reinforced epoxy composites using a novel thermal recycling process. Processes 2020, 8, 954. [Google Scholar] [CrossRef]
- EUWebsite. Electricity Price Statistics. Available online: https://ec.europa.eu (accessed on 22 October 2021).
- Duflou, J.; Deng, Y.; Van Acker, K.; Dewulf, W. Do fibre-reinforced polymer composites provide environmentally benign alter-natives? A life-cycle-assessment-based study. MRS Bull. 2012, 37, 374–382. [Google Scholar] [CrossRef]
- Bicer, Y.; Dincer, I. Life cycle evaluation of hydrogen and other potential fuels for aircrafts. Int. J. Hydrogen Energy 2017, 42, 10722–10738. [Google Scholar] [CrossRef]
- Larsen, l.; Schuster, A.; Kim, J.; Kupke, M. Path planning of cooperating industrial robots using evolutionary algorithms. Procedia Manuf. 2018, 17, 286–293. [Google Scholar] [CrossRef]
- Airliners Website. Aircraft Technical Data and Specifications. Airbus A320. Available online: https://www.airliners.net (accessed on 22 October 2021).
- Saidani, M.; Yannou, B.; Leroy, Y.; Cluzel, F. How to Assess Product Performance in the Circular Economy? Proposed Requirements for the Design of a Circularity Measurement Framework. Recycling 2017, 2, 6. [Google Scholar] [CrossRef]
- Rigamonti, L.; Mancini, E. Life cycle assessment and circularity indicators. Int. J. Life Cycle Assess. 2021, 26, 1937–1942. [Google Scholar] [CrossRef]
- Corona, B.; Shen, L.; Reike, D.; Carreón, J.R.; Worrell, E. Towards sustainable development through the circular economy—A review and critical assessment on current circularity metrics. Resour. Conserv. Recycl. 2019, 151, 104498. [Google Scholar] [CrossRef]
- Kirchherr, J.; Reike, D.; Hekkert, M. Conceptualizing the circular economy: An analysis of 114 definitions. Resour. Conserv. Recycl. 2017, 127, 221–232. [Google Scholar] [CrossRef]
- Moraga, G.; Huysveld, S.; Mathieux, F.; Blengini, G.A.; Alaerts, L.; Van Acker, K.; de Meester, S.; Dewulf, J. Circular economy indicators: What do they measure? Resour. Conserv. Recycl. 2019, 146, 452–461. [Google Scholar] [CrossRef]
- Zhao, D.; Guo, Z.; Xue, J. Research on scrap recycling of retired civil aircraft. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2021; Volume 657, p. 012062s. [Google Scholar]
- Zardari, N.H.; Ahmed, K.; Shirazi, S.M.; Yusop, Z.B. Introduction. In Weighting Methods and their Effects on Multi-Criteria Decision Making Model Outcomes in Water Resources Management; Springer Briefs in Water Science and Technology; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation; McGraw-Hill: New York, NY, USA, 1980; 287p. [Google Scholar]
- Ighravwe, D.E.; Oke, S.A. A multi-criteria decision-making framework for selecting a suitable maintenance strategy for public buildings using sustainability criteria. J. Build. Eng. 2019, 24, 100753. [Google Scholar] [CrossRef]
- Jarek, S. Removing Inconsistency in Pairwise Comparisons Matrix in the AHP. Mult. Criter Decis. Mak. 2016, 11, 63–76. [Google Scholar] [CrossRef]
- Hasan, M.; Gulzarul, Z.; Mohammad, F. Multi-choice best-worst multi-criteria decision-making method and its applications. Int. J. Intell. Syst. 2021, 37, 1129–1156. [Google Scholar] [CrossRef]
- Srdjevic, B.; Srdjevic, Z.; Reynolds, K.M.; Lakicevic, M.; Zdero, S. Using Analytic Hierarchy Process and Best–Worst Method in Group Evaluation of Urban Park Quality. Forests 2022, 13, 290. [Google Scholar] [CrossRef]
- Talukder, B.; Hipel, K.W.; W. vanLoon, G. Developing Composite Indicators for Agricultural Sustainability Assessment: Effect of Normalization and Aggregation Techniques. Resources 2017, 6, 66. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023; Available online: https://www.R-project.org/ (accessed on 9 January 2023).
| Semantics | Grade | Reciprocal |
|---|---|---|
| Extremely preferred | 9 | 1/9 |
| Very strongly to extremely | 8 | 1/8 |
| Very strongly preferred | 7 | 1/7 |
| Strongly to very strongly | 6 | 1/6 |
| Strongly preferred | 5 | 1/5 |
| Moderately to strongly | 4 | 1/4 |
| Moderately preferred | 3 | 1/3 |
| Equally to moderately | 2 | 1/2 |
| Equally preferred | 1 | 1 |
| Component Type | Elastic Modulus (GPa) | Density (g/cm3) | Specific Stiffness (GPa/(g/cm3)) | Resulting Weight (kg) |
|---|---|---|---|---|
| Woven virgin | 70 | 1.6 | 43.75 | 1000 |
| Recycled aligned | 60.8 | 1.5 | 40.53 | 1080 |
| Recycled random | 39.8 | 1.44 | 27.64 | 1580 |
| Component Type | Primary Material Production (kgCO2eq- Mass) | Component Manuf. (kgCO2eq-Mass) | Use Phase (kgCO2eq-Mass-Lifetime Km) | Recycling (kgCO2eq-Mass) | |||
|---|---|---|---|---|---|---|---|
| Kerosene | Liquid Hydrogen | Liquid Hydrogen Wind | Liquid Hydrogen Geothermal | ||||
| Woven virgin | 20,440 | 103,000 | 52,920,000 | 5,544,000 | 3,024,000 | 756,000 | 1540 |
| Recycled aligned | 1921 | 1717 | 57,153,600 | 5,987,520 | 3,265,920 | 816,480 | 1663 |
| Recycled random | 3549 | 2512 | 83,613,600 | 8,759,520 | 4,777,920 | 1,194,480 | 2433 |
| Component Type | Primary Material Production (€-Mass) | Component Manuf. (€-Mass) | Use Phase (kgCO2eq-Mass-Lifetime Km) | Recycling (€-Mass) | |||
|---|---|---|---|---|---|---|---|
| Kerosene | Liquid Hydrogen | Liquid Hydrogen Wind | Liquid Hydrogen Geothermal | ||||
| Woven virgin | 17,905 | 3340 | 4,032,000 | 7,056,000 | 21,168,000 | 21,168,000 | 499 |
| Recycled aligned | 1560 | 1858 | 4,354,560 | 7,620,480 | 22,861,440 | 22,861,440 | 539 |
| Recycled random | 2882 | 2718 | 6,370,560 | 11,148,480 | 33,445,440 | 33,445,440 | 788 |
| Component Id | Ranking Order | ||||
|---|---|---|---|---|---|
| No | Component Type | Fuel | Min–Max | z-Score | Proportionate |
| 1 | Woven virgin | Kerosene | 5 | 5 | 10 |
| 2 | Woven virgin | LH2 (conventional source) | 1 | 1 | 1 |
| 3 | Woven virgin | LH2 (wind source) | 4 | 4 | 4 |
| 4 | Woven virgin | LH2 (geothermal source) | 3 | 3 | 3 |
| 5 | Recycled aligned | Kerosene | 8 | 8 | 11 |
| 6 | Recycled aligned | LH2 (conventional source) | 2 | 2 | 2 |
| 7 | Recycled aligned | LH2 (wind source) | 7 | 7 | 7 |
| 8 | Recycled aligned | LH2 (geothermal source) | 6 | 6 | 5 |
| 9 | Recycled random | Kerosene | 12 | 12 | 12 |
| 10 | Recycled random | LH2 (conventional source) | 9 | 9 | 6 |
| 11 | Recycled random | LH2 (wind source) | 11 | 11 | 9 |
| 12 | Recycled random | LH2 (geothermal source) | 10 | 10 | 8 |
| Scenario 1—Equal Weighting | ||||
|---|---|---|---|---|
| Environmental Impact | Costs | Circularity | Weight Factor/Priority | |
| Environmental Impact | 1 | 1 | 1 | ≈33.3% |
| Costs | 1 | 1 | 1 | ≈33.3% |
| Circularity | 1 | 1 | 1 | ≈33.3% |
| Scenario 2—environmental impact prioritization | ||||
| Environmental Impact | 1 | 5 | 3 | ≈66% |
| Costs | 1/5 | 1 | 1 | ≈16% |
| Circularity | 1/3 | 1 | 1 | ≈18% |
| Scenario 3—circularity prioritization | ||||
| Environmental Impact | 1 | 3 | 1/5 | ≈21% |
| Costs | 1/3 | 1 | 1/5 | ≈10% |
| Circularity | 5 | 5 | 1 | ≈69% |
| Scenario 4—costs prioritization | ||||
| Environmental Impact | 1 | 1/5 | 2 | ≈18% |
| Costs | 5 | 1 | 5 | ≈70% |
| Circularity | 1/2 | 1/5 | 1 | ≈12% |
| Component Identifier | Ranking Order | |||
|---|---|---|---|---|
| Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | |
| virgin ker. | 5 | 10 | 2 | 4 |
| virgin hyd. | 1 | 1 | 1 | 1 |
| virgin wind | 4 | 4 | 8 | 3 |
| virgin geo. | 3 | 2 | 7 | 2 |
| aligned ker. | 8 | 11 | 4 | 8 |
| aligned hyd. | 2 | 3 | 3 | 5 |
| aligned wind | 7 | 6 | 10 | 7 |
| aligned geo. | 6 | 5 | 9 | 6 |
| random ker. | 12 | 12 | 6 | 12 |
| random hyd. | 9 | 7 | 5 | 9 |
| random wind | 11 | 9 | 12 | 11 |
| random geo. | 10 | 8 | 11 | 10 |
| Reference Scenario | ||||
|---|---|---|---|---|
| Environmental Impact | Costs | Circularity | Weight Factor/Priority | |
| Environmental Impact | 1 | 5 | 3 | ≈66% |
| Costs | 1/5 | 1 | 1 | ≈16% |
| Circularity | 1/3 | 1 | 1 | ≈18% |
| Alternative Scenario 1 | ||||
| Environmental Impact | 1 | 4 | 3 | ≈63% |
| Costs | 1/4 | 1 | 1 | ≈18% |
| Circularity | 1/3 | 1 | 1 | ≈19% |
| Alternative Scenario 2 | ||||
| Environmental Impact | 1 | 5 | 3 | ≈64% |
| Costs | 1/5 | 1 | 2 | ≈21% |
| Circularity | 1/3 | 1/2 | 1 | ≈15% |
| Alternative Scenario 3 | ||||
| Environmental Impact | 1 | 6 | 3 | ≈67% |
| Costs | 1/6 | 1 | 1/2 | ≈11% |
| Circularity | 1/3 | 2 | 1 | ≈22% |
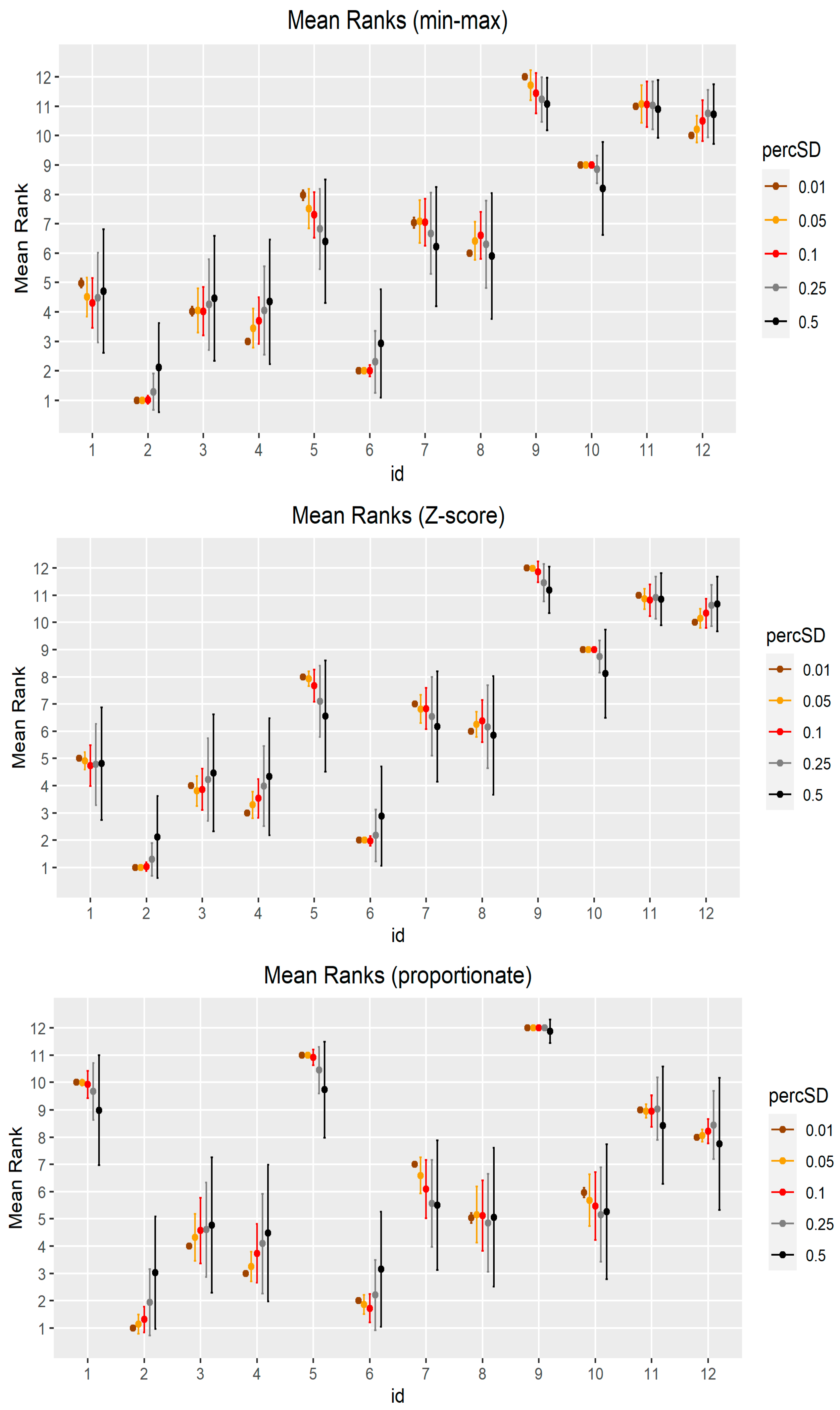
| Mean Rank | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.01 | 0.05 | 0.1 | 0.25 | 0.5 | |||||||
| Id No | Initial Rank | Min–Max | z-Score | Min–Max | z-Score | Min–Max | z-Score | Min–Max | z-Score | Min–Max | z-Score |
| 1 | 5 | 4.98 | 5.00 | 4.51 | 4.91 | 4.30 | 4.73 | 4.48 | 4.78 | 4.71 | 4.81 |
| 2 | 1 | 1.00 | 1.00 | 1.00 | 1.00 | 1.02 | 1.03 | 1.29 | 1.30 | 2.11 | 2.12 |
| 3 | 4 | 4.02 | 4.00 | 4.05 | 3.80 | 4.02 | 3.86 | 4.25 | 4.23 | 4.46 | 4.46 |
| 4 | 3 | 3.00 | 3.00 | 3.45 | 3.29 | 3.70 | 3.53 | 4.04 | 3.98 | 4.35 | 4.33 |
| 5 | 8 | 7.97 | 8.00 | 7.51 | 7.93 | 7.30 | 7.67 | 6.82 | 7.09 | 6.40 | 6.55 |
| 6 | 2 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 1.98 | 2.30 | 2.17 | 2,93 | 2.88 |
| 7 | 7 | 7.03 | 7.00 | 7.08 | 6.82 | 7.05 | 6.83 | 6.67 | 6.54 | 6.22 | 6.17 |
| 8 | 6 | 6.00 | 6.00 | 6.42 | 6.25 | 6.60 | 6.37 | 6.30 | 6.16 | 5.90 | 5.85 |
| 9 | 12 | 12.00 | 12.00 | 11.71 | 11.99 | 11.44 | 11.86 | 11.23 | 11.46 | 11.08 | 11.19 |
| 10 | 9 | 9.00 | 9.00 | 9.00 | 9.00 | 9.00 | 9.00 | 8.85 | 8.75 | 8.21 | 8.11 |
| 11 | 11 | 11.00 | 11.00 | 11.08 | 10.86 | 11.06 | 10.81 | 11.02 | 10.91 | 10.91 | 10.85 |
| 12 | 10 | 10.00 | 10.00 | 10.21 | 10.15 | 10.50 | 10.33 | 10.75 | 10.63 | 10.73 | 10.67 |
| 0.01 | 0.05 | 0.25 | 0.5 | ||
|---|---|---|---|---|---|
| Mean Rank | Mean Rank | Mean Rank | Mean Rank | ||
| Id No | Initial Rank | Prop | Prop | Prop | Prop |
| 1 | 10 | 10.00 | 9.99 | 9.67 | 8.98 |
| 2 | 1 | 1.00 | 1.14 | 1.94 | 3.02 |
| 3 | 4 | 4.00 | 4.32 | 4.61 | 4.77 |
| 4 | 3 | 3.00 | 3.25 | 4.09 | 4.48 |
| 5 | 11 | 11.00 | 11.00 | 10.45 | 9.73 |
| 6 | 2 | 2.00 | 1.86 | 2.21 | 3.15 |
| 7 | 7 | 7.00 | 6.59 | 5.56 | 5.50 |
| 8 | 5 | 5.03 | 5.16 | 4.85 | 5.06 |
| 9 | 12 | 12.00 | 12.00 | 12.00 | 11.88 |
| 10 | 6 | 5.97 | 5.68 | 5.16 | 5.26 |
| 11 | 9 | 9.00 | 8.96 | 9.04 | 8.43 |
| 12 | 8 | 8.00 | 8.05 | 8.44 | 7.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Markatos, D.N.; Malefaki, S.; Pantelakis, S.G. Sensitivity Analysis of a Hybrid MCDM Model for Sustainability Assessment—An Example from the Aviation Industry. Aerospace 2023, 10, 385. https://doi.org/10.3390/aerospace10040385
Markatos DN, Malefaki S, Pantelakis SG. Sensitivity Analysis of a Hybrid MCDM Model for Sustainability Assessment—An Example from the Aviation Industry. Aerospace. 2023; 10(4):385. https://doi.org/10.3390/aerospace10040385
Chicago/Turabian StyleMarkatos, Dionysios N., Sonia Malefaki, and Spiros G. Pantelakis. 2023. "Sensitivity Analysis of a Hybrid MCDM Model for Sustainability Assessment—An Example from the Aviation Industry" Aerospace 10, no. 4: 385. https://doi.org/10.3390/aerospace10040385
APA StyleMarkatos, D. N., Malefaki, S., & Pantelakis, S. G. (2023). Sensitivity Analysis of a Hybrid MCDM Model for Sustainability Assessment—An Example from the Aviation Industry. Aerospace, 10(4), 385. https://doi.org/10.3390/aerospace10040385






