Abstract
The stall aerodynamic model based on Kirchhoff’s theory of flow separation is widely used in the identification and modeling of stall aerodynamic parameters. However, it has two defects. First, its model structure is significantly different from the pre-stall model used for a small attack angle, meaning the identification results cannot be combined with the pre-stall model to form the full flight envelope model. Second, the pitching moment model, which is used in conjunction with the Kirchhoff lift model, cannot accurately describe the aircraft stall pitching moment characteristics. To ensure the compatibility of the two models, this paper proposes a method to determine some unknown parameters in the stall model. The mechanism for the pitching moment generation of the aircraft stall is analyzed, and two high-order correction terms are added to the pitching moment model to better describe the longitudinal stall aerodynamic characteristics. Based on the identification of aerodynamic parameters, a longitudinal stall aerodynamic modeling method used for the aircraft stall process is developed. The identification and simulation validation results based on the quasi-steady stall flight data of a civil aircraft show that the improved stall model can accurately describe the quasi-steady stall pitching moment. The established stall aerodynamic model can accurately characterize the longitudinal quasi-steady stall aerodynamic characteristics of aircraft under different stall degrees.
1. Introduction
In order to carry out the airworthiness certification of civil aircraft, it is necessary to establish an accurate high angle of attack (AOA) stall aerodynamic model, which requires flight test data reflecting the aircraft’s stall characteristics through quasi-steady maneuvers which are safe and easy to operate, such as wings-level symmetric, accelerated stalls [1,2,3]. Although there are several well-developed stall aerodynamic models, almost all of them are based on complex and comprehensive wind tunnel test data. Due to the limited maneuvers that can be used in the stall flight test and the far smaller range of AOA and motion frequency covered by the flight test than the wind tunnel test, it is difficult to use these models to carry out the identification and modeling of stall aerodynamic parameters based on the test flight data.
Therefore, the nonlinear stall aerodynamic model based on Kirchhoff’s theory of flow separation is still one of the most widely used models in parameter identification and the modeling of stall aerodynamic characteristics. It combines aerodynamic forces with the physical phenomena of flow by using ordinary differential equations (ODE), and describes the aerodynamic hysteresis generated by flow separation and vortex breakup through the relative position X (0 ≤ X ≤ 1) of the ideal flow separation point of the upper surface of the wing on the mean aerodynamic chord (MAC) [4]. Based on the conventional steady aerodynamic model of small AOA, the lift characteristics in stall are characterized by introducing the relation of the lift curve slope varying with X. That is the typical Kirchhoff lift model. The drag and pitching moment models which are used in conjunction with Kirchhoff’s lift model are mainly based on the linear model, and the stall drag and pitching moment characteristics are described through the drag correction term CDX(1 − X) and pitching moment correction term CmX(1 − X).
The stall aerodynamic model has many advantages, such as a simple structure and definite physical meaning. However, it has two major defects in stall aerodynamic parameter identification and aerodynamic modeling. First, the structure of the stall model is obviously different from that of the steady pre-stall aerodynamic model. As a result, some parameters of steady aerodynamic characteristics obtained by stall model identification cannot be compatible with the pre-stall model [1], which will cause errors in the proportion of the aerodynamic steady and unsteady components of the aerodynamic model, leading to the identification error of X and correction terms.
Second, the pitching moment model used in conjunction with the Kirchhoff lift model cannot accurately describe the nonlinear characteristics of the pitching moment during the aircraft stall. In references [5,6,7,8], the existing stall aerodynamic model has evident fitting errors regarding the measurement values of pitching moment coefficients, which fully illustrate this problem. Because of this defect, the identification results cannot accurately reflect the characteristics of the stall pitching moment. As a result of the above factors, it is difficult to directly establish a stall aerodynamic model that can accurately describe the aerodynamic characteristics of the whole process from entering and recovery of stall.
In order to solve the problem of incompatibility between the pre-stall model and the identification results of stall aerodynamic parameters, the general method at present is for engineers to modify the identification results to ensure compatibility with the pre-stall model as much as possible. Next, the stall aerodynamic model which is not directly related to the pre-stall model will be established based on the modified identification results [9,10]. Then, the pre-stall model and the stall model are switched with respect to AOA, and the smooth transition and continuity from the pre-stall model to the stall model are ensured by linearly blending in a transition region of AOA [11,12]. This method cannot eliminate the identification errors of X and correction terms caused by the incompatibility, and the correction of the identification results greatly depends on the experience of engineers.
Aiming at solving the problem that the pitching moment model in the stall aerodynamic model cannot accurately describe the nonlinear characteristics of the pitching moment during stall, a theoretical model of the stall pitching moment coefficient with X as the main independent variable is presented in references [13,14]. Since X is the main independent variable of the lift coefficient and the pitching moment coefficient model, it is difficult to fit the pitching moment without affecting the fitting of the lift, so the practical application of this model is not ideal. References [5,6,7,8,15,16,17] hold that the nonlinear pitching moment of the aircraft during stall changes in proportion to the 1 − X. Based on the conventional linear model, the pitching moment correction term CmX(1 − X) is added to describe the nonlinear pitching moment. However, in fact, the magnitude and aerodynamic center of the lift generated by the wing change simultaneously during stall, and the change of the pitching moment characteristics, are the superposition of the two effects above, rather than only related to 1 – X. Obviously, it is difficult to describe the nonlinear variation of the pitching moment during stall with the added CmX(1 – X) correction term only.
In references [18], the model structure selection algorithm is used to assess the influence of different correction terms on pitching moment fitting. However, this method is limited by flight test data and researchers’ experience, and there is no fixed form of correction term. In references [19,20,21,22], the nonlinear characteristics of stall pitching moment are characterized by polynomial composed of coupling terms and higher-order terms of variables, such as AOA and angular velocity. However, the polynomial contains too many unknown parameters, making it difficult to identify the unknown parameters accurately. The nonlinear fitting of the model can be improved effectively by adding the AOA spline function [23,24,25,26]. However, the spline function here is similar to “patch”, which is only used to reduce the fitting error under some specific AOA knots, without clear physical meaning.
In the second section of the paper, the structure of the stall aerodynamic model is improved. The critical AOA αcr for switching between the extended stall model and the pre-stall model is defined. The unknown aerodynamic parameters representing steady aerodynamics at small AOA in the stall aerodynamic model are replaced with the known parameters of the pre-stall model at αcr. Then, the theoretical model given in reference [27] is analyzed. The unsteady pitching moment coefficient terms, in the form of ODE, which are difficult to identify and model, are transformed into high-order correction terms that can easily be identified and modeled. Thus, the aerodynamic parameter identification method based on an improved stall aerodynamic model is developed.
In the third section of the paper, based on the identification results of the stall aerodynamic parameters obtained through the improved stall aerodynamic model, the distribution of the identification results of characteristic parameters of X under different stall degrees are analyzed. It is determined that the changes of X under different stall degrees could be described by the same set of parameters characterizing X. On this basis, a set of optimal X characteristic parameters that can fit all the observation data of the lift coefficient under different stall degrees are determined first, and a model of X is established. Next, the correction coefficients are modeled by spline function with X as the independent variable. Then, the Oswald factor and downwash rate at horizontal tail are approximately set as constant values. Thus, a longitudinal stall aerodynamic modeling method used for the mathematical simulation of the aircraft stall process is developed. In the fourth section of the paper, the established identification and modeling method of stall aerodynamic parameters are validated by comparing the mathematical simulation and flight test data of a large civil aircraft’s quasi-steady stall maneuver.
2. Improvement of Stall Aerodynamic Model and Identification of Aerodynamic Parameters
2.1. Determination of Critical Angle of Attack for Model Switching and Steady Aerodynamic Parameters
Kirchhoff’s flow separation theory is applicable to conventional aircraft with turbulent boundary layers (flow separation starts at the trailing-edge progressing upstream to the leading-edge until flow separation on the entire upper surface occurs). The aircraft studied in this paper is a large twin-engine civil aircraft with a conventional layout, which adopts a high subsonic airfoil with a thick trailing edge, and the maneuver adopted in the stall flight test is a typical quasi-steady stall maneuver, which fully applies to the Kirchhoff stall aerodynamic model. The trailing edge separation phenomenon is shown in Figure 1.
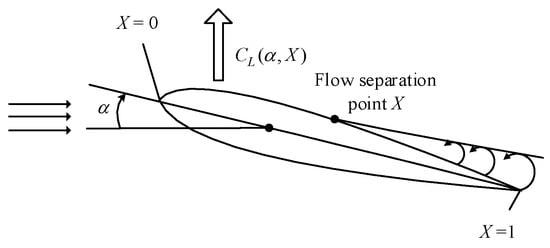
Figure 1.
Trailing edge flow separation phenomenon.
As shown in Figure 1, flow separation starts at the trailing-edge progressing upstream to the leading-edge until flow separation on the entire upper surface occurs. X = 1 when the flow is not separated, and X = 0 when the flow is completely separated [28,29].
The pre-stall aerodynamic model used for small AOA is mainly composed of a linear interpolation table and spline function, usually including static aerodynamic forces and moments and other aerodynamic forces and moments generated by steady rotation, control surfaces and other factors such as aeroelasticity. Evidently, the pre-stall model consisting of a linear interpolation table and spline function cannot accurately characterize the nonlinear characteristics and hysteresis effect of the aerodynamic force during stall. Therefore, it is necessary to establish a high AOA stall aerodynamic model based on the stall flight test data of aircraft in order to form a full-enveloped aerodynamic model of an aircraft together with the pre-stall model.
In order to ensure that the established high AOA stall aerodynamic model is compatible with the pre-stall aerodynamic model of small AOA, the two models should have the same aerodynamic characteristics when switching. According to the steady aerodynamic theory, when the AOA is small and the air flow on the upper surface of the wing is not separated, the aerodynamic characteristics of the aircraft are linear and steady, which can be described by the fixed aerodynamic coefficient/derivative. Hence, the aerodynamic coefficients/derivatives representing the steady aerodynamic force at small AOA in the stall aerodynamic model are replaced by the aerodynamic coefficient/derivative values of the pre-stall model at the switching AOA (denoted as the critical AOA αcr). After such improvement, when the flow on the upper surface of the wing is not separated at all, that is, X≈1, the aerodynamic characteristics of the stall aerodynamic model are almost the same as those of the pre-stall model, and the two models can be switched smoothly. When the AOA increases to the point where the upper surface of the wing begins to generate flow separation, i.e., X < 1, the linear and steady aerodynamic characteristics of the aircraft are still regarded as unchanged, while the nonlinear and unsteady aerodynamic increments are all described by X-related correction terms.
In order to ensure that the pre-stall model is accurate during model switching, the switching AOA should be within the envelope of the pre-stall model; that is, the aerodynamics of the aircraft at αcr should be steady, and the X of αcr should be as close to 1 as possible. Under different change rates of AOA, the value of X is not the same even if the AOA is same, so αcr is not a fixed value, which needs to be determined according to the degree of flow separation, that is, the value of X. When determining αcr according to the magnitude of X, it is necessary to determine the threshold of X firstly; that is, when the value of X is less than the threshold, flow separation is considered to lead to non-negligible aerodynamic nonlinearity, and the calculation error of X and the measurement error of AOA should also be taken into account. Generally, the X-threshold range of the aircraft’s stall buffeting that the pilot can notice is about 0.7~0.9 [29], that is, the aerodynamic force has begun to show clear nonlinear characteristics at this time, so the X corresponding to αcr should be greater than 0.9 at least. Further considering the calculation error of X and the measurement error of AOA (usually greater than 1°), the selection of the critical AOA requires a certain margin, so αcr is determined as the AOA corresponding to X = 0.95 multiplied by 0.8.
In summary, a stall aerodynamic model compatible with the aerodynamic characteristics of the pre-stall model at αcr can be obtained:
where the subscript cr indicates that the value of a parameter is the value of the pre-stall model at the critical AOA αcr, e is the Oswald factor, Λ is the aspect ratio and CDX and CmX are the empirical correction coefficients of the drag and pitching moment, respectively. Subscripts wb, t and δe, respectively, represent the wing-body, horizontal tail and elevator. ΔCLt, ΔCLδe, ΔCmt and ΔCmδe represent the lift force and pitch moment coefficient increment generated by the horizontal tail and elevator, respectively (relative to the trim deflection angle of the horizontal tail and elevator at αcr):
where I = L, m. αt and εt are the local AOA and downwash angle, respectively, at the horizontal tail. ε0 is the downwash angle corresponding to zero lift AOA. After integrating Equation (2), we can get:
Because the forms of Cmαt∂εt/∂X(1 − X) and Cmδe∂εt/∂X(1 − X) in the Equation are similar to the form of CmX(1 − X) in Equation (1), ∂εt/∂X and CmX are collinear. Therefore, ∂εt/∂X and CmX can be combined into CmX for identification, rather than the identification of the two parameters separately.
X can be described as ODE [4]:
where τ1 is the time constant of the unsteady separation process and represents the transient characteristics of the aerodynamic force. τ2 is the time constant of flow separation hysteresis, which represents the hysteresis effect caused by flow separation and reattachment. The separation time of flow is mainly related to the separation characteristics of flow and the flight speed of aircraft. /V, the ratio of MAC to airspeed, is used as the units of τ1 and τ2 to avoid the change of time constant caused by the difference of airspeed, so as to reflect the separation characteristics of flow more directly. X0(α) is the flow separation point under steady flow, which represents the change of the separation point coordinates with AOA in steady flow. X0 is mainly determined by aircraft airfoil and flap/slat configuration, and can be approximated by the hyperbolic-tangent function [28].
where a1 represents the stall characteristics of airfoil and mainly affects the slope of the X-curve at different AOA and change rates of AOA, and α* is the AOA when the flow separation point X0 is equal to 0.5. A complete X expression is formed by combining Equations (4) and (5). The four constants τ1, τ2, a1 and α* can describe the change characteristics of X under different stall degrees when the aircraft configuration and Ma are constant.
2.2. The Modification of the Pitching Moment Model and Improved Stall aerodynamic Model
It is difficult to achieve a good fitting of the observation data of the stall pitching moment when using model (1) for aerodynamic parameter identification, so it is necessary to modify the pitching moment model in model (1).
Based on a well-developed theoretical model of the pitching moment established from the wind tunnel test presented in Reference [27], the missing pitching moment components in model (1) are analyzed and determined by comparing the pitching moment model in model (1) with the theoretical model, and then adding the corresponding correction terms to model (1) to complete the modification. The pitching moment model given in Reference [27] is as follows:
where subscript b represents the fuselage (body), w represents the wing and and , respectively, represent the horizontal tail area and the moment arm length from the horizontal tail pressure center to the center of gravity of the aircraft. Cmb(α) is the pitching moment coefficient of the fuselage; Cmw0 is the constant pitching moment coefficient of the wing. CLw is the lift coefficient of the wing; Xw(α) is the coordinate of the wing pressure center relative to the gravity center position in MAC fraction. CLαt(α) is the lift curve slope of the horizontal tail; αt is the local AOA at the horizontal tail, which is the same as Equation (2). Cmq(α) is the pitch damping derivative varying with the AOA.
CLw consists of the steady linear lift CLw1 and the unsteady nonlinear lift CLw2 [27]:
CLw2 can be expressed by ODE [27]:
where τ1(α) is the characteristic time varying with the AOA, and describes the transient characteristic of CLw2. CLw20(α) is the steady dependency between the nonlinear lift force and the AOA.
Xw(α) is also represented by ODE [27]:
where τ2(α) is the characteristic time varying with the AOA, and describes the transient characteristic of Xw. Xw0(α) is the corresponding steady dependency of the pressure center of the wing upon AOA.
αt includes the influence of the downwash angle εt, which can also be expressed by ODE [27]:
where τ3(α) is the characteristic time varying with the AOA, and describes the transient characteristic of εt. εt0(α) is the steady dependency of the downwash angle upon AOA.
In summary, model (6) is mainly composed of the pitching moment coefficient and derivative which varies with the AOA, and some parameters in model (6) need to be solved by ODE. Therefore, it is difficult to directly use model (6) for parameter identification. By analyzing the pitching moment component contained in model (6), the missing pitching moment component in model (1) can be supplemented, so that it can better fit the characteristics of the stall pitching moment, and thus complete the identification and modeling of aerodynamic parameters.
The added correction terms should have the following characteristics: They should not affect the fitting of the linear model; They can accurately describe the pitching moment generated by the simultaneous change of aerodynamic force and aerodynamic center; They can describe the pitching moment generated by the change of AOA, rate of change of AOA and angular velocity; Their structure is simple and easy to be adjusted manually. By comparing and analyzing the pitching moment model in model (6) and model (1), it can be seen that model (1) lacks the following pitching moment components:
- The Cmcr and Cmαwb_cr(α − αcr) of model (1) represent the linear pitching moment of the wing-body, and can represent the linear components of Cmw0 and Cmb(α) of model (6), but the nonlinear components of Cmb(α) are missing. Considering that the nonlinear pitching moment characteristics of the fuselage, which is a conventional body of revolution, are not very significant [27], this part of the pitching moment can be compensated by CmX(1 − X).
- In model (1), ΔCmt represents the pitching moment of the horizontal tail. It can be seen from Equation (2) that εt in model (1) includes the term (1 − X)∂εt/∂X of the downwash angle varying with X, which is similar to Equation (10) and can characterize the influence of downwash on the pitching moment of the horizontal tail. The CLα of model (1) is constant and cannot represent the change of the slope of the lift curve of the horizontal tail. Therefore, ΔCmt in model (1) cannot accurately represent the in model (6). Considering that the maximum AOA in civil aircraft flight tests is generally less than 25°, the local AOA at the horizontal tail is not large due to the effect of the flow downwash of the wing; hence, the change of CLαt(α) is slight. Meanwhile, the pitch moment of the horizontal tail is the main component of the pitch damping moment of the aircraft. Therefore, the ΔCmt error caused by CLαt(α) can be attributed to the pitch damping moment error. Thus, the model correction terms could be simplified without another separate correction of ΔCmt.
- The and in model (1) can only represent the pitch damping moment coefficient at αcr. When the AOA increases, the value of Cmq(α) will change greatly compared with that of Cmq_cr [3], which leads to easily noticed errors of the stall pitch damping moment characteristics.
- CmX(1 − X) in model (1) can represent the pitching moment CLw1Xw(α) generated by a linear aerodynamic force with the change of aerodynamic center position, but it lacks the pitching moment term specifically corresponding to CLw2Xw(α), that is, the nonlinear pitching moment generated by the simultaneous change of lift force and aerodynamic center position.
To sum up, model (1) lacks a pitch damping moment at a higher AOA and a pitch moment correction term for CLw2Xw(α). The forms of Equations (8) and (9) are similar to those of Equation (4), both of which are related to flow separation. Therefore, it can be considered that CLw2 and Xw(α) are positively correlated with (1 − X), namely:
Multiply CLw2 with Xw(α):
For conventional civil aircraft, the pitch damping moment and the damping moment of the lag of wash are mainly generated by the horizontal tail. When the aircraft rotates in pitch, there will be an additional change of AOA at the horizontal tail, which further generates extra lift:
where
where the subscript ro is rotation, Vt is the local velocity at the horizontal tail, and Δαtq and Δαtε are the changes of local AOA at the horizontal tail, caused by the change of pitch angle velocity and downwash angle, respectively. lht is the distance from the aerodynamic center of the horizontal tail to the gravity center of the aircraft. α(t) and α(t − τ) are the AOAs without and with the lag of wash, respectively. The additional lift force ΔLt_ro multiplied by lht is the increment of the pitch damping moment and damping moment of the lag of wash.
Equation (14) divided by 0.5ρV2S is the increment of the pitch damping moment coefficient and damping moment coefficient of the lag of wash:
As can be seen from Equations (13) and (15), the stall pitch damping moment is mainly determined by the lift derivative of the horizontal tail CLαt, local velocity Vt at the horizontal tail, downwash rate ∂ε/∂α and the lag time of downwash τ. CLαt, Vt and ∂ε/∂α are all related to flow separation, and τ is determined by Vt. Similarly, CLαt, ∂ε/∂α are positively correlated with (1 − X), and the ratio of Vt to V is also positively correlated with (1 − X):
Let Δα = α(t) − α(t − τ) ≈ , and combine with Equations (13) and (15):
Since qlht and K5(1 − X)lht have similar effects, they can be combined, then Equation (17) is transformed into:
So far, through the analysis of the generation mechanism of the stall pitching moment, the second order correction term CmX2(1 − X)2 is proposed to describe the pitching moment generated by the simultaneous change of the lift force and the aerodynamic center position. The third order correction term CmX3(1 − X)3 is proposed to describe the variation of the pitch damping moment due to the variation of AOA and pitch velocity. Since X is close to 1, 1 − X is close to 0 in the steady flight state, and the order of magnitude of (1 − X)2 and (1 − X)3 is small in this case, and the two higher order correction terms have no significant impact on the fitting in the steady flight state.
After adding two high-order pitching moment coefficient correction terms CmX2(1 − X)2 and CmX3(1 − X)3 to the pitching moment model, an improved stall aerodynamic model is established:
After improvement, the steady aerodynamic parameters at small AOA are known quantities of the pre-stall model at αcr, and are no longer iterated as unknowns. This not only greatly reduces the calculation amount, but also reduces the identification errors of the X characteristic parameters, correction coefficients and other parameters caused by incompatible steady aerodynamic parameters, which can effectively improve the reliability of the identification results.
2.3. Identification of Aerodynamic Parameters Based on Improved Stall aerodynamic Model
At the beginning of the flight test of wings-level symmetric, the aircraft should first keep steady and level flight, then the power setting is changed to the idle position to keep the aircraft at 1 kt/s for deceleration flight. The pilot should push stick for stall recovery until the AOA increases to the point where the aircraft enters stall. In the flight test of wings-level symmetric, the aircraft is almost in a steady state before the occurrence of significant stall buffeting, and the angular velocity and the change rate of AOA can be approximately regarded as 0.
When using the improved stall aerodynamic model for stall aerodynamic parameter identification, the parameter vector θ to be identified includes four correction coefficients, CDX, CmX1, CmX2 and CmX3, and four X characteristic parameters, a1, α*, τ1, τ2; e and ∂εt/∂α. It is difficult to obtain the dynamic data needed to identify τ1 by a quasi-steady stall maneuver, so it is impossible to obtain accurate τ1, and the lack of identifiability of τ1 may affect the estimation of τ2. Therefore, in order to obtain more accurate τ2, identification should start with a simplified model with τ1 removed. Special attention should be paid to the identification of CmX1, CmX2 and CmX3: when flow separation is not clear (such as X > 0.8), 1 − X, (1 − X)2, (1 − X)3 have obvious collinearity, and accurate identification results of CmX2 and CmX3 cannot be obtained at this time. In order to obtain more accurate estimates, the collinearity of 1 − X, (1 − X)2, (1 − X)3 should be assessed through VIF, and CmX2 and CmX3 should be removed from the model when significant collinearity exists among the three. For data with easily noticed flow separation (such as X < 0.6), CmX2 and CmX3 should be retained.
Hence, there are seven or nine parameters to be identified in total. The rest of the aerodynamic parameters are directly taken as known values of the pre-stall model at αcr, which no longer need to be identified.
Based on the improved stall aerodynamic model (19), the conventional maximum likelihood method can be used to identify the unknown parameters. This method has been widely used in the identification of aerodynamic parameters, which will not be described here and can be referred to Reference [30]. The fitting values for CL, CD and Cm of model (19) constitute the output vector Y, and the measurement data of CL, CD and Cm of aircraft constitute the observation vector Z. The measurement data of CL, CD and Cm are calculated by acceleration and angular acceleration flight test data.
where m is the aircraft mass, is the dynamic pressure and T is the engine thrust. The cost function of the maximum likelihood method is as follows [30]:
where N is the length of data.
The observation data of the lift, drag and pitching moment are calculated using the acceleration, angular acceleration, dynamic pressure and other data recorded in flight tests. In addition to using different sets of stall data for identification, different sets of quasi-steady stall maneuver data can also be concatenated to obtain a single set of average results directly (but leave a couple stall tests for validation, one abrupt and one smooth). The average result can be used to validate the accuracy of each set of identification result.
3. Aerodynamic Modeling Method for Longitudinal Stall Process
In different quasi-steady stall flight tests, the pilot’s controls and the aircraft’s stall states are different, and the nonlinear and unsteady hysteresis characteristics of the aerodynamic force reflected by the flight test data are not exactly the same. And the value of the correction coefficient in the correction term is directly related to the value of the stall degree 1 − X. When 1 − X is different, the identification results of the correction coefficient are also different. Therefore, the correction coefficient identification results obtained from the data of a single stall flight test are not applicable to the whole process from entering to recovery of stall.
In order to establish a model that can characterize the aerodynamic characteristics of the whole stall process of an aircraft, it is necessary to use the aerodynamic parameter identification results of the flight test data of different stall degrees to carry out the modeling in three parts. The first is the modeling of X; the second is the modeling of correction coefficients CDX, CmX1, CmX2 and CmX3; and the third is the modeling of e and ∂εt/∂α. Because the identification results of the correction coefficients and e and ∂εt/∂α vary with the stall degree 1 − X, X modeling needs to be completed firstly, and then the modeling of the correction coefficient and e and ∂εt/∂α with the change of 1 − X can be completed.
3.1. Modeling Method of X
According to Equations (4) and (5), X is mainly determined by stall characteristic parameters a1, α*, τ1 and τ2. a1, α* and τ2 are mainly determined by airfoil and wing configuration. τ1 is mainly determined by the characteristics of the flow field at infinity and the trailing edge flow characteristics of the wing-body, i.e., τ1 is mainly related to Ma and is independent of the airfoil and wing configuration [28,31]. Therefore, a1, α*, τ1 and τ2 are constants that do not change with the stall degree when the configuration is the same and Ma is similar. Through the change of X, the existing stall aerodynamic model can well describe the quasi-steady stall lift characteristics of aircraft without adding additional correction terms. This means that a set of optimal a1, α*, τ1, τ2 can characterize the lift stall characteristics at different stall degrees. That is, it is necessary to obtain a set of optimal a1, α*, τ1, τ2 by using flight data of different stall degrees.
Although the characteristics of X are determined by a1, α*, τ1, τ2, in the quasi-steady stall process, except the stall and recovery stage, the change rate of the AOA is small, and the flow separation point changes slowly, that is, in most of the data, dX/dt ≈ 0, ≈ 0, and X and have strong changes only in the stall and recovery stage. Since τ1 is the coefficient of dX/dt and τ2 is the coefficient of , most flight test data of a quasi-steady stall cannot fully reflect the effects of τ1 and τ2 on X characteristics. Therefore, when the quasi-steady stall data is used to identify a1 and α*, the impact of data measurement errors and atmospheric disturbance is small, and the identification results are relatively accurate. On the contrary, the identification results of τ1 and τ2 will be significantly affected, and the accuracy of the identification results is relatively low. Therefore, a1 and α* with higher accuracy values are first determined here.
Although a1 and α* do not vary with the change of stall degree, the identification results obtained through different data are theoretically the same. However, the identification results of a1 and α* obtained through different data are not exactly the same due to the impact of measurement error, atmospheric disturbance and other factors, and distribute in a certain area. The statistical test method can be used to determine the value of the identification results. Ideally, a1 and α* identification results obtained through flight test data with different stall degrees should only be affected by random errors and show normal distribution. If the identification results do not meet the normal distribution, it indicates that the identification results are not accurate, and some identification results that are too deviated should be eliminated. The K-S one-sample test is a test method to determine whether the overall sample of the identification results shows a certain distribution through a set of observed values. In this paper, the one-sample K-S test is used to test whether the discrete identification results show normal distribution.
If the identification results of stall maneuver data with different stall degrees show the given normal distribution, then the steady separation characteristics of flow at different stall degrees can be characterized by the same set of a1 and α* when the configuration is the same and Ma is similar. In a quasi-steady stall, the steady separation characteristics of the flow, that is, the change characteristic of X when ≈ 0 and dX/dt ≈ 0, are determined by a1 and α*. Therefore, the test of the distribution characteristics of the two identification results is also carried out in no order simultaneously. In practice, the values of a1 and α* in the X model can be taken as the mean value of the identification results according to the actual fitting of the aircraft flight dynamic model to the flight test data.
After determining the values of a1 and α*, the modeling of the transient characteristics and hysteresis characteristics of X when ≠ 0 and dX/dt ≠ 0, namely the determination of values of τ1 and τ2, should be further completed. It is necessary to extract the data segments that can fully characterize the transient stall characteristics and aerodynamic hysteresis effect of aircraft, that is, the data of aircraft entering stall with strong buffeting until it recovers from stall, to determine τ1 and τ2. However, one data segment is not enough to determine τ1 and τ2 because these data segments account for a small proportion of the whole quasi-steady stall data (usually the length of these data segments is only a few seconds), so it is necessary to extract multiple (at least two) lift coefficient observation data segments with significant unsteady separation and hysteresis. In addition, in order to eliminate the impact of the changes of a1 and α* values on the results of τ1 and τ2, a1 and α* should be fixed as known quantities after the exact values of a1 and α* are determined. Then, τ1 and τ2 are optimized by the optimization function (such as fmincon in Matlab), so that the lift model can fit all the extracted observation data segments of the lift coefficient. Finally, a set of optimal τ1 and τ2 are used to characterize the unsteady separation characteristics of flow at different stall degrees.
3.2. Modeling Method of Correction Coefficients
Correction coefficients include the drag correction coefficient CDX and pitching moment correction coefficients CmX1, CmX2 and CmX3. The correction terms include the correction of the stall aerodynamic force or moment coefficients of different components such as wing-body, horizontal tail and elevator. On the other hand, they also include the correction of different types of derivatives, such as static derivative, dynamic derivative and control derivative. Therefore, the values of correction terms are different under different stalling degrees. The reference [1] holds that the correction coefficient varies proportionally with flow separation. Considering that the aerodynamic characteristics of stall show clear nonlinear characteristics with the change of the flow separation, this proportional model will have nonnegligible errors in the stall and recovery stages. Therefore, knots spline functions are needed for modeling. The general form of the m-order knots spline function of a single variable is [23]:
where
where xi is the knot of spline function. X is used as the independent variable to represent the stall degree. First, 1, X, X2, …, Xm are taken as the candidate set of independent variables, and then the significance test is used to determine whether there is an evident correlation between each independent variable and the identification results of the correction coefficients at different stall degrees. Then, the independent variables with significant correlations with the identification results of each correction coefficient are determined, and the correction coefficient model is established by fitting the identification results through Equation (23). The results of this paper show that the best fitting can be obtained when m is set to three. Finally, according to the difference between the mathematical simulation results of the constructed aircraft motion model and the test flight data, the parameters of each coefficient Ci and Di in Equation (23) can be adjusted to complete the correction coefficient modeling.
3.3. Modeling of e and ∂εt/∂α
E and ∂εt/∂α mainly affect the accuracy of the drag and pitching moment models, but have little influence on the lift model. Different from the stall characteristic parameters in X and the correction terms of the drag and pitching moment, e and ∂εt/∂α also have significant contributions to CD and Cm when the flow is completely unseparated (i.e., X = 1). In addition, the nonlinear characteristics of the drag model are mainly characterized by and CDX; the nonlinear characteristics of the pitching moment model are mainly represented by CmX1, CmX2, CmX3. Hence, the identification results of e and ∂εt/∂α do not contain evident nonlinear characteristics of the drag and pitching moment models. Therefore, in order to ensure the accuracy of the drag and pitching moment models before stall occurs and simplify the model structure as much as possible, e and ∂εt/∂α of different stall degrees are mainly regarded as constants independent of X.
In summary, the longitudinal stall aerodynamic modeling procedure based on quasi-steady stall flight test data is as follows:
- a1 and α* are identified by the whole quasi-steady stall data. Then, it is checked whether the identification results of stall maneuver data with different stall degrees show normal distribution. If these identification results show the normal distribution, the values of a1 and α* are determined near the mean value of the normal distribution. If so, a1 and α* are taken as the mean of normal distribution. If the normal distribution is not followed, the identification results that are too discrete are eliminated and the mean value of the normal distribution is reset. The remaining identification results are tested to determine the values of a1 and α*.
- The flight test data segments of at least two groups of aircraft from deep stall to stall recovery are extracted, and the τ1 and τ2 optimization are carried out to make the lift model fit all the extracted observation data segments well. Then, X modeling is carried out using a1, α*, τ1 and τ2.
- After X modeling is completed, knots splines with 1, X, X2 and X3 as independent variables are used to carry out the modeling of CDX, CmX1, CmX2 and CmX3 under different stall degrees. e and ∂εt/∂α are determined as constants.
The aerodynamic modeling procedure of the longitudinal stall is shown in Figure 2.
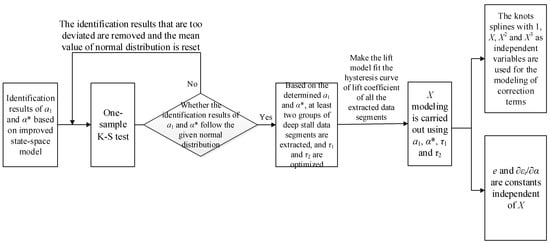
Figure 2.
The modeling procedure of longitudinal stall aerodynamic of civil aircraft.
4. Stall Aerodynamic Parameter Identification and Modeling Example
4.1. Identification of Stall Aerodynamic Parameter
In this paper, the stall aerodynamic characteristic parameters are identified and modeled using the flight test data of a conventional layout large twin-engine jet civil aircraft. The aircraft has a wing area of 128 m2 and a wingspan of 35 m. Because the deflection of the slat can reduce the adverse pressure gradient of the upper airfoil, eliminate the separation vortex of the upper airfoil, delay the separation of flow and increase the maximum lift coefficient and the critical AOA, the flight test data with more obvious aerodynamic nonlinear and hysteresis characteristics at a larger AOA could be obtained. Hence, the flap deflection angle of 25° and the slat deflection angle of 21° configuration (Configuration 3 of the test aircraft) is used as an example to discuss the identification and modeling methods of aerodynamic parameters. In order to obtain the aerodynamic characteristics of the aircraft at different stall degrees, the quasi-steady stall maneuver flight tests with different maximum AOA were carried out. The aerodynamic parameters are identified using the stall maneuver flight test data of Configuration 3 with different stall degrees at the same Ma. There are 15 sets of evident stall flight test data with a flight altitude of 4500~5500 m, Ma = 0.275~0.30 and a maximum AOA of 15.4°–21.8°.
The initial values of a1, α*, τ1, τ2, CDX, CmX1, CmX2, CmX3, e and ∂εt/∂α are given as 20, 20°, 15 c/V, 5 c/V, 0.1, 0, 0, 0, 0.75 and −0.3, respectively. Then, iterating the unknown parameters to minimize the cost function (22). The identification results of stall aerodynamic parameters are shown in Table 1.

Table 1.
Identification results of stall aerodynamic parameters.
s(θ) represents the standard deviation of θ. As can be seen from Table 1, when the maximum AOA is greater than 18.5° and Xmin < 0.82, the identification results of a1, α*, e and ∂εt/∂α are concentrated. This means that although the degrees of stall during the flight test are different, the identified stall characteristics of the aircraft, the characteristics of drag generated by lift and the downwash characteristics at the horizontal tail are similar. The standard deviations of τ2 identification results are large. It should be pointed out that due to the strong buffeting in the stall and recovery, the acceleration data at this stage contains strong noise generated by buffeting. Hence, the CL hysteresis curve calculated by acceleration also contains strong noise. As a result, the standard deviation of τ2 is excessively large (the estimation of τ2 is mainly determined by a hysteresis curve, and the quasi-steady data with low noise has no evident influence on the estimate of τ2). However, the buffeting is approximated as white noise and has little impact on the mean of the estimated results. Therefore, the distribution range of estimated τ2 obtained from tests 6 to 15 is closer to the real standard deviation of τ2, namely, s(τ2) ≈ 2.39 c/V.
The AOA of tests 1–5 is small and the flow separation is slight, so only Cmx1 is retained in the model, and Cmx2 and Cmx3 are removed. When αmax is greater than 18.5° and Xmin is less than 0.82, Cmx2 and Cmx3 are retained. Taking the 11th group of data as an example, the fitting of the identification model on CL and CD observation data is shown in Figure 3.
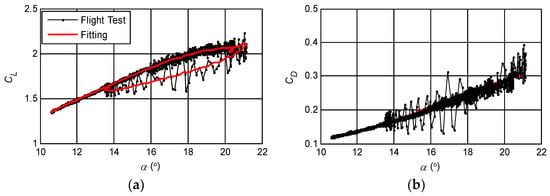
Figure 3.
Fitting of the improved stall aerodynamic model to the observation data (αmax = 21.1°). (a) CL~α; (b) CD~α.
As can be seen from Figure 3, when the AOA is greater than 14°, the observation data of CL and CD contain relatively strong noise. This is mainly because the aircraft is accompanied by strong buffeting when it is stalling, so the recorded overload data contains the disturbance generated by buffeting, and the observed CL and CD values calculated from the overload data contain strong noise. The improved stall aerodynamic model can accurately fit the CL and CD observation data at the same time, so the identification results of a1, α*, CDX and e, which are directly related to the fitting of CL and CD observation data, are reliable.
The fitting of the pitching moment model in the unimproved and improved stall aerodynamic models to Cm observation data is shown in Figure 4.
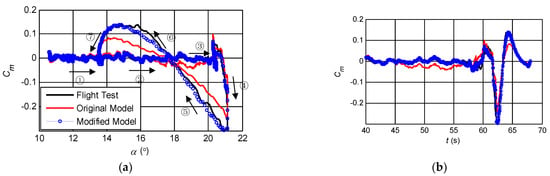
Figure 4.
Fitting of unimproved/improved stall aerodynamic model to the pitching moment observation data. (a) Cm−α; (b) Cm−t.
Figure 4a,b, respectively, show the curves of Cm observation data with the AOA and time. In Figure 4a, Cm observation data changed in the order of arrow direction and serial number. The pitch angular acceleration required to calculate Cm observation data is obtained by smoothing the angular velocity data and differentiating it. Detailed processing methods of angular velocity data can be referred to Reference [32]. Therefore, Cm observation data does not contain significant noise.
Since there is no clear stall before 40 s in Figure 4b, the Cm observation data is approximately 0, and the Cm curves of the unimproved pitching moment model and the improved model are almost coincident, so only the comparison of the fitting curves after 40 s is given. In the quasi-steady stall flight test, the aircraft speed slowly decreases and the AOA slowly increases. Before entering the deep stall, the aircraft maintains a steady state. Therefore, there are more data points in the quasi-steady flight test, and relatively few data points at the state of deep stall and stall recovery. In Figure 4a, it can be seen that the curves of stages ①, ② and ③ are thick, and the curves of stages ④~⑦ are thin. In Figure 4b, it can be seen that the curve before 55 s is thick and after 55 s is thin.
In the linear aerodynamic region with small AOA, the Cm observation data of aircraft can be fitted by using the unimproved pitching moment model. When the AOA increases to the point where obvious stall buffeting occurs (i.e., stages ② and ③ in Figure 4a and 45 s~60 s in Figure 4b), the fitting error of Cm increases significantly. The error is more apparent during the stall recovery (i.e., the stages ④~⑦ in Figure 4a, and the stage after 60 s in Figure 4b). This means that CmX obtained from the unimproved pitching moment model cannot accurately describe the characteristics of the aircraft stall pitching moment. The error of Cm will lead to the error of pitch angle velocity, which will further lead to a rapid increase of the error of pitch angle, airspeed, AOA and other state variables over time. Compared with CL and CD, Cm error has more clear adverse effects on the accuracy of simulation calculation.
CmX2(1 − X)2 is used to characterize the increment of the pitching moment resulting from the simultaneous change of aerodynamic force and aerodynamic center. CmX3(1 − X)3 is used to characterize the nonlinear increment of the pitch damping moment due to the change of AOA and pitch velocity. The fitting of the improved pitching moment model on Cm observation data is obviously improved. The maximum Cm fitting error decreases from 0.027 to 0.013 when entering stall (i.e., stages ② and ③ in Figure 4a and 45 s~60 s in Figure 4b). The maximum Cm fitting error is reduced from 0.086 to 0.034 when recovering stall (stages ④~⑦ in Figure 4a and the stage after 60 s in Figure 4b). The two high-order pitching moment correction terms have little effect on the fitting during steady flight (stage ① in Figure 4a and the stage before 45 s in Figure 4b). It shows that the improvement of the pitching moment model proposed in this paper makes sense. The identification results of ∂εt/∂α, CmX1, CmX2 and CmX3 obtained by using the improved pitching moment model can more accurately characterize the characteristics of the aircraft’s stall pitching moment.
4.2. Aerodynamic Modeling of Stall Process
4.2.1. Modeling of X
When the confidence level is 0.90, the identification results of a1 in Table 1 show the normal distribution of x~N(22.5,102). The identification results of α* follow the normal distribution of x~N(20,0.42). Therefore, the steady separation characteristics of quasi-steady stall maneuvers with different stall degrees can be characterized by the same set of a1 and α*. Based on the analysis above, a1 and α* can be set as 22.5 and 20.0°, respectively.
On the basis of determining the values of a1 and α*, two sets of flight test data segments in the interval from the beginning of evident buffeting to the complete recovery of stall (maximum angles of attack are 20.6° and 21.8°, the duration from stall to recovery is 8.2 s and 9.5 s, respectively) are selected for the optimization of τ1 and τ2. The resulting τ1 and τ2 are 11.93 c/V and 6.66 c/V, respectively. Combined with a1 and α* already established, X modeling can be completed. In order to validate the optimization results, the optimized τ1 and τ2 are substituted into the lift model to fit another flight test data segment with different hysteresis characteristics and a maximum AOA of 21.1°. The optimization results and validation results are shown in Figure 5.
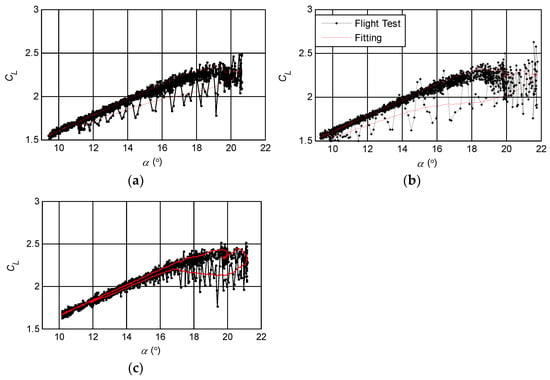
Figure 5.
Lift coefficient fitting after optimization of stall aerodynamic parameters. (a) CL hysteresis curve for optimization of τ1 and τ2 (αmax = 21.8°); (b) CL hysteresis curve for optimization of τ1 and τ2 (αmax = 20.6°); (c) CL hysteresis curve for validation of τ1 and τ2 (αmax = 21.1°).
The hysteresis curve of the lift coefficient in Figure 5c is quite different from the two hysteresis curves used for optimization in Figure 5a,b, but the lift model can still fit its hysteresis characteristics well. This indicates that a set of optimized a1, α*, τ1 and τ2 can make model (19) meet the lift characteristics of aircraft at different stall degrees.
4.2.2. Modeling of Correction Coefficient and e, ∂εt/∂α
After the modeling of X is completed, the identification results of the mean value and the 95% confidence interval of CDX, CmX1, CmX2 and CmX3 are listed by taking Xmin, the minimum value of X achieved in the flight test, as the abscissa, as shown in Figure 6.
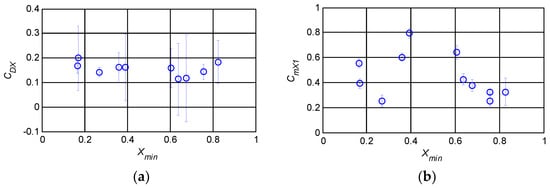
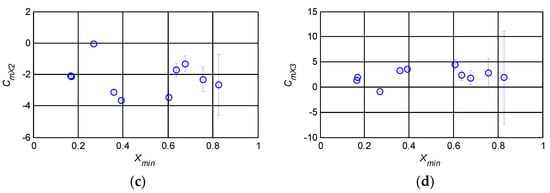
Figure 6.
Identification results of correction coefficients. (a) CDX−Xmin; (b) CmX1−Xmin; (c) CmX2−Xmin; (d) CmX3−Xmin.
When Xmin is large, the flow separation is not obvious, the nonlinear characteristics of aerodynamic force are not significant, and the accuracy of the identification results of the correction coefficient is low. Therefore, only the identification results of a correction coefficient with Xmin less than 0.82 are given in Figure 6. As can be seen from Figure 6a, when Xmin < 0.8, CDX identification results have no clear knots change characteristics, so nonlinear functions can be adopted for fitting. Most of the nonlinear components of the drag are characterized by the induced drag CL2/(eπΛ). The proportion of nonlinear components described by CDX(1 − X) is relatively small, and the absolute value of the estimated result of CDX is smaller (compared with CmX1). Although the s(CDX)/CDX is relatively large, variations in CD are still acceptable for stall aerodynamic modeling.
It can be seen from Figure 6b–d) that the identification results of CmX1, CmX2 and CmX3 under different Xmin are quite different, and the knots spline with X as the independent variable can be used to fit such nonlinear change characteristics. For large civil aircraft, it is too dangerous for the flight test when the flow on the upper surface of the wing is completely separated (i.e., Xmin is close to 0). Therefore, the minimum Xmin achieved in the flight test is 0.16, which is not significantly less than 0.2. Hence, the X knots are initially determined to be 0.6 and 0.4, according to the distribution characteristics of the identification results. Then, the knots and function forms are adjusted according to the fitting of the stall aerodynamic model on the Cm observation data.
It should be noted that when X < 0.16, the aircraft is almost completely stalled, and the risk of flight test is great. Therefore, it is generally impossible to obtain flight test data when X < 0.16 through a flight test, nor can it directly obtain identification results, and it is impossible to determine the characteristics of the stall drag and pitching moment within this range. At this point, extrapolation of the spline function between 0.16 ≤ X ≤ 0.43 may lead to the wrong drag and pitching moment correction coefficient. In order to ensure that the drag and pitching moment model can accurately describe the characteristics of the stall drag and pitching moment when X is near 0.16, the spline function of the correction coefficients of the drag and pitching moment when X < 0.16 are taken as a constant.
- (1)
- CDX modeling
The spline is fitted by using the identification results, and the coefficients in the spline are adjusted according to the actual simulation results. The final form of CDX spline function is Equation (25).
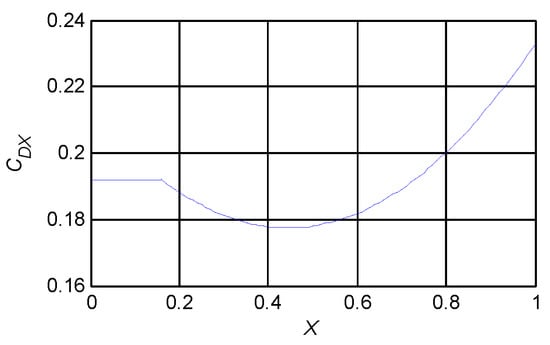
Figure 7.
Spline curve of CDX.
- (2)
- Modeling of CmX1, CmX2 and CmX3
When the flow separation is not easily noticed, 1 − X is small and the identification accuracy of the correction coefficient is poor. In this case, the correction coefficients are fixed as constants, which can simplify the model structure and obtain good fitting. According to the knots characteristics presented by the identification results, when X ≥ 0.6, the spline function of the correction coefficient of the pitching moment obtained by fitting the identification results and adjusting parameters based on the mathematical simulation of aircraft motion is:
When the AOA increases to generate clear nonlinear aerodynamic characteristics, the stall pitching moment characteristics cannot be well represented only by the constant term. When 0.43 ≤ X < 0.6:
The nonlinear characteristics of the pitching moment are enhanced with the further separation of flow. When 0.16 ≤ X < 0.43:
When X < 0.16:
The spline curves of the correction coefficients of pitching moment are shown in Figure 8.
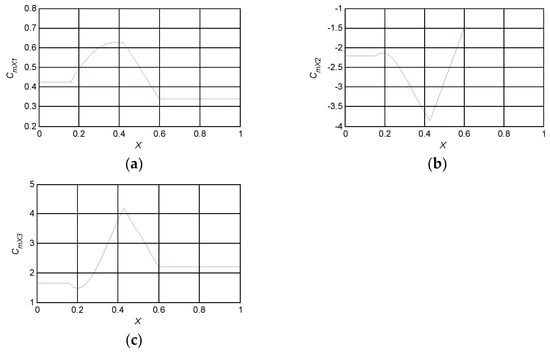
Figure 8.
Spline curves of correction coefficients of pitching moment. (a) CmX1−X; (b) CmX2−X; (c) CmX3−X.
- (3)
- Modeling of e and ∂εt/∂α
It can be seen from Table 1 that the distribution interval of e and ∂εt/∂α under different Xmin is small and does not change with Xmin, so it can be regarded as constant. Based on the identification results, parameters are adjusted according to the comparison between the flight dynamics simulation and test flight data, and the value of e is finally determined to be 0.785 and the value of ∂εt/∂α is 0.347. So far, an aerodynamic model is established for a large civil aircraft configuration 3 at 4500~5500 m altitude and an initial Ma = 0.275~0.30, which can describe the longitudinal stall aerodynamic characteristics of different stall degrees.
4.3. Mathematical Simulation Validation of Quasi-Steady Stall Flight
After the stall aerodynamic modeling of the example aircraft is completed, the comparison between the 6-DOF mathematical simulation results of the quasi-steady stall and flight test data (the initial altitude is 5500 m and the initial Mach is 0.29) is shown in Figure 9. The main control data of the aircraft are shown in Figure 10.
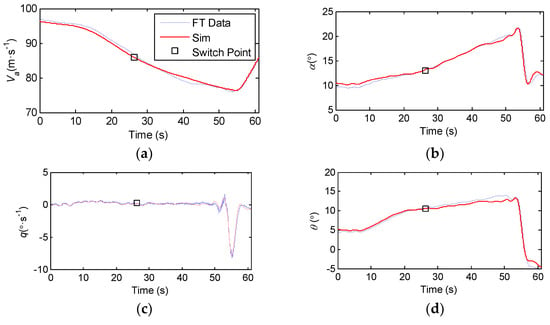
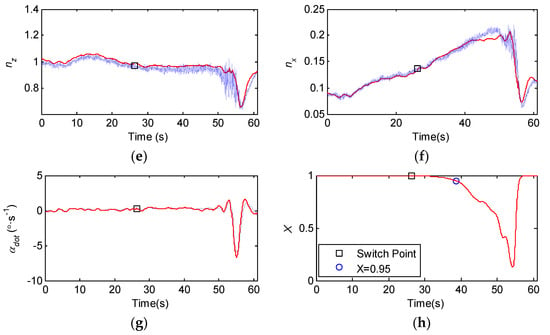
Figure 9.
The comparison of response of motion model and flight test data. (a) Airspeed; (b) Angle of attack; (c) Pitch angular velocity; (d) Pitch angle; (e) z−axis overload; (f) x−axis overload; (g) Change rate of AOA; (h) Change of X.
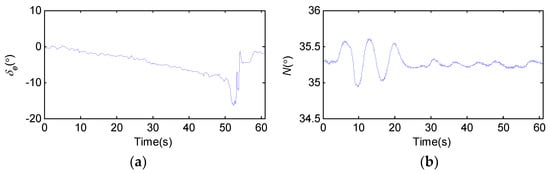
Figure 10.
Flight test data of main control variables. (a) Deflection angle of elevator; (b) High-pressure rotor speed of engine.
Thrust variation is represented by the high-pressure rotor speed of the engine in Figure 10b. During the whole quasi-steady stall process, N almost remains constant. Hence, the influence of the thrust change on stall can be ignored.
As can be seen from Figure 9h, at 38.8 s, X = 0.95, the corresponding AOA is 15.7°. By multiplying this AOA by 0.8, the αcr at entering stall is 12.6°, and the corresponding switching time between the pre-stall model and the extended stall model is 26.2 s. In the range of 0 s to 26.2 s, X ≈ 1, the flow on the upper surface of the wing does not separate, and the aerodynamic model of the motion model is the pre-stall aerodynamic model. The responses of the motion model at this stage are almost exactly consistent with the flight test data, which indicates that the pre-stall aerodynamic model has good accuracy and can accurately characterize the aerodynamic characteristics of the aircraft at small AOA.
During the switching between the pre-stall model and the extended model in 26.2 s, the responses of the motion model before and after the switching are continuous, and the jump can be ignored, which indicates that the high AOA extended stall aerodynamic model established based on the identification results has the same aerodynamic characteristics as the pre-stall model at αcr. In the range of 26.2 s~38.8 s, 0.95 ≤ X ≤ 1, it can still be approximated that there is no flow separation, and the aerodynamic characteristics are steady. However, at this time, the aerodynamic model of the motion model has been switched to the extended stall model. At this stage, the responses of the motion model almost coincide with the flight test data, which indicates that the established stall aerodynamic model has high accuracy in the steady aerodynamic region where the flow is not separated.
In the range of 38.8 s~50 s, 0.6 ≤ X ≤ 0.95, the flow appears to show evident separation. However, the airspeed, AOA and pitch rate of the aircraft are changing stably, and the aircraft is approaching stall. At this stage, the maximum error between the response of the motion model’s AOA and pitch angle and the flight test data is 0.7° and 1.5°, respectively. The maximum error of the velocity response is 1.1 m/s. This indicates that the extended stall aerodynamic model can accurately characterize the longitudinal stall aerodynamic characteristics approaching stall.
As can be seen from Figure 9c,e,f, after 50 s (corresponding to X < 0.6), the aircraft’s stall buffeting is obviously enhanced, uncontrolled pitching motion is generated and the aircraft enters the stall. According to Figure 9b and Figure 10a, the AOA increases to a maximum of 21.7° at 53.8 s and then begins to recover. As can be seen from Figure 9h, X reaches the minimum value of 0.16 at 54.3 s. By 57 s, the aircraft almost recovers from stall. During stall to recovery, the maximum error of the responses of AOA and pitch angle from the flight test data are 1.8° and 1.4°, respectively, and the maximum error of the velocity response is only 0.6 m/s, all of which can fit the flight test data well. This indicates that the aerodynamic model can accurately characterize the longitudinal stall aerodynamic characteristics from stall to recovery.
It should be noted in particular that the maximum error between the pitch angular velocity response of the motion model and the flight test data is only 0.3°/s in the stages of approaching stall, stall and stall recovery. This indicates that CmX1(1 − X), CmX2(1 − X)2 and CmX3(1 − X)3, the three high-order correction terms for the pitching moment, can well represent the characteristics of the stall pitching moment of the aircraft, which significantly reduces the error, which is caused by pitching moment error, between the responses of the motion model and the flight test data.
A set of data not used for identification and modeling (the initial Ma = 0.28, the initial altitude = 4900 m) is used to assess the predictive capability of the stall aerodynamic model. When using the identical input as the flight test data (as shown in Figure A2), the comparison between the dynamic model response and the test flight data is shown in Figure A1. As can be seen from Figure A1, the pitch angle and AOA response of the dynamic model all meet the tolerance requirements of plus or minus 2° for the flight test data of the pitch angle and AOA given in 14 CFR Part 60 [33]. This indicates that the established aerodynamic model has good predictability.
In summary, the improvement of the stall aerodynamic model in this paper makes sense. The longitudinal stall aerodynamic model can accurately characterize the aerodynamic characteristics of the aircraft at the state of approaching stall, stall and stall recovery.
5. Conclusions
(1) The identification method of the stall aerodynamic parameters of civil aircraft based on the improved stall aerodynamic model is established. When the flow separation point of the upper surface of the wing X = 0.95, the corresponding AOA multiplied by 0.8 is defined as the αcr of the switch between the pre-stall model and the extended model. Based on the steady aerodynamic theory at small AOA, the values of unknown aerodynamic parameters representing the steady aerodynamic forces/moments in the stall aerodynamic model are determined. In addition, CmX2(1 – X)2 and CmX3(1 – X)3, two high-order correction terms, are added to the pitching moment model. An improved stall aerodynamic model is established. Then, the observation values of lift, drag and pitching moment are calculated using the overload and angular acceleration data from the flight test. Finally, based on the improved stall aerodynamic model, the maximum likelihood method is used to identify four correction coefficients, CDX, CmX1, CmX2 and CmX3, four X characteristic parameters a1, α*, τ1 and τ2, and e, ∂εt/∂α.
(2) The longitudinal stall aerodynamic modeling method used for the mathematical simulation of a quasi-steady stall is established. Firstly, the identification results of a1 and α* of stall maneuver data with different stall degrees are tested to check whether they show the given normal distribution, and the values of a1 and α* are determined. Then, at least two groups of flight data segments from deep stall to stall recovery are extracted, and the lift model is made to fit the hysteresis curves of these data segments through the optimization of τ1 and τ2. The optimal solution is the values of τ1 and τ2, and the X modeling is established by using a1, α*, τ1 and τ2. Finally, knots splines with 1, X, X2 and X3 as independent variables are used to model correction terms under different stall degrees. The Oswald factor and the downwash rate at the horizontal tail are set as constants.
(3) The comparison of the quasi-steady stall maneuver response of a civil aircraft 6-DOF dynamic model and flight test data shows that the extended stall model based on the identification results of the improved stall aerodynamic model is compatible with the pre-stall model. The aerodynamics and responses of motion are consistent when the two models switch. The quasi-steady stall motion response of the 6-DOF motion model is highly consistent with the flight test data, especially the pitch angular velocity response based on the motion model that almost coincides with the flight data. In summary, the aerodynamic model based on the proposed stall aerodynamic parameter identification method and the stall aerodynamic modeling method can accurately characterize the longitudinal aerodynamic characteristics of the aircraft at the state of approaching stall, stall and stall recovery.
Author Contributions
Conceptualization, L.W. and R.Z.; methodology, R.Z. and K.X.; validation, R.Z., K.X. and Y.Z.; formal analysis, L.W. and T.Y.; investigation, R.Z. and K.X.; resources, Y.Z.; data curation, T.Y. and Y.Z.; writing, L.W. and R.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data sharing is not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Notation
The following abbreviations and symbols are used in this manuscript.
| AOA | angle of attack |
| MAC | mean aerodynamic chord |
| ODE | ordinary differential equation |
| DOF | degree of freedom |
| α | angle of attack (°) |
| V | airspeed (m/s) |
| q | pitch velocity (°/s) |
| dimensionless pitch velocity | |
| dimensionless change rate of AOA | |
| change rate of AOA (°/s2) | |
| dynamic pressure (Pa) | |
| S | reference wing area (m2) |
| wing area of horizontal tail (m2) | |
| mean aerodynamic chord length (m) | |
| δt | horizontal tail deflection angle (°) |
| δe | elevator deflection angle (°) |
| e | Oswald factor |
| Λ | aspect ratio |
| X | relative position of the ideal flow separation point of the upper surface of the wing on the mean aerodynamic chord |
| αt | local AOA at horizontal tail (°) |
| εt | downwash angle at horizontal tail (°) |
| ε0 | downwash angle corresponding to zero lift AOA (°) |
| τ1 | time constant of unsteady separation process (/V) |
| τ2 | time constant of flow separation hysteresis (/V) |
| a1 | stall characteristics parameter of airfoil |
| α* | the AOA when flow separation point is equal to 0.5 (°) |
| ∂εt/∂α | derivative of downwash angle with respect to AOA |
| ∂εt/∂X | derivative of downwash angle with respect to X |
| CL | lift coefficient |
| CD | drag coefficient |
| Cm | pitching moment coefficient |
| CLαwb | lift curve slope of wing-body |
| CDX | empirical correction coefficient of drag |
| CmX | empirical correction coefficient of pitching moment |
| CmX1 CmX2 CmX3 | 1-order, 2-order, 3-order pitching moment correction term |
| Cmα | pitching static stability derivative |
| CLq | lift derivative due to pitching |
| lift derivative due to | |
| Cmq | pitching damping derivative |
| pitching damping derivative of lag of wash | |
| CLαt | lift derivative of horizontal tail |
| Cmδe | pitch control derivative of elevator |
| Cmδt | pitch control derivative of horizontal tail |
| Cmb | pitching moment coefficient of fuselage |
| Cmw0 | zero lift pitching moment coefficient of wing |
| CLw | lift coefficient of wing |
| Xw | the coordinate of wing pressure center relative to gravity center position in MAC fraction |
| lht | the distance from the aerodynamic center of the horizontal tail to the gravity center of the aircraft |
| Vt | local airspeed at horizontal tail |
| ax | longitudinal acceleration (m/s2) |
| T | thrust (N) |
| Ixx | moment of inertia with respect to roll axis (kg × m2) |
| Iyy | moment of inertia with respect to pitch axis (kg × m2) |
| Izz | moment of inertia with respect to yaw axis (kg × m2) |
| Ixz | product of inertia (kg × m2) |
Appendix A
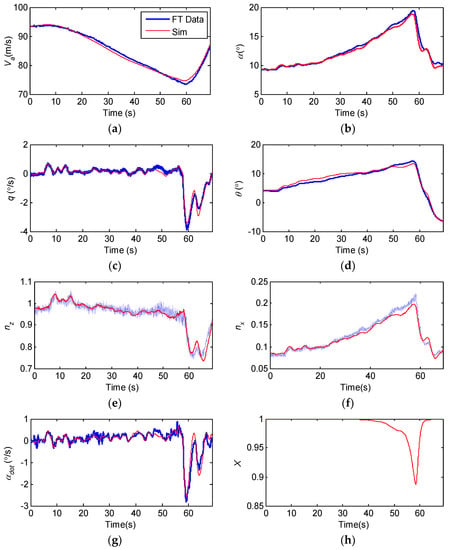
Figure A1.
Model predictive capability validation. (a) Airspeed; (b) Angle of attack; (c) Pitch angular velocity; (d) Pitch angle; (e) z−axis overload; (f) x−axis overload; (g) Change rate of AOA; (h) Change of X.
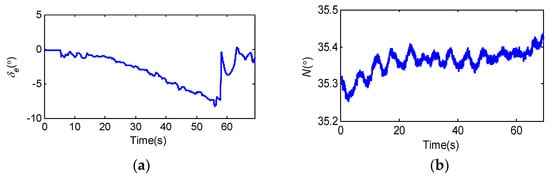
Figure A2.
Flight test data of main control variables. (a) Deflection angle of elevator; (b) High-pressure rotor speed of engine.
References
- Jategaonkar, R.; Moennich, W. Identification of DO-328 aerodynamic database for a Level D flight simulator. In Proceedings of the Modeling and Simulation Technologies Conference, New Orleans, LA, USA, 11–13 August 1997. [Google Scholar]
- Gingras, D.R.; Ralston, J.N.; Oltman, R.; Wilkening, C.; Watts, R.; Derochers, P. Flight Simulator Augmentation for Stall and Upset Training. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar]
- Abramov, N.B.; Goman, M.; Khrabrov, A.N.; Soemarwoto, B.I. Aerodynamic Modeling for Poststall Flight Simulation of a Transport Airplane. J. Aircr. 2019, 56, 1427–1440. [Google Scholar] [CrossRef]
- Goman, M.; Khrabrov, A. Stall aerodynamic representation of aerodynamic characteristics of an aircraft at high angles of attack. J. Aircr. 1994, 31, 1109–1115. [Google Scholar] [CrossRef]
- Dias, N.J. Unsteady and Post-Stall Model Identification Using Dynamic Stall Maneuvers. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Dallas, TX, USA, 22–26 June 2015. [Google Scholar]
- Dias, N.J.; Almeida, F.A. High Angle of Attack Model Identification Without Air Flow Angle Measurements. In Proceedings of the AIAA Atmospheric Flight Mechanics (AFM) Conference, Boston, MA, USA, 19–22 August 2013. [Google Scholar]
- Kumar, A.; Ghosh, A.K. GPR-based novel approach for non-linear aerodynamic modelling from flight data. Aeronaut. J. 2018, 123, 79–92. [Google Scholar] [CrossRef]
- Jategaonkar, R.V.; Fischenberg, D.; Von Gruenhagen, W. Aerodynamic Modeling and System Identification from Flight Data-Recent Applications at DLR. J. Aircr. 2004, 41, 681–691. [Google Scholar] [CrossRef]
- Ingen, J.V.; Visser, C.C.; Pool, D.M. Stall Model Identification of a Cessna Citation II from Flight Test Data Using Orthogonal Model Structure Selection. In Proceedings of the AIAA Scitech 2021 Forum, 11–15 & 19–21 January 2021. [Google Scholar] [CrossRef]
- Horssen, L.J.; Visser, C.C.; Pool, D.M. Aerodynamic Stall and Buffet Modeling for the Cessna Citation II Based on Flight Test Data. In Proceedings of the 2018 AIAA Modeling and Simulation Technologies Conference, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Liu, S.F.; Luo, Z.; Moszczynski, G.; Grant, P.R. Parameter Estimation for Extending Flight Models into Post-Stall Regime-Invited. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Teng, T.; Zhang, T.; Liu, S. Representative Post-Stall Modeling of T-tail Regional Jet and Turboprop Aircraft for Flight Training Simulator. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Singh, J.; Jategaonkar, R. Flight determination of configurational effects on aircraft stall behavior. In Proceedings of the 21st Atmospheric Flight Mechanics Conference, San Diego, CA, USA, 29–31 July 1996. [Google Scholar]
- Nguyen, D.H.; Goman, M.; Lowenberg, M.H.; Neild, S.A. Evaluation of Unsteady Aerodynamic Effects in Stall Region for a T-Tail Transport Model. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA & Virtual, 3–7 January 2022. [Google Scholar]
- Seo, G.-G.; Kim, Y.; Saderla, S. Kalman-filter based online system identification of fixed-wing aircraft in upset condition. Aerosp. Sci. Technol. 2019, 89, 307–317. [Google Scholar] [CrossRef]
- Dias, N.J. High Angle of Attack Model Identification with Compressibility Effects. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Saderla, S.; Dhayalan, R.; Ghosh, A. Non-linear aerodynamic modelling of unmanned cropped delta configuration from experimental data. Aeronaut. J. 2017, 121, 320–340. [Google Scholar] [CrossRef]
- Smets, S.C.; Visser, C.C.; Pool, D.M. Subjective Noticeability of Variations in Quasi-Steady Aerodynamic Stall Dynamics. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Grauer, J.A.; Morelli, E.A. Generic Global Aerodynamic Model for Aircraft. J. Aircr. 2015, 52, 13–20. [Google Scholar] [CrossRef]
- Morelli, E.A. Global nonlinear aerodynamic modeling using multivariate orthogonal functions. J. Aircr. 1995, 32, 270–277. [Google Scholar] [CrossRef]
- Brandon, J.M.; Morelli, E.A. Real-Time Onboard Global Nonlinear Aerodynamic Modeling from Flight Data. J. Aircr. 2016, 53, 1261–1297. [Google Scholar] [CrossRef]
- Boschetti, P.J.; Neves, C.; Ramirez, P.J. Nonlinear Aerodynamic Model in Dynamic Ground Effect at High Angles of Attack. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA & Virtual, 3–7 January 2022. [Google Scholar]
- Morelli, E.A. Efficient Global Aerodynamic Modeling from Flight Data. In Proceedings of the 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012. [Google Scholar]
- Morelli, E.A.; Cunningham, K.; Hill, M.A. Global Aerodynamic Modeling for Stall/Upset Recovery Training Using Efficient Piloted Flight Test Techniques. In Proceedings of the AIAA Modeling and Simulation Technologies (MST) Conference, Boston, MA, USA, 19–22 August 2013. [Google Scholar]
- Garcia, A.R.; Vos, R.; Visser, C. Aerodynamic Model Identification of the Flying V from Wind Tunnel Data. In Proceedings of the AIAA AVIATION 2020 FORUM, Virtual Event, 15–19 June 2020. [Google Scholar]
- Leung, J.M.; Moszczynski, G.J.; Grant, P.R. A State Estimation Approach for High Angle-of-Attack Parameter Estimation from Certification Flight Data. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Khrabrov, A.; Vinogradov, Y.; Abramov, N. Mathematical Modelling of Aircraft Unsteady Aerodynamics at High Incidence with Account of Wing-Tail Interaction. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Providence, RI, USA, 16–19 August 2004. [Google Scholar]
- Fischenberg, D. Identification of an unsteady aerodynamic stall model from flight test data. In Proceedings of the 20th Atmospheric Flight Mechanics Conference, Baltimore, MD, USA, 7–10 August 1995. [Google Scholar]
- Imbrechts, A.; Visser, C.C.; Pool, D.M. Just Noticeable Differences for Variations in Quasi-Steady Stall Buffet Model Parameters. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA & Virtual, 3–7 January 2022. [Google Scholar]
- Jategaonkar, R.V. Output Error Method. In Flight Vehicle System Identification: A Time Domain Methodology; AIAA: Reston, VA, USA, 2006; pp. 79–119. [Google Scholar]
- Luchtenburg, D.M.; Rowley, C.W.; Lohry, M.W.; Martinelli, L.; Stengel, R.F. Unsteady High-Angle-of-Attack Aerodynamic Models of a Generic Jet Transport. J. Aircr. 2015, 52, 890–895. [Google Scholar] [CrossRef]
- Klein, V.; Morelli, E.A. Data Analysis. In Aircraft System Identification—Theory and Practice; AIAA Education Series; AIAA: Reston, VA, USA, 2006; pp. 355–357. [Google Scholar]
- Federal Aviation Administration. Flight Training Device (FTD) Objective Tests. In CFR Part 60, Flight Simulation Training Device Initial and Continuing Qualification; Federal Aviation Administration: Washington, DC, USA, 2016; pp. 302–303. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).