Abstract
The deployment of electro-mechanical actuators plays an important role towards the adoption of the more electric aircraft (MEA) philosophy. On the other hand, a seamless substitution of EMAs, in place of more traditional hydraulic solutions, is still set back, due to the shortage of real-life and reliability data regarding their failure modes. One way to work around this problem is providing a capillary EMA prognostics and health management (PHM) system capable of recognizing failures before they actually undermine the ability of the safety-critical system to perform its functions. The aim of this work is the development of a model-based prognostic framework for PMSM-based EMAs leveraging a metaheuristic algorithm: the evolutionary (differential evolution (DE)) and swarm intelligence (particle swarm (PSO), grey wolf (GWO)) methods are considered. Several failures (dry friction, backlash, short circuit, eccentricity, and proportional gain) are simulated by a reference model, and then detected and identified by the envisioned prognostic method, which employs a low fidelity monitoring model. The paper findings are analysed, showing good results and proving that this strategy could be executed and integrated in more complex routines, supporting EMAs adoption, with positive impacts on system safety and reliability in the aerospace and industrial field.
1. Introduction
Aviation subsystem architectures are evolving substantially as a result of the more electric aircraft (MEA) concept, which, among other improvements, calls for the gradual replacement of hydraulic and electro-hydraulic actuators (EHA) with electro-mechanical actuators (EMA). In fact, it is believed that this paradigm shift would result in significant weight reductions, substantial life cycle cost (LCC) savings [1,2], lower repercussion on the environment, and, last but not least, increased reliability of the entire aircraft system [3].
Flight control surfaces in commercial aircrafts are currently actuated using FBW (fly-by-wire) technology: the pilot commands are translated into low-power electrical signals that are then managed by a computer and passed to hydraulic servovalves, which finally drive the appropriate aerodynamic surface and close the position control loop. The result is an electrical control, which, however, still leverages hydraulic power [4,5]. The core concept is aiming at an all-in-one electrical solution that can meet the necessary safety criteria [6,7], encompassing the most power-demanding aircraft subsystems. The authors in [8] provided a brief overview of the usage of EMAs and electro-hydraulic actuators (EHA) on the most widespread aircraft platforms. In what is considered the forefather of the electric aircraft par excellence, the Boeing 787, EMAs and EHAs are already taking the place of hydraulic actuators. The latest versions of the Airbus A350 and A380 follow the same principle, but EMAs are still only used for secondary flight controls (e.g., flaps, slats, spoilers), while EHAs are installed for both primary and secondary flight controls. It is clear that some challenges still limit a seamless replacement of EMAs in place of hydraulically driven actuation devices [7,9] for primary flight controls. This article follows the ideas presented in [10] and aims to propose a possible step forward by exploiting prognostics. De facto, it is critical to evaluate the implications of the substitution of an hydraulic subsystem with its electrical alternative, in terms of the usage, implementation, monitoring, and the equipment’s reliability and safety. In the case of hydraulic systems, a potential failure (for example, a pressure drop caused by a leak) can be detected far before a load is demanded by appropriate pressure sensors.
Electrical system failures give rise to completely different problems from the power electronics point of view [11], as well as from the actuation one: new safety concerns are raised because no preventive mitigation plan can be implemented to reduce the impact of the fault itself if no additional auxiliary system is envisioned. As a consequence, the system must be exceedingly fault-tolerant. On top of that, EMAs show some issues that are less influential for hydraulic actuators, such as EMC, the mechanical jamming of the overall subsystem, and overheating problems, due to the high currents. A possible solution could be represented by hardware redundancy; however, this would result in weight increases, as well as incompatibilities with actuation requirements [12], therefore reducing the benefits of MEA principles.
Prognostics main selling point stands in the capability of detecting and identifying component early failures and track down their progression during the equipment use. This result brings a lot of positive outcomes with it; one of the most important is definitely the possibility of exploring innovative types of maintenance strategies (CBM, opportunistic and predictive maintenance [13,14,15]). On top of that, prognostics and health management (PHM) strategies could really be useful to back EMAs up, in order for them to reach the required safety standards for safety-critical applications, such as primary flight control actuation. Prognostics can be then seen as an effective mean to assist EMAs, thanks to its ability to identify hidden faults and prevent the related potential hazardous or catastrophic failure conditions. Prognostics sphere of influence stands in the monitoring and tracking of component or system parameters during their operation [16]: in this way, by checking the operational values and physical outputs, incipient failures can be detected resulting in the improvement of mission readiness, upgrade of RAMS capabilities, and a reduction of LCCs [17,18]. There is an ongoing substantial effort in the research community that focuses on the development of PHM systems for EMAs: a very detailed literature review on the matter can be found in [19]. Prognostics can be categorized based on many different criteria. The most general one is linked to the way the data used for the comparison is generated: data-driven [20], model-based [21,22], or hybrid. The method followed by the authors in this work is strictly model-based, due to the lack of enough real-life data to build the prognostic framework upon. The developed prognostic strategy is envisioned within an operational scenario and, as such, a general concept of operation (ConOps) is proposed, along with the high-level failure detection and identification (FDI) methodology. After that, a detailed explanation of the employed metaheuristic search algorithms (MSAs) and a brief overview of the models is reported. Two different models are used in this work: an high fidelity one (RM—-reference model) and a low fidelity counterpart (MM—monitoring model), the latter being in the core of the prognostic framework. This work continues the ongoing effort started in [23], where a similar strategy was applied on brushless BLDC trapezoidal motors: in this case, the employed motor is a sinusoidal PMSM motor. Finally, the results and comparisons between the algorithms are reported.
2. Related Work
Metaheuristic algorithms for prognostics are only partially approached due to the limitations linked to the computational cost. However, there are many studies that already focused on MSAs to solve prognostic challenges. For instance, the authors already applied a similar strategies to a BLDC motor [23]. The literature on MSA is vast and covers almost every field of academic and industrial research. Furthermore, it must be said that the field of mathematical optimization using MSA is an extremely fast paced research area where new algorithms applied on very different application are being published continuously. We focused our literature review on MSA application in the prognostic field. In [24], a PHM framework for lithium-ion batteries has been developed using an improved PSO. PSO has been used also in [25] for power transformers PHM and in [26] for wind turbine gearbox RUL estimation. The same application on lithium-ion batteries has been the focus of [27,28], which proposed the use of teaching–learning-based optimization (TLBO) for multiple degradation factors condition and hunger game search (HGS), respectively. The authors in [29] proposed a fuel cell health estimation strategy using, among other technique, a very popular MSA: the cuckoo search algorithm (CSA), inspired by cuckoo species parasitism. In [30], the authors used PSO to optimize the objective function related to rotating component prognostics. MSAs can also be used to optimize neural network parameters, as performed in [31], with landslide mapping, prediction, and prognostics or in [31], where CSA was employed.
As far as aerospace applications are concerned, a few works have been found and examined. A very interesting approach has been proposed in [32], where a combination of genetic algorithms (GAs) and a bio inspired artificial immune system has been used to schedule predictive maintenance tasks in a PHM framework. The same authors approached GAs and variable neighbourhood search (VNS) to solve the same problem in [33]. Aircraft motion planning issues have been the focus of [34], where a review of different population-based MSAs has been carried out, showing that PSO is the most used approach. A very relevant study [35] proposed ant colony optimization (ACO), in order to integrate PHM in aircraft maintenance planning, from a CBM perspective.
After a detailed literature review, which focused the fundamental queries “Prognostics”, “Metaheuristic Algorithm”, “Bio-inspired”, and a wide range of secondary keyworkds, no work that focused the prognostic area applied to the EMA/aerospace domain using MSA has been found, to the best of our knowledge.
3. Materials and Methods
The proposed PHM strategy is built around the MM, whose simulations can be run almost in real time [36,37]. The other inputs for the prognostic strategy are, of course, the signals coming from the sensors mounted on the physical system (as shown in Figure 1).
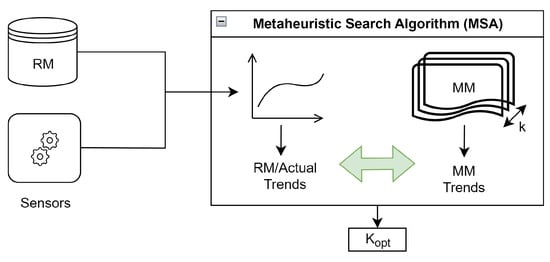
Figure 1.
FDI methodology overview [10].
However, real-life actuator data is difficult to obtain, and the failures are very rare indeed. Therefore, in this study, data have been generated through the aforementioned RM, which has been used as a NTB. The authors set up the RM and generated the failure data; the prognostic algorithm was then employed to detect and identify the failures and, after its run, the results were compared and the errors were calculated. Figure 1 shows the overview of the overall methodology. On the right, the reader can notice data coming from sensors or from the database created by the NTB.
The RM and MM are two physical-based models, developed in Simulink starting from equations implementing the real physical behaviours: actual equations are implemented in Simulink blocks (e.g., EM motor equations, dynamic equations, etc.). A more in depth description will be provided in Section 3.2. The models are defined by a set of top level parameters (TLPs), grouped inside a vector, as better explained later on. Each component of the vector is linked and can be traced back to a failure in the EMA. By altering these parameters, it is possible to inject failures inside the models. For all intents and purposes, the TLPs change the simulation boundary conditions; hence, it is possible to simulate the actuator behaviours in different conditions. Both models have been verified and experimentally validated under nominal and non nominal settings, proving the models’ capacity to estimate actual trends with high precision.
During a prognostic routine, the MM is then iteratively run with different sets of TLPs. In fact, in each simulation run, the TLPs are updated following the results obtained by the optimization using the MSA. The algorithm tries to find the monitoring TLPs that alter the MM outputs in order to reduce the error between the predicted and actual trends (real or simulated). A real-time solution is not feasible because of the total running time of the high number of simulation runs, as stated better later on. The error is defined using a suitable fitness function (Equation (4)). As a result, after the optimization process is complete, the output of the MM is extremely similar to the actual one. After finding a satisfactory match, the system’s health is evaluated by comparing the related TLPs with the related failures. Therefore, it is possible to execute a basic but effective FDI process by examining TLPs to determine whether a failure is occurring and establish what kind of failure it is.
As stated before, and as [38] explained, the TLPs are grouped inside a normalised vector (Equation (1)): each component is strictly linked to a physical system failure and it can assume values between 0 and 1 to characterize different failure magnitudes.
- : Dry friction. When , the resulting friction is the nominal value multiplied by three.
- : Backlash. When , the backlash magnitude is the nominal value multiplied by one hundred.
- , , : Short circuit (SC). Being a three-phase motor, each coefficient is linked to a short circuit in one phase.
- , : Static eccentricity. These coefficients are linked to the modulus and phase of the eccentricity in the rotor. Under nominal conditions, the phase corresponds to 0 rad, so .
- : Proportional gain drift (PGD). is linked to an increase of 50 per cent in the proportional gain, while determines a 50 per cent decrease. The nominal value is .
Table 1 shows in a schematic way each TLP along with the effects on the system at the relative maximum and minimum values. Note that maximum eccentricity refers to a situation where the eccentricity modulus is equal to the rotor air gap width.

Table 1.
Top level parameters meaning and effects.
As far as the failure implementation is concerned, each k coefficient is used in the MM and in the RM as a parameter that affects the model behaviour in different ways. For instance, is multiplied with the static or dynamic friction coefficients within the coulombian friction implementation. coefficient multiplies the global backlash value inside the model, appropriately modelled by a Simulink block. On the other hand, , , and represent the percentages of each phase affected by short circuit. These coefficients modify the wirings resistance (in a linear way) and inductance (in a quadratic way), hence affecting the electrical modelling of the system, as reported in [39]. The outcome of rotor eccentricity is modelled according to the following formulas [40], shown in Equation (2):
where , , and are the resulting back-EMF coefficient for the three phases, starting from the nominal coefficients , , and . On the other hand, is the mechanical rotor angle. Finally, simply multiplies the proportional gain in the controller block.
The nominal vector (i.e., the vector whose components would lead to a nominal behaviour of the EMA) is, hence, the one reported (Equation (3)):
The fitness function is defined as:
where and are the MM and RM current outputs respectively at the instant time i [41]. Furthermore, the quadratic error between these two currents is evaluated to consider both the error in time and in the signal. Finally, the first order derivative is calculated numerically using Matlab’s gradient command and divided by the integration step . Finally, to avoid the time dependence of the error, it is multiplied by the simulation integration step itself . The current values referred to the two models are considered at each instant of time i.
3.1. Employed Algorithms
The authors used a specific kind of optimization method that falls into the category of metaheuristic bio-inspired algorithms. Optimization algorithms’ primary goal is to reduce or maximize an objective function, also known as a fitness function, by modifying the so-called decision variables: in this case the vector’s components, which are bound by established constraints [42]. Although heuristic techniques cannot always guarantee the optimal result, they aim to produce satisfactory solutions, or solutions that are at least close to the optimal outcome, at a reasonable processing cost. MSAs use a variety of strategies to identify effective solutions to optimize problems starting from a large population of acceptable candidates, while making few assumptions about the problem being optimized [43]. Furthermore, the algorithms are bio-inspired, since they have underlying mechanisms based on biological processes. In fact, natural adaptation might be viewed as a type of optimization. In this work, the authors have approached on the evolutionary (EA) and swarm intelligence (SI) algorithms. Following a careful literature review as reported in Section 2, we selected three different MSA:
- PSO, since it resulted as one of the most used ones;
- DE, to represent the evolutionary algorithm category;
- GWO, which we selected among new algorithms.
3.1.1. Evolutionary Algorithms
Evolutionary algorithms draw their inspiration from the natural evolutionary behavior. They are described by a few key characteristics and parameters:
- Population: The solution “pool”, which is initialized at the start of the process;
- Variety: The population must be varied enough to explore the solution space effectively;
- Heredity: This values is linked to the capability of passing a characteristic to the offspring;
- Selection: For artificial algorithms, selection must only occur in the desired direction, which is a key parameter to ensure that only the best solutions will be reproduced.
Individuals serve as a representation of the different solutions, and a score, known as the fitness value, is assigned to them by means of Equation (4), calculated by analyzing the phenotype, or set of traits, of the subjects in question.
Differential Evolution. One of the most famous EA is the differential evolution strategy [43,44], which is also one of the tested algorithms in this work. The main concept of this algorithm follows the genetic principles.
Figure 2 shows the logical process behind this optimization algorithm. The process starts with a step called mutation: three individuals (three vectors in this case) are selected randomly from the population and a fourth vector is created by calculating the difference (the evolution is differential) between the first two vectors, multiplying it by a mutation factor, and then adding the third one. The recombination or crossover phase begins at this stage, when the altered parameters of the starting vector are combined with those of the so-called target vector to produce the trial vector. The trial and target vectors are compared during the selection phase. If the trial’s score exceeds the target, it will be used as the next target; otherwise, it will be discarded. In the next generation, the vector with the highest fitness value will be maintained. The pseudo-code for this algorithm is reported in Figure 3.
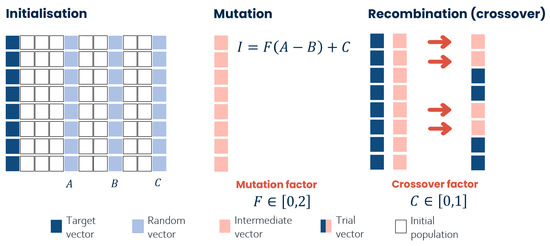
Figure 2.
A schematic representation of the Differential Evolution Algorithm.

Figure 3.
Pseudo-code for DE algorithm, as taken from [41].
Genetic algorithms are another popular EA optimization method (GA). In [23,45], a detailed investigation of the implementation of such algorithms on comparable challenges for PHM techniques was performed. However, in previous tests, the global GA performance (considering the same metrics employed in this work) results were inferior, with respect to other metaheuristic optimization methods [38].
3.1.2. Swarm Intelligence Methods
These methodologies are part of the bio-inspired category because they draw their inspiration from the behavior that may be observed when more than one entity (e.g., animal) interacts with other individuals. As stated before, the biological behaviours linked to the interaction between individual can result in a sort of optimization, in the sense that the resources are shared and, thanks to the mutual collaboration, a solution is reached quicker. The result is a sort of information structure (which would not be present if the problem is approached by a single entity) that can be translated into mathematical formulations and, hence, used in optimization problems.
The difference with EA is that, in this case, the process is interaction-driven by the entities’ behaviours (i.e., collective intelligence) and not controlled by genetic processes. The ability to exchange information and send or receive feedbacks from the other individuals inside the group is what makes the collective intelligence so powerful. In other words, SI methods are the result of a very attentive observation of real-life actions between animals. As said before, two SI methods have been approached in this study: particle swarm optimization (PSO) and gray wolf optimization (GWO). In this case, each individual is seen as a vector and, hence, as a possible solution.
Particle Swarm Optimization. Being a SI algorithm, PSO [46] draws its inspiration from the movement of bird flocks or fish schools. In fact, starting from a population of potential solutions (i.e., particles) and moving them throughout the search space, this methodology can solve optimization problems by following rigid mathematical formulas. As said before, the optimization is guaranteed by the fact that there is a capillary and diffused intelligence: the movement of each particle, and hence, its path, is affected by each particle’s local best known position and the best known locations in the search space (these are known because the knowledge is shared by particles). That is precisely why the swarm is able to iteratively identify the optimum solutions by information sharing. Some initial parameters shall be defined, such as the population size, particle initial placements and speed, and particle inertia. After the initialization set up, each particle is given a random neighborhood, and by travelling, the best overall position is discovered. The position associated with the optimal global location are updated, so that each particle knows it. A detailed examination of the solution space is possible, thanks to the velocities’ inherent stochastic component [47].The pseudo-code for this algorithm is reported in Figure 4. More information on the algorithm implementation can be found in [41]. The employed code routine iteratively runs until 200 iterations are reached or until the error between two successive runs is less than .

Figure 4.
Pseudo-code for PSO algorithm, as taken from [41].
Grey Wolf Optimization. If PSO was generically inspired by birds’ and fishes’ movement, GWO [48] has a more precise inspiring animal: wolves. This optimization technique follows the idea of the rigid hierarchical scales among grey wolf population’s members. After choosing the size of the wolf pack and the initial positions of each “animal”, an initial population hierarchy is defined by looking at the fitness function values. The decision of the number of wolves is crucial, as both the accuracy of the algorithm and the execution time are affected by this parameter. The higher the fitness value, the higher the hierarchical position in the scale. In this way, the individuals with lower scores will be less influential in the optimization process, while the better-positioned animals will lead the process. In other words, each wolf represents a distinct solution to the problem.
The main difference with PSO lies in the fact that, in this case, the wolves cannot communicate their position to the other members of the pack. In order to find the best solution, an adequate population initialization and search method must be adopted [49]. The pseudo-code for this algorithm is reported in Figure 5. The interested reader can find more information on the algorithm implementation in [41]. The size of the population has been set to 50 individuals. The optimization is stopped when the number of iterations reached is 150 or the tolerance of is reached within two successive runs.

Figure 5.
Pseudo-code for GWO algorithm, as taken from [41].
3.2. Models
The general architecture of an aeronautical EMA is extremely complex, characterized by multibody interactions and multiple non linearities and can be summed up as follows: a controller, an electric motor (usually PMSMs or BLDC motors), a gearbox, and an intricate network of sensors for measuring the currents, vibrations, voltages, temperatures, etc. As a result, the system is made up of multiple interconnected hardware and software components. It is also required to investigate their cross-interactions, so that the control system can appropriately fulfill its functions of monitoring, fault detection, and the assessment of a possible divergence route.
As stated before, two models have been assembled in Simulink and then validated, thanks to experimental test rigs. The models are physical-based and each component in real life is treated and modelled thanks to the appropriate equations. In other words, each block encloses the mathematical formulation by means of real formulas (e.g., electromagnetic formulas for the motor, dynamic equations for the physical systems, etc.).
If the RM has been built with a very high degree of precision, the MM has been conceived with approximations and lumped parameters, so that an almost real-time use is more feasible; the computational cost is, hence, reduced. The thorough description of the model is way beyond the scope of this work. The interested reader should see [36,37,50,51], as far as the RM and MM models are concerned, respectively. Furthermore, as explained in [36,37,50,51], the models have been built to represent an existing and experimental test bench located in Politecnico di Torino laboratories. In order to match the models and experimental results, the test bench structure has been reported in Simulink through simulation blocks. The experimental test bench has been pivotal in the model development: in fact, validation is essential to test models simulation performances [52].
The main parameters used in the models are, hence, taken from components data-sheets and technical documents. The hardware configuration is based on the “S120 AC/AC Trainer Package” by Siemens. The motor parameters are reported in Table 2. The PID controller parameters have been calculated according to experimental tests to match the real and simulated behaviours.

Table 2.
PMSM motor parameters. The motor part number is S 1FK7060- 2AC71-1CA0 provided by Siemens. The numbers 60 K and 100 K refer to overtemperature values of 60 K and 100 K.
For reasons of clarity, a simple logical scheme of the RM model is shown in Figure 6, while the four main blocks are quickly analysed below:
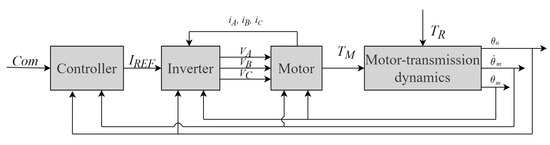
Figure 6.
RM model structure as taken from [41].
- Controller: This block is essentially composed of a PID controller. In fact, even if there are much more advanced and sophisticated control logics (e.g., [53]), PID controllers are still the way to go and they are still chosen even in complex systems, as they are easy to implement and tune. PID controllers are composed of three separated branches, where the proportional, differential, and integral action are calculated. The controller aim is comparing the command signals with the actual signal obtained from the motor transmission dynamics block, hence closing the control loop. In this particular case, both position and speed can be monitored. This block outputs the reference current , obtained from the motor torque thanks to the torque constant, which is finally passed to the inverter.
- Inverter: This block contains Clarke-Park equations, and it provides the motor block with the three voltages (one for each phase) for the PMSM motor by performing the corresponding pulse width modulation (PWM). A very complicated physics-based process is handled by Simscape, a specific Simulink library, capable of providing electrical simulation packages. The main actions inside this block are the calculation of the electrical angle starting from the motor position, the splitting of into the three phase currents (with Clarke-Park equations), the PWM process, and the calculation of the three phase voltages, using the fed-back currents.
- Sinusoidal BLDC motor: This block is able to simulate the electrical and magnetic interactions inside a PMSM. It contains Simscape elements, and it manages three main processes:
- The calculation of the counter-electromotive force coefficient for each phase. This is achieved with the multiplication of the back EMF coefficients (obtained with experimental test campaigns) with three sine waves out of phase from each other.
- The implementation of the motor resitive-inductive circuit. A set of mathematical equations (Equation (5)) that model the three star connected LR branches is solved and phase currents () are, hence, calculated. The resistance and inductance of the motor are taken from equipment data sheets.where and are the currents and voltages across a single j phase.
- The calculation of the motor available torque. Three different electromotive coefficients are used to calculate the motor torque along with the relative phase currents:
- Motor transmission dynamics: this final block compares the available torque with the external requested torque and solves a second-order dynamical system (Equation (7) comprehensive of multiple non linearities, such as dry friction and backlash [52]). The outputs of this block are the motor position and speed, which are looped back to the controller.where represents the motor torque, and represents the external torque. On the other hand, represents the assembly inertia, is the viscous friction coefficient, and is the motor position.
Following the results of a detailed EMA failure mode effect and criticality analysis (FMECA) found in literature [9], it was decided to take into account five distinct failures. These failures show a medium high or high probability and/or criticality for the overall EMA: dry friction, backlash, short circuit, eccentricity, and proportional gain drift. On top of that, they show a quite slow propagation rate, which is desirable when designing failure detection and identification methodologies. For each failure mode, one or more components have been assigned and two different magnitude levels have been simulated: high magnitude () and low one (). In order to complete the analysis, also a condition with multiple failure affecting the EMA has been taken into account: the vector, used in this case is the one shown in Equation (8).
A more in-depth explanation on the failure implementation and the modelling of each failure mode can be found in [40,41].
4. Results
In this section, the mean percentage error and the mean computational cost for each single failure and for the multiple failure situation are presented (Figure 7 and Figure 8). The error has been calculated following Equation (9).
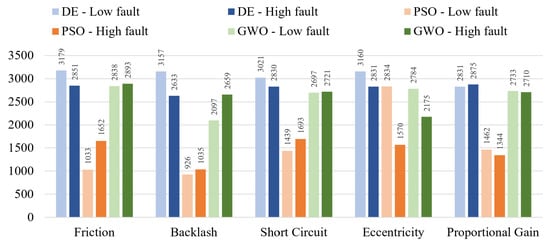
Figure 7.
Comparison between different algorithms: mean percentage error [%]. For each failure mode and for each algorithm, the failure magnitudes are selected as follows: high magnitude () and low one ().
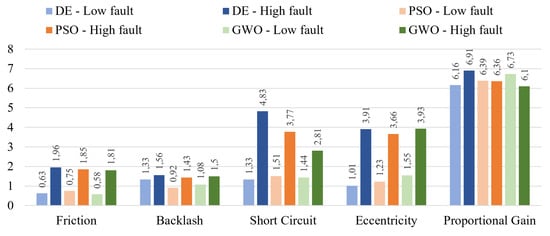
Figure 8.
Comparison between different algorithms: computational cost [s]. For each failure mode and for each algorithm, the failure magnitudes are selected as follows: high magnitude () and low one ().
As stated before, for each failure, a low magnitude and a high magnitude condition have been considered (high magnitude () and low one ()).
These data have been obtained through ten runs of each algorithm for a total of 300 runs to have a minimal statistical relevance. The employed computer is based on a Intel Core i7-8750H CPU @ 2.2 GHz with a RAM of 16 GB and a dedicated GPU NVIDIA GeForce GTX 1050. DE shows a slightly lower error than the other algorithms, as far as the low intensity failures are concerned. On the other hand, GWO seems to be the precise solution for the high level failures (e.g., short circuit and proportional gain). Finally, the PSO algorithm turns out to be the most accurate for backlash faults in general, high static eccentricity, and low proportional gain. Apparently there is not an algorithm able to outperform the others in every situation; this was expected as metaheuristic algorithms, despite being very versatile, are not the panacea for every problem. However, if we look at the computational cost, since a first glance, it is clear that PSO is the most efficient algorithm. In fact, apart in case of the static low eccentricity failure, this optimization technique shows computational burdens almost halved, with respect to the other algorithms, with an average 25 min to detect and identify the failures. If we now consider the other two remaining algorithms, GWO is slightly faster than DE, but the last one seems to provide more stable and repetitive results.
The authors then used a predefined performance coefficient (PC) (first defined in [38] and reported in Equation (10)) to take into the account both the accuracy (mean percentage error) and the computational cost in a single parameter, thus providing an objective criterion useful to choose the best solution overall.
As regards Equation (10), the formula expresses the PC for the i-th algorithm, is the average computational time of the i-th algorithm for the considered fault, and is the average percentage error of the i-th algorithm. The rationale behind the formula is as follows: the denominator is added to make the result non-dimensional, while the multiplication and the subtraction are added to transform it in a percentage value. The results of this further investigation are reported in Table 3, along with other data to sum up the analysis. For reasons of brevity, the reported values of average percentage error and computational costs are obtained by an average between the two magnitude failures. As expected by linking the best results, in terms of accuracy and efficiency, PSO shows the highest figures for every failure. This happens not so much because of the error, as to the significantly lower computational cost related to the PSO-based solution.

Table 3.
Different optimization algorithms outcomes with single failures [10]. The values related to best performing algorithm (PSO) are highlighted in bold, along with the relative PCs.
On the opposite side of the ranking, there is clearly the DE algorithm. This is due to the very high computational cost.
The multiple failure condition results are reported in Table 4. Once again, it is clear that PSO is the leading algorithm, both in terms of efficiency and accuracy. Interestingly, it has to be highlighted that the multiple failure condition requires less than the single failure technique to reach a result. This was probably due to the stochastic operating principles of the algorithms. In fact, as the vector contains random values (Equation (8)), rather than just one component dissimilar from its nominal value, it is believed that the algorithms are able to approach the error tolerance more quickly.

Table 4.
Different optimization algorithms outcomes with multiple failures [10]. The values related to best performing algorithm (PSO) are highlighted in bold, along with the relative PCs.
5. Discussion
By looking at the results, PSO is the leading algorithm, providing the best results for the single and multiple failure condition. It is deemed that this algorithm is able to outperform the others, due to the main constructive principle behind it: unlike GWO, there is a strong collaboration and sharing of information between particles. Each particle contributes to the creation of the aforementioned collective intelligence by sharing the information on the best position it has found in the solution space and, hence, the likelihood to find always better solution rises drastically. This does not happen with GWO, which has a strong hierarchical law. DE showed incomparably worse results, and its implementation is quite challenging, too. It has to be noted that, even though the algorithms are metaheuristic and they pose few assumption on the application, they are very sensible to the problem statement; thus, an algorithm could behave very badly on a specific situation, but could provide excellent results when approaching an even slightly different problem.
The most challenging failure to detect and identify is the proportional gain drift. This particular phenomenon can be led back to the fact that a controller issue affects every single aspect of the actuation system; hence, the prognostic system struggles to identify the specific problems. Percentage errors for this failure mode, albeit higher than the ones relative to the other failures, are restrained around 8%, which is a satisfactory result, indeed.
After checking the results of the different algorithms, the authors envisioned a wider and more comprehensive concept of operations that could provide a practical application of the prognostic checks. The proposed monitoring framework could be easily implemented in a check routine that could be run when the aircraft is on the ground and during the flight to check the EMA subsystem health status. For instance a monitoring procedure can be run while the aircraft is at the gate waiting for the passengers, during maintenance checks, even 24-h or walk-around checks. Additionally, throughout the flying phase, a test procedure can be carried out at predetermined intervals. In this way, EMA health status is assessed and the mission safety is guaranteed. As seen before the proposed checks can not be run in real-time due to the needed number of simulation runs; on the other hand, a real-time monitoring capability is deemed superfluous and unnecessary as failures usually have a progression curve that can be monitored. The proposed prognostic strategy is applicable to a wide range of actuators and do not require the installation of any additional sensors, which is a very researched requirement. A prognostic and health management computer (PHMC) in the avionic bay is needed to perform the calculations.
6. Conclusions
In this paper, a set of three different metaheuristic search algorithms have been considered for failure detection and identification purposes. This work was aimed at testing new algorithms to identify some suitable ones. After having introduced the scenario in which this kind of PHM system could provide useful insights, a brief description of the models have been reported. Particular attention has been given to failure description and implementation, as well as the general methodology overview. A detailed description of the three algorithm has also been reported, in order to enable the reader to understand the most important aspect of each MSA, without the need of additional resources. Finally, the results are shown in a schematic way, highlighting the methodology performance with the use of purpose built coefficients. Further research should focus on the ideal interval between prognostic checks, in order not to jeopardize mission safety and not overloading the PHMC. On top of that, the running time of these routines can definitely be improved with other models or with more performing algorithms. This is why future work should consider other MSAs and other failures inside the EMA, as well as investigate on the unexpected result, regarding the multiple failure condition running time. Finally, if we compare the results of this study (specifically for PMSM-based EMAs) with the outcomes obtained in [23] for BLDC-based EMAs, it is clear that PSO is confirmed as the best performing algorithm, even though the core of the system has changed.
Author Contributions
Conceptualization, M.D.L.D.V.; methodology, M.D.L.D.V.; software, M.D.L.D.V.; validation, I.Q.; formal analysis, I.Q.; investigation, I.Q.; resources, I.Q.; data curation, I.Q.; writing—original draft preparation, L.B.; writing—review and editing, L.B.; visualization, L.B.; supervision, M.D.L.D.V.; project administration, M.D.L.D.V.; funding acquisition, P.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare that they have no known conflict of interest nor competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Abbreviations
The following abbreviations are used in this manuscript:
| MEA | More Electric Aircraft |
| EMA | Electro-Mechanical Actuator |
| PHM | Prognostic and Health Management |
| PMSM | Permanent Magnet Syncrhonous Motor |
| DE | Differential Evolution |
| PSO | Particle Swarm Optimization |
| GWO | Grey Wolf Optimization |
| NTB | Numerical Test Bench |
| LCC | Life Cycle Costs |
| EHA | Electro-Hydraulic Actuators |
| CBM | Condition-Based Maintenance |
| RAMS | Reliability, Availability, Maintenability, and Safety |
| TLBO | Teaching–Learning-Based Optimization |
| HGS | Hunger Game Search |
| VNS | Variable Neighbourhood Search |
| ACO | Ant Colony Optimization |
| CSO | Cuckoo Search Optimization |
| MM | Monitoring Model |
| RM | Reference Model |
| SC | Short Circuit |
| FDI | Failure Detection and Identification |
| ConOps | Concept of Operation |
| TLP | Top Level Parameter |
| MSA | Metaheuristic Search Algorithm |
| EA | Evolutionary Algorithm |
| SI | Swarm Intelligence |
| GA | Genetic Algorithm |
| BLDC | BrushLess Direct Current |
| PID | Proportional Integral Derivative |
| PWM | Pulse Width Modulation |
| FMECA | Failure Mode Effect and Criticality Analysis |
| PC | Performance Coefficient |
| PHMC | Prognostic and Health Management Computer |
| EMF | Electro-Motive Force |
References
- Vercella, V.; Fioriti, M.; Viola, N. Towards a methodology for new technologies assessment in aircraft operating cost. Inst. Mech. Eng. Part J. Aerosp. Eng. 2021, 235, 879–892. [Google Scholar] [CrossRef]
- Hölzel, N.B.; Gollnick, V. Cost-benefit analysis of prognostics and condition-based maintenance concepts for commercial aircraft considering prognostic errors. In Proceedings of the Annual Conference of the Prognostics and Health Management Society, PHM, Coronado, CA, USA, 18–24 October 2015. [Google Scholar]
- Berri, P.C.; Dalla Vedova, M.D.; Mainini, L. Computational framework for real-time diagnostics and prognostics of aircraft actuation systems. Comput. Ind. 2021, 132, 103523. [Google Scholar] [CrossRef]
- Gp Capt Atul, G.; Rezawana Islam, L.; Tonoy, C. Evolution of Aircraft Flight Control System and Fly-By-Light Flight Control System. Int. J. Emerg. Technol. Adv. Eng. 2013, 3, 12. [Google Scholar]
- Sutherland, J.P. Fly-by-Wire Flight Control Systems. Air Force Flight Dyn. Lab Wright-Patterson Air Force Base Ohio 1968, 3, 2250–2459. [Google Scholar]
- Telford, R.D.; Galloway, S.J.; Burt, G.M. Evaluating the reliability & availability of more-electric aircraft power systems. In Proceedings of the 2012 47th International Universities Power Engineering Conference (UPEC), Uxbridge, UK, 4–7 September 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Qiao, G.; Liu, G.; Shi, Z.; Wang, Y.; Ma, S.; Lim, T.C. A review of electromechanical actuators for More/All Electric aircraft systems. Inst. Mech. Eng. Part J. Mech. Eng. Sci. 2018, 232, 4128–4151. [Google Scholar] [CrossRef]
- Wang, C.; Fan, I.S.; King, S. Failures Mapping for Aircraft Electrical Actuation System Health Management. In Proceedings of the PHM Society European Conference, London, UK, 27–29 May 2022; Volume 7, pp. 509–520. [Google Scholar] [CrossRef]
- Balaban, E.; Saxena, A.; Bansal, P.; Goebel, K.F.; Curran, S. A Diagnostic Approach for Electro-Mechanical Actuators in Aerospace Systems. In Proceedings of the 2009 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2009; pp. 1–13. [Google Scholar]
- Baldo, L.; Querques, I.; Dalla Vedova, M.D.L.; Maggiore, P. Prognostics of aerospace electromechanical actuators: Comparison between model-based metaheuristic methods. In Proceedings of the 12th EASN International Conference on Innovation in Aviation & Space for Opening New Horizons, Barcelona, Spain, 18–21 October 2022. [Google Scholar]
- Wileman, A.J.; Aslam, S.; Perinpanayagam, S. A road map for reliable power electronics for more electric aircraft. Prog. Aerosp. Sci. 2021, 127, 100739. [Google Scholar] [CrossRef]
- Kuznetsov, V.E.; Khanh, N.D.; Lukichev, A.N. System for Synchronizing Forces of Dissimilar Flight Control Actuators with a Common Controller. In Proceedings of the 2020 23rd International Conference on Soft Computing and Measurements, SCM 2020, St. Petersburg, Russia, 27–29 May 2020. [Google Scholar] [CrossRef]
- Benedettini, O.; Baines, T.S.; Lightfoot, H.W.; Greenough, R.M. State-of-the-art in integrated vehicle health management. Proc. Inst. Mech. Eng. Part J. Aerosp. Eng. 2009, 223, 157–170. [Google Scholar] [CrossRef]
- Lee, J.; de Pater, I.; Boekweit, S.; Mitici, M. Remaining-Useful-Life prognostics for opportunistic grouping of maintenance of landing gear brakes for a fleet of aircraft. In Proceedings of the PHM Society European Conference, London, UK, 27–29 May 2022; Volume 7, pp. 278–285. [Google Scholar]
- Scott, M.J.; Verhagen, W.J.C.; Bieber, M.T.; Marzocca, P. A Systematic Literature Review of Predictive Maintenance for Defence Fixed-Wing Aircraft Sustainment and Operations. Sensors 2022, 22, 7070. [Google Scholar] [CrossRef]
- Swerdon, G.; Watson, M.J.; Bharadwaj, S.; Byington, C.S.; Smith, M.; Goebel, K.; Balaban, E. A Systems Engineering Approach to Electro-Mechanical Actuator Diagnostic and Prognostic Development. In Proceedings of the Machinery Failure Prevention Technology (MFPT) Conference, Dublin, Ireland, 23–25 June 2009. [Google Scholar]
- Rosero, J.A.; Ortega, J.A.; Aldabas, E.; Romeral, L. Moving towards a more electric aircraft. IEEE Aerosp. Electron. Syst. Mag. 2007, 22, 9380100. [Google Scholar] [CrossRef]
- Garcia Garriga, A.; Ponnusamy, S.S.; Mainini, L. A multi-fidelity framework to support the design of More-Electric Actuation. In Proceedings of the 2018 Multidisciplinary Analysis and Optimization Conference, Atlanta, GA, USA, 25–29 June 2018; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018. [Google Scholar] [CrossRef]
- Yin, Z.; Hu, N.; Chen, J.; Yang, Y.; Shen, G. A review of fault diagnosis, prognosis and health management for aircraft electromechanical actuators. IET Electr. Power Appl. 2022, 16, 1249–1272. [Google Scholar] [CrossRef]
- Kaplan, H.; Tehrani, K.; Jamshidi, M. A Fault Diagnosis Design Based on Deep Learning Approach for Electric Vehicle Applications. Energies 2021, 14, 6599. [Google Scholar] [CrossRef]
- Sutharssan, T.; Stoyanov, S.; Bailey, C.; Yin, C. Prognostic and health management for engineering systems: A review of the data-driven approach and algorithms. J. Eng. 2015, 2015, 215–222. [Google Scholar] [CrossRef]
- Berri, P.C.; Dalla Vedova, M.D.L.; Mainini, L. Learning for predictions: Real-time reliability assessment of aerospace systems. Aiaa J. 2022, 60, 566–577. [Google Scholar] [CrossRef]
- Dalla Vedova, M.D.; Berri, P.C.; Re, S. Metaheuristic Bio-Inspired Algorithms for Prognostics: Application to on-Board Electromechanical Actuators. In Proceedings of the 2018 3rd International Conference on System Reliability and Safety, ICSRS 2018, Barcelona, Spain, 24–26 November 2018. [Google Scholar] [CrossRef]
- Ma, Y.; Yao, M.; Liu, H.; Tang, Z. State of Health estimation and Remaining Useful Life prediction for lithium-ion batteries by Improved Particle Swarm Optimization-Back Propagation Neural Network. J. Energy Storage 2022, 52, 104750. [Google Scholar] [CrossRef]
- Li, A.; Yang, X.; Dong, H.; Xie, Z.; Yang, C. Machine Learning-Based Sensor Data Modeling Methods for Power Transformer PHM. Sensors 2018, 18, 4430. [Google Scholar] [CrossRef] [PubMed]
- Gougam, F.; Chemseddine, R.; Benazzouz, D.; Benaggoune, K.; Zerhouni, N. Fault prognostics of rolling element bearing based on feature extraction and supervised machine learning: Application to shaft wind turbine gearbox using vibration signal. Proc. Inst. Mech. Eng. Part J. Mech. Eng. Sci. 2021, 235, 5186–5197. [Google Scholar] [CrossRef]
- Rodrigues, L.R.; Coelho, D.B.P.; Gomes, J.P.P. A Hybrid TLBO-Particle Filter Algorithm Applied to Remaining Useful Life Prediction in the Presence of Multiple Degradation Factors. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Jin, Z.; Li, X.; Yu, D.; Zhang, J.; Zhang, W. Lithium-ion battery state of health estimation using meta-heuristic optimization and Gaussian process regression. J. Energy Storage 2023, 58, 106319. [Google Scholar] [CrossRef]
- Chen, K.; Laghrouche, S.; Djerdir, A. Health state prognostic of fuel cell based on wavelet neural network and cuckoo search algorithm. ISA Trans. 2021, 113, 175–184. [Google Scholar] [CrossRef]
- Zhong, J.; Long, J.; Zhang, S.; Li, C. Flexible Kurtogram for Extracting Repetitive Transients for Prognostics and Health Management of Rotating Components. IEEE Access 2019, 7, 55631–55639. [Google Scholar] [CrossRef]
- Hong, H.; Tsangaratos, P.; Ilia, I.; Loupasakis, C.; Wang, Y. Introducing a novel multi-layer perceptron network based on stochastic gradient descent optimized by a meta-heuristic algorithm for landslide susceptibility mapping. Sci. Total Environ. 2020, 742, 140549. [Google Scholar] [CrossRef]
- Ladj, A.; Benbouzid-Si Tayeb, F.; Varnier, C. An integrated prognostic based hybrid genetic-immune algorithm for scheduling jobs and predictive maintenance. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 2083–2089. [Google Scholar] [CrossRef]
- Ladj, A.; Tayeb, F.B.S.; Varnier, C. Hybrid of metaheuristic approaches and fuzzy logic for the integrated flowshop scheduling with predictive maintenance problem under uncertainties. Eur. J. Ind. Eng. 2021, 15, 675–710. [Google Scholar] [CrossRef]
- Wu, Y. A survey on population-based meta-heuristic algorithms for motion planning of aircraft. Swarm Evol. Comput. 2021, 62, 100844. [Google Scholar] [CrossRef]
- Rodrigues, L.R.; Gomes, J.P.P.; Ferri, F.A.S.; Medeiros, I.P.; Galvão, R.K.H.; Nascimento Júnior, C.L. Use of PHM Information and System Architecture for Optimized Aircraft Maintenance Planning. IEEE Syst. J. 2015, 9, 1197–1207. [Google Scholar] [CrossRef]
- Berri, P.C.; Dalla Vedova, M.D.L.; Maggiore, P. A Simplified Monitor Model for EMA Prognostics. In Proceedings of the MATEC Web of Conferences, Osaka, Japan, 21–22 September 2018; EDP Sciences: Les Ulis, France, 2018. [Google Scholar]
- Berri, P.C.; Dalla Vedova, M.D.L.; Maggiore, P.; Viglione, F. A simplified monitoring model for PMSM servoactuator prognostics. In Proceedings of the MATEC Web of Conferences, Osaka, Japan, 21–22 September 2018; EDP Sciences: Les Ulis, France, 2019; p. 04013. [Google Scholar]
- Dalla Vedova, M.D.; Berri, P.C.; Re, S. A comparison of bio-inspired meta-heuristic algorithms for aircraft actuator prognostics. In Proceedings of the 29th European Safety and Reliability Conference, ESREL, Hannover, DE, USA, 22–26 September 2019. [Google Scholar] [CrossRef]
- Kim, B.W.; Kim, K.T.; Hur, J. Simplified Impedance Modeling and Analysis for Inter-Turn Fault of IPM-type BLDC motor. J. Power Electron. 2012, 12, 10–18. [Google Scholar] [CrossRef]
- Berri, P.C. Design and Development of Algorithms and Technologies Applied to Prognostics of Aerospace Systems. Ph.D. Thesis, Politecnico di Torino, Torino, Italy, 2021. [Google Scholar]
- Querques, I. Prognostics of On-Board Electromechanical Actuators: Bio-Inspired Metaheuristic Algorithms; Technical Report; Politecnico di Torino: Torino, Italy, 2021. [Google Scholar]
- Wahde, M. Biologically Inspired Optimization Methods: An Introduction; WIT Press: Ashurst, UK, 2008. [Google Scholar]
- Ahmad, M.F.; Isa, N.A.M.; Lim, W.H.; Ang, K.M. Differential evolution: A recent review based on state-of-the-art works. Alex. Eng. J. 2022, 61, 3831–3872. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Aimasso, A.; Berri, P.C.; Dalla Vedova, M.D. A genetic-based prognostic method for aerospace electromechanical actuators. Int. J. Mech. Control 2021, 22, 195–206. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Darwish, A. Bio-inspired computing: Algorithms review, deep analysis, and the scope of applications. Future Comput. Inform. J. 2018, 3, 231–246. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Kumar, V.; Kumar, D. An astrophysics-inspired Grey wolf algorithm for numerical optimization and its application to engineering design problems. Adv. Eng. Softw. 2017, 112, 231–254. [Google Scholar] [CrossRef]
- Berri, P.C.; Dalla Vedova, M.D.L.; Maggiore, P.; Scanavino, M. Permanent Magnet Synchronous Motor (PMSM) for Aerospace Servomechanisms: Proposal of a Lumped Model for Prognostics. In Proceedings of the 2018 2nd European Conference on Electrical Engineering and Computer Science (EECS), Bern, Switzerland, 20–22 December 2018; pp. 471–477. [Google Scholar]
- Berri, P.C.; Dalla Vedova, M.D.; Maggiore, P. A lumped parameter high fidelity EMA model for model-based prognostics. In Proceedings of the 29th European Safety and Reliability Conference, ESREL 2019, Hannover, Germany, 22–26 September 2019; Research Publishing Services: Singapore, 2020; pp. 1086–1093. [Google Scholar] [CrossRef]
- Baldo, L.; Berri, P.C.; Dalla Vedova, M.D.L.; Maggiore, P. Experimental Validation of Multi-fidelity Models for Prognostics of Electromechanical Actuators. In Proceedings of the PHM Society European Conference, Turin, Italy, 6–8 July 2022; Volume 7, pp. 32–42. [Google Scholar]
- Bendjedia, M.; Tehrani, K.A.; Azzouz, Y. Design of RST and Fractional Order PID Controllers for an Induction Motor Drive for Electric Vehicle Application. In Proceedings of the 7th IET International Conference on Power Electronics, Machines and Drives, Manchester, UK, 8–10 April 2014. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).