Design and Experiment of a Seamless Morphing Trailing Edge
Abstract
1. Introduction
2. Design Approach
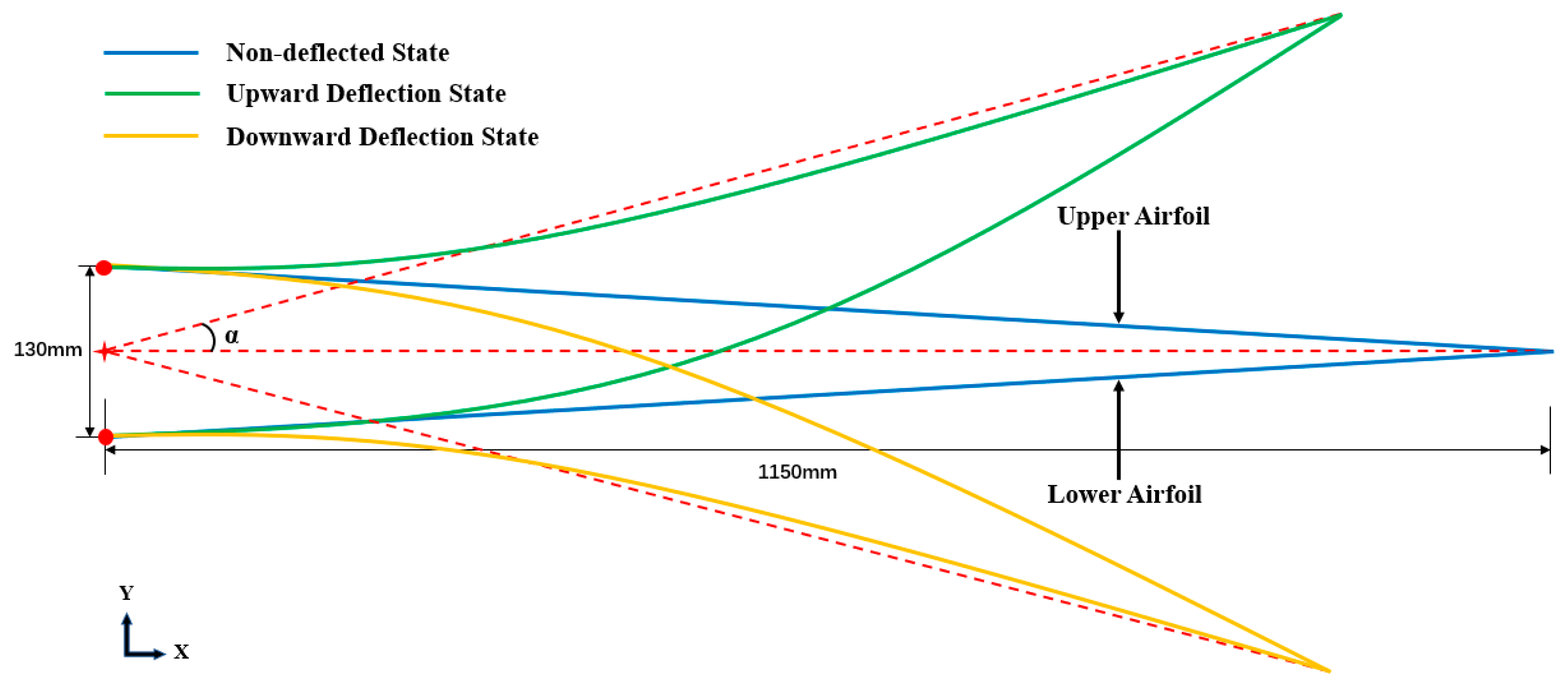
2.1. The Morphing Concept
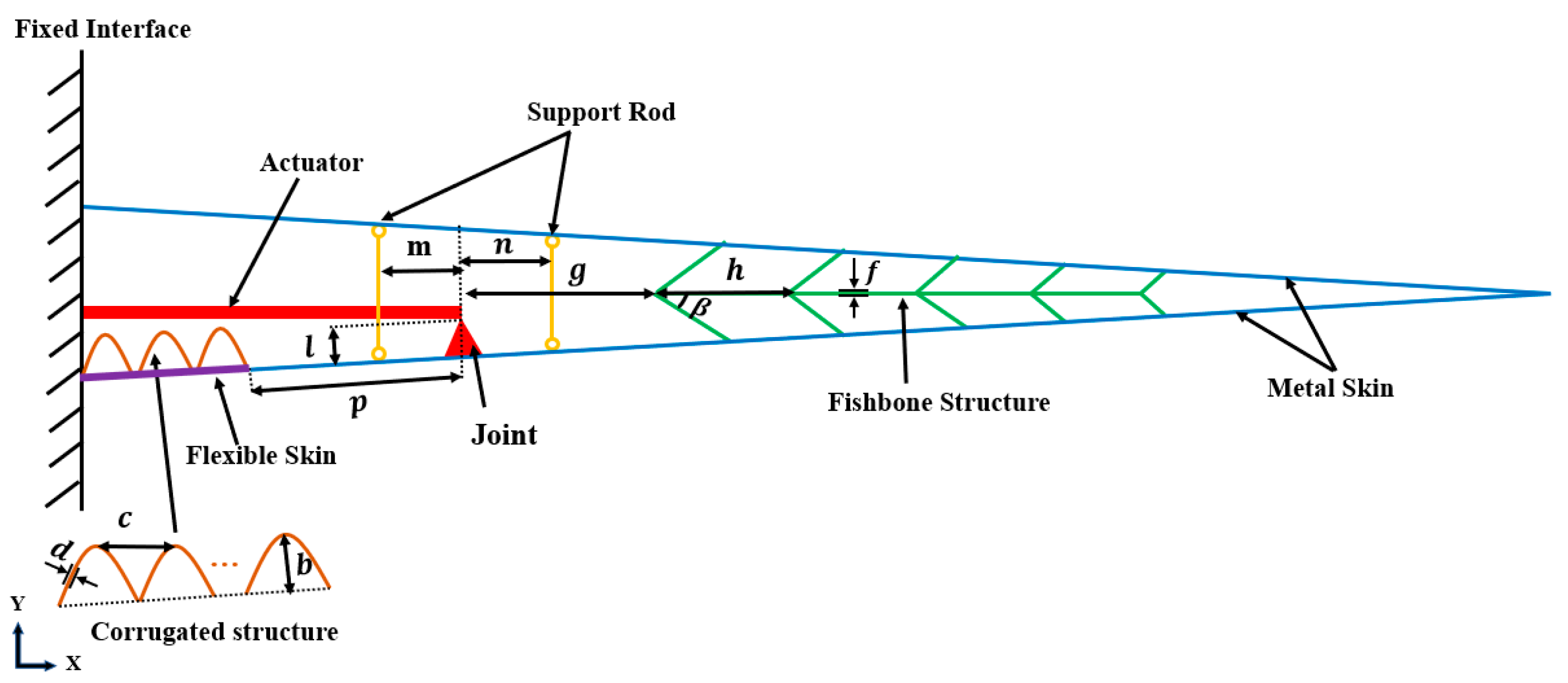
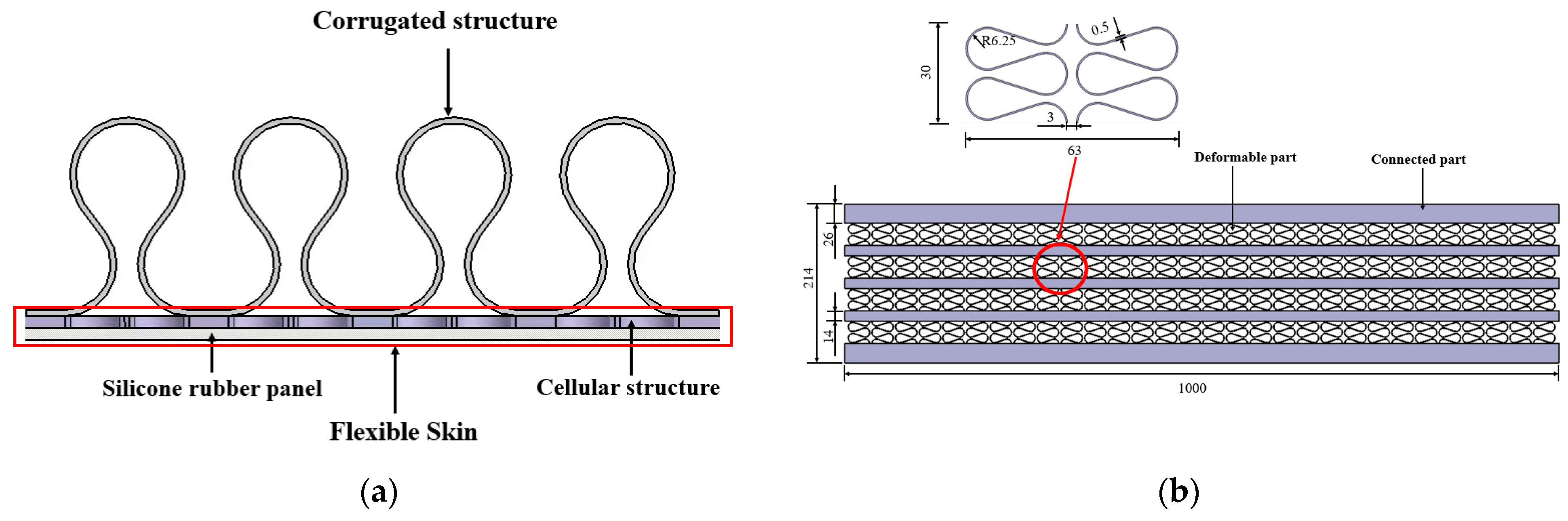
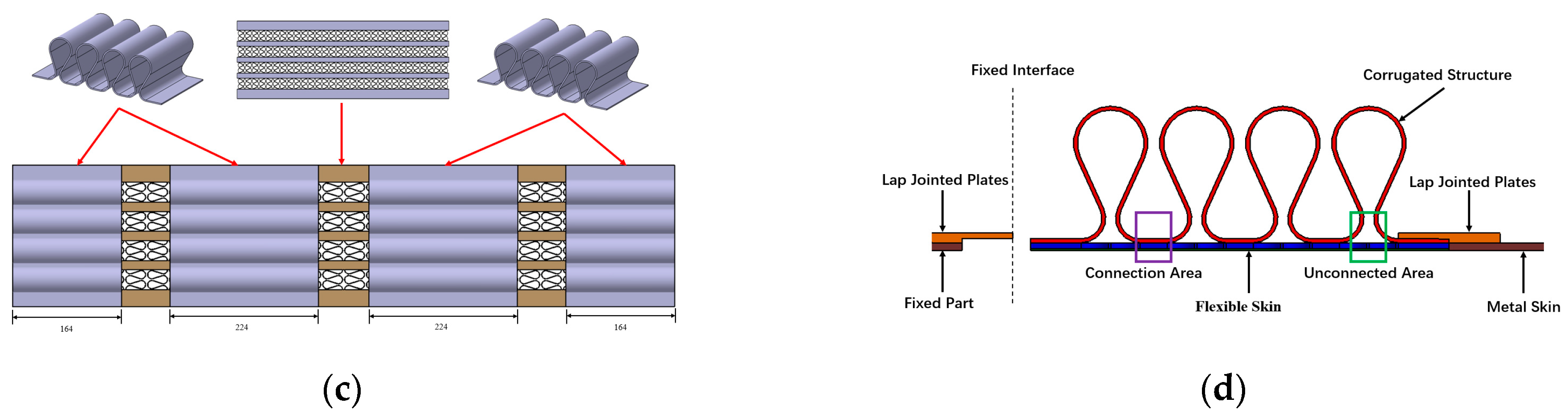
2.2. 2D Structural Layout
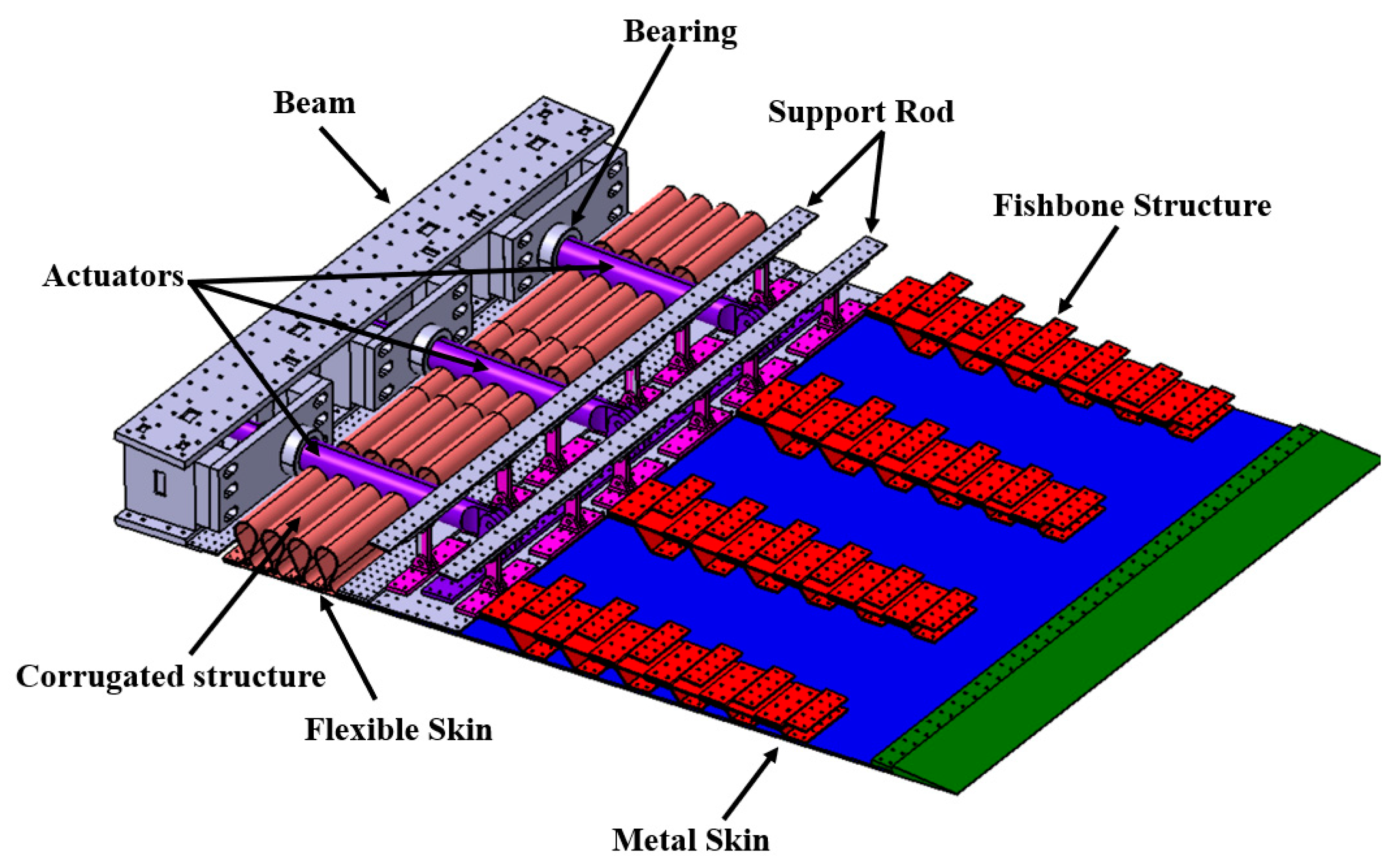
2.3. 3D Structural Layout
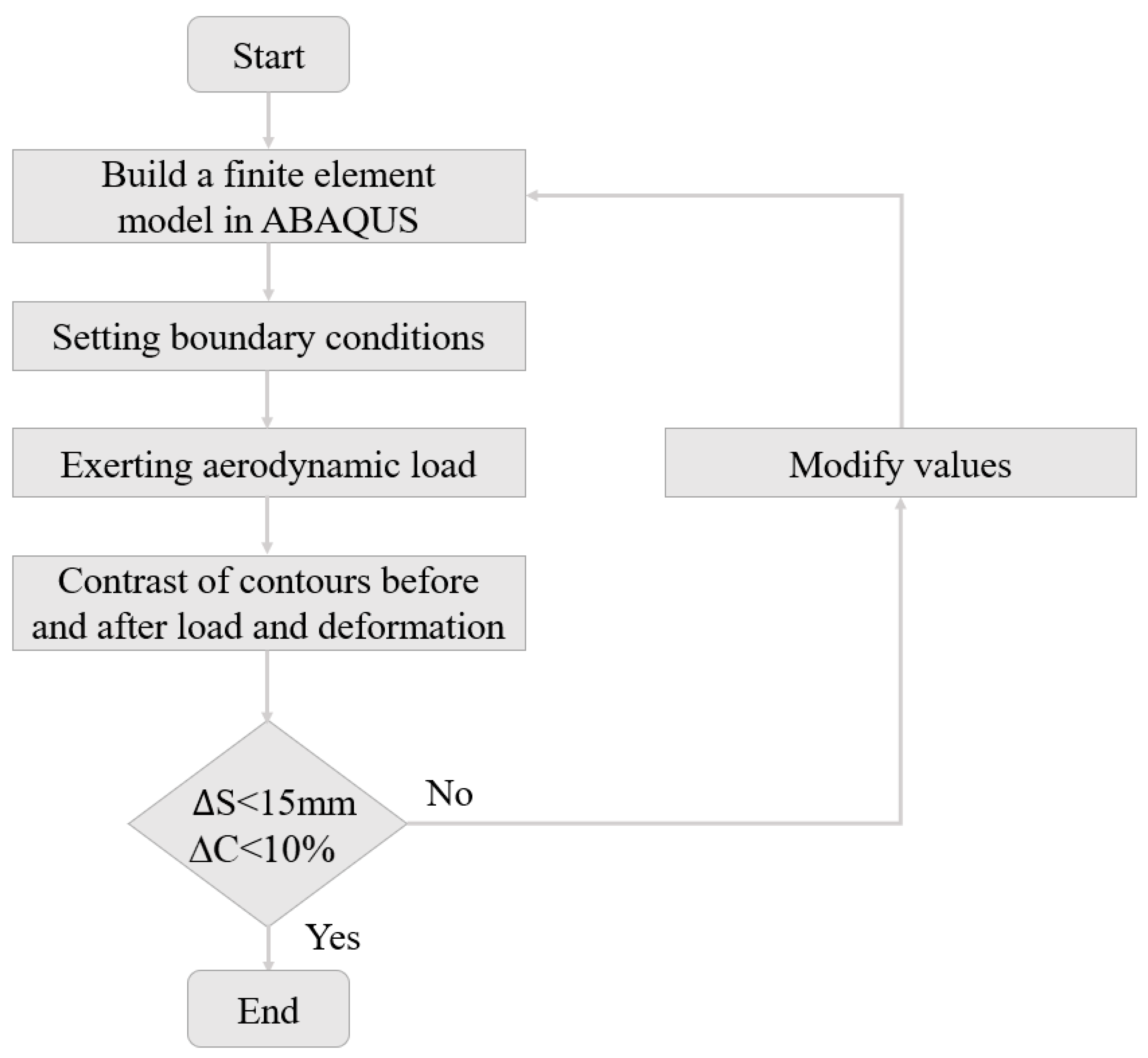
3. Finite Element Simulation Studies and Parametric Design
3.1. Parametric Design of 2D Morphing Trailing Edge
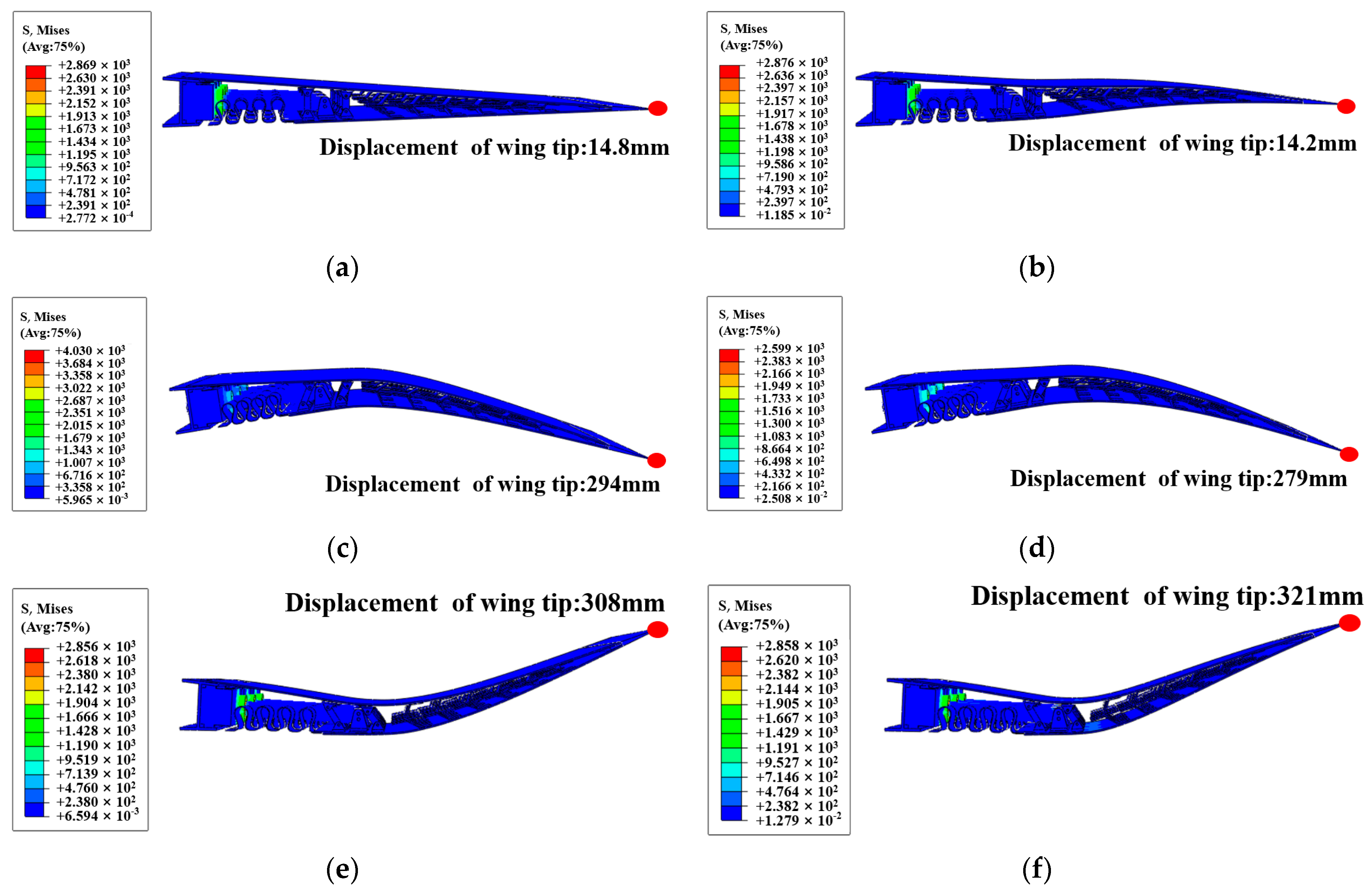
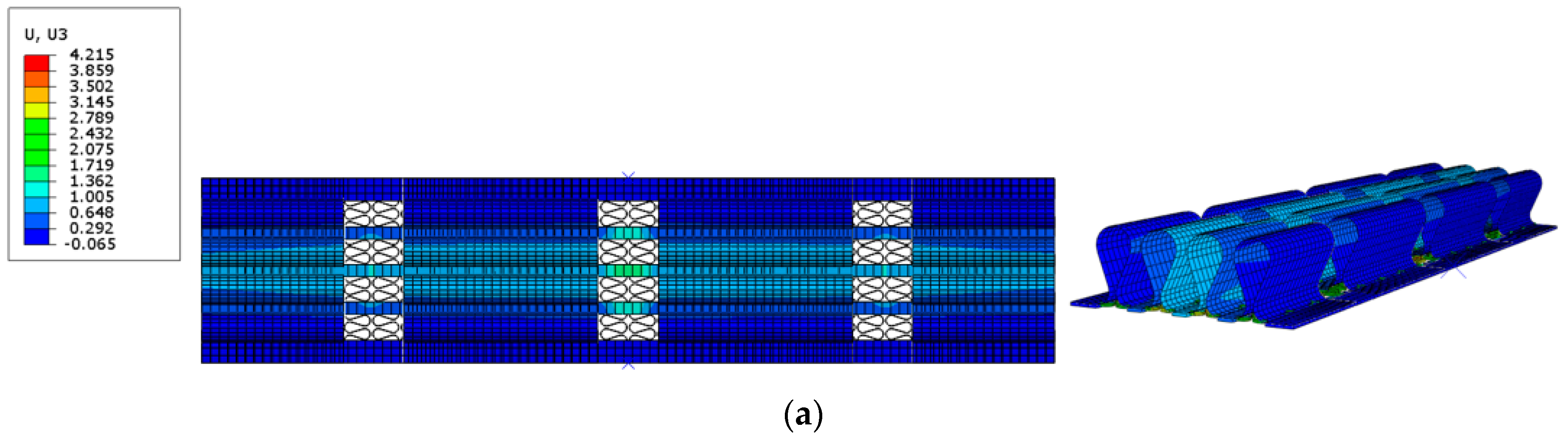
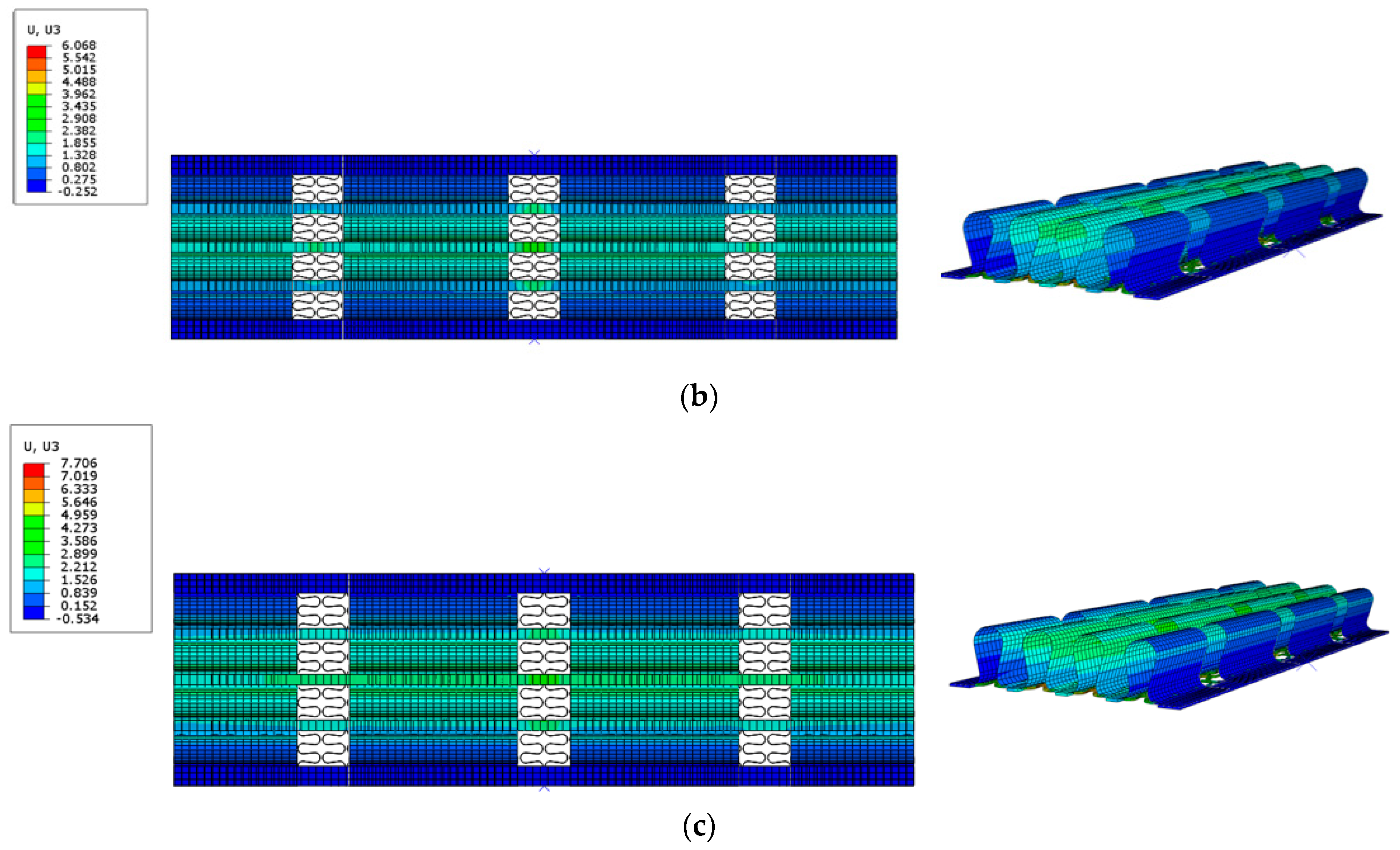
3.2. Finite Element Simulation Studies of the 3D Morphing Trailing Edge
4. Manufacturing and Testing
4.1. Assembly and Integration
4.2. Deformation Testing and Load Testing
5. Conclusions
- A seamless camber morphing trailing edge with flexible skin is designed based on the local deformation principle;
- The position and size of key structures are determined by parametric analysis and verified by finite element analysis of a 3D model;
- A prototype is designed and manufactured, and a deformation test and load test are conducted. The test results show that the prototype can achieve 15° deflection and bear a 0.015 MPa aerodynamic load.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sofia, A.Y.N.; Meguid, S.A.; Tan, K.T.; Yeo, W.K. Shape morphing of aircraft wing: Status and challenges. Mater. Des. 2010, 31, 1284–1292. [Google Scholar]
- Oliviu, S.G.; Andreea, K.; Mihaela, B.R. Optimization of an Unmanned Aerial System’ Wing Using a Flexible Skin Morphing Wing. Sae Int. J. Aerosp. 2013, 2013, 115–121. [Google Scholar]
- Gu, X.; Yang, K.-K.; Wu, M.; Zhang, Y. Integrated optimization design of smart morphing wing for accurate shape control. Chin. J. Aeronaut. 2021, 34, 135–147. [Google Scholar] [CrossRef]
- Previtali, F.; Arrieta, A.F.; Ermanni, P. Performance of a three-dimensional morphing wing and comparison with a conventional wing. AIAA J. 2014, 52, 2101–2113. [Google Scholar] [CrossRef]
- Li, D.; Zhao, S.; Da Ronch, A.; Xiang, J.; Drofelnik, J.; Li, Y.; Zhang, L.; Wu, Y.; Kintscher, M.; Monner, H.P.; et al. A review of modelling and analysis of morphing wings. Prog. Aerosp. Sci. 2018, 100, 46–62. [Google Scholar] [CrossRef]
- De Gaspari, A.; Ricci, S. A two-level approach for the optimal design of morphing wings based on compliant structures. J. Intell. Mater. Syst. Struct. 2011, 22, 1091–1111. [Google Scholar] [CrossRef]
- Monner, H.P.; Breitbach, E.; Bein, T.; Hanselka, H. Design aspects of the adaptive wing—The elastic trailing edge and the local spoiler bump. Aeronaut. J. 2000, 104, 89–95. [Google Scholar] [CrossRef]
- Monner, H.P. Realization of an optimized wing camber by using formvariable flap structures. Aerosp. Sci. Technol. 2001, 5, 445–455. [Google Scholar] [CrossRef]
- Icardi, U.; Ferrero, L. SMA actuated mechanism for an adaptive wing. J. Aerosp. Eng. 2011, 24, 140–143. [Google Scholar] [CrossRef]
- Meguid, S.A.; Su, Y.; Wang, Y. Complete morphing wing design using flexible-rib system. Int. J. Mech. Mater. Des. 2017, 13, 159–171. [Google Scholar] [CrossRef]
- Arena, M.; Nagel, C.; Pecora, R.; Schorsch, O.; Concilio, A.; Dimino, I. Static and Dynamic Performance of a Morphing Trailing Edge Concept with High-Damping Elastomeric Skin. Aerospace 2019, 6, 22. [Google Scholar] [CrossRef]
- Bartley-Cho, J.D.; Wang, D.P.; Martin, C.A.; Kudva, J.N.; West, M.N. Development of High-rate, Adaptive Trailing Edge Control Surface for the Smart Wing Phase 2 Wind Tunnel Model. J. Intell. Mater. Syst. Struct. 2004, 15, 279–291. [Google Scholar] [CrossRef]
- Moored, K.W.; Bart-Smith, H. The analysis of tensegrity structures for the design of a morphing wing. J. Appl. Mech. 2007, 74, 668–676. [Google Scholar] [CrossRef]
- Woods BK, S.; Bilgen, O.; Friswell, M.I. Wind tunnel testing of the fish bone active camber morphing concept. J. Intell. Mater. Syst. Struct. 2014, 25, 772–785. [Google Scholar] [CrossRef]
- Woods BK, S.; Dayyani, I.; Friswell, M.I. Fluid/structure-interaction analysis of the fish-bone-active-camber morphing concept. J. Aircr. 2015, 52, 307–319. [Google Scholar] [CrossRef]
- Kumar, D.; Ali, S.F.; Arockiarajan, A. Structural and Aerodynamics Studies on Various Wing Configurations for Morphing. IFAC-Pap. 2018, 51, 498–503. [Google Scholar] [CrossRef]
- Wu, R.; Soutis, C.; Zhong, S.; Filippone, A. A morphing aerofoil with highly controllable aerodynamic performance. Aeronaut. J. 2017, 121, 54–72. [Google Scholar] [CrossRef]
- Wu, R.; Sun, J.; Chang, Z.; Bai, R.; Leng, J. Elastic composite skin for a pure shear morphing wing structures. J. Intell. Mater. Syst. Struct. 2015, 26, 352–363. [Google Scholar] [CrossRef]
- Alsaidi, B.; Joe, W.Y.; Akbar, M. Computational analysis of 3D lattice structures for skin in real-scale camber morphing aircraft. Aerospace 2019, 6, 79. [Google Scholar] [CrossRef]
- Mukherjee, A.; Ali, S.F.; Arockiarajan, A. Modeling of integrated shape memory alloy and Macro-Fiber Composite actuated trailing edge. Smart Mater. Struct. 2020, 29, 085005. [Google Scholar] [CrossRef]
- Elsheikh, M.E. Highly Flexible Wind Turbine Blades Utilizing Corrugated Surface Hinges. Coatings 2021, 11, 635. [Google Scholar] [CrossRef]
- Ghabezi, P. Rectangular and triangular corrugated composite skins. Fibers Polym. 2018, 19, 435–445. [Google Scholar] [CrossRef]
- Ghabezi, P.; Mohammad, G. Mechanical Behavior of Quasi-sinusoidal Corrugated Composite sheets. Iran. J. Polym. Sci. Technol. 2012, 24, 379–389. [Google Scholar]
- Dimino, I.; Flauto, D.; Diodati, G.; Concilio, A.; Pecora, R. Actuation system design for a morphing wing trailing edge. Recent Pat. Mech. Eng. 2014, 7, 138–148. [Google Scholar] [CrossRef]
- Liu, S.; Ge, W.; Li, S. Optimal Design of Compliant Trailing Edge for Shape Changing. Chin. J. Aeronaut. 2008, 21, 187–192. [Google Scholar]
- Campanile, L.F.; Sachau, D. The belt-rib concept: A structronic approach to variable camber. J. Intell. Mater. Syst. Struct. 2000, 11, 215–224. [Google Scholar] [CrossRef]
- Barbarino, S.; Bilgen, O.; Ajaj, R.M.; Friswell, M.I. A review of morphing aircraft. J. Intell. Mater. Syst. Struct. 2011, 22, 823–877. [Google Scholar] [CrossRef]
- Dayyani, I.; Shaw, A.D.; Flores, E.S.; Friswell, M.I. The mechanics of composite corrugated structures: A review with applications in morphing aircraft. Compos. Struct. 2015, 133, 358–380. [Google Scholar] [CrossRef]







| Parameter | Value Range | Selected Parameters |
|---|---|---|
| 3~5 | 4 | |
| 60~80 mm | 70 mm | |
| 20~40 mm | 30 mm | |
| 1~2 mm | 2 mm | |
| 30~50 mm | 40 mm | |
| 70~80 mm | 74 mm | |
| 4~6 | 6 | |
| 80~100 mm | 90 mm | |
| 150~160 mm | 154 mm | |
| 2~3 mm | 3 mm | |
| 45°~50° | 50° | |
| 50 mm~60 mm | 55.7 mm | |
| 50 mm~60 mm | 57 mm | |
| 6~10 mm ∗ 15~20 mm | 8 mm ∗ 18 mm | |
| 3~5 mm | 4 mm |
| State | Value |
|---|---|
| without aerodynamic loads in the non-deflected state | 1070 N |
| with aerodynamic loads in the non-deflected state | 3723 N |
| without aerodynamic loads in upward deflection | −4863 N |
| with aerodynamic loads in upward deflection | −1020 N |
| without aerodynamic loads in downward deflection | 2330 N |
| with aerodynamic loads in downward deflection | 7664 N |
| Time | The Wing Tip Deflection in Experiment | The Wing Tip Deflection in Simulation | The Deflection Angle α in Experiment | The Deflection Angle α in Simulation |
|---|---|---|---|---|
| 0 s | 14 mm | 14.8 mm | 0° | 0° |
| 6.5 s | 307 mm | 308 mm | 15° | 15° |
| 15 s | 14 mm | 14.8 mm | 0° | 0° |
| 20 s | 294 mm | 294 mm | −15° | −15° |
| 25 s | 14 mm | 14.8 mm | 0° | 0° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, G.; Ma, T.; Yang, J.; Chang, N.; Zhou, X. Design and Experiment of a Seamless Morphing Trailing Edge. Aerospace 2023, 10, 282. https://doi.org/10.3390/aerospace10030282
Cheng G, Ma T, Yang J, Chang N, Zhou X. Design and Experiment of a Seamless Morphing Trailing Edge. Aerospace. 2023; 10(3):282. https://doi.org/10.3390/aerospace10030282
Chicago/Turabian StyleCheng, Gui, Tianrui Ma, Jun Yang, Nan Chang, and Xiang Zhou. 2023. "Design and Experiment of a Seamless Morphing Trailing Edge" Aerospace 10, no. 3: 282. https://doi.org/10.3390/aerospace10030282
APA StyleCheng, G., Ma, T., Yang, J., Chang, N., & Zhou, X. (2023). Design and Experiment of a Seamless Morphing Trailing Edge. Aerospace, 10(3), 282. https://doi.org/10.3390/aerospace10030282







