Abstract
The current work investigates the effect of canard geometric characteristics on the performance of a lightweight flying wing Unmanned Aerial Vehicle (UAV), capable of both conventional and Vertical Take-Off and Landing (VTOL) flight. The canards are sized as horizontal stabilizers to enhance the UAV’s longitudinal stability and minimize trimming requirements during cruise. Using a Design of Experiments (DOE) approach and, specifically, the Taguchi method, six canards’ design parameters are investigated on three different levels. These parameters are the sweep angle (Λ), aspect ratio (AR), taper ratio (λ), vertical position in relation to the main wing (vpos), incidence angle (ic), and dihedral angle (Γ). An L27 orthogonal array (OA) is used to investigate the influence of these key design parameters using two performance criteria, namely the Lift-to-Drag ratio (L/D) and the pitching moment coefficient (Cm), at cruise conditions (designated as L/Dcruise and |Cm|cruise). The investigation is conducted by using high-fidelity Computational Fluid Dynamics (CFD) methods for each of the 27 configurations defined by the L27 OA, over a range of angles of attack. Based on the CFD results, two distinct combinations are derived for maximum L/Dcruise and minimum |Cm|cruise using the Signal-to-Noise ratio (SNR) analysis. The optimal design parameter combinations for the two performance criteria are A2B1C1D1E1F1 and A2B2C1D2E2F3, respectively. Finally, the Pareto Analysis of Variance (ANOVA) technique is conducted to define the contribution of each of the six design parameters on the L/Dcruise and the |Cm|cruise. More specifically, ic seems to have the most significant effect on L/Dcruise, whereas Λ is the most important parameter for |Cm|cruise.
1. Introduction
Aircraft designers have always put considerable effort towards improving the aerodynamic efficiency and the performance of aerial vehicles by investigating novel configurations, flow control techniques, as well as unconventional take-off and landing methods. When it comes to manned aviation, the configurations remain more-or-less unchanged in the last 50 years [1], since the incorporation of a novel and unconventional configuration arguably comes at increased business risk [2,3]. However, this is not the case for Unmanned Aerial Vehicles (UAVs), where a large number of novel and unconventional designs exist, thus improving some aspects of their flight performance [4]. In the 21st century, the following two novelties have significantly affected the UAV layout design:
- Hybrid flight. This term refers to a combined fixed-wing and multi-copter operation. This combination grants the benefits of Vertical Take-Off and Landing (VTOL), greatly enhancing deployability and maneuverability when compared to conventional, fixed-wing UAVs. At the same time, though, it allows fixed-wing flight, i.e., using the wing surface for lift generation, thus achieving enhanced cruise efficiency when compared to multi-copters. Most of the UAVs that are capable of hybrid flight feature conventional tail-and-wing configurations with additional motors for the VTOL phase, mounted on external booms [5,6].
- Tailless configurations. This term refers to novel layouts [7], such as the blended-wing-body (BWB) and flying-wing configurations. Their main advantages, compared to conventional, tail-and-wing configurations, are improved aerodynamic efficiency and a larger internal volume-to-wetted area ratio. Preliminary studies indicate an improvement of up to 20% in the Lift-to-Drag ratio, resulting primarily from the absence of empennage [1,7,8].
Not only do these two novelties have a significant impact on UAVs’ performance and operating capabilities on their own but they can potentially be used complementary to each other. The simultaneous implementation of both design choices enables the internal installation of VTOL components (motors and mounting points), thus reducing the parasitic drag [9]. Additionally, the VTOL capability mitigates the risk of stalling and unstable pitch breaks, associated with high angles of attack during conventional take-off and landing [10]. However, to fully exploit the potential of a tailless, fixed-wing VTOL UAV, one big challenge remains, i.e., to tackle the reduced pitch and directional authority due to the absence of empennage and the relatively short moment arms.
A possible solution to these issues is to incorporate canard surfaces in the tailless aerial vehicle designs, which function as horizontal stabilizers. The canards can drastically improve the aerial vehicle’s longitudinal stability, while the associated weight and drag penalty remain small. Additionally, the canards can be used for midflight trimming instead of the conventional control surfaces, which can also result in reduced trim drag [11]. This way, the inherent disadvantages of tailless designs are to some extent negated, while the performance characteristics associated with conventional take-off and landing are also improved (e.g., take-off runway, landing approach angle).
The idea of employing canards as horizontal stabilizers is not new. Initially introduced for delta wing configurations (mostly for fighter jets), several investigations have also been performed for tailless UAV applications. In their work, Nasir et al. [12] have incorporated canards on a BWB UAV design, to increase its static stability as well as lift production, though the overall design of the canards is not described in detail. Furthermore, the influence of the canard incidence angle on the lift force, pitching moment, and longitudinal stability is investigated in [13], using CFD, and compared against previous experimental results. The study of Sunnam et al. [14] is mainly focused on the canard-wing combination, investigating parameters concerning the position of the canards relative to the wing (e.g., canard area, canard sweep angle, and canard position). Moreover, Ali et al. [15] examine, implementing CFD analyses, the effect of the aspect ratio of the canards on the aerodynamic performance of a BWB aircraft, where they are employed to improve the overall stability of the aircraft. Summing up, the use of canards appears to be a robust approach to enhance the stability characteristics of tailless UAV configurations. However, most existing works, as presented above, are limited to studies focusing on specific configuration cases, tailored to the needs of the respective reference platforms, and mostly dealing with a single design parameter at a time. These works provide little-to-no information on the corresponding canard design trends, let alone implement a holistic methodology for trade studies, such as the Design of Experiments (DOE).
In the present work, a parametric investigation is performed, and a CFD-based optimization methodology is described. The effect of some of the most critical canard design parameters is collectively examined through CFD analyses on a tailless UAV [16]. A small, lightweight flying wing UAV capable of hybrid flight, designed in the framework of the Multirole Portable UAS (MPU) project, is used as a reference platform. Its prototype, marked as MPU RX-4, can perform a wide range of missions (e.g., cartography, photogrammetry, precision farming), and conducted its maiden flight in 2022. Using the Taguchi experimental design method, the effect of six design parameters is examined, for the configuration where the canards are used solely as horizontal stabilizers. These parameters are the sweep angle (Λ), aspect ratio (AR), taper ratio (λ), vertical position in relation to the main wing (vpos), incidence angle (ic), and dihedral angle (Γ). The optimum combinations of the design parameter levels are identified for two performance criteria, i.e., the maximization of the Lift-to-Drag ratio and the pitching moment coefficient at cruise conditions (L/Dcruise and |Cm|cruise). Furthermore, the percentage contribution of each design parameter to the performance criteria is defined using the Pareto Analysis of Variance (ANOVA) and the most significant parameters are identified, which can serve as valuable input for future canard designs. The aim of this work is to present an innovative design procedure and provide clear trends for the sizing of canards on a UAV, by employing DOE methods (Taguchi) tailored to the canard design parameters and performance criteria, coupled with high-fidelity CFD analyses. Hence, the presented results aim to assist future UAV designers in the initial design stages (conceptual and early preliminary).
It must be noted at this point that the current manuscript does not present a purely scientific or theoretical subject, but rather deals with a more applied topic of Aeronautical Science. All elements of the study are fully backed up by the corresponding literature, as is evident from the selection of the design parameters and performance criteria, the formulation of the analysis methodology, and the selection of the boundary conditions (including the low-Reynolds turbulence model and the corresponding turbulence inlet conditions), the establishment of the DOE methodology, as well as from the discussion of the results and the corresponding conclusions.
2. Tools and Methods
2.1. Reference Platform & Canards Design
The goal of the MPU research project (2018–2022) was the development of a small UAS capable of hybrid flight. The MPU RX-4 is equipped with various cameras (RGB, Thermal, Multispectral) and can carry a small payload for emergencies (medicine, wireless transceiver, etc.) [17,18]. In order to be compliant with regulations concerning UAV flights in Greece, the MPU RX-4 operates at altitudes of less than 400 ft with a cruise velocity of 65 km/h. As shown in Figure 1, the UAV is based on the flying wing configuration and, as such, has no empennage. This offers the advantage of a reduced wetted area and weight and, consequently, increases its aerodynamic performance in terms of endurance. It also provides adequate volume for a relatively large central fan to be installed at the rear of the platform. However, as also discussed in the previous section, this tailless configuration has the inherent drawback of limited control authority in the longitudinal direction [5,11,15], which leads the design team to the addition of canards. Apart from acting as horizontal stabilizers, the canards are also used as mounting points for the UAV’s main motors.
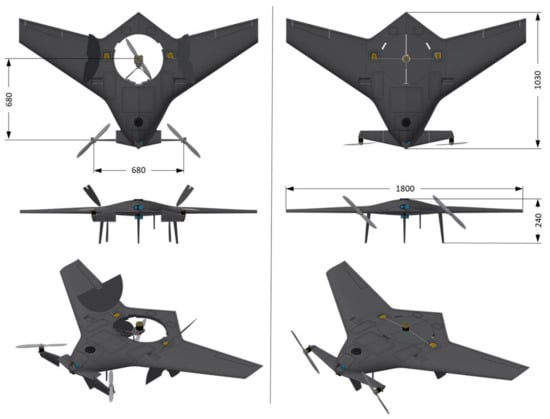
Figure 1.
The MPU RX-4 during the VTOL (left) and fixed-wing (right) phases, with its basic dimensions.
Since the authors of this work want to emphasize the aerodynamic and stability aspects of the canard surfaces, the UAV that serves as a reference platform for the parametric investigations is a simplified version of the MPU RX-4. These simplifications refer to the omission of the landing fins, the internal rotating mechanisms, and the main motors and propellers. The omission of the latter shifts the focus of this study toward cases where the canards are used in a conventional manner (i.e., solely as horizontal stabilizers). Even though the MPU RX-4 features canard-mounted motors/propellers, this does not reflect most canard UAV designs. Therefore, the decision to omit the propeller effect not only reduces the computational effort but also allows for the extrapolation of the study’s results to the majority of canard-using UAV configurations.
Six independent key canard design parameters of this reference platform are investigated. These design parameters are the sweep angle Λ (A), aspect ratio AR (B), taper ratio λ (C), vertical position with respect to the main wing vpos (D), incidence angle ic (E), and dihedral angle Γ (F). These parameters completely define the canards’ design and are indicatively shown in Figure 2 and Figure 3. Another parameter that was initially considered by the authors is the twist angle. However, it was eventually dropped, because the well-established aircraft design textbook methods [11,19] do not consider it as a key design parameter for canards and horizontal stabilizers. The incidence angle ic is instead selected, as a more important horizontal stabilizer design parameter [20]. To produce canard configurations with different design parameter combinations, the following steps are conducted using 3D CAD software. Initially, the tip chord (ctip) is altered to attain the suitable λ, followed by the wingspan (b) to obtain the desired AR, and finally by moving the tip airfoil along the longitudinal axis until the desired Λ is reached. The ic is acquired by selecting the appropriate airfoil incidence at the tip of the canard, whereas the Γ is achieved by changing the vertical position of the tip airfoil. Finally, the vpos is obtained by moving the canards vertically. Three vertical positions are selected, marked as Low, Mid, and High, which refer to the vertical distance of the canard root from the origin point, as is marked in Figure 2. At the Low position, the canard root is placed 5 mm lower from the origin point, whereas at the Mid and High positions, the canard root is placed 7.5 and 20 mm higher, respectively. A comparison between different canards configurations is shown in Figure 3.
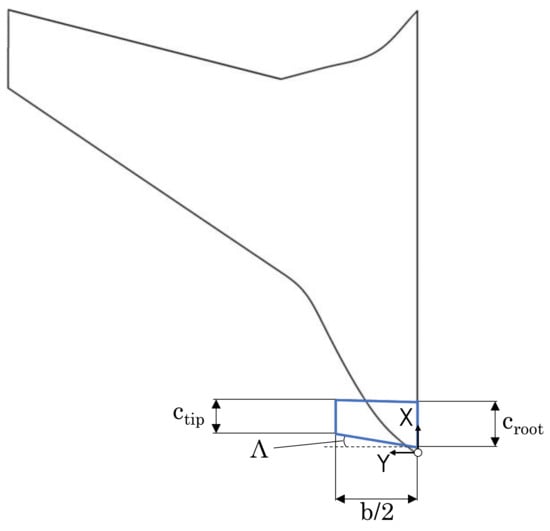
Figure 2.
Definition of key geometrical parameters of canards.
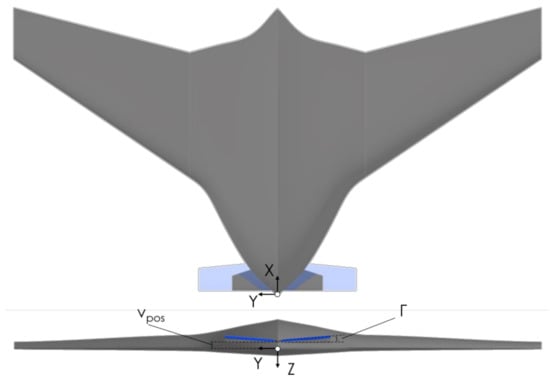
Figure 3.
Comparison between different canards configurations.
2.2. Taguchi Methodology
Advanced engineering optimization problems often tend to require the examination of several design parameters at various levels, leading to a considerable number of combinations. For a full factorial optimization problem, where the whole design space is under investigation, the number N of the possible combinations that occur for L number of levels of the design parameters and m number of design parameters is equal to:
More specifically, where aircraft design is concerned, most platform optimization studies or trade studies, especially the ones conducted during preliminary design, are based on experimental or high-fidelity computational methods. Such studies are demanding, both resource- and time-wise, and also take into consideration a rather restricted design space, such as the winglet sizing presented in [21]. When the design is in progress, there is often the need to reduce the corresponding resources and time without compromising the accuracy of the platform trade studies. Especially when studying more innovative platforms (e.g., flying wing and BWB UAVs), the use of low-fidelity methods tends to lead to a less accurate calculation of the aerodynamic coefficients, such as the drag and moment coefficients [22]. In an attempt to overcome this issue, Taguchi proposed a standardized DOE method [23], which is widely used in industry to design and produce high-quality products. Taguchi’s method maximizes the robustness of products and processes, making them insensitive to the influence of uncontrollable factors, thereby achieving high quality at a relatively low cost. With the implementation of a special set of OAs, the minimum required “experiments” for this set of design parameters are defined (Table 1), ensuring that the conclusions derived from the reduced “experimental” space are valid over the entire design space. It should be noted at this point, that the use of the Taguchi method is not innovative by itself, since it is a well-established DOE method employed by the industry. However, the suggested overall method, which combines Taguchi with ANOVA for the definition of the percentage contribution of canard design parameters on aerodynamic and stability performance, is unique and original, since it has not been discussed in the published canard design literature.

Table 1.
Indicative comparison between a full factorial and a Taguchi experimental design.
The first step in constructing an orthogonal array is the calculation of the total degrees of freedom, which in turn yields the minimum number of “experiments” that need to be executed to examine the selected design parameters. For each design parameter, the degrees of freedom are equal to its number of levels, minus one (Equation (2)), where i stands for the respective parameter (A, B, C, etc.). Consequently, the total degrees of freedom are equal to the sum of the degrees of freedom of the design parameters’ main effects, plus one degree of freedom associated with the overall mean [24].
The second step is to determine the appropriate OA layout, which is defined by the total degrees of freedom and the number of design parameters. The number of rows of an OA must be at least equal to the total degrees of freedom, whereas the number of columns depends on the number of factors and their levels. The design parameters are selected by the design engineers, based on the aspects of the corresponding field, theory, and common practice [11,25]. Concerning the current study, the design parameters defined in the previous section are presented in Table 2. The values of each design parameter level are selected based on reference platform and manufacturability restrictions and general guides for longitudinal stabilizer design [11,15,26]. Concluding, the combination of the design parameters and their levels (five parameters with three levels each) leads to an L27 orthogonal array for the current trade studies (Table 3). Thus, the configurations of 27 different canards are examined and their effect on the aerodynamic performance of the MPU RX-4 platform is extracted. It is worth noting that, through the use of the Taguchi method, the total number of cases that need to be examined is reduced from 729 to merely 27, compared to the full factorial problem, thus drastically reducing the CAD- and CFD-related effort.

Table 2.
Design parameters and their levels under investigation.

Table 3.
L27 Orthogonal Array.
2.3. CFD Methodology
The parametric investigations are performed using high-fidelity CFD computations for the different cases. The employment of CFD is preferred over both semi-empirical/statistical and low-fidelity panel methods. The semi-empirical/statistical methods include an inherent result bias and lack accuracy when employed on UAV configurations [9]. Similarly, the low-fidelity panel methods have several disadvantages, such as the inability to accurately predict viscous effects, which in turn can result in the underprediction of drag force [27]. More specifically, in the present study, the steady-state Reynolds Averaged Navier Stokes (RANS) equations are solved, with the adoption of an appropriate turbulence model necessary for their closure. More specifically, the one-equation eddy viscosity model of Spalart and Allmaras (SA) [28] is selected, which uses one transport equation (Equation (3)) for the calculation of the viscosity variable . It is widely used in external aerodynamics flows and has good agreement with experimental results in low freestream Reynolds number applications [29].
All the required computational meshes are generated using the BETA ANSA pre-processing software (v19.1.0, Root, Switzerland). They are unstructured and consist of tetra-, penta- and hexahedral cells. The SA is a low-Reynolds turbulence model, therefore a structured-like region has been generated near the UAV’s solid surfaces, where the boundary layer develops, with 25 cells in the normal to the wall direction (Figure 4). The first cell height is selected so that the y+ values do not exceed the value of 1 and that at least 5 computational cells are lying within the viscous sublayer. Since the UAV is completely symmetrical, only half of it is modeled, to reduce the computational effort of the CFD analyses. The total number of computational cells is around 10 million for all examined cases and is the result of extensive grid independency studies performed during the conceptual and preliminary design phases of the MPU RX-4 for cruise conditions [16,17]. The solution is performed with the Ansys CFX software (Release 18.2, Academic Multiphysics Campus Solution, Canonsburg, PA, USA), using a coupled pressure-based solver, and second-order spatial discretization schemes for the continuity, x-, y- and z-momentum and viscosity variable transport equations. Each different configuration that is examined, as a result of the Taguchi analysis, is investigated for a range of angles of attack between −4° and 12° at cruise altitude and flight velocity, with a corresponding freestream Reynolds number of 5 × 105 based on the mean aerodynamic chord. Regarding the turbulence boundary condition parameters that correspond to typical flight conditions, only the freestream eddy viscosity ratio is set equal to 0.21, since with the adoption of the Spalart-Allmaras turbulence model, no dedicated equation for the dissipation of the turbulence kinetic energy is used [30]. The CFD computations were performed on an Intel i7-6700 machine, equipped with 32 Gb RAM, in local MPI parallel mode. The average time required for the computations of each configuration (examining the whole angle of attack range described) was equal to ~200 CPU hours. Finally, each case solution was considered converged when all the following criteria were met:
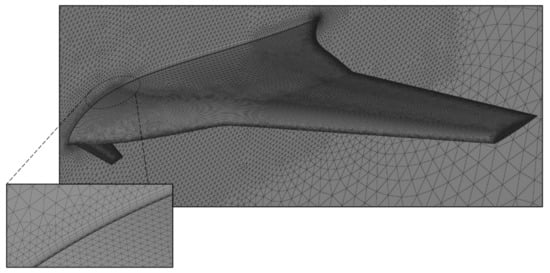
Figure 4.
The computational mesh on the surface of the UAV and detail of the structured region.
- The development of all normalized RMS residuals is consistent for a predefined number of iterations (i.e., 100).
- All RMS residuals reduce by at least four orders of magnitude (<10−4)
- The development of the axial and normal forces is consistent for a predefined number of iterations (i.e., 100).
2.4. SNR and ANOVA
Taguchi suggests the Signal-to-Noise Ratio (SNR) for the analysis of the results. The SNR generally represents the efficiency factor and a quality measure connected with the loss function. By maximizing the SNR, the losses related to the procedure are minimized. The “experimental” observations are converted to SNR, following three basic, different definitions depending on the desirable direction of the results (Equations (4)–(6)). The logarithmic transformation of the observations in SNR strengthens the prediction of the performance criteria improvement.
In this specific case, the term y refers to the estimated performance criteria for each configuration and n to the number of configurations under investigation. Furthermore, is the mean value and is the variance of each performance criterion (Equations (7) and (8)) [20].
Concerning the performance criteria of the current study, for the optimization of the L/Dcruise, the ‘Bigger the better’ definition is used, whereas for the optimization of the |Cm|cruise, the ‘Smaller the better’ definition is applied. For each performance criterion, the combination of the design parameters with the highest SNR is the optimum one and corresponds to the best performance with the minimum variation.
Furthermore, an ANOVA [23,31] is also conducted to analyze the results and draw conclusions regarding the optimum combination for each performance criterion. ANOVA is a statistical method mainly used for the analysis of “experimental” data and the investigation of the effect that the design parameters have on the total variation of the results. In the current work, a simplified version of ANOVA is implemented, called Pareto ANOVA [31,32]. It is based on the Pareto principle and is a quick and easy method to analyze the results of parametric trade studies. The Pareto ANOVA does not need an F-test, consequently, the statistical significance of each design parameter can be determined for each one of the performance criteria. In the current study, an ANOVA is conducted for L/Dcruise and |Cm|cruise, taking into concern the SNR analysis results, yielding the importance and the percentage contribution of Λ, AR, λ, vpos, ic, and Γ.
Following the methodology presented in [31], let i stand for the number of parameters and j stand for the number of levels of each design parameter so that i and j range from 1 to 6 and 1 to 3 respectively (Table 2). Hence, following the well-established ANOVA methodology, the contribution of each design parameter is calculated using Equation (9).
The terms and represent the sum of squares of each design parameter and the total sum of squares, respectively, due to variation about the overall mean. The exact values of and are calculated using Equations (10) and (11).
Finally, is the average SNR of the ith parameter at the jth level, and the overall mean SNR is calculated using Equation (12).
The above procedure is conducted for each one of the performance criteria, yielding two percentage contributions in the current study.
3. Results
As a first step, the results from the CFD computations are extracted for each one of the 27 configurations. All the required aerodynamic coefficients, such as lift, drag, and moment coefficients, are calculated. Next, the drag polar and the Cm-AoA curves are defined for each configuration, and the L/Dcruise and |Cm|cruise are calculated.
In Figure 5, the pressure acting on the surface of the different canard configurations, as well as the local flow field in the canard tip region, are presented. In several cases, a strong variation in pressure distribution is observed and significant tip leakage occurs from the high- to the low-pressure side of the canard (e.g., configurations 12, 24). The aerodynamic performance of all configurations of the L27 OA is presented in Figure 6 and Figure 7, where the drag polars and the lift coefficients as a function of the longitudinal moment coefficients are shown, respectively. For a better presentation of the aerodynamic analysis results, the figures are split into three parts, a, b, and c. These results are for clean canard configurations, where the effect of the propeller slipstream is omitted, and hence they can be exploited in the design of canards as purely horizontal stabilizers. In cases where the UAV motors are mounted in the canard tips, dedicated CFD analyses are required on a case-by-case basis. Indicatively, in the MPU RX-4 case, the effect of the propeller slipstream reduces the aerial vehicle’s L/D by about 4% and increases the pitching moment by about 30%, when considering the modeling methods presented in [16].
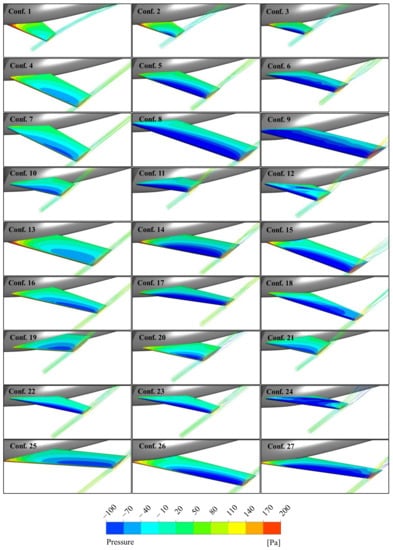
Figure 5.
Pressure contours and streamlines on the canard surface.
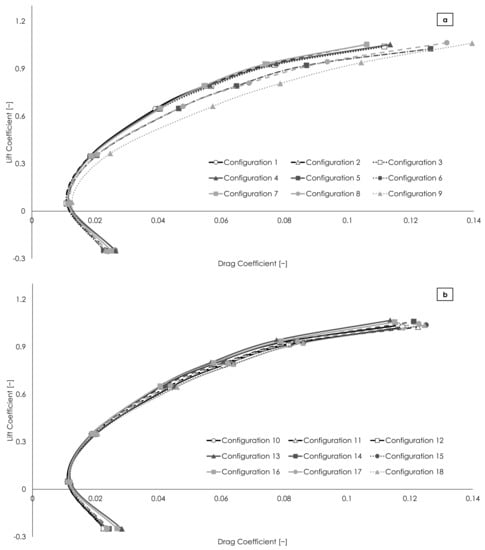
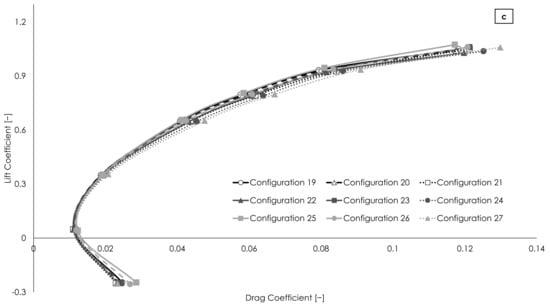
Figure 6.
Drag polars of all examined configurations, split in three parts (a–c).
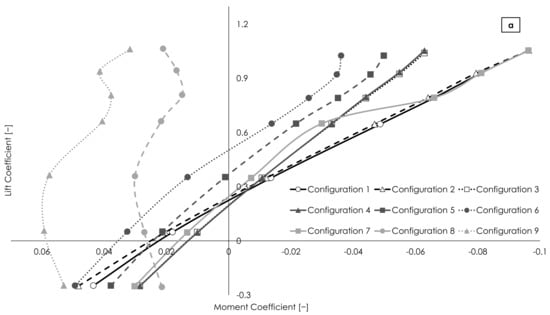
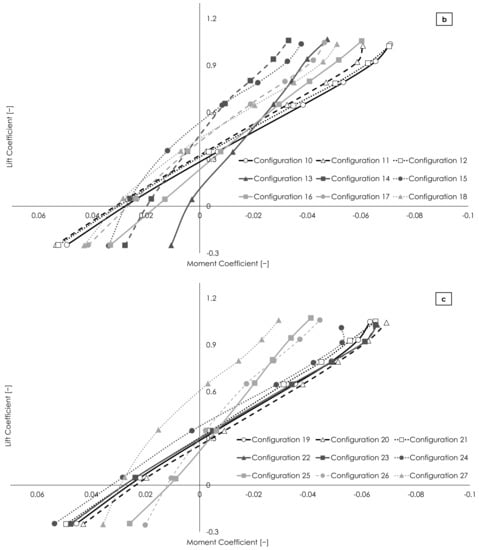
Figure 7.
Trim diagram of all examined configurations, split in three parts (a–c).
The SNR analysis is conducted to define the optimum combination of the design parameters for each performance criterion (L/Dcruise and |Cm|cruise). From the SNR analysis, the SNR of each configuration for each performance criterion is calculated (Table 4). It is found that the mean SNR for L/Dcruise and |Cm|cruise is 25.30 dB and 40.58 dB, respectively.

Table 4.
Performance criteria and calculated SNR.
For the optimization of L/Dcruise, the “Bigger is better” definition of SNR is used, while for |Cm|cruise, the “Smaller is better” definition is selected. The results of the SNR analysis for each parameter individually are presented in Table 5 and Table 6. Delta is equal to the difference between the maximum and the minimum SNR value of each parameter. The rank οf each design parameter reveals which one affects the response characteristic more and it is defined by the fraction of each parameter Delta divided by the sums of all the parameters’ Deltas.

Table 5.
Response table for L/Dcruise.

Table 6.
Response table for |Cm|cruise.
The effect of the design parameters on the performance criteria is shown in plot form in Figure 8 and Figure 9. The optimum level of each parameter for each response characteristic is the one with the maximum SNR. L/Dcruise takes its maximum value at the first level for B (AR), C (λ), D (vpos), E (ic), and F (Γ), and at the second level for A (Λ). |Cm|cruise takes its minimum value at the first level for C (λ), at the second level for parameters A (Λ), B (AR), D (vpos), and E (ic), and at the third level for F (Γ).
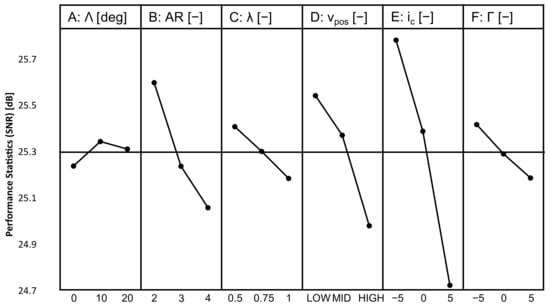
Figure 8.
Effect of the design parameters on L/Dcruise.
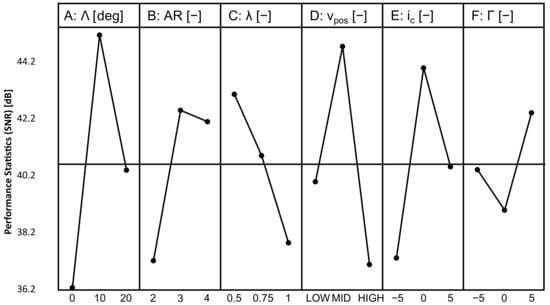
Figure 9.
Effect of the design parameters on |Cm|cruise.
The optimum design parameter levels combinations for each examined performance criterion are summed up in Table 7. The combination A2B1C1D1E1F1 optimizes the L/Dcruise, according to the “Bigger is Better” condition and the corresponding SNR analysis. Similarly, A2B2C1D2E2F3 is the optimum combination for |Cm|cruise, defined by the “Smaller is Better” definition of the SNR. For all optimized configurations, the lowest taper ratio is preferable, whereas for both performance criteria, a medium value of sweep is optimal.

Table 7.
Optimum design parameter combinations for the optimization of the performance criteria.
The Pareto ANOVA results are presented in Table 8 and Table 9, as well as in Figure 10, where the effect of design parameters on each performance criterion is specifically shown. According to the ANOVA, ic (E) is the parameter with the most significant influence at L/Dcruise, whereas the effect of Λ (A), λ (C), and Γ (F) is insignificant for L/Dcruise. On the contrary, Λ (A) has the most significant effect on |Cm|cruise, followed by vpos (D) and ic (E). Finally, Γ (F) appears to have an insignificant influence on both performance criteria.

Table 8.
Contribution ratio of the design parameters on L/Dcruise.

Table 9.
Contribution ratio of the design parameters on |Cm|cruise.
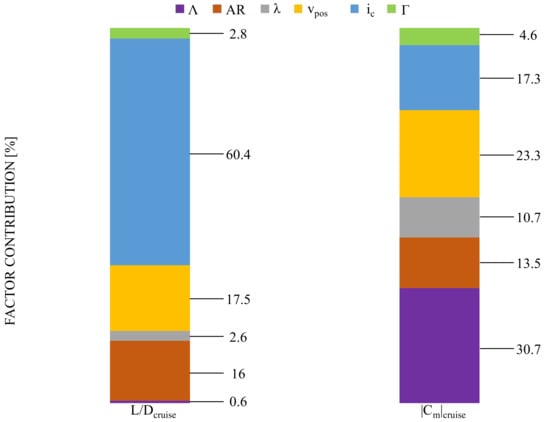
Figure 10.
Contribution of the design parameters on the performance criteria.
4. Conclusions
In the present study, a parametric canard investigation is conducted on a flying wing VTOL UAV, using the Taguchi method. More specifically, the influence of six design parameters on the aerodynamic and stability performance of a flying wing UAV is investigated. These design parameters are the sweep angle (Λ), aspect ratio (AR), taper ratio (λ), vertical position of the canards relative to the main wing (vpos), incidence angle (ic), and dihedral angle (Γ). Two performance criteria are selected, i.e., the lift-to-drag ratio, L/Dcruise, and the moment coefficient, |Cm|cruise, during cruise. The values of the performance criteria are extracted using a high-fidelity, CFD approach. The optimum combinations of design parameters for the maximization of L/Dcruise and minimization of |Cm|cruise are defined using SNR analysis. Finally, a Pareto ANOVA is implemented to calculate the percentage contributions of the design parameters on each performance criterion. The main conclusions of this study are listed as follows:
- The optimum combination of design parameters for the maximization of L/Dcruise is A2B1C1D1E1F1 and the optimum level values are Λ = 10⁰, AR = 2, λ = 0.5, vpos = LOW, ic = −5, and Γ = −5.
- The optimum combination of design parameters for the minimization of |Cm|cruise is A2B2C1D2E2F3, and the optimum level values are Λ = 10⁰, AR = 3, λ = 0.5, vpos = MID, ic = 0, and Γ = 5.
- An ANOVA is conducted for the SNRs of each performance criterion, yielding the effect of every design variable. AR (B), vpos (D), and ic (E) have a significant effect on L/Dcruise and Λ (A), vpos (D), and ic (E) on |Cm|cruise.
- The parameter that affects L/Dcruise the most is ic, with a contribution factor equal to 60.4%.
- The parameter with the most significant effect at |Cm|cruise is Λ, with a contribution factor equal to 46.7%.
In conclusion, by coupling high-fidelity CFD computations with the DOE, the trade studies of the canards are conducted in a considerably lower amount of time, as the design space of the studies is limited from 729 to only 27 configurations. The design space limitation achieved with the implementation of the Taguchi method reduces the total computational effort from around 145,800 CPU-hours to only 5400 CPU-hours. Finally, the design trends for the canards are extracted for the MPU-RX4 platform, which can also act as general guidelines for the canard design on other UAVs performing similar missions.
In future work, more design parameters can be included in the parametric investigation, such as the distance between the canards and the wing, and the twist angle of the canards. Additionally, the effect of the propeller slipstream on canard performance can also be investigated, for specific cases where canard mounted motors are implemented. Structural considerations and limitations can also be assessed. Finally, to extrapolate the results of this methodology to larger-scale applications and aerial vehicles operating at higher Mach numbers, the effects of compressibility can also be investigated.
Author Contributions
Conceptualization, C.B.; methodology, S.K. and P.P.; validation, C.B. and P.K.; formal analysis, S.K. and C.B.; investigation, S.K. and C.B.; data curation, P.K. and P.P.; writing—original draft preparation, S.K. and C.B.; writing—review and editing, P.K. and P.P.; visualization, C.B.; supervision, P.K. and P.P.; project administration, S.K. and K.Y.; funding acquisition, S.K. and K.Y. All authors have read and agreed to the published version of the manuscript.
Funding
The research work was supported by the Hellenic Foundation for Research and Innovation (HFRI) under the 3rd Call for HFRI PhD Fellowships (Fellowship Number: 6179).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liebeck, R.H. Design of the Blended Wing Body Subsonic Transport. J. Aircr. 2004, 41, 10–25. [Google Scholar] [CrossRef]
- Wittmann, R. Passenger Acceptance of BWB Configuration. In Proceedings of the 24th International Congress of the Aeronautical Sciences, Yokohama, Japan, 29 August–3 September 2004; Scientific Research Publishing: Wuhan, China, 2004; pp. 1–10. [Google Scholar]
- Galea, E.R.; Filippidis, L.; Wang, Z.; Ewer, J. Fire and Evacuation Analysis in BWB Aircraft Configurations: Computer Simulations and Large-Scale Evacuation Experiment. Aeronaut. J. 2010, 114, 271–277. [Google Scholar] [CrossRef]
- Abbas, A.; de Vicente, J.; Valero, E. Aerodynamic Technologies to Improve Aircraft Performance. Aerosp. Sci. Technol. 2013, 28, 100–132. [Google Scholar] [CrossRef]
- Bacchini, A.; Cestino, E. Electric VTOL Configurations Comparison. Aerospace 2019, 6, 26. [Google Scholar] [CrossRef]
- Ozdemir, U.; Orkut Aktas, Y.; Vuruskan, A.; Dereli, Y.; Farabi Tarhan, A.; Demirbag, K.; Erdem, A.; Duygu Kalaycioglu, G.; Ozkol, I.; Inalhan, G.; et al. Design of a Commercial Hybrid VTOL UAV System. J. Intell. Robot. Syst. 2014, 74, 371–393. [Google Scholar] [CrossRef]
- Panagiotou, P.; Yakinthos, K. Aerodynamic Efficiency and Performance Enhancement of Fixed-Wing UAVs. Aerosp. Sci. Technol. 2019, 99, 105575. [Google Scholar] [CrossRef]
- Bolsunovsky, A.L.; Buzoverya, N.P.; Gurevich, B.I.; Denisov, V.E.; Dunaevsky, A.I.; Shkadov, L.M.; Sonin, O.V.; Udzhuhu, A.J.; Zhurihin, J.P. Flying Wing—Problems and Decisions. Aircr. Des. 2001, 4, 193–219. [Google Scholar] [CrossRef]
- Götten, F.; Finger, D.F.; Havermann, M.; Braun, C.; Marino, M.; Bil, C. Full Configuration Drag Estimation of Short-to-Medium Range Fixed-Wing UAVs and Its Impact on Initial Sizing Optimization. CEAS Aeronaut. J. 2021, 12, 589–603. [Google Scholar] [CrossRef]
- Kitsios, I.; Dimopoulos, T.; Panagiotou, P.; Yakinthos, K. Longitudinal Dynamics Analysis and Autopilot Design for a Fixed-Wing, Tactical Blended-Wing-Body UAV. In Proceedings of the 2020 International Conference on Unmanned Aircraft Systems, ICUAS, Athens, Greece, 1–4 September 2020; pp. 149–157. [Google Scholar] [CrossRef]
- Raymer, D. Aircraft Design: A Conceptual Approach, 6th ed.; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018. [Google Scholar]
- Nasir, R.E.M.; Kuntjoro, W.; Wisnoe, W.; Ali, Z.; Reduan, N.F.; Mohamad, F.; Suboh, S. Wing-Body (BWB) Unmanned Aerial Vehicle (UAV): Achieving Higher Aerodynamic Efficiency Through Planform Redesign and Low-Fidelity Inverse Twist Method. In Proceedings of the 3rd Engineering Conference on Advancement in Mechanical and Manufacturing for Sustainable Environment (EnCon2010), Chennai, India, 14–16 April 2010; pp. 3–9. [Google Scholar]
- Nasir, R.E.M.; Kuntjoro, W.; Wisnoe, W.; Ali, Z.M.; Reduan, N.; Mohamad, F.; Ramly, R. Static Stability of Baseline-II Blended Wing-Body Aircraft at Low Subsonic Speed: Investigation via Computational Fluid Dynamics Simulation. In Proceedings of the CSSR 2010—2010 International Conference on Science and Social Research, Kuala Lumpur, Malaysia, 5–7 December 2010; pp. 97–102. [Google Scholar] [CrossRef]
- Sunnam, S.; Muthuraj, C.; Ragul, S. Design and Position Sensitivity Analysis of Close-Coupled Canard for Naval Fighter Aircraft. In Advances in Multidisciplinary Analysis and Optimization: Proceedings of the 4th National Conference on Multidisciplinary Analysis and Optimization; Springer: Singapore, 2022. [Google Scholar] [CrossRef]
- Ali, Z.M.; Kuntjoro, W.; Wisnoe, W.; Ishak, I.S.; Katon, M.Z.; Ahmad, N. Aerodynamics Analysis on the Effect of Canard Aspect Ratio on Blended Wing Body Aircraft Using CFD Simulation. IOP Conf. Ser. Mater. Sci. Eng. 2020, 834, 012015. [Google Scholar] [CrossRef]
- Bliamis, C.; Zacharakis, I.; Kaparos, P.; Yakinthos, K. Aerodynamic and Stability Analysis of a VTOL Flying Wing UAV. IOP. Conf. Ser. Mater. Sci. Eng. 2021, 1024, 012039. [Google Scholar] [CrossRef]
- Kaparos, P.; Bliamis, C.; Yakinthos, K. Conceptual Design of a Uav with Vtol Characteristics. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; pp. 1–11. [Google Scholar]
- Tsintotas, K.A.; Bampis, L.; Taitzoglou, A.; Kansizoglou, I.; Kaparos, P.; Bliamis, C.; Yakinthos, K.; Gasteratos, A. The MPU RX-4 Project: Design, Electronics and Software Development of a Geofence Protection System for a Fixed-Wing VTOL UAV. IEEE Trans. Instrum. Meas. 2022, 72, 7000113. [Google Scholar] [CrossRef]
- Roskam, J. Airplane Design, Part VII: Determination of Stability, Control and Performance Characteristics: FAR and Military Requirements; Roskam Aviation and Engineering Corp: Ottawa, ON, Canada, 2006. [Google Scholar]
- Nelson, R.C. Flight Stability and Automatic Control; McGraw-Hill Education: New York, NY, USA, 1997; ISBN 0070462739. [Google Scholar]
- Panagiotou, P.; Kaparos, P.; Yakinthos, K. Winglet Design and Optimization for a MALE UAV Using CFD. Aerosp. Sci. Technol. 2014, 39, 190–205. [Google Scholar] [CrossRef]
- Panagiotou, P.; Yakinthos, K. Parametric Aerodynamic Study of Blended-Wing-Body Platforms at Low Subsonic Speeds for UAV Applications. In Proceedings of the 35th AIAA Applied Aerodynamics Conference, Denver, CO, USA, 5–9 June 2017; pp. 1–19. [Google Scholar] [CrossRef]
- Roy, R.K. Primer on the Taguchi Method, 2nd ed.; Society of Manufacturing Engineers: Deadborn, MI, USA, 2010; ISBN 9780872638648. [Google Scholar]
- Phadke, M.S. Quality Engineering Using Robus, 1st ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 1989; ISBN 0-13-745167-9. [Google Scholar]
- Anderson, J.D. Aircraft Performance and Design, 2nd ed.; WCB/McGraw-Hill: Boston, MA, USA, 1999; ISBN 978-0-07-001971-3. [Google Scholar]
- Handa, S.; Srinivas, G. Recent Developments of Blended Wing Body Aircraft: Experimental, Numerical and Theoretical Approaches. Aerosp. Syst. 2022, 5, 171–183. [Google Scholar] [CrossRef]
- Weierman, J.; Jacob, J.D. Winglet Design and Optimization for UAVs. In Proceedings of the 28th AIAA Applied Aerodynamics Conference, Chicago, IL, USA, 28 June–1 July 2010; Volume 1. [Google Scholar] [CrossRef]
- Spalart, P.R.; Allmaras, S.R.; Reno, J. One-Equatlon Turbulence Model for Aerodynamic Flows. In Proceedings of the 30th Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 6–9 January 1992; p. 23. [Google Scholar]
- Aftab, S.M.A.; Rafie, A.S.M.; Razak, N.A.; Ahmad, K.A. Turbulence Model Selection for Low Reynolds Number Flows. PLoS ONE 2016, 11, e0153755. [Google Scholar] [CrossRef] [PubMed]
- Spalart, P.R.; Rumsey, C.L. Effective Inflow Conditions for Turbulence Models in Aerodynamic Calculations. AIAA J. 2007, 45, 2544–2553. [Google Scholar] [CrossRef]
- Vankanti, V.K.; Ganta, V. Optimization of Process Parameters in Drilling of GFRP Composite Using Taguchi Method. J. Mater. Res. Technol. 2014, 3, 35–41. [Google Scholar] [CrossRef]
- Venkateswarlu, G.; Davidson, M.; Tagore, G. Influence of Process Parameters on the Cup Drawing of Aluminium 7075 Sheet. Int. J. Eng. Sci. Technol. 2011, 2, 41–49. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).