Component Maintenance Planning Optimization in Defense Aviation

Abstract

The primary objective in military aviation is to optimize operational readiness, the capability to perform assigned flight missions. This capability is influenced by aircraft downtime due to preventive maintenance at prescribed flight time intervals. In practice, flight planning incorporates preventive maintenance relative to the aircraft as a whole, but also to specific components that are subject to individual constraints. Optimization models have been developed to address the associated aircraft flight and maintenance planning problem, but none of these models addresses planning at the component level while retaining consistency with the aircraft planning outputs. Furthermore, no existing models adequately incorporate the main components of operational readiness. Lastly, practical approaches to this planning problem are reactive. To address these issues, this paper proposes a mixed integer linear programming model that solves the component flight and maintenance planning problem using component substitution scheduling while being aligned with overall aircraft flight and maintenance planning. In this manner, a pro-active, integrated approach is established. The proposed model has been applied towards Royal Netherlands Air Force CH47D Chinook helicopter fleet data, with results showing substantial improvements in critical operational readiness key performance indicators while showing strong reductions in the variability of the preventive maintenance demand and associated financial expenses.

1. Introduction

Preventive maintenance is a cornerstone element of existing commercial and military aircraft maintenance policies, helping to ensure safe, airworthy flight operations. Preventive maintenance is a periodical process that is performed in accordance with fixed intervals of time in service, which sets it apart from other policies such as corrective maintenance or condition-based maintenance. Given its time-based nature, preventive maintenance can be planned in advance. When considering a fleet of aircraft and a set of maintenance constraints, such as available workforce, facilities, and inventory, a planning process must determine which aircraft to operate and which aircraft to maintain at specific moments in time over the duration of a planning horizon. This process, known as aircraft flight and maintenance planning (FMP), is highly complex and time consuming due to a large number of constraints. Furthermore, FMP output needs to be reassessed frequently as deviations from the initial schedule occur due to unpredictable operational demand, unforeseen failures, and poor weather conditions. From this, it follows that the FMP process must be flexible, fast, and efficient. Several approaches have been proposed to optimize the FMP problem for civil aviation and military aviation contexts [1,2,3,4,5,6,7,8,9,10]. All of these approaches consider the FMP problem with individual aircraft as the unit of analysis. However, individual aircraft themselves consists of a multitude of systems, subsystems, and components, which in turn can be subject to preventive maintenance as well. Note that within the context of this work, for reasons of simplicity the term component is used to denote any subsidiary element of the overall aircraft system and can therefore represent any (sub)system or (sub)structure or contributing parts. Importantly, each component can be subject to specific preventive maintenance intervals, which may differ compared to other components or the aircraft as a whole. While the majority of tasks in the maintenance program will be based on on-condition or corrective approaches, an important minority is governed by hard-time replacement policies, as applicable to so-called life-limited parts (LLPs).

Consequently, a need arises to optimize flight and maintenance planning relative to aircraft and components. Planning must be performed in such a way that the operational program of the aircraft fleet is not adversely influenced by component downtime. For this purpose, the availability of components must be continuously aligned with planned operations of the aircraft fleet. The resulting challenge of proactively assigning components to operational service on aircraft on the one hand, and to preventive maintenance on the other hand, is referred to here as the component maintenance planning (CMP) problem. Solutions to this problem are underrepresented in the state of the art. This has practical implications: given the sheer number of components on the average aircraft, the CMP problem is complicated to tackle for real-life applications. Hence, operators tend to deal with preventive maintenance scheduling of aircraft components on a reactive basis only. This results in an installed component being left installed on the carrying aircraft until its maximum time in service is reached. Subsequently, the component is withdrawn from service in order to receive the required preventive maintenance. With such an approach, spacing of maintenance capacity and inventory are not taken into account; at certain times, maintenance capacity may be underutilized or even idle, whereas at other times, multiple components must be maintained at once. Therefore, a reactive approach may lead to unequal distribution of component usage within the operator’s total inventory and, therefore, to fluctuating and sub-optimal component availability.

A possible means to improve upon this reactive approach is to manipulate the allocation of flight time to components by proactively interchanging components between aircraft in the fleet at specific moments over a planning horizon. Following this approach, components can be swapped between aircraft and spare inventory in such a way that the usage remains controlled, leading to optimized long-term component availability and therefore increased fleet readiness levels. To operationalize this pro-active approach, this paper proposes a mixed integer linear programming model that solves the component maintenance planning problem for defense aviation operators using component substitution scheduling while being aligned with overall aircraft flight and maintenance planning. This constitutes a novel contribution to the state of the art by addressing three research gaps:

• Consideration of component maintenance planning: the majority of existing literature regarding maintenance optimization in aviation considers network and/or route optimization in light of scheduled maintenance requirements. Several models specific to flight and maintenance planning exist, but these focus nearly exclusively on aircraft flight and maintenance planning. The role of component maintenance in the FMP problem has not been considered in detail in the current state of the art (see Section 2).
• Alignment of aircraft and component maintenance planning optimization: current models for maintenance planning optimization cover dependencies between multiple components, but planning optimization for situations where a hierarchical dependency exists between the overall system and subsidiary components is not covered in the literature. This paper proposes a model that ensures an alignment between aircraft-level and component-level maintenance planning.
• Application in military aviation context: civil and military aircraft operators work towards different objectives. Whereas civil operators will generally strive towards profit maximization, and hence maximum availability at minimum cost, military operators place a premium on mission readiness: the capability of an aircraft to conduct its planned operations. This research addresses the unique circumstances of military aviation in more detail while expressing the concept of mission readiness in suitable metrics.

The context, state of the art and research gaps concerning the FMP and CMP optimization problems are discussed in more detail in Section 2, further substantiating the stated novelty. Section 3 introduces an optimization model that can be applied to solve the CMP optimization problem. The proposed model is applied to Royal Netherlands Air Force (RNLAF) data related to the CH-47 Chinook helicopter fleet in Section 4. Finally, conclusions are presented in Section 5.

2. Theoretical Context

The theoretical context of the FMP problem consists of a number of aspects. Section 2.1 covers the state of the art with respect to maintenance optimization models, including applications towards maintenance planning optimization in aviation. Subsequently, Section 2.2 briefly sets out a previously introduced model [3], which covers the aircraft FMP problem and constitutes a necessary basis for the extension of the FMP problem towards components, as discussed from Section 3 onwards.

2.1. State of the Art

Aircraft are highly expensive assets subject to stringent safety and reliability requirements. As a result, various types of maintenance must be performed to ensure that aircraft meet their functionality and safety standards throughout their operational life. These types of maintenance include corrective, preventive, and condition-based maintenance. The focus of the present work is on preventive maintenance: calendar- or usage-based maintenance that aims to prevent systems from failing in order to avoid unplanned downtime and adverse safety effects [11]. Multiple maintenance optimization models have been proposed over the last decades to optimize maintenance, as discussed in more detail in Section 2.1.1. This is followed by the state of the art regarding maintenance planning optimization in aviation.

2.1.1. Maintenance Optimization Models

A voluminous body of work exists relative to the optimization of maintenance, as reviewed by multiple authors [12,13,14]. As defined by Dekker [12], “a maintenance optimization model is a mathematical model in which both costs and benefits of maintenance are quantified and in which an optimum balance between both is obtained.” Objective functions are often centered on cost, but may also incorporate reliability, safety or availability. Ref. [15] mentions eight criteria helpful in classifying maintenance optimization models: (1) information availability, (2) single-unit versus multi-unit systems, (3) time-dependent/action relationships, (4) model types, (5) optimization criteria, (6) methods of solution, (7) planning time horizon (finite/infinite), and (8) maintenance effect (perfect, minimal, imperfect). These criteria mirror other classification schemes mentioned in the literature [12]. With respect to the novelty of the model proposed in this paper, the following aspects are important to address in more depth:

• Single-unit versus multiple-unit systems: optimization can be performed relative to single- or multiple-unit systems. In the case of multiple units, a usual assumption is to consider these as being identical [16]. Furthermore, in the case of multiple-unit systems, the units themselves may act independently or may share a dependency [17]. Notably, some authors assert that the majority of models has been developed for single-unit or identical multi-unit systems [16], which limits applicability towards more complex real-life maintenance systems. In addition, most literature on multi-unit systems considers series or parallel component configurations [18] but neglects hierarchical compositions. In these hierarchical compositions, the top-level system as well as the underlying (systems of) units may each have their own maintenance frequency. However, these frequencies are not always aligned or integrated in an optimal approach.
• Planning time horizon: maintenance optimization models may work on a variety of time horizons. At the top level, the maintenance concept or strategy covers the events associated with the adoption of maintenance types (e.g., replacement, repair, inspection), with many models focusing on this area of research [12]. A maintenance strategy can be determined during and after the design stage. The next level considers the planning of maintenance when products are in operation, with planning being defined as “the determination of the execution moments of (major) maintenance activities, in accordance with other (e.g., production) plans (e.g., planning shutdowns of major refinery units), the work preparation and the determination of the required maintenance capacity” [12]. As such, time horizons are typically finite for planning problems. The FMP problem is a typical planning problem possessing a finite horizon, as discussed in more detail in the next subsection.
• Decision variable: typically, maintenance optimization models use the interval of time between a maintenance intervention as the primary decision variable (e.g., [18,19]). This interval of time—which may be a single fixed value or may be flexible over time [19]—can be associated with various types of maintenance, such as corrective maintenance (length of time between repairs), preventive maintenance (length of time between scheduled replacements), and condition-based maintenance (length of time between inspections). However, in the case of safety-critical systems, it may be the case that the chosen maintenance policy is preventive and adopts mandatory, relatively short intervals between preventive replacement. In such cases, interval length is not a suitable decision variable, and alternatives should be explored, such as residual time.

A number of shortcomings exist with respect to existing models, making them less suitable for application for flight and maintenance planning. First of all, these models tend to focus on interval optimization, whereas the FMP problem (both on the aircraft and component level) is restricted by mandatory intervals on safety-critical items. As such, making changes to maintenance intervals on the basis of cost optimality is often not permitted from a legislative point of view. Second, there is a paucity of work considering planning optimization for multiple-unit, hierarchically dependent systems. In the next section, it will be shown that several models are available for planning optimization relative to the aircraft FMP problem, which considers identical multiple-unit configurations. However, research that covers hierarchical dependencies between systems (e.g., a fleet of multiple identical aircraft) and their subsidiary components (e.g., engines) in combination with mandatory preventive maintenance intervals is, to the best of the authors’ knowledge, lacking in the state of the art.

2.1.2. Maintenance Planning Optimization in Aviation

The aircraft flight and maintenance planning problem (FMP) is considered to be a subset of the flight scheduling and routing research field, a subject of interest in the operations research field for many decades. Levin [20] was the first to formulate a practicable linear integer program (IP) to solve for optimal flight scheduling, routing, and fleet size. This work has served as a basis for researchers to further investigate the optimization of flight scheduling, crew scheduling, equipment selection, usage, and passenger mix. However, relatively few optimization models exist for solving maintenance planning problems. Various authors [9,21,22] integrated flight scheduling and planning considerations with maintenance requirements, typically focused on relatively short planning horizons. More recent work has focused on integrated scheduling and planning for a multi-year planning horizon for heterogeneous fleets while incorporating uncertainty [23,24,25,26], with attention towards decision support aspects for end user applicability [27,28] as well as including dynamic scheduling considerations [29].

Unfortunately, the work covered so far concerns commercial aviation maintenance and is only partially applicable to military aviation, which is the focus of this work. A major difference is that commercial airlines have to deal with routes in a (often complex) network, where the military flight scheme is concentrated around a central base. Even more importantly, military operations revolve around mission readiness, as covered in more detail in Section 2.2.1. This results in a different set of objectives and constraints, the latter of which include safety regulations, maintenance requirements, flight program requirements, personnel and facility capacity, and logistics support [30].

Literature on FMP in military aviation focuses primarily on phase maintenance, a periodical extensive inspection of the aircraft which is the most elaborate of all preventive maintenance processes in military aviation. Phase maintenance typically requires the aircraft to be grounded for a number of weeks. The main tool used to execute FMP in many air forces, typically a manual process, is the phase flow chart. This chart depicts the operational aircraft in a unit’s fleet as well as their residual flight time (RFT), with the latter defined as the total amount of flight hours that may be flown by a specific aircraft before phase maintenance is due to be performed. If the utilization of aircraft in the unit is ideally spaced, the phase flow will be shaped as a straight line. This ideal situation is presented in Figure 1a. However, in practice, this situation is very unlikely to occur, and a realistic chart rather looks like the example in Figure 1b.

Evidently, the phase flow chart varies over time as aircraft in the unit generate flight hours. Furthermore, maintenance is typically performed on a continuous basis. As a result, indices shift position to the right as residual flight times decrease and aircraft that complete phase maintenance (and therefore regain full residual hours) move to the first position. The phase flow chart or the underlying concept of residual flight time are used as a main element to optimize fleet readiness in existing FMP models for military aviation. An overview of existing work for aircraft FMP in a military aviation context is given in

Table 1. Brief overview of objective(s) of, approaches to, and limitations of existing models for FMP optimization in defense aviation. Adapted from [3].

Ref.	Objective(s)	Approach	Limitations
[7]	Achieve maximum availability for an air force unit that consists of multiple subunits by (1) maximizing the number of available aircraft and (2) maximizing the number of available flight hours.	Incorporate residual flight and maintenance time to express (un)availability; maximize available aircraft and flight hours while respecting maintenance capacity constraints.	Does not consider residual flight hour distribution over fleet, although later work [31] adds a heuristic to deal with phase flow chart. Reactive; not resilient to short-term changes; does not include component maintenance considerations.
[8]	Minimize overall number of maintenance actions and evenly distribute capacity and flight hours over time.	Allow consolidation of maintenance tasks by shifting usage-based and calendar-based maintenance actions in order to realize mergers.	Does not consider residual flight hour distribution over fleet; reactive; not resilient to short-term changes; does not include component maintenance considerations.
[4]	Minimizing the maximum number of aircraft in phase maintenance at any given time to balance the variability in phase maintenance demand.	Minimizing aircraft in phase maintenance, while assuring aircraft utilization is evenly distributed by introducing end-of-horizon targets.	Reactive; not resilient to short-term changes; does not include component maintenance considerations.
[2,32]	Optimizes daily flight and maintenance for a small fleet of military aircraft for a planning horizon of 30 days.	Mixed integer linear programming approach with a partitioning heuristic for larger test cases.	Reactive; does not include component maintenance considerations.
[33]	Optimizes engine life management in an analogue approach to the FMP stagger-line.	Proposes a mixed-integer programming (MIP) model for assigning airplanes to missions considering the goal of engine life management.	Reactive; addresses component maintenance but not integrated with FMP.
[34]	Optimizing the FMP problem by scheduling the last check for all aircraft as late as possible and minimizing the deviations from all elastic constraints.	Approach based on a new mixed integer program and the use of both valid cuts generated on the basis of initial conditions and learned cuts based on the prediction of certain characteristics of optimal or near-optimal solutions.	Long-term planning time horizon; does not include component maintenance considerations.
[1]	Maximising the utilisation rate (UR) of aircraft, while satisfying other operational and maintenance constraints, for a multi-year planning horizon.	Applying a genetic algorithm (GA) and a modified artificial bee colony (ABC) algorithm for constrained optimisation.	Reactive; small test case size; does not include component maintenance considerations.

.

It can be observed in Table 1 that these models differ in their capacity to take into account maintenance capacity limitations, the distribution of residual flight hours over the fleet, resilience to short-notice changes to the flight program, and consolidation of maintenance tasks. Furthermore, two general limitations of these models are that (1) they do not take into account the full scope of operational readiness; (2) they do not address component maintenance planning. Relative to the first general limitation, the next Section shows how operational readiness has been operationalized and used to construct an aircraft FMP optimization model. Subsequently, the remainder of this paper focuses on addressing the second general limitation.

2.2. Aircraft Flight and Maintenance Planning Model

2.2.1. Main Concepts

Military aviation has the overall objective to maximize operational readiness: the capability to perform all assigned present and future flight operations. Within the context of the flight and maintenance planning process, operational readiness has three primary components: availability, serviceability, and sustainability.

• Availability: the total duration in which subject aircraft are mission capable, which influences the capacity of the military organization to meet its flight hour requirement. This requirement is derived from the necessity to meet air crew training hour requirements and perform predetermined operational assignments. Availability is an overall measure, considering the full planning horizon.
• Serviceability: the number of mission-capable aircraft at a specific instant of time. This is, therefore, an instantaneous measure describing the capability to perform flight missions at any specific point in time. However, this number alone gives no information on how long the serviceable aircraft remain available for flight operations in the future. In other words, although serviceability might be sufficient, it is unknown if the subject aircraft have sufficient residual flight time left to fulfill a mission requirement.
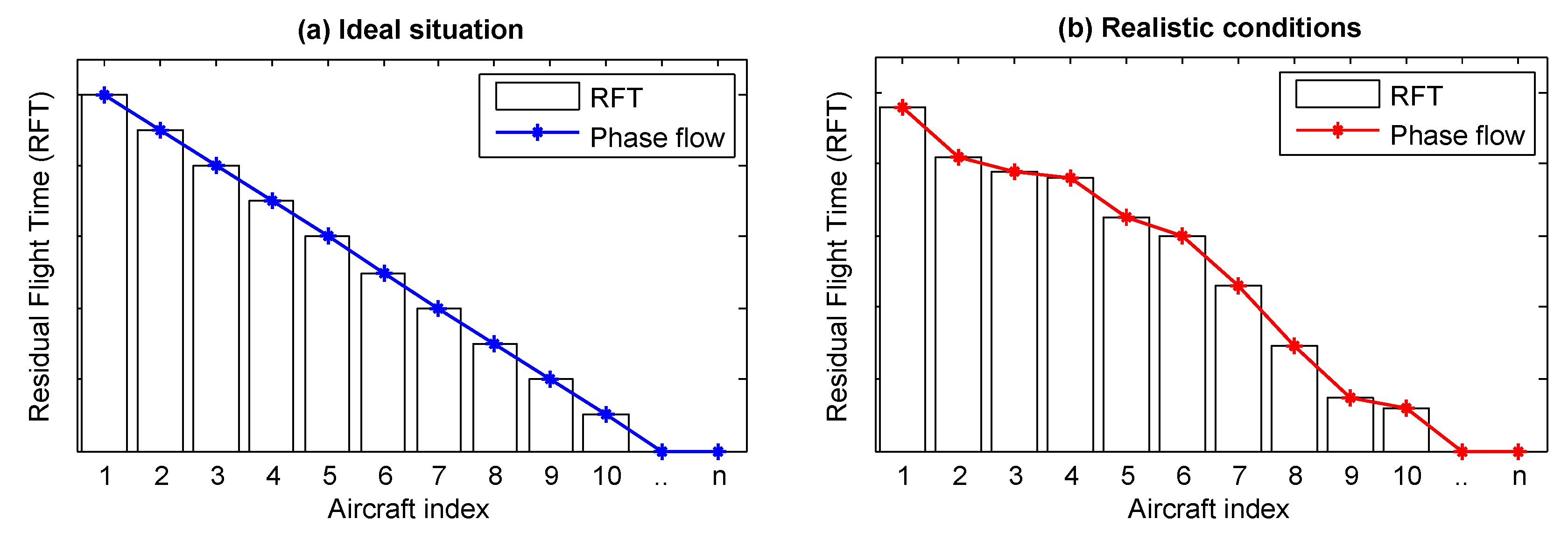
• Sustainability: the total residual flight time of the entire fleet at a specific instant of time. This is also an instantaneous measure, which solves the shortcoming of serviceability. Together, serviceability and sustainability determine how long a tactical unit will remain capable of sustaining a flight mission, starting at an immediate point in time, when no maintenance resources are accessible.

These components have been used in the construction of an aircraft FMP model that produces optimal output with respect to operational readiness. The conceptual model as well as key results are presented in the next subsection.

2.2.2. Aircraft FMP Model and Results

Figure 2 shows a schematic representation of the aircraft FMP optimization framework with the required inputs and outputs. Notably, the model requires the fleet arrangement (i.e., the composition of the fleet of aircraft in terms of numbers and types), the initial fleet status, including residual flight and maintenance times, and various maintenance and operational requirements and constraints. The model delivers output in the form of flight and maintenance assignments; in other words, it specifies which aircraft should fly or undergo maintenance at which point in time in order to produce optimal operational readiness.

The mathematical formulation of the model is represented in detail in [3]. Inputs for the model have been derived from ERP systems and Excel files maintained by the operator involved in the study. Key results include a substantial improvement in sustainability, with a highly decreased variability, as well as automatic generation of coherent, optimal flight and maintenance plans, which take substantially less time to generate compared to the manual process. While the aircraft FMP model successfully addresses the FMP problem from the viewpoint of operational readiness maximization, the larger issues surrounding the CMP problem as discussed in Section 2 remain. These will be addressed in the next sections.

3. Component Flight and Maintenance Planning Model

This section proposes a linear programming model that solves the component flight and maintenance planning problem for defense aviation operations using the optimal scheduling of component substitutions. The CMP optimization model is built to work sequentially on the basis of the aircraft FMP optimization model and its output, as described in Section 2.2. The aircraft FMP model effectively generates adequate and long-term flight and maintenance schedules on the fleet level. The CMP optimization model attempts to assign components to aircraft and to preventive maintenance in such a way that: (1) all mandatory preventive maintenance requirements are satisfied, (2) all operational requirements of the aircraft fleet can be fulfilled through the continuous provision of serviceable components, (3) the maximum availability of the component inventory is maintained, and demand for preventive maintenance is smoothened, and (4) minimum maintenance burden is induced by component substitutions.

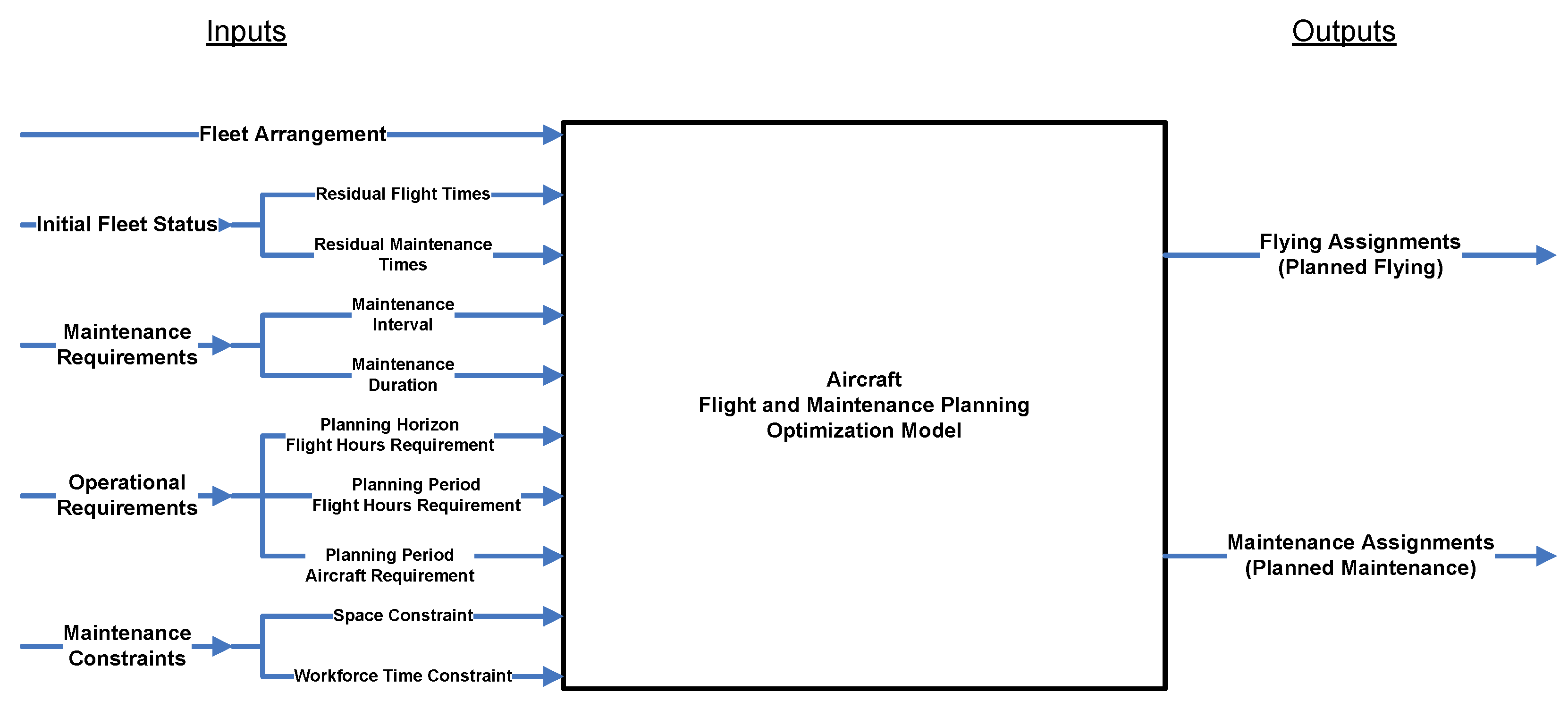
3.1. Model Framework

The framework of the proposed CMP model is represented in Figure 3. As shown, the aircraft FMP model and CMP model are connected, since the outputs of the former guide inputs to the latter. Furthermore, inputs regarding component inventory composition, initial status and maintenance requirements must be provided to produce feasible outputs. The model framework is defined in such way that it is applicable to various problem instances with respect to component type and operator.

The following input values must be provided to the CMP model:

• Aircraft flying assignments reflect the scheduled flight time per planning period for each aircraft in the fleet, which is an output of the aircraft FMP model.
• Aircraft maintenance assignments reflect the scheduled maintenance time per planning period of each aircraft in the fleet, which is an output of the aircraft FMP model.
• The inventory arrangement reflects the quantity of components in the inventory and the separate component identification numbers (serial numbers). This includes items that are installed on aircraft, down for preventive or corrective maintenance, and spares.
• The initial inventory status represents the residual operating and maintenance time and the aircraft configuration of each single component in the inventory. For the CMP model, residual maintenance time due to both preventive and corrective maintenance is of interest. Depending on the serviceability state of the component, the residual operating time or the residual maintenance time is relevant. The initial component/aircraft configuration reflects which components are installed on which aircraft and which are not installed at the start of the planning horizon.
• Maintenance requirements reflect the interval and duration of the preventive maintenance under consideration. The maintenance interval is the prescribed component operating time (COT) between two preventive maintenance actions, or time between maintenance (TBM). The maintenance duration is the amount of maintenance time required to complete a single preventive maintenance action, or scheduled maintenance time (SMT).

The CMP model will generate the following outputs:

• An optimized schedule of component maintenance assignments over a certain planning horizon consisting of separate planning periods. This schedule reflects the maintenance time per individual component for each planning period. A component can only receive maintenance after it has been removed from the carrying aircraft.
• An optimized component substitution scheme. This includes a schedule of all component removals and installations from/on the affected aircraft, which are required to maximize inventory availability, facilitate scheduled component maintenance actions, and ensure the continuous provision of serviceable components to all aircraft.

In this work, it is assumed that the preventive maintenance of components is solely driven by the component operating time, which follows directly from the flight time of the carrying aircraft. Since the allocation of operating time to components follows from the assignment of components to aircraft, both outputs of the model framework are interrelated. For this reason, the scheduling of component substitutions and the assignment to maintenance must be the outputs of a single optimization process.

3.2. Model Dynamics

Every component in the inventory is subject to a separate cycle, which consists of alternating periods of operating uptime and maintenance downtime. As a result, a component can be serviceable, which means that it is available for installation on aircraft, or unserviceable, which means that it is unavailable due to either preventive or corrective maintenance. A serviceable component holds a residual operating time (RFT), and an unserviceable component holds a residual maintenance time (RMT). RFT decreases as a result of allocated operating time, which follows from the flight time (FT) produced by the aircraft on which the subject component is installed. As soon as the RFT reaches (near) zero, the component is removed from the carrying aircraft and scheduled for maintenance at the earliest capacity of the maintenance shop. From this point, the residual maintenance time takes its maximum value, which is equal to the maintenance duration (or scheduled maintenance time (SMT)). RMT decreases proportionally to the amount of maintenance time (MT) allocated, which is assigned per planning period by the model. As soon as maintenance is finished, the RMT reaches zero. Subsequently, the now-serviceable component is available for assignment to an aircraft (with its own residual flight time (RFT)), and the component RFT takes its maximum value, which is equal to the maintenance interval (or time between maintenance (TBM)). From here, the cycle starts over again.

This loop is simultaneously processed by the model for each component in the inventory. The model must run and arrange the separate loops such that the objective for the optimization is optimally satisfied. This cycle requires model inputs 1–3 (Figure 3) to be known parameters. First of all, the input inventory arrangement tells the model how many separate components need to be taken into account, thus informing the model regarding the number of loops that need to be processed simultaneously. Second, the input initial inventory status provides the model with all RFT and RMT data at the start of the planning horizon. Third, the input maintenance requirements defines the maximum RFT and maximum RMT. In addition to these inputs, the length of the complete planning horizon and the duration of a single planning period must be determined.

In addition to these basic dynamics, the model must incorporate the following elements:

• The model must assign components to aircraft such that the scheduled flight time of the carrying aircraft optimally effects the FMP cycle of the installed component. The FT for each aircraft and each period is predefined by the aircraft FMP optimization model;
• Aircraft may carry more than one component of a certain type. Therefore, the model must be able to deal with a variable quantity per aircraft (QPA) per component;
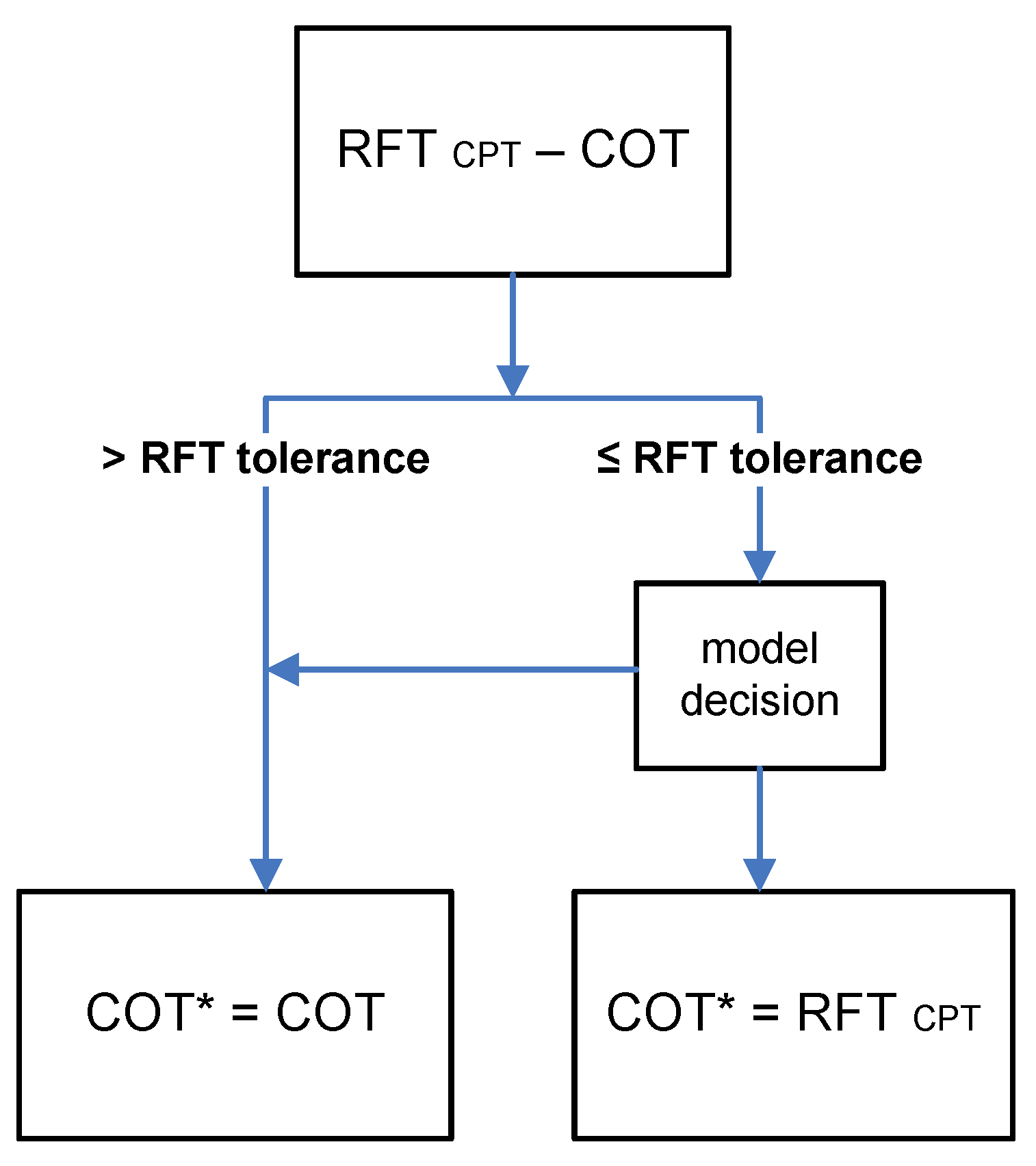
• It is very unlikely that such a combination of predetermined aircraft FT exists that the RFT of each component can be brought to exactly zero after a number of planning periods. For this reason, the model must be allowed to dismiss RFT as soon as it drops under an operator-defined threshold in order to prevent the cycle from stalling;
• The unserviceability of components due to corrective maintenance is of great influence to the scheduling problem since these components may not be installed on aircraft. For this reason, an element must be added to the model that withdraws these components from the serviceable inventory for the remaining duration of the corrective maintenance effort. The COT remains unchanged since this only relates to preventive maintenance;
• The component operating time (COT), which drives preventive maintenance, is not necessarily equal to the flight time of the carrying aircraft. In most cases, COT also contains the time in which the component is running while the aircraft is not flying (e.g., start-up, shut-down, maintenance ground run). As a result, the model must be able to represent COT on the basis of component tracking data or must be able to convert aircraft FT to COT based on an appropriate operator-provided conversion ratio.

Figure 4 provides a schematic representation of the CMP model consisting of the basic dynamics and the described additional elements and inputs.

The first block in Figure 4 uses the input data regarding aircraft flight and maintenance schedule (from the aircraft FMP model), initial component inventory status, and the required quantity per aircraft in order to assign serviceable components to aircraft. Components that are unserviceable due to either preventive or corrective maintenance are not taken into account. This results in a substitution scheme, which serves as the first output of the CMP model. Furthermore, this allocates aircraft FT to the assigned components, which is further converted to COT by block 2, using the operator-defined conversion ratio. This ratio may be statistically determined from past experience. The third block ensures the model’s feasibility by dismissing relatively small amounts of RFT that could otherwise stall the cycle. This results in a corrected COT, which is referred to as COT* in the schematic. The COT* is fed into the fourth and last block that represents the basic FMP cycle, which was described in detail before. Since the COT* has already been defined by the previous blocks, the FMP process will now seek optimal maintenance assignments in order to best satisfy the objective function. A feedback loop enables the FMP block to re-run the component assignment in order to vary the operating time allocation in case the outcome was found to be suboptimal.

In the following sections, the assignment of components to aircraft (block 1) and the relaxation of residual flight time (block 3) will be explained in more detail.

3.2.1. Assignment Problem

The problem of adequately assigning components to aircraft is referred to as the assignment problem. Each aircraft in the fleet must be provided with components in the right quality, namely serviceable, and quantity (QPA). The problem extends beyond the previous considerations since the assignment must be such that the number of component substitutions is minimized, as this introduces maintenance work and downtime.

In operations research theory, problems of this kind are referred to as ‘transportation problems’ [35]. In this perspective, the assignment problem can be considered another variation of the transportation problem. Figure 5 visually presents the assignment problem, where the circles on the left side represent the aircraft in the fleet and the squares on the right side represent the components in the inventory. The aircraft are the ‘sources’ that need to transport their product, which is flight time, to the right ‘destinations’, which are the serviceable components. The ‘supply’ of the aircraft, which is the QPA, must meet the existing ‘demand’ of the component inventory, while minimizing the number of changes in existing aircraft–component relations (substitutions). Using this similarity, the assignment problem for the CMP optimization model can be solved as any other transportation problem with the use of existing mathematical theory.

3.2.2. Residual Flight Time Relaxation

It is very unlikely that all component RFTs can be brought to exactly zero with a combination of the predetermined aircraft FTs. For this reason, the model must have freedom to dismiss the amounts of RFT necessary to prevent stalling of the cycle, as this would result in infeasibility. The necessary relaxation of RFT constraints could be realized by adjusting the FMP cycle. However, a more straightforward approach is to add an element that takes care of this problem before the COT is fed into the FMP cycle (Figure 4).

The new element provides the model with additional decision logic, as displayed in Figure 6. First of all, the result of subtracting the proposed COT from the RFT ($RF{T}_{t+1}$) is evaluated and compared with the operator-defined tolerance for dismissal. If the $RF{T}_{t+1}$ turns out to be larger than the tolerance, the COT will remain unchanged since the user does not allow dismissal of the RFT. In that case, the adjusted operating time, COT*, equals the original COT. In case the $RF{T}_{t+1}$ turns out to be equal to or smaller than the tolerance, the model is given two possibilities: 1. COT* equals COT, or 2. COT* takes the value of the RFT, which brings $RF{T}_{t+1}$ to zero. In all cases, COT* is fed into the FMP cycle. This provides the model with the necessary flexibility to keep the problem feasible while seeking for an optimal output. The amount of wasted residual flight time can be easily observed by evaluating COT*−COT.

3.2.3. Objective

In order to guide the described modeling framework toward a desired state, the dynamics must be complemented with a suitable objective function. The goal of the CMP optimization model is to maintain a state in which: (1) the availability of the component inventory is sufficient to support all scheduled flight operations of the aircraft fleet, (2) the component inventory follows a steady-state flow into preventive maintenance in order to smoothen preventive maintenance demand, and (3) minimum component substitutions on the aircraft fleet are required. A distinction must be made between substitutions on aircraft that are scheduled to be operational, non-operational, and unserviceable (base maintenance).

3.3. Mathematical Formulation

Now that the model dynamics and desired objective have been defined, the mathematical formulation of the model will be presented. The required parameters that contain the set of user-provided data are listed in

Table A1. CMP optimization model input parameters.

Parameter	Description	Domain
$AC$	Set of aircraft in the fleet, indexed by n;	$n\in AC$
$CPT$	Set of components in the inventory, indexed by c;	$c\in CPT$
T	Length of the planning horizon, indexed by t;	$t\in [1,T]$
$RF{T}_{max}$	Maximum residual operating time of a component, equal to the maintenance interval/TBM;
$RM{T}_{max}$	Maximum residual maintenance time of a component, equal to the maintenance duration/SMT;
$M{T}_{max}$	Maximum maintenance time on one component in one period, expressed in fraction of the period’s duration;
$SV{C}_{c,1}$	Binary parameter with value 1 if component c is serviceable at the start of period 1, and 0 if it is in preventive maintenance;	$c\in CPT$
$RF{T}_{c,1}$	Residual operating time of component c at the start of period 1;	$c\in CPT$
$RM{T}_{c,1}$	Residual maint. time of component c at start of period 1;	$c\in CPT$
$SVC{C}_c$	Binary parameter with value 1 if component c is serviceable at the start of period 1, and 0 if it is in corrective maintenance;	$c\in CPT$
$RMT{C}_c$	Residual corrective maint. time of component c at start of period 1;	$c\in CPT$
$FTA{C}_{n,t}$	Scheduled flight time of aircraft n in period t;	$n\in AC,t\in [1,T]$
$SVCA{C}_{n,t}$	Binary parameter with value 1 if aircraft n is scheduled serviceable at the start of period t, and value 0 if it is in maintenance;	$n\in AC,t\in [1,T]$
$OPRA{C}_{n,t}$	Binary parameter with value 1 if aircraft n is scheduled operational at the start of period t, and value 0 otherwise;	$n\in AC,t\in [1,T]$
$QPA$	Quantity per aircraft of the subject component;
$CF{G}_{n,c,1}$	Binary parameter with value 1 if component c is installed on aircraft n at the start of period 1, and value 0 otherwise;	$n\in AC,c\in CPT$
$COT/FT$	Ratio between component operating time and aircraft flight time;
$to{l}_{RFT}$	Fraction of the total component residual operating time that may be dismissed by the model if necessary, $\in [0,1]$;
$pe{n}_{OPR}$	Penalty for a substitution while the aircraft is scheduled operational;
$pe{n}_{SVC}$	Penalty for a substitution while the aircraft is scheduled serviceable;
$pe{n}_{MTX}$	Penalty for a substitution while the aircraft is scheduled for phase maintenance;
$W_1$	Weight factor required for bi-objective function, $\in [0,1]$;
$W_2$	Weight factor required for bi-objective function, $\in [0,1]$;
K	Arbitrary large number ($K>RF{T}_{max},RM{T}_{max},2$).

in Appendix A.

Table A2. CMP optimization model decision variables.

Variable	Description	Domain
$RF{T}_{c,t}$	Residual operating time of component c at the start of period t;	$c\in CPT,t\in [1,T+1]$
$RM{T}_{c,t}$	Residual maintenance time of component c at the start of period t;	$c\in CPT,t\in [1,T+1]$
$SV{C}_{c,t}$	Binary variable that takes value 1 if component c is serviceable at the start of period t, and 0 if it is in maintenance;	$c\in CPT,t\in [1,T+1]$
$F{T}_{c,t}$	Assigned operating time to component c in period t;	$c\in CPT,t\in [1,T]$
$M{T}_{c,t}$	Assigned maintenance time to component c in period t;	$c\in CPT,t\in [1,T]$
$M{S}_{c,t}$	Binary variable that takes value 1 if component c starts to receive maintenance in period t, and 0 otherwise;	$c\in CPT,t\in [1,T+1]$
$M{R}_{c,t}$	Binary variable that takes value 1 if component c finishes maintenance by the start of period t, and 0 otherwise;	$c\in CPT,t\in [1,T+1]$
$CF{G}_{n,c,t}$	Binary variable that takes value 1 if component c is installed on aircraft n in period t, and 0 otherwise;	$n\in AC,c\in CPT,t\in [1,T]$
$sub{s}_{n,t}$	Number of component substitutions on aircraft n in period t;	$n\in AC,t\in [2,T]$
$subs{1}_{n,c,t}$	Substitution scheme that takes value -1 or 1 if component c must be removed or installed, respectively, from/on aircraft n in period t, and value 0 otherwise;	$n\in AC,c\in CPT,t\in [2,T]$
$sub{s}_{tot}$	Total number of component substitutions over the planning horizon;
$sub{s}_{OPR}$	Total number of component substitutions while the affected aircraft is scheduled operational;
$sub{s}_{SVC}$	Total number of component substitutions while the affected aircraft is scheduled serviceable;
$sub{s}_{MTX}$	Total number of component substitutions while the affected aircraft is scheduled for phase maintenance;
$\mathit{costsubs}$	Total penalty cost for all scheduled component substitutions over the planning horizon;
$sus{t}_{min}$	Minimum sustainability over the planning horizon;
$P_{c,t}$	Auxiliary binary variable for component c in planning period t;	$c\in CPT,t\in [1,T]$
$Q_{c,t}$	Auxiliary binary variable for component c in planning period t;	$c\in CPT,t\in [1,T]$
$R_{c,t}$	Auxiliary binary variable for component c in planning period t;	$c\in CPT,t\in [1,T]$
$S_{n,c,t}$	Auxiliary binary variable for affected aircraft n and component c in planning period t;	$n\in AC,c\in CPT,t\in [2,T]$
$FT{1}_{c,t}$	Auxiliary variable for component c in period t.	$c\in CPT,t\in [1,T]$

, also given in Appendix A, lists the variables that may be determined by the model as a means to explore the solution space and maximize the objective function.

The model programming is listed in equation set (1)–(37). First of all, the objective function (1) attempts to smoothen the variability in sustainability while minimizing the inconvenience due to component substitutions, as explained in Section 3.2.3. The first term ($W_1·sus{t}_{min}$) maximizes the minimum sustainability over the planning horizon. The second term ($-W_2·\mathit{costsubs}$) minimizes the total substitution costs. Weights $W_1$ and $W_2$ are added to combine the two conflicting objective functions following the weighted sum method [36]. The weights may be varied as long as the sum of both weight stays equal until a desired outcome has been identified by the user. The first two constraints, (2) and (3), define the variables in the expression.

The second set of constraints, (4)–(14), solve the component assignment problem, which was explained in Section 3.2.1. Constraint (4) ensures that the number of components c that is assigned to each aircraft n in every period t equals the prescribed quantity per aircraft (QPA). Furthermore, constraint (5) ensures that each component can only be installed on one aircraft at a time. These are the two boundaries that must be satisfied by the model while assigning components to aircraft.

Maximize:

$$\begin{array}{cc}\hfill & W_1·sus{t}_{min}-W_2·\mathit{costsubs}\hfill \end{array}$$

(1)

Subject to:

$$\begin{array}{ccc}\hfill sus{t}_{min}& \le {\sum }_c^{}RF{T}_{c,t}\hfill & \hfill ,\forall t\in [1,T]\end{array}$$

(2)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathit{costsubs}& ={\mathit{pen}}_{OPR}·{\mathit{subs}}_{OPR}+{\mathit{pen}}_{SVC}·{\mathit{subs}}_{SVC}\hfill \\ \hfill & +{\mathit{pen}}_{MTX}·{\mathit{subs}}_{MTX}\hfill \end{array}\end{array}$$

(3)

$$\begin{array}{ccc}\hfill QPA& ={\sum }_c^{}CF{G}_{n,c,t}\hfill & \hfill ,\forall n\in AC,t\in [1,T]\end{array}$$

(4)

$$\begin{array}{ccc}\hfill 1& \ge {\sum }_n^{}CF{G}_{n,c,t}\hfill & \hfill ,\forall c\in CPT,t\in [1,T]\end{array}$$

(5)

$$\begin{array}{ccc}\hfill FT{1}_{c,t}& ={\sum }_n^{}(CF{G}_{n,c,t}·\lfloor FTA{C}_{n,t}·COT/FT\rceil )\hfill & \hfill ,\forall c\in CPT,t\in [1,T]\end{array}$$

(6)

$$\begin{array}{ccc}\hfill \mathit{subs}{\mathit{1}}_{n,c,t}& =CF{G}_{n,c,t}-CF{G}_{n,c,t-1}\hfill & \hfill ,\forall n\in AC,c\in CPT,t\in [2,T]\end{array}$$

(7)

$$\begin{array}{ccc}\hfill \mathit{subs}{\mathit{1}}_{n,c,t}& \le -1+K·(1-S_{n,c,t})\hfill & \hfill ,\forall n\in AC,c\in CPT,t\in [2,T]\end{array}$$

(8)

$$\begin{array}{ccc}\hfill \mathit{subs}{\mathit{1}}_{n,c,t}& \ge 0-K·S_{n,c,t}\hfill & \hfill ,\forall n\in AC,c\in CPT,t\in [2,T]\end{array}$$

(9)

$$\begin{array}{ccc}\hfill {\mathit{subs}}_{n,t}& ={\sum }_c^{}(\mathit{subs}{\mathit{1}}_{n,c,t}+S_{n,c,t})\hfill & \hfill ,\forall n\in AC,t\in [2,T]\end{array}$$

(10)

$$\begin{array}{cc}\hfill {\mathit{subs}}_{tot}& ={\sum }_n^{}{\sum }_{t=2}^T{\mathit{subs}}_{n,t}\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill {\mathit{subs}}_{OPR}& ={\sum }_n^{}{\sum }_{t=2}^T(OPRA{C}_{n,t}·{\mathit{subs}}_{n,t})\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill {\mathit{subs}}_{SVC}& ={\sum }_n^{}{\sum }_{t=2}^T((1-OPRA{C}_{n,t})·SVCA{C}_{n,t}·{\mathit{subs}}_{n,t})\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill {\mathit{subs}}_{MTX}& ={\sum }_n^{}{\sum }_{t=2}^T((1-SVCA{C}_{n,t})·{\mathit{subs}}_{n,t})\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill RF{T}_{c,t}-FT{1}_{c,t}& \le to{l}_{RFT}·RF{T}_{max}+Q_{c,t}·K\hfill & \hfill ,\forall c\in CPT,t\in [1,T]\end{array}$$

(15)

$$\begin{array}{ccc}\hfill RF{T}_{c,t}-FT{1}_{c,t}& \le RF{T}_{c,t}-1+Q_{c,t}·K\hfill & \hfill ,\forall c\in CPT,t\in [1,T]\end{array}$$

(16)

$$\begin{array}{ccc}\hfill F{T}_{c,t}& \ge FT{1}_{c,t}\hfill & \hfill ,\forall c\in CPT,t\in [1,T]\end{array}$$

(17)

$$\begin{array}{ccc}\hfill F{T}_{c,t}& \le FT{1}_{c,t}+(1-Q_{c,t})·K\hfill & \hfill ,\forall c\in CPT,t\in [1,T]\end{array}$$

(18)

$$\begin{array}{ccc}\hfill F{T}_{c,t}& \ge RF{T}_{c,t}-Q_{c,t}·K\hfill & \hfill ,\forall c\in CPT,t\in [1,T]\end{array}$$

(19)

$$\begin{array}{ccc}\hfill F{T}_{c,t}& \le RF{T}_{c,t}\hfill & \hfill ,\forall c\in CPT,t\in [1,T]\end{array}$$

(20)

$$\begin{array}{ccc}\hfill F{T}_{c,t}& \le SVC{C}_c·RF{T}_{c,t}\hfill & \hfill ,\forall c\in CPT\\ \hfill & \hfill & \hfill ,t\in [1,RMT{C}_c+SVC{C}_c]\end{array}$$

(21)

$$\begin{array}{ccc}\hfill K& \ge RF{T}_{c,t}+K·P_{c,t}\hfill & \hfill ,\forall c\in CPT,t\in [1,T]\end{array}$$

(22)

$$\begin{array}{ccc}\hfill SV{C}_{c,t+1}& \le (RF{T}_{c,t}-F{T}_{c,t})·K+K·P_{c,t}\hfill & \hfill ,\forall c\in CPT,t\in [1,T]\end{array}$$

(23)

$$\begin{array}{ccc}\hfill K& \ge RM{T}_{c,t}+K·R_{c,t}\hfill & \hfill ,\forall c\in CPT,t\in [1,T]\end{array}$$

(24)

$$\begin{array}{ccc}\hfill 1-SV{C}_{c,t+1}& \le (RM{T}_{c,t}-M{T}_{c,t})·K+K·R_{c,t}\hfill & \hfill ,\forall c\in CPT,t\in [1,T]\end{array}$$

(25)

$$\begin{array}{ccc}\hfill RF{T}_{c,t+1}& =RF{T}_{c,t}-F{T}_{c,t}+M{R}_{c,t+1}·RF{T}_{max}\hfill & \hfill ,\forall c\in CPT,t\in [1,T]\end{array}$$

(26)

$$$$

(27)

$$\begin{array}{ccc}\hfill M{R}_{c,t+1}& \ge SV{C}_{c,t+1}-SV{C}_{c,t}\hfill & \hfill ,\forall c\in CPT,t\in [1,T]\end{array}$$

(28)

$$\begin{array}{ccc}\hfill 0.1& \le SV{C}_{c,t+1}-SV{C}_{c,t}+1.1·(1-M{R}_{c,t+1})\hfill & \hfill ,\forall c\in CPT,t\in [1,T]\end{array}$$

(29)

$$\begin{array}{ccc}\hfill RM{T}_{c,t+1}& =RM{T}_{c,t}-M{T}_{c,t}+M{S}_{c,t+1}·RM{T}_{max}\hfill & \hfill ,\forall c\in CPT,t\in [1,T]\end{array}$$

(30)

$$\begin{array}{ccc}\hfill M{S}_{c,t+1}& \ge SV{C}_{c,t}-SV{C}_{c,t+1}\hfill & \hfill ,\forall c\in CPT,t\in [1,T]\end{array}$$

(31)

$$\begin{array}{ccc}\hfill 0.1& \le SV{C}_{c,t}-SV{C}_{c,t+1}+1.1·(1-M{S}_{c,t+1})\hfill & \hfill ,\forall c\in CPT,t\in [1,T]\end{array}$$

(32)

$$\begin{array}{ccc}\hfill 1-SV{C}_{c,t}& \le M{T}_{c,t}\hfill & \hfill ,\forall c\in CPT,t\in [1,T]\end{array}$$

(33)

$$\begin{array}{ccc}\hfill M{T}_{c,t}& \le M{T}_{max}\hfill & \hfill ,\forall c\in CPT,t\in [1,T]\end{array}$$

(34)

$$\begin{array}{ccc}\hfill RF{T}_{c,t}& \le SV{C}_{c,t}·RF{T}_{max},t\in [1,T+1]\hfill & \hfill ,\forall c\in CPT,t\in [1,T]\end{array}$$

(35)

$$\begin{array}{ccc}\hfill RM{T}_{c,t}& \le (1-SV{C}_{c,t})·RM{T}_{max},t\in [1,T+1]\hfill & \hfill ,\forall c\in CPT,t\in [1,T]\end{array}$$

(36)

$$\begin{array}{ccc}\hfill F{T}_{c,t}& \le SV{C}_{c,t}·RF{T}_{max}\hfill & \hfill ,\forall c\in CPT,t\in [1,T]\end{array}$$

(37)

As soon as the assignment has been completed, constraint (6) calculates the new component operating times. The operations carried out by this constraint can be mathematically expressed as follows for a single period ($t=\mathrm{constant}$) and $QPA=1$:

$$\begin{array}{c}\mathit{FT}{\mathbf{1}}_{\mathit{c}}^{\mathbf{⊺}}\\ c_1\\ c_2\\ c_3\\ ⋮\\ CPT\end{array}\left(\begin{array}{c}\\ CO{T}_{c_1}\\ CO{T}_{c_2}\\ CO{T}_{c_3}\\ ⋮\\ CO{T}_c\end{array}\right)=\sum _n^{}\left(\begin{array}{c}{\mathit{CFG}}_{\mathit{n}\mathbf{,}\mathit{c}}\\ n_1\\ n_2\\ n_3\\ ⋮\\ AC\end{array}\left(\begin{array}{ccccc}{c}_1& c_2& c_3& \cdots & CPT\\ 1& 0& 0& \cdots & 0\\ 0& 1& 0& \cdots & 0\\ 0& 0& 1& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \cdots & 1\end{array}\right)·\begin{array}{c}{\mathit{FTAC}}_{\mathit{n}}\\ n_1\\ n_2\\ n_3\\ ⋮\\ AC\end{array}\left(\begin{array}{c}\\ F{T}_{n_1}\\ F{T}_{n_2}\\ F{T}_{n_3}\\ ⋮\\ F{T}_n\end{array}\right)·COT/FT\right)$$

(38)

For every period, the binary configuration matrix $CF{G}_{n,c,t}$ is multiplied with the array $FTA{C}_{n,t}$ containing all scheduled aircraft flight times. The resulting $n\times c$ matrix is then multiplied with the $COT/FT$ conversion ratio in order to convert aircraft flight times to component operating times. The resulting values are rounded to the nearest integer to keep them suitable for numerical processing by a solver in a later stage. Finally, evaluation of the sum over n of the established matrix leads to the array $FT{1}_{c,t}$, which contains all component operating times for the concerning period.

Constraints (7)–(10) define two major outputs: the substitution scheme with installation and removal instructions and an overview of the number of component substitutions per aircraft per period. The first, $subs{1}_{n,c,t}$, is established by subtracting the configuration matrix of period $t-1$ from the configuration matrix of period t. $subs{1}_{n,c,t}$ is forced to 1 if component c is installed on aircraft n in period t, forced to −1 if component c is removed from aircraft n in period t, and forced to 0 otherwise. Furthermore, constraints (8) and (9) force auxiliary binary variable $S_{n,t,c}$ to 1 if $subs{1}_{n,c,t}$ is equal to −1 and to 0 otherwise. The sum of $S_{n,t,c}$ and $subs{1}_{n,c,t}$ now provides a binary array with a value of 1 for every installation only. Evaluating the sum of this array over all components, c, results in the aircraft substitution overview $sub{s}_{n,t}$. Both operations are carried out by constraint (10). The logic of this routine for all possible combinations is given in

Table 2. Aircraft substitution overview with supporting logic.

${\mathit{CFG}}_{\mathit{n},\mathit{c},\mathit{t}}$	${\mathit{CFG}}_{\mathit{n},\mathit{c},\mathit{t}-1}$	$\mathit{subs}1\mathit{n},\mathit{c},\mathit{t}$	Constr. (8)	Constr. (9)	${\mathit{S}}_{\mathit{n},\mathit{t},\mathit{c}}$	${\mathit{subs}}_{\mathit{n},\mathit{t}}$
		$={\mathit{CFG}}_{\mathit{n},\mathit{c},\mathit{t}}-{\mathit{CFG}}_{\mathit{n},\mathit{c},\mathit{t}-\mathbf{1}}$	${\mathbf{S}}_{\mathit{n},\mathit{t},\mathit{c}}$	${\mathbf{S}}_{\mathit{n},\mathit{t},\mathit{c}}$		$=\mathit{subs}{\mathbf{1}}_{\mathit{n},\mathit{c},\mathit{t}}+{\mathbf{S}}_{\mathit{n},\mathit{t},\mathit{c}}$
1	1	0	0	0, 1	0	0
1	0	1	0	0, 1	0	1
0	1	−1	0, 1	1	1	0
0	0	0	0	0, 1	0	0

.

Constraint (11) counts the number of component substitutes over the full planning horizon by summing $sub{s}_{n,t}$ over all aircraft and periods. Constraints (12)–(14) differentiate component substitutes that are scheduled when the affected aircraft is operational, non-operational, and unserviceable due to base maintenance, respectively.

Constraint set (15)–(19) takes care of the residual flight time relaxation decision logic, which was explained in Section 3.2.2. First of all, constraint (15) evaluates $RF{T}_{c,t+1}$ by subtracting the anticipated COT ($FT{1}_{c,t}$, which is the output of the assignment problem) from the $RF{T}_{c,t}$. If $RF{T}_{c,t+1}$ turns out to be larger than the set tolerance for RFT dismissal, the auxiliary binary variable $Q_{c,t}$ will be forced to 1. If $RF{T}_{c,t+1}$ turns out to be within the tolerance instead, $Q_{c,t}$ can either take a value of 0 or 1. Subsequently, constraints (17)–(19) ensure that the adjusted component operating time, COT* ($F{T}_{c,t}$ in the formulation), is set equal to the COT in case $Q_{c,t}=1$ and set equal to the $RF{T}_{c,t}$ in case $Q_{c,t}=0$. Since $Q_{c,t}$ can be either 0 or 1 when the tolerance requirement is met, the model is provided freedom to decide whether or not to dismiss residual flight time. Constraint (16) ensures that this routine only provides output for the components that had operating time assigned ($FT{1}_{c,t}\ge 1\mathrm{if}{Q}_{c,t}=0$).

Constraint 21 withdraws components that are unserviceable due to corrective maintenance from the assignment problem. This is established by forcing $F{T}_{c,t}$ to zero if $SVC{C}_c$ is zero at the start of the planning horizon and keeping this setting for the duration of the anticipated residual corrective maintenance time $RMT{C}_c$.

The following constraint set, (22)–(32), embodies the actual flight and maintenance planning process. First of all, constraints (22)–(25) make sure that the serviceability at the start of the next period ($SV{C}_{c,t+1}$) takes the proper value. When the residual operating time is larger than zero, constraint (22) forces $P_{c,t}$ to zero. Subsequently, constraint (23) makes sure that the serviceability during the next period is forced to zero whenever $P_{c,t}=0$ and the residual operating time is equal to the assigned operating time in the current period. In a similar way, constraints (24) and (25) force the serviceability during the next period to 1 when the residual maintenance time is larger than zero and the assigned maintenance time is equal to the residual maintenance time in the current period. Following this routine, the serviceability in period t is set to zero when component c is in maintenance, and it is set to one when the component is available for installation on an aircraft.

Constraints (26)–(29) make sure that the residual operating time at the start of the next period is updated based on the residual operating time and the assigned operating time in the current period. Constraint (26) subtracts the assigned operating time from the residual operating time. Additionally, it resets the residual operating time to its maximum value ($RF{T}_{max}$) when the maintenance work on component c is ready by the start of the next period. In order to indicate when the maintenance work is ready, constraints (28) and (29) force $M{R}_{c,t+1}$ to 1 if component c becomes serviceable at the start of the next period and to zero otherwise. The logic of these constraints is further clarified in

Table 3. Constraint (26)–(29) logic.

		Constr. (28)	Constr. (29)
${\mathit{SVC}}_{\mathit{c},\mathit{t}+\mathbf{1}}$	${\mathit{SVC}}_{\mathit{c},\mathit{t}}$	${\mathit{MR}}_{\mathit{c},\mathit{t}+\mathbf{1}}\ge$	${\mathit{MR}}_{\mathit{c},\mathit{t}+\mathbf{1}}$	${\mathit{MR}}_{\mathit{c},\mathit{t}+\mathbf{1}}$
1	1	0	0	0
1	0	1	0, 1	1
0	1	−1	0	0
0	0	0	0	0

.

Following the same procedure, constraints (30)–(32) update the residual maintenance time at the start of the next period based on the residual maintenance time and the assigned maintenance time in the current period. Again, constraint (30) subtracts the assigned maintenance time from the residual maintenance time to create the new value of the residual maintenance time for the next period. When component c starts to receive maintenance in the next period, the updated value of $M{S}_{c,t+1}$ (due to constraints (31) and (32)) forces the residual maintenance time to its maximum value ($RM{T}_{max}$).

Constraint (33) makes sure that each component will start to receive maintenance immediately after it becomes unserviceable. Constraint (34) puts an upper limit on the amount of maintenance time that can be assigned to a component during a single period. The parameter $M{T}_{max}$ is expressed as a fraction of the period’s duration, so $M{T}_{max}=1$ represents a full time workforce period, and $M{T}_{max}=2$ represents a full time maintenance period in a double shift. This parameter thus allows the user to evaluate the impact of single- versus double-shift maintenance allocation in the component maintenance shop.

Finally, constraint set (35)–(37) imposes necessary boundaries to the model dynamics. First, constraint (35) makes sure that the residual operating time of each component stays between zero (in case $SV{C}_{c,t}=0$) and the maximum residual operating time. Similarly, constraint (36) forces the residual maintenance time of each component between zero (in case $SV{C}_{c,t}=1$) and the maximum residual maintenance time. Finally, constraint (37) fixes the operating time to zero in case the component is unserviceable and keeps it below the maximum residual operating time in case the component is serviceable.

4. Results

The following section describes the application of the CMP model for several real problem instances.

4.1. Dataset Characteristics

For this paper, the CMP model was implemented for real problem instances drawn from the Royal Netherlands Air Force (RNLAF) in three consecutive years in the past: 2011–2013. In order to demonstrate the performance of the model, the model outputs were compared with the actual RNLAF actions and associated results in terms of component serviceability and sustainability, effectively enabling a comparison of the real-life, benchmark scenario with a hypothetical scenario where the CMP model outputs would have been adopted over the considered 3-year period. For this reason, actual input data were made available for all parameters in Table A1, related to the Honeywell T55-L-714A gas turbine engine, which is installed in the RNLAF CH-47 Chinook helicopter fleet.

The planning horizon, T, comprises a one year period divided into 13 4-week periods, where the 4-week periods are defined in relation with the related maintenance requirements but also assist in the computational performance of the model (see Section 4.4). The $RF{T}_{max}$ for the T55 engine is 1500 operating hours due to the mandatory overhaul. The $RM{T}_{max}$ was determined to be 24 weeks (6 4-week periods), which is based on the actual average turnaround time. As a rule of thumb, the used threshold for dismissal of $RFT$ is $10\%$, so $to{l}_{RFT}$ is set to 0.1. The ratio between engine operating time and aircraft flight time was statistically determined to be $105\%$. Each CH-47 is equipped with 2 T55 gas turbine engines ($QPA=2$). For this model implementation, the penalties for substitutions while the affected aircraft is scheduled to be operational, non-operational, and unserviceable are set to 100, 10, and 1, respectively. The fleet and inventory arrangement, initial status, and operational values are kept out of this paper for confidentiality reasons.

4.2. Results and Validation

For the model calculations, the real input values for the actual RNLAF situation on 1 January of the years 2011–2013 were used. The model formulation and input parameters are programmed in the AMPL mathematical programming language [37] and solved using the Gurobi solver [38] on a remote high-performance machine available through the NEOS server [39].

In order to fully demonstrate the model’s capabilities, two separate model runs were performed for the RNLAF Chinook problem. Run 1 utilized the real starting input for the years 2011–2013 to validate model performance through a comparison with actual RNLAF figures. However, the starting points for each year are presumed to be suboptimal, which is a downside as they ‘anchor’ the model on an annual basis and leave optimization potential unexplored. In order to work around this drawback, we ran 2 optimizations for multiple years at once while disregarding the objective function values for the first year but still satisfying all constraints. Following this approach, the model has freedom to adjust the sustainability during year 1 in order to produce a maximized and steady-state situation by the start of year 2, leading to better results.

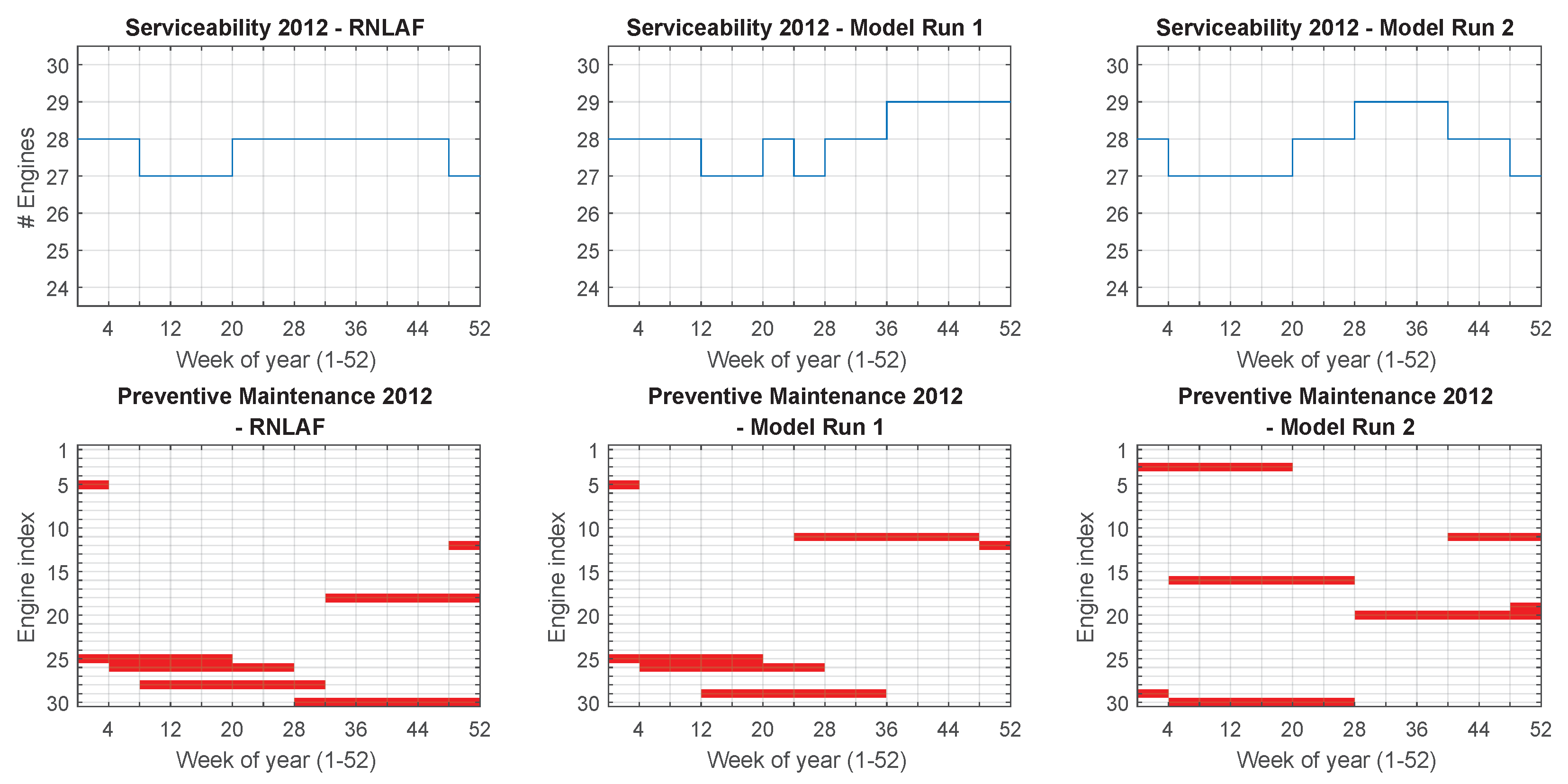
4.2.1. Serviceability and Preventive Maintenance Schedule

In this paper, serviceability is defined as the number of components that are in mission-capable condition at a specific instant of time. For this problem implementation, the serviceability equals the number of engines in the inventory that are available for installation and service on operational aircraft. Since the CMP model takes into account scheduling of preventive maintenance, a specific component is unserviceable if it is scheduled for preventive maintenance at that instant of time, and the component is serviceable otherwise.

Figure 7 provides graphical representations of the output of model runs 1 and 2 for the year 2012 compared to the RNLAF performance. The three plots displayed in the upper half of the figure show the development of the serviceability over the planning horizon. The range of the horizontal axis equals the one-year planning horizon split by 13 4-week periods. The vertical axis displays the number of engines, which is bounded by 30 since this is the inventory size and by 24 as this was found to be the overall minimum achieved serviceability and thus an appropriate lower limit of the axis. The serviceability is represented by the blue line.

The three plots in the lower half of Figure 7 graphically represent the preventive maintenance schedule over the planning horizon. The range of the horizontal axis again equals the one-year planning horizon split by 13 4-week periods. The vertical axis projects the indices of all 30 engines that comprise the inventory. The red bars represent periods of unserviceability due to the preventive maintenance of the corresponding engines. As defined through the input parameter $RM{T}_{max}$, each preventive maintenance effort lasts 24 weeks.

Figure 7 shows that the preventive maintenance schedule that is the output of model run 1 is similar to the schedule resulting from the baseline effort. The minimum serviceability is equal at 27 engines. However, model run 1 achieves a higher serviceability from week 36 onward by implying 3 scheduling changes compared to the baseline. Engine $\#28$ is substituted for engine $\#29$, which enters maintenance 4 weeks later. Engine $\#30$ is swapped for engine $\#11$, which is due for maintenance 4 weeks earlier. Maintenance on engine $\#22$ turns out to be undesired. The maintenance schedule for run 2 is not directly comparable to the baseline and run 1, as it uses a different (optimized) starting point. However, the bandwidth in serviceability, here denoted as $\Delta SVC$, turns out to be identical to run 1. All three FMP efforts result in the completion of 5 preventive maintenance actions in 2012.

4.2.2. Sustainability

In this paper, sustainability is defined as the sum of the residual operating times of all serviceable components in the inventory. It is of importance to maintain an adequate level of component inventory sustainability at all times. This enables the operator to support flight operations into the future.

Figure 8 provides the output of model runs 1 and 2 for the year 2012 compared to the actual RNLAF performance. The three plots displayed in the upper half of the figure show a representation of the ’flow’ into preventive maintenance. The horizontal axis shows the indices of all 30 engines in the inventory, and the vertical axis projects the residual operating time of each engine. The range of the vertical axis is bounded by the $RF{T}_{max}$, which equals 1500 engine operating hours, and zero. Five separate colored lines represent the PM flow at different moments in time: one for the situation at $t=1$ and one for the end of each quarter. The dotted red line along with a gray bar plot project the mean PM flow over the duration of the planning horizon. Furthermore, the dotted black line represents the ideal PM flow. The plot in the upper left corner shows this information for the RNLAF performance, and the two plots beside show the output PM flows of the model.

The three plots in the lower half of Figure 8 represent the distribution of sustainability over the planning horizon. The range of the horizontal axis equals the one-year planning horizon. The total residual operating time (expressed in engine operating hours) of the inventory is projected on the vertical axis and provides a measure of the sustainability. The blue curves represent the actual sustainability, the red curves show the mean values, and the green line projects the minimum sustainability achieved. Again, the black dotted line represents the ideal sustainability based on the input parameters.

The surface below the PM flow curve equals the sustainability at that point in time. As a result, the surface below the mean PM flow equals the mean value of the sustainability. Hence, the two plots are different representations of the same information.

Slight improvements are observed in Figure 8 of model run 1 compared to the RNLAF simulation for 2012. Just one additional engine substitution enables the model to schedule the preventive maintenance efforts such that the production and consumption of operating hours remain nicely balanced for the duration of the planning horizon. Figure 8 clearly shows the model spreads maintenance more equally over the year. This way, the sustainability is brought up with $3.6\%$, and the bandwidth in sustainability, $\Delta sust$, is decreased by $40.5\%$. Nevertheless, the mean PM flow shows a clear dip below the ideal curve, which is also reflected by a low mean sustainability compared to the ideal line. This shows that although the model does a good job smoothing the maintenance actions over the planning horizon, the achieved sustainability remains well below the target level.

It is apparent that model run 2 performs better in terms of sustainability, which is mainly due to a better starting condition. The PM flow curve is brought very close to the ideal curve, and the minimum scheduled sustainability is increased by $14.6\%$. The $\Delta sust$, however, is also increased by $24.0\%$. The mean sustainability is brought to a much more appropriate level above the ideal sustainability, which only required 6 engine substitutions. This is half the number that was required for the RNLAF simulation of the same year, which emphasizes the influence of the improved starting condition for run 2.

4.3. Overall Results

Table 4. Numerical results of the CMP optimization model with respect to serviceability, sustainability and number of substitutions for the years 2011–2013. Actual RNLAF results (left) are presented alongside the results of two optimization model runs for the same years (middle and right).

Parameter	2011			2012			2013
[hrs]	RNLAF	Model 1	Model 2	RNLAF	Model 1	Model 2	RNLAF	Model 1	Model 2
$SV{C}_{min}$	27	27	27	27	27	27	24	25	28
$SV{C}_{max}$	30	30	30	28	29	29	30	29	30
$\Delta SVC$	3	3	3	1	2	2	6	4	2
$sus{t}_{min}$	17,714	19,992	19,772	17,448	18,074	19,993	19,812	19,815	20,037
$sus{t}_{max}$	22,724	22,724	22,724	20,069	19,633	23,243	26,900	26,892	21,930
$\Delta sust$	5010	2732	2952	2621	1559	3250	7088	7077	1893
$sub{s}_{tot}$	3	8	13	12	13	6	8	8	5

gives the overall numerical results of the model runs for the three years. This includes serviceability, sustainability, and the number of engine substitutions required to achieve the optimal outcome.

4.4. Computational Analysis

The required computational time per run was found to be between 4 and 8 h, depending on the input problem (year), using remote computers on the NEOS server [39] equipped with two 2.8 GHz (12 cores total, HT-enabled) processors and 64 GB of RAM.

The model must determine the optimal assignment of components to aircraft, which entails a large number of possible combinations. As elaborated in Equation (39), there exist approximately $5.9·{10}^6$ different possibilities to assign a subset out of 30 engines to 22 aircraft positions. Since the assignment problem must be solved for each single period, the number of periods covered in the planning horizon T is the main driver of problem complexity and computational lead time.

$${\left(\begin{array}{c}30\\ 22\end{array}\right)}^T={\frac{30!}{22!·8!}}^T={5852925}^T$$

(39)

4.5. Assumptions and Limitations

The proposed CMP optimization model must be comprehensive and widely applicable, while at the same time understandable and tractable. As a result, the model in its basic form is subject to a number of assumptions and limitations:

• For the assignment problem, the model does not distinguish between separate components in the inventory. As a result, all serviceable components are assumed to be equivalent and interchangeable in terms of form, fit and function.
• The model can take into account a single component type at a time. Multiple model runs are required to optimize for different components. While the output of multiple runs will be aligned with the aircraft-level FMP, the maintenance of multiple components will not be optimized relative to each other (i.e., component maintenance interventions may not overlap or align).
• The model does not take into account maintenance capacity constraints, since aircraft component maintenance work can usually be sourced to multiple parties.
• The model can handle one set of maintenance requirements, which means that TBM and SMT are assumed to be constants. As a result, the model can handle one type of standardized maintenance work.
• The model is relevant for components maintained under a hard-time maintenance policy or a predictive maintenance policy with sufficiently long prediction periods; for those cases, planned substitutions make sense. The model would have to be adapted to incorporate on-condition maintenance policies.

5. Conclusions

Preventive maintenance of aircraft components must be scheduled in such way that mission readiness is ensured. This paper proposed a mixed integer linear programming model that optimally solves the component flight and maintenance planning problem for defense aviation operators using component substitution scheduling. In doing so, this model addresses several major gaps in the current state of the art as highlighted before.

The established model formulation takes into account all relevant requirements with respect to aircraft operations and component maintenance. Furthermore, the assignment of components to aircraft (assignment problem), necessary dismissal of residual operating time, and unavailability due to corrective maintenance have been addressed. An objective function was defined that attempts to develop a steady-state situation with stable sustainability and smooth maintenance demand against minimum inconvenience due to component substitutions.

The CMP optimization model was found to assign components to operational aircraft and to preventive maintenance in such way that:

• All mandatory preventive maintenance requirements were fulfilled at all times in order to satisfy safety and reliability standards throughout the components’ lifetime;
• All operational requirements of the subject aircraft fleet were fulfilled at all times through the continuous provision of serviceable components to all operational aircraft;
• The availability of the component inventory could be significantly increased in terms of serviceability and sustainability. Model run 1 increased the overall minimum serviceability by $4.2\%$, and run 2 managed to increase the same parameter by $12.5\%$. Sustainability was increased by up to $14.6\%$;
• A smooth and steady-state flow of components into preventive maintenance was established in order to improve maintenance resource planning. The variability on overall preventive maintenance demand was decreased by $33\%$ and $50\%$ by model run 1 and run 2, respectively. This allows both the operator and maintenance station to better anticipate required future logistics and capacity, which ultimately reduces the risk of logistical delay and maintenance overflow. Furthermore, the model demonstrated that variability on financial expenses could be decreased by up to $80\%$, which leads to significant budgetary benefits;
• Unnecessary waste of component operating time due to early withdrawal from service was prevented by providing the model with decision logic based on a threshold for dismissal. The operator remains in control of this process, since the threshold is an operator-defined input parameter;
• The maintenance burden due to component substitutions was minimized by introducing a cost function. This function induces a cost penalty for each component substitution relative to the state of the affected aircraft. It was demonstrated that model run 2 even managed to produce improved scheduling results compared to the RNLAF against lower overall substitution costs.

The CMP optimization model provides any military or response-driven aircraft operator with the capability to generate optimized component flight and maintenance schedules. The interconnection between the aircraft and CMP optimization models ensures that the flight and maintenance planning processes on both levels are executed effectively and coherently. The fast and efficient generation enables the operator to cope with unforeseen circumstances and unpredictability. Furthermore, the model provides an adequate tool for experimentation with different organizational scenarios (e.g., adding or removing spare components to the inventory, in- and outsourcing of component maintenance capability, tweaking maintenance turnaround times, etc.) and long-term forecasting of preventive component maintenance demand.

The mathematical formulation in its current form provides a strong foundation for the further development of more complex or wider adaptable CMP optimization models. In terms of future directions, in particular for larger fleet sizes or longer problem horizons, which increase problem size, the use of appropriate meta-heuristics may be required. Furthermore, future research can be targeted towards the capability to optimize flight and maintenance planning including multiple different components in an integrated fashion. This integration may consider independent components but may also meaningfully address the issue of dependencies, especially when considering system hierarchies involving multiple ’layers’ from system to subsystem to components to individual parts.