1. Introduction
The inspection of aircraft engines is often an extensive and time-consuming task, which is usually carried out manually by trained personnel. In particular, the inspection in confined spaces is in many cases performed manually using handheld video endoscopes and is based on subjective assessments, which may depend on their respective inspector. Therefore, such applications can benefit significantly from automated assistance systems, that enable defined and objective assessments. In this study, a coating damage inspection, which outputs 2D RGB video data from the manual inspection process, is automated by the application of convolutional neural networks (CNNs) for the segmentation of these damages.
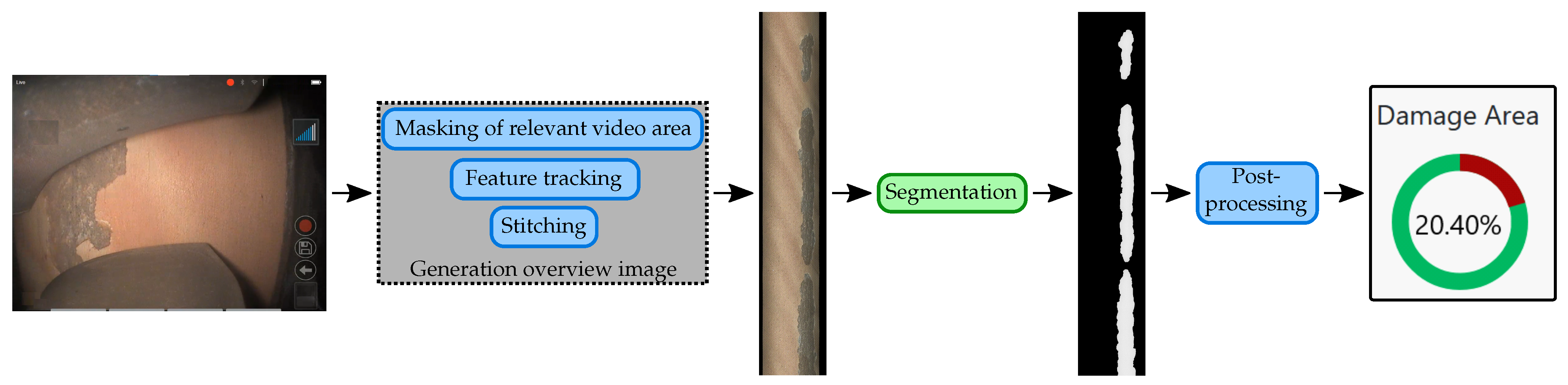
The software application comprises a pipeline, which processes the inspection videos and outputs quantified and visualized damage assessments. This pipeline is depicted in
Figure 1. To enable an adequate quantification of the coating damages, an overview image is generated depicting the whole coating area to be analyzed. For this, the relevant area showing the potential coating area in the video frames is detected and masked. Subsequently, feature tracking, registration and stitching algorithms are applied on the video frames to generate the overview image. After these preprocessing steps, the damage segmentation is performed. This task comprises the application of a CNN or methods applying several CNNs to achieve adequate segmentation results. This damage segmentation thus represents the focus of this study. After the postprocessing steps, the software provides the relative detected damage area and a visualization of the segmentation results. In the end, this software tool can then be utilized within the current inspection process to assist the personnel with the coating analysis and further decision making.
Due to considerable effort in annotating the data, the quantity of image data available for training and validation is limited. Additionally, the image data exhibit significant variations in feature characteristics (e.g., damage and coating) and interference caused by stray light, varying camera positions, motion blur and image compression. Considering the application in aircraft maintenance, this use case demands a robust and adaptive segmentation algorithm. Since conventional computer vision algorithms could not sufficiently detect the coating damages due to the described challenges (evaluated in preliminary investigations), CNNs are implemented. These are particularly suitable due to their adaptability and robustness to environmental influences in the image data. Therefore, different methods are proposed in this study to increase the segmentation accuracy and certainty, by combining the advantages of two CNNs in a pipeline. Specifically, both networks are trained each for a different field of view (FOV), to address the segmentation of the large overview images at different scales. To combine the differing advantageous properties of both CNNs, a two-stage segmentation pipeline is proposed where the first network provides an initial segmentation which is further optimized by a second network at another scale range. The focus of this study is therefore on the methodical application of both networks to generate an optimized segmentation mask and therefore increase the overall accuracy and certainty.
The application of segmentation networks in several stages and different field of views (FOVs) has already been examined in different ways. Wang et al. [
1] proposed a two-stage 3D U-Net framework which defined a region of interest (ROI) in a first stage using downscaled images. In the second stage, a detailed segmentation of the image data in the detected ROI was performed. A similar approach was proposed by Amiri et al., where a comparable two-stage method was applied with U-Nets on breast ultrasound images [
2]. All these approaches aimed for an ROI detection followed by a detailed segmentation of the relevant objects. For the application on which this study is based, these approaches are not applicable since a detailed segmentation of the whole high-resolution image is required. Zhao et al. [
3] introduced a method which evaluated the whole image by two consecutive networks. In a first stage, an attention network was applied. The resulting output, an attention map of the whole image, was then forwarded to a U-Net-like segmentation network. Huang et al. [
4] proposed a novel network structure which created a segmentation and distance map in a first stage. Subsequently, these outputs were concatenated and forwarded into a second segmentation network. Another approach for combining several networks is given by ensemble learning. For instance, Guo et al. [
5] proposed an ensemble learning method, where a weighted voting was implemented to create an ensemble from the segmentation results of several CNNs with different encoder–decoder structures. For this, the networks were applied on the same image data and the results were combined by a weighted voting algorithm. Another ensemble learning technique was proposed by Liu et al. [
6], where an ensemble of several CNNs with identical network architecture but different loss functions applied in training was created. Additionally, a preceding network was used on a large FOV to determine the ROI for the subsequent ensemble application. Setting the whole overview image as the input of the first network is not beneficial nor applicable for the task presented in this study. This is due to the high resolution of the overview images (approx. 1024 × 50,000 pixels), which would require either a considerable downscaling or a large network size. In both cases, preliminary investigations revealed that the accuracy was reduced significantly. Additionally, the overview images differ in width and height, which would complicate an analysis without any loss of information with respect to the downscaling. Therefore, this study proposes a novel method, where the whole area of large individual high-resolution images is analyzed in detail without focusing on one specific region (e.g., ROI).
2. Problem Definition and Hypothesis
The task of a damage inspection using handheld endoscopes poses different challenges when considering a robust automation while a wide range of environmental perturbations are present. The inspection is based on video endoscopes with a chip-on-the-tip design of two different manufacturers. In both devices, the image sensor has a resolution of 1024 × 768 pixels. The other specifications differ.
The tip is manually fixed inside the aircraft engine, which results in differing camera positions. The coating area is located around the circumference of the rotor, which is rotated by hand or semiautomatically during the recording of the video. Due to the large radius of the rotor, this rotation results in an approx. translational motion with a differing velocity of the coating area through the FOV of the camera. The recorded video contains at least a full rotation of the rotor. The camera position is fixed during this process. Since the segmentation of the coating damage area in the video frames does not lead to a precise quantification of the whole area, this entire coating area must be stitched together from the video frames first (refer to
Figure 1). Due to the varying camera position and uncertainties in the stitching process, the resulting overview images differ in shape and size. Therefore, these overview images, which are stitched out of approx. 5000 video frames, have a height ranging from approx. 40,000 to 60,000 pixels. The underlying video data exhibit highly varying properties due to changing environmental variables as well as diverse damage and coating feature occurrences. The environmental variables comprise differing lighting conditions (inhomogeneous illumination of the FOV), camera positions (angle of view, FOV) and movement speed of the coating area, which results in a varying motion blur effect. Additionally, the images feature MP4-compression artifacts due to the restricted video export settings of the applied commercial instrument [
7]. Finally, potential registration or stitching uncertainties as well as the inhomogeneous lighting lead to artifacts in the stitched overview image [
8]. These perturbations result in an increased difficulty for computer vision algorithms and can lead to reductions in segmentation accuracy.
The basis of the quantifiable inspection of the coating area is a binary semantic segmentation task, since only the classes coating damage and intact coating are distinguished. A further specification of damage class or intensity is not useful, as examinations of all available video data have indicated that only one damage class is present, and varying intensities does not provide any further information (e.g., cause of damage). For the considered task, CNNs are particularly suitable, especially due to the challenging fluctuations within the environmental conditions. Therefore, an established encoder–decoder structure was used to predict a binary segmentation mask from an RGB input image with a fixed size. Due to the differing shape of the coating area and its large size, the overview image has to be divided into smaller patches [
8].
All image data used in this work were annotated by trained personnel to allow an accurate evaluation regarding the optimal damage detection. Furthermore, a state-of-the-art encoder and network structure was used to allow a comparison to established baseline methods. Therefore, in all evaluations, the proposed method was compared to the baseline, which was the application of this single-network structure. In order to set the scope of this study specifically on the methodical network application, only this one exact architecture and input size were considered in the proposed method. As a result, the FOV of the input image could only be increased while downscaling the image patch accordingly. Preliminary investigations showed that the FOV and an eventual downscaling of the image data had a significant impact on the resulting accuracy of an applied CNN. Specifically, at different damage and coating properties, these parameters resulted in significant accuracy variations. When further investigated, the following hypothesis could be made: networks achieved higher accuracies if both classes (coating damage and intact coating) were present with a significant number of pixels. This applied especially for networks without a preceding downscaling and thus a smaller FOV, which in turn increased the probability of having only one class present. These networks (without any downscaling) are later referred to as small-scale networks. On the other hand, networks with an input downscaled from larger image patches (later referred to as large-scale networks) featured a larger FOV. This led to a higher probability of both classes being present in an input image, as well as a potentially greater diversity of features needed for a precise prediction. However, details such as fine surface structures were omitted due to the downscaling. Additionally, the resulting segmentation mask had the same downscaled resolution, which may evoke further inaccuracies. Therefore, this study proposes the integration of the two network types into a coherent pipeline for the detailed segmentation of overview images in order to incorporate the mentioned advantages of both types (small-scale and large-scale). Within this pipeline, the overview image is analyzed in different patch sizes with respect to the FOV. The pipeline is designed to directly address the hypothesis that the number of pixels per class has an influence on the segmentation accuracy. For this, by utilizing the segmentation result of a large-scale network, the application of a small-scale network can be optimized to maximize the accuracy. This optimization specifically comprises methods to receive patches with an adequate number of pixels of both classes.
3. Materials and Methods
This section presents prerequisite information for the following experiments regarding the underlying configurations and proposed methods. This comprises the properties of the dataset, experimental settings and a broad description of the proposed methods.
3.1. Dataset
The video data in this study were obtained from handheld endoscopes applied in the confined spaces of aircraft engines. Therefore, the videos differed significantly regarding lighting conditions, endoscope type and camera/tip position. Additionally, the video data featured noise and artifacts due to an inevitable MP4-compression [
7]. As stated in the previous section, the video frames were stitched together to generate a large overview image of the whole coating area to enable an adequate quantification of the damage area. These overview images had a resolution of approx. 1024 × 50,000 pixels (width × height). However, the applied segmentation networks required smaller input images and therefore, the overview images were divided into smaller image patches. In preliminary investigations, an input resolution of 384 × 256 pixels was proven to be optimal regarding the overall accuracy. This investigation was conducted with the same experimental settings as stated in the following. Additionally, a downscaling factor could be applied to get an increased FOV while keeping the same input image resolution. Since in this work, the proposed two-stage pipeline analyzed the overview images with different downscaling factors, the datasets were built accordingly. In total, four configurations were evaluated in this study. These were, on the one hand, a configuration without any downscaling, and on the other hand three configurations with considerable downscaling factors to achieve a significant distinction in the respective FOVs between the small-scale network and large-scale network. All three downscaling factors were selected so that the whole width of the overview image was covered and, depending on the target input image aspect ratio and orientation, a differing height of the overview image was covered. In all configurations the input image size (number of pixels) was the same. The exact parameters are listed in
Table 1. Example images of all used configurations are depicted in
Figure 2.
In total, there were 26 annotated overview images resulting in 11,047 image patches of the nonscaled dataset. The number of image patches for the downscaled datasets continuously decreased with their downscaling factor (refer to
Table 1). The overview images were assigned to either the training & validation or the test dataset. The overview images in the training & validation dataset were bisected horizontally and assigned to either the training or validation dataset. Then, the resulting image patches of the sorted overview images were extracted for the application in training. The images used for testing were only seen by the CNN in a separate test procedure, where images and network were loaded independently. In all training processes in this study, 20 overview images (approx. 77%) were assigned to the training & validation dataset and 6 overview images to the test dataset. With the subsequent patching of these overview images, it should be considered that approx. 50% of the patches regarding each overview image for training & validation were used for training while the others were used for validation. This whole procedure was developed in preliminary investigations and succeeded over a standard randomized distribution of the extracted image patches.
The image data were normalized and augmented during the training process. The normalization was performed with respect to the mean and standard deviation of the whole training dataset for each channel separately. The data augmentation comprised typical geometric transformations, noise, blurring, color channel manipulations and the CutMix operation, where random regions were cut out and inserted randomly over the images of one batch [
9]. The geometric transformations included flipping, rotating, shifting and cropping operations. The color channel manipulations comprised a randomly applied histogram equalization and value shifts within each color channel. The applied augmentations are exemplarily depicted in
Figure A1.
3.2. Experimental Settings
All networks, training and evaluation methods were executed with the same configurations and hyperparameters, if not stated otherwise. In particular, the networks, regardless of their input image properties, had the same size and structure to set the focus on the hypothesis and the proposed methods. Therefore,
DeeplabV3+ [
10] was used with a
RegNetY-120 encoder [
11]. With the standard input image size, this network structure had 53,000,762 trainable parameters, which were initialized with ImageNet weights in all training processes. The network output had per default no activation layer to receive the logit values of each class as the output. Subsequently, the binary segmentation could be extracted.
The used datasets in this study only had a few image data (refer to
Table 1). Further, the available image data had a high diversity regarding the relevant features and possible perturbations. This led to high fluctuations of the resulting accuracy measurement evoked by, e.g., the distribution of the overview images into training and test datasets. Therefore, all experiments in this study were executed with 30 iterations to consider and identify these influences. Additionally, the experiments and evaluations conducted in this study were fully reproducible and deterministic due to the seeding of every function and randomized calculation (including calculations executed on the GPU). The code was written in
Python using the
PyTorch framework and the
Segmentation Models Pytorch repository by Iakubovskii et al. [
12].
As the loss function, a compound function of the binary cross-entropy and the dice similarity coefficient was used in all training procedures [
13,
14]. On the one hand, the binary cross-entropy, which is typically used in most training procedures of segmentation networks, provides continuous and smooth gradients of the prediction error [
15,
16]. With the dice loss, on the other hand, the input class imbalance problems can be handled [
15,
16]. The class distribution in the present dataset equaled approx. 23.97% (of class coating damage in terms of the relative number of pixels of the relevant area). The dice loss is defined as follows:
Here,
N is the number of images in the respective batch,
g is the ground truth,
s is the prediction and
is the sigmoid activation function [
13,
17]. Accordingly, the binary cross-entropy loss is defined as [
13,
16]:
The weighted sum or compound loss function is then defined as follows [
13]:
The setup of the described loss function and its weights was based on results of preliminary investigations, where the weights were determined iteratively regarding a baseline training of a single segmentation network with the described experimental settings. For all accuracy calculations, the standard dice coefficient was used. In all experiments, the accuracy was measured on the stitched segmentation mask with respect to the full overview image. This ensured a correct comparison between the proposed pipeline and the single networks. Segmentation masks obtained from downscaled images were always upscaled again to execute the accuracy calculation with the same resolution. Finally, the same optimizer with the following initialization parameters was used in all training procedures:
AdaBelief (learning rate (
):
, weight decay:
,
:
) [
18].
3.3. Two-Stage Network Pipeline
In the following subsections, the proposed methods are introduced. They comprise a first description of the full pipeline used in the experiments, as well as a detailed overview of the relevant methods inside this pipeline.
The methods regarding the pipeline are based on the hypothesis stated in
Section 2. This involved especially the properties and advantages of both networks, large-scale and small-scale. The large-scale network was utilized to achieve an adequate first prediction since it had a better overview and therefore a sense of damage locations and occurrences compared to the small-scale network. However, the utilization of image details such as surface structures is only possible with the small-scale network. As stated in the hypothesis, the small-scale network had the disadvantage of a significant decrease in accuracy if one of the classes was not present in the input image. This disadvantage had to be addressed in the application of the small-scale network in the pipeline and was further expressed with the class proportion
for each patch:
Here,
is the number of pixels labeled with coating damage inside this patch,
w is the width of the image patch and
h is the height.
had to be in a certain range to ensure a high performance of the small-scale network. This range was determined to be 1–99% in preliminary investigations, so an adequate number of pixels per class was ensured while most patches were still marked as valid. Additionally, the application of both networks had to be managed adequately to achieve a high accuracy while keeping the compute time at a reasonable level.
For this, the pipeline depicted in
Figure 3 was developed, which describes the algorithms applied on an input overview image (
RGB Image) to generate a final segmentation mask (
Final Prediction). Firstly, a single-network application is described by the dark gray box. There, an overview image is inserted and divided into patches by the
Standard Patching algorithm, which is explained later in detail. These patches are eventually downscaled and sequentially forwarded to the respective network. In a single-network application (without the rest of the pipeline), this can also be a small-scale network. In the proposed pipeline in
Figure 3, this is the large-scale network as stated. The output of this network application is a binary segmentation mask of the overview image, which is stitched together from the output patches (
Prediction). In a next step, this segmentation mask is again divided into smaller patches, which are later forwarded to the small-scale network. This patching algorithm works with one of four later introduced techniques:
Standard Patching (
SP),
Global Coordinate Optimization (
GCO),
Local Coordinate Optimum (
LCO) or a
Combined Method (
CM) of the two latter techniques. Depending on the technique, the binary mask information is utilized to overcome the described disadvantage of the small-scale network. Subsequently, a decision block is inserted to decide for each of these small patches, if it should be forwarded to the small-scale network. This is based on the defined class proportion and its valid range for each small patch and therefore also works towards a performance increase of the small-scale network. If valid, the patch is forwarded to the small-scale network and inferred. If nonvalid the existing segmentation mask of this patch is forwarded to the
Confidence Comparison (
CC) block.
This
CC block is an optional decision block (dark gray box in
Figure 3) so that, if not active, the class proportion block decides whether the small-scale network output or the existing segmentation mask of the respective patch is used in the subsequent stitching of the final binary segmentation mask. Otherwise, if active, the
CC block re-evaluates the network output of the small-scale network and the large-scale network. For this, the logit output is used to determine the confidence of both networks and forwards the output with the higher confidence. This is further explained in
Section 3.6. Finally, the whole binary segmentation mask is stitched together. This mask consists of segmentation patches predicted by one of the two networks and has the same size and shape as the overview image given as the input (see
Final Prediction and
RGB Image in
Figure 3). The segmentation mask (“Prediction” in
Figure 3) received from the first network application also has this same size and shape.
The patching algorithms, which are applied a priori to the segmentation networks, are an essential part of the proposed methods. The position and size of the patches may pose a significant impact on the accuracy of the networks. Therefore, different patching algorithms were evaluated, to acquire a comprehensive insight about the correlations and interdependencies. The
Standard Patching algorithm (
SP) was the baseline of this evaluation. Here, patches of the exact size and shape, regarding the subsequent applied network, were arranged to cover the whole area to be analyzed. This was typically the whole RGB image but could be a smaller proportion of it, if the surface area did not cover the whole RGB image (see
Figure 2, images with irrelevant black areas). The patches were arranged in a grid and did not have overlapping regions in the y-direction (except the last row of patches). In the x-direction, the patches featured a uniform overlap, so that the left and right patches of each patch row covered the left and right borders. The
SP was also used a priori in the large-scale network, since at this state of the pipeline no metainformation was available on which one of the more elaborate methods could be based on. A priori, to the small-scale network, a first binary mask was available and could be utilized to execute advanced patching techniques, which eventually contributed to an increase of accuracy with the subsequent network. These methods are introduced in the next subsections.
3.4. Global Coordinate Optimization (GCO)
The
Global Coordinate Optimization (
GCO) algorithm utilized cost functions, which were developed based on the assumptions made in the hypothesis, to optimize the patch locations via differential evolution [
19]. This patching method as well as the other algorithms are depicted in
Figure 4. In this method, the patch’s shape and size were fixed to the input size of the small-scale network. The problem to be optimized was multidimensional (the x- and y-coordinates of each patch) and nonlinear due to the cost functions. Additionally, the differentiation of the problem could not be ensured. Therefore, the global optimization method of differential evolution was selected, because it did not use the gradient of the problem and thus did not require any overall differentiation [
19].
The cost function consisted of two basic principles for this optimization. On the one hand, the coverage of the binary segmentation edges was utilized to describe a necessary criterion while on the other hand, the class proportion of each patch was used to find the optimal configuration for the subsequently applied network. The edge coverage was based on the detected edges gained by a canny edge detector applied on the binary segmentation mask [
20]. The goal and therefore lowest cost was reached when all detected edge pixels were covered by one of the arranged patches. The resulting cost function
could therefore be described with the following equation:
Here,
N is the number of patches,
is the total set of edge pixels resulting from the preceding canny edge detection, and
is the area covered by the respective image patch
. This cost function ensured a coverage of all areas to be further analyzed by the second small-scale network. The second principle addressed the assumption made in
Section 2, that class proportions unequal to zero or one and especially tending to
were advantageous for the subsequently applied small-scale network. This assumption resulted in the following cost function
:
where
is the calculated class proportion of the respective patch
i. Next, both functions were combined to formulate one cost function to be minimized by differential evolution. Here,
was the necessary criterion for a valid patch configuration. Therefore, if a certain threshold of
was not met,
was the function to be optimized, otherwise
was optimized. This was expressed with the combined cost function
as follows:
The threshold of
was determined iteratively in preliminary investigations so that a stable convergence of the optimization was ensured while keeping the threshold as low as possible. To maintain a valid comparison of the different solution vectors in the differential evolution process, a value greater or equal to one (highest cost of
) had to be added to the cost value for the unmet criterion in case one (
).
As it is depicted in
Figure 4, the optimization was initialized with the
SP algorithm to achieve a fast convergence by already meeting the necessary edge coverage criterion. The
SP therefore set the number of patches to be optimized and thus the number of dimensions of the optimization problem. Since the number of patches for the whole overview image exceeded 600 (which would result in a 1200-dimensional problem) the overview image was divided into smaller parts
, where each part was optimized separately. These parts were sections with the whole width and were vertically arranged without overlap. The optimization could then be parallelized to minimize computation time.
Finally, for each optimized patch configuration, a filter was applied to remove invalid patch locations (see
Figure 4,
GCO, yellow box). This was based on two principles. First, patches having a large overlap with others were removed to spare unnecessary computation time. Second, patches with a class proportion not in the valid range were sorted out. This second filter condition was identical to the class proportion block of the full pipeline (see
Figure 3, yellow box, bottom right).
3.5. Local Coordinate Optimum (LCO) and Combined Method (CM)
Another patching technique evaluated in this study was the
Local Coordinate Optimum (
LCO). This method was based on two concepts, where the first comprised the described optimal class proportion of each patch. The second concept was that specific metadata were useful to maximize the prediction accuracy of a certain area. In other words, the surrounding image data of a patch were vital for the optimal prediction. Therefore, in this method, smaller patches (smaller than the default input size of the subsequent network) were arranged by the
SP algorithm and sequentially analyzed (see
Figure 4,
LCO, blue box). These smaller patches are referred to as
LCO patches in the following. For each of these
LCO patches
, the patch with the default input size was placed to enclose the respective
LCO patch. This input patch could then be shifted to minimize the class proportion cost
(see
Figure 4,
LCO, yellow box). Eventually, this input patch was forwarded to the class proportion validation and the small-scale segmentation (see
Figure 3), from which the resulting prediction was cropped to the required smaller
LCO patch size and finally forwarded to the next pipeline block (
CC).
This method is visualized on an exemplary overview image section in
Figure 5. Here, a
LCO patch size of 192 × 128 pixels was selected (compared to the original input image size of 384 × 256 pixels). The
SP of these
LCO patches is depicted in
Figure 5a. For one of these patches, the subsequent input patch placement is depicted in
Figure 5c. The input patch (red) was shifted to minimize the class proportion cost while still enclosing the
LCO patch (gray). This resulted in an upper right shift towards the damage area since the class proportion was generally too low at the other positions. In this method, an optimization algorithm of the x- and y-shifts was obsolete since the search space regarding these shift parameters was of a reasonable size. One of the most crucial parameters regarding the performance of the
LCO was the size and shape of the
LCO patches. Therefore, this parameter is evaluated in detail in
Section 4.
The last patching method proposed in this study is the
combined method (
CM), which was a combination of
GCO and
LCO. Based on the idea of the
LCO algorithm, the
SP of the
LCO patches was replaced with the
GCO method (see
Figure 4,
CM, blue box). Here, the
LCO patches were already optimized to patch locations with low class proportion costs and a high coverage of the segmentation edges. Subsequently, the
LCO method set the input patches (see
Figure 4,
CM, green and yellow box). The optimized
LCO patches in this method are exemplary depicted in
Figure 5b. It can be observed that the patches tended to scatter around the damage edges with an approx. class proportion of
. Patches placed completely on the intact coating area (for example on the left side of the image) were filtered out since the valid class proportion range was not met. Again, for each of these
LCO patches, the input patch was placed (see
Figure 5c).
A variant of the CM algorithm is a combined method without the x-coordinate optimization of the LCO patch coordinates (CM-Y). This reduced compute time and forced the patch arrangement to equally spread over the whole width of the overview image.
3.6. Confidence Comparison
The
Confidence Comparison block (
CC) in the pipeline (see
Figure 3) represents the decision concerning which patch has the higher mean confidence and is therefore selected for the final prediction mask to be stitched. Here, the confidence was defined as the probability of correctness and was calculated based on the nonprobabilistic output or logit of the respective networks [
21]. Usually, only the binary classification of each pixel is used in such a semantic segmentation task. This can be described as follows:
where
is the pixelwise class prediction or binary segmentation result of the respective sample
i,
is the logit matrix or network output and
k is the respective class. Thus, this equation reflects the typical pixelwise selection of the class with the larger logit value. This binary segmentation output does not allow any description of the network’s confidence for the respective prediction. Therefore, a different approach was followed, where the sigmoid function
was first applied on the logit. Subsequently, the maximum class sigmoid was selected pixelwise to gain a description of the network confidence
. This can be described with the following equation:
By combining Equations (
8) and (
9), the general application of a network
h with an input
could be described as
. The confidence
was then used in the pipeline to decide between the existing binary segmentation result and the new prediction to be inserted into the final segmentation mask (see
Figure 3). For this, both mean confidences of the respective patch were compared. This comparison of the confidence of two different networks could lead to complications, since the described uncalibrated approach of the confidence definition did not take this into account.
A possible solution could be the usage of (local) temperature scaling, which was proposed by Guo et al. [
21]. With this temperature scaling (or Platt scaling) approach applied, the logit
in Equation (
9) would first be divided by a single scalar parameter
T (temperature), which was calibrated a priori using the validation dataset. In an advanced development of this approach, the local temperature scaling proposed by Ding et al., the temperature was defined as a matrix instead of a scalar. Here, a separate neural network was needed to calibrate these temperature values based on the validation dataset [
22]. Both approaches were evaluated in preliminary investigations by applying an additional calibration step between the training of the networks and the subsequent test phase. A short analysis showed that the temperature values were optimized close to one, while resulting in a minor decrease in overall accuracy. A temperature equal to one would be the equivalent to omitting the method. Since the analysis did not result in significant improvements of the accuracy in confidence description, these methods were not applied in the further progress of this study. A detailed analysis of these approaches is beyond the scope of this work.
4. Results
In the following section, all experimental results are presented. First, the results of the single networks are shown and decisions for further analysis steps and pipeline configurations are derived. Subsequently, the proposed whole pipeline is analyzed in different configurations regarding their accuracy and compute time.
4.1. Analysis of the Single Networks
In this subsection, the application of single segmentation networks with a
Standard Patching are evaluated (refer to
Figure 3, single-network application). The networks were configured with the different input image shapes and patch sizes as described in
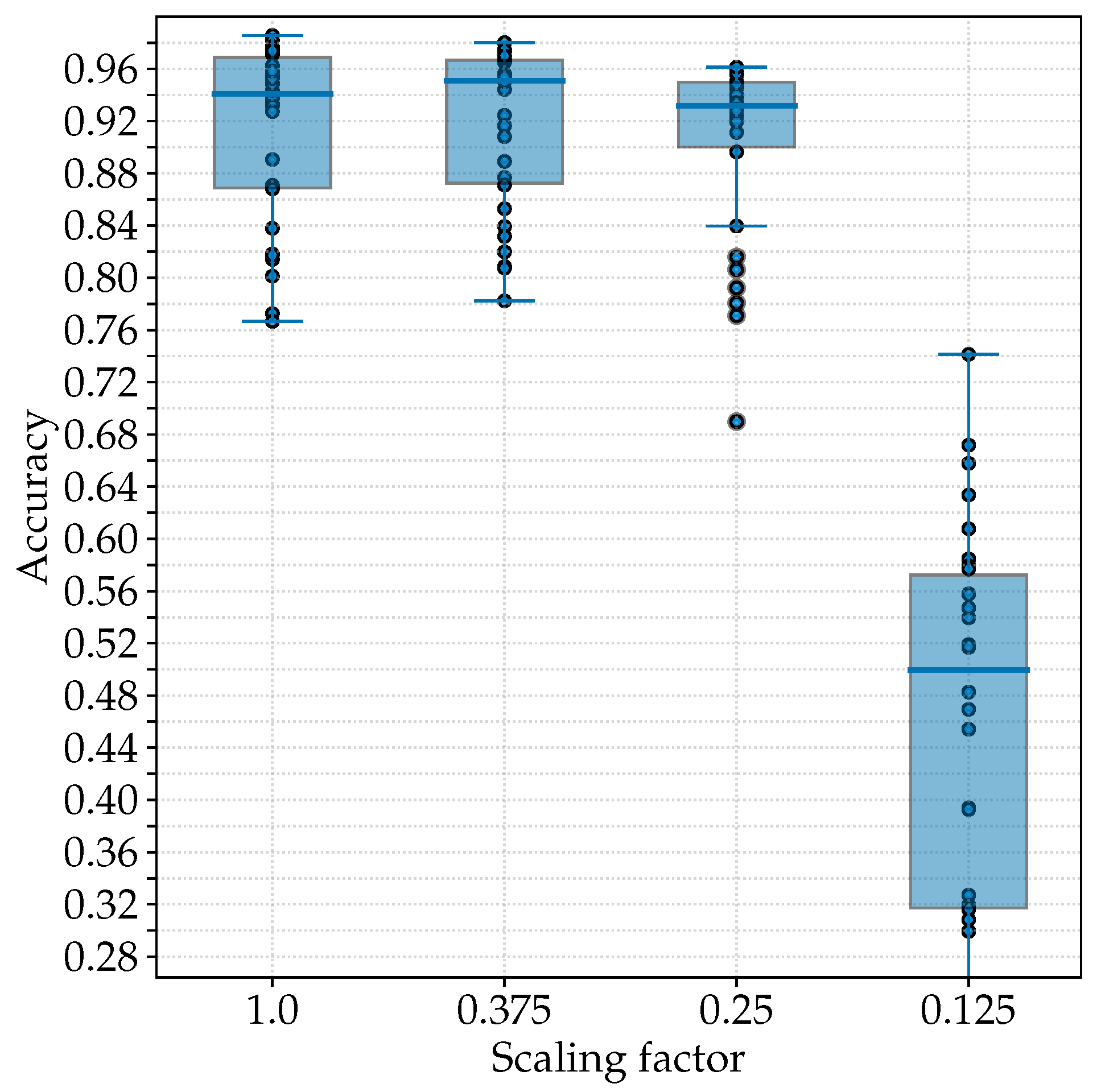
Table 1. The training of each network was executed with 60 epochs and a batch size of 16. The results regarding the different scaling factors are visualized side by side in
Figure 6 as boxplots. The data points represent a single iteration of a training and test process. The accuracy was calculated on the test dataset of each iteration. The first network with a scaling factor of 1.0 achieved a median accuracy of 94.08%. When comparing the networks with a scaling factor lower than 1.0, the network with the lowest scaling factor achieved the overall poorest accuracy of 49.98%. The overall best accuracy with 95.31% was exhibited by the network with the highest scaling factor of 0.375. Higher scaling factors were not considered to obtain a significant difference in FOV between the two networks to be applied, although these could possibly achieve higher accuracies (regarding the single-network application). A possible explanation for the decreasing performance with heavier downscaling, on the one hand, can be the increasing loss of information. On the other hand, the respective dataset size equaled approx. 25% of the preceding configuration resulting in approx. 77 images for training for the last configuration.
According to the proposed pipeline, a large-scale network had to be selected in addition to the small-scale network with a scaling factor of 1.0. The second network depicted in
Figure 6 featured the highest median accuracy. Although the lower whisker of the third network also indicated robust results, there were various lower outliers compared to the second network. Therefore, the second network with a scaling factor of 0.375 was selected as the large-scale network for the whole pipeline and all further evaluations. This first approach of the single-network application is referred to as
single-network small scale (
1S SS) in the following for a scaling factor of 1.0 and
single-network large scale (
1S LS) for a scaling factor of 0.375.
Additionally, a confusion matrix was calculated for the selected network configurations
1S SS and
1S LS (refer to
Table 2). While both networks handled true positive values almost identically,
1S LS achieved less false predictions overall. Furthermore,
1S LS performed better at intact coating (ground truth negative) compared to
1S SS, which can be explained with the advantageously larger FOV. The recall equaled 95.65% for
1S SS and 96.73% for
1S LS, which was consistent with the median accuracies [
23].
Next, the hypothesis formulated in
Section 2 was evaluated on the small-scale network. Thus, the accuracy in each predicted input image was analyzed regarding the class proportion of the respective input image. This is depicted in
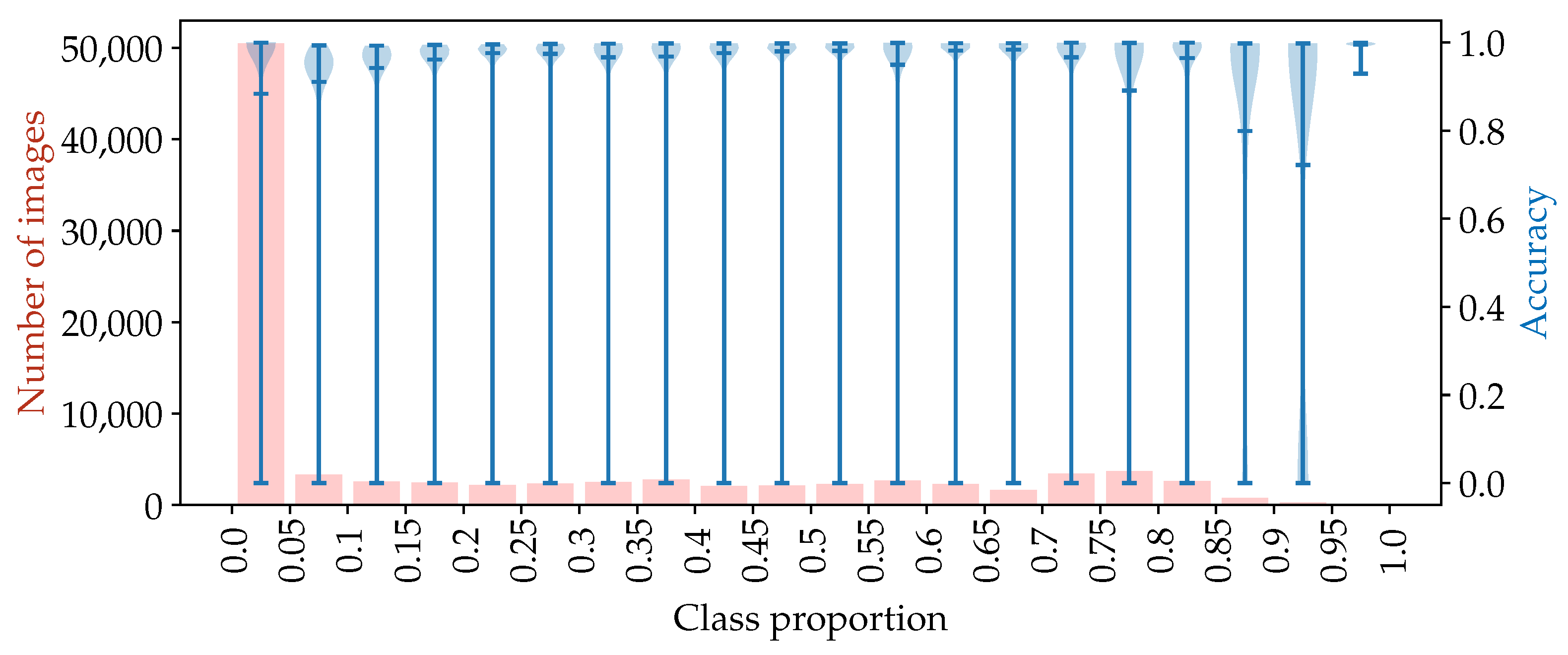
Figure 7, where test accuracy (blue) and number of image patches (red) are visualized over the class proportion of each image patch. With the approach
1S SS, 30 iterations were executed, where each patch in the test dataset was evaluated separately. The resulting violin plot was then generated with the number of patches available. This number of patches is depicted in the histogram for each class proportion (red). In total, 92,838 patches were analyzed. For low decreasing class proportions (approx.
), the mean accuracy decreased continuously down to 88.4% for class proportions between 0.00 and 0.05. A similar behavior was observed for high increasing class proportions (approx.
), where the mean accuracy also decreased down to 72.2% for class proportions between 0.90 and 0.95. One outlier was present at a class proportion between 0.95 and 1.00, where the mean accuracy equaled 99.6%. A possible explanation for this was the disproportionately low number of image patches in that range with only 90 images. This equaled approx. 0.097% of the evaluated image patches and therefore indicated a strongly declined significance. Especially the class proportion range between 0.00 and 0.05 had a high impact on the overall accuracy of an analyzed overview image, since it covered approx. 54.4% of all image patches.
With these results, the hypothesis that the “networks achieve higher accuracies, if both classes (coating damage and intact coating) are present with at least a significant amount of pixels” could therefore be validated by this evaluation. Further, the highest accuracy with over 98.00% could only be achieved with class proportions near 0.50, or more specifically in the range of 0.45 and 0.65, if the outliers at 0.55 to 0.60 and 0.95 to 1.00 were neglected. With these insights, the proposed pipeline and patching methods can be configured and evaluated in the next subsections.
4.2. Analysis of the Two-Stage Pipeline
In this subsection, the application of both networks as it is visualized in
Figure 3 is analyzed. In all following evaluations, the two networks were identical in each iteration as they were presented in the last subsection. This implied that for the following experiments, only evaluations on the test dataset were executed without any training of the networks. The whole pipeline configuration is referred to as
two-stage (
2S) in the following.
Before comparing the
two-stage approaches to each other, the best patch size for the patching of the
LCO patches in
LCO,
CM and
CM-Y had to be identified. This was done by evaluating the whole pipeline configured with
LCO patching and without
CC. The
LCO patch’s height and width were changed in different combinations. The results were compared based on the overall median accuracy of the 30 iterations, which is listed in
Table 3. Here, the configuration with a resolution of 384 × 128 pixels achieved the highest median accuracy. This shape had the same width as the original input image patch shape. Therefore, in the
LCO method as well as in the
CM method, the optimum search regarding the input patch position only had one degree of freedom (y) instead of two (x, y). However, the results in
Table 3 indicated a continuous decrease in accuracy for patch widths lower than 384 pixels. This could be observed for all patch heights. The configuration 384 × 256 pixels corresponded to the
SP algorithm, since the evaluated
LCO patch size must be smaller than the input image patch in
LCO,
CM or
CM-Y to enable the required shifting of the input patch. In the following, these methods were configured with the
LCO patch size of 384 × 128 pixels.
With the crucial parameters adjusted in the above investigations, the
two-stage configurations were evaluated. They comprised the different patching algorithms
SP,
GCO,
LCO,
CM and
CM-Y each with or without
Confidence Comparison. The results with these
two-stage configurations as well as the initially presented single-network applications
1S SS and
1S LS are listed in
Table 4 regarding the overall median accuracy over 30 iterations. Here, it can be observed that the additional
Confidence Comparison improved the median accuracy of every configuration resulting in an average accuracy improvement of approx. 0.6%. The overall highest median accuracy was achieved by the
2S LCO and
CC with 97.07%. This same approach also exhibited the highest accuracy regarding the methods without
CC. The application of
GCO both individually and within
CM and
CM-Y yielded worse results than the application of a simple
SP, if
CC was enabled. With
CC disabled,
SP achieves the poorest results regarding the
two-stage approaches.
In addition to
Table 4, the best
two-stage approaches were further compared to the single-network applications as boxplots in
Figure 8. It can be seen that the box and therefore the certainty of the methods was improved significantly with all compared
two-stage approaches. Additionally, the lower whisker could be increased drastically. This resulted in improvements of 3.83% to 11.48% in accuracy depending on the methods compared. In particular, the method
2S LCO w/ CC achieved a high lower whisker, albeit with several critical outliers. Regarding the already high upper whisker, the
two-stage approaches achieved only a minor increase from 98.1% (
1S LS) or 98.6% (
1S SS) to approx. 98.8% (all
two-stage).
Overall, the median accuracy could be increased by approx. 1.98% resulting in a final median accuracy of 97.07% with method
2S LCO w/ CC. This same method also achieved the best results when comparing the mean accuracy. Here, an improvement of 2.25% in mean accuracy was observed when comparing method
2S LCO w/ CC (93.91%) to the best single-network application (
1S LS, 91.66%). Thus, when outliers were taken into account to a greater extent (when analyzing the mean value), the proposed methods also exhibited advantageous results. The recall, which was similarly calculated using the method described in
Section 4.1, equaled 97.70% for method
2S LCO w/ CC. Thus, an improvement of 0.97% could be achieved. Another improvement could be seen when comparing the worst-case scenario, thus the worst iteration. Here,
1S LS achieved approx. 78.23% while method
2S LCO w/ CC, with approx. 81.04%, increased the accuracy by approx. 2.81%. With all these statistical characteristics, the increased overall robustness of the damage segmentation using the proposed pipeline was demonstrated.
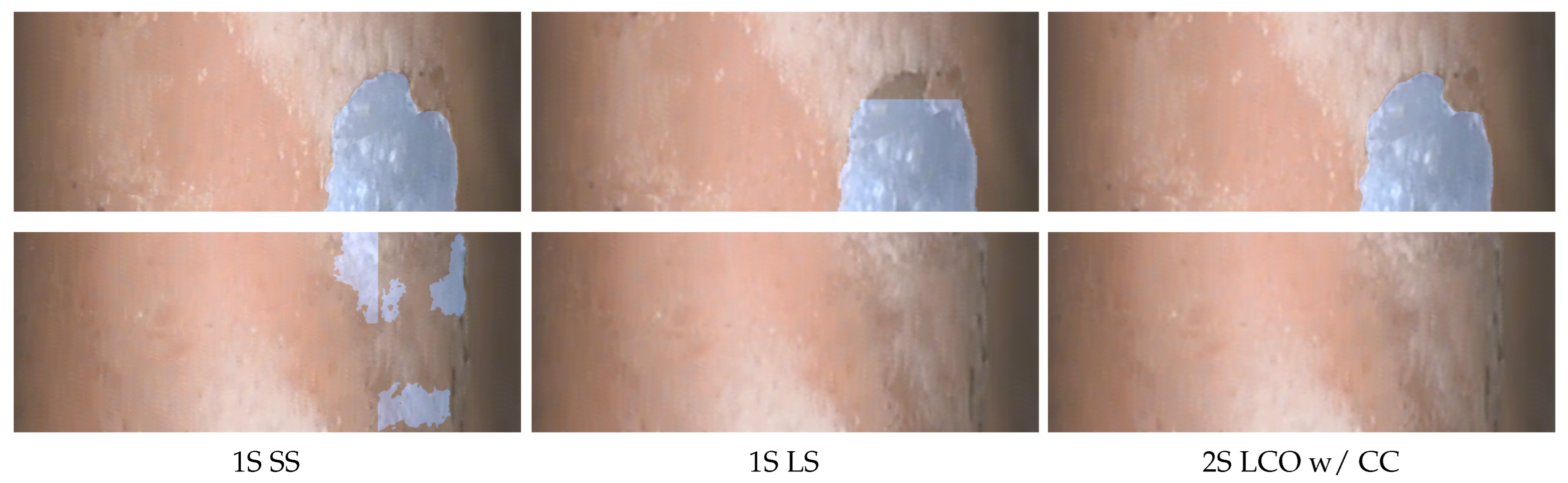
Finally, example segmentation results are depicted in
Figure 9, where the single networks
1S SS and
1S LS are compared to the proposed method
2S LCO w/ CC. Here, two example parts of an overview image (top and bottom row) were analyzed. In the first row, it can be observed that the small-scale network (left) achieved an adequate accuracy since the damage in the right of the image was fully masked (depicted with blue overlay color). The large-scale network (center) exhibited partly false segmentation results. Method
2S LCO w/ CC (right) resulted in a similar mask as that of
1S SS indicating the improvement of the initial large-scale segmentation by the small-scale segmentation in the pipeline (see
Figure 3). In the second row, a false segmentation mask was predicted by the
1S SS, since no damage was present in this image part. However, method
1S LS resulted in the correct segmentation. Again, method
2S LCO w/ CC interpreted both segmentation results correctly and output the segmentation result of the large-scale segmentation.
4.3. Analysis of the Computational Time
In a final experiment, the computational time of the proposed methods was analyzed. Therefore, after two warm-up runs, six runs of feed-forward predictions of the full overview images were timed. These multiple runs were conducted to average several side effects in this experiment. First, each overview image featured a different size and therefore different numbers of patches. Second, for the two-stage approaches, the number of predicted patches differed according to the damage occurrences and depending on the pipeline decision blocks. The experiment was executed on similar hardware as the previous training and evaluation processes, which was an NVIDIA GeForce RTX 3090 GPU (NVIDIA Corporation, Santa Clara, CA, USA) and an AMD Ryzen 5950X CPU (Advanced Micro Devices Inc., Santa Clara, CA, USA). The memory size of the segmentation models (small-scale and large-scale) was the same in all approaches.
The results for the single networks as well as several
two-stage methods are listed in
Table 5. The
1S LS method achieved the lowest computational time, since there were only few patches with a large FOV to be predicted. The other single-network method, required more than twice the time for predicting more than twice the number of patches. The simplest
two-stage method,
2S SP w/o CC, was basically a full large-scale segmentation
1S LS, a selective
1S SS and an algorithm overhead leading to an increase in time. This resulted in a computational time of 50.01 s. The integration of the
LCO method further increased the computational time by approx. 50 s. Finally, the additional implementation of the
GCO method posed a significant load on the compute resources. This resulted in a major increase of approx. 5594 s, if the x- and y-coordinates were optimized for each patch. The optimization of the y-coordinates only, which reduced the dimensions to be optimized by 50%, still led to an increase in compute time of 4132 s. Although the optimization method was parallelized, significant resources were required due to the high number of dimensions. It must be taken into account that the absolute computational times only applied to this specific hardware and may be different in a real-world application depending on the hardware and software implementation of the algorithms.
5. Discussion
The datasets of this study comprised a low number of image data with a wide range of environmental perturbations. This posed the challenge of an adequate training and application of CNNs to achieve high accuracies despite low training data. Since the target image data in this study had a high resolution and size, the proposed methods utilized the advantageous properties of CNNs trained with image patches at different scales. Accordingly, the hypothesis stated in
Section 2 therefore referred to the beneficial application of CNNs in terms of patch position and FOV regarding the different classes present in an image patch to be inserted into the networks. This hypothesis could successfully be proven by the results depicted in
Figure 7. The derived methods and pipeline were evaluated in the subsequent experiments. The goal here was the successful combination of the advantages of both networks applied (small-scale and large-scale). In particular, the
Confidence Comparison proved to be effective by ensuring a correct replacement and a prevention of false decisions based on unknown network application properties, as it was depicted in the results in
Table 4. In other words, without the
CC block, the replacement of the segmentation results from the preceding network was only based on statistical findings and not individual results and confidences. The proposed pipeline in its simplest form,
2s SP w/o CC, already achieved an improvement of 1.16% in median accuracy (see
Table 4). With the proposed patching methods implemented, this could be further increased by 0.42%. With the additional
CC block, the median accuracy was also increased by 0.4% for the
2S LCO method resulting in the overall best median accuracy of 97.07%.
The improvement in accuracy gained by the
two-stage approaches highly differed between the single-overview images. This uncertainty was also evident in the boxplots of all methods (see
Figure 8). There, the range between lower and upper whiskers highlighted that uncertainty and the crucial influence of the image distribution on the datasets. When analyzing the average performance of all methods on the single-overview images, it was observed that on individual overview images, the accuracy was significantly lower (<70%). The distribution of these critical images into the datasets therefore led to significant fluctuations depending on whether these images were sorted into the test dataset. These fluctuations, among others, evoked the uncertainty observed in the boxplots.
Among the proposed patching methods, GCO exhibited the poorest median accuracy, which evoked several possible explanations. First, the implemented class proportion cost function led to an optimization of the patch location towards a class proportion of 0.5, compared to the simple threshold of 1% of each class present, which was implemented in the pipeline. The simple threshold already covered the majority of cases, which was why the cost function was not expected to have a large impact. Second, the optimized patch positions excluded a significant amount of surface area, while covering other areas several times (by various overlapping patches). This was due to the edge coverage cost function focusing only on edges and not on overall coverage. The effect could be partially solved by adjusting the cost function of the optimization by an additional cost of the overall coverage, which however did not achieve better results in preliminary investigations.
The evaluation of the computational time compared the feed-forward time of each method regarding a specific hardware setup used in this study. Nevertheless, assuming an application with this hardware setup, method 2S LCO w/ CC, which achieved the highest performance in accuracy, required 108.49 s in the evaluation and therefore approx. 18.1 s per overview image. This is a reasonable computational time regarding the introduced a posteriori application in inspection software, which does not require an execution in-process.
All methods proposed in this study were developed and evaluated only on the presented image dataset. A possible transfer of this method on other domains or segmentation tasks was not covered in this study. However, a suitable new domain generally has to comprise high-resolution images on the one hand. On the other hand, the class occurrences must consist of wide coherent areas. Otherwise, the patching methods do not have a suitable pattern or gradient for optimization. Further, a successful application of the proposed methods is indicated if the hypothesis is validated on the respective domain.
6. Conclusions and Future Works
Within the scope of this study, the application of CNNs within an automated inspection of coating damages in aircraft engines was analyzed and improved to overcome the challenges posed by limited image data and environmental perturbations. Therefore, a viable method was proposed and validated to improve the segmentation accuracy of CNNs trained on a low number of diverse 2D image data. Specifically, it comprised the analysis of high-resolution images requiring a sequential processing of image patches. The proposed methods therefore introduced a pipeline implementing two segmentation networks, which worked on different scales of the image data to improve the overall accuracy on the large overview images to be analyzed. For this, a hypothesis was formulated regarding the efficient application of CNNs in the present domain, which could be proven in first experiments. Based on this hypothesis, the pipeline and patching methods were developed. It could be shown that each block of the presented pipeline contributed to an increase in accuracy. However, the proposed patching methods exhibited varying results. Nevertheless, the best approach could be identified with method 2S LCO w/ CC, where patch locations were optimized for a beneficial application of the segmentation networks. This result further supported the stated hypothesis and posed a viable method of combining segmentation networks of different properties to overcome a low number of training data in an abstract domain and ensure high accuracies.
As stated in
Section 5, the proposed methods were only evaluated on the domain present in this study. To investigate the generalizability of the methods, further experiments on other domains must be performed. This respective domain should meet the characteristics specified in
Section 5 to ensure a successful implementation. In this study, only one network structure and size was investigated to keep the hyperparameter space at a reasonable size and the network applications comparable. However, for the different network applications (
SS and
LS), other network structures could be more efficient regarding their accuracy and size, which could be investigated in future studies. Another possible investigation addressed the optimization methods (
LCO,
GCO and
CM), which currently only considered the x- and y-coordinates of the image patches. The additional optimization of the individual patch size could yield further advantages. However, this entails that the CNNs would have to be adjusted. A possible extension of the proposed methods is the implementation of multiclass semantic segmentation. Since the segmentation task evaluated here did not cover such a case, this was not further investigated. Nevertheless, an extension of the
two-stage pipeline to multiclass segmentation is especially worthwhile for other domains.
7. Patents
The automation of the inspection process and underlying algorithms of the presented software pipeline in
Section 1 and
Figure 1, specifically the masking, feature tracking, registration and stitching to an overview image, are stated and specified in a pending patent. The scientific research presented here is therefore based on the data generated by the methods of this patent. However, the methods and scientific results of this study are not covered in the patent nor will be covered in the future. The corresponding patent is published in Germany under the title “Verfahren zum Abbilden einer Oberfläche einer Strömungsmaschine und Detektieren einer Schädigung” (DE102021120899.8).
Author Contributions
Conceptualization, K.H.; methodology, K.H. and L.H.; software, K.H.; validation, K.H. and L.H.; formal analysis, investigation, resources, data curation, K.H.; writing—original draft preparation, K.H.; writing—review and editing, K.H., L.H. and E.R.; visualization, K.H. and L.H.; supervision, L.H.; project administration, K.H., L.H. and E.R.; funding acquisition, K.H. and E.R. All authors have read and agreed to the published version of the manuscript.
Funding
The research was funded by the German Federal Ministry of Education and Research as part of the Aviation Research and Technology Program of the Niedersachsen Ministry of Economic Affairs, Employment, Transport and Digitalisation under the grant number ZW 1-80157862. The authors are responsible for the content of this publication.
Data Availability Statement
The data presented in this study, excluding the image data, are available on request from the corresponding author. The image data are subject to confidentiality with the collaborating partner and are therefore not available. The data of this study will be kept for at least 5 years, while the evaluation scripts will be available indefinitely.
Acknowledgments
The authors thank the MTU Maintenance Hannover GmbH for the collaboration, the provided data and the support.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FOV | Field of view |
| ROI | Region of interest |
| CNN | Convolutional neural network |
| 1S | Single-stage |
| 2S | Two-stage |
| SP | Standard patching |
| GCO | Global coordinate optimization |
| LCO | Local coordinate optimum |
| CM | Combined method |
| CM-Y | Combined method (only y-coordinates optimized) |
| CC | Confidence comparison |
| CPU | Central processing unit |
| GPU | Graphics processing unit |
Appendix A
Figure A1.
Visualization of exemplary images (upper row) and labels (lower row) from the training dataset with applied augmentations. On the patch depicted in (a) a color channel shift is applied. In (b), the application of a rotation and histogram equalization can be seen. The patch depicted in (c) shows, among others, an applied CutMix operation, where an ROI of another patch from the same batch is inserted into the shown patch on the upper right. The label is adjusted accordingly. The image patch depicted in (d) is rotated and additionally mirrored in places where black areas would appear otherwise (see lower right corner of the depicted image patch).
Figure A1.
Visualization of exemplary images (upper row) and labels (lower row) from the training dataset with applied augmentations. On the patch depicted in (a) a color channel shift is applied. In (b), the application of a rotation and histogram equalization can be seen. The patch depicted in (c) shows, among others, an applied CutMix operation, where an ROI of another patch from the same batch is inserted into the shown patch on the upper right. The label is adjusted accordingly. The image patch depicted in (d) is rotated and additionally mirrored in places where black areas would appear otherwise (see lower right corner of the depicted image patch).
References
- Wang, C.; MacGillivray, T.; Macnaught, G.; Yang, G.; Newby, D. A two-stage 3D Unet framework for multi-class segmentation on full resolution image. arXiv 2018, arXiv:1804.04341. [Google Scholar]
- Amiri, M.; Brooks, R.; Behboodi, B.; Rivaz, H. Two-stage ultrasound image segmentation using U-Net and test time augmentation. Int. J. Comput. Assist. Radiol. Surg. 2020, 15, 981–988. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Li, P.; Gao, C.; Liu, Y.; Chen, Q.; Yang, F.; Meng, D. TSASNet: Tooth segmentation on dental panoramic X-ray images by Two-Stage Attention Segmentation Network. Knowl.-Based Syst. 2020, 206, 106338. [Google Scholar] [CrossRef]
- Huang, X.; Lin, Z.; Jiao, Y.; Chan, M.T.; Huang, S.; Wang, L. Two-Stage Segmentation Framework Based on Distance Transformation. Sensors 2022, 22, 250. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.; Zhang, N.; Guo, J.; Zhang, H.; Hao, Y.; Hang, J. Automated polyp segmentation for colonoscopy images: A method based on convolutional neural networks and ensemble learning. Med. Phys. 2019, 46, 5666–5676. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Yuan, X.; Hu, R.; Liang, S.; Feng, S.; Ai, Y.; Zhang, Y. Automatic pancreas segmentation via coarse location and ensemble learning. IEEE Access 2019, 8, 2906–2914. [Google Scholar] [CrossRef]
- ISO/IEC 14496-14:2003; Information Technology—Coding of Audio-Visual Objects—Part 14: MP4 File Format. Technical Report. International Organization for Standardization: Geneva, Switzerland, 2003.
- Hedrich, K.; Hinz, L.; Reithmeier, E. Damage segmentation using small convolutional neuronal networks and adversarial training methods on low-quality RGB video data. In Proceedings of the AI and Optical Data Sciences III, San Francisco, CA, USA, 22–27 January 2022; Volume 12019, p. 1201902. [Google Scholar]
- Yun, S.; Han, D.; Oh, S.J.; Chun, S.; Choe, J.; Yoo, Y. Cutmix: Regularization strategy to train strong classifiers with localizable features. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27–28 October 2019; pp. 6023–6032. [Google Scholar]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 801–818. [Google Scholar]
- Radosavovic, I.; Kosaraju, R.P.; Girshick, R.; He, K.; Dollár, P. Designing Network Design Spaces. arXiv 2020, arXiv:2003.13678. [Google Scholar]
- Iakubovskii, P. Segmentation Models Pytorch. 2019. Available online: https://github.com/qubvel/segmentation_models.pytorch (accessed on 24 October 2022).
- Ma, J.; Chen, J.; Ng, M.; Huang, R.; Li, Y.; Li, C.; Yang, X.; Martel, A.L. Loss odyssey in medical image segmentation. Med. Image Anal. 2021, 71, 102035. [Google Scholar] [CrossRef]
- Dice, L.R. Measures of the amount of ecologic association between species. Ecology 1945, 26, 297–302. [Google Scholar] [CrossRef]
- Jadon, S. A survey of loss functions for semantic segmentation. In Proceedings of the 2020 IEEE Conference on Computational Intelligence in Bioinformatics and Computational Biology (CIBCB), Virtual, 27–29 October 2020; pp. 1–7. [Google Scholar]
- Taghanaki, S.A.; Zheng, Y.; Zhou, S.K.; Georgescu, B.; Sharma, P.; Xu, D.; Comaniciu, D.; Hamarneh, G. Combo loss: Handling input and output imbalance in multi-organ segmentation. Comput. Med. Imaging Graph. 2019, 75, 24–33. [Google Scholar] [CrossRef] [PubMed]
- Khvedchenya, E. PyTorch Toolbelt. 2019. Available online: https://github.com/BloodAxe/pytorch-toolbelt (accessed on 24 October 2022).
- Zhuang, J.; Tang, T.; Ding, Y.; Tatikonda, S.C.; Dvornek, N.; Papademetris, X.; Duncan, J. Adabelief optimizer: Adapting stepsizes by the belief in observed gradients. In Proceedings of the Advances in Neural Information Processing Systems, Virtual, 6–12 December 2020; Volume 33, pp. 18795–18806. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, PAMI-8, 679–698. [Google Scholar] [CrossRef]
- Guo, C.; Pleiss, G.; Sun, Y.; Weinberger, K.Q. On calibration of modern neural networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 1321–1330. [Google Scholar]
- Ding, Z.; Han, X.; Liu, P.; Niethammer, M. Local temperature scaling for probability calibration. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 6889–6899. [Google Scholar]
- Makhoul, J.; Kubala, F.; Schwartz, R.; Weischedel, R. Performance measures for information extraction. In Proceedings of the DARPA Broadcast News Workshop, Herndon, VA, USA, 28 February–3 March 1999; pp. 249–252. [Google Scholar]
Figure 1.
Visualization of the pipeline implemented in the resulting software tool. Here, the video (on the left) is inserted, processed and evaluated by the segmentation algorithms. After a subsequent postprocessing, a relative damage quantification and a visualization of the whole coating area and the detected damages are provided. The overview image (center) is depicted considerably smaller in height than originally. The proposed methods are implemented in the Segmentation block (green).
Figure 1.
Visualization of the pipeline implemented in the resulting software tool. Here, the video (on the left) is inserted, processed and evaluated by the segmentation algorithms. After a subsequent postprocessing, a relative damage quantification and a visualization of the whole coating area and the detected damages are provided. The overview image (center) is depicted considerably smaller in height than originally. The proposed methods are implemented in the Segmentation block (green).
Figure 2.
Example images of the used datasets with the different downscaling factors (see
Table 1).
Upper left: 384 × 256 pixels (rotated) without downscaling;
center: 384 × 256 pixels (rotated) with a scaling factor of 0.375;
upper right: 256 × 384 pixels with a scaling factor of 0.25;
bottom: 128 × 768 pixels (rotated) with a scaling factor of 0.125.
Figure 2.
Example images of the used datasets with the different downscaling factors (see
Table 1).
Upper left: 384 × 256 pixels (rotated) without downscaling;
center: 384 × 256 pixels (rotated) with a scaling factor of 0.375;
upper right: 256 × 384 pixels with a scaling factor of 0.25;
bottom: 128 × 768 pixels (rotated) with a scaling factor of 0.125.
Figure 3.
Visualization of the full pipeline starting with the RGB overview image (orange, upper left) and finishing with the final stitched segmentation mask (red, upper right). The light gray boxes represent the iterative execution over the patches defined beforehand (green boxes). Blue boxes depict the execution of CNNs; yellow boxes represent a decision or comparison based on the input data or initially defined thresholds. Dark gray boxes represent optional or separately executable algorithm steps.
Figure 3.
Visualization of the full pipeline starting with the RGB overview image (orange, upper left) and finishing with the final stitched segmentation mask (red, upper right). The light gray boxes represent the iterative execution over the patches defined beforehand (green boxes). Blue boxes depict the execution of CNNs; yellow boxes represent a decision or comparison based on the input data or initially defined thresholds. Dark gray boxes represent optional or separately executable algorithm steps.
Figure 4.
Visualization of the different patching methods applied in the full pipeline (see
Figure 3). The input is defined as the respective overview image and a first binary segmentation (not necessary for the first method). All methods return the entire patch coordinates. In green, the algorithm steps are depicted; the blue boxes represent common or previously defined algorithms; the yellow boxes are filters or decision-making blocks based on initially defined cost functions, thresholds or criteria.
Figure 4.
Visualization of the different patching methods applied in the full pipeline (see
Figure 3). The input is defined as the respective overview image and a first binary segmentation (not necessary for the first method). All methods return the entire patch coordinates. In green, the algorithm steps are depicted; the blue boxes represent common or previously defined algorithms; the yellow boxes are filters or decision-making blocks based on initially defined cost functions, thresholds or criteria.
Figure 5.
Visualization of the algorithm steps for methods
LCO and
CM. (
a)
SP result with smaller patches (
LCO patches with a shape of 192 × 128 pixels). (
c) Selection of the best patch location by shifting, depicted for one patch
(refer to
Figure 4,
LCO, green and yellow box). Here, the gray patch was fixed while the red patch was shifted to achieve a low class proportion cost. Thereafter, the red patch was forwarded towards the small-scale segmentation. (
b) Result of the applied
GCO method with
LCO patches in the
CM algorithm (see
Figure 4,
CM, blue box). The patches were arranged to achieve a low class proportion cost while covering all edges of the existing binary damage segmentation.
Figure 5.
Visualization of the algorithm steps for methods
LCO and
CM. (
a)
SP result with smaller patches (
LCO patches with a shape of 192 × 128 pixels). (
c) Selection of the best patch location by shifting, depicted for one patch
(refer to
Figure 4,
LCO, green and yellow box). Here, the gray patch was fixed while the red patch was shifted to achieve a low class proportion cost. Thereafter, the red patch was forwarded towards the small-scale segmentation. (
b) Result of the applied
GCO method with
LCO patches in the
CM algorithm (see
Figure 4,
CM, blue box). The patches were arranged to achieve a low class proportion cost while covering all edges of the existing binary damage segmentation.
Figure 6.
Boxplots depicting the test accuracy of networks with different scaling factors of the image patch to be inserted. The x-axis is not proportional. Network input size, network size and number of parameters are identical for every configuration.
Figure 6.
Boxplots depicting the test accuracy of networks with different scaling factors of the image patch to be inserted. The x-axis is not proportional. Network input size, network size and number of parameters are identical for every configuration.
Figure 7.
Accuracy (violin plot with mean value, blue) and number of images (histogram, red) over the class proportion regarding all tested image patches. The data depict the application of the small-scale network in 30 iterations on the test datasets. All predicted image patches were analyzed separately (not gathered in batches or overview images). It can be observed that the mean accuracy significantly decreases for low (approx. ) and high (approx. ) class proportions.
Figure 7.
Accuracy (violin plot with mean value, blue) and number of images (histogram, red) over the class proportion regarding all tested image patches. The data depict the application of the small-scale network in 30 iterations on the test datasets. All predicted image patches were analyzed separately (not gathered in batches or overview images). It can be observed that the mean accuracy significantly decreases for low (approx. ) and high (approx. ) class proportions.
Figure 8.
Boxplots depicting the overall results compared amongst the different methods. The highest overall median accuracy is achieved by the 2S LCO w/ CC method, where the full pipeline with Local Coordinate Optimization and Confidence Comparison was applied.
Figure 8.
Boxplots depicting the overall results compared amongst the different methods. The highest overall median accuracy is achieved by the 2S LCO w/ CC method, where the full pipeline with Local Coordinate Optimization and Confidence Comparison was applied.
Figure 9.
Example segmentation results on two parts of one overview image from the test dataset (top and bottom). The applied networks are all from the same iteration. The final binary segmentation mask of each method is visualized with a blue overlay.
Figure 9.
Example segmentation results on two parts of one overview image from the test dataset (top and bottom). The applied networks are all from the same iteration. The final binary segmentation mask of each method is visualized with a blue overlay.
Table 1.
Patch sizes to be evaluated. All scaling factors (lower than 1.0) and input image sizes were selected to achieve an identical number of input pixels while covering the whole width of the overview images. For example images, see
Figure 2.
Table 1.
Patch sizes to be evaluated. All scaling factors (lower than 1.0) and input image sizes were selected to achieve an identical number of input pixels while covering the whole width of the overview images. For example images, see
Figure 2.
| Scaling Factor | Patch Size (Width × Height) (Px) | Input Image Size (Width × Height) (Px) | Dataset Size (No. of Images) |
|---|
| 1.0 | 384 × 256 | 384 × 256 | 11,047 |
| 0.375 | 1024 × 682 | 384 × 256 | 1729 |
| 0.25 | 1024 × 1536 | 256 × 384 | 784 |
| 0.125 | 1024 × 6144 | 128 × 768 | 208 |
Table 2.
Confusion matrix for 1S SS and 1S LS calculated over the single-image-patch predictions from the single-network application on the test datasets in 30 iterations.
Table 2.
Confusion matrix for 1S SS and 1S LS calculated over the single-image-patch predictions from the single-network application on the test datasets in 30 iterations.
| | | Predicted |
|---|
| | 1S SS (1S LS) | Positive | Negative |
|---|
| Ground
Truth | Positive | 27.06% (27.03%) | 1.23% (0.91%) |
| Negative | 1.29% (1.05%) | 70.41% (71.00%) |
Table 3.
Median accuracy calculated over 30 iterations on the test datasets for different LCO patch size configurations. Tested with patching method LCO without CC. (* at that patch size, only the SP was applied).
Table 3.
Median accuracy calculated over 30 iterations on the test datasets for different LCO patch size configurations. Tested with patching method LCO without CC. (* at that patch size, only the SP was applied).
| Height \Width (Px) | 384 | 192 | 96 | 48 |
|---|
| 256 | 96.25% * | 95.41% | 95.42% | 95.42% |
| 170 | 96.57% | 95.62% | 95.84% | 95.90% |
| 142 | 96.55% | 95.57% | 95.76% | 95.90% |
| 128 | 96.67% | 95.51% | 95.79% | 95.95% |
| 85 | 96.62% | 95.62% | 95.80% | 96.01% |
| 64 | 96.61% | 95.36% | 95.78% | 95.99% |
| 51 | 96.59% | 95.39% | 95.77% | 96.04% |
| 32 | 96.53% | 95.40% | 95.80% | 96.06% |
Table 4.
Median accuracy calculated over 30 iterations on the test datasets for the different approaches. The methods using an additional
LCO patching were configured with the best patch size stated in
Table 3.
Table 4.
Median accuracy calculated over 30 iterations on the test datasets for the different approaches. The methods using an additional
LCO patching were configured with the best patch size stated in
Table 3.
| Patching Method | With Confidence Comparison | Without Confidence Comparison |
|---|
| 1S SS | - | 94.08% |
| 1S LS | - | 95.09% |
| 2SSP | 96.92% | 96.25% |
| 2SGCO | 96.41% | 95.61% |
| 2SLCO | 97.07% | 96.67% |
| 2SCM | 96.69% | 95.78% |
| 2SCM-Y | 96.79% | 96.57% |
Table 5.
Computational time (feed-forward time) of the used models with two warm-up predictions and six timed predictions of overview images. Tested on a GeForce RTX 3090 GPU and a Ryzen 5950X CPU.
Table 5.
Computational time (feed-forward time) of the used models with two warm-up predictions and six timed predictions of overview images. Tested on a GeForce RTX 3090 GPU and a Ryzen 5950X CPU.
| Approach | Time (s) |
|---|
| 1S SS | 35.12 |
| 1S LS | 13.35 |
| 2S SP w/o CC | 50.01 |
| 2S LCO w/ CC | 108.49 |
| 2S CM w/ CC | 5702.78 |
| 2S CM-Y w/ CC | 4240.41 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).