Abstract
The electric transmission failure induced by the electrostatic migration and deposition of the friction-pair-produced abrasive dusts in the Solar Array Drive Assembly (SADA) is studied for the first time by integrating experiments and Finite Element Method (FEM) simulation. Particle morphology and composition are characterized by SEM and X-ray EDS, respectively. The size, distribution and average charge of the abrasive dusts are characterized by PSDA as well as the home-made particle charge measurement device. The results show that the dusts’ sizes are in the range of 10–40 μm, and the dusts are primarily composed of Ag and a small amount of Cu and S. Sliced abrasive dusts with an average diameter of 30 μm and a charge of 85 e are used for the FEM prediction of particle trajectory, which is consistent with the theoretical calculation results. The electromagnetic field distribution in the SADA and the electrostatic migration and deposition of abrasive dusts are predicted and analyzed by adopting the FEM method. The experimentally observed dusts’ trajectories in a vacuum chamber with 0.02 Pa vacuum degree are consistent with the simulation results, which qualitatively verifies the accuracy of the FEM model. The predicted results show that the irradiation-induced conductivity increase in polyimide material has little influence on the electric field distribution and the migration and deposition of the abrasive dusts but has great influence on the local current density. Both the potential differences between the two adjacent conducting rings and the loose contact between the electric brush and the conducting rings have significant influence on the migration and deposition of the abrasive dusts, which may greatly increase the surface discharge risk and the electrical transmission instability in the SADA. This study is conducive to the safe and stable operation of the on-orbit spacecrafts.
1. Introduction
The Solar Array Drive Assembly (SADA) is the key component to ensure the normal operation of spacecraft [1,2]. It is located between the solar panel and the spacecraft body, and plays a crucial role in the transmission of the electric power and electric signal by driving the solar panel rotation and then tracking the sun for energy [3,4]. The conductive slip ring is one of the most important components of the SADA for electric transmission. Whether for the disk or the column conductive slip rings, the electric power and the electric signal are transferred primarily by the sliding electrical contact between the electric brush and the conductive ring [5,6,7]. However, due to the rough contact surface, the long-time sliding contact accelerates the wear of the SADA. According to previous studies, Greenwood et al. found that the current-carrying friction pair between the conductive ring and the electric brush can cause adhesive and abrasive wear on the contact surface, and accordingly generate a great amount of abrasive dusts [8]. In order to solve the problem of abrasive dust generation, researchers increased the wear resistance and smoothness of the conductive ring by plating a small amount of antimony salt and other materials on the surface, but this method only reduced the generation of abrasive dusts and could not prevent their generation [9,10].
The abrasive dusts generated by the friction pair can potentially migrate to the electrode gaps of the conductive rings, leading to the gap breakdown and surface flashover under the combined action of electric field and magnetic field as well as electrochemical corrosion [11,12,13]. In addition, as an electronic device, the SADA is directly exposed to the space environment and is easily affected by electromagnetic radiation and high-energy charged particles in space [14]. The spatial high-energy charged particles penetrate the aluminum shield shell and then are deposited in the insulating medium, increasing the conductivity of the insulating medium as well as the internal discharge risk [15,16]. Up to now, several satellite power system faults caused by the SADA discharge have been identified [17]. From the above, it is clear that for a long-life stable operation of spacecraft in orbits, guaranteeing the electric transmission security of the SADA is of vital importance and has recently received more and more attention from researchers.
The migration and deposition of the friction-pair-generated abrasive dusts are predicted to be important factors triggering the internal discharge in the SADA under the combined conditions of microgravity and a complicated electromagnetic field. However, due to the complexity of multi-physical fields’ interaction, the characteristics of the charging, migration and deposition of abrasive dusts in the SADA have not been fully understood. Until now, several studies on the migration behavior of conductive metal particles driven by an electromagnetic field have mainly focused on the particle dynamics caused by inelastic collisions between metal particles and insulating media in gas-insulated transmission lines (DC-GIL) and gas-insulated switches (GIS). Compared with the AC electric field, the migration of conductive particles in GIS and GIL driven by a DC electric field is more random, which has become a serious concern of researchers [18,19].
In the study of the dynamics of abrasive particles, Metwally et al. used wedge electrodes to simulate the DC transmission field with axial inhomogeneity, and developed the charging and migration model of spherical metal particles but did not consider other shapes of particles [20,21]. Nojima et al. focused on the motion behavior of linear conducting particles in an electric field but did not consider the influence of insulating medium shape and electrode spacing [22,23]. Sakai et al. established a detailed dynamics model for conductive particles in consideration of the influencing factors such as the coated film on an electrode plate, particle shapes (sheet, spherical and cylindrical, etc.), particle starting position, transmission line voltage, insulating medium shapes and other influencing factors [23,24]. However, the dynamic behavior of the charged particles subjected to the action of a vacuum, microgravity and a DC unipolar field has not been reported. To the authors’ knowledge, so far, not enough research has been conducted on the charging and migration of the abrasive dusts in the SADA.
Accordingly, in this paper, the migration and deposition of the friction-pair-generated abrasive dusts under the action of the microgravity and the electromagnetic field inside the SADA are investigated by integrated studies of experiment and simulation. Firstly, the morphology, composition and particle size distribution for the SADA abrasive dusts are characterized by scanning electron microscope (SEM), X-ray EDS and laser particle size analyzer (PSDA), respectively. Charge capacities of the abrasive dusts with different diameters are experimentally measured by a home-made particle charge measurement device, which provides an initial charge boundary for dust migration simulation. Secondly, based on the analysis of the space radiation, the migration and deposition of the abrasive dusts in consideration of the action of the microgravity and the electromagnetic field inside the SADA are demonstrated by the Finite Element Method (FEM). The particle trajectory recognized by the FEM model has a good agreement with the experimental observation. Finally, the FEM calculation is carried out to analyze the possible satellite power system faults caused by the migration and deposition of the abrasive dusts inside the SADA.
2. Experimental Setup and Simulation Method
2.1. Experimental Setup
Figure 1 shows the schematic diagram of the experimental setup. The experimental system is mainly composed of a charge measurement device, a ground simulated device for dust migration and deposition and a driving power supply. The servo motor provides the SADA with the rotation speed. The DC power supply applies rated current and voltage on the conductive slip ring of the SADA. The high-speed camera is used to observe and record the particle trajectory and the deflection angle inside the SADA. The friction-pair-generated abrasive dusts are removed from the SADA and then transferred to the home-made charge measuring device for charge measurement under insulation conditions. Oscilloscope is used to monitor the current and voltage change in the circuit. The parallel plate electric field is produced by a DC power supply. The vacuum chamber is used to eliminate the influence of air flow on dust migration and deposition.
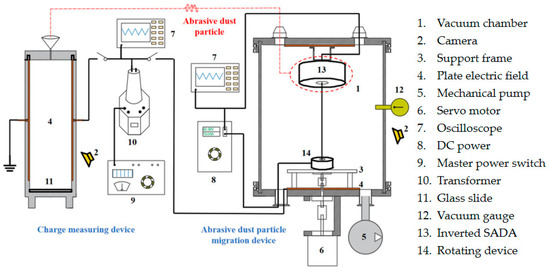
Figure 1.
Schematic diagram of the experimental setup.
The dust charge measurement experiment, as shown in the left part of Figure 1, is carried out in atmospheric environment. Main body of the charge measuring device is composed of two parallel metal plates, forming a uniform electric field between two plates. The value range of the electric field strength can be changed by adjusting the applied voltages of the DC power supply. The charged dusts deflect towards the electrically opposite electrode, while the abrasive dusts pass through the funnel formed by the parallel plates. The uncharged dusts, however, fall to the funnel bottom vertically. According to deflection angle of the charged dusts as well as the electric field intensity between the two parallel plates, the charge-to-mass ratio of the abrasive dusts can be calculated, as shown in Equation (1),
where q/m is the charge-to-mass ratio, θ is the deflection angle of the abrasive dusts, L is the gap distance between two plates (10 mm in this work), V is the applied voltage (0–3000 V) and E is the electric field intensity.
As shown in the right part of Figure 1, the migration trajectories of the abrasive dusts are observed by a high-speed camera. In order to eliminate the influence of air flow on dust migration and deposition, the observation experiment is carried out in the vacuum chamber with 0.02 Pa vacuum degree. Here, positively charged conductive slip ring is inverted, ensuring the charged dusts move downward. The high-speed camera-recorded trajectories of the abrasive dusts are used to qualitatively verify the FEM calculation results in this study.
2.2. Simulation Method for Abrasive Dusts’ Migration
Electromagnetic field distribution in the SADA is solved based on Maxwell’s equations. COMSOL Multiphysics software based on FEM is adopted to solve the Maxwell’s equations. Characterization results of the abrasive dusts charge and the electrical properties of materials irradiated by the space irradiation environment are taken as the inputs to ensure the accuracy of the predicted results. The mathematical model used in this simulation is as follows:
where is the conduction current density, E is the electric field intensity and the unit is V/m, B is the magnetic flux density, and σ is the conductivity of the material. B = μ0μrH, where μr is the relative permeability of the material. D = ε0εrE, where εr is the relative dielectric constant of the material. According to the characterization results of the abrasive dusts by X-ray EDS analysis and SEM, μr and εr for both the conductive ring and the electric brush are taken as 0.99 and 1, respectively. For the insulating material made of polyimide, μr and εr are taken as 1 and 3.5, respectively.
Because of the geometry symmetry, half SADA is modeled. The model structure is modeled by 1:1 with the actual disc slip ring structure, and the thickness and width of the conducting ring are determined to be 1.75 and 3.5 mm, respectively, as shown in Figure 2a,b. Periodic continuity condition is set to the axial truncation surface. Terminal current boundary is set to the end of the upper electric brushes, the current is set as 10 A, the current source is set to the brush head, and grounded boundaries are set to the lower electric brushes. The applied voltages on the upper electric brush and the lower electric brush are 42 and 0 V, respectively. The steady-state iterative solver named “FGMRES” was used for electromagnetic field simulation. The transient iteration solver named “GMRES” was used in the simulation of abrasive dusts’ trajectory. The output time was set as 150 s, the step size was 5 s. In view of the great influence of particle shape on the simulation results [25], the particle shape of the particle is not a single shape according to the characterization results. Therefore, the default spherical particle shape of the software is adopted firstly, and the average mass of the particle size of 10 μm to 40 μm is set as the mass of the simulation particle, that is the mass of the simulation particle is 4.7 × 10−11 kg, and the charge number of the simulation particle is set as 85 e.
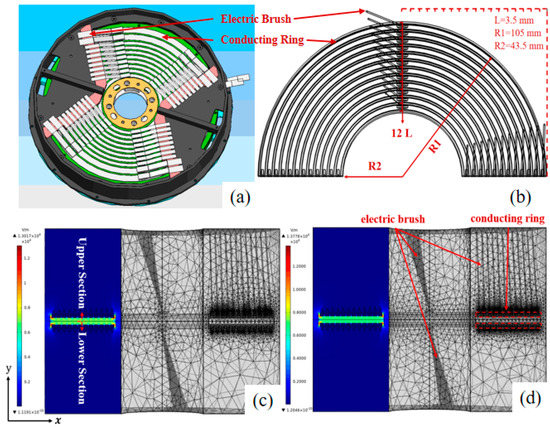
Figure 2.
Geometry and mesh generation for the modelling (a) structural geometry, (b) simulation model, (c) regular mesh and (d) refined mesh of SADA.
Grid refinement is performed to improve the calculation accuracy and ensure the accuracy of simulation results. Figure 2c uses a conventional grid, containing 239,606 domain units, 90,665 boundary units and 15,306 side units, and Figure 2b uses a refined grid, containing 437,450 domain units, 92,621 boundary units and 21,548 side units. By comparing the simulation electric field results, the maximum electric field simulation result of the conventional grid is 13,017 V/m, and the maximum electric field simulation result of the refined grid is 13,778 V/m. As such, the difference between the two results is less than 6%. In order to improve the calculation efficiency, the conventional grid method is chosen.
2.3. Space Irradiation Simulation Method
Monte Carlo method (CASINO computing platform) is used to simulate the interaction between the space high-energy electrons and the SADA materials [26]. By using the MD method, trajectories of high-energy electrons deposited in the materials can be obtained [27,28]. The CASINO platform takes into account the distance of particles after two consecutive collisions, and the formula is as follows:
where L is the distance after two collisions. is the electron level transition wavelength, and this parameter can be eliminated in (3). Ci is the atomic proportion of element i, is the atomic weight of element i, is the workpiece density and the unit is , is Avogadro’s constant, is the collision cross-section area and the unit is nm2, the value sets can be found in the table in literature [29].
After penetrating the metal shielding shell of the SADA, high-energy electrons deposit at a certain depth inside the polyimide material. The incidence depth of high-energy incident electrons can be calculated by Weber Semiempirical Formula [30], as shown below.
where R is the maximum incident depth of high-energy electron, Ep is the incident electron energy, is the material density, and , and are constants (, , ). The energy deposition per unit distance can be solved according to the maximum incident depth of high-energy electrons, and the formula is as follows.
2.4. Force Analysis for Abrasive Dusts
The abrasive dusts inside the SADA are affected by Coulomb force, Lorentz force, gravity force, drag force and adhesion force near wall. Freezing boundary is set while the particles colliding with the wall, so, the adhesion force is not considered in this calculation. By referring to the FEM calculation of the electromagnetic fields and the experimentally characterized morphology, density and charge of the abrasive dusts, force analysis for abrasive dusts’ migration inside the SADA with varied particle diameter is calculated and shown in Figure 3. When the air pressure drops to 0.01 atm, the influence of the drag force on the abrasive dusts’ migration is greatly weakened. Specifically, with the average particle diameter of 30 μm and the vacuum degree of 0.02 pa in the vacuum tank in this study, influence of the drag force on the abrasive dusts’ migration can be ignored. Note that in the microgravity environment in orbit, the dust movement is primarily driven by the coulomb force; however, in the gravity environment on ground, the dust movement is primarily driven by the gravity force. As such, in order to observe the charged dusts’ movement in the ground experiment, the disk SADA is placed upside down, as shown in Figure 1.
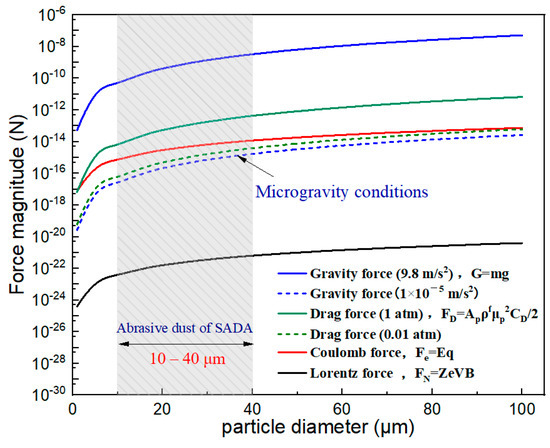
Figure 3.
Force analysis for abrasive dusts in SADA.
3. Results and Discussion
3.1. Experimental Characterization of Abrasive Dusts
As described above, the dust charge measurement device is utilized to characterize the dust charging. Taking the particle diameter of 30 μm as an example, when the voltage applied on the High Voltage Electrode is 1 kV, most of the abrasive dusts deflect towards the ground electrode, and only a few deflect towards the High Voltage Electrode. From this, it can be seen that most of the positive friction-pair-produced dusts are positively charged. Further observation finds that when the applied voltage is increased to 2 kV, all the abrasive dusts deflect to the ground electrode. According to the relation between the charge-to-mass ratio and the deflection angle of the charged dusts as well as the electric field intensity, particle charge can be obtained, as shown in Figure 4.
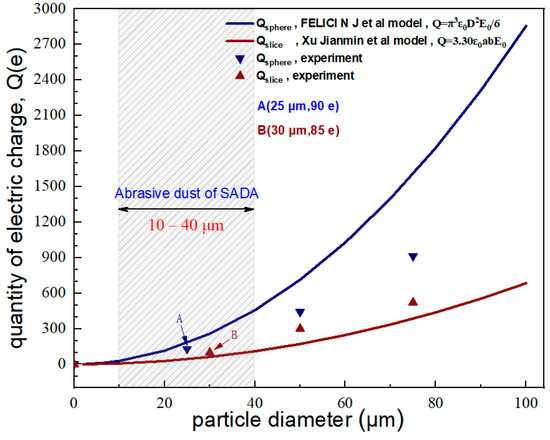
Figure 4.
Comparison of the particle charge between theoretical calculation and experimental measurement.
Theoretical calculation of the abrasive dusts’ charge based on different theoretical models is simultaneously carried out [31,32], as presented in Figure 4. Qsphere represents the conduction charge of a sphere particle. Qslice represents the conduction charge of a sliced particle. According to the FEM prediction, the electric field intensity near the conductive slip surface is set to 1000 V/m. From Figure 4, in the particle diameter range of 0–100 μm, the experimental measurements and the theoretical calculations of the abrasive dusts’ charge are at the same order of magnitude. Specifically, for the sliced particles with an average particle diameter of 30 μm, the theoretically calculated charge is 61 e, and the experimentally measured charge is 85 e. Abrasive dusts with an average diameter of 30 μm and charge of 85 e are finally used for FEM prediction of the particle trajectory.
Figure 5 shows the particle morphology characterized by JSM-6301F SEM and the particle composition analyzed by INCA-300 X-ray EDS. The SEM characterization results show that most of the abrasive dusts are featured with a 10–40 μm size distribution, a thin-sliced shape and sharp corners. According to the X-ray EDS results, the abrasive dusts are mainly composed of Ag, containing a small amount of Cu and S, which indicates that the abrasive dusts are mainly produced from the electric brush.

Figure 5.
Characterization of the abrasive dusts’ (a) morphology, (b) single dust morphology and component analysis.
The particle size distribution is measured by the MASTERSIZER2000 laser particle size analyzer. The sample is wet injected with water as a dispersing medium. As shown in Figure 6, the average particle size measured by the laser particle size analyzer is 20.734 μm, and the specific surface area is 0.576 m2/g. In addition, the measured particle sizes are primarily distributed within a 10–40 μm range. In order to ensure the accuracy of the characterization results, the laser diffraction principle is adopted to correct the raw measured results of the laser particle size analyzer. After correction, the actual average particle size is 29.62 μm and the particles are concentrated in the range of 14.29–57.14 μm. The characterization results of the morphology, composition and particle size for the abrasive dusts provide more accurate and detailed inputs for FEM modelling.
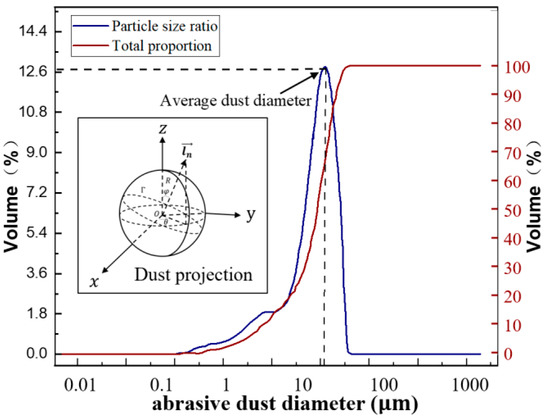
Figure 6.
Particle size distribution of the abrasive dusts measured by the laser diffraction particle size analyzer.
3.2. Damage Effect of Space Energetic Particles on SADA
The shielding shell of the SADA is usually made of super-hard aluminum material, aiming to prevent the space energetic particle radiation and then generate charging and discharging. Despite this, when the radiant energy is large enough, the space energetic particles can still penetrate the shell and damage the SADA material.
The space-radiation-induced charging–discharging phenomenon is herein carried out based on CASINO software to simulate the physical process of the high-energy electron beam acting with the shielding shell as well as the SADA polyimide material. High-energy electrons act on the surface of the shell material in a vertical direction. The Al material density is set to 2.702 × 103 kg/m3 and the thickness is 5 mm [33]. The number of electrons is set to 100,000 and the electron energy varies from 1 to 7 MeV. The simulation results are shown in Figure 7.
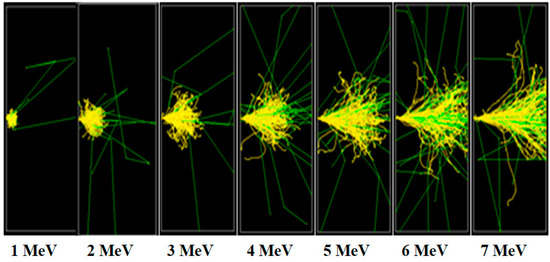
Figure 7.
Predicted results of the spacecraft shielding shell damage irradiated by high-energy electrons.
The yellow lines represent the motion of electrons and the green lines represent the motion of neutral particles in the material. It can be seen from the simulation results that with the increase in electron energy, the depth of electron incident in the shielding shell increases gradually. When the electron energy reaches 3 MeV, a small number of the electrons begin to penetrate the shielding shell. When the electron energy reaches 7 MeV, almost all the electrons penetrate the shell material. Due to the randomness of energy distribution, electrons have a large range of motion inside the shielding shell.
As can be seen in Figure 8a, when the electron energy is less than 4 MeV, the high-energy electrons have energy loss along the shielding shell. However, when the electron energy is greater than 4 MeV, barely no energy loss occurs. Further observation finds the high-energy electrons present a parabolic deposition law and the maximum deposition energy is reached at a certain depth. With the increase in electron energy, the position of the maximum deposition energy is gradually deepened. As can be seen in Figure 8b, with the increase in the energy of electrons, the number of electrons deposited on the shielding shell surface decreases. More and more electrons pass through the shielding shell and enter the SADA polyimide material.
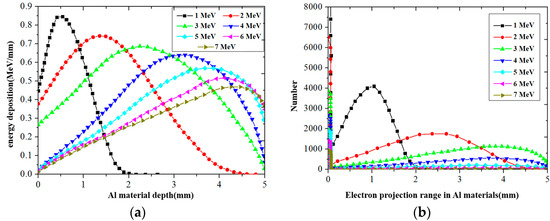
Figure 8.
Energy and electron distribution in spacecraft shielding shell (a) energy deposition, (b) electron projection range.
When the SADA polyimide material is exposed to the strong radiation, its conductivity increases significantly. Considering the energy and the flux of the high-energy particles in the orbits of the spacecraft, the relation between the radiation-induced conductivity and the electron deposition depth can be obtained, as shown in Figure 9, which is used as the inputs for the radiation-damaged material for the following simulation.
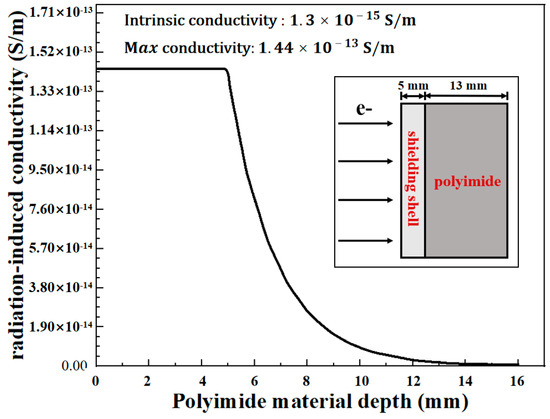
Figure 9.
Radiation-induced conductivity change in the polyimide materials.
3.3. Model Validity
Based on the FEM method, the motion and migration of the abrasive dusts driven by the electromagnetic field of the SADA are simulated and analyzed. Figure 10a and Figure 11a show the axial cross-section view of the magnetic field distribution of the SADA in its perfect working order. It can be seen that the maximum magnetic field intensity is 0.01 T. Correspondingly, the Lorentz force is calculated to be between 10−23 N~10−20 N. It is therefore determined that the Lorentz force has little effect on the abrasive dusts’ movement and migration and can be ignored.
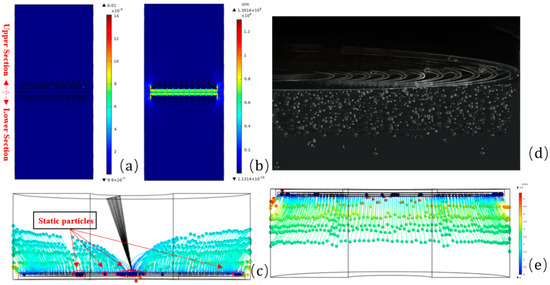
Figure 10.
FEM simulation of (a) axial electric field intensity, (b) magnetic field intensity of electric brushes and (d) experimentally observed dusts’ movement in the vacuum chamber and (c,e) migration of abrasive dusts in the SADA.
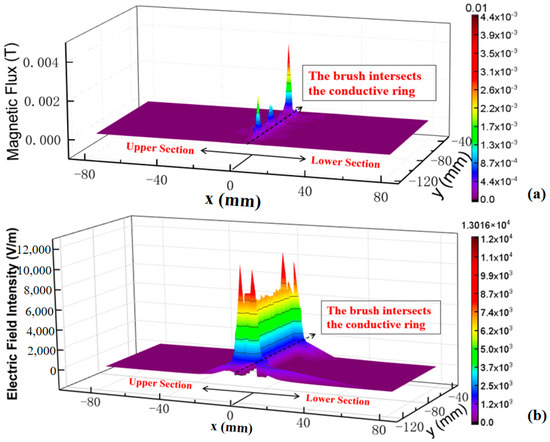
Figure 11.
Spatial distributions of (a) the magnetic flux and (b) the electric field intensity in the axial section of the electric brush in a perfect working order.
Figure 10b illustrates the electric field distribution of the axial section of the electric brush of the SADA in its perfect working order. The maximum electric field inside the SADA is about 1.3017 × 104 V/m, and the calculated electric field force is 10−16 N~10−13 N. Considering the size and weight of the abrasive dusts and the microgravity environment in space, it is concluded that the electric field has a great influence on the movement and migration of the abrasive dusts. As observed in Figure 11b, the electric field intensity reaches the maximum at the positions where the insulating medium makes contact with the inner and outer conductive rings, and gradually weakens while the insulating medium is away from the conductive rings. In addition, the electric field intensity on both sides of the insulating medium is much greater than that away from it, which implies that the abrasive dusts generated on the innermost and outermost conductive rings are significantly affected by the local electric field.
Figure 10c indicates the simulation of the movement and migration trends of the abrasive dusts under the action of the SADA electromagnetic field. As can be seen from the figure, the maximum velocity of the abrasive dusts is about 5.4 × 10−3 m/s. Almost all the abrasive dusts move from the conductive ring to the outer shell, resulting in the accumulation of abrasive particles on the outer shielding shell. Correspondingly, a small part of the abrasive dusts are stationary on the surface of the conductive ring. This means that the electric field is the main factor influencing the motion of the abrasive dusts.
Figure 10d,e show the motion trajectories of the abrasive dusts obtained by the experimental observation and the simulation calculation, respectively. Comparatively, the experimentally observed dusts’ trajectories are consistent with the simulation results, which qualitatively verifies the accuracy of the FEM model.
3.4. Migration and Deposition of Abrasive Dusts under Fault Conditions
According to the analysis results in Figure 9, the maximum irradiation-induced conductivity of 1.453 × 10−13 S/m is selected as the simulation input. As shown in Figure 12a,c, due to the increase in conductivity in the polyimide material induced by the space irradiation, the maximum electric field decreases from 13,017 to 13,016 V/m. The current density increases by 36.6% from 8.4945 × 106 to 1.16 × 107 A/m2. However, because of the similar vector distribution of the electric field inside the SADA, the movement and migration of the abrasive dusts are kept consistent with or without space irradiation. Thus the irradiation-induced polyimide conductivity has great influence on the local current density but has little impact on the movement and migration of the abrasive dusts. Therefore, the electrical transmission fault induced by the electrostatic migration and deposition of the abrasive dusts under the space irradiation can be ignored.
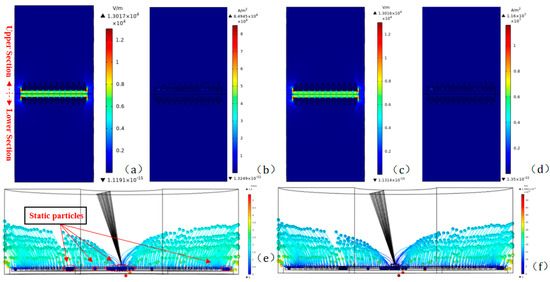
Figure 12.
Spatial distributions of (a,c) electric field intensity, (b,d) current density and (e,f) dust migration in the axial section of the electric brush in perfect working order as well as space charging condition.
Figure 13a–d analyze the effects of the potential differences between two adjacent conducting rings on the electric field distribution as well as the migration trends of abrasive dusts. In contrast with Figure 10, applying a potential difference on the two adjacent conducting rings, the position with the maximum electric field strength transfers from the junction between the insulating medium and the conductive rings to the local insulating medium. When the potential difference increases from 2 to 20 V, the maximum electric field increases by about 64.3% from 13,017 to 21,389 V/m. Correspondingly, the maximum velocity of the abrasive dusts increases from 5.4 × 10−3 to 5.81 × 10−3 m/s. At the same time, the motion trajectories of the abrasive dusts are shifted upward. The potential difference between the adjacent conducting rings has a significant influence on the electric field as well as the movement and migration of the abrasive dusts. As can be seen in Figure 13b,d, when the potential difference increases, the number of stationary abrasive dusts on the surface of the conductive ring increases, indicating the increased surface discharge risk and the instability of the electrical transmission in the SADA induced by deposited particles.
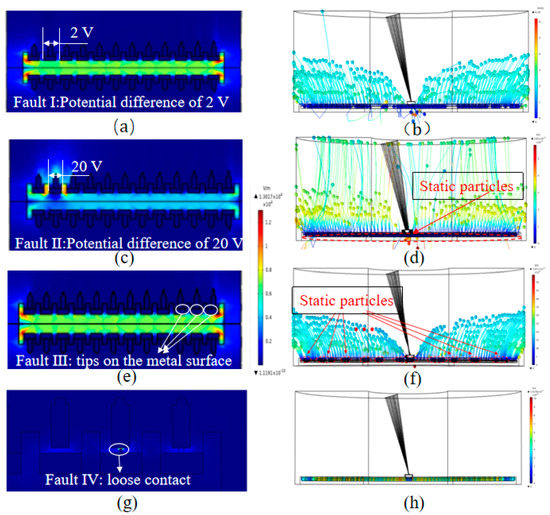
Figure 13.
Spatial distributions of (a,c,e,g) electric field intensity and (b,d,f,h) dust migration in the axial section of the electric brush under different fault conditions.
Figure 13e,f show the effects of the metal surface tips on the electric field distribution as well as the migration trends of abrasive dusts. Compared with Figure 10, the maximum electric field intensity of the axial section of the brush decreases by about 5.1% from 13,017 to 12,347 V/m. Further observation finds that the adhesion positions of the particles moving to the wall are basically the same and the maximum velocity of the abrasive dusts remains largely the same. Therefore, the metal surface tips have a small influence on the electric field as well as the movement and migration of the abrasive dusts. Nonetheless, particles deposited on the conducting slips still have a great possibility to trigger the surface discharge.
Figure 13g,h describe the effects of the loose contact between the electric brush and the conducting rings on the electric field distribution as well as the migration trends of abrasive dusts. Suppose that all three of the outer conductive rings have loose contacts. In particular, as shown in the white circle in Figure 13g, the abrasive dusts are deposited in the gap between the brush and the conductive ring. In contrast with Figure 10, the local electric field gradient between the brush and the conductive ring is greatly increased under the condition of the loose contact. In particular, with the particle deposition in the gap between the brush and the conductive ring, the local electric field rises sharply up to 1.1112 × 106 V/m, greatly increasing the risk of surface discharge.
4. Conclusions
By integrating experiments and FEM simulation, the electric transmission failure of the SADA induced by the electrostatic migration and deposition of the abrasive dusts is studied. JSM-6301F scanning electron microscope and INCA-300 energy spectrum are used to characterize the particle morphology and composition of the abrasive dusts. MASTERSIZER2000 laser particle size analyzer as well as the home-made dust charge measurement device are used to characterize the particle size and distribution and the average charge. The characterization results show that most of the abrasive dusts feature a 14.29–57.14 μm size distribution, a thin-sliced shape and sharp corners. The results also show the abrasive dusts are mainly composed of Ag, yet contain a small amount of Cu and S, which indicates that the abrasive dusts are mainly produced from the electric brush. Furthermore, for a sliced particle with an average diameter of 30 μm, the experimentally measured charge is 85 e, and the theoretically calculated charge is 61 e. Sliced abrasive dusts with an average diameter of 30 μm and charge of 85 e are finally used for FEM prediction of particle trajectory.
Using the FEM method, the electromagnetic field distribution and the movement and migration of abrasive dusts generated by the friction pair in the SADA are analyzed. The results show that the maximum magnetic field intensity inside the SADA is 0.01 T, and the maximum electric field is 1.3017 × 104 V/m. It is thus determined that the electric field is the main influencing factor on the abrasive dusts’ migration. The relationship between the irradiation-induced conductivity and the electron deposition depth is obtained and further used as the input for simulation analysis by considering the energy and flux of high-energy particles in the orbits of spacecraft. The FEM results show that the irradiation-induced conductivity increase in polyimide material has little influence on the electric field distribution and the migration and deposition of the abrasive dusts but has great influence on the local current density.
Several typical faults of the SADA including the potential differences between two adjacent conducting rings, the metal surface tips and the loose contact between the electric brush and the conducting rings are simulated and analyzed. The predicted results show that both the potential differences between two adjacent conducting rings and the loose contact between the electric brush and the conducting rings have significant influence on the electric field as well as the migration and deposition of the abrasive dusts. The surface discharge risk as well as the electrical transmission instability in the SADA may thus be greatly increased. In addition, in the case of tips on the metal surface, more particles deposited on the conducting slips have an equal possibility to trigger the surface discharge. By studying the migration of abrasive dusts under electric transmission failure, the motion trajectories of abrasive dusts are obtained. It is hoped that this study can provide some reference for future research, such as the collection of abrasive dusts and other research directions.
Author Contributions
Conceptualization, T.W. and Q.C.; methodology, Q.C.; software, T.W.; validation, T.W.; formal analysis, Q.C. and T.W.; investigation, Q.C.; resources, Z.M. and J.J.; data curation, T.W.; writing—original draft preparation, T.W.; writing—review and editing, Q.C.; visualization, Q.C.; supervision, Z.M. and J.J.; project administration, Z.M. and J.J.; funding acquisition, Q.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Opening Foundation of Shanghai Key Laboratory of Spacecraft Mechanism: YY-F805202111043; And National Natural Science Foundation of China: 21975018.
Data Availability Statement
All data used during the study appear in the submitted article.
Acknowledgments
The authors would like to thank the grant support from the Opening Foundation of Shanghai Key Laboratory of Spacecraft Mechanism (No. YY-F805202111043) and the National Natural Science Foundation of China (No. 21975018).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cao, Y.; Cao, D.; Wei, J.; Huang, W. Modeling for solar array drive assembly system and compensating for the rotating speed fluctuation. Aerosp. Sci. Technol. 2019, 84, 131–142. [Google Scholar] [CrossRef]
- Wang, X.; Min, D.; Pan, S.; Zheng, S.; Hou, X.; Wang, L.; Li, S. Coupling effect of electron irradiation and operating voltage on the deep dielectric charging characteristics of solar array drive assembly. IEEE Trans. Nucl. Sci. 2021, 68, 1399–1406. [Google Scholar] [CrossRef]
- Chen, J.P.; Cheng, W.; Wang, Y.F. Modeling and simulation of solar array drive assembly disturbance driving a flexible load. In Applied Mechanics and Materials; Trans Tech Publications: Zurich, Switzerland, 2014; Volume 565, pp. 67–73. [Google Scholar]
- Zhang, Y.; Meng, L.; Liu, M. Finite angle multichannel space slip ring design. IOP Conf. Ser. Earth Environ. Sci. 2019, 252, 022108. [Google Scholar] [CrossRef]
- Li, R.; Guo, F.; Yu, C.; He, Y.; Ye, Z.; Yuan, S. Development and validation of a mechatronic solar array drive assembly for mini/micro-satellites. Acta Astronaut. 2017, 134, 54–64. [Google Scholar] [CrossRef]
- Avino, F.; Martens, P.; Howling, A.A.; Bommottet, D.; Furno, I. Gas breakdown mitigation in satellite slip rings. Aerosp. Sci. Technol. 2019, 85, 229–233. [Google Scholar] [CrossRef]
- Zhao, X.; Nie, Y.; Chen, M.; Qin, H.; Xu, X. Analysis of contact characteristics of carbon brush/slip ring under eccentric oscillation of hydrogenerator rotor. Shock Vib. 2021, 2021, 1–12. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Tripp, J.H. The contact of two nominally flat rough surfaces. Proc. Inst. Mech. Eng. 1970, 185, 625–633. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, X.; Cheng, B.; Zhao, Y. Storage life modeling and analysis for contacting slip ring based on physics of failure. IEEE Trans. Compon. Packag. Manufact. Technol. 2017, 7, 1969–1980. [Google Scholar] [CrossRef]
- Grandin, M.; Wiklund, U. Wear and electrical performance of a slip-ring system with silver–graphite in continuous sliding against PVD coated wires. Wear 2016, 348–349, 138–147. [Google Scholar] [CrossRef]
- Dorsey, G. Fretting possibility in slip rings: A review. In Proceedings of the 2017 IEEE Holm Conference on Electrical Contacts, Denver, CO, USA, 10–13 September 2017; pp. 93–101. [Google Scholar]
- Zhang, D.R.; Jin, D. Slip-ring failure mechanism analysis and solution of airborne platform inertial navigation system. Chin. Inert. Technol. 2010, 18, 645–647. [Google Scholar]
- Song, K.; Ma, B.; Yang, G.; Jiang, J.; Wei, R.; Zhang, H.; Zhu, C. A Rotation-lightweight wireless power transfer system for solar wing driving. IEEE Trans. Power Electron. 2019, 34, 8816–8830. [Google Scholar] [CrossRef]
- Luza, L.M.; Wrobel, F.; Entrena, L.; Dilillo, L. Impact of atmospheric and space radiation on sensitive electronic devices. In Proceedings of the 2022 IEEE European Test Symposium (ETS), Barcelona, Spain, 23–27 May 2022; pp. 1–10. [Google Scholar]
- Lai, S.T. Fundamentals of Spacecraft Charging: Spacecraft Interactions with Space Plasmas; Princeton University Press: Princeton, NJ, USA, 2012; ISBN 978-1-4008-3909-4. [Google Scholar]
- Gupta, S.B.; Kalaria, K.R.; Vaghela, N.P.; Mukherjee, S.; Joshi, R.S.; Puthanveettil, S.E.; Shankaran, M.; Ekkundi, R.S. An overview of spacecraft charging research in india: Spacecraft plasma interaction experiments—SPIX-II. IEEE Trans. Plasma Sci. 2014, 42, 1072–1077. [Google Scholar] [CrossRef]
- Tafazoli, M. A Study of on-orbit spacecraft failures. Acta Astronaut. 2009, 64, 195–205. [Google Scholar] [CrossRef]
- Wang, J.; Li, Q.; Li, B.; Chen, C.; Liu, S.; Ji, H. Motion analysis of spherical metal particle in AC gas-insulated lines: Random effects and resistance of the SF6/N2 mixture. IEEE Trans. Dielect. Electr. Insul. 2016, 23, 2617–2625. [Google Scholar] [CrossRef]
- Khan, Y.; Sakai, K.; Okabe, S.; Suehiro, J.; Hara, M. Importance of the consideration of electrical gradient force in the deactivation of free conducting particle under dc voltage. In Proceedings of the IEEE/PES Transmission and Distribution Conference and Exhibition, Yokohama, Japan, 6–10 October 2002; pp. 904–908. [Google Scholar]
- Metwally, I.A.; A-Rahim, A.A. Dynamic analysis of motion of spherical metallic particles in non-uniform electric field. IEEE Trans. Dielect. Electr. Insul. 2002, 9, 282–293. [Google Scholar] [CrossRef]
- Yan, D.; Zhang, Z.; Gong, H.; Ya, Y. Effect of barbed tubular electrode corona discharge EHD flow on submicron particle collection in a wide-type ESP. J. Electrost. 2021, 109, 103545. [Google Scholar] [CrossRef]
- Nojima, K.; Zhang, X.; Sato, M.; Yasuoka, T.; Shiiki, M.; Takei, M.; Boggs, S.A. Forces affecting metallic particle motion in GIS. In Proceedings of the 2014 International Symposium on Electrical Insulating Materials, Niigata, Japan, 1–5 June 2014; pp. 132–135. [Google Scholar]
- Sakai, K.; Labrado Abella, D.; Khan, Y.; Suehiro, J.; Hara, M. Experimental studies of free conducting wire particle behavior between non-parallel plane electrodes with Ac voltages in air. IEEE Trans. Dielect. Electr. Insul. 2003, 10, 418–424. [Google Scholar] [CrossRef]
- Arif, S.; Branken, D.J.; Everson, R.C.; Neomagus, H.W.J.P.; Noras, M.A.; le Grange, L.A.; Arif, A. An experimentally validated computational model to predict the performance of a single-channel laboratory-scale electrostatic precipitator equipped with spiked and wire discharge electrodes. J. Electrost. 2021, 112, 103595. [Google Scholar] [CrossRef]
- Moradnouri, A.; Vakilian, M.; Hekmati, A.; Fardmanesh, M. HTS transformer’s partial discharges raised by floating particles and nitrogen bubbles. J. Supercond. Nov. Magn. 2020, 33, 3027–3034. [Google Scholar] [CrossRef]
- Drouin, D.; Couture, A.R.; Joly, D.; Tastet, X.; Aimez, V.; Gauvin, R. CASINO V2.42—A fast and easy-to-use modeling tool for scanning electron microscopy and microanalysis users. Scanning 2007, 29, 92–101. [Google Scholar] [CrossRef]
- Carriere, P.R.; Yue, S. Energy absorption during pulsed electron beam spot melting of 304 stainless steel: Monte-Carlo simulations and in-situ temperature measurements. Vacuum 2017, 142, 114–122. [Google Scholar] [CrossRef]
- Arat, K.T.; Hagen, C.W. Model sensitivity analysis of Monte-Carlo based SEM simulations. Results Phys. 2020, 19, 103545. [Google Scholar] [CrossRef]
- Hovington, P.; Drouin, D.; Gauvin, R. CASINO: A new Monte Carlo code in C language for electron beam interaction—Part I: Description of the program. Scanning 2006, 19, 1–14. [Google Scholar] [CrossRef]
- Pan, S.; Min, D.; Wang, X.; Hou, X.; Wang, L.; Li, S. Effect of electron irradiation and operating voltage on the deep dielectric charging characteristics of polyimide. IEEE Trans. Nucl. Sci. 2019, 66, 549–556. [Google Scholar] [CrossRef]
- Wu, Y.; Castle, G.S.P.; Inculet, I.I.; Petigny, S.; Swei, G. Induction charge on freely levitating particles. Powder Technol. 2003, 135, 59–64. [Google Scholar] [CrossRef]
- Li, J.; Lu, H.; Xu, Z.; Zhou, Y. A model for computing the trajectories of the conducting particles from waste printed circuit boards in corona electrostatic separators. J. Hazard. Mater. 2008, 151, 52–57. [Google Scholar] [CrossRef]
- Zalevsky, Z.; Rudnitsky, A.; Haran, A.; Zentner, A.; David, D.; Noter, Y. Irradiation test results of components selected from novel optical rotman lens configuration for space systems. Aerosp. Sci. Technol. 2011, 15, 261–268. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).