A Novel Optimization Strategy for Reducing the Initial Error of a Quasi-Steady Algorithm for Conjugate Heat Transfer
Abstract
1. Introduction
2. Numerical Methods
2.1. Baseline Solver for CHT
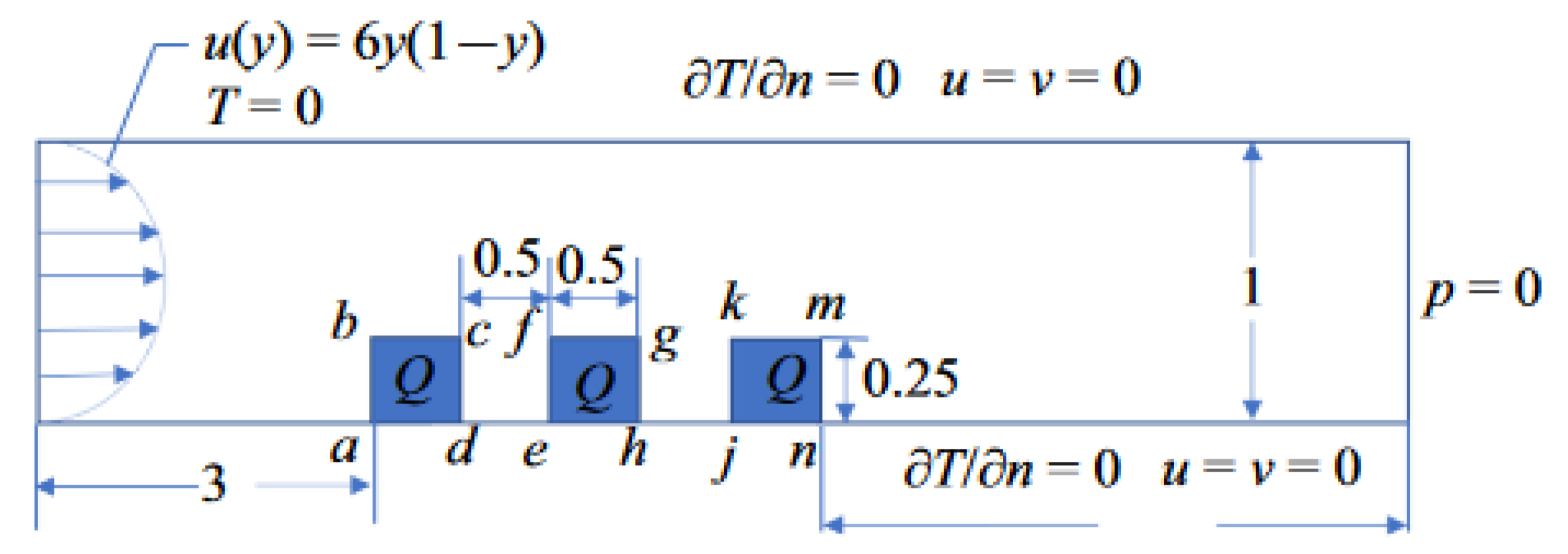
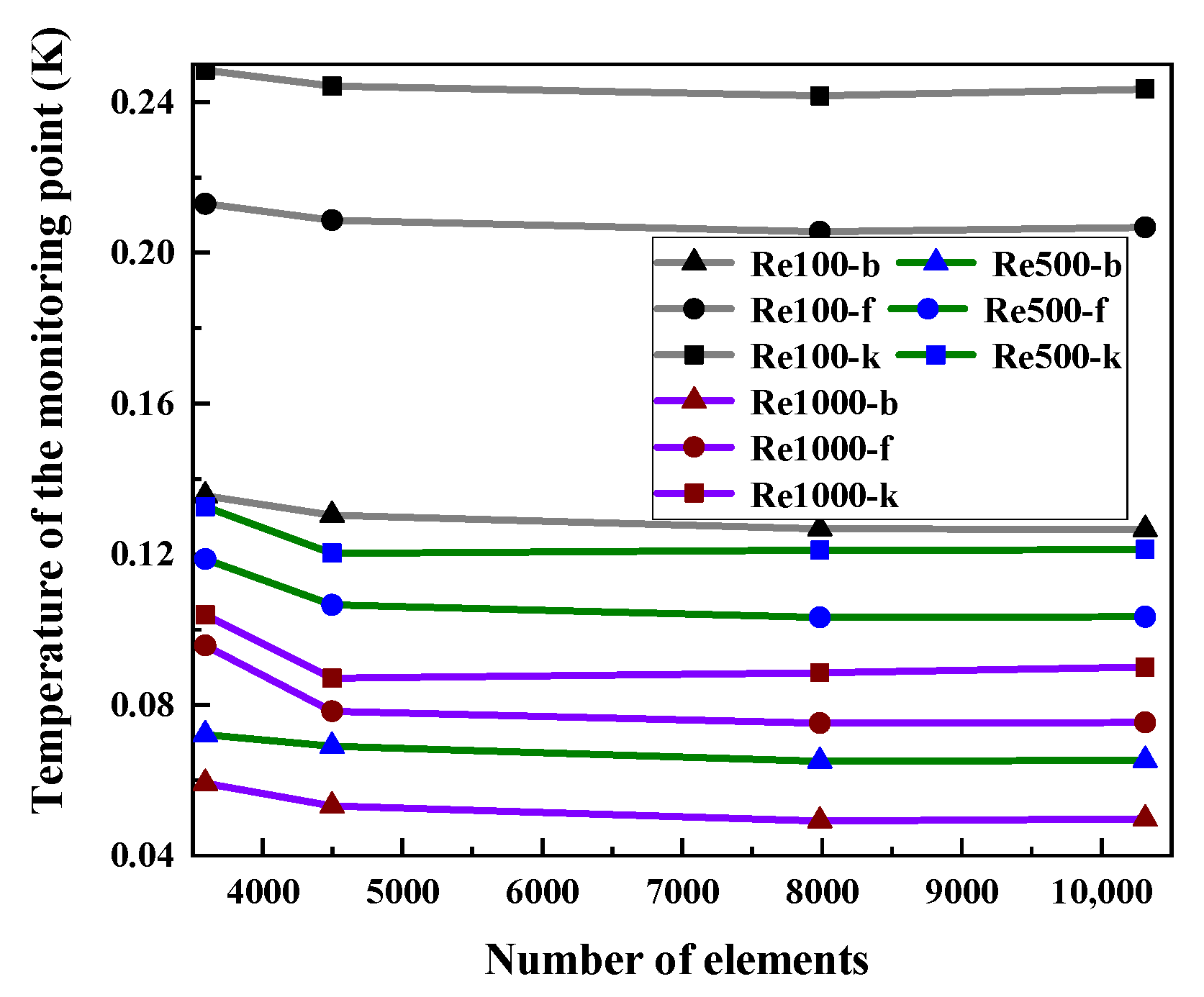
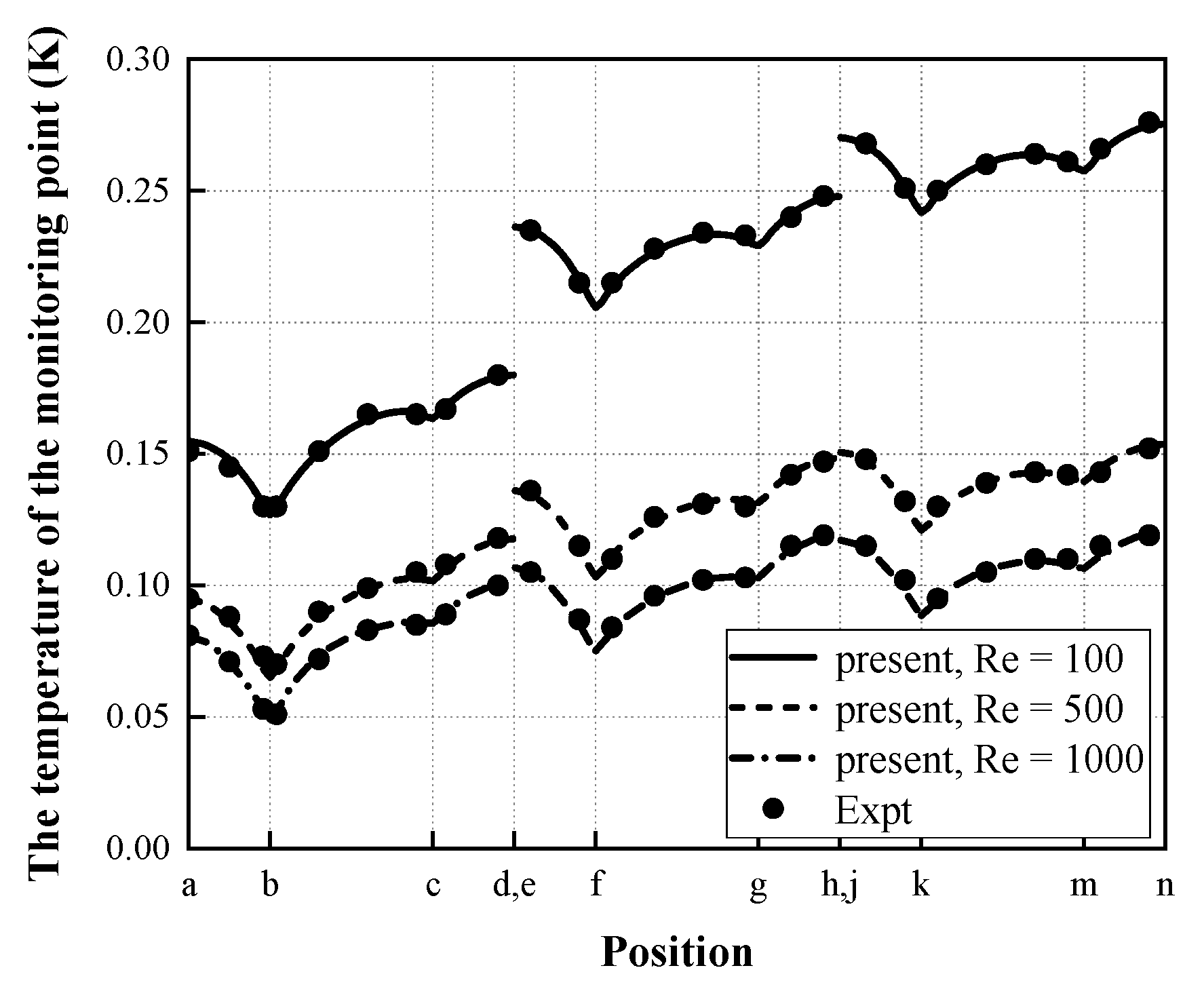
2.2. Solver Validation
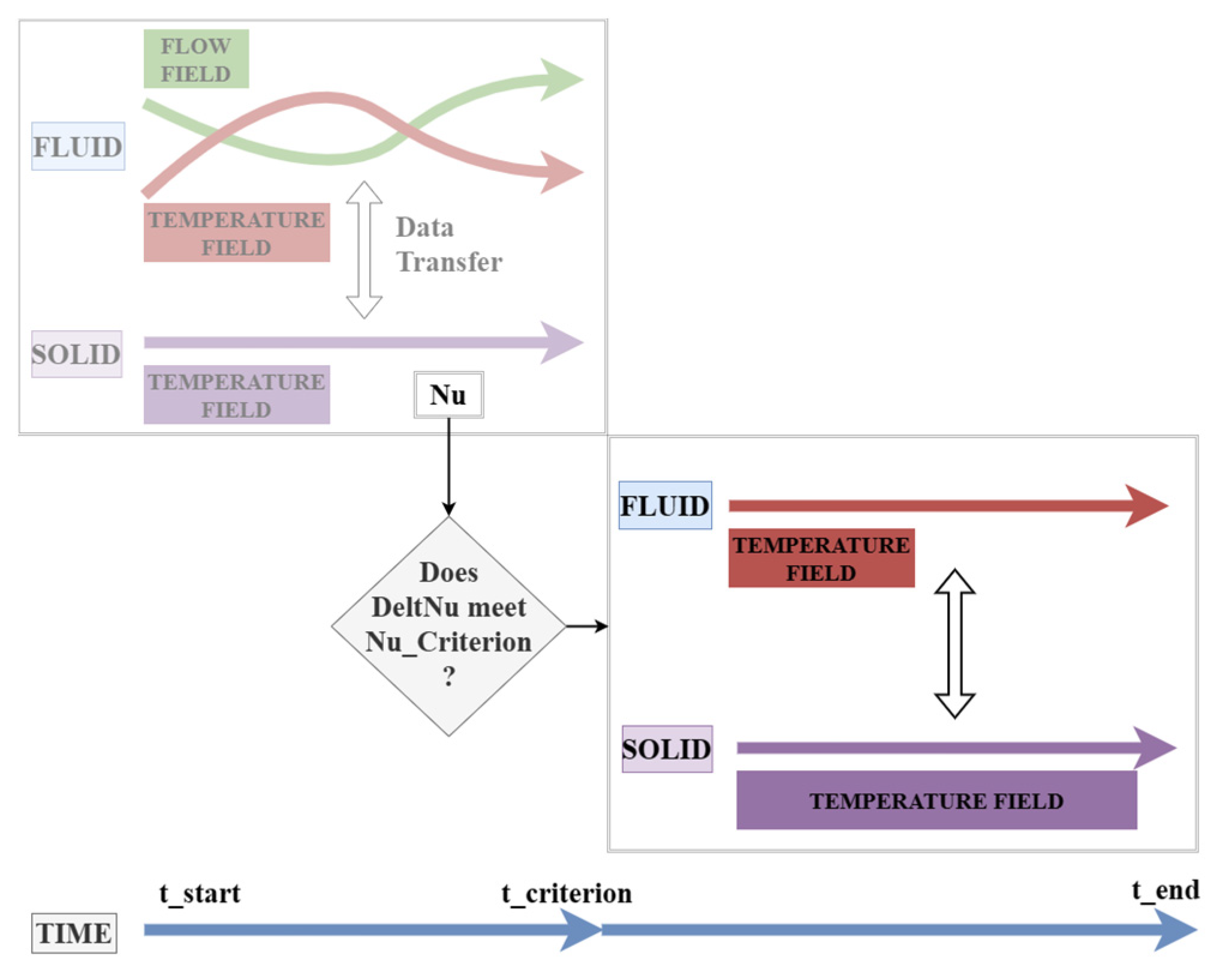
3. New Optimization Strategy
3.1. Description of the Optimization Strategy
3.2. Validation of the Optimization Strategy
4. Test Case and Results
5. Limitations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| u | velocity component (unit: m/s) |
| p | pressure (unit: Pa) |
| v | kinematic viscosity (unit:m2/s) |
| c | specific heat capacity (unit: J/(kg·K)) |
| k | thermal conductivity (unit: W/(m·K)) |
| Q | thermal source terms (unit: W) |
| q | heat flux (unit: W/m2) |
| t | time (unit: s) |
| T | thermodynamic temperature (unit: K) |
| Nu | Nusselt number |
| h | heat transfer coefficient (unit: W/(m2·K)) |
| L | characteristic length (unit: m) |
| Pr | Prandtl number |
| Re | Reynolds number |
| x, y, z | coordinate axis |
| Greek letters | |
| ρ | density (unit: kg/m3) |
| Subscripts | |
| i | serial number |
| j | tensor subscript |
| n | total number of elements for solid boundaries |
| in | entry boundary |
| f | fluid |
| s | solid |
| p | pressure surface, constant pressure |
| pre | previous time step |
| now | current time step |
References
- Afzal, A.; Samee, A.D.M.; Razak, R.K.A. Steady and transient state analyses on conjugate laminar forced convection heat transfer. Arch. Comput. Methods Eng. 2020, 27, 135–170. [Google Scholar] [CrossRef]
- Hotte, F.; Haupt, C. Transient 3D conjugate heat transfer simulation of a rectangular GOX—GCH4 rocket combustion chamber and validation. Aerosp. Sci. Technol. 2020, 105, 106043. [Google Scholar] [CrossRef]
- Wang, X.; Xu, H.Z.; Wang, J.H.; Song, W.; Wang, M. Multi-objective optimization of discrete film hole arrangement on a high pressure turbine end-wall with conjugate heat transfer simulations. Int. J. Heat Fluid Flow. 2019, 78, 108428. [Google Scholar] [CrossRef]
- Amini, Y.; Mokhtari, M.; Haghshenasfard, M. Heat transfer of swirling impinging jets ejected from Nozzles with twisted tapes utilizing CFD technique. Case Stud. Therm. Eng. 2015, 6, 104–115. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Naganthran, K.; Azizul, F.M. Numerical study of conjugate natural convection heat transfer of a blood filled horizontal concentric annulus. Int. Commun. Heat Mass Transf. 2020, 114, 104568. [Google Scholar] [CrossRef]
- Das, S.; Panda, A.; Deen, N.G. A sharp-interface immersed boundary method to simulate convective and conjugate heat transfer through highly complex periodic porous structures. Chem. Eng. Sci. 2018, 191, 1–18. [Google Scholar] [CrossRef]
- Dbouk, T. A new technology for CPU chip cooling by concentrated suspension flow of non-colloidal particles. Appl. Therm. Eng. 2019, 146, 664–673. [Google Scholar] [CrossRef]
- Qing, A.I.; Xia, X.L. Numerical simulation of transient temperature field in the airborne radar cabin. J. Harbin Inst. Technol. 2008, 40, 1767–1772. [Google Scholar]
- Perelman, T.L. On conjugated problems of heat transfer. Int. J. Heat Mass Tran. 1961, 3, 293–303. [Google Scholar] [CrossRef]
- Verstraete, T.; Alsalihi, Z.; Van den Braembussche, R.A. Numerical study of the heat transfer in micro gas turbines. J. Turbomach. 2007, 129, 835–841. [Google Scholar] [CrossRef]
- Dees, J.E.; Bogard, D.G.; Ledezma, G.A.; Laskowski, G.M. The effects of conjugate heat transfer on the thermal field above a film cooled wall. In Proceedings of the ASME Turbo Expo: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 6–10 June 2011; Volume 6, p. GT2011-46617. [Google Scholar]
- He, L.T.; Oldfield, M.L.G. Unsteady conjugate heat transfer modeling. ASME J. Turbomach. 2011, 133, 031022.1–031022.12. [Google Scholar] [CrossRef]
- Ganine, V.; Javiya, U.; Hills, N.; Chew, J. Coupled fluid-structure transient thermal analysis of a gas turbine internal air system with multiple cavities. J. Eng. Gas Turbines Power. 2012, 134, 1025108. [Google Scholar] [CrossRef]
- Beausoleil-Morrison, I. The adaptive coupling of computational fluid dynamics with whole-building thermal simulation. In Proceedings of the 7th International IBPSA Conference, Rio de Janeiro, Brazil, 13–15 August 2001. [Google Scholar]
- Zhai, Z.; Chen, Q. Impact of determination of convective heat transfer coefficient on the coupled energy and CFD simulation for buildings. Proc. Build. Simul. Confer. 2003, 3, 1467–1474. [Google Scholar]
- Chen, Q.; Zhai, Z.; Wang, L. Computer modeling of multiscale fluid flow and heat and mass transfer in engineered spaces. Chem. Eng. Sci. 2007, 62, 3580–3588. [Google Scholar] [CrossRef]
- Rahman, F.; Visser, J.A.; Morris, R.M. Capturing sudden increase in heat transfer on the suction side of a turbine blade using a Navier-Stokes solver. ASME J. Turbomach. 2005, 127, 552–556. [Google Scholar] [CrossRef]
- Luo, J.; Razinsky, E.H. Conjugate heat transfer analysis of a cooled turbine vane using the V2F turbulence model. ASME J. Turbomach. 2007, 129, 773–781. [Google Scholar] [CrossRef]
- Goormans-Francke, C.; Carabin, G.; Hirsch, C. Mesh generation for conjugate heat transfer analysis of a cooled high pressure turbine stage. In Proceedings of the ASME Turbo Expo: Power for Land, Sea, and Air, Berlin, Germany, 9–13 June 2008; Volume 9, p. GT2008-50660. [Google Scholar]
- Shi, Y.; Ding, S.; Qiu, T. Bi-Fo time scaling method in the numerical simulation of transient conjugate heat transfer. Propuls. Power Res. 2021, 10, 15. [Google Scholar] [CrossRef]
- Kazemi-Kamyab, V.; van Zuijlen, A.H.; Bijl, H. Accuracy and stability analysis of a second-order time-accurate loosely coupled partitioned algorithm for transient conjugate heat transfer problems. Int. J. Numer. Methods Fluid. 2014, 74, 113–133. [Google Scholar] [CrossRef]
- Henshaw, W.D.; Chand, K.K. A composite grid solver for conjugate heat transfer in fluid-structure systems. J. Comput. Phys. 2009, 228, 3708–3741. [Google Scholar] [CrossRef]
- Maffulli, R.; He, L.; Stein, P.; Marinescu, G. Fast conjugate heat transfer simulation of long transient flexible operations using adaptive time stepping. ASME J. Turbomach. 2018, 140, 091005.1–091005.10. [Google Scholar] [CrossRef]
- Wang, Z.; Corral, R.; Chaquet, J.M.; Pastor, G. Analysis and improvement of a loosely coupled fluid-solid heat transfer method. In Proceedings of the ASME Turbo Expo: Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013; p. GT2013-94332. [Google Scholar]
- Kazemi-Kamyab, V.; van Zuijlen, A.H.; Bijl, H. A high order time accurate loosely-coupled solution algorithm for unsteady conjugate heat transfer problems. Comput. Methods Appl. Mech. Eng. 2013, 264, 205–217. [Google Scholar] [CrossRef]
- Kazemi-Kamyab, V.; Zuijlen, A.H.; Bijl, H. Analysis and application of high order implicit Runge-Kutta schemes for unsteady conjugate heat transfer: A strongly-coupled approach. J. Comput. Phys. 2014, 272, 471–486. [Google Scholar] [CrossRef]
- Sun, Z.X.; Chew, J.W.; Hills, N.J.; Volkov, K.N.; Barnes, C.J. Efficient finite element analysis/computational fluid dynamics thermal coupling for engineering applications. ASME J Turbomach. 2010, 132, 031016.1–031016.9. [Google Scholar] [CrossRef]
- Ganine, V.; Amirante, D.; Hills, N.J. Aero-thermo-mechanical modelling and validation of transient effects in a high pressure turbine internal air system. In Proceedings of the ASME Turbo Expo: Turbomachinery Technical Conference and Exposition, Seoul, Republic of Korea, 13–17 June 2016; p. GT2016-57739. [Google Scholar]
- Errera, M.P.; Turpin, G. Temporal multiscale strategies for conjugate heat transfer problems. J. Coupled. Syst. Multiscale Dyn. 2013, 1, 89–98. [Google Scholar] [CrossRef]
- Errera, M.P.; Baqué, B. A quasi-dynamic procedure for coupled thermal simulations. Int. J. Numer. Methods Fluid. 2013, 72, 1183–1206. [Google Scholar] [CrossRef]
- Meng, F.; Dong, S.; Wang, J. A new algorithm of global tightly-coupled transient heat transfer based on quasi-steady flow to the conjugate heat transfer problem. Theor. Appl. Mech. Lett. 2016, 6, 233–235. [Google Scholar] [CrossRef]
- Davalath, J.; Bayazitoglu, Y. Forced convection cooling across rectangular blocks. J. Heat Transfer. 1987, 109, 321–328. [Google Scholar] [CrossRef]
- Malatip, A.; Wansophark, N.; Dechaumphai, P. Fractional four-step finite element method for analysis of thermally coupled fluid-solid interaction problems. Appl. Math. Mech. 2012, 33, 99–116. [Google Scholar] [CrossRef]

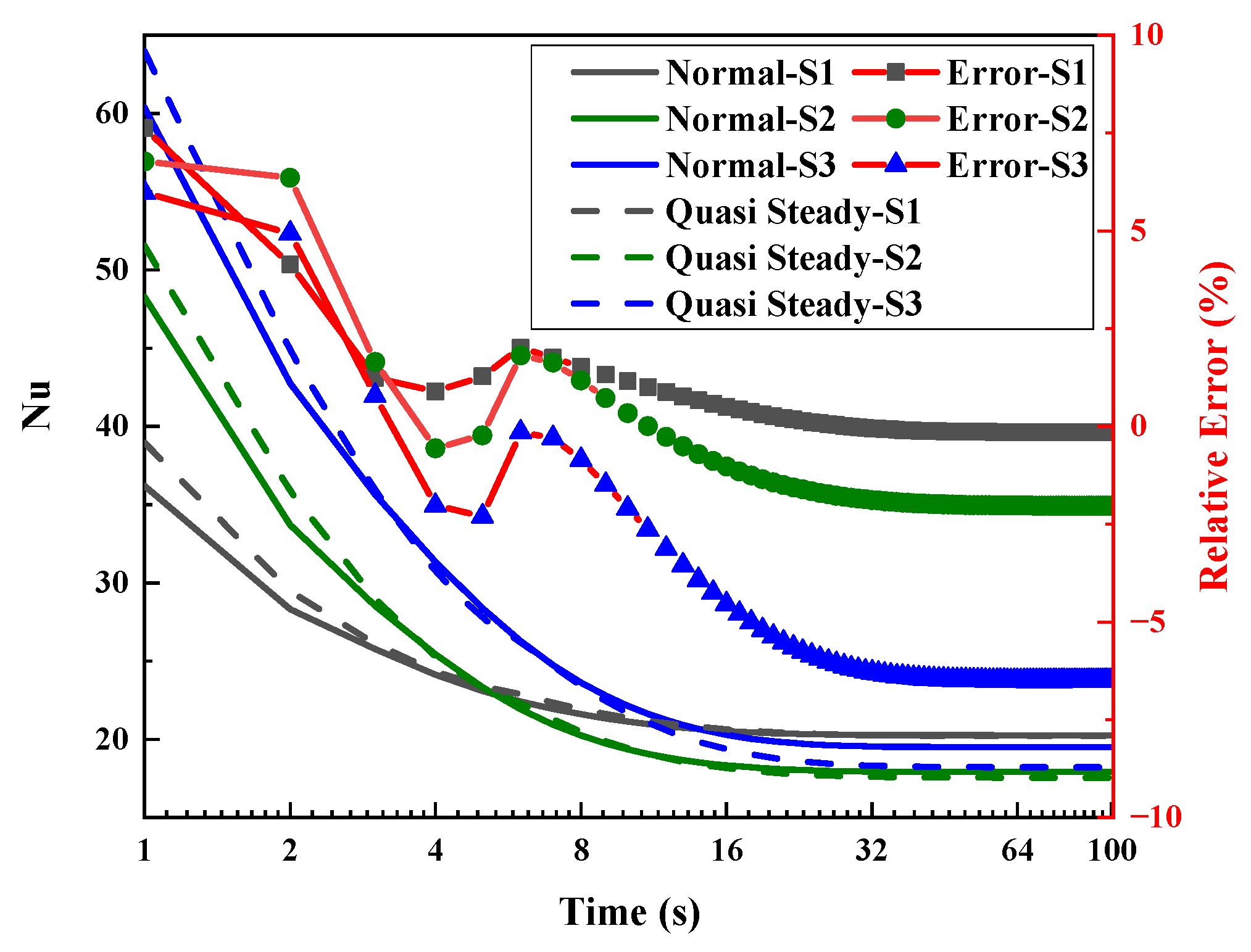
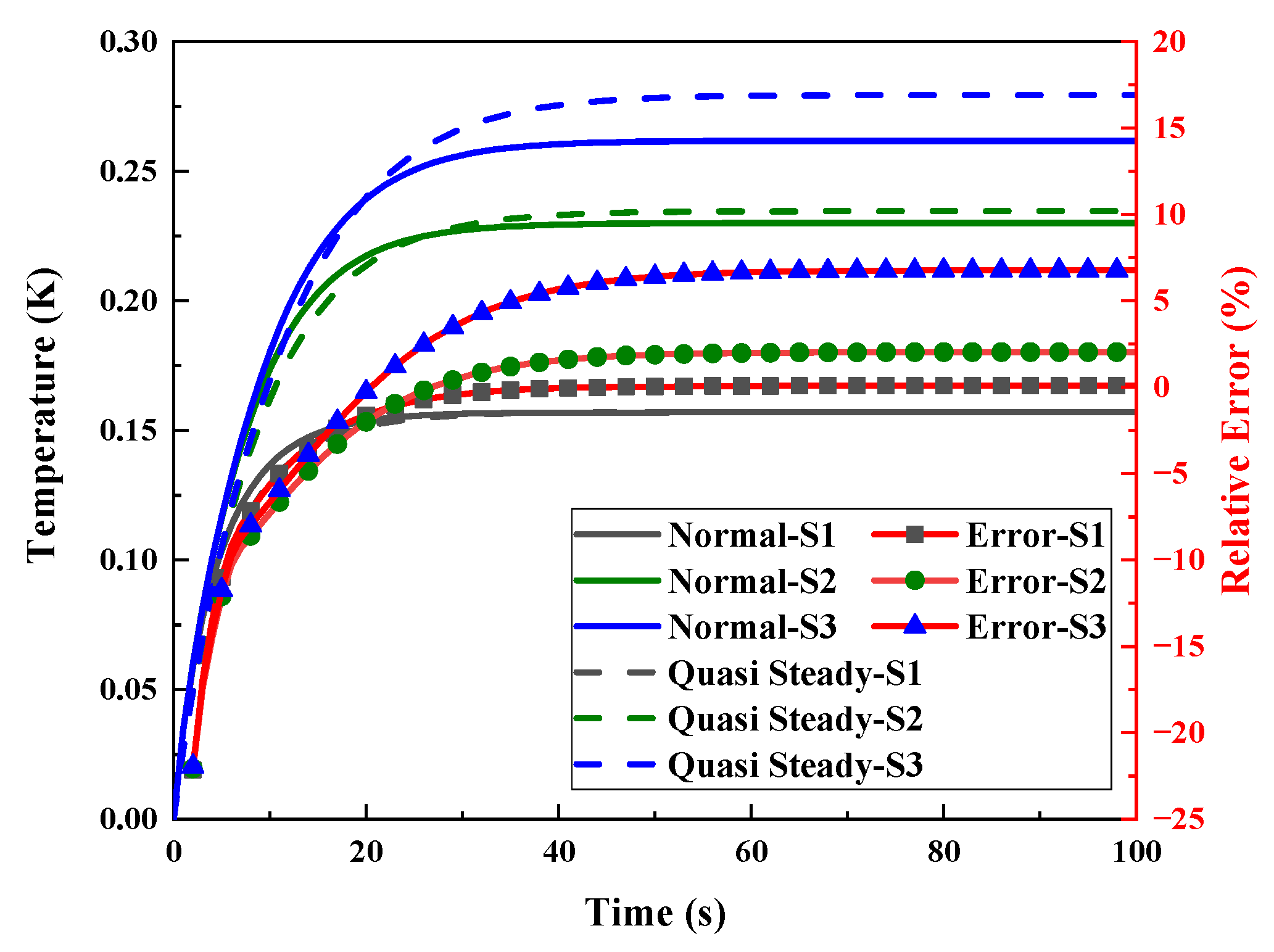
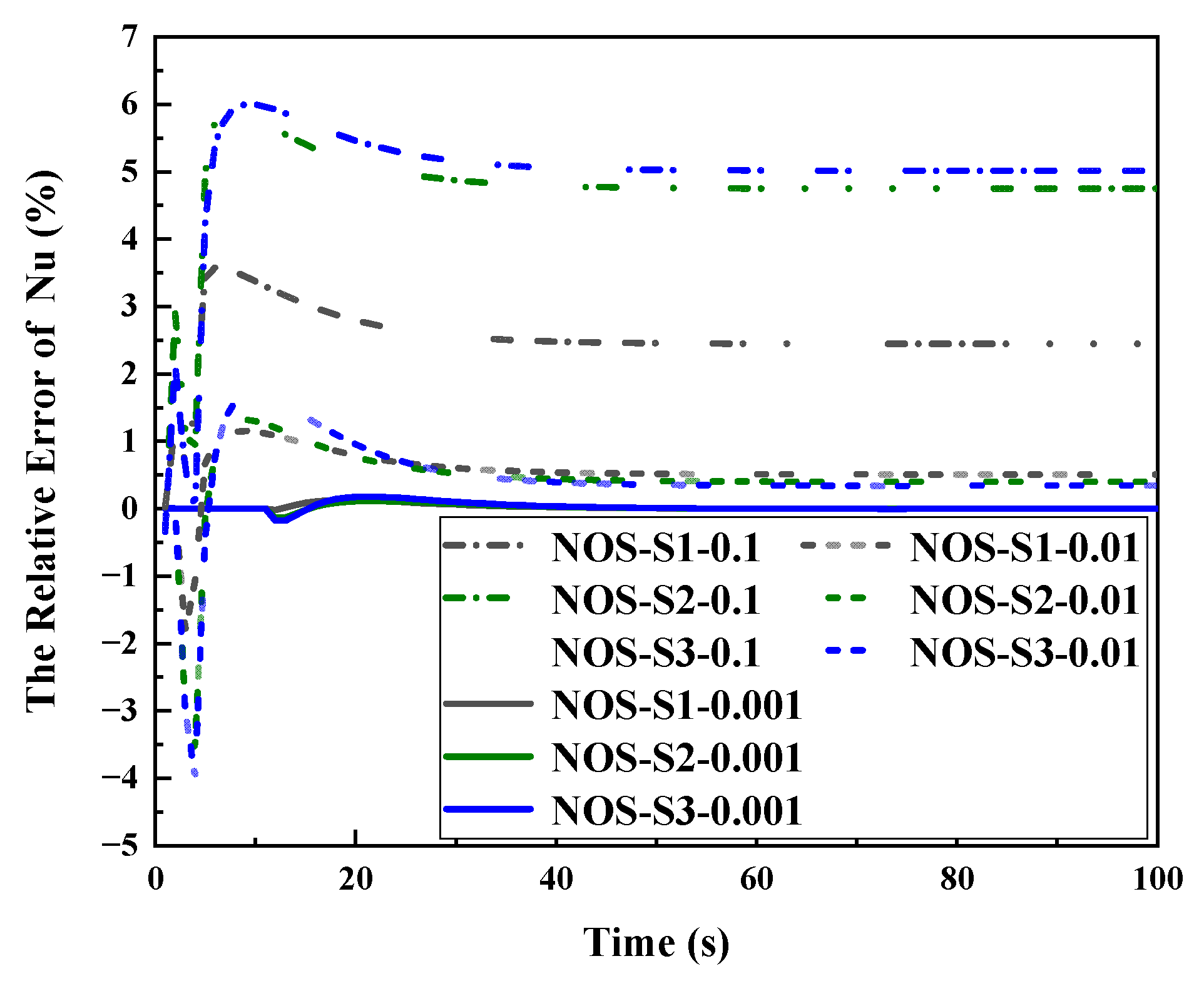
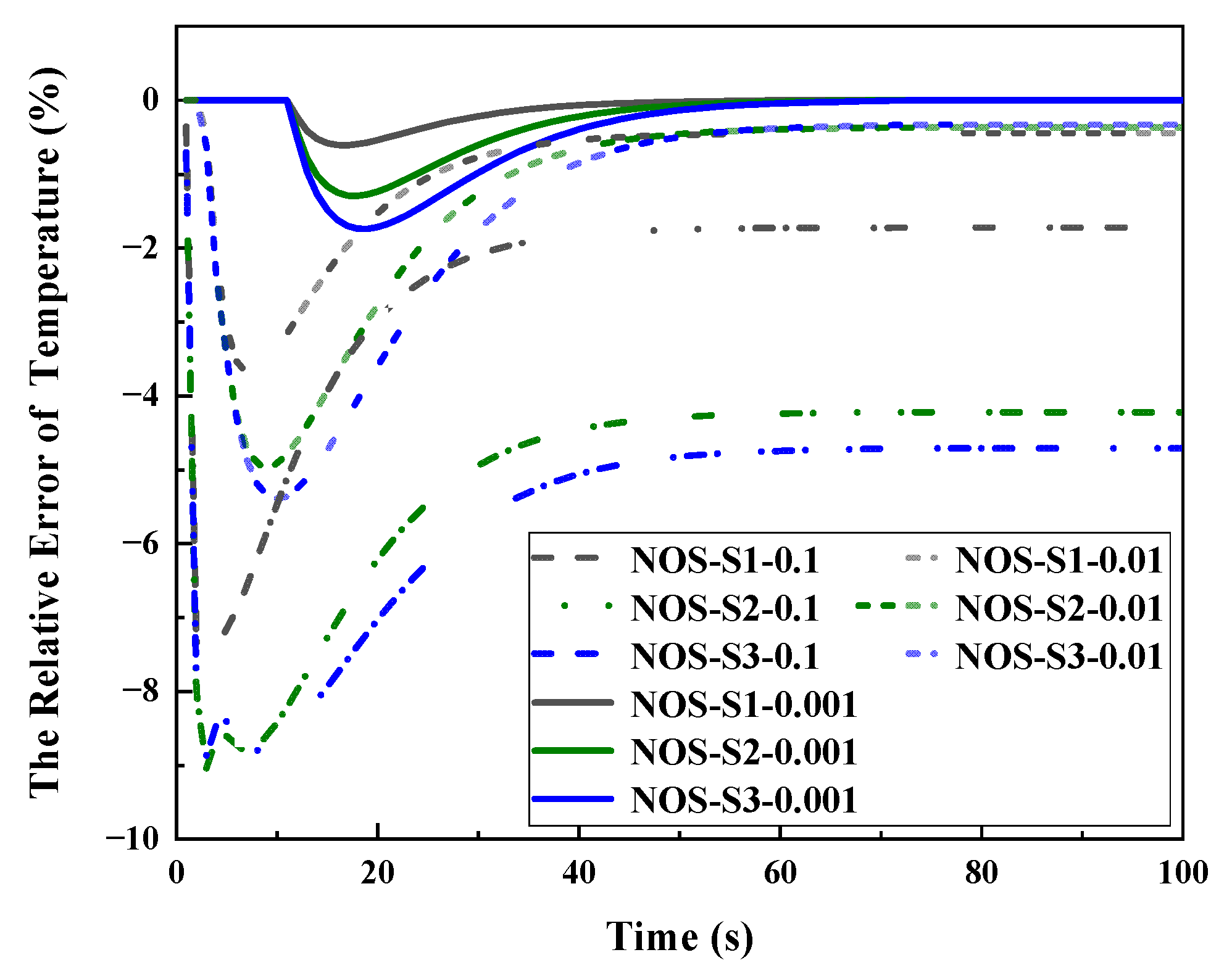
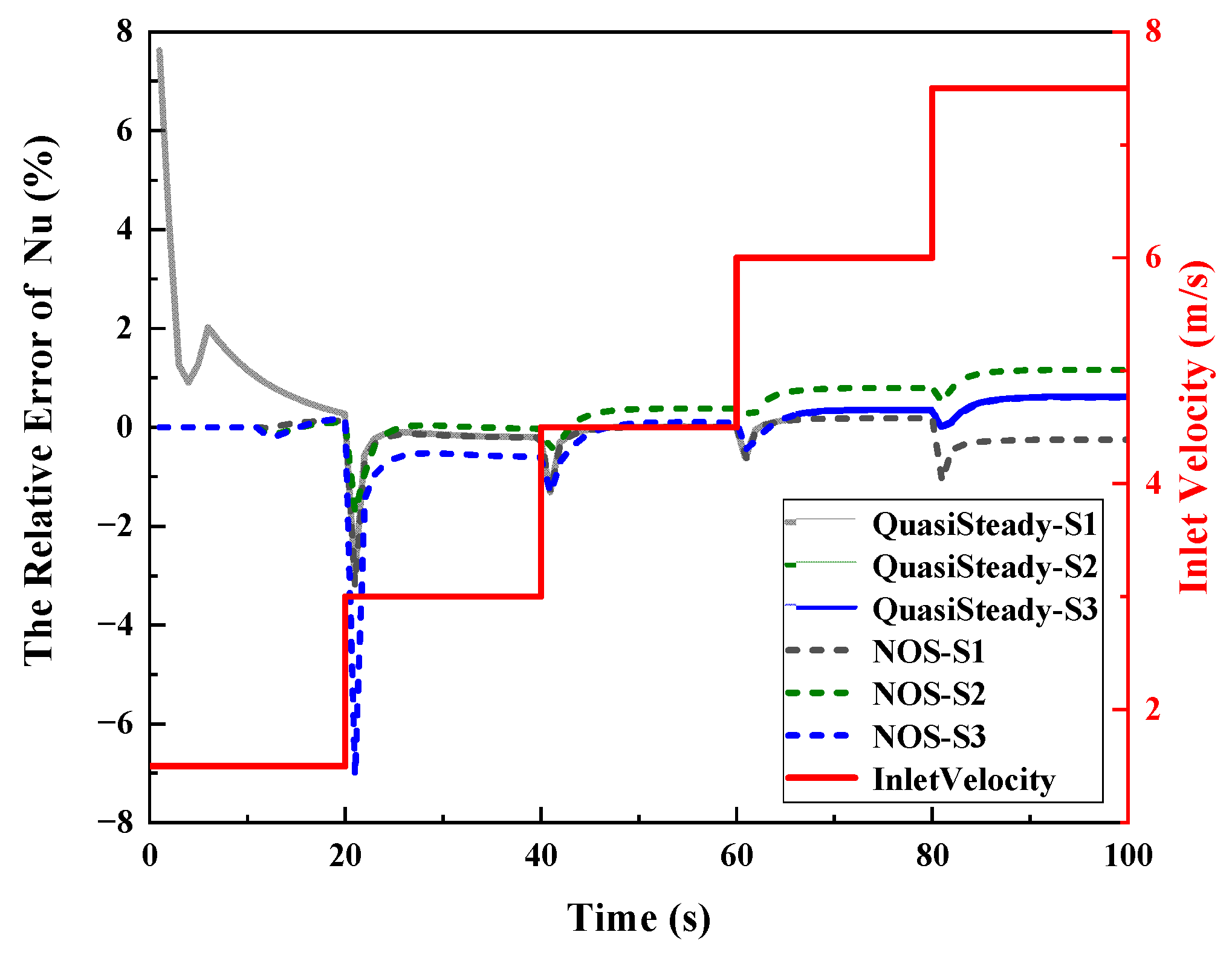
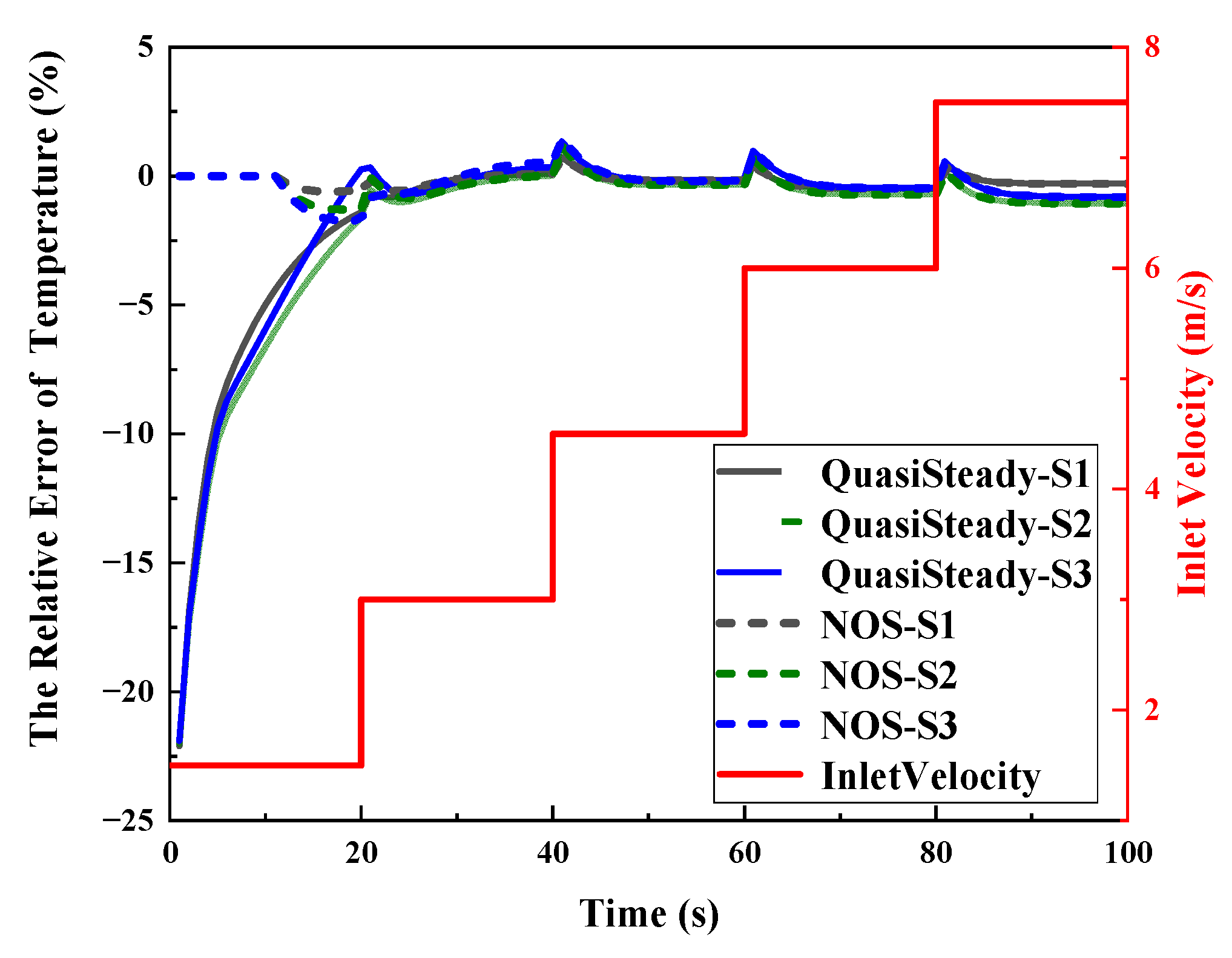
| Algorithm | Nu_Criterion | t_criterion (s) | Computational Time (s) |
|---|---|---|---|
| Normal | - | - | 218 |
| Quasi Steady | - | - | 41 |
| NOS | 0.1 | 0.96834 | 43 |
| NOS | 0.01 | 2.84694 | 66 |
| NOS | 0.001 | 11.2444 | 99 |
| Algorithm | 0–20 s | 20–40 s | 40–60 s | 60–80 s | 80–100 s | Total Time (s) |
|---|---|---|---|---|---|---|
| Normal | 77 | 155 | 215 | 272 | 323 | 1042 |
| Quasi Steady | 36 | 75 | 78 | 81 | 89 | 359 |
| NOS | 72 | 67 | 85 | 87 | 89 | 400 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, B.; Dong, S.; Ding, C.; Cui, Z. A Novel Optimization Strategy for Reducing the Initial Error of a Quasi-Steady Algorithm for Conjugate Heat Transfer. Aerospace 2023, 10, 214. https://doi.org/10.3390/aerospace10030214
Zhao B, Dong S, Ding C, Cui Z. A Novel Optimization Strategy for Reducing the Initial Error of a Quasi-Steady Algorithm for Conjugate Heat Transfer. Aerospace. 2023; 10(3):214. https://doi.org/10.3390/aerospace10030214
Chicago/Turabian StyleZhao, Banghua, Sujun Dong, Chen Ding, and Zhiliang Cui. 2023. "A Novel Optimization Strategy for Reducing the Initial Error of a Quasi-Steady Algorithm for Conjugate Heat Transfer" Aerospace 10, no. 3: 214. https://doi.org/10.3390/aerospace10030214
APA StyleZhao, B., Dong, S., Ding, C., & Cui, Z. (2023). A Novel Optimization Strategy for Reducing the Initial Error of a Quasi-Steady Algorithm for Conjugate Heat Transfer. Aerospace, 10(3), 214. https://doi.org/10.3390/aerospace10030214





