Propagation of Interactions among Aircraft Trajectories: A Complex Network Approach
Abstract
1. Introduction
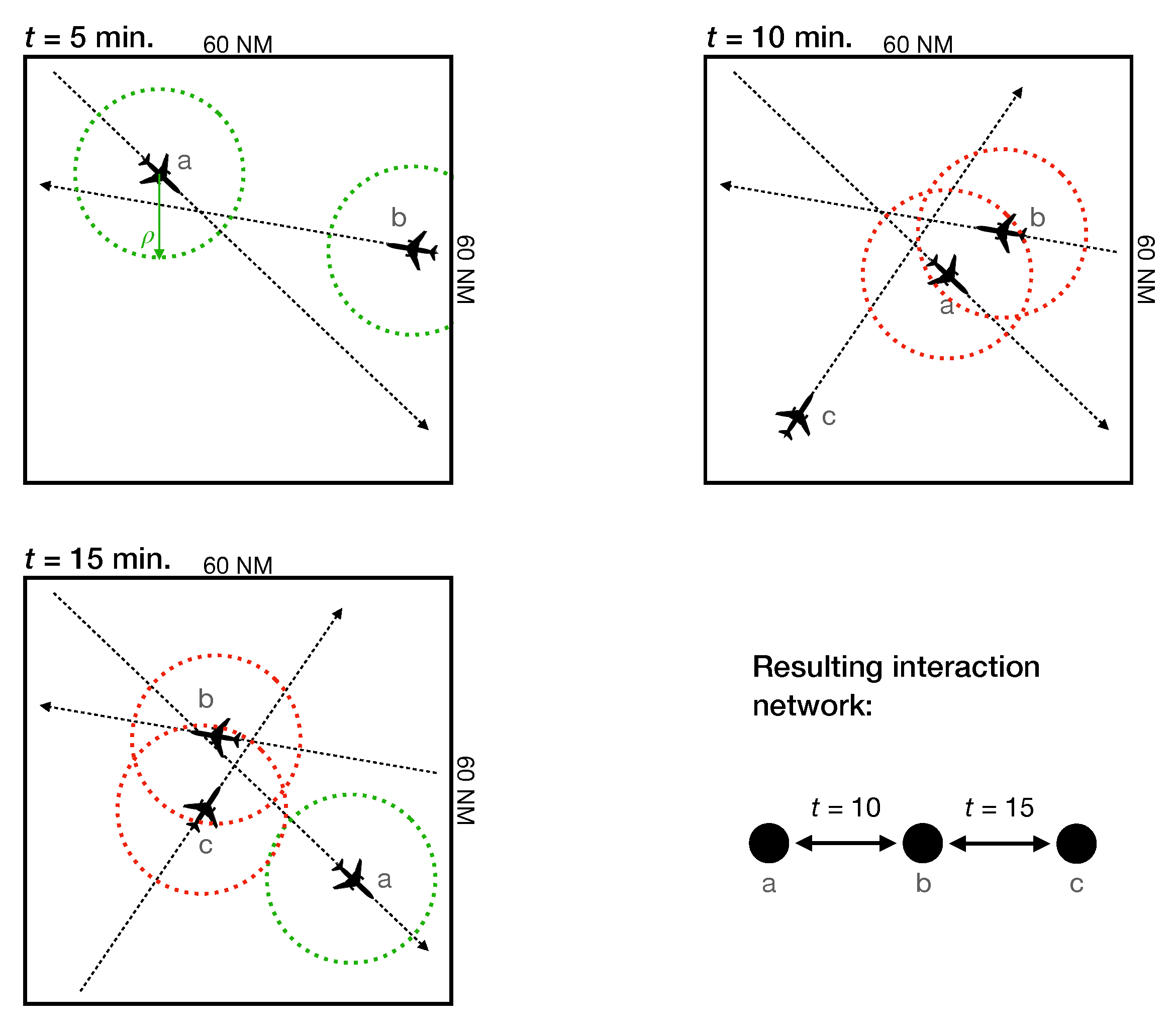
2. Reconstructing and Analysing Interaction Propagation Networks
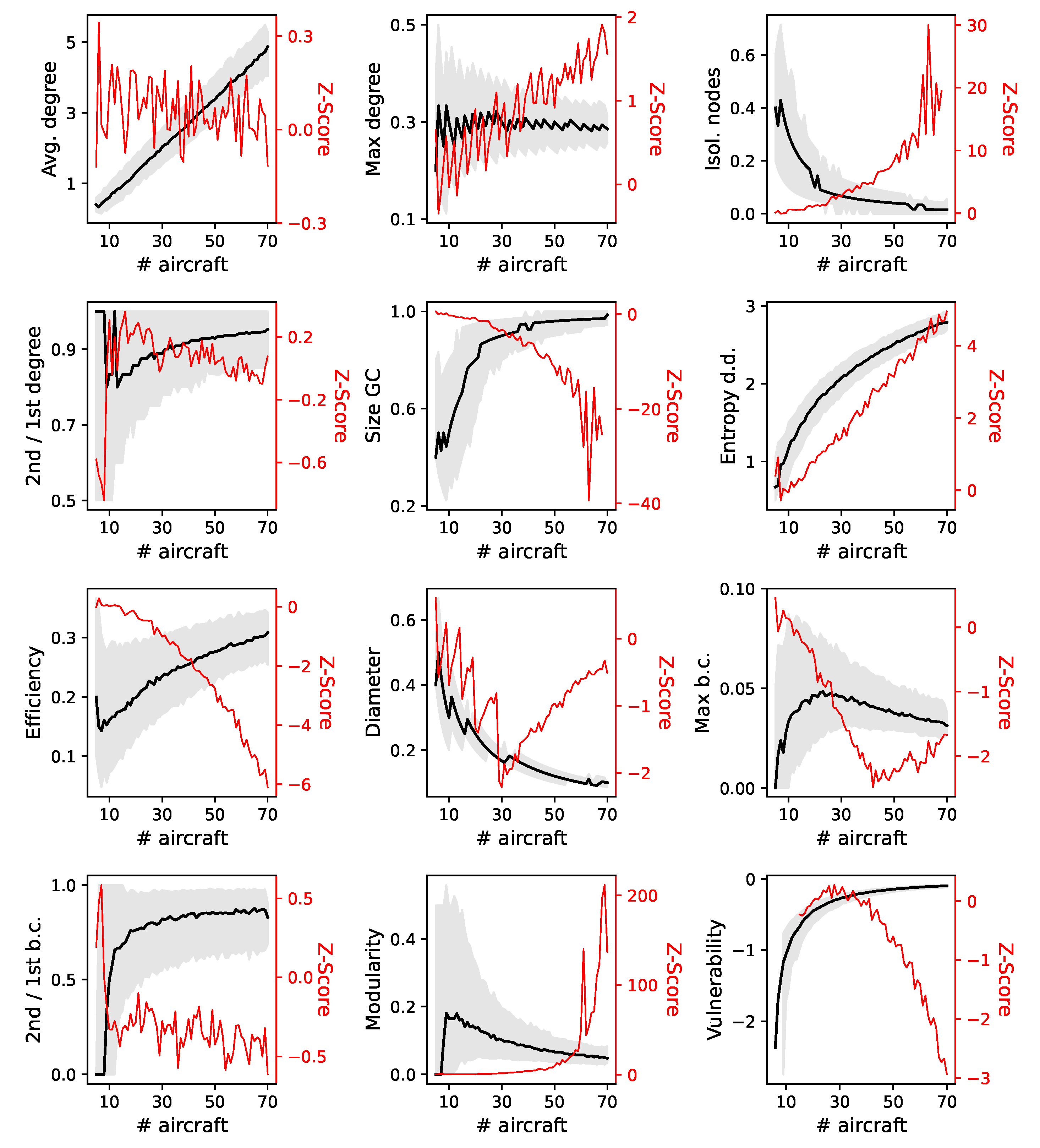
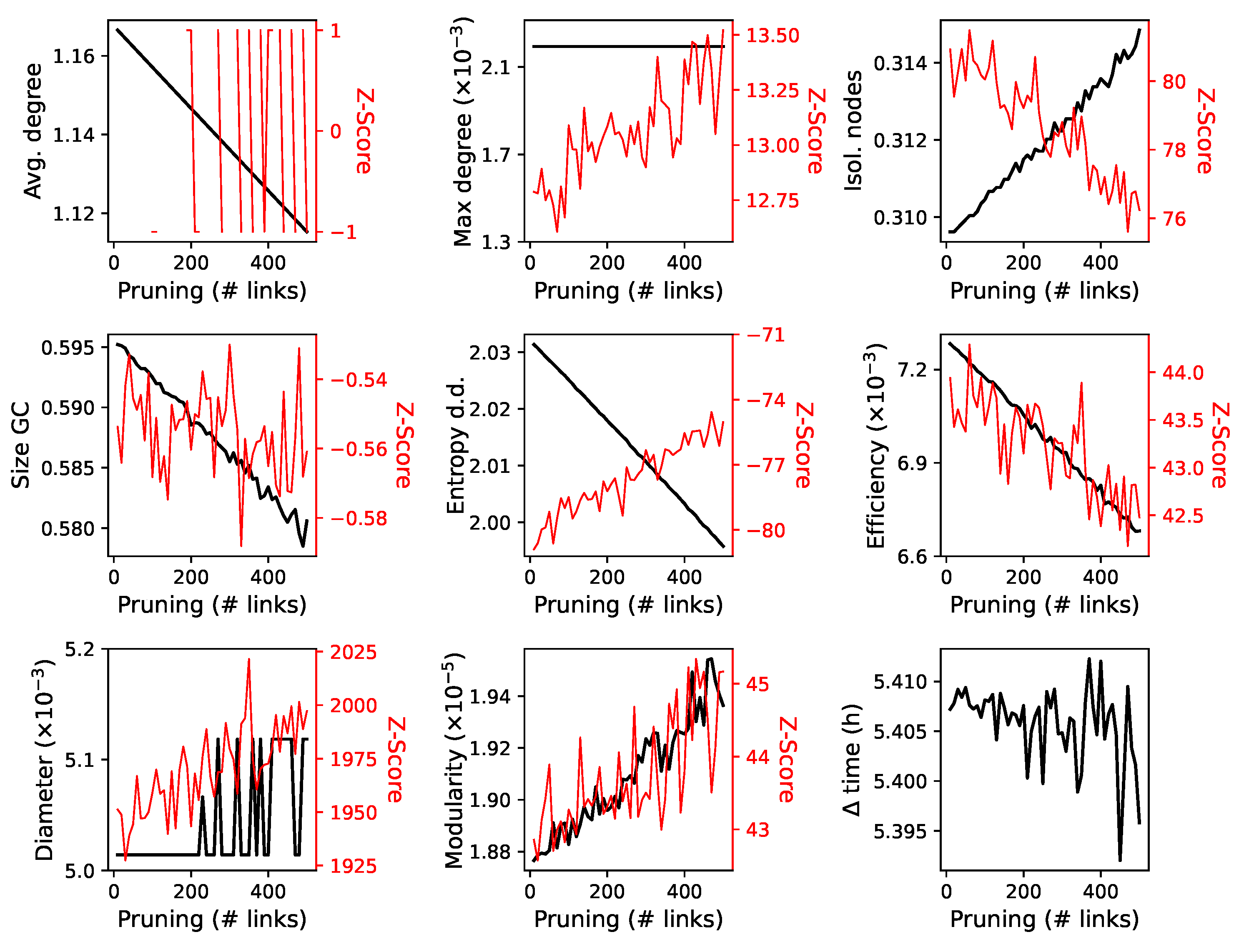
- Degree. The number of interactions in which one node (i.e., aircraft) is involved. This metric is further synthesized at the network level by calculating the mean degree, i.e., the average number of interactions, and the maximum degree (normalized by the total number of nodes).
- Isolated nodes. The number of nodes that have experienced no interactions with other nodes, hence for which the degree is zero. It is here expressed as a fraction over the total number of nodes.
- 2nd/1st degree. The ratio between the degree of the second most connected node of the network, and the degree of the most connected one—i.e., of the second most and most interacting aircraft, respectively. Values close to one indicate that the two most connected nodes have a similar degree, and hence that the network is more homogeneous; conversely, small values suggest that the most connected node is especially well connected.
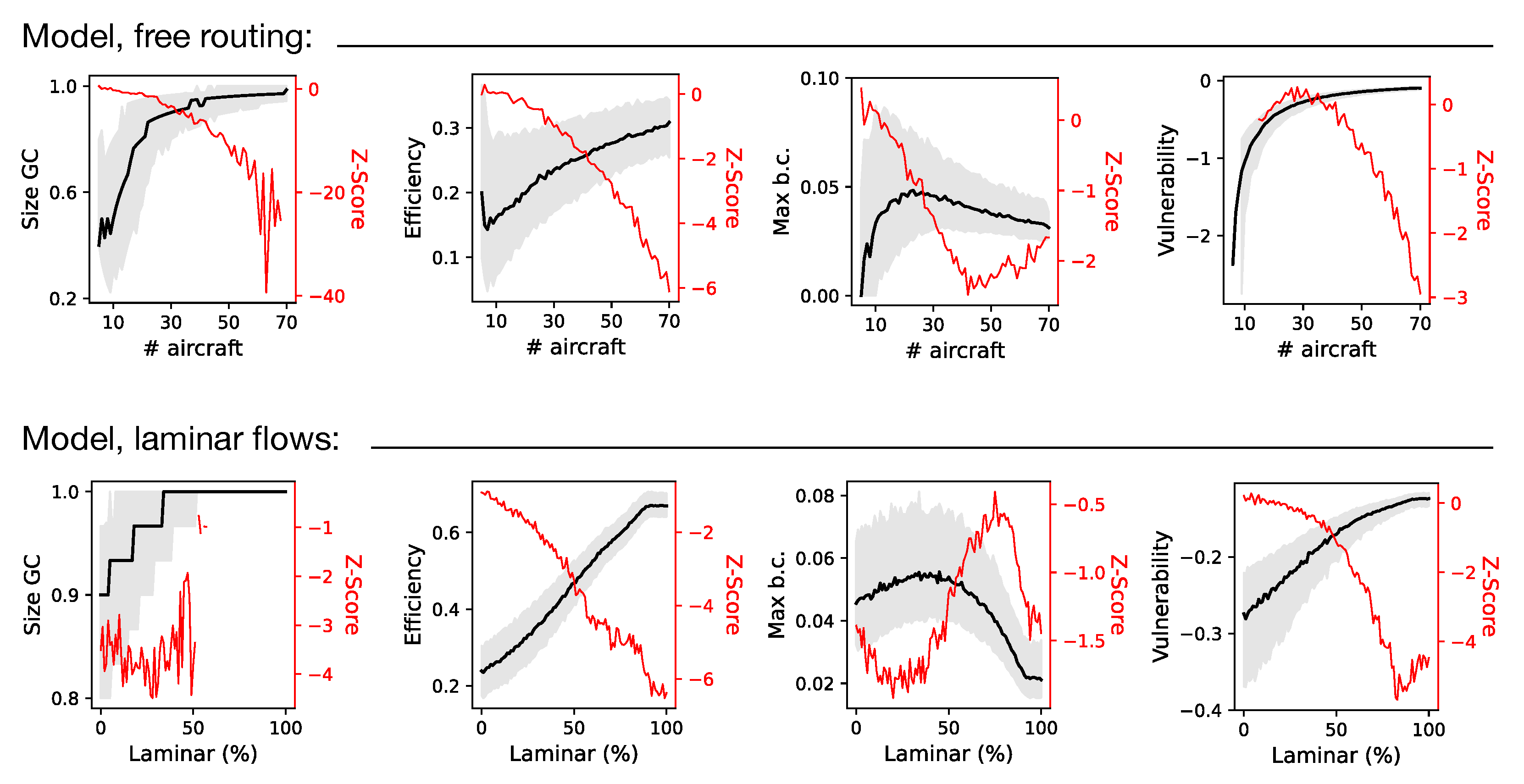
- Giant Component. Nodes that compose the largest set of connected nodes. It thus represents the largest set of nodes that are mutually reachable, that is, the largest set of aircraft among which perturbations can propagate. The size of the giant component is here expressed as the fraction of the number of these nodes over the total number of nodes in the network.
- Entropy of the degree distribution. The entropy S of a probability distribution represents the degree of uncertainty that we have about the values k extracted from it, and is mathematically defined as:when applied to the distribution of the degrees of nodes, it describes how heterogeneous these are. In other words, the larger S is, the closer the degree distribution is to a uniform one; conversely, when S approaches 0, all aircraft are involved in the same number of interactions. Large values of the entropy thus indicate that the network is more heterogeneous, and this has been proven to be related to its vulnerability [20].
- Efficiency. The global efficiency of a network is defined as the normalized sum of the inverse of the distances between every pair of nodes [21]:with N being the total number of nodes. By convention, pairs of aircraft not connected by a path yield , and thus do not contribute to the final metric value [21]. The distance is the minimum number of interactions needed to move from aircraft i to aircraft j, taking into account their temporal direction. To illustrate, in Figure 1 the distance between a and c is 2, while the distance between c and a is undefined (due to the temporal dimension, a propagation cannot go from c to a). E is thus defined between 0 and 1, the former indicating that the nodes are completely disconnected, and 1 that a direct link exists between all pairs of nodes. The name comes from the fact that this metric measures how efficient the network is in transmitting information. In the context of this work, the efficiency assesses how easily perturbations are propagated in the system.
- Diameter. The largest value of the distance between all possible pairs of nodes. In the context of this work, it quantifies the longest possible chain of propagation of interactions.
- Betweenness centrality. A measure of the centrality of nodes, i.e., how important they are within the network structure. For a given node i, it is proportional to the number of shortest paths connecting every pair of nodes j and k (with ) that pass through i [22]. Note that the metric is calculated on unweighted networks, i.e., links have no weight (or distance) associated to them. Aircraft with large betweenness centrality play a key role in what is known as the “shortest path structure”, as they are mostly responsible for the propagation of interactions. We here consider two derived metrics: the betweenness centrality of the most central node; and the ratio between the centrality of the second and first most central nodes.
- Modularity. The magnitude that measures the tendency of a network to organize into communities, i.e., groups of nodes strongly connected between them and loosely connected to the remainder of the network [23,24]. It is calculated as the normalized difference between the actual number of edges that connect nodes of the same community, and the expected number of them (if the network was constructed randomly). Thus, a modularity close to zero implies that the community structure is comparable to that of a random network, i.e., that no significant structure is observed; conversely, a modularity of 1 indicates a structure with disconnected modules. The algorithm here used to calculate the communities is the celebrated Louvain algorithm [25].
- Vulnerability. This measures how resilient the network is to the elimination of individual nodes [26]; in other words, how much the propagation of perturbations would be hindered if a single aircraft would be excluded from the system. It is calculated by evaluating, for each node, the logarithm of the ratio between the efficiency of the network without that node, and the one of the unaltered network. The smallest value, i.e., the largest loss of efficiency, is taken as the measure of vulnerability of the network.
- Δ time. Given a propagation network, this metric represents the maximum time a perturbation can propagate in the network. It is thus the temporal equivalent to the diameter.
3. The Model
4. Analysis of Real Trajectories
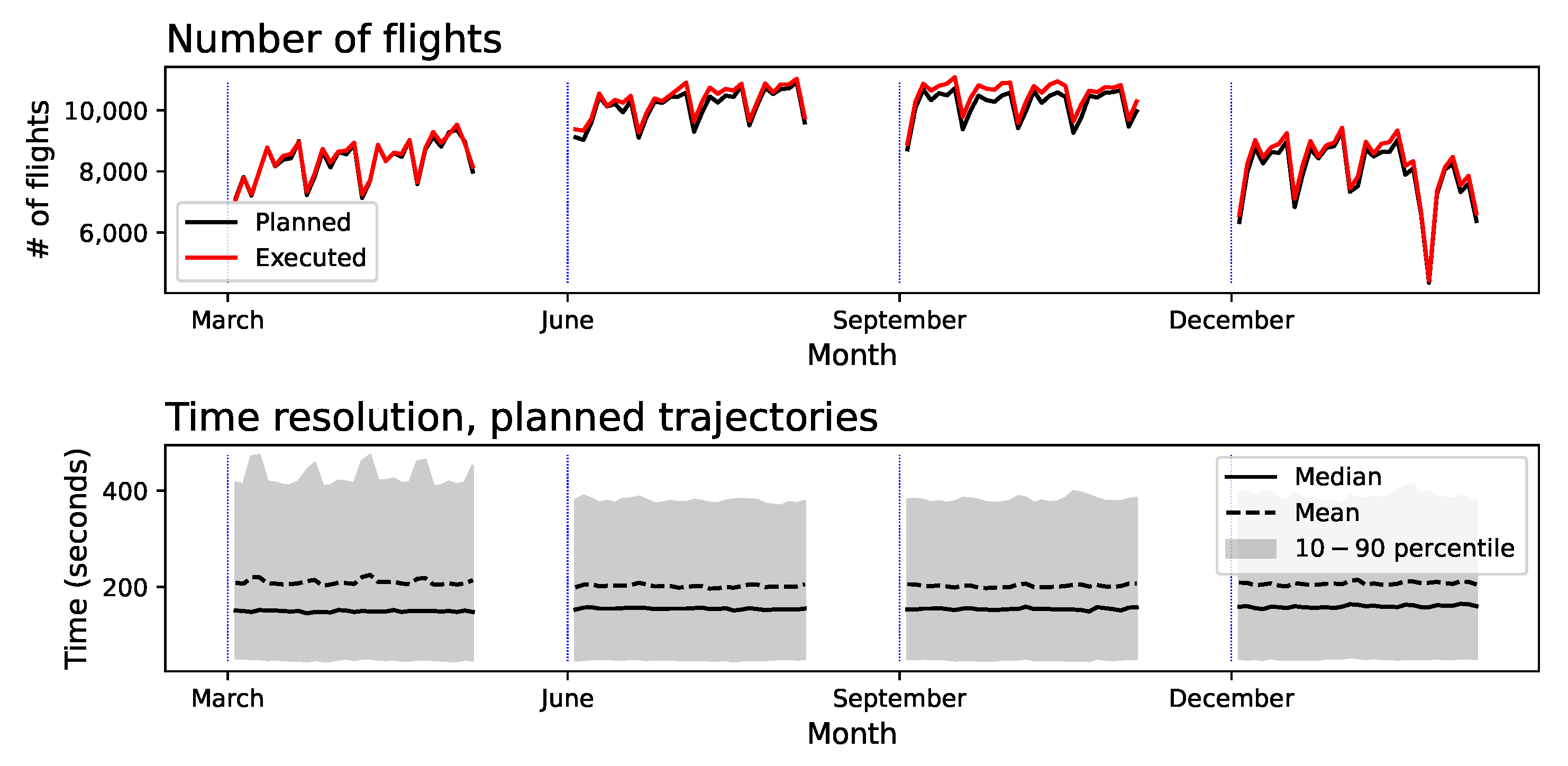
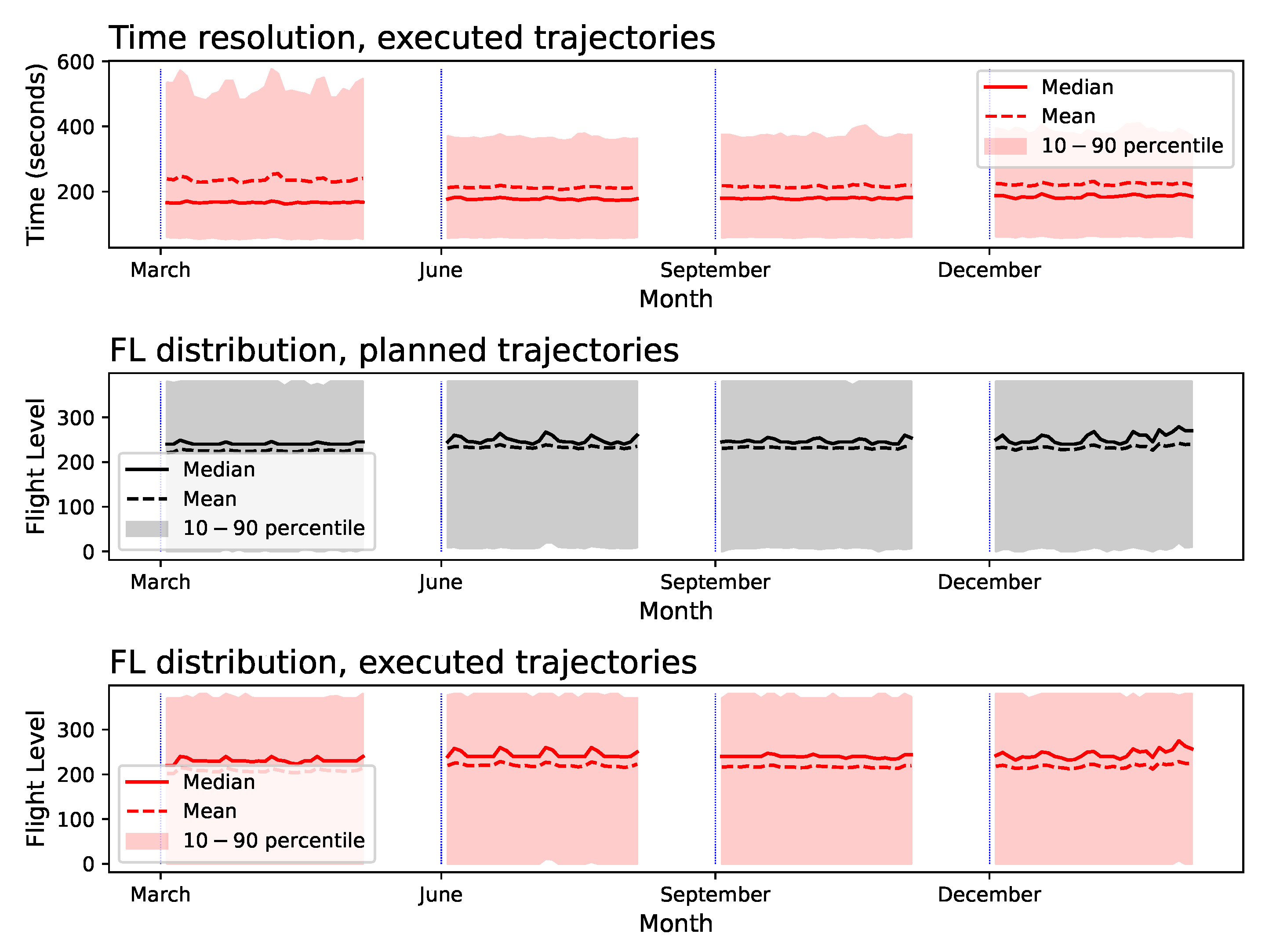
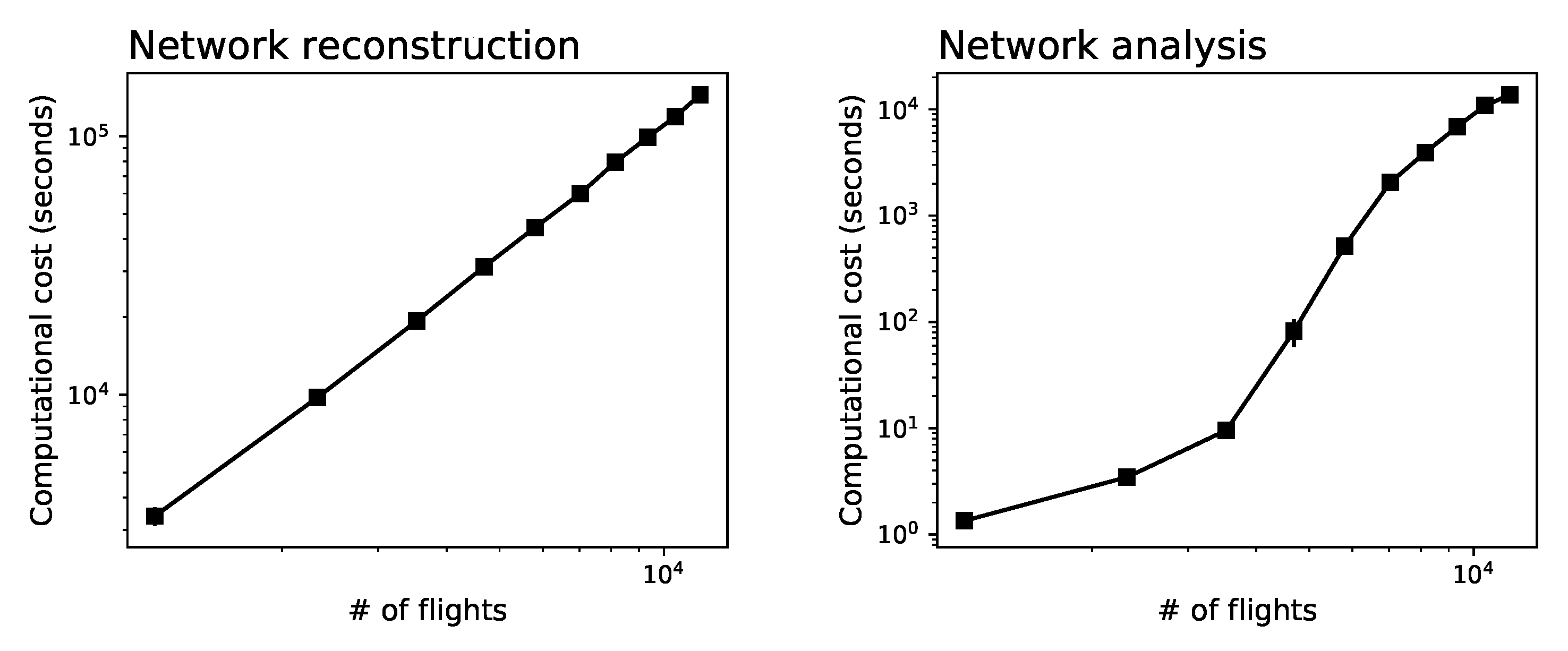
4.1. Trajectory Data and Preprocessing
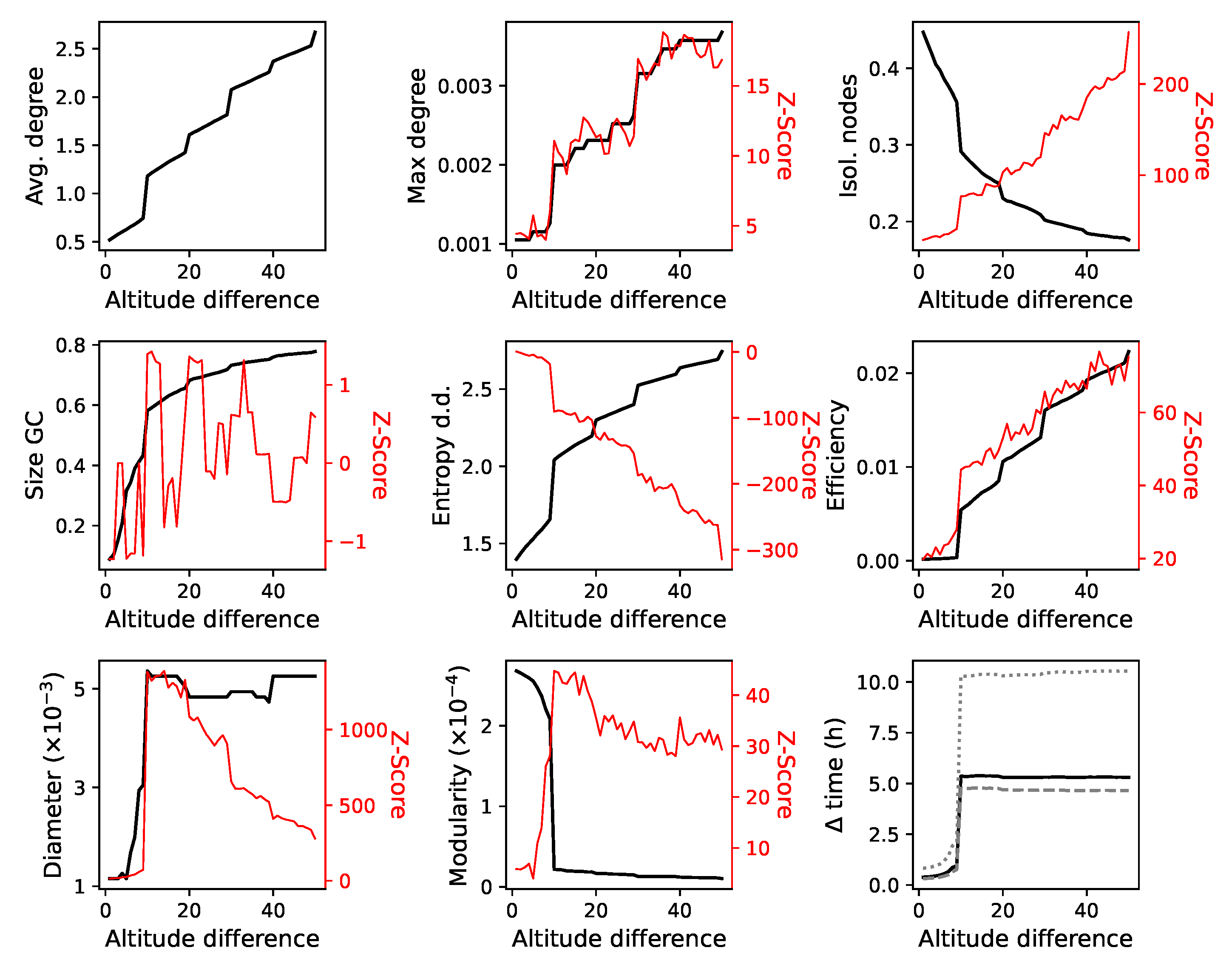
4.2. Basic Results: Interaction Radius and Altitude Difference
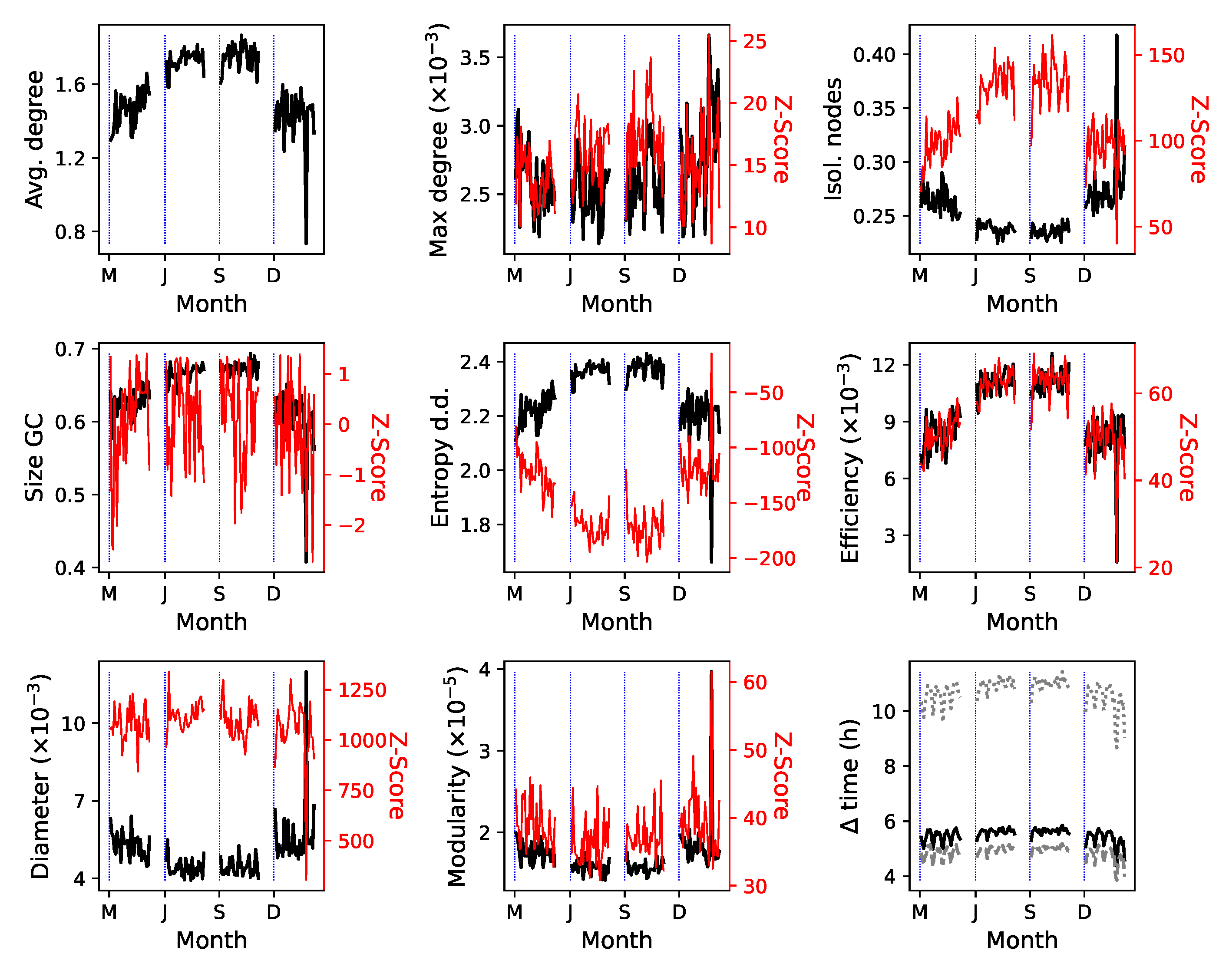
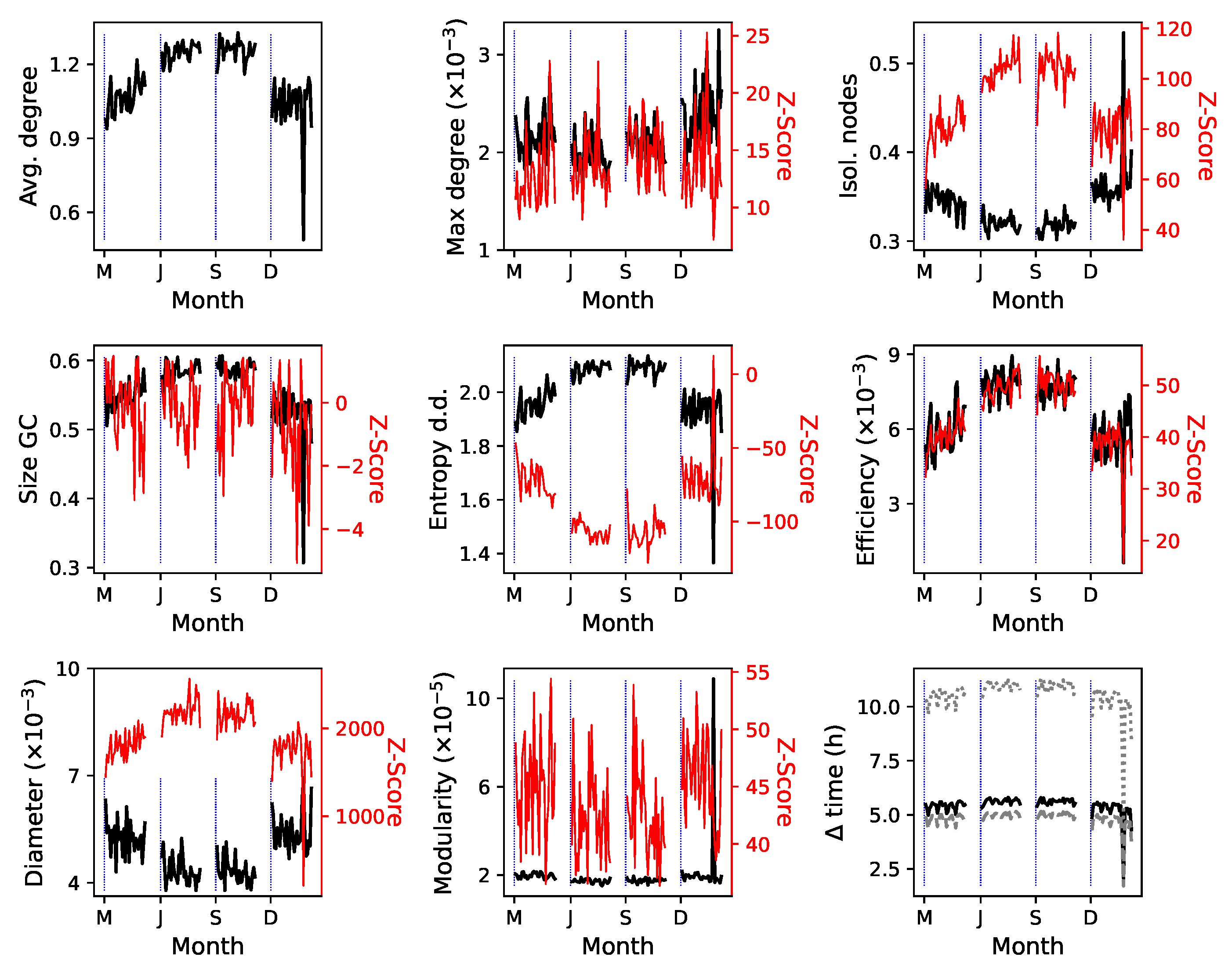
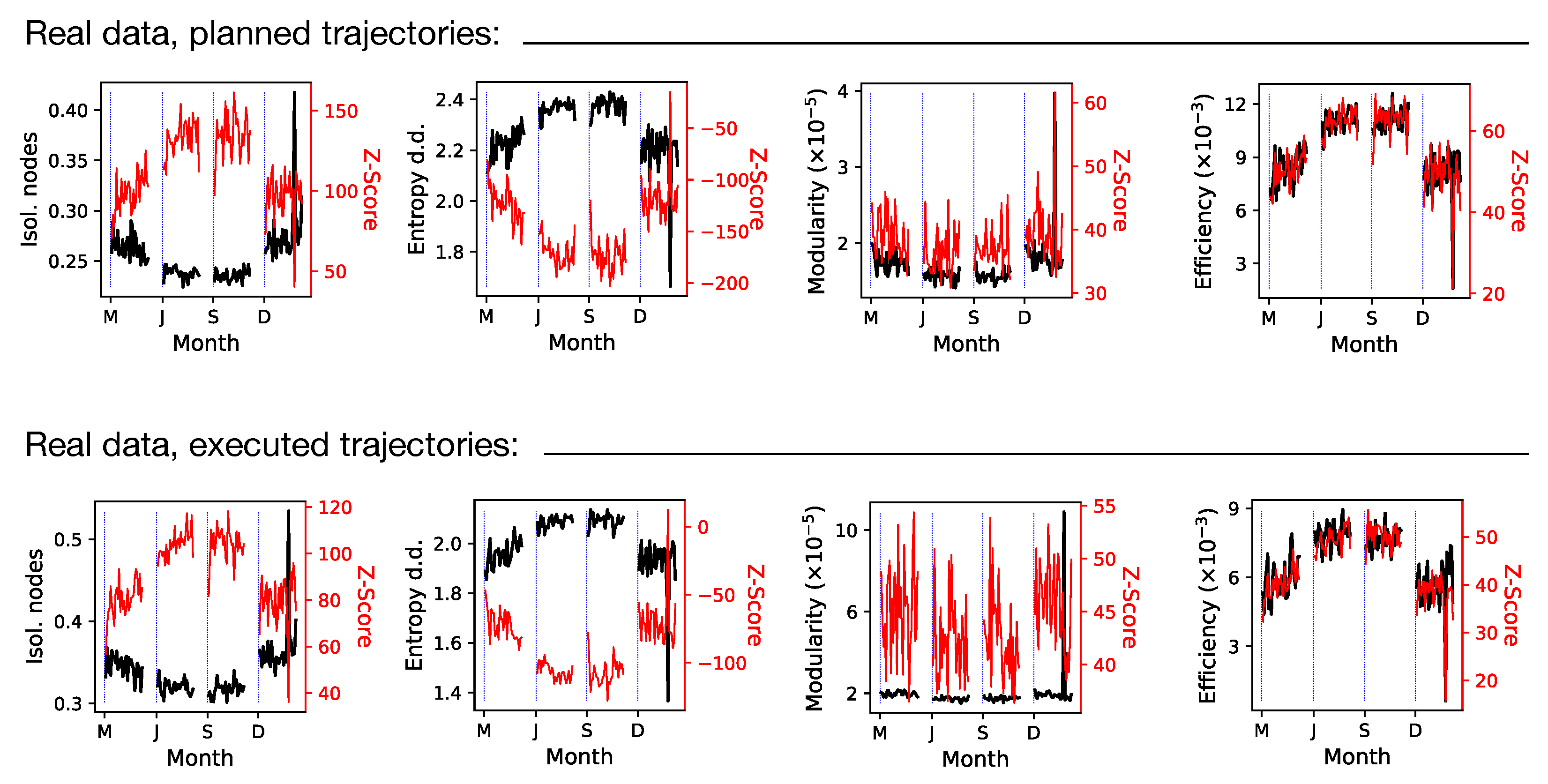
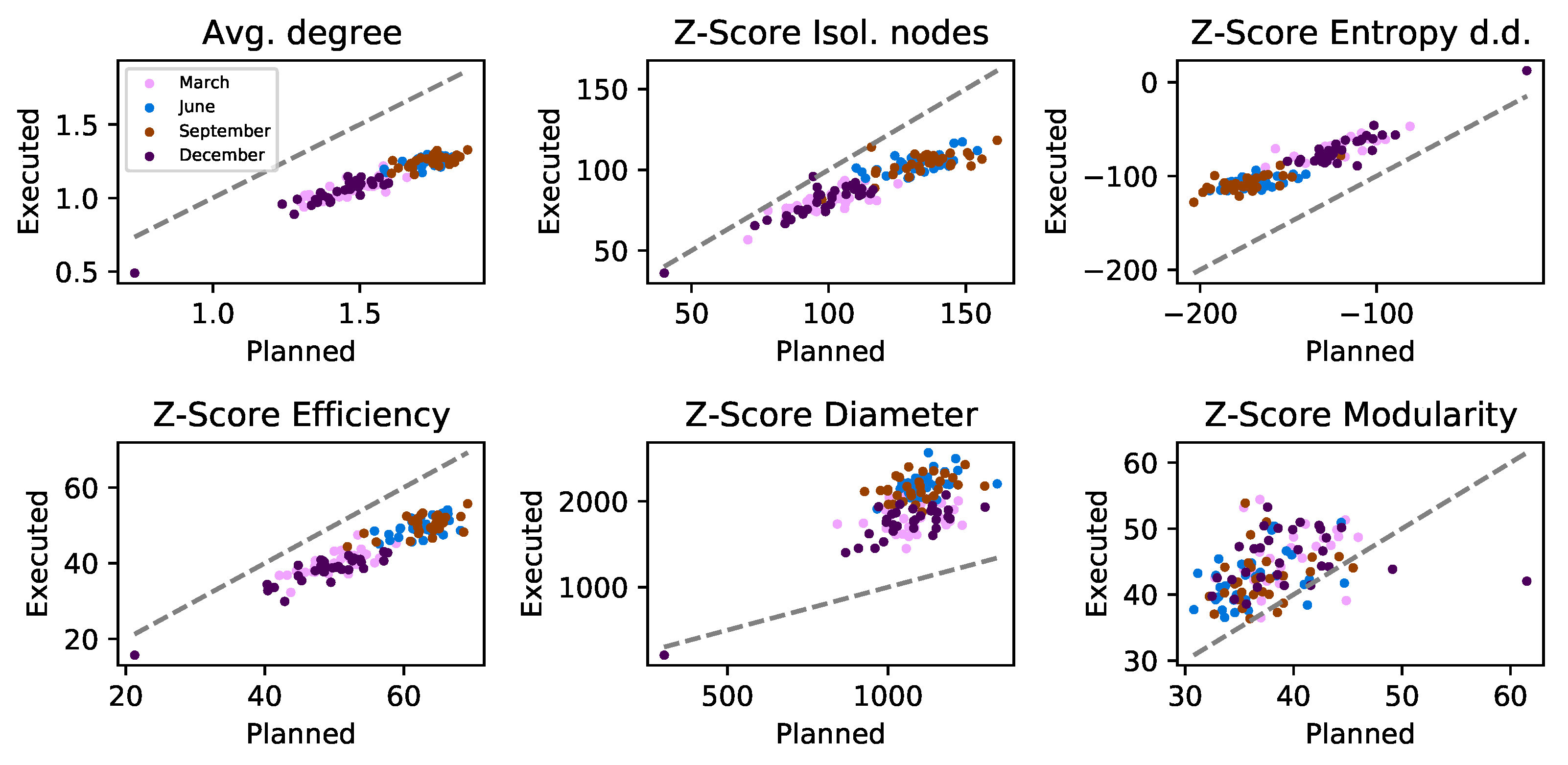
4.3. Properties of Planned and Executed Trajectories
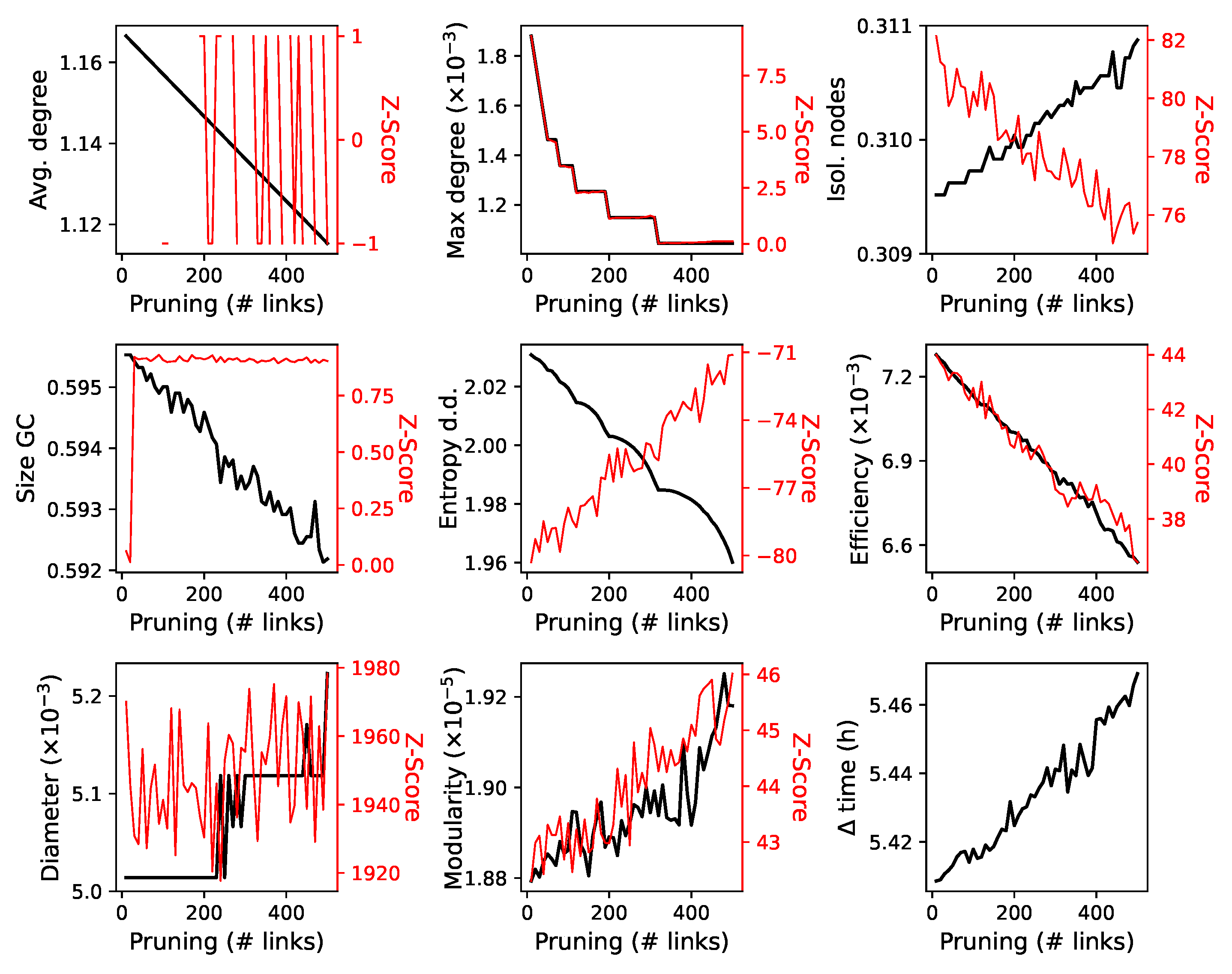
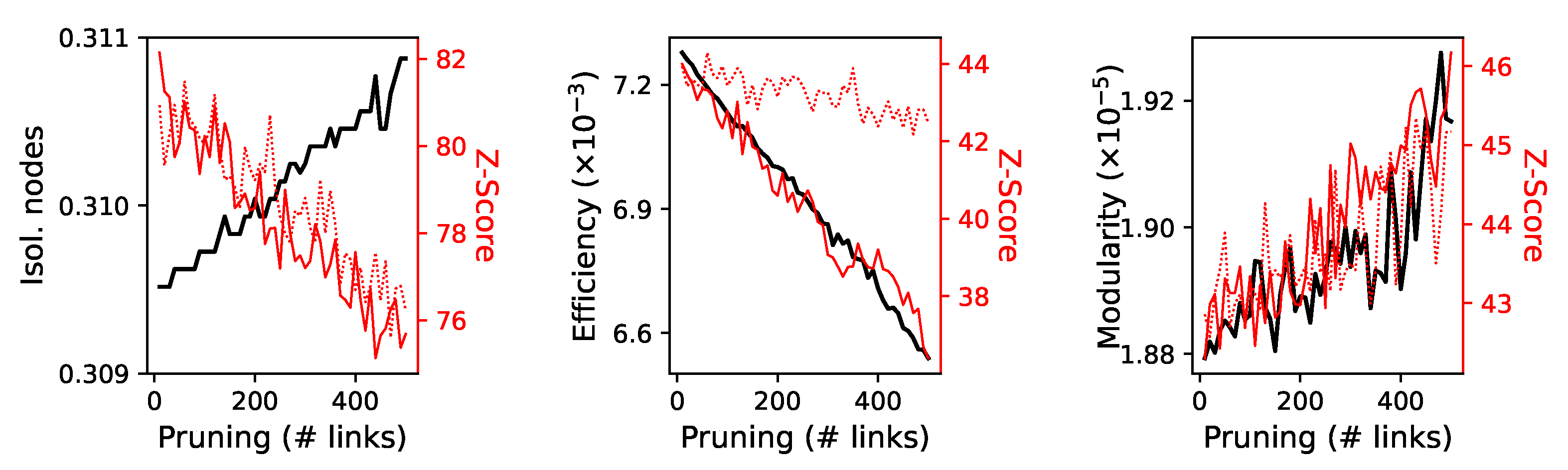
4.4. Robustness of the Interaction Network
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A




References
- Nolan, M.S. Fundamentals of Air Traffic Control; Cengage Learning: Belmont, CA, USA, 2011. [Google Scholar]
- Galster, S.M.; Duley, J.A.; Masalonis, A.J.; Parasuraman, R. Air traffic controller performance and workload under mature free flight: Conflict detection and resolution of aircraft self-separation. Int. J. Aviat. Psychol. 2001, 11, 71–93. [Google Scholar] [CrossRef]
- Radanovic, M.; Eroles, M.A.P.; Koca, T.; Gonzalez, J.J.R. Surrounding traffic complexity analysis for efficient and stable conflict resolution. Transp. Res. Part C Emerg. Technol. 2018, 95, 105–124. [Google Scholar] [CrossRef]
- Jun, T.; Piera, M.A.; Ruiz, S. A causal model to explore the ACAS induced collisions. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2014, 228, 1735–1748. [Google Scholar] [CrossRef]
- Lizarraga, M.; Elkaim, G. Spatially deconflicted path generation for multiple UAVs in a bounded airspace. In Proceedings of the 2008 IEEE/ION Position, Location and Navigation Symposium, Monterey, CA, USA, 5–8 May 2008; IEEE: New York, NY, USA, 2008; pp. 1213–1218. [Google Scholar]
- Gariel, M.; Srivastava, A.N.; Feron, E. Trajectory clustering and an application to airspace monitoring. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1511–1524. [Google Scholar] [CrossRef]
- Gardi, A.; Sabatini, R.; Ramasamy, S.; Kistan, T. Real-time trajectory optimisation models for next generation air traffic management systems. Appl. Mech. Mater. Trans. Tech. Publ. 2014, 629, 327–332. [Google Scholar] [CrossRef]
- Wei, J.; Sciandra, V.; Hwang, I.; Hall, W.D. Design and evaluation of a dynamic sectorization algorithm for terminal airspace. J. Guid. Control. Dyn. 2014, 37, 1539–1555. [Google Scholar] [CrossRef]
- Schuster, H.G.; Just, W. Deterministic Chaos: An Introduction; John Wiley & Sons: New York, NY, USA, 2006. [Google Scholar]
- Zanin, M. Network analysis reveals patterns behind air safety events. Phys. A Stat. Mech. Its Appl. 2014, 401, 201–206. [Google Scholar] [CrossRef]
- Monechi, B.; Servedio, V.D.; Loreto, V. Congestion transition in air traffic networks. PLoS ONE 2015, 10, e0125546. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, J.; Wu, C. From trees to forest: Relational complexity network and workload of air traffic controllers. Ergonomics 2015, 58, 1320–1336. [Google Scholar] [CrossRef]
- Wang, H.; Song, Z.; Wen, R.; Zhao, Y. Study on evolution characteristics of air traffic situation complexity based on complex network theory. Aerosp. Sci. Technol. 2016, 58, 518–528. [Google Scholar] [CrossRef]
- Wang, H.; Song, Z.; Wen, R. Modeling air traffic situation complexity with a dynamic weighted network approach. J. Adv. Transp. 2018, 2018, 5254289. [Google Scholar] [CrossRef]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47. [Google Scholar] [CrossRef]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Newman, M.E. The structure and function of complex networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Costa, L.D.F.; Rodrigues, F.A.; Travieso, G.; Villas Boas, P.R. Characterization of complex networks: A survey of measurements. Adv. Phys. 2007, 56, 167–242. [Google Scholar] [CrossRef]
- Holme, P.; Saramäki, J. Temporal networks. Phys. Rep. 2012, 519, 97–125. [Google Scholar] [CrossRef]
- Wang, B.; Tang, H.; Guo, C.; Xiu, Z. Entropy optimization of scale-free networks’ robustness to random failures. Phys. A Stat. Mech. Its Appl. 2006, 363, 591–596. [Google Scholar] [CrossRef]
- Latora, V.; Marchiori, M. Efficient behavior of small-world networks. Phys. Rev. Lett. 2001, 87, 198701. [Google Scholar] [CrossRef]
- Barthelemy, M. Betweenness centrality in large complex networks. Eur. Phys. J. B 2004, 38, 163–168. [Google Scholar] [CrossRef]
- Fortunato, S. Community detection in graphs. Phys. Rep. 2010, 486, 75–174. [Google Scholar] [CrossRef]
- Lambiotte, R.; Schaub, M.T. Modularity and Dynamics on Complex Networks; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 2008, P10008. [Google Scholar] [CrossRef]
- Holme, P.; Kim, B.J.; Yoon, C.N.; Han, S.K. Attack vulnerability of complex networks. Phys. Rev. E 2002, 65, 056109. [Google Scholar] [CrossRef] [PubMed]
- Maslov, S.; Sneppen, K. Specificity and stability in topology of protein networks. Science 2002, 296, 910–913. [Google Scholar] [CrossRef] [PubMed]
- Zanin, M.; Sun, X.; Wandelt, S. Studying the topology of transportation systems through complex networks: Handle with care. J. Adv. Transp. 2018, 2018, 3156137. [Google Scholar] [CrossRef]
- Halpern, N.; Graham, A. The Routledge Companion to Air Transport Management; Routledge: London, UK, 2018. [Google Scholar]
- Sun, X.; Wandelt, S.; Linke, F. Temporal evolution analysis of the European air transportation system: Air navigation route network and airport network. Transp. B Transp. Dyn. 2015, 3, 153–168. [Google Scholar] [CrossRef]
- Basora, L.; Olive, X.; Dubot, T. Recent advances in anomaly detection methods applied to aviation. Aerospace 2019, 6, 117. [Google Scholar] [CrossRef]
- Ho, T.; Shigeru, S. Mobile Ad-Hoc Network Based Relaying Data System for Oceanic Flight Routes in Aeronautical Communications. Int. J. Comput. Netw. Commun. 2009, 1, 10803862. [Google Scholar]
- Murca, M.C.R.; Hansman, R.J. Identification, characterization, and prediction of traffic flow patterns in multi-airport systems. IEEE Trans. Intell. Transp. Syst. 2018, 20, 1683–1696. [Google Scholar] [CrossRef]
- Chatterji, G.; Sridhar, B. Measures for air traffic controller workload prediction. In Proceedings of the 1st AIAA, Aircraft, Technology Integration, and Operations Forum, Los Angeles, CA, USA, 16–18 October 2001; p. 5242. [Google Scholar]
- Hilburn, B. Cognitive complexity in air traffic control: A literature review. EEC Note 2004, 4, 1–80. [Google Scholar]
- Loft, S.; Sanderson, P.; Neal, A.; Mooij, M. Modeling and predicting mental workload in en route air traffic control: Critical review and broader implications. Hum. Factors 2007, 49, 376–399. [Google Scholar] [CrossRef]
- Durand, N.; Alliot, J.M.; Noailles, J. Automatic aircraft conflict resolution using genetic algorithms. In Proceedings of the 1996 ACM Symposium on Applied Computing, Philadelphia, PA, USA, 17–19 February 1996; pp. 289–298. [Google Scholar]
- Cafieri, S.; Durand, N. Aircraft deconfliction with speed regulation: New models from mixed-integer optimization. J. Glob. Optim. 2014, 58, 613–629. [Google Scholar] [CrossRef]
- Courchelle, V.; Soler, M.; González-Arribas, D.; Delahaye, D. A simulated annealing approach to 3D strategic aircraft deconfliction based on en-route speed changes under wind and temperature uncertainties. Transp. Res. Part C Emerg. Technol. 2019, 103, 194–210. [Google Scholar] [CrossRef]
- Kivelä, M.; Arenas, A.; Barthelemy, M.; Gleeson, J.P.; Moreno, Y.; Porter, M.A. Multilayer networks. J. Complex Netw. 2014, 2, 203–271. [Google Scholar] [CrossRef]
- Boccaletti, S.; Bianconi, G.; Criado, R.; Del Genio, C.I.; Gómez-Gardenes, J.; Romance, M.; Sendina-Nadal, I.; Wang, Z.; Zanin, M. The structure and dynamics of multilayer networks. Phys. Rep. 2014, 544, 1–122. [Google Scholar] [CrossRef]
- Wandelt, S.; Sun, X.; Feng, D.; Zanin, M.; Havlin, S. A comparative analysis of approaches to network-dismantling. Sci. Rep. 2018, 8, 13513. [Google Scholar] [CrossRef]



| Parameter | Meaning |
|---|---|
| N | Number of simulated aircraft. |
| Radius of interaction, i.e., the distance below which a pair of aircraft is assumed to be interacting. | |
| Laminar percentage, defining how constrained (in terms of the entrance spatial window and angle) the aircraft entrance to the airspace is. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-Martín, R.; Zanin, M. Propagation of Interactions among Aircraft Trajectories: A Complex Network Approach. Aerospace 2023, 10, 213. https://doi.org/10.3390/aerospace10030213
López-Martín R, Zanin M. Propagation of Interactions among Aircraft Trajectories: A Complex Network Approach. Aerospace. 2023; 10(3):213. https://doi.org/10.3390/aerospace10030213
Chicago/Turabian StyleLópez-Martín, Raúl, and Massimiliano Zanin. 2023. "Propagation of Interactions among Aircraft Trajectories: A Complex Network Approach" Aerospace 10, no. 3: 213. https://doi.org/10.3390/aerospace10030213
APA StyleLópez-Martín, R., & Zanin, M. (2023). Propagation of Interactions among Aircraft Trajectories: A Complex Network Approach. Aerospace, 10(3), 213. https://doi.org/10.3390/aerospace10030213







