Distributed and Scalable Cooperative Formation of Unmanned Ground Vehicles Using Deep Reinforcement Learning

Abstract

Cooperative formation control of unmanned ground vehicles (UGVs) has become one of the important research hotspots in the application of UGV and attracted more and more attention in the military and civil fields. Compared with traditional formation control algorithms, reinforcement-learning-based algorithms can provide a new solution with a lower complexity for real-time formation control by equipping UGVs with artificial intelligence. Therefore, in this paper, a distributed deep-reinforcement-learning-based cooperative formation control algorithm is proposed to solve the navigation, maintenance, and obstacle avoidance tasks of UGV formations. More importantly, the hierarchical triangular formation structure and the newly designed Markov decision process for UGV formations of leader and follower attributes make the control strategy learned by the algorithm reusable, so that the formation can arbitrarily increase the number of UGVs and realize a more flexible expansion. The effectiveness and scalability of the algorithm is verified by formation simulation experiments of different scales.

1. Introduction

Multiagent systems [1,2] are often more efficient than a single agent in many fields. As a typical example, unmanned ground vehicles (UGVs) frequently appear in logistics warehouses and search and rescue scenes, and will play an important role as planetary robots in the exploration of planetary surfaces. In these application environments, the cooperative control of the rover swarm will inevitably be involved, and the UGVs may need to create a formation to complete the navigation task safely and fast.

The solutions to the formation problem are diverse, and the most commonly used one is the leader-following approach [3,4], which has the advantage of a simple operation. Traditional control methods include behavior-based formation control methods [5,6], potential functions [7,8], etc. Some of these methods are difficult to implement on actual low-cost UGV hardware by using complex nonlinear control algorithms, although they can achieve good control performance.

In recent years, machine learning, especially reinforcement learning, has been gradually applied to the control [9,10] of UGV, using a linear function with low complexity [11], and learning behavior strategies through trial-and-error interaction with a dynamic environment without any prior samples and rules [12]. However, conventional reinforcement learning methods, such as Q-learning [13] and SARSA, need to record the expected value of the state–action value function by constructing a Q table. Under such a strategy, the cost of storage and maintenance quickly becomes expensive as the state/action dimension increases, making it difficult to solve continuous problems [14]. Using an artificial neural network instead of a Q table to approximate state–action values is a model to solve this problem, which includes Deep Q-Network (DQN), deep deterministic policy gradient (DDPG), etc.

At present, the application of reinforcement learning in agent control mainly focuses on the path planning of a single vehicle. Reference [15] realized the autonomous navigation and obstacle avoidance of an unmanned aerial vehicle (UAV) in three-dimensional space based on the DDPG algorithm. Reference [16] used the actor–critic dual-network architecture to optimize the agent’s control strategy to plan a collision-free optimal path in an unknown environment. Based on the reinforcement learning strategy applied with prior knowledge, reference [17] proposed a length-first optimal path selection method and improved the search direction of the A-star algorithm to help different types of intelligent vehicles find the most optimal path in the transportation network.

In addition, the application of deep reinforcement learning to formations has gradually attracted attention. Reference [18] realized the perception of any number of obstacles by applying long short-term memory (LSTM) and realized an anticollision formation control based on deep reinforcement learning. Reference [19] proposed a multirobot double-layer formation control framework based on deep reinforcement learning. The executive layer realized the robot’s obstacle avoidance and navigation through the deep network trained by the reinforcement learning method, and the decision layer was responsible for the formation’s organization and target location assignment. Reference [20] proposed a DQN-based path planning algorithm for UAV and USV formations, which used a centralized approach to the triangular formation and obstacle avoidance. However, with discrete actions, the control accuracy of the algorithm was limited, and the centralized control method had difficulties meeting the simplicity of formation expansion.

By summarizing the current research on UGV control using deep reinforcement learning, especially in formation control, some research gaps remain as follows:

• Most research works only focus on one or several simple formation shapes, without considering the scalability for different formations, and the formation scheme needs to be redesigned when the number of UGVs or the formation shape changes.
• Most of the formation algorithms based on deep reinforcement learning have limited scalability, and any change in formation requires redesigning the deep reinforcement learning network and rerunning the training process. Therefore, the scalability of the formation is of great significance. By introducing a distributed control method, the trained network can be easily applied to the newly added UGV, which would facilitate the adjustment of the formation.

Based on the above discussion, a scalable cooperative formation control algorithm using distributed deep reinforcement learning is proposed in this paper. Compared with the existing cooperative formation control algorithms, the scalability, portability and real-time aspect of the algorithm are considered, and the complexity of the algorithm is reduced, which can be used for the cooperative formation control of large-scale unmanned systems. In addition, reinforcement learning, previously mainly used in single-agent training, is now used to solve multiagent coordination problems, and the general Markov decision process (MDP) design makes it possible to realize a role change of the leader-following relationship in the dynamic process, which is more characteristic of actual humanlike behavior than existing methods. The main contributions include the following:

• A multi-UGV layered and scalable formation framework is proposed, using distributed deep reinforcement learning for navigation, obstacle avoidance, and formation tasks.
• To realize the coordination and scalability of the formation, a new MDP is designed for the UGV with a follower attribute so that the same type of UGV can reuse the learned control strategy, thus making the formation expansion easier.
• Simulation experiment results demonstrate that the proposed formation algorithm generalizes well in formations of different number of vehicles and shapes.

The following structure of this paper is as follows. Section 2 introduces the problem that needs to be solved in this paper, the layered formation structure, and the basic knowledge of reinforcement learning, including the Markov decision processes, policy gradient, and the DDPG algorithm. Section 3 introduces the deep-reinforcement-learning-based distributed and scalable cooperative formation control algorithm in detail, including the design of an MDP and the methods of formation expansion, training, and testing. Section 4 verifies the effectiveness of the proposed algorithm through simulation experiments. Section 5 concludes the paper and discusses future work.

2. Preliminaries

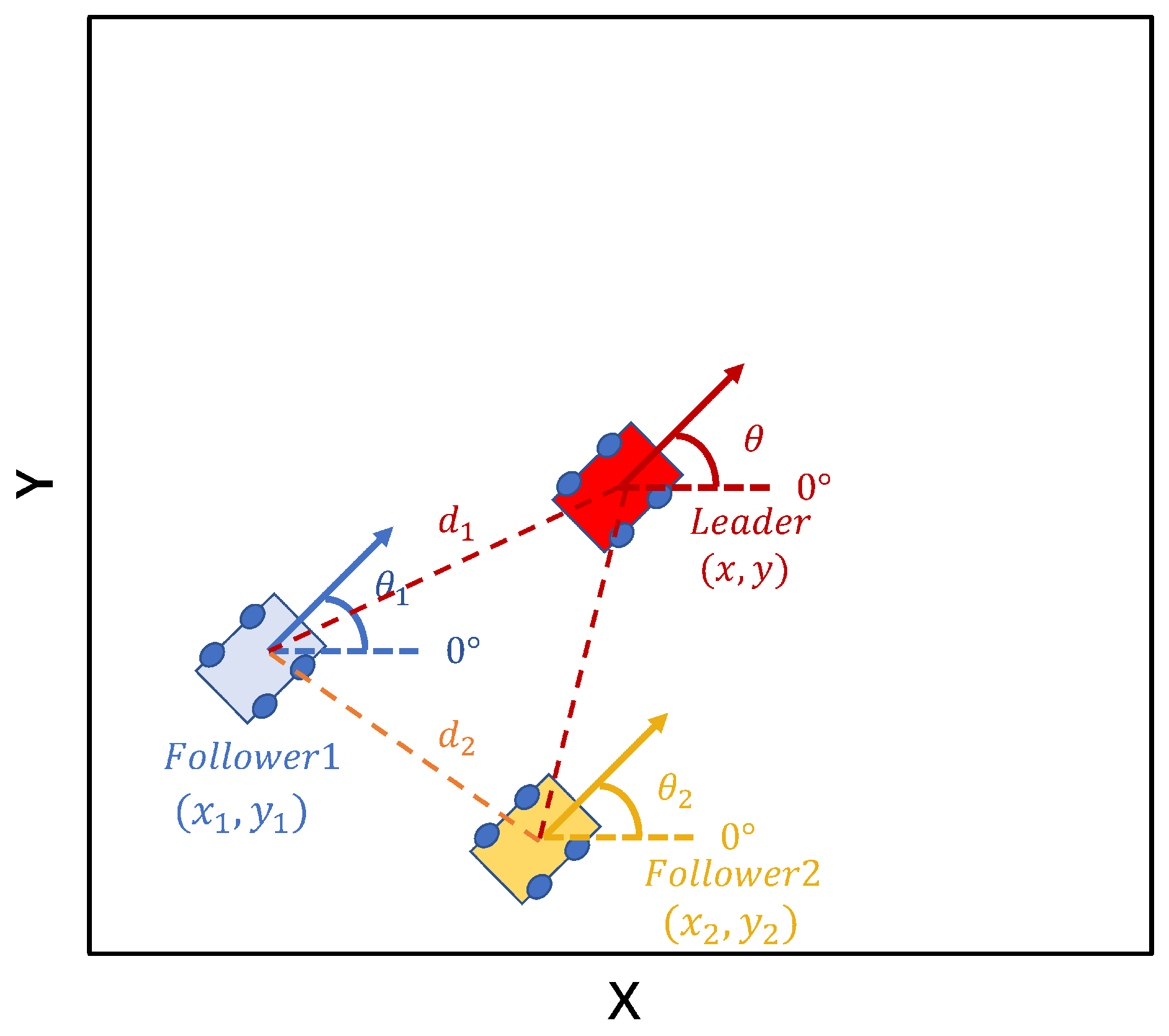
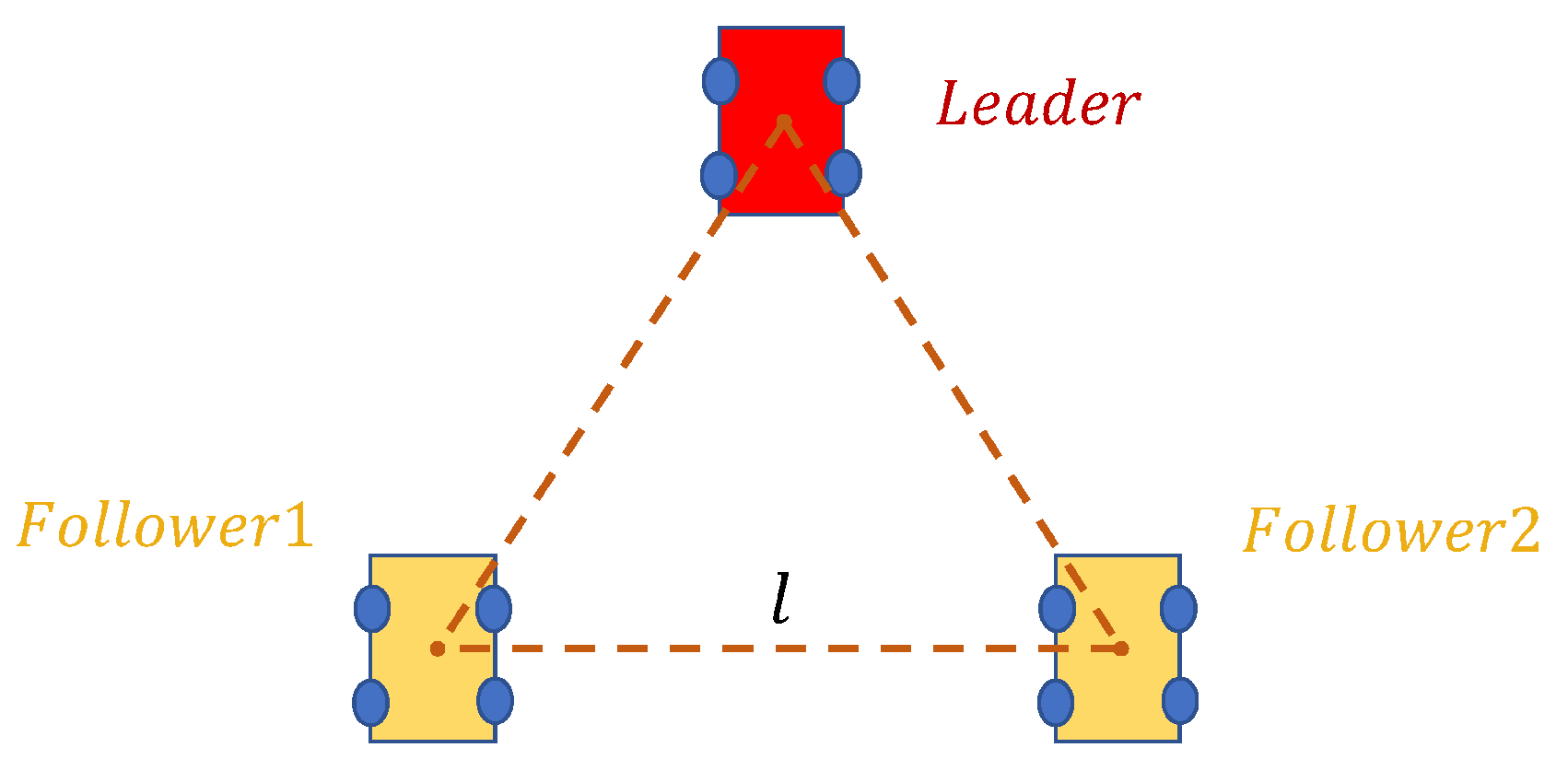
2.1. Problem Formulation

As shown in Figure 1, the problem addressed in this paper is the cooperative control of a UGV formation in an environment with obstacles. The UGVs have the requirement of maintaining the formation and need to move from the initial position to the target position together, while avoiding collisions with each other and obstacles.

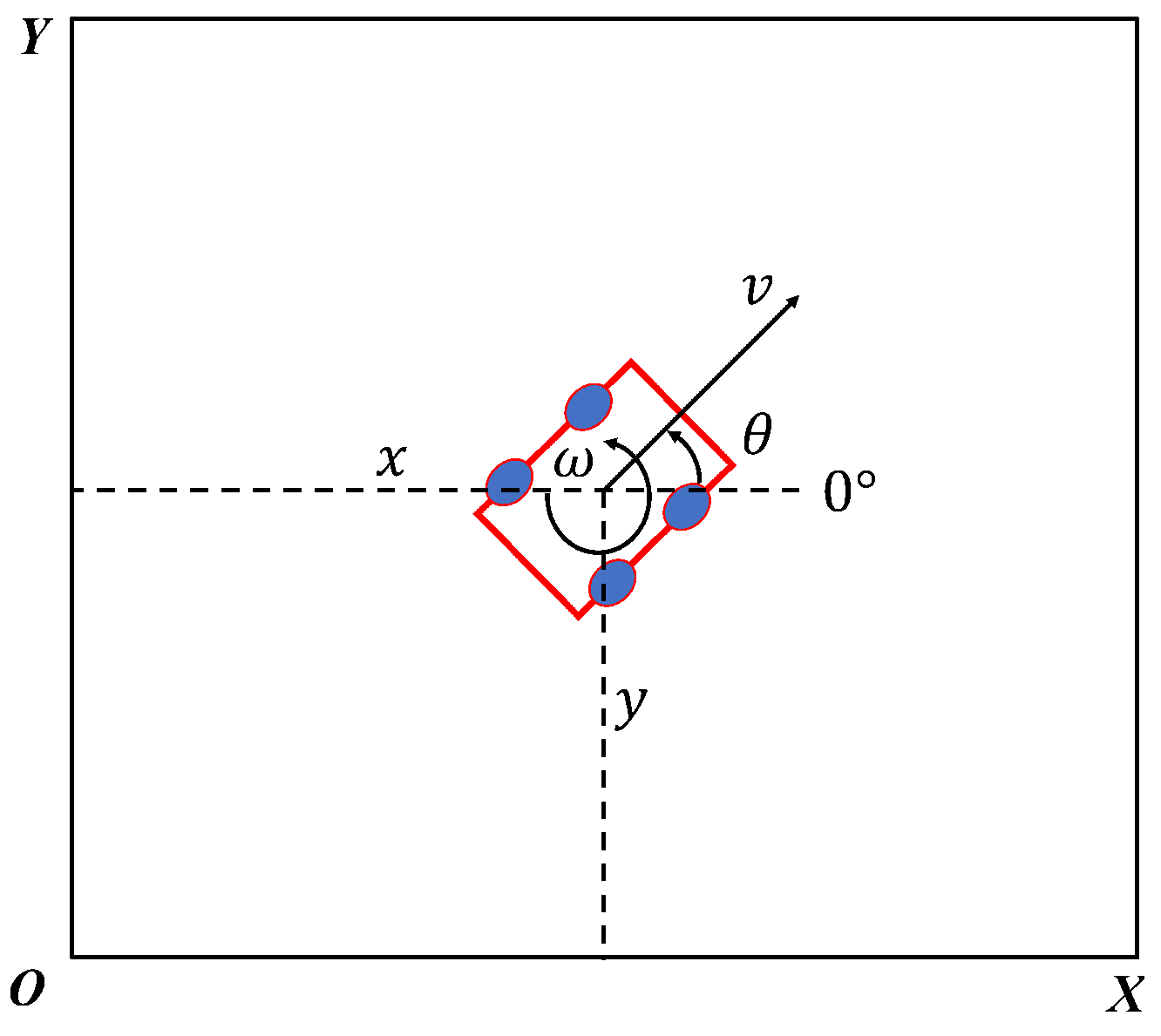
2.2. UGV Model

The UGV model is shown in Figure 2. The position of a UGV on the two-dimensional plane is expressed as $\mathbf{p}=[x,y]$ and the direction is expressed as $\theta$. The velocity vector is expressed as $\mathbf{v}=[v,\omega ]$, where v is the linear velocity and $\omega$ is the angular velocity. Therefore, the motion of a UGV can be written as:

$$\begin{array}{c}{x}_{t+1}=x_t+v_{t+1}Tcos{\theta }_{t+1}\hfill \\ y_{t+1}=y_t+v_{t+1}Tsin{\theta }_{t+1}\hfill \\ v_{t+1}=v_t+a_{t}T\hfill \\ {\theta }_{t+1}={\theta }_t+{\omega }_{t}T\hfill \end{array}$$

(1)

where $a_t$ and ${\omega }_t$ are the control inputs of the UGV at time t. T is the sampling time for a system.

In addition, it is necessary to limit the range of control inputs as:

$$\begin{array}{c}a\in [-a_{max},a_{max}]\hfill \\ \omega \in [-{\omega }_{max},{\omega }_{max}]\hfill \end{array}$$

(2)

where $a_{max}$ and ${\omega }_{max}$ are the maximum acceleration and angular velocity of the UGV, respectively. Its specific value is determined by the actual vehicle dynamics’ characteristics so that the planned path can make the UGV run more smoothly.

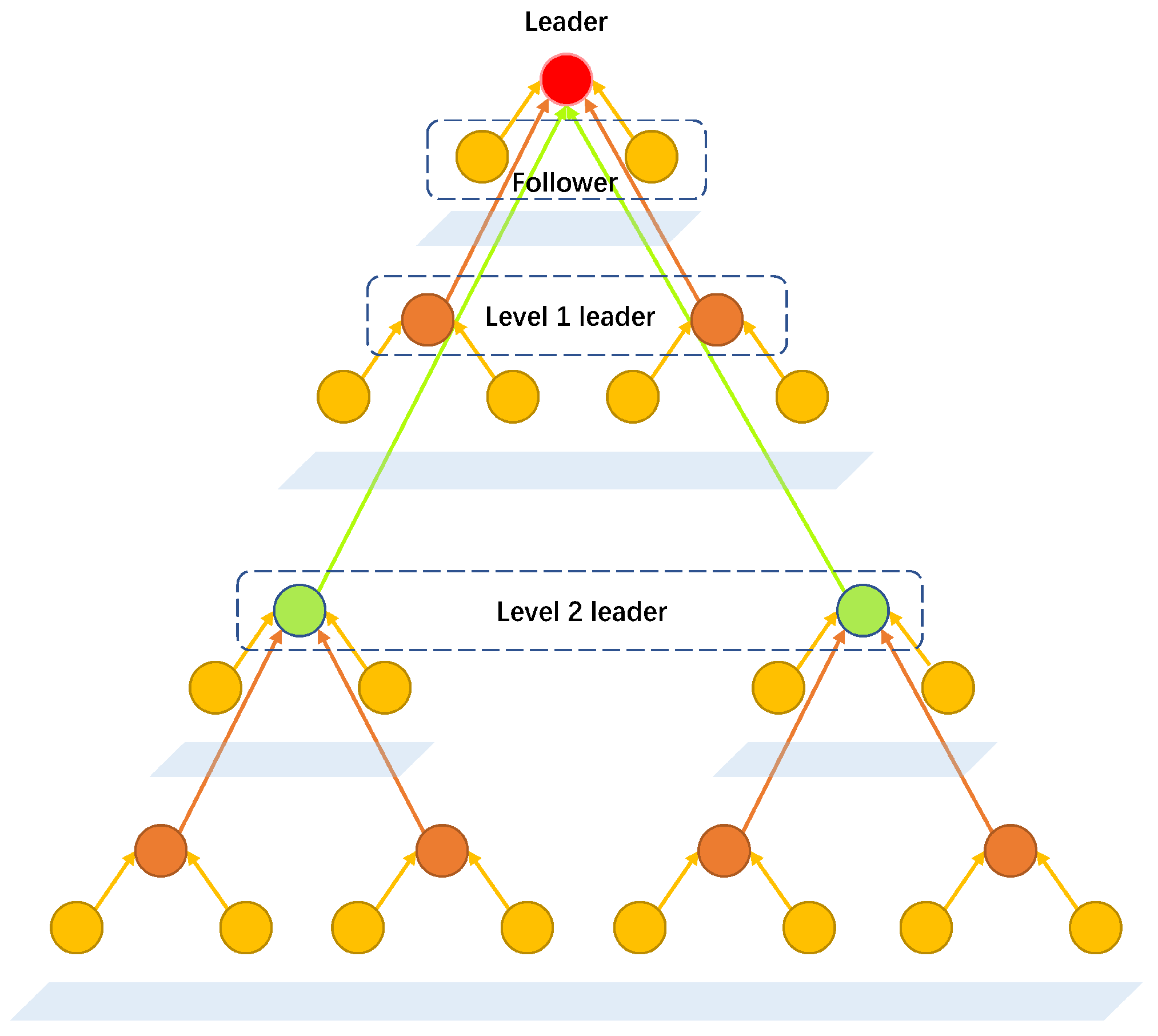
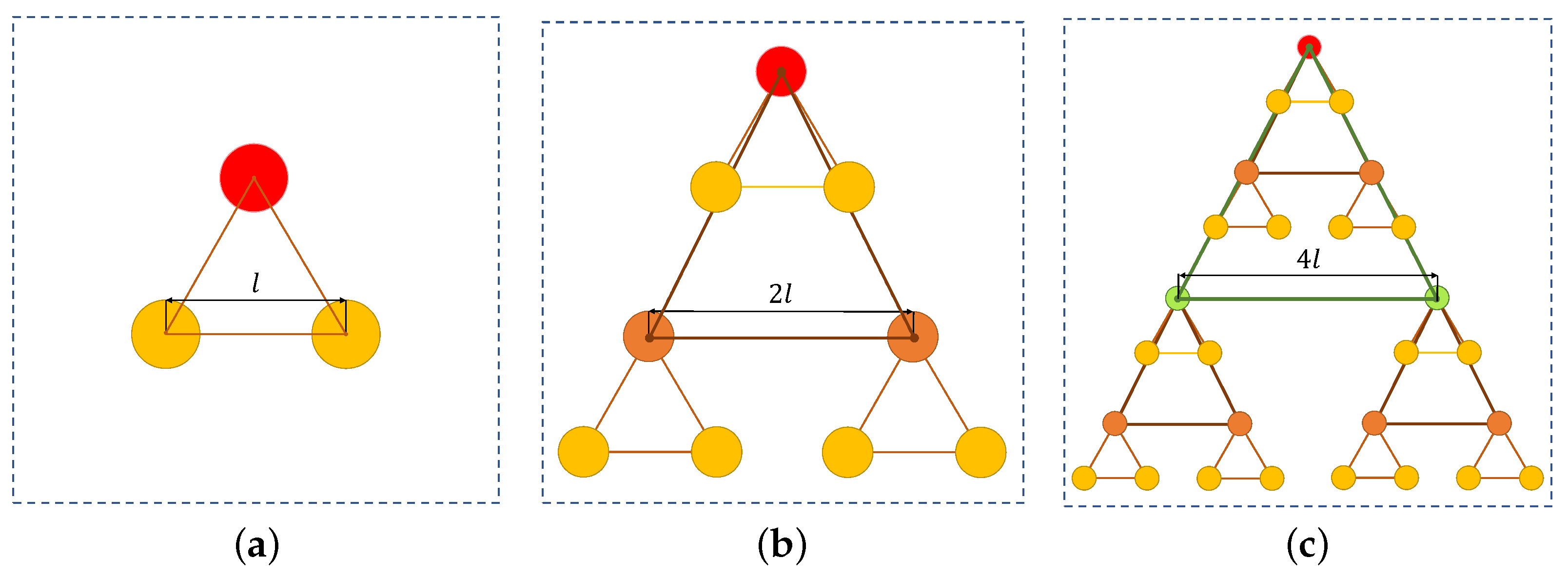
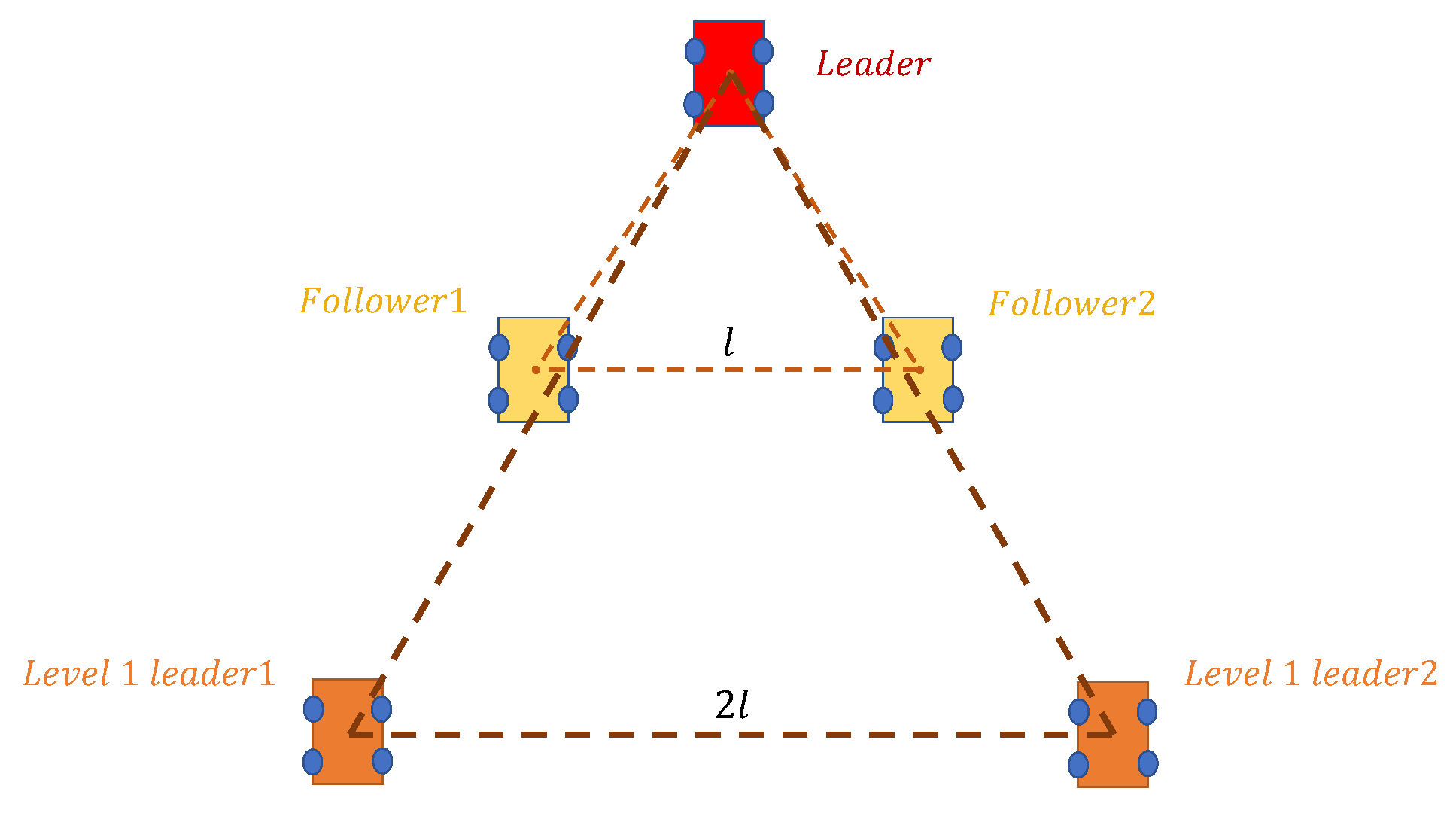
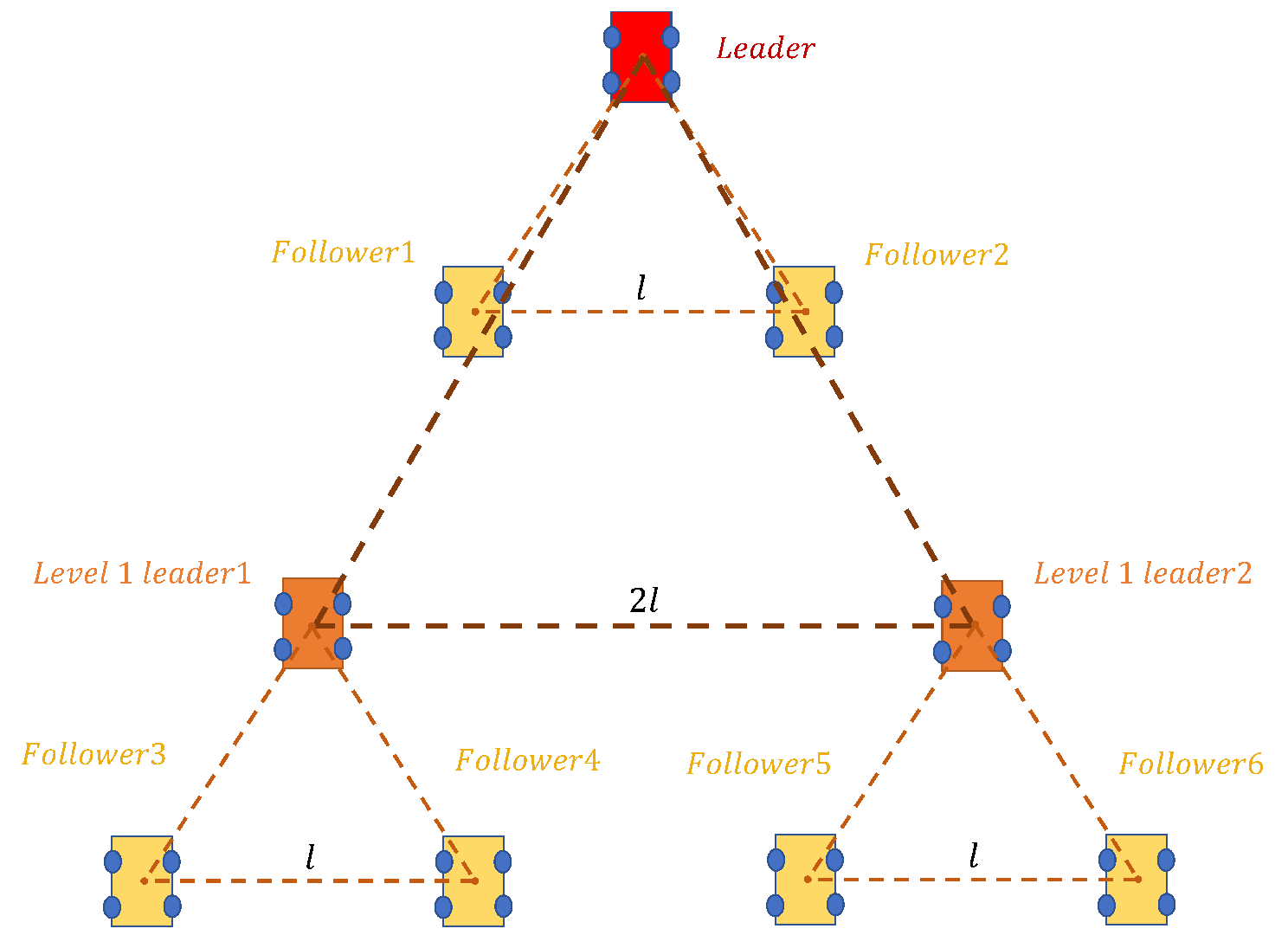
2.3. A Layered Formation Structure

In the leader-following approach, generally speaking, the leader is the only one who knows the team goal, while the followers are committed to maintaining a certain formation or distance relationship. Then, as the leader moves towards the target, the follower will move with it naturally.

As shown in Figure 3, a layered leader-following structure is used to establish the relationship between UGVs in the formation: the leader’s role as the commander of the whole group, and the leaders of other level’s roles as followers of a higher-level leader. The level number increases as the distance the UGV needs to maintain from its leader increases.

At the same time, in the problem of multiagent control, the distributed control method [21,22] has proved its potential compared with the centralized method already [23,24]. Under this formation structure, in this work, a distributed training and execution strategy was adopted, so as to facilitate the formation control and expansion.

2.4. Fundamentals in Reinforcement Learning

2.4.1. Markov Decision Process

The origin of the Markov decision process can be traced back to the research on optimal control problems in dynamic systems in the 1950s, and now it has been widely used in reinforcement learning. One of the reasons is that the MDP has the Markov property, which means that the state of the next moment is only related to the state and action of the current moment. At the same time, the essence of reinforcement learning is to improve strategies through all states, actions, and rewards in history, and select the actions that are expected to obtain the maximum cumulative reward for the current state. Using the Markov hypothesis in a model reinforcement learning problem can simplify the model and speed up the efficiency of the calculation.

Generally speaking, an MDP can be represented using a five-element tuple:

$$M=<S,A,P,R,\gamma >$$

(3)

where $S=s_1,s_2,\dots ,s_t$ represents the finite set of states in the MDP environment, and $s_t$ represents the state at time t. $A=a_1,a_2,\dots ,a_n$ represents the set of all possible actions performed by the agent. $P=(s_t,a_t,s_{t+1})$ represents the probability of a state transition to $s_{t+1}$ after performing action $a_t$ in state $s_t$. R is the reward function and $\gamma \in [0,1]$ is used in the cumulative reward function to adjust how much emphasis the model places on current and future rewards.

The interaction between the agent and the environment in reinforcement learning is shown in Figure 4. The agent chooses an action $a_t$ according to the policy under the observed environmental state $s_t$; the action selected by the agent acts on the environment and causes the state to be updated from $s_t$ to $s_{t+1}$ and returns an immediate reward $r_{t+1}$; finally, the agent updates its policy according to $<s_t,a_t,s_{t+1},r_{t+1}>$ to expect a larger cumulative reward [25].

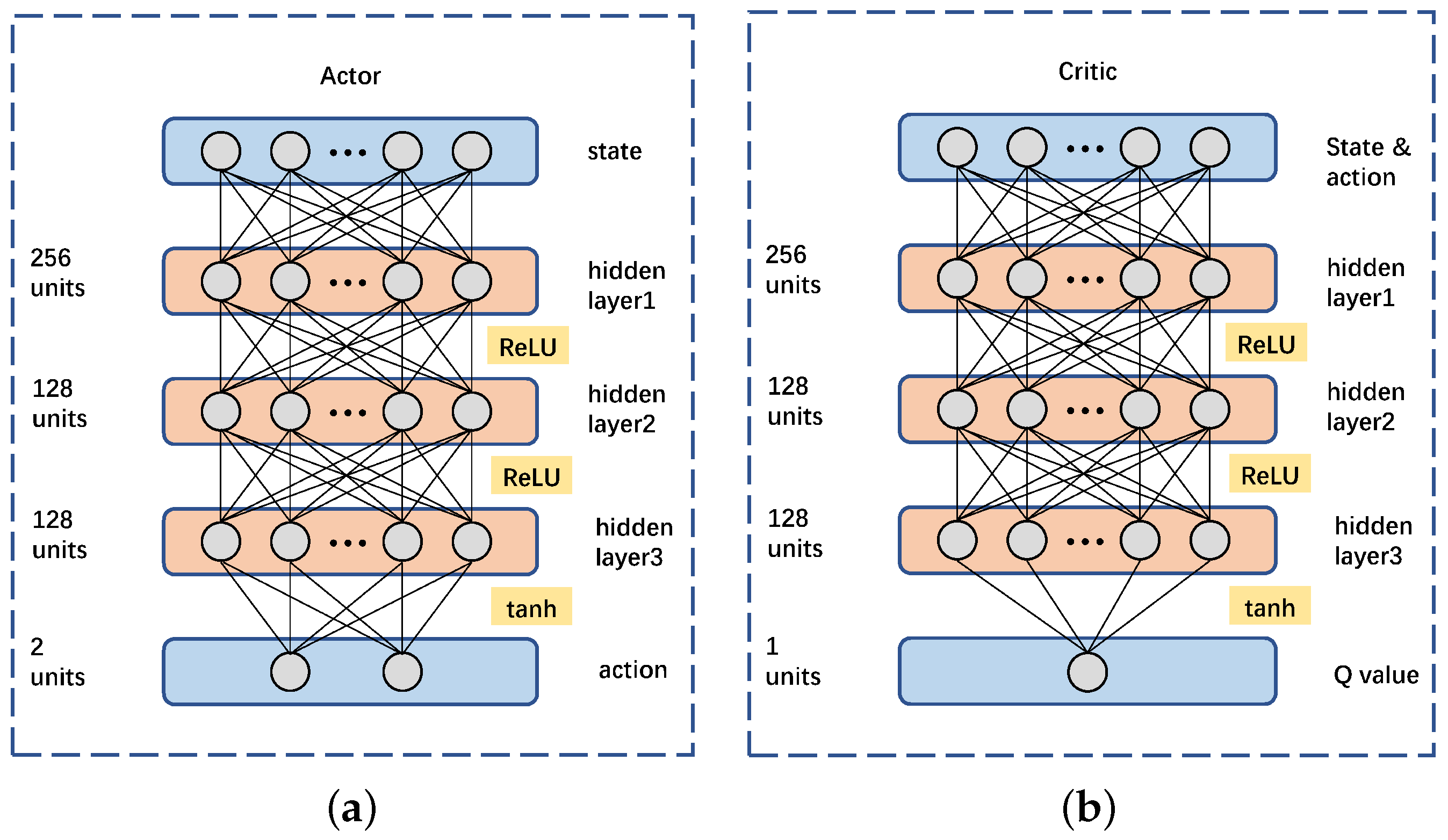
2.4.2. Deep Deterministic Policy Gradient

As mentioned before, the Q-learning algorithm needs to record the expectations of the state–action value function by building a Q table, so it is more suitable for dealing with small state and action space dimensions, such as mazes and some simple game controls problems. However, many problems in the real world have a large state and action space, such as Go and autonomous driving problems, which makes Q-learning encounter the problem of the curse of dimensionality in the way of table records.

The DQN [26] algorithm is a model to solve this dilemma. It uses a deep neural network instead of a Q table to approximate the value of an action and solve the problem with a high-dimensional state space well. However, when it faces the problem of a continuous action space, the way of discretizing the continuous action will make the iterative calculation cost high and the convergence weak, which is not suitable for problems that require continuous and smooth control, such as UGV formation control.

To solve this problem, a reinforcement learning method based on policy gradient (PG) has been proposed. The basic idea is that the optimal policy of each step ${\pi }_{\theta }\left(a_t\mid s_t\right)$ can be expressed as:

$${\pi }_{\theta }\left(a_t\mid s_t\right)=Pr\left(a=a_t\mid s=s_t,\theta \right)$$

(4)

where $Pr$ is a parameterized probability distribution and $\theta$ is its parameter vector. Then, the current optimal action value $a_t$ obtained by sampling can be expressed as:

$$a_t\sim {\pi }_{\theta }\left(a_t\mid s_t\right)$$

(5)

where the process of generating action values is essentially a random process, and the learned policy is also called stochastic policy, which has a natural advantage in the face of an uncertain environment and is conducive to obtaining the optimal policy through exploration. However, with the increase of the dimension of the action space, a high computational complexity caused by sampling in a high-dimensional space occurs. To solve this problem, a deterministic policy gradient (DPG) algorithm [27] using the actor–critic method has been proposed. The DPG algorithm adopts a deterministic policy, and the action value in each step can be directly obtained as:

$$a_t={\mu }_{\theta }\left(s_t\right)$$

(6)

where $\mu$ is the optimal policy and $\theta \in R^n$. The performance objective of the DPG algorithm can be defined as:

$$\begin{array}{cc}J\left({\mu }_{\theta }\right)\hfill & ={\int }_{\mathcal{S}}{\rho }^{\mu }\left(s\right)r\left(s,{\mu }_{\theta }\left(s\right)\right)\mathrm{d}s\hfill \\ \hfill & ={\mathbb{E}}_{s\sim {\rho }^{\mu }}\left[r\left(s,{\mu }_{\theta }\left(s\right)\right)\right]\hfill \end{array}$$

(7)

where ${\rho }^{\mu }\left(s\right)$ is the discounted state distribution and $r(s,{\mu }_{\theta }\left(s\right))$ is the reward function. The gradient of $J\left({\mu }_{\theta }\right)$ can be calculated as:

$$\begin{array}{cc}{\nabla }_{\theta }J\left({\mu }_{\theta }\right)\hfill & ={\int }_{\mathcal{S}}{\rho }^{\mu }\left(s\right){\nabla }_{\theta }{\mu }_{\theta }\left(s\right){\nabla }_a{Q}^{\mu }{(s,a)|}_{a={\mu }_{\theta }\left(s\right)}\mathrm{d}s\hfill \\ \hfill & ={\mathbb{E}}_{s\sim {\rho }^{\mu }}\left[{\left.{\nabla }_{\theta }{\mu }_{\theta }\left(s\right){\nabla }_a{Q}^{\mu }(s,a)\right|}_{a={\mu }_{\theta }\left(s\right)}\right]\hfill \end{array}$$

(8)

Based on the DPG and DQN algorithms, a model-free deep deterministic policy gradient (DDPG) [28] algorithm using an actor–critic method is proposed. Continuing the idea of a DQN fixed network, the DDPG algorithm can be divided into an actor network and a critic network. Each network is composed of a main network and a target network with the same network structure, and the skills of experience replay and freezing the parameters of the target network are adopted to stabilize the learning of the Q function.

At the same time, to make a satisfactory exploration of the state and action space in the training stage, noise $\mathcal{N}$ is added when selecting an action through policy ${\mu }_{\theta }\left(s\right)$:

$$a={\mu }_{\theta }\left(s\right)+\mathcal{N}$$

(9)

In addition, unlike a DQN which adopts a hard update strategy by periodically copying the main network parameters to the target network, the DDPG algorithm adopts a soft update strategy to update the parameters $\theta$ of the target network:

$${\theta }^{\prime }=\tau \theta +(1-\tau ){\theta }^{\prime }$$

(10)

where $\tau$ is a constant and $\tau \ll 1$.

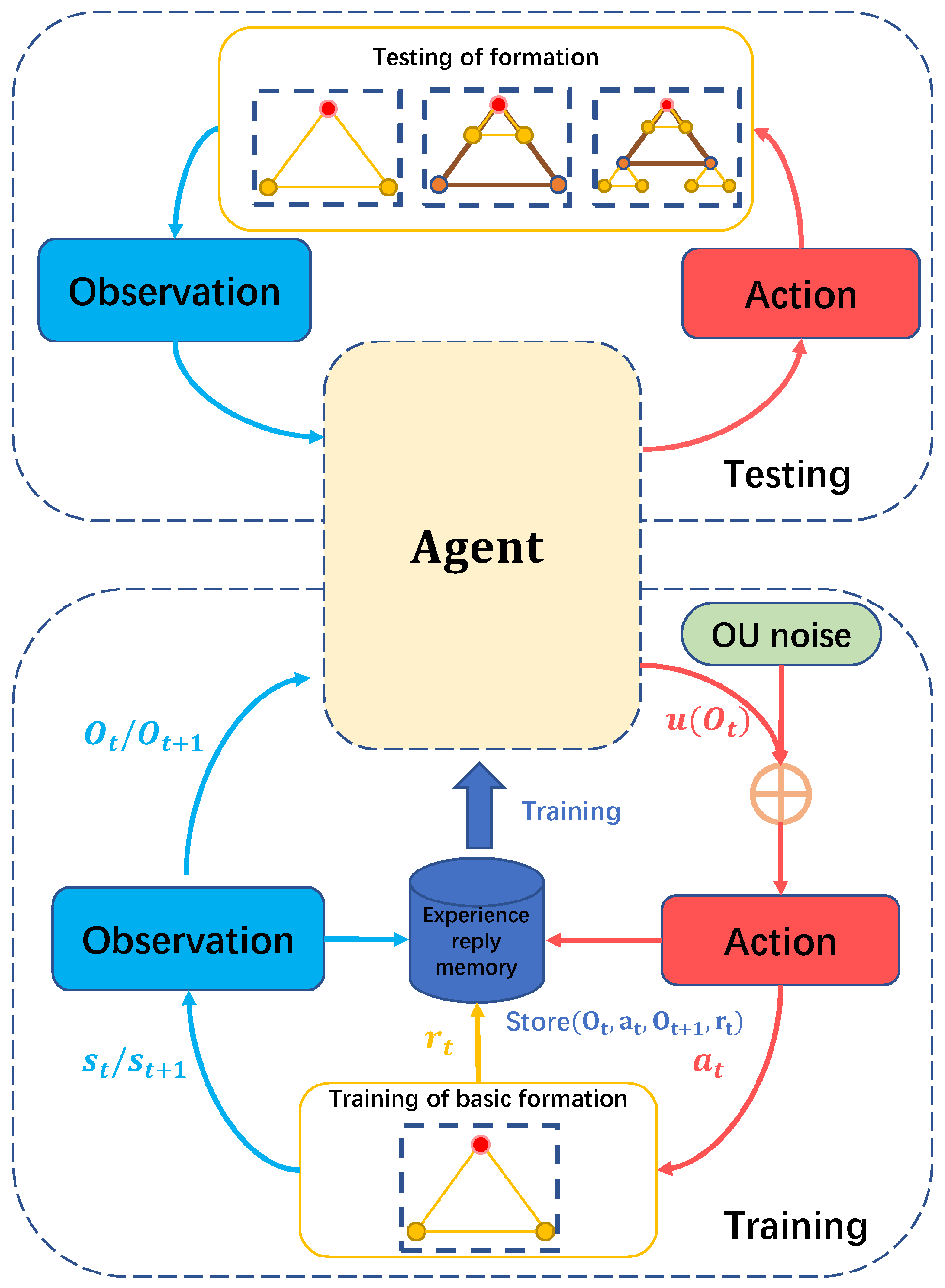
3. Deep-Reinforcement-Learning-Based Distributed and Scalable Cooperative Formation Control Algorithm

In this section, to realize the scalability of the UGV formation, according to different tasks, general MDP models are designed for the leader and other UGVs with follower attributes, respectively, including the state space, action space, and reward function. In addition, the deep-deterministic-policy-gradient-based distributed training and execution strategy will be explained.

3.1. State Space

Consider any UGV in the basic formation, as shown in Figure 5, in which the reinforcement learning training is conducted in a 500 m × 500 m two-dimensional environment. For the leader, the main goal was to reach the target point, and the state space was defined as:

$$S_{leader}=[x,y,\theta ]$$

(11)

where $(x,y)$ is the position coordinates of a UGV and $\theta$ is the heading angle. It should be noted that the coordinate value needed to be normalized.

For the other UGVs with follower attributes, they were divided into two types: a UGV on the left side and a UGV on the right side of its leader. Both of them used the same state space as:

$$S_{follower}=[\frac{\Delta d_1}{d_{req}},\frac{\Delta v_1}{v},\Delta {\theta }_1,\frac{\Delta d_2}{d_{req}},\frac{\Delta v_2}{v},\Delta {\theta }_2]$$

(12)

where $\Delta d_1=d_1-d_{req}$ and $\Delta d_2=d_2-d_{req}$, $d_1$ is the distance between the follower and its leader, $d_2$ is the distance between the follower and the follower at the same level under the same leader (the same relationship as $Follower1$ and $Follower2$ in Figure 5), and $d_{req}$ is the required formation distance corresponding to its level. $\Delta v_1=v_1-v$, where $v_1$ is the velocity of the follower and v is the velocity of its leader (the same definition of the follower’s partner UGV applies to $\Delta v_2$). $\Delta {\theta }_1={\theta }_1-\theta$ with ${\theta }_1$ the heading angle of the follower and $\theta$ the heading angle of its leader (the same definition of the follower’s partner UGV applies to $\Delta {\theta }_2$).

3.2. Action Space

Different from the previous work of path planning using Q-learning, where the action space consisted of 4 or 8 discrete actions due to the limitation of the curse of dimensionality [29], the action space in this work was defined in the continuous space. On the basis of the UGV model, the leader adopted a control strategy of maintaining a constant speed while adjusting its heading angle, and its action space was defined as:

$$A_{leader}=\left[\omega \right]$$

(13)

where $\omega$ is the angular velocity of the leader.

For other UGVs with follower attributes, the actions taken were acceleration a and angular velocity $\omega$ to change the speed and direction of the UGV, so the action space was defined as:

$$A_{follower}=[a,\omega ]$$

(14)

3.3. Reward Functions

The reward function, as the environment feedback to the agent’s behavior, plays a crucial role in reinforcement learning. In this work, a set of subreward functions were designed for the distributed leader and other UGVs to achieve the goal of a cooperative formation and meet the premise of obstacle avoidance. The total reward was composed of all subrewards.

For the leader UGV, its main purpose was to ensure its safety while reaching the target point. The total reward function of the leader consisted of three subreward functions:

Arrival reward function (${\mathit{r}}_{\mathit{arrival}}$): the reward function was designed to encourage a UGV to reach the target and only applied a large positive value to $r_{arrival}$ as a reward when UGV reached the target position.

Distance reward function (${\mathit{r}}_{\mathit{distance}}$): To avoid the problem of slow learning or even nonconvergence due to the sparse rewards, the distance reward function was designed to provide dense rewards for the leader’s exploration, so as to guide the leader to move towards the target position. The formula for calculating the reward function was:

$$\begin{array}{cc}\hfill distanc{e}_t\hfill & =\sqrt{{\left(x_t-x_{goal}\right)}^2+{\left(y_t-y_{goal}\right)}^2}\hfill \\ \hfill distanc{e}_{t+1}\hfill & =\sqrt{{\left(x_{t+1}-x_{goal}\right)}^2+{\left(y_{t+1}-y_{goal}\right)}^2}\hfill \\ \hfill r_{distance}\hfill & ={\lambda }_{distance}(distanc{e}_t-distanc{e}_{t+1})\hfill \end{array}$$

(15)

where $(x_t,y_t)$ and $(x_{t+1},y_{t+1})$ are the coordinate positions of UGV at time t and time $t+1$, respectively, $(x_{goal},y_{goal})$ is the coordinate position of the target point, and ${\lambda }_{distance}$ is a constant, which was used to adjust the importance of the reward. Therefore, when the distance between a UGV and the target was shortened, the positive calculated value was assigned to $r_{distance}$ as a reward; otherwise, the behavior far away from the target was punished by a negative calculated value.

Safety protection reward function (${\mathit{r}}_{\mathit{safe}}$): Safety is one of the core keys in path planning, requiring no obstacles on the planned path, and further expected to maintain a certain distance to obtain redundant safety and avoid collision accidents.

First, consider the handling of collision events. In the environment of continuous space and discrete time, it is necessary to give corresponding rewards as feedback for three situations generated by the interaction between the UGV and obstacles:

• No collision: if there is no collision with obstacles in the next state, no penalty is given.
• Collision: when the next state collides with an obstacle, the UGV is given a large negative reward $r_{obs1}$ as a punishment to guide it to reduce the selection of similar actions in this state.
• Collision along the route: Compared with the continuous real world, discrete time brings some special situations: the next state of the UGV does not collide with the obstacle, but there is an overlap between the connecting line of the two states and the obstacle. Therefore, checking for such collisions is easily overlooked but necessary, and $r_{obs1}$ was also assigned as a penalty for collision along the route.

In addition, to obtain safety redundancy, it was necessary for the UGV to avoid getting too close to the obstacle to reduce the possibility of collision. Assuming that $minL$ was the minimum safe distance between the UGV and the obstacle, when the distance between the UGV and the obstacle was less than $minL$ but no collision occurred, the negative reward $r_{obs2}$ was assigned to the UGV as a penalty to guide safer choices in the future. The value of $r_{obs2}$ was configured according to the importance of safety redundancy.

In summary, the safety protection reward function could be expressed as:

$$\begin{array}{c}{r}_{safe}=r_{obs1}+r_{obs2}\hfill \end{array}$$

(16)

Summarizing the reward function proposed for the leader UGV, including the three subreward functions, in which $r_{arrival}$ and $r_{distance}$ are positive rewards, $r_{safe}$ is a negative reward, the total reward function of the leader could be expressed as:

$$r_{leader}=r_{arrival}+r_{distance}+r_{safe}$$

(17)

For other UGVs with follower attributes, their main purpose was to maintain the shape of the formation while also ensuring safety. The total reward function of the distributed follower consisted of four subreward functions:

Formation distance reward function (${\mathit{r}}_{\mathit{fd}}$): For the distributed follower, keeping the shape of the formation is one of its main tasks. Corresponding to the layered leader-following structure mentioned above, the triangular shape was naturally selected as the target formation. Consider a basic triangular formation consisting of a leader and two followers, as shown in Figure 6, $d_1$ and $d_2$ represent the distance between the follower 1 and its leader and follower 2, respectively, and the closer the distance is to the formation demand, the smaller the penalty. The specific formation achievement reward was calculated as:

$$\begin{array}{cc}{r}_{fd}\hfill & =-{\lambda }_{fd1}|\frac{d_1-d_{req}}{d_{req}}|-{\lambda }_{fd2}|\frac{d_2-d_{req}}{d_{req}}|\hfill \end{array}$$

(18)

where $d_{req}$ is the required formation distance corresponding to its level. ${\lambda }_{fd1}$ and ${\lambda }_{fd2}$ are constant coefficients, which were used to adjust the importance of the two distance-keeping rewards in the triangular formation.

Safety protection reward function (${\mathit{r}}_{\mathit{safe}}$): Safety is also a critical issue for followers. We basically adopted the same solution as that of the leader, including collision prevention and safety redundancy.

Formation position function (${\mathit{r}}_{\mathit{fp}}$): Corresponding to the state space, the followers were divided into two categories: the left follower UGV and the right follower UGV. As shown in Figure 7, the main goal of this reward function was to adjust the relative position relationship between the followers and the leader, so that the left follower UGV and the right follower UGV were more inclined to be on the left and right sides of the ray formed by the leader’s coordinates and heading, respectively, thus avoiding the instability of the formation and the collision risk inside the formation caused by the exchange of positions between the two followers during the advance. If the follower was on the correct side of the ray, zero reward was distributed; otherwise, a negative value was assigned to $r_{fp}$. The relative position relationship could be calculated as:

$$\begin{array}{cc}relationalvalue=\hfill & (y-y_{ray})\ast x_1+(x_{ray}-x)\ast y_1\hfill \\ & +x\ast y_{ray}-x_{ray}\ast y\hfill \end{array}$$

(19)

where $x_{ray}$, $y_{ray}$ is the coordinate of any point on the ray. If the $relationalvalue$ was greater than 0, the follower was on the right side; if the $relationalvalue$ was less than 0, the follower was on the left side; otherwise, the follower was on the ray.

Action reward function (${\mathit{r}}_{\mathit{action}}$): Different from the previous awards that were all for completing the formation and safety, an action reward function was introduced to keep the formation shape more stable, so as to avoid repeated oscillation of the formation between the completed and incomplete states. Considering the formation task under the leader-following structure, if the speed and heading of the UGV and its leader were more consistent, the shape of the formation would be more stable, and the reward function could be expressed as:

$$\begin{array}{cc}{r}_{action}\hfill & =-{\lambda }_{action1}|\frac{v_1-v}{v}|-{\lambda }_{action2}|{\theta }_1-\theta |\hfill \end{array}$$

(20)

where $v_1$ is the velocity of the follower and v is the velocity of its leader. ${\theta }_1$ is the heading angle of the follower and $\theta$ is the heading angle of its leader. ${\lambda }_{action1}$ and ${\lambda }_{action2}$ are constant coefficients, which were used to adjust the importance of keeping the speed and heading consistently. Note that to avoid the follower UGV adopting this strategy when the formation is incomplete, $r_{action}$ should be configured to a smaller value.

Summarizing the reward function proposed for UGVs with follower attributes, including the four subreward functions, in which $r_{fd}$, $r_{safe}$, and $r_{fp}$ are negative rewards and $r_{action}$ is a positive reward. The total reward function of followers could be expressed as:

$$r_{follower}=r_{fd}+r_{safe}+r_{fp}+r_{action}$$

(21)

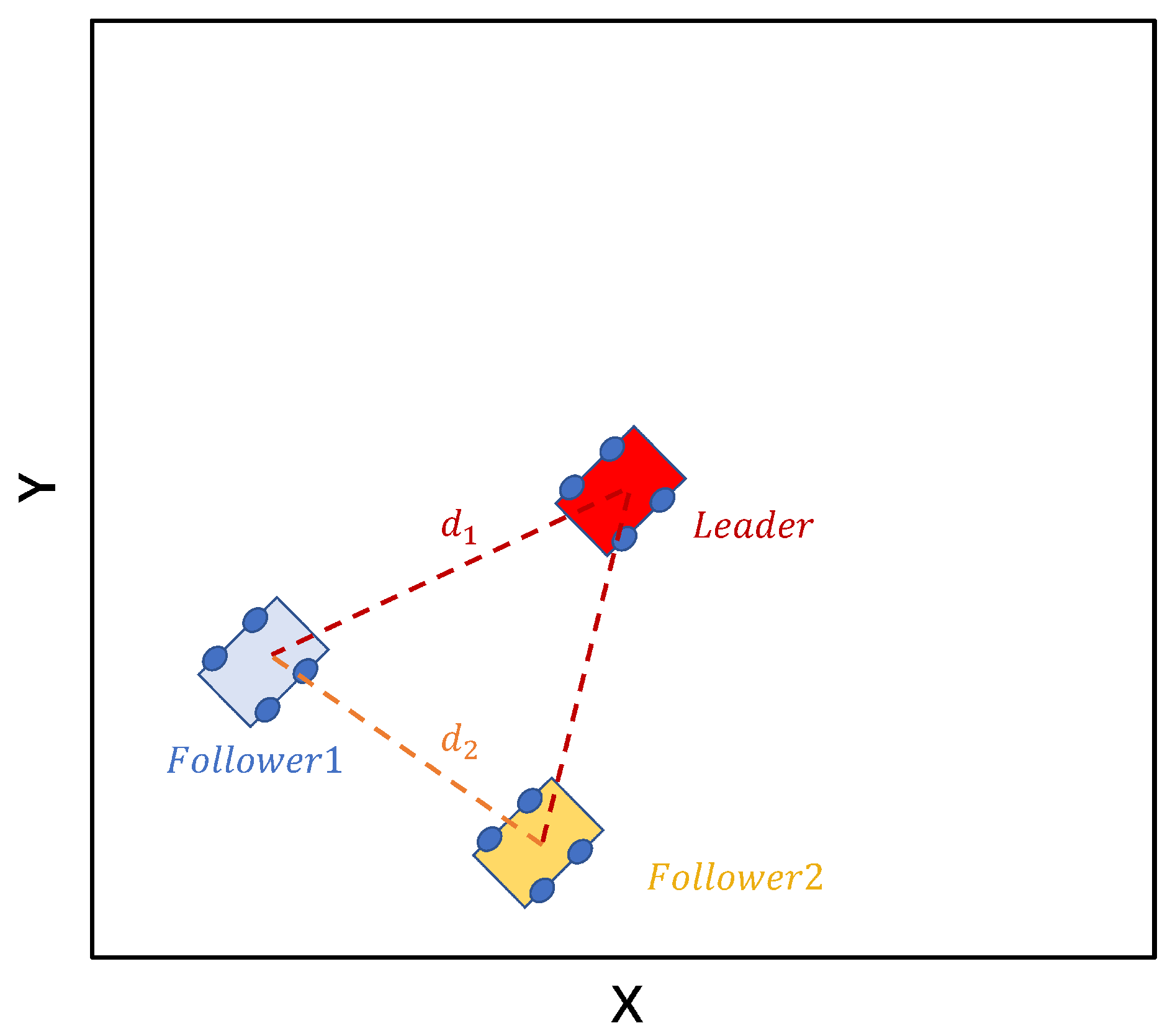
3.4. Formation Expansion Method

In order to satisfy the requirement of formation expansion and reduce the possibility of collision within the formation, a hierarchical triangular formation structure under the layered leader-following structure was designed. Its core was that each agent formed a triangular formation with its leader and follower, respectively, when the leader or follower existed.

Specifically, consider the basic single-layer triangular formation consisting of three UGVs, as shown in Figure 8a. The formation is divided into a leader and two followers, and the distance of the triangular formation is set to l.

On this basis, it is extended to a double-layer formation consisting of nine UGVs, as shown in Figure 8b. At that time, the formation consists of leader, level 1 leaders, and followers, and the distance of the triangular formation consisting of the leader and level 1 leaders is set to $2l$.

Furthermore, it is extended to a three-layer formation consisting of 27 UGVs, as shown in Figure 8c, and the distance of the triangular formation consisting of the leader and level 2 leaders is set to $4l$.

To conclude, for an n-layer formation with a maximum capacity of $3^n$, the level i leader needs to form a triangular formation with a distance $2^{i}l$ from its leader, while followers keep a distance l from their leader.

3.5. Cooperative Formation for Distributed Training and Execution Using Deep Deterministic Policy Gradient

In this work, a distributed and extensible cooperative formation method using DDPG was implemented. Corresponding to the layered formation structure proposed above, instead of adopting a centralized strategy where all UGVs were treated as one agent, a distributed training and execution strategy was designed as shown in Figure 9. Each UGV had their own actor and critic networks. Instead of using global state information, each agent obtained its own observations $O_n$ and rewards $r_n$ by performing actions and interacting with the environment, allowing each network to learn an optimal control strategy to achieve a cooperative formation.

In addition, such a training strategy could largely meet the scalability requirements of UGV formations. Once the network was trained on the base formation shape, the trained network could be easily reused by adjusting the formation distance to meet the needs of other levels of UGV to achieve formation expansion without retraining.

The training and testing framework is shown in Figure 10. Its purpose was to implement reinforcement learning training on simple UGV formations and complete more complex formation tasks with the learned knowledge in the testing phase. Specifically, in the training process, actor–critic networks of the leader, left follower, and right follower were trained by a basic triangular UGV formation, respectively. In the testing phase, different numbers and shapes of formation cases (testing block in Figure 10) were designed to verify the advantages of the scalability of the proposed algorithm. Due to the great benefits of the designed state space and reward function, UGVs of different levels belonging to the left or right followers could reuse the strategies learned from the basic formation in the training phase by allocating the required formation distance. The workflow of the proposed distributed and scalable cooperative formation control algorithm is shown in Algorithm 1.

Algorithm 1 DDPG for Distributed and Scalable Cooperative Formation.

Set the number of UGVs in the formation and determine the category for each UGV Configure the distance of the UGV formation forUGV i = 1, 2, …, n do    Initialize replay buffer $R_i$    Randomly initialize critic network $Q_i(s,a|{\theta }_i^Q)$ and actor ${\mu }_i(s|{\theta }_i^{\mu })$ with weights ${\theta }_i^Q$ and ${\theta }_i^{\mu }$    Initialize target network $Q_i^{\prime }$ and ${\mu }_i^{\prime }$ with weights ${\theta }_i^{Q^{\prime }}\leftarrow {\theta }_i^Q$, ${\theta }_i^{{\mu }^{\prime }}\leftarrow {\theta }_i^{\mu }$ end for forepisode = 1: max-episodedo    Reset the training scenario settings    Initialize a random process $\mathcal{N}$ for action exploration    for step = 1: max-step do      for UGV i = 1, 2, …, n do         Receive observation state $s_i^t$         Select action $a_i^t={\mu }_i(s_i^t|{\theta }_i^{\mu })+\mathcal{N}$         Execute action $a_i^t$ in the training scenario and observe reward $r_i^t$ and new state $s_i^{t+1}$         Store transition $(s_i^t,a_i^t,r_i^t,s_i^{t+1})$ in $R_i$         Sample a random minibatch of N transitions $(s_i^j,a_i^j,r_i^j,s_i^{j+1})$ from $R_i$         Set $y_i^j=r_i^j+\gamma Q_i^{\prime }(s_i^{j+1},{\mu }_i^{\prime }(s_i^{j+1}|{\theta }_i^{{\mu }^{\prime }})|{\theta }_i^{Q^{\prime }})$         Update critic by minimizing the loss: $L_i=\frac{1}{N}{\sum }_j{\left(y_i^j-Q_i\left(s_i^j,a_i^j\mid {\theta }_i^Q\right)\right)}^2$         Update the actor policy using the sampled policy gradient:         ${\nabla }_{{\theta }_i^{\mu }}{J}_i\approx \frac{1}{N}{\sum }_j{\nabla }_a{Q}_i(s,a\mid {\theta }_i^Q){{|}_{s=s_i^j,a={\mu }_i(s_i^j)}{\nabla }_{{\theta }_i^{\mu }}{\mu }_i(s\mid {\theta }_i^{\mu })|}_{s_i^j}$         Update the target networks:         ${\theta }_i^{Q^{\prime }}\leftarrow \tau {\theta }_i^Q+(1-\tau ){\theta }_i^{Q^{\prime }}$         ${\theta }_i^{{\mu }^{\prime }}\leftarrow \tau {\theta }_i^{\mu }+(1-\tau ){\theta }_i^{{\mu }^{\prime }}$      end for      if leader UGV arrives at goal point then         Break      end if    end for end for

In the design of the actor and critic networks of the DDPG algorithm, based on the dimensions of the state space and action space mentioned above, a network structure with three hidden layers (each layer containing 256, 128, and 128 neurons, respectively) was adopted to approximate the policy and state–action value function, as shown in Figure 11.

Table 1. List of Parameters Used in DDPG Algorithm.

ID	Parameter	Value
1	Actor learning rate	0.001
2	Critic learning rate	0.002
3	Discount rate	0.95
4	Soft update $\tau$	0.005
5	Memory size	100,000
6	Batch size	256

lists the other relevant parameters used by the DDPG algorithm.

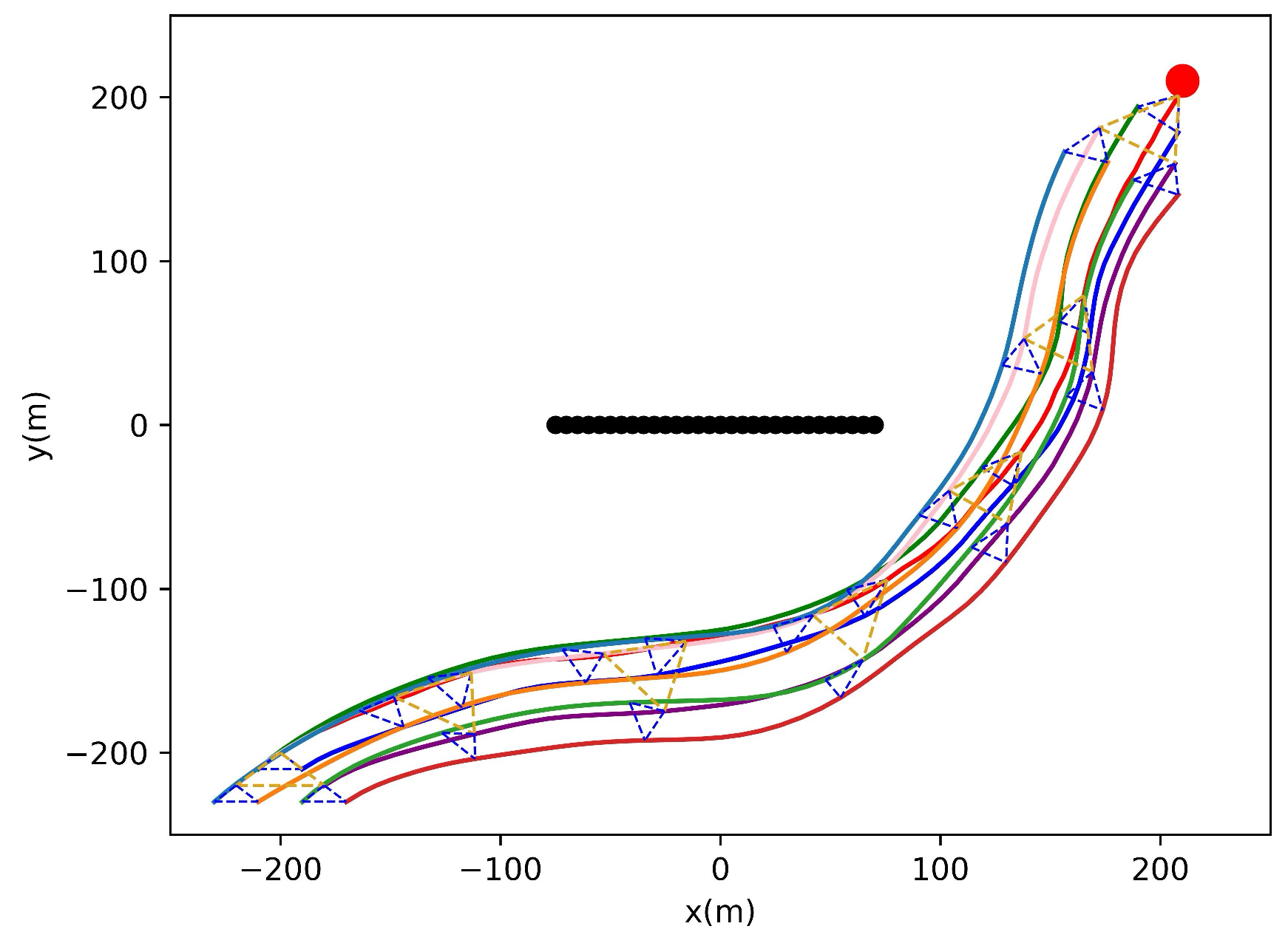
4. Simulation Results and Analysis

To verify the effectiveness of the proposed algorithm, a set of simulation experiments were carried out, and the results are discussed and analyzed in detail in this section. The basic purpose of this work was, first, to verify that the cooperative formation of UGVs could be realized by adopting a distributed deep reinforcement learning architecture; more importantly, it was to verify that the trained actor–critic network could be directly applied to different levels of UGVs with follower attributes by adjusting the formation demand distance in the state space, and the formation could be expanded arbitrarily according to the hierarchical triangular formation structure. Based on this, the simulation results in this section consisted of two parts:

• Training and testing the performance of the cooperative formation control algorithm under the distributed deep reinforcement learning architecture on a basic formation in Section 4.1.
• Testing the scalability of the proposed algorithm on expanded formations in Section 4.2.

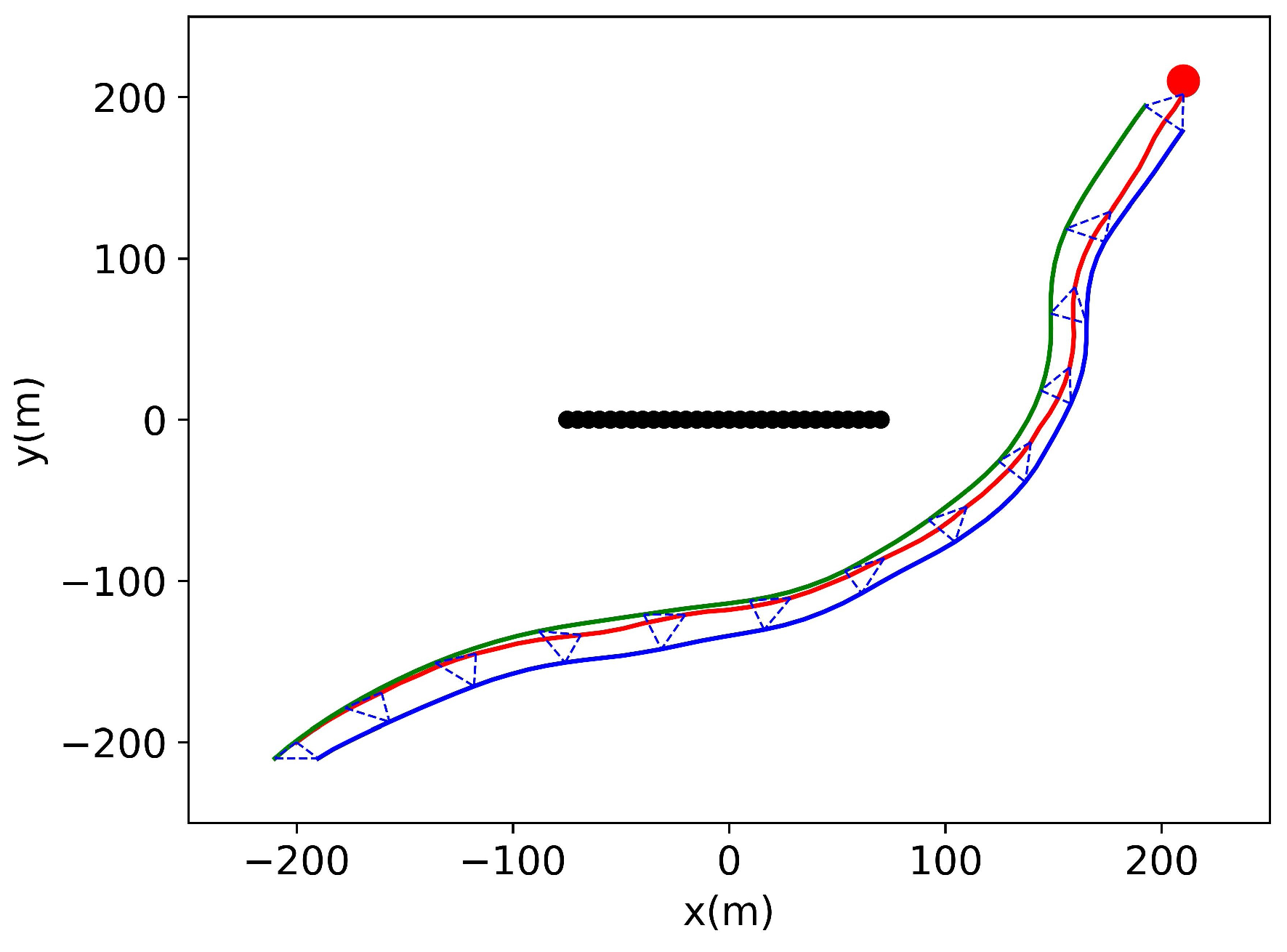
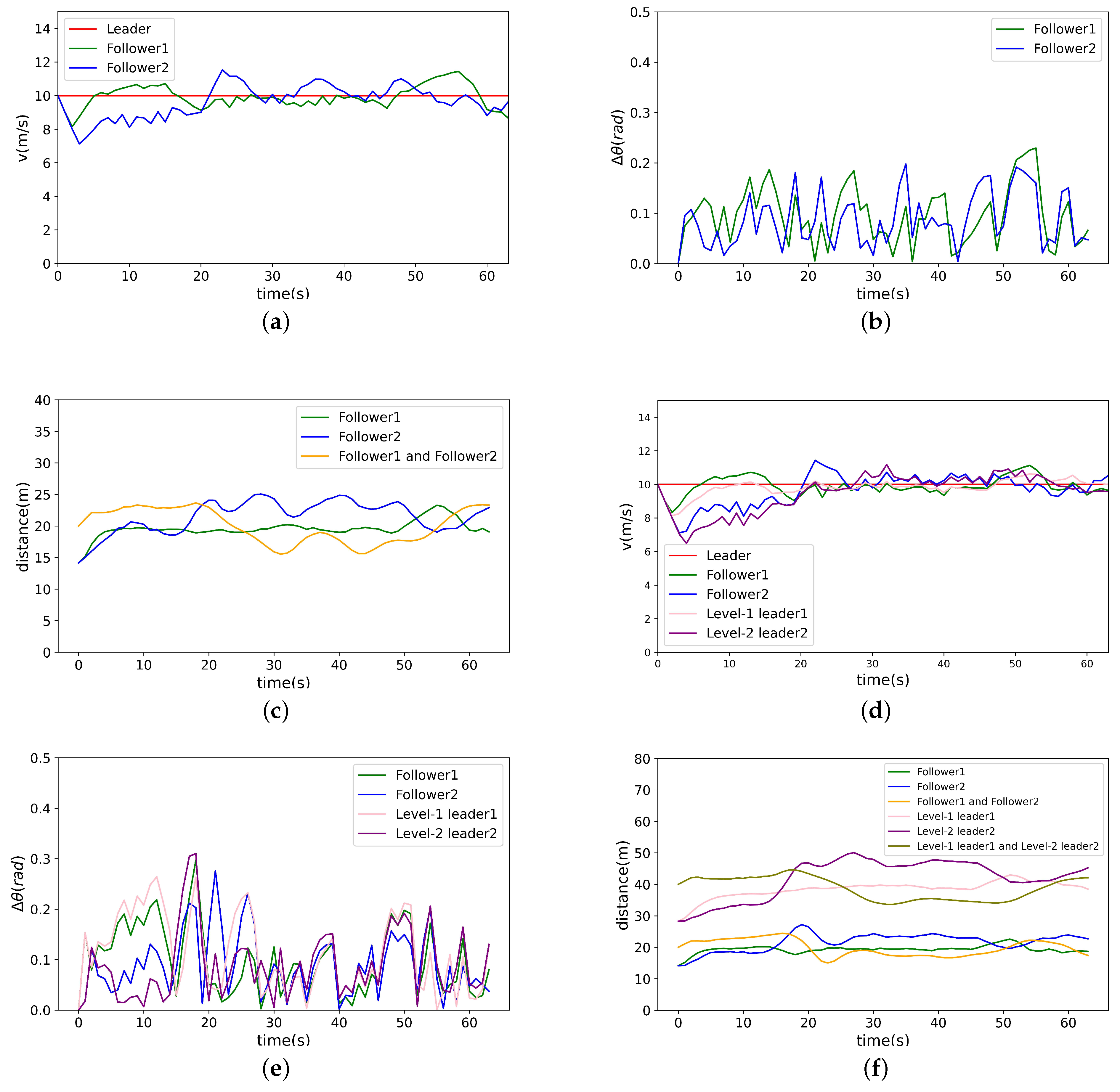
4.1. Training and Testing of Basic Formation

As shown in Figure 12, three actor–critic networks conducted distributed training on a basic triangular formation composed of three UGVs, which were divided into a leader, a left follower, and a right follower. Corresponding to the definition that was previously introduced in the action space, the leader adopted the control method of adjusting the heading at a fixed speed, and the follower could adjust the speed and heading at the same time. The parameters related to the formation are shown in

Table 2. List of Parameters Used in DDPG Algorithm.

ID	Parameter	Value
1	Map range	500 m × 500 m
2	Initial position of the leader	(−200,−200) m
3	Initial position of follower 1	(−210,−210) m
4	Initial position of follower 2	(−190,−210) m
5	Position of the target	(210,210) m
6	Initial speed	10 m/s
7	Initial heading	${90}^{\circ }$
8	Angular velocity range of the leader	${[-5,5]}^{\circ }$/s
9	Angular velocity range of the followers	${[-6,6]}^{\circ }$/s
10	Acceleration range of the followers	[−1,1] m/${\mathrm{s}}^2$
11	Distance requirements of followers in formation	20 m

.

The multi-UGV cooperative formation control policy was trained on a computer with a 5600X CPU and the whole training process took 35 min. Figure 13 shows the moving average cumulative reward of follower 2 with a moving window of 100 episodes during the specific training process. Note that similar reward trends were also observed on the leader and follower 1. During the exploration phase of the training runs from the beginning to about 3000 episodes, under the influence of the actor network with randomly initialized parameters and noise, the UGVs randomly explored the environment without network training to fill the experience pool. After this, with the gradual reduction of noise, the training gradually transitioned to the exploitation phase. The parameters of the actor–critic network were iteratively updated by randomly sampling samples from the experience pool, and the average cumulative reward quickly converged to about −10, which indicated that the training of the algorithm was successful.

We used the trained network on the basic formation to test the performance of the strategy learned by the algorithm, and the parameters used in this formation are shown in

Table 3. List of Parameters Used in the Testing of a Basic Single-layer Triangle Formation.

UGV ID	Initial Position	UGV Type	Formation Distance
Leader	(−200,−200) m	Leader	-
Follower 1	(−210,−210) m	Left	20 m
Follower 2	(−190,−210) m	Right	20 m

. As shown in Figure 14, obstacles are represented by black areas, the red line represents the trajectory of the leader UGV, and the green and blue lines represent the trajectory of the follower 1 UGV and the follower 2 UGV, respectively. It can be seen that a collision-free trajectory could be generated for the UGV formation by using the trained strategy, and the triangle shape could be well maintained in the whole process. In addition, the performance of the algorithm can be further verified in Figure 15a–c. Figure 15a,b show that the follower could keep pace with the leader’s speed and angle to a certain extent. On this basis, the distance of the triangular formation was dynamically stabilized on the required distance of the formation, as shown in Figure 15c.

4.2. Testing of Expanded Formation

The main purpose of the simulation tests in this subsection was to verify the scalability of the proposed formation algorithm. As shown in Figure 16, level 1 leader 1 and level 1 leader 2 were added to the formation to form a double-layer triangular formation consisting of five UGVs, and the parameters related to this formation are shown in

Table 4. List of Parameters Used in the Testing of a Double-layer Triangle Formation.

UGV ID	Initial Position	UGV Type	Formation Distance
Leader	(−200,−200) m	Leader	-
Follower 1	(−210,−210) m	Left	20 m
Follower 2	(−190,−210) m	Right	20 m
Level 1 leader 1	(−220,−220) m	Left	40 m
Level 1 leader 2	(−180,−220) m	Right	40 m

.

The test was performed in the same simulation environment, where level 1 leader1 and level 1 leader2 were directly controlled using the actor–critic networks of follower 1 and follower 2 were trained from the basic triangle formation, respectively. As shown in Figure 17, the expanded formation could still maintain the layered triangle shape while advancing towards the target point. Figure 15d–f show the specific performance of the algorithm in the double-layer triangle formation. It can also be seen that the actor–critic network trained on the follower UGV could still achieve good results in the control of the speed, angle, and formation distance (Figure 15d–f) of the level 1 leader UGV.

On this basis, the scalability of the formation was further verified by increasing the number of UGVs. As shown in Figure 18, a full double-layer triangular formation composed of nine UGVs was constructed for testing, and the relevant parameters of the formation are shown in

Table 5. List of Parameters Used in the Testing of a Full Double-layer Triangle Formation.

UGV ID	Initial Position	UGV Type	Formation Distance
Leader	(−200,−200) m	Leader	-
Follower 1	(−210,−210) m	Left	20 m
Follower 2	(−190,−210) m	Right	20 m
Level 1 leader 1	(−220,−220) m	Left	40 m
Level 1 leader 2	(−180,−220) m	Right	40 m
Follower 3	(−230,−230) m	Left	20 m
Follower 4	(−210,−230) m	Right	20 m
Follower 5	(−190,−230) m	Left	20 m
Follower 6	(−170,−230) m	Right	20 m

. Figure 19 shows the trajectory of the UGV formation and it can be seen that the formation could better maintain the double-layer triangle shape in the process of approaching the target point, which further verified the scalability of the algorithm.

5. Conclusions

In this work, a scalable cooperative formation control algorithm using distributed deep reinforcement learning was proposed. Based on the leader-following structure, a special layered triangular formation structure was designed to formalize the formation construction and expansion. In order to realize the distributed control and scalability of the formation, a new MDP was designed for UGVs with follower attributes, which enabled UGVs belonging to the same category to directly reuse the control strategies learned from the simple formation, thereby enabling more complex formations.

An important direction in future work is to learn the inherent logic of a UGV’s obstacle avoidance by designing a more advanced MDP, so as to realize the safe completion of cooperative formation tasks in a complex environment with variable obstacles without retraining, while maintaining the plug-and-play expansibility of the formation.