Abstract
With satellite systems rapidly developing in multiple satellites, multiple tasks, and high-speed response speed requirements, existing computing techniques face the following challenges: insufficient computing power, limited computing resources, and weaker coordination ability. Meanwhile, most methods have more significant response speed and resource utilization limitations. To solve the above problem, we propose a distributed collaborative computing framework with a genetic algorithm-based task scheduling model (DCCF-GA), which can realize the collaborative computing between multiple satellites through genetic algorithm. Specifically, it contains two aspects of work. First, a distributed architecture of satellites is constructed where the main satellite is responsible for distribution and scheduling, and the computing satellite is accountable for completing the task. Then, we presented a genetic algorithm-based task scheduling model that enables multiple satellites to collaborate for completing the tasks. Experiments show that the proposed algorithm has apparent advantages in completion time and outperforms other algorithms in resource efficiency.
1. Introduction
With the rapid development of satellite systems, effectively coordinating multiple satellites to improve their computational efficiency is an urgent need to be addressed. As shown in Figure 1, the traditional satellite computation is planned in advance by the ground station with corresponding instructions [1], which is subsequently uploaded to the satellite and executed offline through a suitable uplink from the ground station. Meanwhile, it requires precise and serial instructions as well as sufficient communication time between the satellite and the ground, which is a relatively stable operating environment.
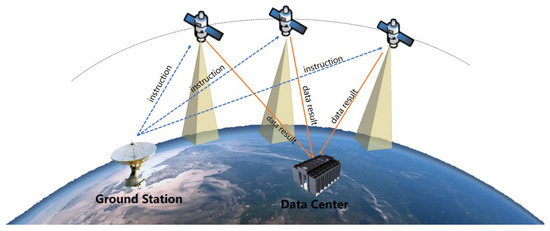
Figure 1.
The traditional satellite computation fashion, where single-satellite calculation is the common mode. The ground station transmits instructions, the satellite calculates itself, and then the satellite sends the result back to the data center.
The rapid development of space–Earth integration makes space information networks [2] a hot spot of research all over the world. It takes space platforms as carriers and supports network infrastructure. Therefore, we can achieve a real-time collection, transmission, and processing of massive space information through inter-satellite as well as on-earth integrated network interconnection. At present, satellite network technology has developed to the stage of a space-based information network. At the same time, with the rapid development of satellite networking technology of inter-satellite links [3,4], the on-board routing switching technology and the integrated satellite network management technology [5,6,7] of space and earth, the satellite network can be better independent of the ground communication system and become an actual space information path.
Multi-satellite collaborative computing [8,9,10,11] is hot research. The continuous development of satellite networks makes interaction between satellites possible, and computational data can be downloaded to satellites autonomously. Most satellite systems consist of multiple satellites. The satellite orbits form a stable spatial geometry, and the satellites maintain a fixed space–time relationship to accomplish specific space tasks.
As an independent agent, each satellite can realize multi-satellite collaborative computing. Compared with a single satellite, multi-satellite collaboration can give full play to the role of satellites and expand the application form of satellites. Therefore, the multiple satellites’ advantages in globality, diversity, timeliness, and continuity are incomparable to a single satellite.
The research on collaborative computing within multi-satellite still needs to be made available. The existing related work includes distributed architectures [12,13], edge computing models [14,15], agent models [16], and other optimization algorithms. Aiming at the problems of inflexible routing strategy, poor compatibility, and high deployment cost of satellite networks, [17,18,19,20,21,22,23,24,25,26] regard the satellite as an intelligent body and build a multi-satellite collaborative computing framework around the agent body. Those methods have significantly superior performance in terms of computation time and success rate, but each satellite has the same role, increasing each satellite’s load. It is only suitable for scenarios with a small amount of computation. A distributed architecture is proposed in the satellite system to study the collaboration between multiple satellites [27,28,29,30]. Focusing on the architectural design of satellite systems. Mobile edge computing is applied in satellite systems [31,32,33,34,35,36,37,38,39]. It solves the collaborative problem of mobile edge computing clusters in the dynamic satellite environment. The introduction of mobile edge computing offloads tasks to each satellite, reducing the dependence on the ground station and the computing pressure of a single satellite. There are also studies for the collaborative method of LEO satellite system [40,41,42,43,44]. According to the high dynamic and non-centered characteristics of LEO satellite network, they proposed some algorithms suitable for high dynamic non-centered scenarios. Respectively, MSABGCT [45], NSGA-II [46], TABU search heuristic [47], and tap water injection algorithm [48] are proposed to solve the problem of multi-satellite collaborative computing. In these studies, optimization algorithms suitable for satellite systems are designed, but the constraints of applicable scenarios and assumptions are somewhat simple. In addition, [49,50,51,52,53,54] proposed effective algorithms to solve the task allocation strategy by studying resource collaboration, realizing multi-satellite collaborative computing, and improving computing efficiency.
The above works have effectively improved the computing efficiency of multi-satellite collaborative computing. However, in the process of multi-satellite collaborative computing, static scenarios cannot only be considered, because the status of satellites and tasks will change. In addition, the effectiveness of the algorithm can be increased by conducting simulation experiments with real satellite data. Though the existing research is deviated from a want to study. The difficulties for this issue are three folds as follows:
- Satellite functions need to be clearly divided. Divide the types of satellites and give them different functions to reduce the load pressure on satellites.
- The satellite environment is dynamically changing, where emergencies such as dynamic changes in satellite time windows, changes in satellite computing status, and changes in computing task queues need to be taken.
- The multi-satellite collaboration algorithm is oriented to satellites in actual scenarios. Measured only from one evaluation index, it lacks rigor. In addition, simulation experiments are required.
To address the above issues, we construct a multi-satellite-oriented distributed collaborative computing framework. With the distributed architecture, a multi-satellite collaborative computing algorithm is proposed to minimize the completion time and optimize energy consumption by scheduling the tasks performed on each satellite.
When studying multi-satellite collaborative computing algorithms, this paper focuses on the unique computing environment of satellite networks, and considers some factors in the real scenario, such as periodic dynamic changes in network topology, limited satellite computing capabilities, and relatively single network structure. The algorithm realizes multi-satellite collaborative computing and improves the execution efficiency of satellites. Meanwhile it enables each satellite to achieve interconnection at the computing level. In general, the contributions of this work are as follows:
- We construct a distributed architecture to model the multi-satellite collaborative computing, and clearly describe the multi-satellite collaboration process. The functions of the main satellite and computing satellite are clear.
- We propose a Distributed Collaborative Computing Framework with a Genetic Algorithm-based task scheduling model (DCCF-GA) to reduce energy consumption and completion time. Specifically, the computing tasks are distributed to satellites under the constraints of tasks and satellite tuples, so multiple satellites can collaborate to complete them, reducing energy consumption and completion time.
- Experiments and simulations are conducted on BEIDOU-3 satellite data. The results show that our proposed algorithm is better than other scheduling algorithms in terms of completion time and energy consumption.
The rest of this paper is organized as follows. Section 2 presents the distributed framework of satellite collaborative computing and the mathematical model of the problem. The proposed DCCF-GA is shown in Section 3. Experimental validation and Simulation are performed in Section 4, and conclusions and future work are given in Section 5.
2. System Model and Problem Formalization
2.1. Problem Definition
Collaborative computing is the entire computing process, where the satellites make interconnection and reach mutual perception to collaborate. In this process, the distributed environment of the satellite network should be able to understand the task planning scheme expressed in certain specifications. Then, they can advance the autonomous computation according to the instruction needs and enable the interaction between different satellites to complete the whole computing task queue collaboratively. So, satellite systems can achieve the minimum energy consumption and minimum completion time.
The resources of the satellite network change dynamically, and the availability of satellite computing nodes also varies over time due to the orbit, satellites’ operation, and the visible time window. Unlike the previous studies, this paper proposes the concept of ‘Time Slice’ and considering the dynamic changes in satellites and tasks. It selects a time period as the research object, and studies multi-satellite collaborative computing within this time slice.
Firstly, a collaborative computing framework for satellite networks is constructed based on the distributed environment of satellite networks. With the computing framework, the collaborative computation process in the satellite network is mainly for collaboration among multiple satellites to complete the tasks for minimizing energy consumption and minimum completion time.
As shown in Figure 2, satellites are divided into the main satellite and the computing satellite:
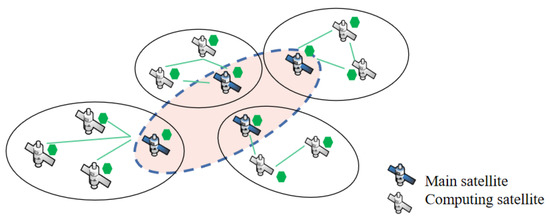
Figure 2.
The collaborative fashion in the main satellites and computing satellites, where the main satellites need to distribute tasks to computing satellites so that they can achieve collaborative computing between multiple satellites.
- Main satellite: A satellite which distributes computing task queues to computing satellites, resource scheduling management, and supervises the situation of the remaining computing satellites.
- Computing satellite: A satellite that acts as a computing satellite generally refers to a satellite with robust computation and communication capabilities, which can communicate with the main satellite. It also allows the main satellite to understand the situation of each computing satellite and make proper resource scheduling.
The multi-satellite collaborative computing problem can be divided into three processes: computational task queue reconstruction, multi-satellite collaborative computation, and computational result aggregation. We mainly study multi-satellite collaborative computation.
The ground station sends a scheduling command, and then the command reaches the main satellite. The computing task queue in the main satellite will be reconstructed first, and then through the scheduler, the main satellite will distribute unexecuted tasks to other satellites. Computing satellites can perform the computation function, and the task queue exists in the main satellite.
The selection of the scheduling satellite is the result of multi-satellite negotiation. The main satellite will execute the most reasonable distribution strategy and allocation scheme according to the particular environmental constraints on the satellite so as to reduce the pressure of single satellite computing. Thus, it can make the computing load of the satellite reaches a balanced level and effectively improve the overall computing efficiency of satellites. For a better description, Table 1 shows the names of the variables that can be used in the multi-satellite collaborative computation process.

Table 1.
Variable noun description used in this paper.
The computing task queue exists only in the main satellite, where the sub-tasks are non-divisible atomic tasks. Multiple tasks can form task blocks, and they form a computing task queue. We need a scheduling algorithm that minimizes the satellite system’s energy consumption and completion time. The initialization of the computing task queue, for each task in the computing task queue, consists of a tuple of attributes: T = {TID, RT, FT, L, Q}, where RT is the task start time, and FT is end time. Q represents which task queue it belongs to.
The reconfiguration of computing task queue is mainly a sorting of the operable time range of the sub-tasks, where the tasks in the same field constitute a task block, and multiple task blocks are sorted to form reconfigured computing task queue. Each computing satellite’s existing and assigned tasks are considered and assigned to the first satellite to complete the computation using polling. In the satellite system of real environment, satellites’ characteristic attributes and trajectories are cumbersome. To facilitate theoretical calculations, multiple satellites in a unified orbit are divided into the same satellite system. The orbital parameters of the satellites in the same orbit are consistent. For different satellites, their load resources determine the computational capability of the satellite. The visible time window of satellite determines its workable time, and the satellite can perform computation only within the visible time range.
To facilitate modeling, we define the satellite property tuple as S = {SID, SRT, SFT, VT, Sp} and the task property tuple as T = {TID, RT, FT, L, Q}. The main satellite receives the task command from the ground station in the multi-satellite collaborative computing process. It will perform a reordering initialization operation on the task queue, sorted by combining the RT and FT of each atomic task. In the dynamic environment, when a new computing task arrives, it will be inserted into the computing task queue according to the time. So, satellites can compute more tasks within the visible time range of the satellite with minimal energy consumption and completion time. The executable time range of each satellite compute node is obtained from SRT, and SFT is called VT.
As shown in Figure 3, the main satellite will distribute tasks to computing satellites according to the tuple information of computing satellites and tasks. The distribution strategy depends on the time window of the computing satellites, the calculation speed, the time of the task, and the size, which enables collaborative computing between multiple satellites.
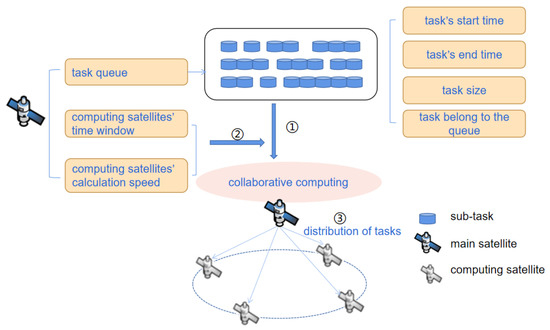
Figure 3.
In the process of multi-satellite collaborative computing, the main satellite distributes tasks to the computing satellites according to the tuple information of computing satellites and tasks.
The model of the whole system is described above, and the collaborative computing model is presented next.
2.2. Multi-Satellite Collaborative Computing Model
The main satellite will distribute the sub-tasks stored in its computing task queue to the computing satellites through the scheduling procedure. It is necessary to consider constraints such as task time and satellite visible time window to minimize energy consumption and minimum completion time. Setting Aij means that task Sj executes, then
In collaborative computing, each computational task is assigned to a computing satellite which cannot execute another task until the execution is completed. At a particular moment, there can only be 0 or 1 task on each satellite to ensure the execution of the collaborative process, so the following restrictions exist:
The energy consumption of multi-satellite collaborative computing is mainly divided into computational energy consumption and transmission energy consumption. For the satellite system and computational tasks described in this paper, the data transmission consumption is ignored for the time being because the amount of input data is usually larger than the amount of output data. Therefore, when we measure the energy consumption of multi-satellite collaborative computing, we focus on the energy consumed by the satellites to perform the tasks. The formula is expressed as follows:
As we can see, Sj represents the computing speed of satellite j, and Cj represents the energy consumption per second of satellite j performing computing tasks. Li represents the size of task i, Ecalj represents the energy consumption of satellite j to calculate the task.
In the multi-satellite collaborative computing scenario, the sum of the energy consumption of the entire satellite system after completing the computing task queue is the total energy consumption.
The satellites cooperatively process sequential related coupled computing tasks, and the satellites can only perform computing tasks within the visible time window.
In addition, the start time of task i is the larger value of the transmission time of the task and the end time of the previous sequence-dependent computing task i, so the execution time of computing task i is:
Therefore, when we measure the completion time of satellite collaborative computing, the start time of the first computing task Ti is within the visible time window of the assigned satellite. We make the following constraints, and the end time of task Ti can be expressed
In the satellite system, the completion time only considers the computing task’s calculation time and waiting time. The waiting time of the task is related to the start execution time. Therefore, the completion time can be calculated after all tasks have been executed. CTical represents the computing task’s calculation time, so the completion time of computing task i can be expressed as (8), and we can use (9) to express the completion time of the satellite system. In (9), min Ct depends on the maximum value of variable FT minus the minimum value of variable RT.
We propose to measure the algorithm’s effectiveness with the minimum total computational energy consumption and completion time. As shown above, the energy consumption objective function of this paper is Formula (4). The completion time objective function of this paper is Formula (9). The constraints are (1), (3), (5), (6) and (7). This function describes the completion time and energy consumption required by multiple satellites to complete collaborative calculations. We can evaluate the effectiveness of the algorithm by observing the results.
Therefore, the collaborative computing of multiple satellites can be formulated as the above problem.
3. The Proposed DCCF-GA Algorithm
The collaborative computing problem for multi-satellites in a satellite system can be statute as a mixed integer nonlinear programming problem. The objective is to obtain a scheduling strategy that minimizes the completion time and energy consumption after completing the computation of tasks. There is no better solution in this field. The specific algorithm is shown Algorithm 1 and its steps can be briefly as follows:
- Randomly generate the population,
- Determine the fitness of individuals with roulette strategy,
- Judge whether it meets the optimization criterion,
- If it does, output the best individual and optimal solution, then end,
- Otherwise, proceed to the next step,
- Select the regenerated individuals based on their fitness, the individuals with high fitness are selected with high probability, and those with low fitness are eliminated,
- According to the crossover probability and crossover method, new individuals are generated until the maximum number of iterations is reached, or the result is stabilized.
According to the algorithm DCCF-GA (Distributed Collaborative Computing Framework with a Genetic Algorithm-based task scheduling model), we first obtain the satellite tuple and task tuple information. Then, we use the DCCF-GA algorithm to distribute tasks to each satellite. The satellites perform a loop operation on the tasks, and iteratively obtains the completion time and energy consumption results by completing all the tasks in collaboration with the satellites. Finally, we can get the performance of the entire satellite system, which are minimum completion time and energy consumption, and the strategy that produces the best result is used as the distribution strategy.
| Algorithm 1. Distributed Collaborative Computing Framework with a Genetic Algorithm-based task scheduling model. |
| Input: multiple satellites performing collaborative computing, queue of computing tasks to be executed, maximum number of species, the maximum number of iterations. Output: minimum completion time CT, minimum energy consumption E. 1: initialize E = 0, CT = RT0 2: get tasks T = {TID, RT, FT, L} 3: get satellites S = {SID, SRT, SFT, VT, Sp} 4: while T ≠ ∅do 5: select task Ti in T with RT, FT satisfies satellite Sj ’s VT 6: if S ≠ ∅ 7: for each task in T 8: combined with GA algorithm, select satellite, which need to be satisfied with minimum CT or E 9: assign Ti to the satellite for execution 10: update the satellite’s status 11: end for 12: end if 13: break 14: get the execution result of the collaborative calculation 15: end while |
3.1. Encoding Decoding
The initialization process of the computing task queue is shown in Figure 4. Based on the start and end time of the task in a front-to-back order, which is located at the top of the queue, it will be assigned to the computing satellites first. This way has a well-balanced initial task queue. Each individual in the task queue represents a batch of possible scheduling of task blocks, and the sub-computing tasks in the task blocks can contain more than one, as shown in Figure 4. The task blocks are separated by a 0 symbol, where Sj represents the computed satellite j.
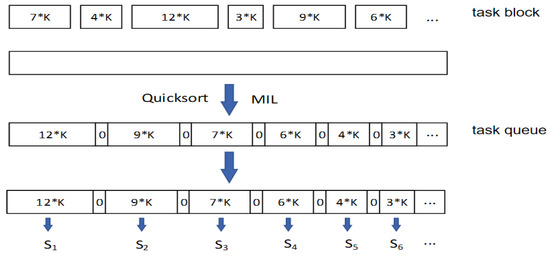
Figure 4.
The illustration about the constructed order of tasks.
3.2. Selection, Crossover and Mutation
Selection is used in genetic algorithms to inherit the optimized individual (or solution) directly to the next generation. The roulette wheel selection algorithm is a widely used selection algorithm by researchers in DCCF-GA for task scheduling. The algorithm in this paper uses the standard weighted roulette wheel selection algorithm. As shown in Figure 5, Each individual i in the task queue is assigned a slot between 0 and 1. The size of the slot is
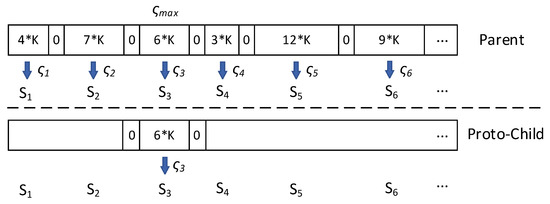
Figure 5.
Selection of tasks, where perform a “select” operation on tasks in the queue.
Crossover is the core function of DCCF-GA algorithm, which refers to replacing and recombining part of the structure of two individuals to generate a new individual. as shown in Figure 6, By crossover, the search ability of DCCF-GA algorithm can be improved by leaps and bounds. After the selection process is completed, a round-robin approach is used to facilitate the search.
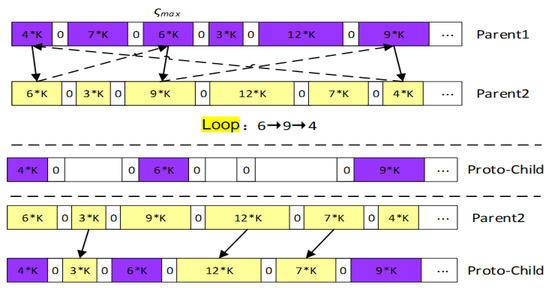
Figure 6.
Crossover of tasks. The tasks’ crossover after performing the selection operation. Through these steps, we can gradually get the best result.
- Select the task block in Parent1, correspondingly find the task block in the corresponding position of Parent2, and then find the same task block in Parent1 from the task block in the corresponding position of Parent2, and repeat the work until a ring is formed;
- Use Parent1 Proto-Child is generated from the selected task block in, to ensure the corresponding position;
- Put the remaining task blocks in Parent2 into Proto-Child.
As shown in Figure 7, the mutation operation is performed by randomly changing the number of computational tasks in individual j. This random mutation method perturbs the search area of the algorithm in the solution space. A certain percentage amount mutates the individuals in each generation stage, and the mutation rate is increased if the energy consumption of the computation does not improve after the corresponding x generations. Once the computed minimum energy consumption decreases again, the mutation rate is reduced. It reduces the probability that the genetic algorithm will fall into a local minimum. The energy consumption of the computation is then reduced using a load-balancing mutation method. It is achieved by distributing the load more evenly over the computation nodes by swapping satellites with high task load to the satellites with low load and swapping. It produces a balanced random initial queue of computational tasks.
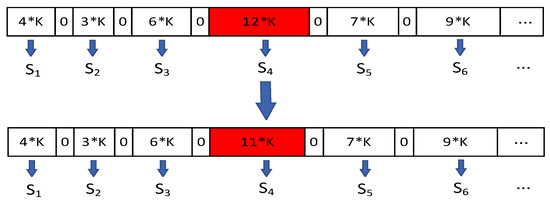
Figure 7.
Mutation of tasks. It is achieved by distributing the load more evenly over the computation nodes by swapping satellites with high task load to the satellites with low load and swapping.
3.3. Fitness Function
Fitness refers to the ability of an individual to adapt to the environment. The fitness function of the genetic algorithm, which is an index used to determine the degree of excellence of the individuals in the population, and the population of this algorithm refers to the computing task queue. The fitness function adds an additional value to each computing node in the system, indicating the goodness of the scheduling plan. This algorithm uses the relative error to generate the fitness value, hoping to calculate the fitness of each computing node to judge whether the individual scheduling is good.
The relative error of individual j is: judging that the scheduling of individual j is
τc(y,j) is the cost of computing satellite j when scheduling is y. The fitness value of individual j is Fj. The larger the value Fj, the smaller the relative error, and the better the scheduling of individual j.
3.4. Termination Conditions
Since the resource usage of the satellite network is precious, the genetic algorithm must generate the schedule reasonably. In this paper, two termination conditions are used. In the experiment, the algorithm converges if the total time and energy consumption fluctuate within a small range. Additionally, set the number of stabilization iterations. When the algorithm’s total energy consumption and completion time stay mostly the same within the specified number of iterations, the algorithm is considered to have converged and stopped. The maximum number of iterations (MNI) setting also considers operability. The algorithm also stops when the maximum number of iterations is exceeded.
4. Experimental
4.1. Algorithm Implementation
In the experiment, some variable values need to be set first. Although the dynamic topology of the satellite network is changing in real time, and the satellite nodes are operating at high speed, the topology is characteristic of periodic changes. The basic parameters of the current significant satellites are shown in Table 2, and the average number of satellite nodes in each constellation is 20. Therefore, we will obtain the satellite ephemeris data, as shown in Table 2, for experimental analysis. Under the constraints of 20 computing nodes and communication delay, we will gradually increase the amount of computing tasks to observe the execution efficiency of the scheduling algorithm and change the task size.

Table 2.
Basic parameters of major satellites. From left to right, they represent satellites’ name, numbers, orbit numbers, orbital inclination, satellite orbital pitch, orbit averaged height and averaging period.
Algorithm DCCF-GA proposed in this paper is implemented programmatically in combination with simulation data and deployed under a computing node with multiple simulations. Every node is assigned different computing and communication capabilities through threaded pass-through parameters. Varying factors, such as the number of computing nodes, the amount of computing tasks, and the communication delay, and the results are evaluated by two evaluation metrics: computational energy consumption and completion time. The total energy consumption is equal to the product of execution time and execution speed consumption per satellite, which is related to the completion time. To improve the reliability of experiments, when implementing genetic algorithm-based scheduling, the default scheduling algorithm in the simulation environment is compared, each group of experiments is repeated several times, and the average results are calculated each time.
4.2. Results Comparison with Other Algorithms
As shown in Figure 8, the maximum completion time index is displayed and analyzed. We verify that our proposed DCCF-GA is superior to SS from three aspects, as shown in the figure. As the number of tasks, communication delay, and the number of computing nodes increase, in terms of maximum completion time, the performance of DCCF-GA is better than SS. As shown in Figure 9, the energy consumption index is displayed and analyzed. When the number of tasks increases, energy consumption also increases. Therefore, we chose to analyze the number of tasks as a variable. By varying the number of tasks, we can observe that as the number of tasks increases, the energy consumption of DDCF-GA is lower than that of SS.
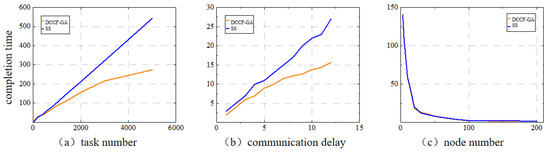
Figure 8.
Performance comparison of DCCF-GA and SS in completion time. (a) Comparing the completion time of DCCF-GA and SS when the number of tasks is different; (b) Comparing the completion time of DCCF-GA and SS when communication delay is different. (c) Comparing the completion time of DCCF-GA and SS when the number of satellite nodes is different.
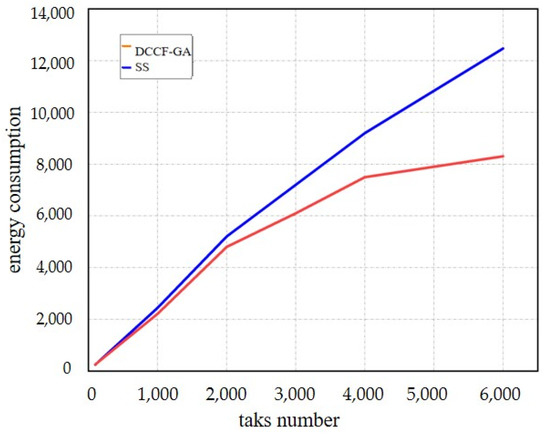
Figure 9.
Performance comparison of DCCF-GA and SS in energy consumption.
The experimental results regarding the number of computational tasks are first analyzed. The basic parameters of the current significant satellites are shown in Table 2. 20 satellite nodes are averaged. The maximum completion time is calculated and compared by gradually increasing computational tasks under the constraint of the same number of 20 computational nodes and communication delays. The maximum completion time of SS in the results grows in a simple linear positive correlation with the increase in the number of tasks. In order to reduce the influence of other factors, a smaller number of computational tasks and the same number of computational nodes are selected for repeated experiments. The results show that DCCF-GA has a significant computation speed advantage in low and high latency environments. After the first two rounds of experiments, the maximum completion time of DCCF-GA and SS is similar when the number of tasks is 400, and the communication delay is 3 s. Under this constraint, the maximum completion time is gradually increased, and the results show that the maximum completion time of the two scheduling algorithms is quite similar. In the early stage, the computation speed improved significantly with the increase in the number of nodes. Still, when the number of nodes was increased to 30, a time bottleneck appeared on both sides. The computation speed improvement began to slow down, which required further comparison and analysis in terms of efficiency. Additionally, as shown in Figure 8, this paper mainly selects the number of tasks to compare the performance of DCCF-GA and SS. When the number of tasks gradually increases, the growth rate of DCCF-GA gradually slows down. Additionally, the energy consumption of DCCF-GA is lower than SS. In real satellite scenarios, the number of tasks is a crucial factor.
In general, the completion time and energy consumption above can directly judge the superiority and inferiority of the scheduling algorithm from the subjective perspective. Based on the results shown in the figure, the algorithm DCCF-GA has considerable advantages over the default Sequential Scheduling (SS) algorithm in the simulation environment after 36 sets of repeated experiments of three kinds.
Comparing the DCCF-GA scheduling algorithm used in this paper with some common batch and immediate mode heuristic scheduling algorithms in distribution. EF scheduling algorithm (Earliest First) is a direct mode scheduler. When a task is to be processed, the scheduler will consider the existing load on each satellite. Then, it will assign the task to the satellite, which completes the calculation first. Lightest Loaded (LL) is an immediate mode scheduling that will assign tasks to the satellites with the lowest current load, regardless of the task size. The Round Robin (RR) algorithm is the most basic immediate mode scheduling, and tasks are allocated to satellites in a round-robin manner. Use empty load or task information when making scheduling decisions. The Max-Min (Max-Min, MX) scheduling algorithm is a batch mode heuristic scheduling. It adopts task batches based on FCFS and sorts these tasks in descending order according to their size. The largest task is then assigned to the node that will complete the computation first, and the operation repeats until the task queue is empty. Then, another task queue is considered. The main purpose of this schedule is to schedule the largest tasks as early as possible and fill the gaps with smaller tasks. Min-min (MM) algorithm is similar to MX, except that the tasks are sorted in ascending order of size. ZO is a batch scheduler that creates schedules based on particle swarm optimization.
The two critical indicators of execution energy consumption and completion time are still used to evaluate DCCF-GA and the six scheduling algorithms introduced above. The experimental results are compared in repeated simulation experiments with the same number of computing nodes and high computing task volume. Figure 10a shows that the maximum completion time of different scheduling algorithms is compared. Figure 10b shows the efficiency comparison of different scheduling algorithms as the amount of computing tasks changes. According to the experimental results, the DCCF-GA algorithm is superior to other algorithms in energy consumption and maximum completion time.
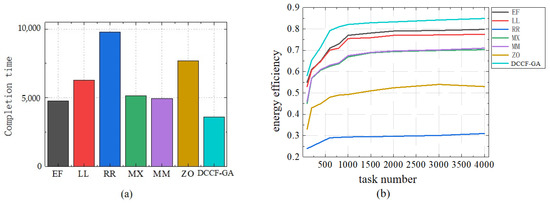
Figure 10.
Performance comparison results with other algorithms. (a) Calculate the completion time of other six algorithms; (b) Calculate the energy consumption ratio of other six algorithms. By comparing the experimental results, it can be seen that DCCF-GA is superior to others.
4.3. Simulation Environment
In the distributed computing environment of satellite networks, the main external constraints are the dynamically changing network topology and the communication visibility between satellites. Although the dynamic topology of the satellite network changes in real-time and the satellite nodes operate at high speed, its topology structure has the characteristics of periodic oscillations so that the parameters of each satellite orbit can be obtained through calculation. Visibility between satellites is to test the feasibility of interstellar calculations.
In terms of setting up the simulation environment of the satellite network, STK is currently a standard analysis software in the aerospace field. STK includes a variety of space element databases such as satellites, radars, and ground stations. Users can set multiple parameters of satellite orbits to create satellite entities. It has a 3D optical module, which can comprehensively display the operating status of the constellation within the specified time range and provide detailed reports.
Satellite ephemeris (TLE, Two-Line Orbital Element) is used to describe spaceflight objects’ position and velocity. TLE records the six parameters of the satellite’s orbit. The STK-Java API can realize STK and Java interconnection for secondary development, obtain the parameters of each satellite by reading and cleaning TLE data, and create satellites in batches. As is shown in Figure 11, which is simulating the BEIDOU-3 satellite.
Figure 11.
The simulation experiment scene of BEIDOU-3 satellite. We created some BEIDOU-3 satellite and they run in orbit.
4.4. Simulation Results
Based on the satellite computing platform, this paper imported the ephemeris data of 25 satellites of the BEIDOU-3 satellite constellation. So, we can simulate the construction of the BEIDOU-3 satellite constellation environment and the scheduling of data computing tasks in the navigation task. Each satellite randomly allocates threads to provide computing power. The computing data in the navigation task generates 1000 computing tasks of different magnitudes by constructing simulated computing task classes. Those tasks are divided into four computing task queues, each queue contains 250 sub-tasks. The visibility of inter-satellite communication uses the satellite data report generated by STK to calculate each satellite. The straight-line distance of the satellite’s relative position and the parameter distance of visible communication is set, and the relative distance determines the communication delay. After constructing the constraints of the DCCF-GA algorithm, the final scheduling assignment result is shown in Figure 12.
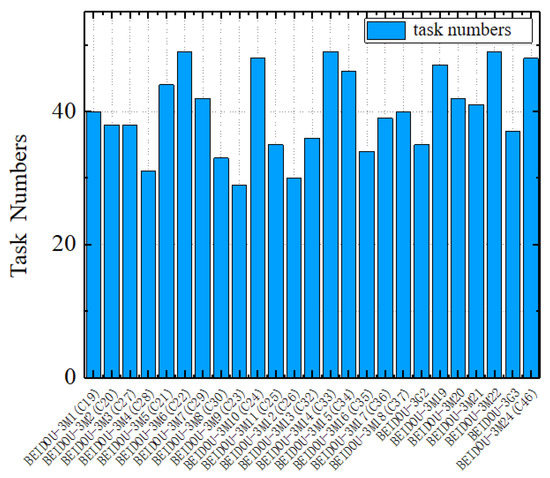
Figure 12.
The simulation results. Set DCCF-GA on the simulation platform, and then get the final collaborative result.
After the satellites performed 1000 computing tasks, Figure 12 shows the number of tasks assigned to each satellite. Finally, we also got the simulation experiment’s completion time and energy consumption. As shown in Table 3, the DCCF-GA algorithm was applied to the simulation experiment, and the simulation results are close to the experimental results as shown on Figure 8a and Figure 9 in Section 4.2.

Table 3.
The simulation results, completion time and energy consumption of the BEIDOU-3 satellite.
5. Conclusions and Future Work
In this paper, we propose a collaborative computing algorithm DCCF-GA. It adapts to the satellite’s environment to accomplish the problem of scheduling computing tasks for multi-satellite collaborative computing, to make the collaborative computing achieve energy minimization and minimum completion time. Under the actual on-satellite environment constraints, DCCF-GA algorithm provides an efficient method. We develop an energy consumption and a completion time model for multi-satellite collaborative computing. We use DCCF-GA algorithm to obtain the optimal solution of the objective function within the number of iterations by crossover variation. DCCF-GA outperforms different algorithms in energy consumption and completion time through repeated experiments and comparison with other scheduling algorithms. It can achieve near-optimal efficiency, which verifies the correctness and effectiveness of the algorithm.
The following issues will be addressed in our future research: First, we will further improve the model for satellite collaborative computing, e.g., by considering constraints over a longer dynamic time. Furthermore, we will extend our experiments to practical applications. Finally, the problems related to resource diversity, data transmission loss, etc., will be fully considered to improve the algorithm.
Author Contributions
Conceptualization, X.Z. and H.F.; methodology, X.Z. and H.F.; formal analysis, L.L.; Funding acquisition, J.L. and L.L.; Investigation, Y.W.; Supervision, L.L.; Validation, H.F. and J.L.; Visualization, X.Z. and L.L.; Writing—original draft, X.Z.; Writing—review and editing, X.Z. and Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xing, J.W.; Wang, B.; Li, J. SAMPGA task scheduling algorithm in cloud computing. In Proceedings of the 36th Chinese Control Conference, Wuhan, China, 26–28 July 2017; pp. 5633–5637. [Google Scholar]
- Yu, Q.; Wang, J.C.; Bai, L. Architecture and critical technologies of space information networks. J. Commun. Inf. Netw. 2016, 1, 1–9. [Google Scholar] [CrossRef]
- Radhakrishnan, R.; Edmonson, W.; Afghah, F.; Rodriguez-Osorio, R.M.; Pinto, F.; Burleigh, S.C. Survey of inter-satellite communication for small satellite systems: Physical layer to network layer view. IEEE Commun. Surv. Tutor. 2016, 18, 2442–2473. [Google Scholar] [CrossRef]
- Chen, Q.; Giambene, G.; Yang, L.; Fan, C.; Chen, X. Analysis of Inter-Satellite Link Paths for LEO Mega-Constellation Networks. IEEE Trans. Veh. Technol. 2021, 70, 2743–2755. [Google Scholar] [CrossRef]
- Cao, Y.; Guo, H.; Liu, J.; Kato, N. Optimal Satellite Gateway Placement in Space-Ground Integrated Networks. IEEE Netw. 2018, 32, 32–37. [Google Scholar] [CrossRef]
- Tang, F. Dynamically adaptive cooperation transmission among satellite-ground integrated networks. In Proceedings of the Conference on Computer Communications, Honolulu, Hawaii, 3–6 August 2020; pp. 1559–1568. [Google Scholar]
- Zhao, Y.; Zhao, Q.; Yang, F.; Yue, H.; Yang, X.; Li, H. Design and Analysis of a Compression and Separation Device for Multi-Satellite Deployment. Aerospace 2022, 9, 446. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, R.; Yu, F.R. Sharded Blockchain for Collaborative Computing in the Internet of Things: Combined of Dynamic Clustering and Deep Reinforcement Learning Approach. Internet Things J. 2022, 9, 16494–16509. [Google Scholar] [CrossRef]
- Fu, S.; Wu, B.; Wu, S. Multi-resources management in 6G-oriented terrestrial-satellite network. China Commun. 2021, 18, 24–36. [Google Scholar] [CrossRef]
- Sarno, S.; Iervolino, M.; Fasano, G. An Adaptive Approach for Impulsive Formation Maintenance Relevant to Distributed SAR Missions. Aerospace 2022, 9, 142. [Google Scholar] [CrossRef]
- Shangguan, B.; Liu, W.; Yue, P.; Wang, M.; Jiang, H.; Yan, Z. An Approach of Spatial Information Network Oriented Satellite-Ground Collaborative Computing Migration. Geomat. Inf. Sci. Wuhan Univ. 2019, 44, 459–466. [Google Scholar]
- Liu, Y.; Dai, Y.; Liu, G. Distributed Space Remote Sensing and Multi-satellite Cooperative On-board Processing. In Proceedings of the International Sensing, Measurement & Data Analytics in the era of Artificial Intelligence, Xi’an, China, 15–17 October 2020; pp. 551–556. [Google Scholar]
- Zheng, Z.; Guo, J.; Gill, E. Distributed onboard mission planning for multi-satellite systems. Aerosp. Sci. Technol. 2019, 89, 111–122. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, J.; Guo, X.; Qu, Z. Satellite edge computing for the internet of things in aerospace. Sensors 2019, 19, 4375. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, G.; Zhao, F. Summary of Satellite Collaborative Planning Algorithm. Int. J. Future Comput. Commun. 2020, 9, 35–43. [Google Scholar] [CrossRef]
- Zhang, G.; Li, X.; An, J. Summary of Research on Satellite Mission Planning Based on Multi-Agent-System. Conf. Ser. 2021, 1802, 022032. [Google Scholar] [CrossRef]
- Ding, Z.; Long, J.; Xie, F.; Qian, Z. Cooperative Control Method of Multi Agent Satellite System Based on SDN. In Proceedings of the International Conference on Smart Grid and Electrical Automation, Kunming, China, 29–30 May 2021; pp. 189–193. [Google Scholar]
- Cui, F.Z.; Zhong, C.Q.; Wang, X.K. A collaborative design method for satellite module component assignment and layout optimization. J. Aerosp. Eng. 2019, 233, 5471–5491. [Google Scholar] [CrossRef]
- Du, B.; Li, S. A new multi-satellite autonomous mission allocation and planning method. Acta Astronaut. 2019, 163, 287–298. [Google Scholar] [CrossRef]
- Chen, J.; Liu, S.; Zhang, Y. Inter-satellite token ring Ad hoc network technology for micro-nano satellite cluster collaboration. Inf. Sci. Commun. 2021, 3, 125–131. [Google Scholar]
- Feng, P.; Chen, H.; Peng, S. A method of distributed multi-satellite mission scheduling based on improved contract net protocol. In Proceedings of the International Conference on Natural Computation, Zhangjiajie, China, 15–17 August 2015; pp. 1062–1068. [Google Scholar]
- Luo, Y.; Jiang, X.; Zhong, S.; Ji, Y.; Sun, G. Multi-satellite Task Allocation and Orbit Planning for Asteroid Terminal Defence. Aerospace 2022, 9, 364. [Google Scholar] [CrossRef]
- Jiang, W.; Pang, X.L.; Yuan, Z.Q. Multi agent-based networking satellite tasks scheduling with department collaborative mechanism. In Proceedings of the International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery, Zhangjiajie, China, 15–17 August 2017; pp. 989–996. [Google Scholar]
- Bonnet, J.; Gleizes, M.P.; Kaddoum, E. Multi-satellite mission planning using a self-adaptive multi-agent system. In Proceedings of the International Conference on Self-Adaptive and Self-Organizing Systems, Cambridge, MA, USA, 21–25 September 2015; pp. 11–20. [Google Scholar]
- Dong, Y.; Wei, X.; Liu, F. Novel collaborative optimization framework with a negotiation model for satellite system design. Eng. Optim. 2018, 50, 1395–1414. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Y.; Zhang, C. The state-space model identification-based adaptive collaborative multi-satellite simulation system. In Proceedings of the Fourth World Congress on Software Engineering, Hong Kong, China, 3–4 December 2013; pp. 293–297. [Google Scholar]
- Long, J.; Qian, Z.M.; Xie, F. An Improved Multi-Satellite Cooperative Task Planning Method Based on Distributed Multi-agent System. Meas. Technol. Mechatron. Autom. 2021, 539–542. [Google Scholar]
- Sinha, P.K.; Dutta, A. Multi-satellite task allocation algorithm for earth observation. In Proceedings of the Region 10 Conference, Hong Kong, China, 15 July–9 September 2016; pp. 403–408. [Google Scholar]
- Chen, Q.; Liao, S.; Wu, W. Research on Collaborative Planning for Distributed Satellite System Formation Adjusting. J. Astronaut. 2009, 2–12. [Google Scholar]
- Liu, L.; Dong, Z.; Su, H. A Study of Distributed Earth Observation Satellites Mission Scheduling Method Based on Game-Negotiation Mechanism. Sensors 2021, 21, 6660. [Google Scholar] [CrossRef]
- Ma, L.; Liu, M.; Li, C. A cloud-edge collaborative computing task scheduling algorithm for 6g edge networks. J. Beijing Univ. Posts Telecommun. 2020, 43, 66–73. [Google Scholar]
- Jia, X.H.; Lv, T.; He, F. Collaborative data downloading by using inter-satellite links in LEO satellite networks. Trans. Wirel. Commun. 2017, 16, 1523–1532. [Google Scholar] [CrossRef]
- Wang, H.; Han, J.; Cao, S.; Zhang, X. Computation Offloading Strategy of Multi-satellite Cooperative Tasks Based on Genetic Algorithm in Satellite Edge Computing. In Proceedings of the 2021 International Conference on Space-Air-Ground Computing (SAGC), Huizhou, China, 23–25 October 2021; pp. 22–28. [Google Scholar]
- Qiao, W.; Liu, Y.; Xi, L. A Novel Method for Resource Efficient Security Service Chain Embedding Oriented to Cloud Datacenter Networks. Access 2021, 9, 77307–77324. [Google Scholar] [CrossRef]
- Wang, F.; Jiang, D.; Qi, S. Fine-grained resource management for edge computing satellite networks. In Proceedings of the Global Communications Conference, Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar]
- Fadlallah, G.; Mcheick, H.; Rebaine, D. Layered Architectural Model for Collaborative Computing in Peripheral Autonomous Networks of Mobile Devices. Procedia Comput. Sci. 2019, 155, 201–209. [Google Scholar] [CrossRef]
- Qin, J.; Guo, X.; Ma, X.; Li, X.; Yang, J. Application and Performance Evaluation of Resource Pool Architecture in Satellite Edge Computing. Aerospace 2022, 9, 451. [Google Scholar] [CrossRef]
- He, C.; Zheng, M. Cloud-Edge Collaboration Feature Extraction Framework in Satellite Multi-access Edge Computing. Electron. Inf. Emerg. Commun. 2021, 61–64. [Google Scholar]
- Song, Z.; Hao, Y.; Sun, X. Computation Offloading and Resource Allocation Algorithm for Collaborative LEO Satellite Multi-Access Edge Computing. Acta Electonica Sin. 2022, 50, 567. [Google Scholar]
- Zhao, Q.; Jiang, B.; Yu, X. Collaborative mission optimization for ship rapid search by multiple heterogeneous remote sensing satellites. J. Ind. Manag. Optim. 2021, 18, 2805–2826. [Google Scholar] [CrossRef]
- Zhao, G.; Kang, Z.; Huang, Y.; Wu, S. A Routing Optimization Method for LEO Satellite Networks with Stochastic Link Failure. Aerospace 2022, 9, 322. [Google Scholar] [CrossRef]
- Wang, F.; Jiang, D.; Qi, S. A dynamic resource scheduling scheme in edge computing satellite networks. Mob. Netw. Appl. 2021, 26, 597–608. [Google Scholar] [CrossRef]
- Leng, T.; Li, X.; Hu, D. Collaborative Computing and Resource Allocation for LEO Satellite-Assisted Internet of Things. Wirel. Commun. Mob. Comput. 2021, 2021, 4212548. [Google Scholar]
- Wang, C.; Ren, Z.; Cheng, W.; Zheng, S.; Zhang, H. Time-Expanded Graph-Based Dispersed Computing Policy for LEO Space Satellite Computing. In Proceedings of the 2021 IEEE Wireless Communications and Networking Conference, Nanjing, China, 29 March–1 April 2021; pp. 1–6. [Google Scholar]
- Xu, A.; Ju, C.; Qian, J.; Zhang, Q.; Shen, Y.; Tao, Y.; Chen, D.; Cao, G.; Liu, Q. Multi-satellite Spectrum Allocation Algorithm Based on Graph Coloring Theory. In Proceedings of the 2020 International Conference on Aviation Safety and Information Technology, Weihai, China, 14–16 October 2020; pp. 622–627. [Google Scholar]
- Chen, Y.; Xu, M.; Shen, X.; Zhang, G.; Lu, Z.; Xu, J. A Multi-Objective Modeling Method of Multi-Satellite Imaging Task Planning for Large Regional Mapping. Remote Sens. 2020, 12, 344. [Google Scholar] [CrossRef]
- Bianchessi, N.; Cordeau, J.F.; Desrosiers, J. A heuristic for the multi-satellite, multi-orbit and multi-user management of Earth observation satellites. Eur. J. Oper. Res. 2007, 177, 750–762. [Google Scholar] [CrossRef]
- Fu, S.; Gao, J.; Zhao, L. Collaborative multi-resource allocation in terrestrial-satellite network towards 6G. Trans. Wirel. Commun. 2021, 20, 7057–7071. [Google Scholar] [CrossRef]
- Cui, Y.; Chen, Z.; Li, L.; Zhang, Q.; Luo, S.; Lu, Z. An efficient parallel computing strategy for the processing of large GNSS network datasets. GPS Solut. 2021, 25, 36. [Google Scholar] [CrossRef]
- Hu, F.; Gao, X. Development trend analysis of remote sensing small satellite of surveying and mapping application. Sci. Surv. Mapp. 2019, 44, 136–142. [Google Scholar]
- Zhang, S.; Cui, G.; Long, Y. Optimal resource allocation for satellite-aided collaborative computing among multiple user pairs. Int. J. Satell. Commun. Netw. 2021, 39, 500–508. [Google Scholar] [CrossRef]
- Fan, H.; Yang, Z.; Wu, S. An Efficient Satellite Resource Cooperative Scheduling Method on Spatial Information Networks. Mathematics 2021, 9, 3293. [Google Scholar] [CrossRef]
- Fan, H.; Yang, Z.; Zhang, X. A novel multi-satellite and multi-task scheduling method based on task network graph aggregation. Expert Syst. Appl. 2022, 205, 117565. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, W.; Fan, H. A Spatio-Temporal Graph Neural Network Approach for Traffic Flow Prediction. Mathematics 2022, 10, 1754. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).