Path Planning of Multiple Unmanned Aerial Vehicles Covering Multiple Regions Based on Minimum Consumption Ratio
Abstract
1. Introduction
2. Related Works
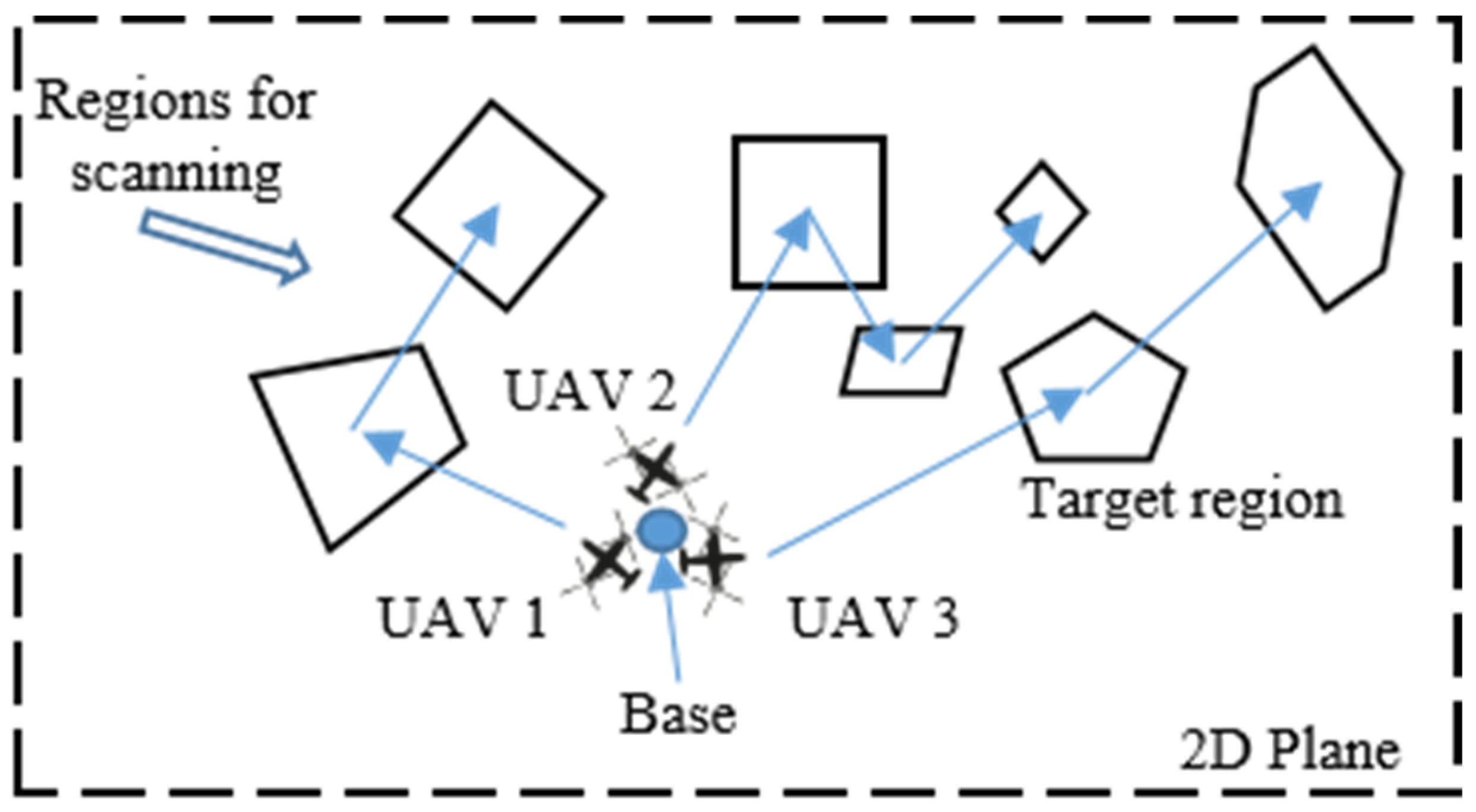
3. Problem Formulation
4. Methodology
4.1. Minimum Consumption Ratio for Coverage Path Planning
| Algorithm 1 Minimum Consumption Ratio Algorithm | |
| Input: | UAV set: ; Target Regions set: . |
| Output: | Set of mission areas for each UAV |
| 1 | Number the UAVs according to the coverage capability from small to large |
| 2 | Initialize region accessible variable |
| 3 | Initialize the number of regions variable = 0 |
| 4 | While |
| 5 | ← the first drone completes covering the current mission area |
| 6 | |
| 7 | |
| 8 | Calculate the MCR of the corresponding node for |
| 9 | |
| 10 | |
| 11 | Select the region with an MCR and labeled as |
| 12 | ← 0 |
| 13 | ← |
| 15 | |
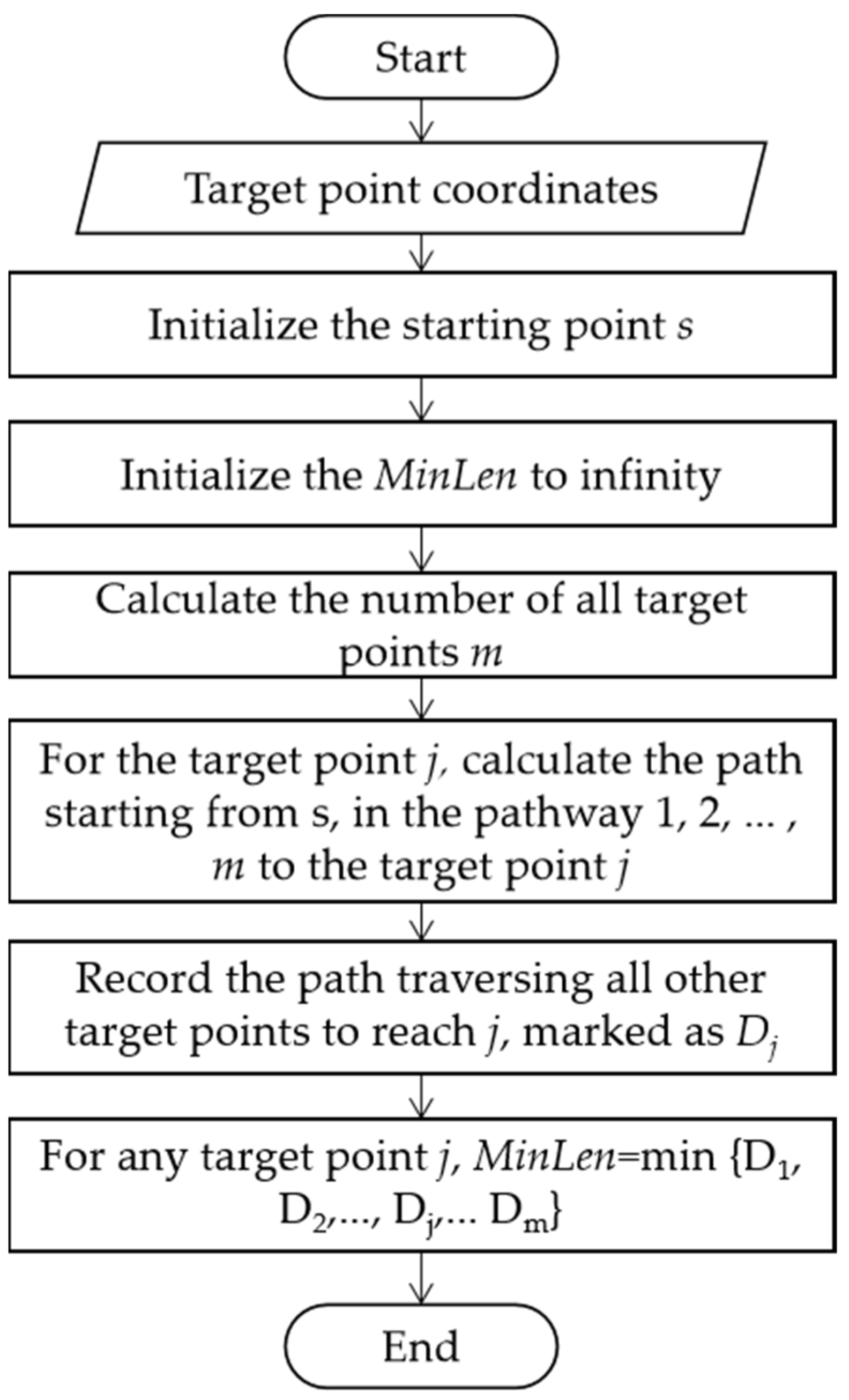
4.2. Coverage Path Replanning by Dynamic Planning
5. Numerical Experiments
6. Results and Discussion
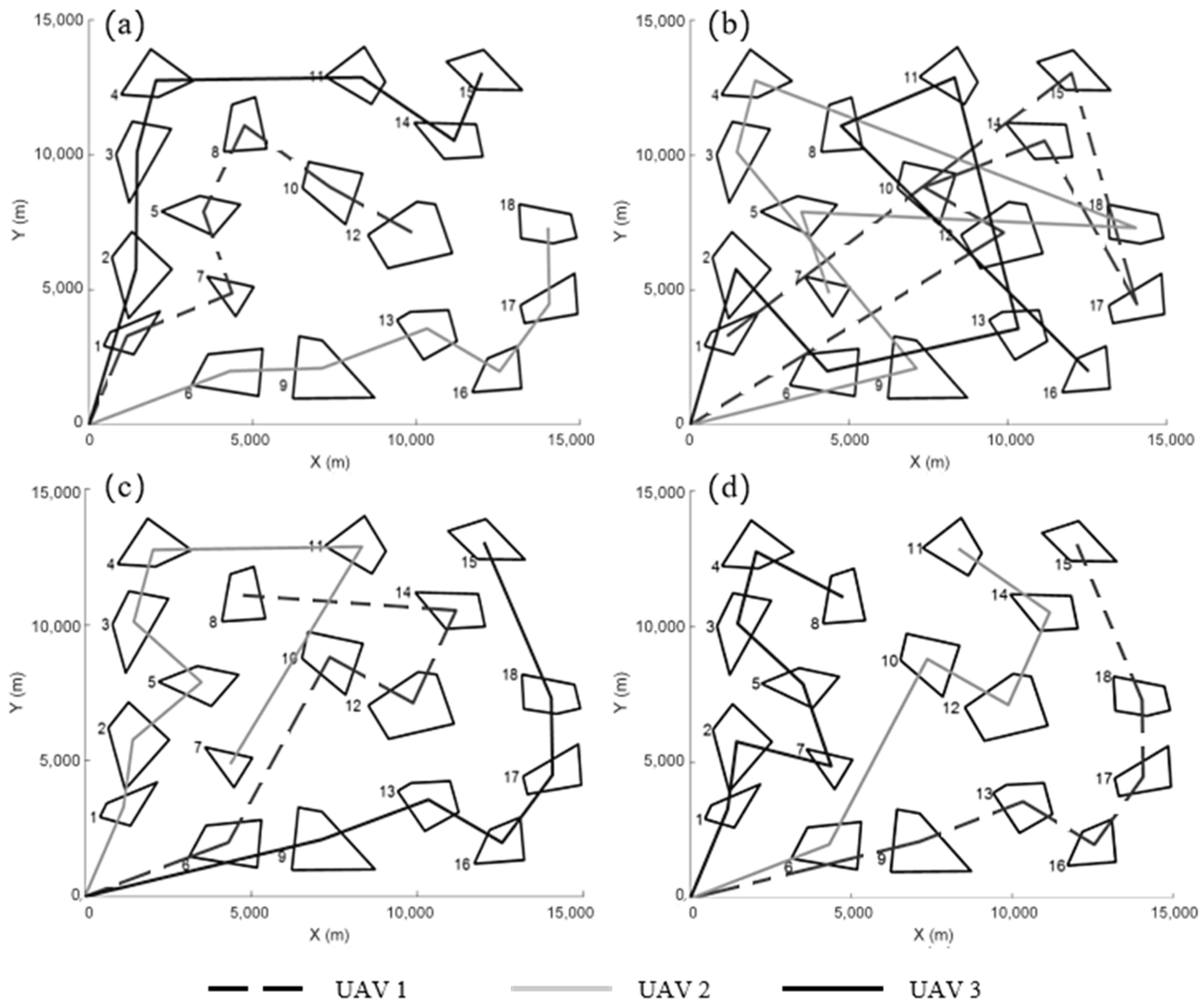
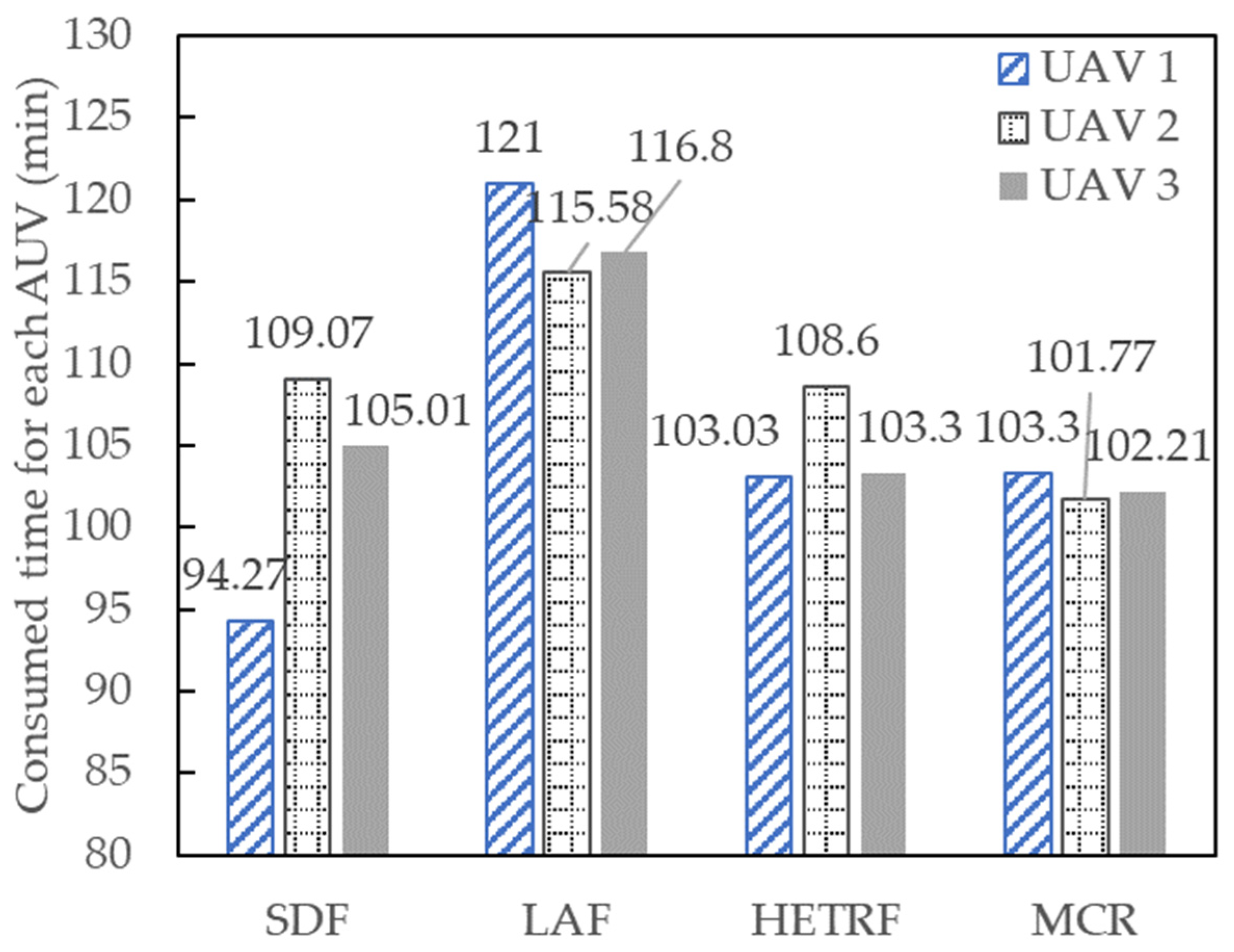
6.1. Homogeneous UAVs
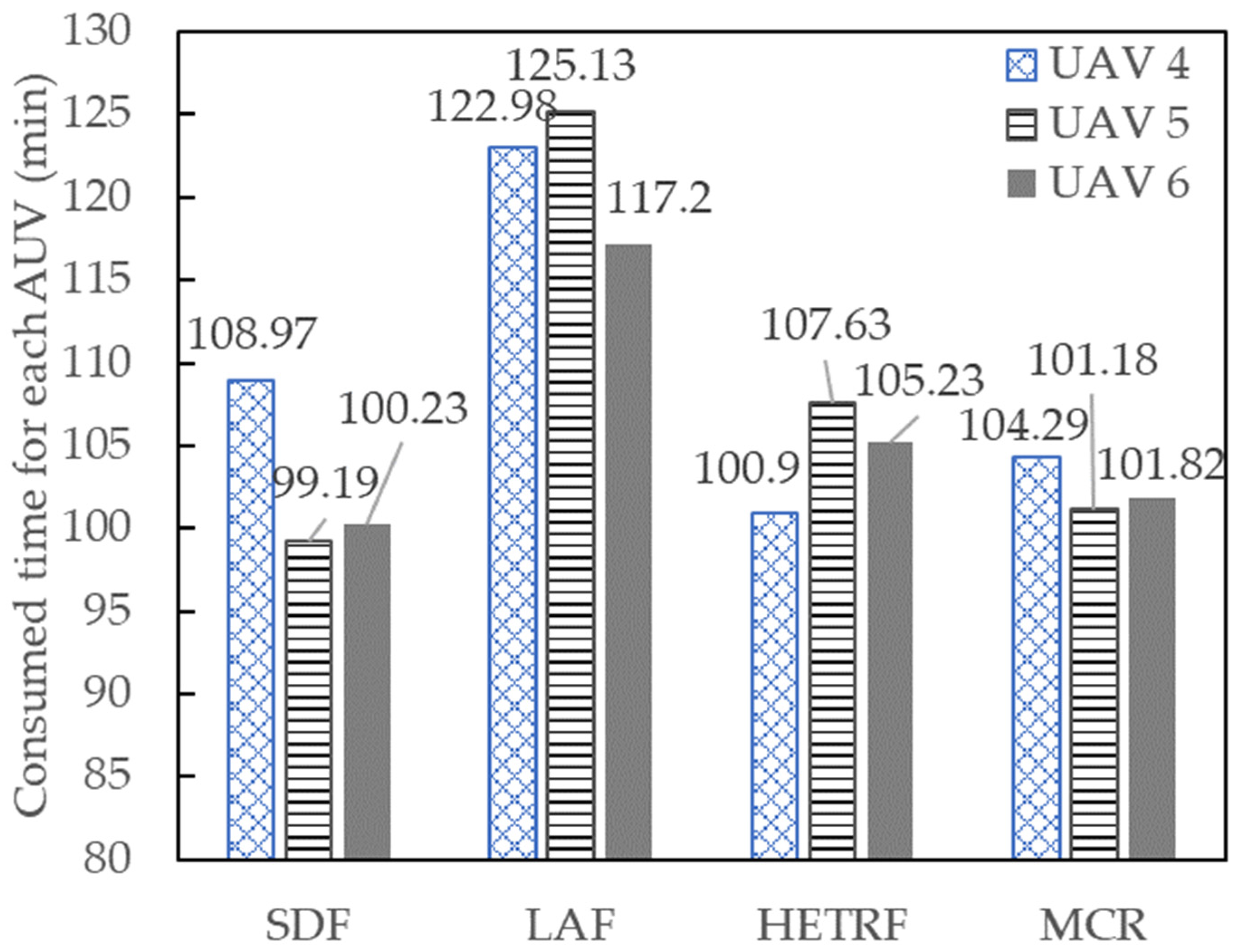
6.2. Heterogeneous UAVs
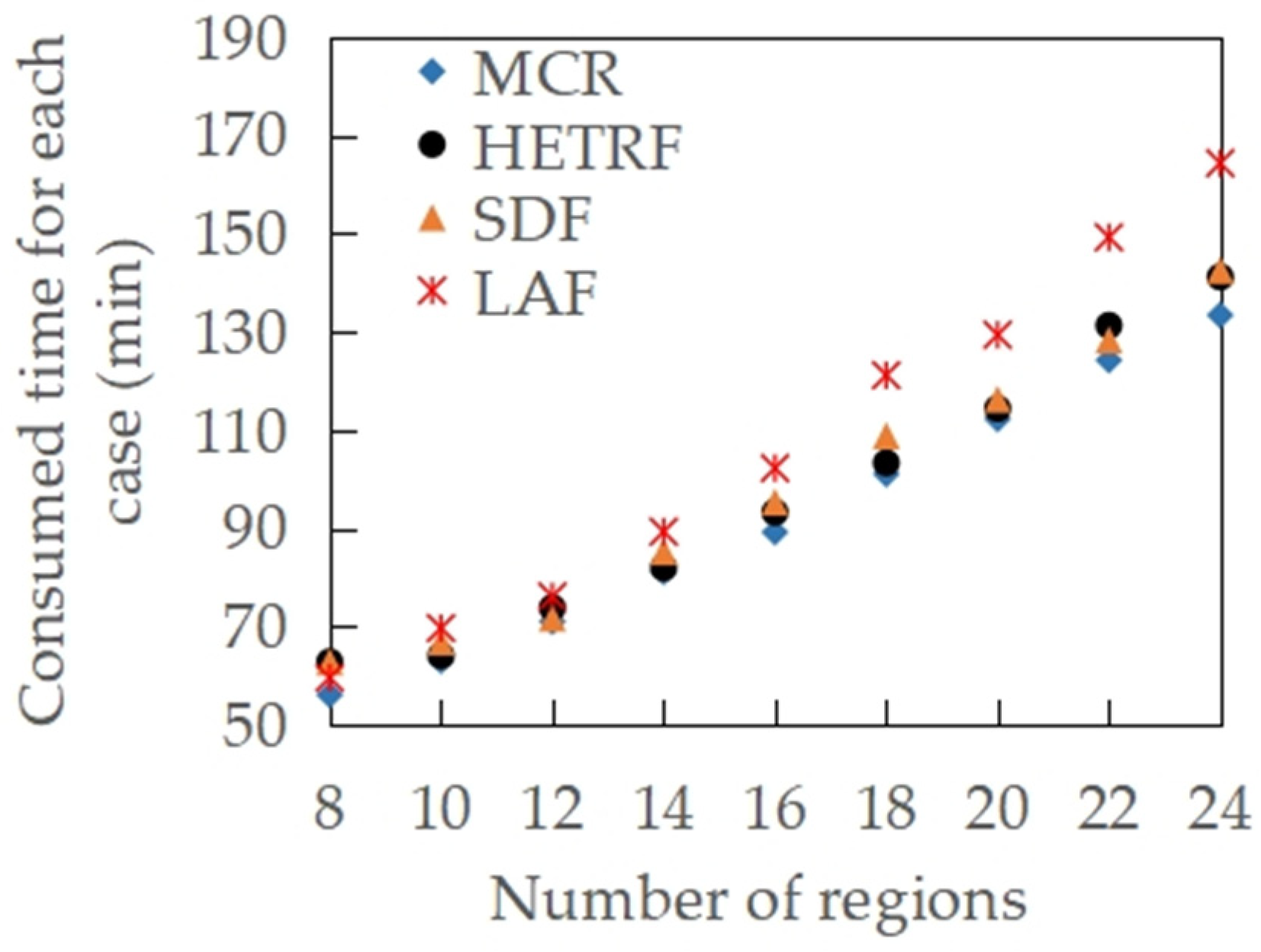
6.3. Effect of the UAV Number and Region Number
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| corresponding regions areas | |
| distance from point x to y. | |
| distance between any two regions | |
| D(x, V’) | the shortest distance from the starting point s, passing all target points in V’ once and arriving at x. |
| ℎ | height of the UAV from the ground |
| number of regions | |
| number of UAVs | |
| regions need to be covered | |
| A set of UAVs with different speed and scan camera performance | |
| V | set of all vertices |
| rear width of the scan area | |
| front width of the UAV scanning area | |
| control variables | |
| α | mounting angle of the UAV imaging sensor |
| β | horizontal field of view angle |
| γ | vertical field of view angle of the UAV imaging sensor |
| θ | elevation angle of the UAV |
| BETR | Balanced Effective Task Rate |
| CPP | Coverage Path Planning |
| HETRF | High Effective Time Rate First |
| MCR | Minimum Consumption Ratio |
| TSP | travel salesman problem |
| UAV | unmanned aerial vehicle |
Appendix A
| Base | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Base | 0 | ||||||||||||||||||
| 1 | 3490 | 0 | |||||||||||||||||
| 2 | 5945 | 2492 | 0 | ||||||||||||||||
| 3 | 10,220 | 6829 | 4345 | 0 | |||||||||||||||
| 4 | 12,923 | 9510 | 7018 | 2708 | 0 | ||||||||||||||
| 5 | 8633 | 5161 | 2960 | 3011 | 5082 | 0 | |||||||||||||
| 6 | 4753 | 3412 | 4748 | 8606 | 11,005 | 5955 | 0 | ||||||||||||
| 7 | 6549 | 3582 | 3067 | 5988 | 8221 | 3138 | 2884 | 0 | |||||||||||
| 8 | 12,063 | 8583 | 6267 | 3420 | 3177 | 3432 | 9107 | 6224 | 0 | ||||||||||
| 9 | 7426 | 6082 | 6768 | 9809 | 11,811 | 6833 | 2809 | 3910 | 9300 | 0 | |||||||||
| 10 | 11,481 | 8300 | 6657 | 6029 | 6617 | 3965 | 7469 | 4941 | 3462 | 6720 | 0 | ||||||||
| 11 | 15,334 | 11,967 | 9898 | 7391 | 6281 | 6937 | 11,600 | 8924 | 3999 | 10,846 | 4176 | 0 | |||||||
| 12 | 12,176 | 9519 | 8543 | 8916 | 9642 | 6416 | 7566 | 5942 | 6476 | 5732 | 3027 | 5953 | 0 | ||||||
| 13 | 10,931 | 9177 | 9163 | 11,018 | 12,377 | 8085 | 6220 | 6102 | 9368 | 3530 | 6031 | 9523 | 3590 | 0 | |||||
| 14 | 15,345 | 12,345 | 10,826 | 9698 | 9381 | 8100 | 10,944 | 8834 | 6434 | 9351 | 4172 | 3677 | 3639 | 7014 | 0 | ||||
| 15 | 17,726 | 14,583 | 12,828 | 10,932 | 9961 | 9941 | 13,462 | 11,177 | 7513 | 11,985 | 6282 | 3680 | 6288 | 9622 | 2649 | 0 | |||
| 16 | 12,704 | 11,463 | 11,737 | 13,741 | 15,047 | 10,804 | 8232 | 8672 | 11,989 | 5426 | 8578 | 11,682 | 5798 | 2722 | 8660 | 11,073 | 0 | ||
| 17 | 14,759 | 12,957 | 12,691 | 13,796 | 14,594 | 11,099 | 10,059 | 9698 | 11,422 | 7336 | 7984 | 10,170 | 4958 | 3840 | 6714 | 8809 | 2918 | 0 | |
| 18 | 15,890 | 13,537 | 12,723 | 12,870 | 13,144 | 10,563 | 11,146 | 10,009 | 10,004 | 8735 | 6841 | 7914 | 4192 | 5352 | 4254 | 5990 | 5635 | 2936 | 0 |
Appendix B
References
- Park, W.; Lee, K.; Im, K. A Proposal on the Aviation Rules of the Military UAV in the National Airspace System. J. Korean Soc. Aviat. Aeronaut. 2014, 22, 22–31. [Google Scholar] [CrossRef]
- Bejiga, M.B.; Zeggada, A.; Nouffidj, A.; Melgani, F. A convolutional neural network approach for assisting avalanche search and rescue operations with UAV imagery. Remote Sens. 2017, 9, 100. [Google Scholar] [CrossRef]
- Wang, S.; Han, Y.; Chen, J.; Pan, Y.; Cao, Y.; Meng, H. A Transfer-learning-based Feature Classification Algorithm for UAV Imagery in Crop Risk Management. Desalin. Water Treat. 2020, 181, 330–337. [Google Scholar]
- Ollero, A.; Kondak, K. 10 Years in the Cooperation of Unmanned Aerial Systems. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots & Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; IEEE: New York, NY, USA, 2012; pp. 5450–5451. [Google Scholar]
- Huang, H.; Savkin, A.V.; Li, X. Reactive autonomous navigation of UAVs for dynamic sensing coverage of mobile ground targets. Sensors 2020, 20, 3720. [Google Scholar] [CrossRef]
- Mansouri, S.S.; Kanellakis, C.; Fresk, E.; Kominiak, D.; Nikolakopoulos, G. Cooperative coverage path planning for visual inspection. Control Eng. Pract. 2018, 74, 118–131. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, C.; Coombes, M. Spraying Coverage Path Planning for Agriculture Unmanned Aerial Vehicles. In Proceedings of the 26th International Conference on Automation and Computing (ICAC), Portsmouth, England, 2–4 September 2021; IEEE: New York, NY, USA, 2021; pp. 1–6. [Google Scholar]
- Wang, C.; Liu, P.; Zhang, T.; Sun, J. The Adaptive Vortex Search Algorithm of Optimal Path Planning for Forest Fire Rescue UAV. In Proceedings of the 2018 IEEE 3rd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 October 2018; IEEE: New York, NY, USA, 2018; pp. 400–403. [Google Scholar]
- Vazquez-Carmona, E.V.; Vasquez-Gomez, J.I.; Herrera-Lozada, J.C.; Antonio-Cruz, M. Coverage path planning for spraying drones. Comput. Ind. Eng. 2022, 168, 108125. [Google Scholar] [CrossRef]
- Maini, P.; Sundar, K.; Singh, M.; Rathinam, S.; Sujit, P.B. Cooperative aerial–ground vehicle route planning with fuel constraints for coverage applications. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 3016–3028. [Google Scholar] [CrossRef]
- Galceran, E.; Carreras, M. A survey on coverage path planning for robotics. Robot. Auton. Syst. 2013, 61, 1258–1276. [Google Scholar] [CrossRef]
- Yang, C.H.; Tsai, M.H.; Kang, S.C.; Hung, C.Y. UAV path planning method for digital terrain model reconstruction—A debris fan example. Autom. Constr. 2018, 93, 214–230. [Google Scholar] [CrossRef]
- Cabreira, T.M.; Brisolara, L.B.; Paulo, R.F.J. Survey on coverage path planning with unmanned aerial vehicles. Drones 2019, 3, 4. [Google Scholar] [CrossRef]
- Ho, Y.-H.; Tsai, Y.-J. Open Collaborative Platform for Multi-Drones to Support Search and Rescue Operations. Drones 2022, 6, 132. [Google Scholar] [CrossRef]
- Yuan, J.; Liu, Z.; Lian, Y.; Chen, L.; An, Q.; Wang, L.; Ma, B. Global Optimization of UAV Area Coverage Path Planning Based on Good Point Set and Genetic Algorithm. Aerospace 2022, 9, 86. [Google Scholar] [CrossRef]
- Shivgan, R.; Dong, Z. Energy-Efficient Drone Coverage Path Planning Using Genetic Algorithm. In Proceedings of the 2020 IEEE 21st International Conference on High Performance Switching and Routing (HPSR), Newark, NJ, USA, 11–14 May 2020; IEEE: New York, NY, USA, 2020; pp. 1–6. [Google Scholar]
- Jing, W.; Deng, D.; Wu, Y.; Shimada, K. Multi-uav Coverage Path Planning for the Inspection of Large and Complex Structures. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; IEEE: New York, NY, USA, 2020; pp. 1480–1486. [Google Scholar]
- Wang, J.; Chen, W.; Temu, V. Multi-vehicle motion planning for search and tracking. In Proceedings of the 2018 IEEE conference on multimedia information processing and retrieval (MIPR), Miami, FL, USA, 10–12 April 2018; IEEE: New York, NY, USA, 2018; pp. 352–355. [Google Scholar]
- Huang, J.; Fu, W.; Luo, S.; Wang, C.; Zhang, B.; Bai, Y. A Practical Interlacing-Based Coverage Path Planning Method for Fixed-Wing UAV Photogrammetry in Convex Polygon Regions. Aerospace 2022, 9, 521. [Google Scholar] [CrossRef]
- Valente, J.; Sanz, D.; Del Cerro, J.; Barrientos, A.; de Frutos, M. Near-optimal coverage trajectories for image mosaicing using a mini quad-rotor over irregular-shaped fields. Precis. Agric. 2013, 14, 115–132. [Google Scholar] [CrossRef]
- Apuroop, K.G.S.; Le, A.V.; Elara, M.R.; Sheu, B.J. Reinforcement learning-based complete area coverage path planning for a modified hTrihex robot. Sensors 2021, 21, 1067. [Google Scholar] [CrossRef]
- Theile, M.; Bayerlein, H.; Nai, R.; Gesbert, D.; Caccamo, M. UAV Coverage Path Planning Under Varying Power Constraints Using Deep Reinforcement Learning. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2021; pp. 1444–1449. [Google Scholar]
- Wu, Q.; Zhou, S.; Yan, S. Research on multi UAV coverage reconnaissance method in complex area. Tactical Missile Technol. 2016, 1, 50–55. (In Chinese) [Google Scholar]
- Gao, C.; Kou, Y.; Li, Z.; Xu, A.; Li, Y.; Chang, Y. Cooperative coverage path planning for small UAVs. Syst. Eng. Electron. Technol. 2019, 41, 1294–1299. (In Chinese) [Google Scholar]
- Luo, C.; Yang, S. A real-time cooperative sweeping strategy for multiple cleaning robots. In Proceedings of the 2002 IEEE International Symposium on Intelligent Control, Vancouver, BC, Canada, 27–30 October 2002; IEEE: New York, NY, USA, 2002; pp. 660–665. [Google Scholar]
- Geiger, B.; Schmidt, E.; Horn, J. Use of neural network approximation in multiple-unmanned aerial vehicle trajectory optimization. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Chicago, CA, USA, 10–13 August 2009; p. 6103. [Google Scholar]
- Applegate, D.L.; Bixby, R.M.; Chvátal, V.; Cook, W.J. The Traveling Salesman Problem. In The Traveling Salesman Problem; Princeton University Press: Princeton, NJ, USA, 2011; ISBN 978–0-691–12993–8. [Google Scholar]
- Steinerberger, S. New Bounds for the Traveling Salesman Constant. Adv. Appl. Probab. 2015, 47, 27–36. [Google Scholar] [CrossRef]
- Yao, J.; Li, X.; Zhang, Y.; Ji, J.; Wang, Y.; Zhang, D.; Liu, Y. Three-Dimensional Path Planning for Unmanned Helicopter Using Memory-Enhanced Dueling Deep Q Network. Aerospace 2022, 9, 417. [Google Scholar] [CrossRef]
- Koenig, D.; Tsvietkova, A. NP–hard problems naturally arising in knot theory. T Am. Math. Soc. Ser. B 2021, 8, 420–441. [Google Scholar] [CrossRef]
- Chen, J.; Ling, F.; Zhang, Y.; You, T.; Liu, Y.; Du, X. Coverage path planning of heterogeneous unmanned aerial vehicles based on ant colony system. Swarm Evol. Comput. 2022, 69, 101005. [Google Scholar] [CrossRef]
- Majeed, A.; Hwang, S.O. A Multi-Objective Coverage Path Planning Algorithm for UAVs to Cover Spatially Distributed Regions in Urban Environments. Aerospace 2021, 8, 343. [Google Scholar] [CrossRef]
- Chen, J.; Du, C.; Lu, X.; Chen, K. Multi-region Coverage Path Planning for Heterogeneous Unmanned Aerial Vehicles Systems. In Proceedings of the 2019 IEEE International Conference on Service-Oriented System Engineering (SOSE), San Francisco East Bay, CA, USA, 4–9 April 2019; IEEE: New York, NY, USA, 2019; pp. 356–361. [Google Scholar]
- Xie, J.; Chen, J. Multi-regional coverage path planning for robots with energy constraint. In Proceedings of the 2020 IEEE 16th International Conference on Control & Automation (ICCA), Sapporo, Hokkaido, Japan, 9–11 October 2020; IEEE: New York, NY, USA, 2020; pp. 1372–1377. [Google Scholar]
- Yu, X.; Jin, S.; Shi, D. Balanced multi-region coverage path planning for unmanned aerial vehicles. In Proceedings of the 2020 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Toronto, ON, Canada, 11–14 October 2020; IEEE: New York, NY, USA, 2020; pp. 3499–3506. [Google Scholar]
- Sundar, K.; Venkatachalam, S.; Rathinam, S. Formulations and algorithms for the multiple depot, fuel-constrained, multiple vehicle routing problem. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; IEEE: New York, NY, USA, 2016; pp. 6489–6494. [Google Scholar]
- Chen, J.; Du, C.; Zhang, Y.; Han, P.; Wei, W. A clustering-based coverage path planning method for autonomous heterogeneous UAVs. IEEE Trans. Intell. Transp. Syst. 2021, 23, 25546–25556. [Google Scholar] [CrossRef]
- Li, J.; Xiong, Y.; She, J.; Wu, M. A path planning method for sweep coverage with multiple UAVs. IEEE Internet Things J. 2020, 7, 8967–8978. [Google Scholar] [CrossRef]
- Peng, H.; Shen, L.; Huo, X. Research on Multiple UAV Cooperative Area Coverage Searching (In Chinese). J. Syst. Simul. 2007, 19, 2472–2476. [Google Scholar] [CrossRef]
- Huang, H.; Savkin, A.V. Aerial Surveillance in Cities: When UAVs Take Public Transportation Vehicles. IEEE Trans. Autom. Sci. Eng (Early Access) 2022, 1–12. [Google Scholar] [CrossRef]
- Yu, K.; O’Kane, J.M.; Tokekar, P. Coverage of an Environment Using Energy-Constrained Unmanned Aerial Vehicles. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; IEEE: New York, NY, USA, 2019; pp. 3259–3265. [Google Scholar]





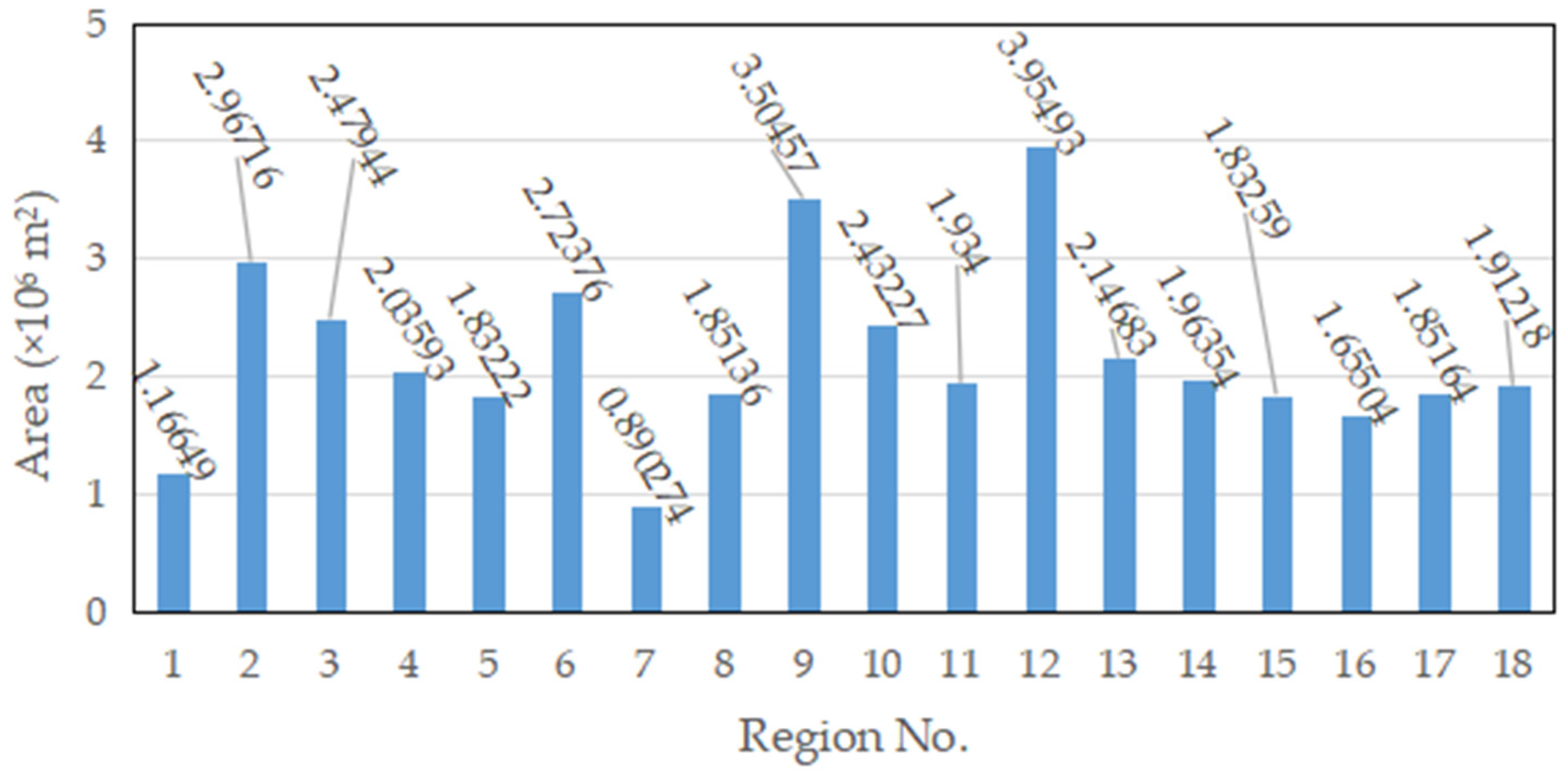
| No. | Edge Number | Vertex Coordinate Distribution (Counterclockwise) |
|---|---|---|
| 1 | 4 | (451,2924), (1370,2608), (2172,4206), (651,3428) |
| 2 | 4 | (700,6210), (1208,3942), (2534,5769), (1315,7152) |
| 3 | 4 | (829,10023), (1226,8231), (2510,10965), (1326,11237) |
| 4 | 4 | (978,12231), (2123,12143), (3205,12751), (1890,13917) |
| 5 | 4 | (2205,7910), (3802,7008), (4621,8164), (3386,8481) |
| 6 | 4 | (3134,1465), (5182,1067), (5308,2819), (3641,2613) |
| 7 | 3 | (3602,5501), (4484,4017), (5036,5107) |
| 8 | 4 | (4120,10120), (5429,10231), (5083,12140), (4374,11863) |
| 9 | 4 | (6225,973), (8723,1004), (7128,3125), (6421,3280) |
| 10 | 4 | (6524,8771), (7840,7425), (8361,9310), (6715,9743) |
| 11 | 4 | (7214,12900), (8635,11883), (9054,12710), (8414,14008) |
| 12 | 5 | (8524,7035), (9136,5802), (11100,6359), (10586,8169), (10023,8263) |
| 13 | 5 | (9405,3882), (10224,2411), (11243,3101), (10983,4251), (9815,4180) |
| 14 | 4 | (9930,11196), (10854,9853), (12034,9936), (12034,9936) |
| 15 | 4 | (11804,12421), (13237,12401), (12059,13891), (10926 13452) |
| 16 | 4 | (11708,1206), (13214,1345), (13094,2917), (12181 2458) |
| 17 | 4 | (13180,4424), (13309,3767), (14928,4105), (14841,5606) |
| 18 | 5 | (13142,8175), (13203,6908), (14181,6721), (14900,6927), (14726,7801) |
| No. | (m/s) | (m) | |
|---|---|---|---|
| Homogeneous UAV | UAV1 | 25 | 100 |
| UAV2 | 25 | 100 | |
| UAV3 | 25 | 100 | |
| Heterogeneous UAV | UAV4 | 20 | 100 |
| UAV 5 | 25 | 90 | |
| UAV 6 | 30 | 110 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Zhang, R.; Zhao, H.; Li, J.; He, J. Path Planning of Multiple Unmanned Aerial Vehicles Covering Multiple Regions Based on Minimum Consumption Ratio. Aerospace 2023, 10, 93. https://doi.org/10.3390/aerospace10020093
Chen J, Zhang R, Zhao H, Li J, He J. Path Planning of Multiple Unmanned Aerial Vehicles Covering Multiple Regions Based on Minimum Consumption Ratio. Aerospace. 2023; 10(2):93. https://doi.org/10.3390/aerospace10020093
Chicago/Turabian StyleChen, Jian, Ruikang Zhang, Hongqiang Zhao, Jiejie Li, and Jilin He. 2023. "Path Planning of Multiple Unmanned Aerial Vehicles Covering Multiple Regions Based on Minimum Consumption Ratio" Aerospace 10, no. 2: 93. https://doi.org/10.3390/aerospace10020093
APA StyleChen, J., Zhang, R., Zhao, H., Li, J., & He, J. (2023). Path Planning of Multiple Unmanned Aerial Vehicles Covering Multiple Regions Based on Minimum Consumption Ratio. Aerospace, 10(2), 93. https://doi.org/10.3390/aerospace10020093







