Abstract
The aerospace electro-hydraulic servo simulator is used to simulate the air load received during flight, and is used for the performance test and acceptance test of aerospace servo actuators on the ground. The force loading accuracy of the load simulator is an important assessment index. Because the loading system and the actuator system to be tested are coupled together, the free displacement of the system to be tested during loading will bring huge disturbance to the loading system, thus how to suppress external interference has always been a hot issue in the control field. This paper addresses this issue under the influence of nonlinear friction and uncertain external disturbance. First, the exact mathematical model of the system is derived, and the characteristics of the system are described by the state equations. Second, in order to obtain the relevant parameters in the controller, the system parameters are identified. Third, the parameter adaptive sliding mode force control based on the reaching law is proposed, and the performance of the control algorithm is analyzed theoretically. Finally, the new control method is applied in the aerospace electro-hydraulic servo simulator, and the results show that the new control algorithm can suppress the external interference by 95% or more, and the control accuracy is more than 97%, which fully demonstrates the effectiveness of the control method.
1. Introduction
In the aerospace field, the air rudder of a rocket is an important component to control the flight attitude. The core component of the air rudder is the servo actuator, which is used to control the deflection angle of the air rudder. Therefore, the test of the servo actuator plays an important role in the product development and delivery stage. In order to accurately simulate the air load on the air rudder during flight, it is necessary to develop a corresponding load simulator to load the servo actuator with rated force or torque.
The loading modes of the load simulator are mainly divided into mechanical loading, electro-hydraulic loading and electric loading, among which electro-hydraulic servo loading is the most widely used. The advantages of mechanical loading are high precision, high reliability and stable performance, but its disadvantages are its complex structure and the limitation of only being able to load linear load. The advantages of electro-hydraulic loading are large power-to-weight ratio, simple mechanical structure, fast response speed and the ability to follow complex loading signals, while the disadvantages are the interference of surplus force. The earliest electro-hydraulic load simulator was built by Japanese scholars, such as Koji Ikega, and has been applied in practical situations. The control technology of the load simulator mainly aims to solve two kinds of problems: one is the control problem of the loading system itself, and the other is the unavoidable problem of surplus force suppression in the load simulator. In the electro-hydraulic load simulator, the loading system has a strong nonlinearity [1,2,3], and the system parameters also have uncertainties: changes in oil temperature [4,5] and medium bubble content [6,7], changes in sensor and controller parameters with time [8,9], etc., will cause changes in system parameters. To solve these problems, many scholars have tried a variety of solutions, mainly from the hardware structure and control strategy to solve and compensate for the problem of surplus force.
To solve the loading problem of the load simulator through the control strategy, the advantage is that there is no change to the external system, the required cost is small, and the design and debugging are relatively convenient. Therefore, many scholars have done a lot of theoretical research, analysis and experimental verification in this regard. A structure invariance compensation (SIC) control method is used to suppress the surplus force in Ref. [10]; its idea is to add a feed-forward link in the control, thus improving the controller performance. Another kind of effective control method is the compensation control method based on disturbance observer [11,12,13,14]. The disturbance observer is designed to estimate the unknown disturbance and compensate it in the feed-forward channel to effectively suppress the disturbance. The controller consists of two parts: a feedback controller and a feed-forward controller based on a disturbance observer. However, this kind of control method has some problems in the design process, such as dependence on the system model and difficulty in system parameter identification.
In recent years, intelligent control has been widely used in many fields and achieved good results. Therefore, some scholars also apply intelligent control methods to the loading system of the load simulator, mainly involving learning control algorithm [15,16], fuzzy control algorithm [17,18], neural network control algorithm [19,20], etc. However, this kind of control algorithm needs a certain learning time to adjust the control parameters to the best value, and the system control effect can reach the best, thus it cannot respond quickly.
The sliding mode control method appeared in the 1950s and became a typical method in the field of automatic control. This control method makes the system states slide along the sliding surface by switching the control variables, which makes the system invariant when the parameters are perturbed and external disturbances occur [21]. Sliding mode variable structure control is widely used in the field of motion control because of its simple algorithm, good robustness and high reliability. Yang et al. applied a sliding mode controller based on an external disturbance observer in the power system to minimize the frequency deviation by controlling the governor of the generation unit [22]. Xu et al. used a sliding mode control using a fractional-order operator (SMCFO) method for the hysteresis of a piezoelectric (PZT) micro-nano platform, achieving a no-load high precision tracking control effect [23]. Chehaidia et al. gives a global state of the art of application of sliding mode control (SMC) for wind turbines and proposes a new application of terminal integral sliding mode control (TISMC) for variable speed wind turbines, which has a good effect in maximizing output power and reducing load [24]. Kang et al. used a finite-time adaptive sliding mode force control method to improve the influence of friction on the electro-hydraulic servo load simulator [25].
The aforementioned studies based on sliding mode control have achieved certain results in their respective fields. Combined with the advantages of sliding mode control, considering that the space load simulator requires high control accuracy, good residual force suppression effect, strong robustness and other characteristics, the control algorithm based on sliding mode control can be used in the control design of the loading system.
The main contributions of this paper are as follows:
(1) In view of the load simulator with medium load (2000 N–8000 N), the hydrodynamic and mechanical characteristics of the system are comprehensively analyzed, the system state equation and accurate mathematical model are established, the root cause of the surplus force is found, and the corresponding suppression methods are proposed.
(2) The design of the controller depends on some parameters of the system, thus the open-loop identification method of the system is designed. The random white noise signal is used as the stimulus signal, and the system parameters are identified using the least square method (LSM) according to the input data and output data of the system. The dynamic characteristics of the identification model and the original system are compared to verify the correctness of the identification parameters.
(3) The sliding surface based on exponential reaching law is designed, and a parameter adaptive control algorithm is proposed based on it; the sliding mode controller of the load simulator is designed, and a good control effect is achieved in practical application.
2. System Introduction and Mathematical Model
2.1. Mechanical System Design and Construction
The space load simulator needs to simulate the air load on the air rudder during flight, thus it needs to load some conventional signals with high accuracy, such as square wave signal, sine signal, etc. At the same time, in order to test the performance of the servo actuator to the maximum extent, it is necessary to load some complex composite signals. In addition to force loading, the simulator also needs to simulate the moment of inertia load and friction load.
Based on the system requirements detailed above, the mechanical system of the load simulator is designed. The mechanical system is mainly composed of the main frame, rotating shaft, swing arm, cantilever, mass block, friction mechanism, etc. The overall 3D design diagram of the system is shown in Figure 1. The force loading system and the servo actuator to be tested are installed on both sides of the swing arm, respectively. Through this coupling mode, the loading system can load the force on the servo actuator to be tested. The mechanical structure of the loading system is shown in Figure 2.
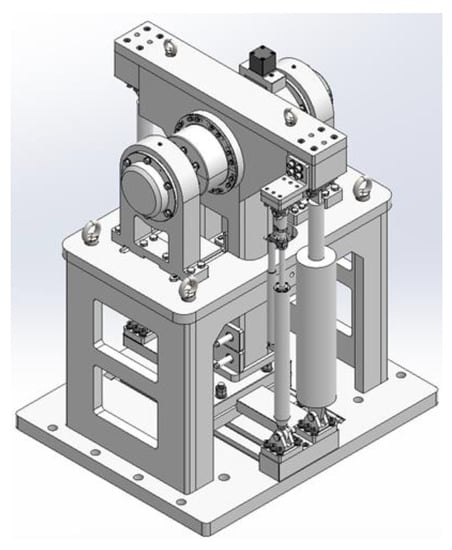
Figure 1.
System 3D design drawing.
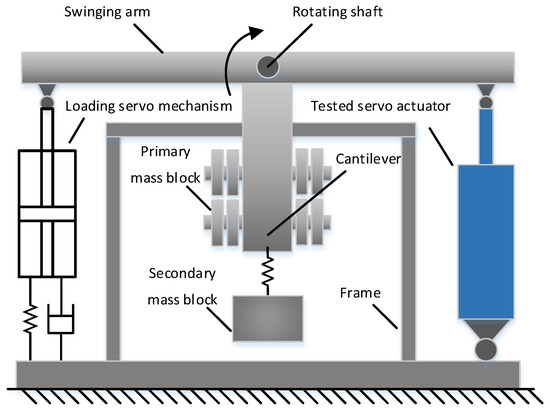
Figure 2.
Structure sketch of the system.
In order to simulate the moment of inertia of the system, a cantilever is designed below the swing arm. Multiple primary mass blocks can be fixed on the cantilever to adjust the moment of inertia of the system. At the same time, the system also needs to simulate the secondary resonance phenomenon under the real load, thus there are springs and secondary mass blocks under the cantilever.
2.2. Establishment of System Mathematical Model
Because the force loading system needs high loading accuracy and can follow complex loading signals, the loading system uses an electro-hydraulic servo system. The loading schematic diagram of the electro-hydraulic servo loading system is shown in Figure 3. The controlled electric signal drives the displacement of the servo valve spool to further control the pressure and flow of the left and right chambers of the servo hydraulic cylinder, and to finally achieve the purpose of controlling the loading force.
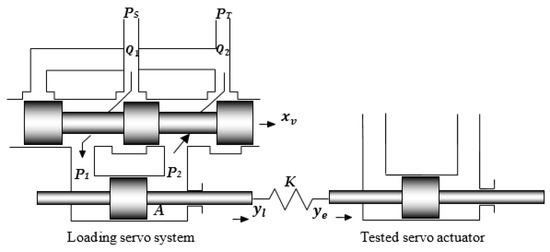
Figure 3.
Schematic diagram of electro-hydraulic servo loading system.
According to the hydraulic loading principle and the relevant theories of fluid mechanics, the flow Equations (1) and (2) of the left and right chambers of the force loading system can be derived.
where [m3/s] and [m3/s] are the flow of the left and right chambers. [Pa] is the system supply oil pressure. [Pa] is the system return oil pressure. [Pa] and [Pa] are the pressure of the left and right chambers. is the discharge coefficient, [m] is the spool valve area gradient and [kg/m3] is the density of the hydraulic oil. [m] is the displacement of the servo valve spool. Furthermore, from the equations , and , Equation (3) can be derived.
This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn.
Under the following assumptions (a), (b) and (c), the flow continuity equation of the system can be expressed by Equations (4) and (5) [26].
(a) Friction loss inside all connecting pipes, factors of fluid quality and dynamic state of the oil circuit are ignored.
(b) The internal pressure of the two working chambers of the hydraulic cylinder is the same everywhere, and the temperature and volume elastic modulus are considered to be constant.
(c) The internal and external leakage of the hydraulic cylinder is laminar flow.
where [(m3/s)/Pa] and [(m3/s)/Pa] are the internal and external leakage coefficients, respectively, [Pa] is the elastic modulus of the hydraulic oil, [m3] is the oil supply cavity volume, and [m3] is the oil return cavity volume.
Assuming that the piston position of the hydraulic cylinder is in the middle position, and the initial volume of the oil inlet cavity and the oil return cavity is equal to half of the total volume, the volumes of the oil inlet cavity and oil return cavity are written as Equations (6) and (7).
where [m2] is the effective area of the hydraulic cylinder piston. [m] is the piston displacement of the servo hydraulic cylinder in the loading system. [m3] is the total volume of the load servo hydraulic cylinder.
The flow continuity equation of the system can be derived from the load flow definition of the system and Equations (4)–(7), as shown in Equation (8).
where [(m3/s)/Pa] is the total leakage coefficient of the system.
Combining Equations (3) and (8), we can get a new Equation (9).
Because the load system and the loading system are coupled together through the swing arm, the force balance formula of the system can be established as shown in Equation (10).
where [N] is the equivalent friction of the system, which includes the friction of the piston of the hydraulic cylinder, the friction of the shaft, and the friction of the tested system. [N] is the unknown surplus force of the system, which is generally caused by the autonomous displacement of the tested servo actuator.
The servo valve selected in the loading system is the servo valve of MOOG. Because the frequency bandwidth of the system is far lower than that of the servo valve, the servo valve can be simplified as a first-order link [27], and the differential equation of spool displacement can be expressed by Equation (11).
where [A] is the servo valve’s input current, is the natural frequency of the servo valve, is the equivalent gain coefficient of servo valve.
Based on the above equations, the system state equations can be derived. Define the state vector of the system as , define the output of the system as . Then Equations (9) and (10) can be rewritten as Equations (12) and (13).
According to the definition of vector and Equations (11)–(13), the state equations of the system can be finally deduced as follows.
To facilitate discussion and simplify Equation (14), define a vector , where , , , , . Then Equation (14) can be simplified into Equation (15).
Equation (15) is the final expression of the system state space equation. It can be seen from the mathematical model of the system that the friction force of the system and external interference superfluous force is the unknown interference of the system. It is expected to find a robust control algorithm with a strong suppression effect on external interference, which can compensate for the friction interference of the system and suppress the excessive force caused by the position disturbance of the tested system, so as to achieve a better control effect and improve the loading accuracy.
3. Identification of System Parameters
From the system mathematical model, it can be seen that some parameters of the system can be obtained through the component manual, but some parameters are difficult to obtain directly, thus the system identification method can be used for parameter identification.
The principle of system identification is to treat the system as a black box and obtain the corresponding output signal through a group of stimulus input signals. Then, a mathematical model that can describe the system is constructed, and the parameters in the mathematical model are identified by using the input signal and output signal through some mathematical estimation algorithms, such as the least square method, maximum likelihood method, etc. System identification is a very mature method, which has been applied in many systems [28,29].
In order to obtain the relevant parameters in the system mathematical model, the transfer function of the load simulator can be established first.
According to Equations (1) and (2), partial derivative Equations (16) and (17) can be obtained
where [(m3/s)/m] is the flow gain of the servo valve near the steady-state operating point, [(m3/s)/Pa] is the flow pressure coefficient of the servo valve. Linearize Equations (1) and (2) to get Equation (18).
Take the load flow as , which can obtain the linearized load flow equation.
The transformed Equations (21)–(23) can be obtained by Laplace transformation of Equations (8), (10) and (20).
where , , , are the Laplace transform of , , .
Equation (24) can be derived from the above three equations.
The model to be identified of the system can be described by Equation (25) without the interference of external excessive force and ignoring the influence of system friction. The system’s input signal is , which is the driving current of the servo valve. The relationship between and spool displacement is described by Equation (26).
where [m/A] is the current gain of the servo valve.
From the transfer function of the system, the loading torque system is a third-order system with six parameters to be identified. In the actual control system, the system is a discrete system. Therefore, the continuous transfer function can be converted into a discrete transfer function through mathematical method. According to Equation (25), the discrete transfer function of the system can be represented by Equation (27).
where and are the system’s output and input at time The equation that rewrites Equation (27) as a vector is as follows.
where , . When , the vector equation represented by Equation (29) can be obtained.
where , .
The purpose of system identification is to estimate the system parameter through groups of observation data . Assume that the estimated value of is , . Then, the identified discrete transfer function of the system is described by Equation (30).
where is called equation error and is a random value.
The least squares system identification method is used in this paper. The purpose is to obtain the minimum value of the criterion function of , as shown in Equation (32).
where . Using the necessary conditions of extreme value and calculating the partial derivative of Equation (32), Equation (33) can be further deduced.
Therefore, , and , namely, according to the observed system input and output data, the system parameter value is finally estimated. The parameter value of the discrete transfer function is obtained, and the parameter value of the continuous transfer function can also be calculated.
The open loop identification method is adopted for the system, and the stimulus signal is a random white noise signal between [−0.002, 0.002]. The sampling time of the data acquisition system is 0.0001 s. The curve of a section of the stimulus signal is shown in Figure 4.
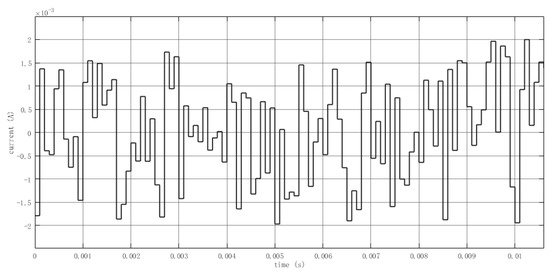
Figure 4.
Schematic diagram of stimulus signal.
According to the corresponding relationship between Equations (24) and (25), and the identified system parameters, the values of each parameter in the final system mathematical model are listed in Table 1.

Table 1.
System parameter table.
In the identification process, 10 s of data were collected. Under the action of the stimulus signal, the output signal of the system is shown in Figure 5. The collected input data and output data of the system are calculated by the least square method, and the specific values of each parameter in the transfer function can finally be obtained, where ,, , , , .
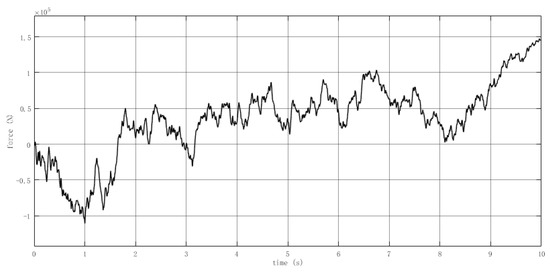
Figure 5.
Identification output signal diagram of the system.
In order to verify the correctness of the parameters of the identification model, general closed-loop control is adopted and the same control parameters are set. Given an 8000 N follow signal, the output of the actual system and the output of the identification model are shown in Figure 6. It can be seen from the figure that the dynamic characteristics of the identification model are basically consistent with the original system, but there are partial differences in some parts due to the identification error; however, the error is within the receiving range. Therefore, we believe that the identified system parameters are correct and available.
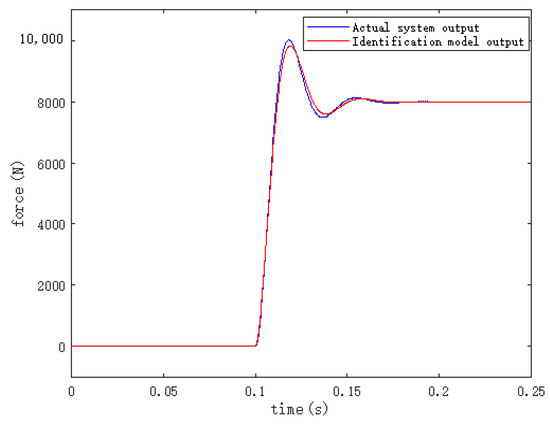
Figure 6.
Comparison of step output between identification model and actual system.
So far, the identification of the system has been completed, making preparations for the design and implementation of the following controller.
It should be noted that in the hydraulic servo system, some parameters will change with time, such as oil viscosity, system damping, etc. However, the range of its value change can be ignored compared with other control parameters, thus the influence on the parameters of the controller can be ignored.
4. Proposal and Implementation of Control Strategy
4.1. Controller Design
Sliding mode control (SMC), also known as variable structure control, is a special kind of nonlinear control, and the nonlinear performance is the discontinuity of the control. Sliding mode control has the advantages of fast response, strong robustness and simple physical implementation. Considering these factors, the controller can be designed based on sliding mode control in the force loading system of the aerospace load simulator.
In Section 2, the equation of the state of the system has been derived and described by Equation (15). First, we define the tracking error of the system as . is the expected ideal value of . Secondly, in order to ensure that the loading system has good dynamic performance and better static accuracy, it is necessary to select a sliding surface suitable for the system. In this paper, the sliding surface is represented by Equation (34).
where () is the parameter of the sliding surface. Take the derivative of and we will get the following equation.
where .
Sliding mode control makes the motion of the system divided into two processes: approaching motion and sliding mode motion. According to the principle of sliding mode variable structure, the reachability condition of sliding mode only guarantees that the moving point at any position in the state space can reach the switching surface in a limited time, and there is no restriction on the specific trajectory of the approaching motion. The dynamic quality of the approaching motion can be improved by using the sliding mode control method of approach law [30]. In this paper, a sliding mode control strategy based on the exponential approach law is designed. We can define the derivative of sliding surface as the following equation.
where and are the control parameters.
According to Equations (35) and (36), we can further design the controller of the system. The output of the controller is described by Equations (37)–(39).
where and are the control parameters of the exponential function.
Note that , the derivative of this state quantity is related to the unknown external interference and , and it is difficult to directly measure and obtain in the actual system. Therefore, in the actual control system, the derivative of for time can be used indirectly, which is . Because is very sensitive to noise signals, special signal filtering is carried out in the signal hardware processing module to reduce the system noise during the acquisition of system displacement and speed. At the same time, it is difficult to directly measure the spool displacement in the common servo valve because the spool is encapsulated in the servo valve. In the control system of this paper, the servo valve is modified, part of the shell of the servo valve is removed, and a micro-displacement sensor is connected in series on the spool to measure the spool displacement. The schematic diagram of the measuring device for spool displacement is shown in Figure 7.
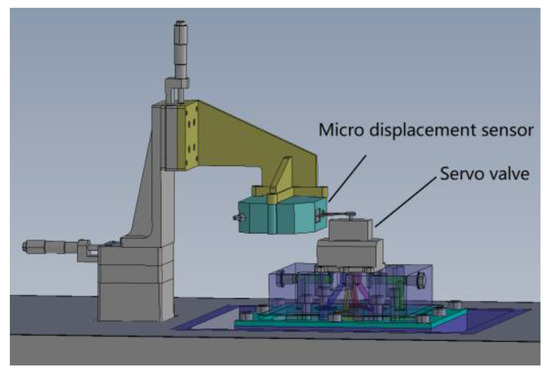
Figure 7.
Schematic diagram of spool displacement measuring device.
is the key control parameter of the controller, which has a great impact on the control performance of the system. If its value is too small, the response speed of the system will not be fast enough and the ability to suppress external interference will be weak. If the value is too large, it will cause chattering problems in the system. Therefore, it is necessary to design a parameter adaptive control strategy in the system. Chattering is always the key issue in sliding mode control, and its essence is caused by the nonlinear switching of control surfaces. In order to solve this problem, many scholars have put forward many effective methods, among which sliding mode control combined with the adaptive control algorithm is an effective solution. In Ref. [31], a novel adaptive sliding mode control method has been designed and applied to the load frequency control, through comparative experiments, and it is proven that it has a good effect on solving the chattering problem. In Ref. [32], a novel ASMC methodology is proposed, which does not require a priori bounded uncertainty. The authors of Refs. [33,34] also used the adaptive control method, which has good control effect against unknown external interference. The above three references have proposed some special control methods in adaptive control and achieved good results.
In the test experiment of the aerospace air rudder, it is unknown when the external interference occurs and how large the interference value is. Because the parameter plays a decisive role in the control effect of the controller, we hope that the designed controller can adjust the parameter adaptively according to the actual control error in order to achieve the best control effect. When the control error of the system is large, the value of can be automatically adjusted to a larger value, and when the system error is small, its value can be adjusted to a smaller value, which can not only have a fast response and strong interference suppression ability, but also solve the problem of chattering well. Finally, an exponential change function is designed, as shown in Equation (39), and the influence of the and parameters on the function is shown in Figure 8, where .
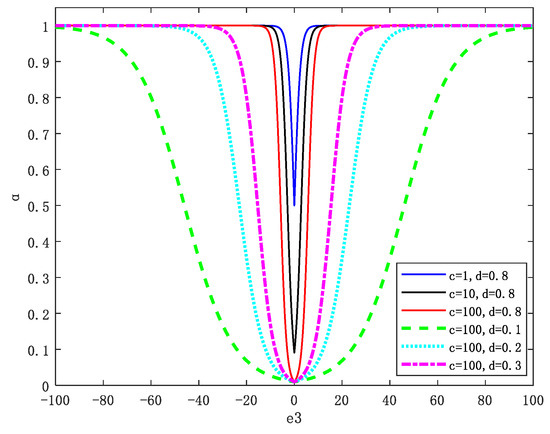
Figure 8.
Diagram of influence of control parameters on adaptive function.
Parameter will affect the minimum value of , and parameter will affect the parameter adjustment speed of the adaptive function. The parameter adaptation method shown in Equation (39) can not only react and suppress external interference quickly, but also reduce the chattering of the system as much as possible.
4.2. Analysis of Control Performance
The convergence of the system is analyzed, and the Lyapunov function is defined as , thus its derivative can be written as the following equation.
Obviously, , therefore the system is convergent and stable.
Equation (40) can be further deduced to Equation (41).
Lemma 1.
For, the solution of inequality equation,is, whereis an arbitrary constant [35].
According to Lemma 1, the solution to inequality (41) is:
It can be seen that converges to 0 by exponential convergence, and the rate of convergence depends on . The exponential term can ensure that when is large, the system state can approach the sliding mode at a large speed. It should be noted that the approach speed is generally reduced from the initial value to 0, which not only shortens the approach time but also makes the speed of the moving point when it reaches the switching surface smaller. In the sliding surface, there is also a constant velocity approach term , so that when is close to 0, the approach speed is a rather than 0, which can ensure that the sliding surface can be reached in a finite time.
In this system, parameters and are two key control parameters, which have a decisive effect on the performance of the controller. If does not consider adaptive adjustment, the value of is a fixed value. When parameters and take different values, the influence on the system control error and error distribution is shown in Figure 9. We tested 841 sets of different initial parameters and counted the maximum error in each control process, thus obtaining the max error distribution diagram in Figure 9. The value range of parameter is [100, 1000], and the step size is 100. The value range of parameter is [1000, 30,000], and the step size is 1000. Take the maximum error in each group of experiments for statistics, and obtain the three-dimensional distribution of the maximum error with the change of parameters and . Through this experimental result, we can easily find the best value range of parameters and .
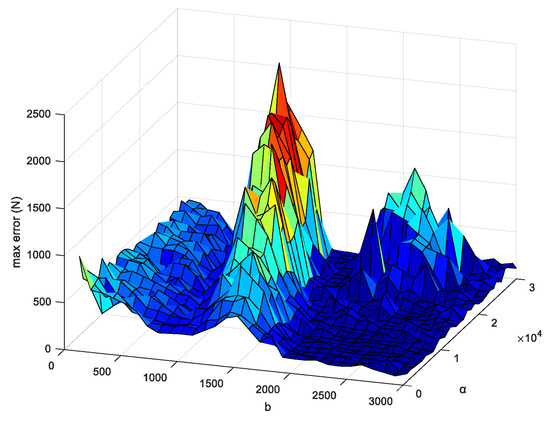
Figure 9.
Influence of control parameters on control error.
From the control error distribution diagram, the control performance of the controller will reach the best when the two key parameters are within a certain value range. When parameter is within the range of [2000, 2500] and parameter is within the range of [5000, 10,000], the control error of the system is within the optimal range. The specific values of control parameters need to be comprehensively considered from the system response speed, interference suppression ability, steady-state accuracy and other aspects in order to select the most appropriate value of control parameters.
It can also be seen from Figure 9 that there are certain requirements for the value of control parameters and . Specifically, within a certain value range, the controller can control the error and automatically adjust the parameters to achieve better results. When the value range of the control parameters is not appropriate, it will exceed the self-regulation ability of the system, and will affect the control effect. The parameter self-adaptive control algorithm proposed in this paper aims to make the controller not only suppress external interference quickly and effectively, but also reduce system chattering as much as possible. As for the full adaptation of parameters in the whole control process, the current intelligent control methods need to be combined, which is also a follow-up study of this paper.
5. Experimental Verification and Results
The mechanical design and construction of the system are completed. After the design of the controller, it is necessary to carry out experimental verification in the loading system of the actual load simulator. The real object diagram of the load simulator is shown in Figure 10. In addition, the loading system is an electro-hydraulic servo system, and the energy of the system is provided by the hydraulic pump station. Its photo is shown in Figure 11.

Figure 10.
Photos of load simulator.

Figure 11.
Photos of the hydraulic pump station of the loading system.
The first experiment is the loading experiment without interference. The purpose is to check the tracking ability of the controller to the input signal and verify whether its control accuracy and system performance meet the requirements. Let the loading system follow several classical input signals, square wave signal, sine wave signal and triangle wave signal, respectively. Set the value of the control parameter as a = 100, b = 1000, c = 50, d = 0.0016, = 11,000, and the system control output in these three cases is shown in Figure 12. It can be seen from the output curve of the system that the control algorithm proposed in this paper has a good tracking effect without interference and can track three types of expected signals well.
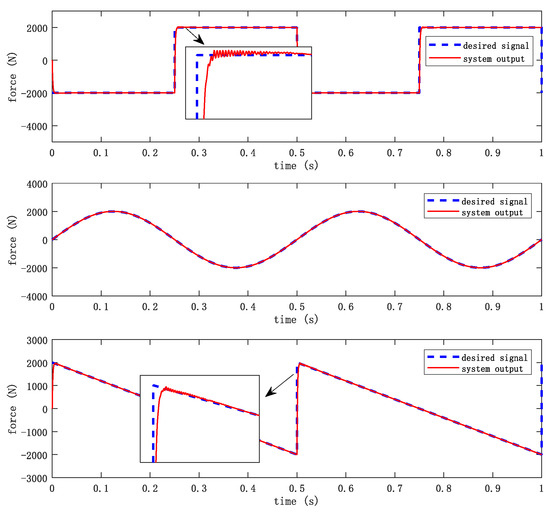
Figure 12.
Control effect diagram without system interference.
In addition to testing signals with fixed frequency, it is also necessary to test loading signals with a certain frequency range. In this group of experiments, according to the requirements of the tested servo products, the sinusoidal signals of 5 Hz, 10 Hz and 20 Hz are selected for loading, and the output signals of the system are shown in Figure 13.
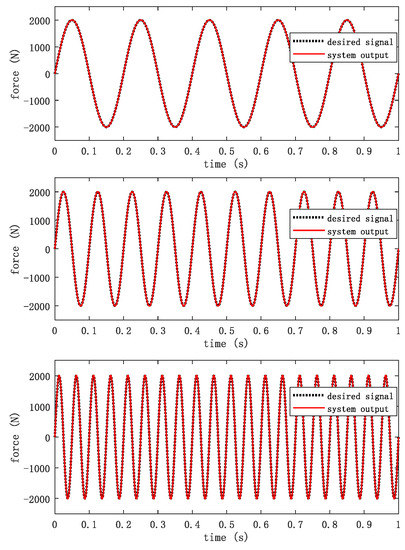
Figure 13.
System output curves at different frequencies.
The system loading errors under various conditions are listed in Table 2 for comparison. It can be seen from the table that the control method used in this paper can track the expected signal well under various circumstances, and the loading error is within 2.5%, which is completely better than the 5% accuracy requirement of the system.

Table 2.
System control error without interference.
However, in the real working environment, the load simulator works in the presence of interference. Therefore, when the tested product starts to move freely, it is the key test for this verification. We set a typical working condition. First, let the loading system load a step signal with an amplitude of 8000 N, and then the tested product starts to move with a 5 Hz square wave displacement at 0.2 s, which will cause a huge interference in the loading system. Through such experiments, test the controller’s ability to suppress external interference and check whether the loading error of the system meets the requirements. In the contrast experiment, the system loading conditions under the three control methods are compared. The three control methods are general closed-loop control, sliding mode control without parameter adaptation, and sliding mode control with parameter adaptation. The loading output of the system is shown in Figure 14.
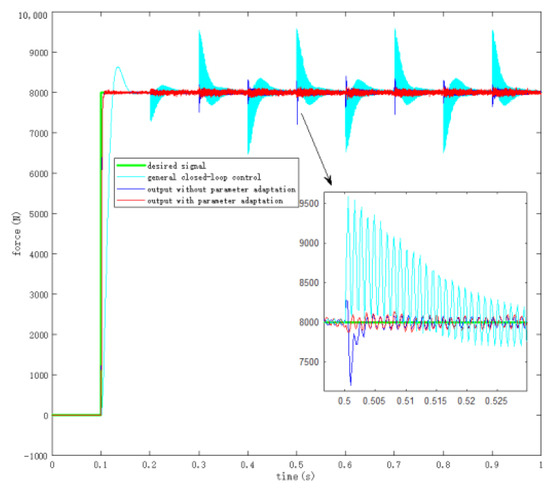
Figure 14.
System output under different control methods.
From the output curve of the system, it can be seen that the response speed of the sliding mode control is faster than that of general closed-loop control, and there is no overshoot. When external interference occurs in the system, the parameter adaptive sliding mode control method proposed in this paper can effectively suppress the external interference from 1581 N to 107 N.
Compared with sliding mode control without parameter adaptation, the new method has obvious advantages in control performance and interference suppression, and can reduce the excess force from 793 N to 107 N.
In this loading experiment, the output curves of the controller and the displacement curves of the servo valve spool are given, as shown in Figure 15. The range of the current drive signal of the servo valve is [−20 mA, +20 mA]
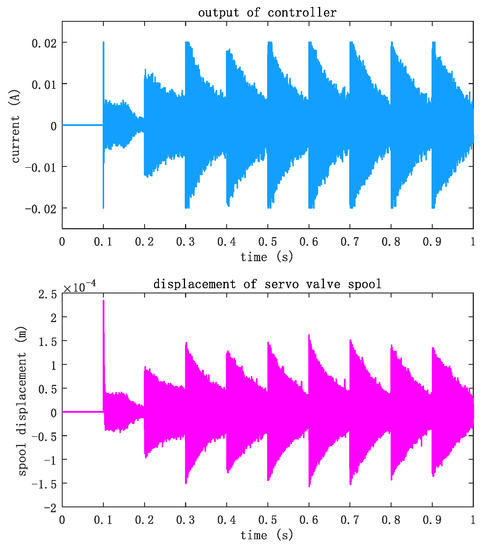
Figure 15.
Controller output and spool displacement curve.
The loading errors under these three control methods are compared, the comparison diagram is shown in Figure 16 and the loading errors are listed in Table 3. The figure shows the loading error under the condition of displacement disturbance of the tested product after the system reaches a stable state 0.2 s later.
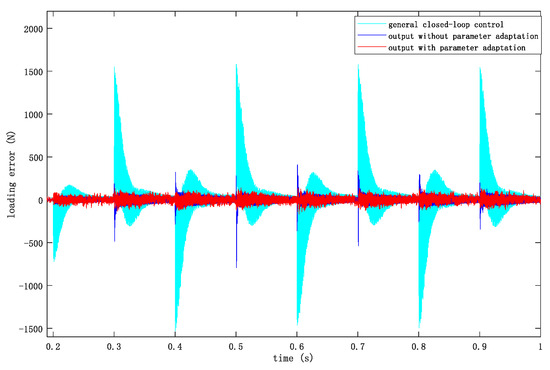
Figure 16.
Loading error comparison under different control methods.

Table 3.
System loading error comparison.
According to the test experiment of the servo product under test, the loading system also needs to load sine waves of different frequencies. We selected the loading conditions of three typical frequency (3 Hz, 10 Hz, and 20 Hz) points for verification. The tested servo product on the other side of the swing arm still moves independently, and the input signal it follows is a square wave signal with a frequency of 5 Hz. Finally, the output of the system at three frequency points is shown in Figure 17, Figure 18 and Figure 19.
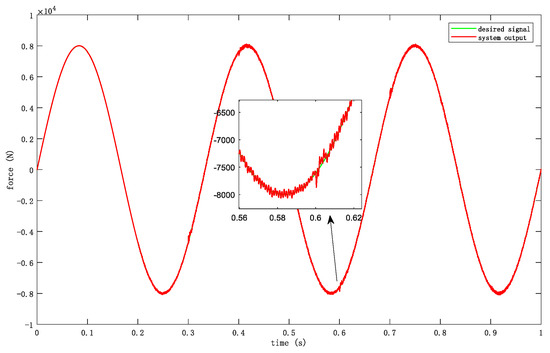
Figure 17.
System loading output at 3 Hz frequency.
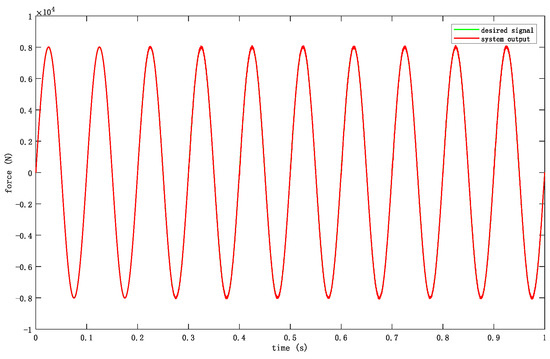
Figure 18.
System loading output at 10 Hz frequency.
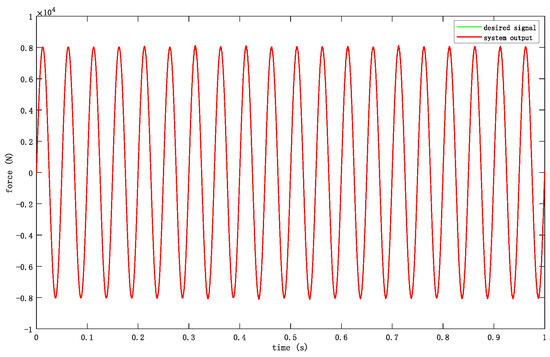
Figure 19.
System loading output at 20 Hz frequency.
According to the output of the system, the controller designed in this paper has a good loading effect and can track the desired signal well from low frequency to high frequency. Although there will be some interference when the tested servo product moves freely, the controller has a good suppression effect on external interference, making the loading error of the system better than 5% of the system requirements.
The loading error curve of the system is shown in Figure 20, and the maximum loading error at each frequency point is listed in Table 4.
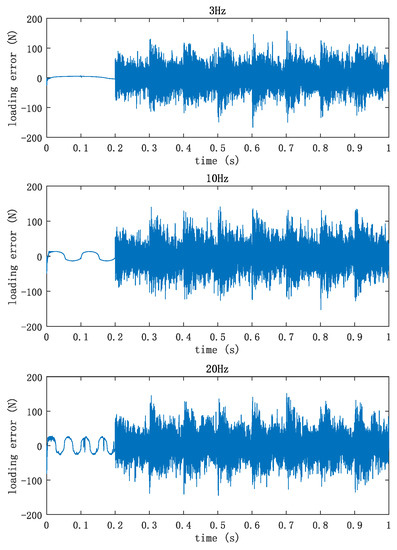
Figure 20.
System loading error at different frequencies.

Table 4.
System loading error comparison.
From the output and loading errors of all the experiments shown above, we can draw the following conclusions: the parameter adaptive sliding mode control algorithm and controller proposed in this paper can control the loading system of the load simulator well, and they have a good control effect. In the actual servo product test experiment, the control algorithm has a strong suppression effect on external interference, making the final loading accuracy reach 1.96%, which is better than the 5% requirement of the system.
6. Conclusions
In this work, the mechanical system and electro-hydraulic servo loading system of the load simulator are designed and built, and the accurate system mathematical model and state equations are established. Then, in order to obtain the relevant parameters of the system itself, the system identification experiment is designed. Through the collected data and the system mathematical model, the parameters required for the controller design are identified. Based on the full understanding and analysis of the system, the sliding mode control algorithm is adopted in the design of the system controller, and a sliding mode control algorithm with adaptive parameters is proposed. The control algorithm and controller are verified in the actual loading experiment on the experimental site of the aerospace load simulator. The results show that the control algorithm has good loading accuracy and strong interference suppression ability. Its loading accuracy is better than the system requirements, and the load simulator finally delivered for use completely meets the technical requirements.
Author Contributions
Conceptualization, J.H. and C.Q.; methodology, J.H. and C.Q.; software, J.H.; validation, Q.T.; investigation, H.G.; data curation, J.W.; writing—original draft preparation, J.H.; writing—review and editing, J.H.; supervision, Z.S.; project administration, C.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data will not be published for privacy reasons. Contact the author if necessary.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jin, B.Q. Study on the Fuzzy Sliding Mode Control Method of Electro-Hydraulic Position Servo Control System. Ph.D. Dissertation, Taiyuan University of Technology, Taiyuan, China, 2010. [Google Scholar]
- Bu, F.P.; Yao, B. Observer based coordinated adaptive robust control of robot manipulators driven by single-rod hydraulic actuators. In Proceedings of the IEEE International Conference on Robotics and Automation, San Francisco, CA, USA, 24–28 April 2000; pp. 3034–3039. [Google Scholar]
- Gan, C.; Pan, S. Nonlinear adaptive robust control of single-rod electro-hydraulic actuator with unknown nonlinear parameters. IEEE Trans. Control. Syst. Technol. 2008, 16, 434–445. [Google Scholar] [CrossRef]
- Jing, C.H.; Xu, H.G.; Jiang, J.H. Practical torque tracking control of electro-hydraulic load simulator using singular perturbation theory. ISA Trans. 2020, 102, 304–313. [Google Scholar] [CrossRef] [PubMed]
- Du, H.; Cheng, Y.; Huang, S.; Wu, M.; Huang, H.; Li, Y. Pressure control of electro-hydraulic servo loading system in heavy vehicle steering testboard based on integral sliding mode control. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 458–468. [Google Scholar] [CrossRef]
- Yu, B.; Yao, J.; Zhu, Q.; Zhang, J.; Huang, Z.; Jin, Z.; Wang, X. Design, Mathematical Modeling and Force Control for Electro-Hydraulic Servo System with Pump-Valve Compound Drive. IEEE Access 2020, 8, 171988–172005. [Google Scholar] [CrossRef]
- Cheng, L.; Zhu, Z.C.; Shen, G.; Wang, S.; Li, X.; Tang, Y. Real-Time Force Tracking Control of an Electro-Hydraulic System Using a Novel Robust Adaptive Sliding Mode Controller. IEEE Access 2020, 8, 13315–13328. [Google Scholar] [CrossRef]
- Yang, H.; Cong, D.; Yang, Z.; Han, J. Continuous Swept-Sine Vibration Realization Combining Adaptive Sliding Mode Control and Inverse Model Compensation for Electro-hydraulic Shake Table. J. Vib. Eng. Technol. 2022, 10, 1007–1019. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Dai, D.; Wang, X.; Wang, S. Review of electro-hydraulic hitch system control method of automated tractors. Int. J. Agric. Biol. Eng. 2021, 14, 1–11. [Google Scholar] [CrossRef]
- Matsui, T.; Mochizuki, Y. Effect of Positive Angular Velocity Feedback on Torque Control of Hydraulic Actuator. Trans. Jpn. Soc. Mech. Eng. 2008, 57, 1604–1609. [Google Scholar] [CrossRef]
- Zhang, W.S.; Ping, Z.L.; Fu, Y.L.; Zheng, S.; Zhang, P. Observer-Based Backstepping Adaptive Force Control of Electro-Mechanical Actuator with Improved LuGre Friction Model. Aerospace 2022, 9, 415. [Google Scholar] [CrossRef]
- Jin, H.Y.; Zhao, X.M.; Wang, T.H. Novel Load Disturbance Observer-based Global Complementary Sliding Mode Control for a Precision Motion Stage Driven by PMLSM. Int. J. Control. Autom. Syst. 2021, 19, 3676–3687. [Google Scholar] [CrossRef]
- Liu, H.; Liu, H.; Shan, X. Linear active disturbance rejection control with torque compensation for electric load simulator. J. Power Electron. 2020, 21, 195–203. [Google Scholar] [CrossRef]
- Liu, L.; Chen, M.; Li, T. Disturbance Observer-based LQR Tracking Control for Unmanned Autonomous Helicopter Slung-load System. Int. J. Control. Autom. Syst. 2022, 20, 1166–1178. [Google Scholar] [CrossRef]
- Dai, M.; Qi, R.; Zhao, Y.; Li, Y. PD-Type Iterative Learning Control with Adaptive Learning Gains for High-Performance Load Torque Tracking of Electric Dynamic Load Simulator. Electronics 2021, 10, 811. [Google Scholar] [CrossRef]
- Panetsos, F.; Karras, G.C.; Kyriakopoulos, K.J. A Deep Reinforcement Learning Motion Control Strategy of a Multi-rotor UAV for Payload Transportation with Minimum Swing. In Proceedings of the 30th Mediterranean Conference on Control and Automation (MED), Vouliagmeni, Greece, 28 June–1 July 2022; pp. 368–374. [Google Scholar]
- Li, C.C.; Pan, X.D.; Wang, G.L. Torque tracking control of electric load simulator with active motion disturbance and nonlinearity based on T-S fuzzy model. Asian J. Control. 2020, 22, 1280–1294. [Google Scholar] [CrossRef]
- Sun, Z.; Ling, Y.W.; Sun, Z.X.; Zhou, Y.; Sun, Z. Designing and application of type-2 fuzzy PID control for overhead crane systems. Int. J. Intell. Robot. Appl. 2021, 5, 10–22. [Google Scholar] [CrossRef]
- Zhang, D.; Feng, W.; Wei, L.; Hu, X. RBF Neural Network PID Space Vector Control of Linear Servo Load Simulator. Mechatron. Syst. Control. 2020, 48, 207–215. [Google Scholar] [CrossRef]
- Asgharnia, A.H.; Jamali, A.; Shahnazi, R.; Maheri, A. Load mitigation of a class of 5-MW wind turbine with RBF neural network based fractional-order PID controller. ISA Trans. 2020, 96, 272–286. [Google Scholar] [CrossRef]
- Liu, J. Sliding Mode Control Design and MATLAB Simulation, 3rd ed.; The Basic Theory and Design Method; Tsinghua University Press: Beijing, China, 2015; pp. 2–4. [Google Scholar]
- Yang, F.; Shao, X.; Muyeen, S.M.; Li, D.; Lin, S.; Fang, C. Disturbance Observer Based Fractional-Order Integral Sliding Mode Frequency Control Strategy for Interconnected Power System. IEEE Trans. Power Syst. 2021, 36, 5922–5932. [Google Scholar] [CrossRef]
- Xu, R.; Pan, W.; Wang, Z.S.; Tian, D. High-Precision Tracking Control of a Piezoelectric Micro-nano Platform Using Sliding Mode Control with the Fractional-Order Operator. Int. J. Precis. Eng. Manuf. 2020, 21, 2277–2286. [Google Scholar] [CrossRef]
- Chehaidia, S.E.; Kherfane, H.; Cherif, H.; Boukhezzar, B.; Kadi, L.; Chojaa, H.; Abderrezak, A. Robust Nonlinear Terminal Integral Sliding Mode Torque Control for Wind Turbines Considering Uncertainties. IFAC Pap. 2022, 55, 228–233. [Google Scholar] [CrossRef]
- Kang, S.; Yan, H.; Dong, L.; Li, C. Finite-time adaptive sliding mode force control for electrohydraulic load simulator based on improved GMS friction model. Mech. Syst. Signal Process. 2018, 102, 117–138. [Google Scholar] [CrossRef]
- Merritt, H.E. Hydraulic Control. Systems; Wiley: New York, NY, USA, 1967. [Google Scholar]
- Shen, W.; Shen, C. An extended state observer-based control design for electro-hydraulic position servo mechanism. Control. Eng. Pract. 2021, 109, 104730. [Google Scholar] [CrossRef]
- Jamaludin, Z.; Brussel, H.V.; Swevers, J. Friction Compensation of an XY feed table using friction-model-based feedforward and an inverse-model-baseddisturbance observer. IEEE Trans. Ind. Electron. 2009, 56, 3848–3853. [Google Scholar] [CrossRef]
- Mugabo, I.; Barbosa, A.R.; Sinha, A.; Higgins, C.; Riggio, M.; Pei, S.; van de Lindt, J.W.; Berman, J.W. System Identification of UCSD-NHERI Shake-Table Test of Two-Story Structure with Cross-Laminated Timber Rocking Walls. J. Struct. Eng. 2021, 147, 04021018. [Google Scholar] [CrossRef]
- Gao, W. Theory and Design Method of Variable Structure Control; Science Press: Beijing, China, 1996. (In Chinese) [Google Scholar]
- Guo, J. Application of a novel adaptive sliding mode control method to the load frequency control—ScienceDirect. Eur. J. Control. 2021, 57, 172–178. [Google Scholar] [CrossRef]
- Roy, S.; Baldi, S.; Fridman, L.M. On adaptive sliding mode control without a priori bounded uncertainty. Automatica 2020, 111, 108650. [Google Scholar] [CrossRef]
- Roy, S.; Baldi, S.; Ioannou, P.A. An Adaptive Control Framework for Underactuated Switched Euler-Lagrange Systems. IEEE Trans. Autom. Control. 2022, 67, 4202–4209. [Google Scholar] [CrossRef]
- Sankaranarayanan, V.N.; Roy, S.; Baldi, S. Aerial Transportation of Unknown Payloads: Adaptive Path Tracking for Quadrotors. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 7710–7715. [Google Scholar]
- Ioannou, P.A.; Jing, S. Robust Adaptive Control; PTP Prentice-Hall: Hoboken, NJ, USA, 1996; pp. 75–76. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).