Predefined-Performance-Based Full-Process Control for Ultra-Close and High-Precision Formation Flying
Abstract
:1. Introduction
2. Dynamics Model of SFF
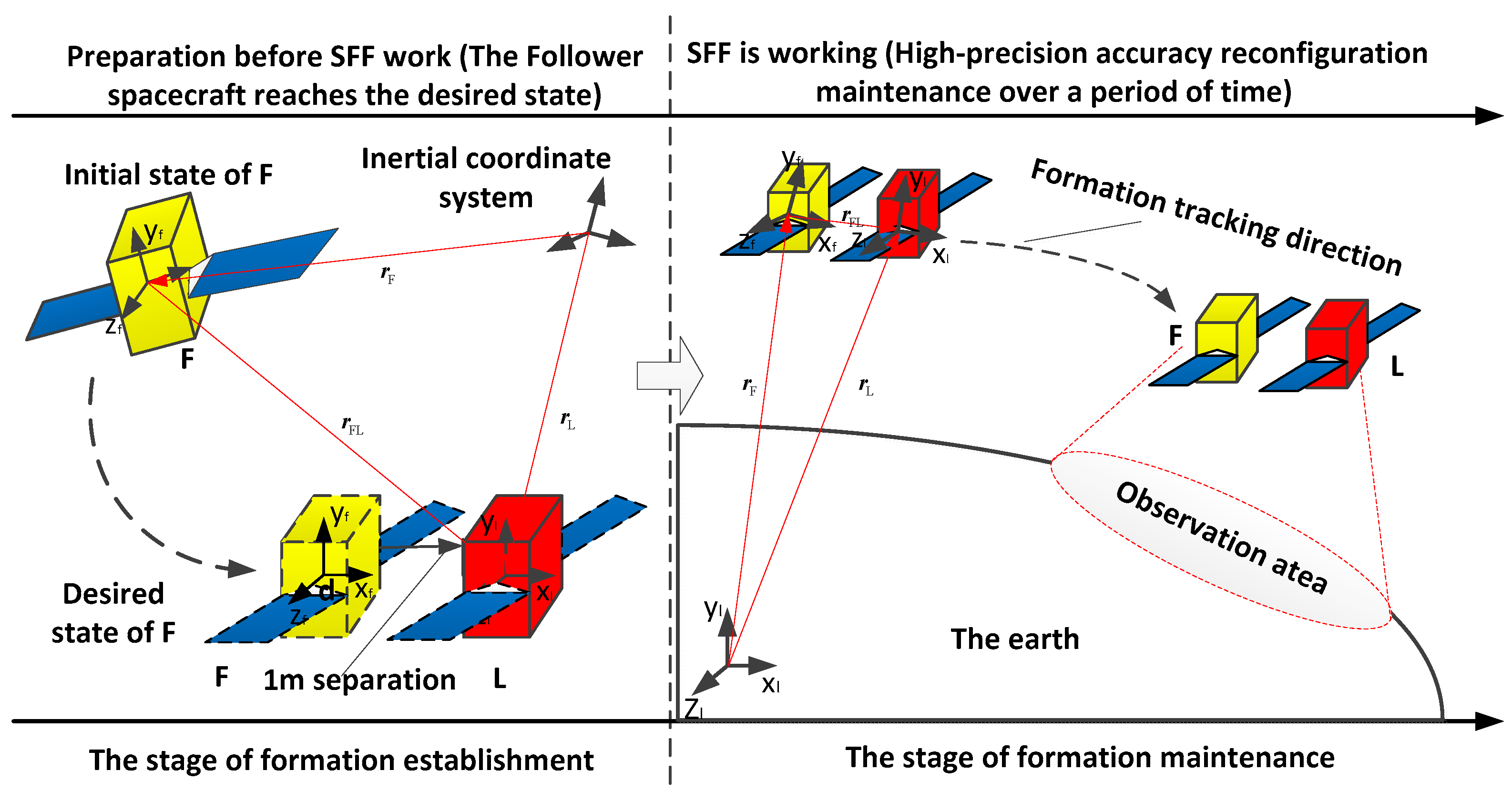
2.1. Coordinate Frames
2.2. Relative Orbit Motions of SFF
2.3. Relative Attitude Motions of SFF
2.4. 6-DOF Motions of SFF
2.5. Problem Statement
3. Full-Process Controller Design
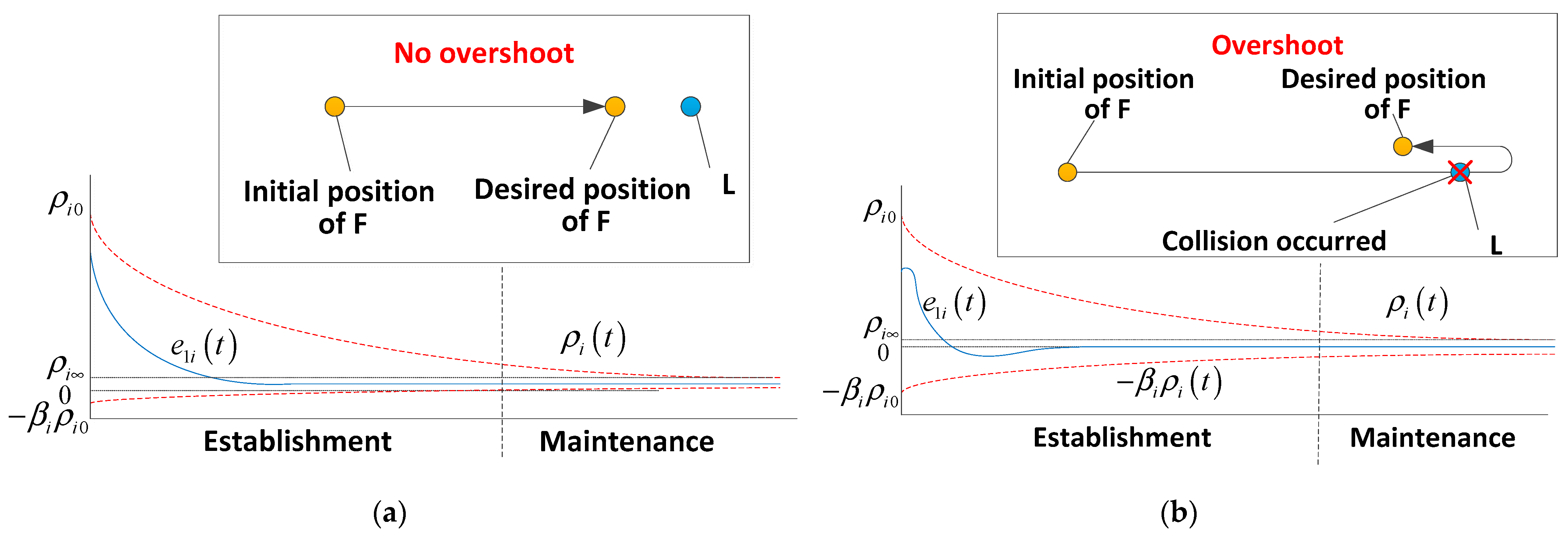
3.1. Predefined Performance Function
3.2. Error Transformation
3.3. Controller Design
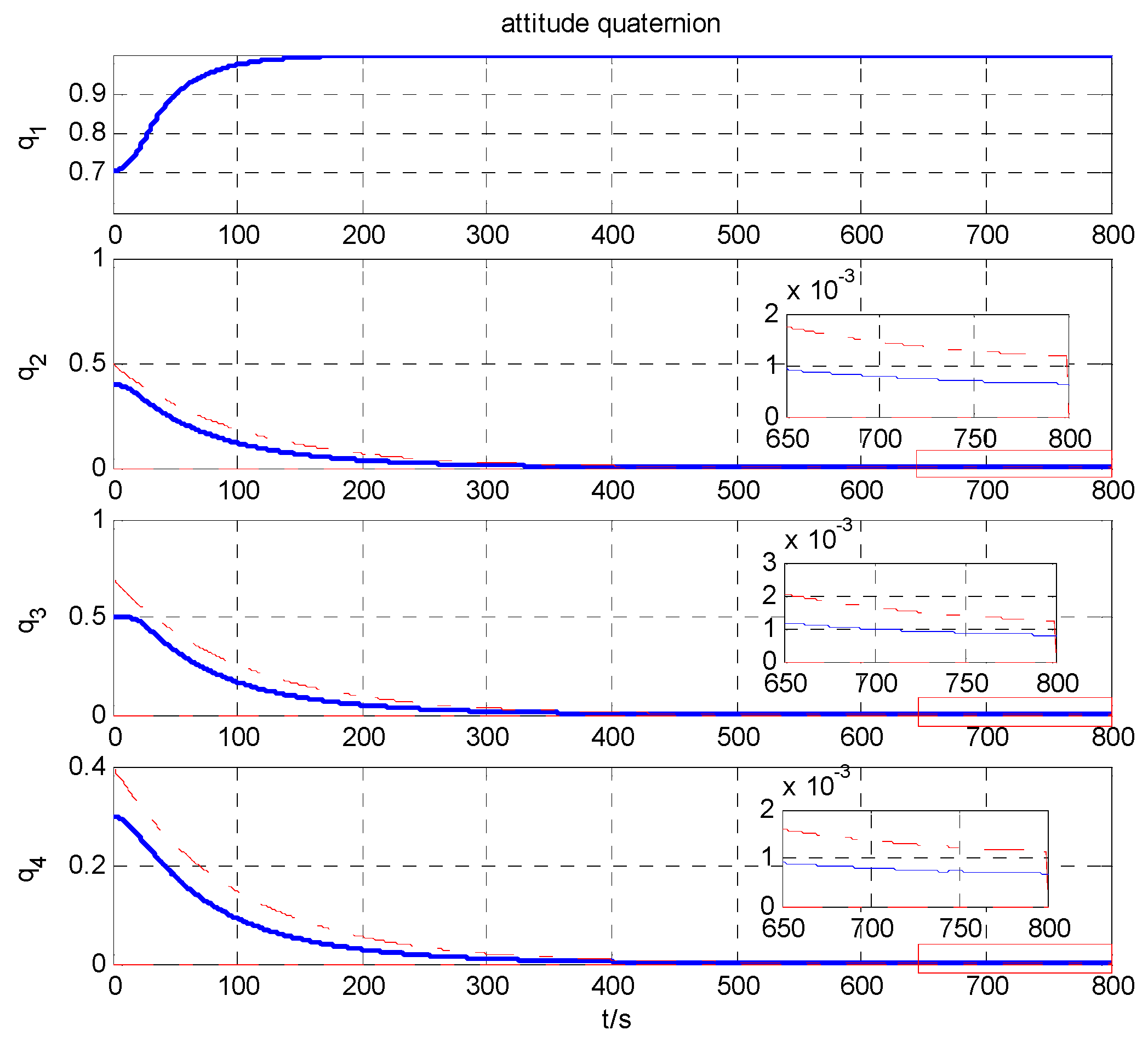
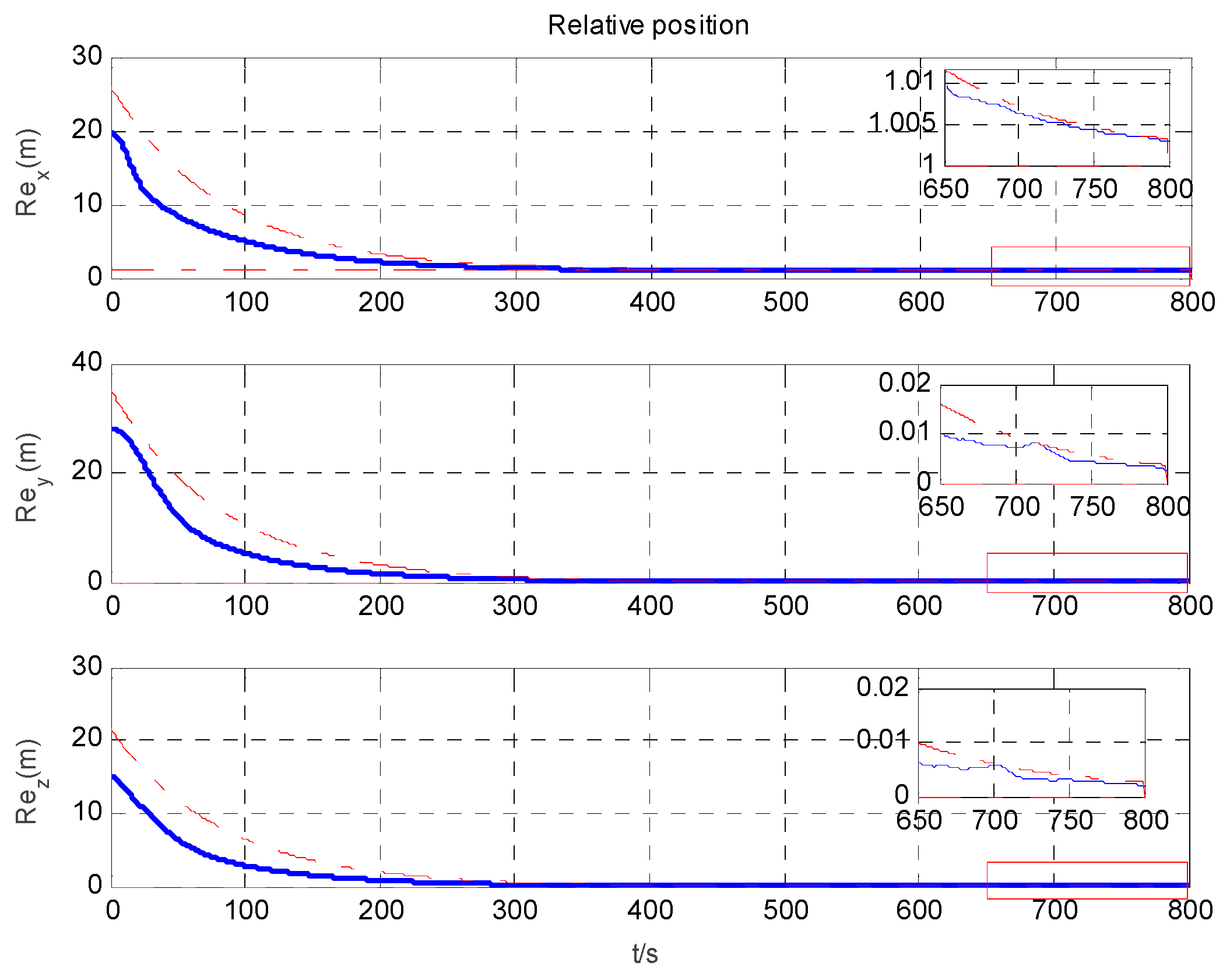
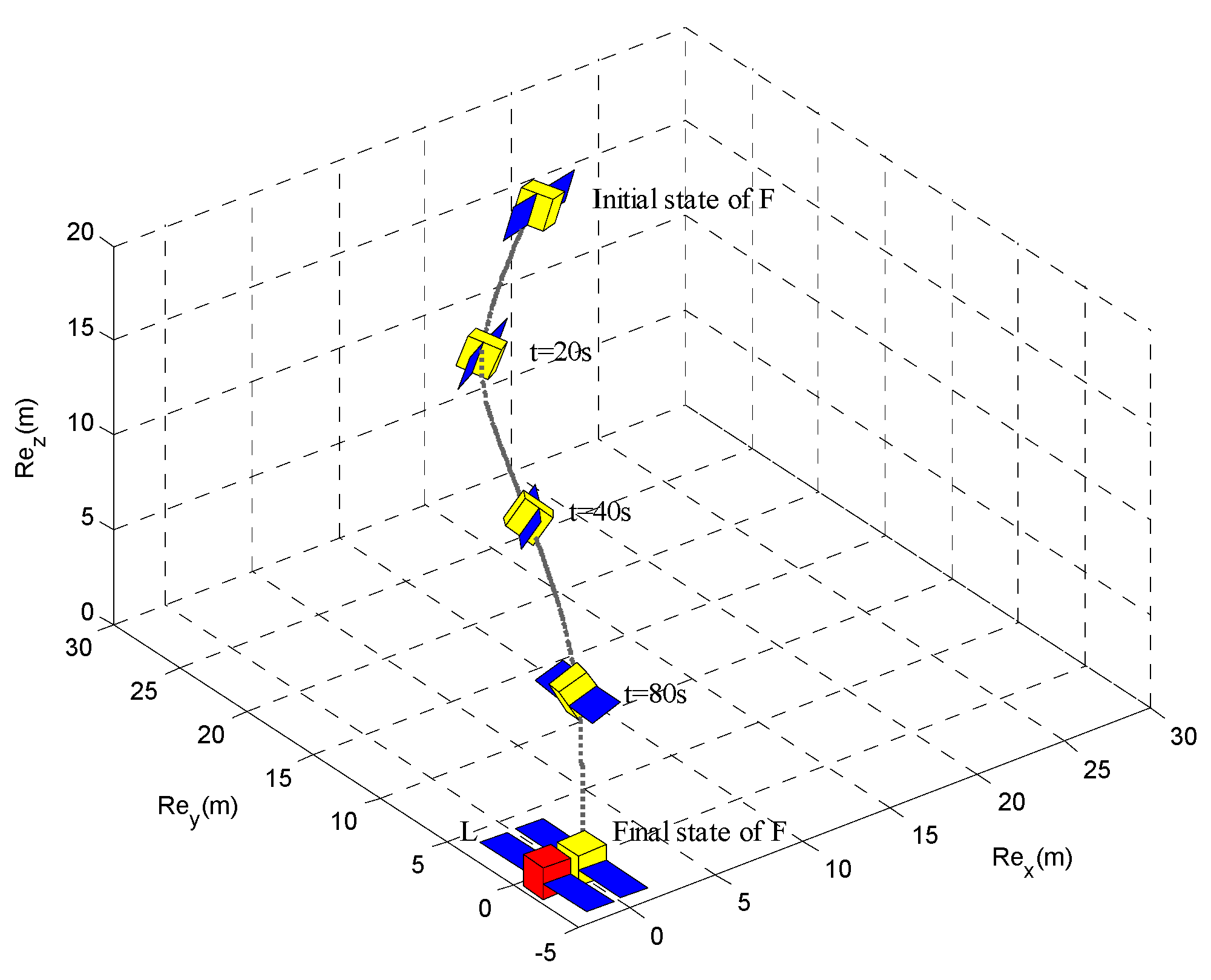
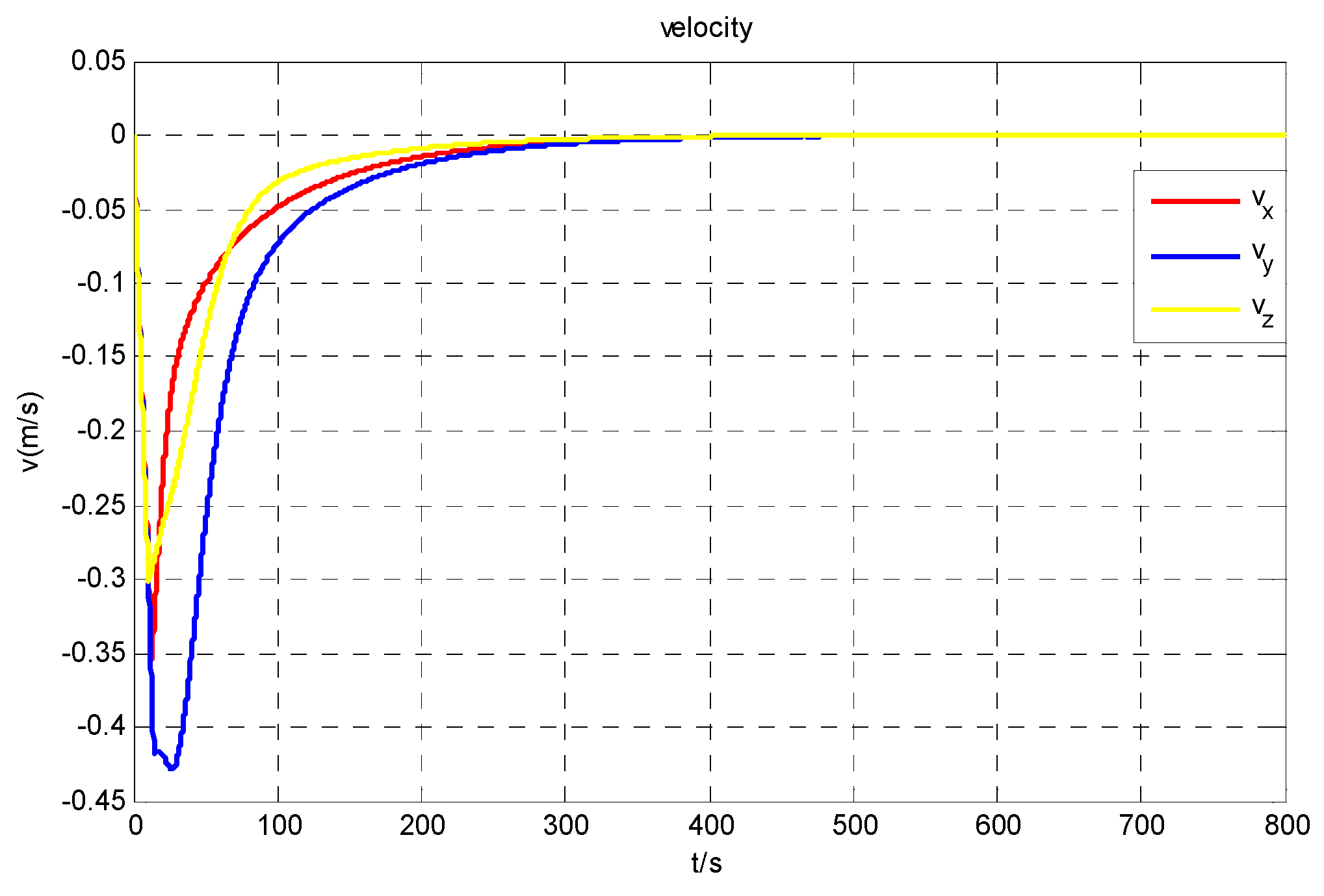
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Vu, T.; Rahmani, A. Analysis of a distributed estimation and control scheme for formation flying spacecraft. Aerosp. Sci. Technol. 2018, 73, 232–238. [Google Scholar] [CrossRef]
- Chung, S.; Bandyopadhyay, S.; Foust, R.; Subramanian, G. Review of formation flying and constellation missions using nanosatellites. J. Guid. Control Dyn. 2017, 53, 567–578. [Google Scholar]
- Wu, X.; Yang, Y.; Sun, Y.; Xie, Y.; Song, X.; Huang, B. Dynamic regional splitting planning of remote sensing satellite swarm using parallel genetic PSO algorithm. Acta Astronaut. 2022; in press. [Google Scholar]
- Larbi, M.; Stoll, E. Spacecraft formation control using analytical finite-duration approaches. CEAS Space J. 2018, 10, 63–77. [Google Scholar] [CrossRef]
- Scharf, D.; Hadaegh, F.; Ploen, S. A Survey of spacecraft formation flying guidance and control (Part 2): Control. In Proceedings of the American Control Conference, Boston, MA, USA, 30 June–2 July 2004. [Google Scholar]
- Roscoe, C.; Westphal, J.; Griesbach, J. Formation establishment and reconfiguration using differential elements in J2-Perturbed orbits. J. Guid. Control Dyn. 2015, 38, 1725–1740. [Google Scholar] [CrossRef]
- Ran, D.; Chen, X.; Misra, A. Finite time coordinated formation control for spacecraft formation flying under directed communication topology. Acta Astronaut. 2017, 136, 125–136. [Google Scholar] [CrossRef]
- Vaddi, S.; Alfriend, K.; Vadali, S.; Sengupta, P. Formation establishment and reconfiguration using impulsive control. J. Guid. Control Dyn. 2005, 28, 262–268. [Google Scholar] [CrossRef]
- Qiu, H.; Duan, H. Pigeon interaction mode switch-based UAV distributed flocking control under obstacle environments. ISA Trans. 2017, 71, 93–102. [Google Scholar] [CrossRef] [PubMed]
- Gallehdari, Z.; Meskin, N.; Khorasani, K. Distributed reconfigurable control strategies for switching topology networked multi-agent systems. ISA Trans. 2017, 71, 51–67. [Google Scholar] [CrossRef]
- Hua, Y.; Dong, X.; Li, Q.; Ren, Z. Distributed fault-tolerant time-varying formation control for high-order linear multi-agent systems with actuator failures. ISA Trans. 2017, 71, 40–50. [Google Scholar] [CrossRef]
- Liu, X.; Meng, Z.; You, Z. Adaptive collision-free formation control for under-actuated spacecraft. Aerosp. Sci. Technol. 2018, 79, 223–232. [Google Scholar] [CrossRef]
- Shastia, B.; Alastya, A.; Assadianb, N. Robust distributed control of spacecraft formation flying with adaptive network topology. Acta Astronaut. 2017, 136, 281–296. [Google Scholar] [CrossRef]
- Sun, H.; Li, S.; Fei, S. A composite control scheme for 6 DOF spacecraft formation control. Acta Astronaut. 2011, 69, 595–611. [Google Scholar] [CrossRef]
- Huang, X.; Yan, Y.; Zhou, Y.; Yang, Y. Dual-quaternion based distributed coordination control of six-DOF spacecraft formation with collision avoidance. Aerosp. Sci. Technol. 2017, 67, 443–455. [Google Scholar] [CrossRef]
- Zhu, Z.; Guo, Y. Adaptive coordinated attitude control for spacecraft formation with saturating actuators and unknown inertia. J. Frankl. Inst. 2018, 356, 1021–1037. [Google Scholar] [CrossRef]
- Yang, H.; You, X.; Hua, C. Attitude tracking control for spacecraft formation with time-varying delays and switching topology. Acta Astronaut. 2016, 126, 98–108. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, Q.; Wang, D.; Xie, W. Robust attitude coordinated control for spacecraft formation with communication delays. Chin. J. Aeronaut. 2017, 30, 1071–1085. [Google Scholar] [CrossRef]
- Agarwal, S.; Sinha, A. Formation Control of Spacecraft under Orbit Perturbation. In Proceedings of the 4th IFAC Conference on Advances in Control and Optimization of Dynamical Systems, Tiruchirappalli, India, 1–5 February 2016; Volume 49, pp. 130–135. [Google Scholar]
- Lee, D. Nonlinear disturbance observer-based robust control for spacecraft formation flying. Aerosp. Sci. Technol. 2018, 76, 82–90. [Google Scholar] [CrossRef]
- Ran, D.; Chen, X.; Misra, A.K.; Xiao, B. Relative position coordinated control for spacecraft formation flying with communication delays. Acta Astronaut. 2017, 137, 302–311. [Google Scholar] [CrossRef]
- Zhao, H.; Wu, X.; Xie, Y.; Du, Y.; Zhang, Z.; Li, Y. Rotation matrix-based finite-time attitude synchronization control for flexible spacecrafts with unknown inertial parameters and actuator faults. ISA Trans. 2022, 128 Pt A, 276–289. [Google Scholar] [CrossRef]
- Warier, R.R.; Sinha, A.; Srikant, S. Line-of-sight based formation keeping and attitude control of two spacecraft. Acta Astronaut. 2016, 127, 131–140. [Google Scholar] [CrossRef]
- Bechlioulis, C.; Kyriakopoulos, K. Robust Model-Free Formation Control with Prescribed Performance for Nonlinear Multi-Agent Systems. In Proceedings of the IEEE International Conference on Robotics and Automation, Seattle, WA, USA, 26–30 May 2015; pp. 1268–1273. [Google Scholar]
- Sui, S.; Tong, S.; Li, Y. Observer-based fuzzy adaptive prescribed performance tracking control for nonlinear stochastic systems with input saturation. Neurocomputing 2015, 158, 100–108. [Google Scholar] [CrossRef]
- Yang, Y.; Tan, J.; Yue, D. Prescribed performance tracking control of a class of uncertain pure-feedback nonlinear systems with input saturation. IEEE Trans. Syst. Man Cybern.: Syst. 2020, 50, 1733–1745. [Google Scholar] [CrossRef]
- Lee, D.; Sanyal, A.K.; Butcher, E.A. Asymptotic tracking control for spacecraft formation flying with decentralized collision avoidance. J. Guid. Control Dyn. 2015, 38, 587–600. [Google Scholar] [CrossRef]
- Calhoun, P.; Novo-Gradac, A.; Shah, N. Spacecraft alignment determination and control for dual spacecraft precision formation flying. Acta Astronaut. 2018, 153, 349–356. [Google Scholar] [CrossRef]
- Bechlioulis, C.; Rovithakis, G. Prescribed performance adaptive control for multi-input multi-output affine in the control nonlinear systems. IEEE Trans. Autom. Control. 2010, 55, 1220–1226. [Google Scholar] [CrossRef]
- Yang, Y.; Fu, R.; Huang, L. Robust analysis and synthesis for a class of uncertain nonlinear systems with multiple equilibria. Syst. Control Lett. 2004, 53, 89–105. [Google Scholar] [CrossRef]
- Pan, H.; Kapila, V. Adaptive nonlinear control for spacecraft formation flying with coupled translational and attitude dynamics. In Proceeding of the 40 th IEEE Conference on Decision and Control, Orlando, FL, USA, 4–7 December 2001. [Google Scholar]



| Parameters of Mass and Inertial Matrix | Orbital Parameters | Initial States |
|---|---|---|
| |
| Controller Gains |
|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Bai, W.; Xie, Y.; Zhang, X.; Song, T. Predefined-Performance-Based Full-Process Control for Ultra-Close and High-Precision Formation Flying. Aerospace 2023, 10, 152. https://doi.org/10.3390/aerospace10020152
Wu X, Bai W, Xie Y, Zhang X, Song T. Predefined-Performance-Based Full-Process Control for Ultra-Close and High-Precision Formation Flying. Aerospace. 2023; 10(2):152. https://doi.org/10.3390/aerospace10020152
Chicago/Turabian StyleWu, Xiande, Wenbin Bai, Yaen Xie, Xianliang Zhang, and Ting Song. 2023. "Predefined-Performance-Based Full-Process Control for Ultra-Close and High-Precision Formation Flying" Aerospace 10, no. 2: 152. https://doi.org/10.3390/aerospace10020152
APA StyleWu, X., Bai, W., Xie, Y., Zhang, X., & Song, T. (2023). Predefined-Performance-Based Full-Process Control for Ultra-Close and High-Precision Formation Flying. Aerospace, 10(2), 152. https://doi.org/10.3390/aerospace10020152







