Abstract
A model-free control method is applied to the attitude and orbital operation of the post-capture combined spacecraft, which consists of a space robot and debris. The main contribution of this paper lies in the following three aspects. Firstly, the discrete dynamic linearization method of the motion equation for a post-capture combined spacecraft is proposed, and then, the standardized expression form of multiple input and multiple output system for the attitude and orbital dynamics motions of post-capture combined spacecraft are presented. Secondly, the data mapping model of the post-capture combined spacecraft is defined, and based on this, an initial value online optimization method for the data mapping model is provided, which is key for the convergence of model-free control. Finally, a test system based on the ground-based three-axis spacecraft simulator is built to simulate the attitude and orbital operation of post-capture combined spacecraft, and the experimental system is implemented to verify the validation of the model-free control method proposed in this paper. The results show that the model-free control has a good control effect on the attitude and orbit of the post-capture combined spacecraft, even if the configuration of the spacecraft is time-varying.
1. Introduction
Post-capture control is a high-priority task in missions of on-orbit debris clearance [1,2,3]. Sandberg [4] proposed online optimization of a combined attitude orbital motion, while Raigoza [5] augmented the method with autonomous orbital motion for multiple debris collision avoidance. Considering that the geometric shape of the capture point is irregular and unpredictable in the capture process, a combination spacecraft (PCCS) would undergo different configurations during post-capture operation [6,7]. We conducted a simulation analysis on the configuration change in the combined spacecraft during post-capture control, as shown in Figure 1 and Table 1. Details of this simulation are the same as the experimental parameters in Section 5, and the experiment is performed under standard conditions with 1 atmosphere pressure and at 25 degrees centigrade. The space robot used a robotic arm to capture the geometric irregularities of space debris, such as the docking ring of the scrapped spacecraft. During the post-capture operation process, it can be found that the configuration of the combined spacecraft was time-varying. This time-varying configuration would cause the inertial parameters to change, making it difficult to construct the dynamics of the combined spacecraft. It further affects the success of the post-capture control. Therefore, a proper control method for all configurations is critical to achieve accurate orbital and attitude operation. Investigations of space robots have focused on the collision avoidance control of module transportation [8,9,10], disturbance robust control [11,12] and model uncertainty adaptive control [13,14]. Few methodologies or design practices are in place to help engineers design with space operation in mind. For example, very little work has been carried out on the benefits and disadvantages of control system algorithms for space operation applications.
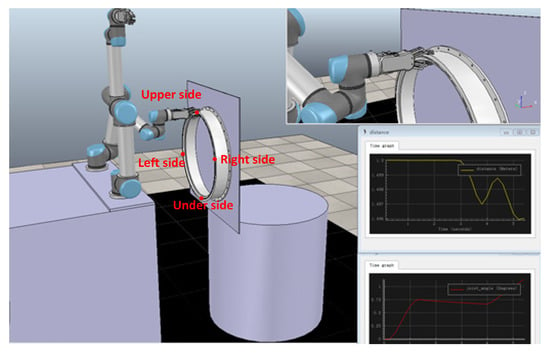
Figure 1.
Post-capture control of space debris.

Table 1.
Configuration change in the combined spacecraft (single-arm capture).
Mohan et al. [15] proposed a dynamic control model generation method for on-orbit assembly tasks. A dynamic model was built of different stages, such as the capture, transport, and docking phases. On the basis of this, the dynamic control model generation method of the space robot was proposed. Maybeck et al. [16] proposed the reconfigurable flight control based on the multi-model adaptive control method, which solved the control problem of the entry module of the Mars Science Laboratory. She et al. [17] designed an adaptive controller for on-orbit service missions dependent of the model generation method. Model generation architectures were classified by the amount of a priori information by designer. Additionally, unknown parameters identification of each stage is required.
The dynamical parameters identification method is a mainstream technique for space operation, and a large number of investigations have been carried out using this method. As an example of the space robot estimation algorithms, Nguyen-Huynh et al. [18] developed an online momentum-based estimation method for inertia parameter identification after the space manipulator grasps an unknown target. On the basis of this, an adaptive reactionless control algorithm was provided for the combined spacecraft attitude stabilization. Norman et al. [19] provided an onboard parameter estimation scheme based on measurement equations describing the angular momentum and kinetic energy states of the rigid-body system. Mortari et al. [20] provided an optimal linear attitude estimator algorithm of spacecraft attitude using the minimum-element attitude parameterization. According to the above investigations, the diagonal elements of spacecraft inertia matrix identification can be successfully realized. However, as reported in [21], the takeover of a non-cooperative target can also have significant effects on the non-diagonal elements of the inertia matrix, and the effects may impart large amounts of error on the control of the combined systems. In response to this problem, Thienel et al. [22] presented a spacecraft inertia adaptive identification method, which could estimate all spacecraft inertia components instead of only estimating the diagonal elements of the inertia matrix. Crassidis et al. [23] made a survey of nonlinear attitude estimation methods.
The dynamic control model generation and unknown parameters identification methods can theoretically solve the control problem of space operation. However, the control precision is affected by the particle degree of the dynamic classification, and strongly related to the prior experience of the designer. In contrast to the above model-dependent control methods, Hou et al. [24] put forward a MFC method, which can achieve convergence without a dynamics model. Bu et al. [25] studied the stability of the MFC method in the case of data loss. Wang et al. [26] proposed a MFC method considering external environmental disturbance, which eliminated the influence of environmental disturbance on the motion of space robots. Vikas et al. [27] proposed a control framework of a soft robot based on the model-free theory to solve the time-varying problem of the model in the operation process. Han et al. [28,29] applied the model-free control (MFC) method to the post-capture combined spacecraft for the first time. In Refs. [28,29], researchers believed that the configuration change only caused the inertia of the combined spacecraft to change and, based on this assumption, the MFC was designed and verified. However, She et al. [17] proposed that the relatively non-linear motion inside the combined spacecraft was the most important influence caused by the configuration change. The above investigations show that the application MFC to PCCS has not yet formed a unified cognition, and that it would benefit from further research. Compared with Refs. [28,29], the main contributions of this paper are as follows:
- (1)
- The standardized expression form of a multiple input and multiple output (MIMO) system for the attitude and orbital dynamics of PCCS is proposed;
- (2)
- An online optimization method of the data mapping model is provided to guarantee the rapid convergence of MFC;
- (3)
- The test system based on the ground-based three-axis spacecraft simulator is built to verify the effectiveness of the application of the MFC method to the attitude and orbital control of PCCS.
In the development that follows, the mission scenario and problem statement were provided in Section 2. The discrete dynamic linearization proof method of the PCCS system was derived in Section 3. In Section 4, the online optimization method of the data mapping model is presented for the MFC of PCCS. In Section 5, a test system based on the ground-based three-axis spacecraft simulator was built to verify the effectiveness of application of the MFC method to the operation of PCCS. Finally, in Section 6, concluding remarks summarize presented results.
2. Mission Scenario and Problem Statement
The mission scenario is designed to be an on-orbit operation of PCCS, which includes two control process, namely attitude control and orbital control. Figure 2 depicts the mission system. Three coordinate frames are introduced in the scenario. Their definitions are given as follows.
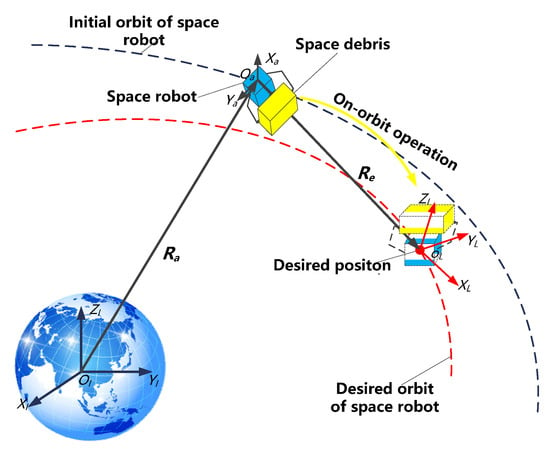
Figure 2.
Configurations of the space robot.
The Earth centered inertial (ECI) frame . This frame is attached to the Earth, where axis points to the vernal equinox, axis points to the North Pole, and axis is in the equatorial plane and complies with the right-hand rule.
The body centered (BC) frame . This frame, shown in Figure 1, is attached to the space robot, where origin is the combined spacecraft center, and the three axes , , and are along the inertial principal axes of the space robot, respectively.
The virtual centered (VC) frame . The origin is the virtual desired point, and its axes are parallel to the inertial coordinate system.
When applying MFC method to this mission scenario, further control flow was represented in Figure 3.
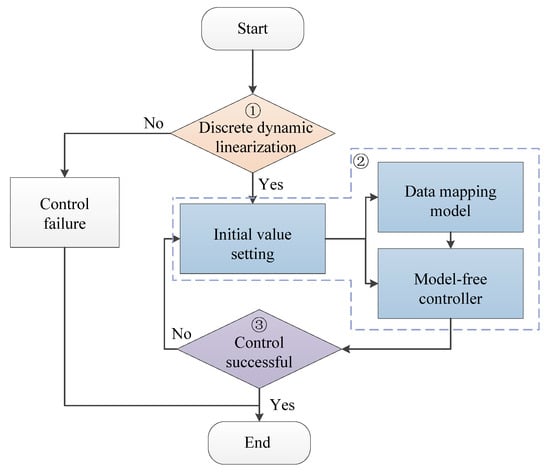
Figure 3.
Control flow of the model-free control method.
It can be seen from Figure 3 that the control process has three key links, as follows:
① Discrete dynamic linearization—based on the input and output variables, the MFC method is applicable only when the nonlinear dynamic equation of the space robot can be discretely and dynamically linearized;
② Initial values assignment of data mapping model and MFC—initial values assignment is key for the convergence of MFC, since the convergence time of the MFC method is positively related to the accuracy of the data mapping model, and the appropriate initial assignment can realize the rapid construction of the data mapping model;
③ Control effectiveness verification—the MFC method investigated in this paper was aimed at a PCCS, which had a variable configuration and time-varying dynamics. Control effectiveness was difficult to verify by the method of numerical modeling. It is necessary to construct the PCCS simulator with space–ground consistency to verify the effectiveness of control.
In response to the above three issues, the discrete dynamic linearization method of the dynamics model for PCCS was proposed in this paper. Then, an initial value online optimization method was proved. On the basis of this, a test system based on the ground-based three-axis spacecraft simulator was built to verify the effectiveness of control.
3. Discrete Dynamic Linearization
3.1. Dynamics of PCCS
When configuration change is not considered, the orbit dynamical equation of PCCS in terms of components along the BC frame can be expressed as follows:
where denotes the space robot mass; is the orbital radius vector of the space robot; denotes the external disturbance acting on the space robot; is the total control force acting on the space robot; is the gravitational constant.
Define as the attitude quaternion of the space robot. Here, is the real part of ; is the vector part of ; denotes the attitude angular velocity represented in the body frame. The attitude kinematic motion of space robot can be expressed as follows:
where ; ; denotes the third-order identity matrix; denotes a 3×3 skew-symmetric matrix, which is as follows:
The attitude dynamics of the space robot can be expressed as follows:
where denotes the moment of inertia matrix of the space robot; and denote the total control torque and external disturbance torque acting on the space robot, respectively.
Define , and . According to Equation (4), the six-degree-of-freedom motions of PCCS can be expressed as follows:
where the following are true:
Based on Equation (5), considering the nonlinear effects caused by the configuration change in PCCS, the dynamics of PCCS can be expressed as follows:
where denotes the nonlinear elements of the dynamics model caused by the configuration change.
3.2. Discrete Dynamic Linearization of PCCS
Equation (6) can further be expressed as follows:
Define , and we can obtain the following:
By substituting Equation (8) into Equation (7), we can obtain the following:
Equation (9) can further be expressed as follows:
Discretize Equation (10), and we can obtain the following:
where denotes the discrete time; is the sampling period.
Equation (11) can further be expressed as follows:
Then, we can obtain the following:
Based on Equation (13), the general multiple-input multiple-output discrete time form of the PCCS can be expressed in a compact form as follows:
where , denote the input and output data at time , respectively; is the nonlinear function corresponding to Equation (13). Equation (14) is the standardized expression form of MIMO system for the attitude and orbital dynamics of PCCS.
In order to design a model-free controller of the nonlinear system in Equation (14), the following assumptions should be satisfied:
Assumption 1.
The partial derivative ofwith respect to control inputis continuous.
Assumption 2
. System (14) is a generalized Lipschitz system, that is, for any and with , , and is a positive constant.
In systems (13) and (14), if the nonlinear element satisfies the following assumption:
Assumption 3
. The value of is bounded for any time . then, assumption 1 and assumption 2 of systems (13) and (14) are satisfiable.
Remark 1.
During the post-capture process of a combined spacecraft, Assumption 3 is reasonable and acceptable from a practical viewpoint. In the PCCS control system, since the change in the configuration, including relative position change and relative attitude changes, is bounded, the effects on the motion of PCCS caused by the nonlinear element cannot go to infinity. Therefore, there exists a positive constantthat satisfies.
Theorem 1.
The multiple-input multiple-output nonlinear system that satisfies assumptions 1 and 2 can be dynamically linearized. That is, there must exist a, called the pseudo-partial derivative (PDD), such that if, System (14) can be described as follows:
whereis an unknown bounded pseudo-gradient matrix;, andare the pseudo-orders of System (14).
3.3. Model-Free Controller Design of PCCS
According to the MFC theory, the model-free controller of System (14) can be designed as follows:
where , denote the parameters of a model-free controller. Here, is the desired output of the system.
The PDD of system (14) can be designed as follows:
where , denote the parameters of PDD.
4. Online Optimization of the Data Mapping Model
As shown in Equation (16), the model-free controller is constructed by using the input data and the output . The advantage of this method is that, based on a limited number of input and output data, the MFC method can realize its control objective in real-time without pre-training. However, in Equation (16), in addition to the constant parameters , , the controller also includes the time-varying matrix . In particular, is key for the convergence characteristics of the controller. Considering that is the dynamic linear relationship matrix between input data and output data, as shown in Equation (15). In this paper, is defined as the data mapping model.
As far as the researchers know, there is no research on the optimal assignment of in MFC theory. In engineering applications, the initial value of is usually set to a very small value to ensure that the initial control input is too large to cause the combined spacecraft to lose control. However, the result of this method is that it will lead to control divergence due to external interference. In this paper, combining the discrete linearization equation of the PCCS in Chapter 3, the initial assignment of the data mapping model is optimized to ensure that the control process can converge without causing the combined spacecraft to lose control.
According to Equation (13), we can obtain the following:
Based on Equations (15) and (18), the initial value of the data mapping model can be optimized as follows:
where is the initial value of the data mapping model ; denotes the initial value of ; and denote the initial estimate of and , respectively.
The mass and moment of inertia of the PCCS are unknown, since the operation object is a non-cooperative target. Therefore, is an unknown value. The purpose of the following development is to propose an estimation method for .
In Equation (19), , , and consist of , , , , , and , where , , , and is measurable. Here, can be directly estimated using the input and output data at the first moment. Equation (20) is as follows:
When estimating , the nonlinear influence caused by the configuration change and the external influence are ignored. Based on the Equation (4), the formula can then be developed as follows:
where , .
In the post-capture control task of non-cooperative targets, the matrix is completely unknown. As mentioned in Section 1, the traditional solution for this problem is to estimate the matrix. However, it is determined that Equation (21) is unsolvable if one considers the nine elements of matrix as unknowns. Therefore, the previous investigations assume that the inertia matrix has a symmetric form, that is , , , and the number of unknowns is reduced to six. Then, the least squares method or Kalman filter method are used to estimate the six unknown parameters. However, it is obvious that the PCCS is not a regular rigid body in actual situations, which means that the assumption that the matrix is symmetrical does not hold. This is also an important reason why traditional dynamic parameter identification and model-based control methods are difficult to apply to PCCS operation.
The model-free controller used in this paper has the function of data model self-adaptation and does not need to obtain the precise dynamic parameters of the combination. In the actual situation, considering the actual situation, the parameters of the inertia principal axis are much larger than other parameters and, thus, . Therefore, we only estimate the parameters of the principal axis of inertia. Then, Equation (21) can be further expressed as follows:
The initial value of the data mapping model, , was obtained though the above method. This method can provide an exact initial value of parameter , instead of the initial value given by the researcher based on experience.
5. Experimental Results
This section will apply the proposed control and optimization method to the problem of post-capture combined spacecraft attitude and orbital control, along with accompanying experimental results.
To test the proposed control and optimization method on the ground, firstly, a three-degree-of-freedom simulator of PCCS was developed. Figure 4 shows the structure of the simulator. The space robot used two robotic arms to capture the docking ring of the space debris. The mass of the space robot and the space debris are roughly equal, at about 120 kg. The single-axis attitude freedom of the simulator is actuated by a flywheel. The theoretical maximum torque of the flywheel is 0.1 N·m, and the maximum speed is 6000 revolutions per second. The two-axis position freedom of the simulator is actuated by eight sets of thrusters. The theoretical maximum force of the thrusters is 0.1 N. The control torque of the flywheel and the control force of thrusters (the input data of PCCS) are transferred to the control computer through the RS232 serial port. The position data and attitude date (the output data of PCCS) are measured by eight cameras and transferred to the control computer through the RS232 serial port. The sampling period is 0.1 s. In the experimental system, a personal computer was used as the control computer to develop the control program by using Simulink software. During the control process, the configuration of the simulator changes with time.

Figure 4.
Control flow of the model-free control method.
To test the proposed control and optimization method on the ground, secondly, an orbit change task was designed. In this task, the space debris was dragged off the origin orbit to a new orbit. Figure 5 shows the flow of this task. As shown in Figure 5, this task was divided into two stages. The first stage is the attitude adjustment of PCCS. The purpose of this stage was to adjust the attitude of the combined spacecraft and to provide a feasible attitude condition for the orbit change in PCCS. The second stage is the orbit control of PCCS and, in this step, the combined spacecraft maneuvered into a new orbit by using its orbit control thruster. Orbit change is a common method for space debris removal missions to free up precious orbital resources occupied by space debris. In the experiment, two cases were designed to simulate the two stages of orbit change task, namely attitude maneuver control and position maneuver control.
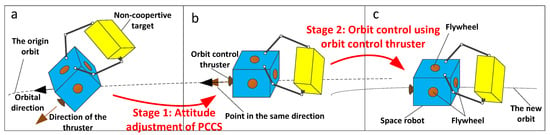
Figure 5.
Flow of the orbit change task. (a) Initial state of PCCS. (b) Attitude adjustment of PCCS. (c) Orbit maneuver of PCCS.
Case 1. Attitude maneuver control
In this case, two groups of tests are provided. In the first group of tests, the initial angle and angular velocity of the simulator are and , respectively. The desired angle and angular velocity of the simulator are set to and , respectively. The parameters of controller , , , , and these parameters are defined in Equations (16) and (17). In addition, based on the three-degree-of-freedom simulator of PCCS shown in Figure 4, the attitude maneuver control around the z-axis was realized by using the flywheel installed on the space robot simulator. The tests results are shown as Figure 6, Figure 7, Figure 8 and Figure 9.
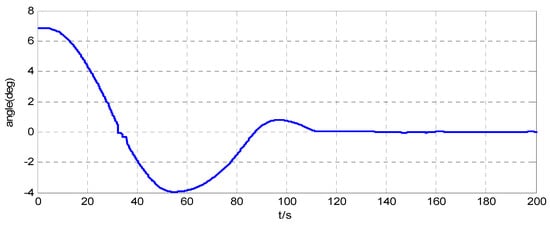
Figure 6.
Angle around the z-axis of the simulator when .
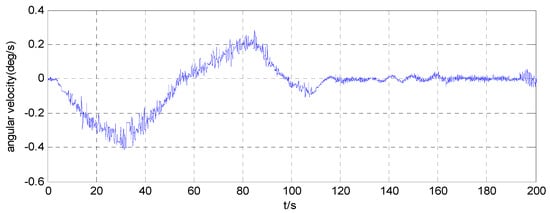
Figure 7.
Angular velocity around the z-axis of the simulator when .
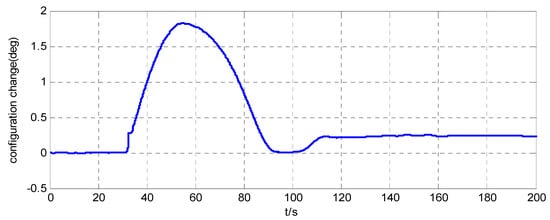
Figure 8.
Relative angle error inside the simulator when .
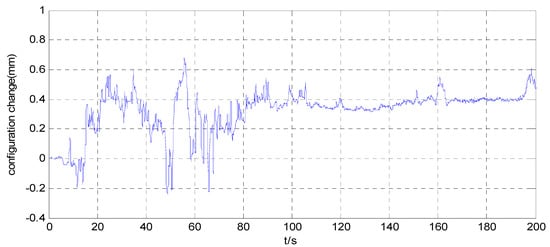
Figure 9.
Relative position error inside the simulator when .
In the second group of tests, the initial angle and angular velocity of the simulator are and , respectively. The desired angle and angular velocity of the simulator and parameters of the controller are the same as that of the first group of tests. The tests results are shown as Figure 10, Figure 11, Figure 12 and Figure 13.
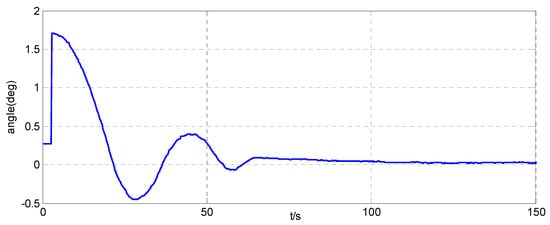
Figure 10.
Angle around the z-axis of the simulator when .
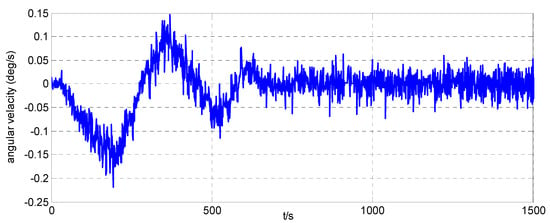
Figure 11.
Angular velocity around the z-axis of the simulator when .
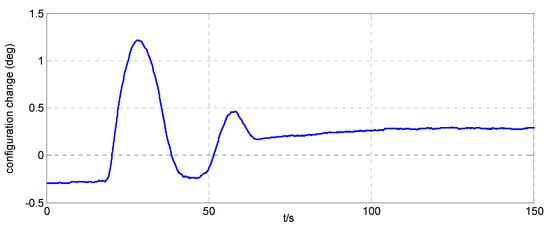
Figure 12.
Relative angle error inside the simulator when .
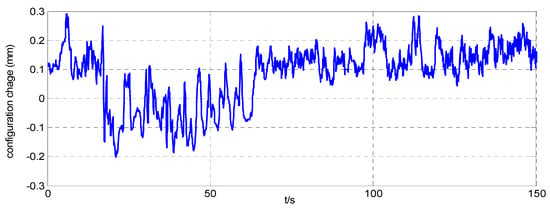
Figure 13.
Relative position error inside the simulator when .
Case 2. Position maneuver control
In this case, two groups of tests are provided. In the first group of tests, the initial position and velocity of the simulator are and , respectively. The desired position and velocity of the simulator are set to and , respectively. The parameters of controller , , , , and these parameters are defined in Equations (16) and (17). The position maneuver control along the x-axis was realized by using the thruster installed on the space robot simulator. Test results are shown as Figure 14, Figure 15, Figure 16 and Figure 17.
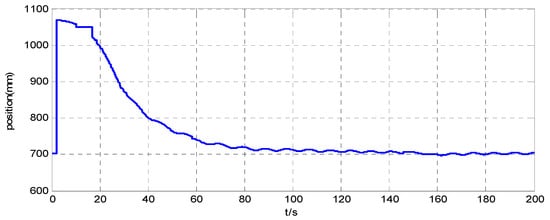
Figure 14.
Position along the x-axis of the simulator when .
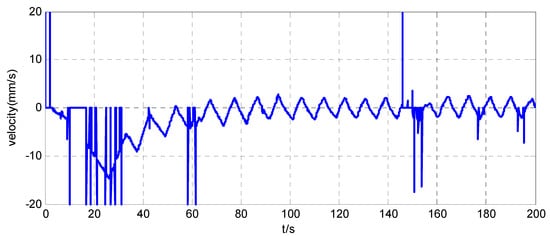
Figure 15.
Velocity along the x-axis of the simulator when .
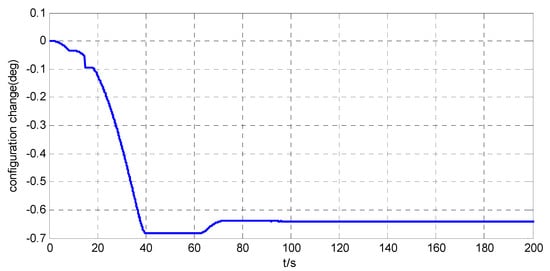
Figure 16.
Relative angle error inside the simulator when .
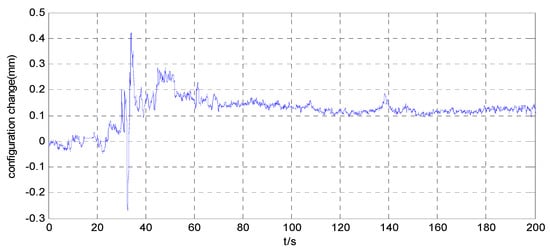
Figure 17.
Relative position error inside the simulator when .
In the second group of tests, the initial position and velocity of the simulator are and , respectively. The desired position and velocity of the simulator are set to and , respectively. The parameters of the controller are the same as those of the first group of tests. Test results are shown as Figure 18, Figure 19, Figure 20 and Figure 21.
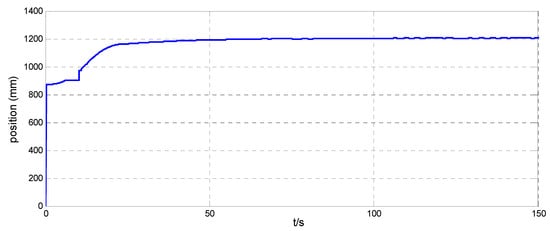
Figure 18.
Position along the x-axis of the simulator when .
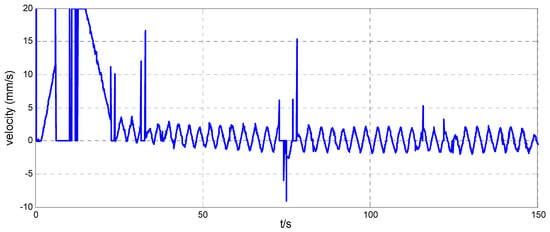
Figure 19.
Velocity along the x-axis of the simulator when .
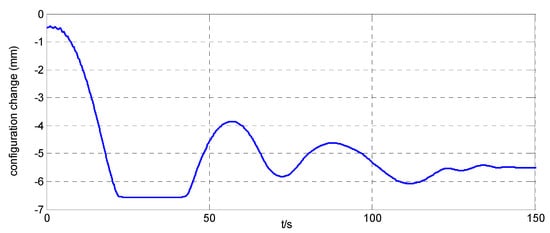
Figure 20.
Relative angle error inside the simulator when .
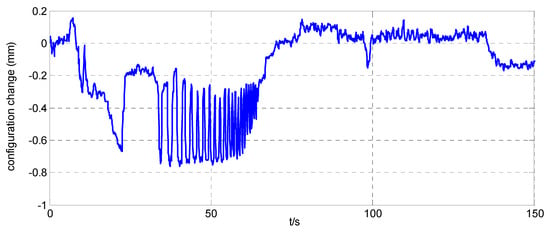
Figure 21.
Relative position error inside the simulator when .
The attitude maneuver control experimental results are shown in Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10. Figure 6 and Figure 10, and Figure 7 and Figure 11, are the angle curve and angular velocity curve of the simulator, respectively. Figure 8, Figure 9, Figure 12 and Figure 13, show the configuration change inside the combined spacecraft during the attitude maneuver. From Figure 6, Figure 7, Figure 10 and Figure 11, it can be observed that the angle and angular velocity of the simulator converge to the desired states asymptotically. The attitude configuration change can reach nearly during the control process, as shown in Figure 8 and Figure 12. Compared with attitude configuration, the position configuration change in the simulator is relatively small, at about 1 mm, as shown in Figure 9 and Figure 13. In the case of the above configuration changes, the attitude control of the spacecraft still achieves very high accuracy by using the MFC method, as shown in Figure 6, Figure 7, Figure 10 and Figure 11. In addition, we adjusted the initial angle of the simulator and carried out several groups of tests. The test results show that model-free control algorithm can also achieve a good control effect, if the energy of the actuator is sufficient. That is, the control effect is independent of the initial state of the system.
The position maneuver control experimental results are shown in Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21. Figure 14 and Figure 18, and Figure 15 and Figure 19, show the position curve and velocity curve of the simulator, respectively. Figure 16, Figure 17, Figure 20 and Figure 21, show the configuration change inside the combined spacecraft during the position maneuver. As shown in Figure 14, Figure 15, Figure 18 and Figure 19, the position control of combined spacecraft is achieved by using the control and optimization method proposed in this paper, in the case of measurement errors in individual data. Furthermore, during the position maneuver control, the simulator has a configuration change. The maximum angle configuration change can reach nearly . From the above experimental results, the effectiveness of the application of the MFC and optimization method to the operation of PCCS is proved.
According to the ground test results, the advantage of MFC in spacecraft attitude and orbit control is its fault tolerance. That is, even if the measured data is distorted at a certain time, the control curve is still smooth and good control effect can be achieved finally. In contrast, the weaknesses of MFC is that it has many parameters, which makes it difficult to achieve a good control effect. As shown in Figure 6 and Figure 10, the attitude curve has overshoot, and this is a result of non-optimal parameter selection. To solve this problem, our next work is to design an adaptive parameter adjustment algorithm to achieve the optimal control effect of MFC.
6. Conclusions
The application of the MFC method to the attitude and orbital operation of the PCCS was proved in this paper. Two innovations were proposed in this paper. First, the standardized expression form of the MIMO system for the attitude and orbital dynamics of PCCS was presented. Then, an initial value online optimization method for the data mapping model was provided. From the experimental results, the feasibility of the control and optimization method proposed has been verified in this paper. The experimental results show that the model-free data-driven control method can achieve accurate attitude and orbit operation of PCCS by using input and output data, in cases where the dynamic model of PCCS is difficult to construct. Even when there are measurement errors in individual data, the controller still works well. Due to the lack of output capacity in the current simulator’s actuators, the experimental results in this paper have been achieved under a small range of configuration changes. Next, we will replace the actuator with a larger output to verify the effectiveness of the MFC method under a wide range of configuration changes.
Author Contributions
Conceptualization, T.S. and Z.Z.; methodology, T.S. and Y.G.; software, T.S. and Z.Z.; validation, T.S.; formal analysis, Y.G.; investigation, Y.G.; resources, J.Y.; data curation, J.Y.; writing—original draft preparation, T.S.; writing—review and editing, T.S. and Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number: 62003269.
Data Availability Statement
Not applicable.
Acknowledgments
We would like to thank the Shanghai Key Laboratory of Space Intelligent Control Technology for providing the data used in the model tests described in this paper.
Conflicts of Interest
We confirm that this manuscript has not been published elsewhere and is not under consideration by another journal. All authors have approved the manuscript and agree with its submission to Aerospace.
Nomenclature
Abbreviations and defining variables in this paper are summarized in the following table.
| MFC | Model-free control |
| PCCS | Post-capture combination spacecraft |
| MIMO | Multiple input and multiple output |
| PDD | Pseudo-partial derivative |
| Mass of PCCS | |
| Position vector of PCCS | |
| Gravitational constant | |
| Control force of PCCS | |
| Attitude quaternion of PCCS | |
| Estimated value of | |
| Real part of | |
| , | Parameters of MFC |
| Vector part of | |
| Angular velocity of PCCS | |
| Third-order identity matrix | |
| Moment of inertia matrix of PCCS | |
| Disturbing force of PCCS | |
| Disturbing torque of PCCS | |
| Translational velocity of PCCS | |
| Control torque of PCCS | |
| System output at time k | |
| System input at time k | |
| PDD at time k | |
| Desired system output | |
| , | Parameters of PDD |
| , | Pseudo-orders |
References
- Reintsema, D.; Thaeter, J.; Rathke, A.; Naumann, W.; Rank, P.; Sommer, J. DEOS—The German Robotics Approach to Secure and De-Orbit Malfunctioned Satellites from Low Earth Orbits; I-SAIRAS: Sapporo, Japan, 2010. [Google Scholar]
- Louembet, C.; Arzelier, D.; Deaconu, G. Robust rendezvous planning under maneuver execution errors. J. Guid. Control Dyn. 2015, 38, 76–92. [Google Scholar] [CrossRef]
- Abiko, S.; Hirzinger, G. An adaptive control for a free-floating space robot by using inverted chain approach. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007. [Google Scholar]
- Sandberg, A.; Sands, T. Autonomous trajectory generation algorithms for spacecraft slew maneuvers. Aerospace 2022, 9, 135. [Google Scholar] [CrossRef]
- Raigoza, K.; Sands, T. Autonomous trajectory generation comparison for de-orbiting with multiple collision avoidance. Sensors 2022, 22, 7066. [Google Scholar] [CrossRef] [PubMed]
- Nenchev, D.; Yoshida, K. Impact analysis and post-impact motion control issues of a free-floating space robot subject to a force impulse. IEEE Trans. Robot. Autom. 1999, 15, 548–557. [Google Scholar] [CrossRef]
- Jiao, C.; Liang, B.; Wang, X. Adaptive reaction null-space control of dual-arm space robot for post-capture of non-cooperative target. In Proceedings of the 29th Chinese Control and Decision Conference, Chongqing, China, 28–30 May 2017. [Google Scholar]
- Chen, T.; Wen, H.; Hu, H.; Jin, D. Output consensus and collision avoidance of a team of flexible spacecraft for on-orbit autonomous assembly. Acta Astronaut. 2016, 121, 271–281. [Google Scholar] [CrossRef]
- Stastny, T.; Garcia, G.; Keshmiri, S. Collision and obstacle avoidance in unmanned aerial systems using morphing potential field navigation and nonlinear model predictive control. J. Dyn. Syst. Meas. Control. 2015, 137, 014503-1. [Google Scholar] [CrossRef]
- Falconi, R.; Sabattini, L.; Secchi, C.; Fantuzzi, C.; Melchiorri, C. Edge-weighted consensus-based formation control strategy with collision avoidance. Robotica 2015, 33, 332–347. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, W.; Wu, X.; Song, T.; Xie, Y.; Zhao, H. In-space structural assembly using predefined performance based method. J. Aerosp. Eng. 2020. ahead-of-print. [Google Scholar] [CrossRef]
- Oh, K.; Park, M.; Ahn, H. A survey of multi-agent formation control. Automatica 2015, 53, 424–440. [Google Scholar] [CrossRef]
- Cao, Y.; Yu, W.; Ren, W.; Chen, G. An overview of recent progress in the study of distributed multi-agent coordination. IEEE Trans. Ind. Inform. 2013, 9, 427–438. [Google Scholar] [CrossRef]
- Ginoya, D.; Shendge, P.; Phadke, S. Sliding mode control for mismatched uncertain systems using an extended disturbance observer. IEEE Trans. Ind. Electron. 2014, 61, 1983–1992. [Google Scholar] [CrossRef]
- Mohan, S.; Miller, D. Dynamic control model calculation: A model generation architecture for autonomous on-orbit assembly. J. Spacecr. Rocket. 2014, 51, 1430–1453. [Google Scholar] [CrossRef]
- Maybeck, P.; Stevens, R. Reconfigurable flight control via multiple model adaptive control methods. IEEE Aerosp. Electron. Syst. Mag. 1991, 27, 470–480. [Google Scholar] [CrossRef]
- She, Y.; Sun, J.; Li, S.; Li, W.; Song, T. Quasi-model free control for the post-capture operation of a non-cooperative target. Acta Astronaut. 2018, 147, 59–70. [Google Scholar] [CrossRef]
- Nguyen-Huynh, T.; Sharf, I. Adaptive Reactionless motion and parameter identification in postcapture of space debris. J. Guid. Control Dyn. 2013, 36, 404–414. [Google Scholar] [CrossRef]
- Norman, M.; Peck, M.; O’shaughnessy, D. In-orbit estimation of inertia and momentum-actuator alignment parameters. J. Guid. Control Dyn. 2011, 34, 1798–1814. [Google Scholar] [CrossRef]
- Mortari, D.; Markley, F.; Singla, P. Optimal linear attitude estimator. J. Guid. Control Dyn. 2007, 30, 1619–1627. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Chung, S. Nonlinear attitude control of spacecraft with a large captured object. J. Guid. Control Dyn. 2016, 39, 754–769. [Google Scholar] [CrossRef]
- Thienel, J.; Luquette, R.; Sanner, R. Estimation of spacecraft inertia parameters. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, HI, USA, 18–21August 2008. [Google Scholar]
- Crassidis, J.; Markley, F.; Cheng, Y. Survey of nonlinear attitude estimation methods. J. Guid. Control Dyn. 2007, 30, 12–28. [Google Scholar] [CrossRef]
- Hou, Z.; Wang, Z. From model-based control to data-driven control: Survey, classification and perspective. Inf. Sci. 2013, 235, 3–35. [Google Scholar] [CrossRef]
- Bu, X.; Hou, Z. The robust stability of model free adaptive control with data dropouts. In Proceedings of the IEEE International Conference on Control and Automation, Xiamen, China, 9–11 June 2010. [Google Scholar]
- Wang, Z.; Behal, A.; Marzocca, P. Model-free control design for multi-input multi-output aeroelastic system subject to external disturbance. J. Guid. Control Dyn. 2011, 34, 446–457. [Google Scholar] [CrossRef]
- Vikas, V.; Grover, P.; Trimmer, B. Model-free control framework for multi-limb soft robots. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Hamburg, Germany, 28 September–2 October 2015. [Google Scholar]
- Gao, H.; Ma, G.; Lv, Y.; Guo, Y. Forecasting-based data-driven model-free adaptive sliding mode attitude control of combined spacecraft. Aerosp. Sci. Technol. 2019, 86, 364–374. [Google Scholar] [CrossRef]
- Han, G.A.O.; Guangfu, M.A.; Yueyong, L.Y.U.; Yanning, G.U.O. Data-driven model-free adaptive attitude control of partially constrained combined spacecraft with external disturbances and input saturation. Chin. J. Aeronaut. 2019, 32, 1281–1293. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).