Surrogate Aerodynamic Wing Modeling Based on a Multilayer Perceptron
Abstract
:1. Introduction
2. Materials and Methods
2.1. Design Space and Output Data Determination
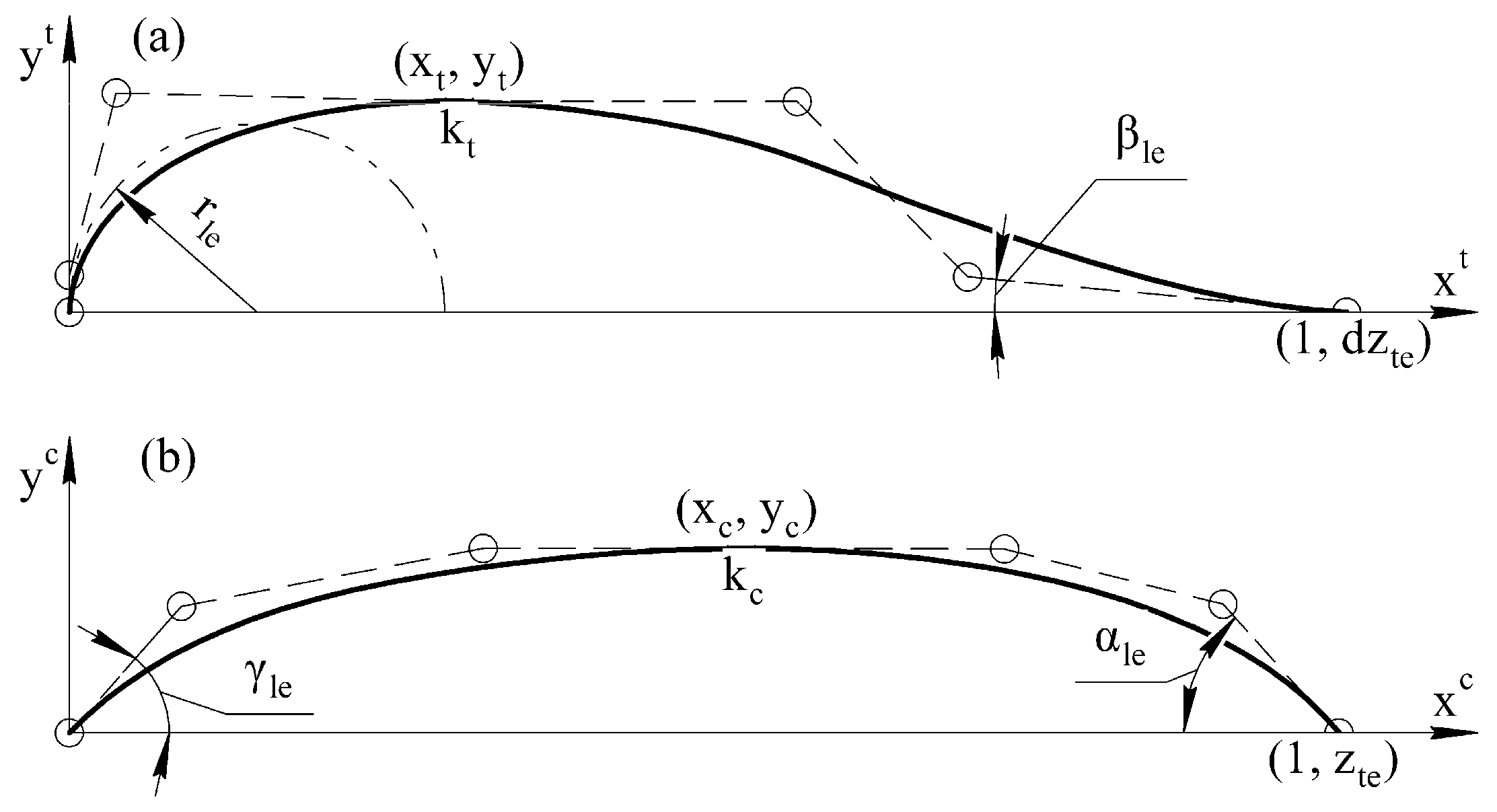
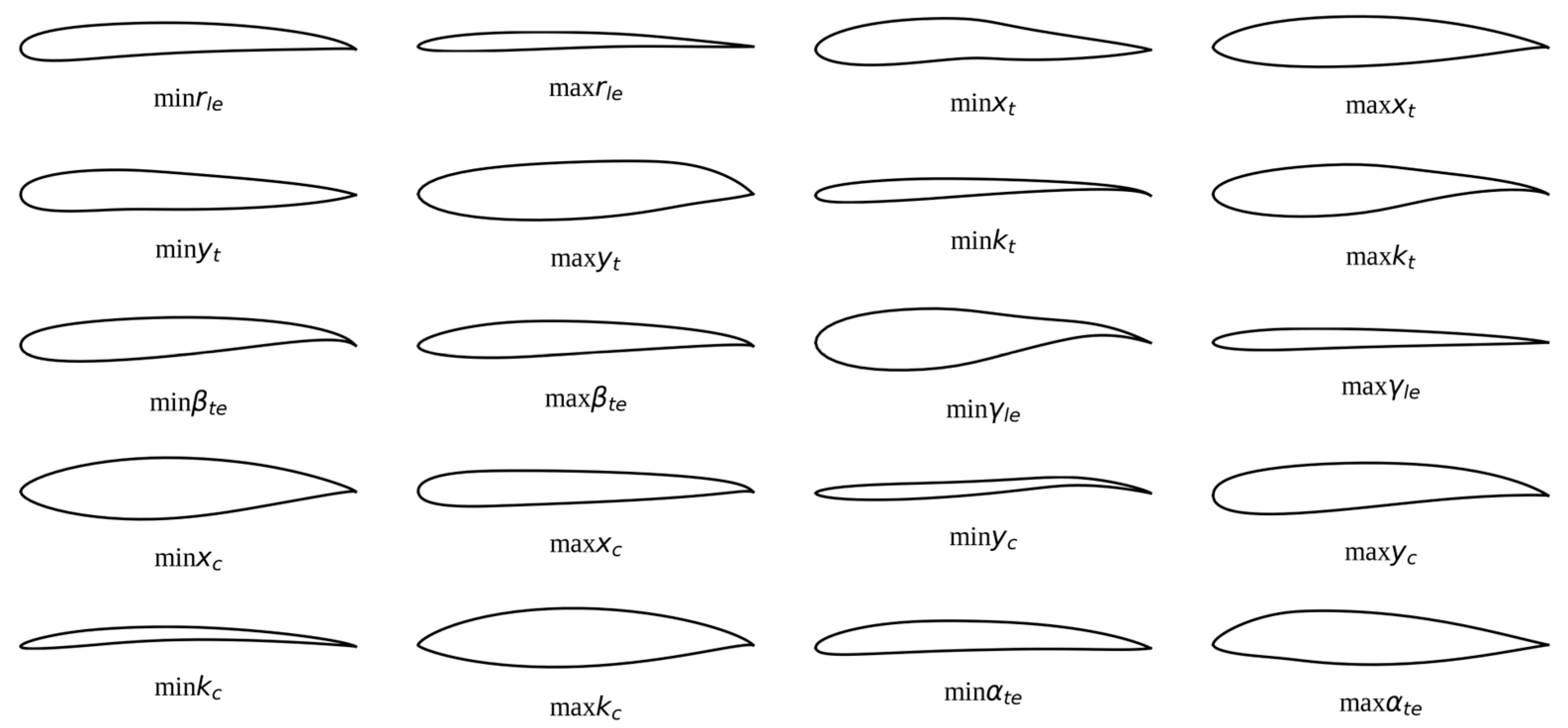
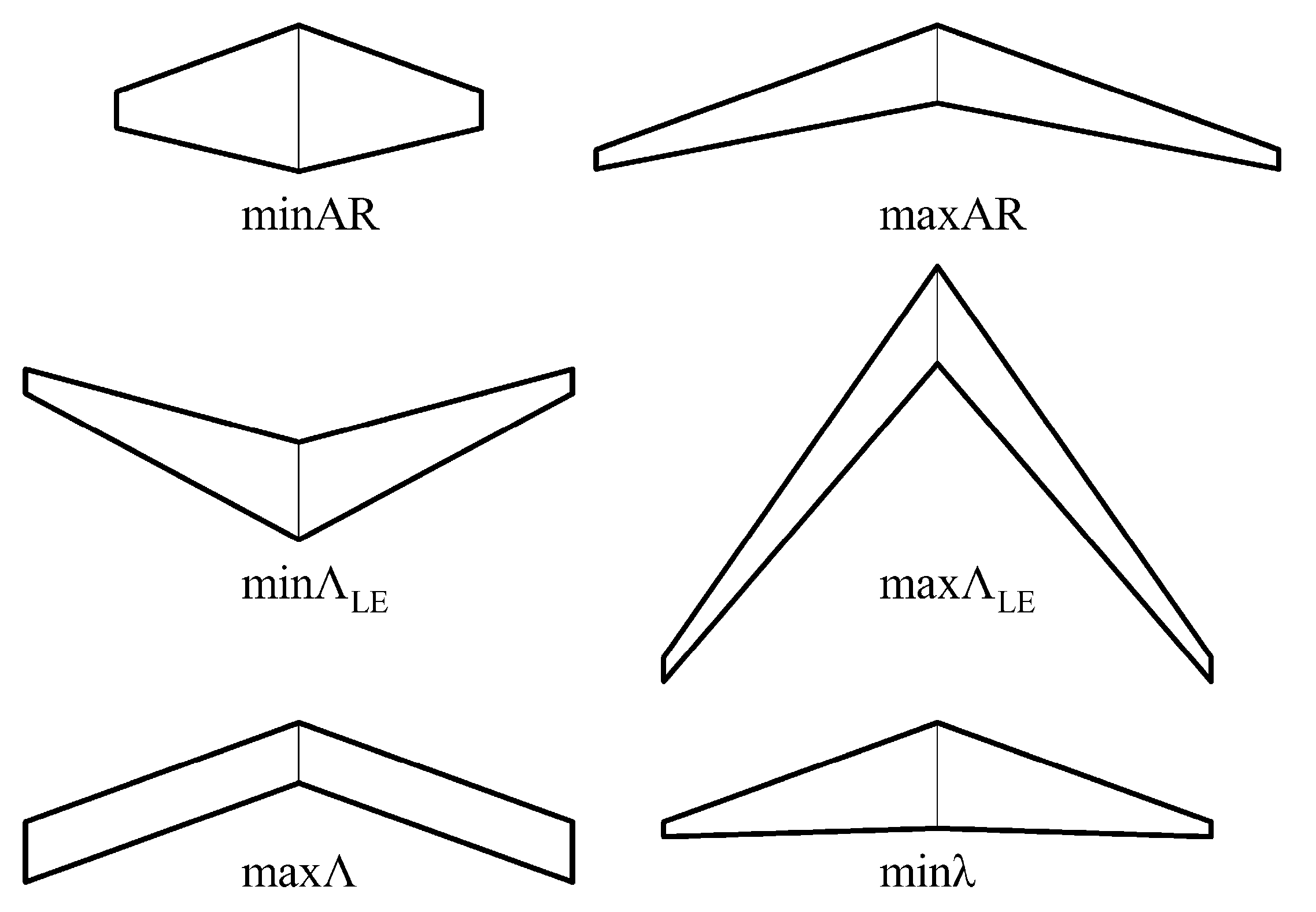
2.1.1. Design Variables
2.1.2. Aerodynamic Coefficient Calculation
2.2. Verification of the Aerodynamic Mathematical Model
2.2.1. Databases Creation
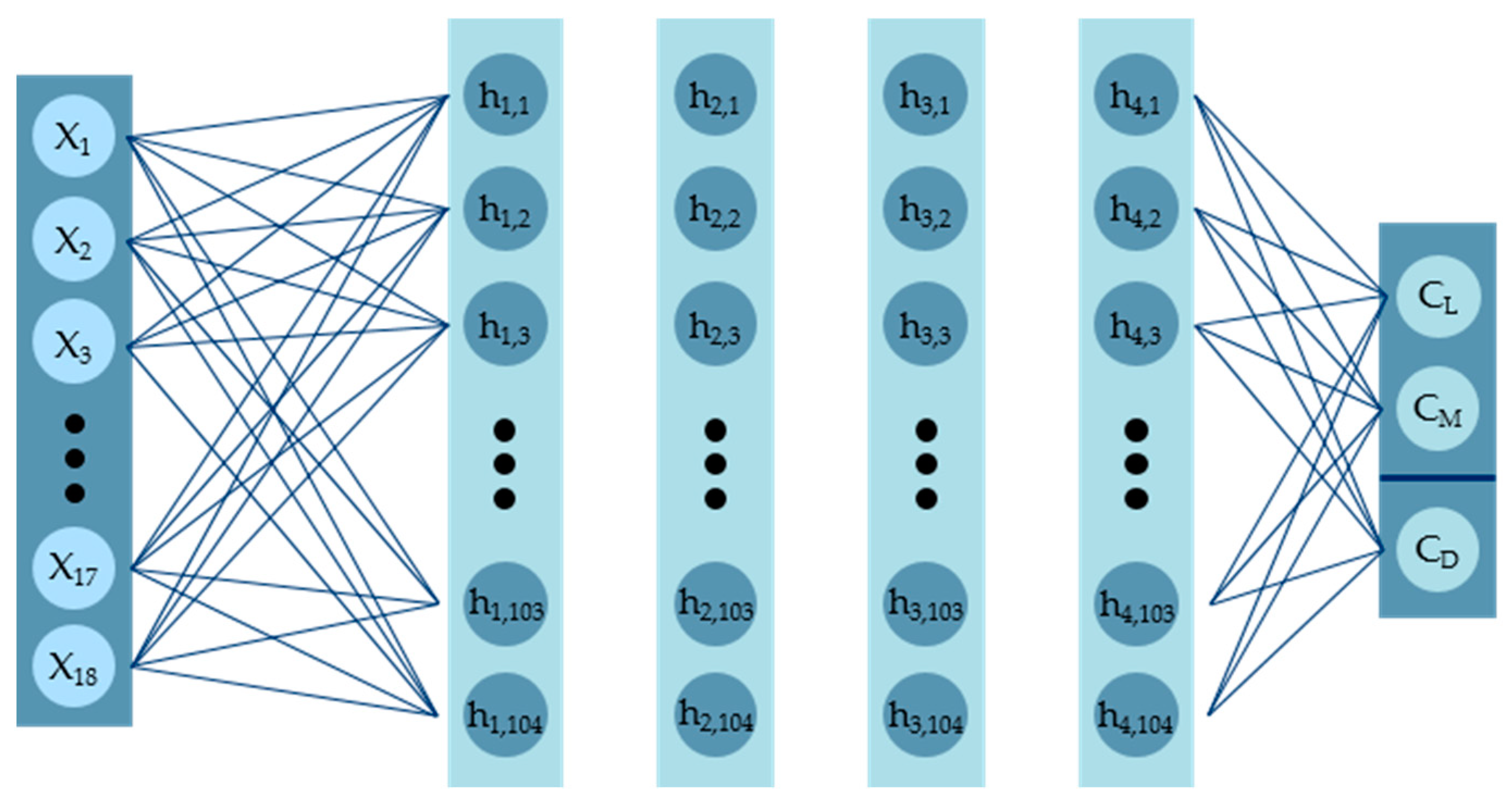
2.2.2. MLP Hyperparameters Determination
- The activation function for all hidden layers was the rectified linear unit (RELU) function due to its computational simplicity and effectiveness in handling of vanishing gradients [9].
- The output layer was composed of two concatenated layers with different activation functions: the first sublayer was composed of a neuron (CD) with the exponential linear unit (ELU) function [30], which prevents predictions from being less than zero; this is of extreme importance, since physically, the CD value is never less than zero. The second sublayer is composed of two neurons (CL and CM) with the linear function.
- The mean square error (MSE) was chosen as the loss function, which is commonly used for regression analysis. Since the MSE often refers to the mean squared prediction error or out of the sample mean squared error, it can refer to the mean of the squared deviations of the predictions of the true values, over a space outside the test sample, generated by an estimated model during a particular sample space [9,18,31].
- The optimizer chosen was adaptive moment estimation (Adam), which is an algorithm for first-order gradient-based optimization of stochastic objective functions, based on adaptive estimates of lower-order moments. The method is straightforward to implement, is computationally efficient, has few memory requirements, is invariant to diagonal rescaling of the gradients, and is well suited for problems that are large in terms of data and/or parameters. The method is also appropriate for nonstationary objectives and problems with very noisy and/or sparse gradients [32].
- The learning rate was fixed at 0.001, predetermined by the Adam optimizer function in Keras [33].
- A batch size of 20 was chosen for all evaluations, as is not expected to use very large database sizes (above the order of 104).
- The number of hidden layers was determined by evaluating five architectures, ranging from one to five hidden layers. Each architecture was assigned 64 neurons per layer.
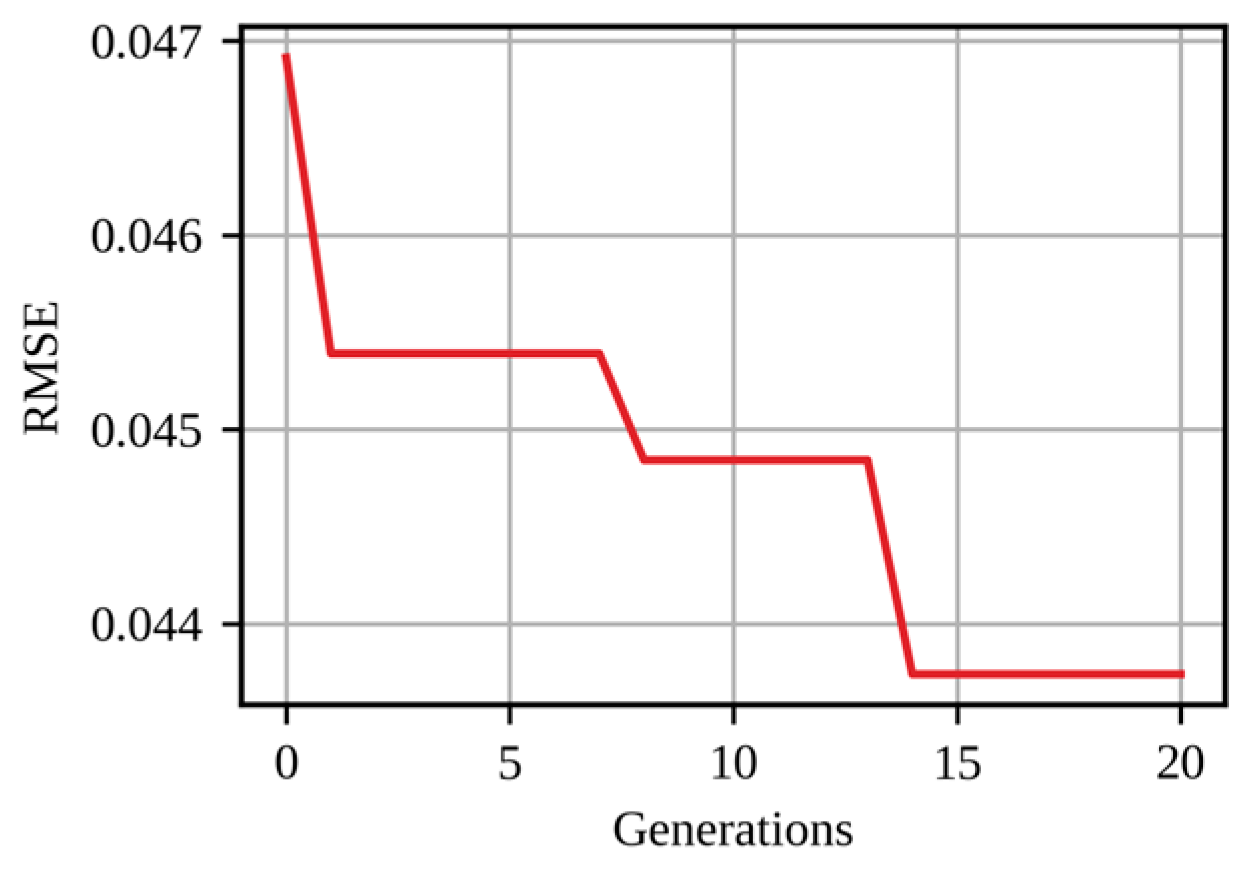
- To define the number of neurons per layer, the integer encoding differential evolution (IEDE) algorithm was used. This algorithm was used because it uses integer variables. The number of variables corresponds to the number of hidden layers obtained in the previous process. The IEDE algorithm, like the DE algorithm, consists of three evolutionary operators: mutation, crossover, and selection. These operators can be observed in more detail in Algorithm A1 [20], which is provided in Appendix A. The mutation operator operates with a scale factor (F) of 0.85, while the crossover operator requires a crossover constant (CR) of 0.85. Other initial parameters of the algorithm include: number of variables (D), which is based on the number of hidden layers determined in the previous process; the design interval of each variable ([Dmin, Dmax]) [9,16]; the population size of each generation (N), which was set to 10 times the number of variables; the cost function to be minimized (f), defined by the average RSME value provided by the k-fold cross-validation method; and the stopping condition, which was set as a limit of 20 generations (G = 20).
3. Results and Discussion
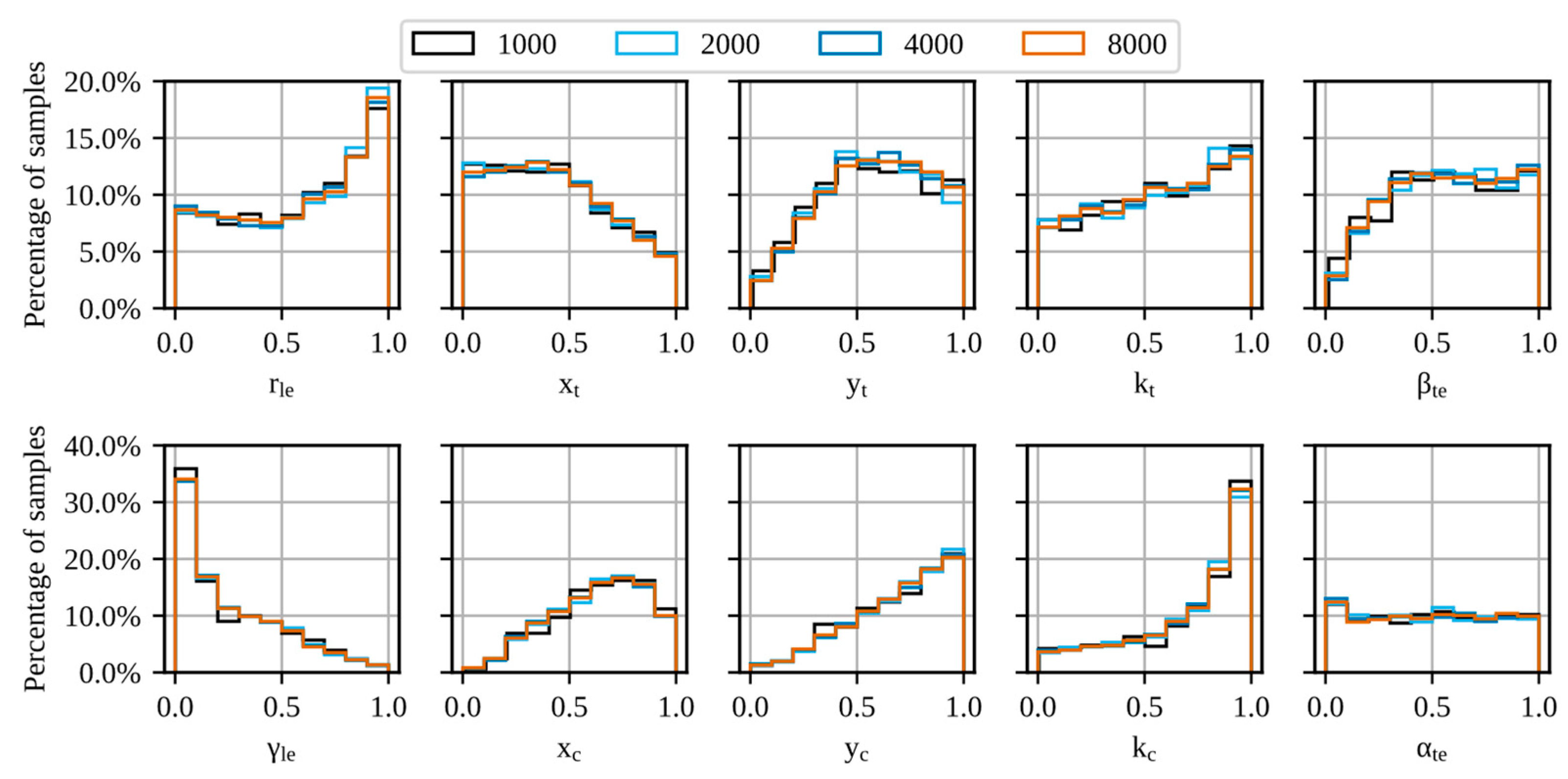
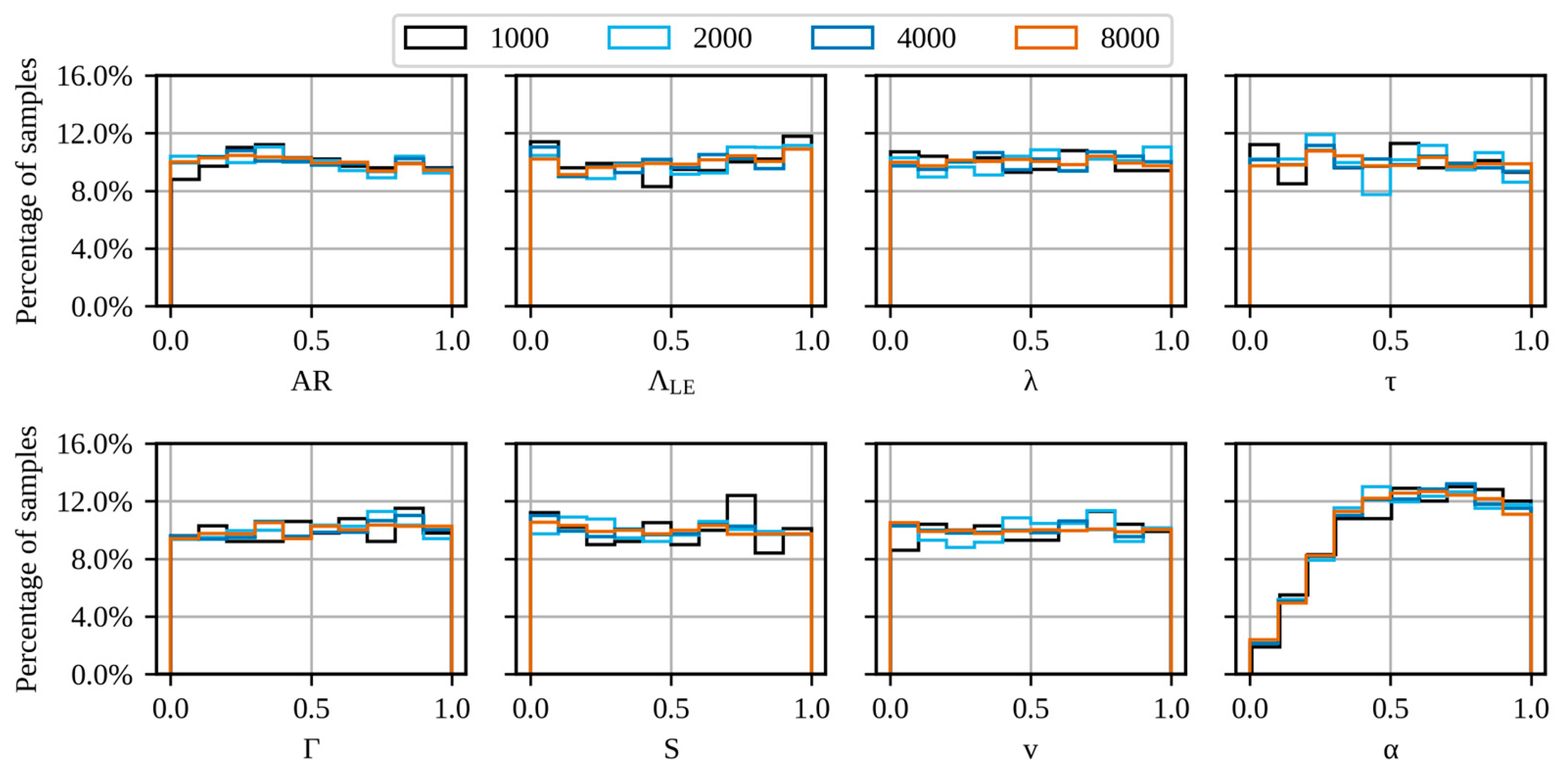
3.1. Databases
3.2. Hidden Layers Determination
3.3. Neurons Number Determination
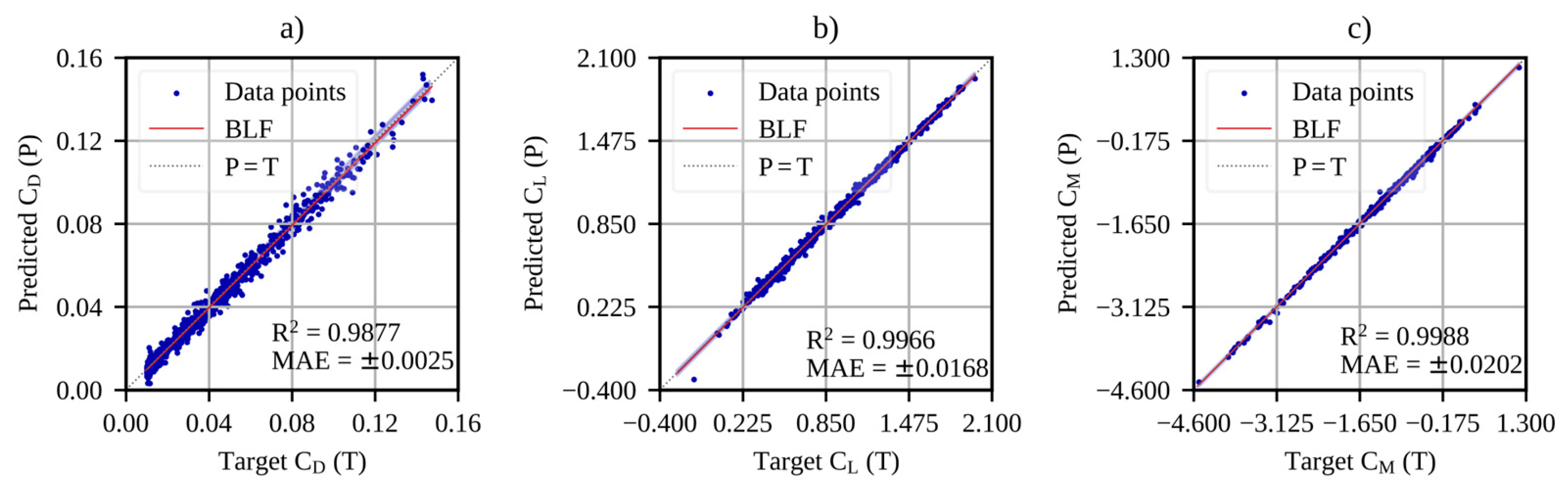
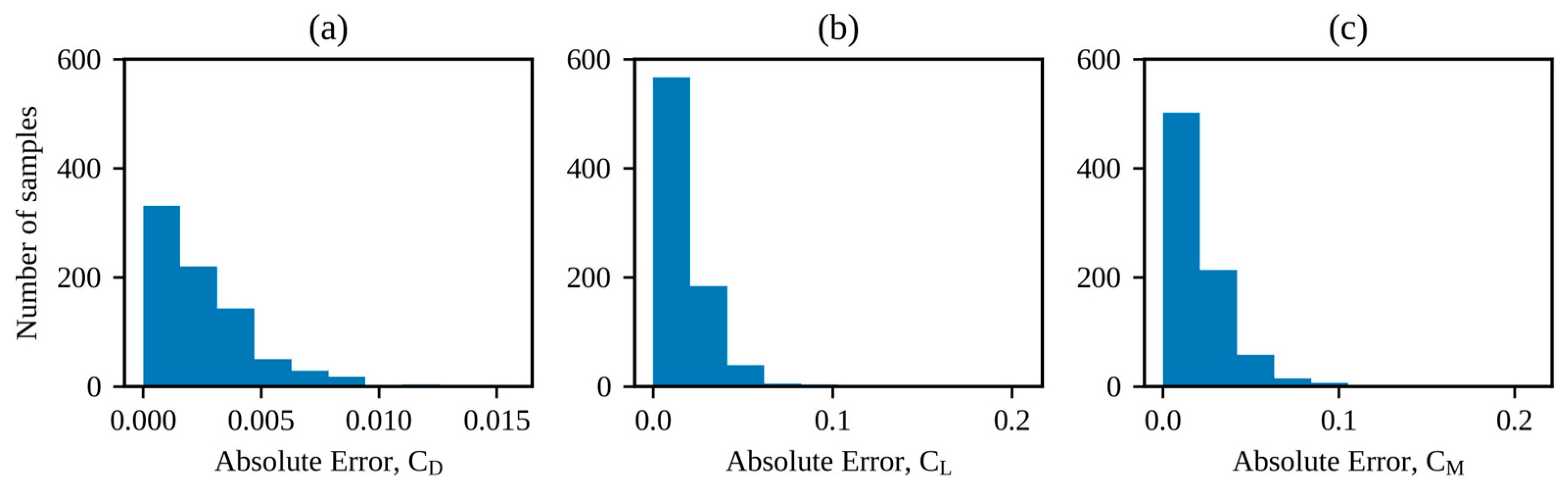
3.4. MLP Performance with Different Database Sizes
3.5. Computing Performance
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Algorithm A1. IEDE algorithm. |
| Input: N, d, [Dmin, Dmax], F, CR, G |
| Output: xopt, fopt |
| Initialize the population randomly Pg = P(randint(x1,g,…,xN,g)); Calculate f(x1,g,…,xN,g) with k-fold cross-validation method for g = 1 to G do for i = 1 to N do //Mutation Choosing xr1, xr2 and xr3 vectors randomly from Pg without replacement; δ = F (xr2 – xr3); for j = 1 to D do if rand() < δj – int ↑ (δj) then vj,i,g = xj,r1 + int ↑ (δj); else vj,i,g = xj,r1 + int ↓ (δj); end if end for end for for i = 1 to N do //Crossover for j = 1 to d do if rand() < CR or j == randint([0, d]) then uj,i,g = vj,i,g; else uj,i,g = xj,i,g; end if end for end for Calculate f(u1,g,…,uN,g) with k-fold cross-validation method; for i = 1 to N do //Selection if f(ui,g) ≤ f(xi,g) then xi,g+1 = ui,g; else xi,g + 1 = xi,g; end if end for end for |
References
- Poghosyan, M.; Liseytsev, N.; Strelets, D.; Kiselev, V.; Tarasov, A.; Dolgov, O.; Dudar, E.; Timoshenko, V.; Eremin, N.; Penkov, E.; et al. Aircraft Design, 5th ed.; Pogosyan, M., Liseytsev, N., Strelets, D., Eds.; Innovatsionnoye Mashinostroyeniye: Moscow, Russia, 2018; ISBN 978-5-6040281-5-5. [Google Scholar]
- Roskam, J. Airplane Design. Part V: Component Weight Estimation; DARcorporation: Lawrence, KS, USA, 2018; ISBN 9781884885693. [Google Scholar]
- Torenbeek, E. Advanced Aircraft Design: Conceptual Design, Technology and Optimization of Subsonic Civil Airplanes; Wiley: Hoboken, NJ, USA, 2013; ISBN 978-1-118-56811-8. [Google Scholar]
- Keane, A.J.; Nair, P.B. Computational Approaches for Aerospace Design: The Pursuit of Excellence; Wiley: Hoboken, NJ, USA, 2005; ISBN 0470855401. [Google Scholar]
- Martins, J.R.R.A. Aerodynamic Design Optimization: Challenges and Perspectives. Comput. Fluids 2022, 239, 105391. [Google Scholar] [CrossRef]
- Schulz, V.; Schillings, C. Optimal Aerodynamic Design under Uncertainty. In Management and Minimisation of Uncertainties and Errors in Numerical Aerodynamics: Results of the German Collaborative Project MUNA; Eisfeld, B., Barnewitz, H., Fritz, W., Thiele, F., Eds.; Springer Berlin: Berlin, Germany, 2013; pp. 297–338. ISBN 978-3-642-36185-2. [Google Scholar]
- Peng, X.; Zhu, H.; Xu, D.; Xiao, M.; Wang, W.; Cai, G. Aerodynamic Performance Uncertainty Analysis and Optimization of a Conventional Axisymmetric Vehicle Based on Parallel Polynomial Chaos Expansions. Aerospace 2022, 9, 396. [Google Scholar] [CrossRef]
- Mavris, D.N.; Pinon, O.J. An Overview of Design Challenges and Methods in Aerospace Engineering. In Complex Systems Design & Management; Springer Berlin: Berlin, Germany, 2012; pp. 1–25. [Google Scholar]
- Moin, H.; Khan, H.Z.I.; Mobeen, S.; Riaz, J. Airfoil’s Aerodynamic Coefficients Prediction Using Artificial Neural Network. arXiv 2021, arXiv:2109.12149v1. [Google Scholar]
- Balla, K.; Sevilla, R.; Hassan, O.; Morgan, K. An Application of Neural Networks to the Prediction of Aerodynamic Coefficients of Aerofoils and Wings. Appl. Math. Model 2021, 96, 456–479. [Google Scholar] [CrossRef]
- Huang, S.; Miller, L.; Steck, J. An Exploratory Application of Neural Networks to Airfoil Design; American Institute of Aeronautics and Astronautics (AIAA): Reston, VA, USA, 1994. [Google Scholar]
- Sun, G.; Sun, Y.; Wang, S. Artificial Neural Network Based Inverse Design: Airfoils and Wings. Aerosp. Sci. Technol. 2015, 42, 415–428. [Google Scholar] [CrossRef]
- Yang, S.; Lee, S.; Yee, K. Inverse Design Optimization Framework via a Two-Step Deep Learning Approach: Application to a Wind Turbine Airfoil. Eng. Comput. 2022. [Google Scholar] [CrossRef]
- Khurana, M.S.; Winarto, H.; Sinha, A.K. Application of Swarm Approach and Artificial Neural Networks for Airfoil Shape Optimization the Direct Numerical Optimization (DNO) Approach for Airfoil Shape Design Requires the Integration of Modules: A) A Geometrical Shape Function; b). In Proceedings of the 12th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Victoria, BC, Canada, 10–12 September 2008. [Google Scholar]
- Bouhlel, M.A.; He, S.; Martins, J.R.R.A. Scalable Gradient–Enhanced Artificial Neural Networks for Airfoil Shape Design in the Subsonic and Transonic Regimes. Struct. Multidiscip. Optim. 2020, 61, 1363–1376. [Google Scholar] [CrossRef]
- Kharal, A.; Saleem, A. Neural Networks Based Airfoil Generation for a given Cp Using Bezier-PARSEC Parameterization. Aerosp. Sci. Technol. 2012, 23, 330–344. [Google Scholar] [CrossRef]
- Secco, N.R.; de Mattos, B.S. Artificial Neural Networks to Predict Aerodynamic Coefficients of Transport Airplanes. Aircr. Eng. Aerosp. Technol. 2017, 89, 211–230. [Google Scholar] [CrossRef]
- Elgeldawi, E.; Sayed, A.; Galal, A.R.; Zaki, A.M. Hyperparameter Tuning for Machine Learning Algorithms Used for Arabic Sentiment Analysis. Informatics 2021, 8, 79. [Google Scholar] [CrossRef]
- Hu, L.; Zhang, J.; Xiang, Y.; Wang, W. Neural Networks-Based Aerodynamic Data Modeling: A Comprehensive Review. IEEE Access 2020, 8, 90805–90823. [Google Scholar] [CrossRef]
- Deng, C.; Zhao, B.; Yang, Y.; Deng, A. Integer Encoding Differential Evolution Algorithm for Integer Programming. In Proceedings of the 2010 2nd International Conference on Information Engineering and Computer Science, Wuhan, China, 25–26 December 2010; pp. 1–4. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Müller, A.; Nothman, J.; Louppe, G.; et al. Scikit-Learn: Machine Learning in Python. arXiv 2012. [Google Scholar] [CrossRef]
- Derksen, R.W.; Rogalsky, T. Bezier-PARSEC: An Optimized Aerofoil Parameterization for Design. Adv. Eng. Softw. 2010, 41, 923–930. [Google Scholar] [CrossRef]
- Drela, M.; Youngren, H. MIT AVL User Primer—AVL 3.36 1–43. Available online: https://web.mit.edu/drela/Public/web/avl/ (accessed on 5 February 2023).
- Kholyavko, V. Calculation of the Aerodynamic Characteristics of the Aircraft. Part 1; Kharkiv Aviation Institute: Kharkiv, Ukraine, 1991. [Google Scholar]
- Espinosa Barcenas, O.U.; Quijada Pioquinto, J.G.; Kurkina, E.; Lukyanov, O. Multidisciplinary Analysis and Optimization Method for Conceptually Designing of Electric Flying-Wing Unmanned Aerial Vehicles. Drones 2022, 6, 307. [Google Scholar] [CrossRef]
- Anderson, R.F. Determination of the Characteristics of Tapered Wings; National Advisory Committee for Aeronautics: Boston, MA, USA, 1937.
- Quijada Pioquinto, J.G.; Shakhov, V. Acceleration of Evolutionary Optimization for Airfoils Design with Population Size Reduction Methods. In Proceedings of the 20th International Conference “Aviation and Cosmonautics”, Samara, Russia, 22–26 November 2021. [Google Scholar]
- Selig, M. UIUC Airfoil Data Site. Available online: https://m-selig.ae.illinois.edu/ads/coord_database.html (accessed on 5 May 2022).
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 1979, 21, 239. [Google Scholar] [CrossRef]
- Clevert, D.-A.; Unterthiner, T.; Hochreiter, S. Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs). arXiv 2015, arXiv:1511.07289v5. [Google Scholar]
- Quadros, J.D.; Khan, S.A.; Aabid, A.; Alam, M.S.; Baig, M. Machine Learning Applications in Modelling and Analysis of Base Pressure in Suddenly Expanded Flows. Aerospace 2021, 8, 318. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980v9. [Google Scholar]
- Chollet, F. Others Keras. 2015. Available online: https://github.com/fchollet/keras (accessed on 5 February 2023).
- Berrar, D. Cross-Validation. In Encyclopedia of Bioinformatics and Computational Biology; Elsevier: Amsterdam, The Netherlands, 2019; pp. 542–545. [Google Scholar]
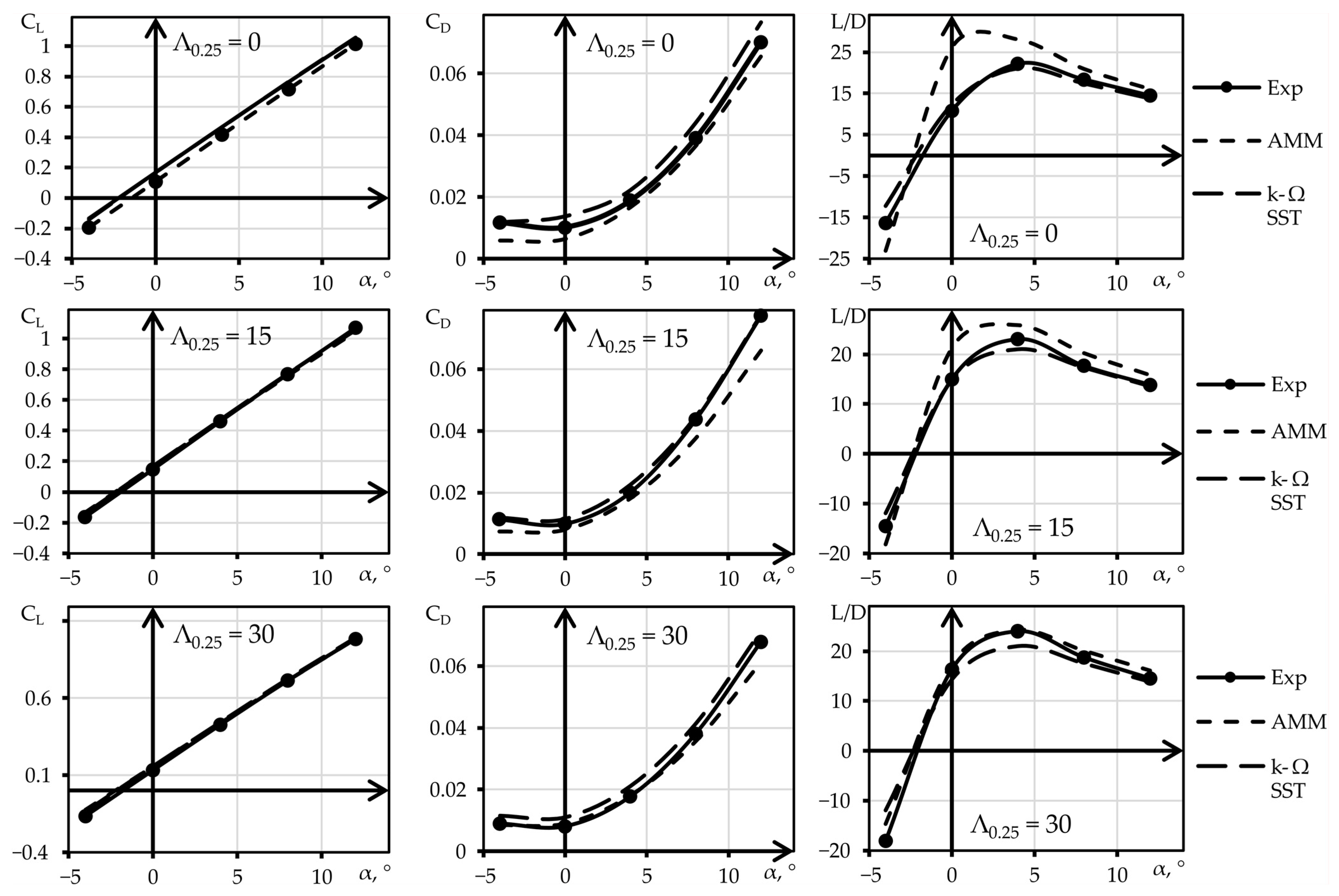


| Aerodynamic Characteristic | MAE | |
|---|---|---|
| AMM | k-Ω SST | |
| CL | 0.029 | 0.008 |
| CD | 0.003139 | 0.006074 |
| L/D | 3.29 | 4.73 |
| Specifications | |
|---|---|
| Processor | Intel® CoreTM i7-6700 CPU @ 3.40 GHz x 8 |
| Memory | 62 GB RAM |
| Hard disk | 500 GB |
| Operating system | GNU/Linux Ubuntu 20.04.4 LTS |
| BP3333 Parameter | Interval |
|---|---|
| rle | [−0.05, −0.001] |
| xt | [0.2, 0.45] |
| yt | [0.02, 0.12] |
| kt | [−0.9, −0.2] |
| βte | [0.01, 0.4] |
| γle | [0.002, 0.04] |
| xc | [0.2, 0.85] |
| yc | [0.005, 0.07] |
| kc | [−1.75, −0.025] |
| αte | [0.002, 0.7] |
| Wing Geometric Characteristics and Flight Conditions | Interval |
|---|---|
| AR | [4, 14] |
| ΛLE, ° | [−15, 55] |
| λ | [0.143, 1] |
| τ, ° | [−5, 2] |
| Γ, ° | [−3, 9] |
| S, m2 | [10, 100] |
| v, m/s | [10, 204] |
| α, ° | [−5, 15] |
| Specifications | |
|---|---|
| Processor | Intel® CoreTM i9−9940 CPU @ 3.30 GHz x 14 |
| Memory | 125 GB RAM |
| Hard disk | 2 TB |
| Operating system | GNU/Linux Ubuntu 18.04.5 LTS |
| Architecture | MSE | RMSE | R2 | ||
|---|---|---|---|---|---|
| CD | CL | CM | |||
| 18-64-3 | 0.0056 | 0.0750 ±0.0279 | 0.8621 ±0.0944 | 0.9503 ±0.0355 | 0.9760 ±0.0106 |
| 18-64-64-3 | 0.0028 | 0.0525 ±0.0291 | 0.9287 ±0.0389 | 0.9776 ±0.0119 | 0.9877 ±0.0081 |
| 18-64-64-64-3 | 0.0023 | 0.0483 ±0.0272 | 0.8987 ±0.0573 | 0.9777 ±0.0136 | 0.9899 ±0.0071 |
| 18-64-64-64-64-3 | 0.0022 | 0.0479 ±0.0202 | 0.9192 ±0.0348 | 0.9809 ±0.0137 | 0.9899 ±0.0097 |
| 18-64-64-64-64-64-3 | 0.0026 | 0.0514 ±0.0207 | 0.9205 ±0.0357 | 0.9720 ±0.0178 | 0.9911 ±0.0060 |
| Database Size | MSE | RMSE | R2 | ||
|---|---|---|---|---|---|
| CD | CL | CM | |||
| 1000 | 0.0019 | 0.0438 ±0.0200 | 0.9527 ±0.0193 | 0.9842 ±0.0101 | 0.9911 ±0.0080 |
| 2000 | 0.0015 | 0.0387 ±0.0161 | 0.9609 ±0.0167 | 0.9866 ±0.0102 | 0.9919 ±0.0081 |
| 4000 | 0.0009 | 0.0304 ±0.0096 | 0.9772 ±0.0097 | 0.9916 ±0.0043 | 0.9961 ±0.0026 |
| 8000 | 0.0010 | 0.0325 ±0.0091 | 0.9733 ±0.0105 | 0.9916 ±0.0028 | 0.9960 ±0.0022 |
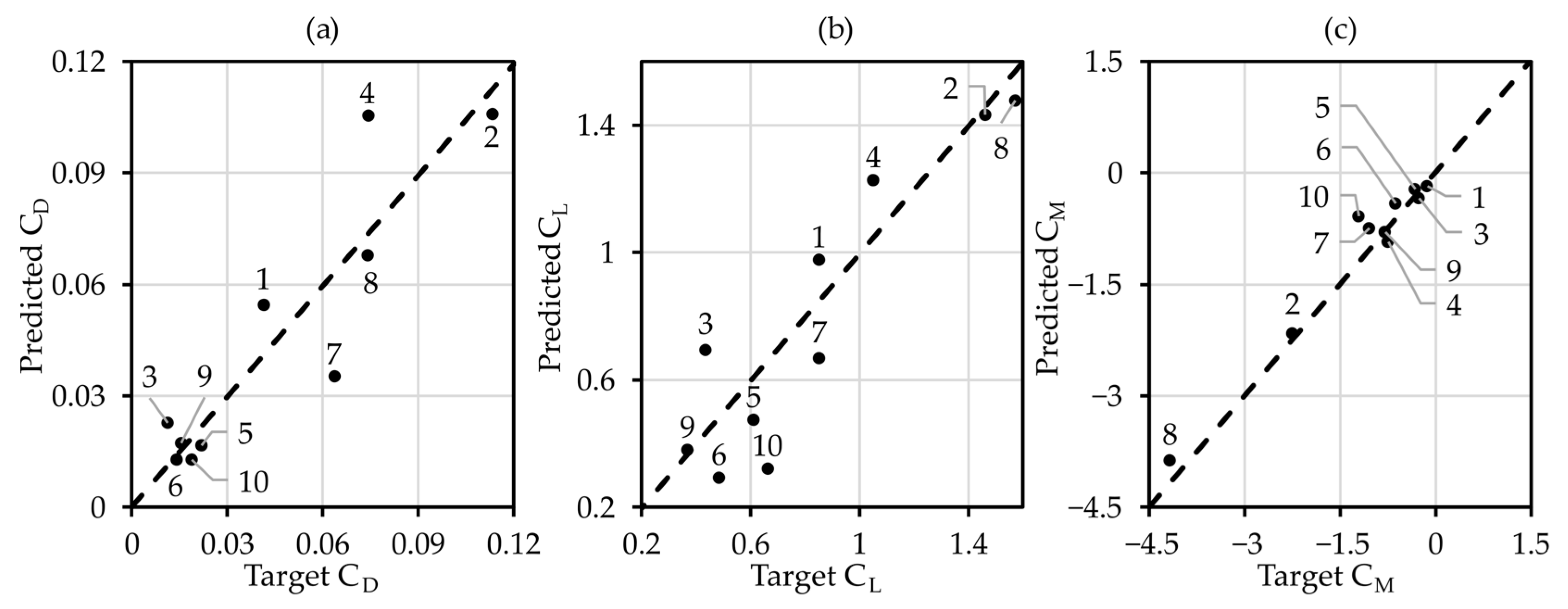
| № | Top View | AR | Leading-Edge Sweep Angle, ° | Taper Ratio | Dihedral Angle, ° | Twist Angle, ° | Wing Area, m2 | Velocity, m/s | Angle of Attack, ° |
|---|---|---|---|---|---|---|---|---|---|
| 1 |  | 7.25 | −13.3 | 0.198 | −1.5 | −4.1 | 21.250 | 102.15 | 5.5 |
| 2 |  | 6.75 | 39.3 | 0.377 | 5.1 | 0.8 | 34.750 | 82.75 | 13.5 |
| 3 |  | 11.25 | −2.8 | 0.241 | 3.9 | −4.5 | 12.250 | 24.55 | −0.5 |
| 4 |  | 5.25 | 21.8 | 0.225 | 1.5 | −0.3 | 93.250 | 199.15 | 10.5 |
| 5 |  | 7.75 | 0.8 | 0.187 | −0.9 | 1.1 | 16.750 | 150.65 | 1.5 |
| 6 |  | 9.75 | 18.3 | 0.308 | 8.1 | −3.1 | 39.250 | 131.25 | −1.5 |
| 7 |  | 4.25 | 42.8 | 0.426 | 6.3 | 0.4 | 66.250 | 34.25 | 9.5 |
| 8 |  | 12.25 | 46.3 | 0.168 | −2.1 | −1.0 | 43.750 | 179.75 | 11.5 |
| 9 |  | 6.25 | 53.3 | 0.282 | 7.5 | −2.7 | 97.750 | 121.55 | 2.5 |
| 10 |  | 11.75 | 32.3 | 0.146 | 5.7 | 1.5 | 84.250 | 92.45 | 0.5 |
| № | Airfoil | rle | xt | yt | kt | βte | γle | xc | yc | kc | αte |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 |  | −0.0215 | 0.3617 | 0.0881 | −0.7334 | 0.3685 | 0.0262 | 0.7131 | 0.0396 | −0.6138 | 0.4248 |
| 2 |  | −0.0024 | 0.3507 | 0.0718 | −0.7682 | 0.2899 | 0.0284 | 0.7591 | 0.0264 | −0.4728 | 0.4370 |
| 3 |  | −0.0080 | 0.4172 | 0.0575 | −0.3747 | 0.2516 | 0.1573 | 0.6086 | 0.0362 | −0.0404 | 0.5869 |
| 4 |  | −0.0258 | 0.3511 | 0.0876 | −0.4184 | 0.3482 | 0.0109 | 0.6535 | 0.0274 | −0.7995 | 0.4292 |
| 5 |  | −0.0288 | 0.2210 | 0.0529 | −0.6247 | 0.3999 | 0.0244 | 0.4986 | 0.0304 | −0.5358 | 0.2399 |
| 6 |  | −0.0288 | 0.3406 | 0.0898 | −0.8768 | 0.3973 | 0.0150 | 0.6009 | 0.0368 | −1.0749 | 0.1877 |
| 7 |  | −0.0163 | 0.2560 | 0.0613 | −0.6530 | 0.1533 | 0.0509 | 0.3475 | 0.0296 | −0.6915 | 0.0272 |
| 8 |  | −0.0173 | 0.2731 | 0.0583 | −0.7552 | 0.2224 | 0.0530 | 0.7971 | 0.0231 | −0.0422 | 0.6824 |
| 9 |  | −0.0432 | 0.3069 | 0.0824 | −0.2910 | 0.3548 | 0.0451 | 0.6134 | 0.0246 | −0.0950 | 0.2217 |
| 10 |  | −0.0402 | 0.2757 | 0.0721 | −0.3157 | 0.3554 | 0.0854 | 0.4247 | 0.0395 | −0.8755 | 0.0408 |
| Specifications | Time, s (Table 2 CPU) | Speedup |
|---|---|---|
| AMM simulation for one case | 0.141 | - |
| Training: MLP with k-fold cross validation | 31.315 | - |
| Prediction: Batch size = 10 | 0.135 | 9.47 |
| Prediction: Batch size = 100 | 0.140 | 90.42 |
| Prediction: Batch size = 1000 | 0.159 | 797.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Espinosa Barcenas, O.U.; Quijada Pioquinto, J.G.; Kurkina, E.; Lukyanov, O. Surrogate Aerodynamic Wing Modeling Based on a Multilayer Perceptron. Aerospace 2023, 10, 149. https://doi.org/10.3390/aerospace10020149
Espinosa Barcenas OU, Quijada Pioquinto JG, Kurkina E, Lukyanov O. Surrogate Aerodynamic Wing Modeling Based on a Multilayer Perceptron. Aerospace. 2023; 10(2):149. https://doi.org/10.3390/aerospace10020149
Chicago/Turabian StyleEspinosa Barcenas, Oscar Ulises, Jose Gabriel Quijada Pioquinto, Ekaterina Kurkina, and Oleg Lukyanov. 2023. "Surrogate Aerodynamic Wing Modeling Based on a Multilayer Perceptron" Aerospace 10, no. 2: 149. https://doi.org/10.3390/aerospace10020149
APA StyleEspinosa Barcenas, O. U., Quijada Pioquinto, J. G., Kurkina, E., & Lukyanov, O. (2023). Surrogate Aerodynamic Wing Modeling Based on a Multilayer Perceptron. Aerospace, 10(2), 149. https://doi.org/10.3390/aerospace10020149






