Mass-Conserved Solution to the Ffowcs-Williams and Hawkings Equation for Compact Source Regions
Abstract
:1. Introduction
2. Acoustic Analogy Theory
3. Mass Conserved Formulation
4. Results and Discussion
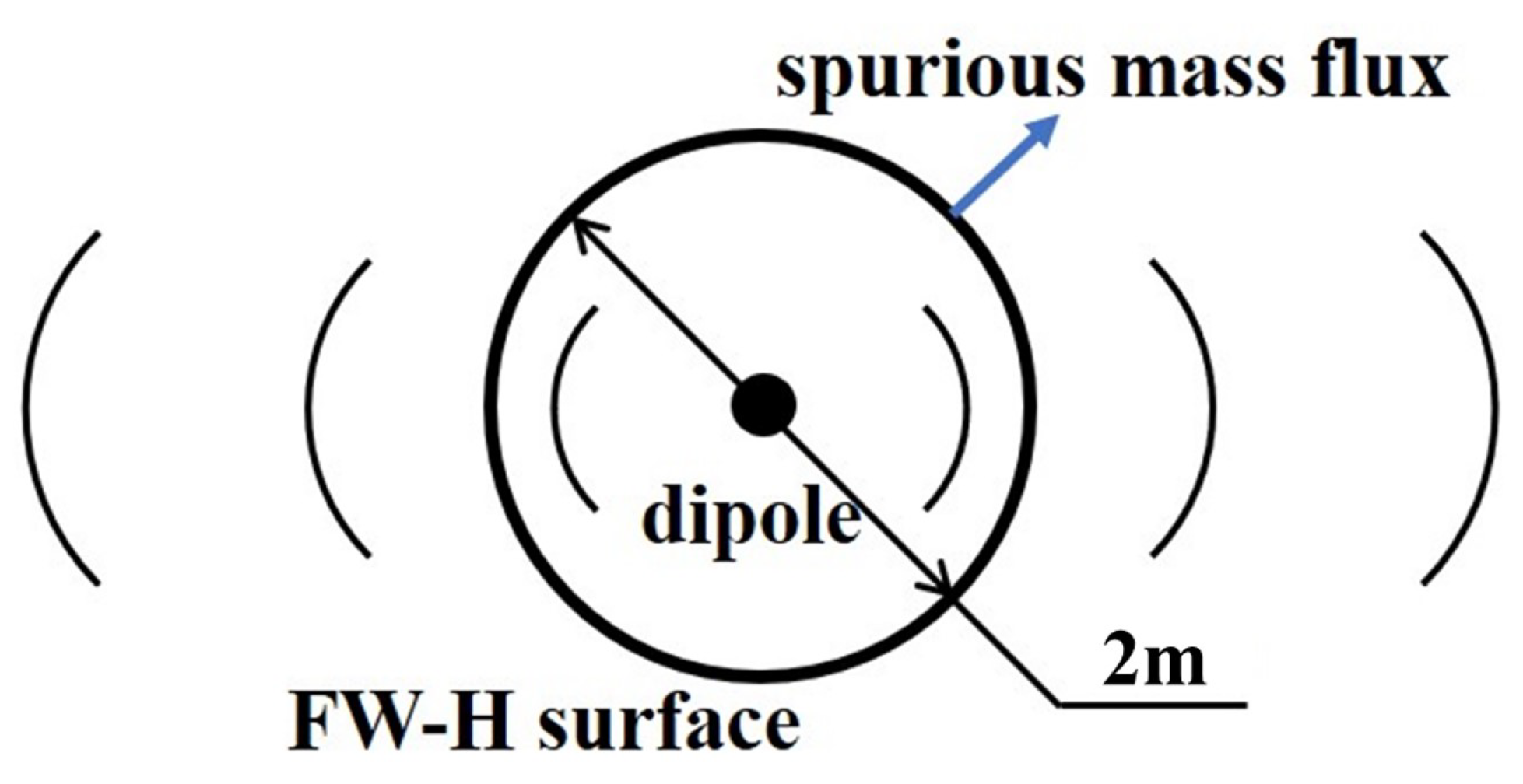
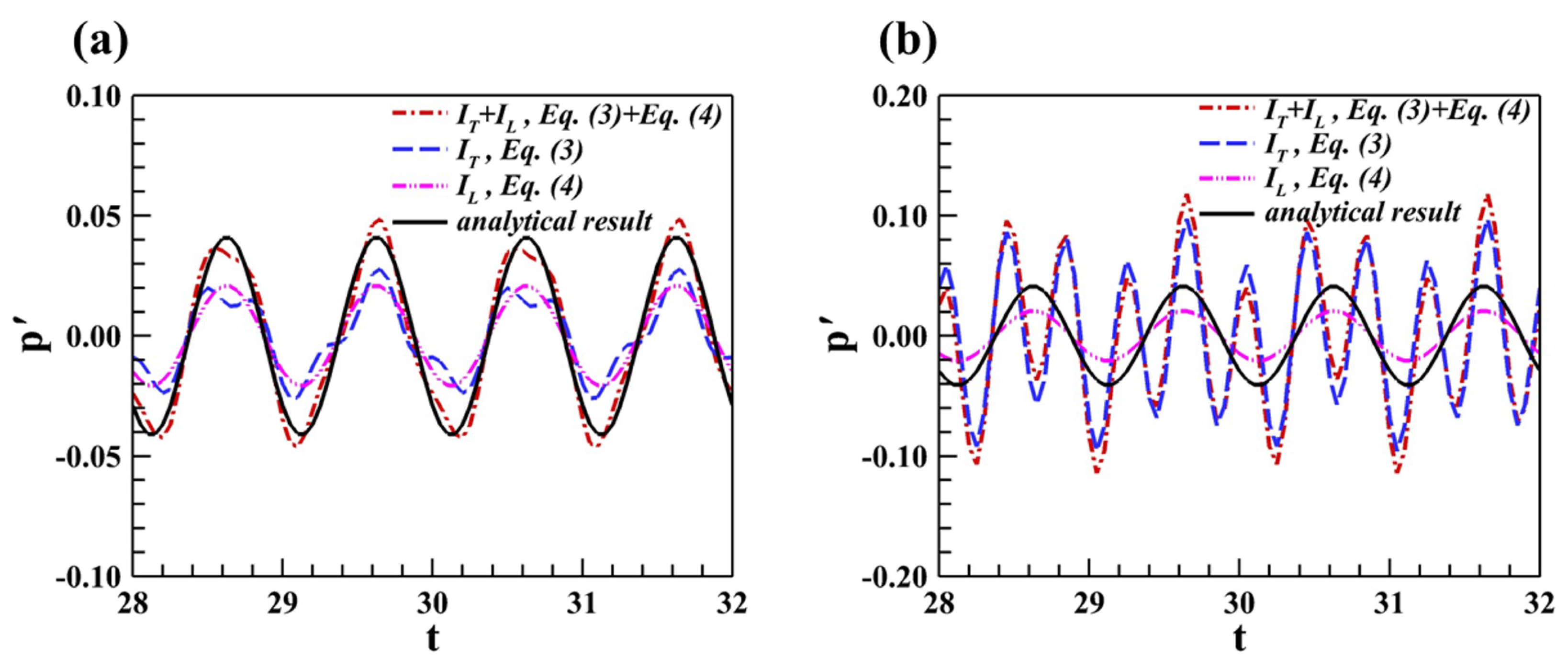
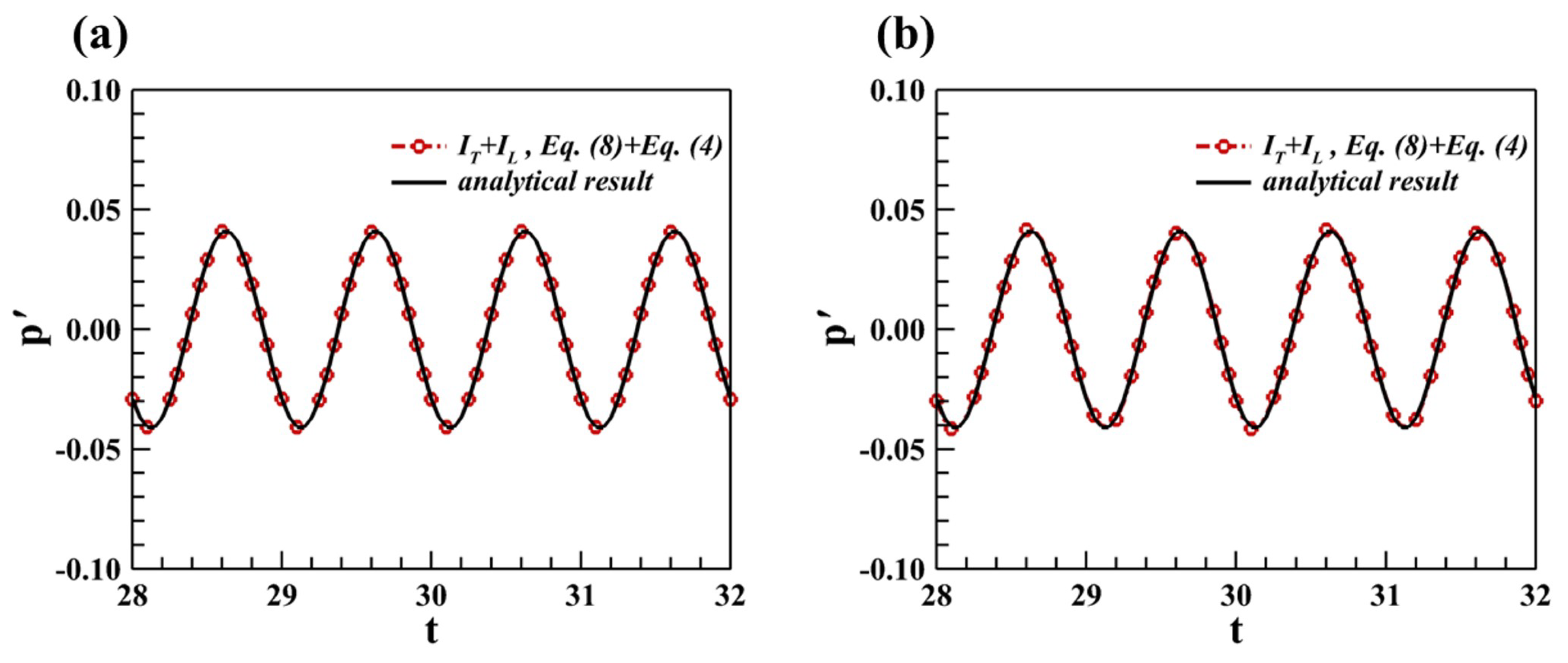
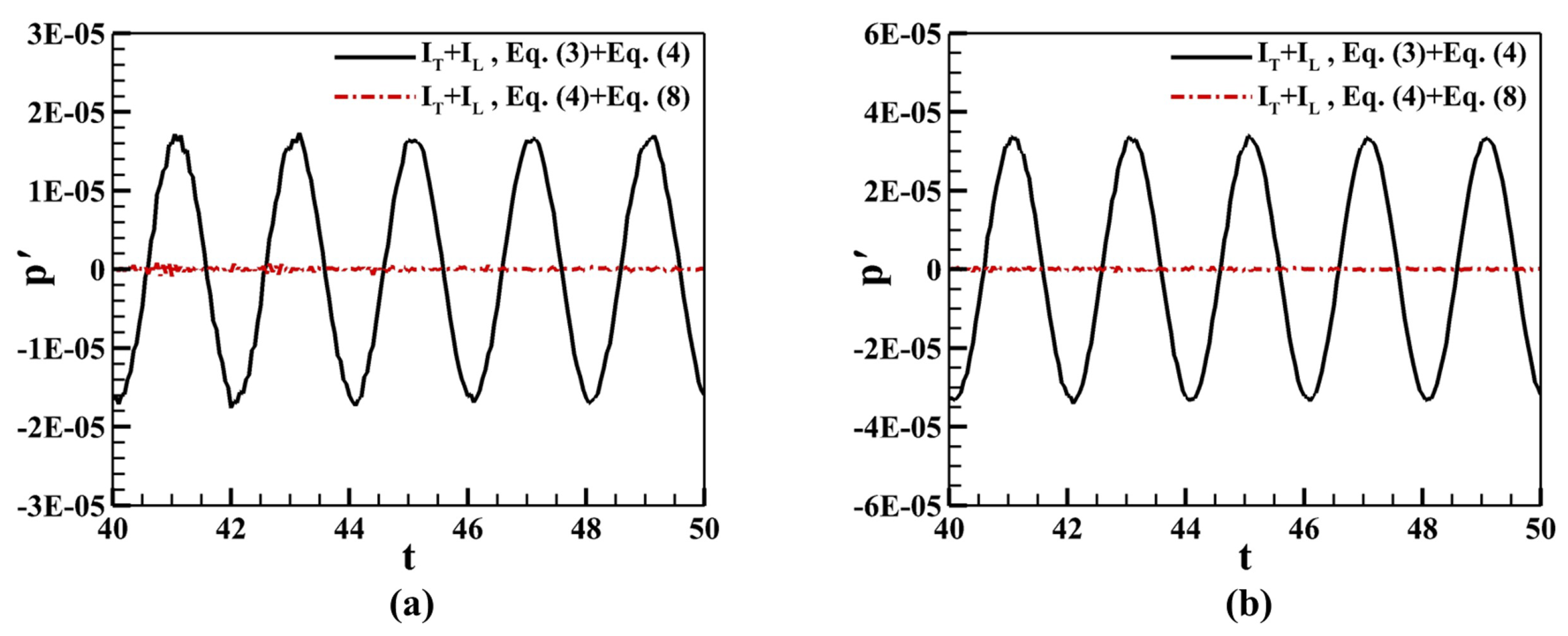
4.1. Unsteady Dipole in a Steady Ambient Flow
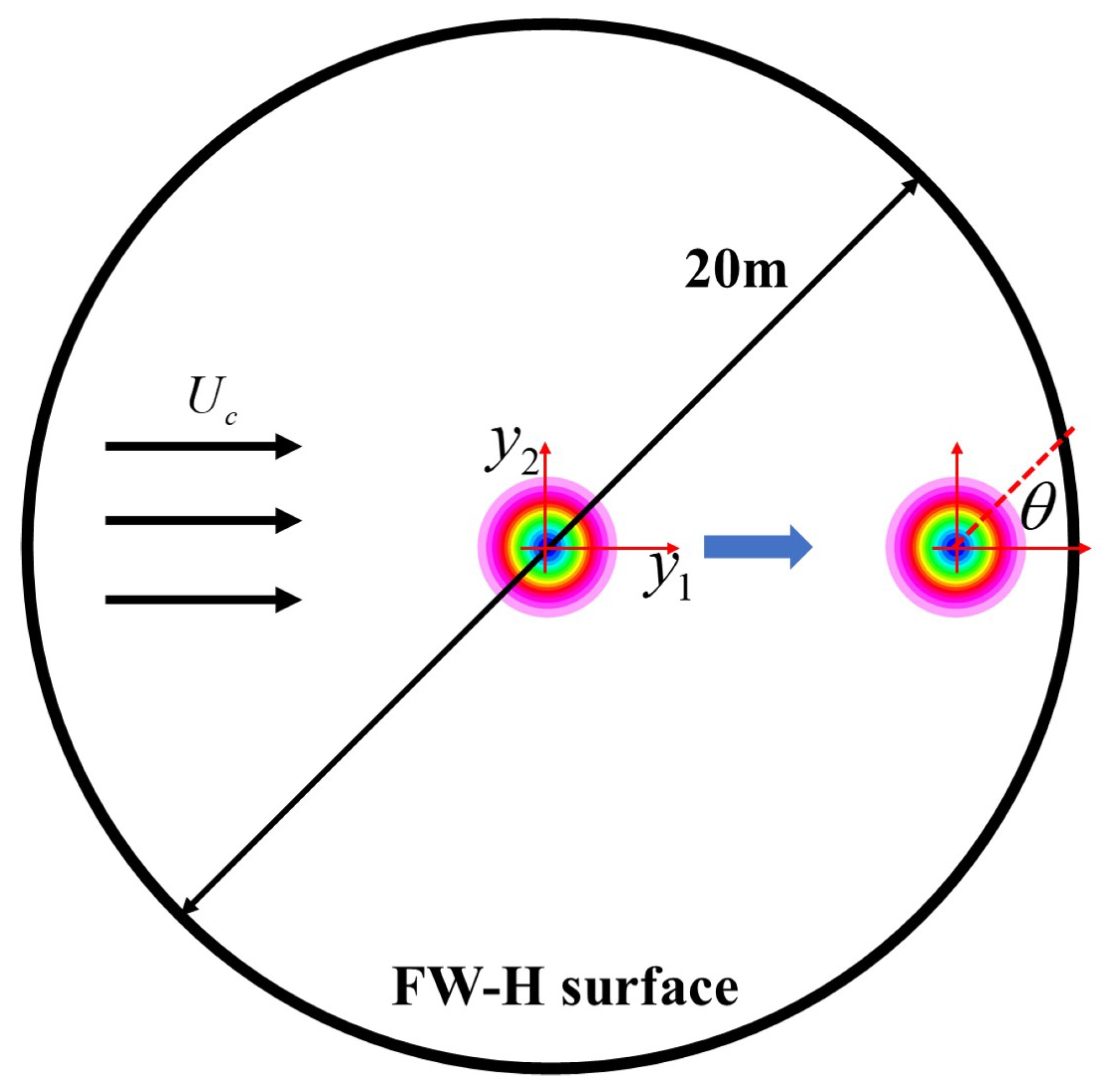
4.2. 2D Incompressible Convecting Vortex
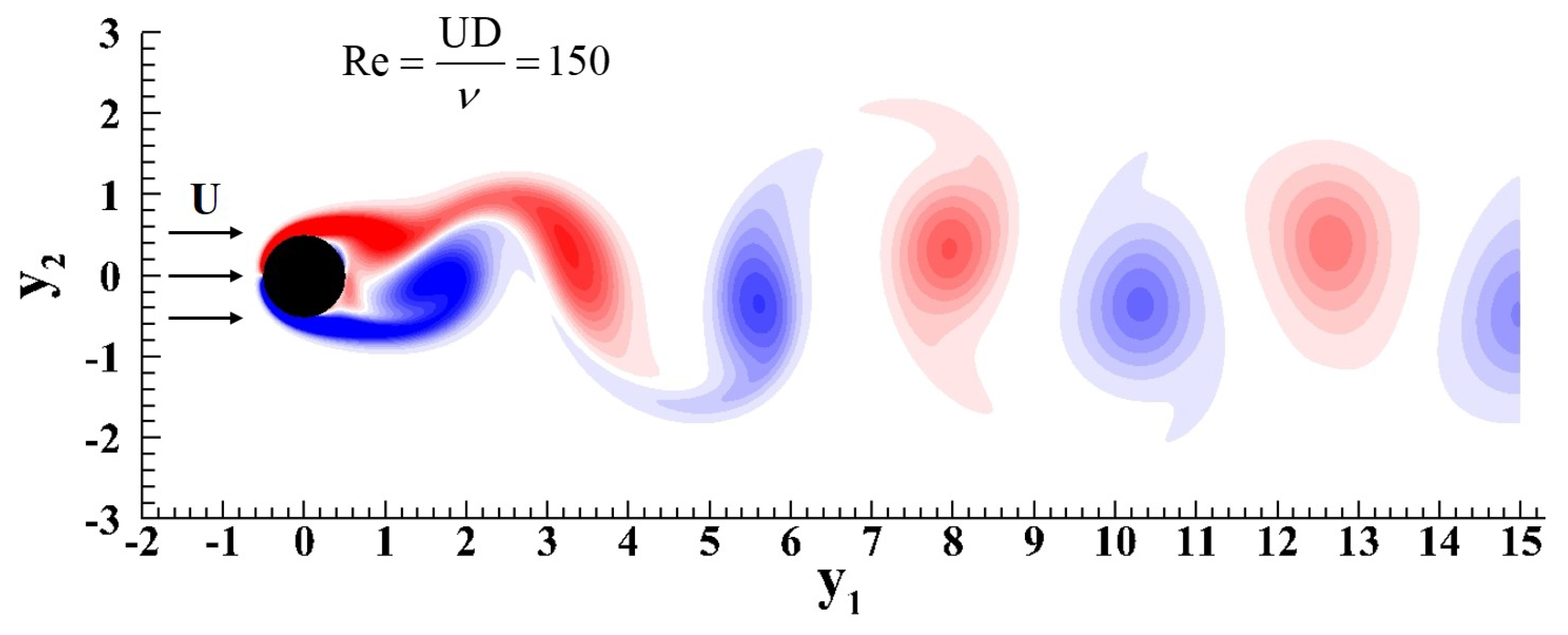
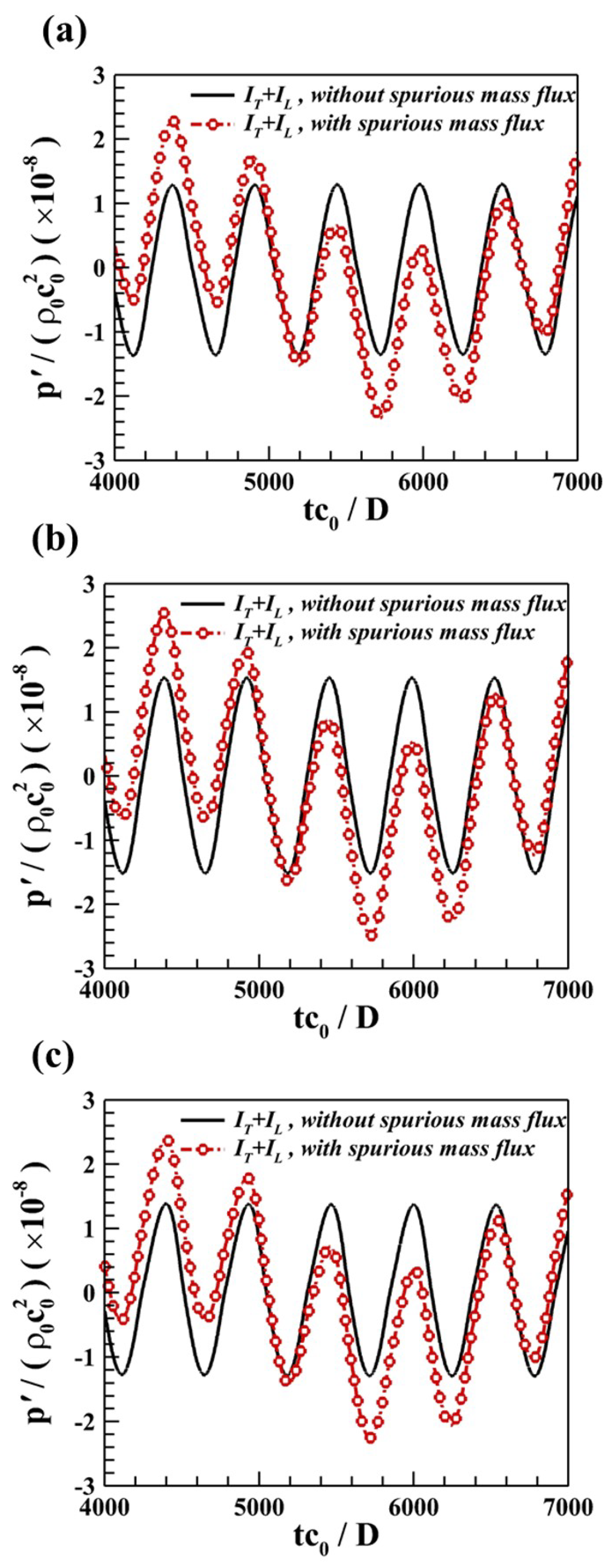
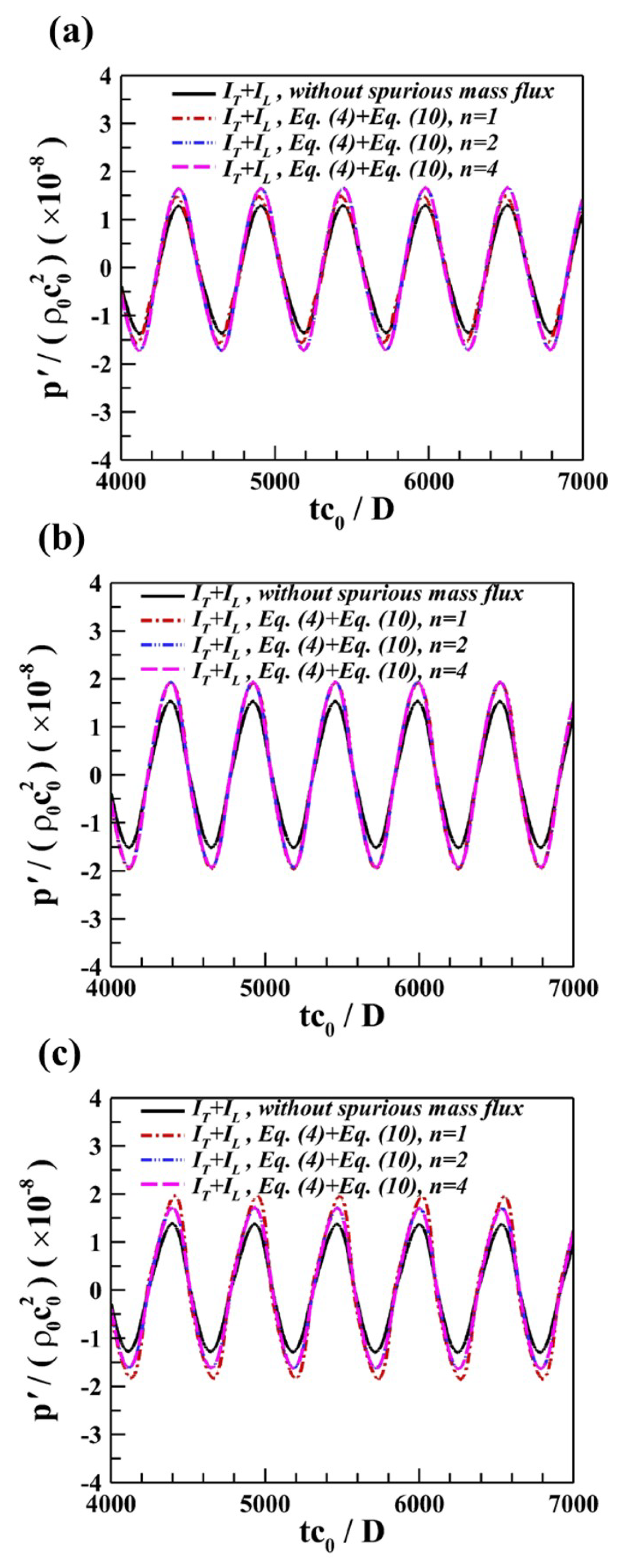
4.3. Flows over a Circular Cylinder
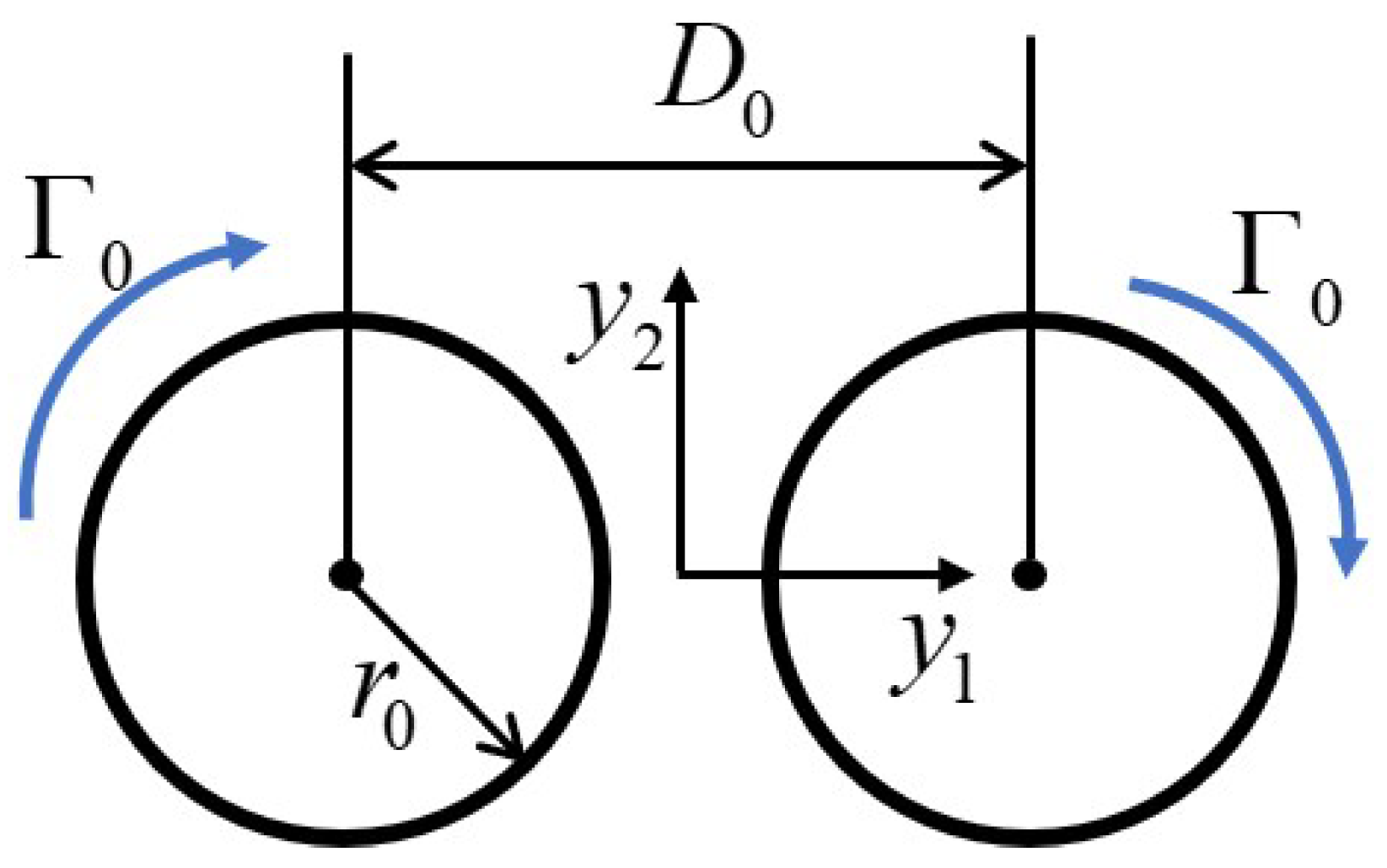
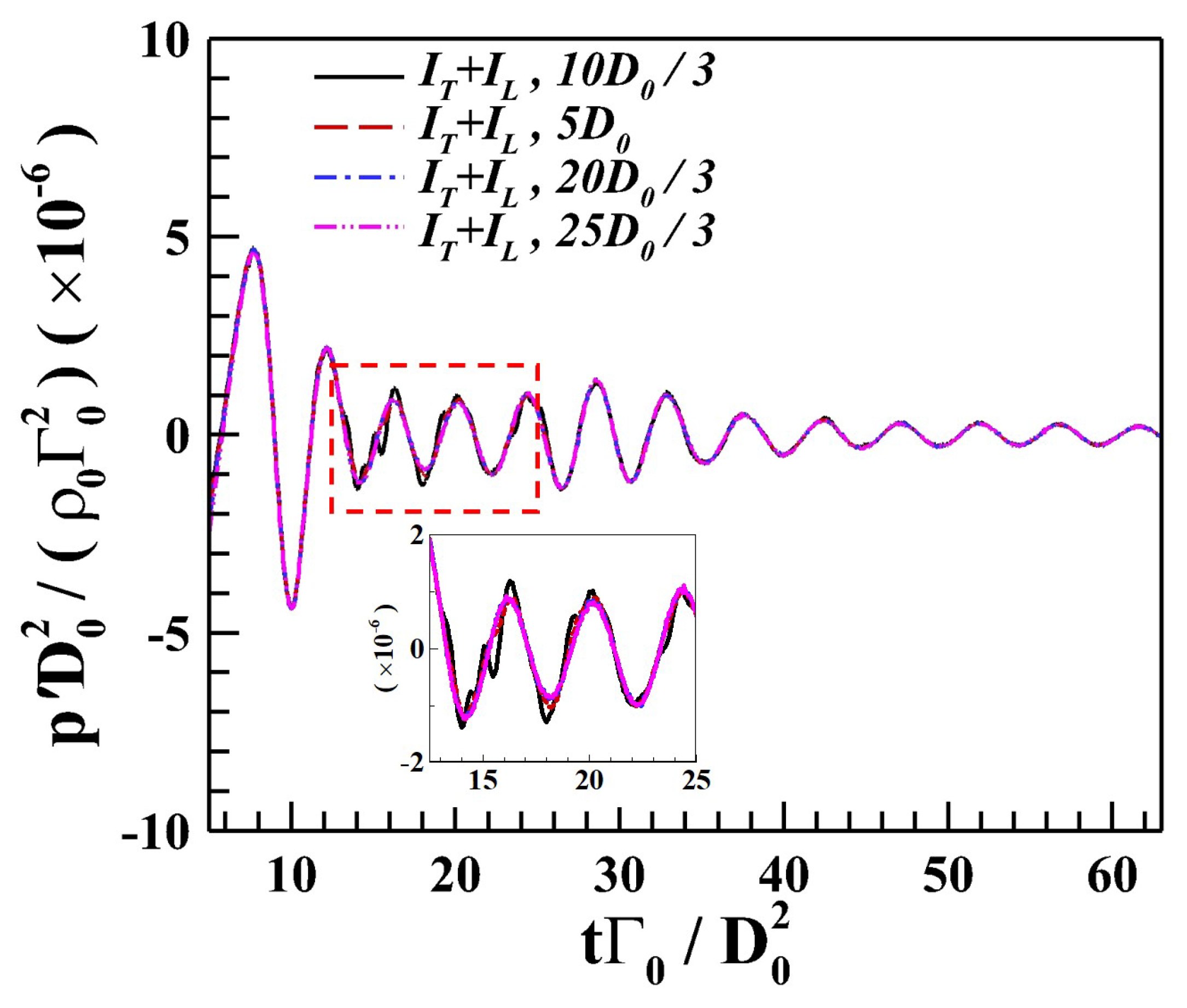
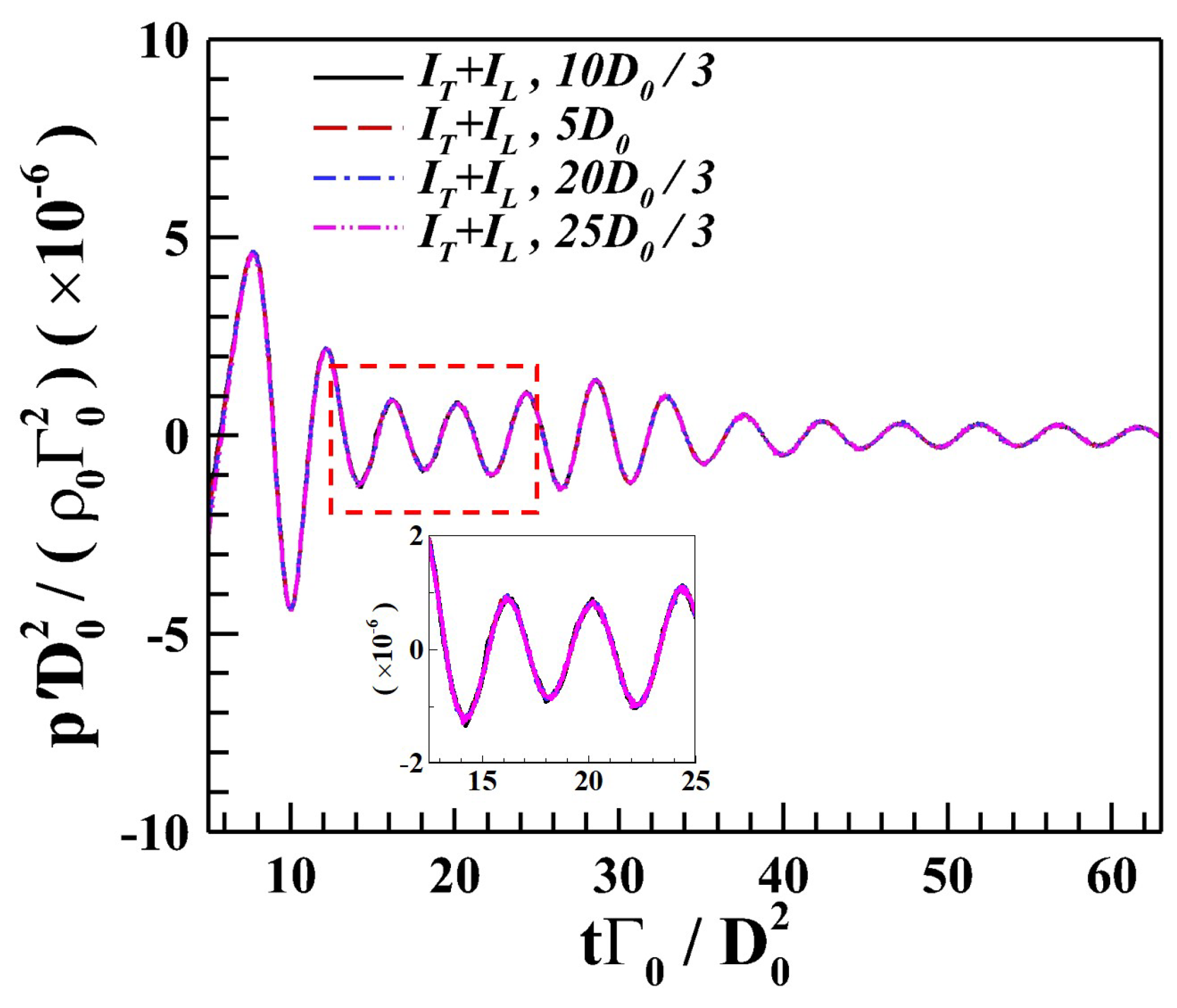
4.4. Co-Rotating Vortex Pair
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Keller, J.; Kumar, P.; Mahesh, K. Examination of propeller sound production using large eddy simulation. Phys. Rev. Fluids 2018, 3, 064601. [Google Scholar] [CrossRef]
- Lidtke, A.K.; Turnock, S.R.; Humphrey, V.F. Characterisation of sheet cavity noise of a hydrofoil using the Ffowcs Williams–Hawkings acoustic analogy. Comput. Fluids 2016, 130, 8–23. [Google Scholar] [CrossRef]
- Zhou, Z.T.; Xu, Z.Y.; Wang, S.Z.; He, G.W. Wall-modeled large-eddy simulation of noise generated by turbulence around an appended axisymmetric body of revolution. J. Hydrodyn. 2022, 34, 533–554. [Google Scholar] [CrossRef]
- Wang, X.; Huang, Q.; Pan, G. Numerical research on the influence of sail leading edge shapes on the hydrodynamic noise of a submarine. Appl. Ocean. Res. 2021, 117, 102935. [Google Scholar] [CrossRef]
- Powell, A. Theory of vortex sound. J. Acoust. Soc. Am. 1964, 36, 177–195. [Google Scholar] [CrossRef]
- Möhring, W. On vortex sound at low Mach number. J. Fluid Mech. 1978, 85, 685–691. [Google Scholar] [CrossRef]
- Schram, C.; Hirschberg, A. Application of vortex sound theory to vortex-pairing noise: Sensitivity to errors in flow data. J. Sound Vib. 2003, 266, 1079–1098. [Google Scholar] [CrossRef]
- Williams, J.F.; Hawkings, D.L. Sound generation by turbulence and surfaces in arbitrary motion. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1969, 264, 321–342. [Google Scholar]
- Cianferra, M.; Ianniello, S.; Armenio, V. Assessment of methodologies for the solution of the Ffowcs Williams and Hawkings equation using LES of incompressible single-phase flow around a finite-size square cylinder. J. Sound Vib. 2019, 453, 1–24. [Google Scholar] [CrossRef]
- Wang, M.; Lele, S.K.; Moin, P. Computation of quadrupole noise using acoustic analogy. AIAA J. 1996, 34, 2247–2254. [Google Scholar] [CrossRef]
- Zhou, Z.; Wang, H.; Wang, S.; He, G. Lighthill stress flux model for Ffowcs Williams–Hawkings integrals in frequency domain. AIAA J. 2021, 59, 4809–4814. [Google Scholar] [CrossRef]
- Lockard, D.; Casper, J. Permeable surface corrections for Ffowcs Williams and Hawkings integrals. In Proceedings of the 11th AIAA/CEAS Aeroacoustics Conference, Monterey, CA, USA, 23–25 May 2005; p. 2995. [Google Scholar]
- Nitzkorski, Z.; Mahesh, K. A dynamic end cap technique for sound computation using the Ffowcs Williams and Hawkings equations. Phys. Fluids 2014, 26, 115101. [Google Scholar] [CrossRef]
- Testa, C.; Porcacchia, F.; Zaghi, S.; Gennaretti, M. Study of a FWH-based permeable-surface formulation for propeller hydroacoustics. Ocean. Eng. 2021, 240, 109828. [Google Scholar] [CrossRef]
- Zhong, S.; Zhang, X. A sound extrapolation method for aeroacoustics far-field prediction in presence of vortical waves. J. Fluid Mech. 2017, 820, 424–450. [Google Scholar] [CrossRef]
- Zhong, S.; Zhang, X. A generalized sound extrapolation method for turbulent flows. Proc. R. Soc. A Math. Phys. Eng. Sci. 2018, 474, 20170614. [Google Scholar] [CrossRef]
- Yao, H.D.; Davidson, L.; Eriksson, L.E. Noise radiated by low-Reynolds number flows past a hemisphere at Ma= 0.3. Phys. Fluids 2017, 29, 076102. [Google Scholar] [CrossRef]
- Ricciardi, T.R.; Wolf, W.R.; Spalart, P.R. On the Application of Incomplete Ffowcs Williams and Hawkings Surfaces for Aeroacoustic Predictions. AIAA J. 2022, 60, 1971–1977. [Google Scholar] [CrossRef]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K. Noise prediction for increasingly complex jets. Part I: Methods and tests. Int. J. Aeroacoustics 2005, 4, 213–245. [Google Scholar] [CrossRef]
- Zhou, Z.; Zang, Z.; Wang, H.; Wang, S. Far-field approximations to the derivatives of Green’s function for the Ffowcs Williams and Hawkings equation. Adv. Aerodyn. 2022, 4, 12. [Google Scholar] [CrossRef]
- Zhou, Z.; Wang, H.; Wang, S.; He, G. Quadrupole source term corrections based on correlation functions for Ffowcs Williams and Hawkings integrals. Acta Aerodyn. Sin. 2020, 38, 1129–1135. [Google Scholar]
- Brentner, K.S.; Farassat, F. Modeling aerodynamically generated sound of helicopter rotors. Prog. Aerosp. Sci. 2003, 39, 83–120. [Google Scholar] [CrossRef]
- Lockard, D.P. An efficient, two-dimensional implementation of the Ffowcs Williams and Hawkings equation. J. Sound Vib. 2000, 229, 897–911. [Google Scholar] [CrossRef]
- Zhou, Z.; Wang, H.; Wang, S. Simplified permeable surface correction for frequency-domain Ffowcs Williams and Hawkings integrals. Theor. Appl. Mech. Lett. 2021, 11, 100259. [Google Scholar] [CrossRef]
- Najafi-Yazdi, A.; Brès, G.A.; Mongeau, L. An acoustic analogy formulation for moving sources in uniformly moving media. Proc. R. Soc. A Math. Phys. Eng. Sci. 2011, 467, 144–165. [Google Scholar] [CrossRef]
- Inoue, O.; Hatakeyama, N. Sound generation by a two-dimensional circular cylinder in a uniform flow. J. Fluid Mech. 2002, 471, 285–314. [Google Scholar] [CrossRef]
- Gloerfelt, X.; Pérot, F.; Bailly, C.; Juvé, D. Flow-induced cylinder noise formulated as a diffraction problem for low Mach numbers. J. Sound Vib. 2005, 287, 129–151. [Google Scholar] [CrossRef]
- Wang, S.; Vanella, M.; Balaras, E. A hydrodynamic stress model for simulating turbulence/particle interactions with immersed boundary methods. J. Comput. Phys. 2019, 382, 240–263. [Google Scholar] [CrossRef]
- Yao, H.D.; Davidson, L.; Eriksson, L.E.; Peng, S.H.; Grundestam, O.; Eliasson, P.E. Surface integral analogy approaches for predicting noise from 3D high-lift low-noise wings. Acta Mech. Sin. 2014, 30, 326–338. [Google Scholar] [CrossRef]
- Feng, F.; Meng, X.; Wang, Q. Sound generation by a pair of co-rotating vortices using spectral acoustic analogy. J. Sound Vib. 2020, 469, 115120. [Google Scholar] [CrossRef]
- Mao, F.; Kang, L.; Wu, J.; Yu, J.L.; Gao, A.; Su, W.; Lu, X.Y. A study of longitudinal processes and interactions in compressible viscous flows. J. Fluid Mech. 2020, 893. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Liu, Y.; Wang, H.; Wang, S. Mass-Conserved Solution to the Ffowcs-Williams and Hawkings Equation for Compact Source Regions. Aerospace 2023, 10, 148. https://doi.org/10.3390/aerospace10020148
Zhou Z, Liu Y, Wang H, Wang S. Mass-Conserved Solution to the Ffowcs-Williams and Hawkings Equation for Compact Source Regions. Aerospace. 2023; 10(2):148. https://doi.org/10.3390/aerospace10020148
Chicago/Turabian StyleZhou, Zhiteng, Yi Liu, Hongping Wang, and Shizhao Wang. 2023. "Mass-Conserved Solution to the Ffowcs-Williams and Hawkings Equation for Compact Source Regions" Aerospace 10, no. 2: 148. https://doi.org/10.3390/aerospace10020148
APA StyleZhou, Z., Liu, Y., Wang, H., & Wang, S. (2023). Mass-Conserved Solution to the Ffowcs-Williams and Hawkings Equation for Compact Source Regions. Aerospace, 10(2), 148. https://doi.org/10.3390/aerospace10020148




