Performance-Seeking Control of Aero-Propulsion System Based on Intelligent Optimization and Active Disturbance Rejection Fusion Controller

Abstract

To investigate the performance potential of the aero-propulsion system and the problem of control mode conversion, this paper takes the inlet/engine integrated component-level model as the research object, and a performance-seeking control (PSC) scheme based on the neighborhood-based speciation differential evolution–grey wolf optimization (NSDE-GWO) algorithm is designed and combined with an active disturbance rejection control (ADRC) to establish a multivariable fusion closed-loop control system. The analysis reveals that the NSDE-GWO hybrid algorithm, which takes advantages of the two algorithms, significantly improves the computing efficiency and optimization accuracy, achieving better optimization solutions in three different modes. The intelligent fusion controller is able to achieve a smooth transition of performance modes to ensure that the engine is provided with a stable thrust during operation under supersonic conditions, and the potential for performance optimization is maintained at a reasonable level. Maximum installed thrust mode capable of achieving no thrust loss and a maximum fluctuation rate within 2000 N/s, with the largest variation in thrust during the conversion being less than 0.9% under the minimum turbine temperature mode and the minimum specific fuel consumption mode. This study presents a theoretical foundation and engineering applications for the design of supersonic propulsion system controllers.

1. Introduction

With the rapid development of supersonic aero technology, the propulsion system controller requires increased reliability and performance potential, and the control system object increasingly transfers from engine to comprehensive propulsion system [1,2]. The present control system mostly uses sensor-based control design principles to handle non-measurable parameters, including thrust, temperature, and safety margins indirectly through measurable parameters. Propulsion systems are characterized by complex structures and wide operating envelopes that cannot be fully exploited by conventional controllers, necessitating the use of fusion optimization approaches. performance-seeking control (PSC) [3,4] is an essential mode of intelligent engine control, which is implemented by using optimization algorithms to find the maximum performance potential (maximum thrust, minimum fuel consumption, or minimum turbine temperature) of the model while satisfying various operating limitations. Therefore, research on comprehensive performance-seeking control algorithms for supersonic propulsion systems is required, and the fusion and conversion of performance-seeking controls with sensor-based controllers necessitates concentrated effort.

Scholars have long researched and experimented with PSC, attempting to apply it to the propulsion system [5]. Nobbs. S [6] applied the full envelope PSC to PW1128 powered F-15 aircraft. NASA Dryden Flying Test Center’s Orme J.S [7] conducted the PSC supersonic flight test. Under supersonic conditions, thrust can be enhanced by 9%, fuel consumption can be lowered by 8%, and turbine temperature can be reduced by 48K. In terms of the numerical simulation study, the linear programming (LP) approach is employed as the performance optimization algorithm in the NASA report [8], and Orme, J.S [7] used LP in the airborne adaptive model. Later, numerous academics engaged in the research and expansion of LP, including SLP [9], FSQP [10], and SQCQP [11]. According to Chen HY [12], the FSQP could obtain the optimal operating conditions of the double bypass variable cycle engine in different conditions. With the rapid growth of artificial intelligence, intelligence algorithms have been gradually applied to the PSC, overcoming the initial value dependence of traditional methods. Several academics have used GA and EA to tackle optimization issues [13,14]. PSO provides an ideal optimization effect under maximum thrust optimization condition [15], but it depends on multiple-parameter tweaking, which cannot adapt to the multiple operating states. Other methods, such as the direct method [16], the Beetle Antennae Search algorithm [17], and IA [18] are also proposed. The above study focuses more on the PSC of turbofan engines and less on multivariable propulsion systems; the initial value sensitivity and the local convergence problems of the traditional algorithm will be more prominent due to the increased number of control variables and the harsh constraints of aero-propulsion modeling. The preceding study is primarily concerned with optimizing potential, a lack of quantitative analysis of stability, and the global convergence of intelligent PSC.

Although the PID controller is still employed in actual engines, it has drawbacks while dealing with strongly coupled multivariable objects. The research focus is on the construction of a multivariable controller with a wide flight envelope under supersonic conditions. NASA Glenn Research Center [19] argued that the multivariable control is mainly used for the requirements of engines in specific high-performance engine conditions. The earliest multivariable control study on aero engines was demonstrated by the LQR method [20] but suffered from accuracy dependence on mathematical models. Compared with LQR, LTR [21] has a better response speed and robustness of disturbance suppression but still exposes the defects in practical application conditions [22]. Richter H [23,24] carried out a study of sliding mode control, which is highly robust to parameter fluctuations and disturbances yet is prone to chattering. Active disturbance rejection control (ADRC) was invented by Han JQ [25]. Based on the approximate bandwidth concept, Gao ZQ [26] presented a simpler parameter setting approach for ADRC. Miklosovic R [27] integrated ADRC into turbofan engine control and validated anti-interference performance using NASA’s highly reliable model. Li SQ [28] compared ADRC to PID and determined that ADRC had superior control performance. Zhang HB [29] achieved turbofan engine decoupling control by integrating a decoupling matrix with ADRC. Xue WC [30] utilized ADRC to adjust the engine fuel ratio. It is clear that ADRC can be employed for decoupling and the robust control of turbofan engines, and its anti-interference performance is superior to PID. Previous research has focused on controller performance and robustness analysis rather than the combination of multivariable controllers and PSC. Nevertheless, the process of transitioning control systems to performance modes has received little attention.

To summarize, the performance-seeking control effects of NSDE-GWO and various swarm-intelligence algorithms are compared first, and then the benefits and application value of NSDE-GWO are analyzed. Finally, under typical supersonic conditions, a fusion-control system using the NSDE-GWO optimization algorithm and ADRC was created to accomplish a seamless transition from the PSC mode to quick reaction and low thrust loss.

2. Materials and Methods

The design of the fusion-control system basically contains the inlet/engine integrated model module, the control system module, and PSC modules. Considering the feasibility and cost of validation, the component-level model is commonly used in studies instead of actual engines. In this paper, a military turbofan engine with a variable geometry inlet and small bypass ratio is adopted, and an integrated component-level model of the inlet and engine is developed. The real engine model is commonly replaced by a component-level model in this paper, and a turbofan engine with a variable geometry inlet and small culvert ratio is adopted; the control system module contains an ADRC closed-loop controller and an inlet open-loop controller. The PSC module contains an online model and an intelligent optimization program, among which the online model is replaced by a component-level model, and the optimization program is adopted by the improved NSDE-GWO method. Figure 1 illustrates the operation principle of the fusion controller.

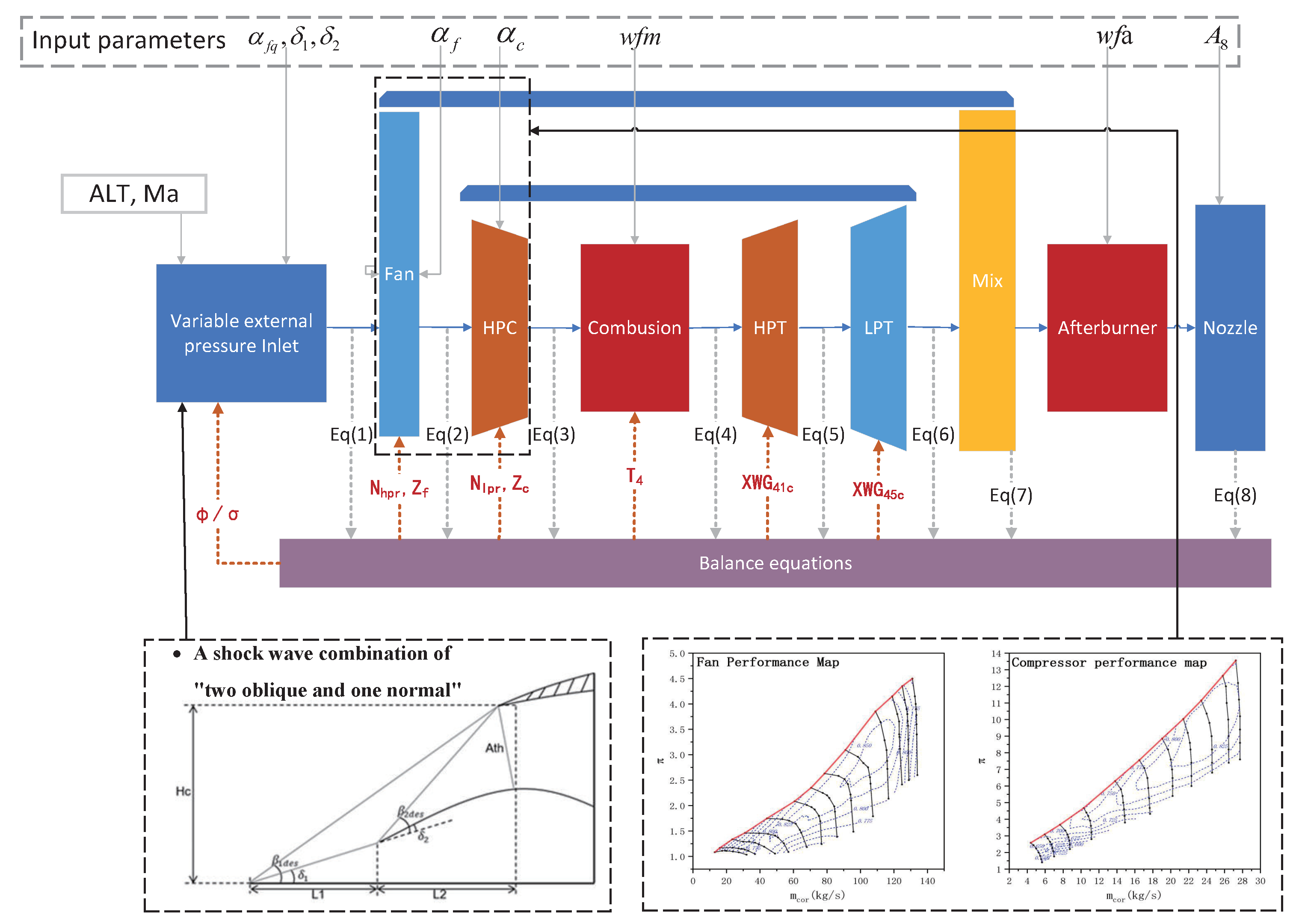
2.1. Supersonic Inlet/Engine Integrated Component-Level Model

Aero-propulsion systems are multivariable, nonlinear, and time-varying, and their models for control generally adopt component-level methods, specifically, models of multiple components based on their characteristic diagrams and aerodynamic-thermodynamic relationships. This paper describes the principle of building an inlet/engine integrated component-level model, which mainly includes two parts: the inlet system and the engine. The main workflow is shown in Figure 2. The main air path components include the external pressure inlet, fan, high-pressure compressor, combustion, high-pressure turbine, low-pressure turbine, mixing chamber, afterburner combustion, and nozzle.

Most of the conventional inlet components are calculated using idealized empirical formulas, which cannot satisfy the requirements of calculation accuracy at supersonic conditions. Considering the shock structure and drag calculation method, quasi one-dimensional flow theory is used to calculate the inlet performance [31]. Combined with basic flight conditions, an external pressure inlet with a combination of “two oblique and one normal” shock waves is selected. Through the geometric relationship of the two-dimensional plane, the structural dimension parameters are determined to seal the shock wave, where the first-stage ramp angle and second-stage ramp angle are adjustable variables and the bleed valve opening is represented by the relative bleed adjustment.

The object is a military small bypass ratio turbofan engine with an operating range of 0–2.5 Mach number interval, in which the fan-guide vane angle, the compressor-guide vane angle, and the nozzle area can be adjusted. The performance parameters of the fan and compressor components are realized using the characteristic interpolation, and the characteristic curves are shown in Figure 2. Simplified linearized characteristics were used for the high-pressure turbine and low-pressure turbine to improve the real-time performance, considering that the turbine mostly works at larger operating conditions and similarity exists in efficiency and flow rate at different speeds.

In addition, the output parameters of each gas path component model are governed by a common set of operating equations. Typical common equations include the pressure balance between the pressurized combustion chamber and nozzle, and the flow balance between the compressors of the fan; the power consumed on the same shaft should form a balance with the power generated. To achieve the inlet/engine matching, the residuals of the inlet and fan flows are taken as the balancing equations, and the ratio of the flow coefficient/total pressure recovery coefficient ($\frac{\varphi }{\sigma }$) is chosen as the starting guess for the iteration. If the number of iterative variables is the same as the balancing equations, the problem is transformed into a nonlinear implicit set of equations with unknown independent variables, and the component-level model is considered to have a reliable solution when the residuals tend to zero. The hybrid iterative algorithm of the damping Newton method [32] is utilized to solve the issue due to the rise in iterative variables. ${[x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8]}^T$ denotes the independent assignment variables for the iterative process. The iterative variables (e) are selected, and co-working equations (Eq) are solved in association, expressed as

$$\left\{\begin{array}{c}Eq\left(1\right):f_1(x_0,x_1,x_2,\dots ,x_8)=W_{inlet}-W_{fan,f}=e_1\hfill \\ Eq\left(2\right):f_2(x_0,x_1,x_2,\dots ,x_8)=W_{fan,a}-W_{HPC,f}=e_2\hfill \\ Eq\left(3\right):f_3(x_0,x_1,x_2,\dots ,x_8)=I_H·N_{hpr}·\frac{d{N}_{hpr}}{dt}-L_{HPT}+L_{HPC}-L_{add}=e_3\hfill \\ Eq\left(4\right):f_4(x_0,x_1,x_2,\dots ,x_8)=W_{comb,a}-W_{HPT,f}=e_4\hfill \\ Eq\left(5\right):f_5(x_0,x_1,x_2,\dots ,x_8)=W_{HPT,a}-W_{LPT,f}=e_5\hfill \\ Eq\left(6\right):f_6(x_0,x_1,x_2,\dots ,x_8)=I_L·N_{l}pr·\frac{d{N}_{lpr}}{dt}-L_{LPT}+L_{fan}=e_6\hfill \\ Eq\left(7\right):f_7(x_0,x_1,x_2,\dots ,x_8)=P_6-P_{16}=e_7\hfill \\ Eq\left(8\right):f_8(x_0,x_1,x_2,\dots ,x_8)=P_8-P_{nozzle}=e_8\hfill \end{array}\right.$$

(1)

$${[x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8]}^T={[\frac{\varphi }{\sigma },N_{hpr},Z_f,N_{lpr},Z_c,T_4,XW{G}_{41c},XW{G}_{45c}]}^T$$

(2)

$$\left\{\begin{array}{c}{W}_{fan,a}=W_{fan,f}-W_{bypass}\hfill \\ W_{comb,a}=W_{comb,f}+Wfm\hfill \end{array}\right.$$

(3)

The formula parameters $W_{inlet}, W_{fan,f}, W_{fan,a}, W_{HPC,f}, W_{comb,f}, W_{comb,a}, W_{HPT,f},$$W_{HPT,a}$, $W_{LPT,f}$ indicate, respectively, inlet outlet flow, fan inlet flow, fan outlet flow, compressor inlet flow, main combustion chamber inlet flow, main combustion chamber outlet flow, high-pressure turbine inlet flow, high-pressure turbine outlet flow, and low-pressure turbine inlet flow. $I_H$, $I_L$ stand for the rotary inertia of high-pressure and low-pressure, and $L_{HPT}$, $L_{LPT}$, $L_{HPC}$, $L_{fan}$ stand for the power of HPT, HPC, HPC, and fan, respectively. $L_{add}$ stands for the additional power of engine starting. $N_{hpr}$, $N_{lpr}$ indicate the high-pressure and low-pressure rotor speed. $Z_f, Z_c, T_4, XW{G}_{41c}, XW{G}_{45c}$ indicate the relative pressure ratio coefficients for fan, HPC, HPT, and LPT components, and initial guesses for characteristic interpolation. Due to the introduction of the external characteristics and taking into account the external resistance of the inlet, the installed thrust and ISFC are obtained by the following equation. $D_{inlet}$ indicates the external resistance calculated for the inlet tract.

$$\left\{\begin{array}{c}{F}_{ITHR}=F_{THR}-D_{inlet}\hfill \\ ISFC=3600·\frac{wfm}{F_{ITHR}}\hfill \end{array}\right.$$

(4)

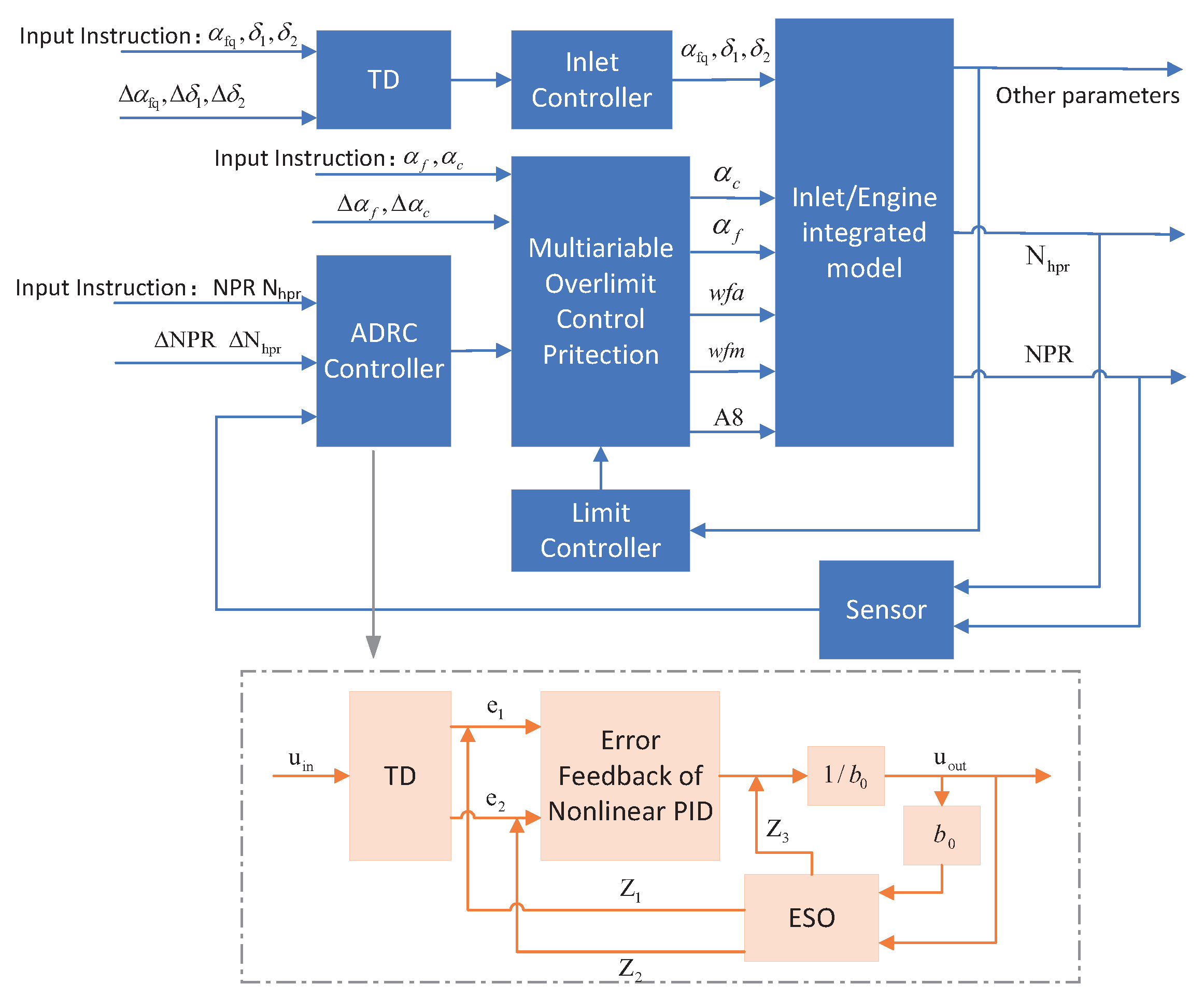
2.2. Performance-Seeking Control in Aero-Propulsion System

Under the supersonic conditions of the aero-propulsion system, the inlet/engine matching seriously affect the installed performance. PSC can optimize the performance by adjusting the inlet geometry parameters and compression parts parameters. At a certain flight altitude and Mach number, the model operating state is mainly determined by the control quantity, X, denoted as the state parameters. The optimized control variables(u) available for the advance integrated propulsion system include the following:

$$\left\{\begin{array}{c}X=f\left(u\right)\hfill \\ u={[wfm,wfa,{\alpha }_{fq},{\delta }_1,{\delta }_2,A_8,{\alpha }_f,{\alpha }_c]}^T\hfill \end{array}\right.$$

(5)

The formula parameters are as follows: relative bleed adjustment ${\alpha }_{\mathrm{fq}}$, first-stage ramp angle ${\delta }_1$, second-stage ramp angle ${\delta }_2$, fan guide vane angle ${\alpha }_{\mathrm{f}}$, compressor guide vane angle ${\alpha }_{\mathrm{c}}$, main fuel flow rate $\mathrm{wfm}$, afterburner fuel flow rate $\mathrm{wfa}$, and exhaust nozzle outlet area ${\mathrm{A}}_8$. The ideal boundary conditions, as well as the stability of the inlet, must be determined while keeping the feasible area of the optimization space and operating limit in mind. If the Inlet flow coefficient ${\phi }_{\mathrm{in}}$ is too low, the inlet will enter an unstable functioning state known as “surge”. The flow coefficient of the surge working state is ${\phi }_{\mathrm{is}}$. Increased inlet distortion may easily cause engine surge and negatively impact engine performance. Formula parameters: low-pressure turbine outlet temperature $T_6$, and fan surge margin SMF, and compressor surge margin SMC. To summarize, the following requirements are guaranteed:

$$M=\left\{\begin{array}{c}{u}_{min}⩽u⩽u_{max}\hfill \\ N_{hpr,min}⩽N_{hpr}⩽N_{hpr,max}\hfill \\ N_{lpr,min}⩽N_{lpr}⩽N_{lpr,max}\hfill \\ T_6⩽T_{6,max}\hfill \\ {\phi }_{is}⩽{\phi }_{in}⩽{\phi }_{max}\hfill \\ SM{F}_{min}⩽SMF\hfill \\ SM{C}_{min}⩽SMC\hfill \end{array}\right.$$

(6)

PSC optimizes the engine operating point in different flight objectives based on the optimization control mode request, as well as the aircraft attitude, flight circumstances, and other information. It is separated into optimization control modes based on various optimization targets, such as maximum thrust, minimum fuel consumption, and minimum turbine temperature. Formula parameters: min ISFC penalty function coefficient K1, min T45 penalty function coefficient K2, optimized installed thrust $F_{ITHR,opt}$, and initial installed thrust $F_{ITHR,ori}$. The penalty function is introduced in the objective function to achieve the optimization objective of constant installation thrust. The penalty function parameters need to adopt suitable values; id they are too large, they may reduce the optimization efficiency, and if they are too small they may weaken the constant thrust effect. Considering the different magnitudes of ISFC and T45, K1 and K2 are taken as 0.1 and 100.

(1) Maximum installed thrust control

$$\begin{array}{c}max F_{ITHR}\hfill \\ \left\{\begin{array}{c}\mathrm{Objective} f\left(u\right)=F_{ITHR}\hfill \\ s.t.\in M,wfm=const,wfa=const\hfill \\ u={[{\alpha }_{fq},{\delta }_1,{\delta }_2,A_8,{\alpha }_f,{\alpha }_c]}^T\hfill \end{array}\right.\hfill \end{array}$$

(7)

(2) Minimum installed specific fuel-consumption control

$$\begin{array}{c}min ISFC\hfill \\ \left\{\begin{array}{c}\mathrm{Objective} f\left(u\right)=ISFC + \mathrm{K}1·\left|F_{ITHR,opt}-F_{ITHR,ori}\right|\hfill \\ s.t.\in M,F_{ITHR}=const\hfill \\ u={[wfm,wfa,{\alpha }_{fq},{\delta }_1,{\delta }_2,A_8,{\alpha }_f,{\alpha }_c]}^T\hfill \end{array}\right.\hfill \end{array}$$

(8)

(3) Minimum low-pressure turbine inlet temperature control

$$\begin{array}{c}min T_{45}\hfill \\ \left\{\begin{array}{c}\mathrm{Objective} f\left(u\right)=T_{45} + \mathrm{K}2·\left|F_{ITHR,opt}-F_{ITHR,ori}\right|\hfill \\ s.t.\in M,F_{ITHR}=const\hfill \\ u={[wfm,wfa,{\alpha }_{fq},{\delta }_1,{\delta }_2,A_8,{\alpha }_f,{\alpha }_c]}^T\hfill \end{array}\right.\hfill \end{array}$$

(9)

2.3. The Principle of Improved NSDE-GWO Hybrid Algorithm

The PSC of the aero-propulsion system is confronted with the problem of increasing control variables and the nonlinearity of the objective function, which necessitates that the control algorithm adapt to a wide range of working conditions while maintaining global convergence and computational efficiency. Grey wolf optimization [33] (GWO) is a heuristic algorithm proposed by Mirjalili in 2014. It offers the advantages of fewer adjustment parameters, as well as being simple and efficient. The differential algorithm (DE) has the characteristics of fast convergence and strong robustness. The NSDE-GWO combines the two algorithms to maximize the global search capability and improve the optimization efficiency by the NS evolutionary principles of the PSC.

Based on GWO, the three individuals $\alpha ,\beta ,\gamma$ with the highest fitness value in the historical population are found as the leading class of the wolf pack. By replicating the exploration and surrounding of prey, each generation of the population is updated. The formula for the behavior of encircling prey is as follows:

$$\overrightarrow{D}=\left|\overrightarrow{C}\times \overrightarrow{X_p}\left(t\right)-\overrightarrow{X}\left(t\right)\right|$$

(10)

$$\overrightarrow{X}(t+1)=\overrightarrow{X_p}\left(t\right)-\overrightarrow{A}·\overrightarrow{D}$$

(11)

$$\overrightarrow{A}=2\overrightarrow{a}·\overrightarrow{r_1}-\overrightarrow{a}$$

(12)

$$\overrightarrow{C}=2·\overrightarrow{r_2}$$

(13)

As the number of iterations increases, $\overrightarrow{\alpha }$ decreases linearly from the initial value of 2 to 0. ${\overrightarrow{\mathrm{r}}}_1$ and ${\overrightarrow{\mathrm{r}}}_2$ are random vectors between [0,1]. To simulate the hunting behavior of grey wolves, other positions need to be updated according to $\alpha ,\beta ,\gamma$. The formula for hunting behavior is as follows:

$$\left\{\begin{array}{c}{\overrightarrow{D}}_{\alpha }=\left|{\overrightarrow{C}}_1·\overrightarrow{X_{\alpha }}-\overrightarrow{X}\right|\hfill \\ {\overrightarrow{D}}_{\beta }=\left|{\overrightarrow{C}}_2·\overrightarrow{X_{\beta }}-\overrightarrow{X}\right|\hfill \\ {\overrightarrow{D}}_{\delta }=\left|{\overrightarrow{C}}_3·\overrightarrow{X_{\delta }}-\overrightarrow{X}\right|\hfill \end{array}\right.$$

(14)

$$\left\{\begin{array}{c}\overrightarrow{X_1}=\overrightarrow{X_{\alpha }}-\overrightarrow{A_1}·\overrightarrow{D_{\alpha }}\hfill \\ \overrightarrow{X_2}=\overrightarrow{X_{\beta }}-\overrightarrow{A_2}·\overrightarrow{D_{\beta }}\hfill \\ \overrightarrow{X_3}=\overrightarrow{X_{\delta }}-\overrightarrow{A_3}·\overrightarrow{D_{\delta }}\hfill \end{array}\right.$$

(15)

$$\overrightarrow{X}(t+1)=\frac{{\overrightarrow{X}}_1+{\overrightarrow{X}}_2+{\overrightarrow{X}}_3}{3}$$

(16)

A new generation of population updates based on the grey wolf algorithm is accomplished using the above formula. The GWO population update mostly relies on the historically best three individual values, disregarding other individuals, whereas DE employs a random update technique for all individuals, which allows it to participate in the grey wolf algorithm. This algorithm’s population update must go through the mutation and crossover procedure. The following is the mutation process formula:

$$\left\{\begin{array}{c}{\mathrm{v}}_{\mathrm{i}}={\mathrm{x}}_{\mathrm{i}1}+{\mathrm{F}}_{\mathrm{i}}·\left({\mathrm{x}}_{\mathrm{i}2}-{\mathrm{x}}_{\mathrm{i}3}\right)\hfill \\ {\mathrm{F}}_{\mathrm{i}}=\left\{\begin{array}{c}{\mathrm{N}}_{\mathrm{i}}\left(0.5,0.5\right), \mathrm{if} {\mathrm{U}}_{\mathrm{i}}\left(0,1\right)\le \mathrm{fp}\hfill \\ {\delta }_{\mathrm{i}}, \mathrm{otherwise}\hfill \end{array}\right.\hfill \end{array}\right.$$

(17)

The formula of the crossover process is as follows:

$${\mathrm{u}}_i\left(j\right)=\left\{\begin{array}{c}{v}_{\mathrm{i}}\left(j\right), \mathrm{if} {\mathrm{U}}_j\left(0,1\right)\le CR\hfill \\ x_{\mathrm{i}}\left(j\right), \mathrm{otherwise}\hfill \end{array}\right.$$

(18)

The greedy algorithm is used for population selection, and a new generation wolf group of the new generation gray wolf algorithm is constructed based on the DE and the GWO new generation population. The next iteration begins, and so on until the model converges. The greedy algorithm selection procedure has the following formula:

$${{\mathrm{x}}^{\prime }}_{\mathrm{i}}=\left\{\begin{array}{c}{\mathrm{u}}_{\mathrm{i}}, \mathrm{if} \mathrm{f}\left({\mathrm{u}}_{\mathrm{i}}\right)\le \mathrm{f}\left({\mathrm{x}}_{\mathrm{i}}\right)\hfill \\ x_{\mathrm{i}}, \mathrm{otherwise}\hfill \end{array}\right.$$

(19)

Figure 3 depicts the calculation flow of NSDE-GWO. The benefit of DE is that the updating process makes use of all individuals’ information, which is stochastic and global. However, DE optimization efficiency is low in the early stages of iteration, and it is possible to fall into local convergence owing to population aggregation in the late stages of iteration. GWO has high optimization efficiency in the early stages, and the randomness of $\tilde{\mathrm{C}}$ is conducive to exploring the global optimal solution in the later stages. The concept of a greedy algorithm is integrated into the population update process, which retains more dominant individuals to engage the following generation, potentially improving the optimization efficiency. Therefore, the NSDE-GWO hybrid algorithm has theoretically better global search capability and optimization efficiency.

2.4. Design of the ADRC Multivariable Controller

In this paper, the ADRC is used as the main closed loop controller in the propulsion system. The main function of ADRC is to use the extended state observer (ESO) to estimate the system disturbance in real time, compensate the disturbance, and improve the robustness. The tracking differentiator (TD) makes the feed-back error change gradually to solve the contradiction between rapidity and over-shoot.

Considering the practical requirements of the engine, the wfa and A8 controlled by sensor-based closed-loop controllers, the turbine total pressure ratio (NPR), and the high-pressure rotor speed ($N_{hpr}$) are chosen as the controlled quantities. The adjustable variable ${\alpha }_{\mathrm{fq}}$, ${\delta }_1$, ${\delta }_2$ of the supersonic inlet and ${\alpha }_{\mathrm{f}}$, ${\alpha }_{\mathrm{c}}$ is controlled by an open-loop controller and incorporates a TD to avoid rapid changes in performance parameters. The operating principle of the control system module is shown in Figure 4 [34]. According to the parameter adjustment principle of the ADRC controller proposed by Gao ZQ [35], the parameters are set at ALT = 12.47 km, Ma = 2.0.

3. Results and Discussion

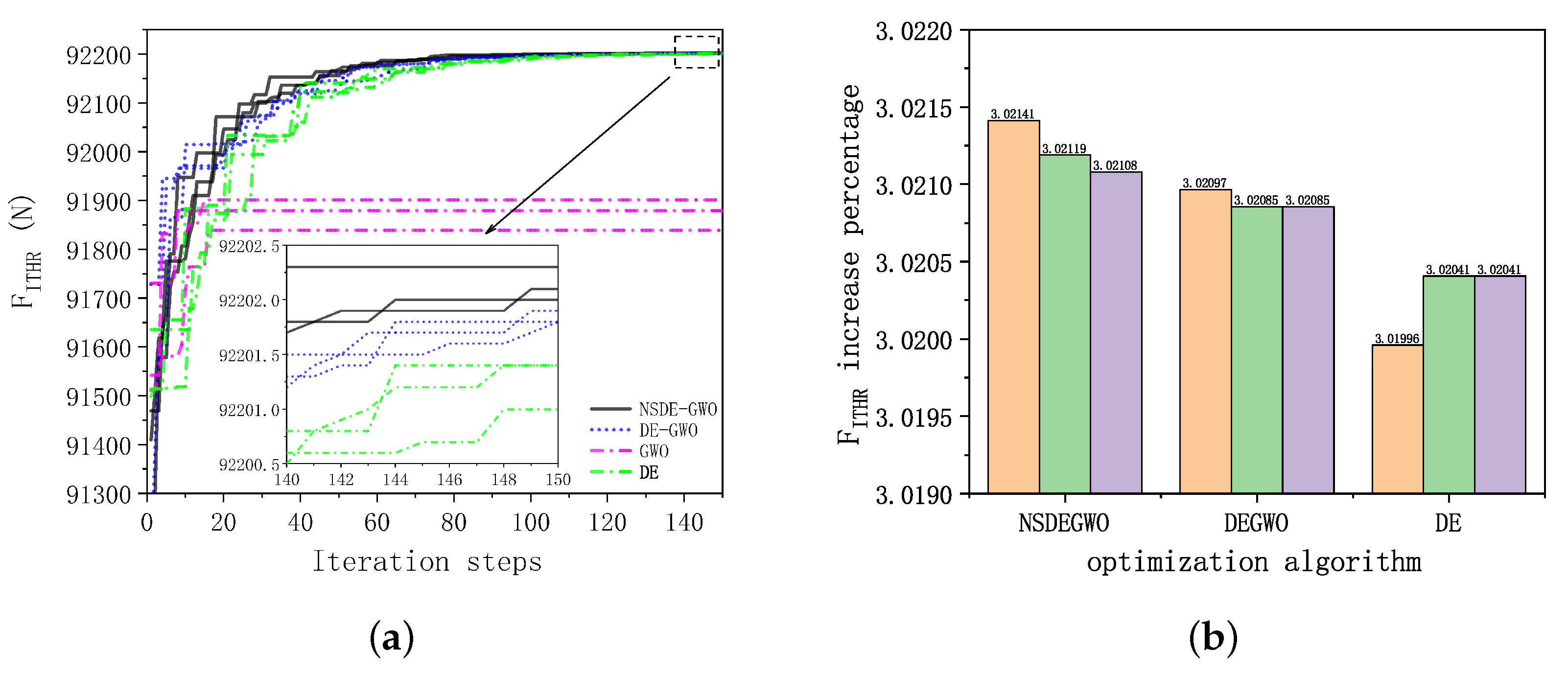
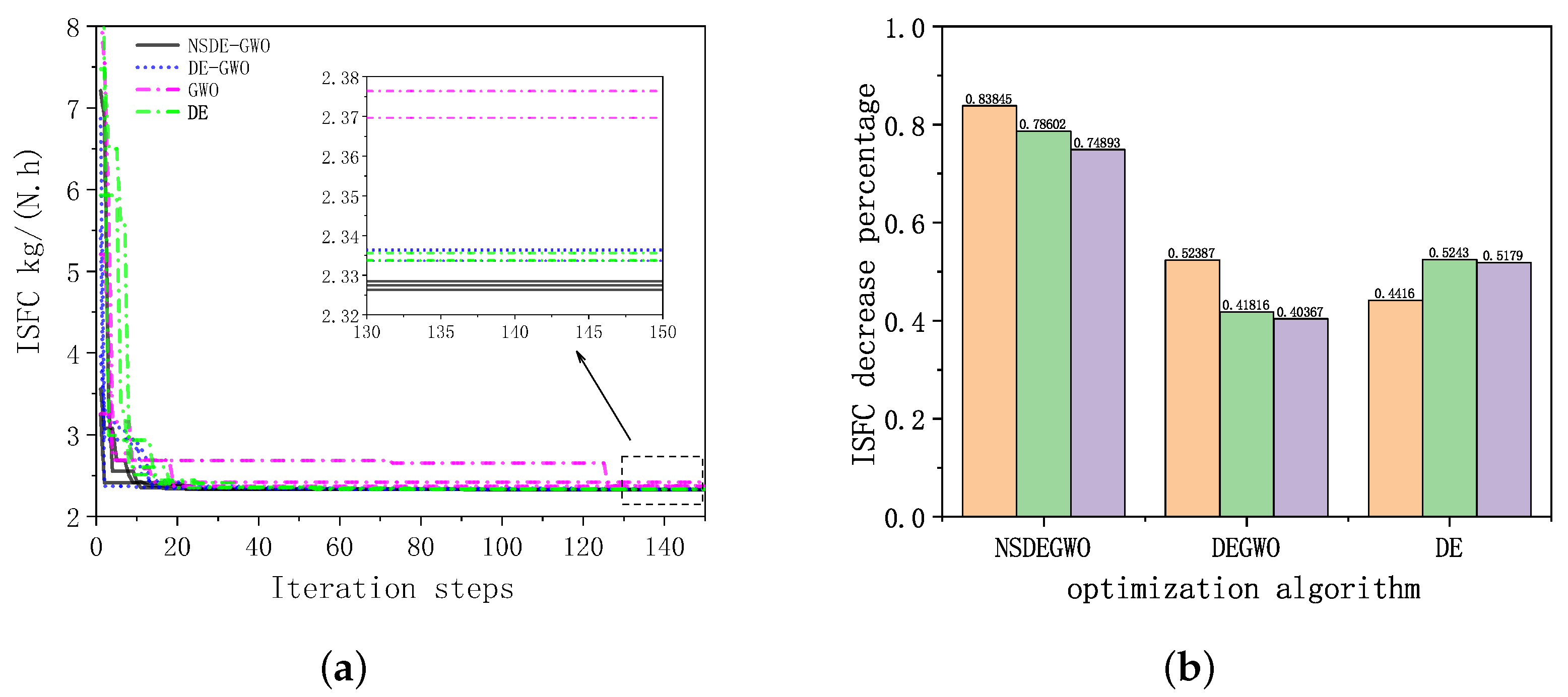
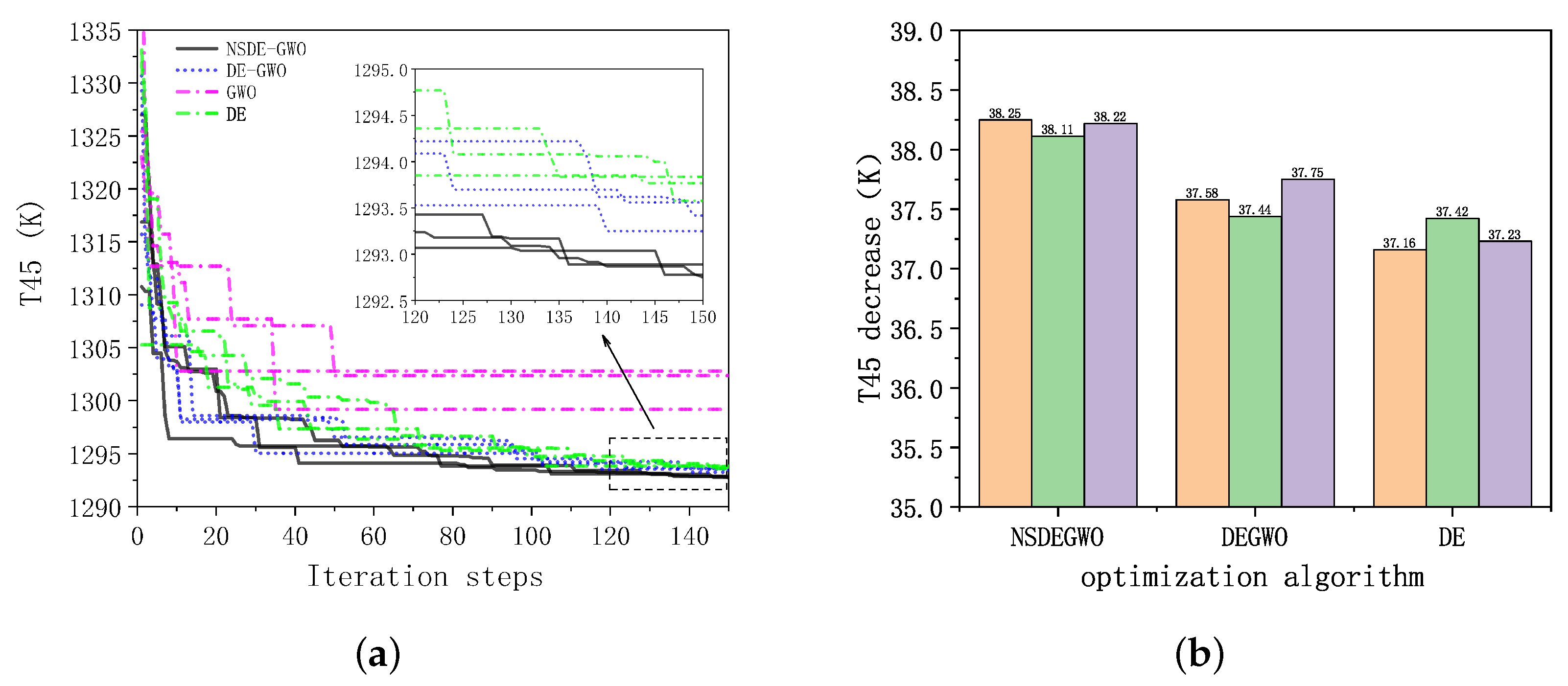
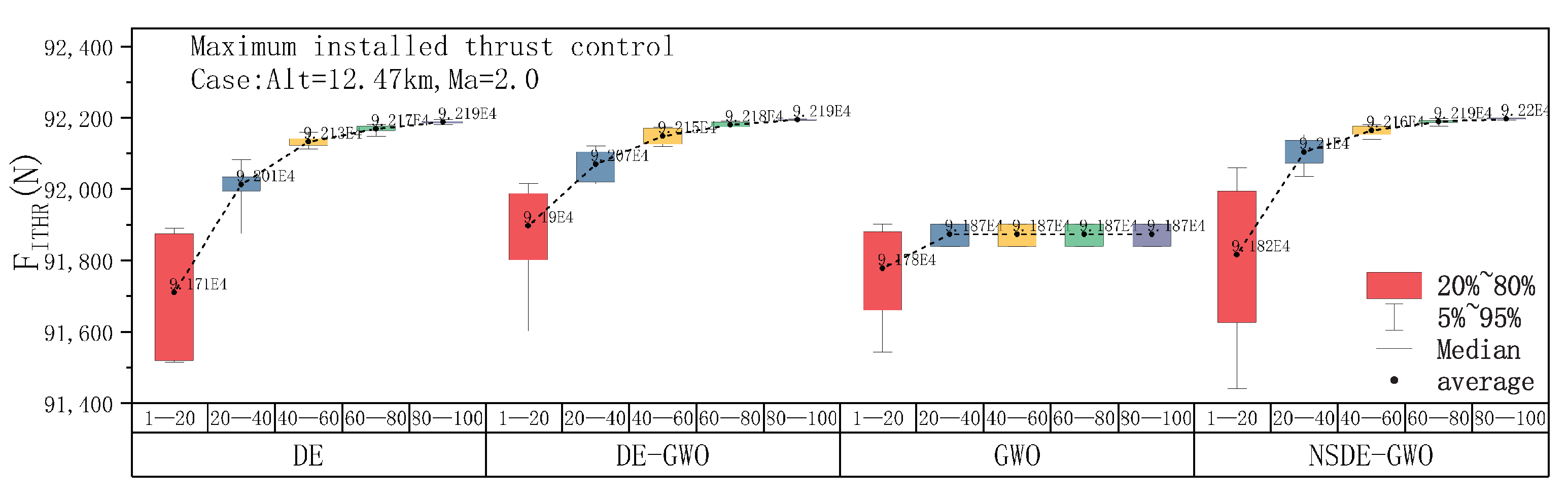
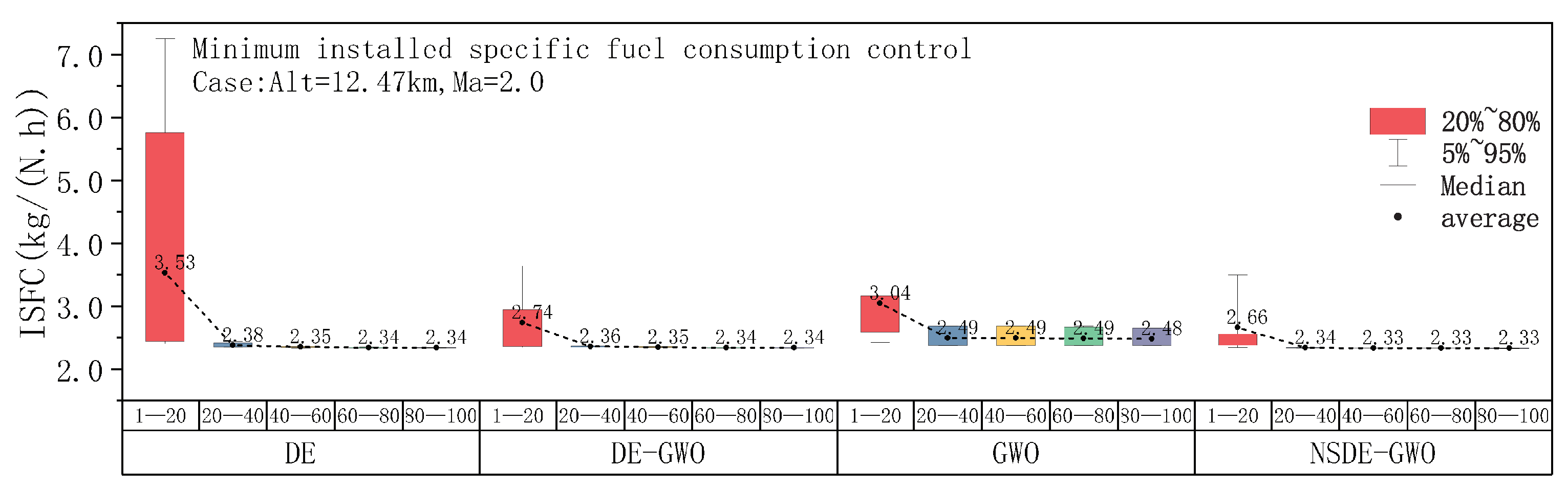
3.1. Comparison of PSC Results of Several Intelligent Algorithms

This research investigates the effects of various intelligent algorithms in the PSC to validate the efficacy of the NSDE-GWO hybrid algorithm. The GWO, DE, DE-GWO, and NSDE-GWO optimization algorithms are all verified. The inlet has a large capture flow under Alt = 12.47 km, Ma = 2.0, but the long inlet size makes the inlet work in the deep subcritical state. The initial population and the number of iteration steps are unchanged in four algorithms to exclude the effects of different parameters. Because of the randomness of the swarm-intelligence algorithm, each algorithm is optimized three times.

Table 1. Optimization of initial conditions and parameter ranges.

Optimization Variables	Initial Data	Optimization Range
Main fuel flow (kg/h)	4125.6	[3713, 4126]
Afterburner fuel flow (kg/h)	16,873.2	[15,187, 16,874]
Nozzle area (m2)	0.6685	[0.50, 0.67]
Fan guide vane angle (deg)	0	[−10, 10]
Compressor guide vane angle (deg)	0	[−10, 10]
Relative bleed adjustment (%)	0	[−10, 20]
First-stage ramp angle (deg)	2	[1, 5]
Second-stage ramp angle (deg)	1	[1, 5]

indicates the optimized initial conditions and the range of the optimization search for the control variables.

According to Figure 5a, DE, DE-GWO, and NSDE-GWO may greatly enhance the installed thrust, but GWO is sensitive to local convergence and has an unstable ultimate value of optimization. NSDE-GWO and DE-GWO combine the advantages of two intelligent algorithms and have a faster convergence speed during the iteration process. Furthermore, compared with DE-GWO, NSDE-GWO has faster calculation efficiency and globality, and the installed thrust of the optimization process is increased quickly, allowing for the ideal optimization result to be obtained within a restricted optimization time. To quantify the improvement effect of the installed thrust of different intelligent algorithms, Figure 5b shows the installed thrust optimization potentials of the three intelligent algorithms are similar; both are about 3%. NSDE-GWO has the largest percentage increase in the installed thrust, and the three optimization effects are close and have good stability.

Figure 6a reveals that DE, DE-GWO, and NSDE-GWO reach a lower fuel consumption level in the early stage of the iteration (about 20 steps), but the optimization speed in the later stage of the iteration is significantly reduced due to the influence of the objective function penalty function intervention. The diversity requirement of the population search is high, while the GWO can easily fall into local convergence, and the final value of the optimization is unstable. Figure 6b shows the percentage analysis of the mini-mum installed fuel consumption optimization potential of the three intelligent algorithms. It shows that NSDE-GWO has the highest minimum installed fuel consumption optimization percentage compared with DE-GWO and DE; it can reduce the minimum installed fuel consumption by 0.838%, which is 0.314% and 0.313% higher than DE and DE-GWO, respectively. The analysis shows that NSDE-GWO improves the randomness of the population updating in the later iteration of the model, and it is easier to search for lower fuel-consumption points.

Figure 7a shows the optimization effect of four intelligent algorithms for minimum turbine temperature control. Because the turbine temperature is mainly affected by the working state of the core components, there may be many groups of optimization input variables under the same turbine temperature conditions, which makes the optimization objective function more complex and presents a significant multi-peak state. The four intelligent algorithms do not achieve global convergence in a limited number of iteration steps. However, NSDE-GWO has faster optimization efficiency because it combines the advantages of the other two algorithms. Figure 7b shows the analysis of the lowest turbine temperature potential of the three intelligent algorithms. After 150 steps, the lowest turbine temperature of NSDE-GWO can be reduced by 38.25 k, while DE-GWO and DE can be reduced by 37.75 k and 37.42 k, respectively.

This study carries out a comprehensive analysis of the iterative process in steps 0–100; the algorithm’s iterative process from 0–100 steps is divided into five parts. The data during every 20 steps is used as a data set to draw a box plot. The median and average of each data set are shown in the graph. The 20% quantile is selected for IQR, and the outliers beyond the maximum and minimum observed values are not displayed. Figure 8 shows that the median and average value of GWO is larger than DE in the process of 1–20 steps, indicating that GWO has high optimization efficiency at the beginning of iteration. The volume of the GWO box is smaller than that of DE, which means that the GWO group of individuals gather faster, while that of DE is more scattered. However, the volume of the GWO box was larger and fell into local convergence during the 20–100 iteration steps, whereas the volume of the DE box gradually shrinks and tends to a fixed value, indicating that DE is better than GWO in global convergence. Compared to DE, DE-GWO has a higher median and average value for each data set, particularly in the early iterations. Although the box volume at the beginning of the iteration becomes larger, the average value of optimized thrust increases in 20–100 iteration steps, and the box volume decreases rapidly, demonstrating that the NSDE-GWO has better global convergence and iteration speed. Figure 9 shows that DE, DE-GWO, and NSDE-GWO can gain the ideal low fuel consumption within 1–20 iteration steps. The median, average, and box volume of the NSDE-GWO in steps 1–20 are significantly smaller, resulting in increased efficiency and stability. Figure 10 shows that the volume of the box does not decrease significantly with the increase in the iteration steps, and it is difficult for the four iterative algorithms to achieve global convergence. However, the NSDE-GWO average value is generally lower in 20–100 steps, indicating that the ideal temperature point can be found in limited iterations.

The above analysis demonstrates that a single intelligent algorithm cannot achieve the computational efficiency and accuracy requirement. The NSDE-GWO combines the benefits of the two methods and achieves the best results within all three control modes.

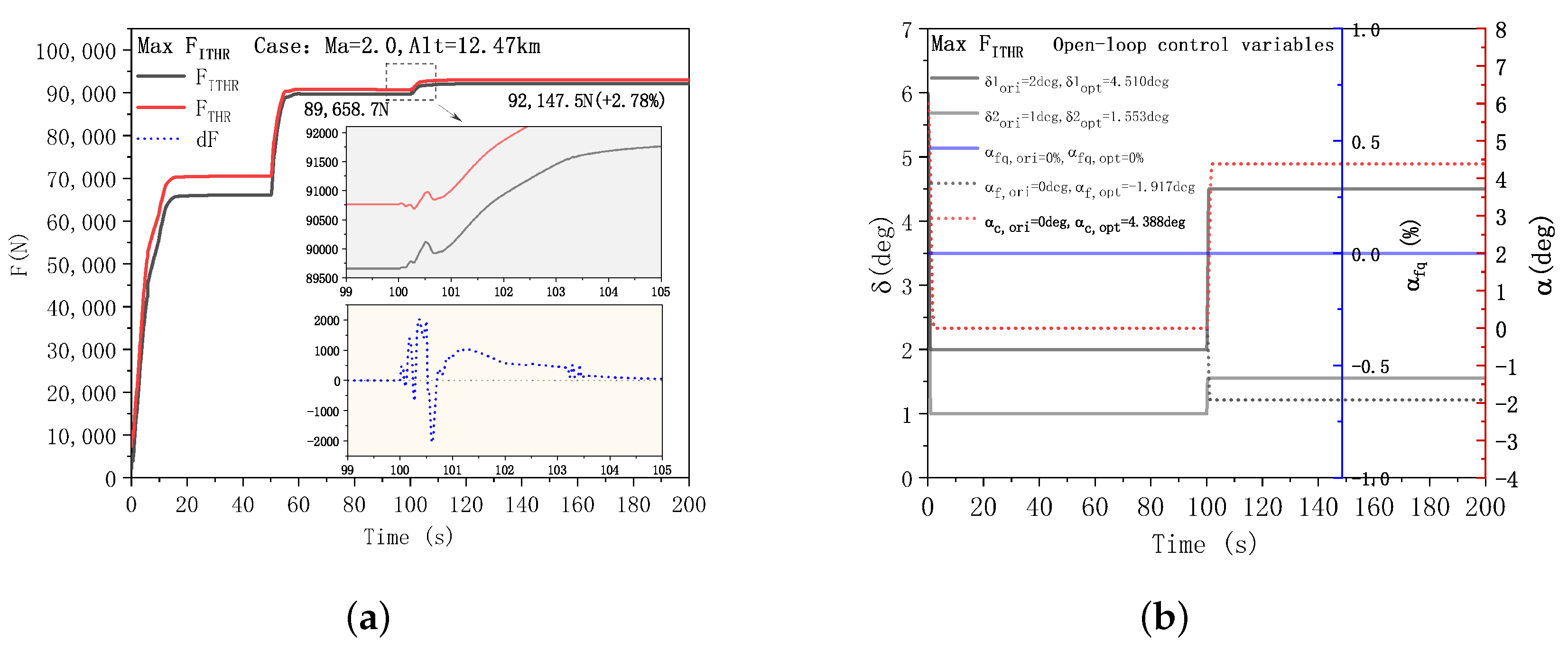
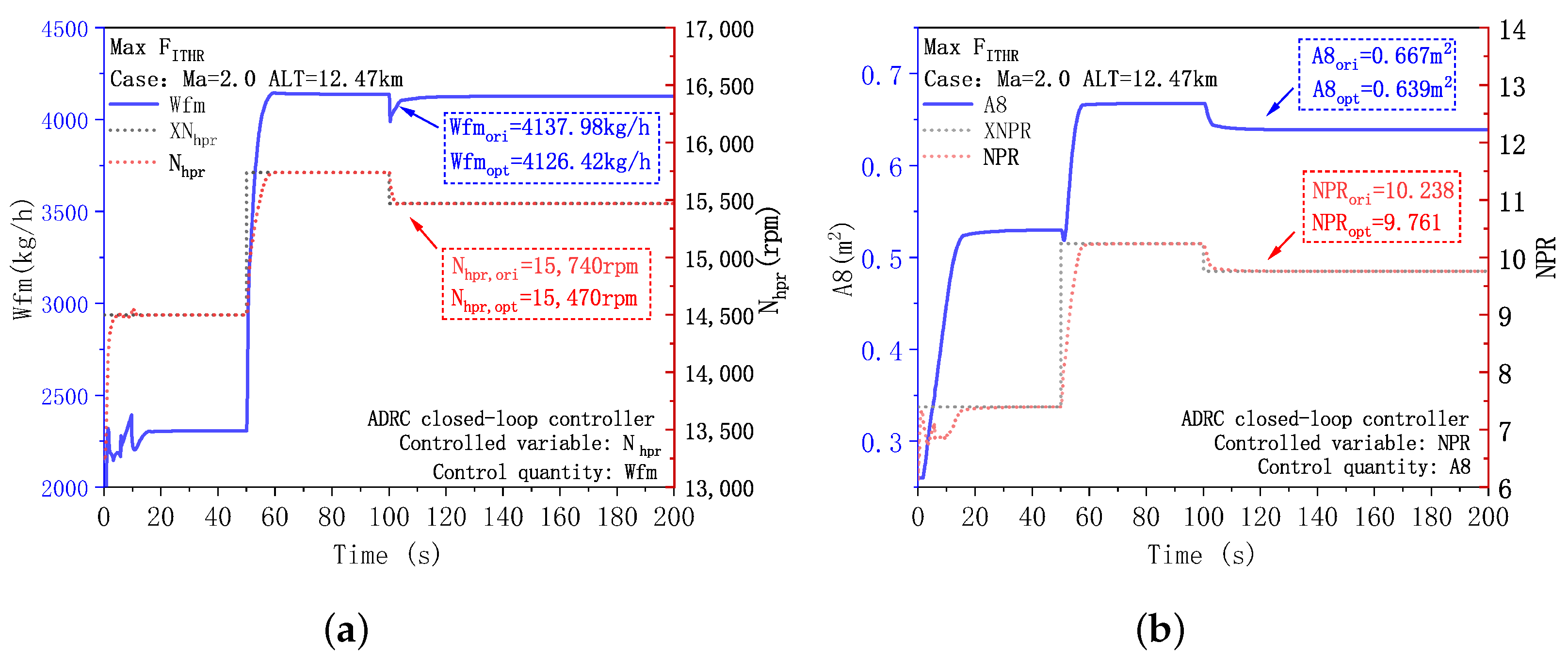
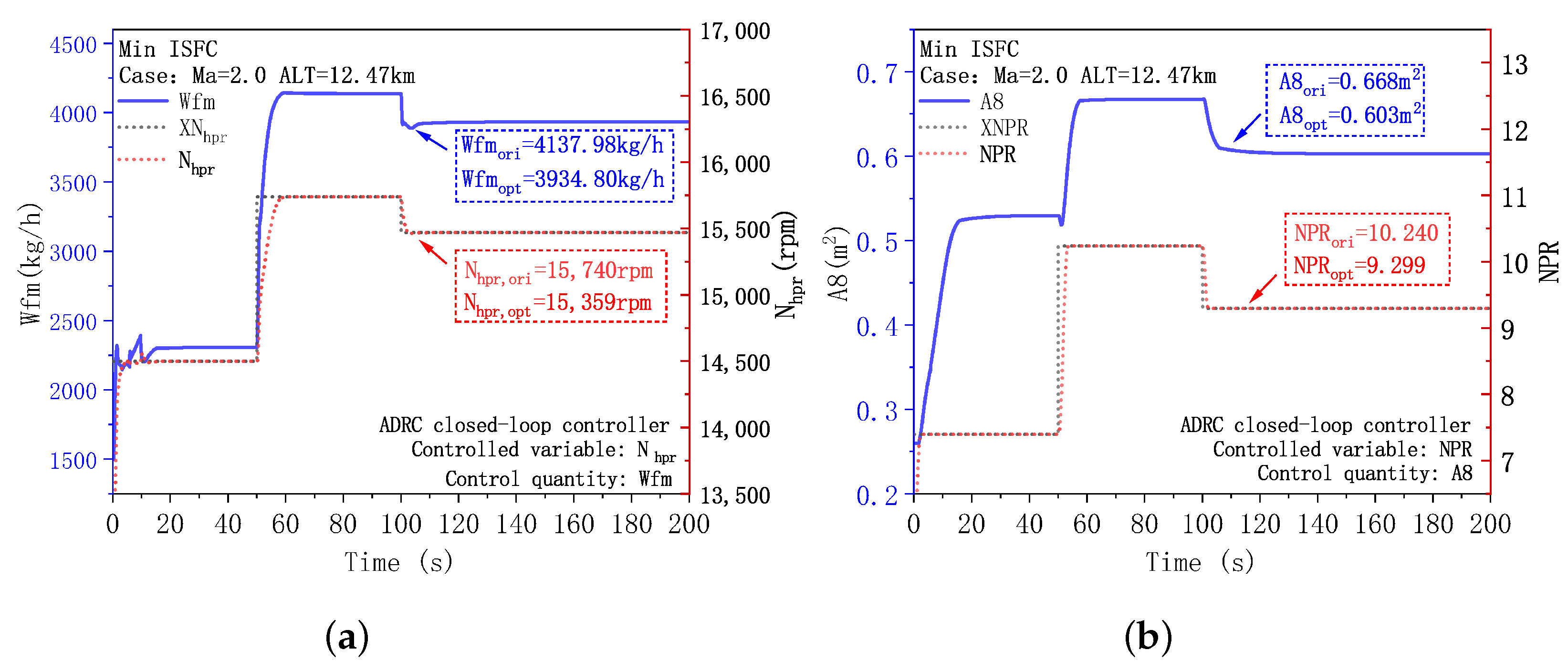
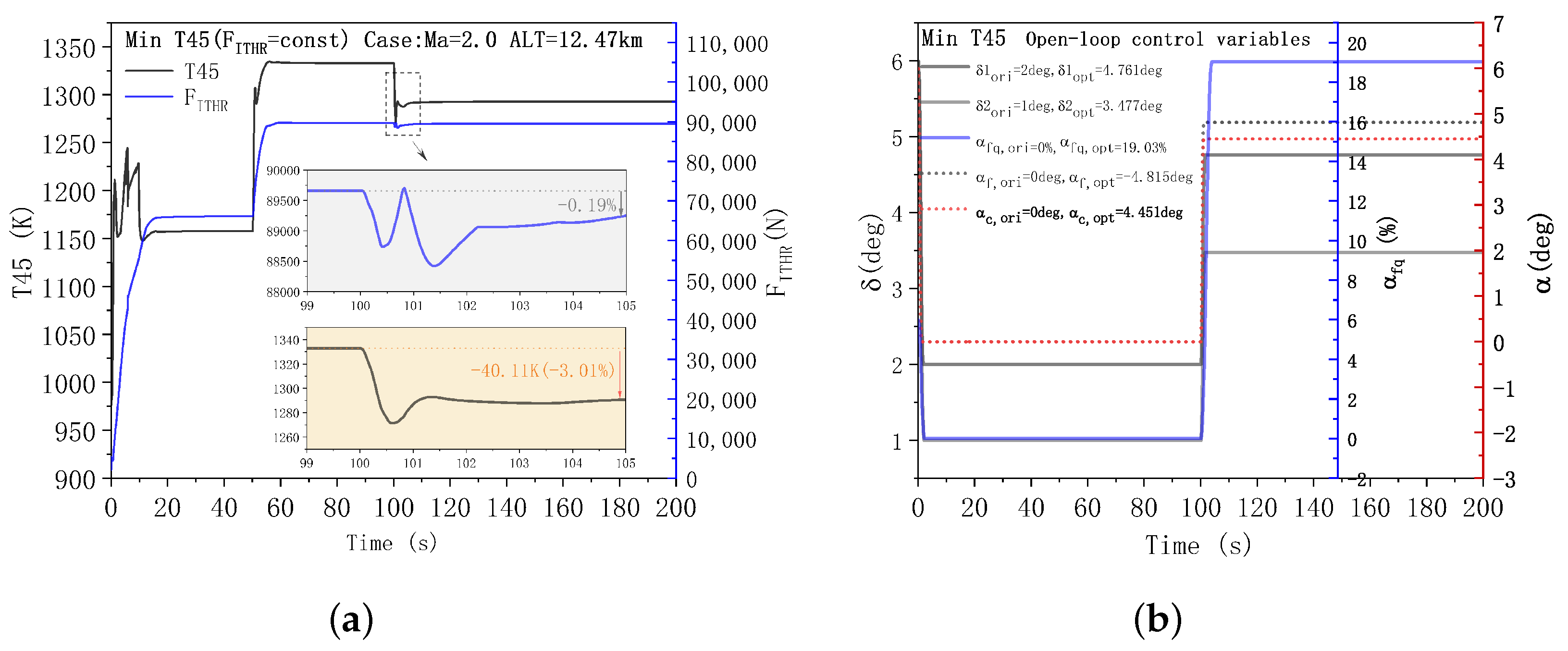
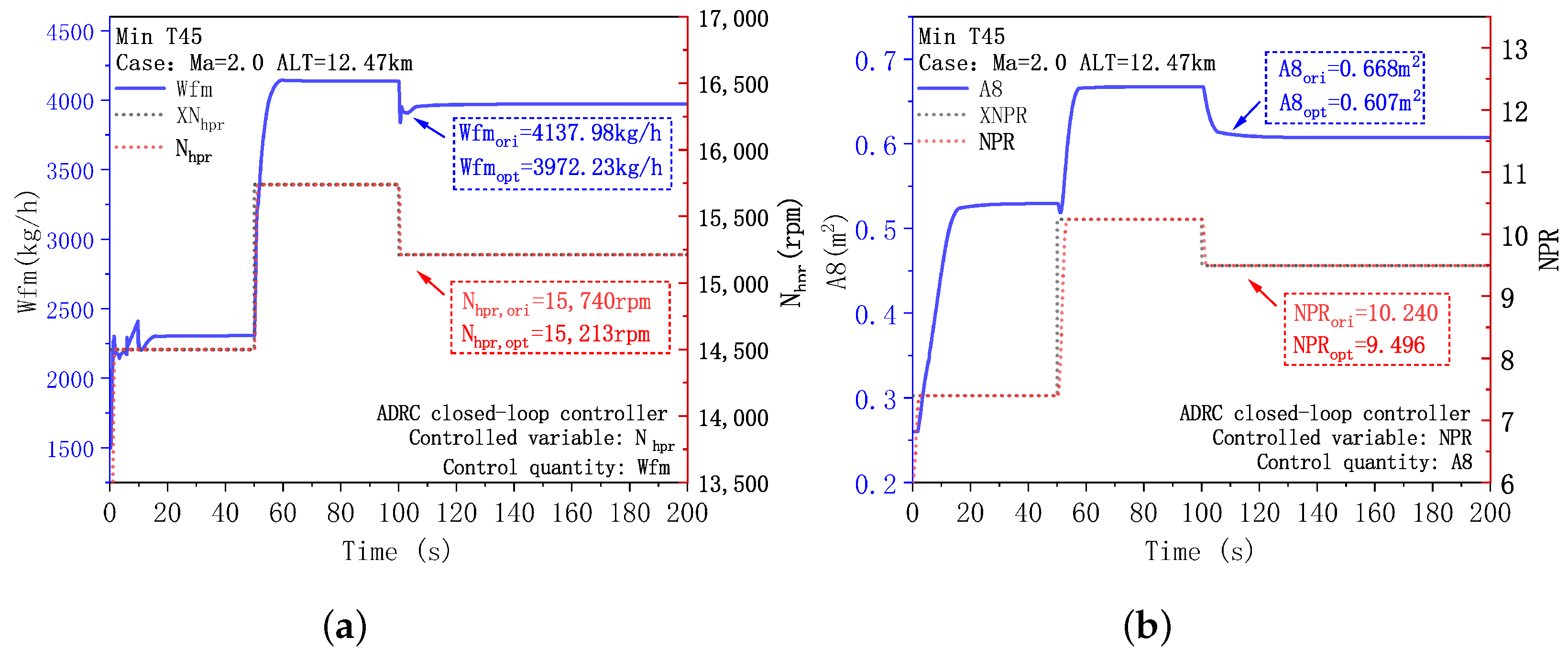
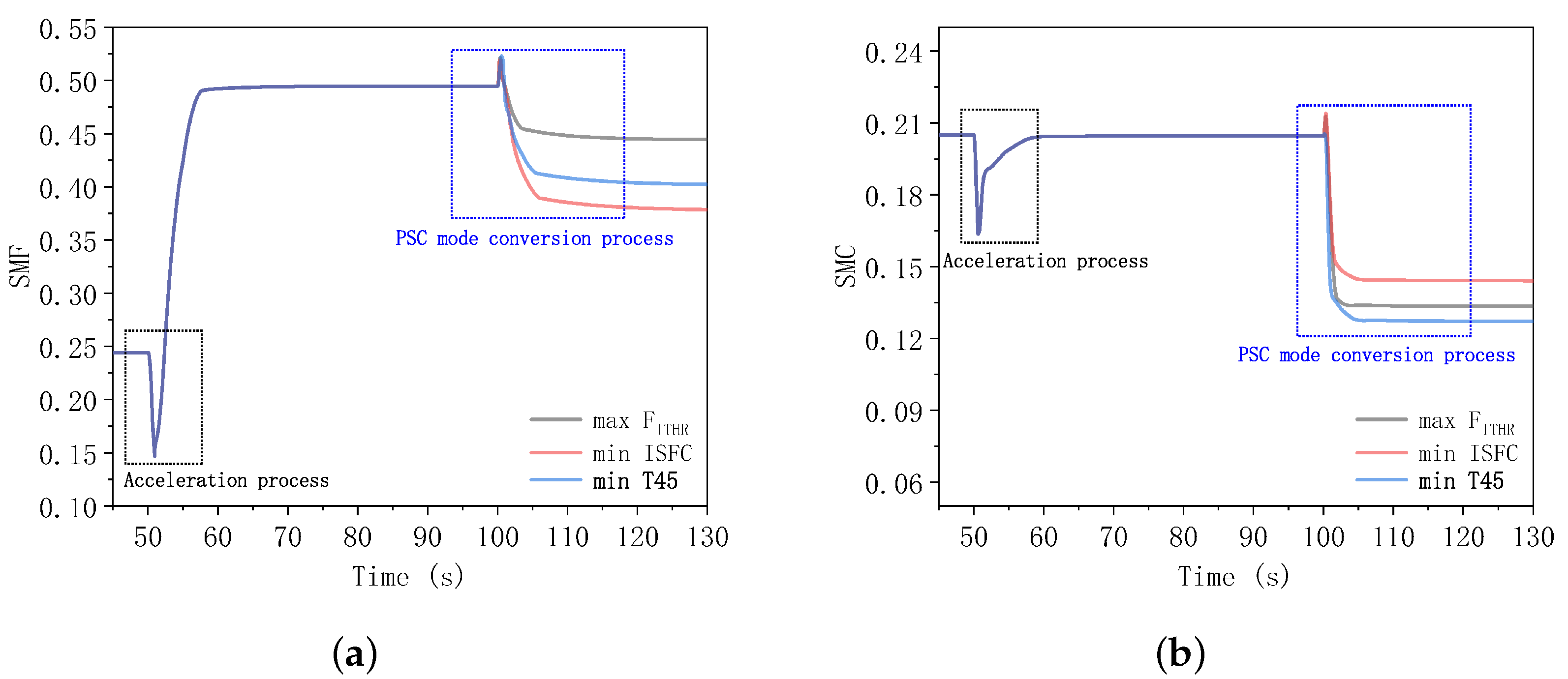
3.2. Analysis of the Performance Mode Transition of the Fusion Controller

In contrast to the previous studies, this study focuses on the analysis of the optimization effect potential brought about by the regulation of the inlet/engine matching at higher Mach number conditions (Ma = 2.0). At the same time, more attention is paid to the smooth switching of the dynamic process fusion controller because the optimization potential varies greatly among engines subject to different constraints and variable ranges. The ADRC closed-loop controller initially simulates the typical acceleration process (Times = 50–60 s) at supersonic conditions and switching from the quasi-steady state to the performance mode (Start time = 100 s). As shown in Figure 11a, the ADRC controller is able to achieve overshoot-free tracking relatively quickly during acceleration. At 100 s, the fusion controller transitions from the quasi-steady state mode to the performance mode, with the implementation of the transition being fed into the ADRC controller via optimized parameters from the PSC module. The maximum variance process during conversion for the dIFN is within 2000 N/s, and thrust smoothing is presented at 103.5 s. This demonstrates that the fusion controller is able to achieve no loss of installed thrust and only minor fluctuations during conversion, as well as obtain maximum thrust performance relatively rapidly. The optimized thrust is increased from 89,658.7 N to 92,147.5 N, about 2.78%, which is slightly below the optimized potential of the steady-state simulation in Section 3.1 and is thought to be caused by the closed-loop controller’s departure from the wfm and A8 dynamic inputs. Figure 11b represents the dynamic change process of multiple open-loop variables; the input process is the change law after the TD module. In Figure 12, X$N_{hpr}$ and XNPR are the controlled variables, wfm and A8 are the control quantities, and Nhc and NPR are the delay curves following the TD module. The TD smooths the target input without creating abrupt changes, and it is tuned using a gradient-optimization approach.

Figure 13 and Figure 14 represent the trends of the performance parameters and optimization variables under the min ISFC mode, and Figure 15 and Figure 16 represent the results under the min T45 mode. Figure 13a and Figure 15a show the results of the dynamic minimum ISFC and minimum T45 modes of the fusion-control system, respectively. Figure 13a reveals that an ISFC reduction of 0.73% can be achieved at 105s, with only a 0.28% reduction in installed thrust, basically achieving the requirement of no loss of thrust performance. The maximum fluctuation in thrust during the transition is within 0.9%, indicating that the fusion controller is able to achieve a smooth transition in the performance mode. Figure 13b indicates that the T45 can drop by 40.11 k, a reduction of 3.01% and a reduction in installed thrust of 0.19%. Compared to the min ISFC mode, the min T45 mode is optimized for high efficiency within Times = 100–101 s. This is due to the reason that the turbine temperature is mainly affected by the adjustment of the fan and compressor guide vane angle, which responds faster than the performance response of the inlet system adjustment. The change pattern of control variables is similar to the max $F_{ITHR}$ mode, which can achieve a faster response and a smoother transition of parameters.

Previous studies on Mach 0.7–1.5 PSC found that the optimization potential gradually decreases as the Mach number increases, with a 5% increase in thrust and a 2% decrease in SFC at Mach 1.4 [36], so the optimization potential of the engine itself will be lower at Mach 2.0 operating conditions, a trend that coincides with the optimization potential results in this paper. The increase in optimization variables leads to greater component potential, and the optimization potential of the lowest turbine temperature is improved compared to previous studies. The experimental study of the supersonic PSC showed a greater optimization potential in terms of thrust and fuel consumption (9%, 8%) due to the elevated amount of enriched fuel and main fuel, while our study kept essentially no increase in the fuel quantity, and the performance optimization potential was achieved mainly through the tuning of accessory components [7].

$Nfan,cor$ and $Ncom,cor$ indicate the fan relative corrected speed and the compressor relative corrected speed, respectively. As can be seen from

Table 2. Comparison of main parameters of PSC under Alt = 12.47 km Ma = 2.0.

Computational Term	Original Data	Optimized Data	Optimization Percentage (%)
Maximum installed thrust control
FITHR(N)	89,658.7	92,147.5	2.78
SMF	0.497	0.444	−10.66
SMC	0.205	0.133	−35.12
Nfan,cor	0.882	0.877	−0.57
Ncom,cor	0.973	0.957	−1.64
Minimum installed specific fuel-consumption control
FITHR(N)	89,658.7	89,410.63	−0.28
ISFC (kg/N.h)	2.343	2.326	−0.73
SMF	0.497	0.378	−23.94
SMC	0.205	0.144	−29.76
Nfan,cor	0.882	0.863	−2.15
Ncom,cor	0.973	0.952	−2.16
Minimum low-pressure turbine inlet temperature control
FITHR(N)	89,658.7	89,492.21	−0.19
T45 (K)	1332.83	1292.72	−3.01
SMF	0.497	0.401	−19.32
SMC	0.205	0.126	−38.54
Nfan,cor	0.882	0.824	−6.58
Ncom,cor	0.973	0.954	−1.95

, the value of $Nfan,cor$ and $Ncom,cor$ varies due to the inletmatching and the change of engine operating point. In addition, SMF and SMC are also significantly reduced, and the optimized point works closer to the surge line, suggesting that PSC redistributes the energy of the high- and low-pressure rotors. In the dynamic process Figure 17, the change of engine surge margin also needs to be demonstrated. During the acceleration process, there is a significant decline in the surge margin, but during the performance mode transition process due to the smooth transition of the fusion controller, a trend of rising and then decreasing surge margin is achieved. To sum up, the optimization path of PSC can be realized by simultaneously relying on inlet/engine matching and the guide vane angle adjustment of compression components; the installed thrust optimization can obtain greater optimization potential. The minimum fuel-consumption control and the minimum turbine temperature control can not only rely on the guide vane angle of the compression part but also compensate for the thrust loss caused by reducing the fuel flow through the inlet/engine matching.

In conclusion, the fusion controller is capable of achieving a smooth transition of performance modes to ensure that the engine maintains a stable thrust during the operation and that the dynamic optimization potential is conservative when compared to the ideal steady-state simulation results but has no effect on the overall control effect.

4. Conclusions

To improve the performance potential of the aero-propulsion system controller, the performance-seeking control effects of NSDE-GWO and different swarm-intelligence algorithms are compared, and a fusion-control system using the NSDE-GWO algorithm and ADRC to realize mode conversion is proposed. The following conclusions were obtained:

• Compared to other intelligent algorithms (DE, GWO, and DE-GWO), the NSDE-GWO hybrid algorithm offers larger potential for optimization, the highest iteration efficiency, and the greatest stability. It can obtain better results in three control modes. Under the conditions of Alt = 12.47 km, Ma = 2.0, the installed thrust is increased by 3.02%, the fuel consumption is reduced by 0.84%, and the temperature after high-pressure turbine is reduced by 3.01%.
• The fusion controller can produce a seamless transition of performance modes to guarantee that the engine maintains a stable thrust throughout operation; the dynamic optimization potential is conservative when opposed to ideal steady-state simulation outputs. The maximum thrust mode is capable of achieving no thrust drop and a maximum fluctuation rate within 2000 N/s. In the minimum installed fuel consumption mode, the greatest fluctuation in thrust during the changeover is less than 0.9%, and the minimum turbine temperature mode also has smaller volatility and higher optimization efficiency.