An Efficient Approach for Parametric Modeling and Prediction of the Hollow Blade Manufacture Shape
Abstract
:1. Introduction
2. Numerical Methodology
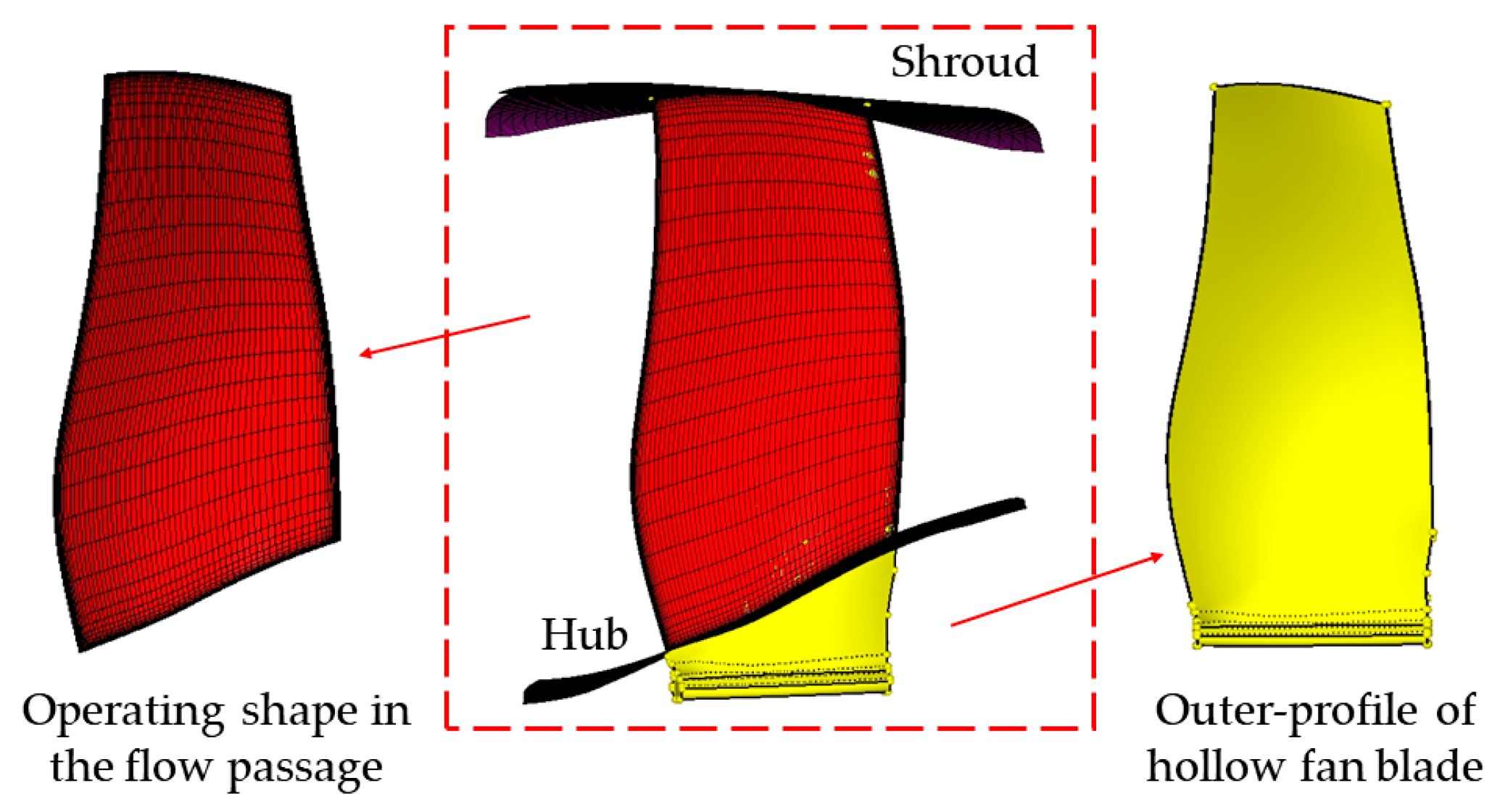
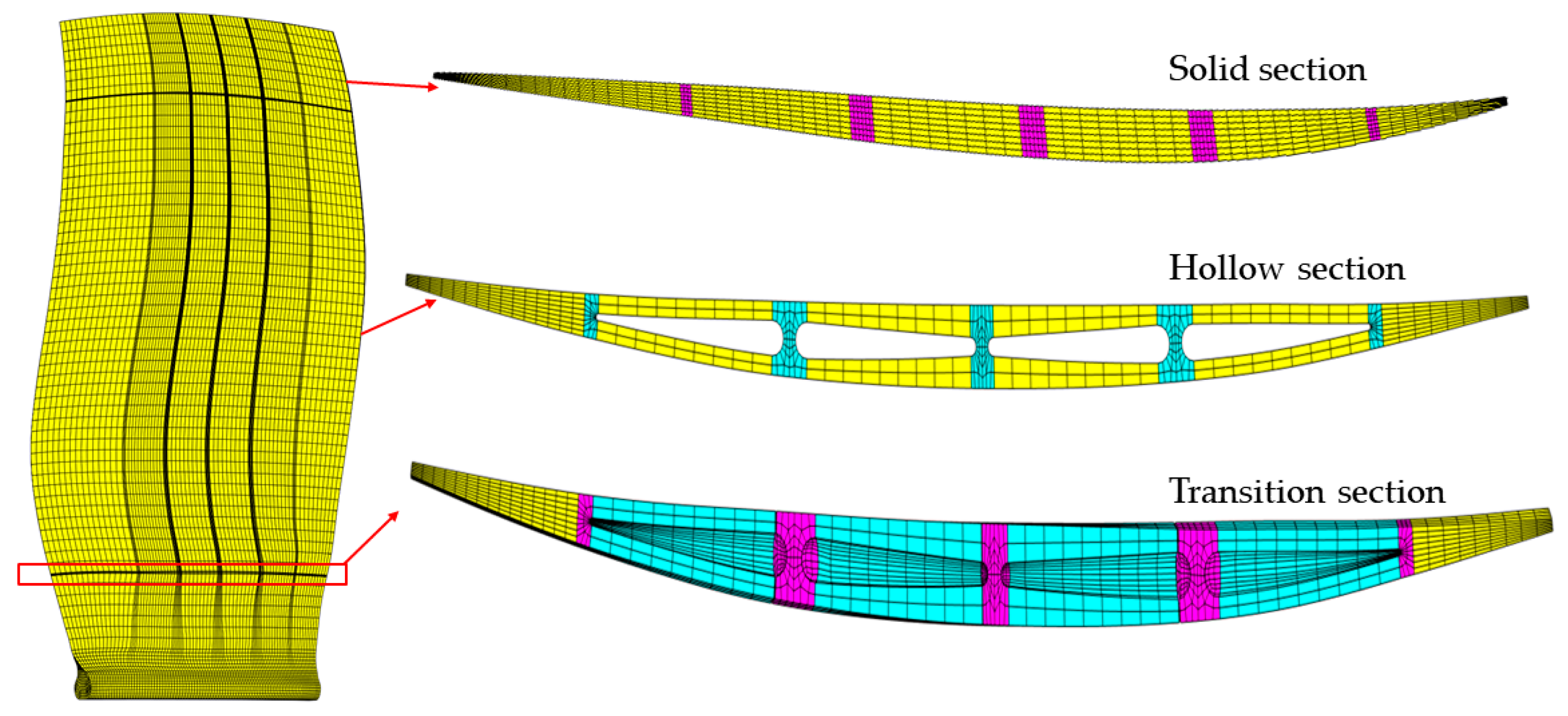
2.1. Model Parameterization of Hollow Fan Blade
2.2. Auto-Generation Method of FEM
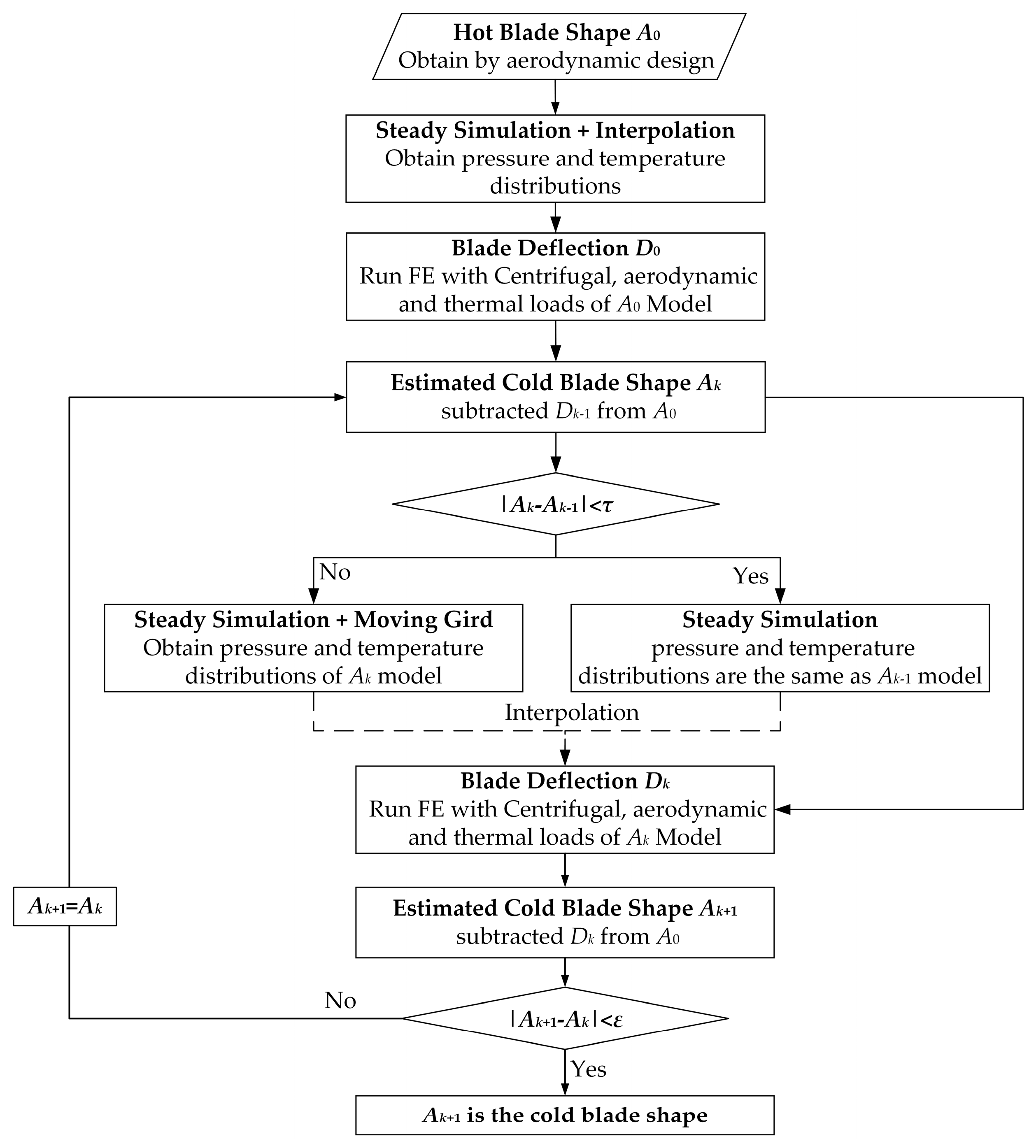
2.3. Hot-to-Cold Analysis Methods
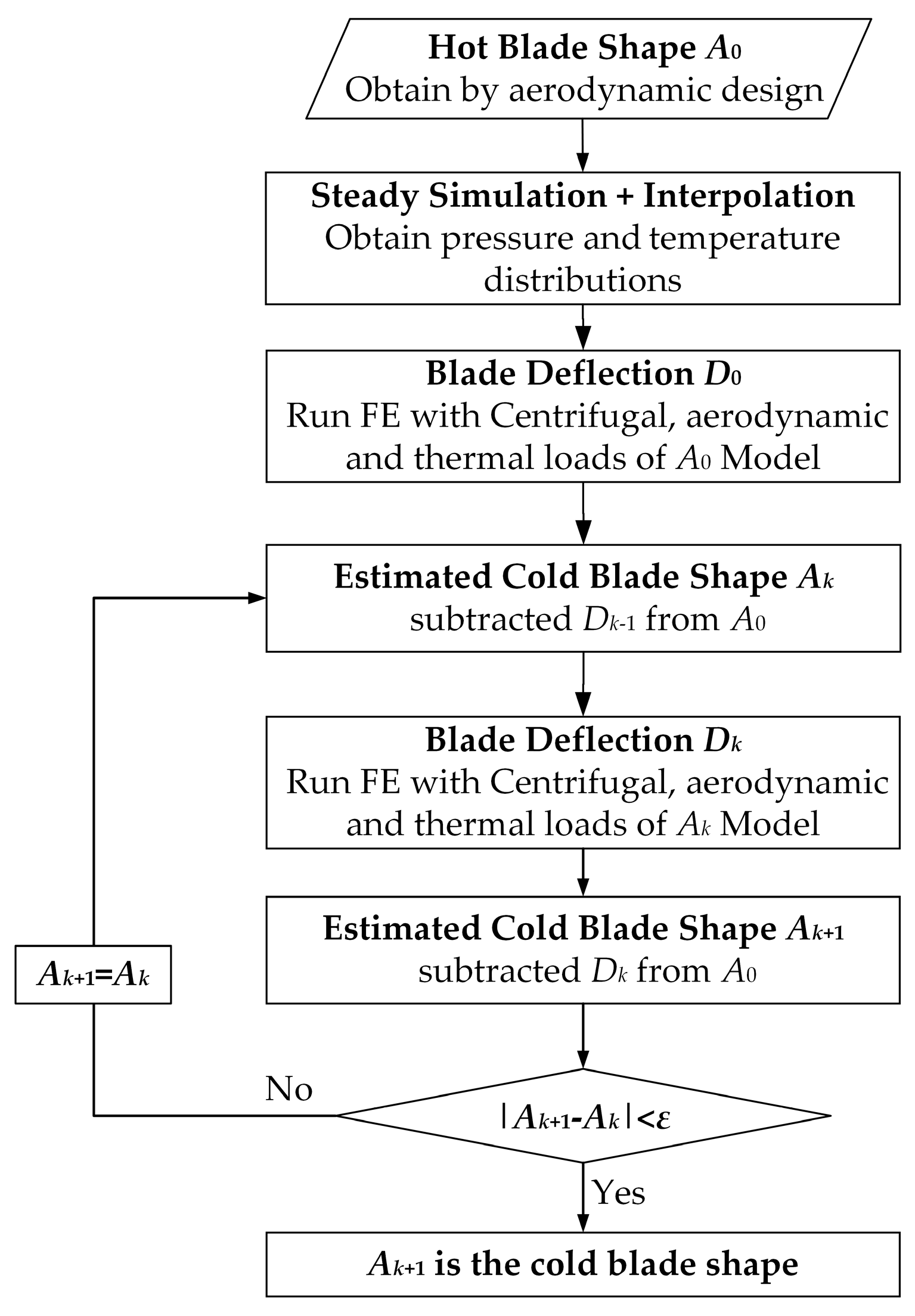
2.3.1. Uncoupling Method without Flow Simulation (UCM)
2.3.2. Weak Coupling Method with Steady Simulation (WCS)
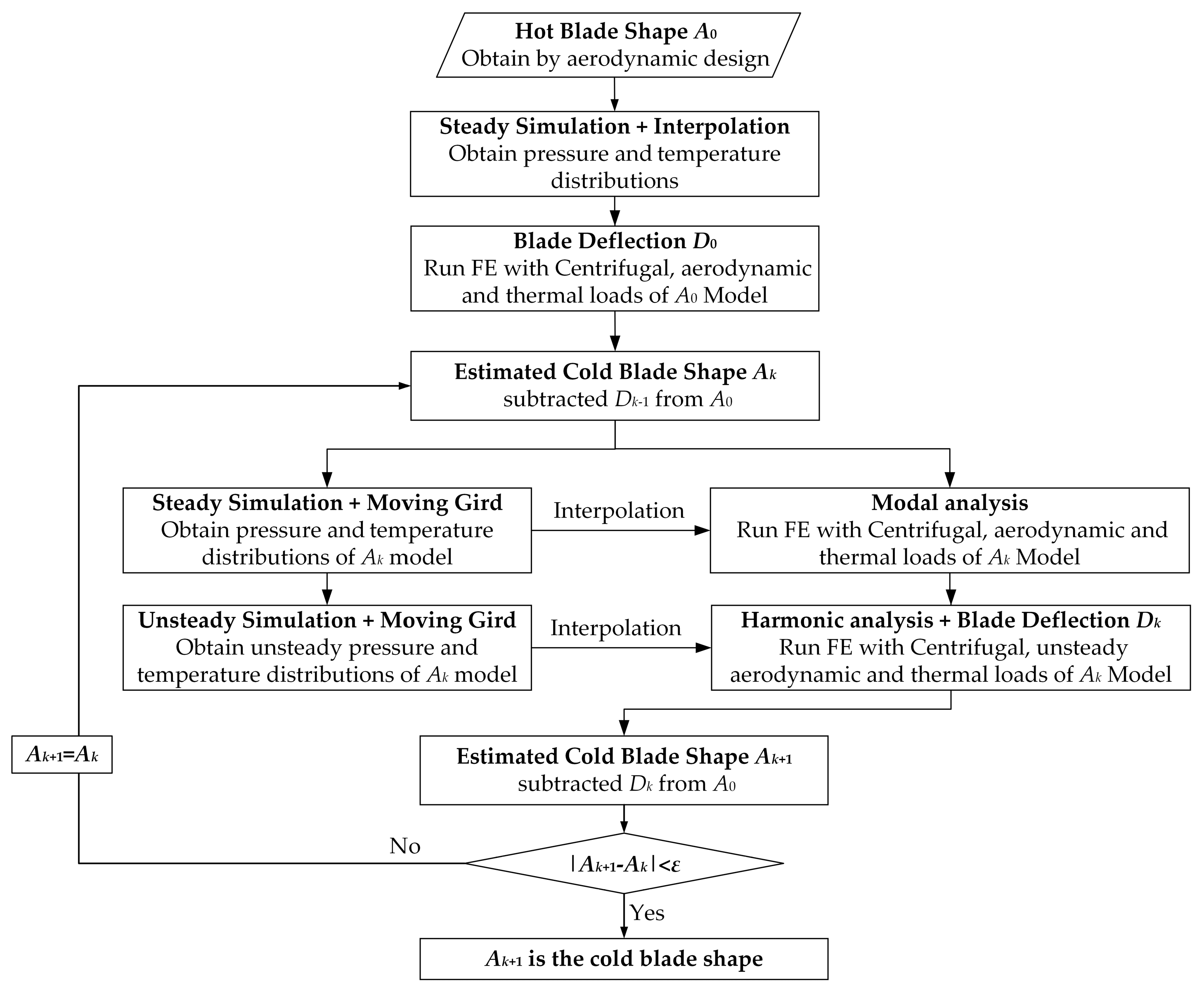
2.3.3. Strong Coupling Method with Unsteady Simulation (SCU)
2.3.4. Strong-Weak Coupling Method with Steady Simulation (SWCS)
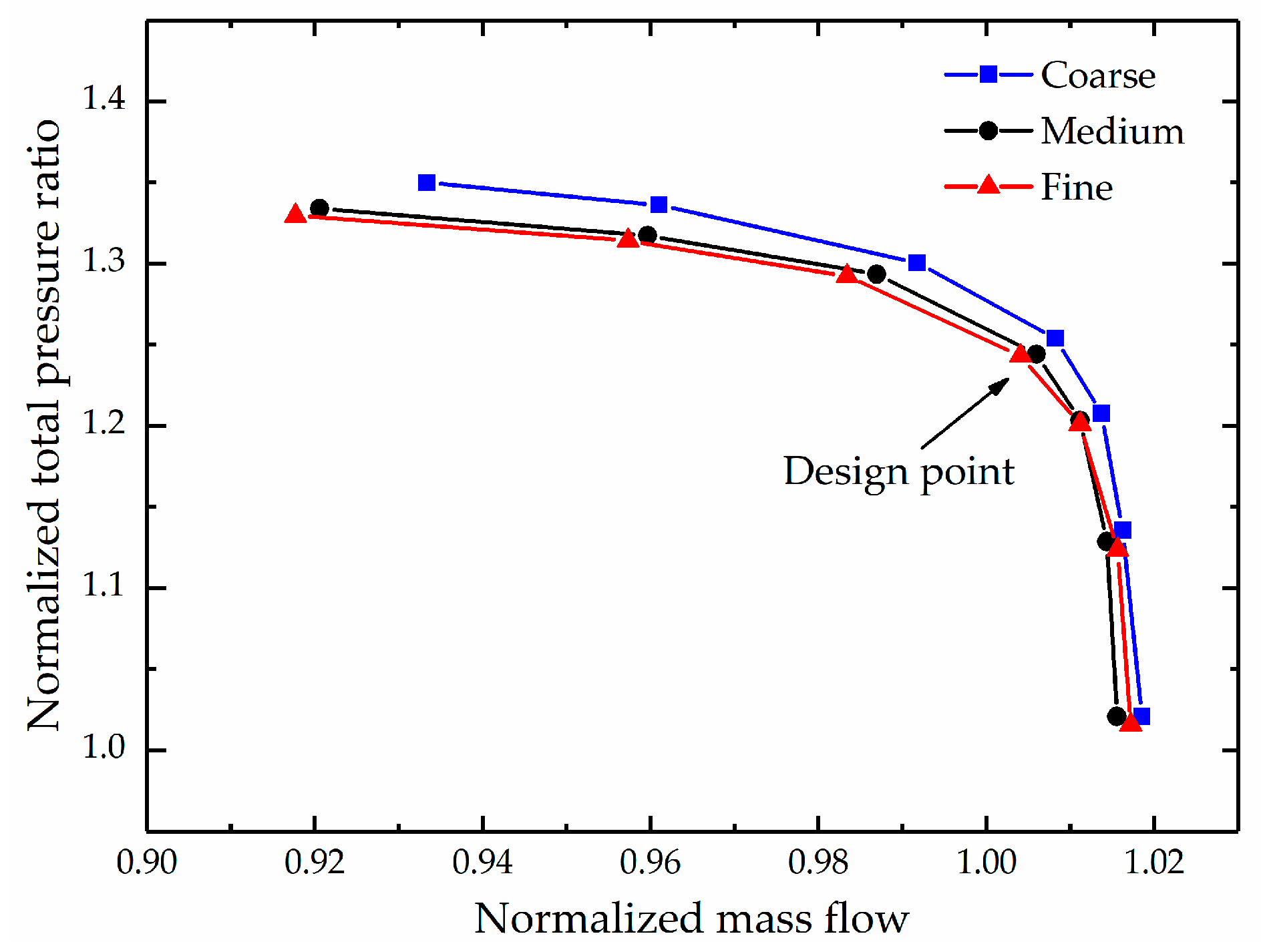
3. Test Case
4. Results and Discussions
4.1. Modeling of Hollow Fan Blade
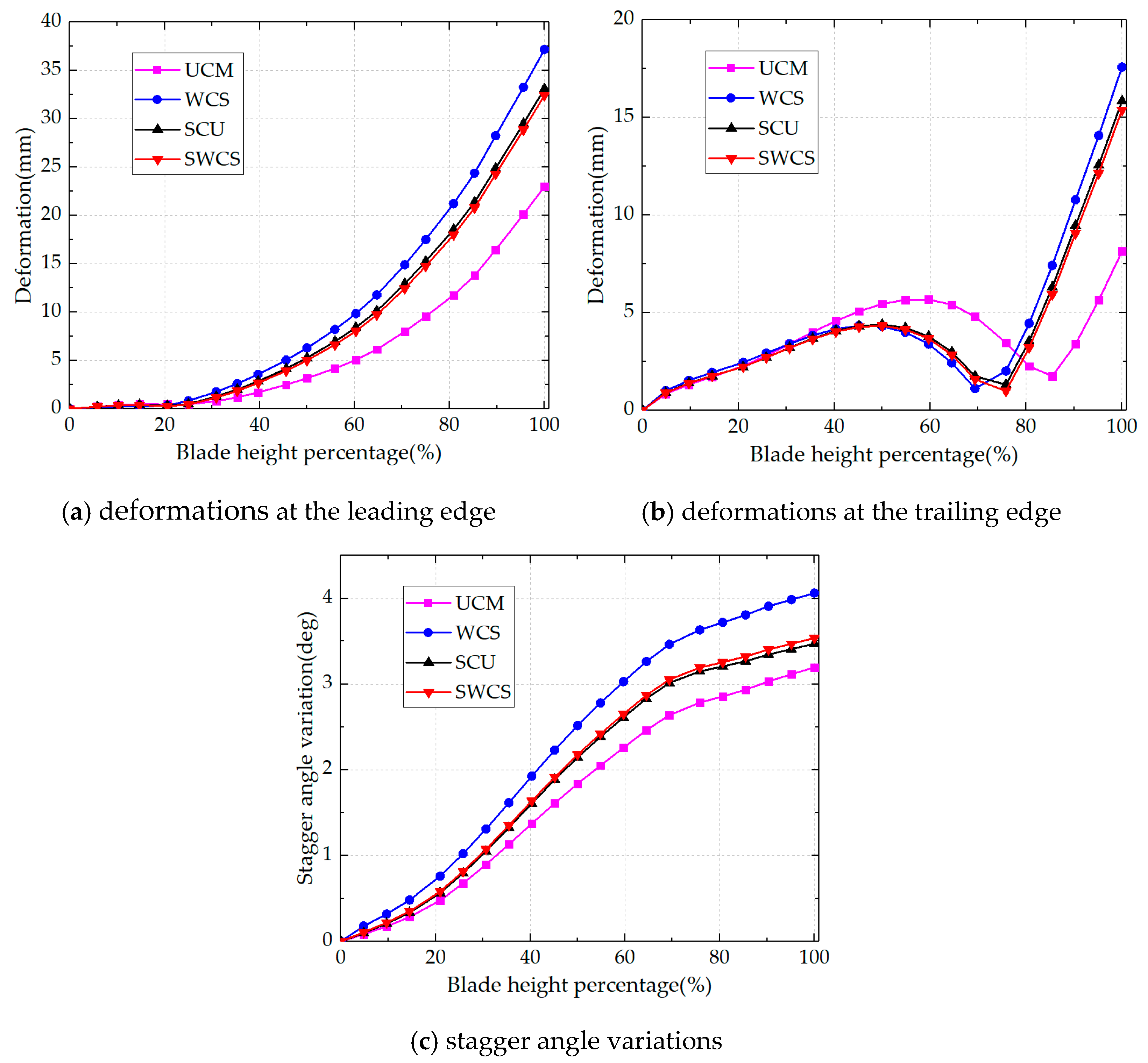
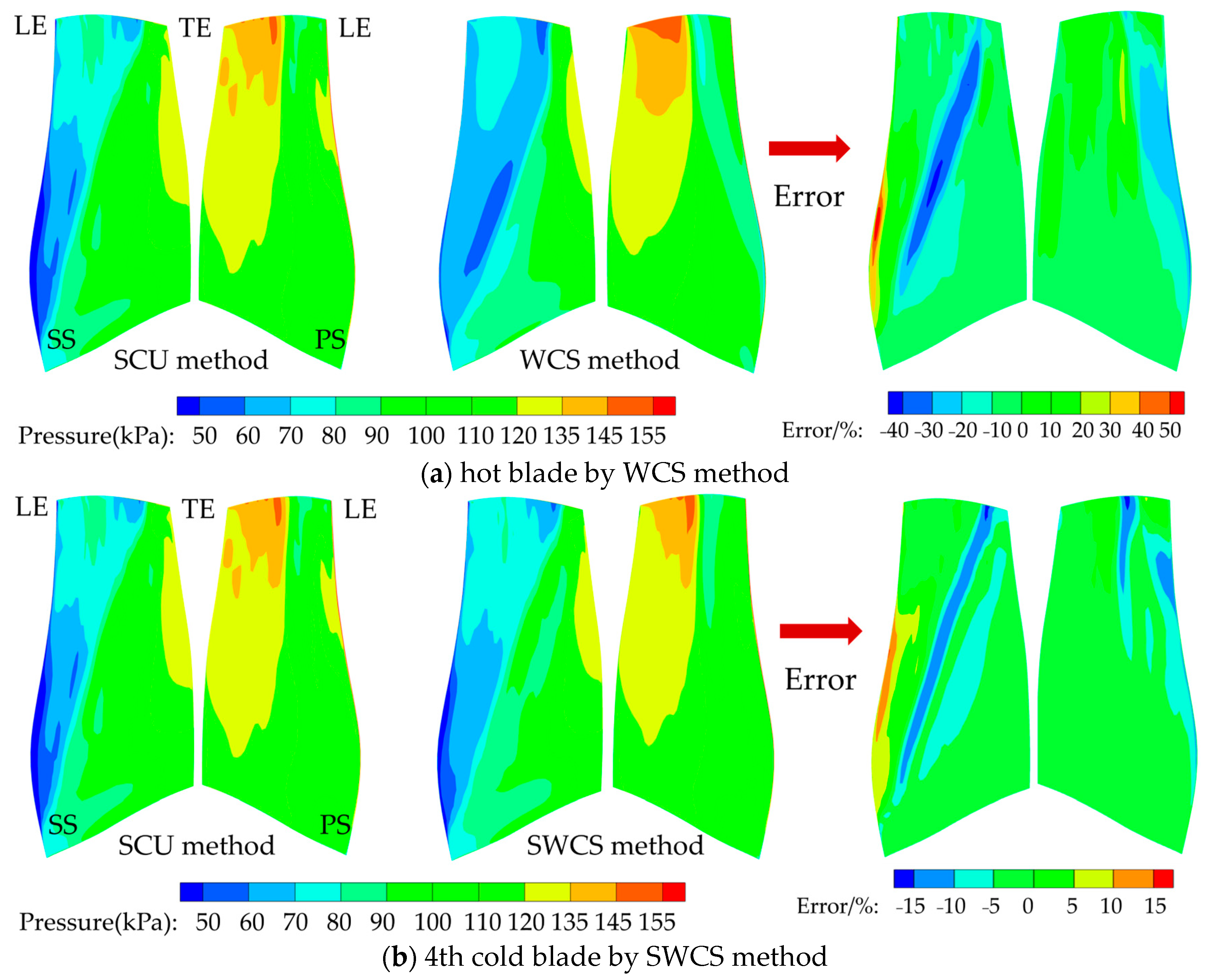
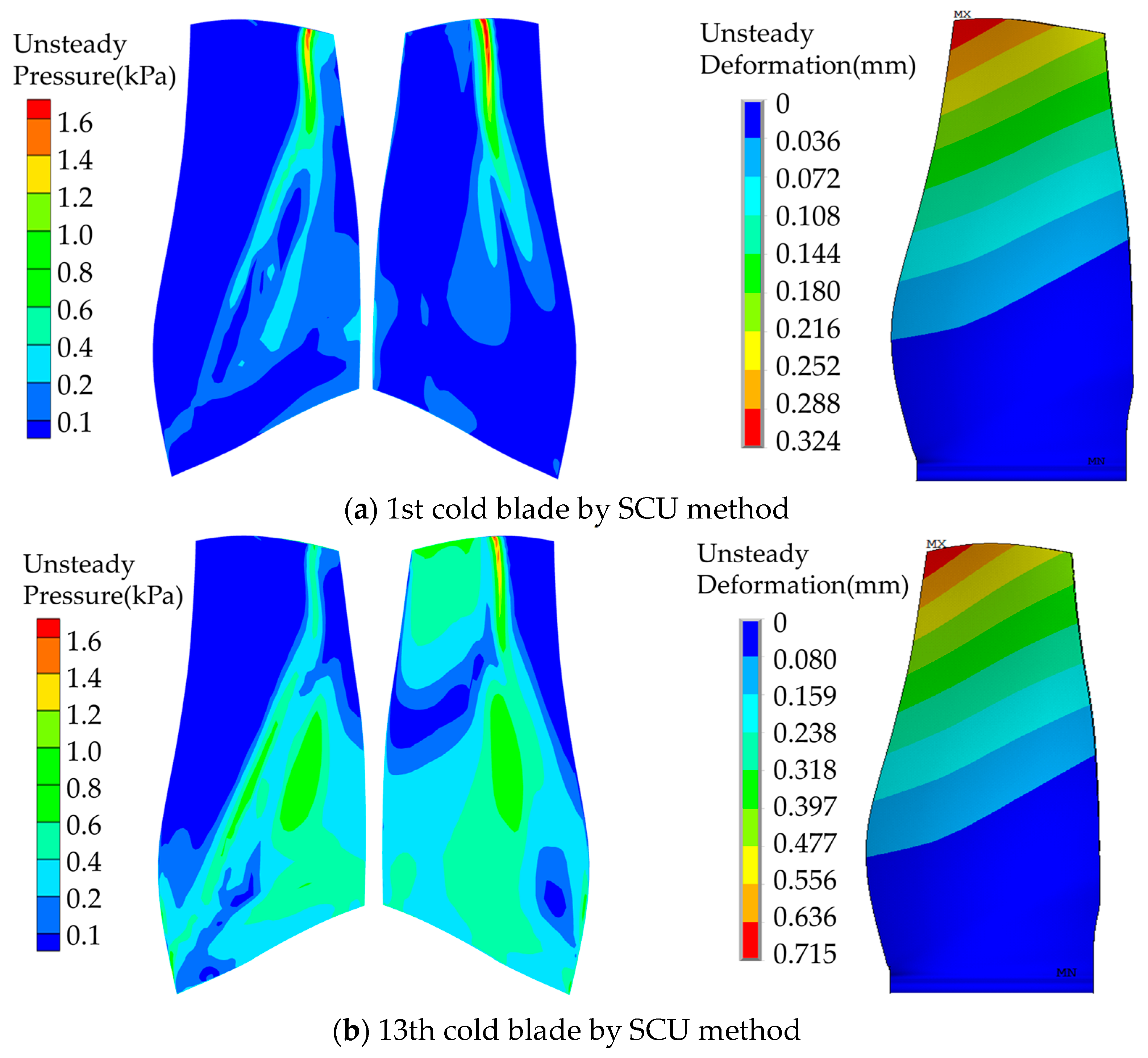
4.2. Comparison of Hot-to-Cold Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fitzgerald, G.; Broughton, T. The Rolls-Royce wide chord fan blade. In Proceedings of the 1st International Conference of the Titanium Products and Applications, San Francisco, CA, USA, 19–22 October 1986; pp. 1–19. [Google Scholar]
- Halle, J.; Michael, C. Energy Efficient Engine Fan Component Detailed Design Report; NASA: Washington, DC, USA, 1981; Report No.: NASA-CR-165466. [Google Scholar]
- Michael, C. Energy Efficient Engine Shroudless, Hollow Fan Blade Technology Report; NASA: Washington, DC, USA, 1982; Report No.: NASA-CR-165586. [Google Scholar]
- Xun, Y.; Tan, M. Applications of superplastic forming and diffusion bonding to hollow engine blades. J. Mater. Process. Technol. 2000, 99, 80–85. [Google Scholar] [CrossRef]
- Li, G.; Tan, M.; Liew, K. Three-dimensional modeling and simulation of superplastic forming. J. Mater. Process. Technol. 2004, 150, 76–83. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Chen, W.; Jiang, X. Parametric study on the flutter sensitivity of a wide-chord hollow fan blade. Chin. J. Aeronaut. 2022, 35, 277–293. [Google Scholar] [CrossRef]
- Kosmatka, J.; Mehmed, O. Development of an integral damping treatment for NASA’s next-generation hollow fan blades. In SPIE 4697, Smart Structures and Materials 2002: Damping and Isolation; SPIE: San Diego, CA, USA, 2002; Volume 4697, pp. 15–24. [Google Scholar]
- Kosmatka, J. Design and spin testing of integrally damped hollow core composite fan blades. In Proceedings of the 46th AIAA Structures, Structural Dynamics and Materials Conference, Austin, TX, USA, 18–21 April 2005; AIAA: Reston, VA, USA, 2005. Report No.: AIAA-2005-2032. [Google Scholar]
- Eberlinc, M.; Širok, B.; Hočevar, M. Experimental investigation of the interaction of two flows on the axial fan hollow blades by flow visualization and hot-wire anemometry. Exp. Therm. Fluid Sci. 2009, 33, 929–937. [Google Scholar] [CrossRef]
- Velicki, A. SPF/DB Hollow Core Fan Blade. United States Patent US 5240376, 31 August 1993. [Google Scholar]
- McKaveney, C.; Wang, L. Hollow Fan Blade Rib Geometry. United States Patent US 0078703 A1, 28 March 2013. [Google Scholar]
- Weisse, M.; McKaveney, C. Hollow Fan Blade Channel Con-Figuration to Reduce Stress. U.S. Patent US 8801367 B2, 12 August 2014. [Google Scholar]
- Ogawa, A.; Sofue, Y.; Isobe, T. Structural Analysis of Hollow Blades: Torsional Stress Analysis of Hollow Fan Blades for Aircraft Jet Engines; NASA: Washington, DC, USA, 1979; Report No.: NASA-TM-75718. [Google Scholar]
- Kajbyshev, O.; Galimov, A.; Kruglov, A.; Lutfullin, R.; Safiullin, R. Numerical analysis of the hollow fan blade design. Probl. Mashinostraeniya I Nadezhnosti. Mashin. 2004, 2004, 90–95. [Google Scholar]
- Kielb, R. Mass balancing of hollow fan blades. J. Eng. Gas Turbines Power 1986, 108, 577–582. [Google Scholar] [CrossRef]
- Meng, J.; Liao, L.; Li, D.; Cao, Y.; Yang, L.; Chen, Y. Topology optimization method research on hollow wide-chord fan blade of a high-bypass turbofan engine. Procedia Eng. 2015, 99, 1228–1233. [Google Scholar] [CrossRef]
- Ma, Y.; Xu, S.; Liu, H.; Wang, X. Optimization of reinforcing ribs of a hollow fan blade using metamodel-based optimization algorithm. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, Republic of Korea, 13–17 June 2016; pp. 1–8. [Google Scholar]
- Audic, S.; Berthillier, M.; Bonini, J. Prediction of bird impact in hollow fan blades. In Proceedings of the 36th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Las Vegas, NV, USA, 24–28 June 2000; pp. 1–7. [Google Scholar]
- Hou, N.; Li, Y.; Liu, J. Numerical simulation of bird impact on hollow blades of titanium fan assembly. J. Aerosp. Eng. 2019, 32, 04019044. [Google Scholar] [CrossRef]
- Wilson, M.; Imregun, M.; Sayma, A. The effect of stagger variability in gas turbine fan assemblies. J. Turbomach. 2007, 129, 404–411. [Google Scholar] [CrossRef]
- Kallesøe, B.; Hansen, M. Some effects of large blade deflections on aeroelastic stability. In Proceedings of the 47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. AIAA 2009-839. [Google Scholar]
- Fu, Z.; Wang, Y.; Jiang, X.; Wei, D. Tip clearance effects on aero-elastic stability of axial compressor blades. J. Eng. Gas Turbines Power 2015, 137, 012501. [Google Scholar] [CrossRef]
- Yang, H.; Zheng, Y. A fluid-structure coupling method for rotor blade unrunning design. In Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013; pp. 1–10. [Google Scholar]
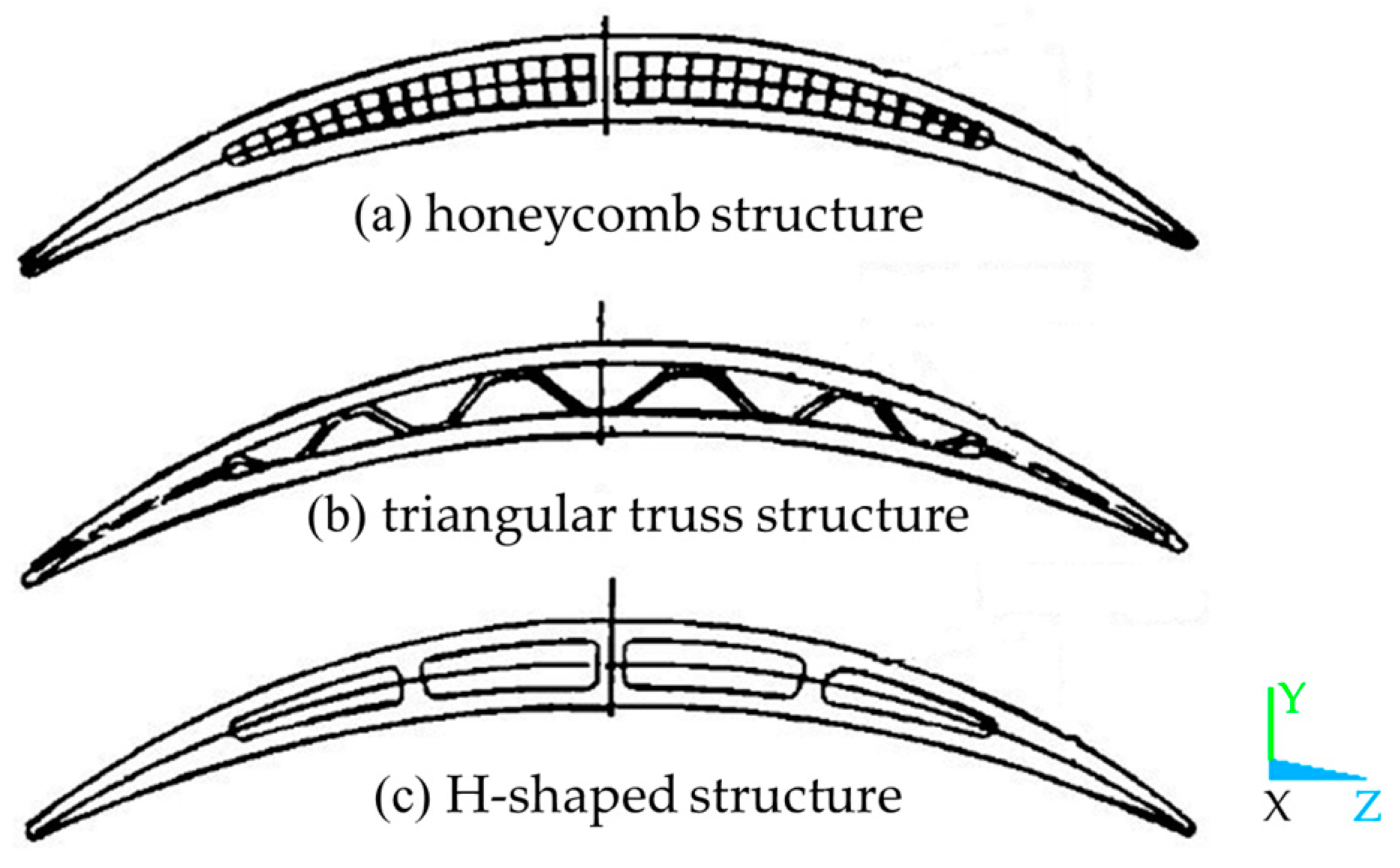



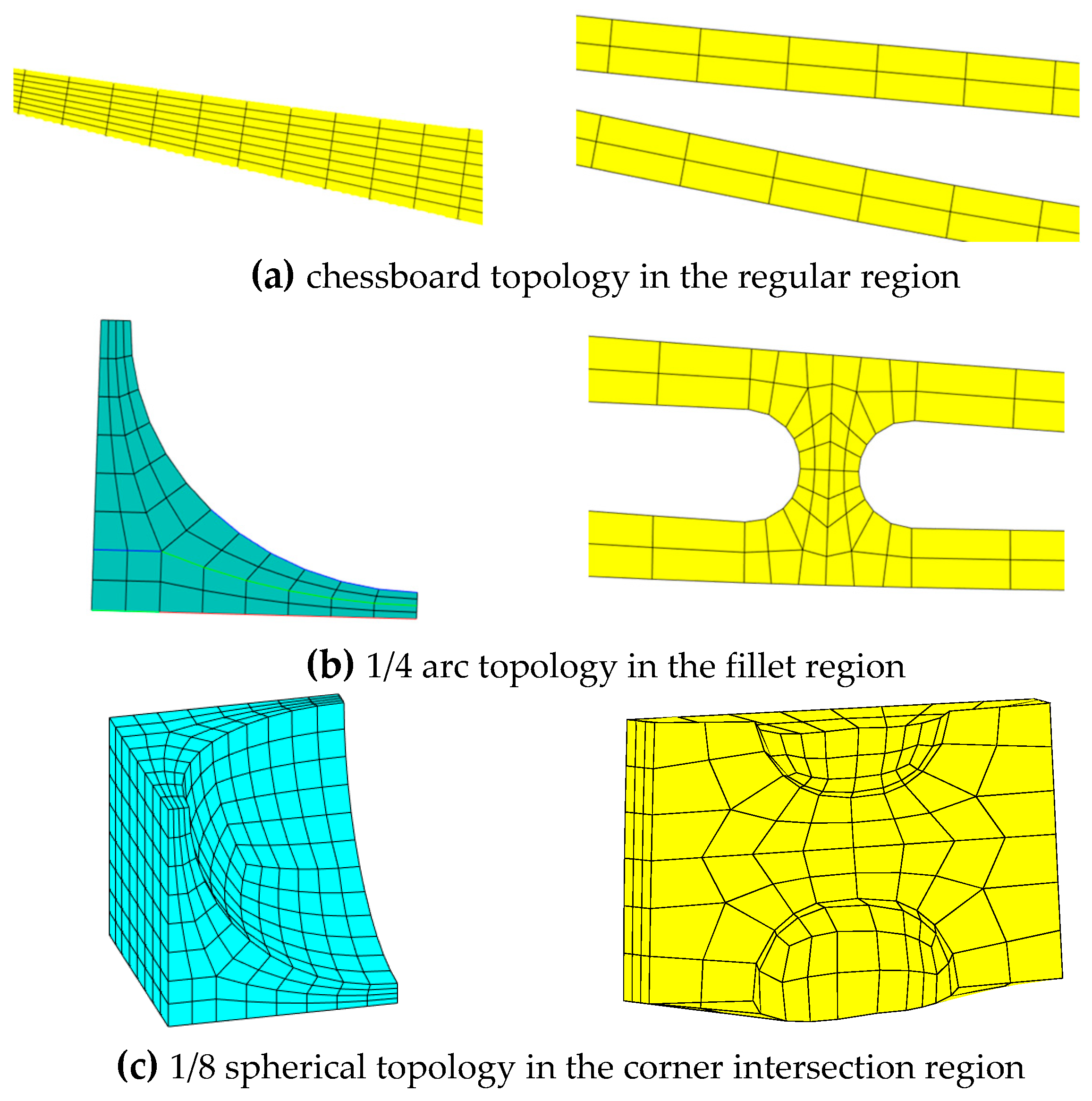




| Symbol | Structural Parameters | Units | Ranges |
|---|---|---|---|
| L | symmetry axis position | - | 0 < L< 1 |
| H | rib position | - | 0 < H< 1 |
| DR | wall thickness of the equal-thickness section | mm | 0 < DR, DC < half of the maximum blade thickness |
| DC | wall thickness of the variable-thickness section | mm | |
| B | rib thickness | mm | B > 0 |
| M1 | distance from the upper boundary of the cavity to blade tip | mm | 0 < M1 < blade height |
| M2 | distance from the lower boundary of the cavity to blade root | mm | 0 < M2 < blade height |
| R | fillet radius | mm | R > 0 |
| Parameter | Value |
|---|---|
| Blade number | 22 |
| Average hub/tip ratio | 0.34 |
| Average aspect ratio | 2.13 |
| Average thickness/chord ratio | 0.06 |
| Tip clearance(mm) | 0.7 |
| Parameter | DR1 | DR2 | DR3 | DR4 | DR5 | DC | M1 | M2 | B(mm) |
| Value | 0.16 | 0.18 | 0.23 | 0.25 | 0.27 | 0.31 | 0.15 | 0.20 | 1.50 |
| Method | Maximum Deformation/mm | Error/% | Computing Time/min |
|---|---|---|---|
| UCM | 22.98 | 30.75 | ~15 |
| WCS | 37.18 | 12.03 | ~50 |
| SCU | 33.19 | 0 | ~7200 |
| SWCS | 32.44 | 2.25 | ~180 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Chen, W.; Hu, D.; Wang, R. An Efficient Approach for Parametric Modeling and Prediction of the Hollow Blade Manufacture Shape. Aerospace 2023, 10, 145. https://doi.org/10.3390/aerospace10020145
Zhang X, Chen W, Hu D, Wang R. An Efficient Approach for Parametric Modeling and Prediction of the Hollow Blade Manufacture Shape. Aerospace. 2023; 10(2):145. https://doi.org/10.3390/aerospace10020145
Chicago/Turabian StyleZhang, Xiaojie, Weiyu Chen, Dianyin Hu, and Rongqiao Wang. 2023. "An Efficient Approach for Parametric Modeling and Prediction of the Hollow Blade Manufacture Shape" Aerospace 10, no. 2: 145. https://doi.org/10.3390/aerospace10020145
APA StyleZhang, X., Chen, W., Hu, D., & Wang, R. (2023). An Efficient Approach for Parametric Modeling and Prediction of the Hollow Blade Manufacture Shape. Aerospace, 10(2), 145. https://doi.org/10.3390/aerospace10020145






