The Influence of Gas Models on Numerical Simulations of Cryogenic Flow
Abstract
:1. Introduction
2. Gas Models
2.1. EOS
2.2. Isentropic Expansion of Cryogenic Nitrogen
2.3. Viscosity Model
2.4. Model of Thermal Conductivity
3. Comparative Analysis of Gas Models
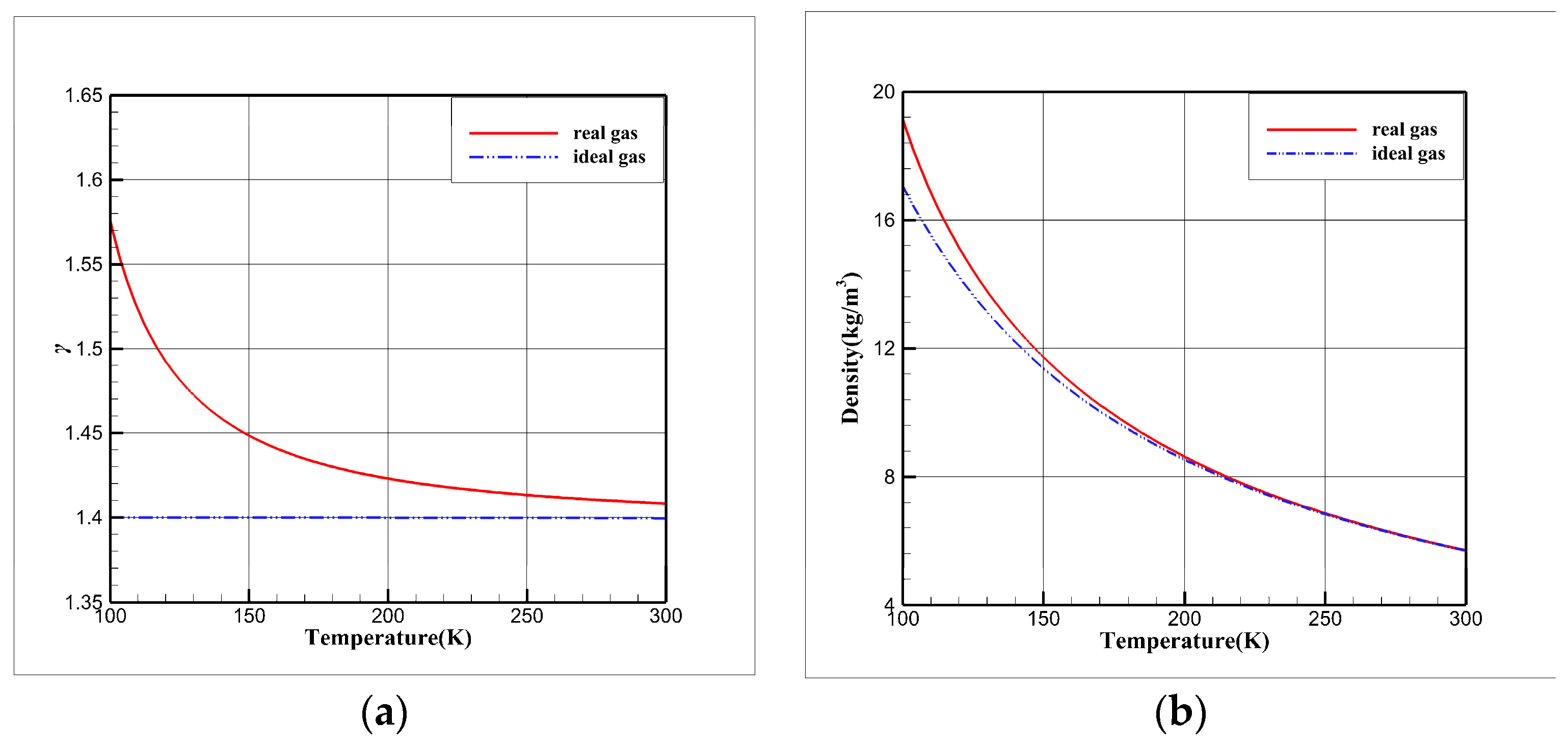
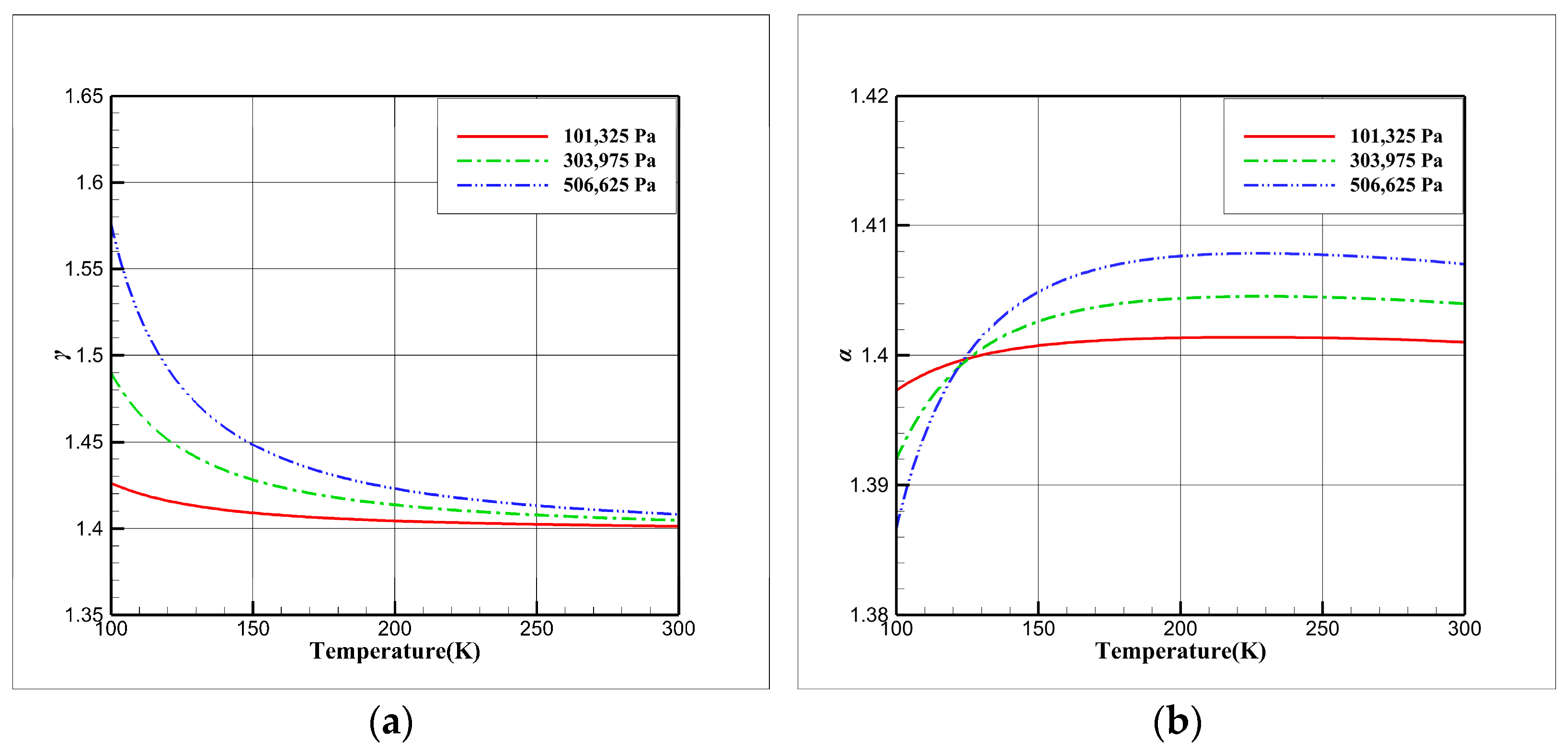
3.1. Comparative Study of Isentropic Relations
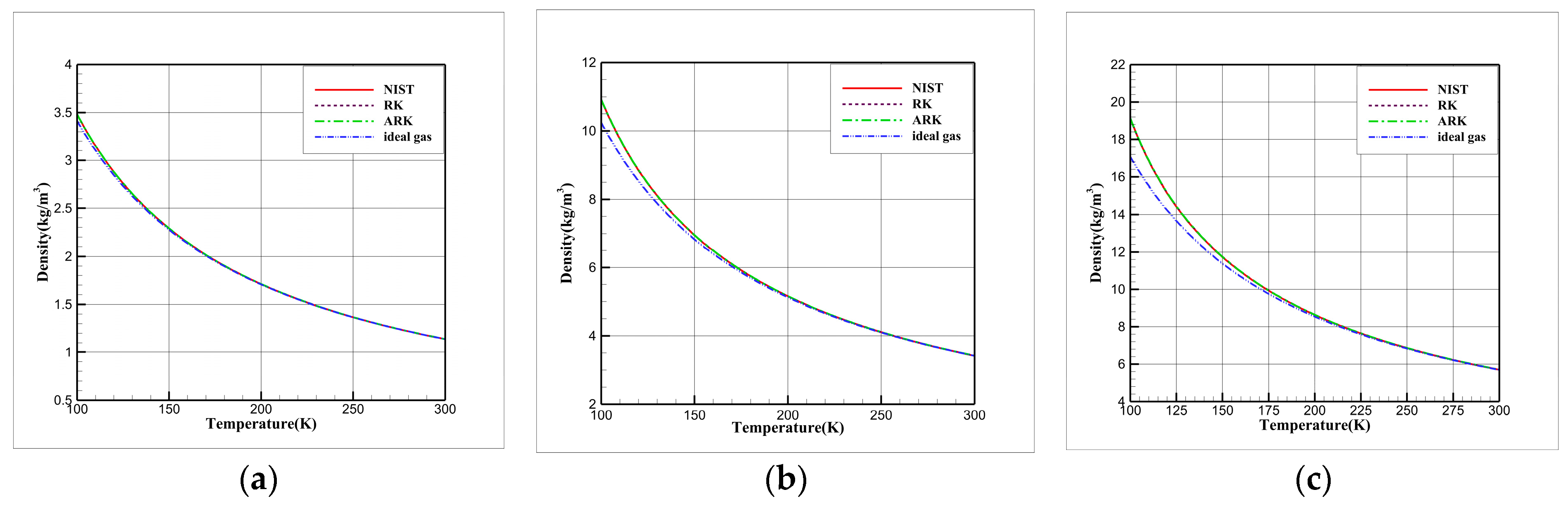
3.2. Comparative Study of EOSs
3.3. Comparative Study of Viscosity Models
3.4. Comparative Study of Thermal Conductivity Models
4. Influence Analysis of Gas Models on Numerical Simulations of Cryogenic Flow
4.1. Governing Equations and Numerical Schemes
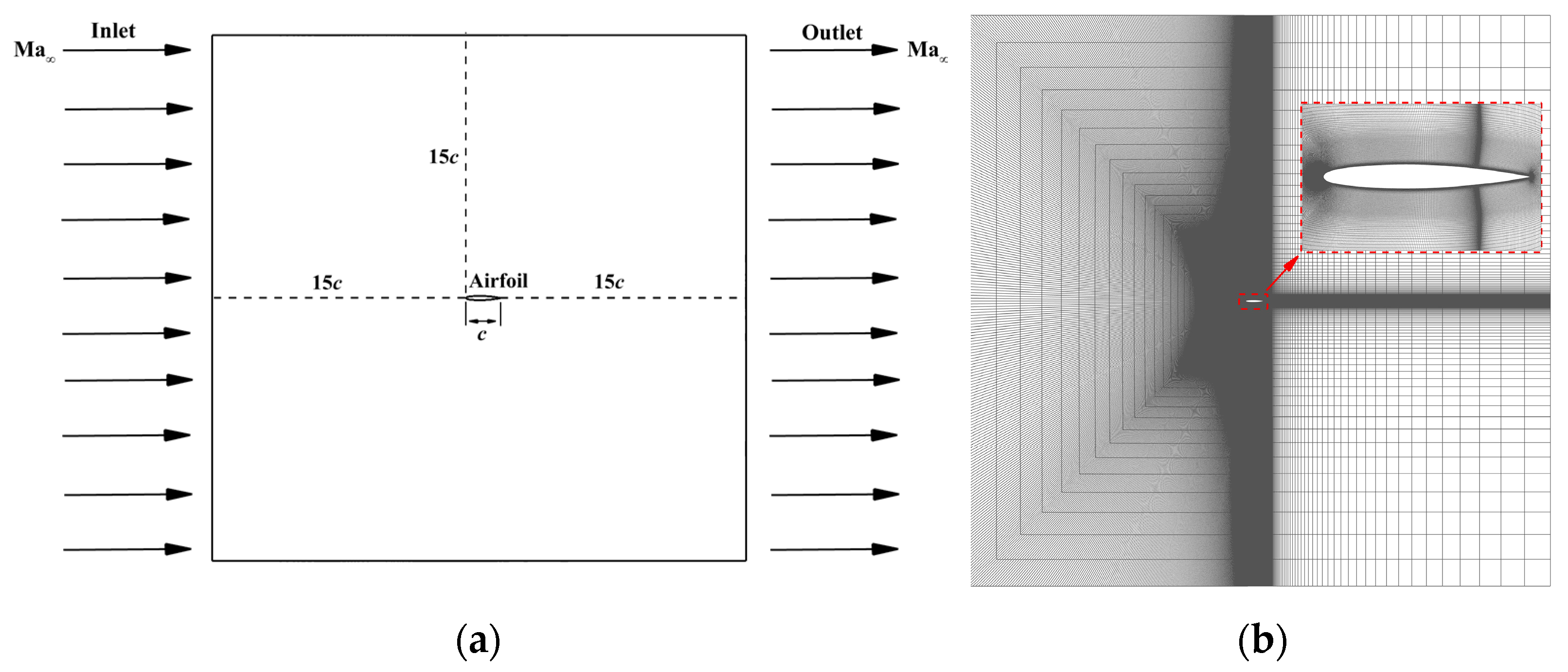
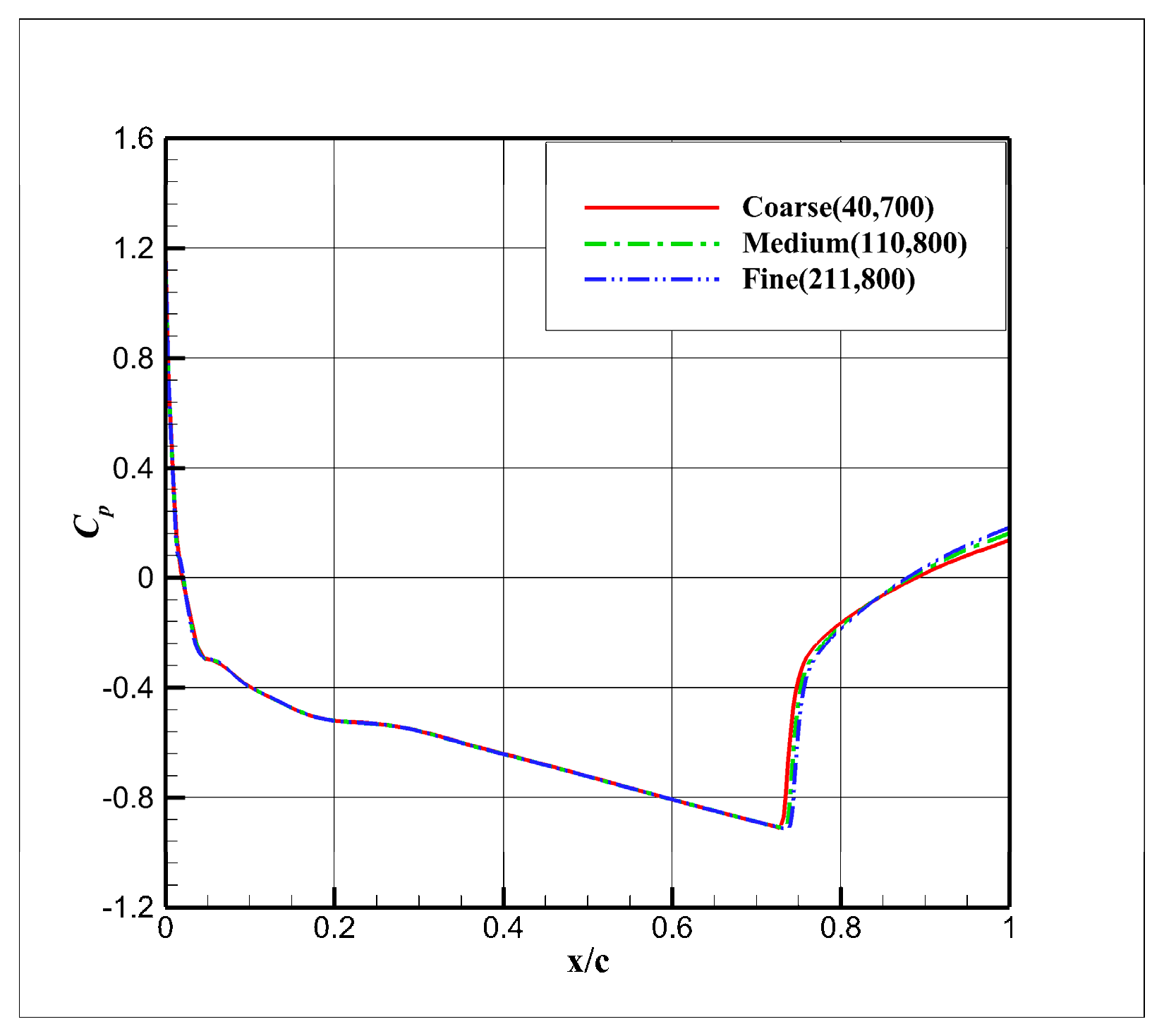
4.2. Grid Independence and the Validity
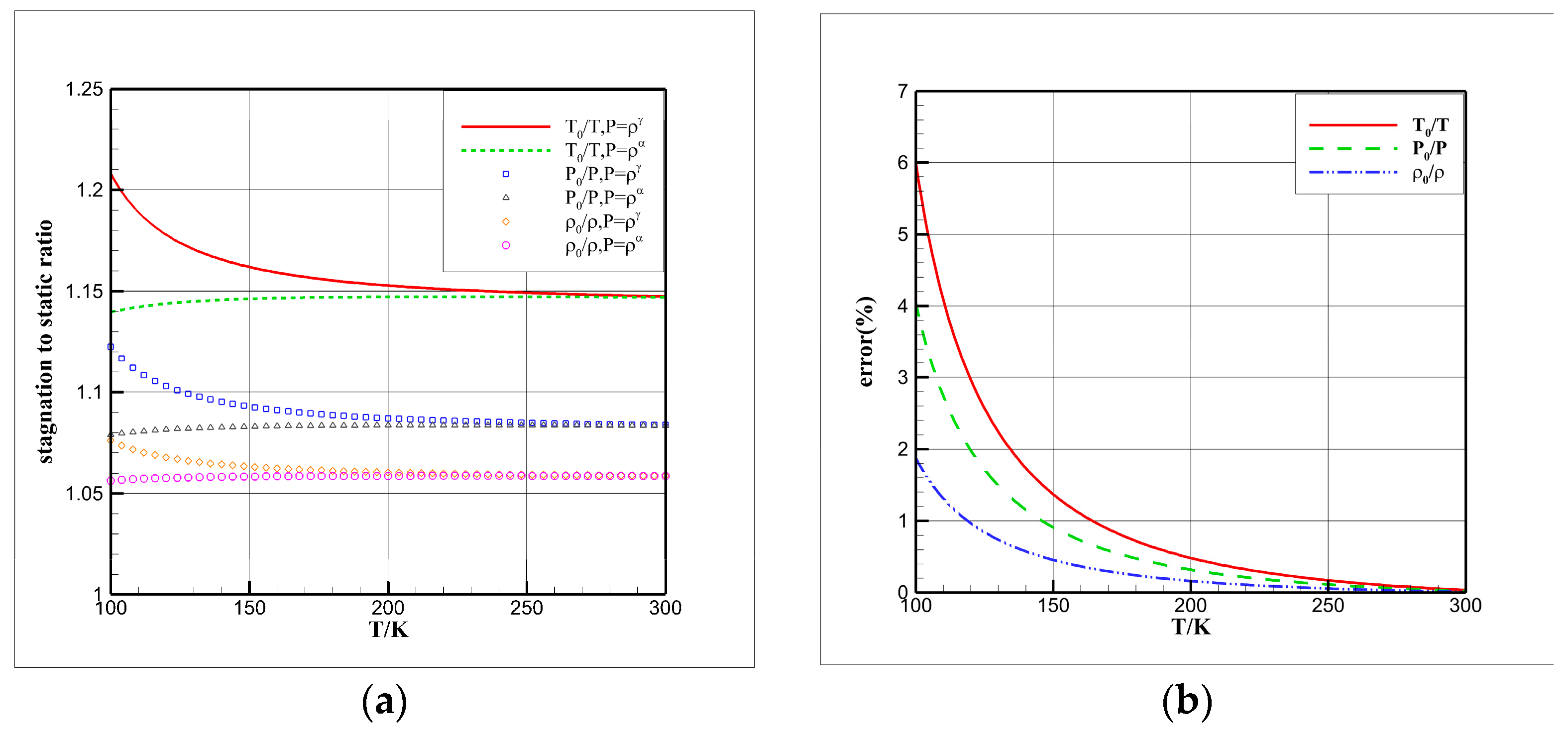
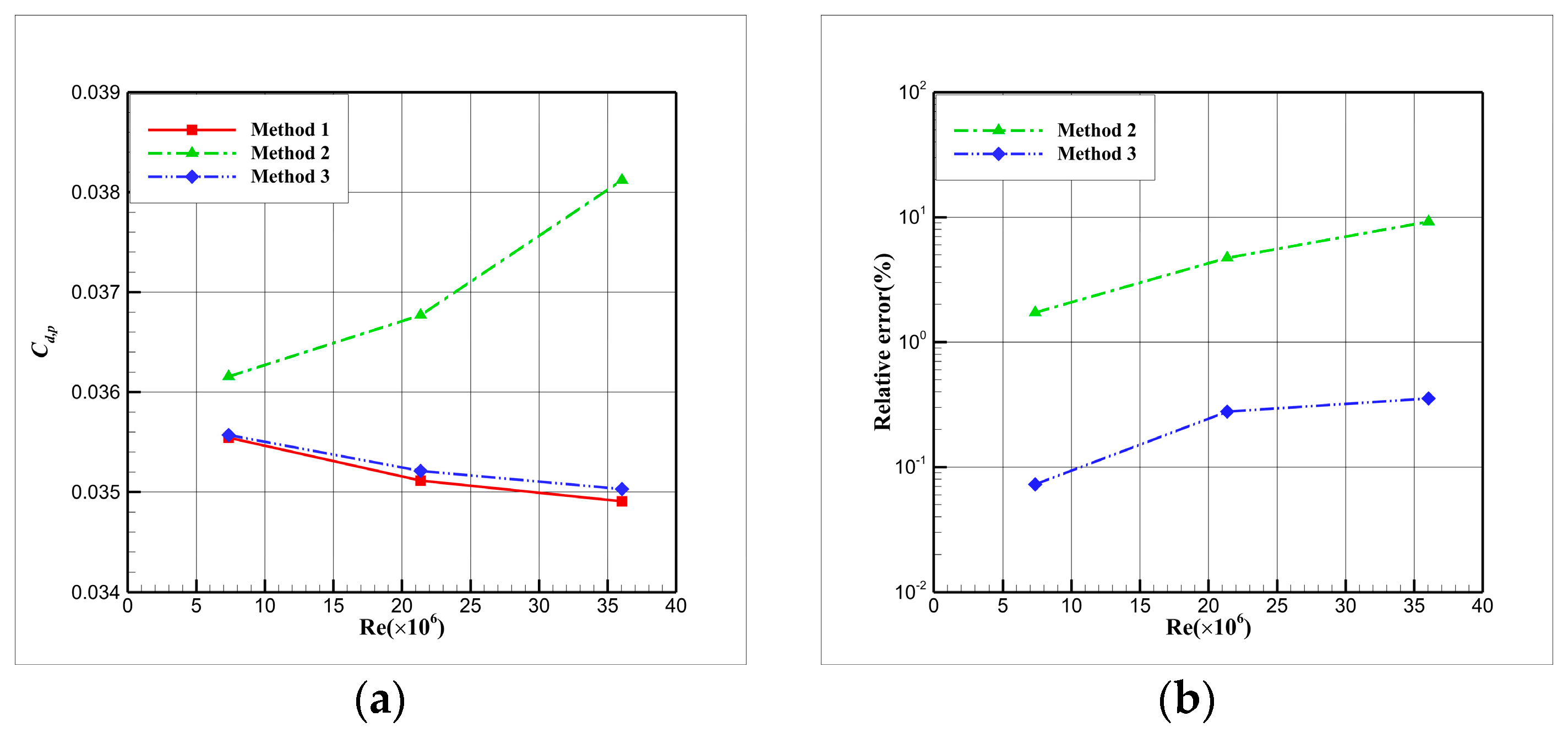
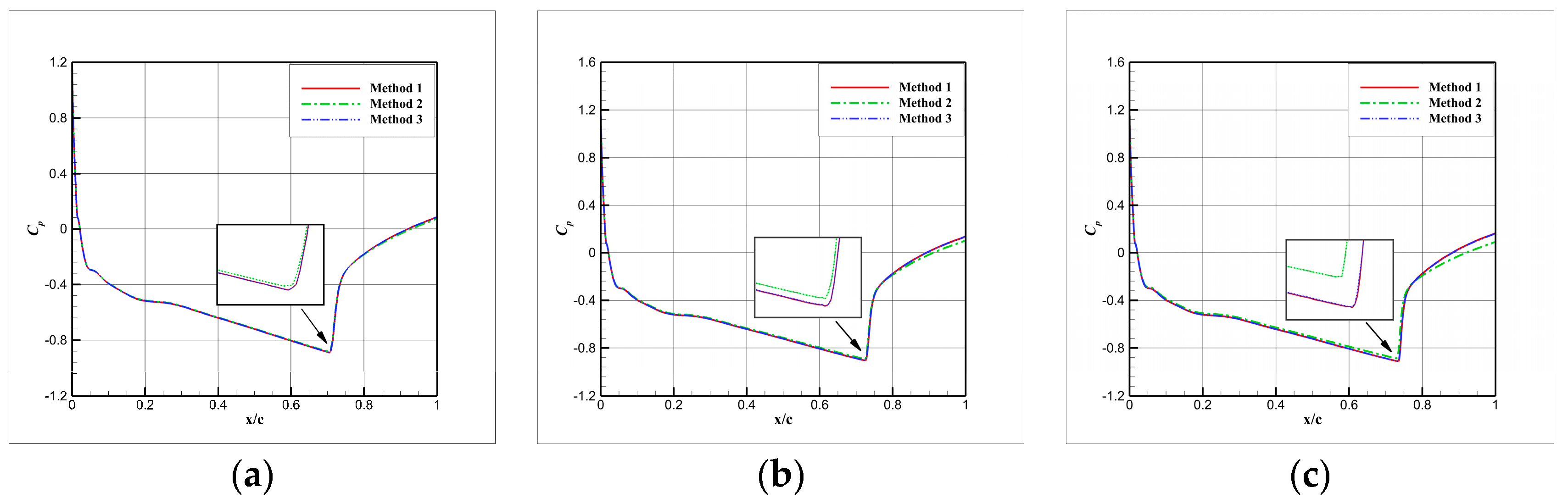
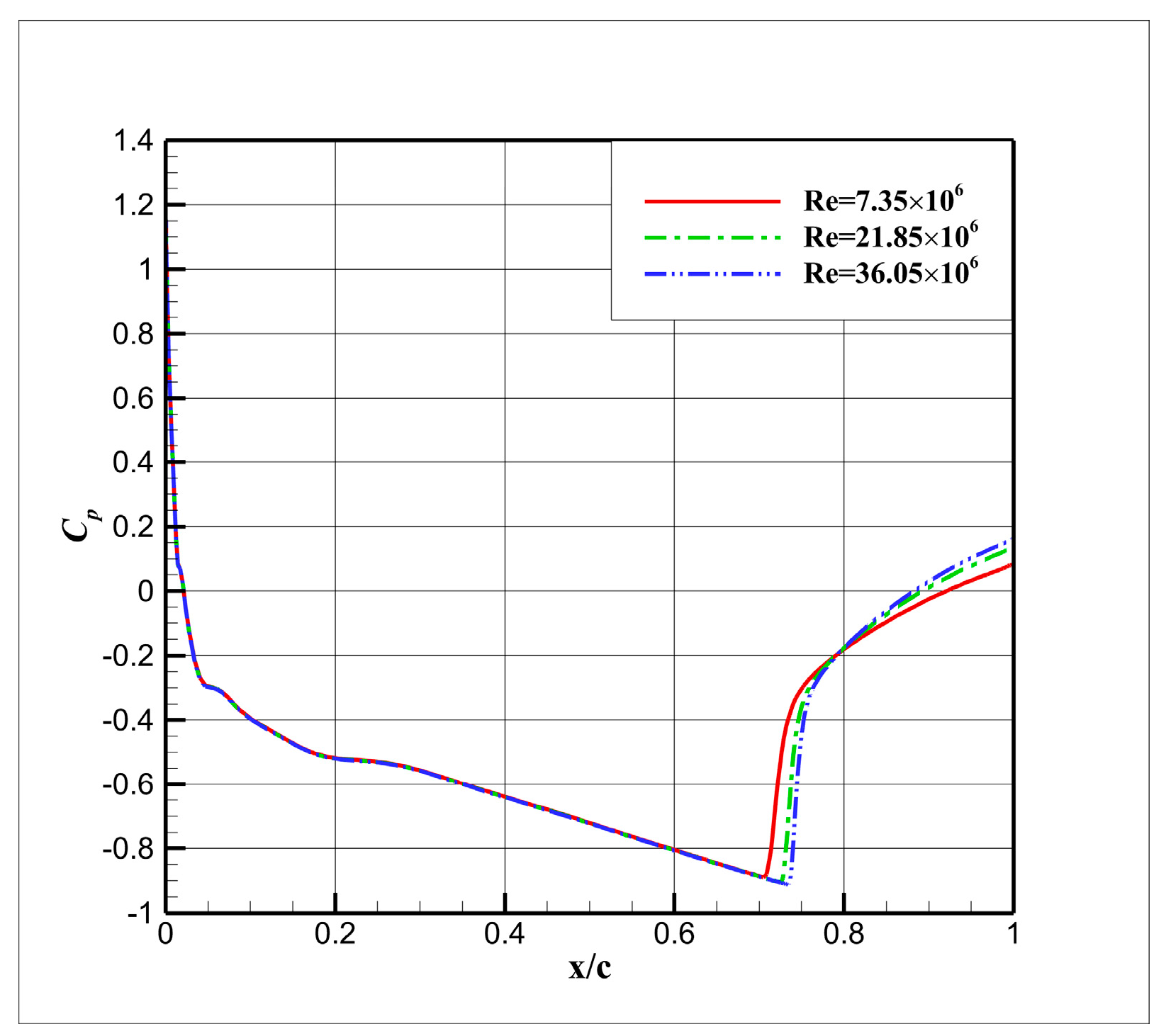
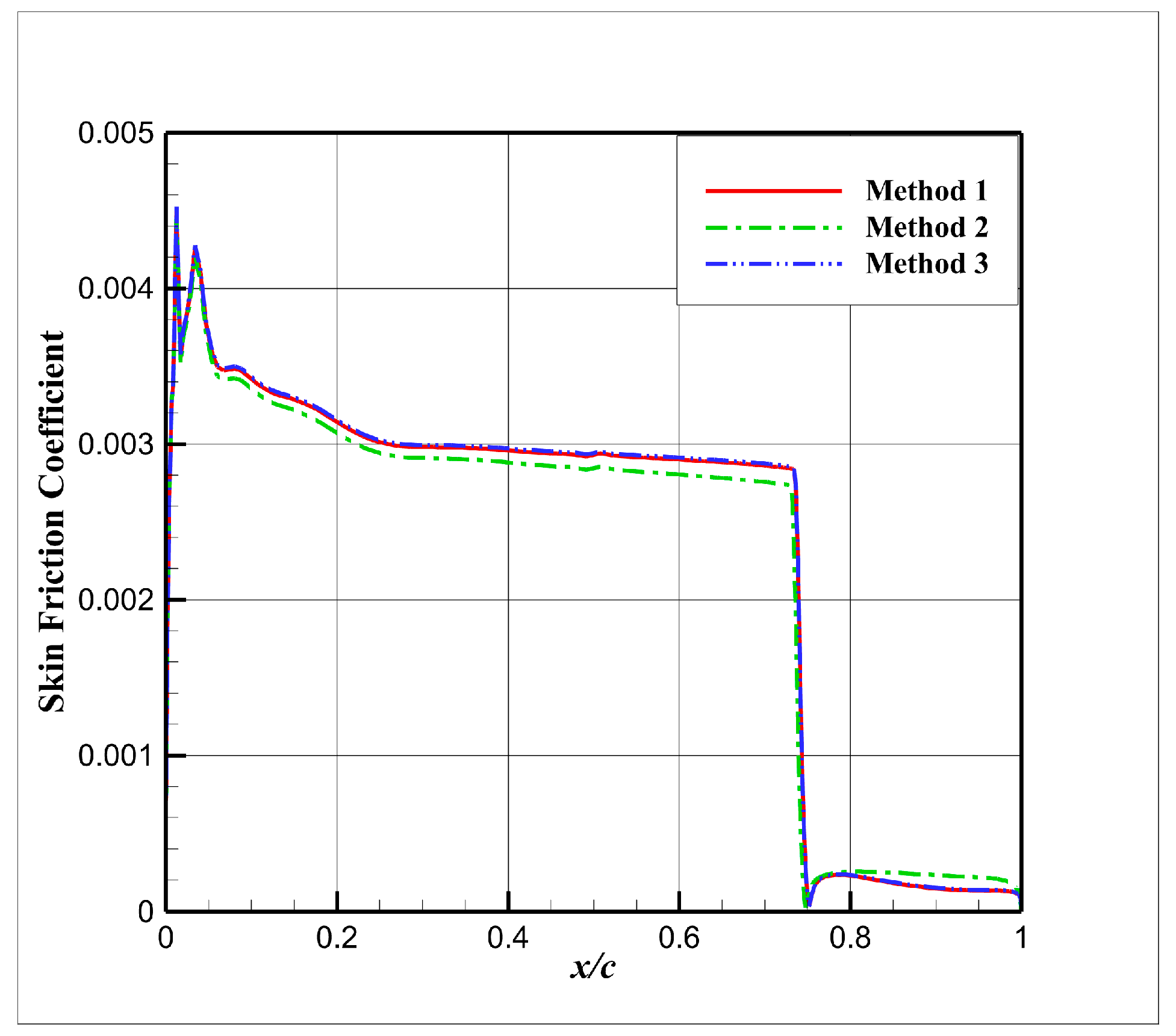
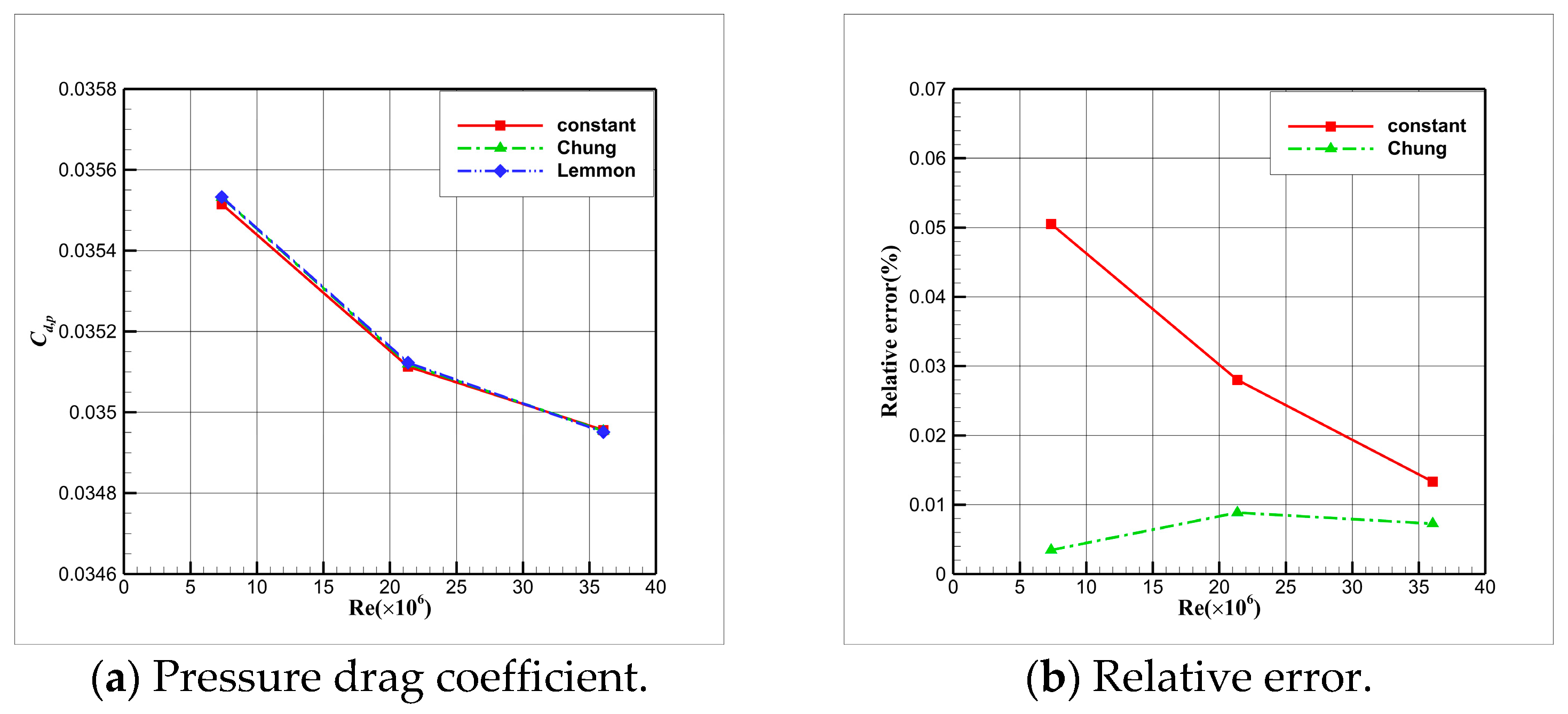
4.3. Influence Analysis of Isentropic Relations on Numerical Simulation
- (1)
- Considering the real gas effect, combining the isentropic relationship in Equation (5) with the thermodynamic properties obtained from the real gas EOS, as shown in Ref. [2];
- (2)
- Considering the real gas effect. However, instead of using the thermodynamic properties obtained from the real gas EOS, the isentropic relationship in Equation (3) is combined with the properties derived from the ideal gas EOS. In this case, the free-stream specific heat ratio in the real gas state is utilized as the expansion coefficient, which was previously used in Ref. [15];
- (3)
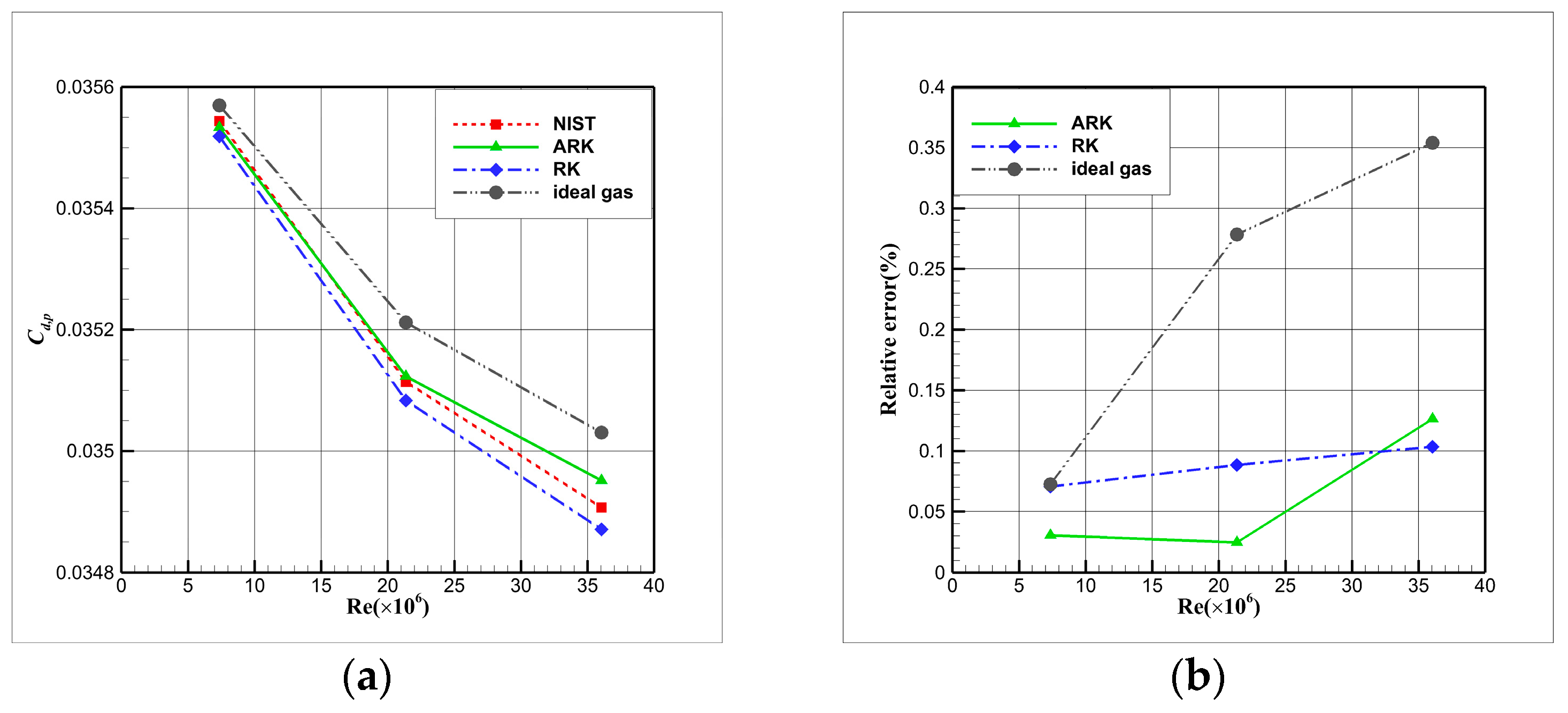
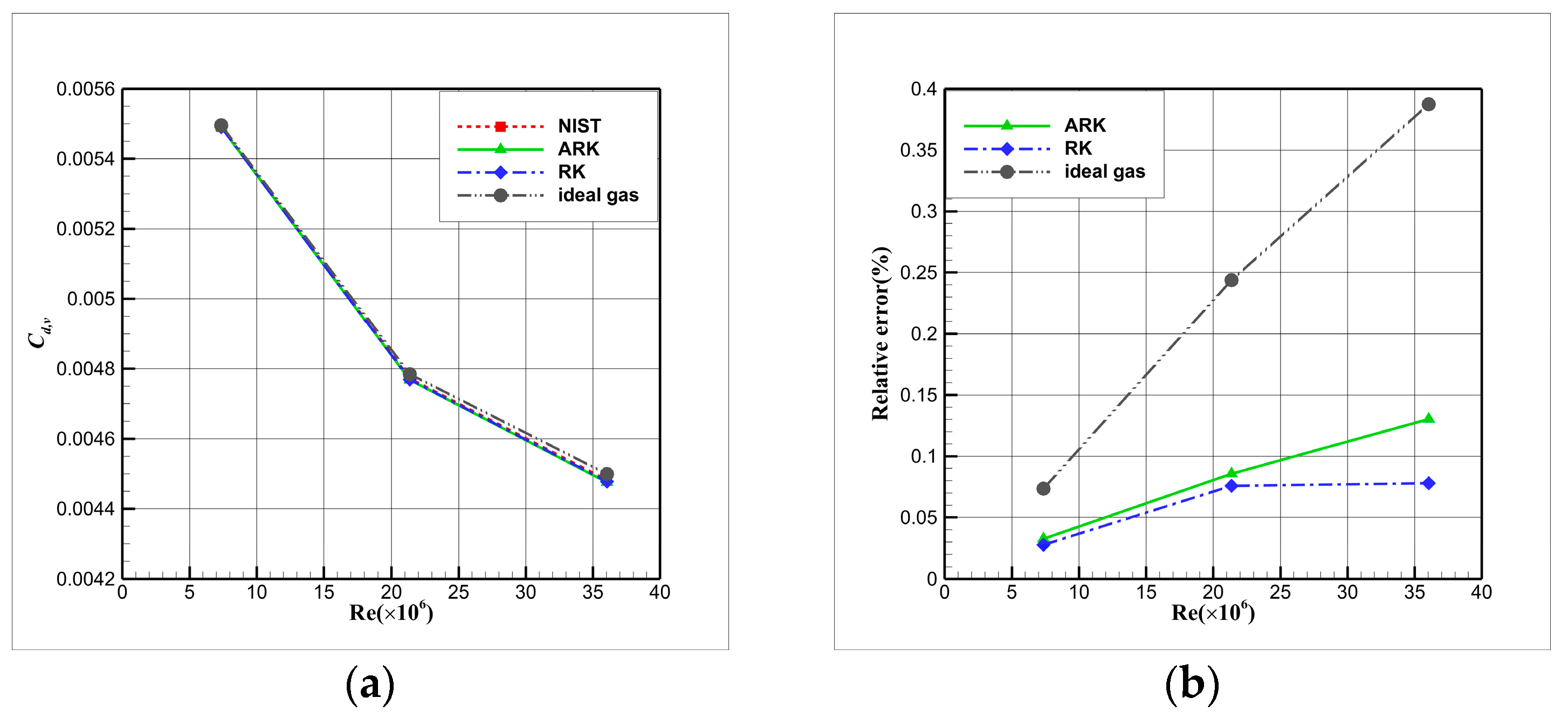
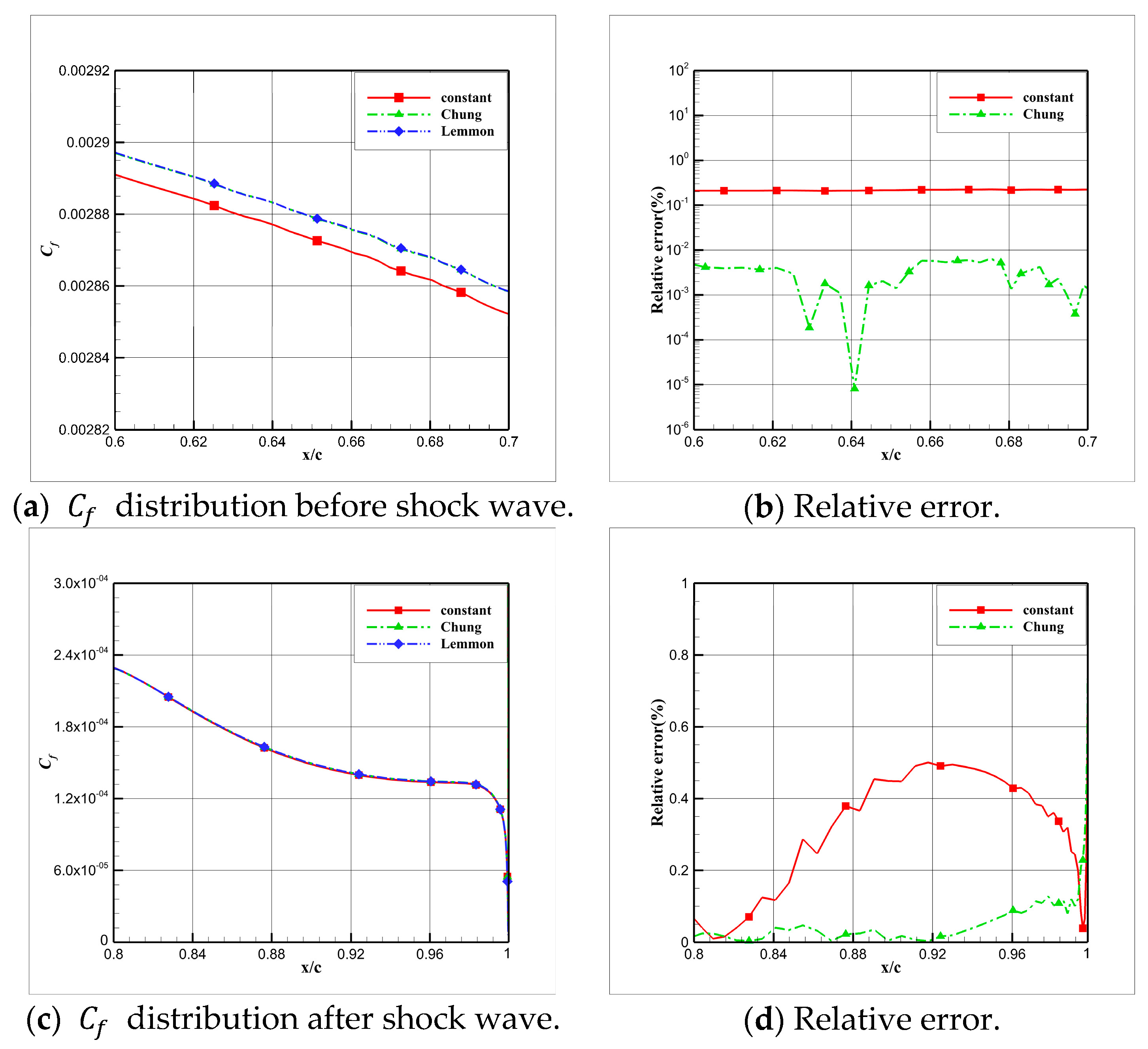
4.4. Influence Analysis of EOSs on Numerical Simulation
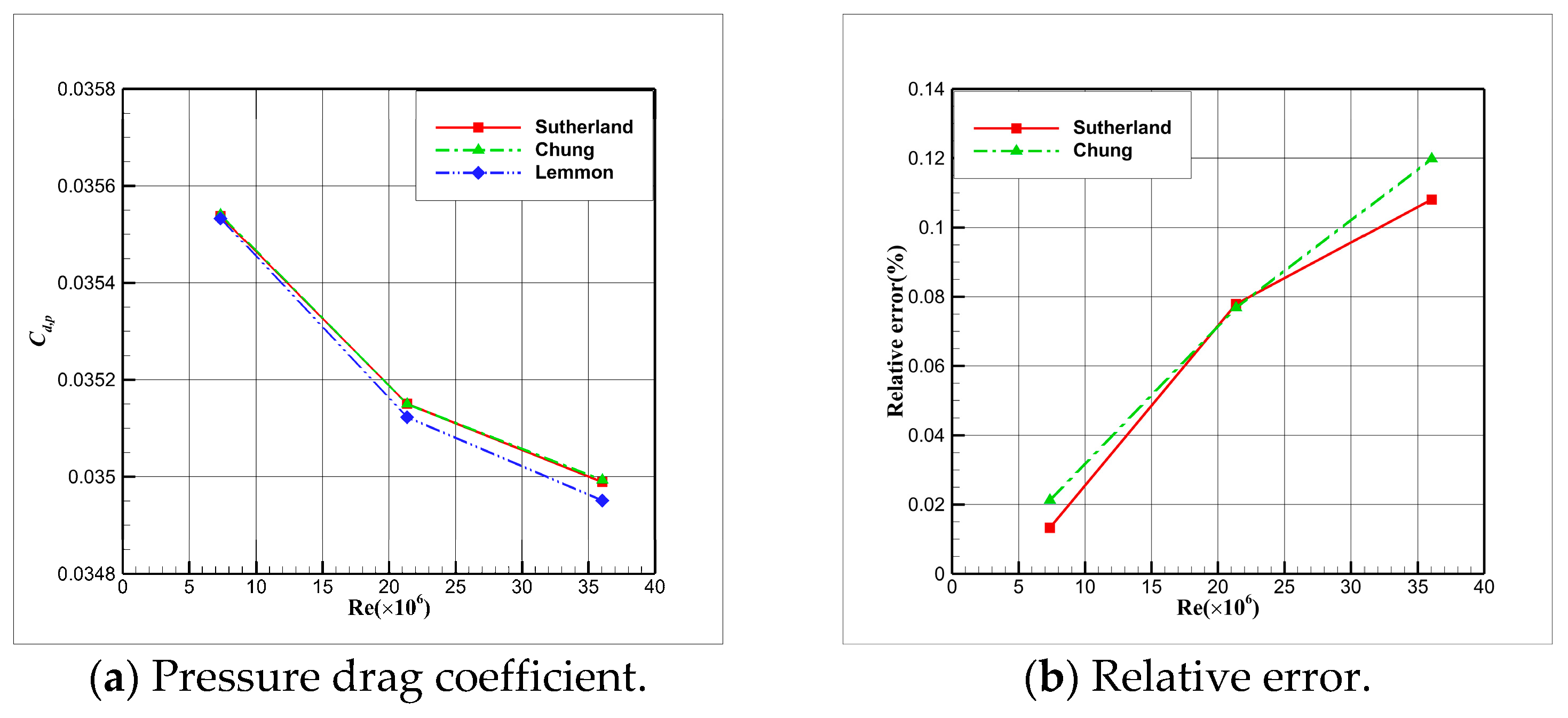
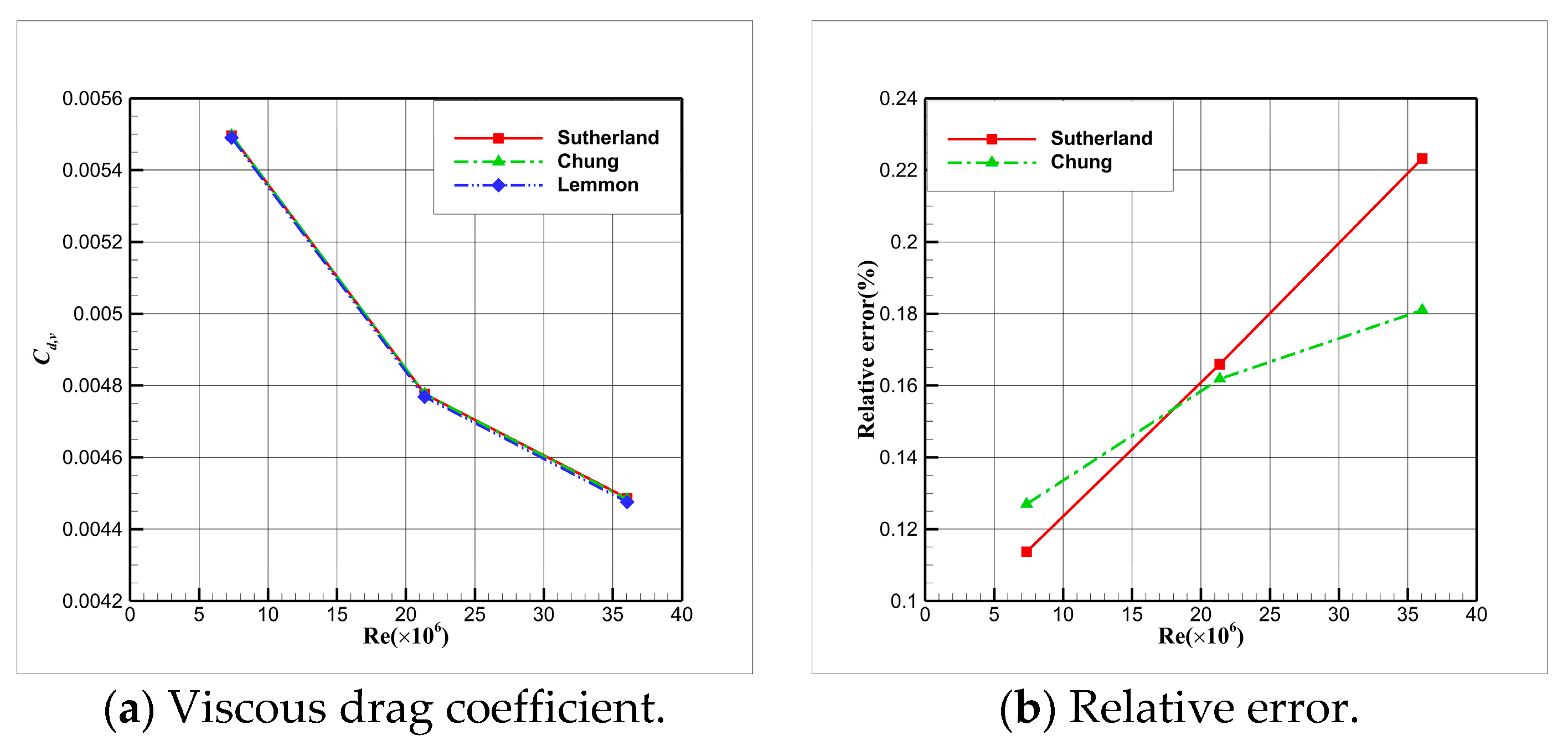
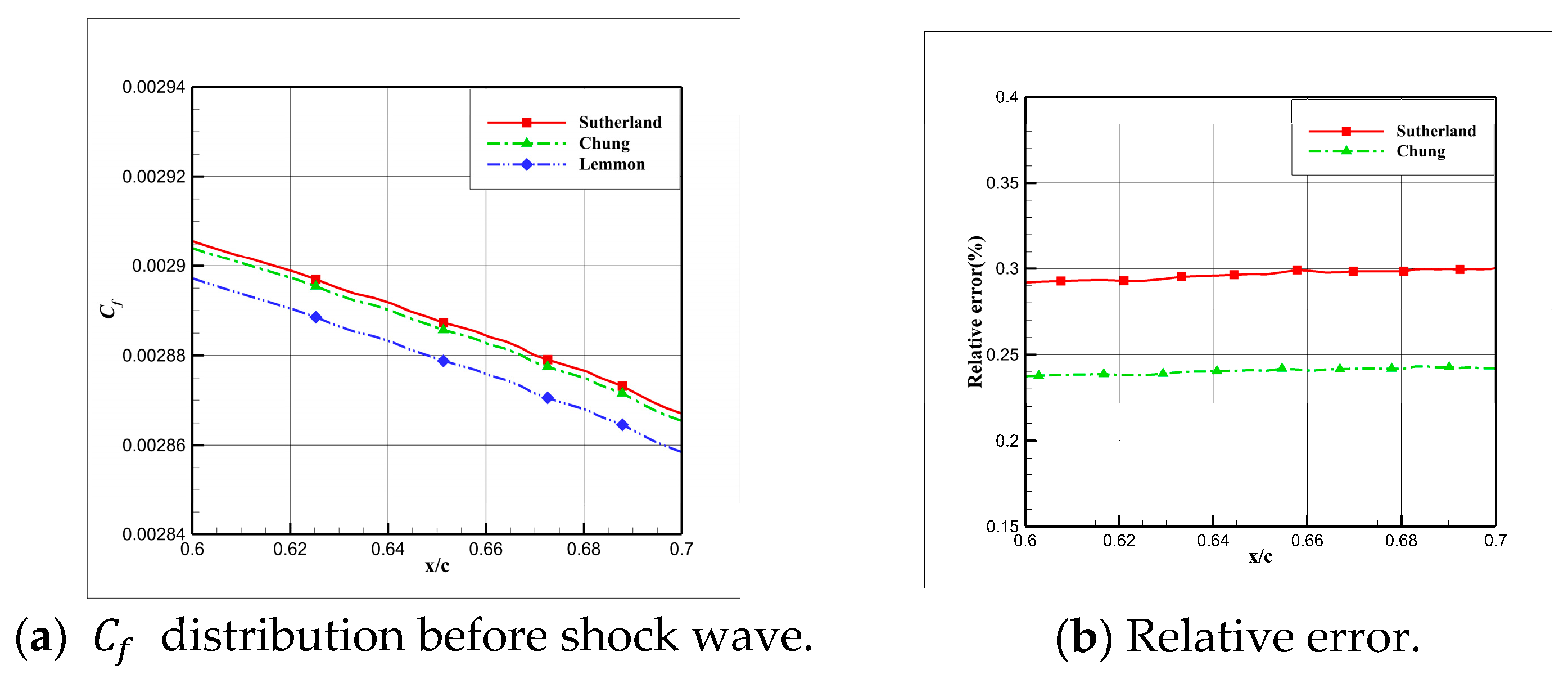
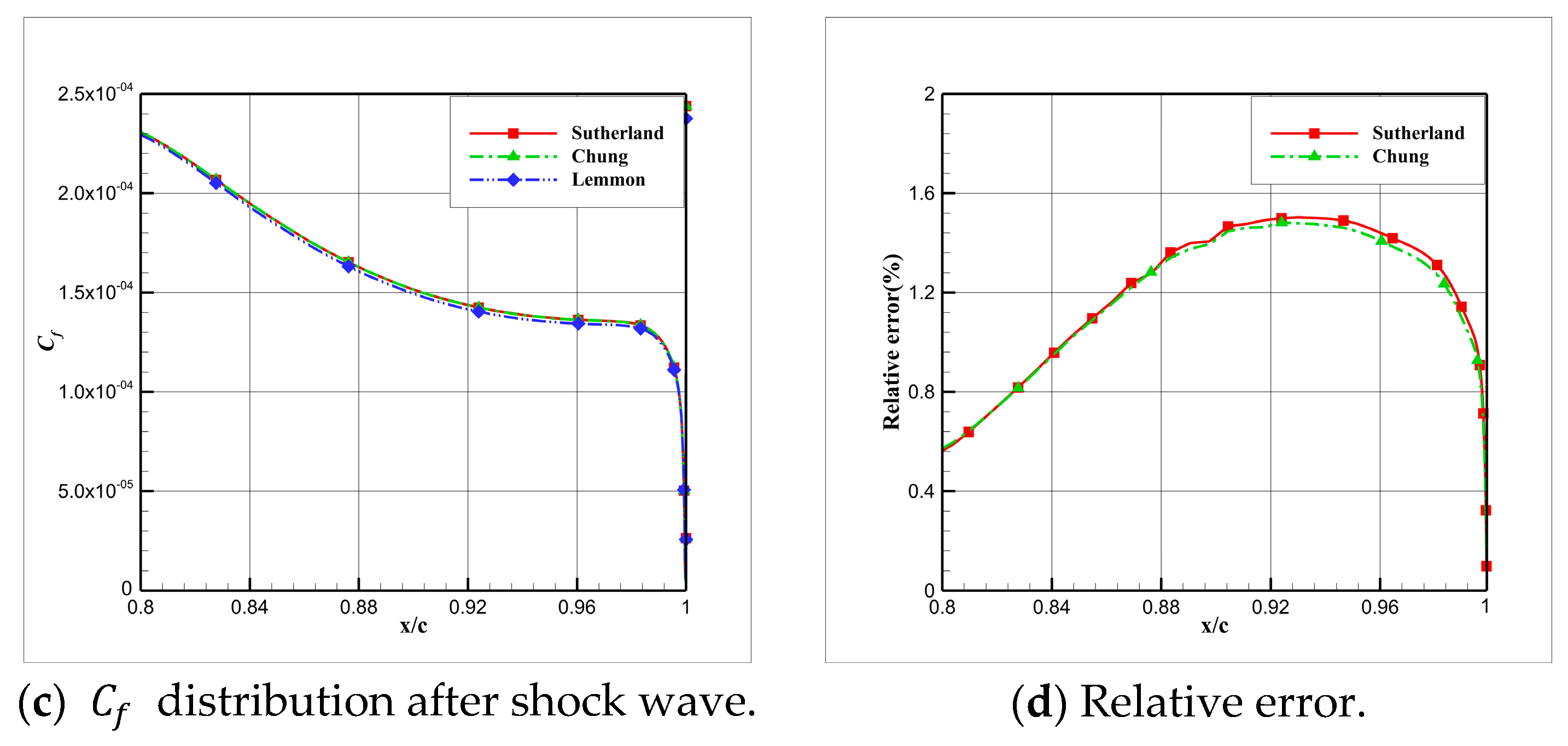
4.5. Influence Analysis of Viscosity Models on Numerical Simulation
4.6. Influence Analysis of Thermal Conductivity Models on Numerical Simulation
5. Conclusions
- (1)
- The isentropic relations of cryogenic nitrogen flow exhibit variations, and combining the ideal gas EOS with the real gas specific heat ratio can result in significant errors, potentially leading to the mistaken belief that the real gas effect is pronounced.
- (2)
- For cryogenic nitrogen flow, the impact of EOSs, viscosity models, and thermal conductivity models on aerodynamic properties like and is relatively small. However, noticeable differences arise when considering the skin friction coefficient, primarily due to the presence of shock waves, with the ideal gas EOS causing the most significant deviation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hall, R.M.; Adcock, J.B. Simulation of Ideal-Gas Flow by Nitrogen and Other Selected Gases at Cryogenic Temperatures; NASA: Washington, DC, USA, 1981.
- Adcock, J.B.; Kilgore, R.A.; Ray, E.J. Cryogenic nitrogen as a transonic wind-tunnel test gas. In Proceedings of the 13th Aerospace Sciences Meeting, Pasadena, CA, USA, 20–22 January 1975. [Google Scholar]
- Lutz, T.; Kleinert, J.; Waldmann, A.; Koop, L.; Yorita, D.; Dietz, G.; Schulz, M. Research Initiative for Numerical and Experimental Studies on High-Speed Stall of Civil Aircraft. J. Aircr. 2023, 60, 623–636. [Google Scholar] [CrossRef]
- Lutz, T.; Gansel, P.; Waldmann, A.; Zimmermann, D.-M.; Hülse, S.S.A. Prediction and Measurement of the Common Research Model Wake at Stall Conditions. J. Aircr. 2016, 53, 501–514. [Google Scholar] [CrossRef]
- Hensch, A.K.; Guntermann, P.; Longo, R.; Klein, C.; Risius, S.; Schaber, S.; Quest, J.; Okfen, P. Investigation of Hybrid Laminar Flow Control (HLFC) on a 2D-Model in the Cryogenic Pilot European Transonic Windtunnel (PETW). In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Klein, C. Boundary layer transition detection on wind tunnel models in PETW during continuous pitch traverse. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Rivers, M.; Quest, J.; Rudnik, R. Comparison of the NASA Common Research Model European Transonic Wind Tunnel test data to NASA National Transonic Facility test data. CEAS Aeronaut J. 2018, 9, 307–317. [Google Scholar] [CrossRef]
- Vrchota, P.; Prachař, A. Using wing model deformation for improvement of CFD results of ESWIRP project. CEAS Aeronaut J. 2018, 9, 361–372. [Google Scholar] [CrossRef]
- Wang, X.; Wu, J.; Chen, J.; Li, Y.; Zhao, Z.; Liu, G.; Tao, Y.; Xiong, N. Numerical Study of Nonadiabatic Wall Effects on Aerodynamic Characteristics of CHN-T1 Standard Model. Aerospace 2023, 10, 372. [Google Scholar] [CrossRef]
- Magalhães, L.B.; Silva, A.R.; Barata, J.M. Computational Analysis of High-Pressure Nitrogen Jets from Transcritical to Supercritical Gas-Like Conditions. In Proceedings of the AIAA Propulsion and Energy 2021 Forum, Online, 9–11 August 2021. [Google Scholar]
- Matheis, J.; Müller, H.; Hickel, S.; Pfitzner, M. Large-Eddy Simulation of Cryogenic Jet Injection at Supercritical Pressures. High-Press. Flows Propuls. Appl. 2020, 260, 531–570. [Google Scholar]
- Traxinger, C.; Banholzer, M.; Pfitzner, M. Real-Gas Effects and Phase Separation in Underexpanded Jets at Engine-Relevant Conditions. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Banuti, D.T.; Hannemann, K. Application of a Real-Gas-Library Multi-Fluid-Mixing Model to Supercritical Single Injector Flow. In Proceedings of the 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cleveland, OH, USA, 28–30 July 2014. [Google Scholar]
- Hall, R.M.; Ray, E.J. Investigation of Minimum Operating Temperatures for Cryogenic Wind Tunnels. J. Aircr. 1977, 14, 560–564. [Google Scholar] [CrossRef]
- Inger, G.R. On the Simulation of Transonic Shock-Turbulent Boundary Layer Interactions in Cryogenic or Heavy Gas Wind Tunnels. In Proceedings of the 10th AIAA Aerodynamic Testing Conference, San Diego, CA, USA, 19–21 April 1978. [Google Scholar]
- Inger, G.R. Transonic Shock-Boundary-Layer Interactions in Cryogenic Wind Tunnels. J. Aircr. 1979, 16, 284–287. [Google Scholar] [CrossRef]
- Adcock, J.B. Simulation of flat-plate turbulent boundary layers in cryogenic tunnels. J. Aircr. 1980, 17, 284–285. [Google Scholar] [CrossRef]
- Wagner, B.; Schmidt, W. Theoretical Investigations of Real Gas Effects in Cryogenic Wind Tunnels. AIAA J. 1978, 16, 580–586. [Google Scholar] [CrossRef]
- Hall, R.M. Preliminary Study of the Minimum Temperatures for Valid Testing in a Cryogenic Wind Tunnel; NASA: Washington, DC, USA, 1975.
- Sun, W.; Xu, T.; Hou, Y.; Ma, Z.Y.; Zhang, L.T. Numerical investigation of nitrogen condensation flow over airfoil in cryogenic wind tunnel. Cryogenics 2020, 111, 103165. [Google Scholar] [CrossRef]
- Ma, J.; Liu, H.S.; Liu, L.; Xie, M.Z. Simulation study on the cryogenic liquid nitrogen jets: Effects of equations of state and turbulence models. Cryogenics 2021, 117, 103330. [Google Scholar] [CrossRef]
- Cengel, Y.; Boles, M. Thermodynamics: An Engineering Approach, 8th ed.; McGraw-Hill Education: New York, NY, USA, 2015; pp. 51–111. [Google Scholar]
- Aungier, R.H. A Fast, Accurate Real Gas Equation of State for Fluid Dynamic Analysis Applications. J. Fluids Eng. 1995, 117, 277–281. [Google Scholar] [CrossRef]
- NIST Standard Reference Database Number 69. Available online: http://webbook.nist.gov/chemistry/ (accessed on 2 October 2023).
- Span, R.; Lemmon, E.W.; Jacobsen, R.T.; Wagner, W.; Yokozeki, A. A Reference Equation of State for the Thermodynamic Properties of Nitrogen for Temperatures from 63.151 to 1000 K and Pressures to 2200 MPa. J. Phys. Chem. Ref. Data 2000, 29, 1361–1433. [Google Scholar] [CrossRef]
- White, F.M. Fluid Mechanics, 8th ed.; McGraw-Hill Education: New York, NY, USA, 2014; pp. 15–39. [Google Scholar]
- Poling, B.E.; Prausnitz, J.M.; O’Connell, J.P. Properties of Gases and Liquids, 4th ed.; McGraw-Hill Education: New York, NY, USA, 2001; pp. 455–623. [Google Scholar]
- Lemmon, E.W.; Jacobsen, R.T. Viscosity and Thermal Conductivity Equations for Nitrogen, Oxygen, Argon, and Air. Int. J. Thermophys. 2004, 25, 21–69. [Google Scholar] [CrossRef]
- Lankford, D.; Powell, S.; Hand, T. Implementation of Real Gas Effects in the Wind-US Flow Solver. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. [Google Scholar]
- Carlson, J.R. Assessment of Using Ideal Gas for Predicting Boattail Flow at Cryogenic Temperatures. In Proceedings of the AIAA SCITECH 2023 Forum, Washington, DC, USA, 23–27 January 2023. [Google Scholar]

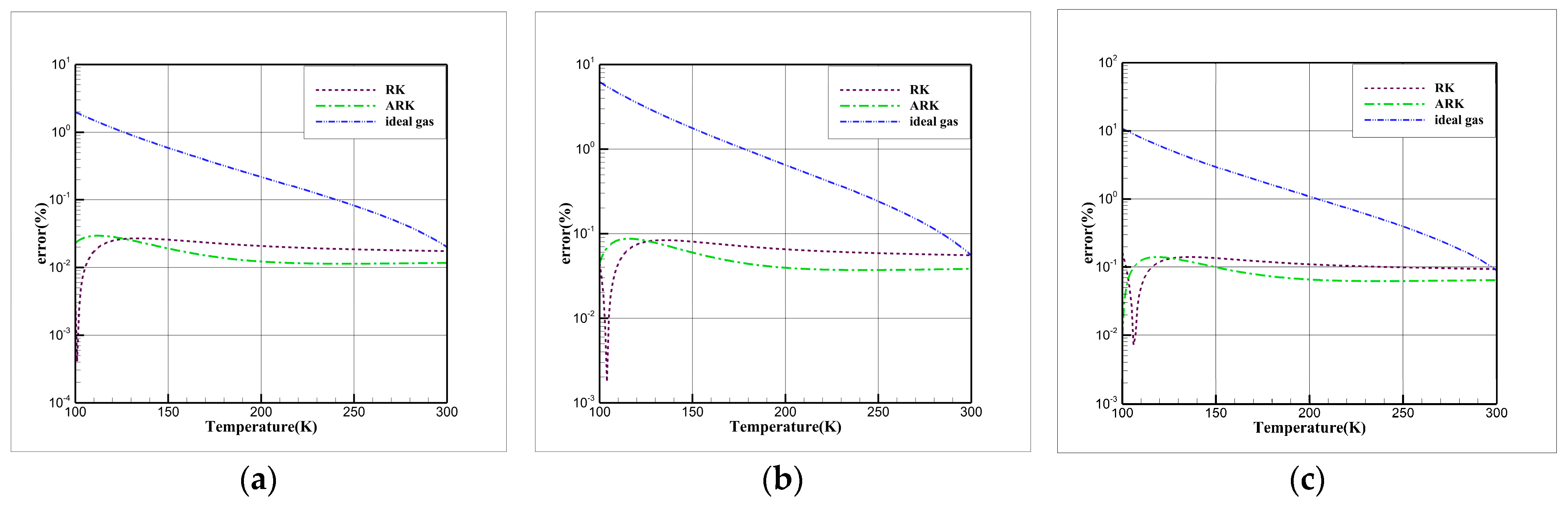
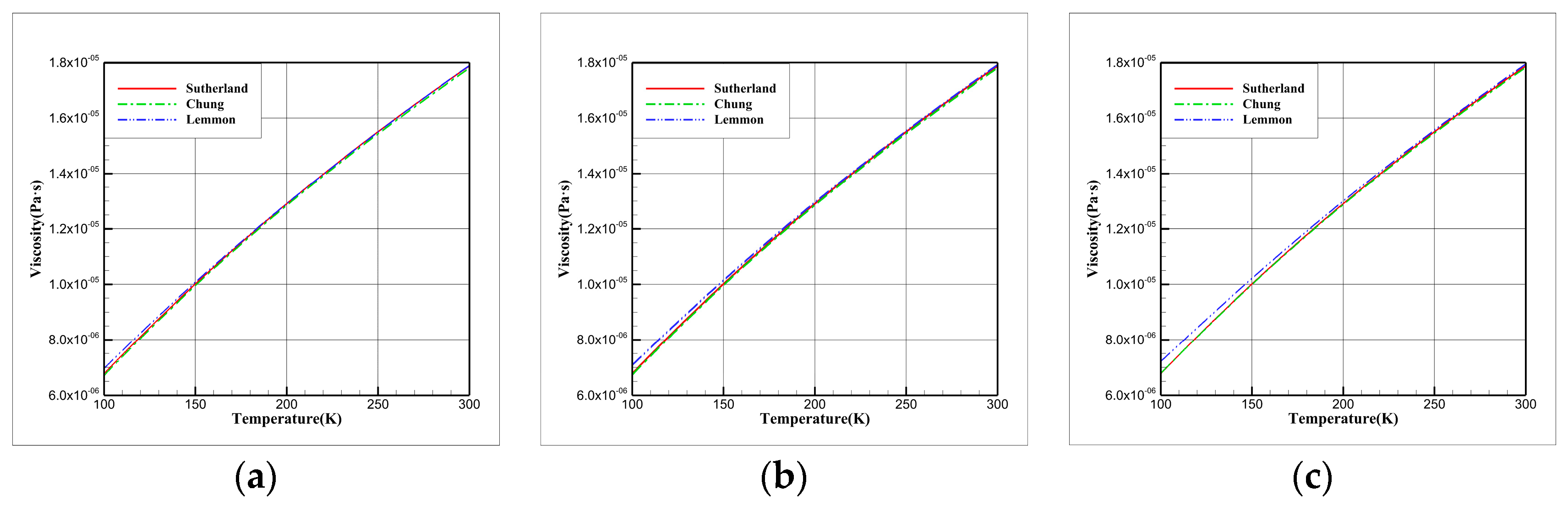
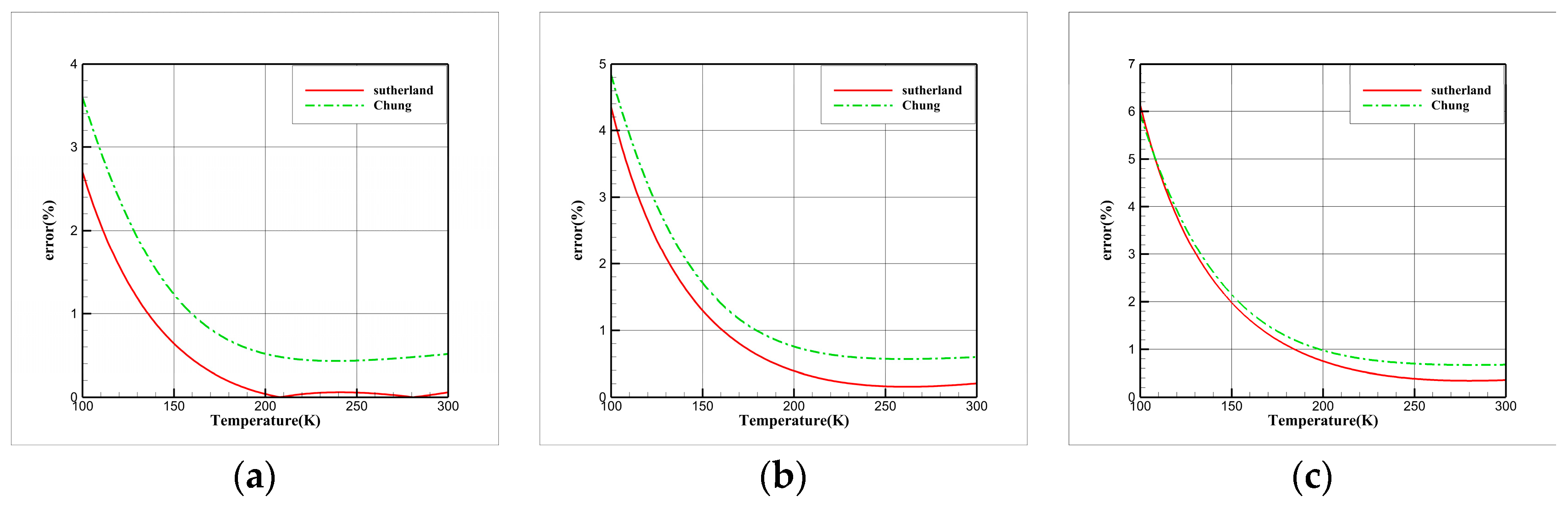

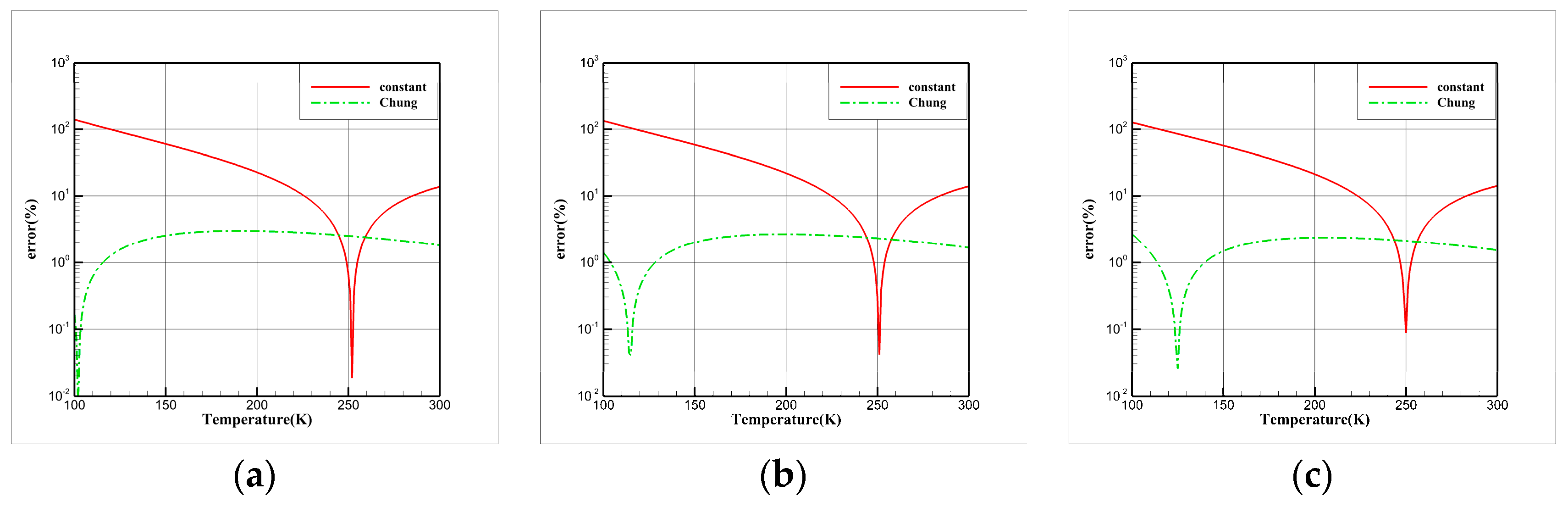




| EOS | |||||
|---|---|---|---|---|---|
| RK | 0 | 0 | |||
| SRK | 0 | 0 | |||
| PR | 0 | ||||
| ARK | 0 |
| Comparison | Isentropic Relation | EOS | Viscosity | Thermal Conductivity | |
|---|---|---|---|---|---|
| Conditions | |||||
| 0.85 | |||||
| 101,325/303,975/506,625 | |||||
| 7.35/21.85/36.05 | |||||
| EOS | Detailed in Table 2 | Different | ARK | ARK | |
| Viscosity model | Lemmon | Lemmon | Different | Lemmon | |
| Thermal conductivity model | Lemmon | Lemmon | Lemmon | Different | |
| Isentropic relation | Detailed in Table 2 | (5) | (5) | (5) | |
| Wall condition | Adiabat | ||||
| Method | 1 | 2 | 3 | |
|---|---|---|---|---|
| Condition | ||||
| EOS | NIST data | Ideal gas | Ideal gas | |
| Isentropic relation | Equation (5) | Equation (3) | Equation (3) | |
| Expansion coefficient | of real gas | |||
| Method | |||
|---|---|---|---|
| 1 | 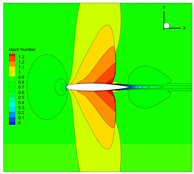 | 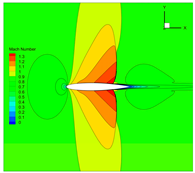 | 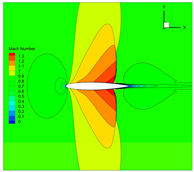 |
| 2 | 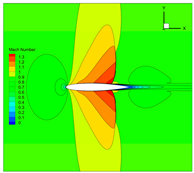 | 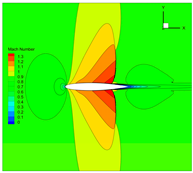 | 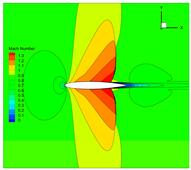 |
| 3 | 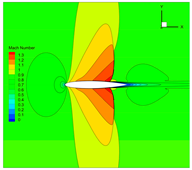 | 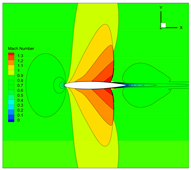 | 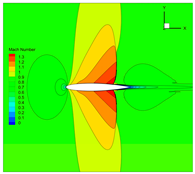 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, R.; Chen, Y.; Wu, J.; Tian, S. The Influence of Gas Models on Numerical Simulations of Cryogenic Flow. Aerospace 2023, 10, 986. https://doi.org/10.3390/aerospace10120986
Hu R, Chen Y, Wu J, Tian S. The Influence of Gas Models on Numerical Simulations of Cryogenic Flow. Aerospace. 2023; 10(12):986. https://doi.org/10.3390/aerospace10120986
Chicago/Turabian StyleHu, Ruifan, Yongliang Chen, Jifei Wu, and Shuling Tian. 2023. "The Influence of Gas Models on Numerical Simulations of Cryogenic Flow" Aerospace 10, no. 12: 986. https://doi.org/10.3390/aerospace10120986
APA StyleHu, R., Chen, Y., Wu, J., & Tian, S. (2023). The Influence of Gas Models on Numerical Simulations of Cryogenic Flow. Aerospace, 10(12), 986. https://doi.org/10.3390/aerospace10120986







