Adaptive Feed-Forward Control for Gust Load Alleviation on a Flying-Wing Model Using Multiple Control Surfaces
Abstract
1. Introduction
2. Aeroservoelastic Modeling of the Flying Wing
2.1. Structural and Aerodynamic Models
2.2. State-Space Open-Loop Aeroservoelastic Equations
3. Design of a MIMO Adaptive Feed-Forward Controller
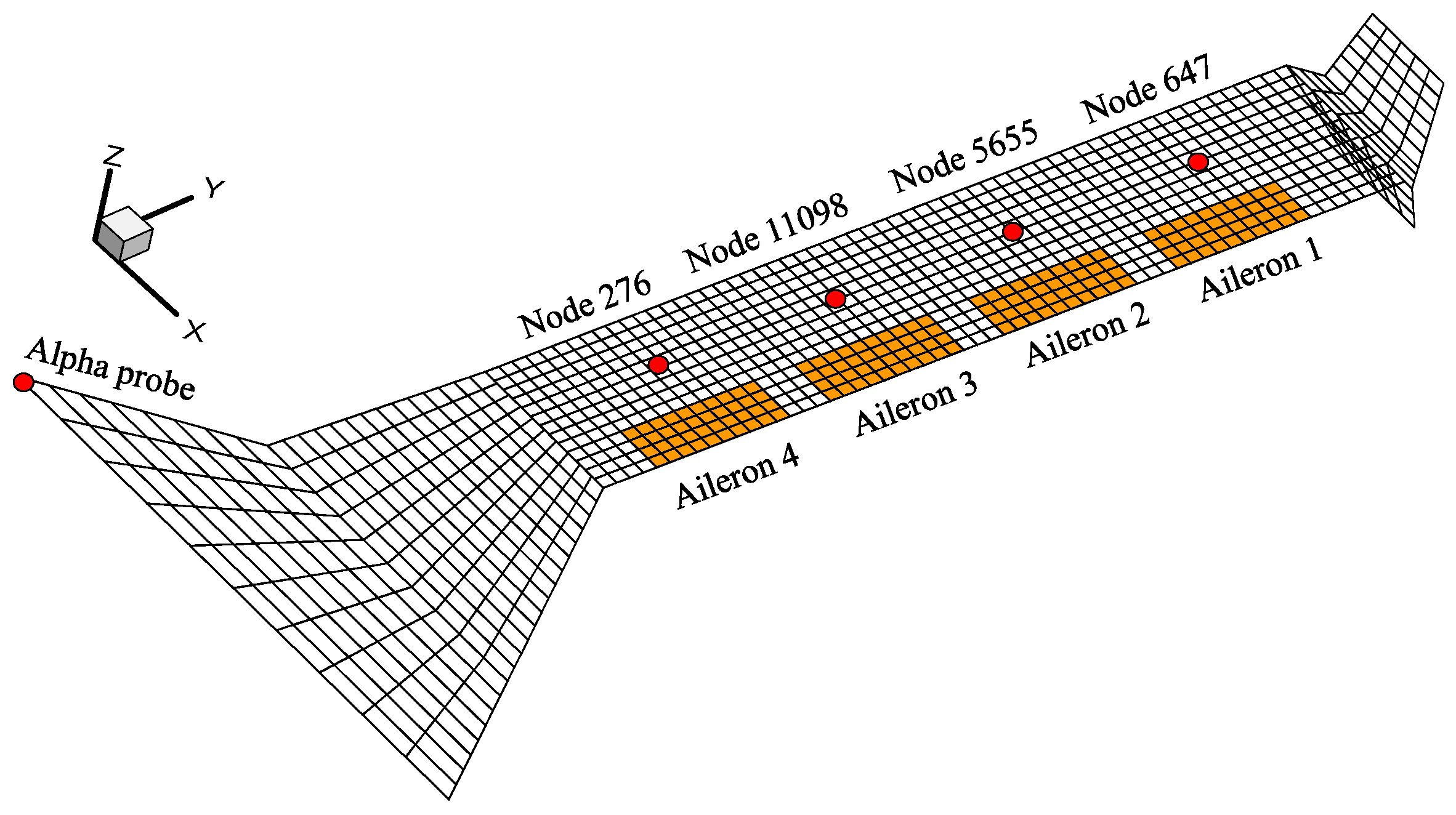
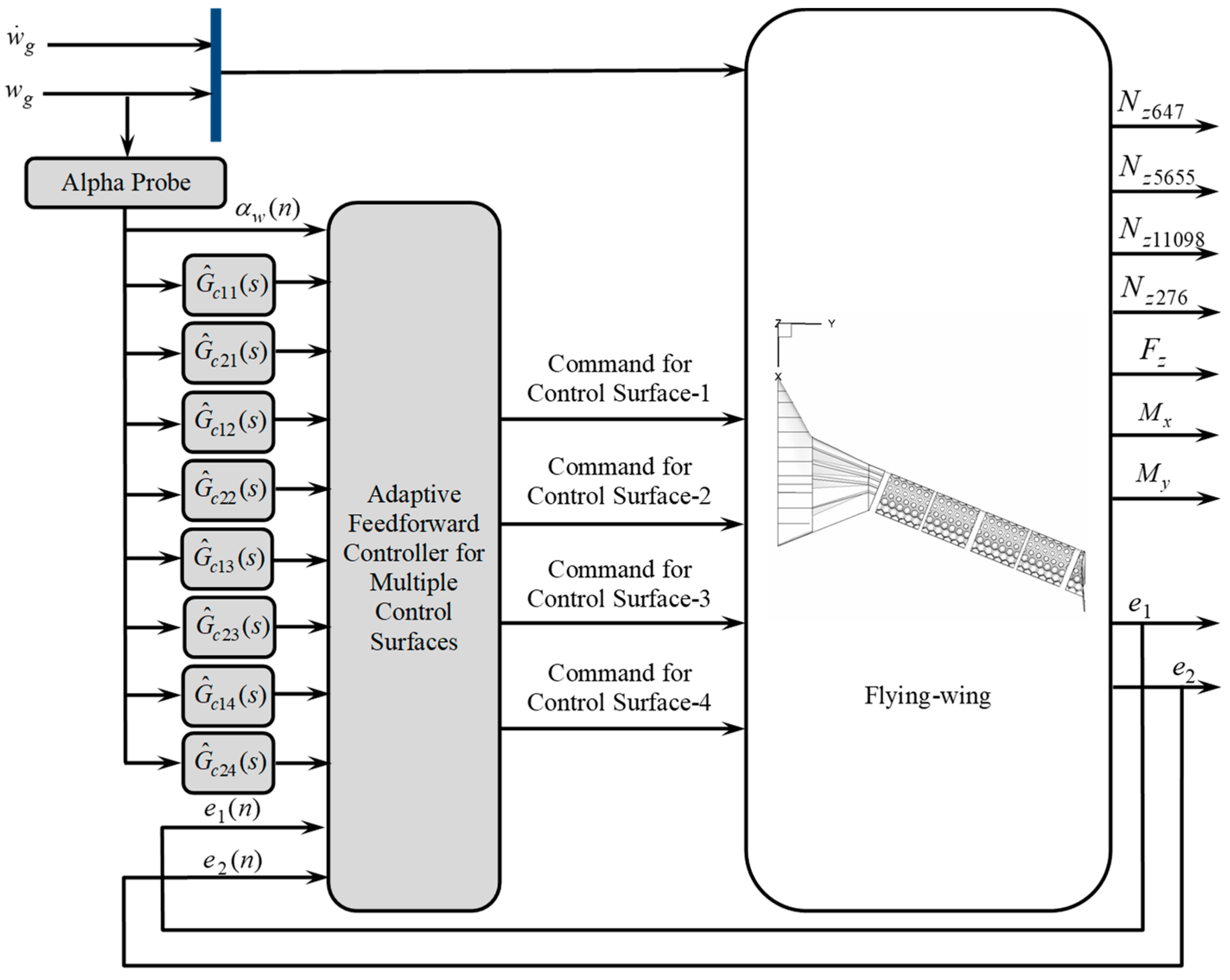
3.1. Control Surface and Sensor Layouts
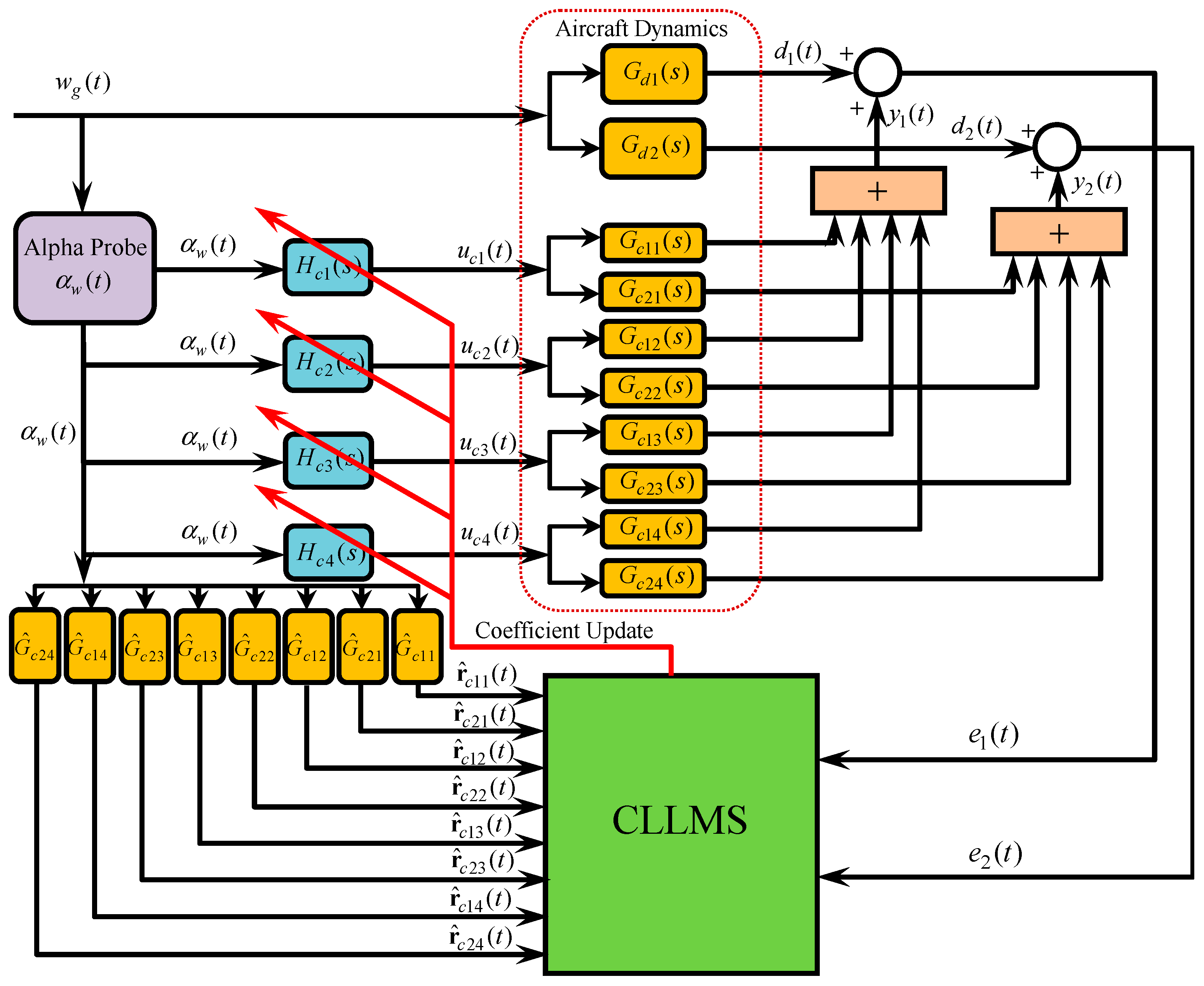
3.2. MIMO Adaptive Feed-Forward Control Scheme
3.3. MIMO Adaptive Feed-Forward Control Algorithm
3.3.1. FIR Filter
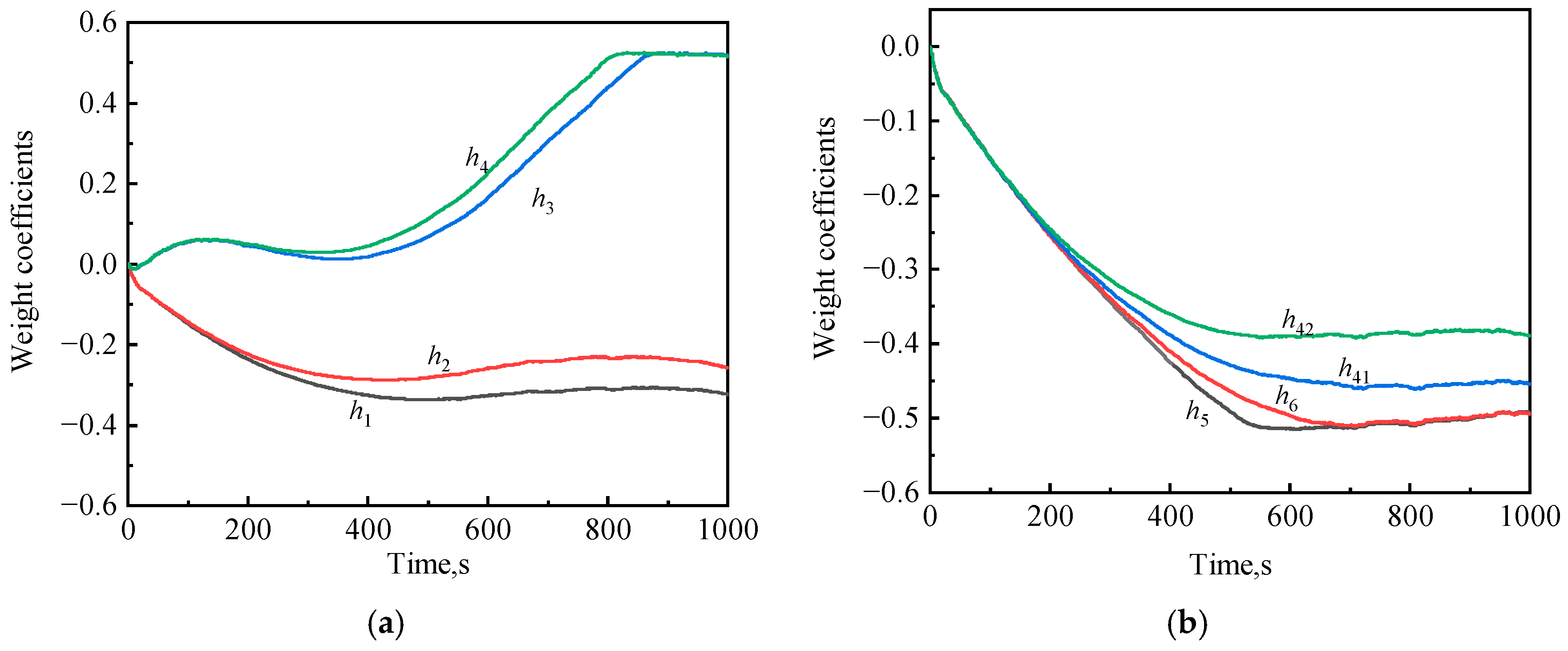
3.3.2. Adaptive Updating Law of the Weight Coefficients
4. Numerical Simulations for GLA Control of the Flying Wing
4.1. Flutter Analysis
4.2. Simulation Environment for GLA Control
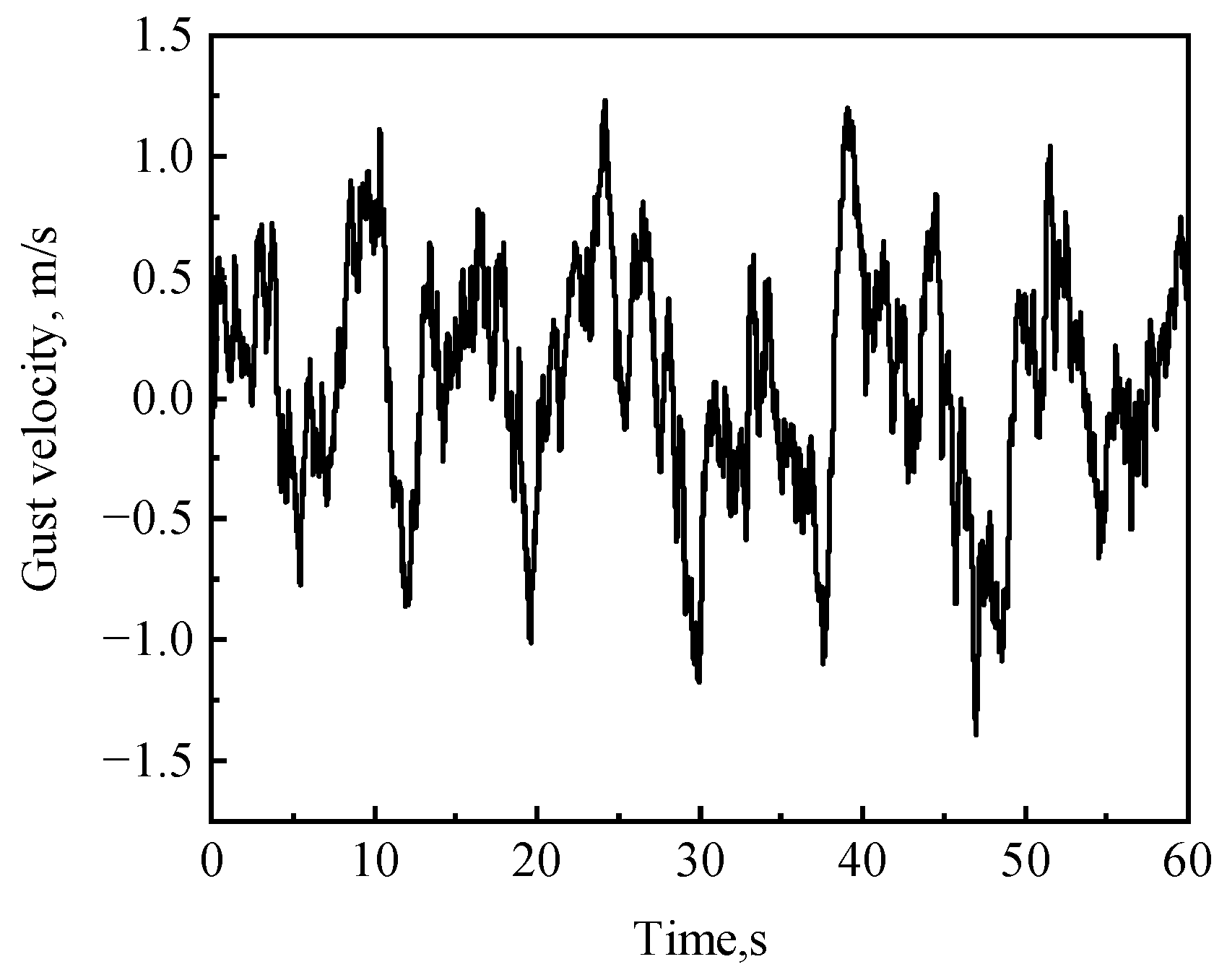
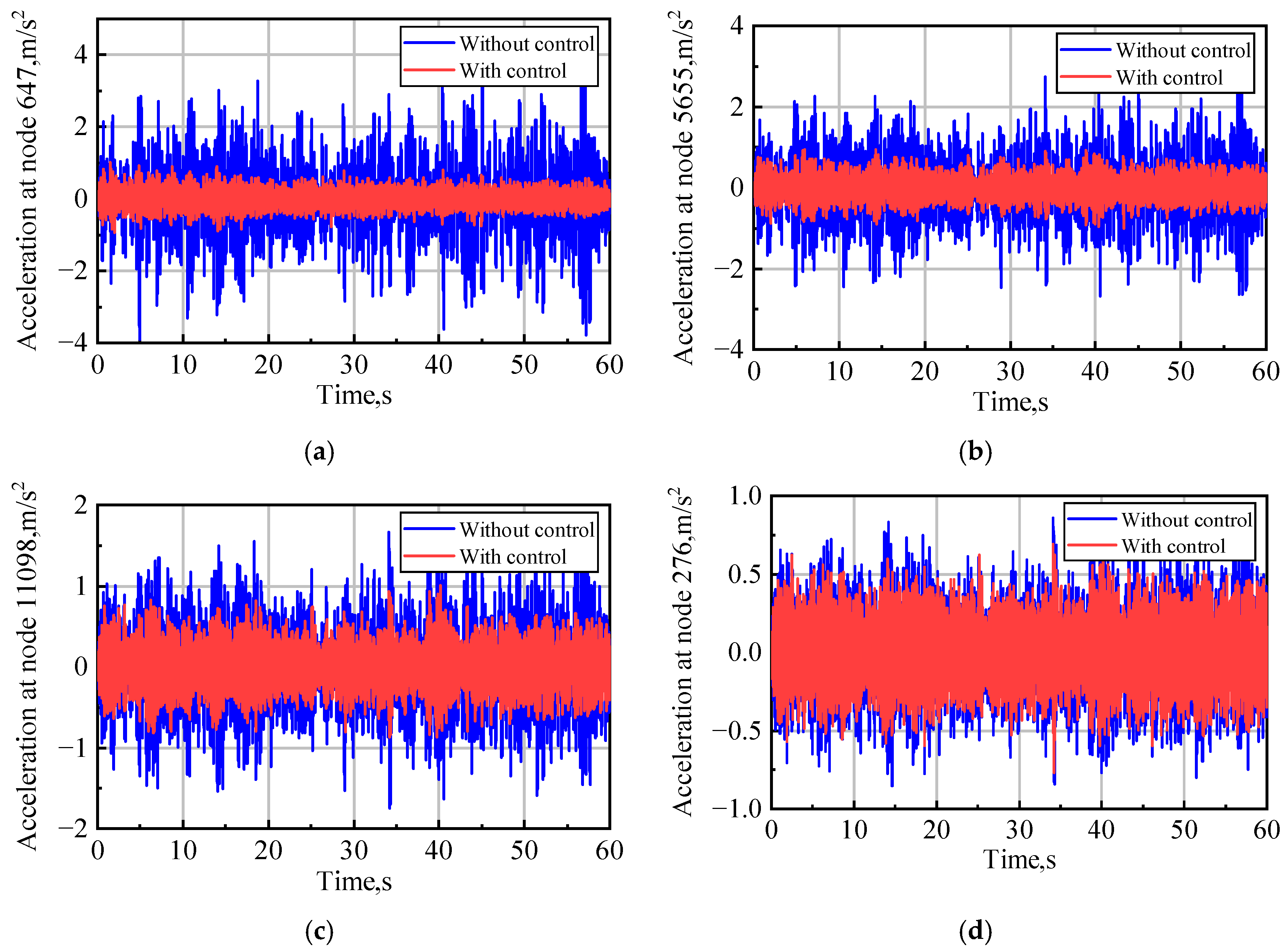
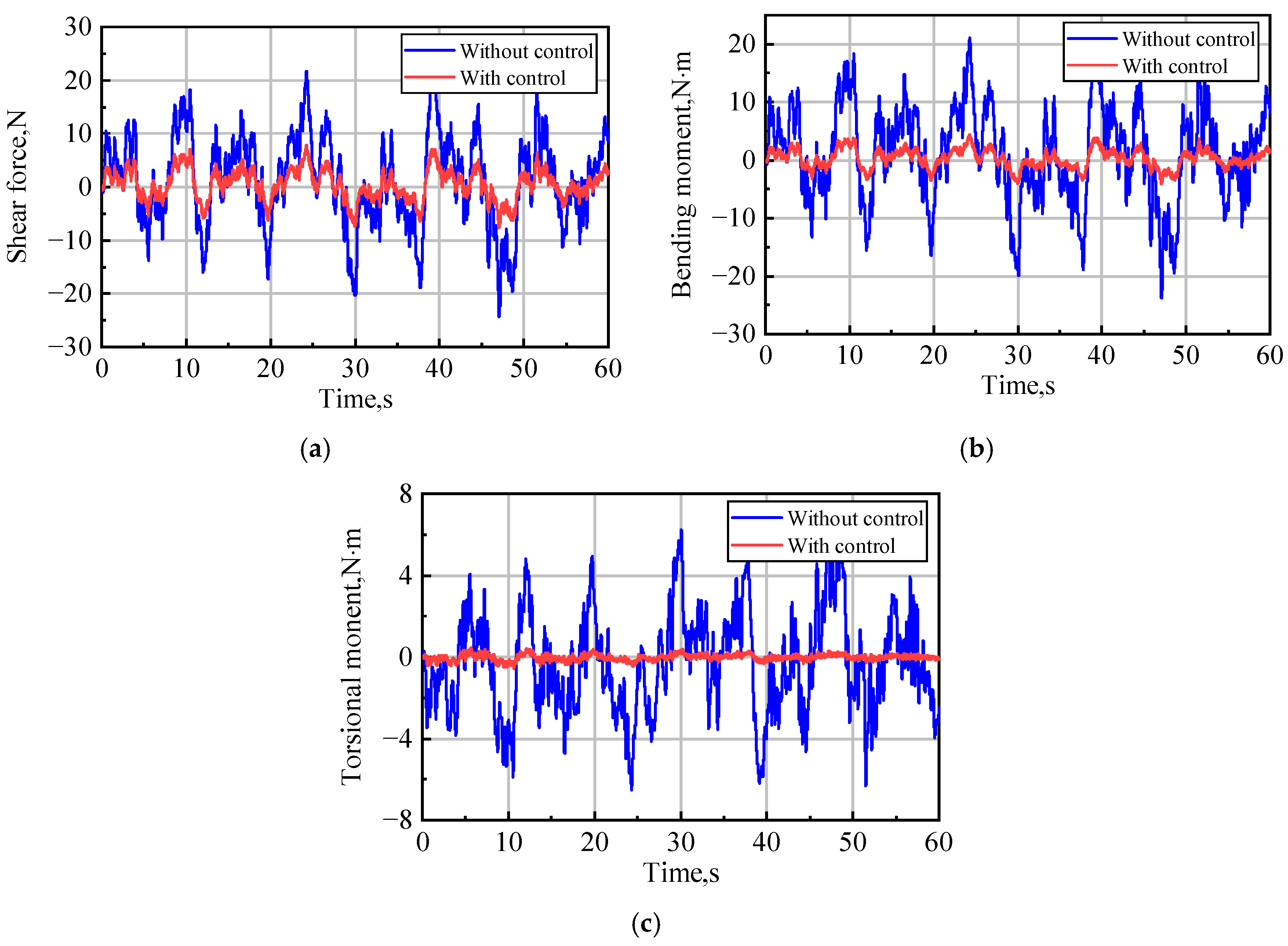
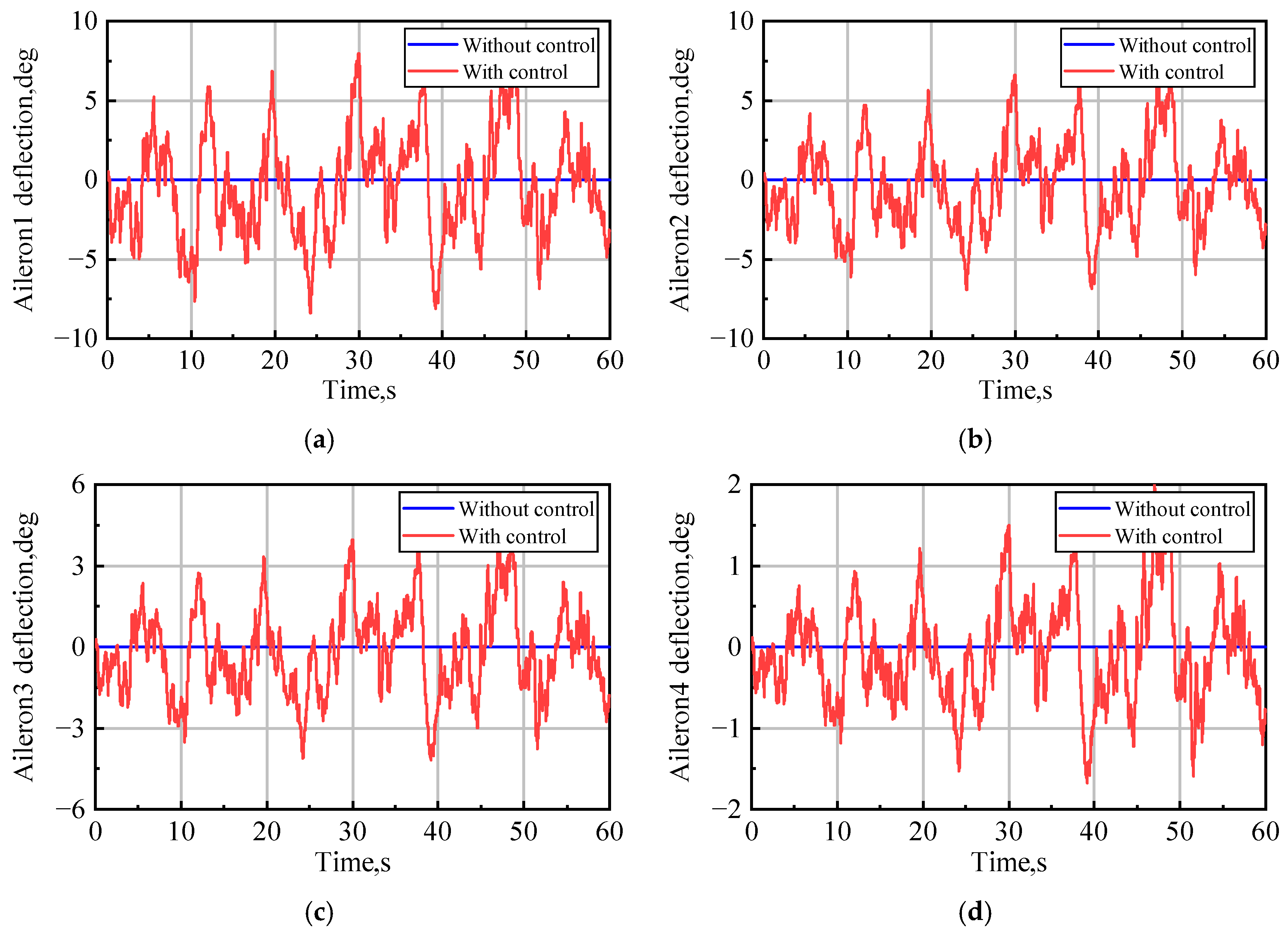
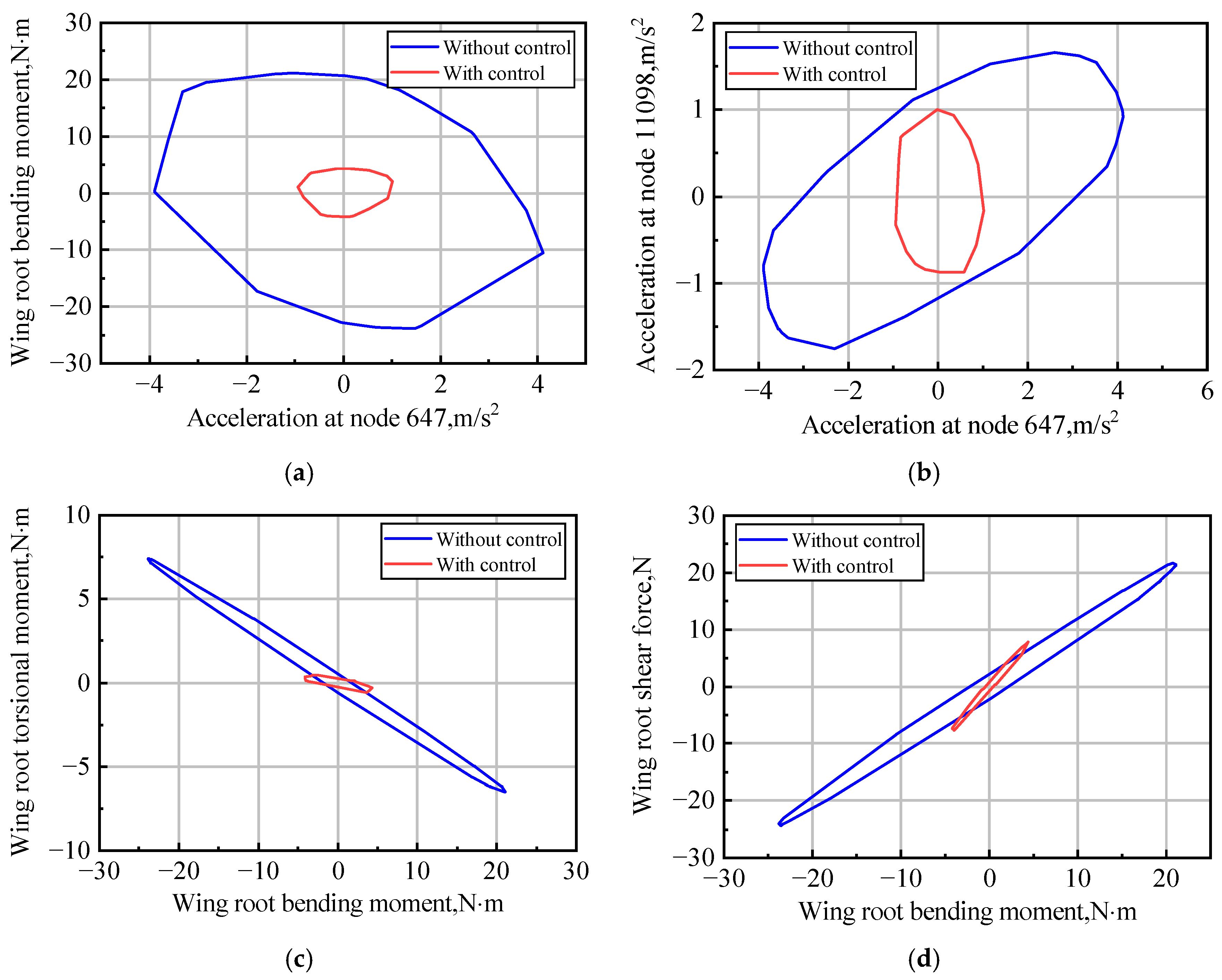
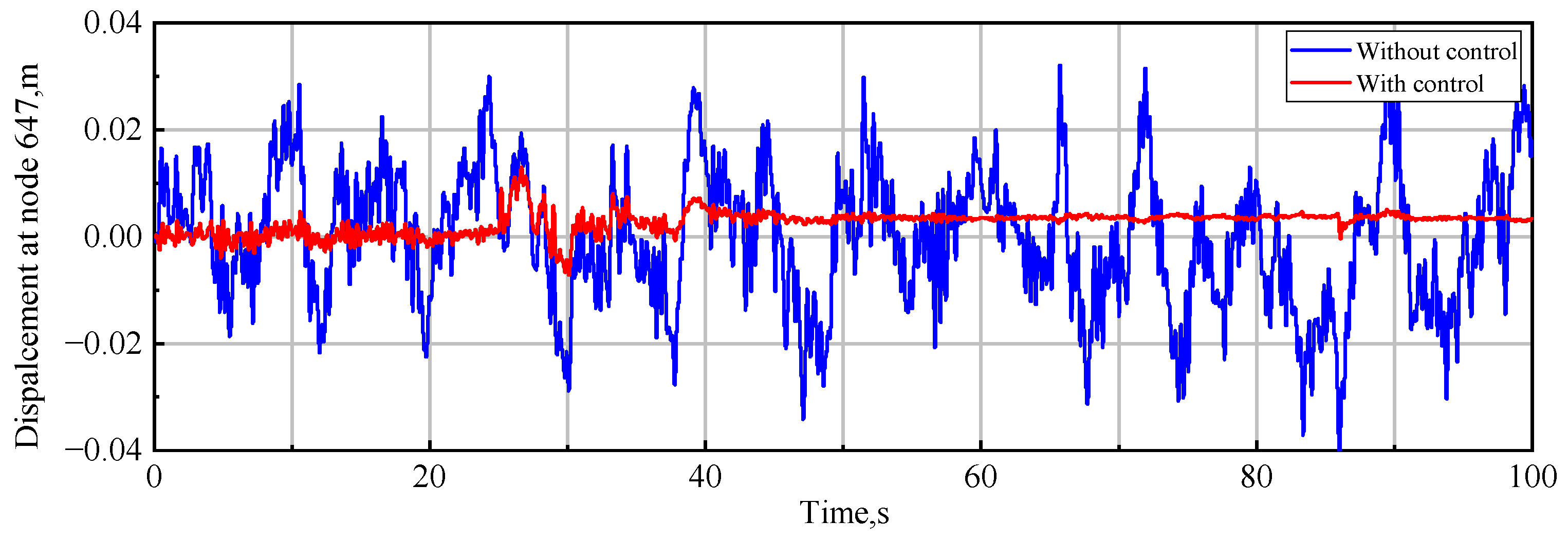
4.3. GLA Control in a Continuous Dryden Gust Field
4.4. GLA Control in a Discrete Gust Field
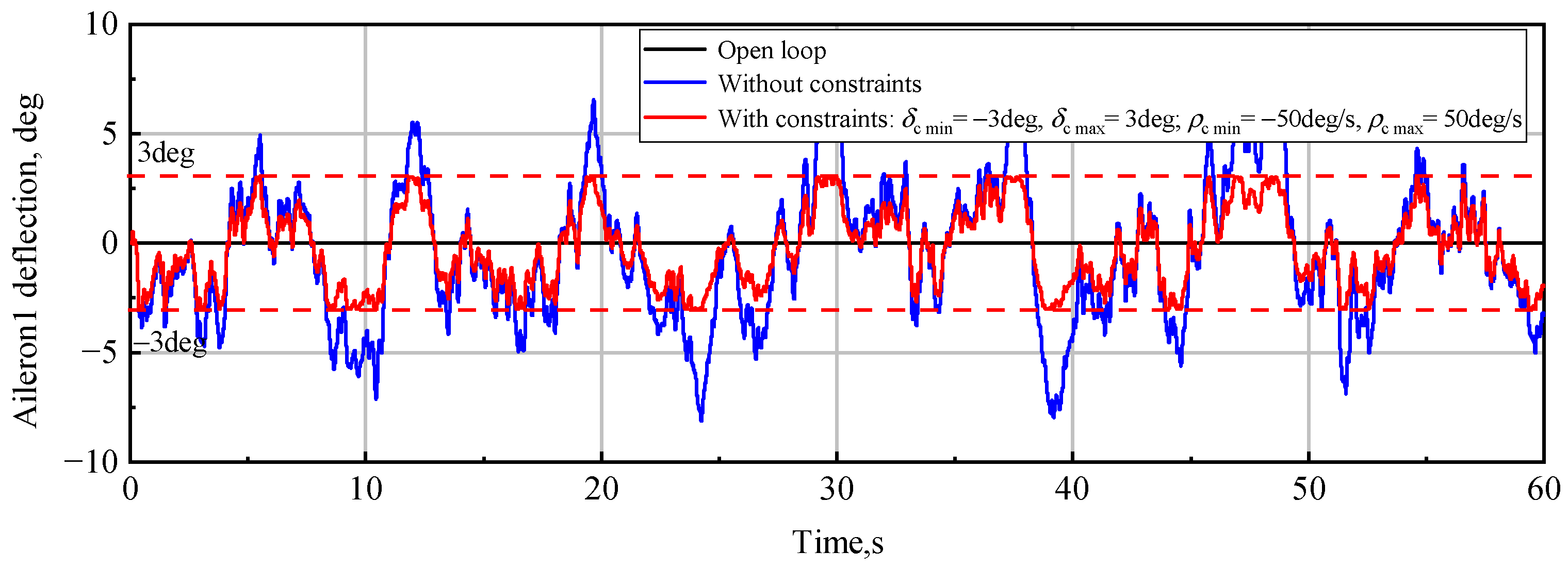
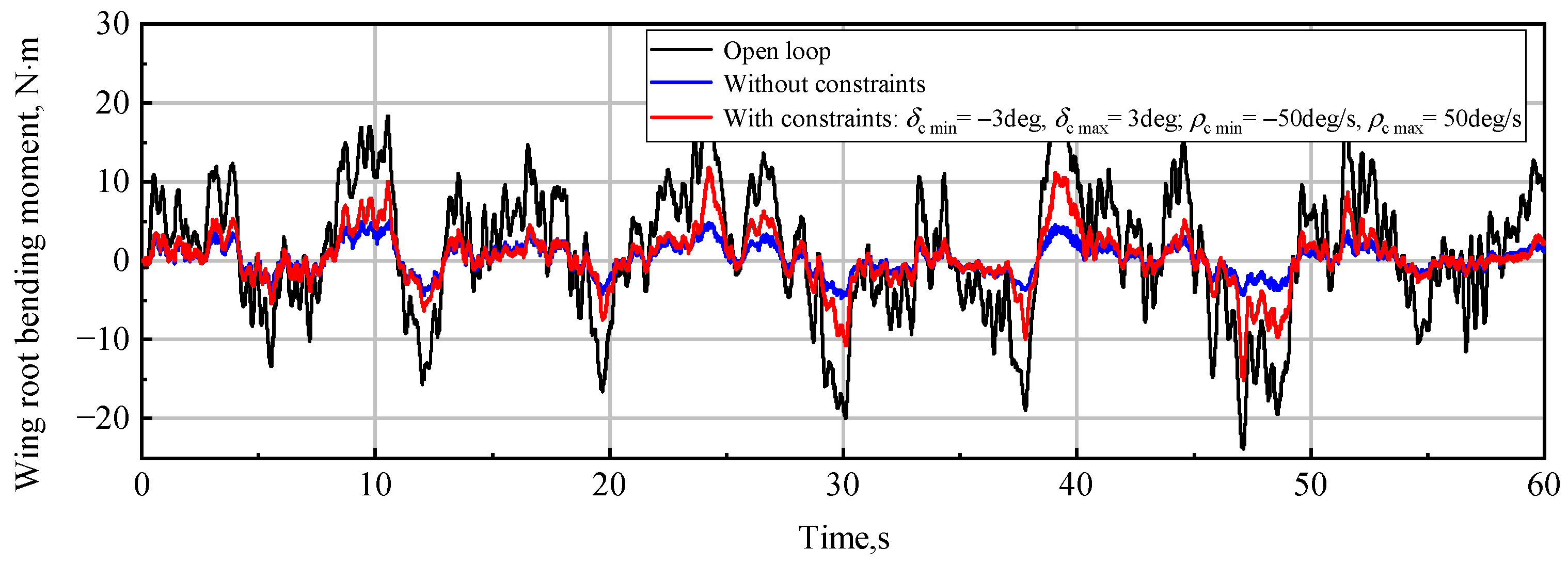
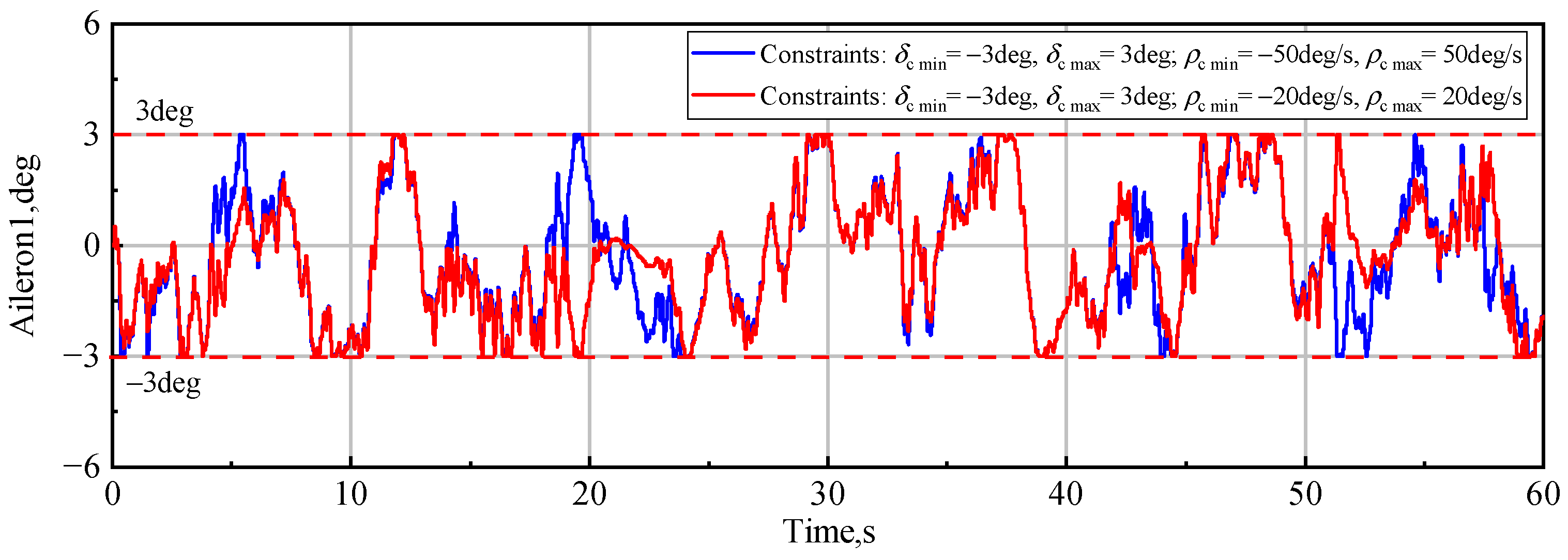
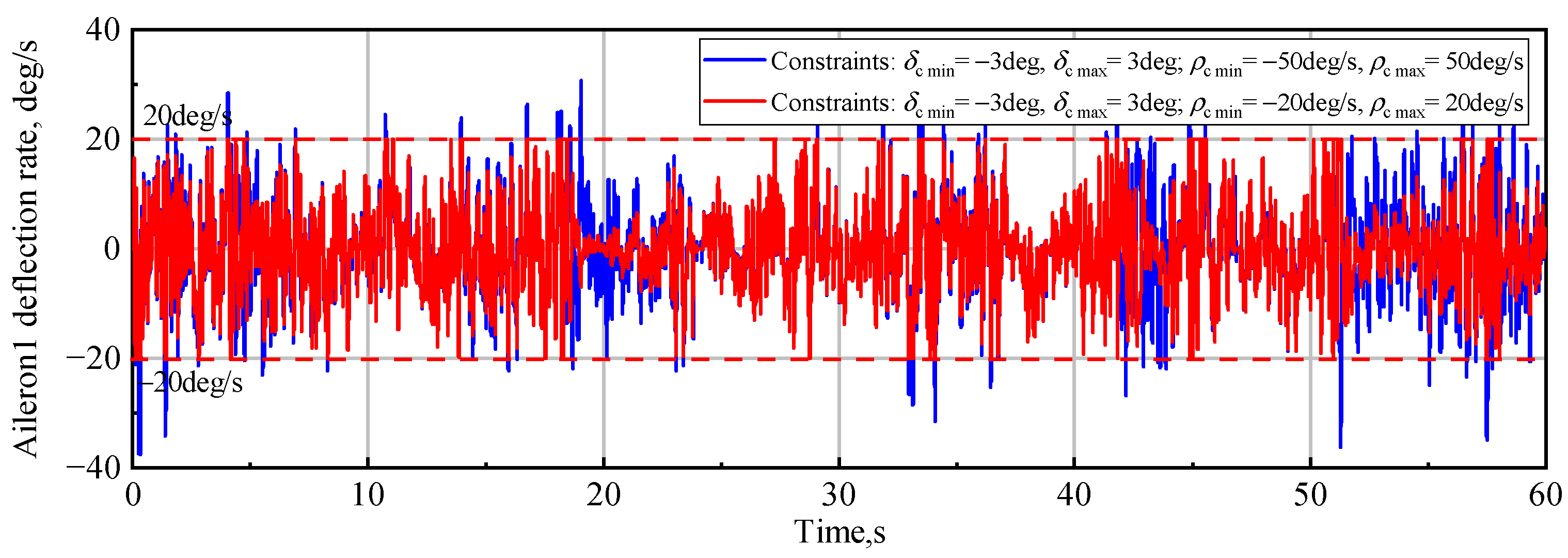
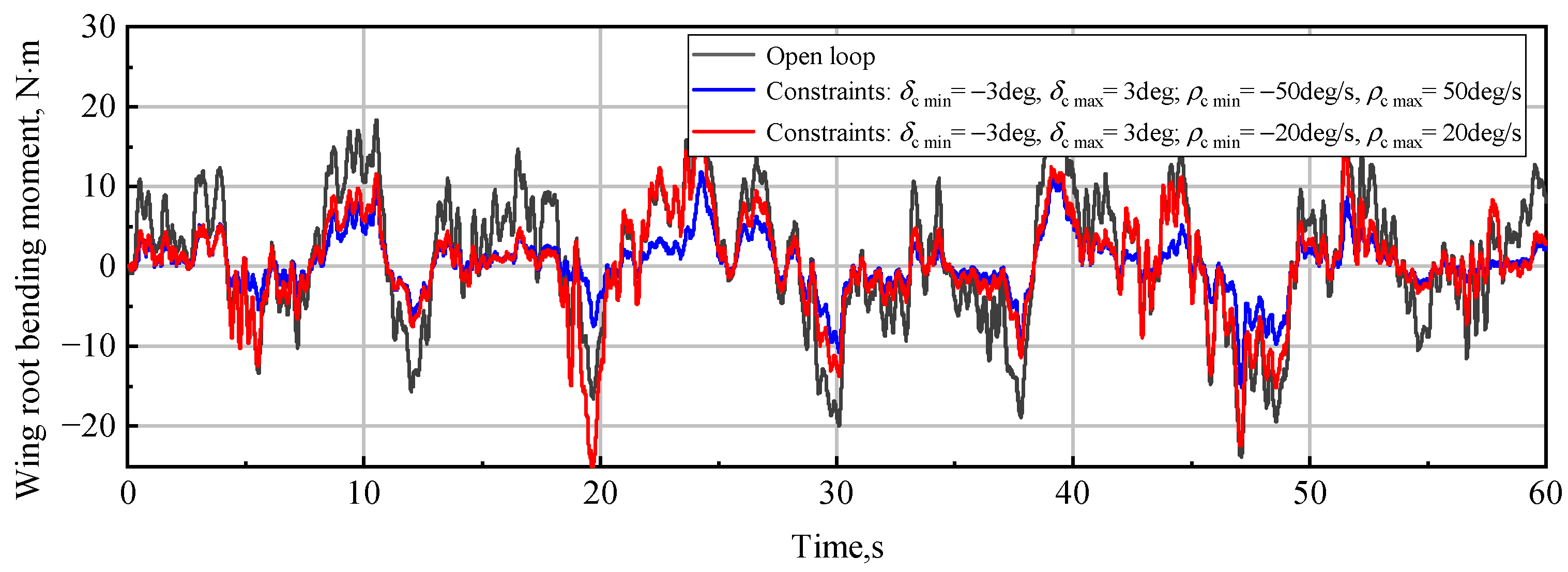
4.5. Constraints on Control Surface Deflections
- If
- Ifwhere is the controller output, namely the command control surface deflection.
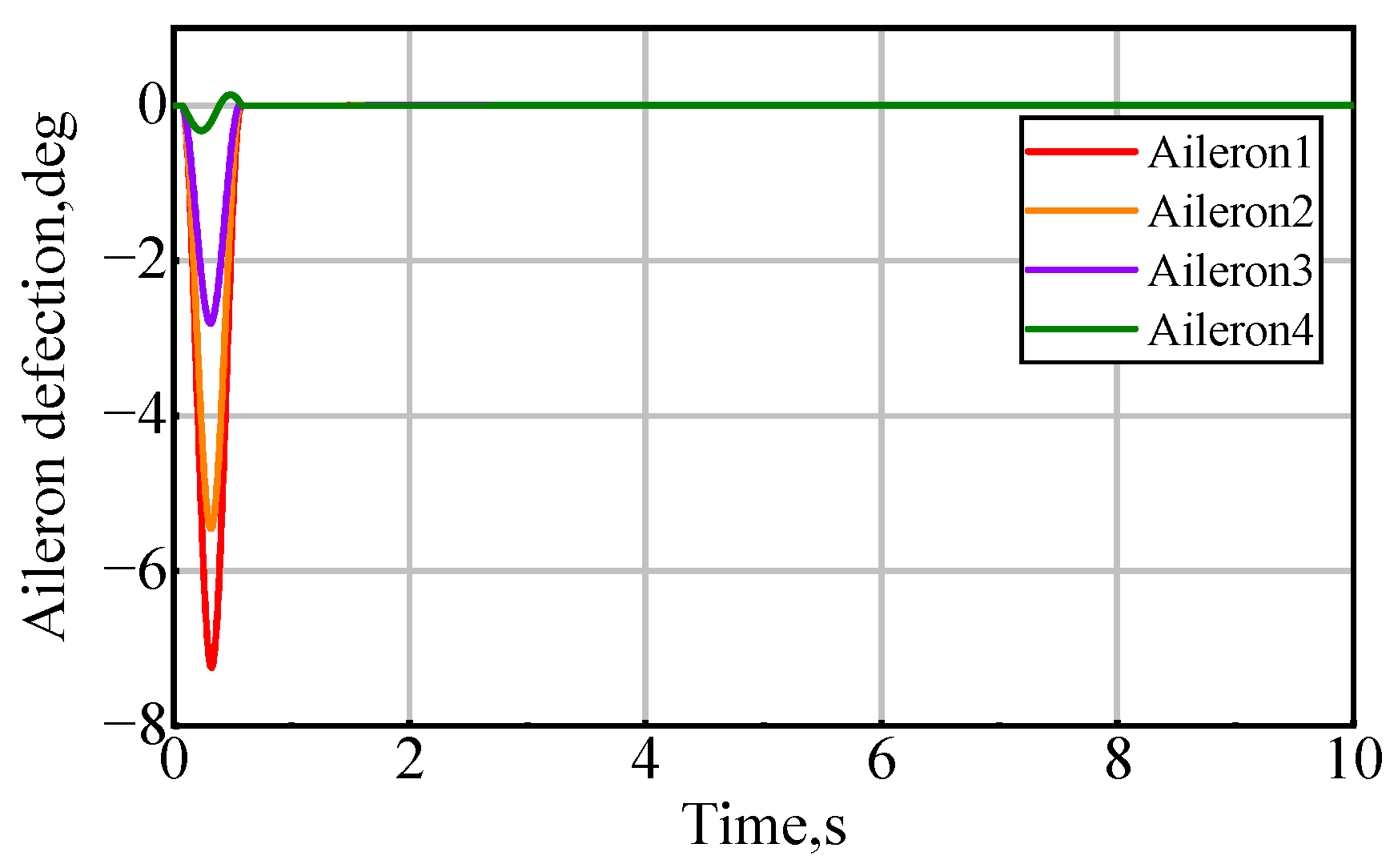
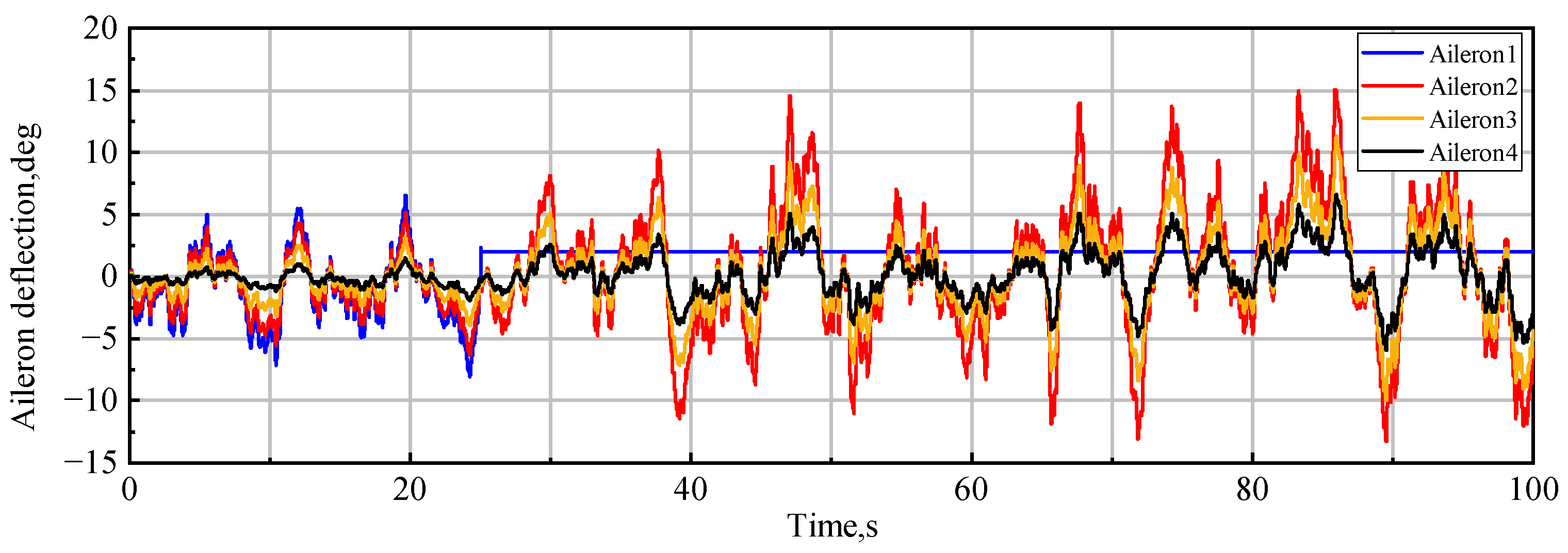
4.6. Case of Partial Failure of Actuators
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| cut-off frequency of the low-pass filter | |
| modal damping matrix | |
| acceleration response | |
| error signal | |
| gust excitation frequency | |
| primary path (PP) transfer function | |
| secondary path (SP) transfer function | |
| estimated transfer functions | |
| adaptive controllers | |
| weight coefficients of the filter | |
| cost function | |
| modal stiffness matrix | |
| continuous gust scale | |
| modal mass matrix | |
| mass coupling matrix | |
| number of the controllers | |
| number of the error signals | |
| matrix of GAF due to structural motion | |
| matrix of GAF due to deflections of control surfaces | |
| matrix of GAF due to gust disturbance | |
| aerodynamic lag root matrix | |
| filtered reference signals | |
| output of the system | |
| Gaussian white noise input | |
| sampling interval in simulations | |
| actual control surface deflection vector | |
| cruise speed | |
| servo-commanded control surface deflection | |
| convergence coefficient | |
| effective angle of attack induced by gust | |
| modal displacement vector | |
| modal velocity vector | |
| actual deflection | |
| , | minimum and maximum allowed deflection, respectively |
| , | minimum and maximum allowed deflection rate, respectively |
| state vector | |
| actuator state vector | |
| output vector | |
| leakage factor | |
| gust disturbance vector | |
| amplitude of gust velocity | |
| angular frequency | |
| RMS value of the gust velocity |
References
- Barnaby, R.S. Gust pre-sensing devices for aircraft gust-alleviation systems. J. Frankl. Inst. 1955, 259, 459–462. [Google Scholar] [CrossRef]
- Fournier, H.; Massioni, P.; Minh, T.P.; Bako, L.; Vernay, R.; Colombo, M. Robust gust load alleviation of flexible aircraft equipped with lidar. J. Guid. Control. Dynam. 2022, 45, 57–72. [Google Scholar] [CrossRef]
- Hoblit, F.M. Gust Loads on Aircraft: Concepts and Applications; American Institute of Aeronautics and Astronautics, Inc.: Washington, DC, USA, 1988. [Google Scholar] [CrossRef]
- Abdelmoula, F. Design of an open-loop gust alleviation control system for airborne gravimetry. Aerosp. Sci. Technol. 1999, 3, 379–389. [Google Scholar] [CrossRef]
- Regan, C.D.; Jutte, C.V. Survey of Applications of Active Control Technology for Gust Alleviation and New Challenges for Lighter-Weight Aircraft; NASA/TM–2012-216008; Dryden Flight Research Center: Edwards, CA, USA, 2012. [Google Scholar]
- Britt, R.T.; Jacobson, S.B.; Arthurs, T.D. Aeroservoelastic analysis of the B-2 bomber. J. Aircr. 2000, 37, 745–752. [Google Scholar] [CrossRef]
- Scott, R.; Coulson, D.; Castelluccio, M.; Heeg, J. Aeroservoelastic wind-tunnel tests of a free-flying, joined-wing Sensorcraft model for gust load alleviation. In Proceedings of the 52nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Denver, CO, USA, 4–7 April 2011; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2011. [Google Scholar] [CrossRef]
- Dillsaver, M.J.; Cesnik, C.E.S.; Kolmanovsky, I.V. Gust load alleviation control for very flexible aircraft. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Portland, OR, USA, 8–11 August 2011; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2011. [Google Scholar] [CrossRef]
- Yue, C.Y.; Zhao, Y.H. Active disturbance rejection controller design for alleviation of gust-induced aeroelastic responses. Aerosp. Sci. Technol. 2023, 133, 108116. [Google Scholar] [CrossRef]
- Alam, M.; Hromcik, M.; Hanis, T. Active gust load alleviation system for flexible aircraft: Mixed feedforward/feedback approach. Aerosp. Sci. Technol. 2015, 41, 122–133. [Google Scholar] [CrossRef]
- Hamada, Y.; Kikuchi, R.; Inokuchi, H. LIDAR-based Gust alleviation control system: Obtained results and flight demonstration plan. IFAC-PapersOnLine 2020, 53, 14839–14844. [Google Scholar] [CrossRef]
- Sleeper, R.K. Spanwise Measurements of Vertical Components of Atmospheric Turbulence; NASA: Washington, DC, USA; Langley Research Center Hampton: Hampton, VA, USA, 1990. [Google Scholar]
- Fuller, C.; Elliott, S.; Nelson, P. Active Control of Vibration; Academic Press: London, UK, 1996. [Google Scholar]
- Wildschek, A. An Adaptive Feed-Forward Controller for Active Wing Bending Vibration Alleviation on Large Transport Aircraft. Ph.D. Dissertation, Technical University of Munich, Munich, Germany, 2008. [Google Scholar]
- Brosilow, C.; Joseph, B. Techniques of Model-Based Control; Prentice Hall: Hoboken, NJ, USA, 2002. [Google Scholar]
- Zhou, Q.; Li, D.; Ronch, A.D.; Chen, G.; Li, Y. Computational fluid dynamics-based transonic flutter suppression with control delay. J. Fluid. Struct. 2016, 66, 183–206. [Google Scholar] [CrossRef]
- Wang, Y.; Ronch, A.D.; Maryam, G. Adaptive feedforward control for gust-induced aeroelastic vibrations. Aerospace 2018, 5, 86–104. [Google Scholar] [CrossRef]
- Wildschek, A.; Maier, R.; Hoffmann, F.; Jeanneau, M.; Baier, H. Active wing load alleviation with an adaptive feed-forward control algorithm. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Keystone, CO, USA, 21–24 August 2006; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2006. [Google Scholar] [CrossRef]
- Wildschek, A.; Maier, R.; Hahn, K.-U.; Leissling, D.; Press, M.; Zach, A. Flight test with an adaptive feed-forward controller for alleviation of turbulence excited wing bending vibrations. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Chicago, IL, USA, 10–13 August 2009; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2009. [Google Scholar] [CrossRef]
- Wildschek, A.; Bartosiewicz, Z.; Mozyrska, D. A multi-input multi-output adaptive feed-forward controller for vibration alleviation on a large blended wing body airliner. J. Sound Vib. 2014, 333, 3859–3880. [Google Scholar] [CrossRef]
- Widrow, B.; Stearns, S. Adaptive Signal Processing; Prentice-Hall: Hoboken, NJ, USA, 1985. [Google Scholar]
- Hansen, C.H.; Snyder, S.D. Active Control of Noise and Vibration; CRC Press: London, UK, 2012. [Google Scholar]
- Tobias, O.J.; Seara, R. Leaky delayed LMS algorithm: Stochastic analysis for Gaussian data and delay modeling error. IEEE Trans. Signal Process. 2004, 52, 1596–1606. [Google Scholar] [CrossRef]
- Zhao, Y.H.; Yue, C.Y.; Hu, H.Y. Gust load alleviation on a large transport airplane. J. Aircr. 2016, 53, 1932–1946. [Google Scholar] [CrossRef]
- Stanford, B.K. Optimal aircraft control surface layouts for maneuver and gust load alleviation. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2020. [Google Scholar] [CrossRef]
- Ricci, S.; De Gaspari, A.; Riccobene, L.; Fonte, F. Design and wind tunnel test validation of gust load alleviation systems. In Proceedings of the 58th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Grapevine, TX, USA, 9–13 January 2017; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2017. [Google Scholar] [CrossRef]
- Berg, J.; Ting, K.Y.; Mundt, T.J.; Mor, M.; Livne, E.; Morgansen, K.A. Exploratory wind tunnel gust alleviation tests of a multiple-flap flexible wing. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2022. [Google Scholar] [CrossRef]
- Kotikalpudi, A.; Danowsky, B.P.; Schmidt, D.; Theis, J.; Seiler, P. Flutter suppression control design for a small flexible flying-wing aircraft. In Proceedings of the Multidisciplinary Analysis and Optimization Conference, Atlanta, GA, USA, 25–29 June 2018; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018. [Google Scholar] [CrossRef]
- Albano, E.; Rodden, W.P. A doublet-lattice method for calculating lift distributions on oscillating surfaces in subsonic flows. AIAA J. 1969, 7, 279–285. [Google Scholar] [CrossRef]
- Karpel, M.; Strul, E. Minimum-state unsteady aerodynamic approximations with flexible constraints. J. Aircr. 1996, 33, 1190–1196. [Google Scholar] [CrossRef]
- Zhao, Y.H. ; Huang. R. Advanced Aeroelasticity and Control; China Science Publishing Press: Beijing, China, 2015. [Google Scholar]
- Wildschek, A.; Hanis, T.; Stroscher, F. L-infinity optimal feedforward gust load alleviation design for a large blended wing body airliner. EUCASS Proc. Ser. 2013, 6, 707–728. [Google Scholar] [CrossRef][Green Version]
- Mayyas, K.; Aboulnasr, T. The leaky LMS algorithm: MSE analysis for Gaussian data. IEEE Trans. Signal Process. 1997, 45, 927–934. [Google Scholar] [CrossRef]
- Nascimento, V.H.; Sayed, A.H. Unbiased and stable leakage-based adaptive filters. IEEE Trans. Signal Process. 1999, 47, 3261–3276. [Google Scholar] [CrossRef]
- ZONA Technology. ZAERO User’s Manual; ZONA Technology Inc.: Scottsdale, AZ, USA, 2011. [Google Scholar]
- Castellani, M.; Lemmens, Y.; Cooper, J.E. Parametric reduced order model approach for rapid dynamic loads prediction. Aerosp. Sci. Technol. 2016, 52, 29–40. [Google Scholar] [CrossRef]

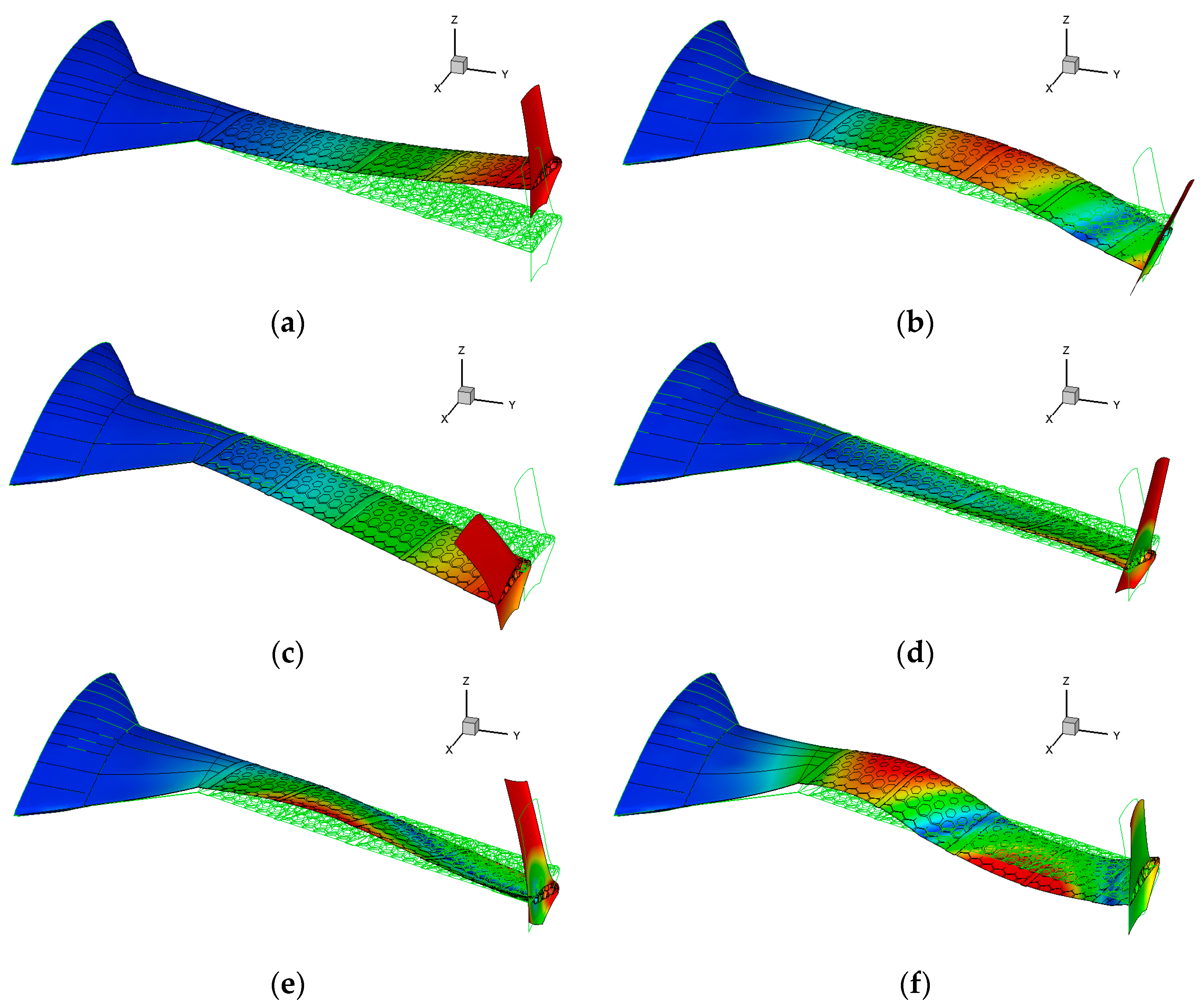
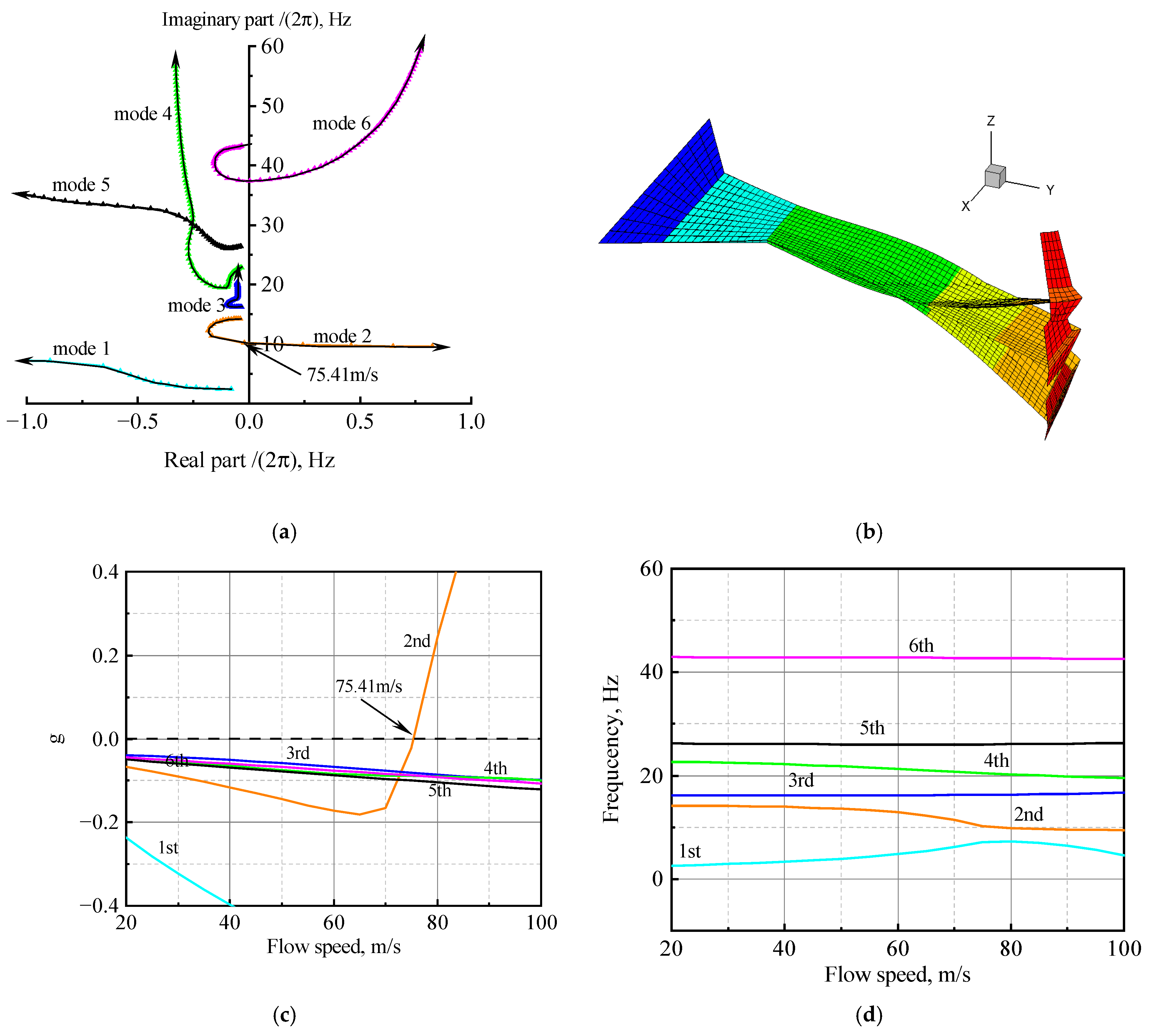



| Mode | Frequency (Hz) | Mode Shape |
|---|---|---|
| 1 | 2.39 | 1st vertical bending |
| 2 | 14.32 | 2nd vertical bending |
| 3 | 16.15 | 1st in-plane bending |
| 4 | 22.87 | 1st torsion |
| 5 | 26.45 | 2nd torsion |
| 6 | 43.35 | 3rd vertical bending |
| Parameter | RMS Reduction | Parameter | RMS Reduction |
|---|---|---|---|
| , | 80.98% | , | 46.62% |
| , | 65.63% | , | 34.44% |
| , | 66.12% | , | 80.72% |
| , | 94.14% | ⸺ | ⸺ |
| Parameter | Reduction of the Maximum Value | Parameter | Reduction of the Maximum Value |
|---|---|---|---|
| , | 83.10% | , | 73.23% |
| , | 90.12% | , | 70.72% |
| , | 77.59% | , | 62.16% |
| Parameter | RMS Reduction with Constraint (without) | Parameter | RMS Reduction with Constraint (without) |
|---|---|---|---|
| , | 61.35% (80.98%) | , | 30.87% (46.62%) |
| , | 48.38% (65.63%) | , | 19.27% (34.44%) |
| , | 55.08% (66.12%) | , | 58.77% (80.72%) |
| , | 65.94% (94.14%) | ⸺ | ⸺ |
| Parameter | RMS Reduction with Constraints (without) | Parameter | RMS Reduction with Constraints (without) |
|---|---|---|---|
| , | 22.80% (80.98%) | , | 14.15% (46.62%) |
| , | 19.78% (65.63%) | , | 8.22% (34.44%) |
| , | 23.99% (66.12%) | , | 28.27% (80.72%) |
| , | 31.43% (94.14%) | ⸺ | ⸺ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Zhao, Y. Adaptive Feed-Forward Control for Gust Load Alleviation on a Flying-Wing Model Using Multiple Control Surfaces. Aerospace 2023, 10, 981. https://doi.org/10.3390/aerospace10120981
Zhang L, Zhao Y. Adaptive Feed-Forward Control for Gust Load Alleviation on a Flying-Wing Model Using Multiple Control Surfaces. Aerospace. 2023; 10(12):981. https://doi.org/10.3390/aerospace10120981
Chicago/Turabian StyleZhang, Liqi, and Yonghui Zhao. 2023. "Adaptive Feed-Forward Control for Gust Load Alleviation on a Flying-Wing Model Using Multiple Control Surfaces" Aerospace 10, no. 12: 981. https://doi.org/10.3390/aerospace10120981
APA StyleZhang, L., & Zhao, Y. (2023). Adaptive Feed-Forward Control for Gust Load Alleviation on a Flying-Wing Model Using Multiple Control Surfaces. Aerospace, 10(12), 981. https://doi.org/10.3390/aerospace10120981







