Investigating Planar and Nonplanar Wing Planform Optimisation for Ground Effect Aircraft
Abstract
:1. Introduction
2. Physics Models
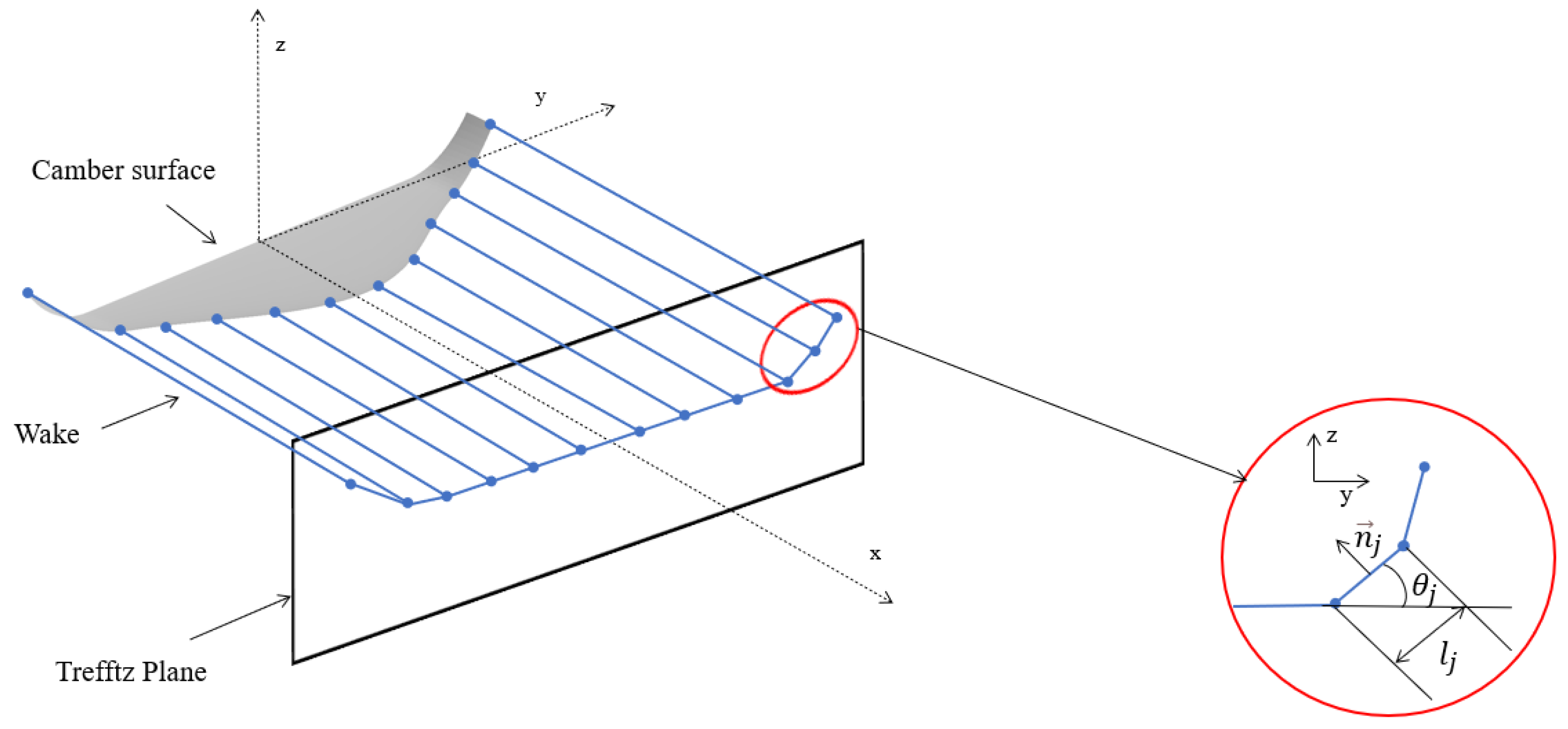
2.1. Vortex Lattice Method
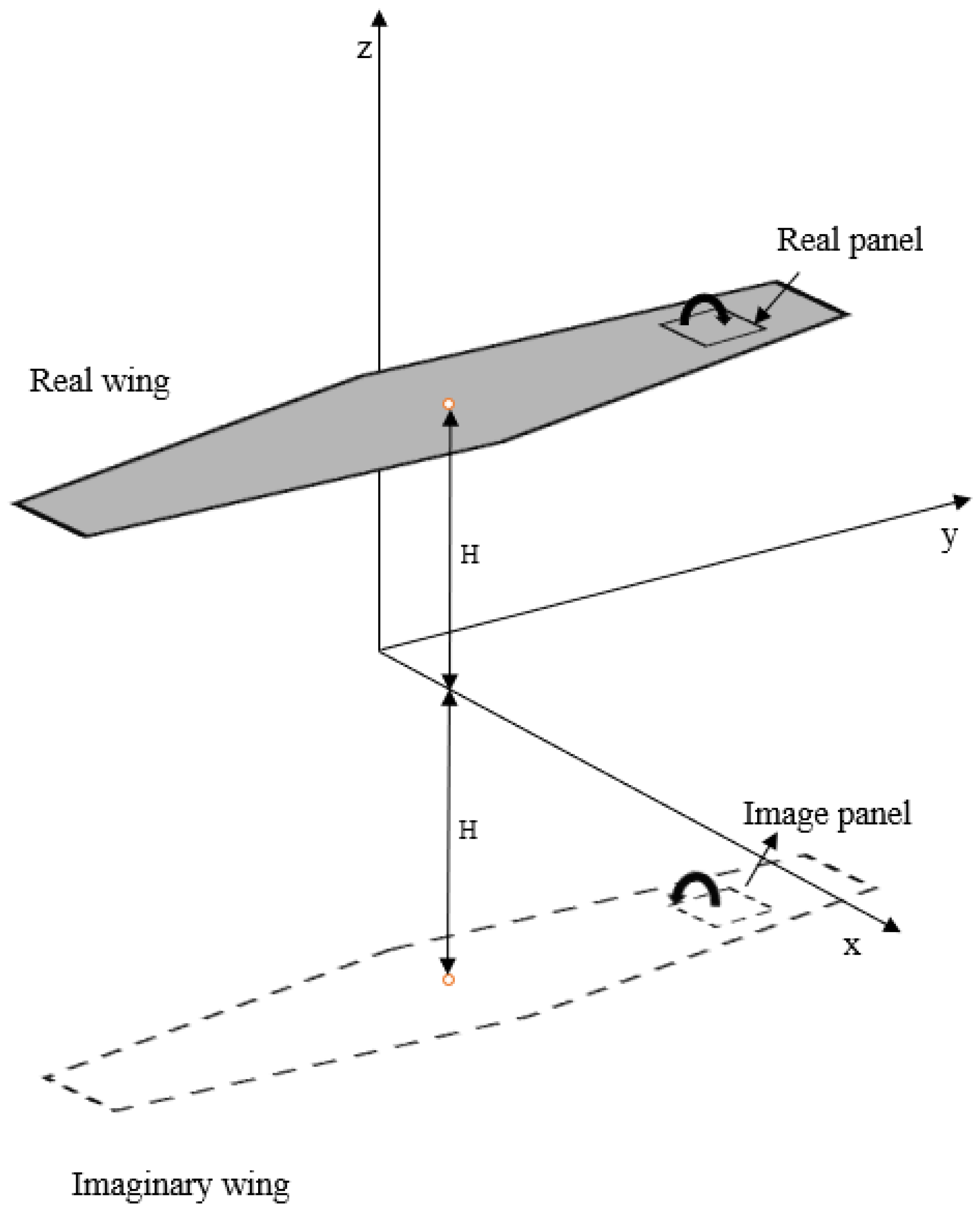
2.2. Method of Images
2.3. Profile Drag
2.4. Longitudinal Static Stability
2.4.1. Pitch Attitude
2.4.2. Static Stability in Pitch
2.4.3. Static Stability in Height
3. Baseline Design and Case Definition
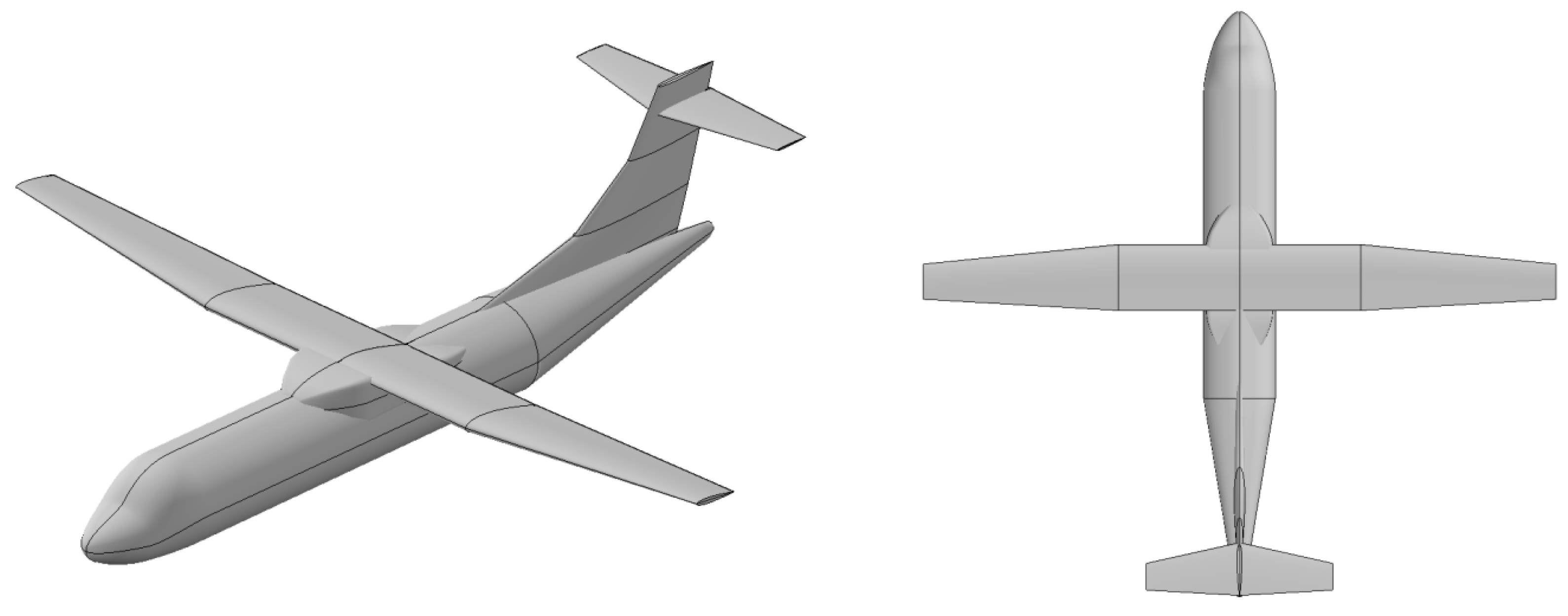
3.1. Baseline Design
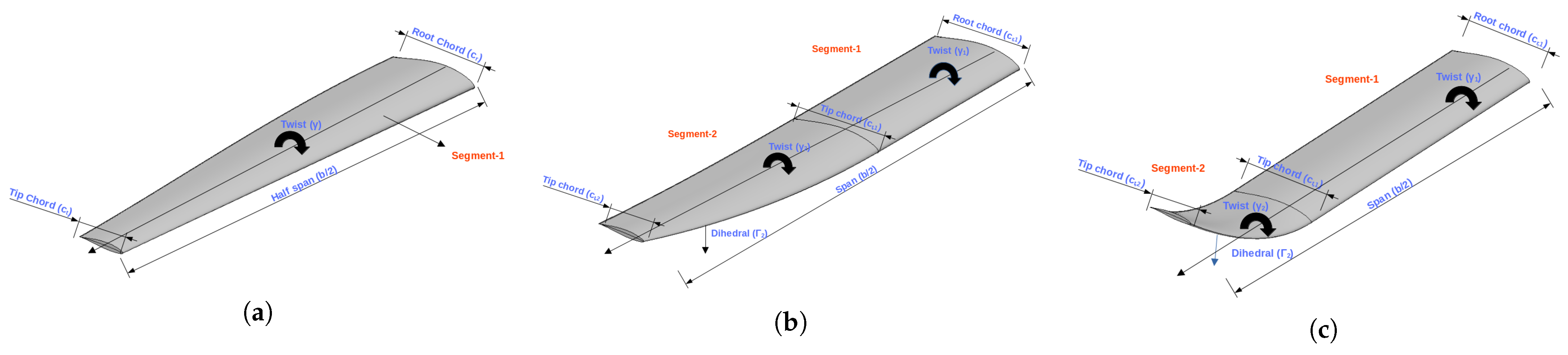
3.2. Geometry Parameterisation Using OpenVSP
3.2.1. Case-1: Planar Optimisation
3.2.2. Case-2: Nonplanar Wing Optimisation
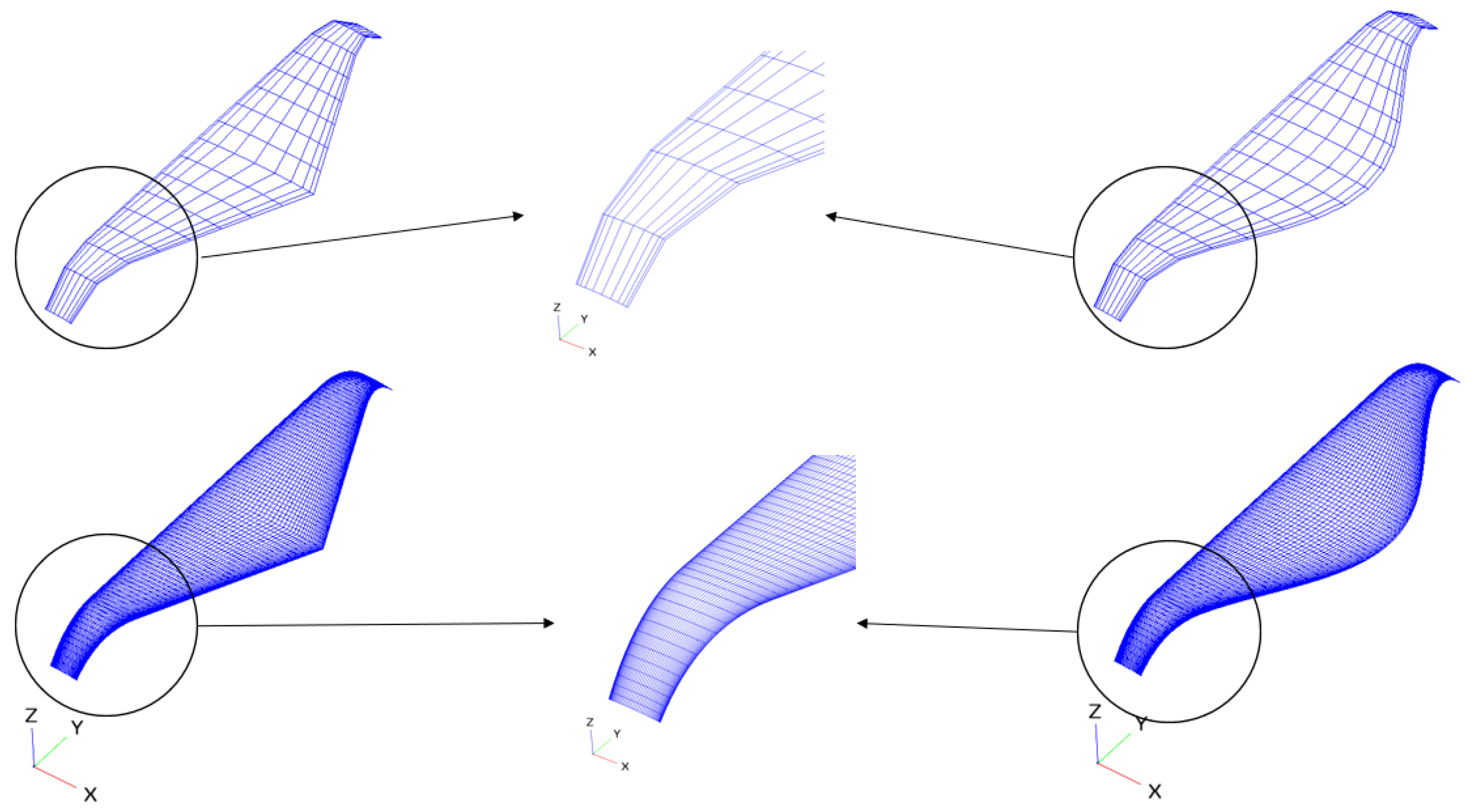
3.2.3. Case-3: Nonplanar Wingtip Optimisation
4. Optimisation Problem Formulation and Framework
4.1. Optimisation Problem Formulation
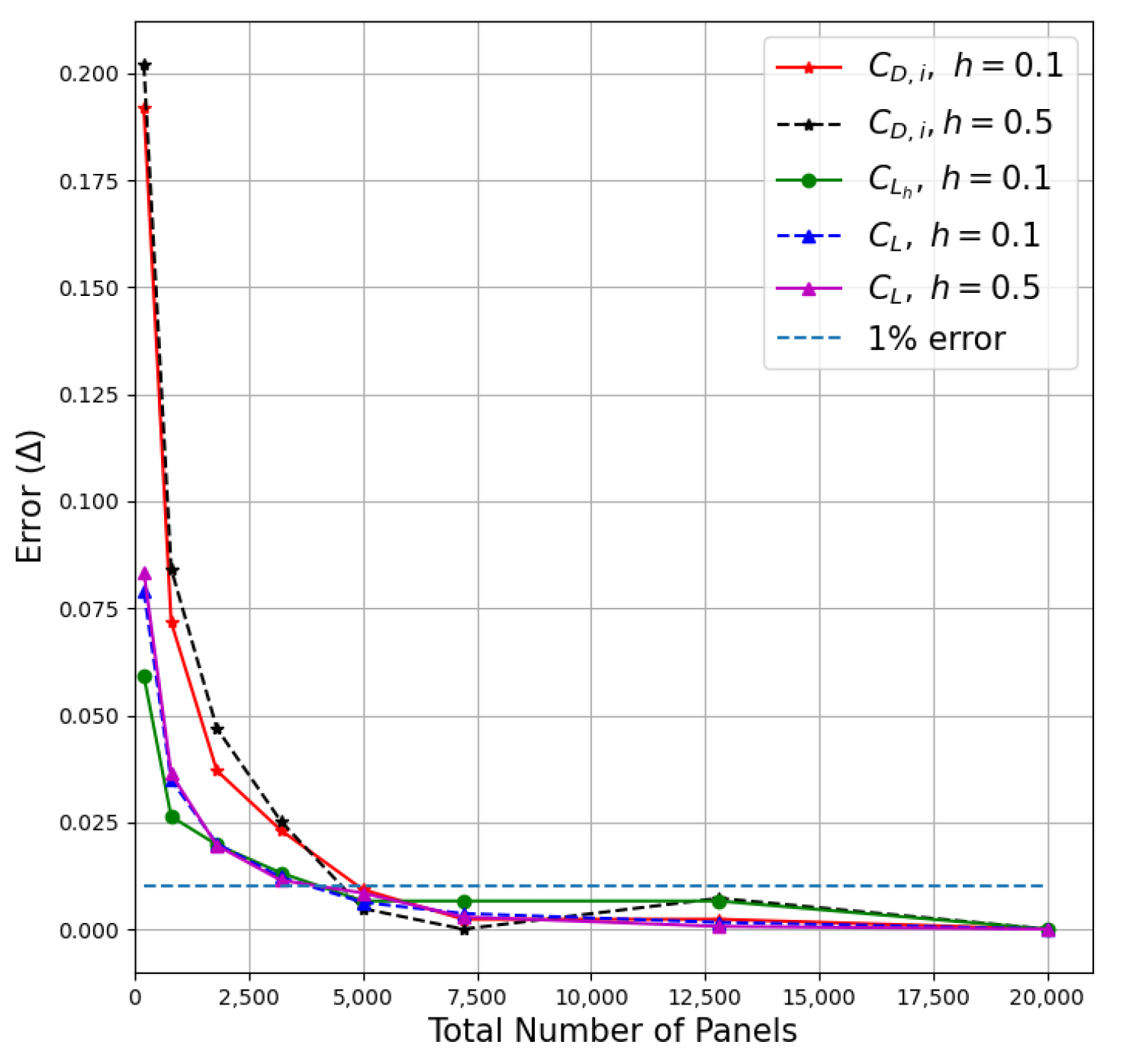
4.2. Mesh Convergence Study
4.3. Optimiser
4.4. Optimisation Framework
5. Results and Discussion
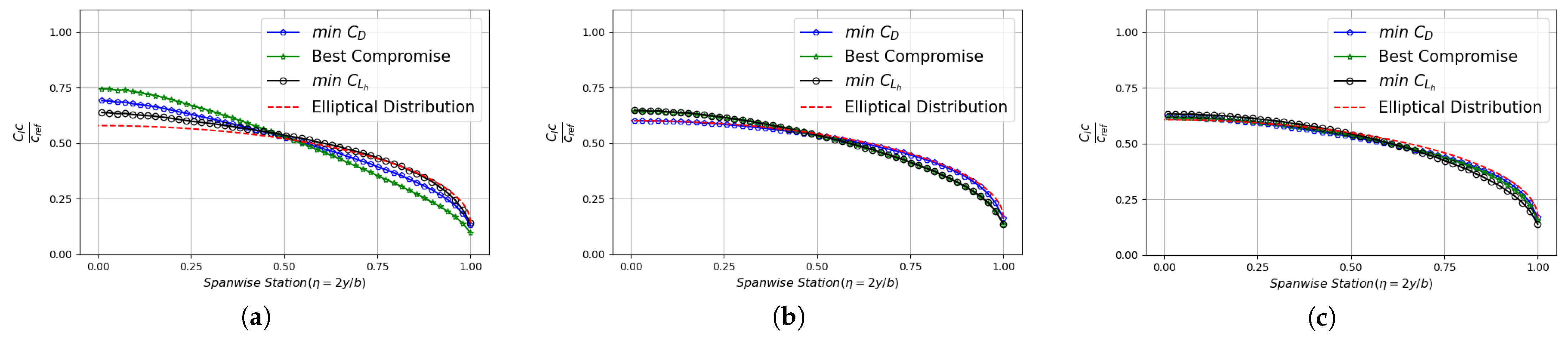
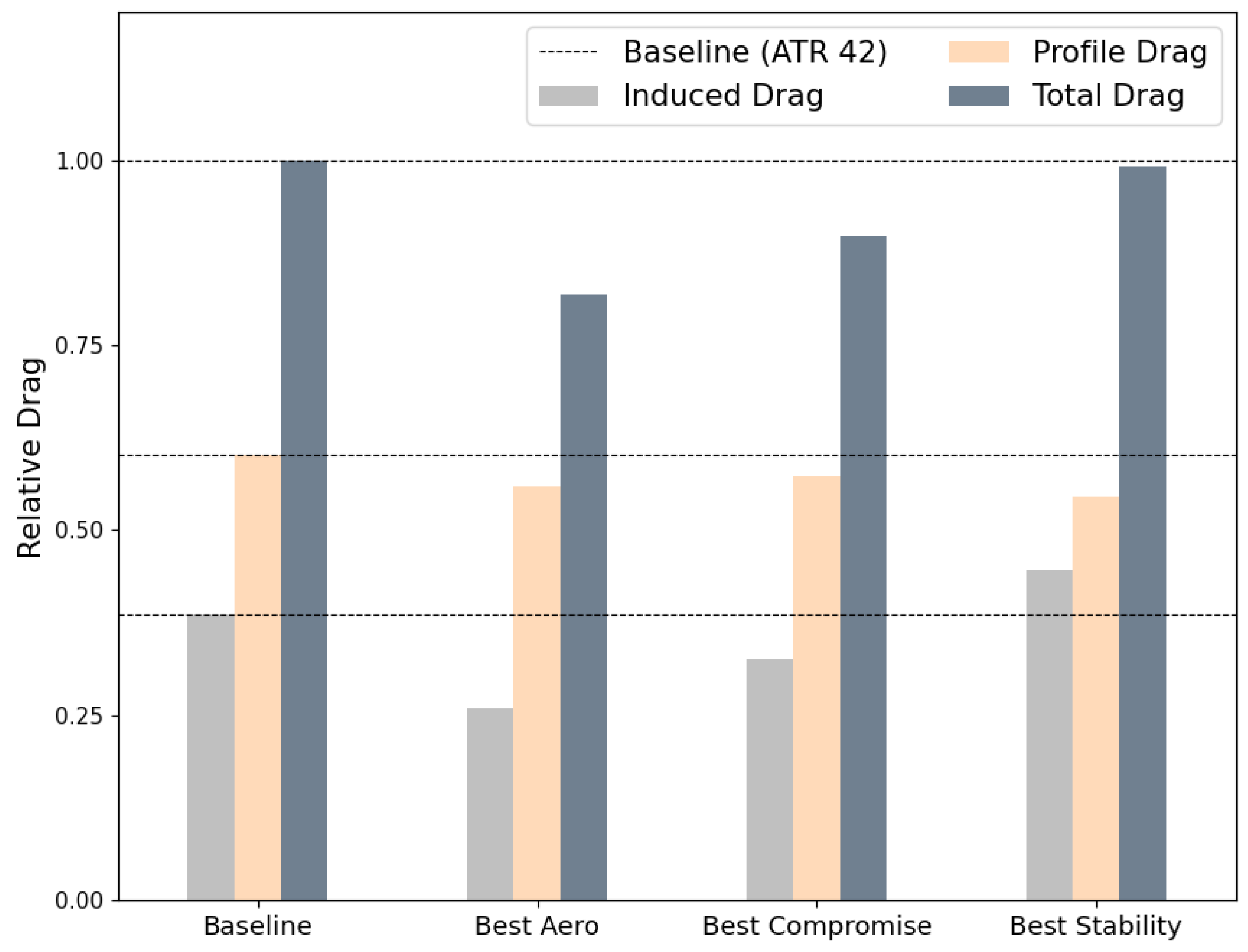
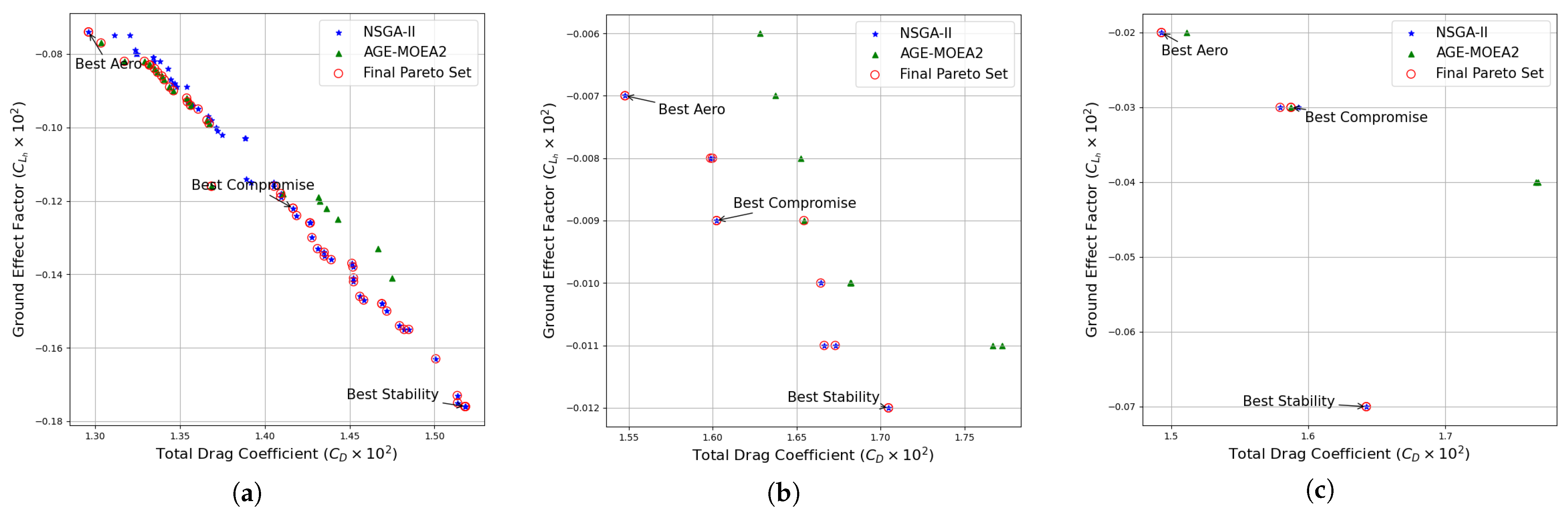
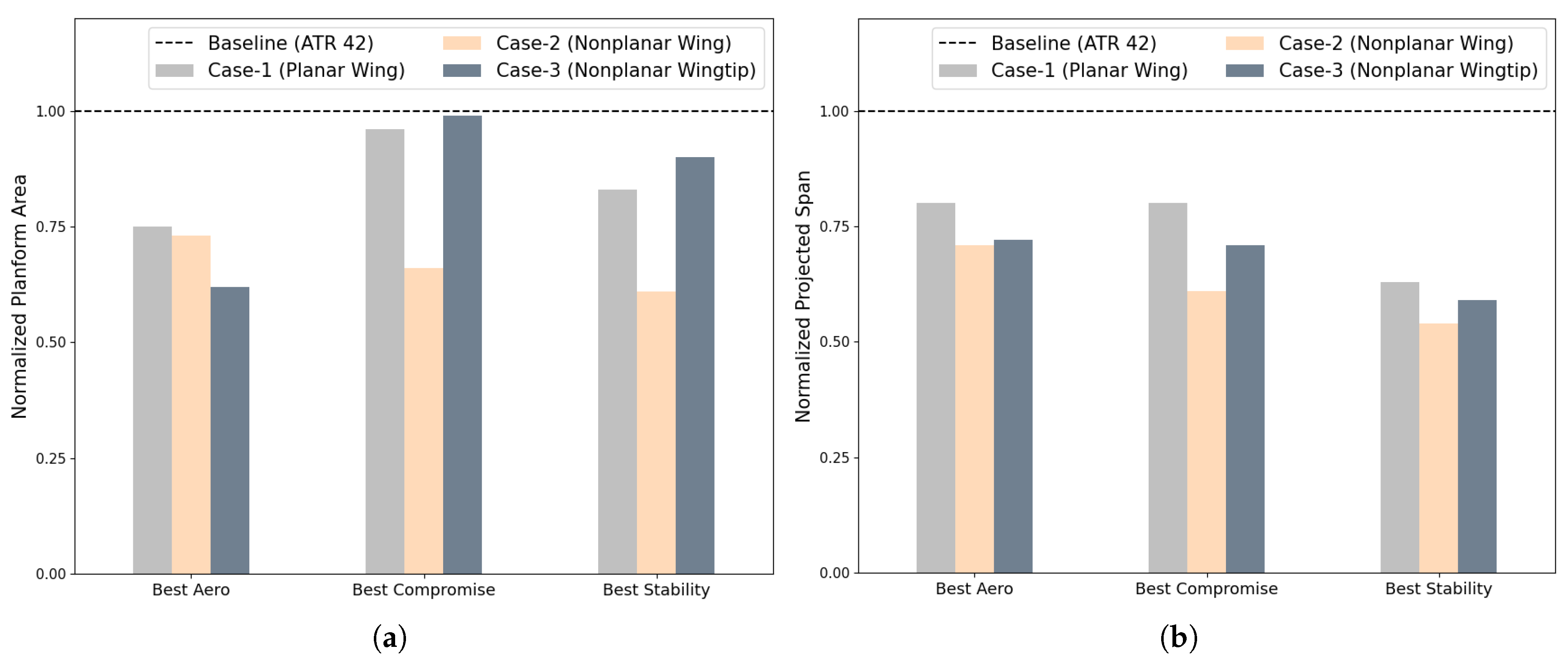
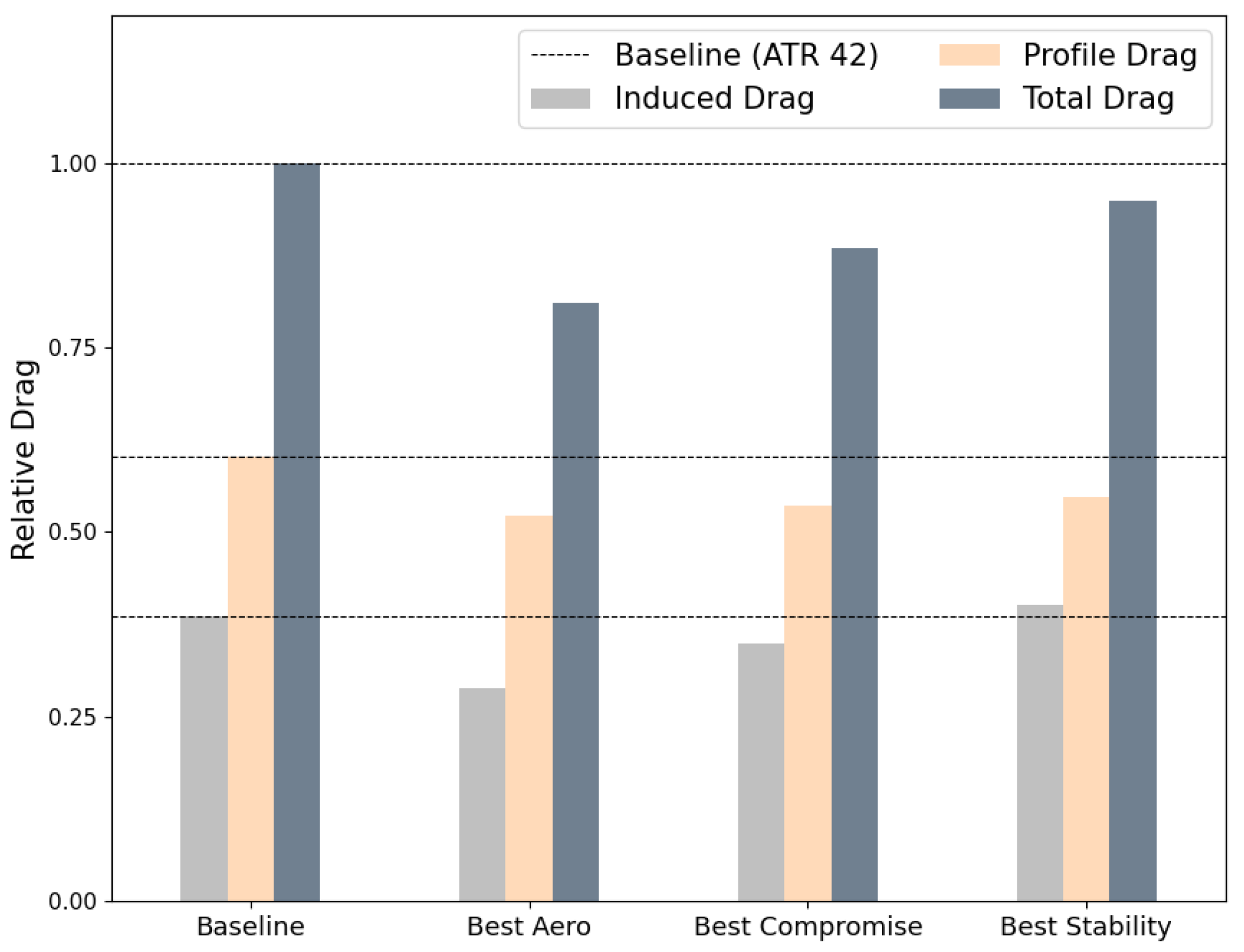
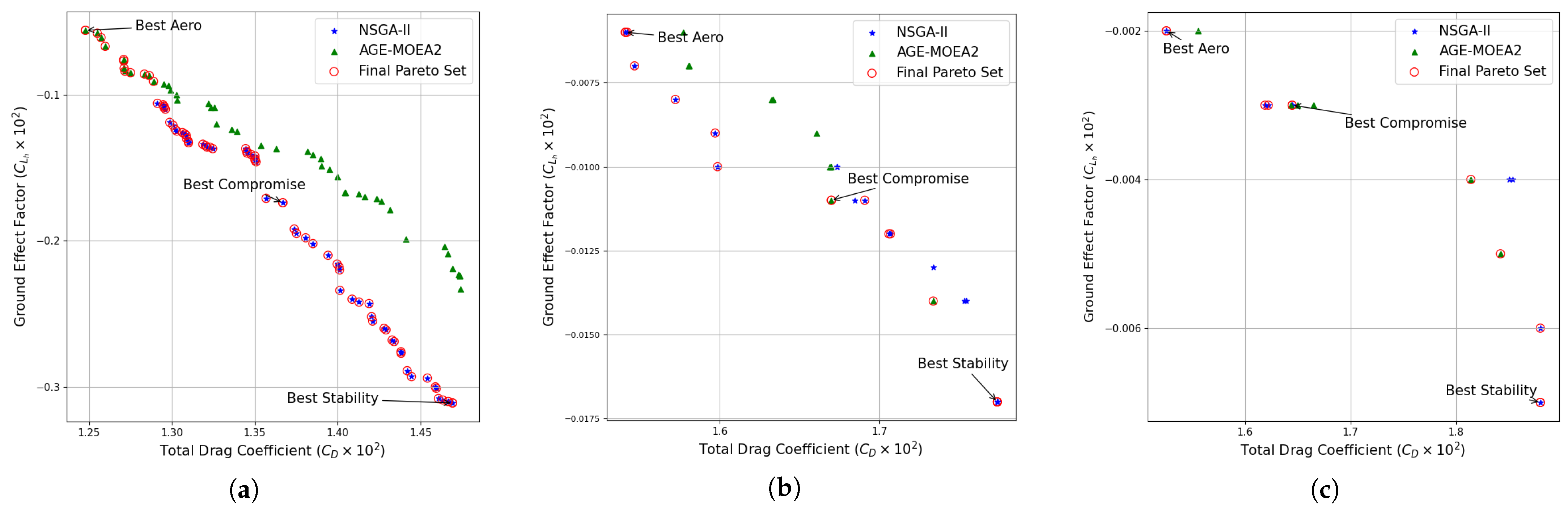
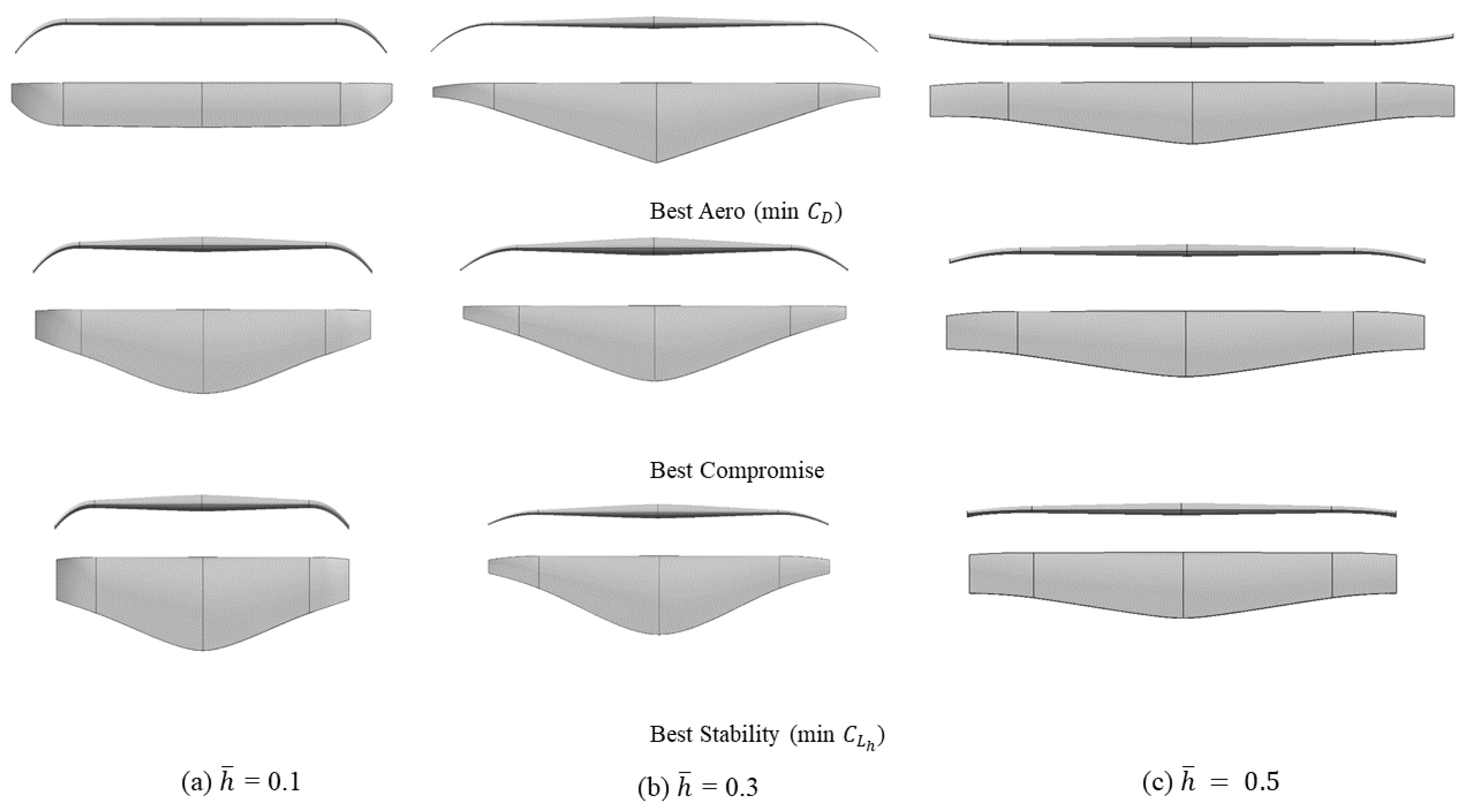
5.1. Case-1: Planar Wing Optimisation
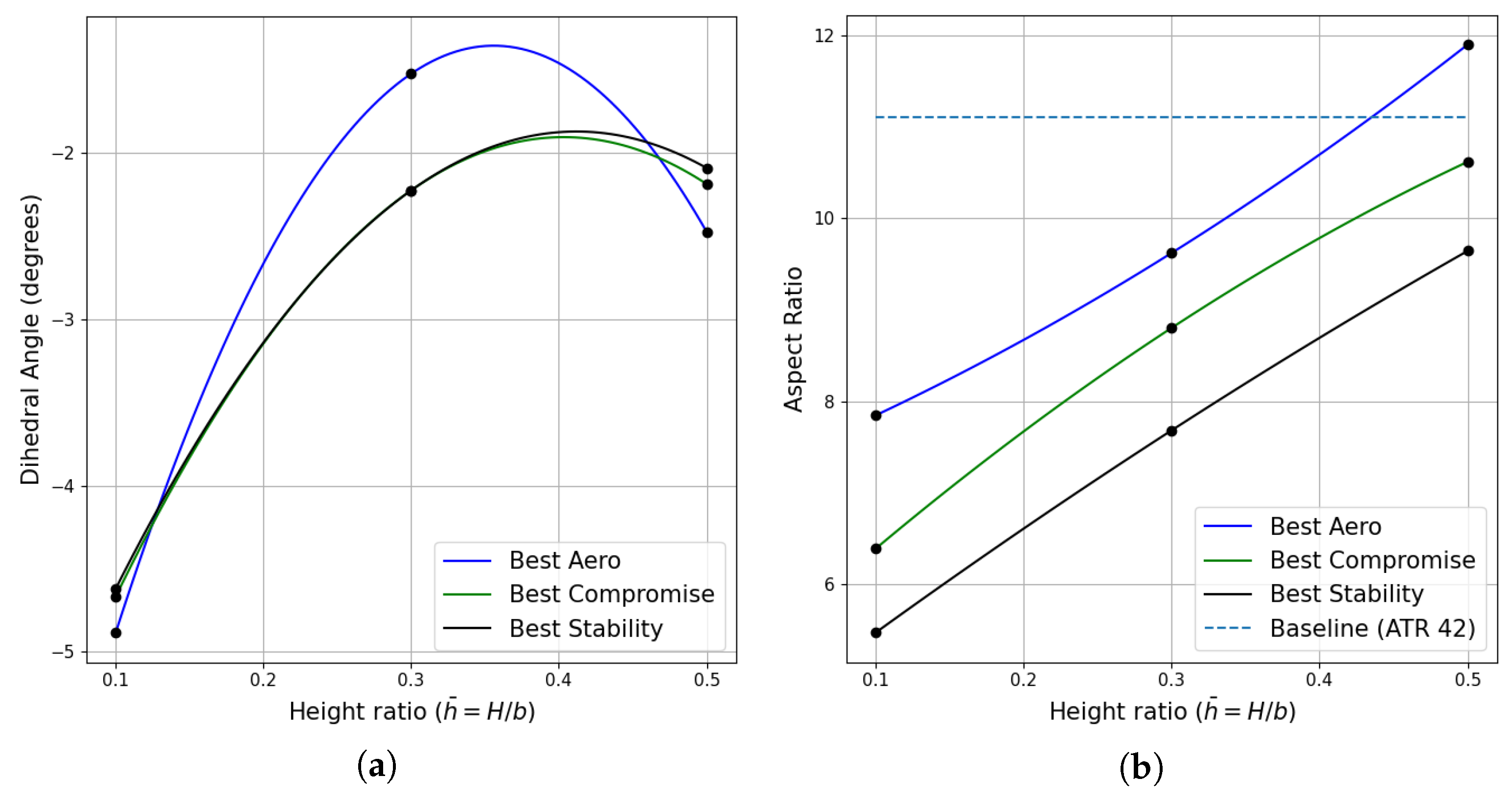
5.2. Case-2: Nonplanar Wing Optimisation
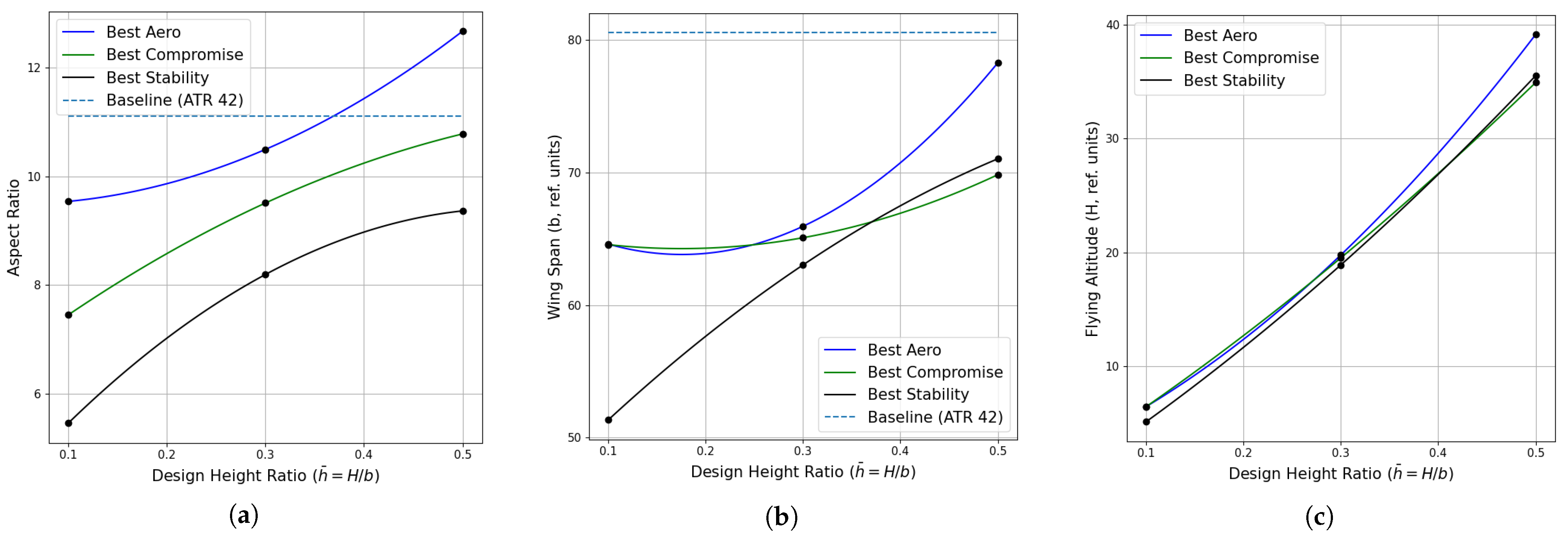
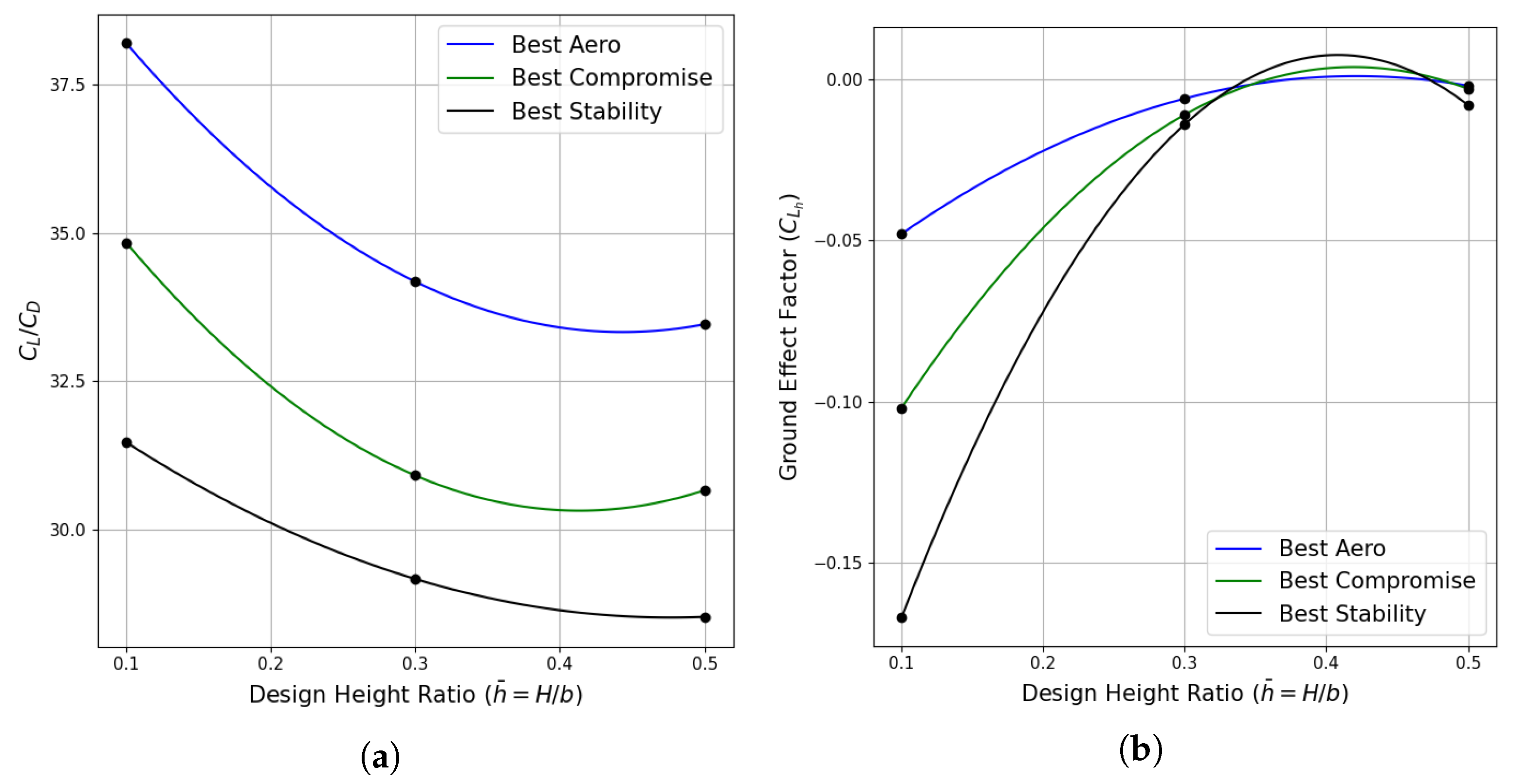
5.3. Case-3: Nonplanar Wingtip Optimisation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CO | Carbon dioxide |
| NO | Nitrogen Oxide |
| WIG | Wing-in-Ground effect |
| MTOW | Maximum Take-Off Weight |
| CAD | Computer Aided Design |
| RANS | Reynolds Averaged Navier Stokes Equations |
| NSGA-II | Non-Dominated Sorting Genetic Algorithm-II |
| AGE-MOEA2 | Adaptive Geometry Estimation based Multi-Objective Evolutionary Algorithm 2 |
| LE, TE | Leading and Trailing Edge |
| VLM | Vortex Lattice Method |
| IGD | Inverted Generational Distance |
| XDSM | eXtended Design Structure Matrix |
| A | Aerodynamic influence coefficient matrix |
| Vortex stength | |
| Vortex stength on the real and image panel | |
| b | Column vector in VLM method |
| w | Induced velocity |
| Normal vector at each panel | |
| Angle of attack | |
| L | Aerodynamic lift |
| H | Distance between center of gravity of the wing and ground |
| mean aerodynamic chord | |
| Non-dimensional height | |
| Freestrem density and velocity | |
| Number of wake panels | |
| Induced drag | |
| and | Orientation and length of the wake panel |
| Lift and total drag coefficients | |
| Design lift coefficient | |
| Total drag coefficient of the reference design | |
| Profile drag and induced drag coefficients | |
| Derivative of lift and moment coefficients with respect to and h | |
| Ground effect factor of the reference design | |
| Dynamic pressure and vehicle speed | |
| Location of neutral point and center of gravity | |
| Residual pitching moment | |
| Moment ratio | |
| Tail volume ratio and efficiency | |
| b | Total curve length along the spanwise direction |
| Root and tip chord of the inner and outer wing segment | |
| Twist of the inner and outer wing segment | |
| Dihedral angle of the outer wing segment | |
| Blending strength parameter of the inner wing segment | |
| Design variable vector for Case-1, Case-2, Case-3 | |
| Sweep angle of the outer wing segment | |
| Design height ratio | |
| Number of populations, design variables, and generations | |
| Pareto front obtained using NSGA-II and AGE-MOEA2 |
References
- Arnaldo Valdes, R.M.; Burmaoglu, S.; Tucci, V.; Braga da Costa Campos, L.M.; Mattera, L.; Gomez Comendador, V.F. Flight path 2050 and ACARE goals for maintaining and extending industrial leadership in aviation: A map of the aviation technology space. Sustainability 2019, 11, 2065. [Google Scholar] [CrossRef]
- Yun, L.; Bliault, A.; Doo, J. WIG craft and ekranoplan. In Ground Effect Craft Technology; Springer: New York, NY, USA, 2010; Volume 2. [Google Scholar]
- Ahmed, M.R.; Takasaki, T.; Kohama, Y. Aerodynamics of a NACA4412 airfoil in ground effect. AIAA J. 2007, 45, 37–47. [Google Scholar] [CrossRef]
- Amir, M.A.U.; Maimun, A.; Mat, S.; Saad, M.; Zarim, M. Wing in ground effect craft: A review of the state of current stability knowledge. In Proceedings of the International Conference on Ocean Mechanical and Aerospace for Scientists and Engineer, Terengganu, Malaysia, 7–8 November 2016. [Google Scholar]
- Rozhdestvensky, K.V. Wing-in-ground effect vehicles. Prog. Aerosp. Sci. 2006, 42, 211–283. [Google Scholar] [CrossRef]
- Staufenbiel, R.; Schlichting, U.J. Stability of airplanes in ground effect. J. Aircr. 1988, 25, 289–294. [Google Scholar] [CrossRef]
- Fevralskikh, A. A development of longitudinal static stability analysis method of a Wing-in-Ground effect vehicle in cruise during the design process. Ocean Eng. 2022, 243, 110187. [Google Scholar] [CrossRef]
- Chun, H.; Chang, C. Longitudinal stability and dynamic motions of a small passenger WIG craft. Ocean Eng. 2002, 29, 1145–1162. [Google Scholar] [CrossRef]
- Kornev, N.; Matveev, K. Complex numerical modeling of dynamics and crashes of wing-in-ground vehicles. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003; p. 600. [Google Scholar]
- Park, K.; Lee, J. Optimal design of two-dimensional wings in ground effect using multi-objective genetic algorithm. Ocean Eng. 2010, 37, 902–912. [Google Scholar] [CrossRef]
- Lee, S.H.; Lee, J. Aerodynamic analysis and multi-objective optimization of wings in ground effect. Ocean Eng. 2013, 68, 1–13. [Google Scholar] [CrossRef]
- Hu, H.; Zhang, G.; Li, D.; Zhang, Z.; Sun, T.; Zong, Z. Shape optimization of airfoil in ground effect based on free-form deformation utilizing sensitivity analysis and surrogate model of artificial neural network. Ocean Eng. 2022, 257, 111514. [Google Scholar] [CrossRef]
- Koo, D.; Zingg, D.W. Investigation into aerodynamic shape optimization of planar and nonplanar wings. AIAA J. 2018, 56, 250–263. [Google Scholar] [CrossRef]
- Conlan-Smith, C.; Ramos-García, N.; Schousboe Andreasen, C. Aerodynamic Shape Optimization of Highly Nonplanar Raised and Drooped Wings. J. Aircr. 2021, 59, 206–218. [Google Scholar] [CrossRef]
- Kim, H.J.; Chun, H.H.; Jung, K.H. Aeronumeric optimal design of a wing-in-ground-effect craft. J. Mar. Sci. Technol. 2009, 14, 39–50. [Google Scholar] [CrossRef]
- Lee, J.; Han, C.S.; Bae, C.H. Influence of wing configurations on aerodynamic characteristics of wings in ground effect. J. Aircr. 2010, 47, 1030–1040. [Google Scholar] [CrossRef]
- Lee, T.; Tremblay-Dionne, V.; Ko, L. Ground effect on a slender reverse delta wing with anhedral. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 1516–1525. [Google Scholar] [CrossRef]
- Lee, S.H.; Lee, J. Optimization of three-dimensional wings in ground effect using multiobjective genetic algorithm. J. Aircr. 2011, 48, 1633–1645. [Google Scholar] [CrossRef]
- Morris, A.; Allen, C.; Rendall, T. Aerodynamic shape optimization of a modern transport wing using only planform variations. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2009, 223, 843–851. [Google Scholar] [CrossRef]
- Lyu, Z.; Martins, J.R. Aerodynamic design optimization studies of a blended-wing-body aircraft. J. Aircr. 2014, 51, 1604–1617. [Google Scholar] [CrossRef]
- Jansen, P.W.; Perez, R.E.; Martins, J.R. Aerostructural optimization of nonplanar lifting surfaces. J. Aircr. 2010, 47, 1490–1503. [Google Scholar] [CrossRef]
- Ning, S.A.; Kroo, I. Multidisciplinary considerations in the design of wings and wing tip devices. J. Aircr. 2010, 47, 534–543. [Google Scholar] [CrossRef]
- Conlan-Smith, C.; Ramos-García, N.; Sigmund, O.; Andreasen, C.S. Aerodynamic shape optimization of aircraft wings using panel methods. AIAA J. 2020, 58, 3765–3776. [Google Scholar] [CrossRef]
- Abu Salem, K.; Palaia, G.; Chiarelli, M.R.; Bianchi, M. A Simulation Framework for Aircraft Take-Off Considering Ground Effect Aerodynamics in Conceptual Design. Aerospace 2023, 10, 459. [Google Scholar] [CrossRef]
- Jesudasan, R.; Mariani, R.; Hanifi, A. Preliminary Aerodynamic Wing Design Optimisation For Wing-in-Ground Effect Aircraft. In Proceedings of the 33rd Congress of the International Council of the Aeronautical Sciences, ICAS 2022, Stockholm, Sweden, 4–9 September 2022; International Council of the Aeronautical Sciences: Bonn, Germany, 2022; pp. 3106–3118. [Google Scholar]
- McDonald, R.A.; Gloudemans, J.R. Open Vehicle Sketch Pad: An Open Source Parametric Geometry and Analysis Tool for Conceptual Aircraft Design. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 4. [Google Scholar]
- Katz, J.; Plotkin, A. Low-Speed Aerodynamics; Cambridge University Press: Cambridge, UK, 2001; Volume 13. [Google Scholar]
- Smith, S.C. A Computational and Experimental Study of Nonlinear Aspects of Induced Drag; Stanford University: Stanford, CA, USA, 1995. [Google Scholar]
- Drela, M. Flight Vehicle Aerodynamics; MIT Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Budziak, K. Aerodynamic Analysis with Athena Vortex Lattice (AVL); Aircraft Design and Systems Group (AERO): Hamburg, Germany, 2015. [Google Scholar]
- Jasa, J.P.; Hwang, J.T.; Martins, J.R. Open-source coupled aerostructural optimization using Python. Struct. Multidiscip. Optim. 2018, 57, 1815–1827. [Google Scholar] [CrossRef]
- Drela, M. XFOIL: An analysis and design system for low Reynolds number airfoils. In Low Reynolds Number Aerodynamics, Proceedings of the Conference, Notre Dame, IN, USA, 5–7 June 1989; Springer: Berlin/Heidelberg, Germany, 1989; pp. 1–12. [Google Scholar]
- Zhao, W.; Kapania, R.K. Static Aeroelastic Optimization of Aircraft Wing with Multiple Surfaces. In Proceedings of the 18th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Denver, CO, USA, 5–9 June 2017; p. 4320. [Google Scholar]
- Gudmundsson, S. General Aviation Aircraft Design: Applied Methods and Procedures; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Nirooei, M. Aerodynamic and static stability characteristics of airfoils in extreme ground effect. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 232, 1134–1148. [Google Scholar] [CrossRef]
- Jackson, P.; Peacock, L. Jane’s All the World’s Aircraft; Janes Information Group: Croydon, UK, 2010. [Google Scholar]
- Sforza, P.M. Commercial Airplane Design Principles; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Kulfan, B.M. Universal parametric geometry representation method. J. Aircr. 2008, 45, 142–158. [Google Scholar] [CrossRef]
- Barrett, R. Statistical Time and Market Predictive Engineering Design (STAMPED) Techniques for Aerospace Preliminary Design: Regional Turboprop Application. J. Aeronaut. Aerosp. Eng. 2014, 3, 135. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Panichella, A. An adaptive evolutionary algorithm based on non-euclidean geometry for many-objective optimization. In Proceedings of the Genetic and Evolutionary Computation Conference, Prague, Czech Republic, 13–17 July 2019; pp. 595–603. [Google Scholar]
- Deb, K. Multi-objective optimisation using evolutionary algorithms: An introduction. In Multi-Objective Evolutionary Optimisation for Product Design and Manufacturing; Springer: Berlin/Heidelberg, Germany, 2011; pp. 3–34. [Google Scholar]
- Blank, J.; Deb, K. Pymoo: Multi-objective optimization in python. IEEE Access 2020, 8, 89497–89509. [Google Scholar] [CrossRef]
- Wierzbicki, A.P. The use of reference objectives in multiobjective optimization. In Multiple Criteria Decision Making Theory and Application, Proceedings of the Third Conference, Hagen/Königswinter, Germany, 20–24 August 1979; Springer: Berlin/Heidelberg, Germany, 1980; pp. 468–486. [Google Scholar]
- Phillips, W.F.; Hunsaker, D.F. Lifting-line predictions for induced drag and lift in ground effect. J. Aircr. 2013, 50, 1226–1233. [Google Scholar] [CrossRef]
- Bons, N.P.; He, X.; Mader, C.A.; Martins, J.R. Multimodality in aerodynamic wing design optimization. AIAA J. 2019, 57, 1004–1018. [Google Scholar] [CrossRef]
- Kocivar, B. Ram-wing X-114: Floats, skims, and flies. Pop. Sci. 1977, 211, 70–73. [Google Scholar]
- Lazos, B.; Visser, K. Aerodynamic comparison of Hyper-Elliptic cambered span (HECS) Wings with conventional configurations. In Proceedings of the 24th AIAA Applied Aerodynamics Conference, San Francisco, CA, USA, 5–8 June 2006; p. 3469. [Google Scholar]
- Park, K.; Lee, J. Influence of endplate on aerodynamic characteristics of low-aspect-ratio wing in ground effect. J. Mech. Sci. Technol. 2008, 22, 2578–2589. [Google Scholar] [CrossRef]







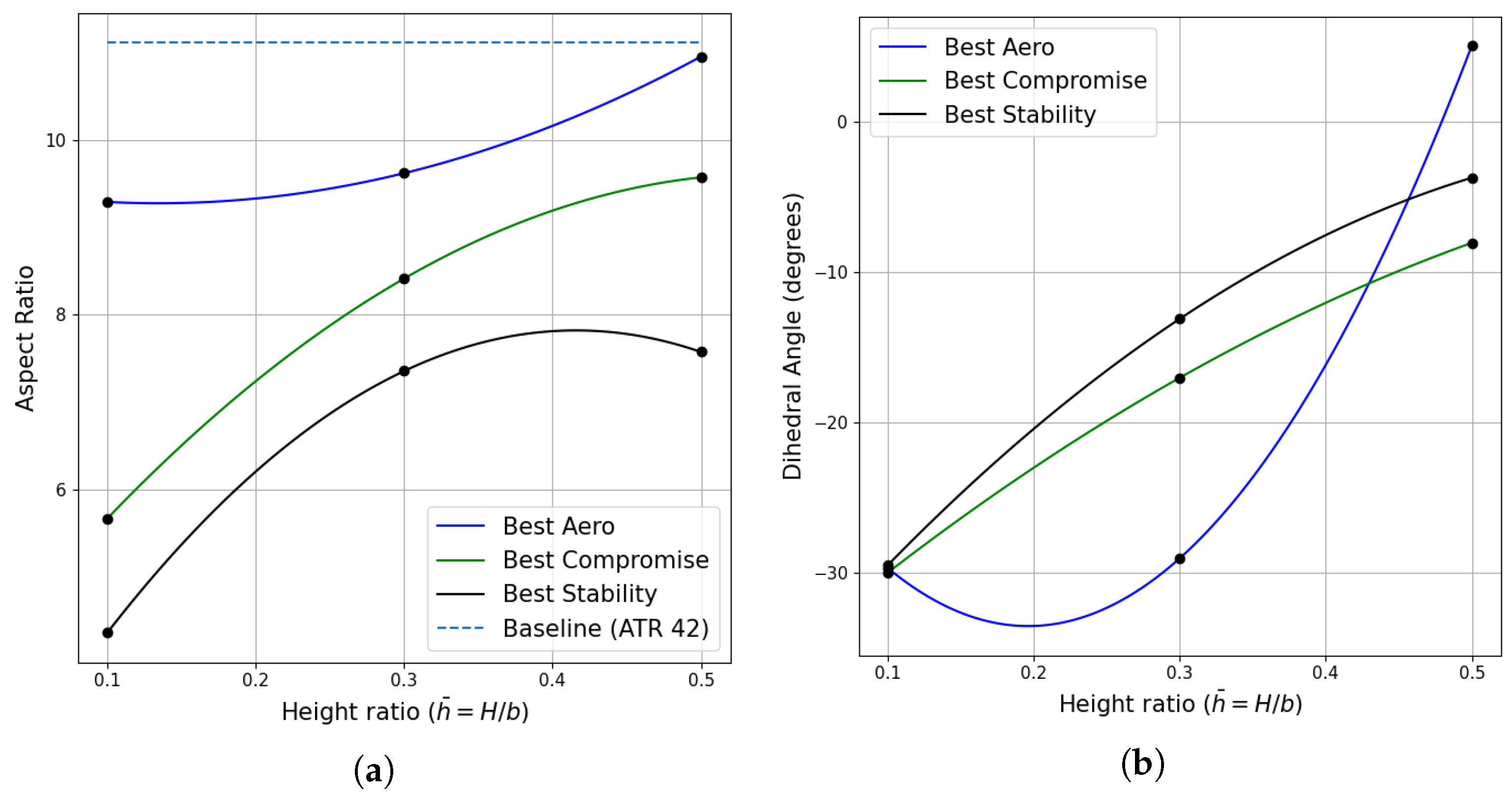
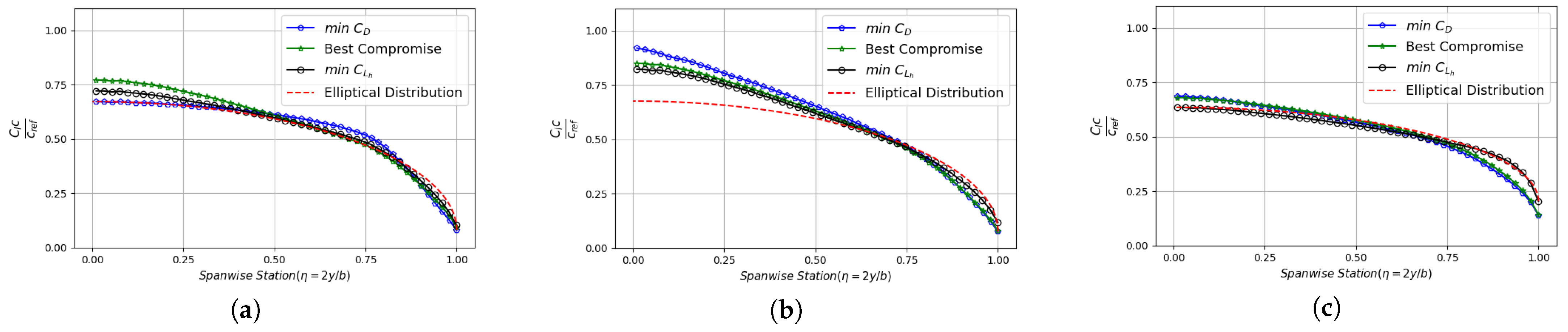
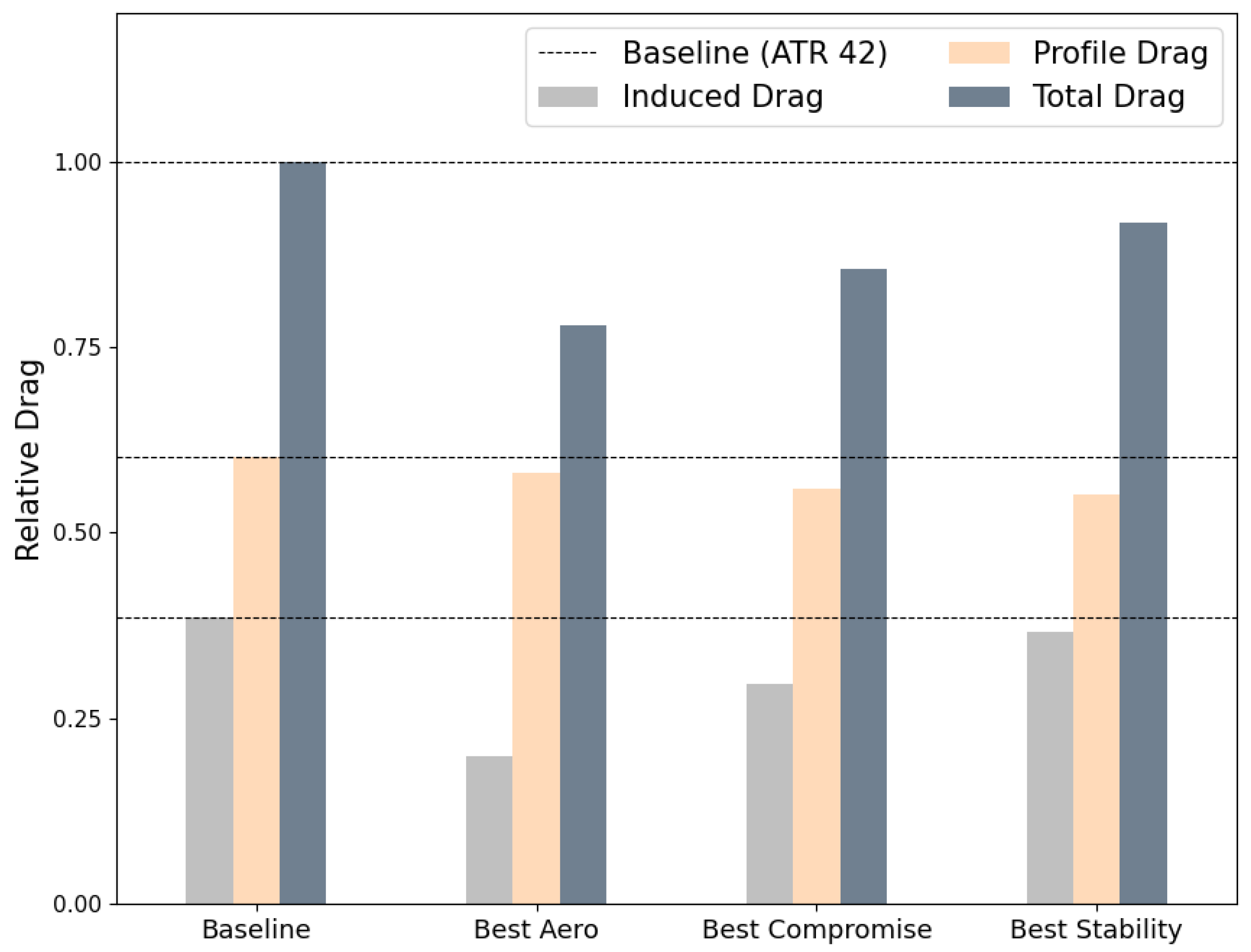
| Design Specifications | Value |
|---|---|
| Wing Reference Area | 587 ft |
| Wing Span | 81 ft |
| Aspect Ratio | |
| Taper Ratio | |
| Root | |
| Tip | |
| Sweep | |
| Dihedral |
| Category | Name | Lower Limit | Upper Limit | Units |
|---|---|---|---|---|
| Objective Function | min | - | ||
| min | - | |||
| Case-1: Design Variables | AOA | 5 | Degrees | |
| Twist | 5 | Degrees | ||
| Root chord | Ref. units | |||
| Tip chord | Ref. units | |||
| Blend Strength | 0 | 1 | Ref. units | |
| Span | Ref. units | |||
| Case 2: Design Variables | 5 | Degrees | ||
| 5 | Degrees | |||
| 0 | 1 | Ref. units | ||
| Ref. units | ||||
| Ref. units | ||||
| 5 | Degrees | |||
| Ref. units | ||||
| 5 | Degrees | |||
| b | Ref. units | |||
| Case 3: Other design variables same as Case 2 | −30 | 30 | Degrees | |
| 0 | 5 | Degrees |
| Parameters | Case | Value |
|---|---|---|
| No. of Populations | Case-1 | 60 |
| Case-2 | 90 | |
| Case-3 | 100 | |
| No. of Generations | Case-1 | 72 |
| Case-2 | 108 | |
| Case-3 | 120 | |
| Crossover Probability | 0.9 | |
| Mutattion Probability | ||
| Solution | Design Height Ratio | Design Height Ratio | Design Height Ratio | ||||||
|---|---|---|---|---|---|---|---|---|---|
| min | 0.1 | −18.17 | 1.2 | 0.3 | −18.72 | 1.0 | 0.5 | −21.35 | 1.0 |
| Best Compromise | −10.28 | 2.5 | −10.14 | 1.8 | −14.19 | 1.5 | |||
| min | −0.71 | 4.1 | −4.78 | 2.3 | −7.78 | 4.0 |
| Solution | Design Height Ratio | Design Height Ratio | Design Height Ratio | ||||||
|---|---|---|---|---|---|---|---|---|---|
| min | 0.1 | −19.0 | 1.9 | 0.3 | −11.0 | 1.2 | 0.5 | −21.42 | 1.0 |
| Best Compromise | −11.45 | 3.1 | −10.24 | 1.5 | −20.46 | 1.5 | |||
| min | −5.1 | 4.4 | −7.53 | 2.0 | −13.55 | 3.5 |
| Solution | Design Height Ratio | Design Height Ratio | Design Height Ratio | ||||||
|---|---|---|---|---|---|---|---|---|---|
| min | 0.1 | −22.0 | 1.4 | 0.3 | −14.39 | 1.0 | 0.5 | −19.71 | 1.0 |
| Best Compromise | −14.56 | 4.34 | −7.22 | 1.8 | −13.43 | 1.5 | |||
| min | −8.16 | 7.7 | −1.46 | 2.8 | −1.05 | 3.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jesudasan, R.; Hanifi, A.; Mariani, R. Investigating Planar and Nonplanar Wing Planform Optimisation for Ground Effect Aircraft. Aerospace 2023, 10, 969. https://doi.org/10.3390/aerospace10110969
Jesudasan R, Hanifi A, Mariani R. Investigating Planar and Nonplanar Wing Planform Optimisation for Ground Effect Aircraft. Aerospace. 2023; 10(11):969. https://doi.org/10.3390/aerospace10110969
Chicago/Turabian StyleJesudasan, Rejish, Ardeshir Hanifi, and Raffaello Mariani. 2023. "Investigating Planar and Nonplanar Wing Planform Optimisation for Ground Effect Aircraft" Aerospace 10, no. 11: 969. https://doi.org/10.3390/aerospace10110969
APA StyleJesudasan, R., Hanifi, A., & Mariani, R. (2023). Investigating Planar and Nonplanar Wing Planform Optimisation for Ground Effect Aircraft. Aerospace, 10(11), 969. https://doi.org/10.3390/aerospace10110969







