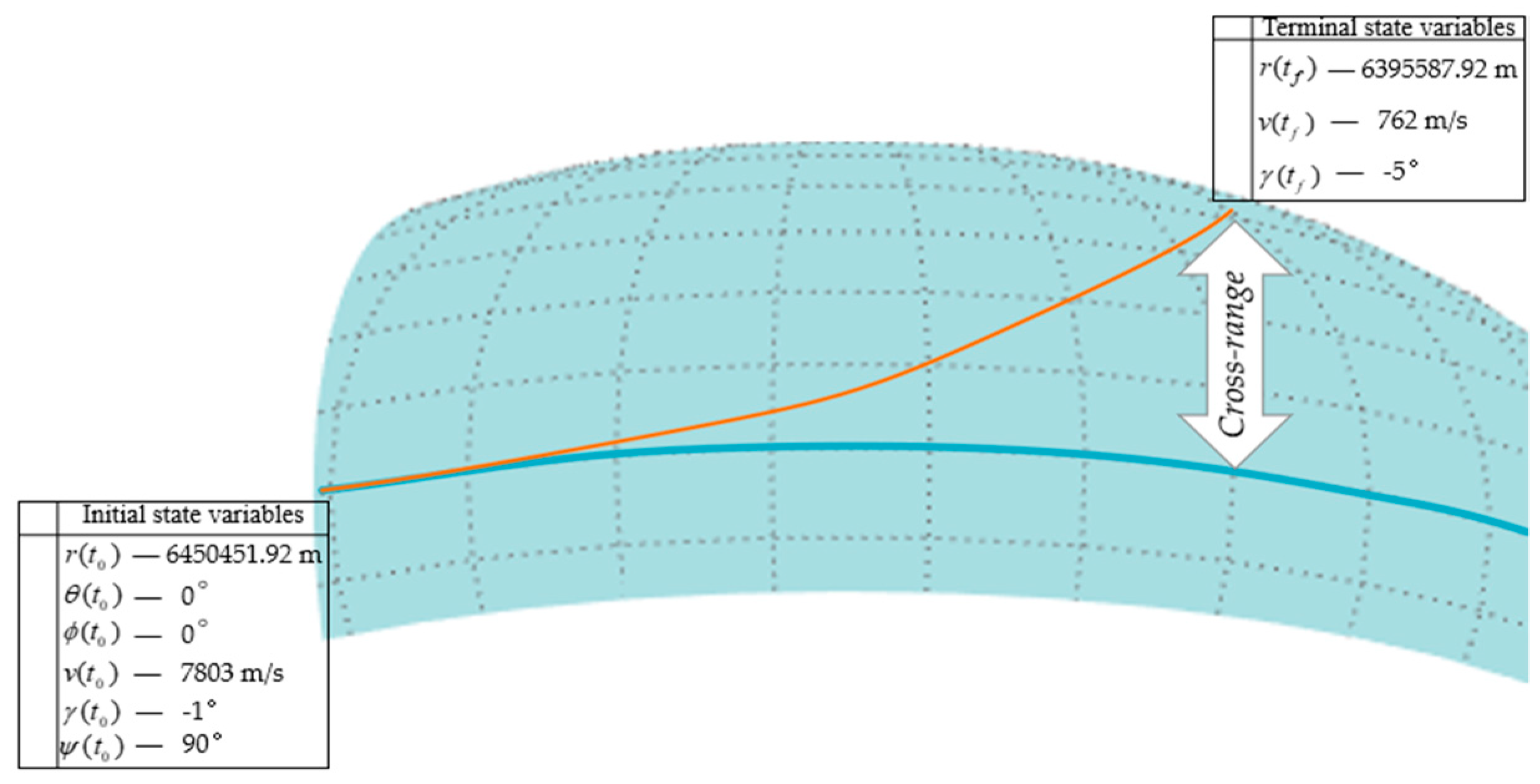
1. Introduction
In recent years, the application of the new generation of artificial intelligence technologies, represented by Deep Neural Networks (DNNs), has made significant progress across various domains. In 2006, Geoffrey Hinton proposed the concept of deep learning, which introduced a model known as a Deep Belief Network (DBN) [
1]. This network consists of multiple stacked Restricted Boltzmann Machines (RBMs) [
2]. He developed a pretraining algorithm for rapid training of DBNs, which was the beginning of the third resurgence of artificial intelligence. In 2012, the AlexNet model proposed by Alex and Geoffrey achieved groundbreaking results in image classification [
3]. They abandoned the layer-wise greedy training algorithm, opting to directly utilize Graphics Processing Units (GPUs) for training. Since the introduction of the AlexNet model, attention has been drawn to the enormous potential of DNNs in computer vision and language processing.
Meanwhile, researchers have begun to explore the potential applications of deep learning in other fields. The application of deep learning in aerospace guidance, control, and dynamics has yielded some research outcomes [
4]. Sánchez, Dario, and others [
5,
6] have systematically studied DNNs in the context of optimal state feedback control for deterministic, continuous-time, and nonlinear systems, including stability analysis of inverted pendulums, precise landing control for quadcopter aircraft and spacecraft, etc. These systems involve cost functions for smooth continuous or discrete optimal control. The research indicates that DNNs can proficiently accomplish tasks, and even when selecting trajectories beyond the training range, the network’s predictions still meet the requirements effectively. This shows the networks’ inherent robustness. In these studies, the authors pointed out that DNNs were not merely interpolating the control data but might have learned the underlying dynamical relationships within the state and control space of nonlinear systems. Dario and his colleagues [
7] extended this research to interplanetary trajectories and investigated how to train DNNs to guide a spacecraft along optimal paths from Earth to Mars. They coined this approach “Guidance and Control Networks” (G&CNETs) [
8], which employed DNNs trained through imitation or supervised learning to achieve optimal trajectory prediction. The authors also provided a differential algebra-based method to elucidate its stability margin and control precision. G&CNETs are simple fully connected feedforward neural networks and they illustrated the potential of using relatively straightforward neural networks to replace current onboard navigation and control algorithms. Based on these studies, Furfaro et al. [
9] devised a Long Short-Term Memory (LSTM) recurrent neural network to predict the fuel-optimal thrust from a sequence of states during powered planetary descent. They validated the algorithm through Monte Carlo simulation experiments in a lunar landing scenario. Another study by Furfaro et al. [
10] utilized Convolutional Neural Networks (CNNs) for excellent image classification performance and applied them to lunar surface image processing. The data from these processes were then fed into LSTMs for spacecraft control during landing, showcasing a comprehensive application of different types of DNNs. While there have been some achievements in employing deep learning for real-time control of spacecraft trajectory landing and orbit transfer [
11,
12,
13,
14,
15], the research on applying deep learning to real-time optimal trajectory generation for hypersonic vehicles remains relatively scarce.
The real-time onboard generation of optimal trajectories for hypersonic vehicles poses an exceptionally intricate challenge due to the intricate nonlinear flight dynamics constraints of hypersonic flight and the uncertainty stemming from initial flight conditions. In practical scenarios, hypersonic aircraft trajectories require rapid responsiveness and adjustments, which imposes stringent demands on the real-time capability of trajectory control systems. Amidst the amalgamation of these factors, it is essential to ensure robustness, rapidity, and guidance accuracy in the application of onboard systems. Thus, the development of efficient online trajectory optimization algorithms capable of fulfilling the demands of complex hypersonic flight missions is an urgent imperative.
One main approach to enhance the performance of online trajectory generation for hypersonic entry flight is the convex optimization technique. Wang et al. [
16] formulated the highly nonlinear problem of planetary-entry optimal control as a series of convex problems and employed an interior-point method to solve these convex optimization problems. The results demonstrated that this solving method converges to the exact solution faster than general-purpose solvers. Wang [
17] further improved the algorithm by introducing line-search and trust-region techniques, fundamentally enhancing the performance of sequential convex programming methods in ballistic trajectory optimization. However, the high computational cost and convergence issues to some extent hinder its onboard application in hypersonic trajectory optimization [
18,
19].
To explore more effective solving methods, researchers have started to experiment with emerging technologies such as artificial intelligence and machine learning. In the field of deep reinforcement learning, Gao et al. [
20] optimized the reentry phase of a Reusable Launch Vehicle (RLV) using a deep reinforcement learning method and validated the feasibility of the Deep Deterministic Policy Gradient (DDPG) algorithm for continuous nonlinear optimization problems through comparisons with the Particle Swarm Optimization (PSO) algorithm. Wu [
21] employed a deep reinforcement learning approach to address the design problem of feedback gains in the entry guidance of hypersonic vehicles. By comparing the results of Monte Carlo simulation, the algorithm achieved real-time adjustment of feedback gains within a certain error range. Solari [
22] investigates the Powered Descent (PD) phase of Mars landings using a reinforcement learning approach with a policy model based on Neural Networks (NNs) with only one hidden layer. The results demonstrate that this algorithm architecture exhibits robustness against disturbances and generalizes effectively to regions of the state space beyond the training domain.
In the deep learning domain, which is the focus of this paper, Yang et al. [
18] following the research methodology of G&CNETs, extending this approach to generating optimal trajectories for a hypersonic vehicle. Simulation results demonstrated that their designed network exhibited favorable control accuracy and robustness. However, their consideration was limited to the two-dimensional longitudinal plane motion trajectory of the hypersonic entry, involving relatively fewer flight states and control variables. Wang et al. [
19] extended Yang’s work to address three-dimensional optimal trajectory planning for hypersonic entry vehicles. They also incorporated terminal states into their training dataset to ensure the generation of trajectories under varying terminal conditions. However, their simulation results indicated that the accuracy in the predicted trajectories of the network model needs to be improved. Due to the absence of the initial flight state range and visually intuitive trajectory fitting curves in simulations, it is hard to validate the robustness of the trajectory generated by the network. Wang et al. [
23], capitalizing on the advantages of deep learning in neural network mapping and real-time performance, utilized the real-time state information of entry vehicles. They employed LSTM models to generate real-time bank angle commands, enhancing computational efficiency while ensuring guidance precision. Cheng et al. [
24] combined DNNs with constraint management techniques, proposing an intelligent multi-constraint prediction–correction guidance algorithm. Simulation results demonstrated the algorithm’s ability to achieve trajectory corrections at a 20 Hz update rate, offering accurate entry guidance for hypersonic flight.
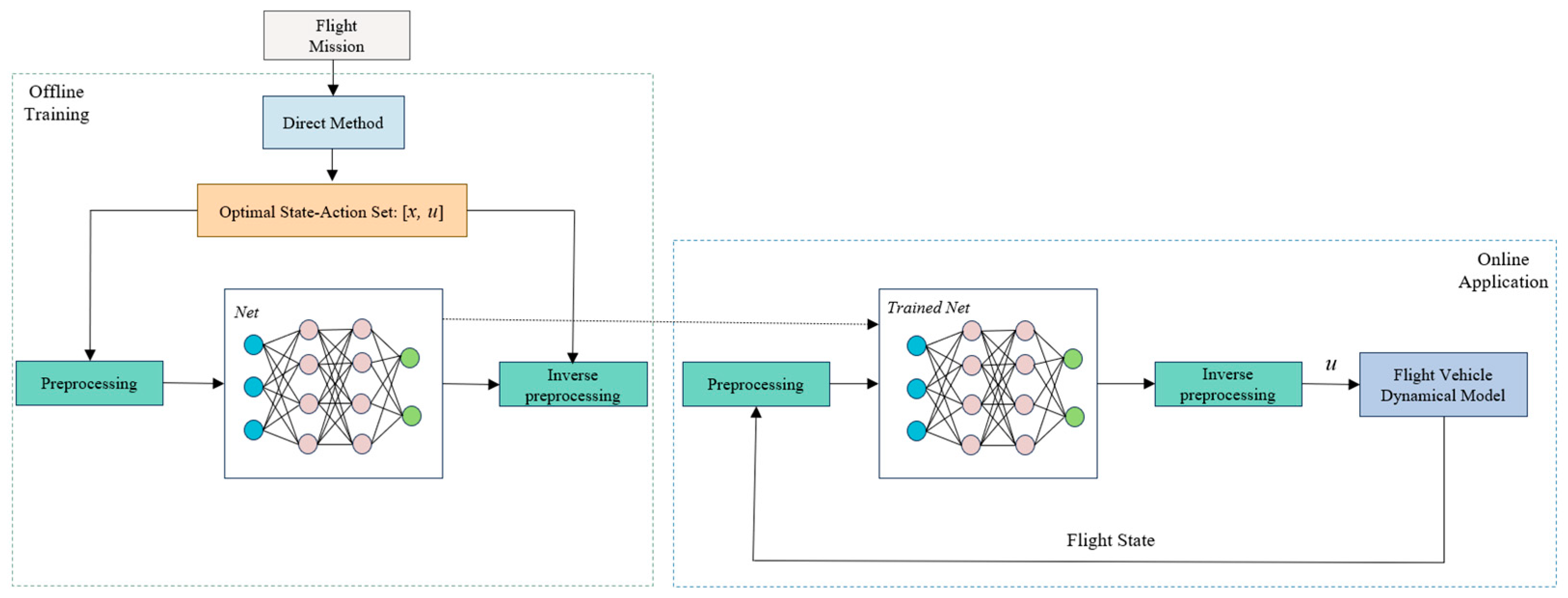
The primary approach in the aforementioned studies is to generate multiple high-precision optimal trajectories using either a direct or indirect method. The optimal state–action sets from these trajectories are then employed as training inputs for the network, with the network outputting optimal control commands for the flight. The network is subjected to offline training. Subsequently, the trained network is integrated into the guidance system to serve as a controller, enabling real-time generation of optimal guidance control commands. In summary, while these studies have yielded promising results for specific problems, they lack comprehensive analyses of sample data reliability, network architecture, and parameter design. In this paper, a simulation verification of the trajectories in the sample database obtained via GPOPS is described based on a 3 Degrees of Freedom (3Dof) flight dynamics model of a hypersonic vehicle. This ensured the reliability of the trajectory data used for network training and testing. Furthermore, the network’s architecture and parameters were determined through cross-validation, and callback functions were introduced to optimize the network, ensuring its excellence in the study case. These efforts effectively enhanced the accuracy and generalization capability of network predictions.
This paper provides an in-depth, comprehensive examination and assessment of the DNN-based generation method for three-dimensional optimal trajectories of hypersonic vehicle entry. Firstly, using the pseudo-spectral method and algorithm package GPOPS II [
25], the optimal flight trajectories of the hypersonic vehicle entry flight are generated. The state–action sets are then extracted from these trajectories and used as training samples for the network model after simulation checking. Verification experiments are designed to ensure the authenticity of the data sample library. Subsequently, the network architecture and hyperparameters are designed and analyzed. The network model is trained offline to effectively learn the underlying mathematical relationships within the hypersonic vehicle’s optimal flight state–action set. This allows the network model to predict optimal control and trajectories. Finally, nonlinear simulations based on the 3Dof flight dynamics model are conducted. Numerical analysis of prediction errors is performed to validate the feasibility of the algorithm and assess its robustness under some uncertain conditions. In this study, the most time-consuming and computationally intensive training process is conducted offline. The trained network solely requires straightforward matrix addition and multiplication operations within its hidden nodes based on the input state set to generate the requisite optimal control commands. Consequently, this algorithm can achieve the generation of the optimal trajectory of the hypersonic vehicle while ensuring expedited execution. The contributions of this paper are mainly in two aspects. Firstly, a detailed analysis of the impact of network structure and parameters on prediction results is conducted. The network model is designed using cross-validation to ensure its quality, effectively enhancing the guidance accuracy of the network. Secondly, the performance of the network and its adaptability to varying initial flight states is evaluated through multiple sets of 3Dof nonlinear simulation experiments. By comparing with numerical optimization methods, the paper demonstrates that the network exhibits significant accuracy and robustness.
The structure of this paper is as follows. In
Section 2, the continuous-time optimal control problem of three-dimensional hypersonic entry flight is presented. Using the GPOPS II package, a large amount of flight trajectories are generated, which serve as training and test samples for the network. In
Section 3, the detailed network design process is given, and the predictive results of the model are analyzed.
Section 4 conducts simulation experiments on the trained network model, followed by a numerical analysis of errors. This section evaluates the performance of the trajectory generation method based on the network model.
4. Simulations and Result Analysis
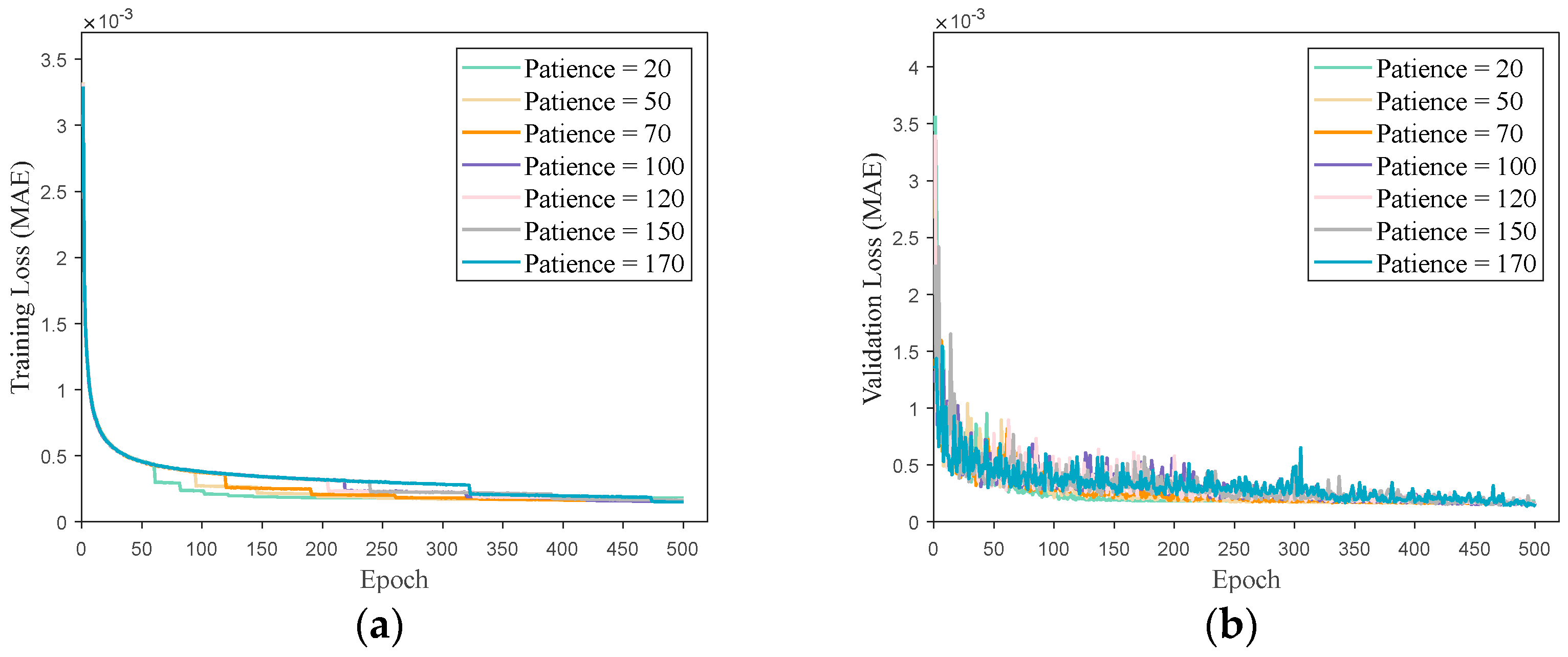
In this section, the effectiveness of the DNN-based optimal trajectory generation algorithm is evaluated through simulation based on the 3Dof flight dynamics. In the preceding section of network design, the MAE was used to assess the gap between the network’s predicted values and the optimized values. However, considering the complexity of actual flight scenarios, a more comprehensive simulation is required to verify the network’s performance. Initially, an analysis of the error between DNN-based prediction and direct numerical optimization results is conducted. Subsequently, a ballistic simulation is designed to validate the accuracy of the network-generated trajectories. Finally, new optimal trajectories are generated beyond the initial value range of the sample data using direct optimization. These new trajectories are compared and analyzed against the trajectories generated by the network to verify the network’s generalization capability and robustness.
4.1. Analysis of Network Prediction Results
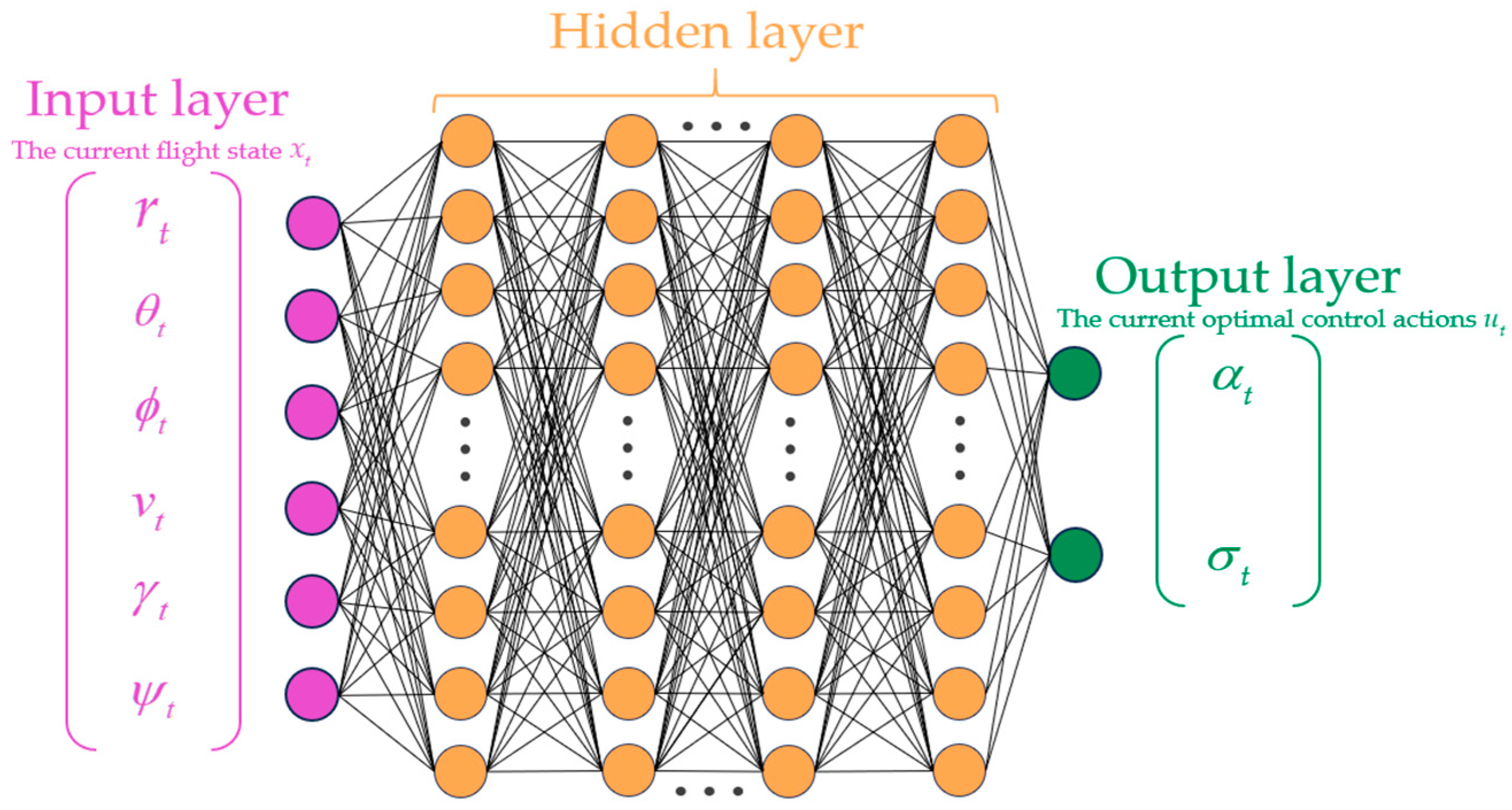
The trained neural network can make predictions based on the current flight state vector
at a given time, providing the control inputs
for the current moment, namely the angle of attack
and bank angle
.
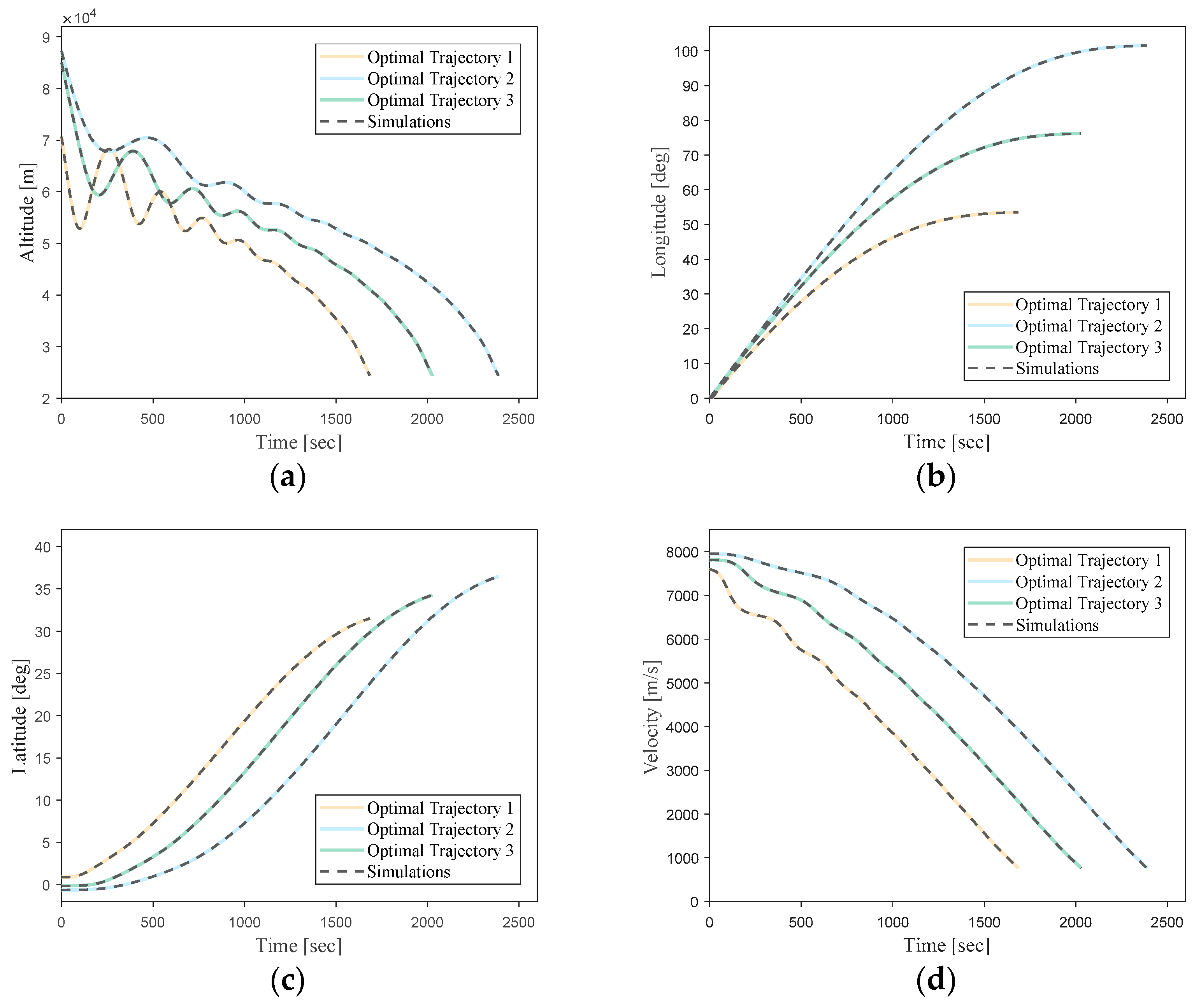
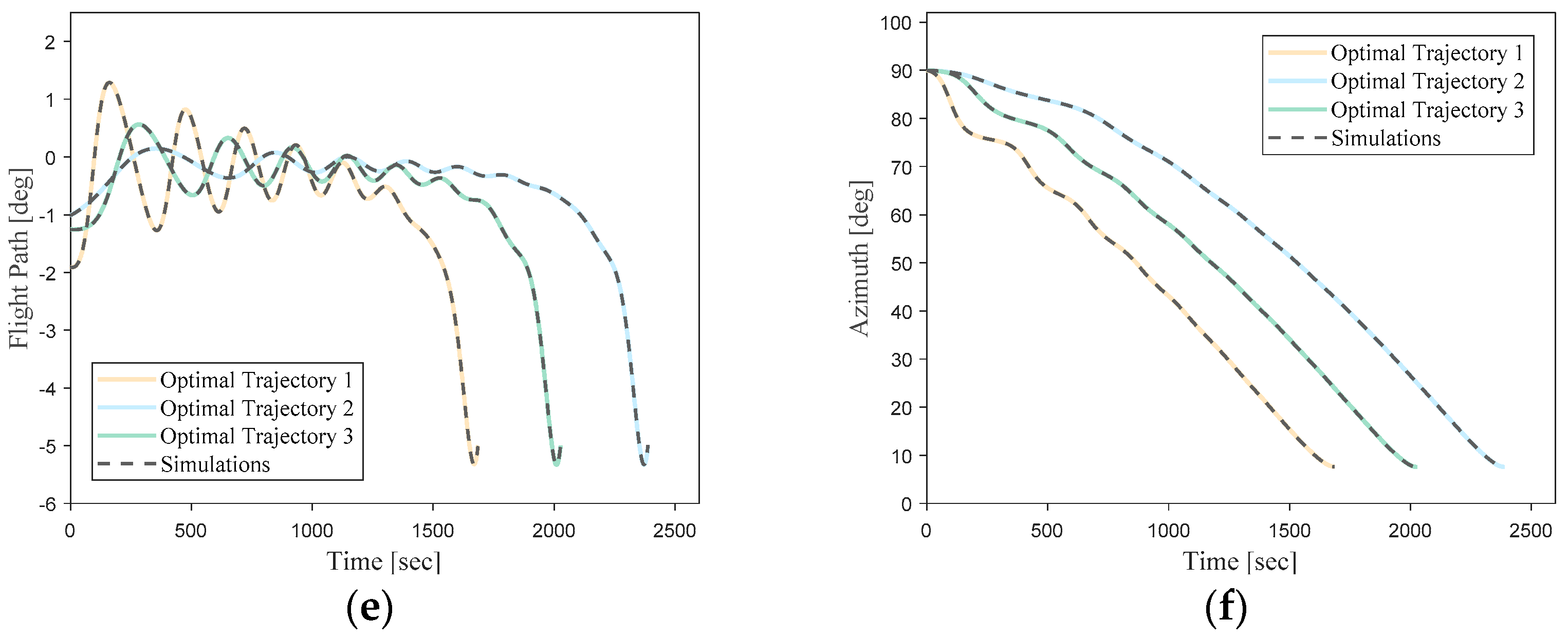
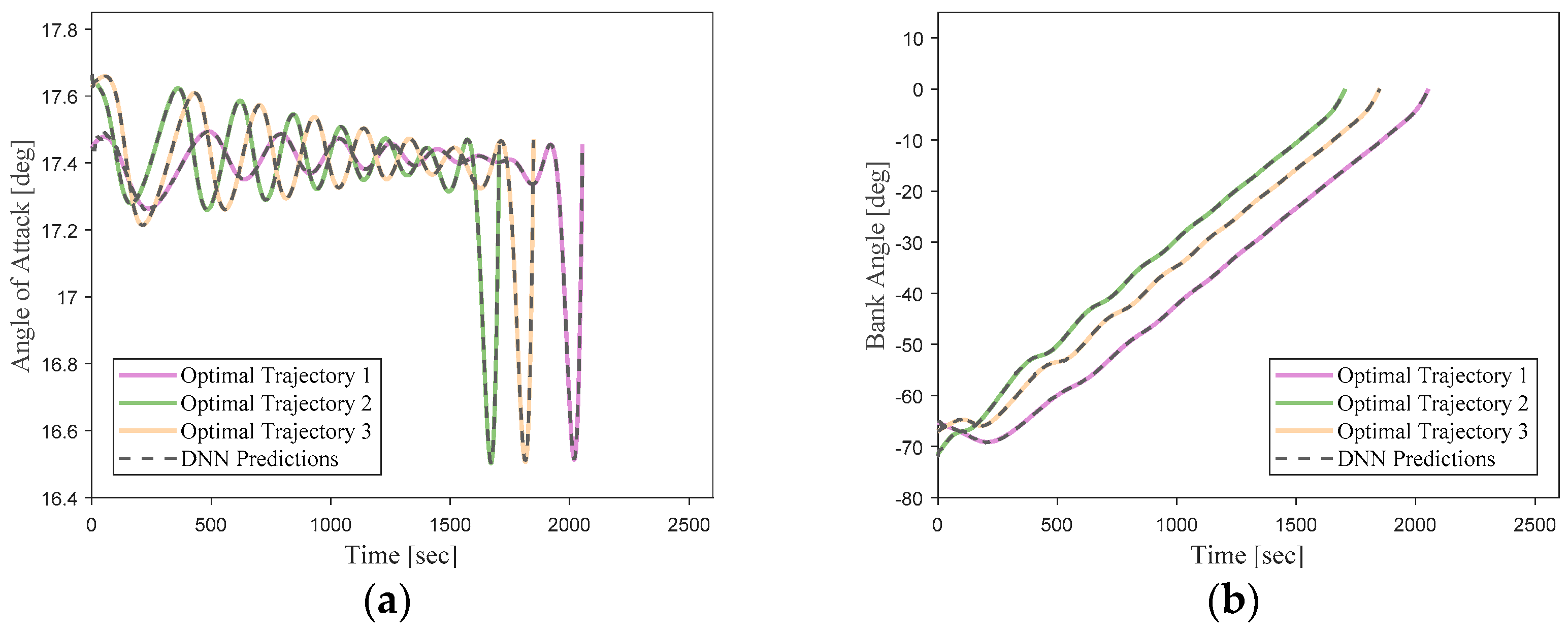
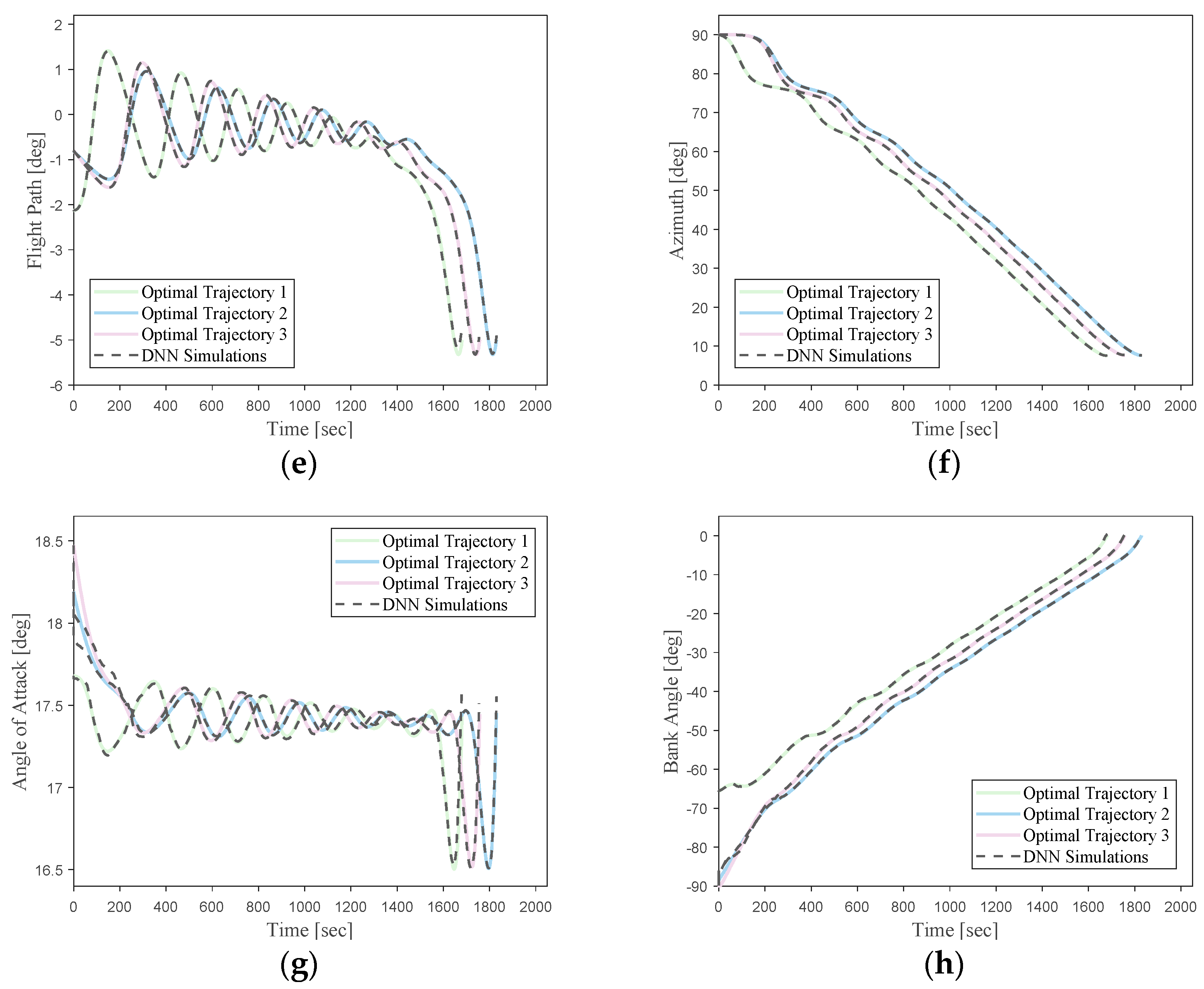
Figure 15 illustrates a comparison between three randomly selected trajectories from the network’s validation dataset and the predicted trajectories generated by the neural network.
The predicted results by the neural network match the optimal trajectories generated using the direct method very closely. This demonstrates a high level of fitting accuracy.
Compared to traditional algorithms, the DNN-based controller offers a simplified computational process and shorter response times. For current DNN models which are developed with TensorFlow in the Python environment, it takes about 0.5 milliseconds to generate a single optimal control instruction on a desktop with an Intel Core i7-12700K processor and a NVIDIA GeForce RTX 3070Ti GPU.
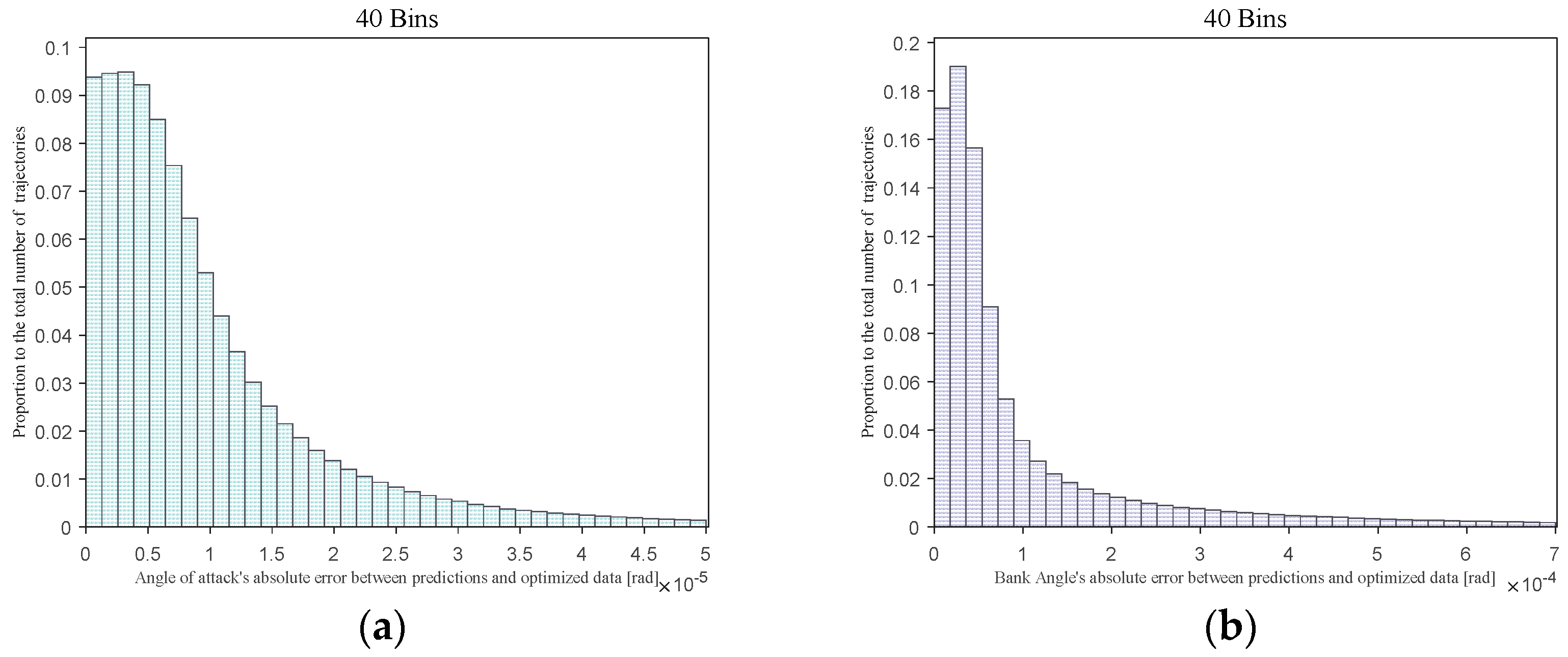
To further quantitatively illustrate the prediction accuracy and errors of the neural network, a histogram of the network prediction absolute errors is presented for another 1000 randomly generated trajectories within the same range as the sample database, as shown in
Figure 16.
Figure 16 illustrates the absolute prediction errors of the neural network for optimal actions across 40 bins. The analysis reveals that in the case of angle of attack
, 96.7% of the absolute errors fall below 0.003°, with 58.9% of the errors being less than 0.0005°, and 12.8% not exceeding 0.0001°. The average prediction error is recorded at 0.001°, with a median of 0.0004° and a standard deviation of 0.005°. As for the bank angle
, 91.2% of the absolute errors are within 0.03°, while 50.9% are limited to 0.003° or less, and 16.8% are below 0.001°. The mean, median, and standard deviation of the prediction errors amount to 0.016°, 0.003°, and 0.11° respectively. The designed DNN model exhibits high accuracy in predicting optimal actions, indicating its potential for achieving precise real-time guidance.
4.2. Analysis of Trajectory Simulation
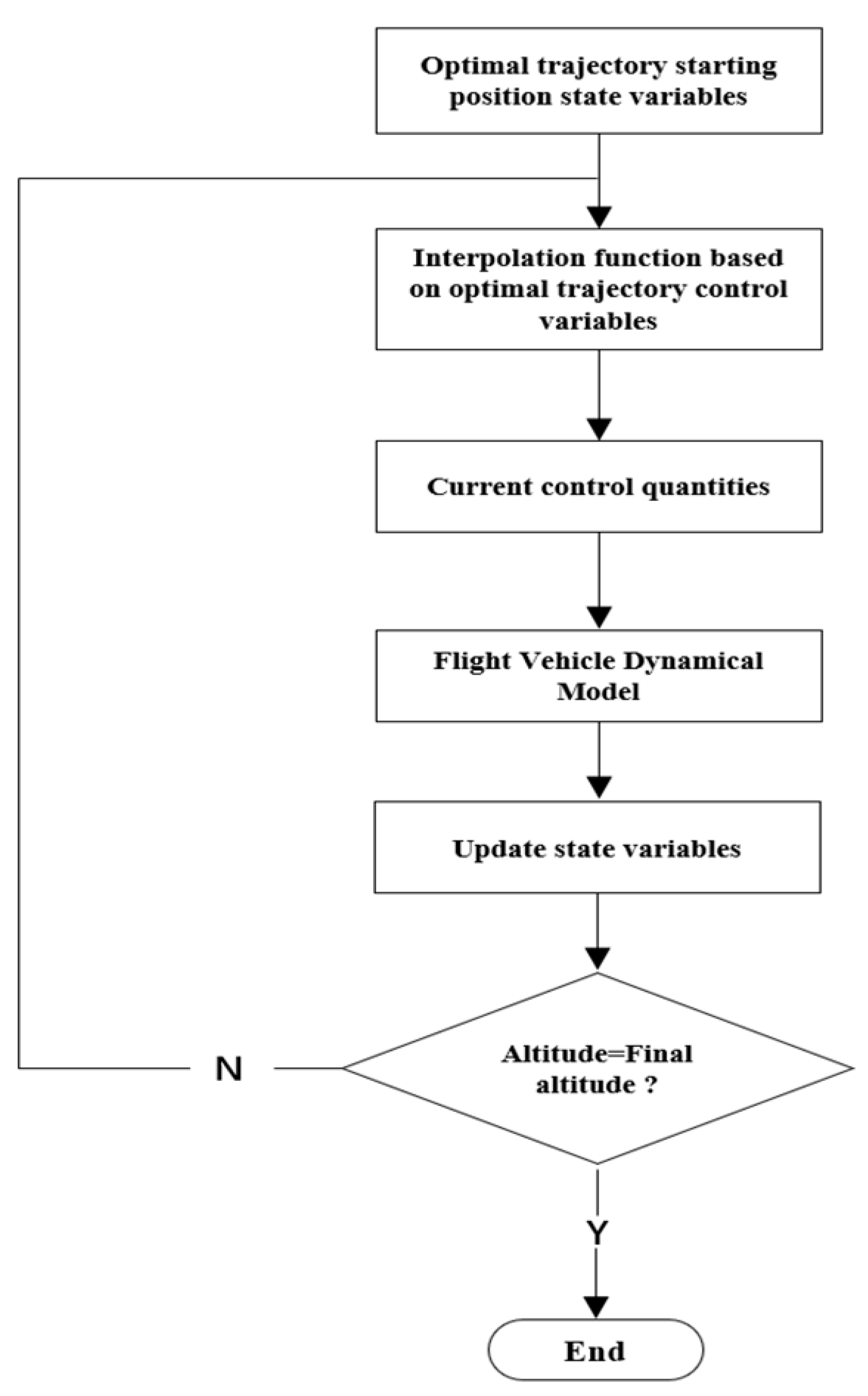
The preceding section analyzed the direct prediction capability of the network model for optimal actions under the current input state. However, when considering the entire flight trajectory, small prediction errors at each moment can accumulate over the whole flight and may lead to significant deviations between the trajectory predicted based on the network and the optimal trajectory, resulting in suboptimal or failed flight missions. Therefore, it is necessary to conduct trajectory simulations based on neural network predictions to evaluate the network’s performance in a given task scenario. Algorithm 1 provides the pseudo-code for the simulation verification process.
| Algorithm 1 Simulation of Trajectory Driving Guided by Deep Neural Networks |
| 1: Load DNN model |
| 2: Set integral step size |
| 3: Initialize state vector |
| 4: While : |
| 5: Preprocess state vector, |
| 6: Get predicted control values from |
| 7: Inverse to |
| 8: Put and into the dynamical equation, obtain |
| 9: Integrate for next state vector (the RK4 method) |
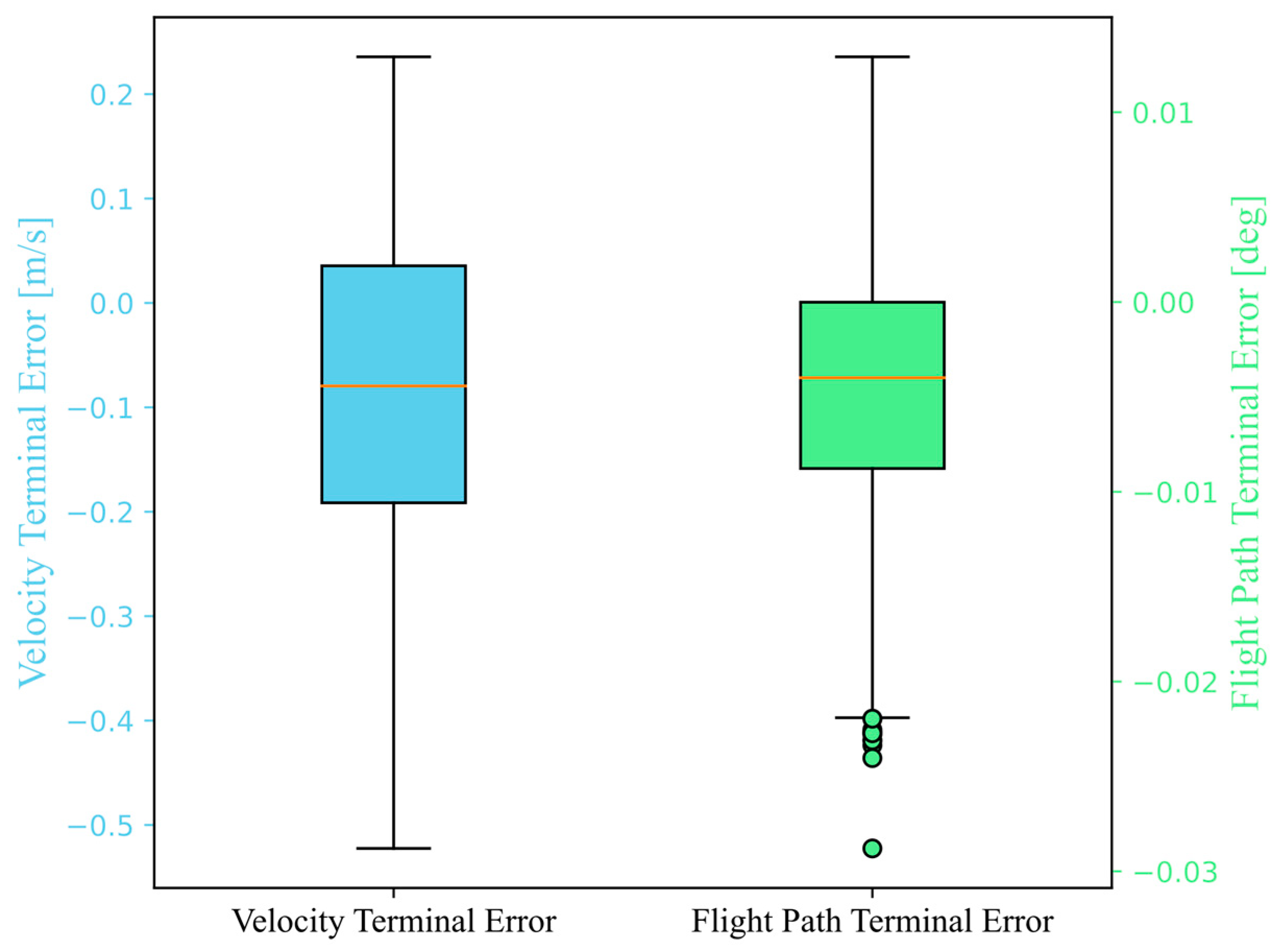
The algorithm implements trajectory generation based on DNNs. By comparing the average absolute errors between the simulated results from the network and the optimal trajectories generated using the direct method, the optimality of the simulated network trajectories can be verified. In order to illustrate the performance of the network, a quantitative analysis of the simulation error of the neural network is conducted. Firstly, the errors in the terminal velocity
and terminal flight path angle
with terminal constraints in the state vector are calculated.
Figure 17 displays the precision analysis of these two variables for trajectories with random initial states. It is worth noting that since the termination condition in Algorithm 1 is the terminal altitude
, there is no precision analysis for the terminal altitude here.
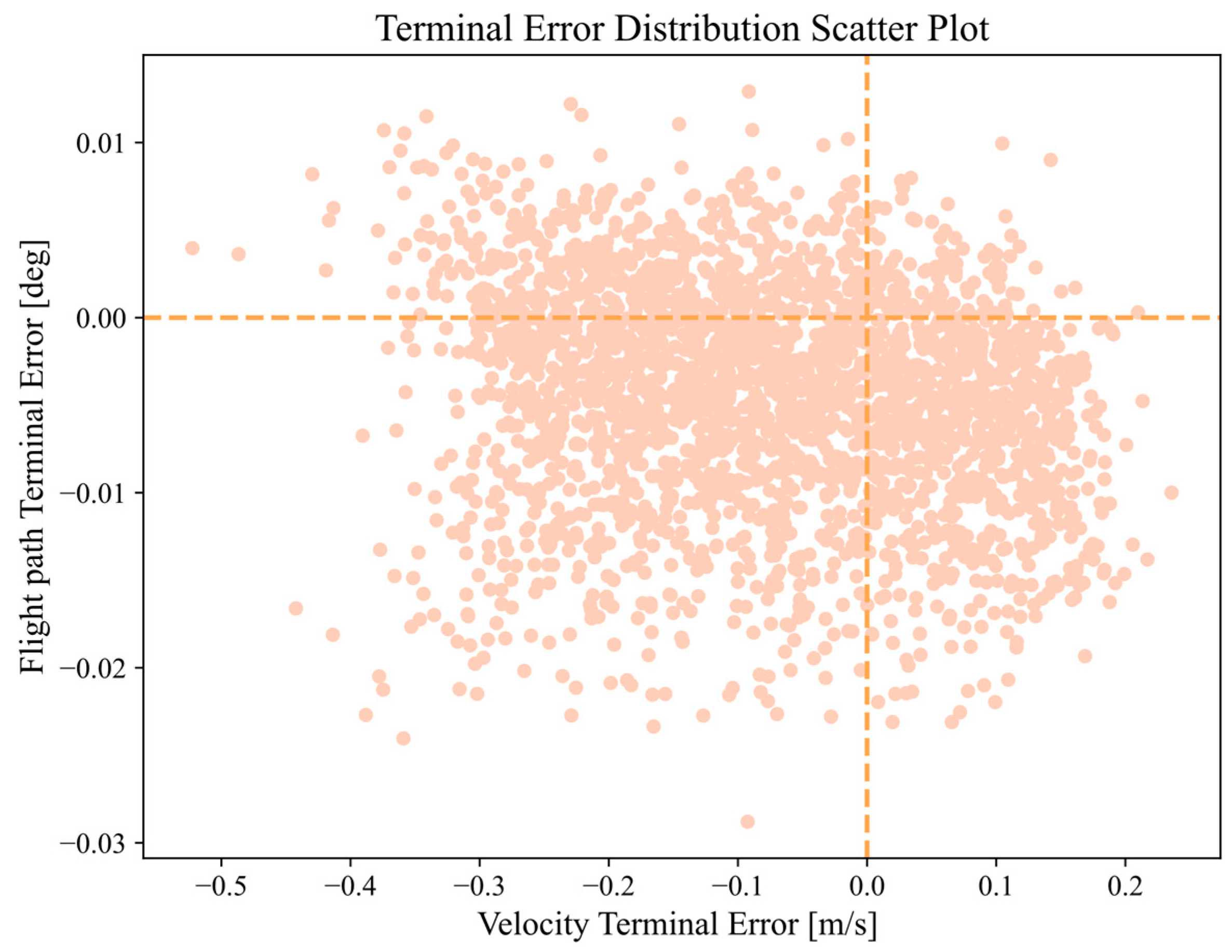
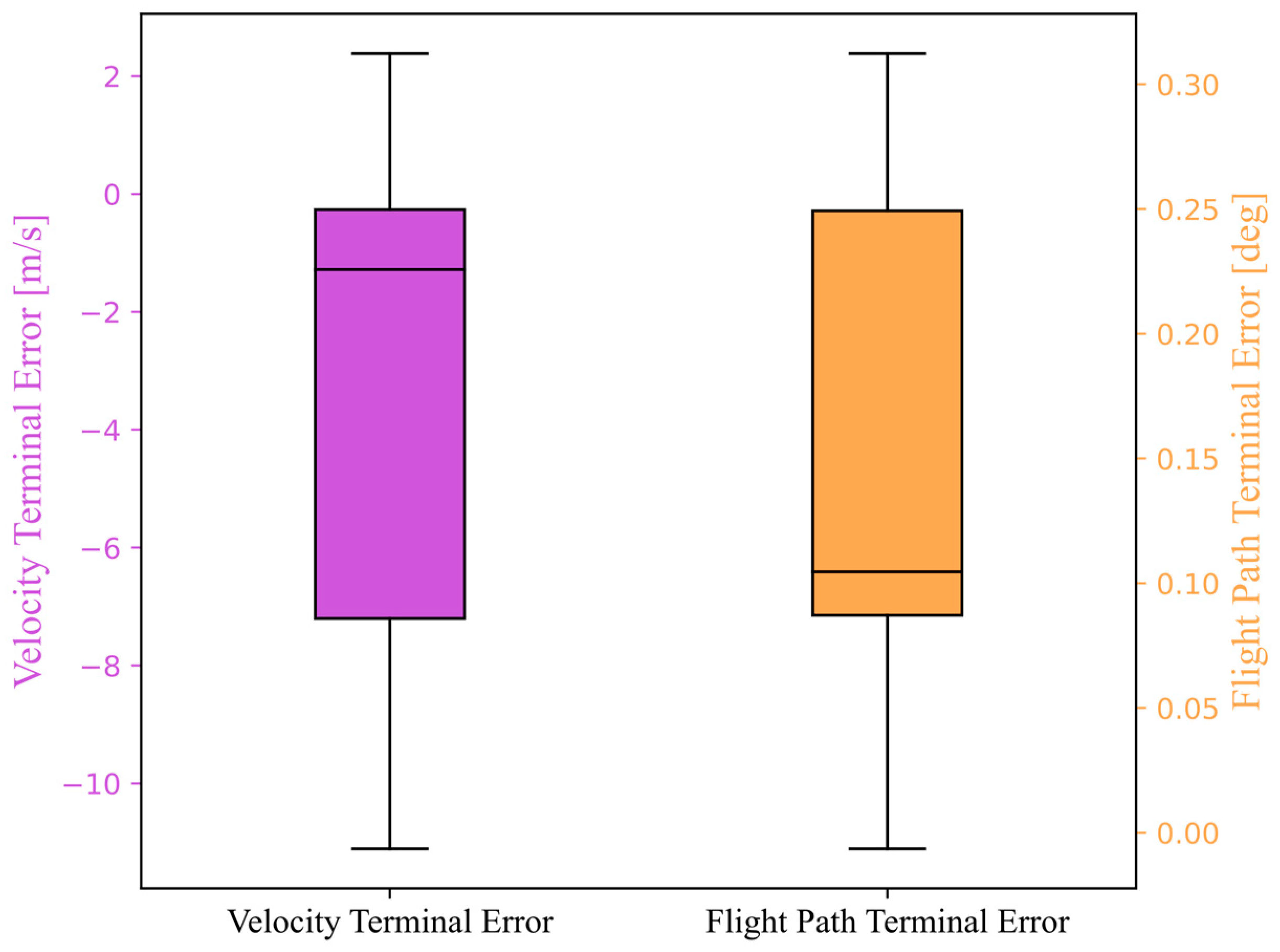
Figure 18 depicts the distribution of trajectory terminal errors in simulation.
The maximum, median, and standard deviation of terminal state errors are provided in
Table 4.
The terminal velocity error ranges from −0.522 to 0.235 m/s, and the terminal flight path angle error ranges from −0.028° to 0.012°. The maximum terminal velocity error is approximately 0.068% of the terminal velocity, and the maximum terminal bank angle error is approximately 0.57% of the terminal bank angle. Additionally, building upon the analysis of terminal errors in DNN simulation, we also analyzed the MAE of state and control variables based on DNN simulation for these trajectories. The specific data are provided in
Table 5.
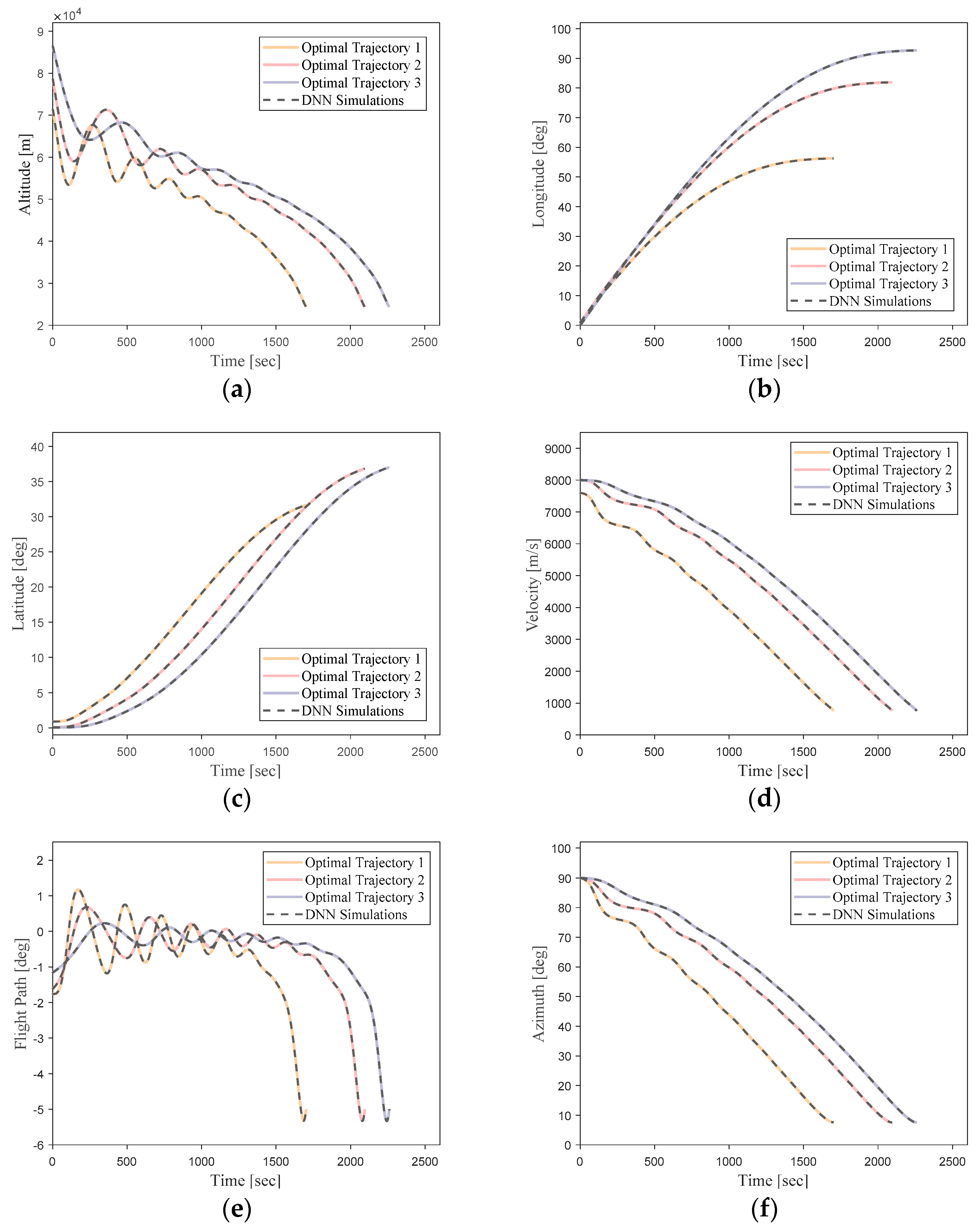
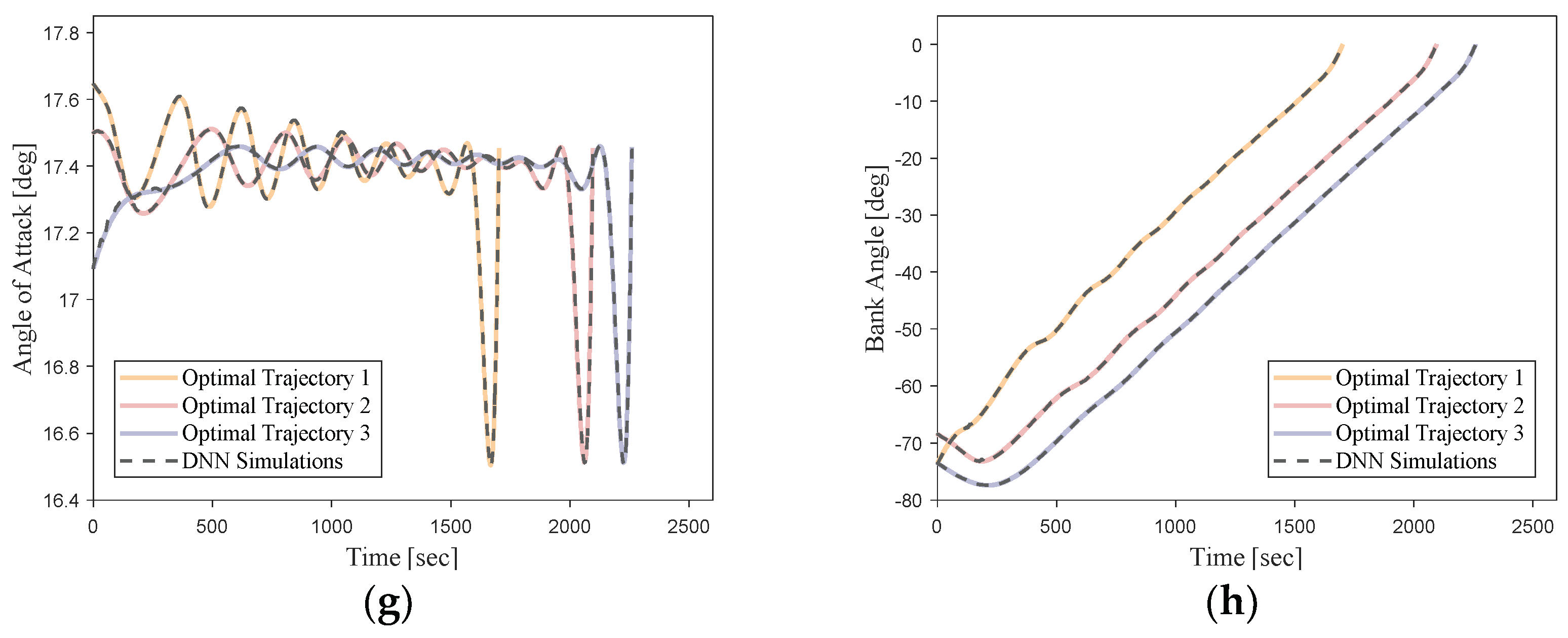
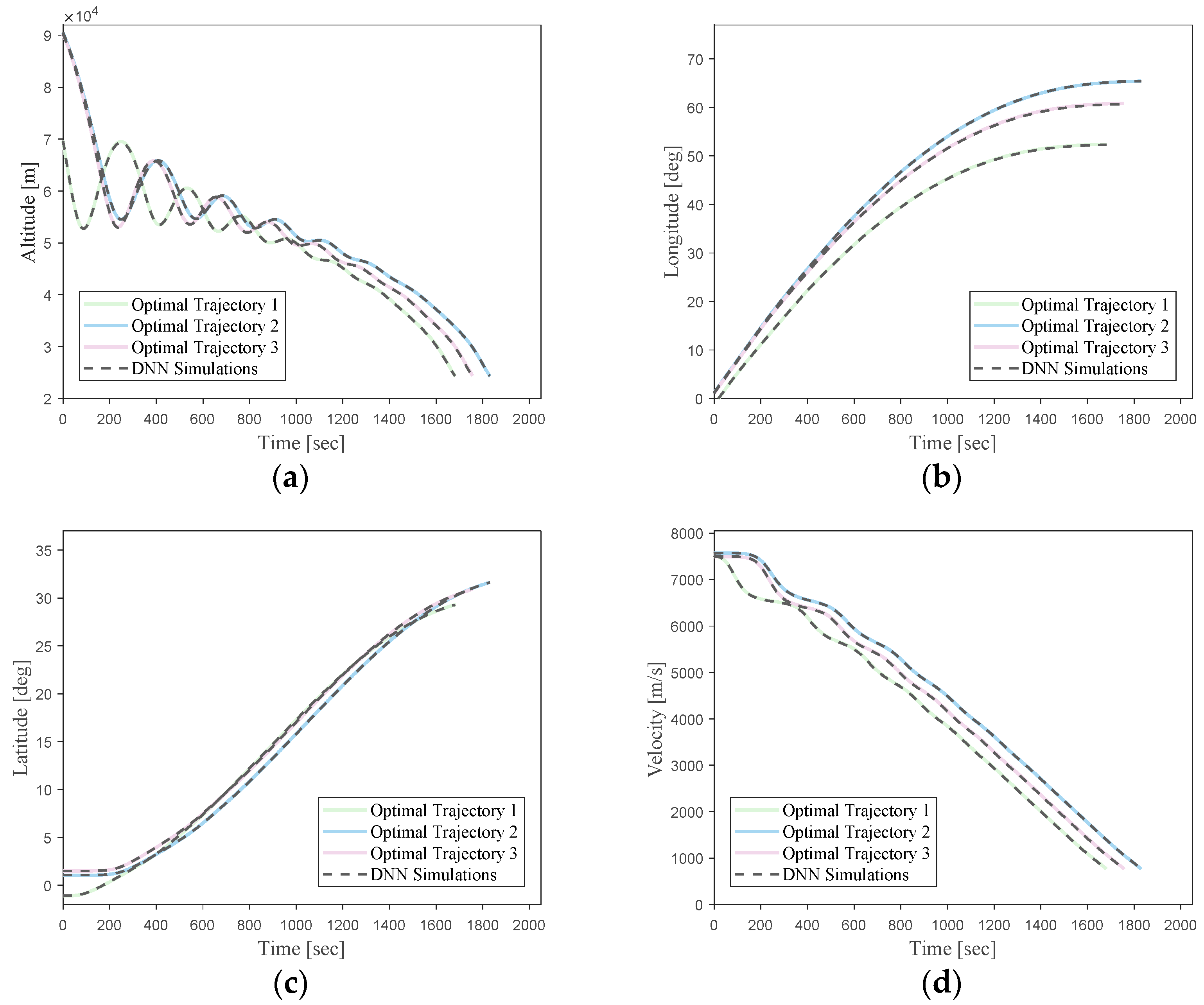
From these error analysis data, it can be shown that the DNN-based optimal trajectory controller for this hypersonic vehicle can ensure trajectory optimality while exhibiting remarkable guidance accuracy under conditions of uncertain initial states. To provide a more intuitive representation of the network’s performance, simulation curves for three trajectories with randomly initialized state vectors are shown in
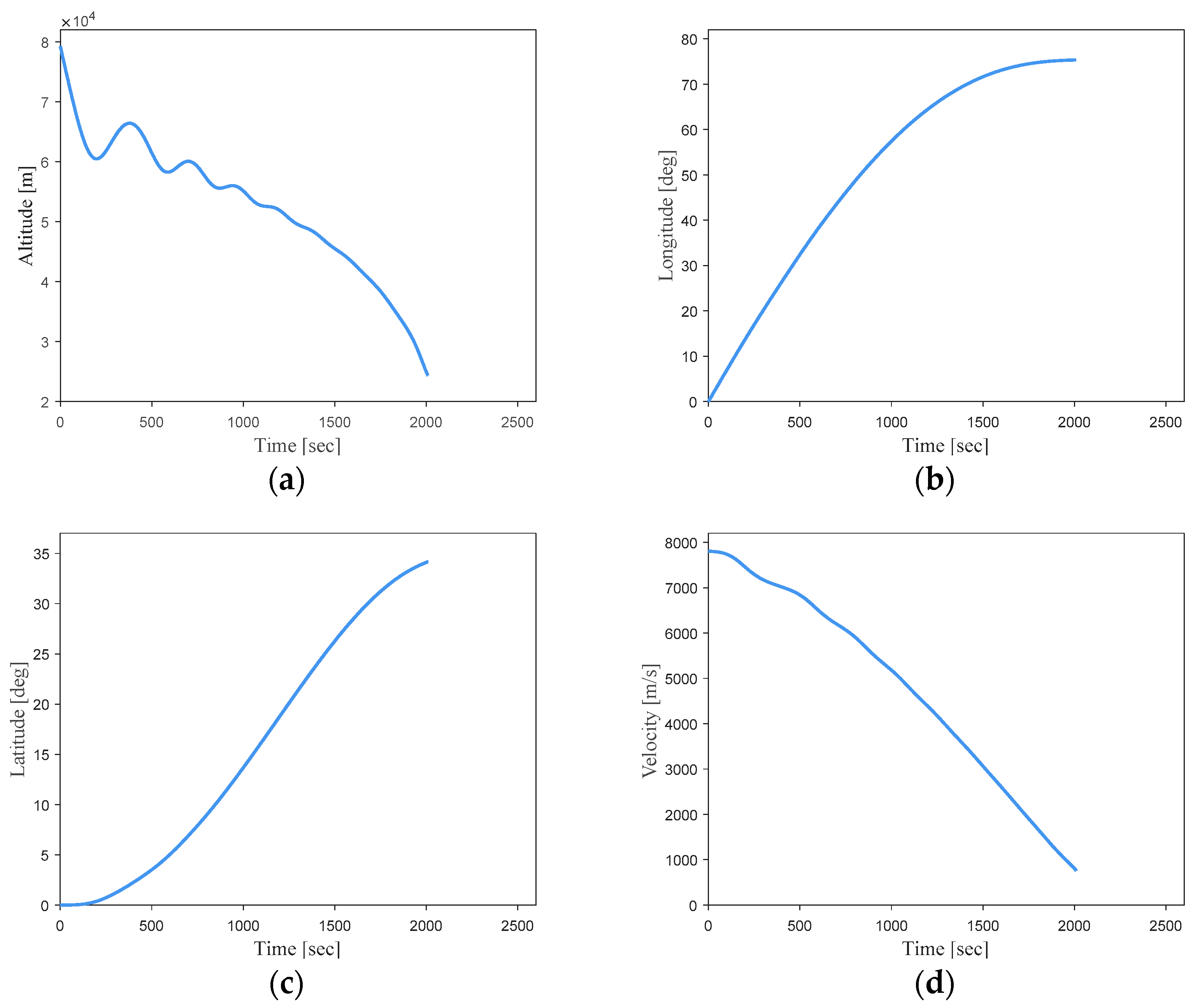
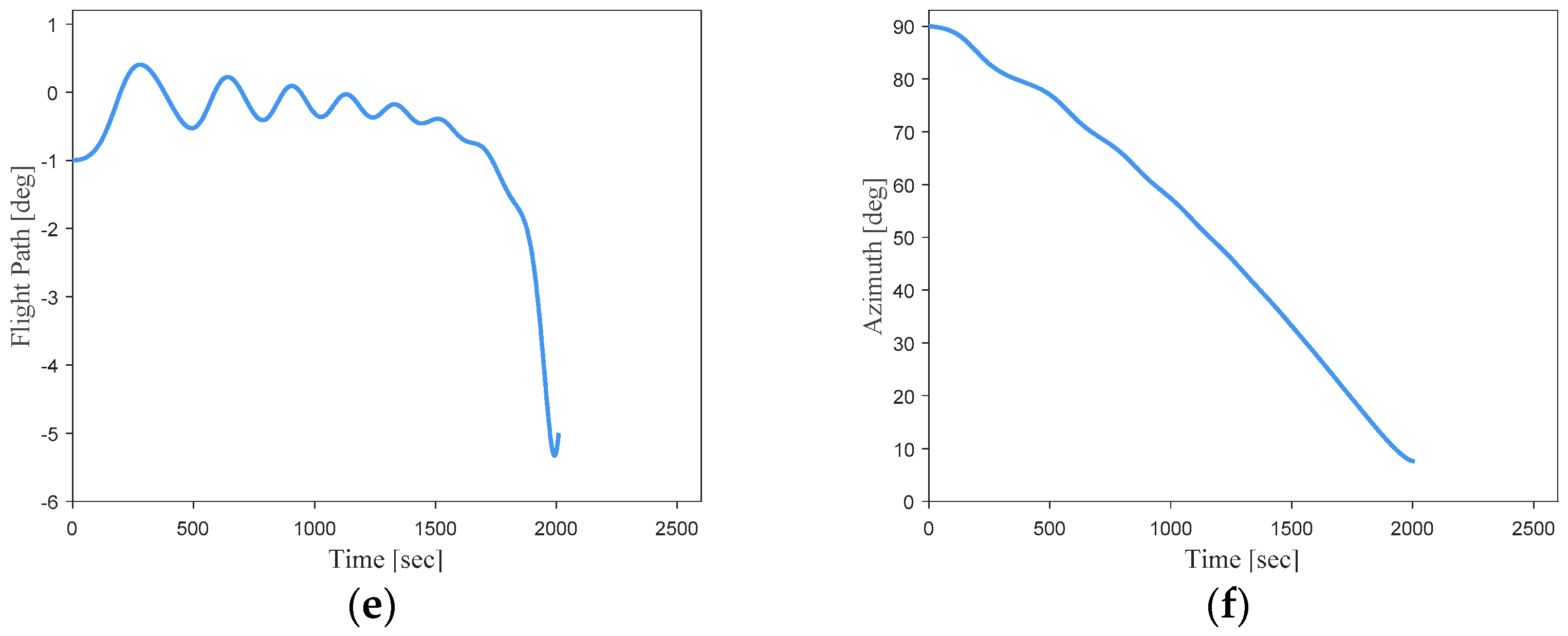
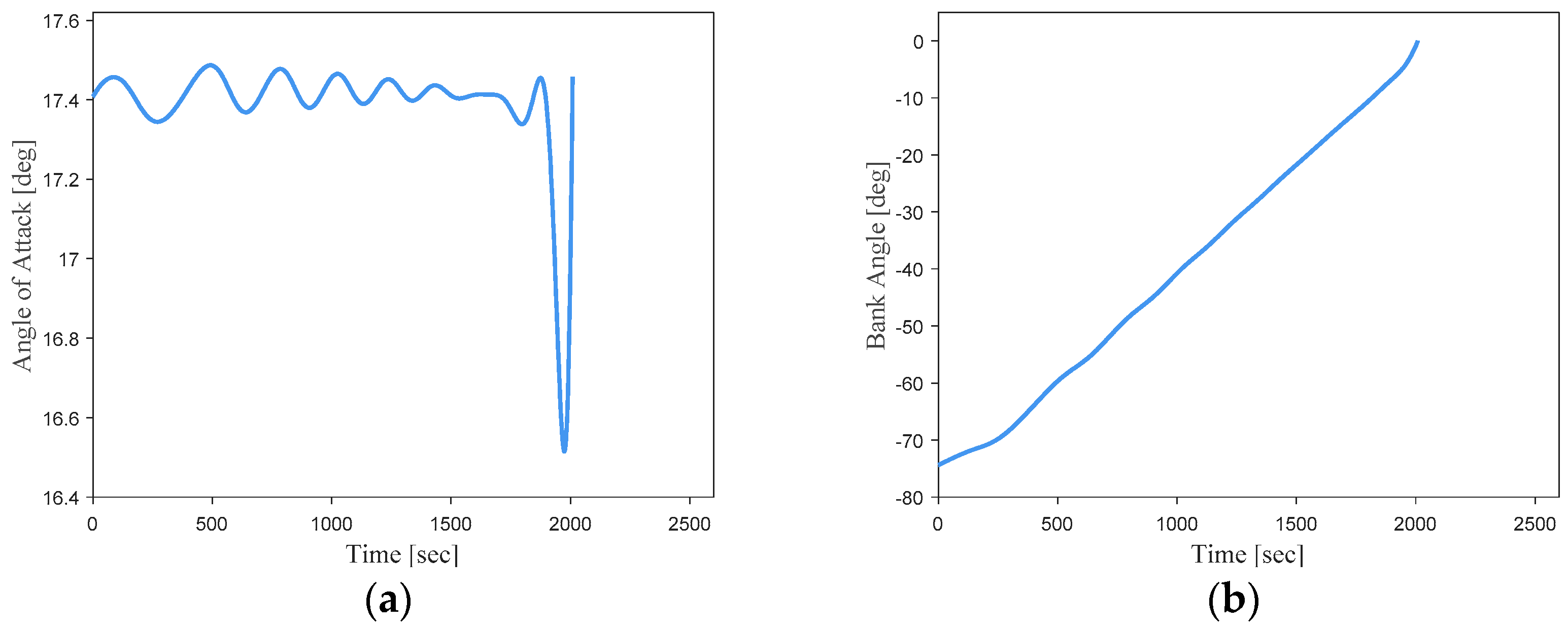
Figure 19.
It can be seen that the simulation trajectories driven by the DNN match the optimal trajectories very well. Under random initial conditions, the DNN can guide the vehicle to complete the flight task along the optimal trajectory for the current state. Additionally, the trajectory simulation time step size of the DNN (0.1 s) is much smaller than the time step size of the optimal trajectories generated using the pseudo-spectral method (about 1 s). This implies that most of the flight state data are not included in the training samples. This indicates that the designed DNN model in this study can effectively learn the nonlinear mapping relationship between the flight state vectors and optimal actions of the hypersonic vehicle in the given task scenario.
4.3. Analysis of Network Robustness
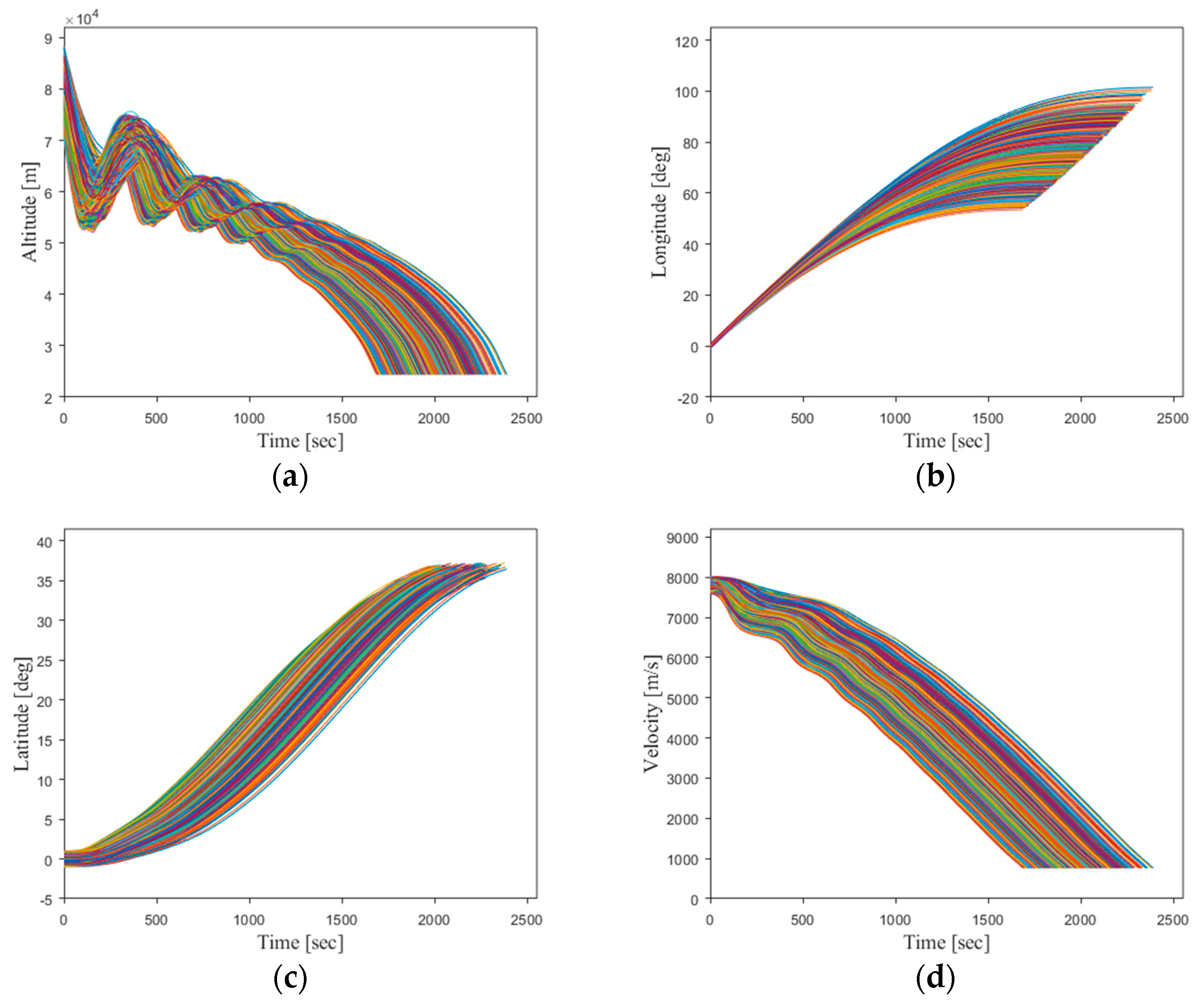
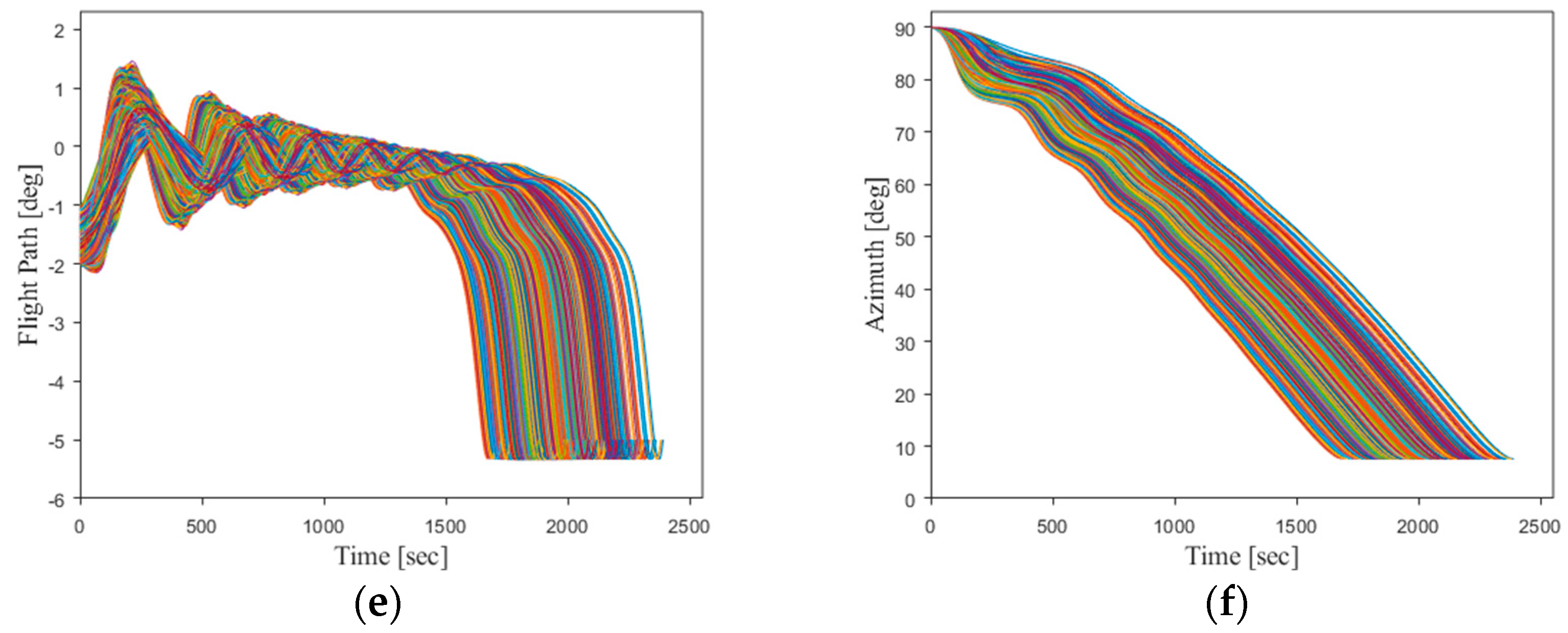
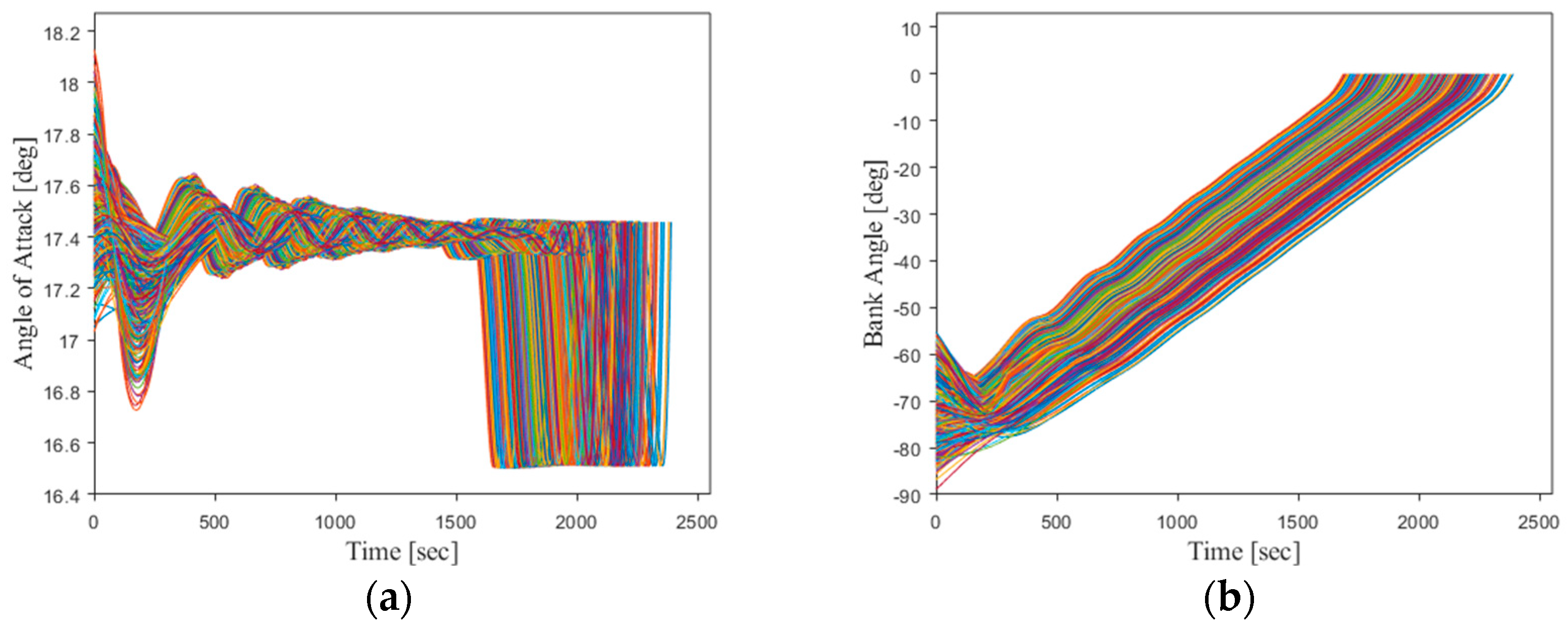
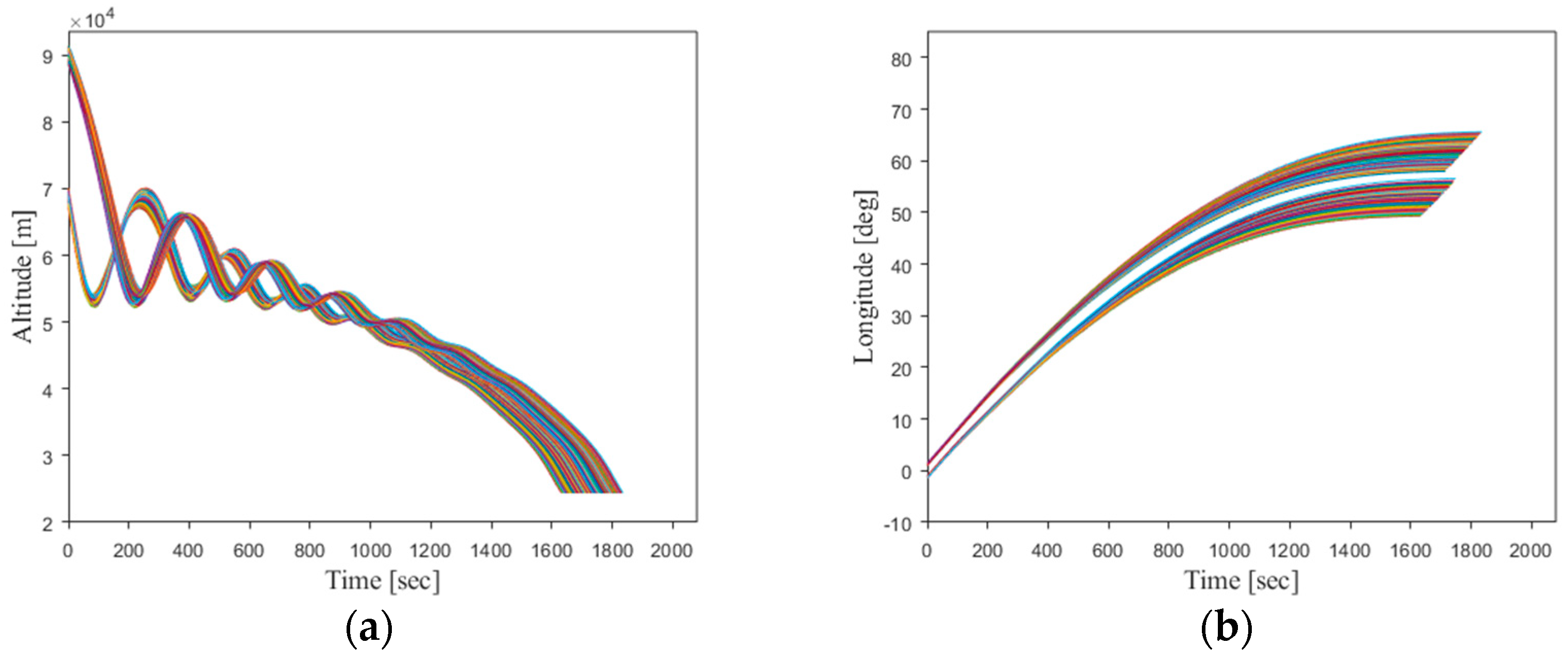
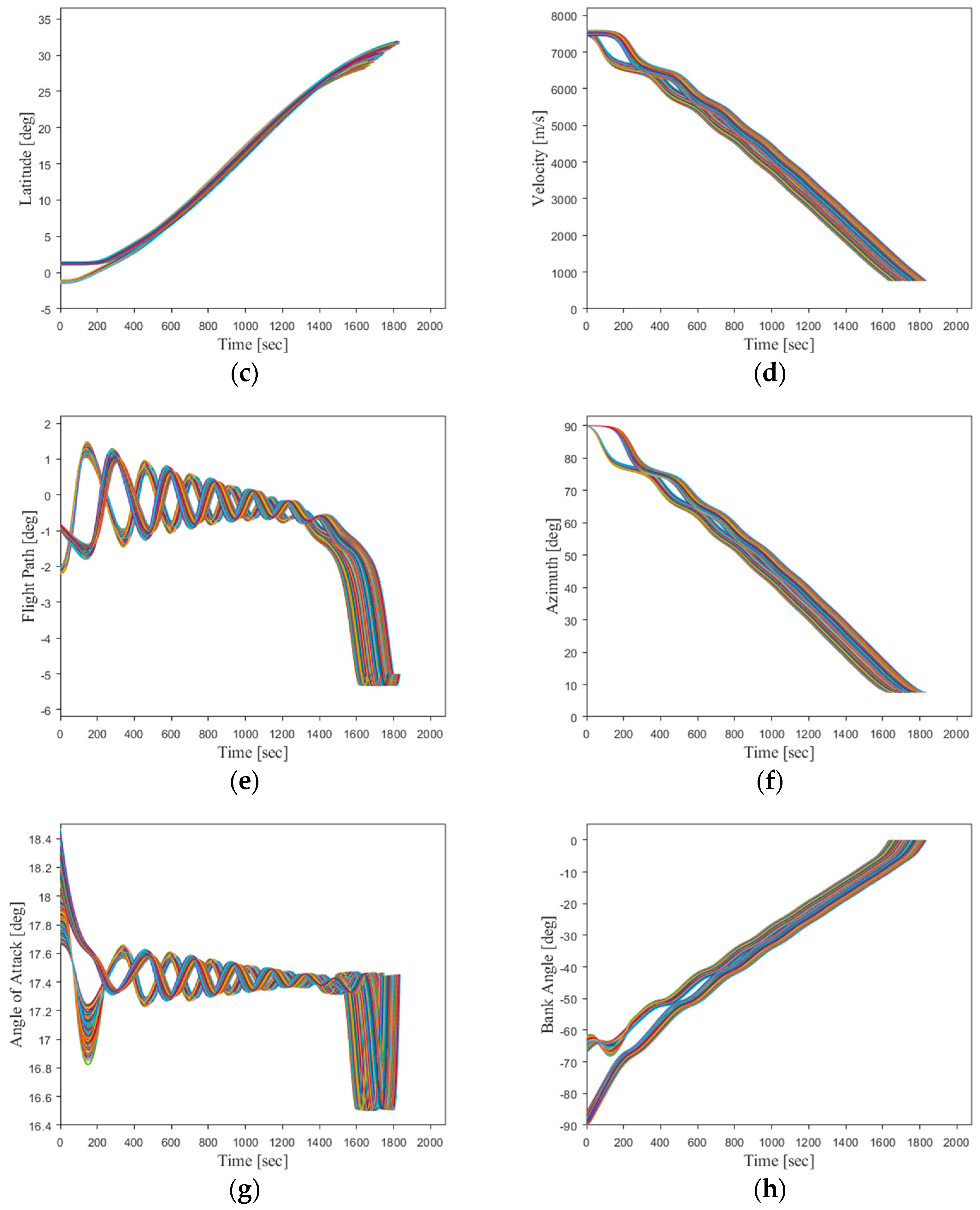
To further explore the network’s performance under unknown initial flight conditions, 500 trajectories are randomly generated outside the original training sample’s initial state range. This is conducted to analyze the network’s generalization capability and its robustness under the uncertainties of the initial flight state. The results are presented in
Figure 20.
The new generated trajectories, in comparison to the original training sample data, have significantly extended the range of flight state values at the entry initial point. The specific value ranges for each initial state variable are provided in
Table 6.
To further illustrate the performance of the DNN-based controller in an unknown initial state region, we conducted a simulation analysis using the DNN model on 500 trajectories from the test dataset.
Figure 21 shows the analysis of terminal errors for trajectories generated by the network in the expanded initial state range. It can be observed that although the terminal errors are relatively larger compared to the results in
Section 4.2, they remain within an acceptable range. The terminal velocity error ranges within [−11.1076, 2.3835] m/s, and the terminal bank angle error falls within the range of [−0.064, 0.3123] degrees. The maximum, mean, median, and standard deviation of terminal errors are provided in
Table 7.
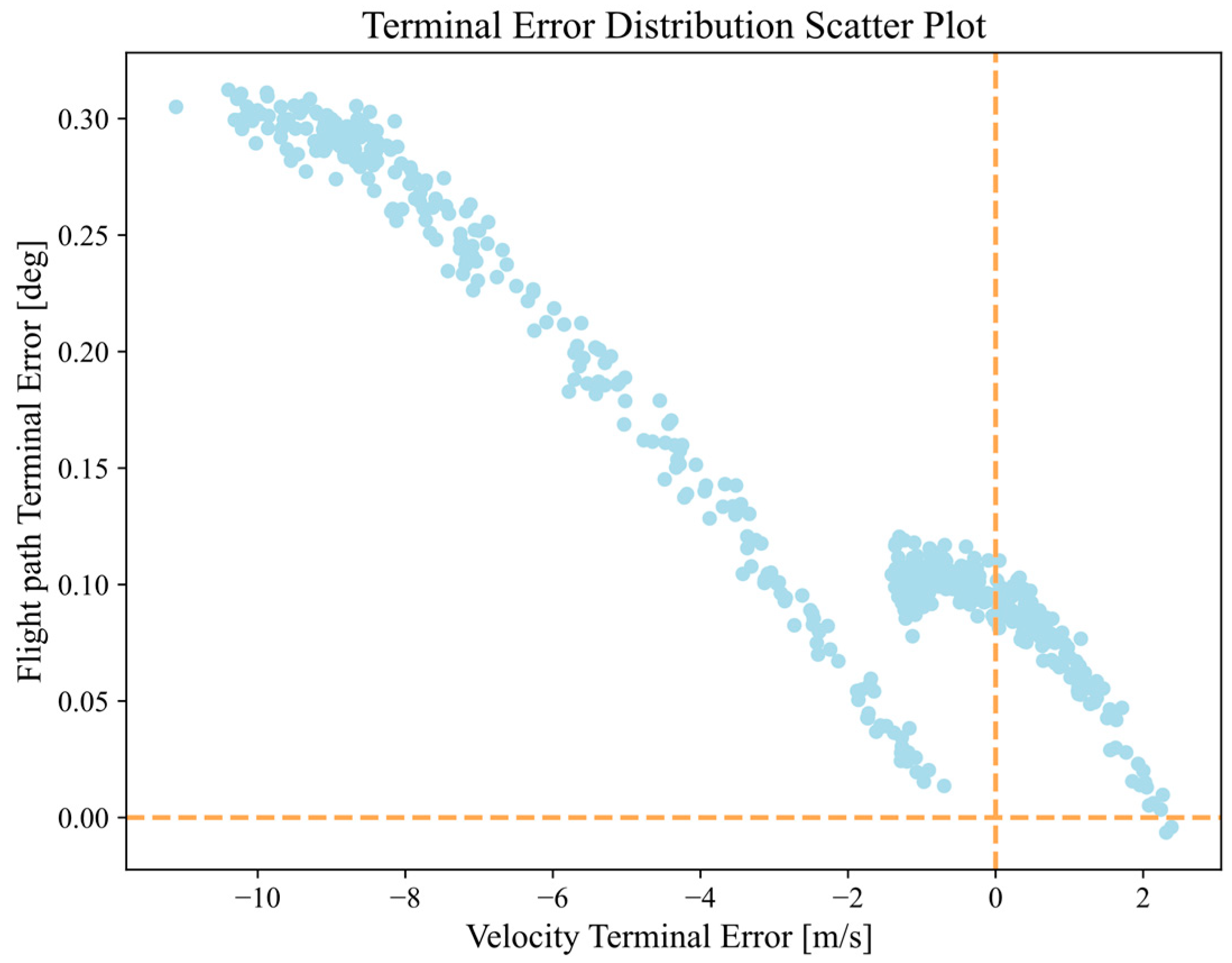
Figure 22 depicts the distribution of trajectory simulation terminal errors in the expanded range. It can be observed that the terminal errors of trajectories generated by the DNN within the current expanded range are not normally distributed, and they exhibit a strip-like distribution. It presents two near linear relationships between velocity terminal error and flight path angle terminal error.
Table 8 presents a statistical analysis of the MAE for all trajectories generated by the DNN within this expanded state range.
From the error analysis data, it can be observed that even beyond the range of training data, the DNN-based controller is still capable of achieving a certain level of guidance accuracy.
To provide a more visual evaluation of the network’s performance outside the training space, three trajectories were randomly selected within the expanded initial space for online simulations based on the DNN. As shown in
Figure 23, a comparison was made between the flight profiles of these trajectories and their corresponding optimal trajectories.
It can be shown that the flight state curves driven by the DNN are smooth and the errors are relatively small. The control variables exhibit larger errors in the initial stages but progressively approach optimal values, with a near-optimal behavior achieved around 270 s. Thus, the proposed DNN-based optimal trajectory controller in this study demonstrates the capability to provide approximate control actions and correct trajectories towards the desired goals, even in cases of significant initial state deviations.
The above results indicate that the designed DNN-based controller can maintain an acceptable level of guidance accuracy even when there are deviations in the initial flight state. It is capable of generating high-quality control commands, demonstrating a certain level of generalization ability and robustness.