Review of Sonic Boom Prediction and Reduction Methods for Next Generation of Supersonic Aircraft
Abstract
1. Introduction
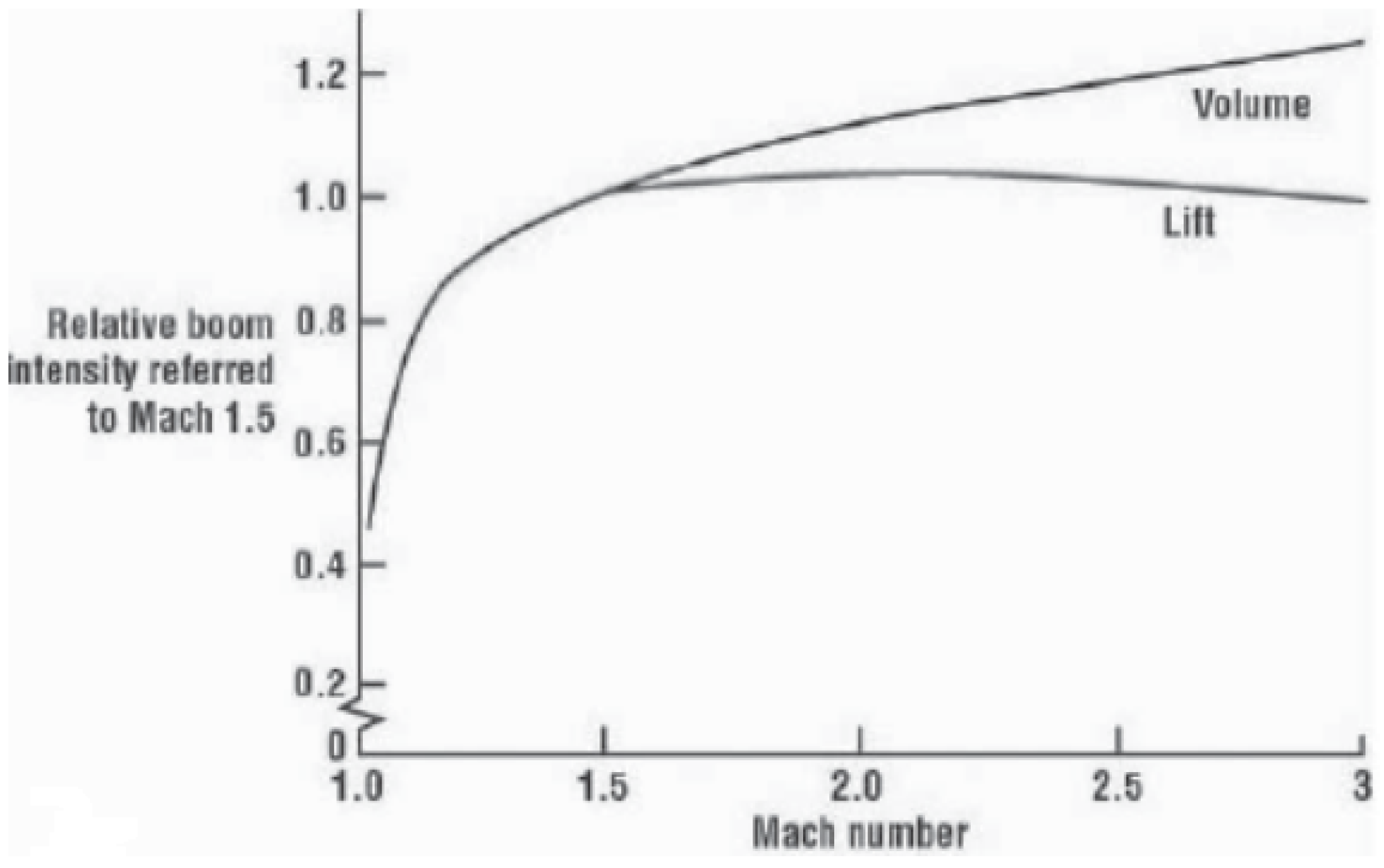
2. Sonic Boom Prediction and Minimization
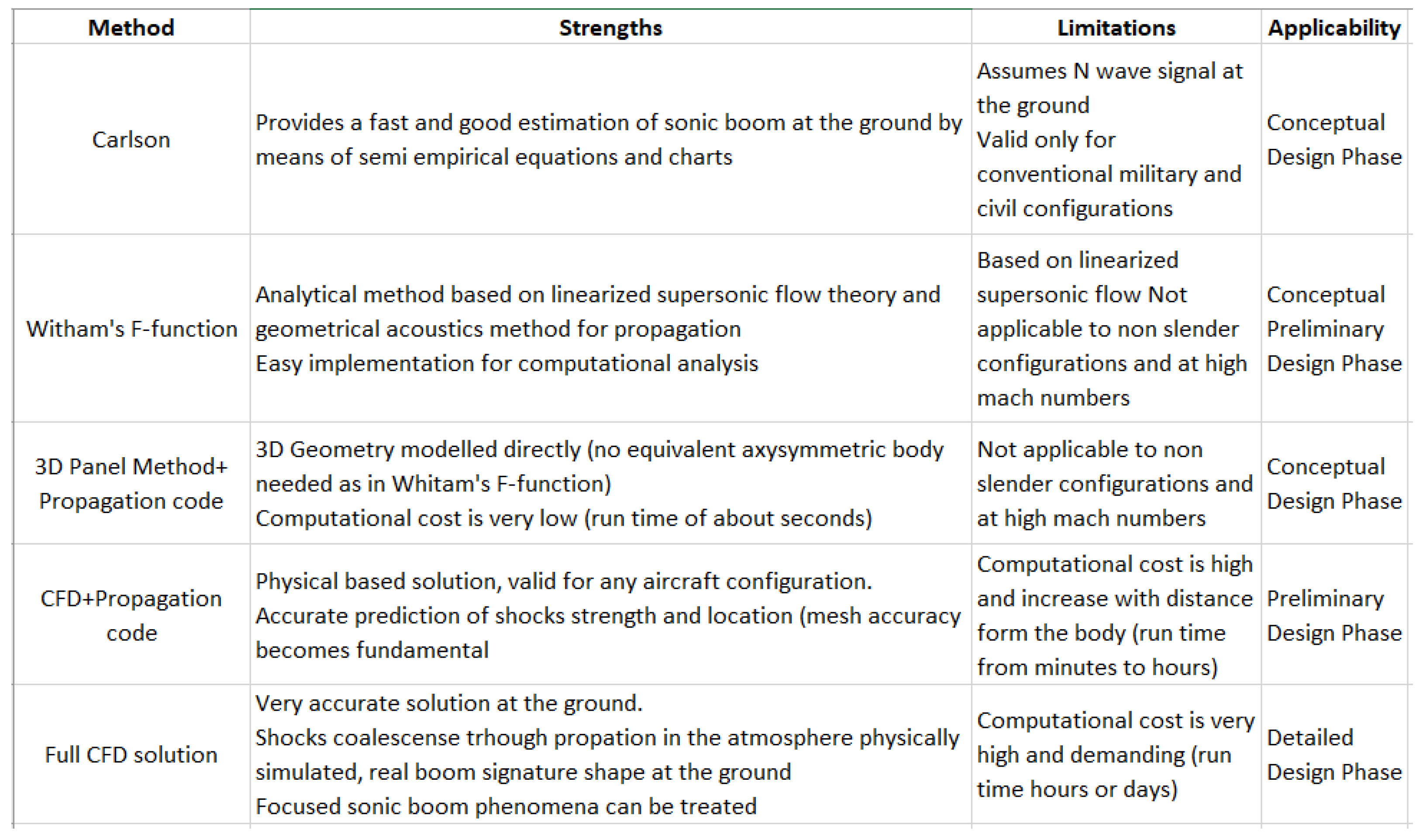
2.1. Prediction Methods
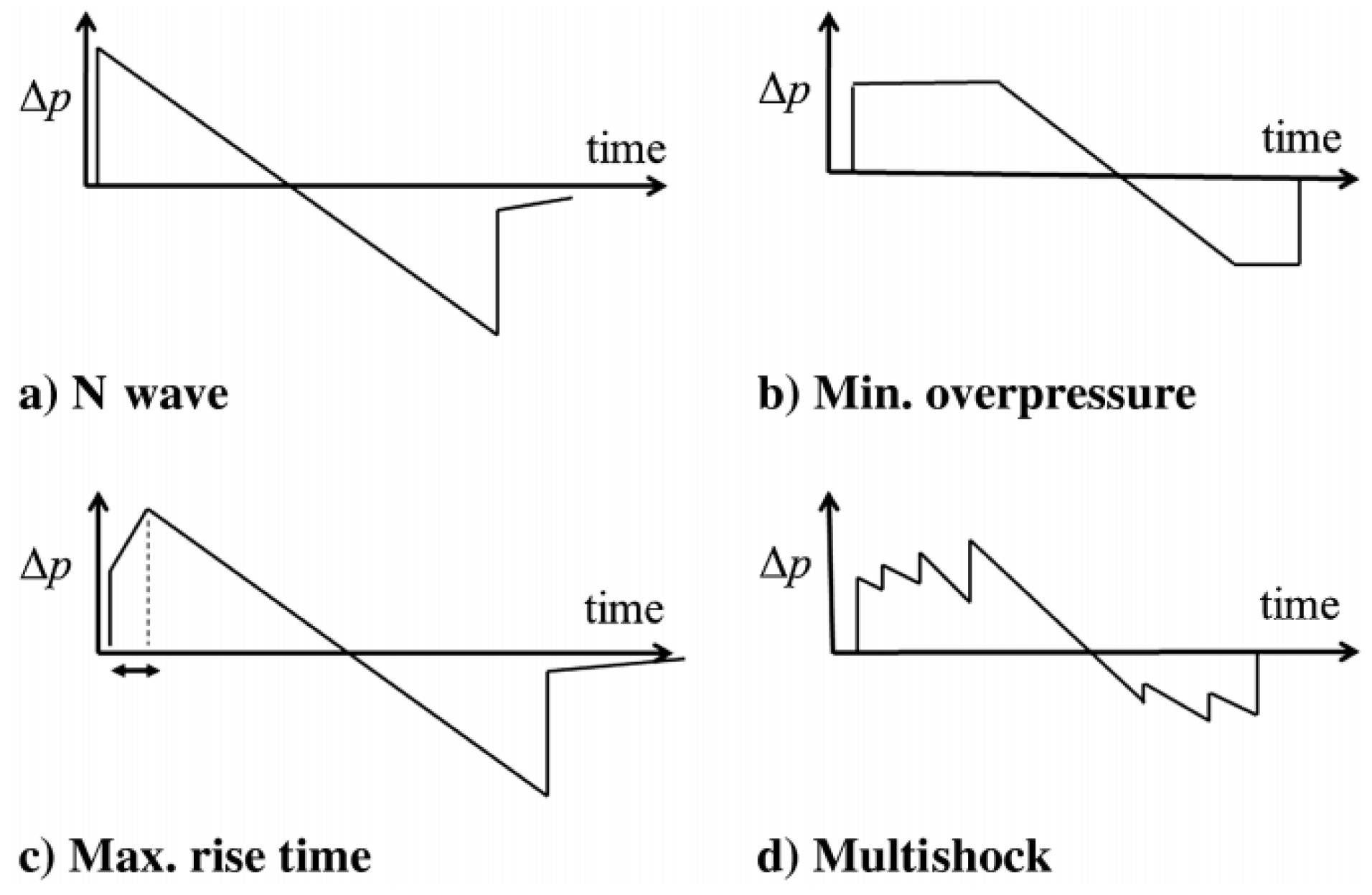
2.1.1. Fundamental Theory
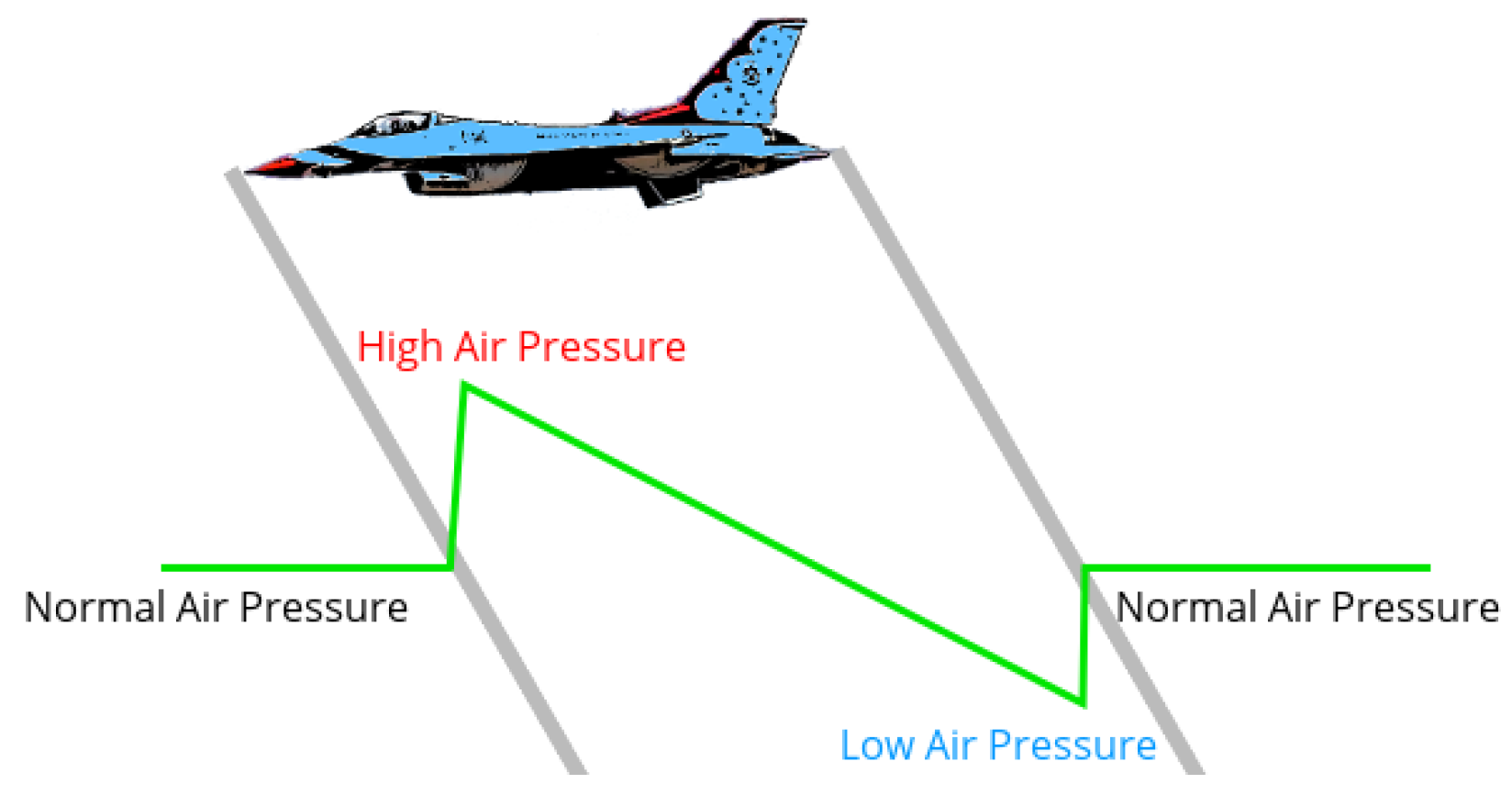
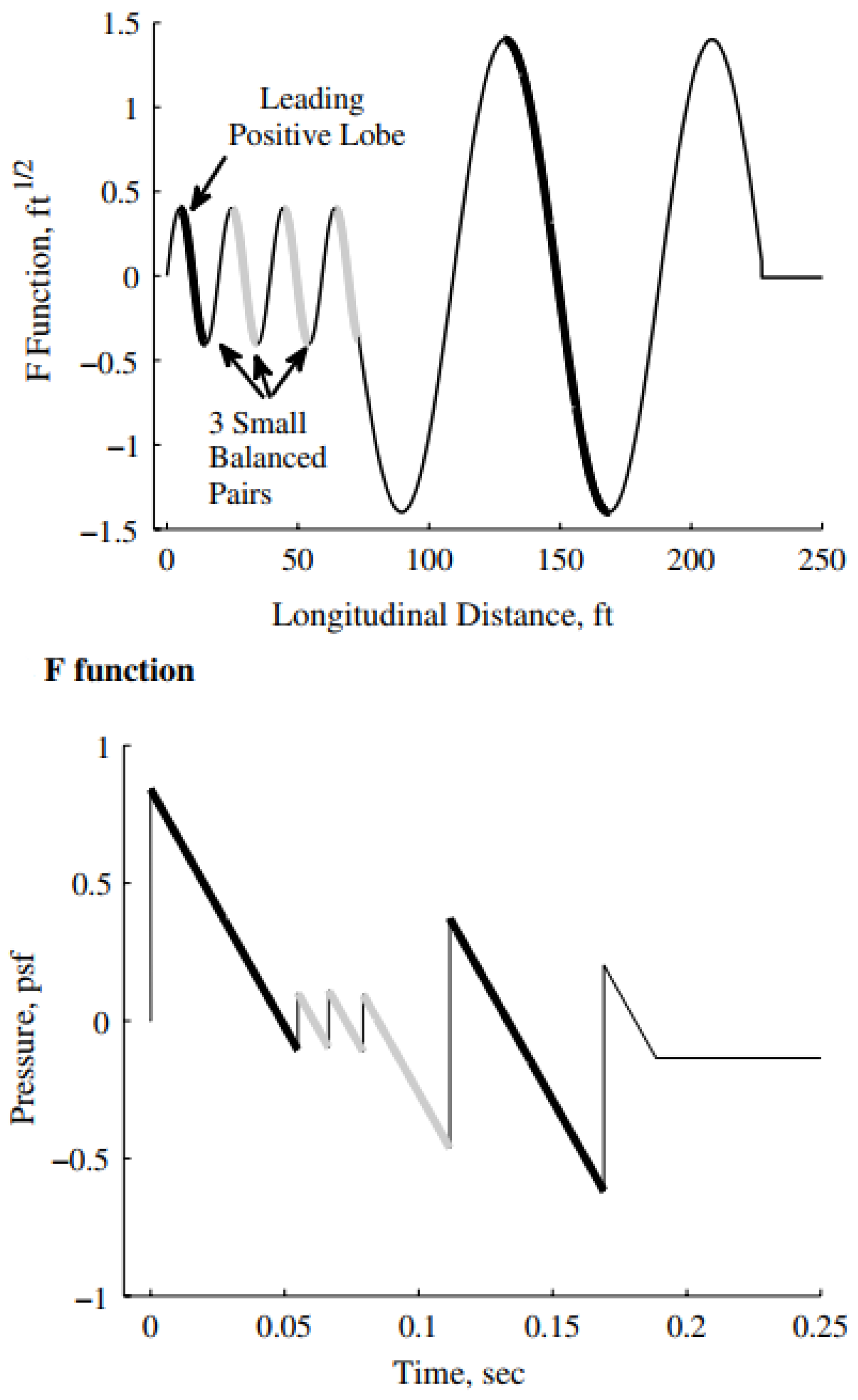
- The acoustic source signature of the vehicle is obtained in terms of a normalized form known as the Whitham F-function. It represents the axisymmetric (or locally axisymmetric) linear acoustic solution in a uniform medium.
- The F-function is extrapolated to large distances by using geometrical acoustics ray tracing, requiring as inputs the vehicle trajectory and the structure of the atmosphere, and according to which the amplitude changes but the shape is fixed.
- In the end, Whitham’s rule is applied to the complete linear acoustic signature. This accounts for nonlinear steepening or “aging” of the signature. Shocks fitting is carried out such that the total area is conserved (‘area balancing’ rule).
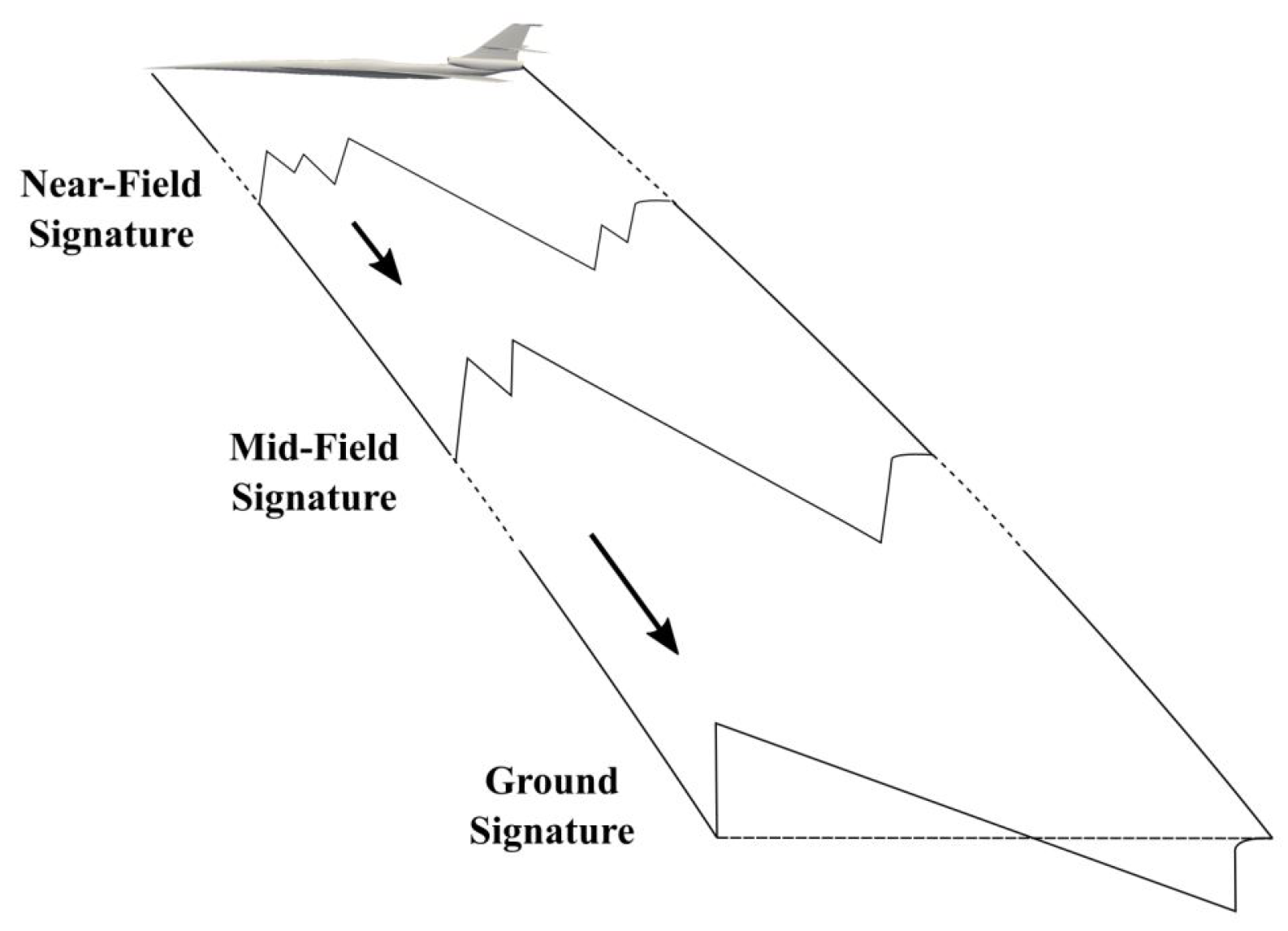
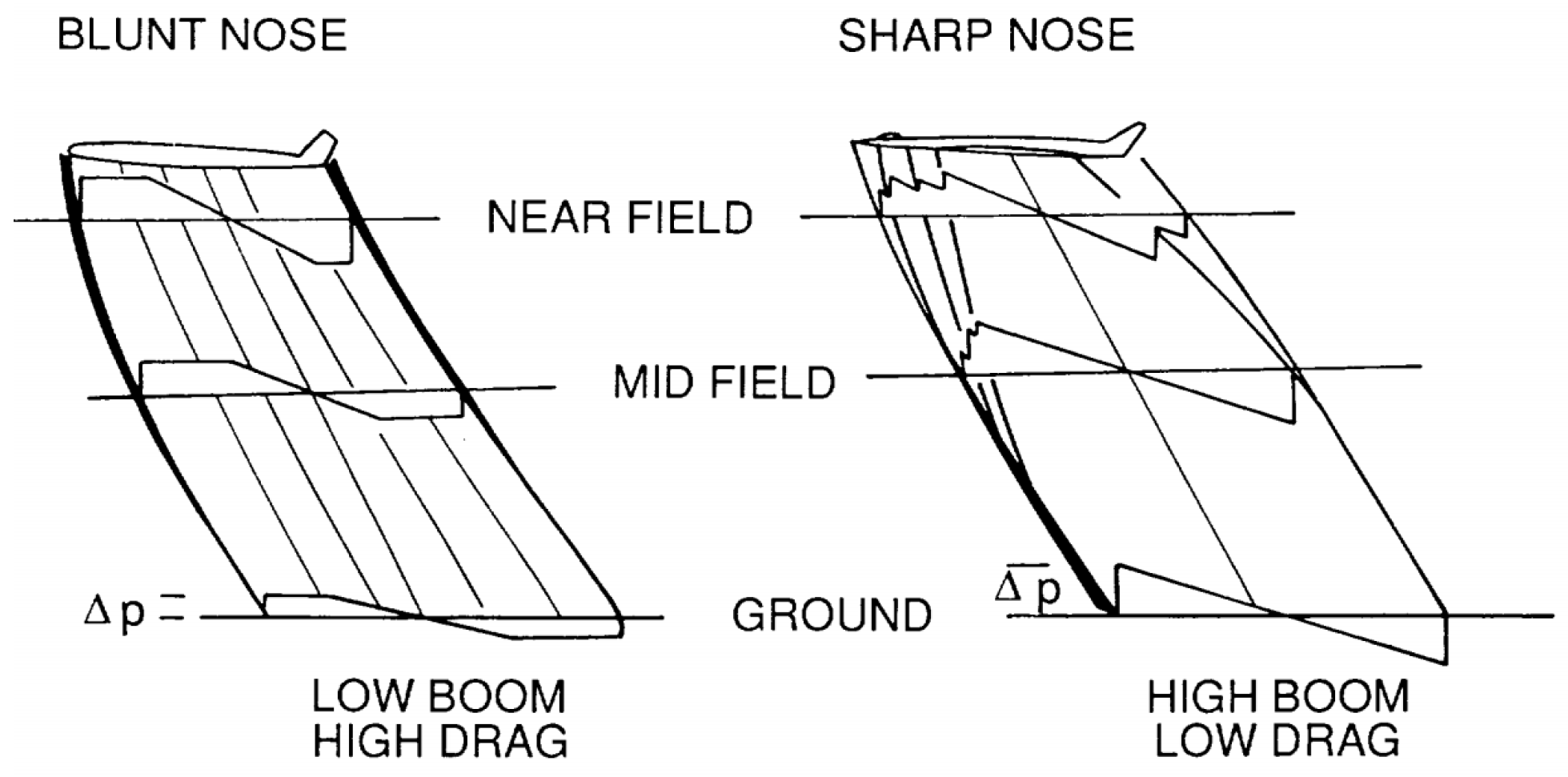
2.1.2. Advances in Near-Field Prediction
2.1.3. Advances in Pressure Propagation
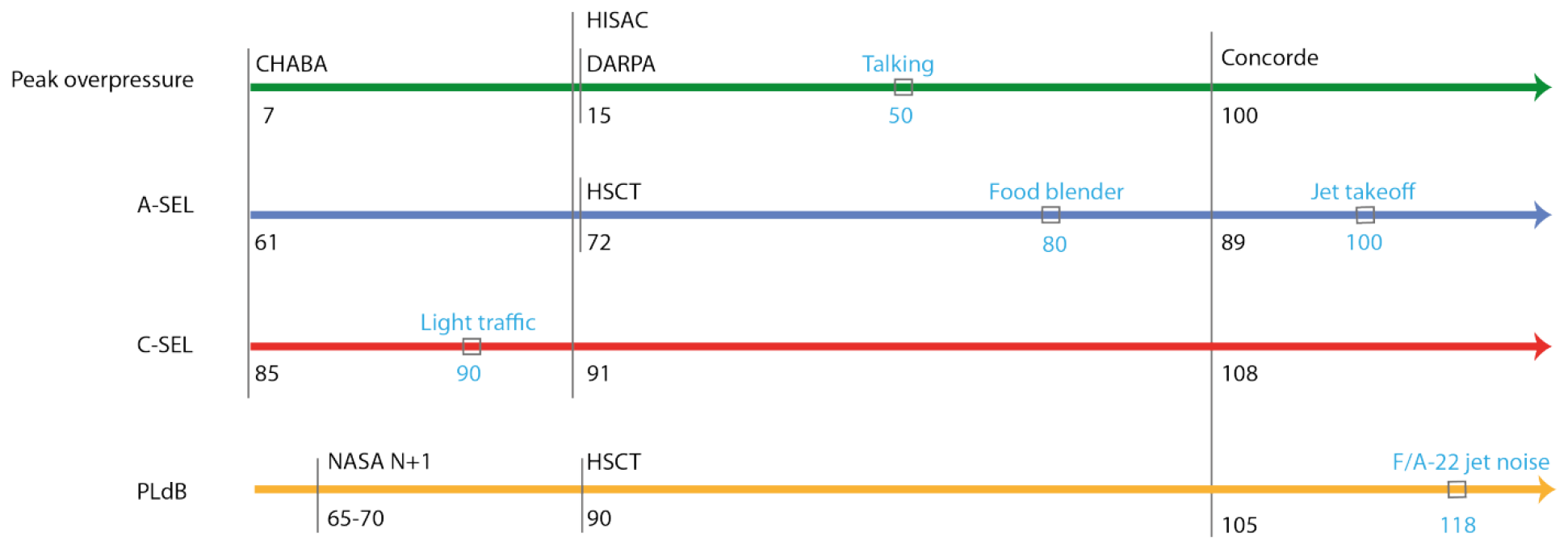
2.2. Loudness and Annoyance Metrics
2.3. Minimization Theory and Techniques
2.4. Critical Review
3. Sonic Boom Reduction
3.1. Aircraft Operations
3.2. Aircraft Configurations for Low Boom
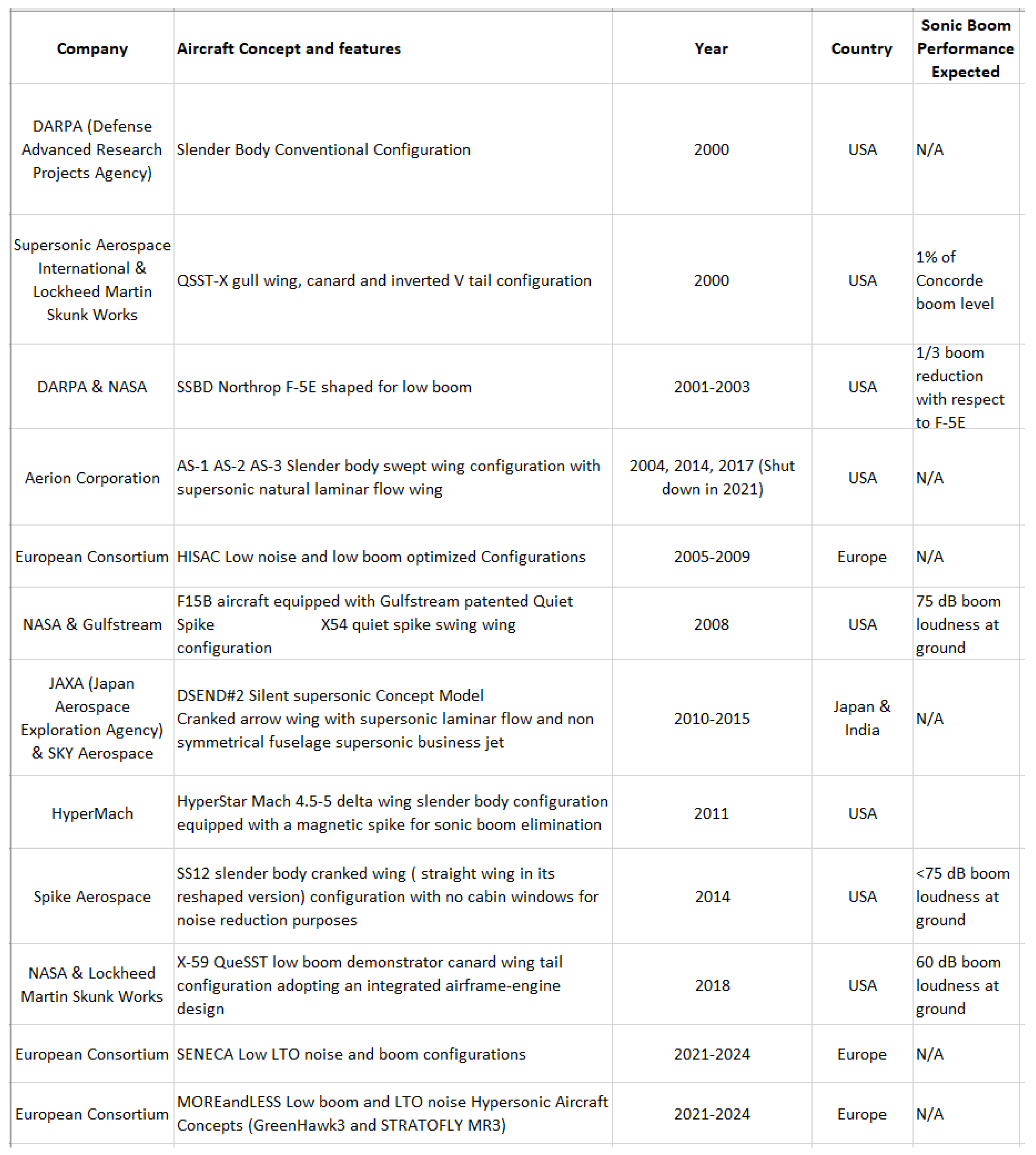
3.2.1. Current Promising Concepts
3.2.2. Forward-Swept Wing Configuration
3.2.3. Oblique Wing Configuration
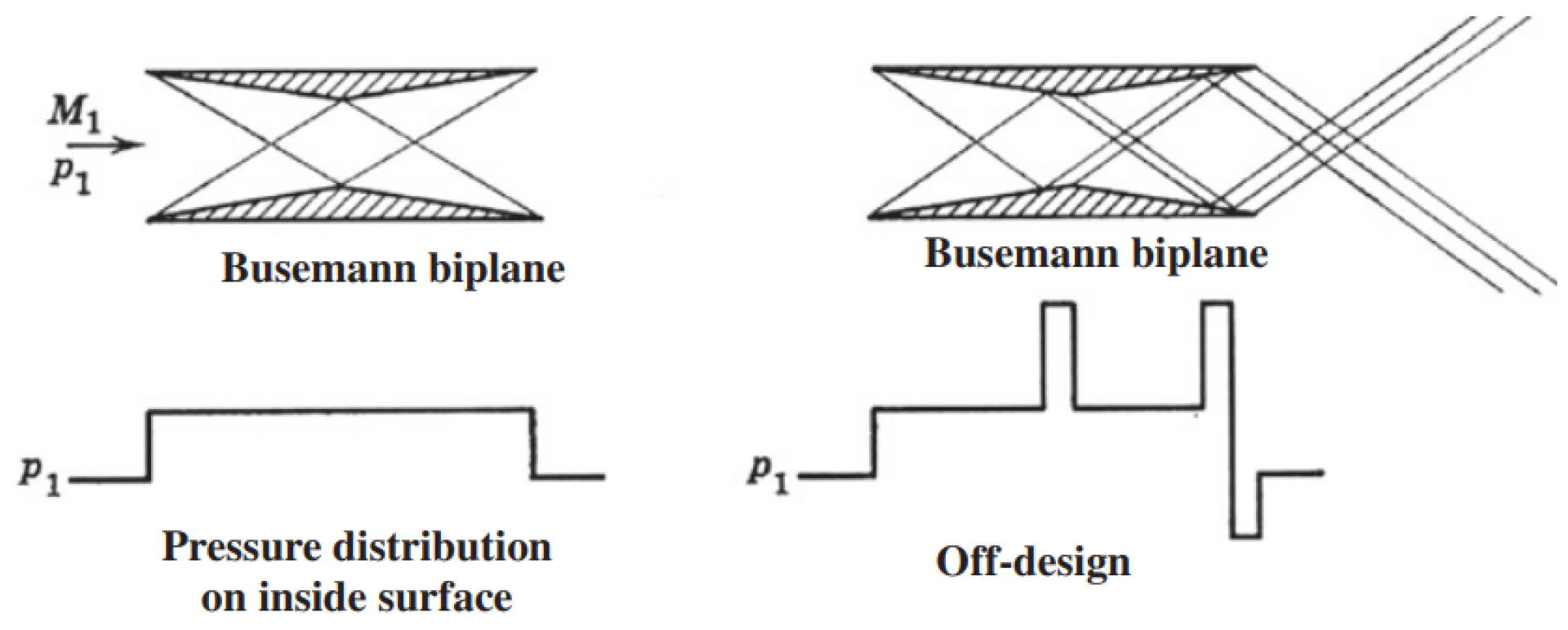
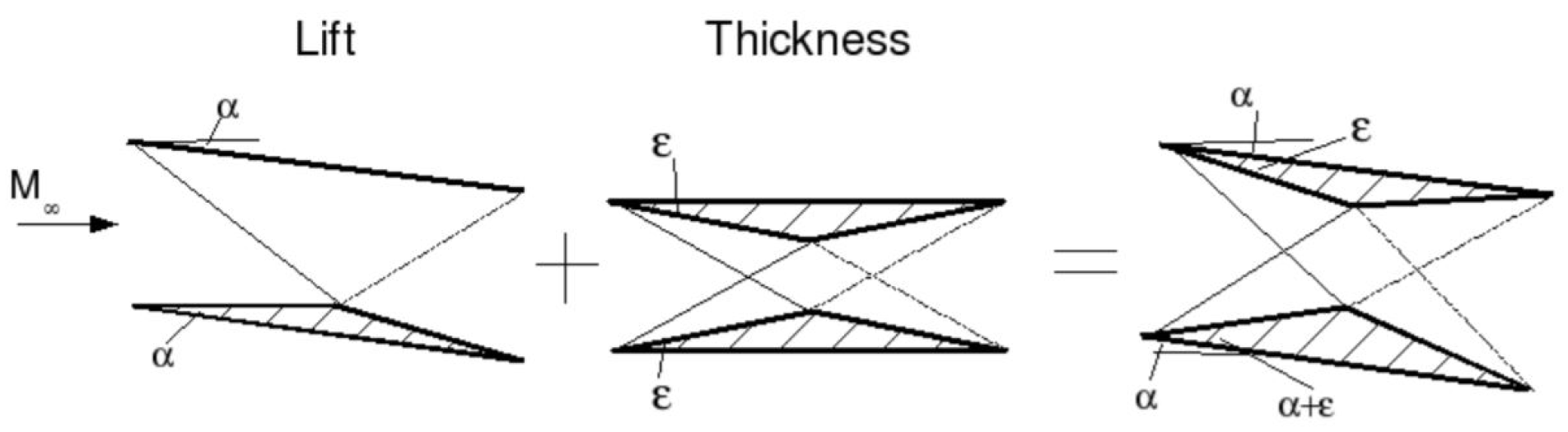
3.2.4. Supersonic Biplane
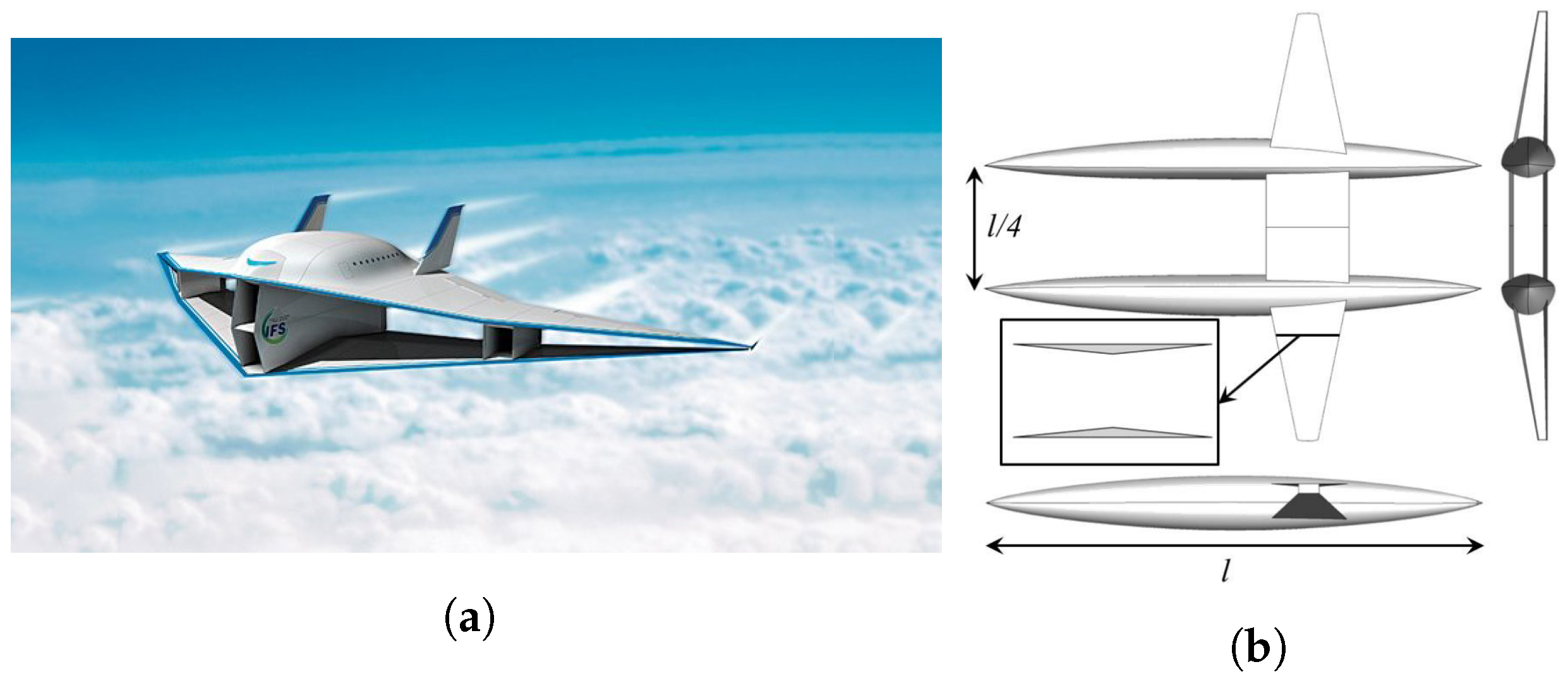
3.2.5. Supersonic Bi-Directional Flying Wing
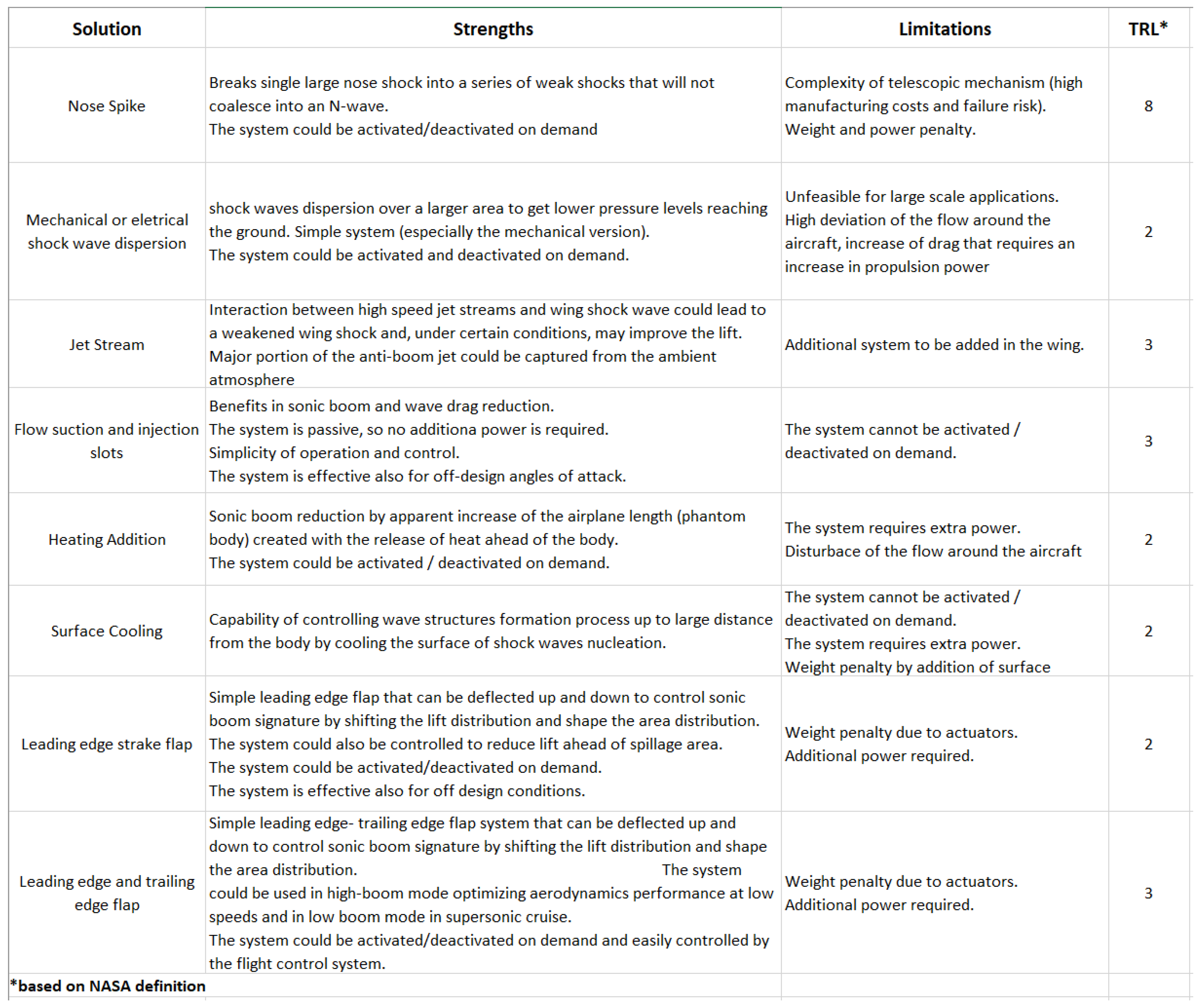
3.3. Noise Reduction Systems and Technologies
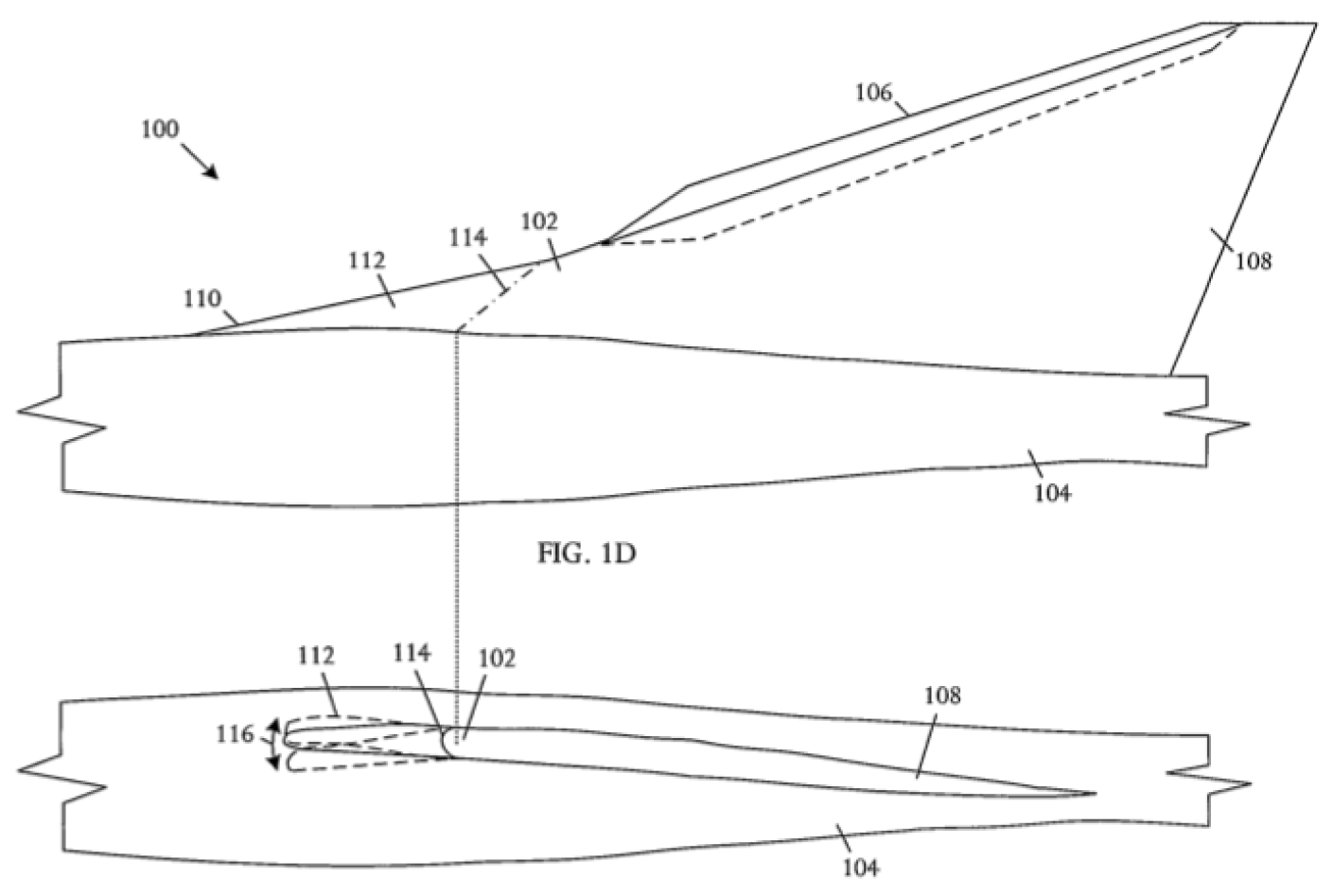
3.3.1. Nose Spike
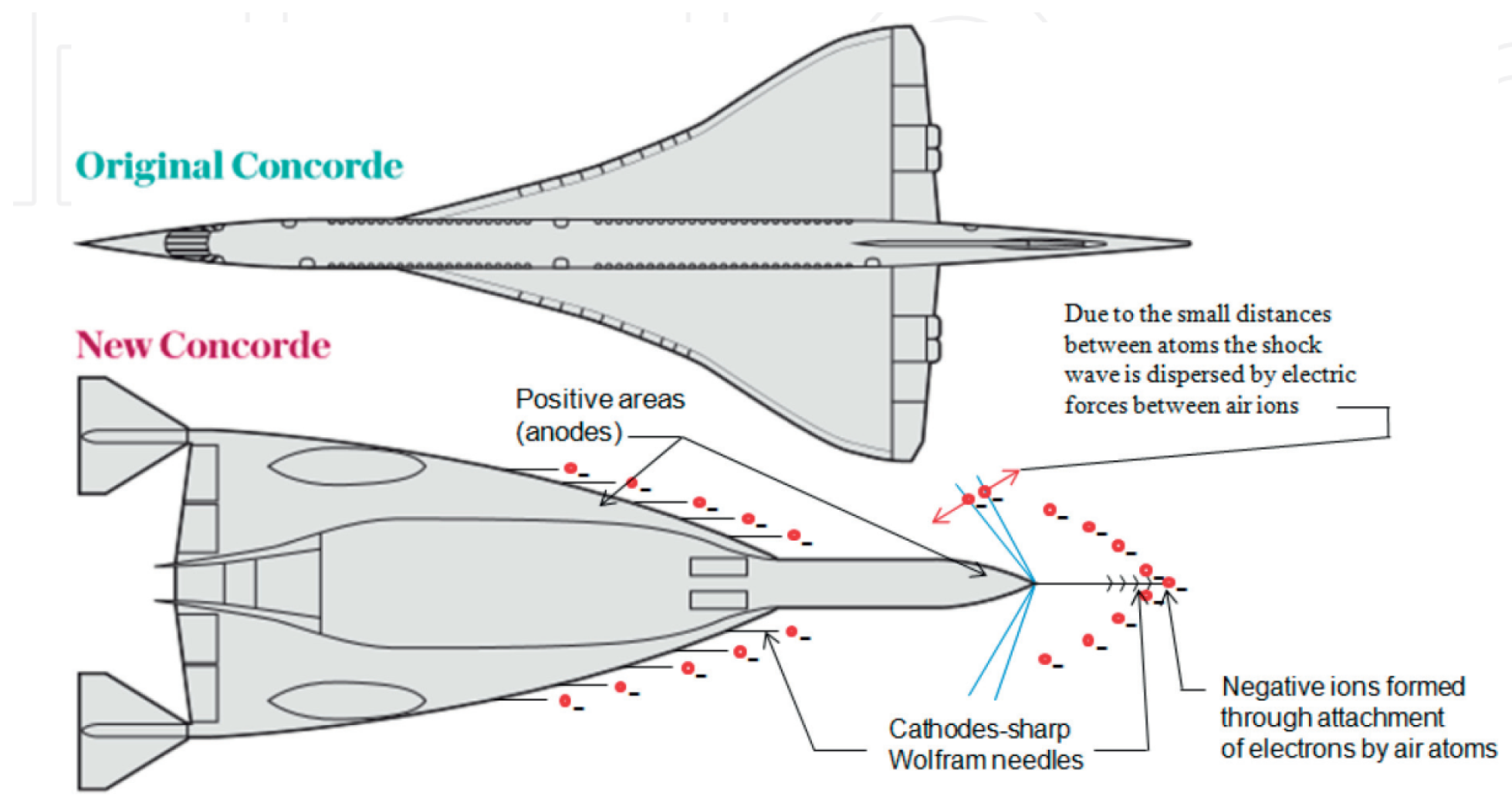
3.3.2. Shock Wave Dispersion
3.3.3. Jet Stream
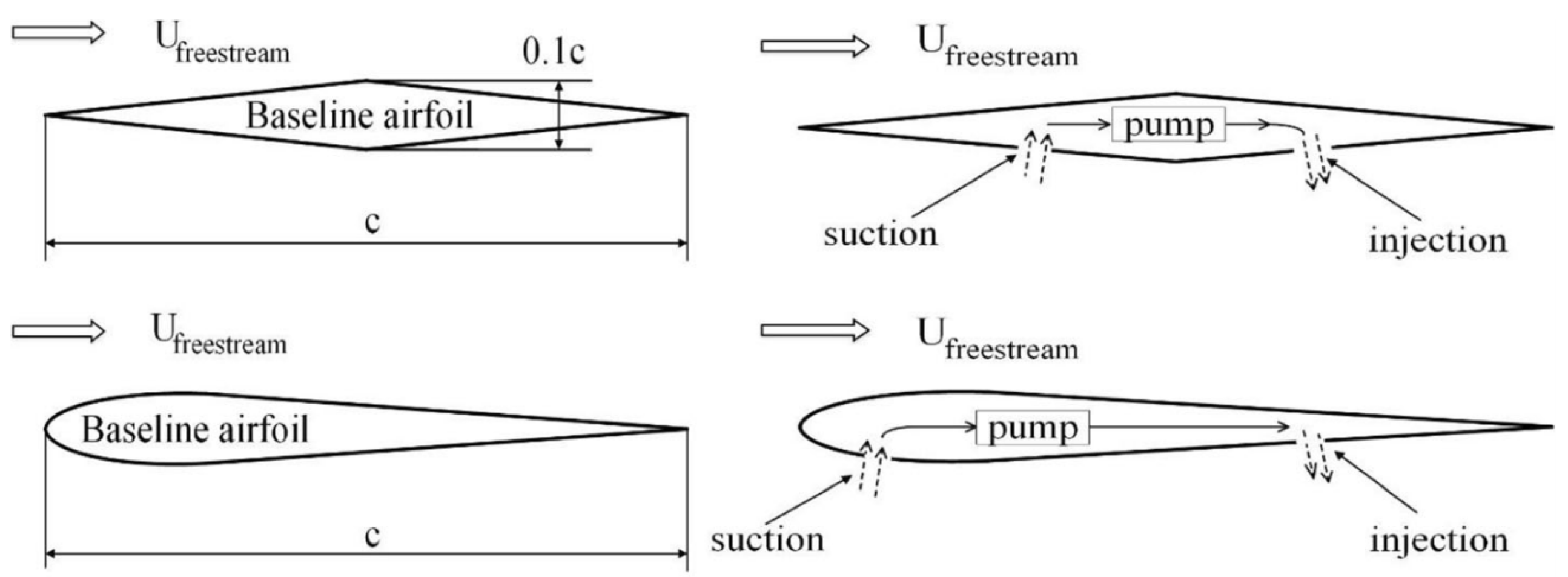
3.3.4. Flow Suction and Injection
3.3.5. Energy and Heating Addition/Cooling
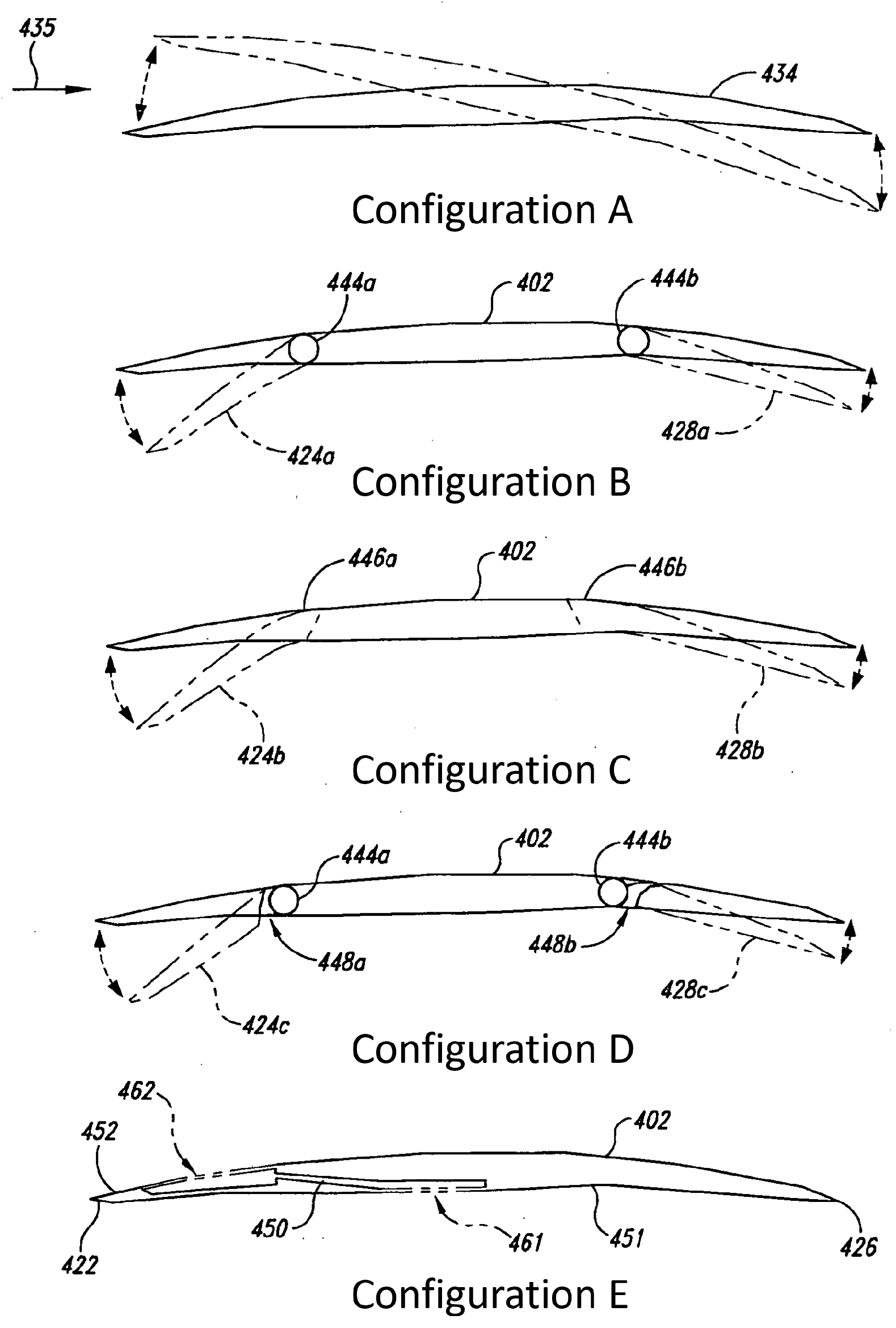
3.3.6. Control Lift Devices
3.4. Critical Review
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- National Air and Space Museum. Available online: https://airandspace.si.edu/collection-objects/bell-x-1 (accessed on 18 October 2023).
- Gibbs, Y. Nasa Armstrong Fact Sheet: Sonic Booms. Available online: https://www.nasa.gov/centers/armstrong/news/FactSheets/FS-016-DFRC.html (accessed on 18 October 2023).
- Coulouvrat, F. The challenges of defining an acceptable sonic boom overland. In Proceedings of the 15th AIAA/CEAS Aeroacoustics Conference (30th AIAA Aeroacoustics Conference), Miami, FL, USA, 11–13 May 2009; p. 3384. [Google Scholar]
- Manci, K.M. Effects of Aircraft Noise and Sonic Booms on Domestic Animals and Wildlife: A Literature Synthesis; US Fish and Wildlife Service, National Ecology Research Center: Oxford, OH, USA, 1988; Volume 88.
- Darden, C.M. Sonic boom theory: Its status in prediction and minimization. J. Aircr. 1977, 14, 569–576. [Google Scholar] [CrossRef]
- FAQBite. What is a Sonic Boom? Available online: https://faqbite.com/what/what-is-a-sonic-boom/ (accessed on 18 October 2023).
- Mabry, J.; Oncley, P. Establishing Certification/Design Criteria for Advanced Supersonic Aircraft Utilizing Acceptance, Interference, and Annoyance Response to Simulated Sonic Booms by Persons in Their Homes; Technical Report; Man-Acoustics And Noise Inc.: Seattle, WA, USA, 1973. [Google Scholar]
- Liu, S.R.; Tong, B. International Civil Aviation Organization Supersonic Task Group overview and status. J. Acoust. Soc. Am. 2017, 141, 3566. [Google Scholar] [CrossRef]
- FAA. Supersonic Flight. Available online: https://www.faa.gov/newsroom/supersonic-flight?newsId=22754 (accessed on 18 October 2023).
- Plotkin, K.J. State of the art of sonic boom modeling. J. Acoust. Soc. Am. 2002, 111, 530–536. [Google Scholar] [CrossRef] [PubMed]
- Abraham, T.A. Sonic Boom Loudness Reduction Through Localized Supersonic Aircraft Equivalent-Area Changes. Ph.D Thesis, Utah State University, Logan, UT, USA, 2021. [Google Scholar]
- Whitham, G.B. The flow pattern of a supersonic projectile. Commun. Pure Appl. Math. 1952, 5, 301–348. [Google Scholar] [CrossRef]
- Whitham, G. On the propagation of weak shock waves. J. Fluid Mech. 1956, 1, 290–318. [Google Scholar] [CrossRef]
- Hayes, W.D. Linearized supersonic flow. Ph.D Thesis, California Institute of Technology, Pasadena, CA, USA, 1947. [Google Scholar]
- Jones, R. Theory of Wing-Body Drag at Supersonic Speeds; (No. NACA-TR-1284); NASA: Washington, DC, USA, 1956.
- Whitcomb, R.T.; Fiscetti, T.L. Development of a Supersonic Area Rule and an Application to the Design of a Wing-Body Combination Having High Lift-to-Drag Ratios; (No. NACA-RM-L53H31a); NASA: Washington, DC, USA, 1953.
- Blokhintzev, D. The propagation of sound in an inhomogeneous and moving medium I. J. Acoust. Soc. Am. 1946, 18, 322–328. [Google Scholar] [CrossRef]
- Carlson, H.W.; Maglieri, D.J. Review of sonic-boom generation theory and prediction methods. J. Acoust. Soc. Am. 1972, 51, 675–685. [Google Scholar] [CrossRef]
- Lomax, H. The Wave Drag of Arbitrary Configurations in Linearized Flow as Determined by Areas and Forces in Oblique Planes; National Advisory Committee for Aeronautics: Hampton, VA, USA, 1955.
- Walkden, F. The shock pattern of a wing-body combination, far from the flight path. Aeronaut. Q. 1958, 9, 164–194. [Google Scholar] [CrossRef]
- Carlson, H.W. An Investigation of Some Aspects of the Sonic Boom by Means of Wind-Tunnel Measurements of Pressures about Several Bodies at a Mach Number of 2.01; National Aeronautics and Space Administration: Hampton, VA, USA, 1959; Volume 161.
- Lina, L.J.; Maglieri, D.J. Ground Measurements of Airplane Shock-Wave Noise at Mach Numbers to 2.0 and at Altitudes to 60,000 Feet; National Aeronautics and Space Administration: Hampton, VA, USA, 1960; Volume 235.
- Smith, H.J. Experimental and Calculated Flow Fields Produced by Airplanes Flying at Supersonic Speeds; National Aeronautics and Space Administration: Hampton, VA, USA, 1960; Volume 621.
- Haefeli, R.; Hayes, W.; Kulsrud, H. Sonic Boom Propagation in a Stratified Atmosphere, with Computer Program; Technical Report; NASA: Hampton, VA, USA, 1969.
- THOMAS, C. Extrapolation of Sonic Boom Pressure Signatures by the Waveform Parameter Method (Extrapolation of Sonic Boom Pressure Signatures by Waveform Parameter Method and Comparison with F-Function Method); No. A-4232; NASA: Washington, DC, USA, 1972.
- Thomas, C.L. Extrapolation of Wind-Tunnel Sonic Boom Signatures without Use of a Whitham F-Function; NASA SP-255; NASA: Washington, DC, USA, 1970; pp. 205–217. [Google Scholar]
- Plotkin, K.J.; Downing, M.; Page, J. USAF single event sonic boom prediction model: PCBOOM. J. Acoust. Soc. Am. 1994, 95, 2839. [Google Scholar] [CrossRef]
- Plotkin, K.J. Pcboom3 Sonic Boom Prediction Model-Version 1.0 c; Technical Report; Wyle Research Lab.: Arlington, VA, USA, 1996. [Google Scholar]
- George, A.; Plotkin, K. Sonic Boom Amplitudes and Waveforms in a Real Atmosphere. AIAA J. 1969, 7, 1978–1981. [Google Scholar] [CrossRef]
- Carlson, H.W. Simplified Sonic-Boom Prediction; Technical Report; NASA: Hampton, VA, USA, 1978.
- Scarselli, G.; Marulo, F.; Averardo, M.; Cafiero, A.; Selmin, V. Numerical comparison between a siimplified method and a full CFD approach for sonic boom evaluation on supersonic innovative configurations. In Proceedings of the 13th AIAA/CEAS Aeroacoustics Conference (28th AIAA Aeroacoustics Conference), Southampton, UK, 14–17 June 2022; p. 3675. [Google Scholar]
- Clare, A.; Oman, R. Sonic Boom Prediction: A New Empirical Formulation and Animated Graphical Model. In Transformational Science And Technology For The Current And Future Force: (With CD-ROM); World Scientific: Singapore, 2006; pp. 565–572. [Google Scholar]
- Lee, R.; Downing, J. Sonic Booms Produced by United States Air Force and United States Navy Aircraft: Measured Data; Technical Report; Armstrong Lab.: Brooks Afb, TX, USA, 1991. [Google Scholar]
- Plotkin, K. Review of sonic boom theory. In Proceedings of the 12th Aeroacoustic Conference, San Antonio, TX, USA, 10–12 April 1989; p. 1105. [Google Scholar]
- McLean, F.E. Some Nonasymptotic Effects on the Sonic Boom of Large Airplanes; National Aeronautics and Space Administration: Hampton, VA, USA, 1965; Volume 2877.
- Jung, T.P.; Starkey, R.P.; Argrow, B. Modified linear theory sonic booms compared to experimental and numerical results. J. Aircr. 2015, 52, 1821–1837. [Google Scholar] [CrossRef]
- Page, J.; Plotkin, K. An efficient method for incorporating computational fluid dynamics into sonic boom prediction. In Proceedings of the 9th Applied Aerodynamics Conference, Baltimore, MD, USA, 23–25 September 1991; p. 3275. [Google Scholar]
- Siclari, M.; Darden, C. Euler code prediction of near-field to midfield sonic boom pressure signatures. J. Aircr. 1993, 30, 911–917. [Google Scholar] [CrossRef]
- Cheung, S.; Edwards, T.; Lawrence, S. Application of CFD to Sonic Boom Near and Mid flow-field prediction. In Proceedings of the 13th Aeroacoustics Conference, Washington, DC, USA, 5 June 1990; p. 3999. [Google Scholar]
- Cliff, S.E.; Thomas, S.D. Euler/experiment correlations of sonic boom pressure signatures. J. Aircr. 1993, 30, 669–675. [Google Scholar] [CrossRef]
- Wintzer, M.; Ordaz, I. Under-Track CFD-Based Shape Optimization for a Low-Boom Demonstrator Concept. In Proceedings of the 33rd AIAA Applied Aerodynamics Conference, Dallas, TX, USA, 22–26 June 2015; p. 2260. [Google Scholar]
- Heath, C.M.; Slater, J.W.; Rallabhandi, S.K. Inlet trade study for a low-boom aircraft demonstrator. J. Aircr. 2017, 54, 1283–1293. [Google Scholar] [CrossRef]
- Plotkin, K.; Page, J. Extrapolation of sonic boom signatures from CFD solutions. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 14–17 January 2002; p. 922. [Google Scholar]
- Rallabhandi, S.K.; Mavris, D.N. New computational procedure for incorporating computational fluid dynamics into sonic boom prediction. J. Aircr. 2007, 44, 1964–1971. [Google Scholar] [CrossRef]
- Ordaz, I.; Li, W. Using CFD Surface Solutions to Shape Sonic Boom Signatures Propagated from Off-Body Pressure. In Proceedings of the 31st AIAA Applied Aerodynamics Conference, San Diego, CA, USA, 24–27 June 2013; p. 2660. [Google Scholar]
- Giblette, T.; Hunsaker, D.F. Prediction of sonic boom loudness using high-order panel methods for the near-field solution. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; p. 0605. [Google Scholar]
- Ehlers, F.; Johnson, F.; Rubbert, P. A higher order panel method for linearized supersonic flow. In Proceedings of the 9th Fluid and PlasmaDynamics Conference, Williamsburg, VA, USA, July 1979; p. 381. [Google Scholar]
- Choi, S.; Alonso, J.J.; Kroo, I.M. Two-level multifidelity design optimization studies for supersonic jets. J. Aircr. 2009, 46, 776–790. [Google Scholar] [CrossRef]
- Chan, M.K.Y. Supersonic Aircraft Optimization for Minimizing Drag and Sonic Boom; Stanford University: Stanford, CA, USA, 2003. [Google Scholar]
- Rallabhandi, S.; Mavris, D. Design and analysis of supersonic business jet concepts. In Proceedings of the 6th AIAA Aviation Technology, Integration and Operations Conference (ATIO), Wichita, KS, USA, 25–27 September 2006; p. 7702. [Google Scholar]
- Ueno, A.; Kanamori, M.; Makino, Y. Multi-fidelity low-boom design based on near-field pressure signature. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; p. 2033. [Google Scholar]
- Rallabhandi, S.K. Advanced sonic boom prediction using the augmented Burgers equation. J. Aircr. 2011, 48, 1245–1253. [Google Scholar] [CrossRef]
- Cleveland, R.O. Propagation of Sonic Booms through a Real, Stratified Atmosphere. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 1995. [Google Scholar]
- Robinson, L.D. Sonic Boom Propagation through an Inhomogeneous, Windy Atmosphere. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 1991. [Google Scholar]
- Pilon, A.R. Spectrally accurate prediction of sonic boom signals. AIAA J. 2007, 45, 2149–2156. [Google Scholar] [CrossRef]
- Lonzaga, J.B. Recent Enhancements to NASA’ s PCBoom Sonic Boom Propagation Code. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; p. 3386. [Google Scholar]
- Yamamoto, M.; Hashimoto, A.; Aoyama, T.; Sakai, T. A unified approach to an augmented Burgers equation for the propagation of sonic booms. J. Acoust. Soc. Am. 2015, 137, 1857–1866. [Google Scholar] [CrossRef]
- Ozcer, I. Sonic boom prediction using Euler/full potential methodology. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007; p. 369. [Google Scholar]
- Stout, T.A. Simulation of N-Wave and Shaped Supersonic Signature Turbulent Variations. Ph.D. Thesis, The Pennsylvania State University, State College, PA, USA, 2018. [Google Scholar]
- Crow, S. Distortion of sonic bangs by atmospheric turbulence. J. Fluid Mech. 1969, 37, 529–563. [Google Scholar] [CrossRef]
- Pierce, A.D. Statistical theory of atmospheric turbulence effects on sonic-boom rise times. J. Acoust. Soc. Am. 1971, 49, 906–924. [Google Scholar] [CrossRef]
- Pierce, A.D.; Maglieri, D.J. Effects of atmospheric irregularities on sonic-boom propagation. J. Acoust. Soc. Am. 1972, 51, 702–721. [Google Scholar] [CrossRef]
- Plotkin, K.J.; George, A. Propagation of weak shock waves through turbulence. J. Fluid Mech. 1972, 54, 449–467. [Google Scholar] [CrossRef]
- Blanc-Benon, P.; Lipkens, B.; Dallois, L.; Hamilton, M.F.; Blackstock, D.T. Propagation of finite amplitude sound through turbulence: Modeling with geometrical acoustics and the parabolic approximation. J. Acoust. Soc. Am. 2002, 111, 487–498. [Google Scholar] [CrossRef] [PubMed]
- Averiyanov, M.; Blanc-Benon, P.; Cleveland, R.O.; Khokhlova, V. Nonlinear and diffraction effects in propagation of N-waves in randomly inhomogeneous moving media. J. Acoust. Soc. Am. 2011, 129, 1760–1772. [Google Scholar] [CrossRef] [PubMed]
- Bradley, K.A.; Hobbs, C.M.; Wilmer, C.B.; Sparrow, V.W.; Stout, T.A.; Morgenstern, J.M.; Underwood, K.H.; Maglieri, D.J.; Cowart, R.A.; Collmar, M.T.; et al. Sonic Booms in Atmospheric Turbulence (SONICBAT): The Influence of Turbulence on Shaped Sonic Booms; (No. NASA/CR–2020–220509); NASA: Washington, DC, USA, 2020.
- Locey, L.L. Sonic Boom Postprocessing Functions to Simulate Atmospheric Turbulence Effects; The Pennsylvania State University: State College, PA, USA, 2008. [Google Scholar]
- Luquet, D. 3D Simulation of Acoustical Shock Waves Propagation through a Turbulent Atmosphere. Application to Sonic Boom. Ph.D Thesis, Université Pierre et Marie Curie, Paris, France, 2016. [Google Scholar]
- Dagrau, F.; Rénier, M.; Marchiano, R.; Coulouvrat, F. Acoustic shock wave propagation in a heterogeneous medium: A numerical simulation beyond the parabolic approximation. J. Acoust. Soc. Am. 2011, 130, 20–32. [Google Scholar] [CrossRef]
- Kanamori, M.; Takahashi, T.; Naka, Y.; Makino, Y.; Takahashi, H.; Ishikawa, H. Numerical Evauation of Effect of Atmospheric Turbulence on Sonic Boom Observed in D-SEND# 2 Flight Test. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; p. 0278. [Google Scholar]
- Kanamori, M.; Takahashi, T.; Ishikawa, H.; Makino, Y.; Naka, Y.; Takahashi, H. Numerical Evaluation of Sonic Boom Deformation due to Atmospheric Turbulence. AIAA J. 2021, 59, 972–986. [Google Scholar] [CrossRef]
- Leconte, R.; Marchiano, R.; Coulouvrat, F.; Chassaing, J.C. Influence of atmospheric turbulence parameters on the propagation of sonic boom. In Proceedings of the Forum Acusticum, Lyon, France, 7–11 December 2021; pp. 979–980. [Google Scholar]
- Kandil, O.; Ozcer, I.; Khasdeo, N. Sonic Boom Prediction, Focusing, and Mitigation. In Proceedings of the 2S Congress of the Aeronautical Sciences 2006, Hamburg, Germany, 3–8 September 2006. [Google Scholar]
- Griffiths, G.W.; Schiesser, W.E. Linear and nonlinear waves. Scholarpedia 2009, 4, 4308. [Google Scholar] [CrossRef]
- Van Hove, B.; Lofqvist, M.; Bonetti, D.; Kokorich, M. Reducing the Noise of Hypersonic Aircraft. 2023. Available online: https://www.researchgate.net/publication/367966282_Reducing_the_Noise_of_Hypersonic_Aircraft (accessed on 18 October 2023).
- Guiraud, J.P. Acoustique geometrique bruit balistique des avions supersoniques et focalisation. J. Mec. 1965, 4, 215. [Google Scholar]
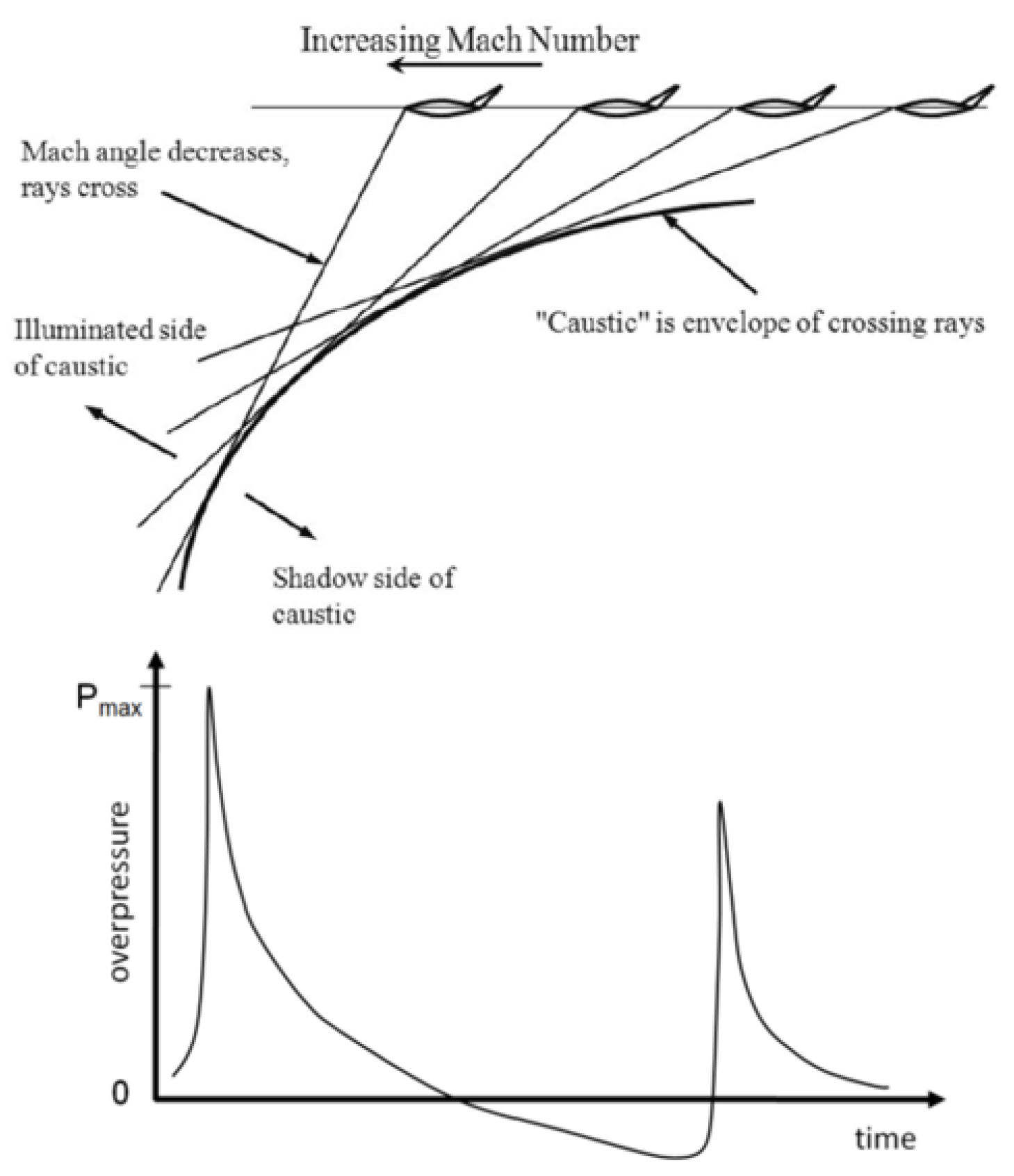
- Seebass, R. Nonlinear Acoustic Behavior at a Caustic; Technical Report; Boeing Scientific Research Labs.: Seattle, WA, USA, 1971. [Google Scholar]
- Gill, P.; Seebass, A. Nonlinear Acoustic Behavior at a Caustic-An Approximate Analytical Solution. In Aeroacoustics: Fan; MIT Press: Cambridge, MA, USA, 1975; pp. 353–386. [Google Scholar]
- Plotkin, K.; Cantril, J. Prediction of sonic boom at a focus. In Proceedings of the 14th Aerospace Sciences Meeting, Washington, DC, USA, 26–28 January 1976; p. 2. [Google Scholar]
- Marchiano, R.; Coulouvrat, F.; Grenon, R. Numerical simulation of shock wave focusing at fold caustics, with application to sonic boom. J. Acoust. Soc. Am. 2003, 114, 1758–1771. [Google Scholar] [CrossRef]
- Auger, T.; Coulouvrat, F. Numerical simulation of sonic boom focusing. AIAA J. 2002, 40, 1726–1734. [Google Scholar] [CrossRef]
- Kandil, O.; Zheng, X. Prediction of Superboom Problem Using Computational Solution of Nonlinear Tricomi Equation. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, San Francisco, CA, USA, 15–18 August 2005; p. 6335. [Google Scholar]
- Kandil, O.; Zheng, X. Computational solution of nonlinear Tricomi equation for sonic boom focusing and applications. In Proceedings of the AIP Conference Proceedings. American Institute of Physics, Mexico City, Mexico, 10–14 July 2006; Volume 838, pp. 607–610. [Google Scholar]
- Piacsek, A.A. A Numerical Study of Weak Step Shocks That Focus in Two Dimensions. Ph.D. Thesis, The Pennsylvania State University, State College, PA, USA, 1995. [Google Scholar]
- Piacsek, A.A. Atmospheric turbulence conditions leading to focused and folded sonic boom wave fronts. J. Acoust. Soc. Am. 2002, 111, 520–529. [Google Scholar] [CrossRef] [PubMed]
- Loubeau, A. Recent progress on sonic boom research at NASA. In Proceedings of the INTER-NOISE and NOISE-CON Congress and Conference Proceedings. Institute of Noise Control Engineering, New York City, NY, USA, 19–22 August 2012; Volume 2012, pp. 3760–3770. [Google Scholar]
- Taylor, A.D. The TRAPS Sonic Boom Program; Department of Commerce, National Oceanic and Atmospheric Administration: Washington, DC, USA, 1980; Volume 87.
- Rallabhandi, S.; Fenbert, J. Numerical simulation of sonic boom focusing and its application to mission performance. J. Acoust. Soc. Am. 2017, 141, 3566. [Google Scholar] [CrossRef]
- E. U. Rumble. H2020. Available online: https://rumble-project.eu/i/dissemination/conference-presentations (accessed on 18 October 2023).
- Töpken, S.; van de Par, S. Loudness and short-term annoyance of sonic boom signatures at low levels. J. Acoust. Soc. Am. 2021, 149, 2004–2015. [Google Scholar] [CrossRef] [PubMed]
- Marshall, A.; Davies, P. A semantic differential study of low amplitude supersonic aircraft noise and other transient sounds. In Proceedings of the International Congress on Acoustics, Madrid, Spain, 2–7 September 2007; pp. 1–6. [Google Scholar]
- Marshall, A.; Davies, P. A comparison of perceptual attributes and ratings of environmental transient sounds in two different playback environments. In Proceedings of the INTER-NOISE and NOISE-CON Congress and Conference Proceedings. Institute of Noise Control Engineering, Shanghai, China, 26–29 October 2008; Volume 2008, pp. 5586–5592. [Google Scholar]
- Marshall, A.; Davies, P. Metrics including time-varying loudness models to assess the impact of sonic booms and other transient sounds. Noise Control. Eng. J. 2011, 59, 681–697. [Google Scholar] [CrossRef]
- Glasberg, B.R.; Moore, B.C. A model of loudness applicable to time-varying sounds. J. Audio Eng. Soc. 2002, 50, 331–342. [Google Scholar]
- Zwicker, E.; Fastl, H. Psychoacoustics: Facts and Models; Springer Science & Business Media: Berlin, Germany, 2013; Volume 22. [Google Scholar]
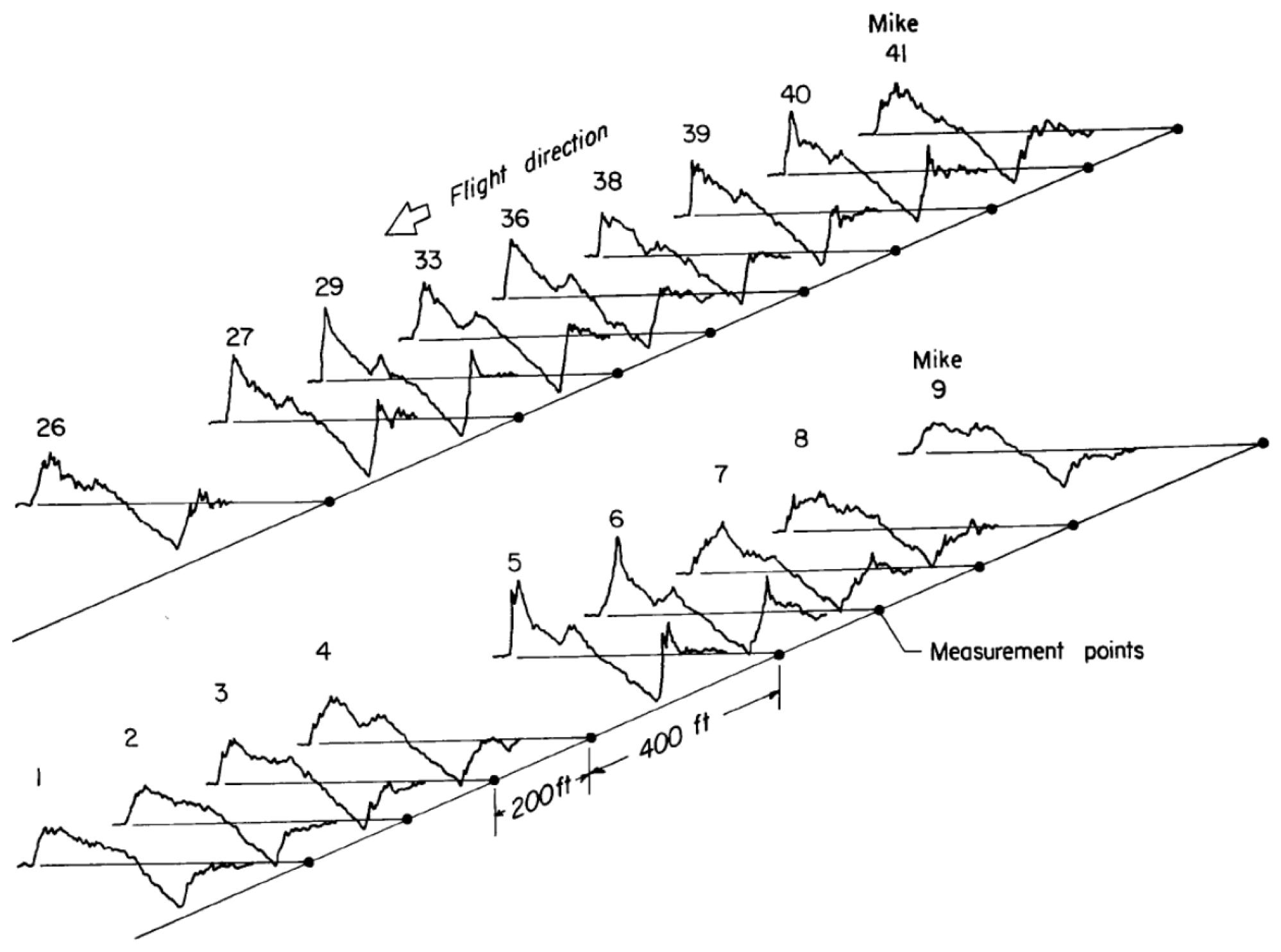
- Maglieri, D.J.; Huckel, V.; Henderson, H.R. Variability in Sonic Boom Signatures Measured Along an 8000-Foot Linear Array; National Aeronautics and Space Administration: Washington, DC, USA, 1969; Volume 5040.
- Doebler, W.J.; Sparrow, V.W. Stability of sonic boom metrics regarding signature distortions from atmospheric turbulence. J. Acoust. Soc. Am. 2017, 141, EL592–EL597. [Google Scholar] [CrossRef]
- Leatherwood, J.D.; Sullivan, B.M. Loudness and Annoyance Response to Simulated Outdoor and Indoor Sonic Booms; No. NASA-TM-107756; NASA: Washington, DC, USA, 1993.
- Stevens, S.S. Perceived level of noise by Mark VII and decibels (E). J. Acoust. Soc. Am. 1972, 51, 575–601. [Google Scholar] [CrossRef]
- Borsky, P.N.; York, N.O.R.C.N. Community Reactions to Sonic Booms in the Oklahoma City Area: Volume 2. Data on Community Reactions and Interpretations; Aerospace Medical Research Laboratories: Brooks AFB, TX, USA, 1965. [Google Scholar]
- Clarkson, B.L.; Mayes, W.H. Sonic-Boom-Induced Building Structure Responses Including Damage. J. Acoust. Soc. Am. 1972, 51, 742–757. [Google Scholar] [CrossRef]
- Sizov, N.V.; Plotkin, K.J.; Hobbs, C.M. Predicting transmission of shaped sonic booms into a residential house structure. J. Acoust. Soc. Am. 2010, 127, 3347–3355. [Google Scholar] [CrossRef]
- Minelli, A. Aero-Acoustic Shape Optimization of a Supersonic Business Jet. Ph.D. Thesis, Université Nice Sophia Antipolis, Nice, France, 2013. [Google Scholar]
- Jones, L. Lower bounds for sonic bangs. Aeronaut. J. 1961, 65, 433–436. [Google Scholar] [CrossRef]
- Carlson, H.W. The Lower Bound of Attainable Sonic-Boom Overpressure and Design Methods of Approaching This Limit; National Aeronautics and Space Administration: Washington, DC, USA, 1962. [Google Scholar]
- Carlson, H.W. Influence of airplane configuration on sonic-boom characteristics. J. Aircr. 1964, 1, 82–86. [Google Scholar] [CrossRef]
- Darden, C.M.; Powell, C.A.; Hayes, W.D.; George, A.R.; Pierce, A.D. Status of sonic boom methodology and understanding. In Proceedings of the Sonic Boom Workshop, Hampton, VA, USA, 1 June 1989. [Google Scholar]
- George, A.; Seebass, R. Sonic boom minimization including both front and rear shocks. AIAA J. 1971, 9, 2091–2093. [Google Scholar] [CrossRef]
- Seebass, R.; George, A.R. Sonic-Boom Minimization. J. Acoust. Soc. Am. 1972, 51, 686–694. [Google Scholar] [CrossRef]
- Darden, C.M. Sonic-Boom Minimization with Nose-Bluntness Relaxation; National Aeronautics and Space Administration, Scientific and Technical: Washington, DC, USA, 1979; Volume 1348.
- Carlson, H.W.; Barger, R.L.; Mack, R.J. Application of Sonic-Boom Minimization Concepts in Supersonic Transport Design; No. NASA-TN-D-7218; NASA: Washington, DC, USA, 1973.
- Mack, R.J. Wind-Tunnel Investigation of the Validity of a Sonic-Boom-Minimization Concept; NASA TP D-1421; NASA: Washington, DC, USA, 1979.
- Mack, R.J.; Needleman, K.E. A Methodology for Designing Aircraft to Low Sonic Boom Constraints; Technical Report; NASA: Washington, DC, USA, 1991.
- Rallabhandi, S.K.; Mavris, D.N. Aircraft geometry design and optimization for sonic boom reduction. J. Aircr. 2007, 44, 35–47. [Google Scholar] [CrossRef]
- Plotkin, K.; Rallabhandi, S.; Li, W. Generalized formulation and extension of sonic boom minimization theory for front and aft shaping. In Proceedings of the 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009; p. 1052. [Google Scholar]
- Jung, T.P.; Starkey, R.P.; Argrow, B. Lobe balancing design method to create frozen sonic booms using aircraft components. J. Aircr. 2012, 49, 1878–1893. [Google Scholar] [CrossRef]
- Farhat, C.; Argrow, B.; Nikbay, M.; Maute, K. Shape optimization with F-function balancing for reducing the sonic boom initial shock pressure rise. Int. J. Aeroacoustics 2004, 3, 361–377. [Google Scholar] [CrossRef]
- Minelli, A.; Salah el Din, I.; Carrier, G. Inverse design approach for low-boom supersonic configurations. AIAA J. 2014, 52, 2198–2212. [Google Scholar] [CrossRef]
- Wintzer, M.; Kroo, I.; Aftosmis, M.; Nemec, M. Conceptual design of low sonic boom aircraft using adjoint-based CFD. In Proceedings of the Seventh International Conference on Computational Fluid Dynamics (ICCFD7), Big Island, HI, USA, 9–13 July 2012. [Google Scholar]
- Feng, X.; Li, Z.; Song, B. Research of low boom and low drag supersonic aircraft design. Chin. J. Aeronaut. 2014, 27, 531–541. [Google Scholar] [CrossRef]
- Li, W.; Rallabhandi, S. Inverse design of low-boom supersonic concepts using reversed equivalent-area targets. J. Aircr. 2014, 51, 29–36. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, J.; Zhenghong, G.; Chao, W.; Bowen, S. Inverse design of low boom configurations using proper orthogonal decomposition and augmented Burgers equation. Chin. J. Aeronaut. 2019, 32, 1380–1389. [Google Scholar] [CrossRef]
- Li, W.; Geiselhart, K. Multidisciplinary design optimization of low-boom supersonic aircraft with mission constraints. AIAA J. 2021, 59, 165–179. [Google Scholar] [CrossRef]
- Goel, N.; Jawahar, S. Towards a Supersonic Transport: Minimization of Sonic Boom. J. Stud. Res. 2022, 11. [Google Scholar] [CrossRef]
- Maglieri, D.J.; Bobbitt, P.J.; Plotkin, K.J.; Shepherd, K.P.; Coen, P.G.; Richwine, D.M. Sonic Boom: Six Decades of Research; Special Publication (SP); NASA: Washington, DC, USA, 2014.
- Oceanic, U.S.N.; Administration, A.; Force, U.S.A. US Standard Atmosphere, 1976; National Oceanic and Atmospheric Administration: Washington, DC, USA, 1976; Volume 76.
- Page JA, L.A. Aircraft Noise Generation and Assessment Section 5-Overall Vehicle System Noise, Part d-Sonic Boom. CEAS Aeronaut J. 2019, 10, 335–353. [Google Scholar] [CrossRef] [PubMed]
- Cliatt, L.J.; Hill, M.A.; Haering, E. Mach cutoff analysis and results from NASA’s Farfield investigation of no-boom thresholds. In Proceedings of the 22nd AIAA/CEAS Aeroacoustics Conference, Lyon, France, 30 May–1 July 2016; p. 3011. [Google Scholar]
- Haering, E.A., Jr.; Smolka, J.W.; Murray, J.E.; Plotkin, K.J. Flight Demonstration Of Low Overpressure N-Wave Sonic Booms and Evanescent Waves. In Proceedings of the AIP American Institute of Physics, Mexico City, Mexico, 10–14 July 2006; Volume 838, pp. 647–650. [Google Scholar]
- Wlezien, R.; Veitch, L. Quiet Supersonic Platform Program Advanced algorithms for design and optimization of Quiet Supersonic Platforms. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 14–17 January 2002; p. 143. [Google Scholar]
- Security, G. Quiet Supersonic Platform (qsp). Available online: https://www.globalsecurity.org/military/systems/aircraft/qsp.htm (accessed on 18 October 2023).
- Komadina, S.; Drake, A.; Bruner, S. Development of a quiet supersonic aircraft with technology applications to military and civil Aircraft. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 14–17 January 2002; p. 519. [Google Scholar]
- NASA. Quiet Spike Project. Available online: https://www.nasa.gov/centers/dryden/multimedia/imagegallery/Quiet_Spike/Quiet_Spike_proj_desc.html (accessed on 18 October 2023).
- NASA. Shaped Sonic Boom Demonstration. Available online: https://www.nasa.gov/centers/dryden/multimedia/imagegallery/SSBD/SSBD_proj_desc.html (accessed on 18 October 2023).
- NASA. Nasa Investigates the ‘Faint’ Side of Sonic Booms. Available online: https://www.nasa.gov/topics/aeronautics/features/faint_sonic_booms.html (accessed on 18 October 2023).
- NASA. Nasa Quiet Sonic Boom Research Effort Ends with a Whisper. Available online: https://www.nasa.gov/centers/dryden/Features/WSPR_research_complete.html (accessed on 18 October 2023).
- Wikipedia. Available online: https://en.wikipedia.org/wiki/Gulfstream_X-54 (accessed on 18 October 2023).
- NASA. Nasa Chat: Taking the “Boom” Out of Booms. Available online: https://www.nasa.gov/connect/chat/sonic_boom_chat.html (accessed on 18 October 2023).
- Security, G. X-54 Relaxed Isentropic Compression. Available online: https://www.globalsecurity.org/military/systems/aircraft/x-54.htm (accessed on 18 October 2023).
- JAXA. D-Send Project(fy2010-fy2015). Available online: https://www.aero.jaxa.jp/eng/research/frontier/sst/d-send.html (accessed on 18 October 2023).
- Sakata, K. Japan’s supersonic technology and business jet perspectives. In Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013; p. 21. [Google Scholar]
- Sakata, K. Challenge for Supersonic Business Jet SKY Mobility Innovation 10/12/12. Available online: https://www.skyaero.jp/ja/research/challenge4ssbj.pdf (accessed on 18 October 2023).
- CORDIS. Environmentally Friendly High Speed Aircraft. Available online: https://cordis.europa.eu/project/id/516132 (accessed on 18 October 2023).
- CORDIS. HISAC Project Publishable Activity Report; Technical Report; CORDIS: Hialeah, FL, USA, 2008. [Google Scholar]
- CORDIS. Mdo and Regulations for Low-Boom and Environmentally Sustainable Supersonic Aviation. Available online: https://cordis.europa.eu/project/id/101006856 (accessed on 18 October 2023).
- Piccirillo, G.; Graziani, S.; Fusaro, R.; Viola, N. Lto noise and sonic boom predictions in early conceptual design phases. In Proceedings of the ICAS 2022, Stockholm, Sweden, 4–9 September 2022. [Google Scholar]
- Rodriguez, D. Propulsion/Airframe integration and optimization on a supersonic business jet. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007; p. 1048. [Google Scholar]
- Technology, A. The Aerion Super Sonic Business Jet Project, USA. Available online: https://www.aerospace-technology.com/projects/aerionsbjsupersonicb/ (accessed on 18 October 2023).
- Masunaga, S. To Get Supersonic Business Jets off the Ground, Aerion Corp. Is Building Planes that Don’t go ‘Boom’. Available online: https://www.latimes.com/business/la-fi-supersonic-aerion-20180911-story.html (accessed on 18 October 2023).
- Technology, A. Aerion as2 Supersonic Business Jet. Available online: https://www.aerospace-technology.com/projects/aerion-as2-supersonic-business-jet/ (accessed on 18 October 2023).
- Sampson, B. Aerion Supersonic Jet Developer Makes Key Appointments. Available online: https://www.businessairportinternational.com/news/aircraft/aerion-supersonic-jet-developer-makes-key-appointments.html (accessed on 18 October 2023).
- Academy, A.S. From Concorde to New Supersonic Aircraft Projects-Dossier 46. Available online: https://academieairespace.com/wp-content/uploads/2019/06/AAE_D46_UK_WEB.pdf (accessed on 18 October 2023).
- George, A. Supersonic Jet Ditches Windows for Massive Live-Streaming Screens. Available online: https://www.wired.com/2014/02/supersonic-jet-video-windows/ (accessed on 18 October 2023).
- Aerospace, S. Quiet & Sustainable Supersonic Flight. Available online: https://www.spikeaerospace.com/s-512-supersonic-jet/quiet-supersonic-flight/ (accessed on 18 October 2023).
- Technology, A. Spike s-512 Supersonic Business Jet. Available online: https://www.aerospace-technology.com/projects/spike-s-512-supersonic-business-jet/ (accessed on 18 October 2023).
- Staff, F. Spike Aerospace s-512 Quiet Supersonic Commercial Business Jet. Available online: https://sofrep.com/fightersweep/spike-aerospace-s-512-quiet-supersonic-commercial-business-jet/ (accessed on 18 October 2023).
- Supersonic, B. Supersonic Passenger Airplanes Boom Supersonic. 2020. Available online: https://boomsupersonic.com/ (accessed on 18 October 2023).
- Wikipedia. Boom Technology. Available online: https://en.wikipedia.org/wiki/Boom_Technology (accessed on 18 October 2023).
- Cook, M. Boom Enters Supersonic Air Force One Race. Available online: https://www.avweb.com/aviation-news/boom-enters-supersonic-air-force-one-race/ (accessed on 18 October 2023).
- Guardian, T. United Airlines Aims to Revive Concorde Spirit with Supersonic Planes. Available online: https://www.theguardian.com/business/2021/jun/03/united-airlines-boom-supersonic-overture-airliner-concorde (accessed on 18 October 2023).
- Supersonic, B. Overture. Available online: https://boomsupersonic.com/overture (accessed on 18 October 2023).
- Banke, J. New Nasa x-Plane Construction Begins Now. Available online: https://www.nasa.gov/lowboom/new-nasa-x-plane-construction-begins-now (accessed on 18 October 2023).
- Giangreco, L. Lockheed and Nasa Move toward Design Review for Supersonic x-Plane. Available online: https://www.flightglobal.com/helicopters/lockheed-and-nasa-move-toward-design-review-for-supersonic-x-plane/123441.article (accessed on 18 October 2023).
- Week, G.N.A.; Technology, S. Final Testing Will Clear Way for Assembly of Supersonic x-59a. Available online: https://aviationweek.com/air-transport/final-testing-will-clear-way-assembly-supersonic-x-59a (accessed on 18 October 2023).
- Gipson, L. Low-Boom Flight Demonstration. Available online: https://www.nasa.gov/mission_pages/lowboom/flights (accessed on 18 October 2023).
- Proponet. Lockheed Martin Begins Manufacturing, Commits to 3-Year Timeline for x-59 Quesst Low-Boom Demonstrator. Available online: https://www.proponent.com/lockheed-martin-manufacturing-x-59-quesst-low-boom-demonstrator/ (accessed on 18 October 2023).
- Wikipedia. Sai Quiet Supersonic Transport. Available online: https://en.wikipedia.org/wiki/SAI_Quiet_Supersonic_Transport#cite_note-popsci2007march-3 (accessed on 18 October 2023).
- Hagerman, E. All Sonic, no Boom. Available online: https://www.popsci.com/military-aviation-space/article/2007-03/all-sonic-no-boom/ (accessed on 18 October 2023).
- Trimble, S. Sai Resurrects Qsst-x as All-First Class Supersonic Airliner, Seeks Investors. Available online: https://www.flightglobal.com/sai-resurrects-qsst-x-as-all-first-class-supersonic-airliner-seeks-investors/110088.article (accessed on 18 October 2023).
- International, S.A. Quiet Supersonic Transport-x. Available online: https://sai-qsstx.com/ (accessed on 18 October 2023).
- Beautiful Life Online Magazine. Sai Quiet Supersonic Transport. Available online: https://www.beautifullife.info/automotive-design/sai-quiet-supersonic-transport/ (accessed on 18 October 2023).
- CNN, J.B. Race to be First with ‘Son of Supersonic’. Available online: http://edition.cnn.com/2011/TECH/innovation/06/21/concorde.hyper.sonic/index.html (accessed on 18 October 2023).
- AINonline, L.M. Paris 2011: HYPERSONIC Hyperbole. Available online: https://www.ainonline.com/aviation-news/business-aviation/2011-06-21/paris-2011-hypersonic-hyperbole (accessed on 18 October 2023).
- JetOptions. Hypermach Now Shooting for Mach 4.0 Business Jet. Available online: https://www.flyjetoptions.com/hypermach-now-shooting-for-mach-4-0-business-jet/ (accessed on 18 October 2023).
- Darren, Q. Hypermach Unveils Sonicstar Supersonic Business Jet Concept. Available online: https://newatlas.com/hypermach-sonicstar-ssbj-concept/18974/ (accessed on 18 October 2023).
- Security, G. Hypermach Aerospace Industries. Available online: https://www.globalsecurity.org/military/systems/aircraft/hypermach.htm (accessed on 18 October 2023).
- Trautvetter, C. Hypermach at ‘Pivotal Stage’ for Its Mach 5 Bizjet. Available online: https://www.ainonline.com/aviation-news/business-aviation/2016-11-01/hypermach-pivotal-stage-its-mach-5-bizjet (accessed on 18 October 2023).
- Gibbs, Y. Nasa Armstrong Fact Sheet: X-29 Advanced Technology Demonstrator Aircraft. Available online: https://www.nasa.gov/centers/armstrong/news/FactSheets/FS-008-DFRC.html (accessed on 18 October 2023).
- Wikimedia. Sukhoi su-47 in 2008. Available online: https://commons.wikimedia.org/wiki/File:Sukhoi_Su-47_in_2008.jpg (accessed on 18 October 2023).
- Winter, G. Kb Sat sr-10 ex-88004. Available online: https://www.flickr.com/photos/57931616@N03/36149040295 (accessed on 18 October 2023).
- Kishi, Y.; Makino, Y.; Kanazaki, M. Numerical Investigation of Sonic Boom for Forward-Swept Wing Based on Euler and Augmented Burgers Equations. Aerosp. Technol. Jpn. Jpn. Soc. Aeronaut. Space Sci. 2020, 19, 1–9. [Google Scholar] [CrossRef]
- Horinouchi, S. Variable Forward-Swept Wing Supersonic Aircraft Having Both Low-Boom Characteristics and Low-Drag Characteristics. U.S. Patent Application Number 11/103, 12 April 2005. p. 549. [Google Scholar]
- Raymer, D. Aircraft Design: A Conceptual Approach; American Institute of Aeronautics and Astronautics Inc.: Reston, VA, USA, 1992; pp. 515–552. [Google Scholar]
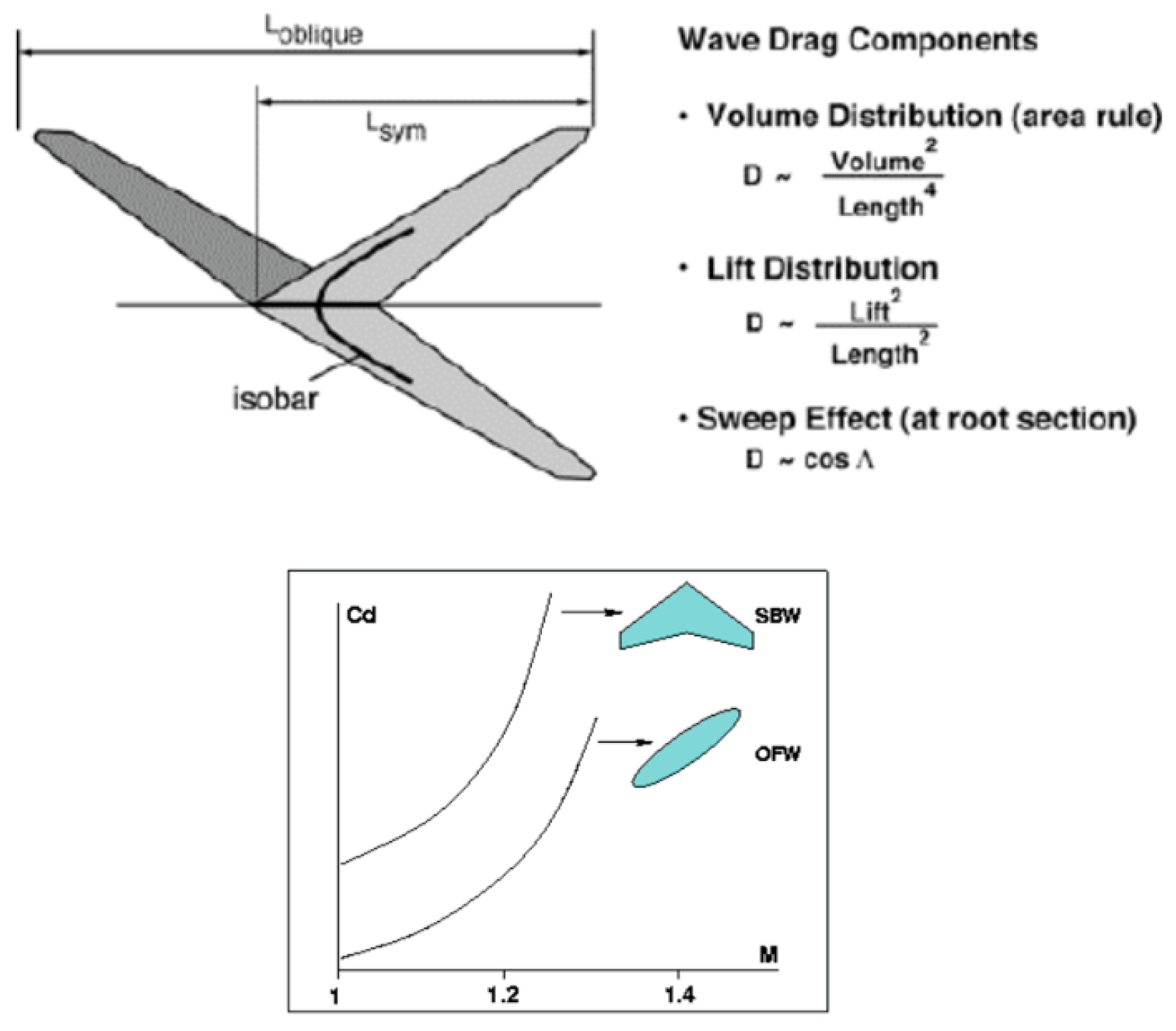
- Desktop Aeronautics Oblique Flying Wings: An Introduction and White Paper; Desktop Aeronautics: Palo Alto, CA, USA, 2005.
- Filippone, A. The Oblique Flying Wing. Available online: https://aerodyn.org/ofw/ (accessed on 18 October 2023).
- Conner, M. Nasa Armstrong Fact Sheet: The ad-1. Available online: https://www.nasa.gov/centers/armstrong/news/FactSheets/FS-019-AFRC.html (accessed on 18 October 2023).
- Reddit. 1970s “Flying Oblique Wing” Concept, Designed by r.t. Jones, art by Rick Guidice, for NASA. Available online: https://www.reddit.com/r/RetroFuturism/comments/aw47jq/1970s_flying_oblique_wing_concept_designed_by_rt/ (accessed on 18 October 2023).
- Hicks, R.M.; Mendoza, J.P. Oblique-Wing Sonic Boom; NASA: Washington, DC, USA, 1973.
- Van der Velden, A.; Kroo, I. Sonic boom of the oblique flying wing. J. Aircr. 1994, 31, 19–25. [Google Scholar] [CrossRef]
- El-Salamony, M. Oblique Flying Wing: Past and Future. In Proceedings of the Proceedings of Extremal and Record-Breaking Aircrafts Workshop (ERBA), Dolgoprudny, Russia, 5–15 July 2016. [Google Scholar]
- Busemann, A. Aerodynamic lift at supersonic speeds. Luftfahrtforschung 1935. [Google Scholar]
- Kusunose, K.; Matsushima, K.; Maruyama, D. Supersonic biplane—A review. Prog. Aerosp. Sci. 2011, 47, 53–87. [Google Scholar] [CrossRef]
- Hu, R.; Jameson, A.; Wang, Q. Adjoint-based aerodynamic optimization of supersonic biplane airfoils. J. Aircr. 2012, 49, 802–814. [Google Scholar] [CrossRef]
- Licher, R. Optimum Two-Dimensional Multiplanes in Supersonic Flow; Douglas Aircraft Company: Santa Monica, CA, USA, 1955. [Google Scholar]
- Ban, N.; Yamazaki, W.; Kusunose, K. Low-boom/low-drag design optimization of innovative supersonic transport configuration. J. Aircr. 2018, 55, 1071–1081. [Google Scholar] [CrossRef]
- Maruyama, D.; Kusunose, K.; Matsushima, K.; Nakahashi, K. Numerical Analysis and Design of Supersonic Wings Based on Busemann Biplane. 2007. Available online: https://www.eucass.eu/component/docindexer/?task=download&id=2992 (accessed on 18 October 2023).
- Yamashita, H.; Yonezawa, M.; Obayashi, S.; Kusunose, K. A study of busemann-type biplane for avoiding choked flow. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007; p. 688. [Google Scholar]
- Maruyama, D.; Kusunose, K.; Matsushima, K. Aerodynamic characteristics of a two-dimensional supersonic biplane, covering its take-off to cruise conditions. Shock Waves 2009, 18, 437–450. [Google Scholar] [CrossRef]
- Zhai, J.; Zhang, C.A.; Wang, F.M.; Zhang, W.W. Design of a new supersonic biplane. Acta Astronaut. 2020, 175, 216–233. [Google Scholar] [CrossRef]
- Yonezawa, M.; Yamashita, H.; Obayashi, S.; Kusunose, K. Investigation of supersonic wing shape using Busemann biplane airfoil. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007; p. 686. [Google Scholar]
- Yonezawa, M.; Obayashi, S. Reducing drag penalty in the three-dimensional supersonic biplane. Proc. Inst. Mech. Eng. Part J. Aerosp. Eng. 2009, 223, 891–899. [Google Scholar] [CrossRef]
- Yamashita, H.; Kuratani, N.; Yonezawa, M.; Ogawa, T.; Nagai, H.; Asai, K.; Obayashi, S. Wind tunnel testing on start/unstart characteristics of finite supersonic biplane wing. Int. J. Aerosp. Eng. 2013, 2013, 231434. [Google Scholar] [CrossRef]
- Maruyama, D.; Kusunose, K.; Matsushima, K.; Nakahashi, K. Aerodynamic analysis and design of Busemann biplane: Towards efficient supersonic flight. Proc. Inst. Mech. Eng. Part J. Aerosp. Eng. 2012, 226, 217–238. [Google Scholar] [CrossRef]
- Utsumi, Y.; Obayashi, S. Design of supersonic biplane aircraft concerning sonic boom minimization. In Proceedings of the 28th AIAA Applied Aerodynamics Conference, Chicago, IL, USA, 28 June–1 July 2010; p. 4962. [Google Scholar]
- Yamazaki, W.; Kusunose, K. Aerodynamic Study of Twin-Body Fuselage Configuration for Supersonic Transport. Trans. Jpn. Soc. Aeronaut. Space Sci. 2013, 56, 229–236. [Google Scholar] [CrossRef]
- Yamazaki, W.; Kusunose, K. Aerodynamic/sonic boom performance evaluation of innovative supersonic transport configurations. J. Aircr. 2016, 53, 942–950. [Google Scholar] [CrossRef]
- Anthony, S. Supersonic Biplanes: More Fuel Efficient, Quieter Sonic Booms. Available online: https://www.extremetech.com/extreme/133259-supersonic-biplanes-more-fuel-efficient-quieter-sonic-booms (accessed on 18 October 2023).
- Yamazaki, W.; Kusunose, K. Innovative supersonic transport configuration by biplane wing/twin-body fuselage. In Proceedings of the 29th ICAS Congress, ICAS Paper, St. Petersburg, Russia, 7–12 September 2014; Volume 735, p. 2014. [Google Scholar]
- Zha, G.; Im, H.; Espinal, D. Toward zero sonic-boom and high efficiency supersonic flight, part I: A novel concept of supersonic bi-directional flying wing. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010; p. 1013. [Google Scholar]
- Espinal, D.; Lee, B.; Sposato, H.; Kinard, D.; Dominguez, J.; Zha, G.C.; Im, H. Supersonic bi-directional flying wing, Part II: Conceptual design of a high speed civil transport. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010; p. 1393. [Google Scholar]
- Berger, C.; Carmona, K.; Espinal, D.; Im, H.; Zha, G. Supersonic bi-directional flying wing configuration with low sonic boom and high aerodynamic efficiency. In Proceedings of the 29th AIAA Applied Aerodynamics Conference, Reston, VA, USA, 27–30 June 2011; p. 3663. [Google Scholar]
- Zha, G.; Cattafesta, L.; Alvi, F.S. Silent and Efficient Supersonic Bi-Directional Flying Wing; Final Report for NASA NIAC Phase I Grant NNX12AR05G8; NASA: Washington, DC, USA, 2013.
- Sandu, C.; Sandu, R.C.; Olariu, C.T. Sonic Boom Mitigation through Shock Wave Dispersion. In Environmental Impact of Aviation and Sustainable Solutions; IntechOpen: London, UK, 2019. [Google Scholar]
- Henne, P.A.; Howe, D.C.; Wolz, R.R.; Hancock, J.L., Jr. Supersonic Aircraft with Spike for Controlling and Reducing Sonic Boom. U.S. Patent 6,698,684, 22 March 2002. [Google Scholar]
- Simmons, F.; Freund, D. Wing morphing for quiet supersonic jet performance-variable geometry design challenges for business jet utilization. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005; p. 1017. [Google Scholar]
- Howe, D. Improved sonic boom minimization with extendable nose spike. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005; p. 1014. [Google Scholar]
- Simmons, F.; Freund, D.; Spivey, N.; Schuster, L. Quiet spike: The design and validation of an extendable nose boom prototype. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Honolulu, HI, USA, 23–26 April 2007; p. 1774. [Google Scholar]
- Sun, Y.; Smith, H. Review and prospect of supersonic business jet design. Prog. Aerosp. Sci. 2017, 90, 12–38. [Google Scholar] [CrossRef]
- Freund, D.; Simmons, F.; Spivey, N.; Schuster, L. Quiet Spike Prototype Flight Test Results. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Honolulu, HI, USA, 23–26 April 2007; p. 1778. [Google Scholar]
- Freund, D.; Simmons, F.; Howe, D.; Cowart, R.; Grindle, T. Lessons Learned-Quiet SpikeTM Flight Test Program. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008; p. 130. [Google Scholar]
- Gulfstream Aerospace Corporation. An Overview of the Gulfstream An Overview of the Gulfstream Supersonic Technology Supersonic Technology Program. 2010. Available online: https://www.faa.gov/sites/faa.gov/files/about/office_org/headquarters_offices/apl/BaltimorePublicMeeting-Gulfstream.pdf (accessed on 18 October 2023).
- Sandu, C.; Brasoveanu, D. New solution for sonic boom mitigation. Concept and testing methodology. Application at European supersonic business jet. In Proceedings of the 33rd Caius Iacob Conference-Fluid Mechanics and Technical Applications, Bucharest, Romania, 29–30 September 2011; pp. 29–30. [Google Scholar]
- Cheng, S. Device for Sonic Boom Reduction and Improving Aircraft Performance. U.S. Patent 3,737,119, 5 June 1973. [Google Scholar]
- Ye, L.Q.; Ye, Z.Y.; Ye, K.; Wu, J.; Miao, S.J. A low-boom and low-drag design method for supersonic aircraft and its applications on airfoils. Adv. Aerodyn. 2021, 3, 1–27. [Google Scholar] [CrossRef]
- Miles, R.B.; Martinelli, L.; Macheret, S.O.; Shneider, M.; Girgis, I.G.; Zaidi, S.H.; Mansfield, D.; Siclari, M.; Smereczniak, P.; Kashuba, R.; et al. Suppression of sonic boom by dynamic off-body energy addition and shape optimization. AIAA Paper 2002, 150, 33. [Google Scholar]
- Zaidi, S.H.; Shneider, M.; Miles, R. Shock-wave mitigation through an off-body pulsed energy deposition. AIAA J. 2004, 42, 326–331. [Google Scholar] [CrossRef]
- Potapkin, A.; Moskvichev, D.Y. Reduction of the sonic boom level by heating the flow in front of the body. Shock Waves 2014, 24, 429–437. [Google Scholar] [CrossRef]
- Fomin, V.; Tretyakov, P. Active methods of affecting a supersonic flow. In Advanced Problems of Science, Proceedings of the Scientific Session of the Siberian Division of the Russian Academy of Sciences and the Siberian Division of the Russian Academy of Medical Sciences, Nauka, Novosibirsk, 25–26 November 2003; IntechOpen: London, UK, 2003; pp. 185–208. [Google Scholar]
- Shneyder, M.; Macheret, S.; Zaidi, S.; Girgis, I.; Miles, R. Steady and unsteady supersonic flow control with energy addition. In Proceedings of the 34th AIAA Plasmadynamics and Lasers Conference, Orlando, FL, USA, 23–26 June 2003; p. 3862. [Google Scholar]
- Fomin, V.; Chirkashenko, V.; Volkov, V.; Kharitonov, A. Reduction of the sonic boom level in supersonic aircraft flight by the method of surface cooling. Thermophys. Aeromech. 2013, 20, 669–678. [Google Scholar] [CrossRef]
- Morgenstern, J.M.; Arslan, A. Aircraft Lift Device for Low Sonic Boom. U.S. Patent 6,935,592, 30 August 2005. [Google Scholar]
- Adamson, E.; Nelson, C. Supersonic Aircraft with Active Lift Distribution Control for Reducing Sonic Boom. U.S. Patent Appl. 11/039,651, 20 July 2006. [Google Scholar]

















Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonavolontà, G.; Lawson, C.; Riaz, A. Review of Sonic Boom Prediction and Reduction Methods for Next Generation of Supersonic Aircraft. Aerospace 2023, 10, 917. https://doi.org/10.3390/aerospace10110917
Bonavolontà G, Lawson C, Riaz A. Review of Sonic Boom Prediction and Reduction Methods for Next Generation of Supersonic Aircraft. Aerospace. 2023; 10(11):917. https://doi.org/10.3390/aerospace10110917
Chicago/Turabian StyleBonavolontà, Giordana, Craig Lawson, and Atif Riaz. 2023. "Review of Sonic Boom Prediction and Reduction Methods for Next Generation of Supersonic Aircraft" Aerospace 10, no. 11: 917. https://doi.org/10.3390/aerospace10110917
APA StyleBonavolontà, G., Lawson, C., & Riaz, A. (2023). Review of Sonic Boom Prediction and Reduction Methods for Next Generation of Supersonic Aircraft. Aerospace, 10(11), 917. https://doi.org/10.3390/aerospace10110917