Modeling and Application of Out-of-Cabin and Extra-Vehicular Dynamics of Airdrop System Based on Kane Equation
Abstract
1. Introduction
2. Methods
2.1. Out-of-Cabin Process Dynamics
- (1)
- Due to the symmetry of the system, only the displacement and pitch motion along the direction of flight and gravity are considered, i.e., the coordinate system is simplified to two dimensions;
- (2)
- The aircraft maintains a horizontal uniform velocity during the airdrop, and an angle of attack can exist;
- (3)
- No aerodynamic influence is considered when the load is moving inside the cabin;
- (4)
- Due to the long traction rope, the influence of the aircraft’s wake flow on the traction parachute and parachute rope characteristics is not considered.
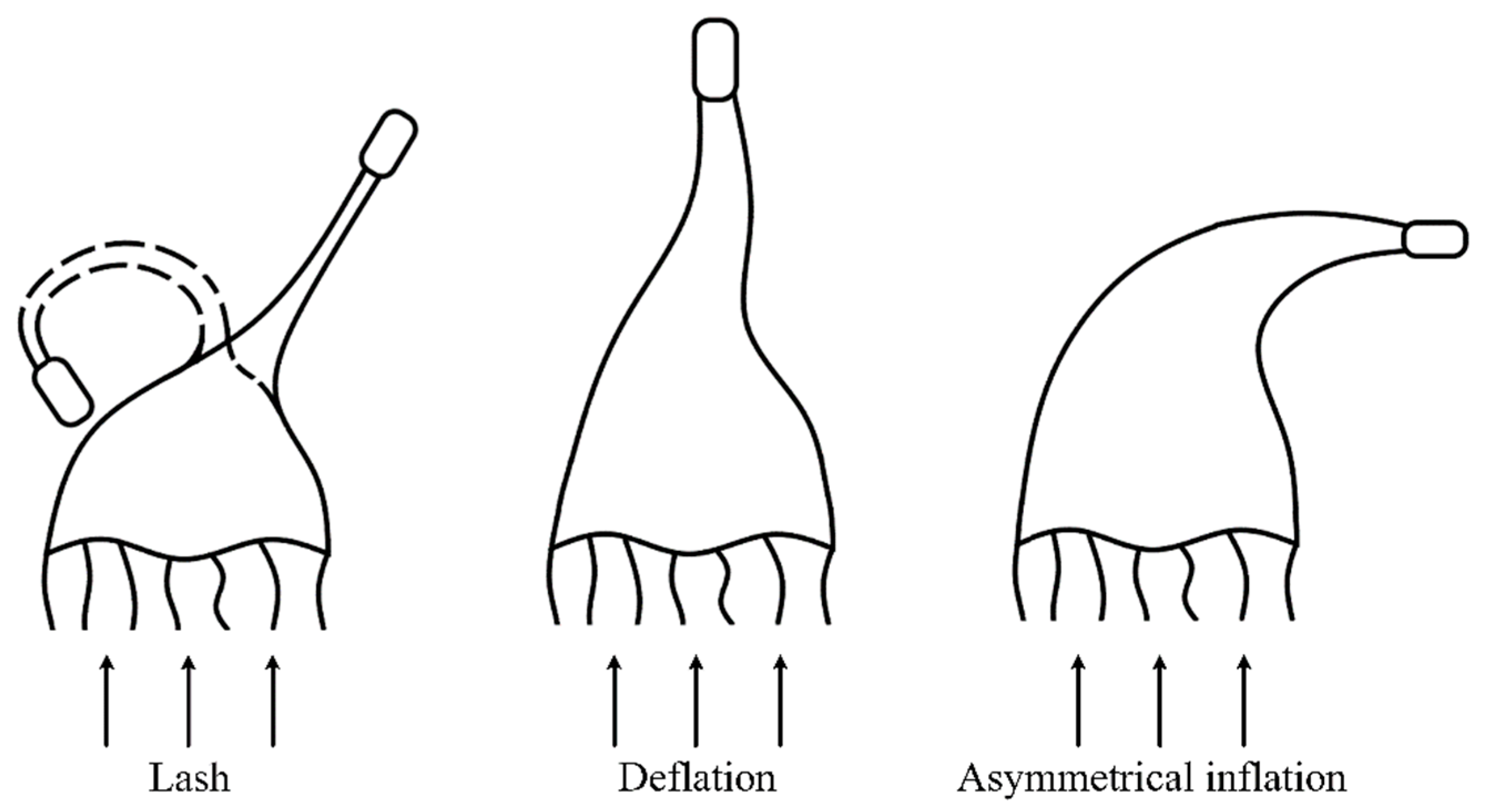
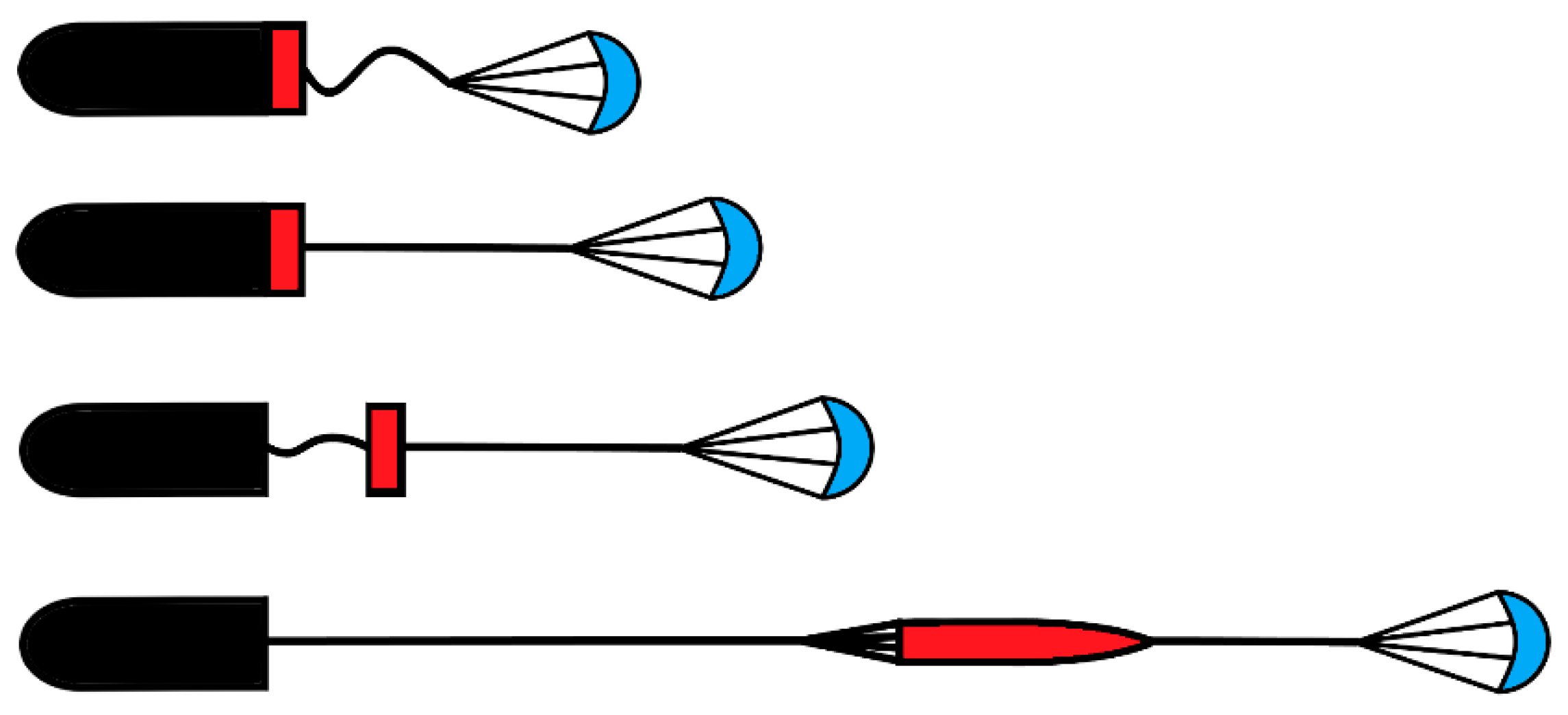
2.2. Extra-Vehicular Process Dynamics of the Line
- (1)
- The rotation of the cargo is not considered. The studies by Wang H. [46] show that its rotation only has an effect on the calculation results of its own attitude and has no effect on the line sail phenomenon generated on the connecting line.
- (2)
- There is no inflation of the main parachute during the straightening process, and it can be regarded as a one-dimensional object in space, similar to the parachute line, whose aerodynamic force is calculated in the same way as that of the parachute attachment line.
- (3)
- It is assumed that the angle of attack of the traction parachute is always zero in the straightening process.
- (4)
- The aerodynamic force acting on the parachute connecting line and the uninflated main parachute is calculated as a cylinder.
3. Results and Discussions
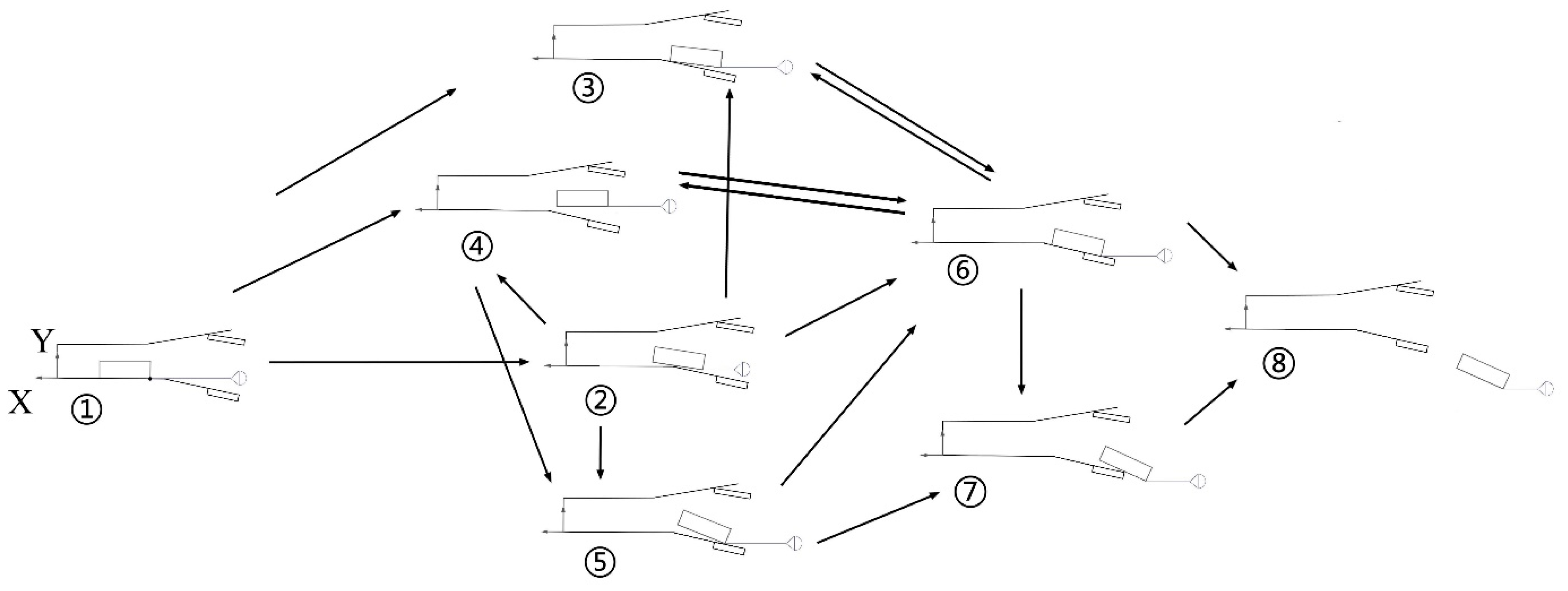
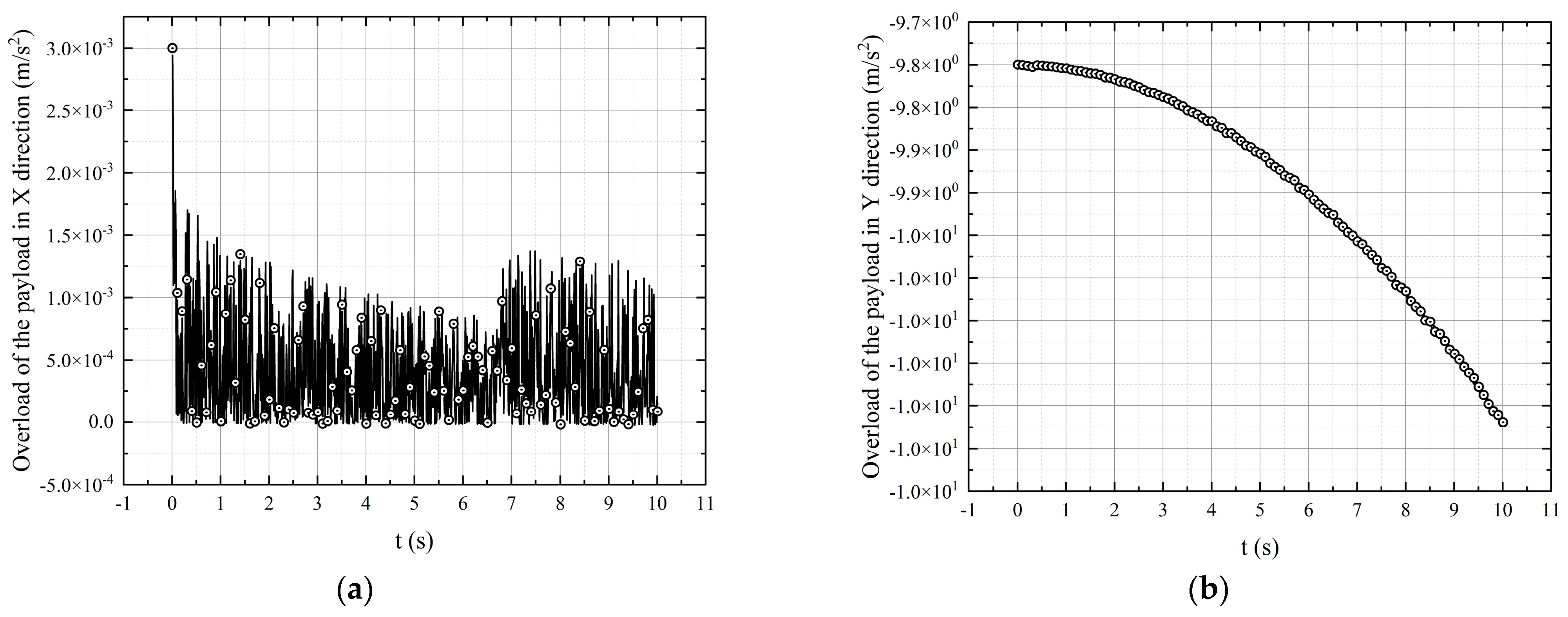
3.1. Results of the Extra-Vehicular Process and Status Identification Analysis
3.1.1. Results of Single Extra-Vehicular Process
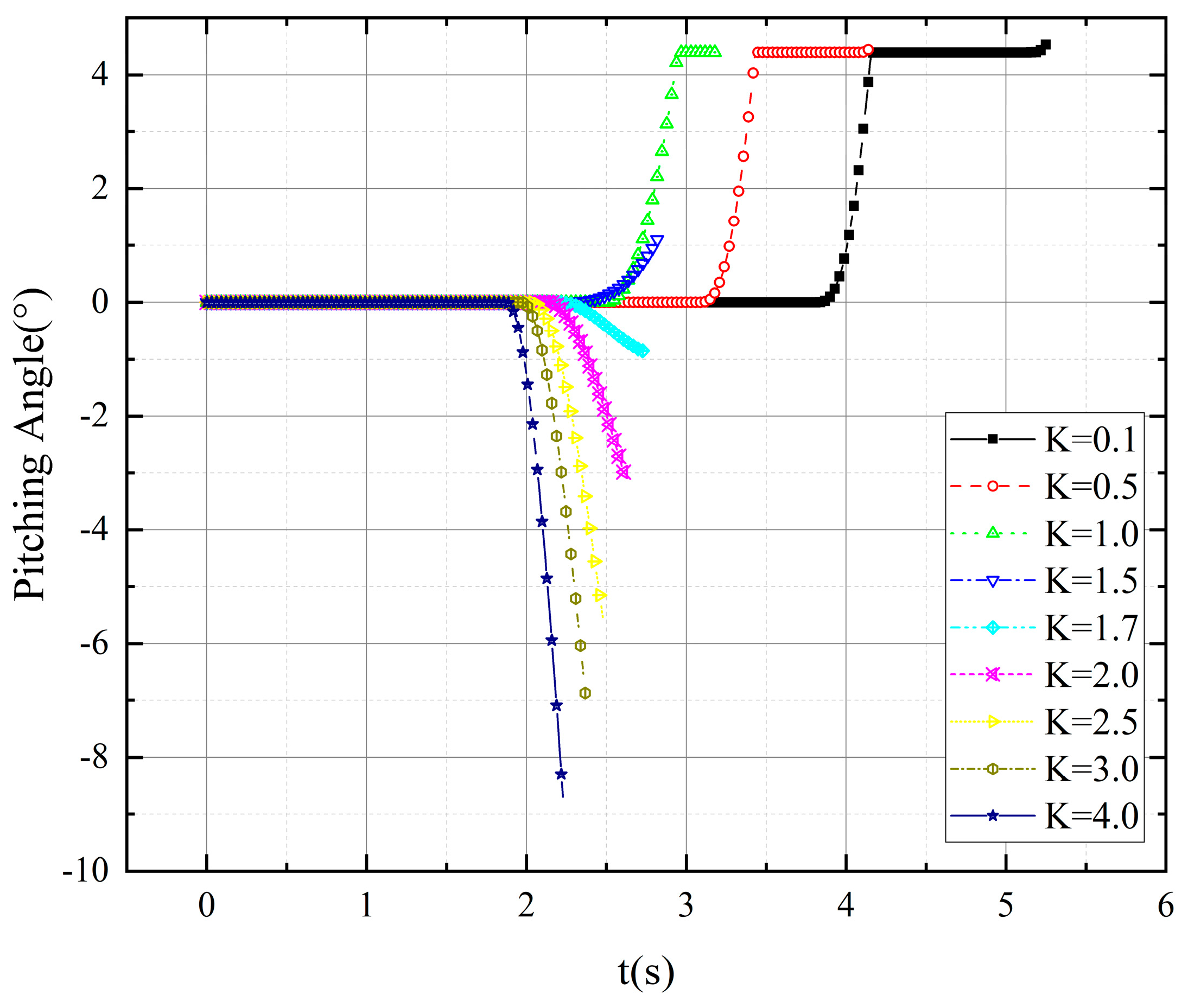
3.1.2. Results of Different Traction Ratios
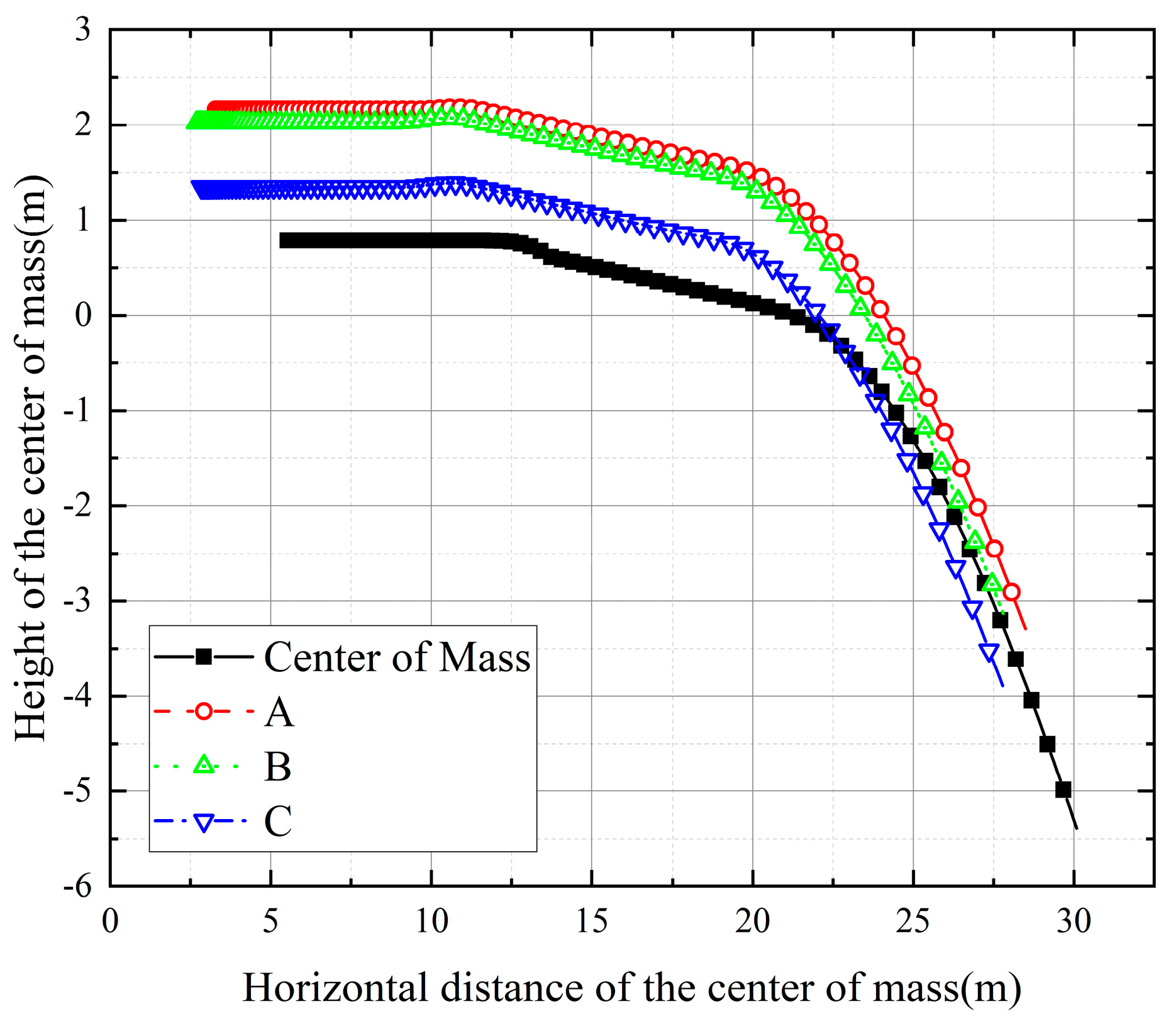
3.1.3. Off-Board Safety Analysis
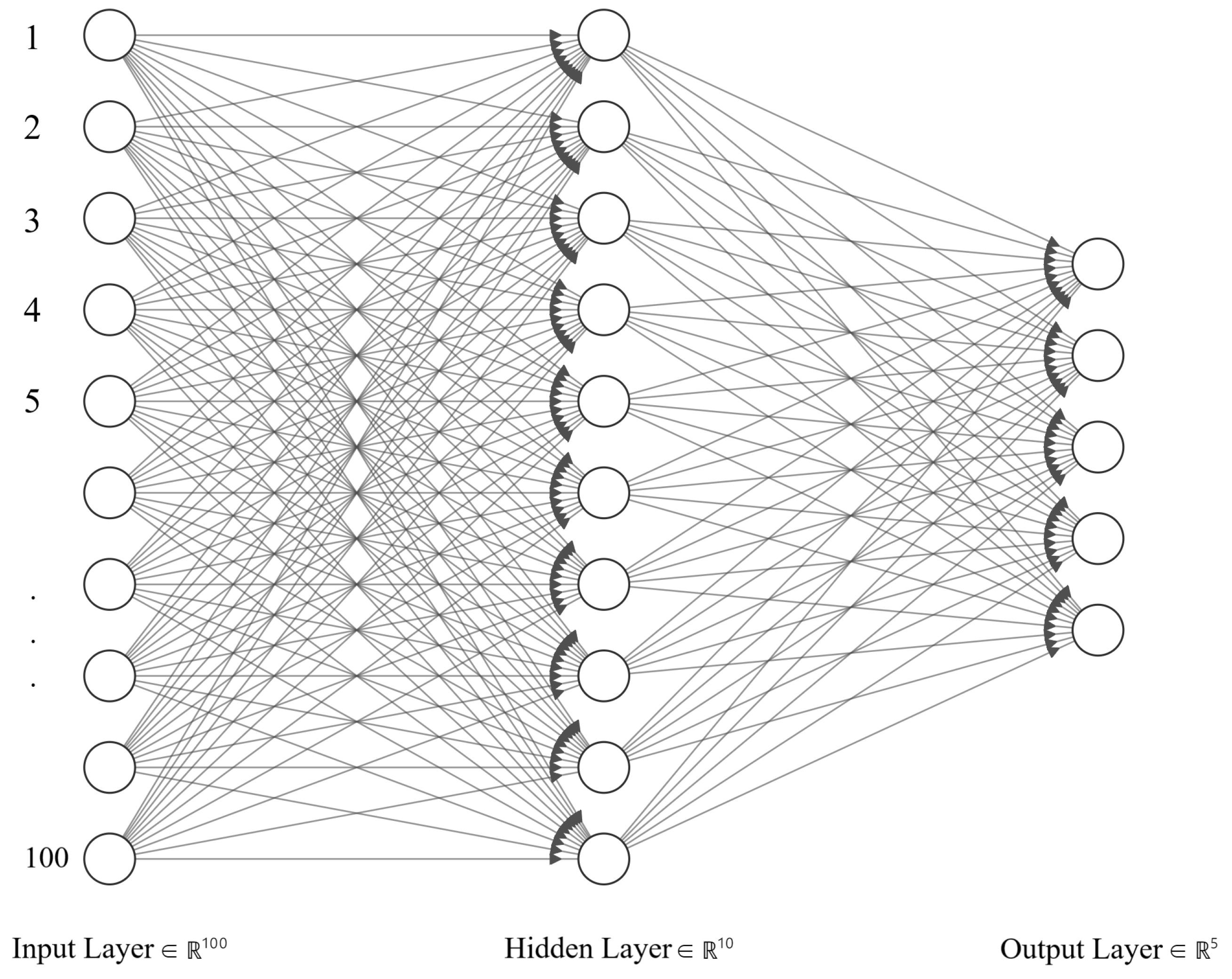
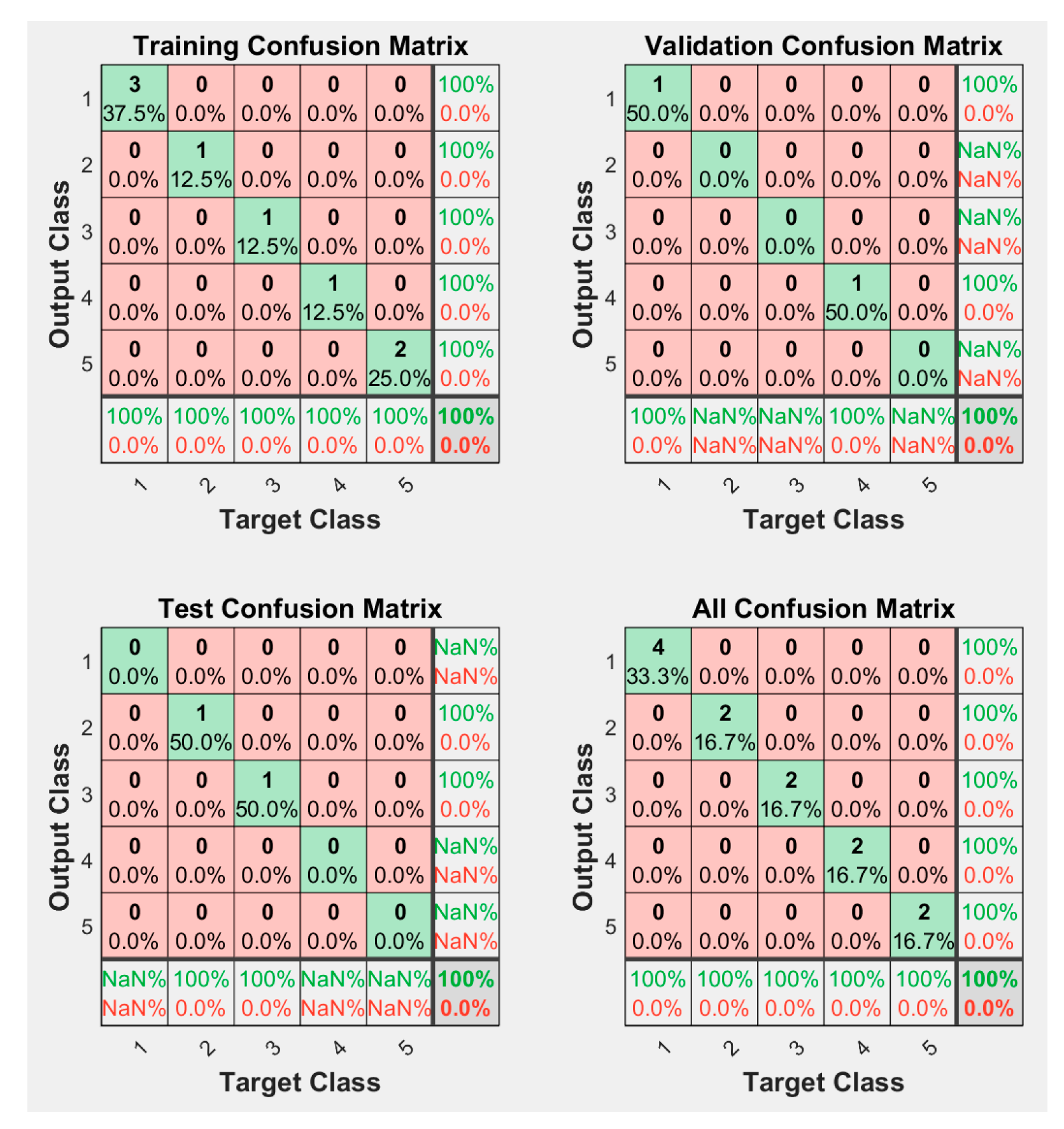
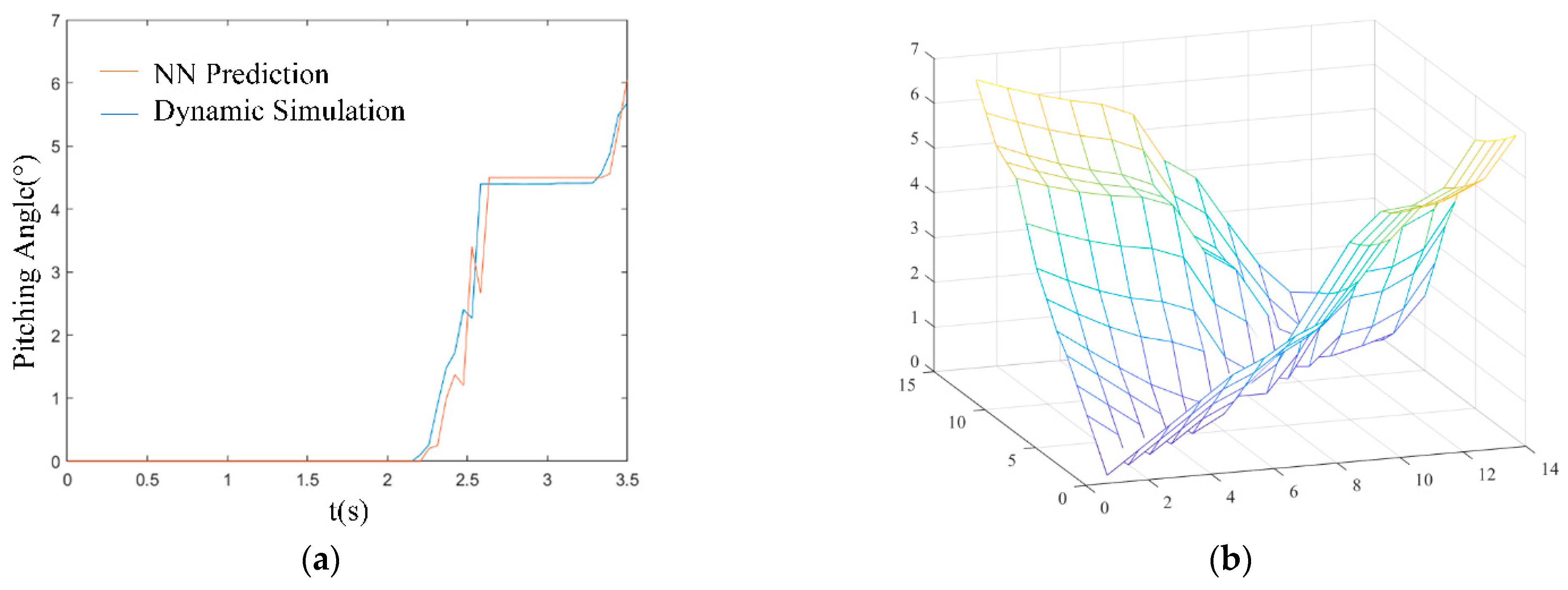
3.1.4. NN Status Recognition
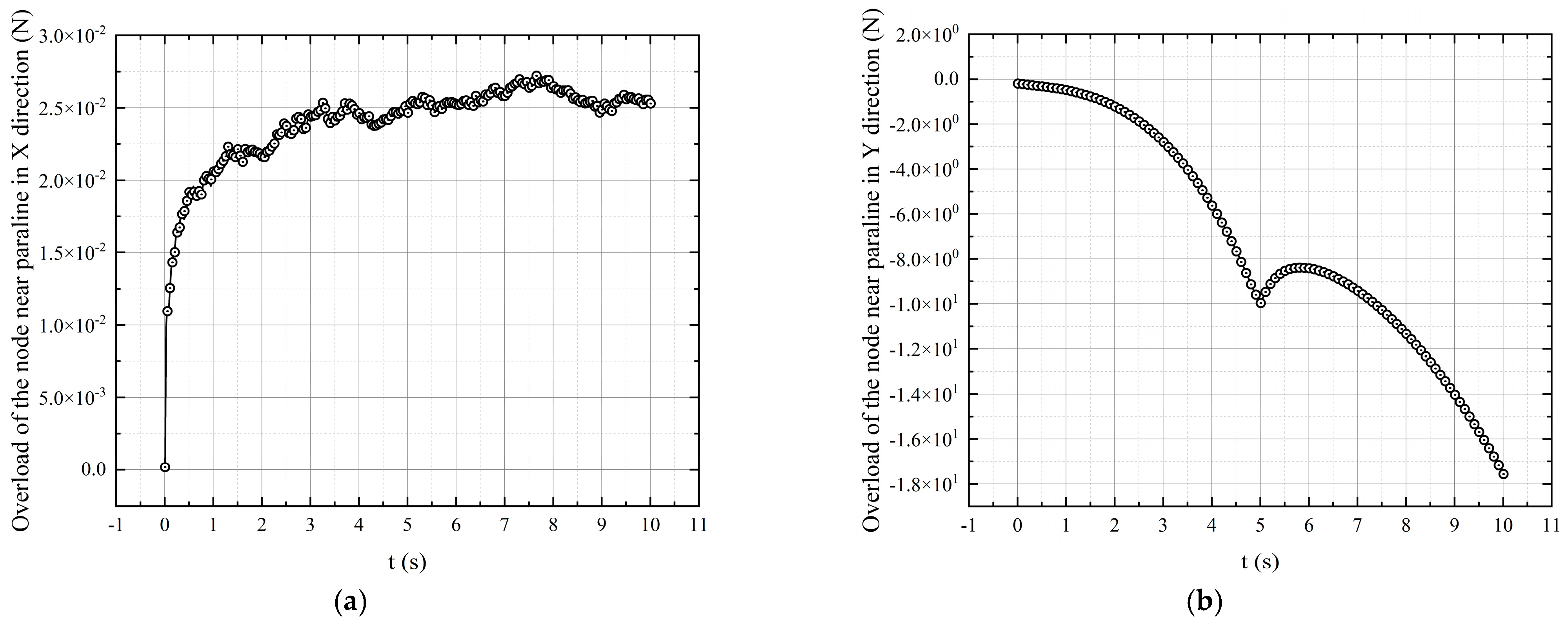
3.2. Results of Parachute Line Motion and Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bergeron, K.; Seidel, J.; Ghoreyshi, M. Numerical Study of Ram Air Airfoils and Upper Surface Bleed-Air Control. In Proceedings of the 32nd AIAA Applied Aerodynamics Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar] [CrossRef]
- Goodrick, T. Theoretical study of the longitudinal stability of high-performance gliding airdrop systems. In Proceedings of the 5th Aerodynamic Deceleration Systems Conference, Albuquerque, NM, USA, 17–19 November 1975. [Google Scholar] [CrossRef]
- Lingard, J.S. The Performance and DESIGN of Ram-Air Parachutes; T.R.-81-103; Royal Aircraft Establishment: Farnborough, UK, 1981. [Google Scholar]
- Goodrick, T. Simulation studies of the flight dynamics of gliding parachute systems. In Proceedings of the 6th Aerodynamic Decelerator and Balloon Technology Conference, Houston, TX, USA, 5–7 March 1979. [Google Scholar] [CrossRef]
- Goodrick, T. Comparison of simulation and experimental data for a gliding parachute in dynamic flight. In Proceedings of the 7th Aerodynamic Decelerator and Balloon Technology Conference, San Diego, CA, USA, 21–23 October 1981. [Google Scholar] [CrossRef]
- Goodrick, T. Scale effects on performance of ram air wings. In Proceedings of the 8th Aerodynamic Decelerator and Balloon Technology Conference, Hyannis, MA, USA, 2–4 April 1984. [Google Scholar] [CrossRef]
- Cockrell, D.; Haidar, N. Influence of the canopy-payload coupling on the dynamic stability in pitch of a parachute system. In Proceedings of the Aerospace Design Conference, Irvine, CA, USA, 16–19 February 1993. [Google Scholar] [CrossRef]
- Machin, R.A.; Iacomini, C.S.; Cerimele, C.J.; Stein, J.M. Flight Testing the Parachute System for the Space Station Crew Return Vehicle. J. Aircr. 2001, 38, 786–799. [Google Scholar] [CrossRef]
- Müller, S.; Wagner, O.; Sachs, G. A high-fidelity nonlinear multibody simulation model for parafoil systems. In Proceedings of the 17th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Monterey, CA, USA, 19–22 May 2003. [Google Scholar] [CrossRef]
- Slegers, N.; Costello, M. Aspects of control for a parafoil and payload system. J. Guid. Control Dyn. 2003, 26, 898–905. [Google Scholar] [CrossRef]
- Moog, R.D. Aerodynamic Line Bowing during Parachute Deployment. In Proceedings of the 5th Aerodynamic Deceleration Systems Conference, Albuquerque, NM, USA, 17–19 November 1975. [Google Scholar] [CrossRef]
- Pillasch, D.W.; Shen, Y.C.; Valero, N. Parachute/submunition system coupled dynamics. In Proceedings of the 8th Aerodynamic Decelerator and Balloon Technology Conference, Hyannis, MA, USA, 2–4 April 1984. [Google Scholar] [CrossRef]
- Fallon, E.J. Parachute dynamics and stability analysis of the Queen Match Recovery System. In Proceedings of the 11th Aerodynamic Decelerator Systems Technology Conference, San Diego, CA, USA, 9–11 April 1991. [Google Scholar]
- Vishniak, A. Simulation of the payload-parachute-wing system flight dynamics. In Proceedings of the Aerospace Design Conference, Irvine, CA, USA, 16–19 February 1993. [Google Scholar] [CrossRef]
- Wolf, D.F. Parachute opening shock. In Proceedings of the 15th Aerodynamic Decelerator Systems Technology Conference, Toulouse, France, 8–11 June 1999. [Google Scholar] [CrossRef]
- Jia, T.; Amirouche, F. Optimum impact force in motion control of multibody systems subject to inequality contraints. Mech. Res. Commun. 1989, 16, 163–173. [Google Scholar] [CrossRef]
- Ider, S.K. Modeling of control forces for kinematical constraints in multibody systems dynamics—A new approach. Comput. Struct. 1991, 38, 409–414. [Google Scholar] [CrossRef]
- Saenger-Zetina, S.; Neiss, K.; Beck, R.; Abel, D. Optimal clutch control applied to a hybrid electric variable transmission with Kane equations. IFAC Proc. Vol. 2007, 40, 87–94. [Google Scholar] [CrossRef]
- Quan, H.; Jia, Y.; Xu, S. A new computer-oriented approach with efficient variables for multibody dynamics with motion constraints. Acta Astronaut. 2012, 81, 380–389. [Google Scholar]
- Salinic, S.; Boskovic, G.; Nikolic, M. Dynamic modelling of hydraulic excavator motion using Kane’s equations. Autom. Constr. 2014, 44, 56–62. [Google Scholar] [CrossRef]
- Chowdhury, D. Kane model parameters and stochastic spin current. Solid State Commun. 2015, 222, 53–57. [Google Scholar] [CrossRef][Green Version]
- Liu, J.; Hearn, G.E.; Chen, X.; Jiang, Z.; Wu, G. Analysis of dynamic response of a restraining system for a powerless advancing ship based on the Kane method. Ocean Eng. 2016, 131, 114–134. [Google Scholar] [CrossRef]
- Pal, R.S. Modelling of Helicopter Underslung Dynamics using Kane’s method. IFAC-Pap. Online 2020, 53, 536–542. [Google Scholar] [CrossRef]
- Sharma, K.K.; Jee, G.; Rajeev, U.P.; Padmakumar, E.S. Modeling of the Helicopter Underslung Aircraft’s Lateral-Directional Dynamics. IFAC-Pap. Online 2022, 55, 174–179. [Google Scholar] [CrossRef]
- Bagdonovich, B.; Desabrais, K.J.; Benney, R. Overview of the Precision Airdrop Improvement Four-Powers Long Term Technology Project. In Proceedings of the 17th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Monterey, CA, USA, 19–22 May 2003. [Google Scholar] [CrossRef]
- Cuthbert, P.A. A software simulation of cargo drop tests. In Proceedings of the 17th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Monterey, CA, USA, 19–22 May 2003. [Google Scholar] [CrossRef]
- Cuthbert, P.A.; Desabrais, J. Validation of a cargo airdrop software simulator. In Proceedings of the 17th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Monterey, CA, USA, 19–22 May 2003. [Google Scholar] [CrossRef]
- Cuthbert, P.A.; Conley G, L. A Desktop Application to Simulate Cargo Drop Tests. In Proceedings of the 18th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Munich, Germany, 23–26 May 2005. [Google Scholar] [CrossRef]
- Taylor, A.P.; Murphy, E. The DCLDYN Parachute Inflation and Trajectory Analysis Tool—An Overview. In Proceedings of the 18th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Munich, Germany, 23–26 May 2005. [Google Scholar] [CrossRef]
- Ke, P.; Yang, C.X.; Yang, X.S. Extraction Phase Simulation of Cargo Airdrop System. Chin. J. Aeronaut. 2006, 19, 315–321. [Google Scholar] [CrossRef]
- Liu, Y.H.; Wang, H.L.; Fan, J.X.; Wu, J.F.; Wu, T.C. Control-oriented UAV highly feasible trajectory planning: A deep learning method. Aerosp. Sci. Technol. 2020, 110, 106435. [Google Scholar] [CrossRef]
- Pereira, G.; Oliveira, M.; Ebecken, N. Genetic Optimization of Artificial Neural Networks to Forecast Virioplankton Abundance from Cytometric Data. J. Intell. Learn. Syst. Appl. 2013, 5, 57–66. [Google Scholar] [CrossRef]
- Hu, L.; Zhang, J.; Xiang, Y.; Wang, W. Neural Networks-Based Aerodynamic Data Modeling: A Comprehensive Review. IEEE Access 2020, 8, 90805–90823. [Google Scholar] [CrossRef]
- Li, K.; Kou, J.Q.; Zhang, W.W. Deep neural network for unsteady aerodynamic and aeroelastic modeling across multiple Mach numbers. Nonlinear Dyn. 2019, 96, 2157–2177. [Google Scholar] [CrossRef]
- Giorgi, M.G.D.; Quarta, M. Hybrid MultiGene Genetic Programming—Artificial neural networks approach for dynamic performance prediction of an aeroengine. Aerosp. Sci. Technol. 2020, 103, 105902. [Google Scholar] [CrossRef]
- Farabet, C.; Coupri, C.; Najman, L. Learning hierarchical features for scene labeling. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1915–1929. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.R. Parachute Theory and Application; Aerospace Press: Beijing, China, 1997. (In Chinese) [Google Scholar]
- Moog, R.D.; Bacchus, D.L.; Utreja, L.R. Performance evaluation of Space Shuttle SRB parachutes from air drop and scaled model wind tunnel tests <149>Solid Rocket Booster recovery system. In Proceedings of the 6th Aerodynamic Decelerator and Balloon Technology Conference, Houston, TX, USA, 5–7 March 1979. [Google Scholar] [CrossRef]
- Purvis, J.W. Prediction of line sail during lines-first deployment. In Proceedings of the 21st Aerospace Sciences Meeting, Reno, NV, USA, 10–13 January 1983. [Google Scholar] [CrossRef]
- Purvi, J.W. Improved prediction of parachute line sail during lines-first deployment. In Proceedings of the 8th Aerodynamic Decelerator and Balloon Technology Conference, Hyannis, MA, USA, 2–4 April 1984. [Google Scholar] [CrossRef]
- Johnson, D.W. Testing of a new recovery parachute system for the F111 aircraft crew escape module: An update. In Proceedings of the 10th Aerodynamic Decelerator Conference, Cocoa Beach, FL, USA, 18–20 April 1989. [Google Scholar] [CrossRef]
- Peterson, C.W. High Performance Parachutes. Sci. Am. 1990, 262, 108–116. [Google Scholar] [CrossRef]
- Maydew, R.C.; Peterson, C.W.; Orlik-Rueckemann, K.J. Design and Testing of High-Performance Parachutes; NATO Advisory Group for Aerospace Research and Development (AGARD): Neuilly-Sur-Seine, France, 1991. [Google Scholar]
- Wang, Y.; Yang, C.; Yang, H. Neural network-based simulation and prediction of precise airdrop trajectory planning. Aerosp. Sci. Technol. 2022, 1, 120. [Google Scholar] [CrossRef]
- Adelfang, S.I.; Smith, O.E. Gust models for launch vehicle ascent. In Proceedings of the 36th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 12–15 January 1998. [Google Scholar] [CrossRef]
- Wang, H. Dynamic Modeling and Simulation of Whipping Phenomenon for Large Parachute. AIAA J. 2018, 56, 1–11. [Google Scholar] [CrossRef]
- Zhang, Q.B.; Cheng, W.K.; Peng, Y.; Qin, Z.Z. A Multi-Rigid-body Model of Parachute Deployment. Chin. Space Sci. Technol. 2003, 23, 45–50. (In Chinese) [Google Scholar]
- Huston, R.L. On the equivalence of Kane’s equations and Gibbs’ Equations for multibody dynamics formulations. Mech. Res. Commun. 1987, 14, 123–131. [Google Scholar] [CrossRef]







| Parameters | Value |
|---|---|
| Mass (kg) | 7000 |
| Profile (m3) | 5.4 × 2.35 × 2.2 |
| Airdrop Height (m) | 600 |
| Airdrop Velocity (km/h) | 320 |
| Installation Position (m) | 8.34 |
| Center of mass position factor | 0.467 |
| Flying Angle (°) | 0 |
| Traction Parachute Line Parameters | |||
| Mass (kg) | 2.83 | Lenth (m) | 3.47 |
| Number of Roots | 60 | Number of Layers | 1 |
| Fracture strength (N) | 4500 | Modulus of elasticity (N) | 15680 |
| Pull-out resistance (N) | 150 | ||
| Traction parachute canopy parameters | |||
| Mass (kg) | 3.47 | Resistance Coefficient | 0.777 |
| Area (m2) | 8 | Pull-out resistance (N) | 300 |
| Traction parachute package parameters | |||
| Mass (kg) | 2.68 | Lenth (m) | 0.5 |
| Resistance characteristic (m2) | 0.5 | ||
| Main parachute package parameters | |||
| Mass (kg) | 8.1 | Resistance characteristic (m2) | 0.14 |
| Lenth (m) | 1.36 | ||
| Dangerous Point | Coordinates | Most Dangerous Position | Most Dangerous Time (s) |
|---|---|---|---|
| A | (4.3, 2.077, 0) | (10.8401, 2.1861, 0) | 3.8370 |
| B | (4.9, 1.938, 0) | (10.5749, 2.0737, 0) | 3.8870 |
| C | (4.746, 1.26, 0) | (10.6265, 1.3885, 0) | 3.8770 |
| Parts | Parameters | Value | Unit |
|---|---|---|---|
| Missile | Mass | 1088.435 | kg |
| Diameter | 0.457 | m | |
| Length | 3.657 | m | |
| Initial angle of attack | 20 | deg | |
| Initial velocity | 1.28 | Ma | |
| Main Parachute | Diameter | 14.020 | m |
| Mass | 80 | kg | |
| Line | Length | 15.239 | m |
| Diameter | 0.006 | m | |
| Mass | 30 | kg | |
| Traction Parachute | Diameter | 1.524 | m |
| Mass | 8.0 | kg |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Yang, C. Modeling and Application of Out-of-Cabin and Extra-Vehicular Dynamics of Airdrop System Based on Kane Equation. Aerospace 2023, 10, 905. https://doi.org/10.3390/aerospace10100905
Wang Y, Yang C. Modeling and Application of Out-of-Cabin and Extra-Vehicular Dynamics of Airdrop System Based on Kane Equation. Aerospace. 2023; 10(10):905. https://doi.org/10.3390/aerospace10100905
Chicago/Turabian StyleWang, Yi, and Chunxin Yang. 2023. "Modeling and Application of Out-of-Cabin and Extra-Vehicular Dynamics of Airdrop System Based on Kane Equation" Aerospace 10, no. 10: 905. https://doi.org/10.3390/aerospace10100905
APA StyleWang, Y., & Yang, C. (2023). Modeling and Application of Out-of-Cabin and Extra-Vehicular Dynamics of Airdrop System Based on Kane Equation. Aerospace, 10(10), 905. https://doi.org/10.3390/aerospace10100905







