Efficient BEM Modeling of the Heat Transfer in the Turbine Blades of Aero-Parts

Abstract

The modeling of the turbine blades in aero-parts presents difficulties in conventional domain solution techniques, especially when internal cooling air passages and a thermal barrier coating (TBC) are applied. This paper presents a very efficient 3D modeling of the anisotropic heat conduction in turbine blades with the boundary element method (BEM), where both the TBC and cooling air passages are considered. The BEM is very ideal for this modeling, since only boundary meshes are required for it; however, a serious problem of nearly singular integration will arise in modeling with coarse meshes. In this article, an efficient modeling and computational algorithm using the BEM is applied for the simulation of heat conduction in the turbine blades of aero-parts. The present work proposes a simplified BEM model to replace multiple thin coating layers on the top of the blade. In the end, the veracity of the implemented BEM code as well as its computational efficiency are illustrated with a few examples, showing that the settled temperature on the substrate can be reduced by 20% by employing a TBC. As compared to the analyses with ANSYS, the percentages of difference were within 2%, while the CPU time spent by the BEM algorithm was about 1/8 of that of ANSYS, not to mention the meshing efforts saved by adopting by a treatment of equivalent convection.

1. Introduction

As is well-known, turbine systems play a crucial role in aircraft performing excellently in the air. The excellent performance of a turbine can only be achieved with an ideally orchestrated combination of mechanical strength, material durability and well-engineered aerodynamic shapes. As an important measure to increase material durability, an ideal cooling design may effectively increase the blades’ endurance under extremely high operational temperatures that may reach up to 1600 °C. When subjected to such extreme temperatures, the blades have to be cooled down to ensure the structural integrity of the gas turbines during operation. One effective means is to apply a very thin layer of coating material with low conductivity, namely a thermal barrier coating (TBC), over the blade surfaces to enhance the blades’ endurance under such high temperatures. Another means is to introduce tiny air passages inside the blades. One may refer to [1] for a literature survey of the heat transfer in turbine blades. Either means of cooling will pose additional modeling difficulties to convectional domain solution techniques (DSTs) such as the finite element method, the finite volume method, the finite difference method, etc. This is because reliable modeling with the DSTs strongly depends on proper aspect ratios of the “cells” and thus, clustered meshes are required to model the blade’s trailing edge, the internal air passages and the TBC (0.5~several μm in thickness). As a consequence, an overwhelming number of meshes is required for this modeling, often incurring overloaded computation. The key factors influencing the settled temperature in the blades are the designs of the internal cooling air passages and the TBC. In principle, introducing more internal passages should help reduce the temperature; however, as a downside, it may also weaken the structural integrity. For the design of the TBC, a thicker coating will provide better protection from the strict ambient temperature, but at the same time, coating delamination/spoiling will be more likely to happen. After all, the accurate prediction of the temperature distribution in turbine blades plays a crucial role in the proper design of TBC blades (see [2]). As such, an efficient numerical simulation of the heat transfer in turbine blades has attracted significant research as to its importance. For example, Li and Kassab [3] have presented a finite-volume method coupled with the BEM to study the conjugate heat transfer in turbine blades. Iacovides and Raisee [4] reported some recent progress in the computation of the heat transfer in the internal cooling air passages of turbine blades. Vo et al. [5] investigated the influences of thickness and coolant on the mainstream hot gas pressure ratio and the temperature ratio in blade film cooling, respectively, by simulating a conjugate heat transfer (CHT) in the first-stage cooling blade of a W501F engine. Wang et al. [6] analyzed thermal stress inside coatings during the thermal cycling of three different structures of TBC designed using finite element simulation. Pu et al. [7] presented a study on the overall thermal performances of the system of TBCs and backward film cooling, conducted through both experiments and predictions in a lab environment.

As an efficient alternative, the boundary element method, usually abbreviated as the BEM, has been widely applied to many engineering problems. Its obvious advantage over DSTs is its boundary discretization, which makes it ideal to model turbine blades coated with TBCs, abbreviated as TBC blades here. This merit makes this modeling much more efficient than the DSTs, regardless of how complicated the internal passages are and how thin the TBC is. Not for a practical design, Figure 1 merely demonstrates a simple 2D example of unstructured grids for the DSTs as well as boundary meshes for the BEM. From this simple 2D demonstration, the merit of applying the BEM to modeling turbine blades is pretty obvious, especially for general 3D cases. However, pertinent BEM works applied for the simulation of heat transfer in 3D anisotropic TBC blades have indeed remained unexplored in the open literature. With reference to Figure 1, it is clear to see that when traditional DSTs are employed in modeling 3D TBC blades with internal cooling air passages, tremendous amounts of “cells” are required, especially for very thin TBC layers. This is because a reliable analysis with DSTs strongly depends upon the constraints of the reasonable aspect ratios of the modeling elements (normally not exceeding 1:20). As such, the DST modeling of complicated TBC blades often requires an overwhelming number of elements, resulting in overloaded computations. Despite the significant efforts saved for the modeling itself, the BEM confronts the numerical difficulty of evaluating nearly singular integrals. This occurs in the BEM modeling of a TBC when the source node on one side is very close to the integration element on its opposite side (Figure 2). This situation may happen in the modeling of the blade’s trailing edge as well as the internal cooling air passages near the blade surface. One simple resolution is to employ clustered elements onto those places to avoid nearly singular integration; however, either a significant decline in computational efficiency or overloaded computation may occur.

To resolve this problem, Letizia and Scuderi [8] have presented a nonlinear transformation for the computation of nearly singular integrals over planar triangles. Zhang et al. [9] also presented a BEM strategy for 3D field problems by coupling least-squares approximation with boundary integral equations. Zhou [10] presented an analytical algorithm for treating anisotropic field problems. Using the strategy of integration by parts, Shiah et al. [11] reduced the strength of singularities such that a reasonably increased number of Gauss points could be used to properly integrate those integrals. This scheme has also been implemented by Shiah et al. [9] to study the heat transfer of composites. Due to the less appealing efficiency of integration by parts, Shiah et al. [12] have presented a new strategy of conformal mapping to reduce the singular strength of the integrals and study the heat conduction in 3D composites. Many other works using the concept of transformation have also been reported (see Chen and Liu [13], Qin et al. [14]), and it is impractical to mention them all in a thorough review, though they are considered important. It is worth mentioning that along with the aforementioned approaches, another scheme, called “self-regularization”, has also been proposed (see Shiah et al. [15]) to treat the problem of near-singularity for the analysis of anisotropic elasticity. The principle of “self-regularization” is to subtract the parameter of the projection point from the field parameter and then add it back for the integration, with the added value then interpolated using the nodal values of the element. However, due to the process of applying uniform stresses for regularization, the accuracy of this method strongly depends on the variation states of the stresses. In other words, when stress distribution varies nonlinearly in a coarse element, the accuracy may also decline significantly. This happens to be the case when a thin body is subjected to transverse loads and flexural deflection changes rapidly in elements. In the analysis of heat transfer, this situation may occur when heat flux propagates in the normal direction of laminated composites. Another potential source of error may also enter when the domain geometry is not uniform: for instance, with a turbine blade.

Although effective under certain circumferences, most past works have involved either pretty mathematically involved transformation or very intricate algorithms. As such, the overall CPU computation time in a complete 3D analysis has turned out to be very costly indeed, especially when significant amounts of meshes are required for practical engineering problems. To expedite these numerical computations, this paper presents a very efficient and general algorithm that does not involve significant transformation in order to properly compute nearly singular integrals. Basically, in the modeling of a very thin medium, the source’s projection will always fall in the vicinity of one node of the integration element. This technique requires only mild sub-division under intrinsic coordinates according to the position of the projected node. For the sub-domain near the source’s projection, integrals are integrated using polar coordinates, whereas the rest are integrated regularly in the usual manner. For those integrated under the polar-coordinate system, a reasonably increased number of Gauss points is employed in the radial direction, r, while a regular number of Gauss points can be used in the angular direction. Using the polar coordinates, the singularity order of integrands will be reduced by one order and the singularity nature will appear only for r. Since the angular parameter will reveal no singularity, regular integration can be applied.

Moreover, to further simplify modeling and expedite the simulation, the present work proposes a methodology to omit the BEM modeling of TBC layers using an equivalent treatment of the boundary condition of forced convection on the top TBC layer. This strategy has been successfully implemented in an existing BEM code. Its validity as well as its computational efficiency are illustrated with a few numerical examples at the end.

2. Analysis of 3D Anisotropic Heat Conduction

As has been well-documented in most textbooks, the temperature change, T, at a source point, P, on a boundary and its normal derivatives, q, at a field point, Q, are related on the boundary surface, S, as follows:

$$C\left(P\right)T\left(P\right)=\int q\left(Q\right) G^{\prime }\left(P,Q\right)dS-\int T\left(Q\right) F^{\prime }\left(P,Q\right)dS$$

(1)

where $C\left(P\right)$ represents the free term at P and $G^{\prime }\left(P,Q\right) \mathrm{a}\mathrm{n}\mathrm{d} F^{\prime }\left(P,Q\right)$ are the fundamental solutions, defined as

$$G^{\prime }(P,Q)=\frac{1}{4\pi r},\hspace{0.33em}{F}^{\prime }(P,Q)=\frac{-r_{,i}\hspace{0.33em}{n}_i}{4\pi r^2}.$$

(2)

In Equation (2), r is the geodesic distance between P and Q and $n_i$ denotes the components of the unit’s outward normal vector at Q. To treat generally anisotropic heat transfer, Equation (1) may still be applied as long as one performs the coordinate transformation of all nodes, as presented by Tuan and Shiah [16]. This transformation array is fundamentally given in terms of the conductivity coefficients, K_ij, of the medium. One may refer to [16] for further details, and no more elaboration will be provided here. Obviously, the integrands of $G^{\prime }$ and $F^{\prime }$ reveal the singularities with the orders of O(1/r) and O(1/r²), respectively. In applying the usual process of collocation, the boundary surface is discretized into M quadratic elements, and the discretized form of Equation (1) is expressed as

$$\begin{array}{c}C(P)\hspace{0.17em}T(P)=\hspace{0.17em}{\displaystyle \sum _{m=1}^M{\displaystyle \sum _{c=1}^{8/6}{q}_m^{(c)}{\displaystyle {\int }_{-1}^1{\displaystyle {\int }_{-1}^1{N}^{(c)}(\xi ,\eta )G^{\prime }(\xi ,\eta )}}\hspace{0.33em}\left|J_m(\xi ,\eta )\right|\hspace{0.17em}d\xi \hspace{0.33em}d\eta }}\\ -{\displaystyle \sum _{m=1}^M{\displaystyle \sum _{c=1}^{8/6}{T}_m^{(c)}{\displaystyle {\int }_{-1}^1{\displaystyle {\int }_{-1}^1{N}^{(c)}(\xi ,\eta )F^{\prime }(\xi ,\eta )}}\hspace{0.33em}\left|J_m(\xi ,\eta )\right|\hspace{0.17em}d\xi \hspace{0.33em}d\eta }}\end{array},$$

(3)

where $N^{(c)}(\xi ,\eta )$ is the shape functions of interpolation under the intrinsic coordinates $(\xi ,\eta )$, $\left|J_m(\xi ,\eta )\right|$ is the Jacobian transformation and $q_m^{(c)}/\hspace{0.33em}{T}_m^{(c)}$ denotes the nodal values of q/T at the cth node of element m. In Equation (3), eight nodes/six nodes are applied for quadrilateral/triangular elements, respectively. Fundamentally, the integrands will fluctuate drastically near the projected position at $({\xi }_0,{\eta }_0)$ when the source approaches the element under integration (Figure 2). As a result, any conventional numerical scheme shall fail to yield proper values. Figure 3 illustrates the rapid fluctuation of the integrands associated with $G^{\prime }(P,Q)$ and $F^{\prime }(P,Q)$ for a typical case. The numerical difficulty of evaluating nearly singular integrals will arise in the modeling of the heat transfer conduction in TBC blades, particularly the thin blade itself, the internal cooling passages close to the blade surface, and the extremely thin coating layer. Generally speaking, the former two do not threaten conventional modeling with any DST; however, the modeling of a TBC will present a challenge if its thickness falls within several orders below that of the mean chord length of the turbine blade.

Except for the substrate material, there are three layers on top of the TBC blade, namely a thin intermediate layer of metallic bond coat (denoted as Layer-1 with thickness, t₁, and conductivity, K₁), another thin intermediate layer of thermally grown oxide (denoted as Layer-2 with thickness, t₂, and conductivity, K₂) and the top TBC layer (denoted as Layer-T with thickness, t_T), as shown in Figure 4 [17]. When t_T is relatively large, the heat flux across Layer-T will not be proportional to the temperature difference between its upper and lower surfaces. Under such circumstances, it will be necessary to model the three layers with an equivalent TBC layer on top and treat the TBC blade as two dissimilarly adjoined media. In practice, single crystals with anisotropic conductivities, denoted as $K_{ij}^{(b)}$ here, are commonly applied as the substrate materials of turbine blades, especially for advanced air fighters. Due to the thinness of the top TBC layer, its conductivity, represented by $K_T$, is usually treated as isotropic. Suppose no thermal resistance exists on the interface. In the conventional BEM sub-region technique, one needs to supply the additional conditions of compatibility/equilibrium for the interface between the blade substrate and the top TBC layer, as below:

$$T^{\left(b\right)}=T^{\left(T\right)},$$

(4)

$$\frac{{\lambda }^{(b)}}{{\mathrm{\Lambda }}^{(b)}{K}_{11}^{(b)}}{q}^{(b)}+K^{(T)}\hspace{0.17em}{q}^{(T)}=0,$$

(5)

where the superscripts (b)/(T) are used to denote the blade/TBC layer, respectively, and the rest of the symbols are defined as follows:

$$\begin{array}{l}{\lambda }^{(b)}=K_{11}^{(b)}{K}_{22}^{(b)}-{\left[K_{12}^{(b)}\right]}^2,\\ {\mathrm{\Lambda }}^{(b)}=\sqrt{\begin{array}{l}{\left(\frac{\sqrt{{\lambda }^{(b)}}}{K_{11}^{(b)}}{n}_1-\frac{K_{12}^{(b)}}{K_{11}^{(b)}}{n}_2+\frac{K_{12}^{(b)}{K}_{13}^{(b)}-K_{11}^{(b)}{K}_{23}^{(b)}}{\sqrt{{\omega }^{(b)}}}{n}_3\right)}^2\\ +{\left(n_2+\frac{K_{12}^{(b)}{K}_{23}^{(b)}-K_{22}^{(b)}{K}_{13}^{(b)}}{\sqrt{{\omega }^{\left(b\right)}}}{n}_3\right)}^2+\frac{{\left[{\lambda }^{(b)}\right]}^2}{{\omega }^{(b)}}{n}_3^2\end{array}},\\ {\omega }^{(b)}=K_{11}^{(b)}\left(K_{33}^{(b)}-K_{22}^{(b)}{\left[K_{13}^{(b)}\right]}^2+2K_{12}^{(b)}{K}_{13}^{(b)}{K}_{23}^{(b)}-K_{11}^{(b)}{\left[K_{23}^{(b)}\right]}^2\right).\end{array}$$

(6)

Instead, one may also introduce an effect of thermal resistance to replace the two intermediate layers and model Layer-T separately as an adjoined medium. For such a treatment, the thermal resistance, R₀, between the substrate and Layer-T is given as

$$R_0=\frac{D_o}{K_0},$$

(7)

where $D_o=t_1+t_2$ and $K_0$ is the equivalent conductivity of the intermediate layers. Considering thermal resistance, the compatibility condition in Equation (4) is modified to be

$$T^{\left(b\right)}-T^{\left(T\right)}=R_0\hspace{0.33em}{K}^{(T)}\hspace{0.17em}{q}^{(T)},$$

(8)

It should be noted that when R₀ approaches null, the compatibility in Equation (8) will be restored back to that in Equation (4). The overall equivalent thermal resistance of the two intermediate layers is thus given as

$$R_0=\left(\frac{t^{(2)}}{K^{(2)}}\right)\hspace{0.33em}\hspace{0.17em}+\left(\frac{t^{(1)}}{K^{(1)}}\right)\hspace{0.33em}.$$

(9)

From Equations (7) and (9), $K_0$ is determined to be

$$K_0=\frac{K^{(1)}{K}^{(2)}\left(t^{(1)}+t^{(2)}\right)}{t^{(2)}{K}^{(1)}+t^{(1)}{K}^{(2)}}.$$

(10)

By substituting Equations (8) and (9), one obtains

$$T^{\left(b\right)}-T^{\left(T\right)}=\left(\frac{t^{(2)}{K}^{(1)}+t^{(1)}{K}^{(2)}}{K^{(1)}{K}^{(2)}}\right)\hspace{0.33em}{K}^{(T)}\hspace{0.17em}{q}^{(T)}.$$

(11)

All the foregoing treatment is to model the TBC blade using two adjoined sub-regions if the individual modeling of Layer-T is inevitable due to the nonlinearity of its heat transfer. However, when the thickness of Layer-T is so small that only linear transfer is considered, the modeling above can be further simplified. Next, the process of model simplification will be elaborated.

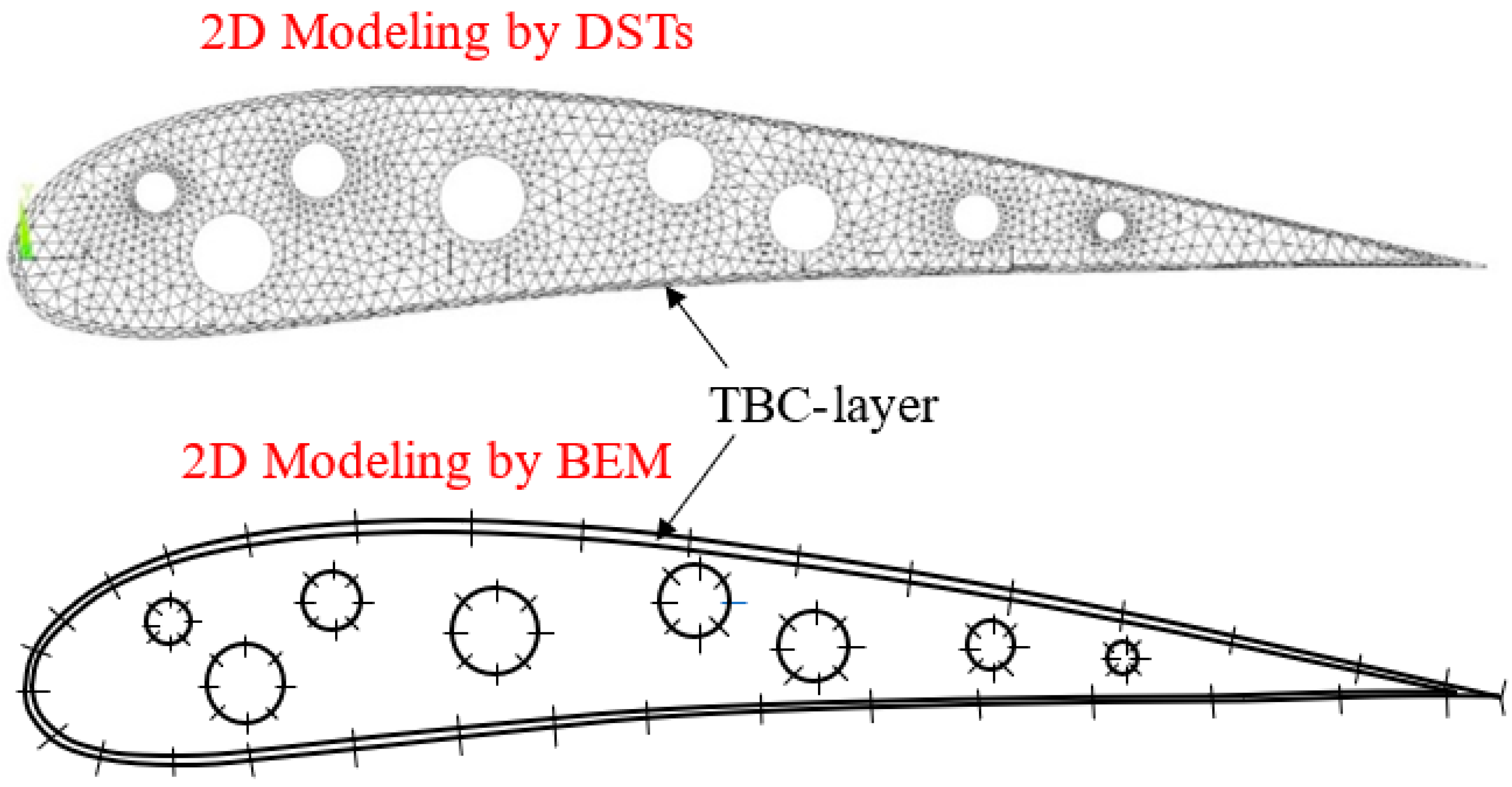
3. Model Simplification of a TBC Blade

With reference to Figure 4, the consideration of the boundary conditions outside the blade is categorized into two separate cases, namely (A) forced convection with ambient temperature $T_{\infty }$ and (B) the Dirichlet condition with prescribed temperature $T_{\infty }$. Treatments for both cases are described in the following.

3.1. Case (A)

As presented previously, case (A) may be treated by modeling the TBC blade as two dissimilarly adjoined media with thermal resistance introduced to replace the two intermediate layers, i.e., Layer-1 and Layer-2. In such modeling, the issue of nearly singular integration will become involved, which will be addressed in the next section. For case (A), the boundary condition of the TBC is expressed as

$$-K^{(T)}\hspace{0.17em}{q}^{(T)}=h_{\infty }\left(T_T-T_{\infty }\right),$$

(12)

where the superscript (T) denotes Layer-T and $h_{\infty }$ denotes the convection coefficient. By performing the usual collocation process for the two sub-regions (i.e., the TBC layer and the blade substrate), one may acquire a system of simultaneous equations. However, the number of obtained equations is smaller than that of the boundary unknowns, including the values of T and/or q on the boundary surface and the interface. In addition to the collocated equations for all boundary nodes, more auxiliary equations are needed to solve for all boundary unknowns. This can be achieved by applying the interfacial conditions, i.e., Equations (5) and (11), and the convection relation on Layer-T, i.e., Equation (12). After collecting all the necessary equations, one may directly solve a combined system of equations for all the unknowns. In such a treatment, however, one needs to properly calculate the nearly singular integrals of modeling the TBC with coarse meshes.

When the TBC thickness is relatively small, the heat flux across Layer-T can be assumed to propagate linearly from the bottom to the top surface. The model for case (A) can be further simplified by introducing an additional pseudo-layer on top, prescribed with the Dirichlet condition of T_∞ outside. With such a substitution, the convective coefficient is treated as an “equivalent conductance” across the pseudo-layer. With the inclusion of the pseudo-layer, the complete model of the TBC blade now comprises four thin layers on top when the convection condition is replaced by the temperature, T_∞, prescribed outside. In treating all the four adjoined layers as one equivalent layer, the overall thermal resistance, $R_0$, is determined with

$$R_0=\left(\frac{t^{(2)}}{K^{(2)}}\right)\hspace{0.33em}\hspace{0.17em}+\left(\frac{t^{(1)}}{K^{(1)}}\right)\hspace{0.33em}+\left(\frac{t^{(T)}}{K^{(T)}}\right)+\left(\frac{1}{h_{\infty }}\right).$$

(13)

As a result, the equivalent thermal conductance, $\stackrel{⌢}{C}$, for the four layers is given by

$$\stackrel{⌢}{C}=\frac{1}{\left(t^{(2)}/K^{(2)}\hspace{0.33em}\hspace{0.17em}+t^{(1)}/K^{(1)}\hspace{0.33em}+t^{(T)}/K^{(T)}+1/h_{\infty }\right)}.$$

(14)

With such an equivalent treatment, one may redefine the equivalent convective coefficient, denoted as $\overline{h_{\infty }}$ here, to be

$$\overline{h_{\infty }}=\frac{1}{\left(t^{(2)}/K^{(2)}\hspace{0.33em}\hspace{0.17em}+t^{(1)}/K^{(1)}\hspace{0.33em}+t^{(T)}/K^{(T)}+1/h_{\infty }\right)}.$$

(15)

Thus, the simplified TBC blade model can be treated by considering only the substrate blade being subjected to the equivalent convection, with its coefficient defined by Equation (15). Now, the auxiliary condition of compatibility is given as

$$\frac{-{\lambda }^{(b)}}{{\mathrm{\Lambda }}^{(b)}{K}_{11}^{(b)}}{q}^{(b)}=\frac{\left(T_b-T_{\infty }\right)}{\left(t^{(2)}/K^{(2)}\hspace{0.33em}\hspace{0.17em}+t^{(1)}/K^{(1)}\hspace{0.33em}+t^{(T)}/K^{(T)}+1/h_{\infty }\right)}.$$

(16)

3.2. Case (B)

When the TBC surface is subjected to the Dirichlet condition (i.e., prescribed with temperature T_∞), one may likewise omit the modeling of all the coating layers. If thermal nonlinearity is present for Layer-T, one still needs to resort to the previous modeling of two adjoined media. If only linear conduction is considered, one may omit modeling the layers via replacing the Dirichlet condition with “equivalent convection”. For this simplified modeling, the equivalent conductivity, $K_0$, of the combined layers (including Layer-1, Layer-2 and Layer-T) is determined with

$$\frac{t^{(1)}+t^{(2)}+t^{(T)}}{K_0}=\left(\frac{t^{(2)}}{K^{(2)}}\right)\hspace{0.33em}\hspace{0.17em}+\left(\frac{t^{(1)}}{K^{(1)}}\right)\hspace{0.33em}+\left(\frac{t^{(T)}}{K^{(T)}}\right).$$

(17)

The algebraic rearrangement of Equation (17) yields

$$K_0=\frac{K^{(1)}{K}^{(2)}{K}^{(T)}\left(t^{(1)}+t^{(2)}+t^{(T)}\right)}{t^{(2)}{K}^{(1)}{K}^{(T)}+t^{(1)}{K}^{(2)}{K}^{(T)}+t^{(T)}{K}^{(1)}{K}^{(2)}}.$$

(18)

Now, the simplified modeling considers only the heat flow propagating from the blade substrate subjected to forced convection with ambient temperature T_∞. In such a treatment, the Dirichlet condition is substituted by the equivalent convection and its coefficient, given as

$${\overline{h}}_{\infty }=\frac{K^{(1)}{K}^{(2)}{K}^{(T)}}{t^{(2)}{K}^{(1)}{K}^{(T)}+t^{(1)}{K}^{(2)}{K}^{(T)}+t^{(T)}{K}^{(1)}{K}^{(2)}}.$$

(19)

With such an equivalent treatment, one may simulate heat conduction simply by modeling the blade substrate, not involving the other coating layers outside. By applying the anisotropic heat flux of the substrate and using Equation (19) for equivalent convection, one will obtain

$$\frac{-{\lambda }^{(b)}}{{\mathrm{\Lambda }}^{(b)}{K}_{11}^{(b)}}{q}^{(b)}=\frac{K^{(1)}{K}^{(2)}{K}^{(T)}}{t^{(2)}{K}^{(1)}{K}^{(T)}+t^{(1)}{K}^{(2)}{K}^{(T)}+t^{(T)}{K}^{(1)}{K}^{(2)}}\left(T_b-T_{\infty }\right).$$

(20)

Thus, Equation (20) can be used to supply additional auxiliary equations that can be combined with all the other collocation equations to solve for unknowns.

At this point, it is clear to see that the problem of 3D heat conduction for TBC blades can be simulated very efficiently using an equivalent treatment of the BEM. The remaining task is to properly calculate the integrals in Equation (3) that appear to be nearly singular when the modeling of Layer-T is necessary, the internal air passages are close to the blade surface or the trailing edge is modeled with coarse elements. To take care of this problem, the approach proposed by Shiah et al. [17] can be applied. However, that approach appears to be, computation-wise, less efficient due to the process of determining new functions by solving Poisson’s equations. To model a sophisticated TBC blade, it is necessary to apply a more efficient algorithm, which will be outlined next.

4. Treatment of Singularity Weakening

As described previously, the integrals in Equation (3) are nearly singular when the source point is very near to the integration element. For the transformation techniques of regularization (e.g., [13,14,15]), computations of the transformed integrals are indeed very costly, and thus, they appear less attractive when the 3D modeling of a TBC blade involves large amounts of meshes. Instead of analytical regularization of the integrals, the strategy for better computational efficiency is to weaken the integrals’ strength such that a slight increase in the Gauss number may overcome this issue in the modeling of the TBC blade. For brevity, the integrals in Equation (3) are denoted as

$$\begin{array}{l}{U}_m^{(c)}={\displaystyle {\int }_{-1}^1{\displaystyle {\int }_{-1}^1{N}^{(c)}(\xi ,\eta )G^{\prime }(\xi ,\eta )\left|J_m(\xi ,\eta )\right|\hspace{0.17em}d\xi \hspace{0.33em}d\eta }},\\ V_m^{(c)}={\displaystyle {\int }_{-1}^1{\displaystyle {\int }_{-1}^1{N}^{(c)}(\xi ,\eta )F^{\prime }(\xi ,\eta )\left|J_m(\xi ,\eta )\right|\hspace{0.17em}d\xi \hspace{0.33em}d\eta }}\end{array}$$

(21)

Firstly, the intrinsic domain, $\left(\xi ,\eta \right)\in \left[-1,1\right]$, for the integration is divided into a few sub-domains, consisting of nonsingular ones and nearly singular ones, where the source point, $P^{\prime }$, is projected. Figure 5 schematically depicts such a domain division; the circular region is for nearly singular integration and the rest (sub-domains 1~4) are for regular integrations.

Note that near-singularity originates directly from the radial distance, r, between the projection $\left({\xi }_0,{\eta }_0\right)$ and the field point in other places. It is clear that the computation will be more efficient if one concentrates all computation resources on r only. Thus, to integrate the nearly singular sub-domain, one may perform Gaussian integration under the polar coordinates, i.e.,

$$\begin{array}{l}{U}_{m0}^{(c)}={\displaystyle {\int }_0^{{\theta }_0}{\displaystyle {\int }_0^{r_0}{N}^{(c)}\left(r\cos \theta ,r\sin \theta \right)G^{\prime }\left(r\cos \theta ,r\sin \theta \right)}}\hspace{0.33em}\left|J_m\left(r\cos \theta ,r\sin \theta \right)\right|\hspace{0.17em}rdr\hspace{0.33em}d\theta ,\\ V_{m0}^{(c)}={\displaystyle {\int }_0^{{\theta }_0}{\displaystyle {\int }_0^{r_0}{N}^{(c)}\left(r\cos \theta ,r\sin \theta \right)F^{\prime }\left(r\cos \theta ,r\sin \theta \right)}}\hspace{0.33em}\left|J_m\left(r\cos \theta ,r\sin \theta \right)\right|\hspace{0.17em}rdr\hspace{0.33em}d\theta ,\end{array}$$

(22)

where the integration limits (r₀, θ₀) depend on the position of $P^{\prime }$. It can be seen that the singular orders of Equation (22) have been reduced by one order because of the multiplication of r in the integrands. As mentioned above, the near-singularity is associated with r only, but, as an effective means of integration, one may slightly increase the number of Gauss points for r only, say, by 32 points, and use a regular number for θ, say, simply eight points. Thus, the formulas of the Gaussian integrations for Equation (22) can be written as

$$\begin{array}{l}{U}_{m0}^{(c)}=\frac{{\theta }_0\hspace{0.33em}{r}_0}{4}{\displaystyle \sum _{i=1}^{32}{\displaystyle \sum _{j=1}^8\overline{G}\left(\frac{r_0}{2}{\zeta }_i+\frac{r_0}{2},\frac{{\theta }_0}{2}{\zeta }_j+\frac{{\theta }_0}{2}\right)}}\hspace{0.33em}{w}_i\hspace{0.33em}{w}_j,\\ V_{m0}^{(c)}=\frac{{\theta }_0\hspace{0.33em}{r}_0}{4}{\displaystyle \sum _{i=1}^{32}{\displaystyle \sum _{j=1}^8\overline{F}\left(\frac{r_0}{2}{\zeta }_i+\frac{r_0}{2},\frac{{\theta }_0}{2}{\zeta }_j+\frac{{\theta }_0}{2}\right)}}\hspace{0.33em}{w}_i\hspace{0.33em}{w}_j,\end{array}$$

(23)

where ${\zeta }_i,\hspace{0.33em}{w}_i$ denote abscissas and weights, respectively, and $\overline{G},\hspace{0.33em}\hspace{0.33em}\overline{F}$ are defined by

$$\begin{array}{l}\overline{G}\left(r,\theta \right)=N^{(c)}\left(r\cos \theta ,r\sin \theta \right)G^{\prime }\left(r\cos \theta ,r\sin \theta \right)\left|J_m\left(r\cos \theta ,r\sin \theta \right)\right|\hspace{0.17em}r,\\ \overline{F}\left(r,\theta \right)=N^{(c)}\left(r\cos \theta ,r\sin \theta \right)F^{\prime }\left(r\cos \theta ,r\sin \theta \right)\left|J_m\left(r\cos \theta ,r\sin \theta \right)\right|\hspace{0.17em}r.\end{array}$$

(24)

respectively.

Here, it should be emphasized that a slight increase in Gauss points for r only will not add a heavy computational burden. For the integration of the nth regular sub-domain (n = 1~4), the conventional Gaussian quadrature rule using eight points can be applied. Thus, by transforming the intrinsic coordinates of the sub-domain nodes to the new local coordinates, $({\xi }^{\prime },{\eta }^{\prime })\in \left[-1,\hspace{0.33em}1\right]$, one obtains

$$U_{mn}^{(c)}={\displaystyle \sum _{i=1}^8{\displaystyle \sum _{j=1}^8\widehat{G}\left({\zeta }_i,{\zeta }_j\right)}}\hspace{0.33em}{w}_i\hspace{0.33em}{w}_j,\hspace{1em}{V}_{mn}^{(c)}={\displaystyle \sum _{i=1}^8{\displaystyle \sum _{j=1}^8\widehat{F}\left({\zeta }_i,{\zeta }_j\right)}}\hspace{0.33em}{w}_i\hspace{0.33em}{w}_j.$$

(25)

In Equation (25), $\widehat{G}\hspace{0.33em}\mathrm{and}\hspace{0.33em}\widehat{F}$ are defined as

$$\begin{array}{l}\widehat{G}\left({\xi }^{\prime },{\eta }^{\prime }\right)=\left[N^{(c)}({\xi }^{\prime },{\eta }^{\prime })G^{\prime }({\xi }^{\prime },{\eta }^{\prime })\left|J_m({\xi }^{\prime },{\eta }^{\prime })\right|\right]\cdot \left|{\widehat{J}}_n({\xi }^{\prime },{\eta }^{\prime })\right|,\\ \widehat{F}\left({\xi }^{\prime },{\eta }^{\prime }\right)=\left[N^{(c)}({\xi }^{\prime },{\eta }^{\prime })F^{\prime }({\xi }^{\prime },{\eta }^{\prime })\left|J_m({\xi }^{\prime },{\eta }^{\prime })\right|\right]\cdot \left|{\widehat{J}}_n({\xi }^{\prime },{\eta }^{\prime })\right|,\end{array}$$

(26)

respectively, where $\left|{\widehat{J}}_n({\xi }^{\prime },{\eta }^{\prime })\right|$ represents the Jacobian transformation of the nth sub-domain.

After the integrals are properly calculated using Equations (23) and (25) for all sub-domains, the field values of T and q inside the sub-domains can be interpolated by the nodal values of the original element under integration. As a result, the original integrals in Equation (21) can be obtained from the interpolation of the sub-domain values calculated with Equations (23) and (25). It should be pointed out that because no analytical transformation of the integrands is involved, all computations using the algorithm are very speedy and straightforward.

5. Numerical Examples

The methodology and algorithm presented above have been implemented in a FORTRAN code for the analysis of heat conduction in a TBC blade. Firstly, to demonstrate the validity of the implemented code, Example I revisits the TBC system presented in [17] but with different boundary conditions prescribed. The reason why different boundary conditions have been prescribed is to test the validity of the BEM treatment of the forced convection that was not considered in [17]. It should be noted that the purpose of prescribing different boundary conditions is to investigate the present treatment of forced convection. In addition, another purpose is to show the temperature profile across the TBC layers, better demonstrating the insulation of the TBC. The TBC system in Figure 6 consists of three thin layers on top of a single crystal substrate, β-Ga₂O₃. The TBC layers include one layer of ZrO₂ on top, an intermediate oxide layer of Al₂O₃ and a bond coat layer of NiCrAlY on the bottom. The conductivities of the coating layers are ZrO₂ = 1.7 (W/m °C) for Layer-T, Al₂O₃ = 12.2 (W/m °C) for Layer-2 and NiCrAlY = 22.5 (W/m °C) for Layer-1. The β-Ga₂O₃ material is used for the substrate medium, with the following principal conductivities:

$$K_{11}^{\ast }=13.3\hspace{0.33em}\left(W/m\hspace{0.33em}°\mathrm{C}\right),\hspace{1em}{K}_{22}^{\ast }=9.5\hspace{0.33em}\left(W/m\hspace{0.33em}°\mathrm{C}\right),\hspace{1em}{K}_{33}^{\ast }=22.5\hspace{0.33em}\left(W/m\hspace{0.33em}°\mathrm{C}\right),$$

(27)

where the asterisk denotes the principal direction. The principal axes of the substrate are successively rotated around the x₃/x₁/x₂ axis by 30°/45°/60°, respectively, clockwise to generate anisotropic properties. The thickness of the three layers is t/L = 10⁻². As listed in

Table 1. Boundary conditions prescribed for Examples I and II.

	Problem I	Problem II
Forced Convection (T∞ = 1000 °C)	Top surface of the TBC (ZrO2)	Blade surfaces on top/bottom
Dirichlet Condition (T = T0)	T0 = 0 °C Outside surfaces of the substrate (β-Ga2O3)	T0 = −50 °C Blade tip and root surfaces at x3 = 0 and −L
Neumann Condition Insulation (q = 0)	Side edges of the top three layers	Tip/root surfaces at x3 = 0 and −L

for the boundary conditions, all outside surfaces of the substrate are insulated and the top coating surface is subjected to forced convection, with its coefficient assumed to be h = 40.79 $(W/m^2\hspace{0.33em}°\mathrm{C})$ and the air temperature taken as T_∞ = 1000 °C. All the other outside surfaces of the thin layers are insulated. Since overloaded computation will happen to ANSYS analysis with a thickness ratio smaller than 10⁻², the present case has considered only a thickness ratio down to 10⁻² for comparison purposes, although BEM modeling is capable of dealing with much smaller thicknesses. For the validation of the BEM analyses, this problem was also analyzed with ANSYS, using a test of grid sensitivity to ensure the convergence of the results. For the modeling, 640 quadratic elements were applied in the BEM analysis for all the thin layers on top, while in ANSYS, 280,000 SOLID226 elements were employed. The complete modeling of all the thin layers was simply to test the validity of the presented algorithm in calculating nearly singular integrals. Using the simplified model to replace the top three layers, the CPU time of the BEM analysis took only a fraction of that of the complete model, while the results remained about the same. These analyses were carried out using a Windows-based PC equipped with the following CPU: AMD–Ryzen5 5600X 6-Core Processor 3.70 GHz (RAM 16 GB). Not mentioning the meshing efforts involved, the CPU time for the BEM analysis was 15.05 s, while that for ANSYS was 1526.11 s. When t/L falls below 10⁻², the BEM approach can still work with the same CPU time, though overloaded computation would happen to ANSYS analysis using elements with an aspect ratio of 1:20. Figure 7 plots the calculated temperature along the midline, $\overline{A{A}^{\prime }}$ (x₁ = 0.25 L), on top of the substrate. The distributions of the computed temperature along $\overline{B{B}^{\prime }}$ and $\overline{C{C}^{\prime }}$ across the coating layers are plotted in Figure 8. From the comparisons in Figure 7 and Figure 8, the BEM analyses are in excellent agreement with those from ANSYS.

As shown in Figure 9, Example II analyzes the anisotropic heat conduction in a NACA2424 blade made of titanium alloy, whose principal conductivities are taken to be

$$K_{11}^{\ast }=20.0\hspace{0.33em}\left(W/m\hspace{0.33em}°\mathrm{C}\right),\hspace{1em}{K}_{22}^{\ast }=15.0\hspace{0.33em}\left(W/m\hspace{0.33em}°\mathrm{C}\right),\hspace{1em}{K}_{33}^{\ast }=18.0\hspace{0.33em}\left(W/m\hspace{0.33em}°\mathrm{C}\right).$$

(28)

The principal axes are rotated in the same manner as the previous case. Suppose there are five internal cooling air passages inside, as shown in Figure 9. The prescribed boundary conditions are listed in Table 1. The radius of the passages should be chosen to be 0.015 $\overline{C}$, since the target is to analyze the heat condition in the blade but not to study the aerodynamic performance. For simplicity, no twisted angle of the blade will factor into the blade design. Here, it should be noted that this example is simply a demonstration of applying the BEM modeling for analysis as compared to ANSYS analysis. As aforementioned, the sophisticated design of a practical TBC blade may lead to overloaded computation for DSTs, especially when the coating layer is very thin. Thus, for ANSYS simulation to provide comparative data, the modeling of a TBC layer should not enter into the design. To expedite the preparation of the input data for the BEM code, an auto-meshing program for the BEM modeling of a turbine blade has been developed in our laboratory. For the BEM modeling, 532 quadratic elements were applied, while 862,375 elements were employed in ANSYS. As the boundary condition, the blade top/bottom surfaces were prescribed T_∞ = 1000 °C, a constant temperature of −50 °C was applied on all cooling air passages and the other surfaces on the tip and the root were insulated. In clocking the CPU times of both approaches, the BEM analysis took only 25.17 s and ANSYS was cost 201.1 s. Figure 10 plots the temperature distribution along the mean chord line, calculated with both approaches. The calculated temperature distribution on the whole plane of x₃ = 0 is plotted in Figure 11. As can be observed from the comparison in Figure 10 and Figure 11, most parts of the blade can be significantly cooled down by introducing internal cooling air passages. However, the proper arrangement of the air passages to meet all requirements of blade design needs further optimizing analysis via more simulations. This comparison shows the perfect agreement of both analyses, though the CPU time of the BEM took only roughly 1/8 of that of ANSYS.

To demonstrate the applicability of the BEM code for the heat conduction analysis of a TBC blade, Example III investigates a typical TBC blade, as shown in Figure 12, whose chord length is denoted as $\overline{C}$. Once again, the aerodynamic design of the blade is not in the present interest, and thus, no discussion about the blade shape is intended here. Even though the twisted angle of a blade is an important parameter of design, the general behavior of heat conduction in each cross-section remained similar, and thus, for simplicity, the analyzed model did not involve the twisted angle. Suppose the titian alloy in Example II is used as the blade substrate and the coating layers include ZrO₂ for Layer-T, with t^(T) = 2.0 $\times {10}^{-3}$$\overline{C}$; Al₂O₃ for Layer-2, with t⁽²⁾ = 4.0 $\times {10}^{-4}$$\overline{C}$; and NiCrAlY for Layer-1, with t⁽¹⁾ = 1.0 $\times {10}^{-3}$$\overline{C}$. The conductivities of all materials used follow those provided in the previous examples. According to Equation (19), the equivalent convective coefficient will be determined to be

$${\overline{h}}_{\infty }=6.38\times {10}^{-3}\hspace{0.33em}\left(\frac{W}{{\overline{C}}^2°C}\right)$$

(29)

All the boundary conditions prescribed remain the same as in Example II. The BEM modeling applied only 532 quadratic elements with 1705 nodes, and the CPU time for this analysis took 27.06 s. Here, it should be emphasized that due to the overloaded computation that occurred in ANSYS when modeling the TBC layers, no comparative data from independent tools are available. This also marks the advantages of applying the present approach for this analysis. However, as expected, when all the TBC layers were modeled for this analysis by applying the algorithm of nearly singular integration, the agreement of the results was observed. Also shown in Figure 12 are the colored contours of temperature distribution in the TBC blade, with two different designs of internal cooling air passage.

6. Conclusions

In providing the excellent performance of a turbine system, the ideally designed blades of aero-parts play a key role. To enhance material endurance under extremely high temperatures, the proper design of cooling/insulation for a blade is of the utmost importance. Despite the BEM’s obvious advantages in engineering analysis, pertinent BEM works on 3D anisotropic heat conduction in TBC blades have remained unexplored in the open literature. The main reasons originate from the difficulty of modeling thin TBC layers and the numerical difficulty of evaluating nearly singular integrals. Regarding the modeling issue, convectional DSTs are also confronted with modeling challenges in the constraints of the proper aspect ratios of elements. Thus, the conventional modeling of TBC layers is often omitted to avoid overloaded computation. This article presents the BEM modeling of TBC layers by posing equivalent boundary/interface conditions to replace the modeling of multiple thin layers. With such treatment, this modeling can be significantly simplified, and the simulation will turn out to be very efficient. Another critical issue, that of nearly singular integration, also enters this analysis in the modeling of the internal passages, the top TBC layer and the trailing edge of the blade. To resolve this issue, the present analysis employs an efficient algorithm of domain sub-division. In the sub-domain with near-singularity, integrals are computed under polar coordinates, whereas in the others, they are directly computed with the standard quadrature rule, simply using eight points. Since no transformation of the integrand is involved, this computation is very speedy indeed. A few final remarks can be made, as follows:

1.

In treating multiple thin layers coated on the TBC blade, the BEM may simply impose equivalent boundary conditions to replace the modeling of the thin layers. With such a treatment, significant modeling efforts can be saved and the computation expedited with much better efficiency.

2.

Regardless of the thinness of TBC layers, the CPU time of the BEM simulation will remain unchanged; however, it shall increase exponentially with any decrease in TBC thinness in convectional DSTs.

3.

Having been verified with ANSYS analysis, our examples have shown that the BEM algorithm is capable of analyzing 3D anisotropic heat conduction in a TBC blade by using modeling with very coarse meshes.

4.

The same meshing scheme using coarse meshes is applicable to various turbine blades with very different geometries. In contrast, when employing conventional DSTs, one needs to model each distinctive case with different meshing adaptively. So far, the BEM algorithm developed has not been commercialized for general design, and thus, meshing still requires laborious modeling. Nevertheless, it is very promising that the BEM code will be developed into friendly software capable of providing auto-meshing for general design.

As a final conclusion, the proposed BEM algorithm is very ideal to be applied in the 3D heat conduction analysis of TBC blades due to its great computational efficiency and the light modeling efforts required.