Fluid-Dynamic and Aeroacoustic Characterization of Side-by-Side Rotor Interaction
Abstract
:1. Introduction
2. Theoretical Background
2.1. Proper Orthogonal Decomposition
2.2. Wavelet Transform
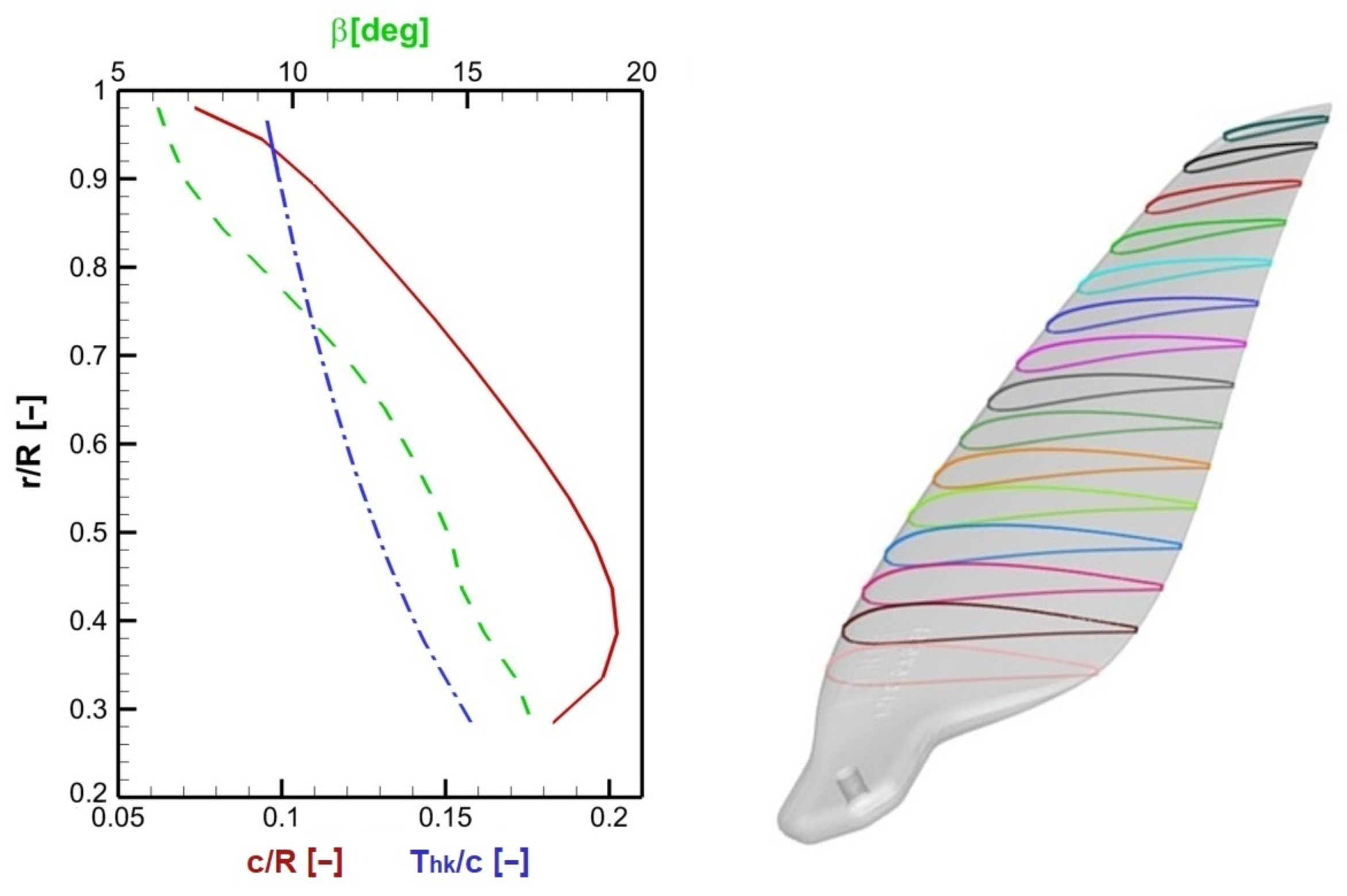
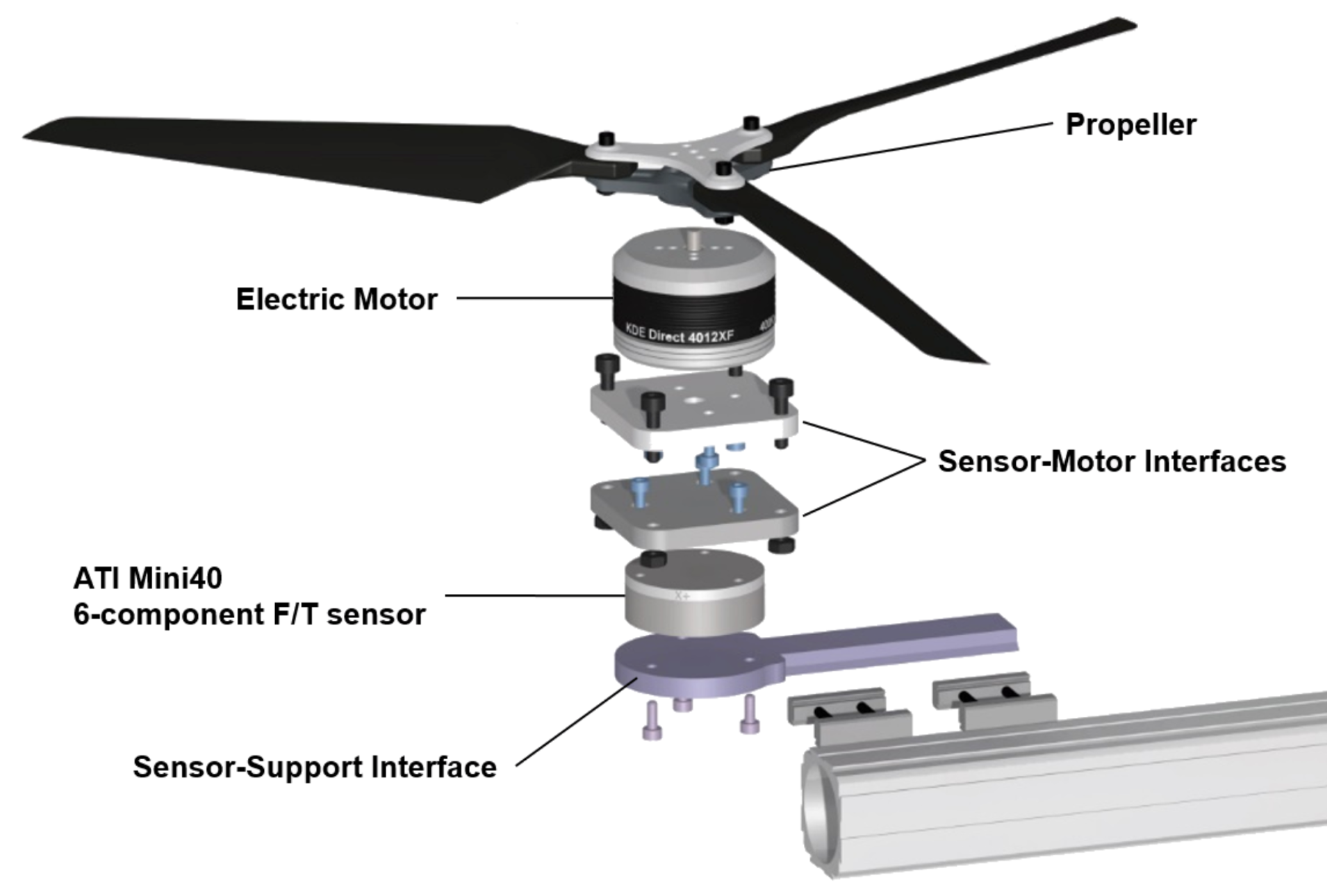
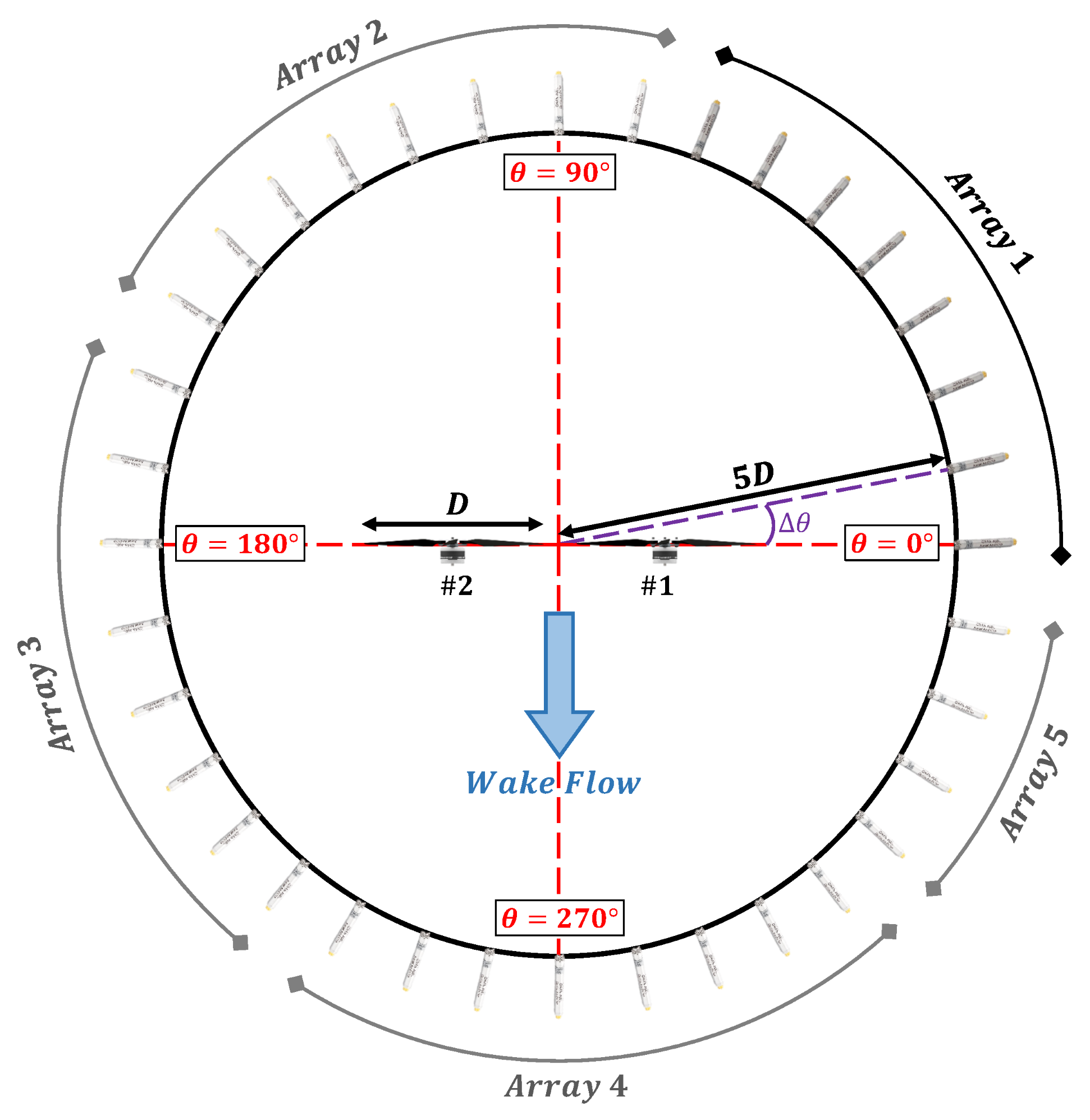
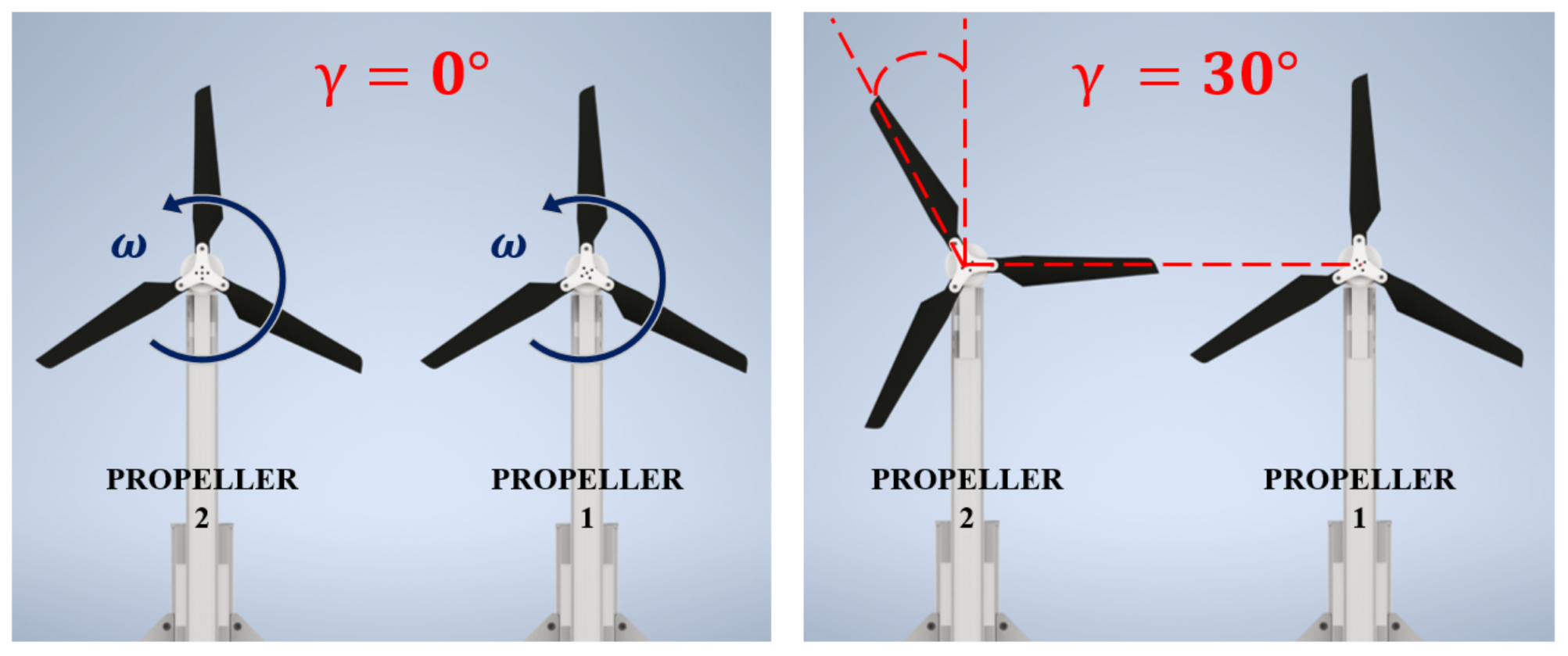
3. Experimental Setup
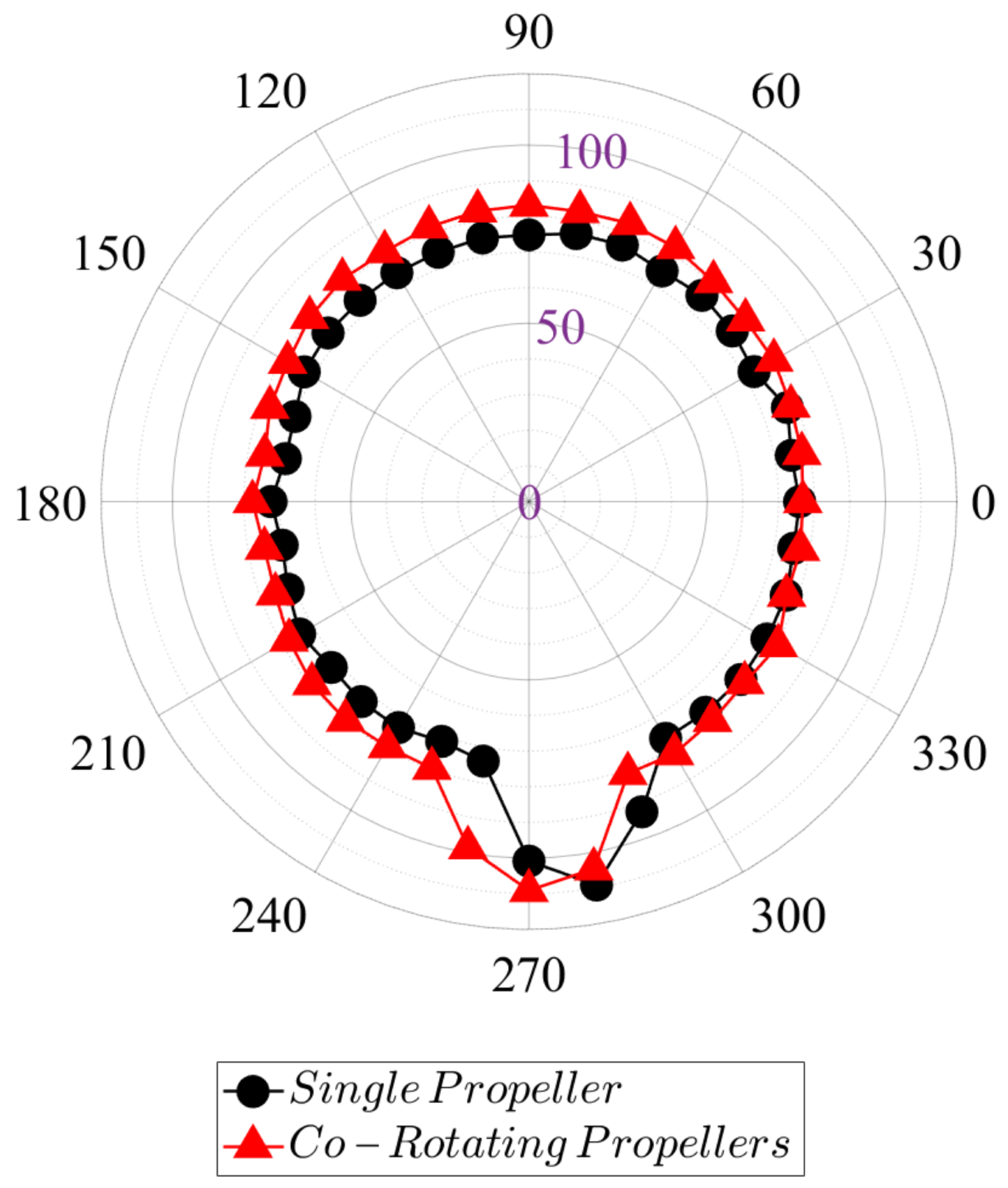
4. Results and Discussion
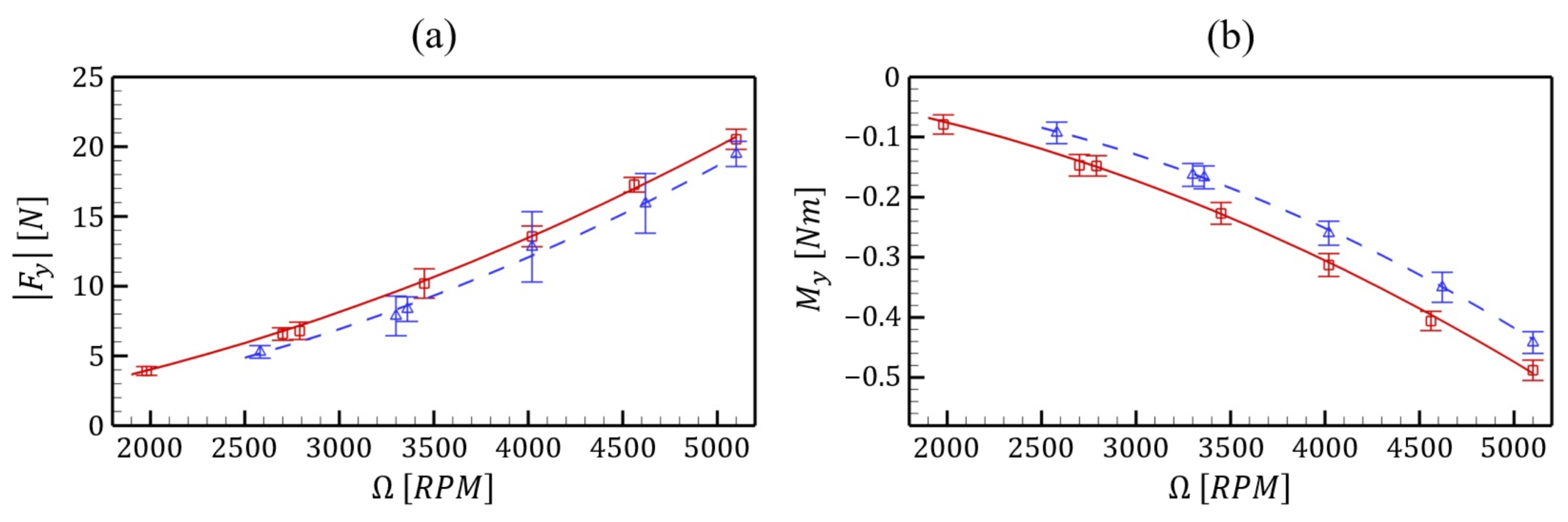
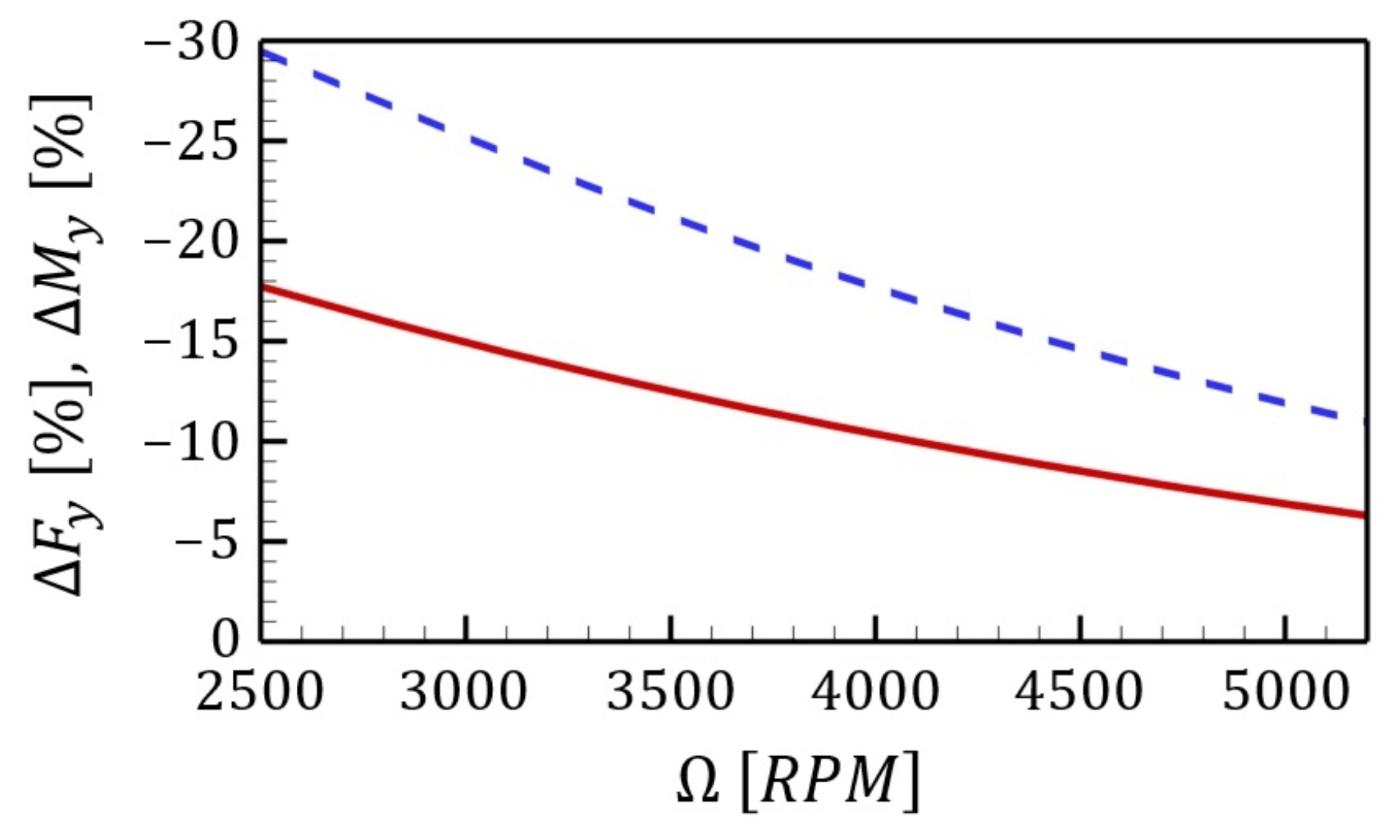
4.1. Dynamic Load Characterization
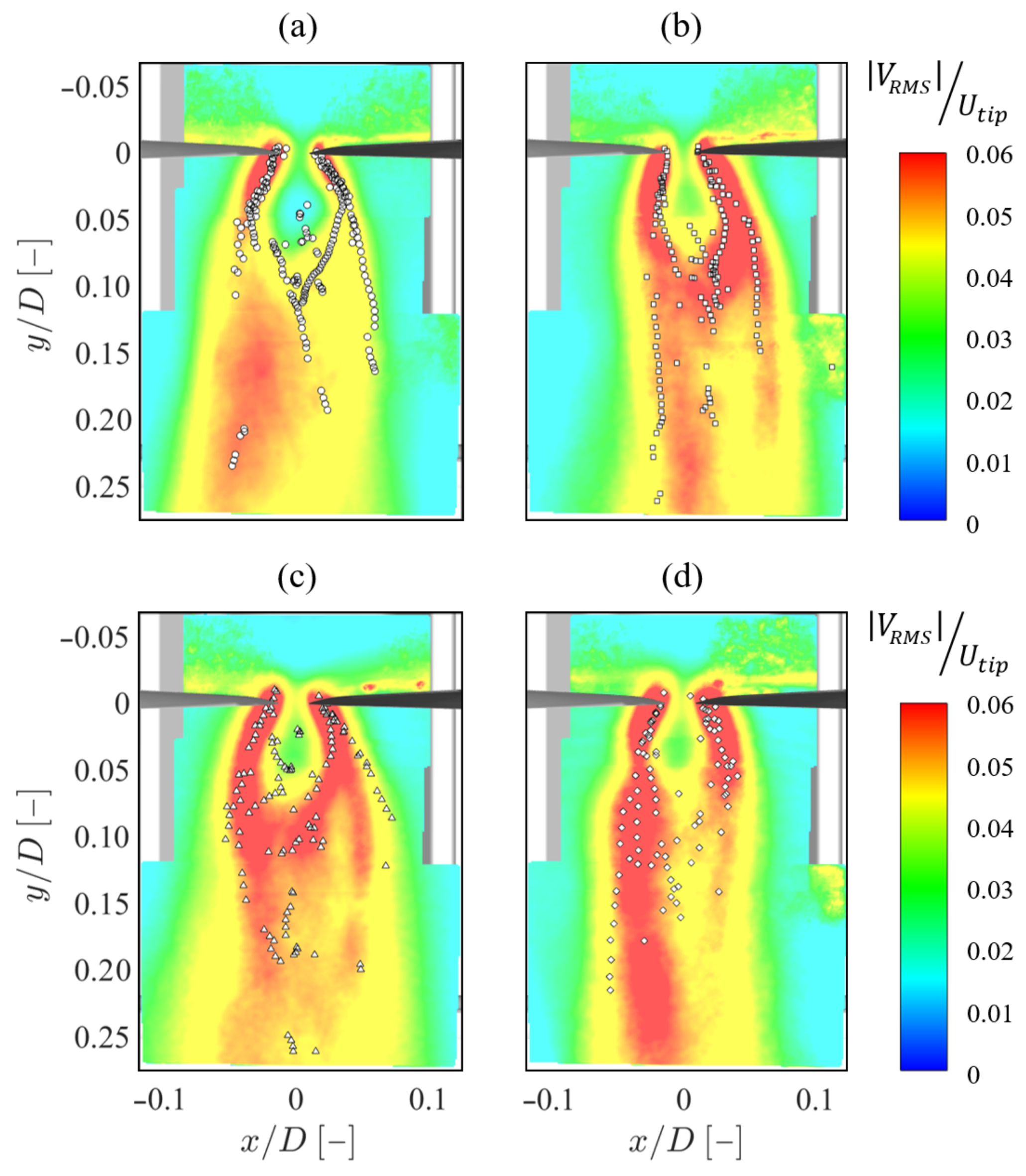
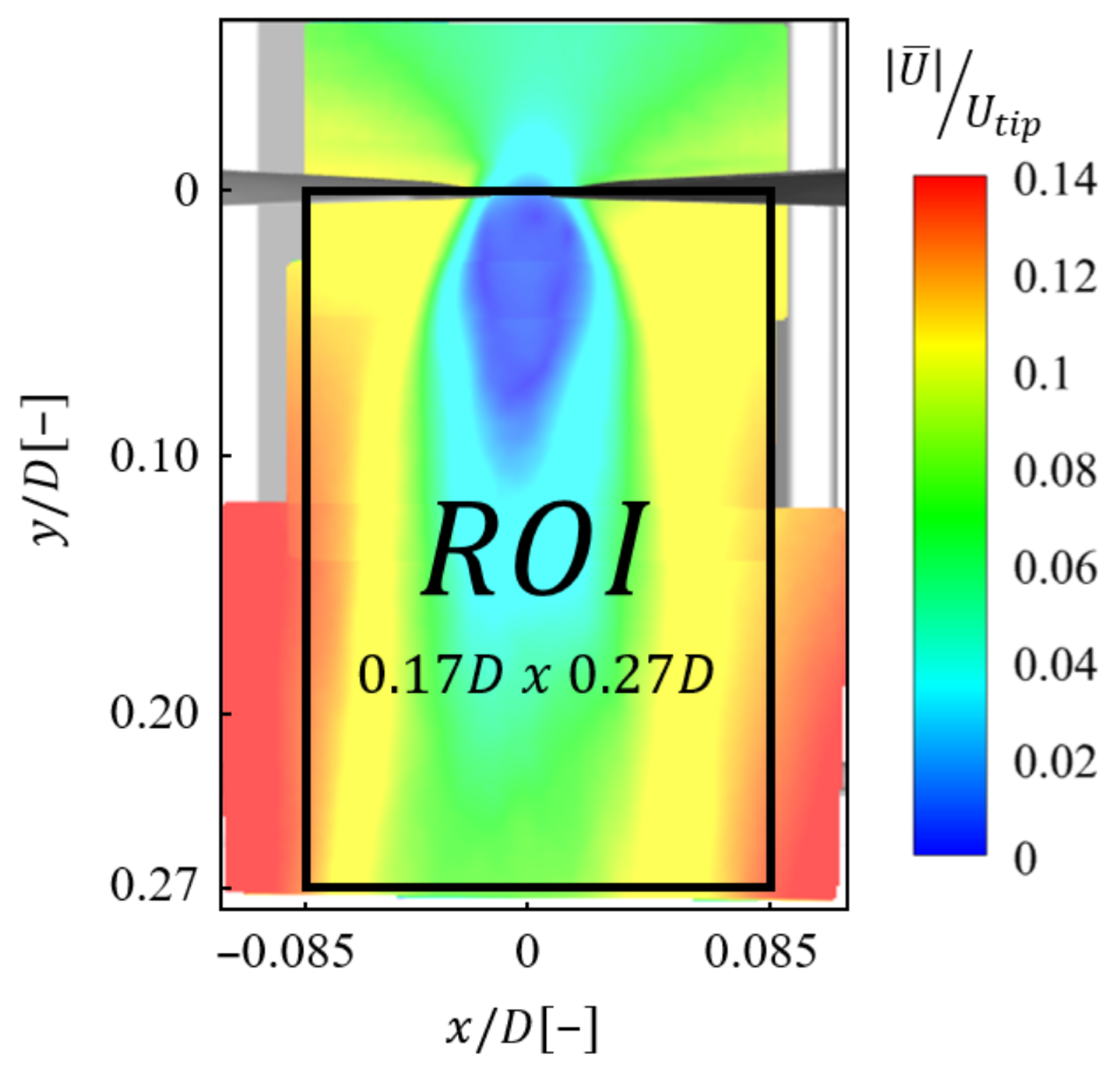
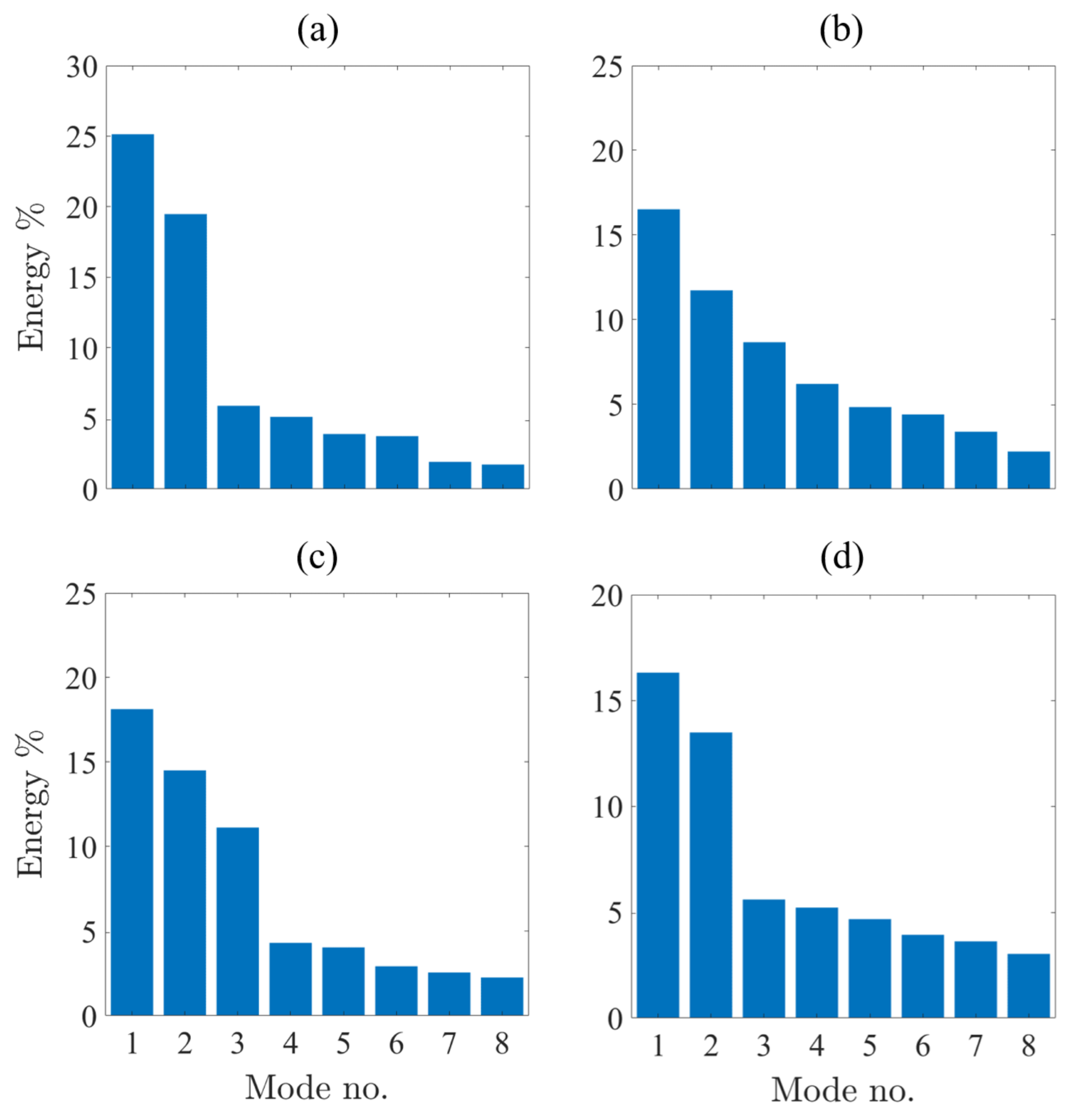
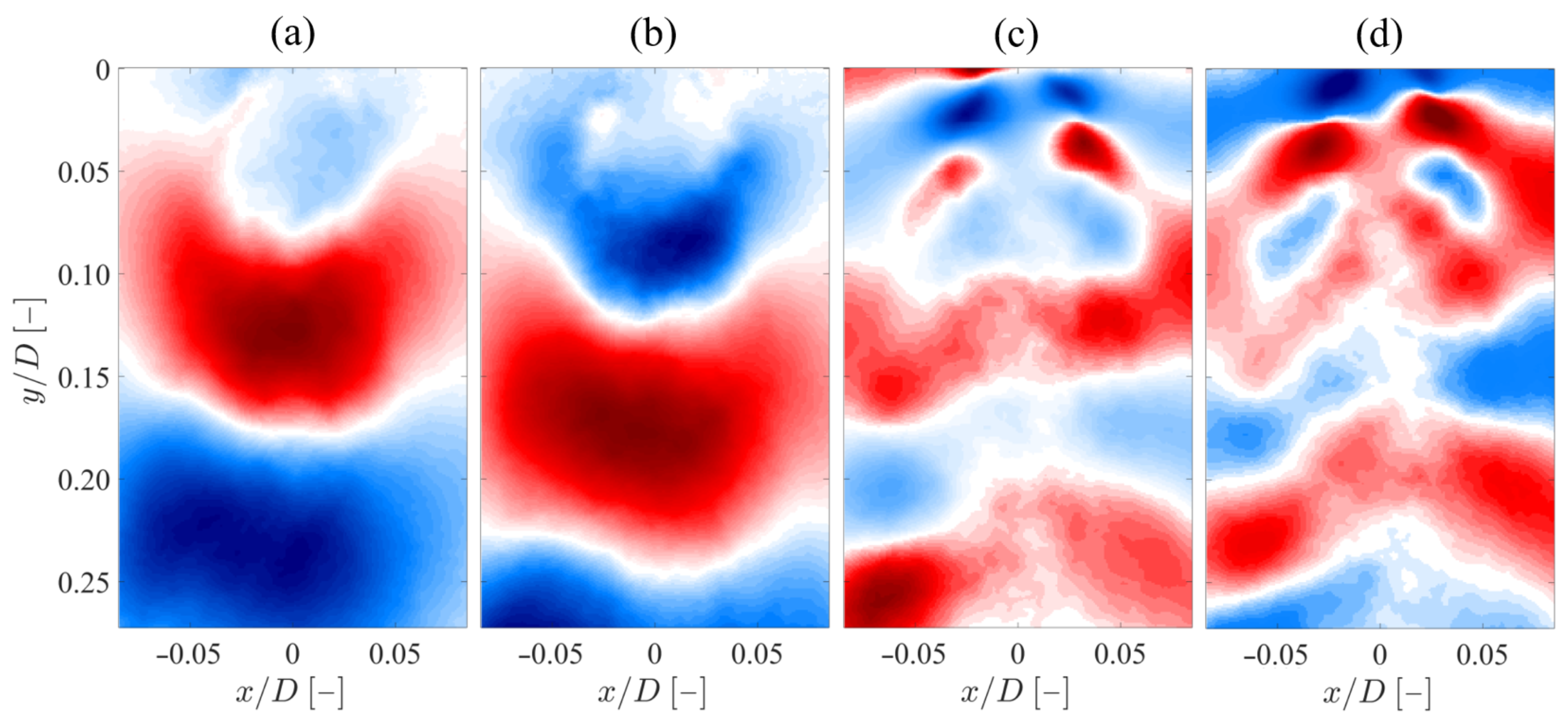
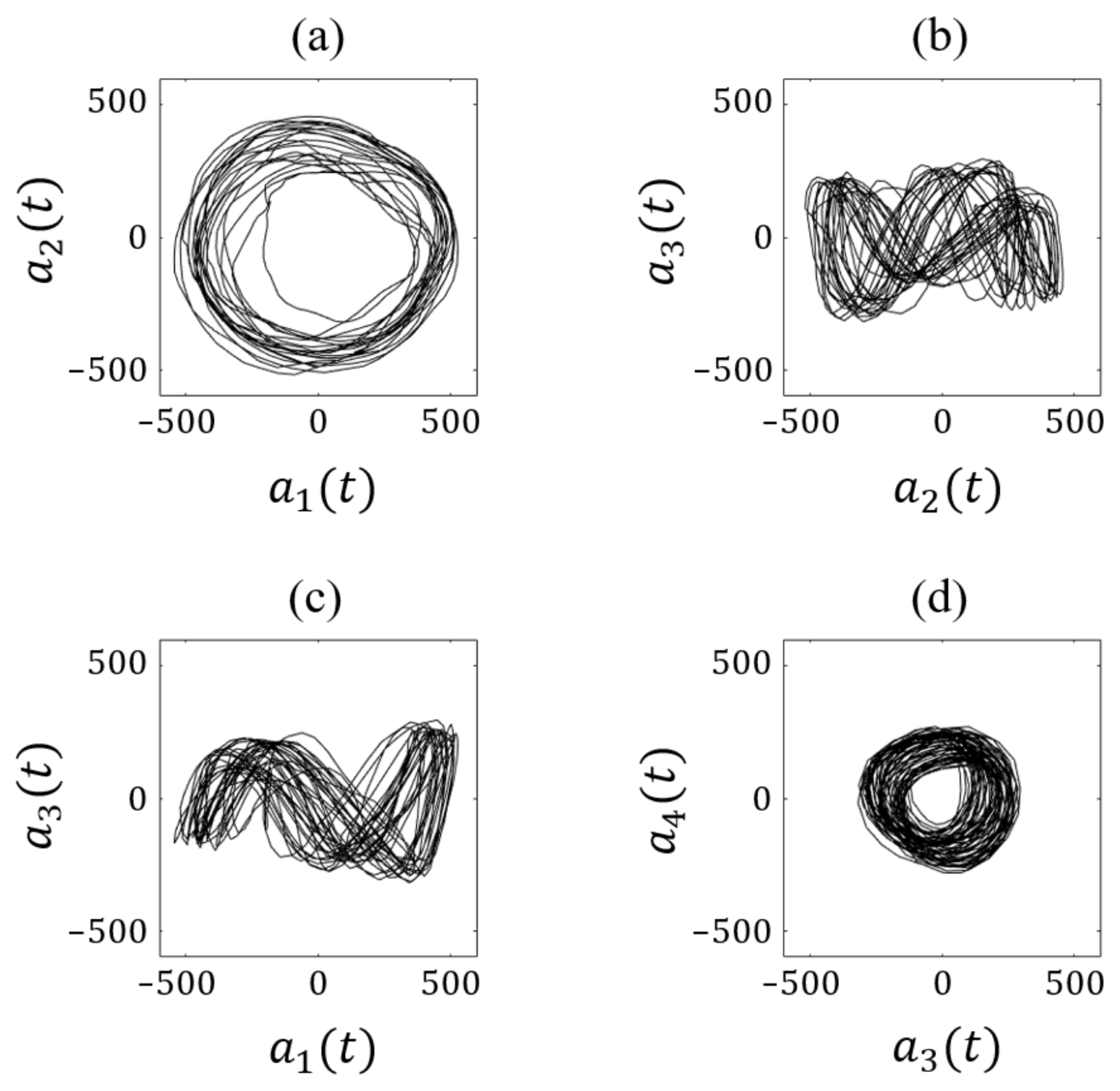
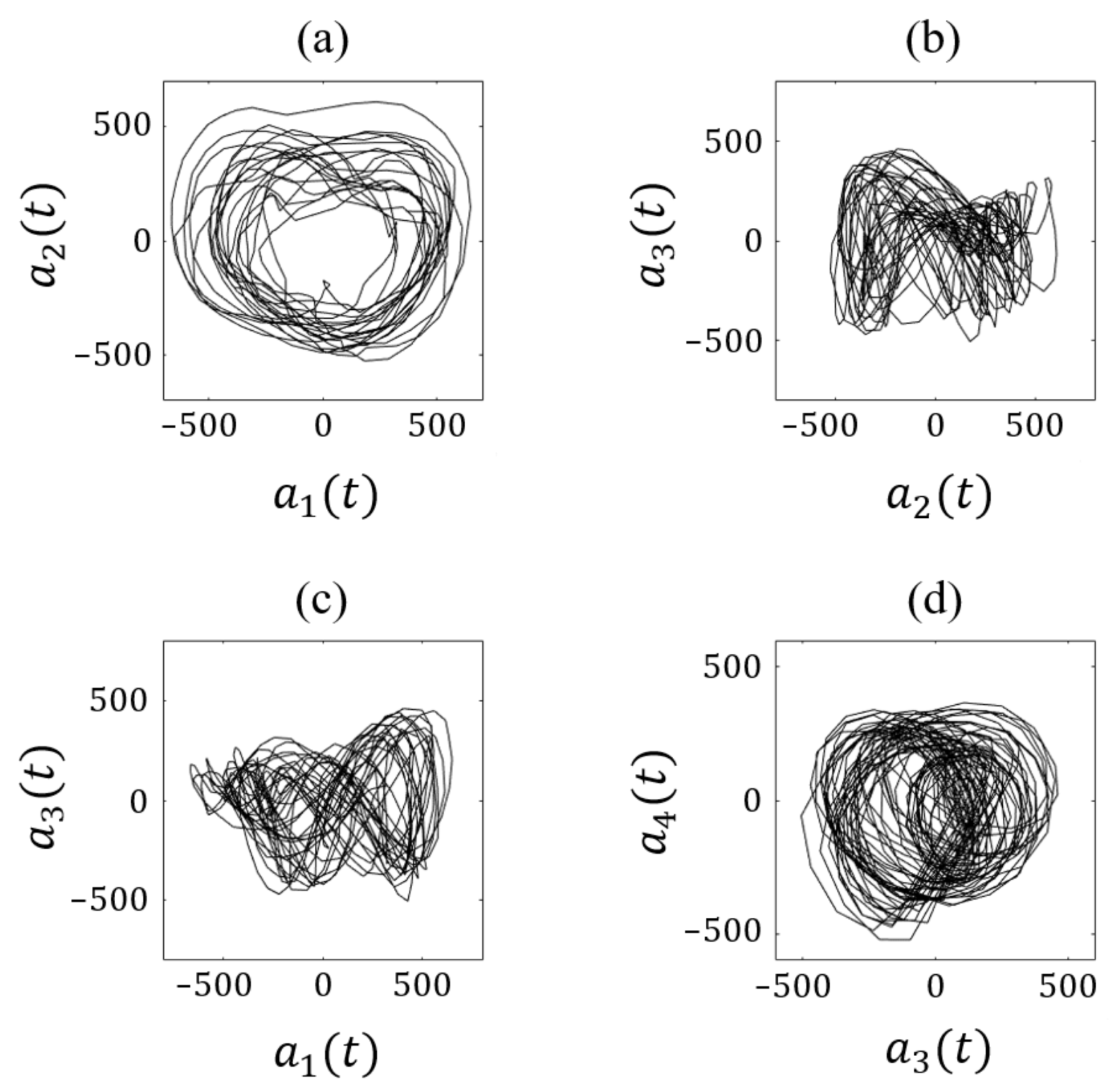
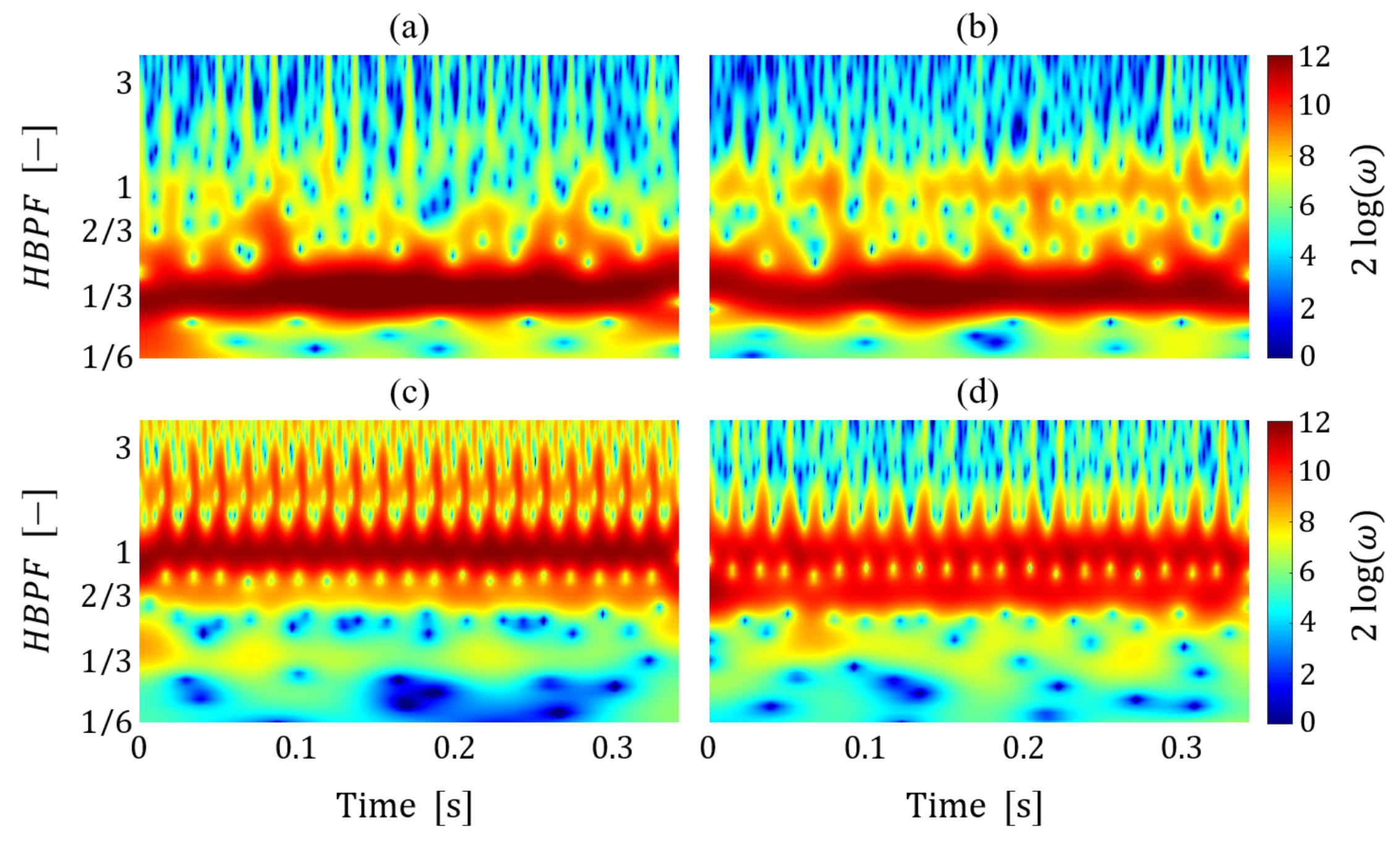
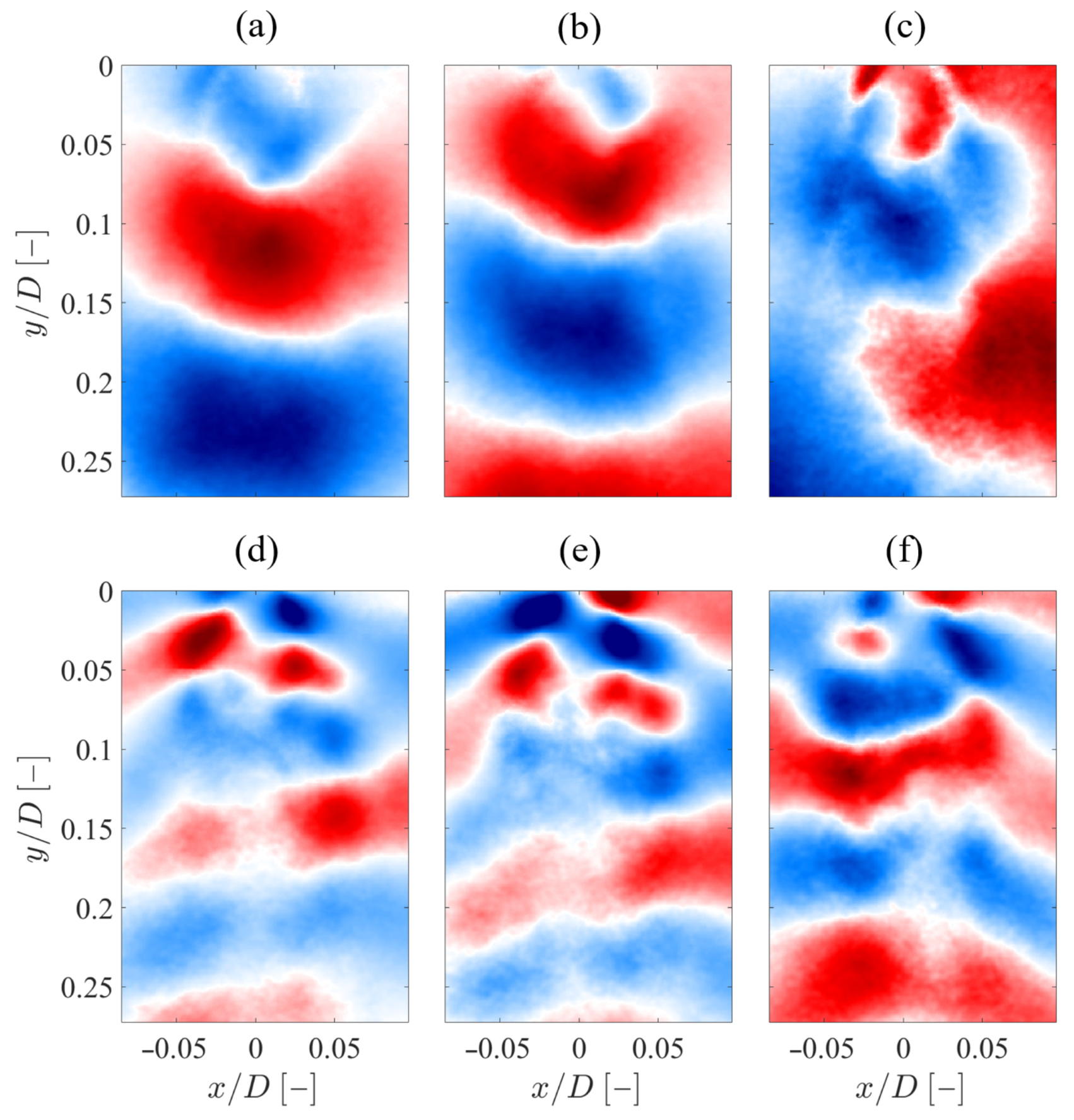
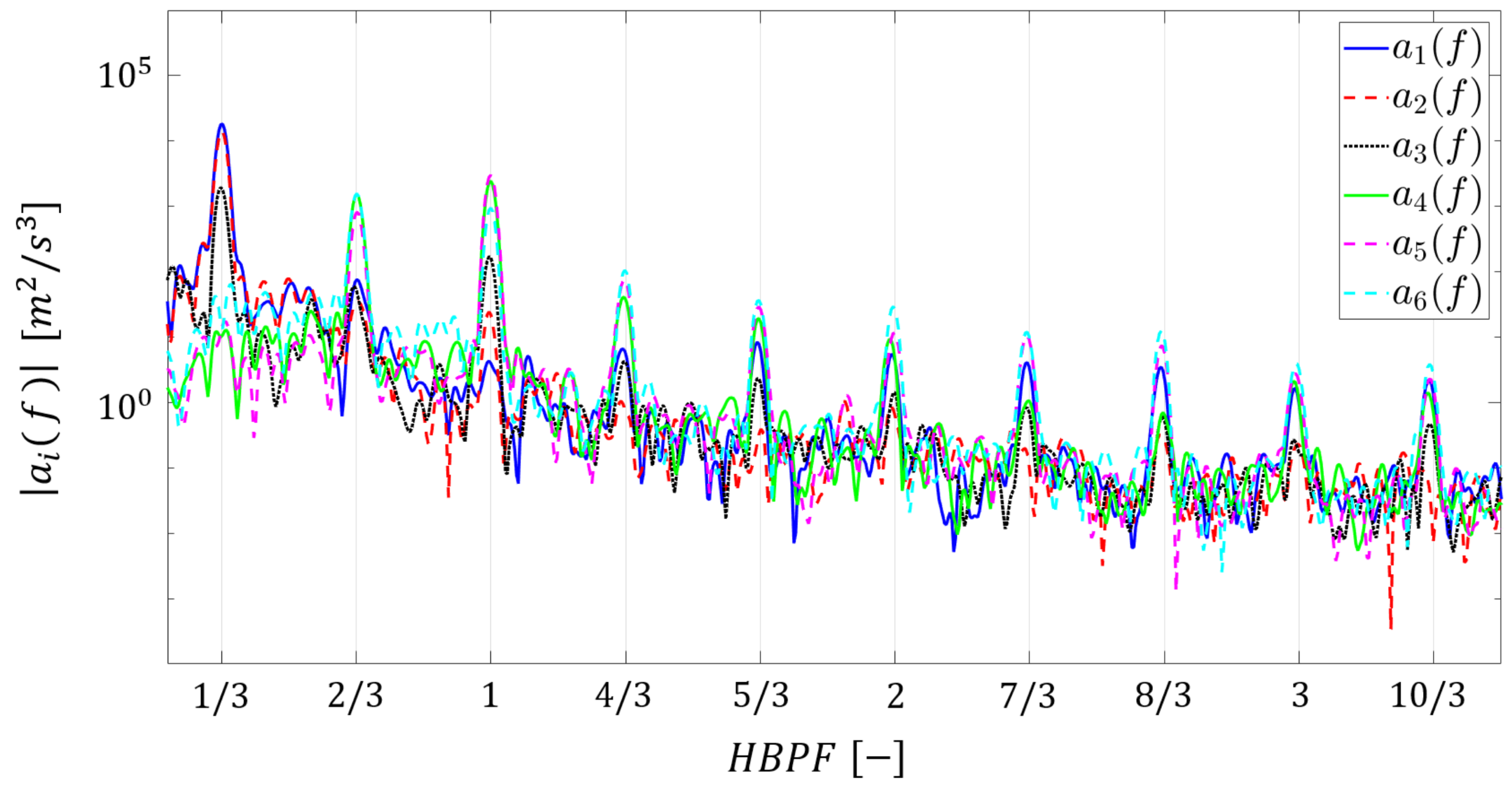
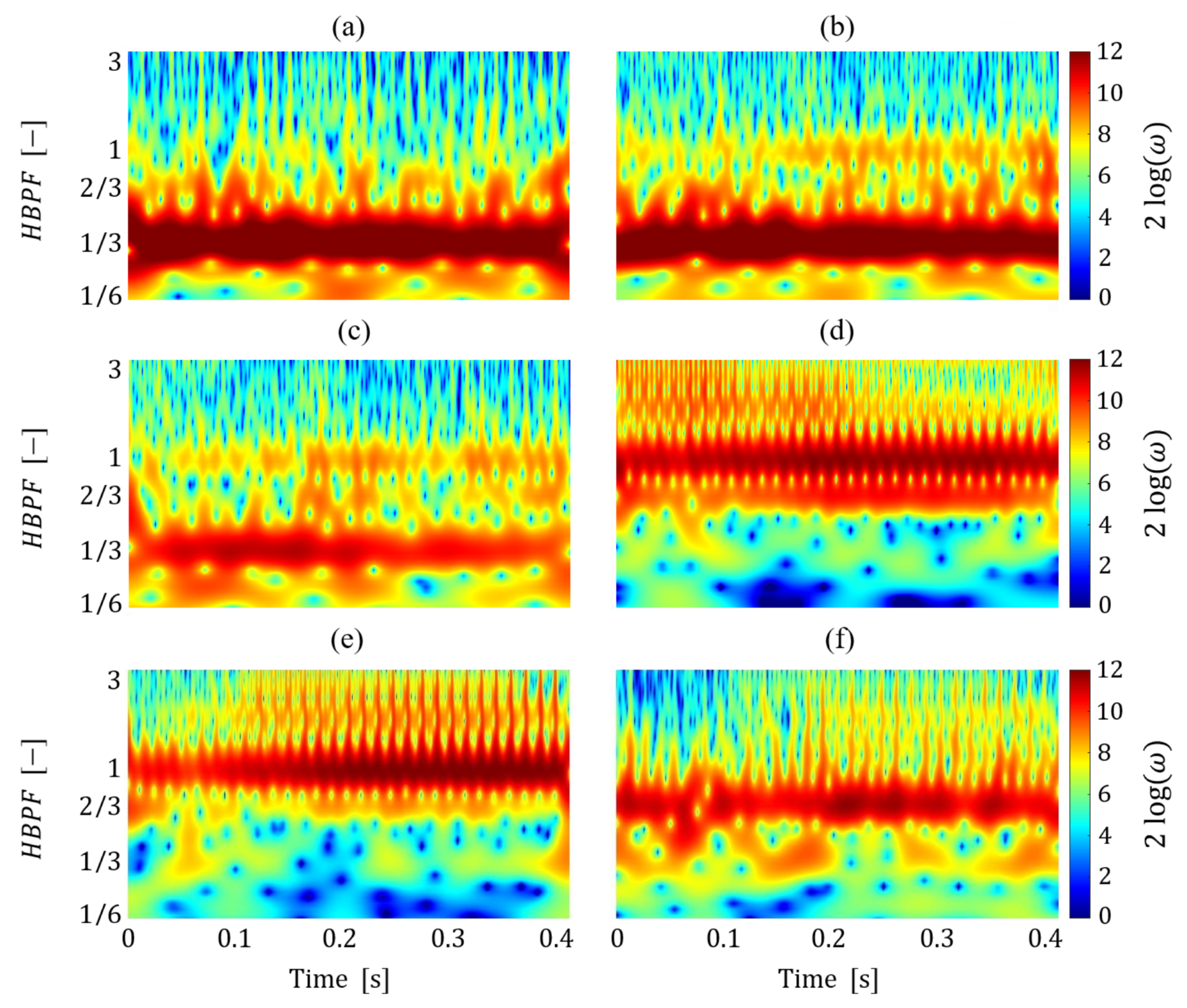
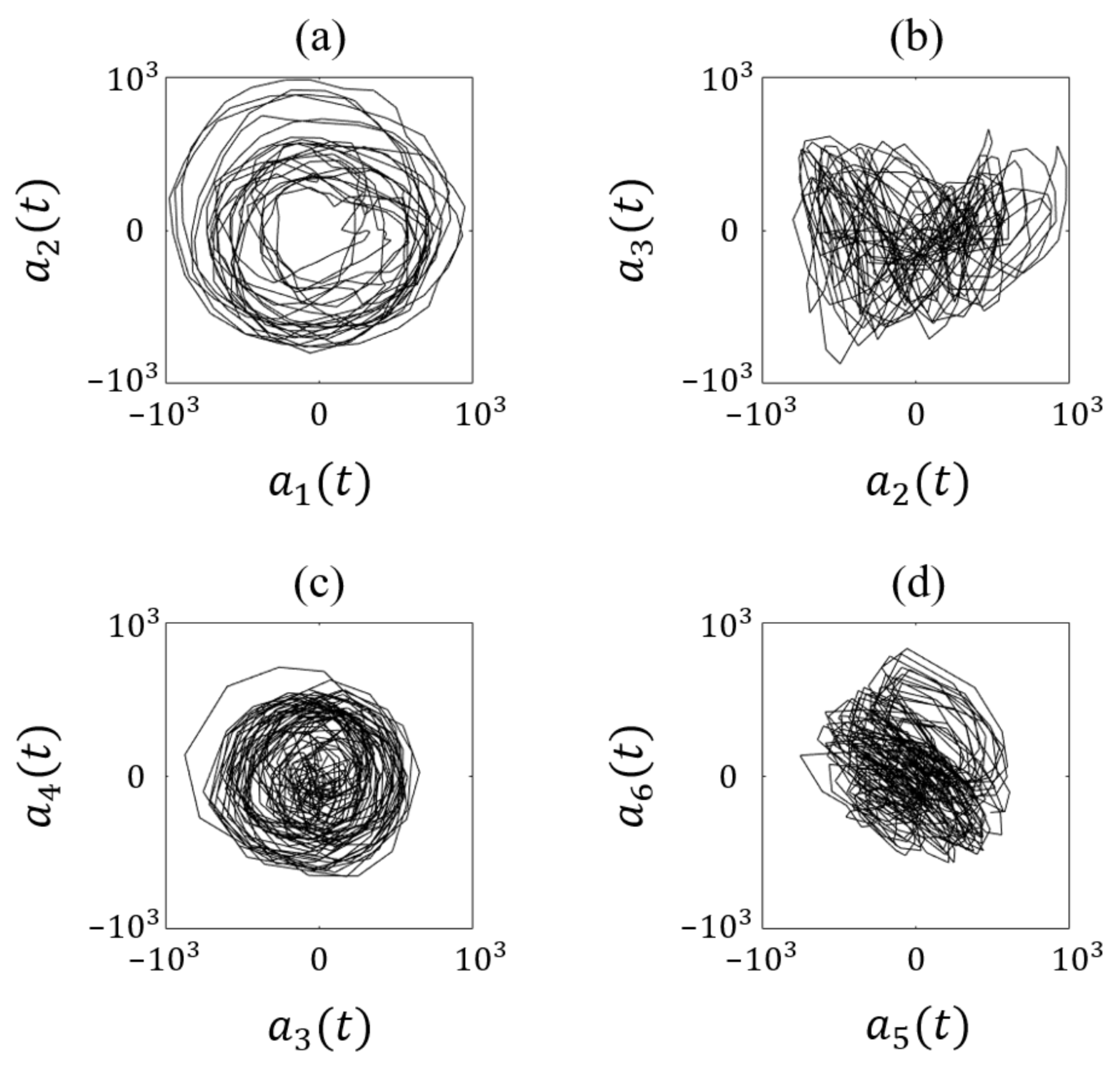
4.2. Flow Field Characterization
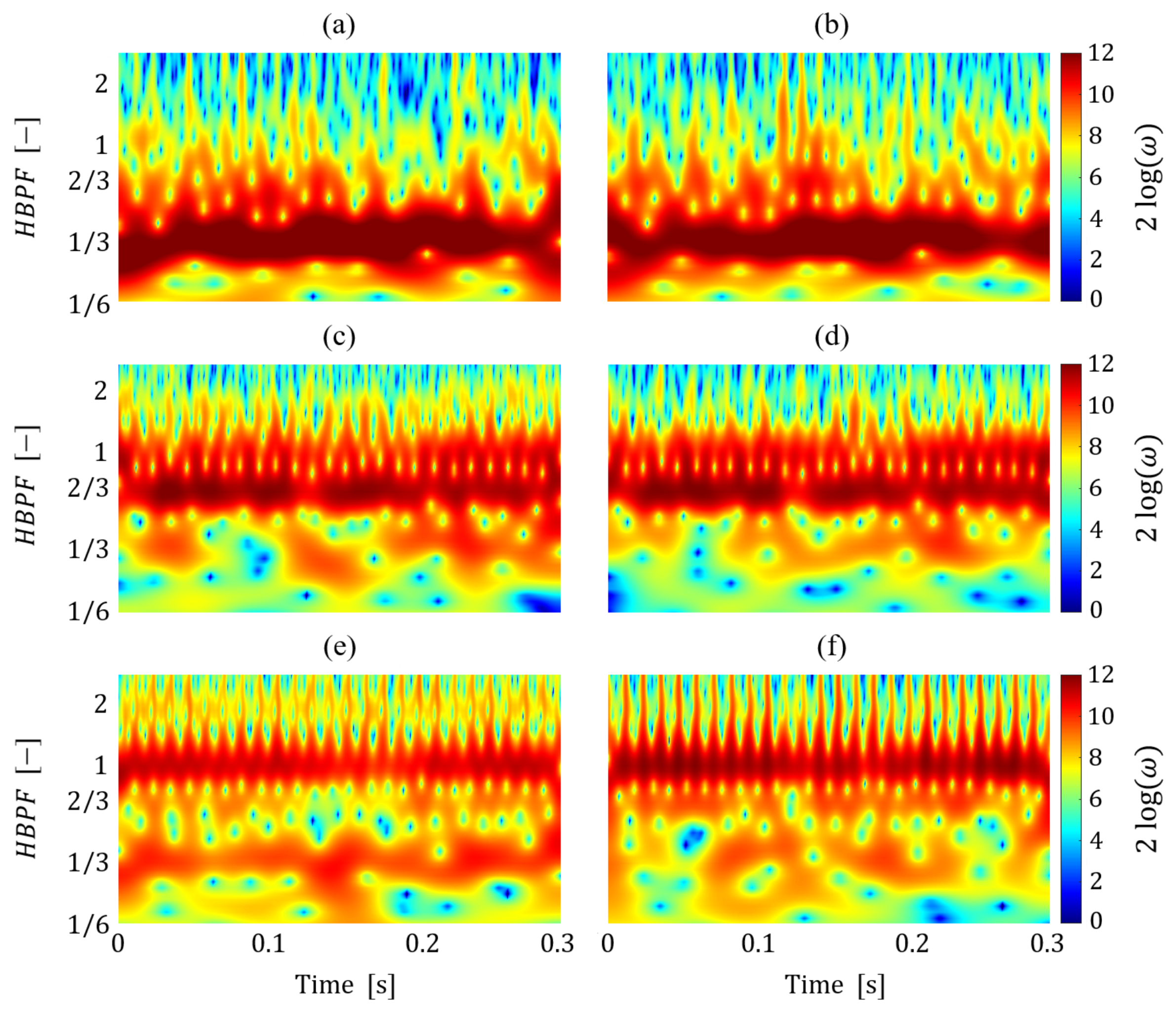
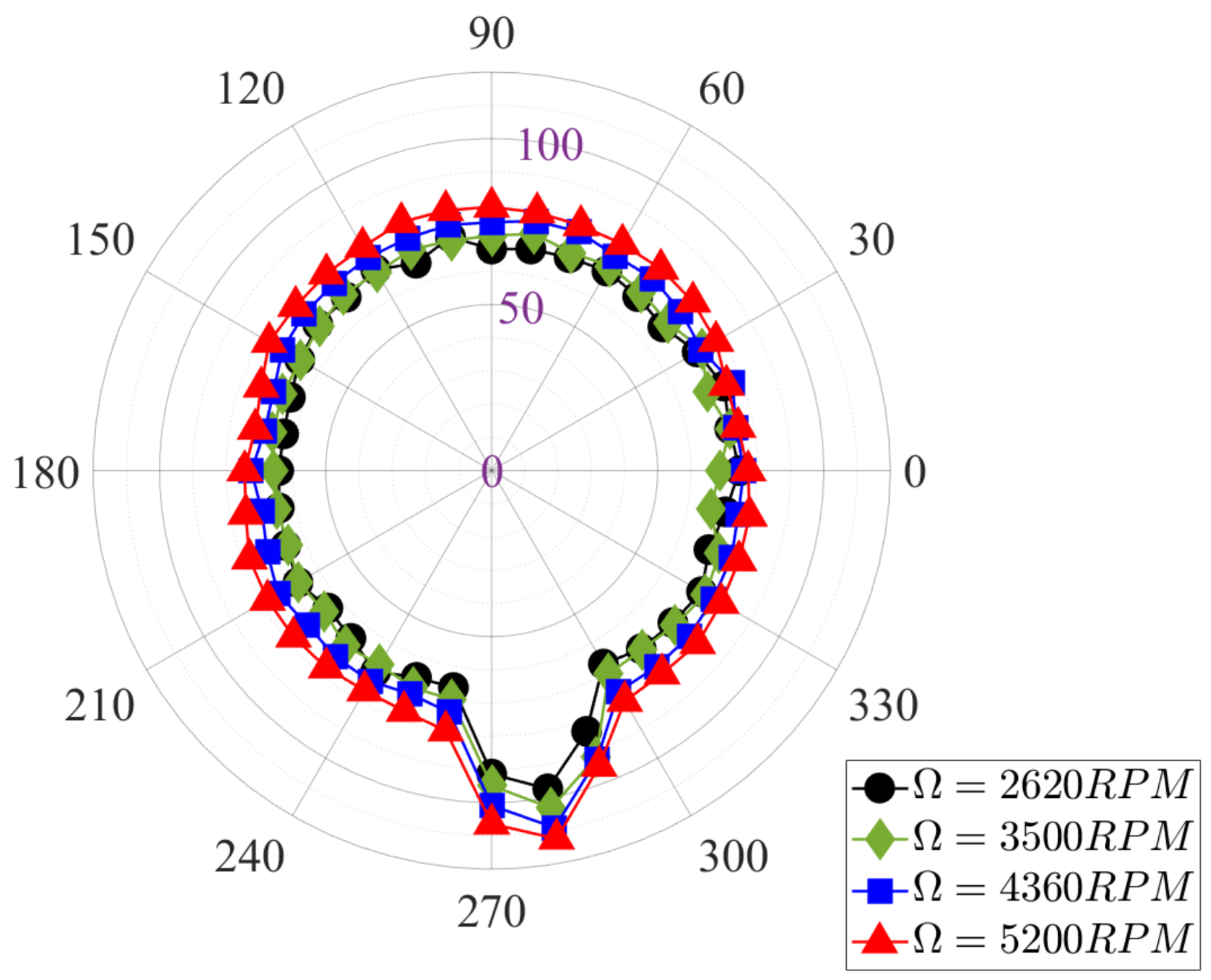
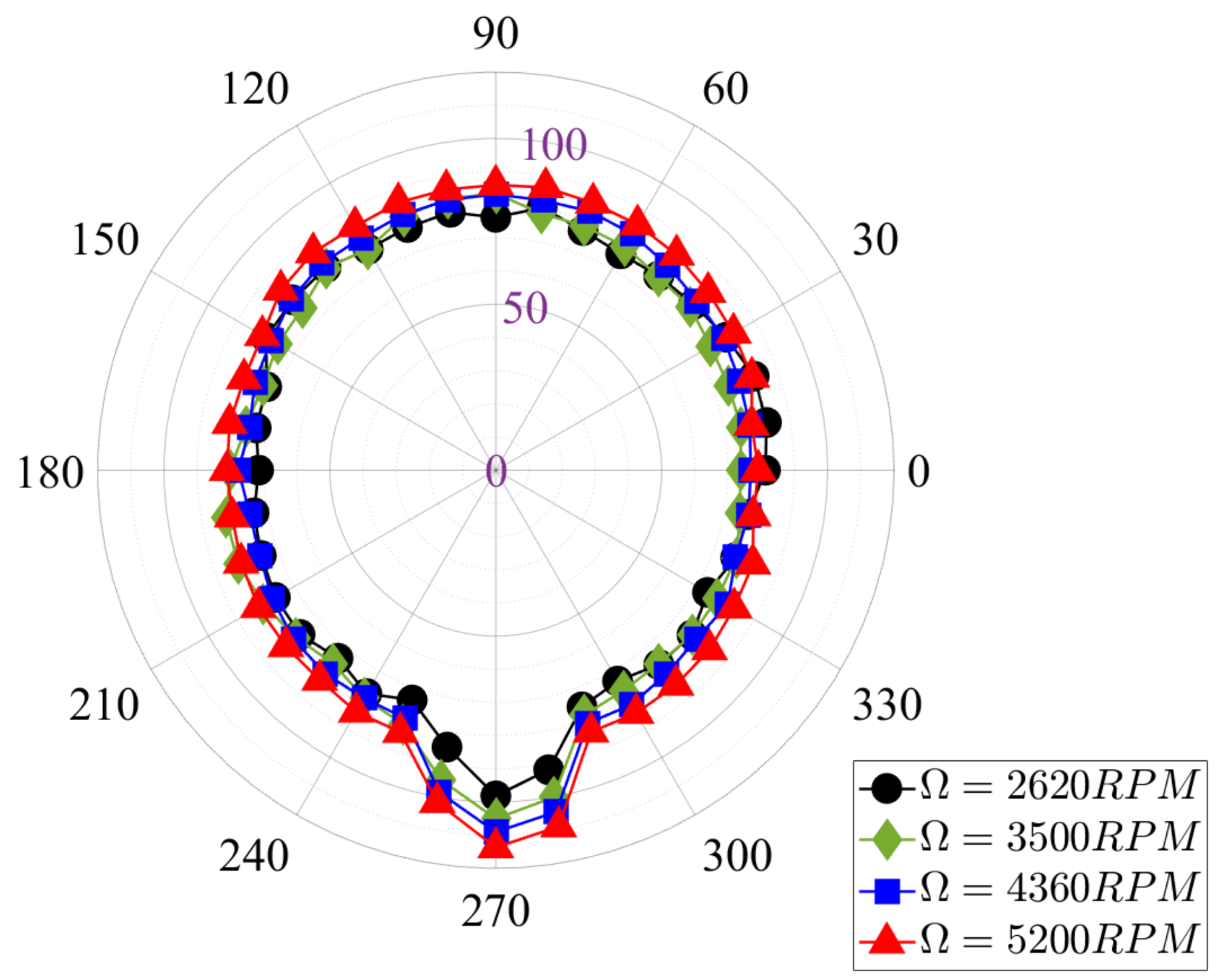
4.3. Aeroacoustic Characterization
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BB | Broad-band |
| CWT | Continuous Wavelet Transform |
| DL | Disk Loading, (N/m) |
| FOV | Field of View |
| HBPF | Harmonics of the Blade Passing Frequency |
| NB | Narrow-band |
| OASPL | Over All Sound Pressure Level, (dB) |
| POD | Proper Orthogonal Decomposition |
| PSD | Power Spectral Density, (Pa/Hz) |
| ppr | Pulses per revolution |
| ROI | Region of Interest |
| SPSL | Sound Pressure Spectral Level, (dB) |
| TR-PIV | Time-Resolved Particle Image Velocimetry |
| UAV | Unmanned Aerial Vehicle |
| WT | Wavelet Transform |
| Symbols | |
| A | Rotor disk area, (m) |
| a | POD time coefficient, (m/s) |
| B | Number of rotor blades, (−) |
| Autocorrelation Matrix | |
| c | Mean aerodynamic chord, (m) |
| D | Diameter of propeller, (m) |
| d | Rotor-to-rotor distance, (m) |
| Thrust, (N) | |
| F-number, (−) | |
| f | Frequency, (Hz) |
| H | Height, (m) |
| M | Number of element of , (−) |
| Mach number, (−) | |
| Torque, (Nm) | |
| N | Number of snapshots, (−) |
| Pressure fluctuation, (Pa) | |
| R | Radius of propeller, (m) |
| Reynolds number, (−) | |
| s | Scaling parameter in WT, (−) |
| Thickness, (m) | |
| t | Temporal coordinate, (s) |
| Velocity vector, (m/s) | |
| Tip velocity, (m/s) | |
| Velocity fluctuating component, (m/s) | |
| Spatial coordinates, (m) | |
| Greek Symbols | |
| Blade pitch, (deg) | |
| Phase angle, (deg) | |
| Azimuthal angle for aeroacoustic measurements, (deg) | |
| Eigenvalue, (−) | |
| Rotor solidity, (−) | |
| Time shifting in WT, (−) | |
| Matrix composed of the POD modes | |
| POD modes, (−) | |
| Mother wavelet | |
| Complex conjugate of the mother wavelet function | |
| Rotating speed, (RPM) | |
| Wavelet frequency, (Hz) |
References
- Bouabdallah, S.; Becker, M.; Siegwart, R. Autonomous miniature flying robots: Coming soon!-research, development, and results. IEEE Robot. Autom. Mag. 2007, 14, 88–98. [Google Scholar] [CrossRef]
- Shukla, D.; Hiremath, N.; Patel, S.; Komerath, N. Aerodynamic interactions study on low-Re coaxial and quad-rotor configurations. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Tampa, FL, USA, 3–9 November 2017; American Society of Mechanical Engineers: New York, NY, USA, 2017; Volume 58424, p. V007T09A023. [Google Scholar] [CrossRef]
- Tulwin, T. Low Reynolds Number Rotor Blade Aerodynamic Analysis. In MATEC Web of Conferences; EDP Sciences: Les Ulis, France, 2019; Volume 252, p. 04006. [Google Scholar] [CrossRef]
- Sinibaldi, G.; Marino, L. Experimental analysis on the noise of propellers for small UAV. Appl. Acoust. 2013, 74, 79–88. [Google Scholar] [CrossRef]
- Zhou, W.; Ning, Z.; Li, H.; Hu, H. An experimental investigation on rotor-to-rotor interactions of small UAV propellers. In Proceedings of the 35th AIAA Applied Aerodynamics Conference, Denver, CO, USA, 5–9 June 2017; p. 3744. [Google Scholar] [CrossRef]
- Ko, J.; Kim, J.; Lee, S. Computational study of wake interaction and aeroacoustic characteristics in multirotor configurations. In INTER-NOISE and NOISE-CON Congress and Conference Proceedings; Institute of Noise Control Engineering: Reston, VA, USA, 2019; Volume 259, pp. 5145–5156. [Google Scholar]
- Tinney, C.; Sirohi, J. Multirotor drone noise at static thrust. AIAA J. 2018, 56, 2816–2826. [Google Scholar] [CrossRef]
- Shukla, D.; Komerath, N. Multirotor Drone Aerodynamic Interaction Investigation. Drones 2018, 2, 43. [Google Scholar] [CrossRef]
- Stokkermans, T.; Usai, D.; Sinnige, T.; Veldhuis, L. Aerodynamic interaction effects between propellers in typical eVTOL vehicle configurations. J. Aircr. 2021, 58, 815–833. [Google Scholar] [CrossRef]
- Zanotti, A.; Algarotti, D. Aerodynamic interaction between tandem overlapping propellers in eVTOL airplane mode flight condition. Aerosp. Sci. Technol. 2022, 124, 107518. [Google Scholar] [CrossRef]
- Nargi, R.E.; De Gregorio, F.; Candeloro, P.; Ceglia, G.; Pagliaroli, T. Evolution of flow structures in twin-rotors wakes in drones by time-resolved PIV. J. Phys. Conf. Ser. 2021, 1977, 012008. [Google Scholar] [CrossRef]
- Kim, H.D.; Perry, A.T.; Ansell, P.J. A review of distributed electric propulsion concepts for air vehicle technology. In Proceedings of the 2018 AIAA/IEEE Electric Aircraft Technologies Symposium (EATS), Cincinnati, OH, USA, 12–14 July 2018; pp. 1–21. [Google Scholar]
- Zanotti, A. Experimental study of the aerodynamic interaction between side-by-side propellers in evtol airplane mode through stereoscopic particle image velocimetry. Aerospace 2021, 8, 239. [Google Scholar] [CrossRef]
- Lumley, J.L. The structure of inhomogeneous turbulent flows. Atmos. Turbul. Radio Wave Propag. 1967, 166–178. [Google Scholar]
- Andrianne, T.; Razak, N.; Dimitriadis, G.; Okamoto, S. Flow visualization and proper orthogonal decomposition of aeroelastic phenomena. In Wind Tunnels; BoD: Paris, France, 2011; pp. 87–104. [Google Scholar] [CrossRef]
- Pagliaroli, T.; Camussi, R. Wall pressure fluctuations in rectangular partial enclosures. J. Sound Vib. 2015, 341, 116–137. [Google Scholar] [CrossRef]
- Pagliaroli, T.; Gambioli, F.; Saltari, F.; Cooper, J. Proper orthogonal decomposition, dynamic mode decomposition, wavelet and cross wavelet analysis of a sloshing flow. J. Fluids Struct. 2022, 112, 103603. [Google Scholar] [CrossRef]
- Berkooz, G.; Holmes, P.; Lumley, J. The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 1993, 25, 539–575. [Google Scholar] [CrossRef]
- Magionesi, F.; Dubbioso, G.; Muscari, R.; Di Mascio, A. Modal analysis of the wake past a marine propeller. J. Fluid Mech. 2018, 855, 469–502. [Google Scholar] [CrossRef]
- Sirovich, L. Turbulence and the dynamics of coherent structures. III. Dynamics and scaling. Q. Appl. Math. 1987, 45, 583–590. [Google Scholar] [CrossRef]
- Meyer, K.; Pedersen, J.; Özcan, O. A turbulent jet in crossflow analysed with proper orthogonal decomposition. J. Fluid Mech. 2007, 583, 199–227. [Google Scholar] [CrossRef]
- Mallat, S. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Daubechies, I. Ten Lectures on Wavelets; SIAM: Philadelphia, PA, USA, 1992. [Google Scholar]
- Lau, K.M.; Weng, H. Climate signal detection using wavelet transform: How to make a time series sing. Bull. Am. Math. Soc. 1995, 76, 2391–2402. [Google Scholar] [CrossRef]
- Mancinelli, M.; Pagliaroli, T.; Marco, A.D.; Camussi, R.; Castelain, T. Wavelet decomposition of hydrodynamic and acoustic pressures in the near field of the jet. J. Sound Vib. 2017, 813, 716–749. [Google Scholar] [CrossRef]
- Pagliaroli, T.; Mancinelli, M.; Troiani, G.; Iemma, U.; Camussi, R. Fourier and wavelet analyses of intermittent and resonant pressure components in a slot burner. J. Sound Vib. 2018, 413, 205–224. [Google Scholar] [CrossRef]
- Tsai, R. A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses. IEEE J. Robot. Autom. 1987, 3, 323–344. [Google Scholar] [CrossRef]
- Westerweel, J.; Dabiri, D.; Gharib, M. The effect of a discrete window offset on the accuracy of cross-correlation analysis of digital PIV recordings. Exp. Fluids 1997, 23, 20–28. [Google Scholar] [CrossRef]
- Wereley, S.T.; Meinhart, C. Second-order accurate particle image velocimetry. Exp. Fluids 2001, 31, 258–268. [Google Scholar] [CrossRef]
- Willert, C.E.; Gharib, M. Digital particle image velocimetry. Exp. Fluids 1991, 10, 181–193. [Google Scholar] [CrossRef]
- Raffel, M.; Willert, C.; Wereley, S.; Kompenhans, J. Particle Image Velocimetry—A Practical Guide; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- Chen, M.; Cranes, D.; Hubner, J. Experimental investigation of rotor-wing interaction at low disk loading and low Reynolds number. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; p. 3034. [Google Scholar] [CrossRef]
- Leishman, J.G.; Baker, A.; Coyne, A. Measurements of rotor tip vortices using three-component laser Doppler velocimetry. J. Am. Helicopter Soc. 1996, 41, 342–353. [Google Scholar] [CrossRef]
- Li, H.; Burggraf, O.; Conlisk, A. Formation of a rotor tip vortex. J. Aircr. 2002, 39, 739–749. [Google Scholar] [CrossRef]
- Nargi, R.E.; De Gregorio, F.; Camussi, R. Four blades rotor model aerodynamic characterization and experimental investigation of rotor wake and sling load interaction. J. Phys. Conf. Ser. 2018, 1110, 012012. [Google Scholar] [CrossRef]
- De Gregorio, F.; Visingardi, A.; Nargi, R. Investigation of a helicopter model rotor wake interacting with a cylindrical sling load. In Proceedings of the 44th European Rotorcraft Forum, Delft, The Netherlands, 18–21 September 2018. [Google Scholar]
- De Gregorio, F.; Visingardi, A. Vortex detection criteria assessment for PIV data in rotorcraft applications. Exp. Fluids 2020, 61, 1–22. [Google Scholar] [CrossRef]
- Graftieaux, L.; Michard, M.; Grosjean, N. Combining PIV, POD and vortex identification algorithms for the study of unsteady turbulent swirling flows. Meas. Sci. Technol. 2001, 12, 1422. [Google Scholar] [CrossRef]
- Ning, Z.; Hu, H. An Experimental Study on the Aerodynamics and Aeroacoustic Characteristics of Small Propellers. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; p. 1785. [Google Scholar] [CrossRef]
- Weightman, J.L.; Amili, O.; Honnery, D.; Soria, J.; Edgington-Mitchell, D. Signatures of shear-layer unsteadiness in proper orthogonal decomposition. Exp. Fluids 2018, 59, 180. [Google Scholar] [CrossRef]
- Yang, Y.; Sciacchitano, A.; Veldhuis, L.; Eitelberg, G. Spatial-temporal and modal analysis of propeller induced ground vortices by particle image velocimetry. Phys. Fluids 2016, 28, 105103. [Google Scholar] [CrossRef]
- Al-Khazali, H.A.; Askari, M.R. Geometrical and graphical representations analysis of lissajous figures in rotor dynamic system. IOSR J. Eng. 2012, 2, 971–978. [Google Scholar] [CrossRef]










| (RPM) | (m/s) | (−) | (−) |
|---|---|---|---|
| 2620 | 54 | 0.157 | |
| 3500 | 72 | 0.210 | |
| 4360 | 90 | 0.262 | |
| 5200 | 107 | 0.313 |
| (N) | (N) | (N) | (Nm) | (Nm) | (Nm) | |
|---|---|---|---|---|---|---|
| Full scale | ±20 | ±20 | ±60 | ±1 | ±1 | ±1 |
| Accuracy (% FS) | 0.25 | 0.25 | 0.60 | 0.0125 | 0.0125 | 0.0125 |
| Test Case (−) | (RPM) | (deg) |
|---|---|---|
| 1 | 2620 | 90 |
| 2 | 3500 | 20 |
| 3 | 4360 | 60 |
| 4 | 5200 | 90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nargi, R.E.; Candeloro, P.; De Gregorio, F.; Ceglia, G.; Pagliaroli, T. Fluid-Dynamic and Aeroacoustic Characterization of Side-by-Side Rotor Interaction. Aerospace 2023, 10, 851. https://doi.org/10.3390/aerospace10100851
Nargi RE, Candeloro P, De Gregorio F, Ceglia G, Pagliaroli T. Fluid-Dynamic and Aeroacoustic Characterization of Side-by-Side Rotor Interaction. Aerospace. 2023; 10(10):851. https://doi.org/10.3390/aerospace10100851
Chicago/Turabian StyleNargi, Ranieri Emanuele, Paolo Candeloro, Fabrizio De Gregorio, Giuseppe Ceglia, and Tiziano Pagliaroli. 2023. "Fluid-Dynamic and Aeroacoustic Characterization of Side-by-Side Rotor Interaction" Aerospace 10, no. 10: 851. https://doi.org/10.3390/aerospace10100851
APA StyleNargi, R. E., Candeloro, P., De Gregorio, F., Ceglia, G., & Pagliaroli, T. (2023). Fluid-Dynamic and Aeroacoustic Characterization of Side-by-Side Rotor Interaction. Aerospace, 10(10), 851. https://doi.org/10.3390/aerospace10100851






