Aerodynamic Robust Design Research Using Adjoint-Based Optimization under Operating Uncertainties
Abstract
:1. Introduction
2. Uncertainty Quantification and Global Sensitivity Analysis Approach
2.1. Polynomial Chaos Expansions
2.2. Gradient-enhanced Polynomial Chaos Expansions
2.3. Global Sensitivity Analysis
2.4. Ishigami Test Case
3. Adjoint-Based Robust Optimization Design Framework
3.1. RANS-Based CFD Solver and Its Adjoint Equation
3.2. Derivatives Computation of Statistic Moment
3.3. ROD Framework
4. Far-Field Drag Decomposition Technique and Verification
4.1. Far-Field Drag Decomposition Method
4.2. Test Case
5. Flying Wing ROD and Aerodynamic Robustness Research
5.1. Optimization Problem Formulation
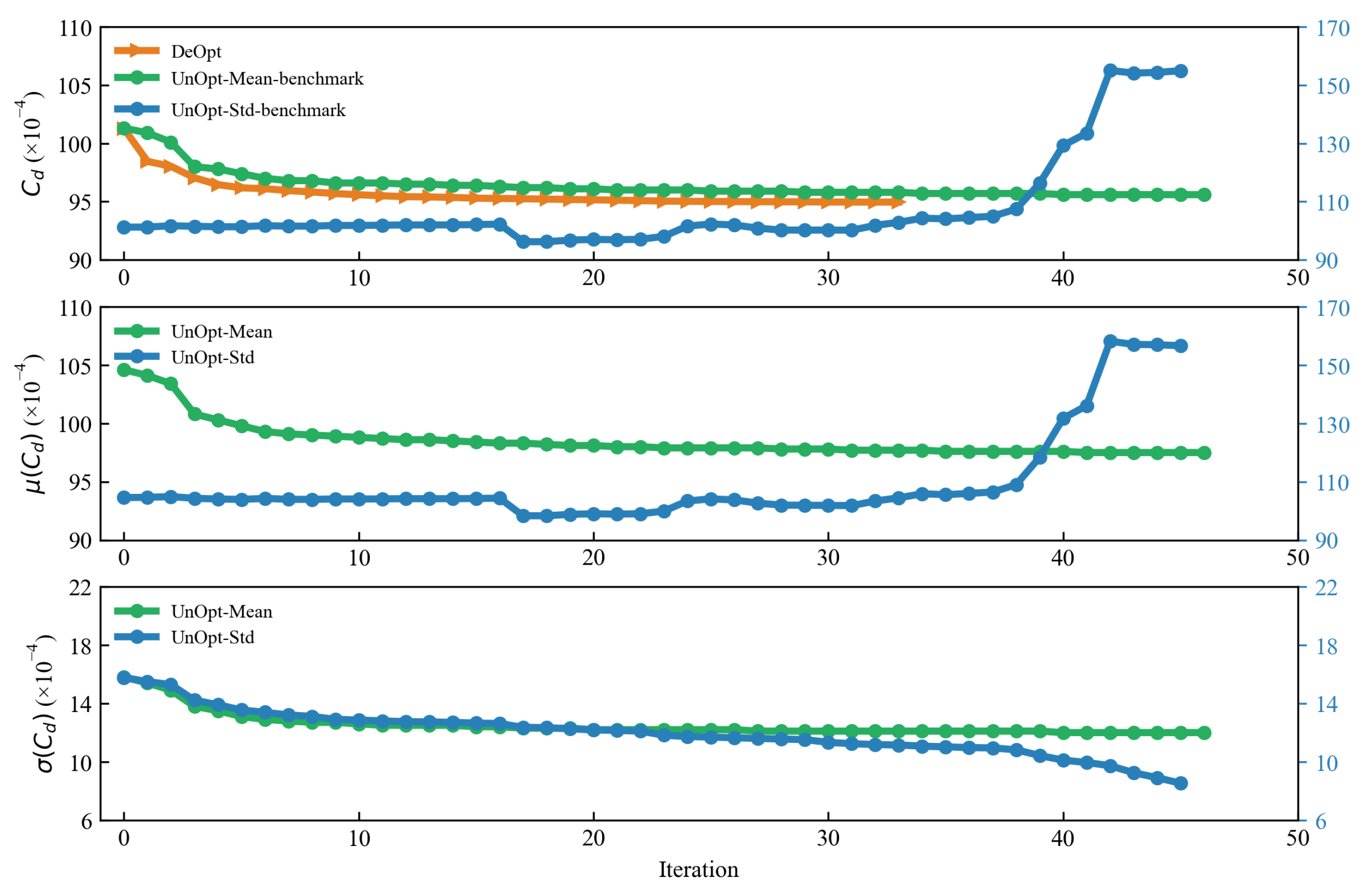
5.2. Deterministic Optimization and ROD under Flight Condition Uncertainties
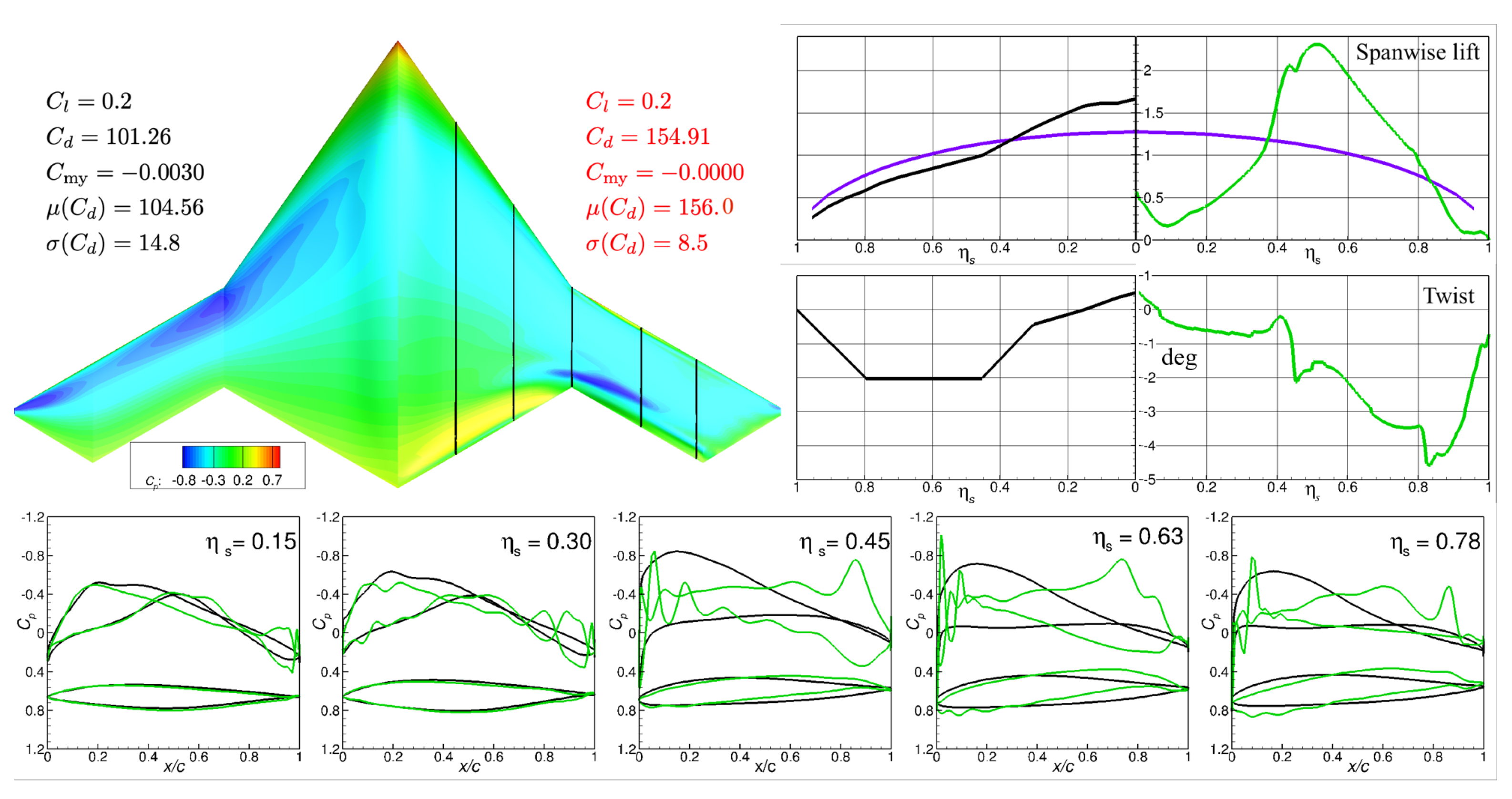
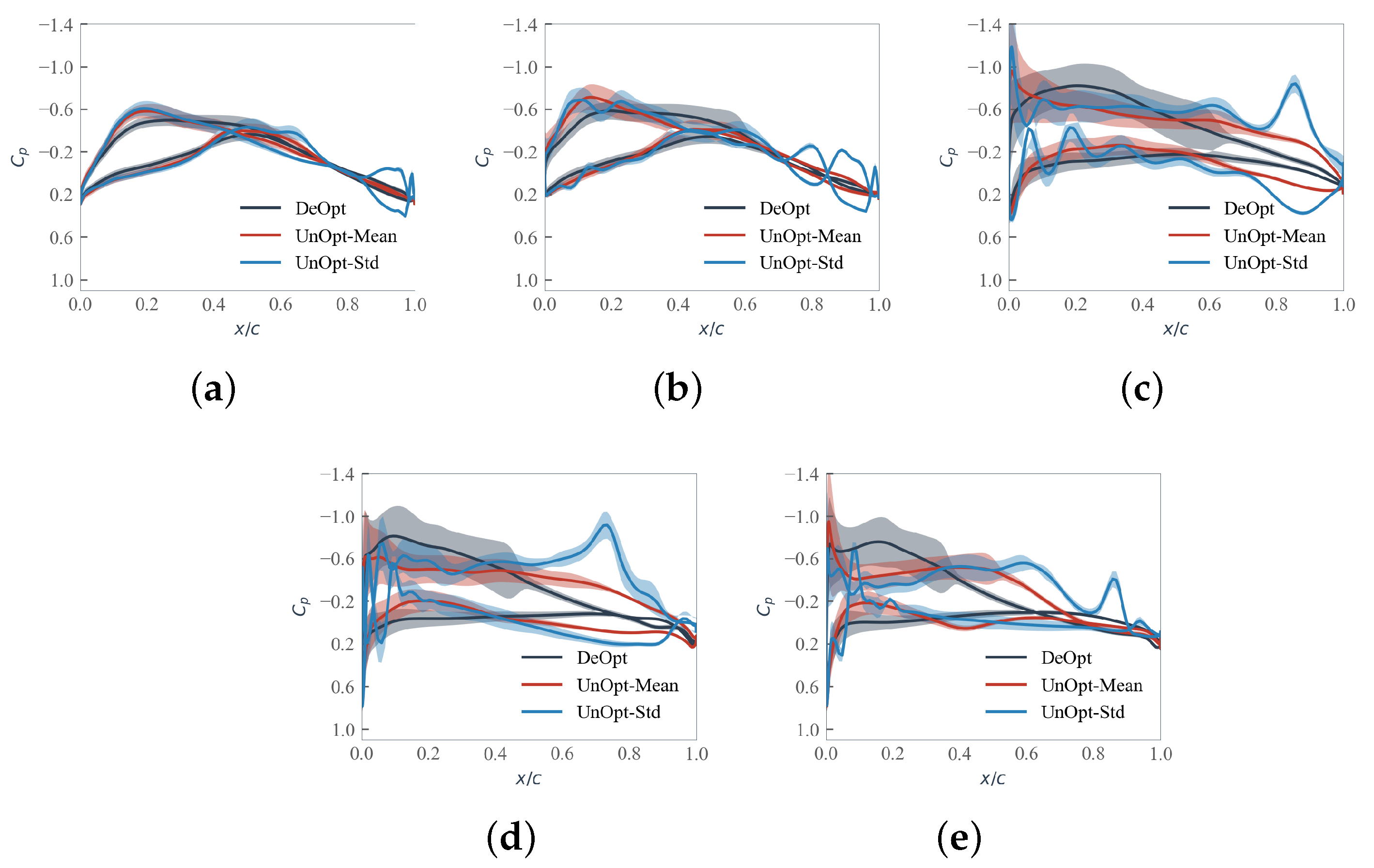
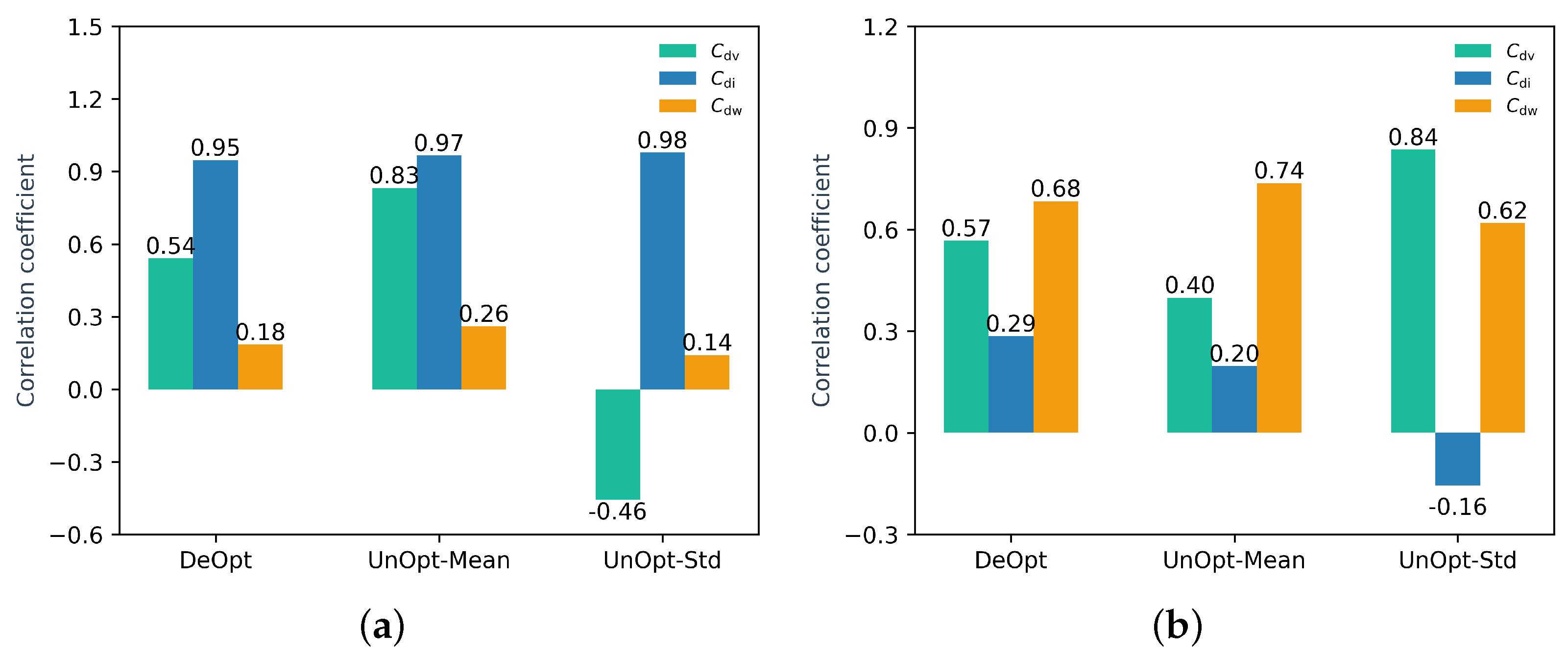
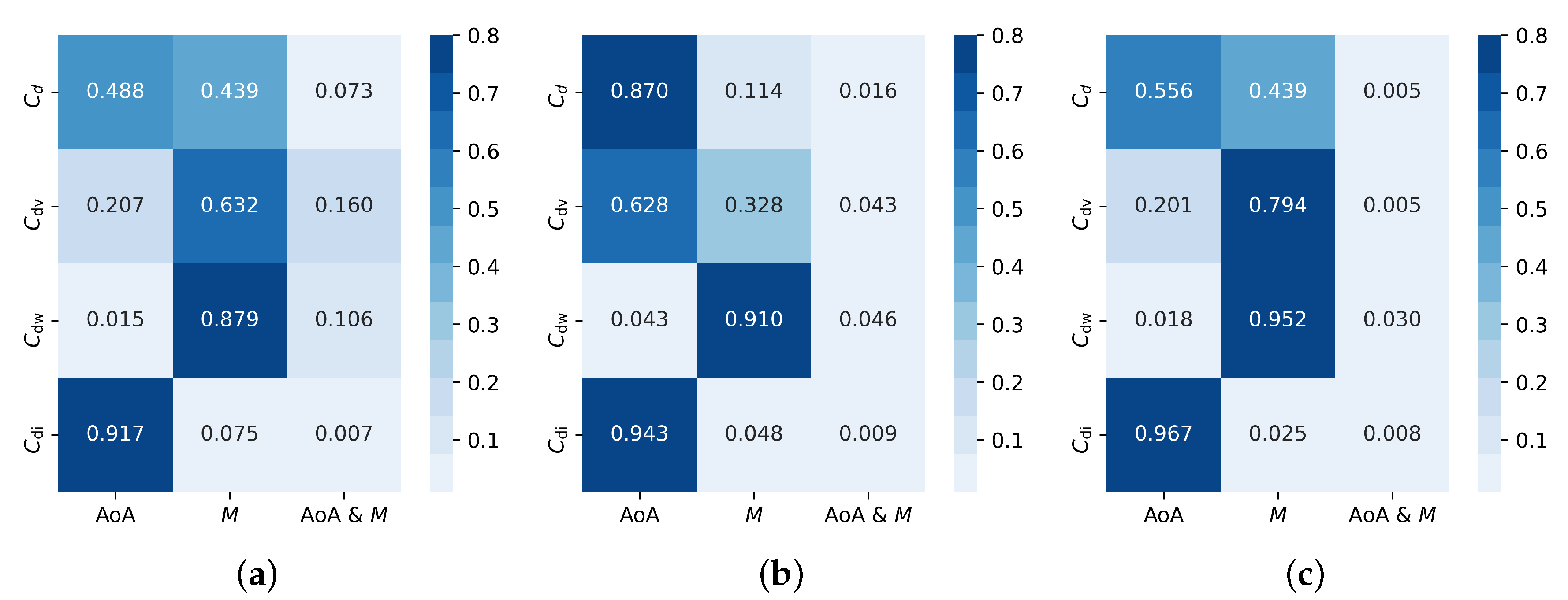
5.3. Aerodynamic Robustness Maintenance Mechanism Research
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Giesing, J.; Barthelemy, J.F. A summary of industry MDO applications and needs. In Proceedings of the 7th AIAA/USAF/NASA/ ISSMO Symposium on Multidisciplinary Analysis and Optimization, St. Louis, MO, USA, 2–4 September 1998; p. 4737. [Google Scholar]
- Zang, T.A. Needs and Opportunities for Uncertainty-Based Multidisciplinary Design Methods for Aerospace Vehicles; National Aeronautics and Space Administration, Langley Research Center: Hampton, VA, USA, 2002. [Google Scholar]
- Huyse, L.; Lewis, R.M. Aerodynamic Shape Optimization of Two-Dimensional Airfoils under Uncertain Conditions; Number 2001; ICASE, NASA Langley Research Center: Hampton, VA, USA, 2001. [Google Scholar]
- Walters, R.W.; Huyse, L. Uncertainty Analysis for Fluid Mechanics with Applications. 2002. Available online: https://www.google.com.hk/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&ved=2ahUKEwj5mMnZocKBAxWetlYBHWajAdcQFnoECBgQAQ&url=https%3A%2F%2Fwww.cs.odu.edu%2F~mln%2Fltrs-pdfs%2Ficase-2002-1.pdf&usg=AOvVaw1nzU3Hu2jZ6kdqYWZbkCYW&opi=89978449 (accessed on 4 August 2023).
- Jameson, A. Aerodynamic Shape Optimization Using the Adjoint Method; Lecture Series; Von Karman Institute for Fluid Dynamics: Rode Saint Genèse, Belgium, 2003. [Google Scholar]
- Kenway, G.K.W.; Mader, C.A.; He, P.; Martins, J.R.R.A. Effective Adjoint Approaches for Computational Fluid Dynamics. Prog. Aerosp. Sci. 2019, 110, 100542. [Google Scholar] [CrossRef]
- Li, J.; Zhang, M. On deep-learning-based geometric filtering in aerodynamic shape optimization. Aerosp. Sci. Technol. 2021, 112, 106603. [Google Scholar] [CrossRef]
- Bernardini, E.; Spence, S.M.; Wei, D.; Kareem, A. Aerodynamic shape optimization of civil structures: A CFD-enabled Kriging-based approach. J. Wind. Eng. Ind. Aerodyn. 2015, 144, 154–164. [Google Scholar] [CrossRef]
- Zhang, X.; Xie, F.; Ji, T.; Zhu, Z.; Zheng, Y. Multi-fidelity deep neural network surrogate model for aerodynamic shape optimization. Comput. Methods Appl. Mech. Eng. 2021, 373, 113485. [Google Scholar] [CrossRef]
- Gariépy, M.; Malouin, B.; Trépanier, J.Y.; Laurendeau, É. Far-field drag decomposition applied to the drag prediction workshop 5 cases. J. Aircr. 2013, 50, 1822–1831. [Google Scholar] [CrossRef]
- Dodson, M.; Parks, G.T. Robust aerodynamic design optimization using polynomial chaos. J. Aircr. 2009, 46, 635–646. [Google Scholar] [CrossRef]
- Wang, X.; Hirsch, C.; Liu, Z.; Kang, S.; Lacor, C. Uncertainty-based robust aerodynamic optimization of rotor blades. Int. J. Numer. Methods Eng. 2013, 94, 111–127. [Google Scholar] [CrossRef]
- Sabater, C.; Bekemeyer, P.; Görtz, S. Robust design of transonic natural laminar flow wings under environmental and operational uncertainties. AIAA J. 2022, 60, 767–782. [Google Scholar] [CrossRef]
- Shankaran, S.; Jameson, A. Robust optimal control using polynomial chaos and adjoints for systems with uncertain inputs. In Proceedings of the 20th AIAA Computational Fluid Dynamics Conference 2011, Honolulu, HI, USA, 27–30 June 2011. [Google Scholar] [CrossRef]
- Padulo, M.; Campobasso, M.S.; Guenov, M.D. Novel uncertainty propagation method for robust aerodynamic design. AIAA J. 2011, 49, 530–543. [Google Scholar] [CrossRef]
- Hwang, J.T.; Jasa, J.; Martins, J.R.R.A. High-fidelity design-allocation optimization of a commercial aircraft maximizing airline profit. J. Aircr. 2019, 56, 1165–1178. [Google Scholar] [CrossRef]
- Mura, R.; Ghisu, T.; Shahpar, S. Least squares approximation-based polynomial chaos expansion for uncertainty quantification and robust optimization in aeronautics. In Proceedings of the AIAA Aviation 2020 Forum, Virtual, 15–19 June 2020; p. 3163. [Google Scholar]
- Jofre, L.; Doostan, A. Rapid aerodynamic shape optimization under uncertainty using a stochastic gradient approach. Struct. Multidiscip. Optim. 2022, 65, 196. [Google Scholar] [CrossRef]
- Albring, T.; Sagebaum, M.; Gauger, N.R. Development of a consistent discrete adjoint solver in an evolving aerodynamic design framework. In Proceedings of the 16th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Dallas, TX, USA, 22–26 June 2015; pp. 22–26. [Google Scholar] [CrossRef]
- Apponsah, K.P.; Zingg, D.W. Aerodynamic Shape Optimization for Unsteady Flows With Application to Laminar Flows. In Proceedings of the AIAA Aviation 2021 Forum, Virtual, 2–6 August 2021; pp. 1–20. [Google Scholar] [CrossRef]
- Secco, N.R.; Kenway, G.K.W.; He, P.; Mader, C.A.; Martins, J.R.R.A. Efficient Mesh Generation and Deformation for Aerodynamic Shape Optimization. AIAA J. 2020, submitted. [CrossRef]
- Yildirim, A.; Gray, J.S.; Mader, C.A.; Martins, J.R.R.A. Boundary Layer Ingestion Benefit for the STARC-ABL Configuration. J. Aircr. 2020. Submitted. [Google Scholar]
- He, X.; Li, J.; Mader, C.A.; Yildirim, A.; Martins, J.R.R.A. Robust aerodynamic shape optimization—from a circle to an airfoil. Aerosp. Sci. Technol. 2019, 87, 48–61. [Google Scholar] [CrossRef]
- Shi, Y.; Mader, C.A.; He, S.; Halila, G.L.O.; Martins, J.R.R.A. Natural Laminar-Flow Airfoil Optimization Design Using a Discrete Adjoint Approach. AIAA J. 2020, 58, 4702–4722. [Google Scholar] [CrossRef]
- Shi, Y.; Mader, C.A.; Martins, J.R.R.A. Natural Laminar Flow Wing Optimization Using a Discrete Adjoint Approach. Struct. Multidiscip. Optim. 2021, 64, 541–562. [Google Scholar] [CrossRef]
- Najm, H.N. Uncertainty quantification and polynomial chaos techniques in computational fluid dynamics. Annu. Rev. Fluid Mech. 2009, 41, 35–52. [Google Scholar] [CrossRef]
- Zuhal, L.R.; Zakaria, K.; Palar, P.S.; Liem, R.P. Polynomial-Chaos—Kriging with Gradient Information for Surrogate Modeling in Aerodynamic Design. AIAA J. 2021, 59, J059905. [Google Scholar] [CrossRef]
- Tang, Z.; Zhang, M.; Hu, X. Optimal shape design and transition uncertainty analysis of transonic axisymmetric natural laminar flow nacelle at high Reynolds number. Aerosp. Sci. Technol. 2022, 121, 107345. [Google Scholar] [CrossRef]
- Peng, J.; Hampton, J.; Doostan, A. On polynomial chaos expansion via gradient-enhanced l1-minimization. J. Comput. Phys. 2016, 310, 440–458. [Google Scholar] [CrossRef]
- Adaptive sparse polynomial chaos expansion based on least angle regression. J. Comput. Phys. 2011, 230, 2345–2367. [CrossRef]
- Guo, L.; Narayan, A.; Zhou, T. A gradient enhanced l1-minimization for sparse approximation of polynomial chaos expansions. J. Comput. Phys. 2018, 367, 49–64. [Google Scholar] [CrossRef]
- Lamboni, M.; Iooss, B.; Popelin, A.L.; Gamboa, F. Derivative-based global sensitivity measures: General links with Sobol’indices and numerical tests. Math. Comput. Simul. 2013, 87, 45–54. [Google Scholar] [CrossRef]
- Sudret, B. Global sensitivity analysis using polynomial chaos expansions. Reliab. Eng. Syst. Saf. 2008, 93, 964–979. [Google Scholar] [CrossRef]
- Buzzard, G.T. Global sensitivity analysis using sparse grid interpolation and polynomial chaos. Reliab. Eng. Syst. Saf. 2012, 107, 82–89. [Google Scholar] [CrossRef]
- Garcia-Cabrejo, O.; Valocchi, A. Global sensitivity analysis for multivariate output using polynomial chaos expansion. Reliab. Eng. Syst. Saf. 2014, 126, 25–36. [Google Scholar] [CrossRef]
- Soize, C.; Ghanem, R. Physical systems with random uncertainties: Chaos representations with arbitrary probability measure. SIAM J. Sci. Comput. 2004, 26, 395–410. [Google Scholar] [CrossRef]
- Torre, E.; Marelli, S.; Embrechts, P.; Sudret, B. Data-driven polynomial chaos expansion for machine learning regression. J. Comput. Phys. 2019, 388, 601–623. [Google Scholar] [CrossRef]
- Spalart, P.; Allmaras, S. A One-Equation Turbulence Model for Aerodynamic Flows. La Rech. Aerosp. 1994, 1, 5–21. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Yildirim, A.; Kenway, G.K.W.; Mader, C.A.; Martins, J.R.R.A. A Jacobian-free approximate Newton–Krylov startup strategy for RANS simulations. J. Comput. Phys. 2019, 397, 108741. [Google Scholar] [CrossRef]
- Lambe, A.B.; Martins, J.R.R.A. Extensions to the Design Structure Matrix for the Description of Multidisciplinary Design, Analysis, and Optimization Processes. Struct. Multidiscip. Optim. 2012, 46, 273–284. [Google Scholar] [CrossRef]
- Destarac, D.; Van Der Vooren, J. Drag/thrust analysis of jet-propelled transonic transport aircraft; definition of physical drag components. Aerosp. Sci. Technol. 2004, 8, 545–556. [Google Scholar] [CrossRef]
- Lovely, D.; Haimes, R. Shock detection from computational fluid dynamics results. In Proceedings of the 14th Computational Fluid Dynamics Conference, Norfolk, VA, USA, 1 January 1999. [Google Scholar] [CrossRef]
- Tognaccini, R. Methods for drag decomposition, thrust-drag bookkeeping from CFD calculations. CFD-Based Aircr. Drag Predict. Reduct. 2003, 2003, 02. [Google Scholar]
- Paparone, L.; Tognaccini, R. Computational fluid dynamics-based drag prediction and decomposition. AIAA J. 2003, 41, 7300. [Google Scholar] [CrossRef]
- Gariépy, M.; Trépanier, J. A new axial velocity defect formulation for a far-field drag decomposition method. Can. Aeronaut. Space J. 2012, 58, 69–82. [Google Scholar] [CrossRef]
- Qiao, L.; He, X.L.; Sun, Y.; Bai, J.Q.; Li, L. Far-field drag decomposition using hybrid formulas and vorticity based area sensors. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2021, 235, 1411–1426. [Google Scholar] [CrossRef]
- Vassberg, J.; Dehaan, M.; Rivers, M.; Wahls, R. Development of a common research model for applied CFD validation studies. In Proceedings of the 26th AIAA Applied Aerodynamics Conference, Honolulu, HI, USA, 18–21 August 2008; p. 6919. [Google Scholar]
- Yamazaki, W.; Matsushima, K.; Nakahashi, K. Drag decomposition-based adaptive mesh refinement. J. Aircr. 2007, 44, 1896–1905. [Google Scholar] [CrossRef]
- Aubeelack, H.; Segonds, S.; Bes, C.; Druot, T.; Bérard, A.; Duffau, M.; Gallant, G. New Methodology for Robust-Optimal Design with Acceptable Risks: An Application to Blended/Wing/Body Aircraft. AIAA J. 2022, 60, 3048–3059. [Google Scholar] [CrossRef]






| q | Gradient-Enhanced | p | Sampling Number | Relative Error | ||
|---|---|---|---|---|---|---|
| PCE | 1.0 | No | 1.0 | 12 | 235 | 0.07% |
| PCE-Sparse0.5 | 0.5 | No | 1.0 | 20 | 181 | 0.27% |
| PCE-Sparse0.7 | 0.7 | No | 1.0 | 15 | 190 | 0.30% |
| PCE-Oversampling | 1.0 | No | 2.0 | 8 | 272 | 0.30% |
| PCE-Sparse0.5-Oversampling | 0.5 | No | 2.0 | 14 | 224 | 0.30% |
| PCE-Sparse0.7-Oversampling | 0.7 | No | 2.0 | 10 | 200 | 0.28% |
| GEPCE | 1.0 | Yes | 1.0 | 8 | 136 | 0.30% |
| GEPCE-Sparse0.5 | 0.5 | Yes | 1.0 | 14 | 112 | 0.29% |
| GEPCE-Sparse0.7 | 0.7 | Yes | 1.0 | 10 | 100 | 0.30% |
| GEPCE-Oversampling | 1.0 | Yes | 2.0 | 8 | 218 | 0.30% |
| GEPCE-Sparse0.5-Oversampling | 0.5 | Yes | 3.0 | 14 | 224 | 0.24% |
| GEPCE-Sparse0.7-Oversampling | 0.7 | Yes | 2.0 | 10 | 200 | 0.28% |
| Indices | Theoretical solutions | GEPCE | GGEPCE q = 0.7, | Relative error GEPCE () | Relative error GEPCE (q = 0.7, ) |
| 0.3139051911 | 0.3153593520 | 0.3140283718 | 0.46% | 0.039% | |
| 0.4424111448 | 0.4408309058 | 0.4414144379 | 0.35% | 0.23% | |
| 0.0 | 0.0000354529 | 0.0000111491 | / | / | |
| 0.5575888552 | 0.5586149844 | 0.5585162896 | 0.18% | 0.17% | |
| 0.4424111448 | 0.4408309058 | 0.4414144379 | 0.35% | 0.23% | |
| 0.2436836641 | 0.2432556324 | 0.2444879178 | 0.17% | 0.33% | |
| Indices | Theoretical solutions | GEPCE | GGEPCE q = 0.7, | Relative error GEPCE () | Relative error GEPCE (q = 0.7, ) |
| 0.3139051911 | 0.3138941796 | 0.3139034836 | 3.5 | 5.4 | |
| 0.4424111448 | 0.4424168140 | 0.4424175374 | 1.3 | 1.4 | |
| 0.0 | 6.2791472705 | 2.0149134521 | / | / | |
| 0.5575888552 | 0.5575831711 | 0.5575824617 | 1.0 | 1.1 | |
| 0.4424111448 | 0.4424168140 | 0.4424175374 | 1.3 | 1.4 | |
| 0.2436836641 | 0.2436889915 | 0.2436789781 | 2.2 | 1.9 |
| Name | Grid Size | |||
|---|---|---|---|---|
| L3 | Coarse | 2,156,544 | 1.33 | 254.6 |
| L2 | Medium | 5,111,808 | 1.00 | 252.1 |
| L1 | Fine | 17,252,352 | 0.67 | 250.3 |
| L0 | Extra-fine | 40,894,464 | 0.50 | 249.8 |
| L0 (ONERA) [49] | Extra-fine | 40,894,464 | 0.50 | 249.9 |
| L3 | L2 | L1 | L0 | L0 (ONERA) [49] | |
|---|---|---|---|---|---|
| 253.1 | 251.5 | 250.5 | 249.8 | 249.7 | |
| 158.6 | 157.0 | 156.1 | 155.5 | 155.3 | |
| 4.4 | 4.4 | 4.4 | 4.4 | 3.8 | |
| 90.1 | 90.1 | 90.0 | 90.0 | 90.6 |
| AoA | ||||||
|---|---|---|---|---|---|---|
| Initial | 0.2 | 101.26 | 3.2737 | −0.0030 | 104.56 | 14.8 |
| DeOpt | 0.2 | 94.96 | 2.8185 | 0.0000 | 98.93 | 17.2 |
| UnOpt-Mean | 0.2 | 95.60 | 3.0155 | 0.0000 | 97.52 | 12.0 |
| UnOpt-Std | 0.2 | 154.91 | 3.1240 | 0.0007 | 156.0 | 8.5 |
| DeOpt | 98.93 | 17.2 | 1.46 | 5.71 | 29.26 | 10.78 | 69.61 | 5.07 |
| UnOpt-Mean | 97.52 | 12.0 | 0.29 | 0.71 | 30.14 | 10.74 | 69.30 | 2.21 |
| UnOpt-Std | 156.0 | 8.5 | 0.24 | 1.02 | 44.83 | 9.13 | 116.72 | 6.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Du, J.; Yang, T.; Shi, Y.; Wang, L.; Wang, W. Aerodynamic Robust Design Research Using Adjoint-Based Optimization under Operating Uncertainties. Aerospace 2023, 10, 831. https://doi.org/10.3390/aerospace10100831
Ma Y, Du J, Yang T, Shi Y, Wang L, Wang W. Aerodynamic Robust Design Research Using Adjoint-Based Optimization under Operating Uncertainties. Aerospace. 2023; 10(10):831. https://doi.org/10.3390/aerospace10100831
Chicago/Turabian StyleMa, Yuhang, Jiecheng Du, Tihao Yang, Yayun Shi, Libo Wang, and Wei Wang. 2023. "Aerodynamic Robust Design Research Using Adjoint-Based Optimization under Operating Uncertainties" Aerospace 10, no. 10: 831. https://doi.org/10.3390/aerospace10100831
APA StyleMa, Y., Du, J., Yang, T., Shi, Y., Wang, L., & Wang, W. (2023). Aerodynamic Robust Design Research Using Adjoint-Based Optimization under Operating Uncertainties. Aerospace, 10(10), 831. https://doi.org/10.3390/aerospace10100831






