Automated Model Hardening with Reinforcement Learning for On-Orbit Object Detectors with Convolutional Neural Networks
Abstract
1. Introduction
- We performed a large-scale fault injection study for representative DL-based object-detection algorithms. We compared the SEU-caused error propagation behaviors based on the detection frameworks, the CNN structures, the position of the layers, and the data types. The performance losses of the object detectors in the presence of multiple errors were also evaluated, providing a practical insight into the vulnerability of DL applications;
- We propose a novel AMHR framework to effectively perform model hardening for CNN-based object-detection algorithms. The usefulness of our AMHR method was evaluated with the SSD and Faster R-CNN detectors. The experimental results showed that the fault tolerance of models hardened with AMHR outperformed the models with other selective hardening strategies.
2. Related Works
2.1. Space AI Applications in EOS
2.2. Object Detection with CNN
2.3. Model-Layer Fault Tolerance for Deep Learning System
3. Fault Tolerance Analysis of CNN-Based Object Detectors
3.1. Exploration of Design Space
- Detection framework and network structure: Each object detector has its own distinct work flow and backbone network structure, which may affect the error propagation. We compared the overall SDC rates of various detectors to explore the impact of the detector frameworks and network structures on the fault tolerance.
- Network layers: Network layers could have different fault tolerance capabilities, since the position and characteristic of a network layer may affect the error propagation. We wanted to understand how the SDC probabilities vary among the convolutional layers in the CNN.
- Data type and bit position: The sensitivity of each bit position is also different due to the different significances. As CNN models can use multiple data types in their implementations, we examined the SDC rate of each bit position with different data types. We sought to find the critical bits for each data type in terms of fault tolerance.
- Multiple errors: Multiple SEUs can have a devastating impact on object detectors. We evaluated the effect of this extreme case through multiple bit-flip error injections into different detectors. We analyzed their performance losses to understand the vulnerability of both region-proposal-based detectors and regression-based detectors.
3.2. Fault Model
3.3. Experiment Setup
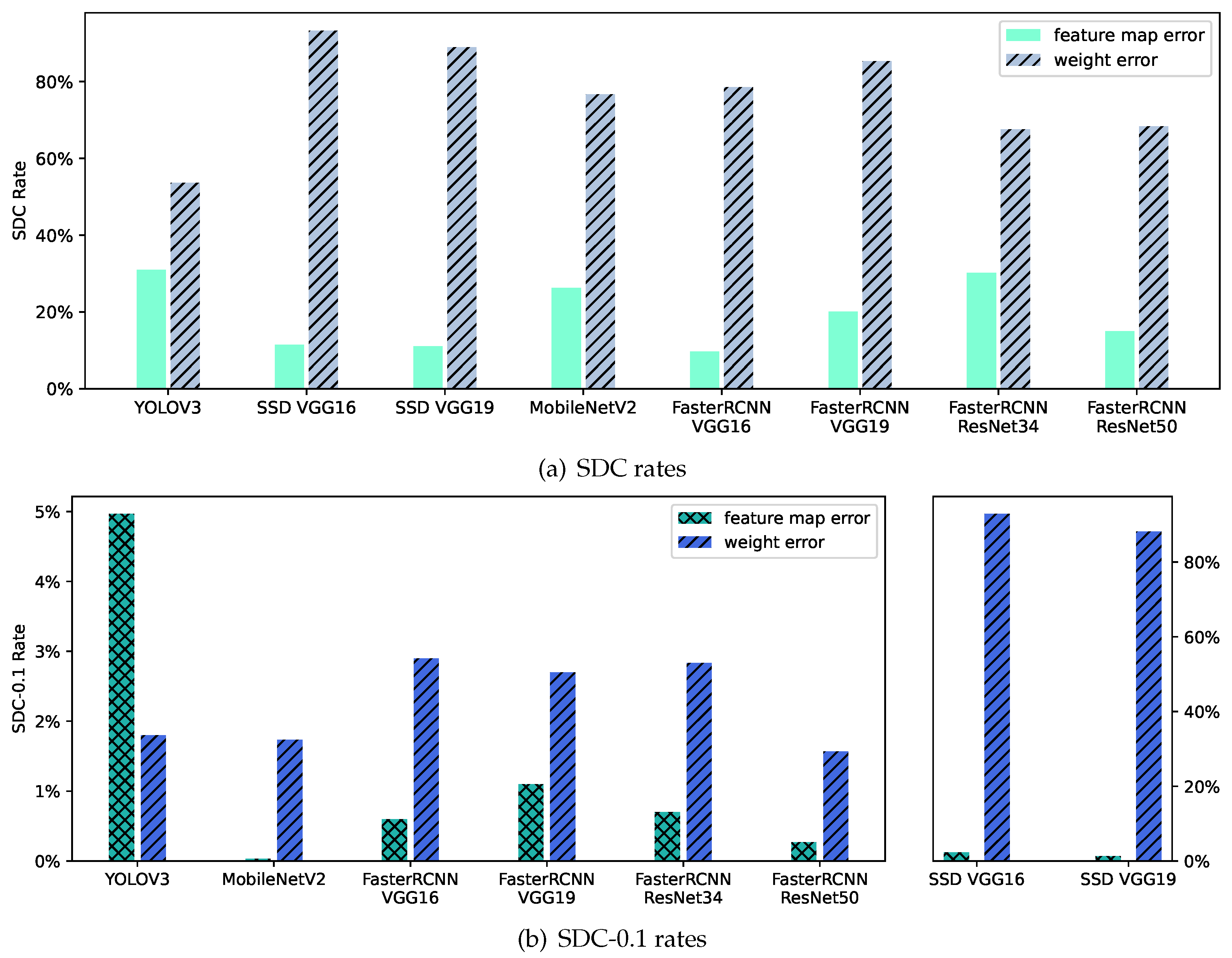
3.4. Detection Framework and Network Structure
3.5. Network Layer
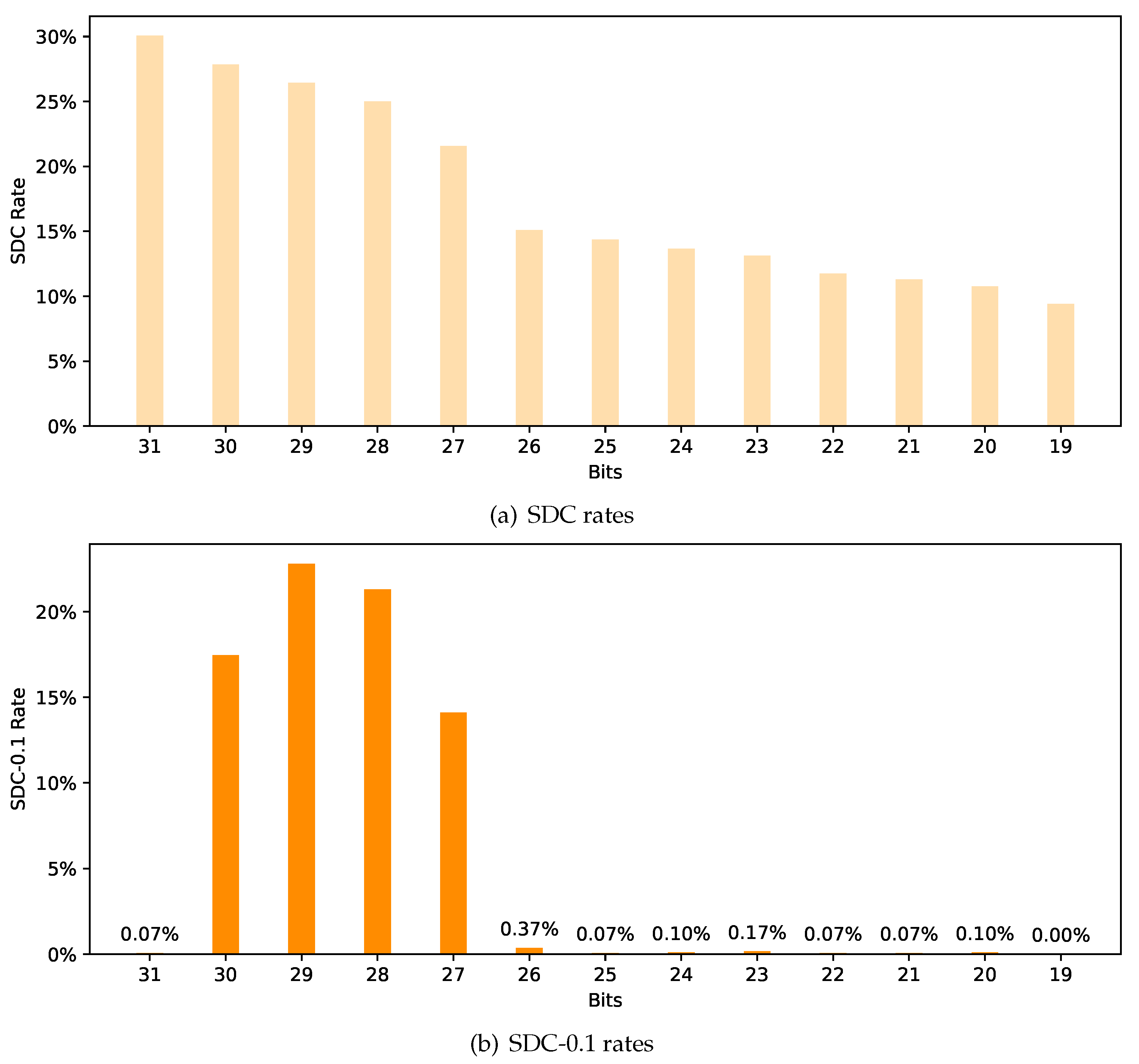
3.6. The Data Type and Bit Position
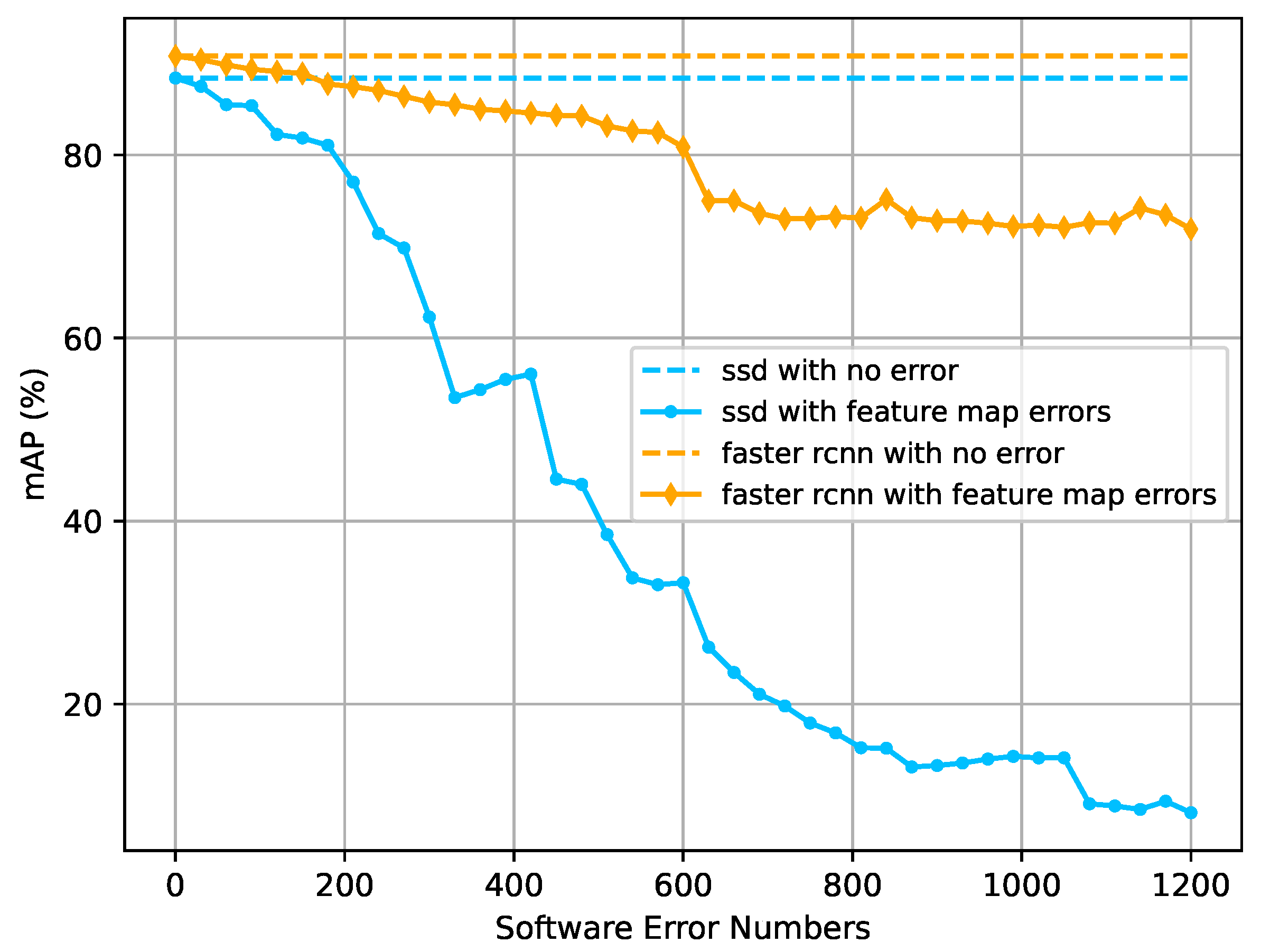
3.7. Multiple Errors
4. Methodology
4.1. Problem Description
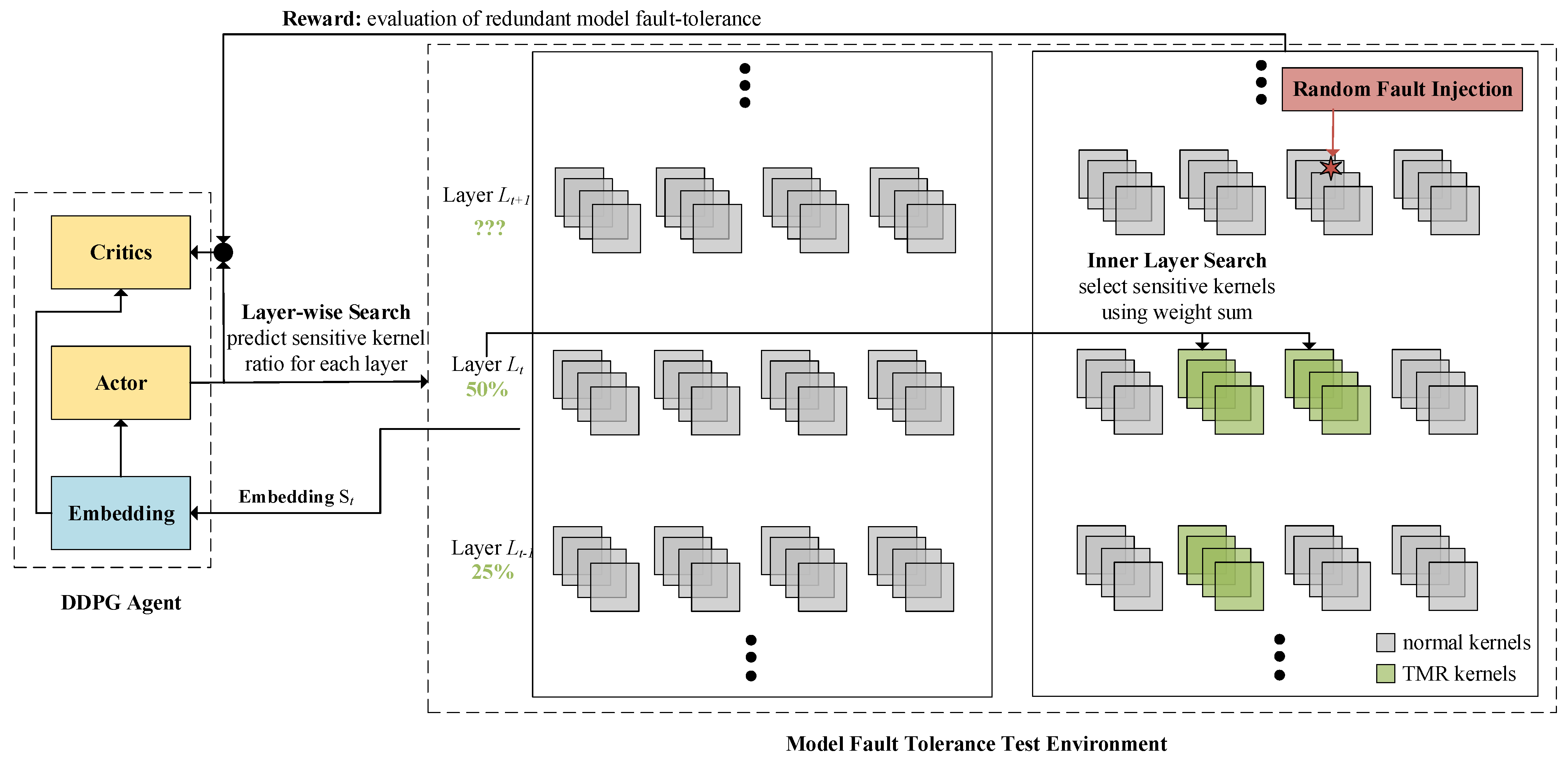
4.2. AMHR Framework
4.3. State Space
4.4. Action Space
4.5. Reward Function
4.6. Training of a DDPG Agent
| Algorithm 1: DDPG training procedure. |
 |
5. Experimental Results
5.1. Experiment Setup
- uniform: Assume error-sensitive kernels are uniformly distributed among layers, and use the weight-sum method to select kernels made redundant in each layer. This uniform assumption is in line with the weight-sum ranking method in [34];
- handcrafted: We manually set the redundancy ratio of each layer based on our knowledge of the network model. For instance, based on the experimental results in Section 3.5, we argue that the bottom few layers in a VGG16 network would have higher importance, and we set higher ratios for those layers accordingly.
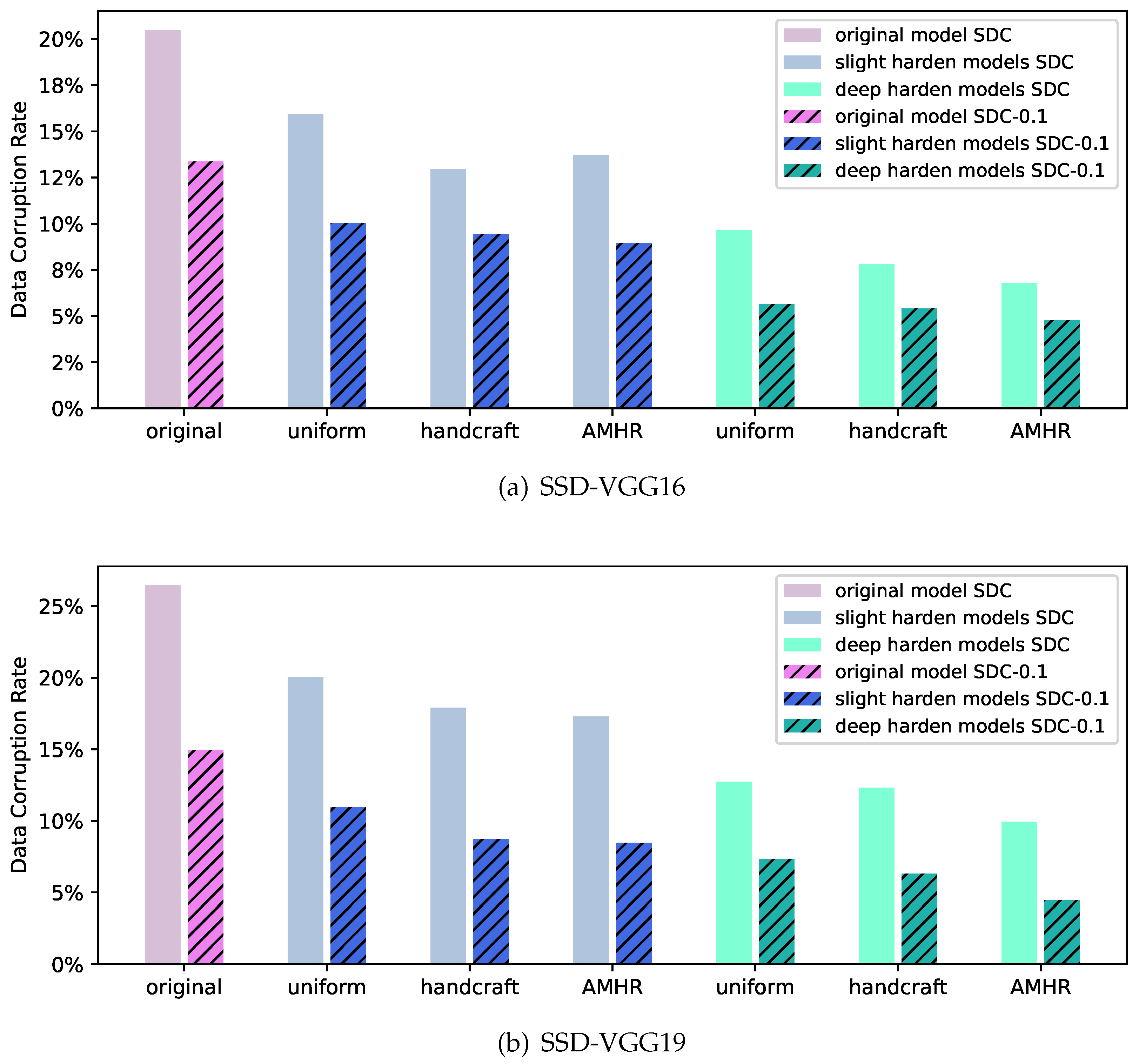
5.2. Single Bit-Flip Error Tolerance Analysis
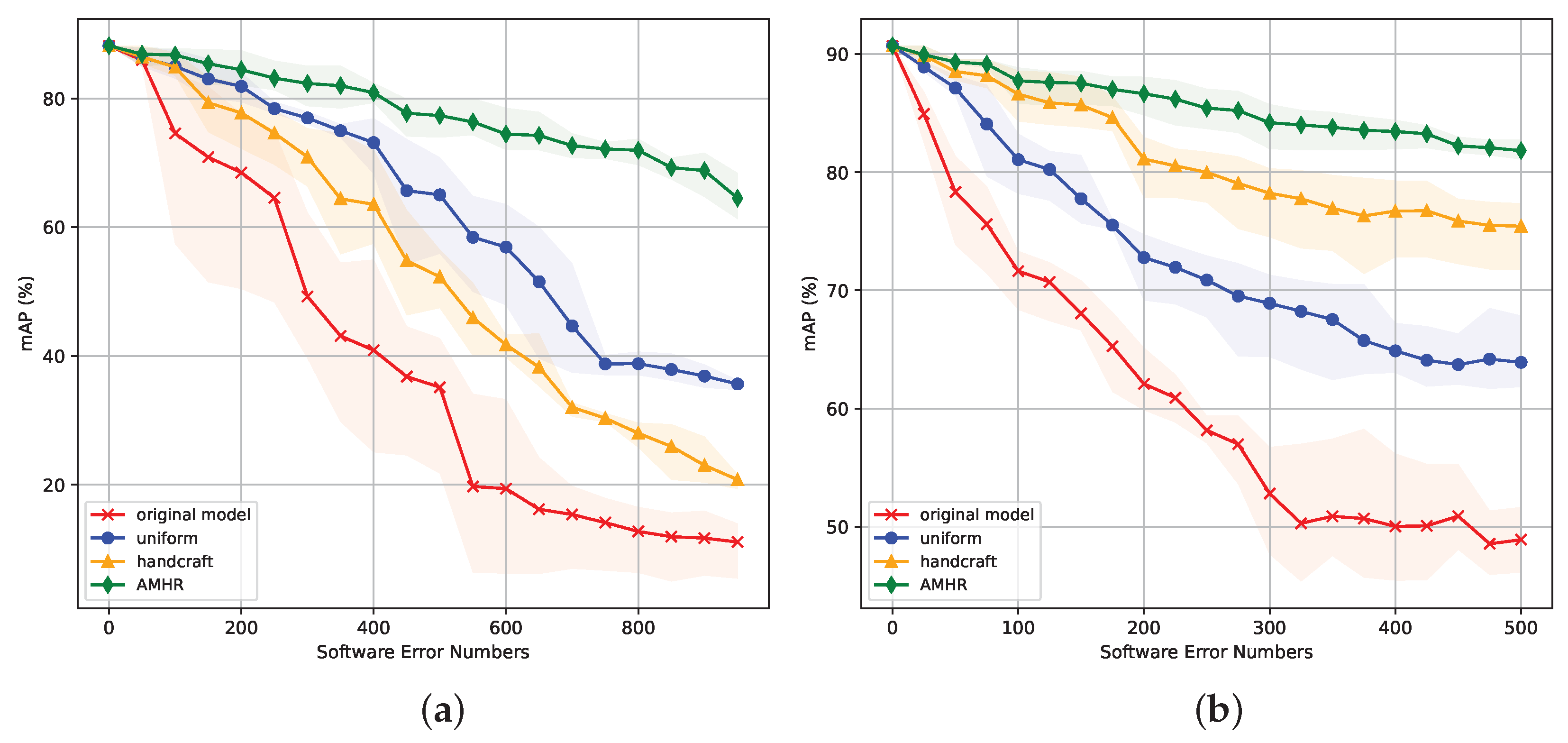
5.3. Multiple-Error Tolerance Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Furano, G.; Meoni, G.; Dunne, A.; Moloney, D.; Ferlet-Cavrois, V.; Tavoularis, A.; Byrne, J.; Buckley, L.; Psarakis, M.; Voss, K.O.; et al. Towards the use of artificial intelligence on the edge in space systems: Challenges and opportunities. IEEE Aerosp. Electron. Syst. Mag. 2020, 35, 44–56. [Google Scholar] [CrossRef]
- Wimmers, A.; Velden, C.; Cossuth, J.H. Using deep learning to estimate tropical cyclone intensity from satellite passive microwave imagery. Mon. Weather Rev. 2019, 147, 2261–2282. [Google Scholar] [CrossRef]
- Manning, J.; Langerman, D.; Ramesh, B.; Gretok, E.; Wilson, C.; George, A.; MacKinnon, J.; Crum, G. Machine-Learning Space Applications on Smallsat Platforms with Tensorflow. 2018. Available online: https://digitalcommons.usu.edu/cgi/viewcontent.cgi?article=4270&context=smallsat (accessed on 1 January 2023).
- Paoletti, M.; Haut, J.; Plaza, J.; Plaza, A. Deep learning classifiers for hyperspectral imaging: A review. ISPRS J. Photogramm. Remote Sens. 2019, 158, 279–317. [Google Scholar] [CrossRef]
- Guirado, E.; Tabik, S.; Rivas, M.L.; Alcaraz-Segura, D.; Herrera, F. Whale counting in satellite and aerial images with deep learning. Sci. Rep. 2019, 9, 1–12. [Google Scholar] [CrossRef]
- Khoshavi, N.; Broyles, C.; Bi, Y. A survey on impact of transient faults on bnn inference accelerators. arXiv 2020, arXiv:2004.05915. [Google Scholar]
- Sterpone, L.; Azimi, S.; Du, B. A selective mapper for the mitigation of SETs on rad-hard RTG4 flash-based FPGAs. In Proceedings of the 2016 16th European Conference on Radiation and Its Effects on Components and Systems (RADECS), Bremen, Germany, 19–23 September 2016; pp. 1–4. [Google Scholar]
- Libano, F.; Wilson, B.; Wirthlin, M.; Rech, P.; Brunhaver, J. Understanding the impact of quantization, accuracy, and radiation on the reliability of convolutional neural networks on FPGAs. IEEE Trans. Nucl. Sci. 2020, 67, 1478–1484. [Google Scholar] [CrossRef]
- Libano, F.; Wilson, B.; Anderson, J.; Wirthlin, M.J.; Cazzaniga, C.; Frost, C.; Rech, P. Selective hardening for neural networks in FPGAs. IEEE Trans. Nucl. Sci. 2018, 66, 216–222. [Google Scholar] [CrossRef]
- Schorn, C.; Guntoro, A.; Ascheid, G. Accurate neuron resilience prediction for a flexible reliability management in neural network accelerators. In Proceedings of the 2018 Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 19–23 March 2018; pp. 979–984. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Li, Y.; Liu, Y.; Li, M.; Tian, Y.; Luo, B.; Xu, Q. D2nn: A fine-grained dual modular redundancy framework for deep neural networks. In Proceedings of the 35th Annual Computer Security Applications Conference, San Juan, PR, USA, 9–13 December 2019; pp. 138–147. [Google Scholar]
- Wagstaff, K.L.; Altinok, A.; Chien, S.A.; Rebbapragada, U.; Schaffer, S.R.; Thompson, D.R.; Tran, D.Q. Cloud filtering and novelty detection using onboard machine learning for the EO-1 spacecraft. In Proceedings of the IJCAI Workshop AI in the Oceans and Space, Melbourne, Australia, 19–25 August 2017; Available online: https://www.semanticscholar.org/paper/Cloud-Filtering-and-Novelty-Detection-using-Onboard-Schaffer-Thompson/4a76832603f0a585bfd85278b34e0ec6d5732cad (accessed on 1 January 2023).
- Gillette, A.; Wilson, C.; George, A.D. Efficient and autonomous processing and classification of images on small spacecraft. In Proceedings of the 2017 IEEE National Aerospace and Electronics Conference (NAECON), Dayton, OH, USA, 27–30 June 2017; pp. 135–141. [Google Scholar]
- Giuffrida, G.; Diana, L.; de Gioia, F.; Benelli, G.; Meoni, G.; Donati, M.; Fanucci, L. CloudScout: A Deep Neural Network for On-Board Cloud Detection on Hyperspectral Images. Remote Sens. 2020, 12, 2205. [Google Scholar] [CrossRef]
- Xu, P.; Li, Q.; Zhang, B.; Wu, F.; Zhao, K.; Du, X.; Yang, C.; Zhong, R. On-board real-time ship detection in HISEA-1 SAR images based on CFAR and lightweight deep learning. Remote Sens. 2021, 13, 1995. [Google Scholar] [CrossRef]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 23 June 2014; pp. 580–587. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. Adv. Neural Inf. Process. Syst. 2015, 28. [Google Scholar] [CrossRef] [PubMed]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. SSD: Single shot multibox detector. In Proceedings of the European Conference on Computer Vision; Springer: Cham, Switzerland, 2016; pp. 21–37. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLO9000: Better, faster, stronger. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 7263–7271. [Google Scholar]
- Bochkovskiy, A.; Wang, C.Y.; Liao, H.Y.M. Yolov4: Optimal speed and accuracy of object detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Zhong, Y.; Han, X.; Zhang, L. Multi-class geospatial object detection based on a position-sensitive balancing framework for high spatial resolution remote sensing imagery. ISPRS J. Photogramm. Remote Sens. 2018, 138, 281–294. [Google Scholar] [CrossRef]
- Yang, X.; Yang, J.; Yan, J.; Zhang, Y.; Zhang, T.; Guo, Z.; Sun, X.; Fu, K. Scrdet: Towards more robust detection for small, cluttered and rotated objects. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 8232–8241. [Google Scholar]
- Xu, Z.; Xu, X.; Wang, L.; Yang, R.; Pu, F. Deformable convnet with aspect ratio constrained nms for object detection in remote sensing imagery. Remote Sens. 2017, 9, 1312. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Liu, C.; Gao, Z.; Liu, S.; Ning, X.; Li, H.; Li, X. Fault-Tolerant Deep Learning: A Hierarchical Perspective. arXiv 2022, arXiv:2204.01942. [Google Scholar]
- Li, G.; Hari, S.K.S.; Sullivan, M.; Tsai, T.; Pattabiraman, K.; Emer, J.; Keckler, S.W. Understanding error propagation in deep learning neural network (DNN) accelerators and applications. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, Denver, CO, USA, 12–17 November 2017; pp. 1–12. [Google Scholar]
- Gao, Z.; Zhang, H.; Yao, Y.; Xiao, J.; Zeng, S.; Ge, G.; Wang, Y.; Ullah, A.; Reviriego, P. Soft Error Tolerant Convolutional Neural Networks on FPGAs with Ensemble Learning. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2022, 30, 291–302. [Google Scholar] [CrossRef]
- Baek, I.; Chen, W.; Zhu, Z.; Samii, S.; Rajkumar, R. FT-DeepNets: Fault-Tolerant Convolutional Neural Networks with Kernel-based Duplication. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2022; pp. 975–984. [Google Scholar]
- Gaitonde, T.; Wen, S.J.; Wong, R.; Warriner, M. Component failure analysis using neutron beam test. In Proceedings of the 2010 17th IEEE International Symposium on the Physical and Failure Analysis of Integrated Circuits, Singapore, 5–9 July 2010; pp. 1–5. [Google Scholar]
- Johnston, A.H. Scaling and Technology Issues for Soft Error Rates. 2000. Available online: https://doi.org/2014/16240 (accessed on 1 January 2023).
- Li, S.; Farooqui, N.; Yalamanchili, S. Software Reliability Enhancements for GPU Applications. In Proceedings of the Sixth Workshop on Programmability Issues for Heterogeneous Multicores, Berlin, Germany, 21–23 January 2013. [Google Scholar]
- Su, H.; Wei, S.; Yan, M.; Wang, C.; Shi, J.; Zhang, X. Object detection and instance segmentation in remote sensing imagery based on precise mask R-CNN. In Proceedings of the IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 1454–1457. [Google Scholar]
- Chen, K.; Wang, J.; Pang, J.; Cao, Y.; Xiong, Y.; Li, X.; Sun, S.; Feng, W.; Liu, Z.; Xu, J.; et al. MMDetection: Open mmlab detection toolbox and benchmark. arXiv 2019, arXiv:1906.07155. [Google Scholar]
- Mahmoud, A.; Aggarwal, N.; Nobbe, A.; Vicarte, J.R.S.; Adve, S.V.; Fletcher, C.W.; Frosio, I.; Hari, S.K.S. Pytorchfi: A runtime perturbation tool for dnns. In Proceedings of the 2020 50th Annual IEEE/IFIP International Conference on Dependable Systems and Networks Workshops (DSN-W), Valencia, Spain, 29 June–2 July 2020; pp. 25–31. [Google Scholar]
- Goldstein, B.F.; Srinivasan, S.; Das, D.; Banerjee, K.; Santiago, L.; Ferreira, V.C.; Nery, A.S.; Kundu, S.; França, F.M. Reliability evaluation of compressed deep learning models. In Proceedings of the 2020 IEEE 11th Latin American Symposium on Circuits & Systems (LASCAS), San Jose, Costa Rica, 25–28 February 2020; pp. 1–5. [Google Scholar]
- He, Y.; Lin, J.; Liu, Z.; Wang, H.; Li, L.J.; Han, S. Amc: Automl for model compression and acceleration on mobile devices. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 784–800. [Google Scholar]
- Zhong, Z.; Yan, J.; Liu, C.L. Practical Network Blocks Design with Q-Learning. arXiv 2017, arXiv:1708.05552. [Google Scholar]
- Cai, H.; Chen, T.; Zhang, W.; Yu, Y.; Wang, J. Reinforcement Learning for Architecture Search by Network Transformation. arXiv 2017, arXiv:1707.04873. [Google Scholar]
- Baker, B.; Gupta, O.; Naik, N.; Raskar, R. Designing neural network architectures using reinforcement learning. arXiv 2016, arXiv:1611.02167. [Google Scholar]





| Detector | Type | Backbone Network |
|---|---|---|
| YOLOv3 | Regression-based | Darknet53 |
| SSD | Regression-based | VGG16 |
| VGG19 | ||
| MobileNetV2 | ||
| Faster R-CNN | Region-proposal-based | VGG16 |
| VGG19 | ||
| ResNet34 | ||
| ResNet50 |
| Model Hardening Method | Masked Software Error Counts | Masked SDC Counts | Masked SDC-0.1 Counts | Masked SDC Ratio (%) | Masked SDC-0.1 Ratio (%) | |
|---|---|---|---|---|---|---|
| slightly hardened model | uniform | 515 | 137 | 100 | 26.6 | 19.42 |
| handcraft | 605 | 226 | 118 | 37.36 | 17.2 | |
| AMHR | 564 | 204 | 132 | 36.17 | 23.4 | |
| deeply hardened model | uniform | 1293 | 326 | 232 | 25.21 | 17.94 |
| handcrafted | 1288 | 381 | 239 | 29.58 | 18.56 | |
| AMHR | 1311 | 412 | 258 | 31.43 | 19.68 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Q.; Li, L.; Feng, J.; Chen, W.; Yu, J. Automated Model Hardening with Reinforcement Learning for On-Orbit Object Detectors with Convolutional Neural Networks. Aerospace 2023, 10, 88. https://doi.org/10.3390/aerospace10010088
Shi Q, Li L, Feng J, Chen W, Yu J. Automated Model Hardening with Reinforcement Learning for On-Orbit Object Detectors with Convolutional Neural Networks. Aerospace. 2023; 10(1):88. https://doi.org/10.3390/aerospace10010088
Chicago/Turabian StyleShi, Qi, Lu Li, Jiaqi Feng, Wen Chen, and Jinpei Yu. 2023. "Automated Model Hardening with Reinforcement Learning for On-Orbit Object Detectors with Convolutional Neural Networks" Aerospace 10, no. 1: 88. https://doi.org/10.3390/aerospace10010088
APA StyleShi, Q., Li, L., Feng, J., Chen, W., & Yu, J. (2023). Automated Model Hardening with Reinforcement Learning for On-Orbit Object Detectors with Convolutional Neural Networks. Aerospace, 10(1), 88. https://doi.org/10.3390/aerospace10010088





