Abstract
As defense technology develops, it is essential to study the pursuit–evasion (PE) game problem in hypersonic vehicles, especially in the situation where a head-on scenario is created. Under a head-on situation, the hypersonic vehicle’s speed advantage is offset. This paper, therefore, establishes the scenario and model for the two sides of attack and defense, using the twin delayed deep deterministic (TD3) gradient strategy, which has a faster convergence speed and reduces over-estimation. In view of the flight state–action value function, the decision framework for escape control based on the actor–critic method is constructed, and the solution method for a deep reinforcement learning model based on the TD3 gradient network is presented. Simulation results show that the proposed strategy enables the hypersonic vehicle to evade successfully, even under an adverse head-on scene. Moreover, the programmed maneuver strategy of the hypersonic vehicle is improved, transforming it into an intelligent maneuver strategy.
1. Introduction
A hypersonic vehicle is an aircraft that flies in near space at a speed of more than 5 Mach; its flying altitude is situated between that of a conventional aircraft and low-orbit satellites. Hypersonic vehicles have the advantages of strong evasion ability, strong mobility, long range and high flight speed, which can realize longer flight distances and rapid striking tasks. At the same time, along with massive developments in related technical fields, such as scramjet technology, composite light and high-temperature resistant material technology [1], hypersonic aerodynamics [2] and navigation [3], and guidance [4] and control technology [5,6], hypersonic vehicles are of research interest to major aerospace countries.
At present, an important problem to be overcome in hypersonic vehicle strategy design is that of the pursuit–evasion (PE) game [7,8] between hypersonic vehicles and their opponent. Moreover, pursuer technology is developing rapidly, thereby posing a threat to the mission execution of hypersonic vehicles. It is, therefore, necessary to conduct a deeper study into the game strategy and evasion methods of hypersonic vehicles to enable their inherent advantages to be fulfilled and to ensure an effective response to the new developments in pursuer technology.
The literature [9,10,11,12] reports that research into corresponding trajectory planning, trajectory optimization and guidance law design was undertaken to address the evasion processes of hypersonic aircrafts. In order to improve guidance accuracy, the use of neural networks to predict interception points and target positions in the future has been reported in the literature [13,14]. The above literature involves programmed trajectory planning and design from either the pursuer’s side or the evader’s side, but a real flying situation is constantly changing, so a single programmed trajectory plan cannot meet rapidly changing battlefield needs. Consequently, there are reports of strategic research being conducted on the direction of attack and defense game confrontation. One report [15] considered the adversarial guidance problem among interceptors, hypersonic vehicles and active defenders and proposed an optimal guidance scheme for each participant in the engagement based on a linear–quadratic differential game strategy. In another report [16], the pursuit problem was described as a differential game, in which a method of intercepting evaders in the capture area by using the approximate optimal guidance law of deep learning was proposed, and simulation cases of evaders with different maneuvering strategies were presented. Furthermore, [17] game-switching strategies were deduced to match the target’s different strategies using complete information obtained by the interceptor. In the interception process, the target switched multiple strategies to avoid the interceptor.
Among scenarios of attack and defense confrontation, however, the head-on scenario is the most serious challenge for a hypersonic vehicle to evade. This is because a hypersonic vehicle possesses lengthy and wide-range maneuvering abilities during flight, and it also has a speed advantage compared with other different types of pursuers. Considering existing interception technology, the pursuer is most likely to adopt the head-on impact strategy; that is, the pursuer approaches the target in the opposite direction of the target velocity vector. In this way, the speed advantage of the hypersonic vehicle is greatly reduced. If the head-on impact situation is not satisfied, the pursuer will not pose enough of a threat to the hypersonic vehicle, and the hypersonic vehicle can easily escape from the threat of the pursuer using its speed advantage [18]. At the same time, it is convenient for the seeker to stably track and intercept the target in this way. When approaching the target, the rendezvous angle is close to zero, so there is a high probability that a low-speed missile could hit a high-speed target.
In a study by [19], based on the model predictive static programming (MPSP) algorithm, the head-on trajectory planning for intercepting high-speed targets met the terminal constraint of terminal arrival at the predicted hit point and consumed less energy. In view of the head-on intercept of the kinetic energy interceptor, another study [20] analyzed the possibility of penetration by the aerodynamic maneuvering of a hypersonic glide vehicle, deriving the penetration guidance law according to the state parameters of the kinetic energy interceptor at the time of boost separation.
The rise of intelligent technology, such as machine learning and artificial intelligence, provides new and feasible solutions to problems such as high dimension, real-time state change and complex input. Reinforcement learning [21], as a branch of machine learning, has developed rapidly in recent years. Reinforcement learning enables the agent to constantly interact with the environment so that it can obtain a reward when each state takes a specific action. Through this process, the agent iteratively updates its own strategy so that the agent can obtain more rewards in the next moment. It is an unsupervised heuristic algorithm that does not need to establish an accurate model and has good generalization ability [22,23]. The use of intelligent algorithms, therefore, facilitates a solution to be found for the PE problem. In the course of combat, the environment changes rapidly. Simple procedural maneuvers cannot adjust the maneuvering time and direction according to the real-time situation; as a result, adaptability is insufficient and does not meet the requirements. In order to improve the intelligence and autonomy of hypersonic vehicles, the penetration strategy should be improved. This can be realized by changing programmed maneuvering to intelligent maneuvering, which can circumvent the limitations of traditional methods, improving the accuracy, and achieving better simulation results, thereby solving several problems that are currently difficult to resolve using such methods.
Aimed at the terminal penetration scenario of ballistic missiles, one study [24] constructed the penetration scenario of targets, missiles and defenders based on deep reinforcement learning, proposing a maneuver penetration guidance strategy that took into account guidance accuracy and penetration ability. Another team [16] studied the 1-to-1 minimax time-track pursuit problem at the given final distance. In order to successfully intercept the evader using any unknown maneuver, a near-optimal track pursuit interception strategy was proposed. In one study [25], to consider the problem of missile penetration control decision-making, a model based on a Markov decision process was established. A deep reinforcement learning model based on the deep deterministic strategy gradient algorithm was given to generate the optimal decision-making network for missile penetration control. In another study [26], an anti-interception guidance method based on deep reinforcement learning (DRL) was also proposed: the problem was modeled as a Markov decision process (MDP), and a DRL scheme composed of actor–critic architecture was designed to solve this problem. Both [26] and [27] improved the reinforcement learning algorithm accordingly.
Based on the above research and analysis, this paper designed a strategy to address the pursuit–evasion problem in hypersonic vehicles under the adverse situation of a head-on scenario. The main contributions to this paper are as follows:
- Unlike simulations in other papers, this paper chose the most unfavorable classic head-on situation for a hypersonic vehicle to design the evasion strategy in the scenario of a pursuit and evasion confrontation; this is because the speed advantage of a hypersonic vehicle in this scenario is greatly weakened, and the evasion process is more dependent on the strategy device.
- Most research on strategy design for hypersonic aircraft has been based on unilateral ballistic planning. However, this paper focuses on the process of game confrontation between the two parties and constructs the problem of a pursuer-and-evasion game.
- Based on the twin delayed deep deterministic (TD3) policy gradient, deep reinforcement learning was used to study the decision-making strategy of evasion control, improving the evasion strategy of a hypersonic vehicle from being a programmed maneuver evasion to an intelligent maneuver evasion.
The paper is arranged as follows: Section 2 describes the model of the hypersonic vehicle and pursuer missile, analyzing and constructing the motion model for the pursuer and evader under the head-on reversal situation scenario. In Section 3, a deep reinforcement learning algorithm based on the TD3 policy gradient network is designed and deduced. In Section 4, the proposed algorithm based on the pursuer-and-evasion scenario is simulated and verified; finally, Section 5 offers a conclusion.
2. PE problem Modeling
2.1. Modeling
According to the dynamic characteristics of a hypersonic vehicle during flight, mechanical analysis and coordinate transformation were performed to establish the centroid dynamics and centroid kinematics models of a hypersonic vehicle, as shown below:
Similarly, the kinetic models and kinematic models of pursuer missiles can be established, as shown below:
Here, subscript and represent evader (hypersonic vehicle) and pursuer projectiles, respectively; is velocity; denotes the ballistic inclination angle; and is the ballistic deflection angle. , , and respectively represent the overload of the three axes of the aircraft under the ballistic coordinate system, and , , and respectively represent the displacement of the three axes of the aircraft under the geographical coordinate system.
To make the simulation of the designed PE confrontation problem more consistent with the actual results, the characteristics of the aircraft autopilot were also taken into account in this process. To simplify the calculation, the aircraft autopilot model was assumed to be a first-order dynamic system. The relationship between the actual overload obtained by the hypersonic vehicle and the overload command can be expressed as follows:
where is the overload order calculated for the hypersonic vehicle, is the overload response of the hypersonic vehicle, and is the responsive time constant of first-order dynamic characteristics.
2.2. The Scenario Description
In this paper, the evasion strategy of the hypersonic vehicle was designed in the situation of a head-on scenario.
If the two sides form a head-on situation, it can be assumed that the velocity direction of the pursuer missile is along the line of pursuer and evader and points to the hypersonic target. At the same time, it is reckoned that the angle between the initial velocity direction of the hypersonic vehicle and the missile target line is small enough or even close to 0; that is, both parties constitute a (standard) head-on situation.
To avoid the influence of a change of speed and altitude on engine thrust during the evasion process, the hypersonic vehicle prefers to complete the evasion through lateral maneuvers. Therefore, the pursuer missile transforming into the final guidance is assumed to be at the same altitude as the hypersonic vehicle. At this time, the pursuer and evader confrontation scenario can be simplified into a two-dimensional plane, based on which the corresponding derivation and research can be performed.
The diagram of the relative motion relation between a hypersonic aircraft and a pursuer missile under the PE state in the two-dimensional plane is shown in Figure 1. Where is the relative distance between the hypersonic vehicle and the pursuer missile, is the line of sight angle between the hypersonic vehicle and the pursuer missile, is the angle between the velocity vector of the aircraft and the line , namely, the lead angle. The lead angle of the hypersonic vehicle and the pursuer missile, respectively, have the following relation:
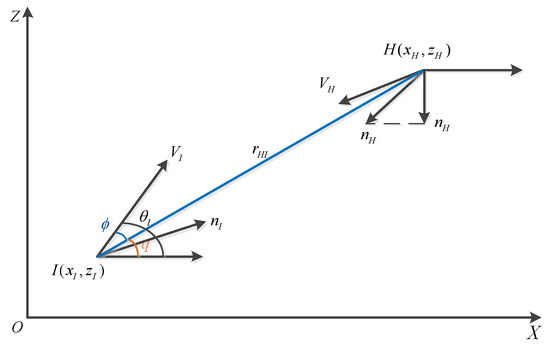
Figure 1.
Schematic diagram of pursuer and evader confrontation in a two-dimensional plane.
According to the geometric relationship, the relative kinematic Equation of pursuer and evader, confrontation can be written as:
In the head-on scenario, there is little change in the deflection of both sides. Based on the small-angle hypothesis, the kinematic model of offensive and defensive confrontation can be linearized at the X-axis. If the state variable is , the linearized model of the pursuit–evasion problem can be obtained as follows:
The corresponding matrix expression in the formula is:
The main content of this paper is about the scenario where the pursuer missile and the evader vehicle have formed a head-on state. Therefore, this paper will only discuss the guidance law adopted by the pursuer missile in the final guidance stage. The most typical and commonly used missile guidance law is proportional guidance (PN), whose longitudinal and lateral overload instructions are shown as follows:
where is the navigation coefficient, and is usually selected between 3 and 5, and is the approach speed of the pursuer and evader.
2.3. The Designing Goal
To make the simulation fit the reality and ensure the simulation results have strong credibility, it is necessary to make assumptions about and place constraints on the performance and conditions of the aircraft.
Here, is supposed to be set as the lowest boundary value of miss distance. In addition, when the present formula is true, the hypersonic vehicle can be considered as making a successful evasion:
The maximum available overload refers to the normal/lateral acceleration generated by the aircraft when the actuator of the aircraft reaches the maximum angle or limitation. Thus, the maximum available overload for the hypersonic vehicle in this paper is assumed to be:
In summary, the whole problem can be described as Problem 1.
Problem 1.
There is a PE game for which the attack and defense models can be expressed, as shown in Equation (7). More specifically, the state-space Equation which is based on the head-on scenario, is given by Equation (8). The evasion strategy should be derived to guarantee that the miss distance satisfies Equation (13) and the control constraint satisfies Equation (14).
3. Method
In reinforcement learning tasks, the types of actions are usually classified into continuous actions and discrete actions. The DQN algorithm can deal with the high-dimensional and observable state space, but the state space must be discrete and have a low-dimensional action space. Managing the huge continuous action space to calculate the probability of each action or the corresponding Q-value is difficult for the DQN network. In view of the defects of the DQN algorithm, David Sliver proposed a Deterministic Policy Gradient (DPG) algorithm in 2014 and proved the effectiveness of this algorithm for continuous action tasks. TP Lillicrap and others proposed a DDPG algorithm based on the Actor–Critic (AC) framework, firstly, by taking advantage of the superiorities of the DPG algorithm to make it possible to critique it in high-dimensional continuous action space; they then combined this with the advantages of the DQN algorithm to take the high-dimensional state space as input. However, the Q-value is always overestimated due to a function approximation error in DDPG algorithm training, so the TD3 algorithm was proposed and produced a better performance.
The remainder of this section is divided into subheadings to provide a concise and precise description of the experimental results, as well as the experimental conclusions.
3.1. TD3 Method
The TD3 algorithm is an optimization algorithm based on DDPG. Therefore, TD3 and DDPG have relatively similar framework algorithms, both of which are updating algorithms based on the actor–critic framework. The characteristics of the TD3 algorithm are as follows:
- The updated value function is different from the DDPG algorithm, which uses the maximum estimation method to estimate value functions; it is, therefore, common for over-estimation problems to occur with the DDPG algorithm. For this reason, the TD3 algorithm was improved. Referring to the idea of two action value functions in twinned Q-learning, the minimum value of two Q-functions was adopted when updating the Q-function of the critic.
- Referring to the experience replay and target network technology in deep Q-learning, the TD3 algorithm stores the data obtained from the system exploration environment and then randomly takes a sample to update the parameters of the deep neural network to reduce the correlation between the data. Moreover, the sample can be reused to improve learning efficiency.
- To ensure its smoothness, regularization of the strategy was carried out, and disturbance was introduced when the TD3 network output the action. Thus, the Twin delayed deep deterministic policy gradient algorithm can be obtained. The algorithm framework is shown in the Figure 2 below:
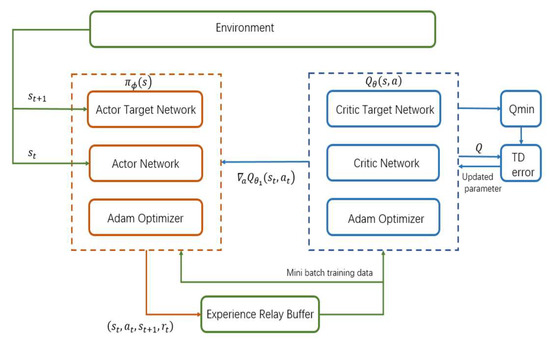 Figure 2. TD3 method structure framework.
Figure 2. TD3 method structure framework.
The detailed structure of the algorithm is described below.
3.1.1. Actor–Critic Structure
DDPG is a value-based reinforcement learning algorithm. Inspired by the idea of value estimating, the actor–critic structure came into being. The actor–critic structure refers to the fact that the reinforcement learning algorithm learns two networks simultaneously: the evaluation network and the strategy network .
The predecessor of the actor network is based on the policy gradient algorithm, which can select the corresponding action in the continuous action space. Its updating mode regenerates at every turn, so learning efficiency is relatively slow. However, the problem of dimension explosion is often encountered using the value-based method of Q-learning updating. Moreover, by using a value-based updating algorithm to select the critic network, a single-step update can be realized. By combining two reinforcement learning algorithms, the policy-based policy gradient and the value-based Q-learning, the actor–critic structure can be formed.
The actor network is responsible for analyzing the data observed by the system from the external environment, obtaining the most suitable action for the current state, and then updating the gradient so that the agent can obtain the best score. The gradient-updating expression of the actor parameter is shown as follows:
where is the parameter in the actor network, and is the parameter in the critic network. To reduce the amount of computation and improve efficiency, the updating data are selected using Mini batch; that is, N groups are extracted from the data obtained from the existing interaction with the environment to train the actor. When the number of training sessions does not reach the set maximum number of sessions, the system generates the action and records the action-state-reward data for each session, which can be recorded as , and the data stored in the replay buffer. At the beginning of training, the parameters in the action network and the parameters in the evaluation network are randomly initialized.
The critic network evaluates the action produced by the current policy network and the current state of the system in the time step. The evaluation network adjusts the parameters within its own network based on feedback from the environment, which is the reward generated by the reward function.
3.1.2. Twin Delayed Deep Deterministic (TD3) Policy Gradient
Based on the above actor–critic framework, by referring to the techniques of experiential replay and target network in deep Q-learning, and the idea of two action value functions in double Q-learning, the twin delayed deep deterministic policy gradient (TD3) algorithm can then be obtained.
To create a more stable network performance, the TD3 algorithm introduces the concept of the target network. The critic network and the actor network each have a target network, and , respectively. The target actor network and the target critic network are only used to calculate the loss function. Two sets of critic networks are adopted, the smaller being taken when calculating the target value, so as to restrain the problem of network overestimation. By using the output value of a relatively stable target network, the target value is constructed to ensure the learning stability of the critic network.
As a supervised learning model, a deep neural network requires data to satisfy characteristics such as independent and homogeneous distribution. To overcome problems with the correlation of empirical data and non-stationary distribution, target networks are able to use experience replay to replace uniform sampling when obtaining data, which would break serial correlation while reusing past experience.
The specific steps are as follows: after a fixed time interval, the algorithm will conduct data sampling for the set of experience replay blocks, and update and with the sampled data as a loss function, according to the following formulas:
In Equation (16), is the second-order norm of output, and rt is the reward function obtained at the current moment. Since this term represents the prediction of the future state and action of the target evaluation network, the future loss rate represents the degree of concern of the algorithm itself to the future benefits. After training updating, the target network should be renewed according to the learning rate.
Above all, it can be known that the algorithm consists of six deep neural networks: the actor network , used to approximate the optimal strategy , and the two value function networks and , used to estimate the action value function. There should be three target networks: , and . Similar to the deep Q learning, the TD3 algorithm firstly needs to collect enough experience data during training and store it in the experience pool. A small batch of data is then randomly sampled from the experience pool to update the , and parameters of the network. The specific structure can be seen in the following Table 1:

Table 1.
The structure of TD3 network.
In some respects, and similar to the double Q-network, the two Q-functions are independently studied, and the smaller Q Value of the two values is used to construct the target value learned by the critic network so as to slow down the overestimation of the critic network; that is:
In the Equation, is the target value of temporal difference; is the noise pruning added to the output of the target policy network. Because the scores obtained by similar actions in the same state are usually not significantly different, for the sake of increasing the stability of the algorithm, is introduced for improvement:
where is the shear function, and it is defined as:
The loss of function of the critic network can be expressed as:
After the introduction of the experience replay mechanism, the loss of function used to update the network parameters of the value function can be defined as:
where represents the length of a small batch of data.
In addition, parameters , and are updated according to the following formula to minimize the loss of functions and .
Different from the hard update mode of DQN, in which parameters are directly copied from the current network to the target network, the TD3 algorithm adopts the updating mode, which is similar to the DDPG soft update mode. The parameters of the three target networks adopt a soft update mode, which can ensure the stability of the training process. To ensure stable training of the actor network, the algorithm of the delayed update is used; in this way, the actor network will be updated after the critic network has been updated many times. Usually, after the critic is updated twice, the actor network will be updated again. The parameters of the actor network , network and network are obtained by running means, respectively, to obtain parameters of the target actor network, the target network and the target network . The calculation formula is shown as follows:
Here is an inertial factor.
3.2. Method Design Based on Head-On Scenario
3.2.1. Design of the State Space and the Motion Space
The input of the actor network in the deep reinforcement learning algorithm is the observable state vector. The actor network can also be expressed as a nonlinear function about the state:
The state space selects the relative state of the hypersonic vehicle and pursuer missile, that is, .
The selection of state variables should ensure that they can be obtained easily in practice. Here is the normalization coefficient, whose function is to ensure that the magnitude of the selected state variables is basically the same; this is more conducive to algorithm convergence.
The output of the actor network is the vertical overload of the hypersonic vehicle ; then:
Here is the limited overload value of a hypersonic vehicle. Thus, the output can be expressed as a function of the state space:
3.2.2. Design of the Reward Function and the Termination Function
During the pursuit–evasion process, the setting of the termination function determines when the simulation and single training ends. Moreover, the setting of the reward function directly affects the learning efficiency and convergence of reinforcement learning. Thus, both have a significant impact on the simulation.
- Termination function
According to the experience and the actual trend, when the relative distance between the hypersonic vehicle and the pursuer missile begins to increase, it can be determined that the pursuit–evasion process is over; that is:
- Reward function
The design of the reward function includes a terminal reward and a process reward. It should be noted that process rewards should not be too sparse; otherwise, the agent may fail to recognize the contribution of an action taken in a certain state to the final reward, thus failing to identify the key actions and resulting in the failure of the final simulation.
where is defined as the reward function of the relevant distance between the pursuer missile and the evader. When the distance decreases, the reward will be given, but when the distance increases, punishment will be given. is defined as a reward function related to the relative angle. In order to ensure that the evader can successfully escape the pursuer, it is necessary to introduce the relative angle information between the hypersonic vehicle and the pursuer missile and give the corresponding punishment and reward. is defined as the termination reward function, when each time the evader escapes from the pursuer successfully, the corresponding reward or punishment is given. In this situation, the success criterion is whether the value of the minimum miss distance meets the requirements.
3.2.3. Design of the Network Structure
Both the policy network and the value function network are realized by the fully connected neural network, which contains three hidden layers, and the activation function of the hidden layer is selected as a ReLU function.
The policy network maps to . Since its overload value is limited, the activation function of the output layer of the policy network is taken as the tanh function, and the scaling layer is superimposed. The scaling range is .
The action value function network takes as input and outputs . Moreover, the activation function of the output layer of the action value network is linear.
The network structure designed in this paper is shown in Table 2. The parameters of the policy and value function networks are adjusted by the Adam optimizer.

Table 2.
Overall network structure in the simulation.
4. Results and Discussion
Simulation parameter settings are shown in Table 3.

Table 3.
The parameters simulation setting table.
The simulation condition for a strict head-on situation was given, which means the initial line-of-sight angle between the hypersonic vehicle and the pursuer missile was 0. The initial ballistic deflection angle of the hypersonic vehicle was set to 0, and the initial ballistic deflection angle of the pursuer missile was set to . The initial position of the hypersonic vehicle was (0,0), and the initial position of the pursuer missile was (100,000).
To truly reflect the scene, the speed of the pursuer was set at 3 Ma, and the speed of the hypersonic aircraft was 6 Ma. Meanwhile, the overload capacity of the hypersonic aircraft was set at 3, while the overload capacity of the pursuer was set at 6. By contrast, the hypersonic aircraft had an overload disadvantage. Thus, under these circumstances, i.e., reduced speed advantage and overload disadvantage, the success of evasion depends more on the active maneuvering time of the hypersonic vehicle.
Using the above strict head-on situation as the simulation conditions, the agent was trained in this case, and the maximum number of training rounds was set at 1000. In the process of each training, some initial quantities were also assigned random deviation to ensure the effectiveness of the training results.
The training process curve for the agent is shown in Figure 3.
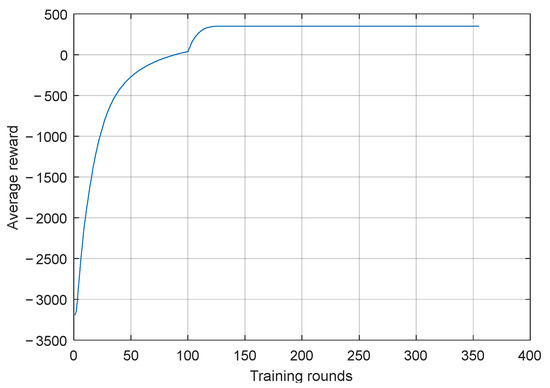
Figure 3.
The curve for agent training during the deep reinforcement learning process.
As seen in Figure 3, as the number of training rounds increases, the average reward value curve gradually increases. In this process, the agent constantly adjusts its strategy due to trial and error. According to the feedback for the reward function and the real-time state information of the environment, the agent was trained and improved iteratively.
After 120 rounds of training, the curve obviously converges and finally stabilizes at a higher value; that is, it converges to a better solution. This indicates that the overall performance of the agent tended to be stable in this process, which means that the training was successful. It can also be further seen from the curve that the deep learning algorithm designed in this paper shows good convergence.
After the completion of the agent training, we chose a relatively strict condition to perform the pursuit and evasion confrontation between aircraft for the agent scene test. The simulation results for the basic indicators are shown in Figure 4.
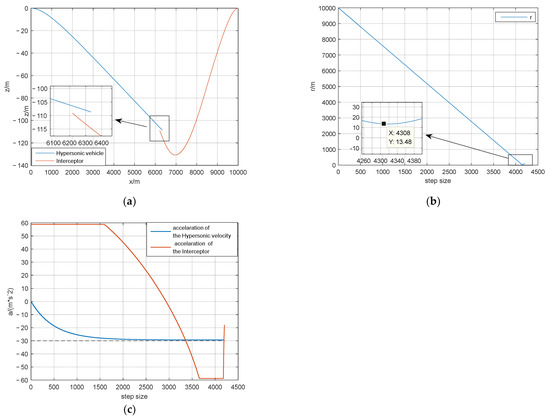
Figure 4.
Simulation results: (a) Two-dimensional plane diagram; (b) Curve of relative distance; (c) Acceleration comparison diagram.
Figure 4a is a two-dimensional plane diagram of attack and defense. The red line represents the plane trajectory of the pursuer missile, which adopts the proportional guidance law, and the blue line represents the plane trajectory of the hypersonic vehicle. As can be seen from Figure 4a, there is no intersection point between the hypersonic vehicle and the pursuer. Figure 4b shows the relative distance changing in the process of attack and defense confrontation. As can be seen from Figure 4b, throughout the entire process, the minimum relative distance between the hypersonic vehicle and interceptor missile was greater than 5 m, which satisfies the index requirements assigned in Section 2.3. According to the design goal in Section 2.3, this miss distance is sufficient to guarantee that the hypersonic vehicle can evade the pursuer.
Figure 4c is a schematic diagram of the acceleration changes of both sides in the process of attack and defense confrontation. The blue line is the acceleration curve of the hypersonic vehicle, and the red line is the acceleration curve of the interceptor missile. As can be seen from Figure 4c, when the head-on situation formed, the hypersonic aircraft tried its best to evade with the overload capability allowed, and the pursuer missile also pursued it with maneuvering advantages. However, even in the case that the head-on situation was not conducive to hypersonic vehicle evasion, and the interceptor capability was stronger than that of a hypersonic vehicle, the hypersonic vehicle still successfully realized evasion through the designed strategy. This demonstrates that the selected state space, action space and the designed reward function were reasonable.
In order to further verify the effectiveness of the trained agent, here, the value range of the initial condition was widened, and the initial line of sight angle and initial trajectory deflection angle that have a greater impact on the initial posture were selected as variables. To ensure that the head-on situation was still established, the selection range of the initial line of sight angle was limited to , and the initial trajectory deflection angle was set in the range of .
A Monte Carlo simulation was conducted 1000 times, and the simulation results for the initial line of sight and initial trajectory deflection angles were selected for combined dispersion. The simulation results are shown in Figure 5 below.
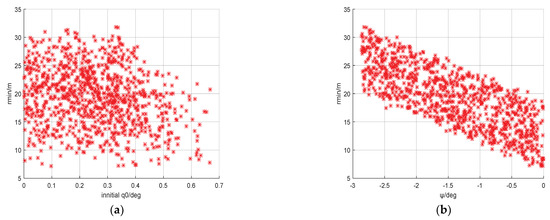
Figure 5.
Monte Carlo simulation results: (a) Miss distance disperses with different initial sight angles; (b) Miss distance disperses with the different initial trajectory deflection angles for the hypersonic vehicle.
As seen in Figure 5, a large number of experimental data illustrate that, in the case of the initial line-of-sight angle and initial trajectory deflection angle distributions, the miss distance of the agent after deep reinforcement learning training can be guaranteed to be greater than 5 m, which demonstrates that the hypersonic vehicle successfully achieved escape in the case of the formation of a head-on situation or an approximate head-on situation. This paper shows the correctness and effectiveness of the reinforcement learning algorithm based on the twin delay deep deterministic gradient to solve this kind of problem.
In fact, the relative distance between the hypersonic vehicle and the pursuer missile at the initial moment should be the biggest factor that influences the miss distance under the head-on situation. In order to qualitatively study the influence of the initial distance between the hypersonic vehicle and the pursuer missile on its miss distance and to provide schemes and suggestions for the maneuvering time of the hypersonic vehicle, the initial relative distance between the hypersonic vehicle and pursuer missile was selected as the variable with a selection range of . The Monte Carlo simulation results (1000 times) are shown in the figure below.
It can be seen in Figure 6 that the miss distance is positively correlated with the initial relative distance dispersion between the hypersonic vehicle and the pursuer missile. The results even present a relatively good linearity. It can be seen that the closer the initial distance between the two sides, the smaller the miss distance in the process of the PE game, and the lower the probability of successful escape for the hypersonic aircraft. Therefore, when a hypersonic vehicle is escaping under adverse head-on conditions, attention should be paid to the timing of the maneuver, that is, the initial relative distance between the evader and the pursuer, which has a great influence on the result. At the same time, it also provides ideas and references for solving related problems, such as decision-making in similar scenarios in the future.
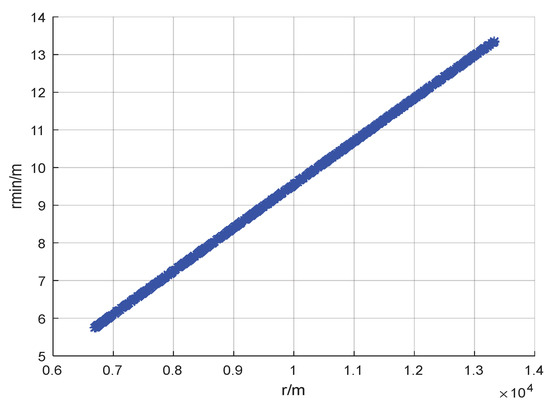
Figure 6.
Miss distance spreads with the initial relative distance.
It should be noted that this paper has several limitations. During the design of the reinforcement learning algorithm, we assumed that the guidance law for the pursuer missile used the proportional guidance and design corresponding to the evasion strategy of the hypersonic vehicle. Although the trained agent had a generalization ability, it was only applicable to classical guidance laws, such as PN or APN, for the pursuer. If the pursuer adopts more advanced guidance laws, the probability of successful evasion remains to be verified. In addition, compared with other algorithms, many parameters in the design process of the deep reinforcement learning algorithm require a certain amount of experience to debug successfully. This limitation will be time-consuming for designers to resolve.
5. Conclusions
In this paper, the evasion strategy of a hypersonic vehicle was studied using deep reinforcement learning under the adverse situation of a head-on scenario. In the actual scene, once the head-on situation formed, the speed advantage of the hypersonic vehicle was greatly weakened, and the evasion strategy of the hypersonic vehicle was more dependent on the design of the strategy. Therefore, based on the head-on situation, the design and simplification of models were conducted, and the delay to the control link was considered to create a more realistic scenario. Thus, the background of the research problem has a high engineering application value. Currently, flight environments and situations are changing rapidly, and a simple programmed maneuver cannot satisfy the actual requirements of real use. Accordingly, the deep reinforcement learning algorithm was used to design an evasion control decision-making strategy so as to improve the aircraft by changing the programmed maneuver to an intelligent maneuver. Based on the twin delayed deep deterministic gradient network, the decision framework for escape control based on the actor–critic method was constructed. The agent was trained and tested based on the deep reinforcement learning of the twin delayed deep deterministic gradient network in an attack-and-defense scenario. The simulation results show that the minimum miss distance between the hypersonic vehicle and the interceptor was greater than 5m. Several of the initial variables deviated, and the minimum miss distances of all the results were greater than 5m; this demonstrates that the trained agent could successfully achieve evasion under different conditions, verifying the effectiveness and feasibility of the strategy based on a reinforcement learning design. Therefore, this paper provides a solution to improving the direction of intelligent and autonomous maneuvering for an aircraft.
The present research limited itself to choosing a maneuvering time for a hypersonic vehicle to evade the adverse situation of a head-on scenario without considering attacking the target. Future research could consider the constraint of attacking the target at the same time as evading. To verify the feasibility of the method, algorithm design and simulation verification were only performed for a 1v1 scenario. In the future, the strategy design could consider coordinated attacks with multiple missiles.
Author Contributions
Conceptualization, all authors; methodology, M.G., T.Y., Q.L. and W.F.; software, M.G., T.Y. and Q.L.; writing—original draft preparation, M.G.; writing—review and editing, M.G., T.Y. and J.Z.; validation, T.Y. and W.F.; investigation, M.G. and J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 61933010) and supported by Fundamental Research Funds for the Central Universities.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data used during the study appear in the submitted article.
Conflicts of Interest
All the authors declare that they have no known competing financial interests or personal relationships that could appear to influence the work reported in this paper.
References
- Zhang, S.; Li, X.; Zuo, J.; Qin, J.; Cheng, K.; Feng, Y.; Bao, W. Research progress on active thermal protection for hypersonic vehicles. Prog. Aerosp. Sci. 2020, 119, 100646. [Google Scholar] [CrossRef]
- Chen, J.; Fan, X.; Xiong, B.; Meng, Z.; Wang, Y. Parameterization and optimization for the axisymmetric forebody of hypersonic vehicle. Acta Astronaut. 2020, 167, 239–244. [Google Scholar] [CrossRef]
- Chen, K.; Pei, S.; Zeng, C.; Ding, G. SINS/BDS tightly coupled integrated navigation algorithm for hypersonic vehicle. Sci. Rep. 2022, 12, 6144. [Google Scholar] [CrossRef]
- Wang, J.; Cheng, L.; Cai, Y.; Tang, G. A novel reduced-order guidance and control scheme for hypersonic gliding vehicles. Aerosp. Sci. Technol. 2020, 106, 106115. [Google Scholar] [CrossRef]
- Liu, J.; Hao, A.; Gao, Y.; Wang, C.; Wu, L. Adaptive control of hypersonicflight vehicles with limited angle-of-attack. IEEE/ASME Trans. Mechatron. 2018, 23, 883–894. [Google Scholar] [CrossRef]
- Zhu, J.; He, R.; Tang, G.; Bao, W. Pendulum maneuvering strategy for hypersonic glide vehicles. Aerosp. Sci. Technol. 2018, 78, 62–70. [Google Scholar] [CrossRef]
- Carr, W.R.; Cobb, R.G.; Pachter, M.; Pierce, S. Solution of a pursuit-evasion game using a near-optimal strategy. J. Guid. Control Dyn. 2018, 41, 841–850. [Google Scholar] [CrossRef]
- Liang, L.; Deng, F.; Peng, Z.; Li, X.; Zha, W. A differential game for cooperative target defense. Automatica 2019, 102, 58–71. [Google Scholar] [CrossRef]
- Shen, Z.; Yu, J.; Dong, X.; Hua, Y.; Ren, Z. Penetration trajectory optimization for the hypersonic gliding vehicle encountering two interceptors. Aerosp. Sci. Technol. 2022, 121, 107363. [Google Scholar] [CrossRef]
- Zhao, B.; Liu, T.; Dong, X.; Hua, Y.; Ren, Z. Integrated design of maneuvering penetration and guidance based on line deviation control. J. Astronaut. 2022, 43, 12. [Google Scholar]
- Zhao, K.; Cao, D.; Huang, W. Integrated design of maneuver, guidance and control for penetration missile. Syst. Eng. Electron. 2018, 40, 8. [Google Scholar]
- Zhou, H.; Li, X.; Bai, Y.; Wang, X. Optimal guidance for hypersonic vehicle using analytical solutions and an intelligent reversal strategy. Aerosp. Sci. Technol. 2022, 132, 108053. [Google Scholar] [CrossRef]
- Xian, Y.; Ren, L.; Xu, Y.; Li, S.; Wu, W.; Zhang, D. Impact point prediction guidance of ballistic missile in high maneuver penetration condition. Def. Technol. 2022. [Google Scholar] [CrossRef]
- Lee, J.Y.; Jo, B.U.; Moon, G.H.; Tahk, M.J.; Ahn, J. Intercept point prediction of ballistic missile defense using neural network learning. Int. J. Aeronaut. Space Sci. 2020, 21, 1092–1104. [Google Scholar] [CrossRef]
- Liang, H.; Li, Z.; Wu, J.; Zheng, Y.; Chu, H.; Wang, J. Optimal Guidance Laws for a Hypersonic Multiplayer Pursuit–Evasion Game Based on a Differential Game Strategy. Aerospace 2022, 9, 97. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, K.; Zhang, Y.; Shi, H.; Tang, L.; Li, M. Near-optimal interception strategy for orbital pursuit-evasion using deep reinforcement learning. Acta Astronaut. 2022, 198, 9–25. [Google Scholar] [CrossRef]
- Tang, X.; Ye, D.; Huang, L.; Sun, Z.; Sun, J. Pursuit-evasion game switching strategies for spacecraft with incomplete-information. Aerosp. Sci. Technol. 2021, 119, 107112. [Google Scholar] [CrossRef]
- Yan, T.; Cai, Y.; Xu, B. Evasion guidance algorithms for air-breathing hypersonic vehicles in three-player pursuit-evasion games. Chin. J. Aeronaut. 2020, 33, 3423–3436. [Google Scholar] [CrossRef]
- Dwivedi, P.N.; Bhattacharya, A.; Padhi, R. Suboptimal midcourse guidance of interceptors for high-speed targets with alignment angle constraint. J. Guid. Control Dyn. 2011, 34, 860–877. [Google Scholar] [CrossRef]
- Liu, K.; Meng, H.; Wang, C.; Li, J.; Chen, Y. Anti-Head-on interception penetration guidance law for slide vehicle. Mod. Def. Tech. 2018, 46, 7. [Google Scholar]
- Hwangbo, J.; Sa, I.; Siegwart, R.; Hutter, M. Control of a quadrotor with reinforcement learning. IEEE Robot. Autom. Lett. 2017, 2, 2096–2103. [Google Scholar] [CrossRef]
- Liu, C.; Dong, C.; Zhou, Z.; Wang, Z. Barrier Lyapunov function based reinforcement learning control for air-breathing hypersonic vehicle with variable geometry inlet. Aerosp. Sci. Technol. 2019, 96, 105537. [Google Scholar] [CrossRef]
- Yoo, J.; Jang, D.; Kim, H.J.; Johansson, K.H. Hybrid reinforcement learning control for a micro quadrotor flight. IEEE Control Syst. Lett. 2020, 5, 505–510. [Google Scholar] [CrossRef]
- Qiu, X.; Gao, C.; Jing, W. Maneuvering penetration strategies of ballistic missiles based on deep reinforcement learning. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2022, 236, 3494–3504. [Google Scholar] [CrossRef]
- Gao, A.; Dong, Z.; Ye, H.; Song, J.; Guo, Q. Loitering munition penetration control decision based on deep reinforcement learning. Acta Armamentarii 2021, 42, 1101–1110. [Google Scholar]
- Jiang, L.; Nan, Y.; Zhang, Y.; Li, Z. Anti-Interception guidance for hypersonic glide vehicle: A deep reinforcement learning approach. Aerospace 2022, 9, 424. [Google Scholar] [CrossRef]
- Li, W.; Zhu, Y.; Zhao, D. Missile guidance with assisted deep reinforcement learning for head-on interception of maneuvering target. Complex Intell. Syst. 2021, 8, 1205–1216. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).