Abstract
Aiming at the attack and defense game problem in the target-missile-defender three-body confrontation scenario, intelligent game strategies based on deep reinforcement learning are proposed, including an attack strategy applicable to attacking missiles and active defense strategy applicable to a target/defender. First, based on the classical three-body adversarial research, the reinforcement learning algorithm is introduced to improve the purposefulness of the algorithm training. The action spaces the reward and punishment conditions of both attack and defense confrontation are considered in the reward function design. Through the analysis of the sign of the action space and design of the reward function in the adversarial form, the combat requirements can be satisfied in both the missile and target/defender training. Then, a curriculum-based deep reinforcement learning algorithm is applied to train the agents and a convergent game strategy is obtained. The simulation results show that the attack strategy of the missile can maneuver according to the battlefield situation and can successfully hit the target after avoiding the defender. The active defense strategy enables the less capable target/defender to achieve the effect similar to a network adversarial attack on the missile agent, shielding targets from attack against missiles with superior maneuverability on the battlefield.
1. Introduction
In recent years, with the development of weapons technology, offensive and defensive confrontation scenarios have become increasingly complex. The traditional one-to-one game problem is also difficult to keep up with the trend of battlefield intelligence. In various new studies, both sides of the confrontation continuously adopt new game strategies to gain battlefield advantages. Among them, the target-missile-defender (TMD) three-body engagement triggered by active target defense has attracted increasing research interest [1,2,3,4,5,6,7]. In a typical three-body confrontation scenario, three types of vehicles are involved: the target (usually a high-value vehicle such as an aircraft or ballistic missile), an attacking missile to attack the target, and a defender missile to intercept the attacking missile. This combat scenario breaks the traditional pursuit-evasion model with greater complexity and provides more possibilities for battlefield games.
The early classical studies of the three-body confrontation problem mainly started from the spatial-geometric relationship. The researchers achieved the goal of defending the target by designing the spatial position of the defender with the target and the attacking missile (e.g., in the middle of the target and the missile). From the line-of-sight (LOS) guidance perspective, a guidance strategy for a defender guarding a target was investigated that enables the defender to intercept an attacking missile at a speed and maneuverability disadvantage [8]. Triangle intercept guidance is also an ingenious guidance law based on the idea of LOS command guidance [9]. In order to avoid the degradation of system performance or the need for additional high-resolution radar assistance due to reduced angular resolution at longer distances, a simpler gain form of the LOS angular rate was derived by optimal control, reducing the capability requirements of the sensing equipment [10,11]. Nonlinear control approaches, such as sliding mode control, can also achieve the control of LOS rotation [12].
The more dominant research idea for the three-body problem is by means of optimal control or differential game. The difference between the two is that the guidance law based on the optimal control theory needs to know the opponent’s control strategy in advance. Although the reliance on a priori information for one-sided optimization can be reduced by sharing information between the target and the defender [13], there are problems such as difficulties in applying numerical optimization algorithms online. In contrast, differential game has received more widespread attention as it does not require additional assumptions about the opponent’s strategy [14,15]. The differential game can obtain the game strategy of the two opponents by finding the saddle point solution, and under the condition of accurate modeling, it can guarantee the optimality of the strategy against the opponent’s arbitrary maneuver [16,17,18]. Considering the drawback that the control of linear quadratic differential game guidance law may go beyond the boundary, the bounded differential game is proposed and verified on a two-dimensional plane and in three-dimensional space [19,20]. The differential game approach can also be applied to analyze the capture and escape regions and the Hamilton–Jacobi–Isaacs equation can be solved to demonstrate the consistency of the geometric approach with the optimal control approach [21,22,23,24]. Based on the analysis of the capture radius, the game can be divided into different stages and the corresponding control strategies can be proposed and the conditions of stage switching are analyzed [25,26]. In addition, in order to be closer to the actual battlefield environment, recent studies have considered the existence of strong constraint limits on capability boundaries [27], state estimation under imperfect information through Kalman filtering [28], the existence of the relative intercept angle constraints on attacking requirements [17,29,30], cooperative multi-vehicle against an active defense target [17,31], weapon-target-allocation strategies [32], and so on.
The existing studies basically must use the model’s linearization and order reduction as the basis to derive a guidance law that satisfies certain constraints and performance requirements. To simplify the derivation, the vehicles are often assumed to possess ideal dynamics [33,34]. However, as participating vehicles adopt more advanced game strategies, the battlefield becomes more complex and the linearization suffers from significant distortion under intense maneuvering confrontations.
Deep reinforcement learning (DRL) developed in recent years has good adaptability to complex nonlinear scenarios and shows strong potential in the aerospace field [35], such as applying DRL to the attitude control of hypersonic vehicles [36], design of missile guidance laws [37,38], asteroid landing [39,40], vehicle path planning [41], and other issues. In addition, there have been many studies applying DRL to the pursuit-evasion game or TMD engagement. The problem of the cooperative capture of an advanced evader by multiple pursuers was studied in [42] using DRL, which is difficult for differential game or optimal control in such a complex uncertain environment. In [43], the researchers applied reinforcement learning algorithms to a particle environment where the attacker was able to evade the defender and eventually capture the target, showing better performance than traditional guidance algorithms. The agents in [42] and [43] all have ideal dynamics with fewer constraints relative to the real vehicle. In [44], from the perspective of the target, reinforcement learning was applied to study the timing of target launching defenders, which has the potential to be solved online. Deep reinforcement learning was also utilized for the ballistic missile maneuvering penetration and attacking stationary targets, which can also be considered as a three-body problem [6,45]. In addition, adaptive dynamic programming, which is closely related to DRL, has also attracted extensive interest in intelligent adversarial games [46,47,48,49,50]. However, the system models studied so far are relatively simple and few studies are applicable to complex continuous dynamic systems with multiple vehicles [51,52].
Motivated by the previous discussion, we apply DRL algorithms to a three-body engagement and obtain intelligent game strategies for both offensive and defensive confrontations, so that both an attacking missile and target/defender can combine evasion and interception performance. The strategy for the attacking missile ensures that the missile avoids the defender and hits the target; the strategy for the target/defender ensures that the defender intercepts the missile before it threatens the target. In addition, the DRL-based approach is highly adaptable to nonlinear scenarios and, thus, has outstanding advantages in further solving more complex multi-body adversarial problems in the future. However, there also exists a gap between the simulation environment and the real world when applying DRL approaches. Simulation environments can improve sampling efficiency and alleviate security issues, but difficulties caused by the reality gap are encountered when transferring agent policies to real devices. To address this issue, research applying DRL approaches to the aerospace domain should focus on the following aspects. On the one hand, sim-to-real (Sim2Real) research is used to close the reality gap and thus achieve more effective strategy transfer. The main methods currently being utilized for Sim2Real transfer in DRL include domain randomization, domain adaptation, imitation learning, meta-learning, and knowledge distillation [53]. On the other hand, in the simulation phase, the robustness and generalization of the proposed methods should be fully verified. In the practical application phase, the hardware-in-the-loop simulation should be conducted to gradually improve the reliability of applying the proposed method to real devices.
In order to assist the DRL algorithm to converge more stably, we introduce curriculum learning into the agent training. The concept of curriculum learning was first introduced at the top conference International Conference on Machine Learning (ICML) in 2009, which caused a great sensation in the field of machine learning [54]. In the following decade, numerous studies on curriculum learning and self-paced learning have been proposed.
The main contributions of this paper are summarized as follows.
- (1)
- Combining the findings of differential game in the traditional three-body game with DRL algorithms enables agent training with clearer direction, while avoiding inaccuracies due to model linearization, and better adapts to complex battlefield environments with stronger nonlinearity.
- (2)
- The three-body adversarial game model is constructed as a Markov Decision Process suitable for reinforcement learning training. Through analysis of the sign of the action space and design of the reward function in the adversarial form, the combat requirements of evasion and attack can be balanced in both missile and target/defender training.
- (3)
- The missile agent and target/defender agent are trained in a curriculum learning approach to obtain intelligent game strategies for both attack and defense.
- (4)
- The intelligent attack strategy enables the missile to avoid the defender and hit the target in various battlefield situations and adapt to the complex environment.
- (5)
- The intelligent active defense strategy enables the less capable target/defender to achieve an effect similar to network adversarial attack on the missile agent. The defender intercepts the attacking missile before it hits the target.
The paper is structured as follows. Section 2 introduces the TMD three-body engagement model and presents the differential game solutions solved on the basis of linearization and order reduction. In Section 3, the three-body game is constructed as a Markov Decision Process with training curricula. In Section 4, the intelligent game strategy for the attacking missile and the intelligent game strategy for the target/defender are solved separately using curriculum-based DRL. The simulation results and discussion are provided in Section 5, analyzing the advantages of the proposed approach. Finally, some final remarks are provided as a conclusion in Section 6.
2. Dynamic Model of TMD Engagement
2.1. Nonlinear Engagement Model
The TMD three-body engagement involves an offensive and defensive confrontation, including an attacking missile (M) on one side and a target (T) and a defender (D) on the other side. The mission of the missile is to attack the target, but the defender will be launched by the target or other platforms to intercept the missile, so the missile is required to evade the defender by maneuvering before attempting to hit the target. The mission of the target/defender is the opposite. In general, the target is weak in maneuvering and has difficulty avoiding being hit by the missile through traditional maneuvering strategies, so the target adopts an active defense strategy of firing the defender to intercept the missile and survive in the battlefield. The engagement geometry of the TMD three-body confrontation in the inertial coordinate system is shown in Figure 1.
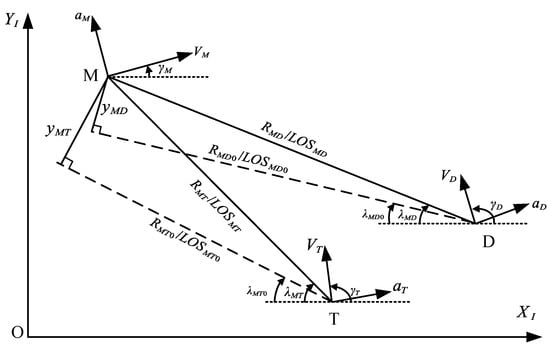
Figure 1.
Three-body confrontation engagement geometry.
As shown in Figure 1, the nonlinear engagement model of missile-target and missile-defender can be represented as
where M stands for the missile and represents the target or defender, i.e., .
The rate of change of flight path angle can be expressed as
The dynamics model of each vehicle can be represented by a linear equation of arbitrary order as
where represents the internal state variables of each vehicle and is the corresponding control input.
2.2. Linearization and Zero-Effort Miss
The three-body engagement generally occurs in the end-game phase, when the relative speeds of the offensive and defensive confrontations are large, the engagement time is short, and the speed of each vehicle can be approximated as a constant. According to [55], by linearizing the engagement geometry near the initial lines of sight and applying differential game theory, the optimal control of each vehicle under a quadratic cost function can be found as
where is the zero-effort miss of missile and target and is the zero-effort miss of defender and missile. The coefficients and () represent the effective navigation gains. The time-to-go between the missile/target pair and the defender/missile pair are donated by and , respectively. The time-to-go can be calculated by and , where the interception time is defined as.
We assume that the engagement of the attacking missile M with the defender D precedes the engagement of the attacking missile M with the target T, i.e., and satisfy in the timeline. This is because, once the missile hits or misses the target, it means that the game is over and the defender no longer needs to continue the engagement.
To derive the expression for the zero-effort miss in Equation (4), we assume that the dynamics of the vehicle in Equation (3) are modeled as a first-order system with a time constant of . Therefore, choosing the state variables as , the equation of motion for the missile to engage the target or defender can be expressed as
where
In Equation (7), the angles between the acceleration and the lines of sight are donated by and , which can be expressed by the flight path angle and the line of sight angle. Using the terminal projection transformation of the linear system, the zero-effort miss and can be expressed as
where is the coefficient matrix and is the state transition matrix. The derived zero-effort miss will be used for the training of the DRL agents, the details of which are presented in Section 3. Up to this point, the only undetermined quantity left in Equation (4) is the effective navigation ratios, which will become the optimization variable for DRL.
3. Curriculum-Based DRL Algorithm
Applying the deep reinforcement learning algorithm to the TMD engagement scenario consists of the following steps. First, the engagement environment is constructed based on the dynamics model, which was outlined in Section 2. Next, the environment is constructed as a Markov decision process, which includes action selection, redirection shaping, and observation selection. This needs to be carefully designed taking full account of the dynamics of the missile and the target/defender. Finally, there is a learning curriculum to ensure training stability.
3.1. Deep Reinforcement Learning and Curriculum Learning
Reinforcement learning, as a branch of machine learning, has received a lot of attention from researchers in various fields in recent years. Classical reinforcement learning is used to solve the Markov Decision Process (MDP) of dynamic interaction between an agent and the environment, which consists of a quintuple , where and denote the state space and action space, denotes the probability matrix of state transfer, denotes the immediate reward, and denotes the reward discount factor. In the MDP, the immediate reward and the next state only depend on the current state and action, which is called Markov property. The solving process of a dynamic system through the integral is essentially consistent with the MDP.
Benefiting from the rapid development of deep learning, reinforcement learning has achieved abundant achievements in recent years and developed into deep reinforcement learning. However, DRL is often plagued by reward sparsity and excessive action-state space in training. In the TMD engagement, we are concerned with the terminal miss distance and not with the intermediate processes. Therefore, the terminal reward in the reward function dominates absolutely, which is similar to the terminal performance index in the optimal control problem. Thus, the reward function in the guidance problem is typically sparse, otherwise the dense intermediate reward may lead to speculative strategies that the designer does not expect. Furthermore, despite the clear problem definition and optimization goals, the nearly infinite action-state space and the huge random initial conditions still pose obvious difficulties for the agent training. In particular, random conditions such as the position, speed, and heading error of each vehicle at the beginning of the engagement add uncertainty to the training.
To solve this problem, we use a curriculum learning approach to ensure the steady progress of training. The learning process of humans and animals generally follows a sequence from easy to difficult and curriculum learning draws on this learning idea. In contrast to the general paradigm of indiscriminate machine learning, curriculum learning mimics the process of human learning by proposing that models start with easy tasks and gradually progress to complex samples and knowledge [56,57]. Curriculum learning assigns different weights to the training samples of different difficulty levels according to the difficulty of the samples. Initially, the highest weights are assigned to the easy samples and, as the training process continues, the weights of the harder samples will be gradually increased. Such a process of dynamically assigning weights to samples is called a Curriculum. Curriculum learning can accelerate training and reduce the training iteration steps while achieving the same performance. In addition, curriculum learning enables the model to obtain better generalization performance, i.e., it allows the model to be trained to a better local optimum state. We will start with simple missions in our training, so that the agent can easily obtain the sparse reward at the end of an episode. Then, the random range of the initial conditions will be gradually expanded to enable the agent to eventually cope with the complex environment.
In the following, we will construct an MDP framework for the TMD engagement, consisting of action selection, reward shaping, and observation selection. The formulation requires adequate consideration of the dynamic model properties, as these have a significant impact on the results.
3.2. Reward Shaping
For the design of the reward function, consider the engagement as the process of the confrontation game between the missile and the target/defender and the advantage of one side on the battlefield is correspondingly expressed as the disadvantage of the other side. Therefore, the reward function should reflect the combat intention of both sides of the game, including positive rewards and negative penalties and, accordingly, the rewards and penalties of one side show the punishments and rewards of the other side. We design the following two forms of reward functions:
where is assigned to indicate an intermediate reward or penalty in an episode and is assigned to indicate a terminal reward or penalty near the end of an episode. The function adopts an exponential form that rises exponentially as approaches zero. The parameters and regulate the rate of growth of the exponential function. The general idea is to obtain continuously varying dense rewards through the exponential function. However, this results in a poor differentiation of the cumulative rewards between different policies and thus affects policy updates. We eventually set the reward to vary significantly as approaches 0, meaning that this will be a sparse reward. The basis of the differential game formulation reduces the difficulty of training and ensures that the agent completes training with sparse rewards. For both the missile and the target/defender, can be chosen as either the distance or the zero-effort miss. Note that using the zero-effort miss in the reward function imposes no additional requirements on the hardware equipment of the guidance system, as this is only used for off-line training. The function adopts a stairs form and , , and are the quantities associated with the kill radius.
3.3. Action Selection
According to the derived Equation (4), when training the missile agent, the action is chosen as a two-dimensional vector ; when training the target/defender agent, the action is chosen as a four-dimensional vector .
Further analysis of Equation (4) reveals that each term in the control law is precisely in the form of the classical proportional navigation guidance law [58]. Thus, each of the effective navigation gains have the meaning in Table 1. Beyond the effective time, that is, after the engagement between the missile and the defender, the corresponding gains are set to zero.

Table 1.
Meanings of the effective navigation gains.
To further improve the efficiency and stability of the training, we further analyze the positive and negative of the effective navigation gains. From the control point of view, the proportional navigation guidance law can be considered as a feedback control system that regulates the zero-effort miss to zero. Therefore, only a negative feedback system can be used to avoid the divergence, as shown in Figure 2a. The simplest step maneuver is often utilized to analyze the performance of a guidance system; the conclusion that the miss distance converges to zero with increasing flight time is provided in [58].
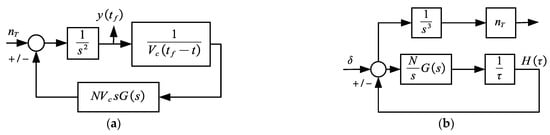
Figure 2.
Block diagram of proportional navigation guidance system. (a) Original guidance system; (b) Adjoint guidance system.
Establish the adjoint system of the negative feedback guidance system, as shown in Figure 2b. For convenience, we allow to be replaced by and, from the convolution integral, we can obtain
Converting Equation (10) from time to the frequency domain, we obtain
Next, integrating the preceding equation yields
When the guidance system is a single-lag system, which means that
we can finally obtain the expression for the miss distance of the negative feedback guidance system in the frequency domain as
Applying the final value theorem, when the flight time increases, the miss distance will tend to zero:
which means that the guidance system is stable and controllable. Similarly, we can find the expression of the miss distance for the positive feedback guidance system in the frequency domain as follows
Again, applying the final value theorem, it can be found that the miss distance does not converge with increasing flight time, but instead diverges to infinity
This conclusion is obvious from the control point of view, since positive feedback systems are generally not adopted because of their divergence characteristics. Therefore, positive feedback is never used in proportional navigation guidance systems and the effective guidance gain is never set to be negative. However, now we are faced with a situation where wants to decrease , and want to decrease , but wants to increase and also and want to increase . Therefore, combining the properties of negative and positive feedback systems, we set the actions , , and to be positive and , , and to be negative.
3.4. Observation Selection
During the flight of a vehicle, not all states are meaningful for the design of the guidance law, nor all states can be accurately obtained by sensors. Redundant observations not only complicate the structure of the network, thus increasing the training difficulty, but also ignore the prior knowledge of the designer. Through radar and filtering technology, information such as distance, closing speed, line-of-sight angle, and line-of-sight angle rate can be obtained, which are also commonly required in classical guidance laws. Therefore, the observation of the agent is eventually selected as
It should be noted that both in training the missile agent and in training the target/defender agent, the selected observation is the in Equation (18). The observation does not impose additional hardware equipment requirements on the vehicle that are capable of interfacing with existing weapons.
In addition, although the TMD engagement is divided into two phases, and , the observations associated with the defender are not set to zero during in order to ensure the stability of the network updating.
3.5. Curricula for Steady Training
Considering the difficulty of training directly, the curriculum learning approach was adopted to delineate environments of varying difficulty, thus allowing the agent to start with simple tasks and gradually adapt to the complex environment. The curricula are set to a different range of randomness for the initial conditions. The randomness of the initial conditions is reflected in the position of the vehicle (both lateral and longitudinal ), the velocity , and the flight path angle including the pointing error. The greater randomness of the initial conditions implies greater uncertainty and complexity of the environment. If the initial conditions are generated from a completely random range at the beginning, it will be difficult to stabilize the training of the agent. The curricula are set up to start training from a smaller range of random initial conditions and gradually expand the randomness of the initial conditions.
Assuming that the variable belongs to , when the total training step reaches , the random range of the variable is
where is the scheduling variable for the curricula difficulty. The training scheduler is depicted in Figure 3, from which it can be seen that the random range keeps expanding, and, by the time the training step reaches , the random range has basically coincided with the complete environment.
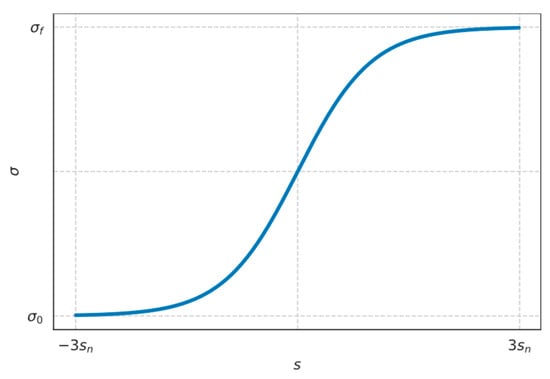
Figure 3.
Curricula training scheduler curve.
The growth rate of the range of random initial conditions is related to the difficulty of the environment. For more difficult environments, is required to be larger. This involves a trade-off between the training stability and training time consumption. For scenarios with difficult initial conditions, the probability distribution of random numbers can be designed to adjust the curricula. In the next training, we will choose the uniform distribution for initialization.
3.6. Strategy Update Algorithm
With the MDP constructed, the reinforcement learning algorithm applied to train the agents is selected. In recent years, along with the development of deep learning, reinforcement learning has evolved into deep reinforcement learning and has made breakthroughs in a series of interactive decision problems. The algorithms that have received wide attention include the TD3 algorithm (Twin Delayed Deep Deterministic Policy Gradient) [59], the SAC algorithm (Soft Actor Critic) [60], and the PPO algorithm (Proximal Policy Optimization) [61]. In this study, we adopt the PPO algorithm, which is insensitive to hyperparameters, stable in the training process, and suitable for training in dynamic environments with continuous action spaces.
At any moment , the agents perform actions based on the current observation from sensors and the embedded trained policy , driving the dynamic system to the next state , and receiving the corresponding reward . The interaction process exists until the end of the three-body game, which is called an episode. The agent and environment concurrently engender a sequence , which is defined as a trajectory.
The goal of the agent is to solve the optimal policy to maximize the expected cumulative discount reward, which is usually formalized by the state-value function and the state-action value function :
The advantage function is also calculated to estimate how advantageous an action is relative to the expected optimal action under the current policy:
In the PPO algorithm, the objective function expected to be maximized is represented as
where is a hyperparameter to restrict the size of policy updates and the probability ratio is . Equation (22) implies that the advantage function will be clipped if the probability ratio between the new policy and the old policy falls outside the range and . The probability ratio measures how different the two policies are. The clipped objective function ensures that excessive policy updates are avoided through clipping the estimated advantage function.
To further improve the performance of the algorithm, a value function loss term for the estimation accuracy of the critic network and an entropy maximum bonus for encouraging exploration are introduced into the surrogate objective
where and are corresponding coefficients. The purpose of the algorithm is to update the parameters of the neural network to maximize the surrogate objective with respect to .
4. Intelligent Game Strategies
4.1. Attack Strategy for the Missile
The mission of an attacking missile is to evade the defender in flight and ultimately hit the target. Therefore, it is important to balance the needs of both evasion and attack during the training process, during which favoring either side will result in mission failure.
The reward function of training missile agent is designed as
where indicates the closing speed between the missile and the defender; when , it indicates that the distance is increasing, meaning that the confrontation between the missile and defender is over. This means that the penalty due to the defender’s proximity to the missile is no longer available after .
The exponential form in Equation (9) is employed as a reward to guide the missile agent to control the zero-effort miss with the target to zero. The vehicle cannot directly measure the zero-effort miss during flight, but choosing as the variable for the reward function does not impose additional requirements on the detection hardware equipment. This is because the reward function is only utilized for offline training and not for online implementation.
In addition, is combined with the stairs form as a penalty to guide the missile agent to avoid the defender’s interception. The variable chosen for the penalty is the distance between the missile and the defender rather than the zero-effort miss . This is because the maneuver moment has a direct effect on the terminal miss. The missile does not have to start maneuvering prematurely when is close to zero, which tends to cause an unnecessary waste of energy while creating additional difficulties for later attacking targets. A better evasion can be achieved by maneuvering when the defender is approaching.
Using and , the first two terms of the reward function can be plotted as Figure 4. When the defender is far from the missile, the reward function encourages the missile to shorten its distance from the target. As decreases, the overall reward also decreases to become negative, which means that the penalty dominates, so the missile’s mission at this time is mainly to evade the defender. Furthermore, using , , , and , the agent will receive a decisive penalty when the defender is close to intercepting the missile.
Figure 4.
Reward shaping for missile agent.
4.2. Active Defense Strategy for the Target/Defender
The target and defender share the common mission of intercepting the incoming missile with the defender, thus ensuring the target’s successful survival. The target-defender cooperative strategy also consists of two parts: on the one hand, the defender attempts to hit the incoming attacking missile and, on the other hand, the target attempts to cause the incoming missile to miss the target as much as possible by maneuvering.
The reward function of training target/defender agent is designed as
For the target/defender, the zero-effort miss is more appropriate for the reward function than the distance. For the defender, the purpose of the guidance is to cause the zero-effort miss to be zero, while, for the target, the purpose of evasion is to maximize the zero-effort miss . Using and , the first two terms of the reward function will be the same as in Figure 4, except that is replaced by and is replaced by . When is small, it means that the target and the missile are already in the intercept triangle, which is extremely detrimental to the target’s survival, so the overall reward then decreases to a negative value. When is relatively large, it means that the target is safe and the purpose of the training is to improve the accuracy of the defender to intercept the missile. Since the zero-effort miss converges faster than the distance, , while , , and are the same as in the case of training missile agent.
5. Simulation Results and Analysis
5.1. Training Setting
The random initial conditions for training are set as listed in Table 2. The initial positions of the target and defender are randomly generated within a certain airspace and the defender is closer to the missile than the target, thus satisfying the timeline assumption . The initial position of the defender is before the target, which can be considered as a missile launched by other platforms or as a missile launched by the target at long-range entering the end guidance phase. The initial position of the missile is fixed because the absolute position of each vehicle is not directly involved in the training, but only its relative position is considered. The data for the initial conditions are samples drawn from a uniform distribution. In other words, any value within a given interval is equally likely to be drawn uniformly. We implement sampling via the uniform function in Python’s random library. In terms of the capabilities of each vehicle, the attacking missile has the greatest available overload and the fastest response time, while the defender and target have weaker maneuvering capabilities than the missile.

Table 2.
Initial parameters for training.
The training algorithm adopts the PPO algorithm with Actor-Critic architecture; the relevant hyperparameters and neural network structure are listed in Table 3.

Table 3.
Hyperparameters for training.
First, the missile agent is trained with a curriculum-based learning approach. As the randomness of the initial conditions increases, the complexity of the environment and the difficulty of the task grows. The target against the missile agent adopts a constant maneuver of random size and the defender employs proportional navigation guidance law. Then, based on the obtained attack strategy of the missile, the missile agent is utilized to train the active defense strategy of the target/defender. That is, the target/defender is confronted with an intelligent missile that has the ability to evade the defender and attack the target from the beginning of the training. All the training and simulations are carried out on a computer with an Intel Xeon Gold 6152 processor and a NVIDIA GeForce RTX 2080 Ti GPU. The environment and algorithm are programmed in Python 3.7 and the neural network is built by using the PyTorch framework. Both the actor network and the critic network for the missile and the target/defender contain three hidden layers with 16 neurons each. The activation function of the network adopts the ReLU function. If the number of multiplication and addition operations in network propagation is used to characterize the time complexity, the complexity of the actor network for the missile can be calculated as 672, the complexity of the actor network for the target/defender as 704, and the complexity of the two critic networks as 656. It can be seen that these networks have relatively simple architectures, occupy little storage space, are fast in operations (each computation lasting about 0.4–0.5 ms on average on a 2.1 GHz CPU), and, therefore, have the potential to be employed onboard.
It should be noted that the rise of the cumulative reward curve will not be accepted as a criterion for training success, since the evolution of the curricula from easy to difficult determines whether the agent can complete easy missions and thus earns high return at the beginning of the training.
5.2. Simulation Analysis of Attack Strategy for Missile
5.2.1. Engagement in Different Scenarios
In order to verify the effectiveness of the attack strategy of the trained missile agent, we set up different scenarios to assess the agent, with the simulation conditions presented in Table 4. The defender adopts a proportional navigation guidance law with an effective navigation ratio of 4. The target adopts a constant maneuver with random direction and magnitude. The simulation results for different target positions and different defender positions are presented in Figure 5.

Table 4.
Initial parameters for training.
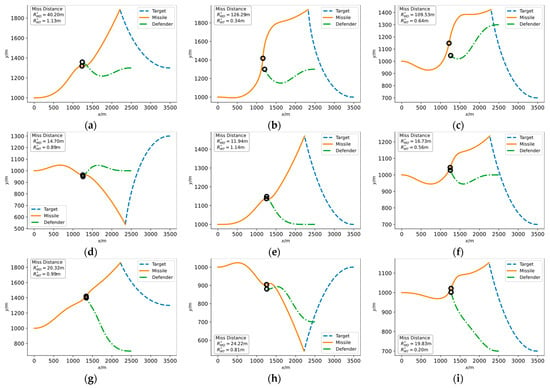
Figure 5.
Engagement trajectories of assessing missile agent under different simulation conditions, i.e., different target longitudinal position and defender longitudinal position : (a) Longitudinal position , ; (b) Longitudinal position , ; (c) Longitudinal position , ; (d) Longitudinal position , ; (e) Longitudinal position , ; (f) Longitudinal position , ; (g) Longitudinal position , ; (h) Longitudinal position , ; and (i) Longitudinal position , .
The relative positions of the target and defender cover most typical scenarios, so the simulation results are representative. Regardless of whether the missile faces a target at high altitude, a target at low altitude, or a target at a comparable altitude and regardless of the direction from which the defender intercepts, the missile can avoid the defender and eventually hit the target. The missile with an intelligent attack strategy will aim at the target in the primary direction, but rapidly maneuvers when the defender threatens itself, causing the defender to fail to intercept the missile.
5.2.2. Analysis of Typical Engagement Process
By further analyzing the engagement process in Figure 5a, we can obtain more insight into the intelligent attack strategy obtained based on DRL. The moment when the defender misses the missile has been marked in Figure 5a as 5.16 s with the miss distance of 40.20 m, which is safe for the missile. The moment the missile finally hit the target is 9.77 s and the off-target amount is 1.13 m, completing the combat mission.
As shown in Figure 6a, the missile quickly maneuvers between capability boundaries as the defender approaches itself and poses a threat, which is a bang-bang form of control law. The sudden and drastic maneuver of the missile does not allow the defender enough time to change the direction of flight and, thus, the interception to the missile fails. As can be seen from the zero-effort miss in Figure 6b, the defender’s zero-effort miss for the missile increases at the last moment due to the missile’s maneuver. Then, the missile rapidly changes its acceleration direction after evading the defender, thus compensating for the deviation in aiming at the target caused by the previous maneuver. The zero-effort miss of the missile to the target eventually converged to zero, although it experienced fluctuations due to the missile’s maneuvers.
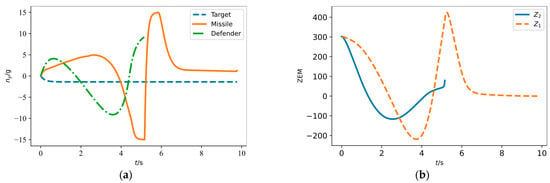
Figure 6.
Engagement process in Figure 5a. (a) The overload of each vehicle; (b) The zero-effort miss and .
5.2.3. Performance under Uncertainty Disturbances
When transferring the trained policy to the practical system, it faces various uncertainty disturbances, among which the observation noise and the inaccurate model used for training can negatively affect the performance of the agent. We count the success rate of the missile agent in the face of disturbances and the results are listed in Table 5. The initial conditions are initialized stochastically and noise disturbances are added to the observation. As for the model uncertainty, the response time constant bias and the higher-order system bias are considered. The higher-order system adopts the binomial form that is commonly adopted in guidance system evaluation, i.e., the third-order system is represented as

Table 5.
Success rate under uncertainty disturbances.
As shown from the simulation results, the trained policy is able to maintain a high success rate for a certain range of disturbances. The error of the response time is more important than the observation noise and the order of the model.
5.3. Simulation Analysis of Active Defense Strategy for Target/Defender
5.3.1. Engagement in Different Scenarios
In the same scenario as for validating the missile agent, we further assess the effectiveness of the intelligent active defense policy for the target/defender agent obtained from DRL training. Considering that the maximum overload and dynamic response of the missile, i.e., maneuverability and agility, are far superior to the target, it is difficult for the target to survive on its own maneuvering next if the defender fails to intercept the attacking missile in time. If the defender fails to intercept, then the target-missile engagement becomes a one-to-one pursuit-evasion game problem, which has been studied in many examples in the literature [62,63,64].
The simulation results for different engagement scenarios are illustrated in Figure 7. The missile utilizes the DRL-based intelligent attack strategy and the target/defender adopts the intelligent active defense strategy trained with the missile agent. In all scenarios, the defender successfully intercepts the missile. Unlike the missile facing a defender employing the proportional navigation guidance law, the missile in these cases does not adopt timely and effective maneuvers to evade the defender. The attack strategy of the missile agent, which is essentially a neural network, seems to be paralyzed. This suggests that the cooperative actions of the target/defender perform an effect similar to network adversarial attack, a widely noticed phenomenon in deep learning classifiers where the researcher can add a little noise to the network input thereby disabling the trained deep network [65,66].
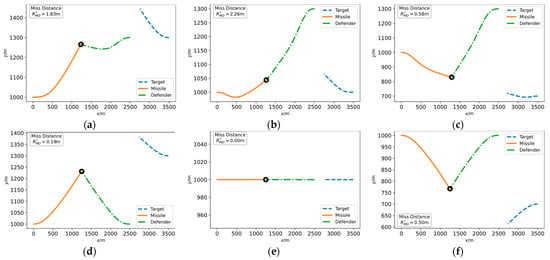
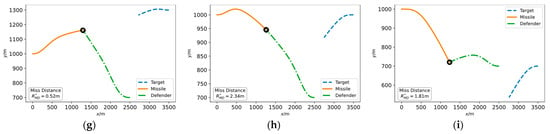
Figure 7.
Engagement trajectories of assessing target/defender agent under different simulation conditions, i.e., different target longitudinal position and defender longitudinal position : (a) Longitudinal position , ; (b) Longitudinal position , ; (c) Longitudinal position , ; (d) Longitudinal position , ; (e) Longitudinal position , ; (f) Longitudinal position , ; (g) Longitudinal position , ; (h) Longitudinal position , ; and (i) Longitudinal position , .
The reinforcement learning agent relies on observation to output action, so the target/defender can maneuver to influence the missile agent’s observation, thus causing the missile agent output to be an invalid action. In the simulation results of Figure 7, (e) is rather special. The target does not maneuver, resulting in a direct head-on attack of the missile and, consequently, the defender intercepts the missile easily. It is because the network inputs to the missile agent are all zero or constant values, which reflects an unexpected flaw of the intelligent strategy obtained from DRL training. The intelligent strategies based on neural networks may be tricked and defeated by very simple adversaries, which should attract sufficient attention in future research.
5.3.2. Analysis of Typical Engagement Process
By further analyzing the engagement process in Figure 7a, we can obtain more insight into the intelligent active defense strategy obtained based on DRL. The moment when the defender intercepts the missile has been marked in Figure 7a as 5.09 s with the miss distance of 1.83 m.
As shown in Figure 8, the missile does not maneuver to its maximum capability as the defender approaches and the timing of the maneuver lags and is eventually intercepted by the defender. Besides, the curves of the zero-effort miss show that the defender has locked the missile on the intercept triangle at about 2 s, while the missile is late in locking the target, which also reflects the failure of the missile attack strategy.
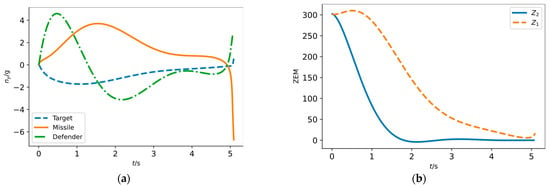
Figure 8.
Block diagram of proportional navigation guidance system. (a) Original guidance system; (b) Adjoint guidance system.
5.3.3. Performance under Uncertainty Disturbances
As in Section 5.2.3, we validate the robustness of the target/defender agent’s policy in the face of observation noise and model inaccuracy. As shown in Table 6, the target/defender agent’s policy is more robust to uncertainty disturbances and achieves a higher success rate in general compared to the missile. This is because the difficulty of the attack is inherently higher than the difficulty of defense and the target/defender’s policy is a targeted adversarial attack training for the missile’s policy.

Table 6.
Success rate under uncertainty disturbances.
Besides, in Table 6, we compare the curriculum-based DRL approach (C-DRL) with the cooperative linear quadratic differential game (CLQDG) guidance law, which is a classical guidance law in the TMD scenario [55]. The gains of the CLQDG guidance law do not involve response time, so we only analyze the effect of input noise and system order. Since ideal dynamics are assumed in the derivation of the gains, the effect of the order of the system is more pronounced. Facing the input noise, the performance of the C-DRL approach decreases insignificantly and the robustness of CLQDG is not as strong as that of the C-DRL approach. In addition, for complex three-dimensional multi-body game problems, the differential game approach to derive an analytic guidance law may not work, so the reinforcement learning approach has greater potential for development.
6. Conclusions
For the scenario of target-missile-defender three-body offensive and defensive confrontation, intelligent game strategies using curriculum-based deep reinforcement learning are proposed, including an attack strategy for attacking missiles and active defense strategy for target/defense. The results of the differential game are combined with deep reinforcement learning algorithms to provide the agent training with clearer direction and enable it them to better adapt to the complex environment with stronger nonlinearity. The three-body adversarial game is constructed as MDP suitable for reinforcement learning training by analyzing the sign of the action space and designing the reward function in the adversarial form. The missile agent and target/defender agent are trained with a curriculum learning approach to obtain the intelligent game strategies. Through simulation verification, we can draw the following conclusions.
- (1)
- Employing the curriculum-based DRL trained attack strategy, the missile is able to avoid the defender and hit the target in various situations.
- (2)
- Employing the curriculum-based DRL trained attack strategy, the less capable target/defender is able to achieve an effect similar to network adversarial attack against the missile agent. The defender intercepts the missile before the it hits the target.
- (3)
- The intelligent game strategies are able to maintain robustness in the face of disturbances from input noise and modeling inaccuracies.
In future research, three-dimensional scenarios with multiple attacking missiles, multiple defenders, and multiple targets will be considered. The battlefield environment is becoming more complicated and the traditional differential game and weapon-target assignment methods will show more obvious limitations, while the intelligent game strategy based on DRL has better adaptability for complex scenarios. A motion analysis in three dimensions can be conducted utilizing vector guidance laws or by decomposing the game problems into two perpendicular channels and solving in the plane, as has been proven to be possible in previous research. Combined with DRL, more complex multi-body game problems are expected to be solved. Technologies such as self-play and adversarial attack will also be applied to the generation and analysis of game strategies. In addition, considering the difficulty of obtaining battlefield observations, the training algorithm needs to be improved to adapt to the scenarios with imperfect information.
Author Contributions
The contributions of the authors are the following: Conceptualization, W.C. and X.G.; methodology, X.G. and Z.C.; validation, Z.C.; formal analysis, X.G.; investigation, X.G.; resources, X.G. and Z.C.; writing—original draft preparation, X.G.; writing—review and editing, W.C. and Z.C.; visualization, X.G.; supervision, W.C.; project administration, W.C.; funding acquisition, Z.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by China Postdoctoral Science Foundation (Grant No. 2021M700321).
Data Availability Statement
All data used during the study appear in the submitted article.
Acknowledgments
The study described in this paper was supported by China Postdoctoral Science Foundation (Grant No. 2021M700321). The authors fully appreciate the financial support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, C.; Wang, J.; Huang, P. Optimal Cooperative Line-of-Sight Guidance for Defending a Guided Missile. Aerospace 2022, 9, 232. [Google Scholar] [CrossRef]
- Li, Q.; Yan, T.; Gao, M.; Fan, Y.; Yan, J. Optimal Cooperative Guidance Strategies for Aircraft Defense with Impact Angle Constraints. Aerospace 2022, 9, 710. [Google Scholar] [CrossRef]
- Liang, H.; Li, Z.; Wu, J.; Zheng, Y.; Chu, H.; Wang, J. Optimal Guidance Laws for a Hypersonic Multiplayer Pursuit-Evasion Game Based on a Differential Game Strategy. Aerospace 2022, 9, 97. [Google Scholar] [CrossRef]
- Shi, H.; Chen, Z.; Zhu, J.; Kuang, M. Model predictive guidance for active aircraft protection from a homing missile. IET Control Theory Appl. 2022, 16, 208–218. [Google Scholar] [CrossRef]
- Kumar, S.R.; Mukherjee, D. Cooperative Active Aircraft Protection Guidance Using Line-of-Sight Approach. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 957–967. [Google Scholar] [CrossRef]
- Yan, M.; Yang, R.; Zhang, Y.; Yue, L.; Hu, D. A hierarchical reinforcement learning method for missile evasion and guidance. Sci. Rep. 2022, 12, 18888. [Google Scholar] [CrossRef]
- Liang, H.; Wang, J.; Wang, Y.; Wang, L.; Liu, P. Optimal guidance against active defense ballistic missiles via differential game strategies. Chin. J. Aeronaut. 2020, 33, 978–989. [Google Scholar] [CrossRef]
- Ratnoo, A.; Shima, T. Line-of-Sight Interceptor Guidance for Defending an Aircraft. J. Guid. Control Dyn. 2011, 34, 522–532. [Google Scholar] [CrossRef]
- Yamasaki, T.; Balakrishnan, S. Triangle Intercept Guidance for Aerial Defense. In AIAA Guidance, Navigation, and Control Conference; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2010. [Google Scholar]
- Yamasaki, T.; Balakrishnan, S.N.; Takano, H. Modified Command to Line-of-Sight Intercept Guidance for Aircraft Defense. J. Guid. Control Dyn. 2013, 36, 898–902. [Google Scholar] [CrossRef]
- Yamasaki, T.; Balakrishnan, S.N. Intercept Guidance for Cooperative Aircraft Defense against a Guided Missile. IFAC Proc. Vol. 2010, 43, 118–123. [Google Scholar] [CrossRef]
- Liu, S.; Wang, Y.; Li, Y.; Yan, B.; Zhang, T. Cooperative guidance for active defence based on line-of-sight constraint under a low-speed ratio. Aeronaut. J. 2022, 1–19, published online. [Google Scholar] [CrossRef]
- Shaferman, V.; Oshman, Y. Stochastic Cooperative Interception Using Information Sharing Based on Engagement Staggering. J. Guid. Control Dyn. 2016, 39, 2127–2141. [Google Scholar] [CrossRef]
- Prokopov, O.; Shima, T. Linear Quadratic Optimal Cooperative Strategies for Active Aircraft Protection. J. Guid. Control Dyn. 2013, 36, 753–764. [Google Scholar] [CrossRef]
- Shima, T. Optimal Cooperative Pursuit and Evasion Strategies Against a Homing Missile. J. Guid. Control Dyn. 2011, 34, 414–425. [Google Scholar] [CrossRef]
- Alkaher, D.; Moshaiov, A. Game-Based Safe Aircraft Navigation in the Presence of Energy-Bleeding Coasting Missile. J. Guid. Control Dyn. 2016, 39, 1539–1550. [Google Scholar] [CrossRef]
- Liu, F.; Dong, X.; Li, Q.; Ren, Z. Cooperative differential games guidance laws for multiple attackers against an active defense target. Chin. J. Aeronaut. 2022, 35, 374–389. [Google Scholar] [CrossRef]
- Chen, W.; Cheng, C.; Jin, B.; Xu, Z. Research on differential game guidance law for intercepting hypersonic vehicles. In Proceedings of the 6th International Workshop on Advanced Algorithms and Control Engineering (IWAACE 2022), Qingdao, China, 8–10 July 2022; Qiu, D., Ye, X., Sun, N., Eds.; SPIE: Bellingham, WA, USA, 2022; p. 94, ISBN 978-1-5106-5775-5. [Google Scholar]
- Rubinsky, S.; Gutman, S. Three-Player Pursuit and Evasion Conflict. J. Guid. Control Dyn. 2014, 37, 98–110. [Google Scholar] [CrossRef]
- Rubinsky, S.; Gutman, S. Vector Guidance Approach to Three-Player Conflict in Exoatmospheric Interception. J. Guid. Control Dyn. 2015, 38, 2270–2286. [Google Scholar] [CrossRef]
- Garcia, E.; Casbeer, D.W.; Pachter, M. Pursuit in the Presence of a Defender. Dyn. Games Appl. 2019, 9, 652–670. [Google Scholar] [CrossRef]
- Garcia, E.; Casbeer, D.W.; Pachter, M. The Complete Differential Game of Active Target Defense. J. Optim. Theory Appl. 2021, 191, 675–699. [Google Scholar] [CrossRef]
- Garcia, E.; Casbeer, D.W.; Fuchs, Z.E.; Pachter, M. Cooperative Missile Guidance for Active Defense of Air Vehicles. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 706–721. [Google Scholar] [CrossRef]
- Garcia, E.; Casbeer, D.W.; Pachter, M. Design and Analysis of State-Feedback Optimal Strategies for the Differential Game of Active Defense. IEEE Trans. Autom. Control 2018, 64, 553–568. [Google Scholar] [CrossRef]
- Liang, L.; Deng, F.; Lu, M.; Chen, J. Analysis of Role Switch for Cooperative Target Defense Differential Game. IEEE Trans. Autom. Control 2021, 66, 902–909. [Google Scholar] [CrossRef]
- Liang, L.; Deng, F.; Peng, Z.; Li, X.; Zha, W. A differential game for cooperative target defense. Automatica 2019, 102, 58–71. [Google Scholar] [CrossRef]
- Qi, N.; Sun, Q.; Zhao, J. Evasion and pursuit guidance law against defended target. Chin. J. Aeronaut. 2017, 30, 1958–1973. [Google Scholar] [CrossRef]
- Shaferman, V.; Shima, T. Cooperative Multiple-Model Adaptive Guidance for an Aircraft Defending Missile. J. Guid. Control Dyn. 2010, 33, 1801–1813. [Google Scholar] [CrossRef]
- Shaferman, V.; Shima, T. Cooperative Differential Games Guidance Laws for Imposing a Relative Intercept Angle. J. Guid. Control Dyn. 2017, 40, 2465–2480. [Google Scholar] [CrossRef]
- Saurav, A.; Kumar, S.R.; Maity, A. Cooperative Guidance Strategies for Aircraft Defense with Impact Angle Constraints. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7 January 2019; American Institute of Aeronautics and Astronautics: Reston: San Diego, CA, USA, 2019. ISBN 978-1-62410-578-4. [Google Scholar]
- Liang, H.; Wang, J.; Liu, J.; Liu, P. Guidance strategies for interceptor against active defense spacecraft in two-on-two engagement. Aerosp. Sci. Technol. 2020, 96, 105529. [Google Scholar] [CrossRef]
- Shalumov, V.; Shima, T. Weapon–Target-Allocation Strategies in Multiagent Target–Missile–Defender Engagement. J. Guid. Control Dyn. 2017, 40, 2452–2464. [Google Scholar] [CrossRef]
- Sun, Q.; Qi, N.; Xiao, L.; Lin, H. Differential game strategy in three-player evasion and pursuit scenarios. J. Syst. Eng. Electron. 2018, 29, 352–366. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, C.; Liu, N.; Zhou, W.; Qi, N. Guidance laws for attacking defended target. Chin. J. Aeronaut. 2019, 32, 2337–2353. [Google Scholar] [CrossRef]
- Chai, R.; Tsourdos, A.; Savvaris, A.; Chai, S.; Xia, Y.; Philip Chen, C.L. Review of advanced guidance and control algorithms for space/aerospace vehicles. Prog. Aerosp. Sci. 2021, 122, 100696. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, H.; Wu, T.; Lun, Y.; Fan, J.; Wu, J. Attitude control for hypersonic reentry vehicles: An efficient deep reinforcement learning method. Appl. Soft Comput. 2022, 123, 108865. [Google Scholar] [CrossRef]
- Gaudet, B.; Furfaro, R.; Linares, R. Reinforcement learning for angle-only intercept guidance of maneuvering targets. Aerosp. Sci. Technol. 2020, 99, 105746. [Google Scholar] [CrossRef]
- He, S.; Shin, H.-S.; Tsourdos, A. Computational Missile Guidance: A Deep Reinforcement Learning Approach. J. Aerosp. Inf. Syst. 2021, 18, 571–582. [Google Scholar] [CrossRef]
- Furfaro, R.; Scorsoglio, A.; Linares, R.; Massari, M. Adaptive generalized ZEM-ZEV feedback guidance for planetary landing via a deep reinforcement learning approach. Acta Astronaut. 2020, 171, 156–171. [Google Scholar] [CrossRef]
- Gaudet, B.; Linares, R.; Furfaro, R. Adaptive guidance and integrated navigation with reinforcement meta-learning. Acta Astronaut. 2020, 169, 180–190. [Google Scholar] [CrossRef]
- He, L.; Aouf, N.; Song, B. Explainable Deep Reinforcement Learning for UAV autonomous path planning. Aerosp. Sci. Technol. 2021, 118, 107052. [Google Scholar] [CrossRef]
- Wang, Y.; Dong, L.; Sun, C. Cooperative control for multi-player pursuit-evasion games with reinforcement learning. Neurocomputing 2020, 412, 101–114. [Google Scholar] [CrossRef]
- English, J.T.; Wilhelm, J.P. Defender-Aware Attacking Guidance Policy for the Target–Attacker–Defender Differential Game. J. Aerosp. Inf. Syst. 2021, 18, 366–376. [Google Scholar] [CrossRef]
- Shalumov, V. Cooperative online Guide-Launch-Guide policy in a target-missile-defender engagement using deep reinforcement learning. Aerosp. Sci. Technol. 2020, 104, 105996. [Google Scholar] [CrossRef]
- Qiu, X.; Gao, C.; Jing, W. Maneuvering penetration strategies of ballistic missiles based on deep reinforcement learning. Proc. Inst. Mech. Eng. Part G: J. Aerosp. Eng. 2022, 236, 3494–3504. [Google Scholar] [CrossRef]
- Radac, M.-B.; Lala, T. Robust Control of Unknown Observable Nonlinear Systems Solved as a Zero-Sum Game. IEEE Access 2020, 8, 214153–214165. [Google Scholar] [CrossRef]
- Zhao, M.; Wang, D.; Ha, M.; Qiao, J. Evolving and Incremental Value Iteration Schemes for Nonlinear Discrete-Time Zero-Sum Games. IEEE Trans. Cybern. 2022, 1–13, published online. [Google Scholar] [CrossRef]
- Xue, S.; Luo, B.; Liu, D. Event-Triggered Adaptive Dynamic Programming for Zero-Sum Game of Partially Unknown Continuous-Time Nonlinear Systems. IEEE Trans. Syst. Man Cybern Syst. 2020, 50, 3189–3199. [Google Scholar] [CrossRef]
- Wei, Q.; Liu, D.; Lin, Q.; Song, R. Adaptive Dynamic Programming for Discrete-Time Zero-Sum Games. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 957–969. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhao, D.; Li, X. Iterative Adaptive Dynamic Programming for Solving Unknown Nonlinear Zero-Sum Game Based on Online Data. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 714–725. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, H.; Han, J.; Zhang, K. Iterative adaptive dynamic programming methods with neural network implementation for multi-player zero-sum games. Neurocomputing 2018, 307, 54–60. [Google Scholar] [CrossRef]
- Wang, W.; Chen, X.; Du, J. Model-free finite-horizon optimal control of discrete-time two-player zero-sum games. Int. J. Syst. Sci. 2023, 54, 167–179. [Google Scholar] [CrossRef]
- Zhao, W.; Queralta, J.P.; Westerlund, T. Sim-to-Real Transfer in Deep Reinforcement Learning for Robotics: A Survey. 2020 IEEE Symposium Series on Computational Intelligence (SSCI), Canber, ACT, Australia, 1–4 December 2020; IEEE: New York, NY, USA, 2020; pp. 737–744, ISBN 978-1-7281-2547-3. [Google Scholar]
- Bengio, Y.; Louradour, J.; Collobert, R.; Weston, J. Curriculum learning. In Proceedings of the 26th Annual International Conference on Machine Learning-ICML ’09, Montreal, QC, Canada, 14–18 June 2009; Danyluk, A., Bottou, L., Littman, M., Eds.; ACM Press: New York, NY, USA, 2009; pp. 1–8, ISBN 978-1-6055-8516-1. [Google Scholar]
- Perelman, A.; Shima, T.; Rusnak, I. Cooperative Differential Games Strategies for Active Aircraft Protection from a Homing Missile. J. Guid. Control Dyn. 2011, 34, 761–773. [Google Scholar] [CrossRef]
- Wang, X.; Chen, Y.; Zhu, W. A Survey on Curriculum Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 4555–4576. [Google Scholar] [CrossRef] [PubMed]
- Soviany, P.; Ionescu, R.T.; Rota, P.; Sebe, N. Curriculum Learning: A Survey. Int. J. Comput. Vis. 2022, 130, 1526–1565. [Google Scholar] [CrossRef]
- Zarchan, P. Tactical and Strategic Missile Guidance, 6th ed.; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2012; ISBN 978-1-60086-894-8. [Google Scholar]
- Fujimoto, S.; van Hoof, H.; Meger, D. Addressing Function Approximation Error in Actor-Critic Methods. In Proceedings of the 35th International Conference on Machine Learning; Dy, J., Krause, A., Eds.; PLMR: Stockholm, Sweden, 2018; pp. 1587–1596. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor. In Proceedings of the 35th International Conference on Machine Learning; Dy, J., Krause, A., Eds.; PMLR: Stockholm, Sweden, 2018; pp. 1861–1870. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv Prepr. 2017, arXiv:1707.06347. Available online: https://arxiv.org/abs/1707.06347v2 (accessed on 28 August 2017).
- Liu, F.; Dong, X.; Li, Q.; Ren, Z. Robust multi-agent differential games with application to cooperative guidance. Aerosp. Sci. Technol. 2021, 111, 106568. [Google Scholar] [CrossRef]
- Wei, X.; Yang, J. Optimal Strategies for Multiple Unmanned Aerial Vehicles in a Pursuit/Evasion Differential Game. J. Guid. Control Dyn. 2018, 41, 1799–1806. [Google Scholar] [CrossRef]
- Shaferman, V.; Shima, T. Cooperative Optimal Guidance Laws for Imposing a Relative Intercept Angle. J. Guid. Control Dyn. 2015, 38, 1395–1408. [Google Scholar] [CrossRef]
- Ilahi, I.; Usama, M.; Qadir, J.; Janjua, M.U.; Al-Fuqaha, A.; Hoang, D.T.; Niyato, D. Challenges and Countermeasures for Adversarial Attacks on Deep Reinforcement Learning. IEEE Trans. Artif. Intell. 2022, 3, 90–109. [Google Scholar] [CrossRef]
- Qiu, S.; Liu, Q.; Zhou, S.; Wu, C. Review of Artificial Intelligence Adversarial Attack and Defense Technologies. Appl. Sci. 2019, 9, 909. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).