Filter Design for Laser Inertial Navigation System Based on Improved Pigeon-Inspired Optimization
Abstract
1. Introduction
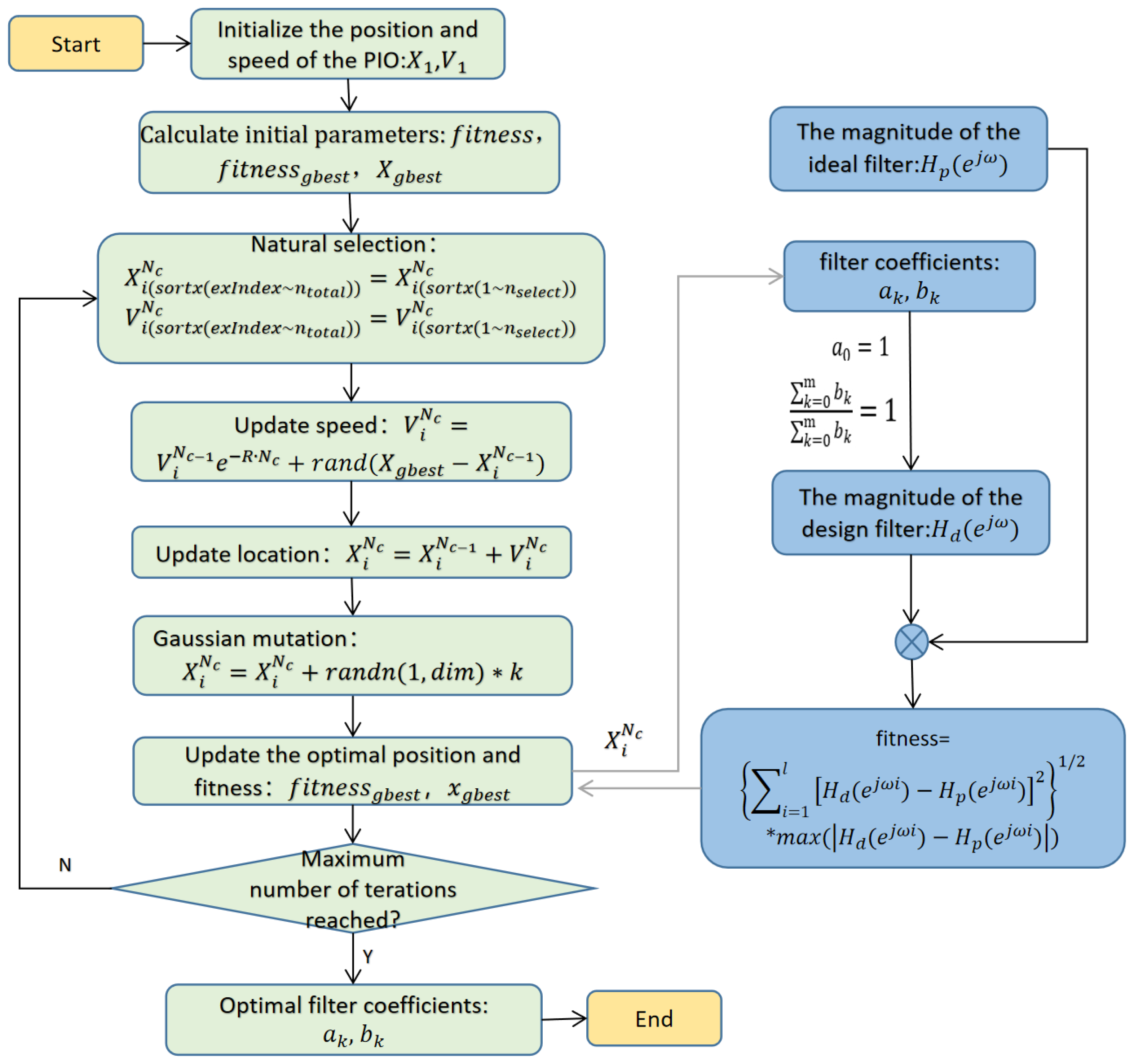
2. Design Method of LINS Filter Based on SMPIO
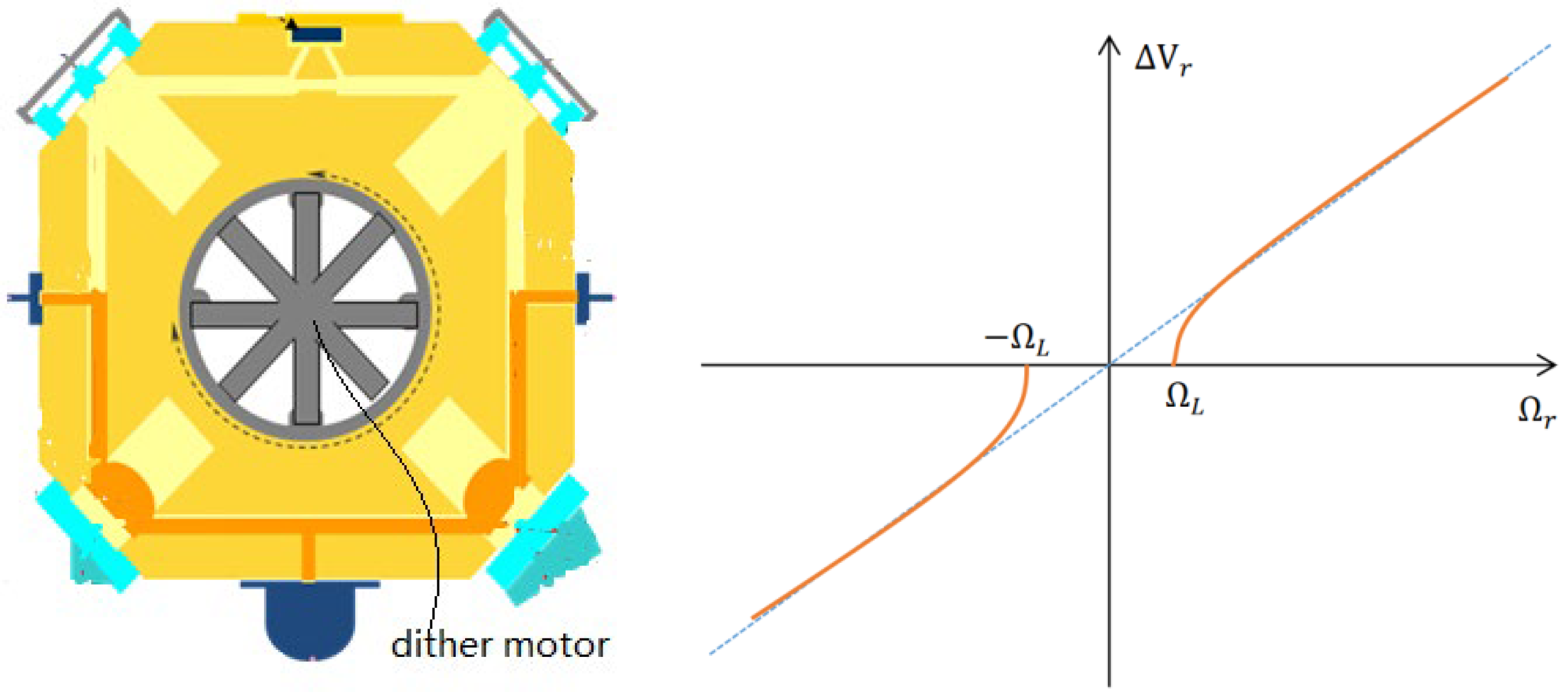
2.1. LINS Filter
2.2. SMPIO Method
- Natural selection of the particle swarm:
- 2.
- Gaussian mutation of the particle swarm:
2.3. Filter Design Method Based on SMPIO
- A set of initial values of particle swarm is randomly generated by Monte Carlo method. The fitness function value of the particle swarm is calculated and compared to find the globally optimal.
- The fitness function of the IIR filter, that is Formula (9), is calculated as follows:
- Obtain the coefficient , of the IIR digital filter according to the particle swarm position data.
- Calculate the amplitude response of each sampling point of the designed filter according to , , then compare it with the amplitude response of the ideal filter, and then calculate the fitness function according to Formula (9).
- Natural selection of the particle swarm: Sort the current generation of particles according to their fitness, from small to large, and update the speed and position of particles with the largest fitness according to Formula (7).
- Update the particle swarm velocity according to Formula (5) and update the particle swarm position according to Formula (6).
- Gaussian mutation of the particle swarm: Mutate the position of the particle swarm according to Formula (8);
- Calculate the fitness function value of the particle swarm after position update, compare and record the global optimal particle position and fitness value.
- Determine whether the specified maximum number of iteration steps is reached. If not, go to step 3, and continue iterative calculation; if so, end the process and save the calculation results.
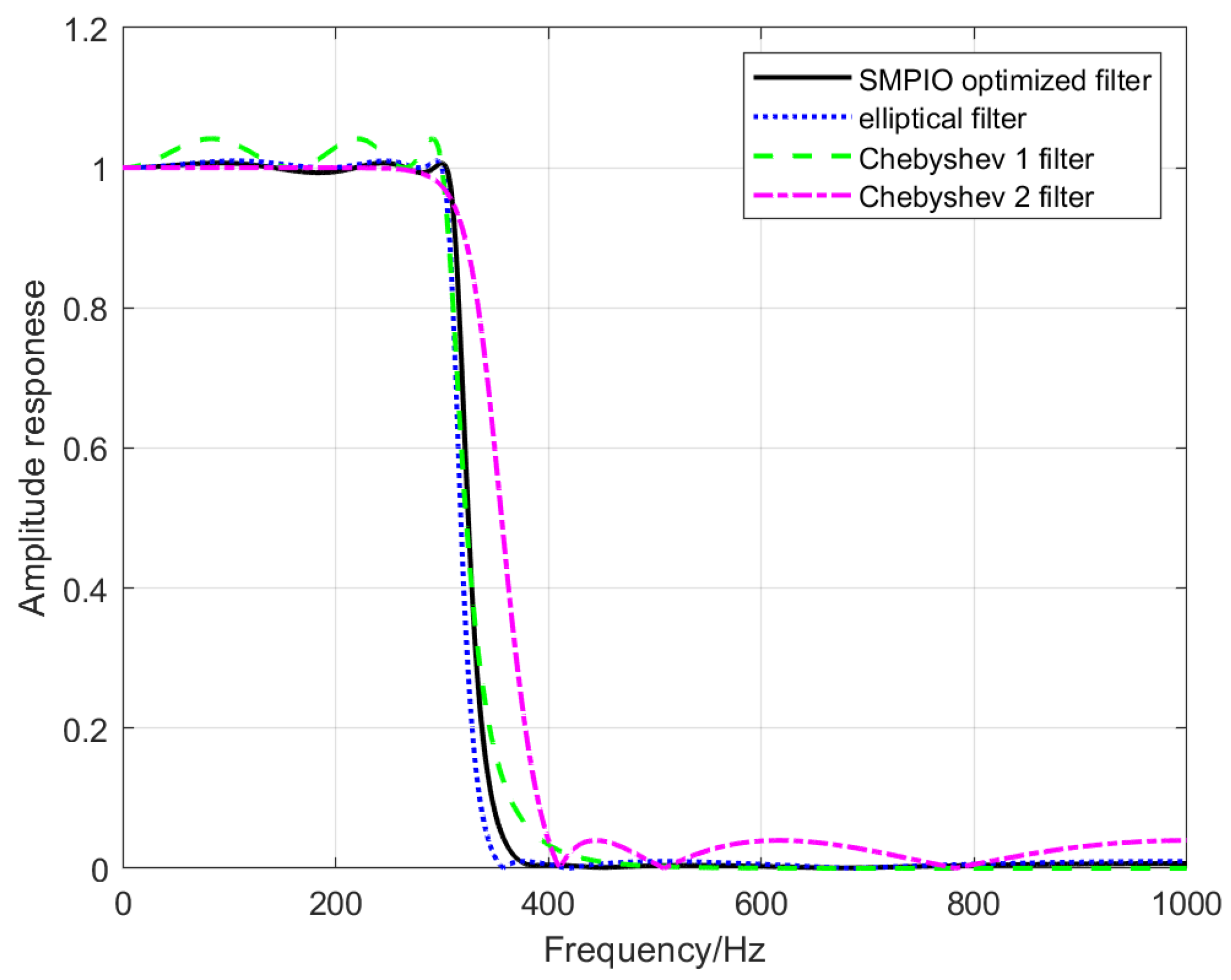
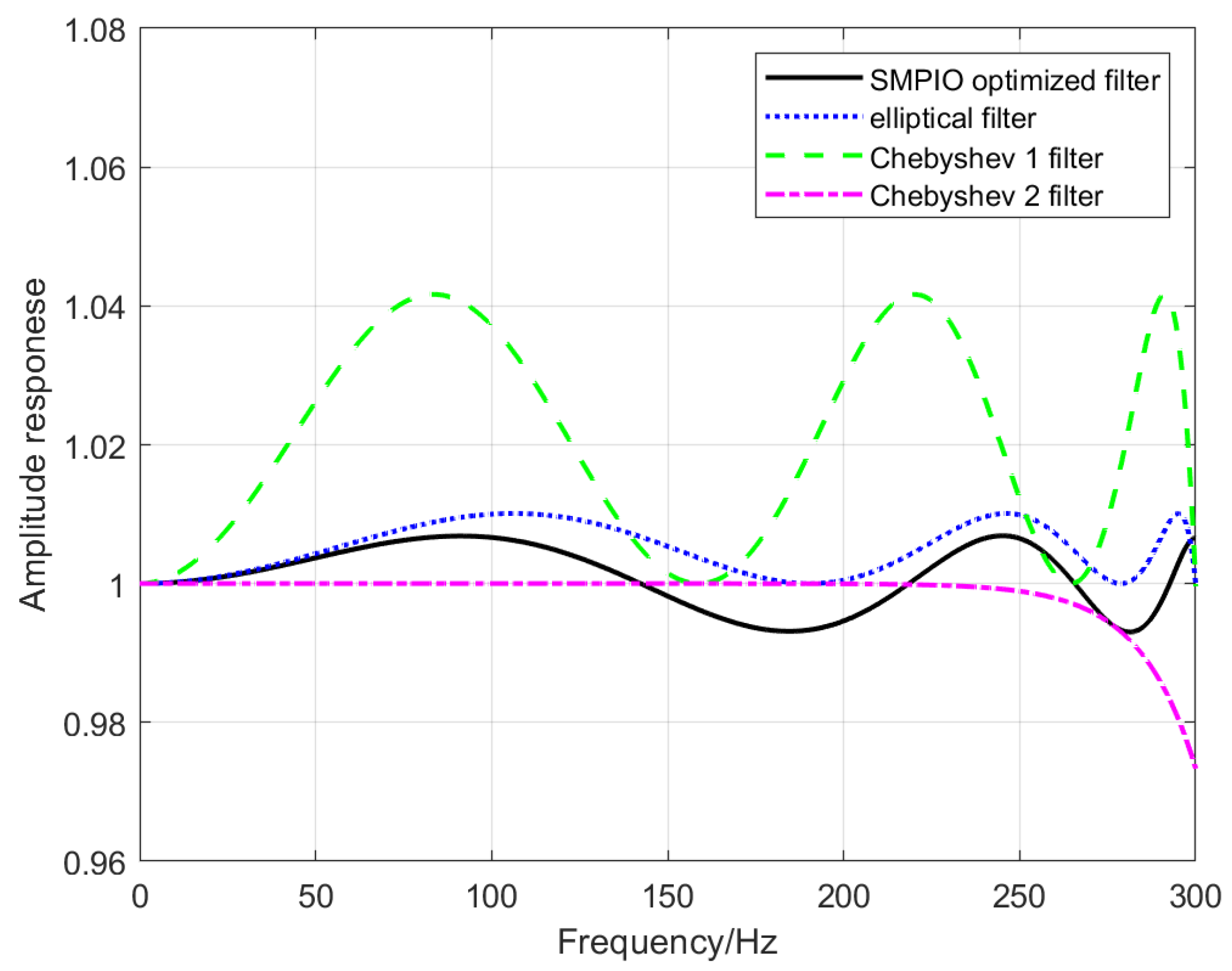
3. Results
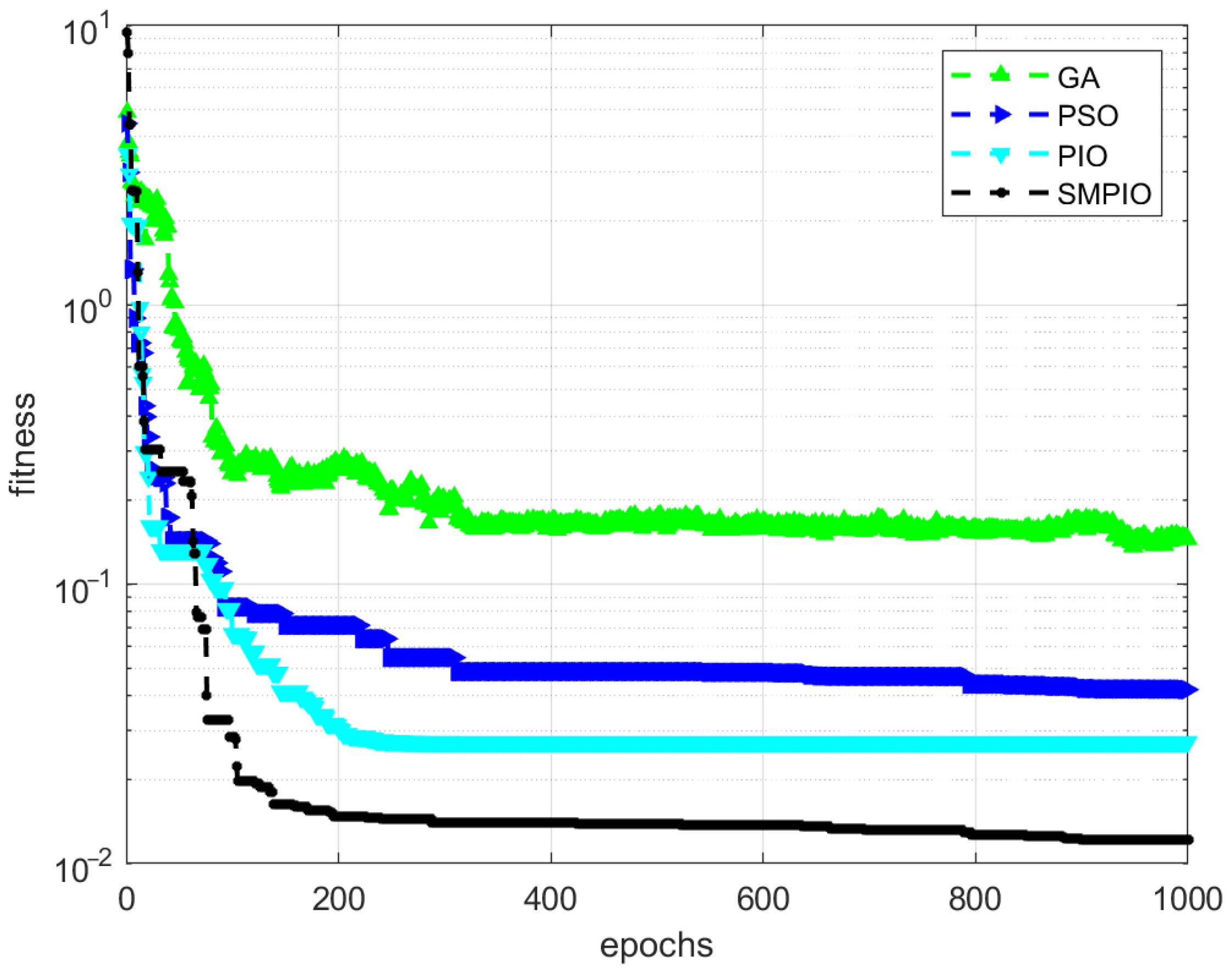
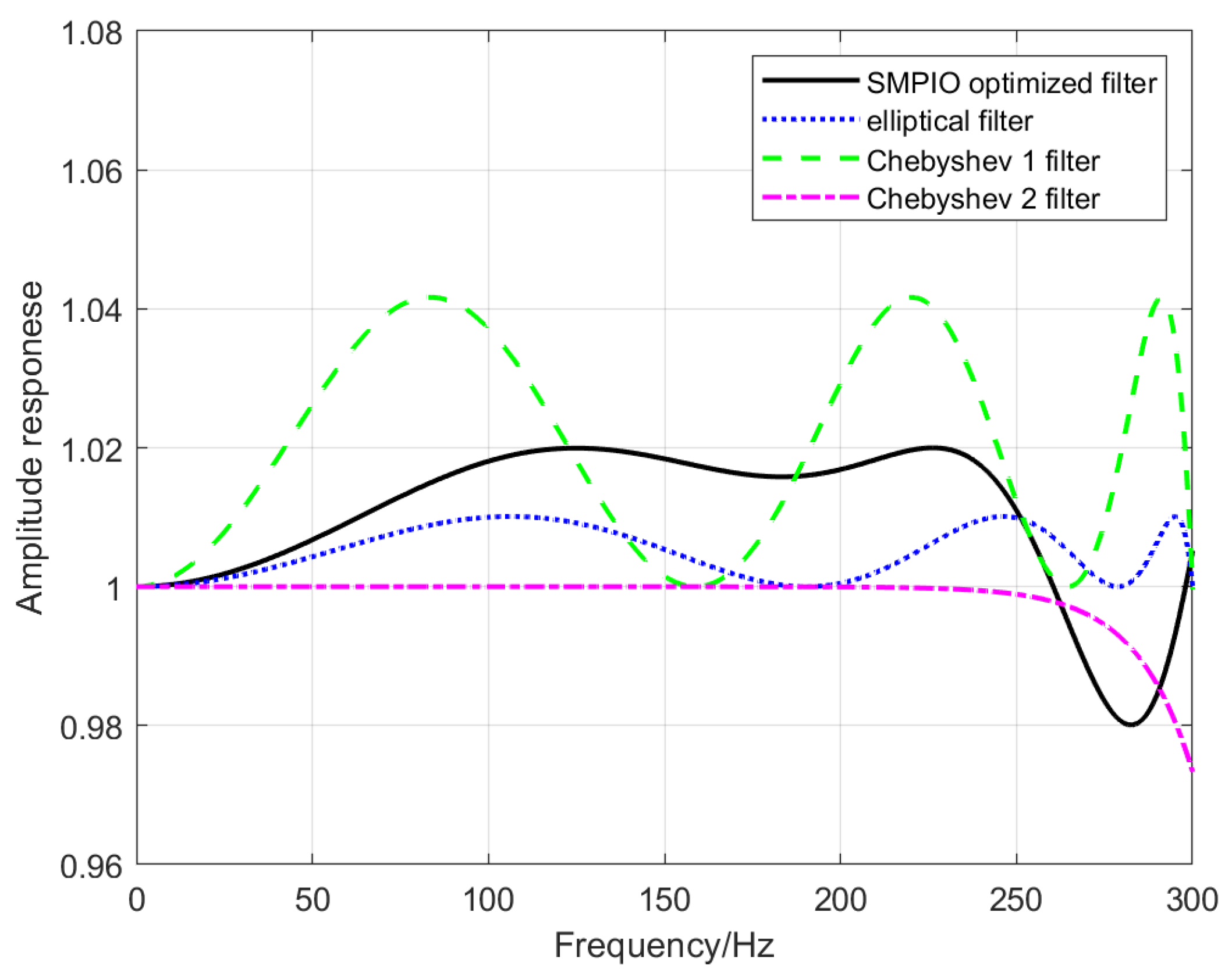
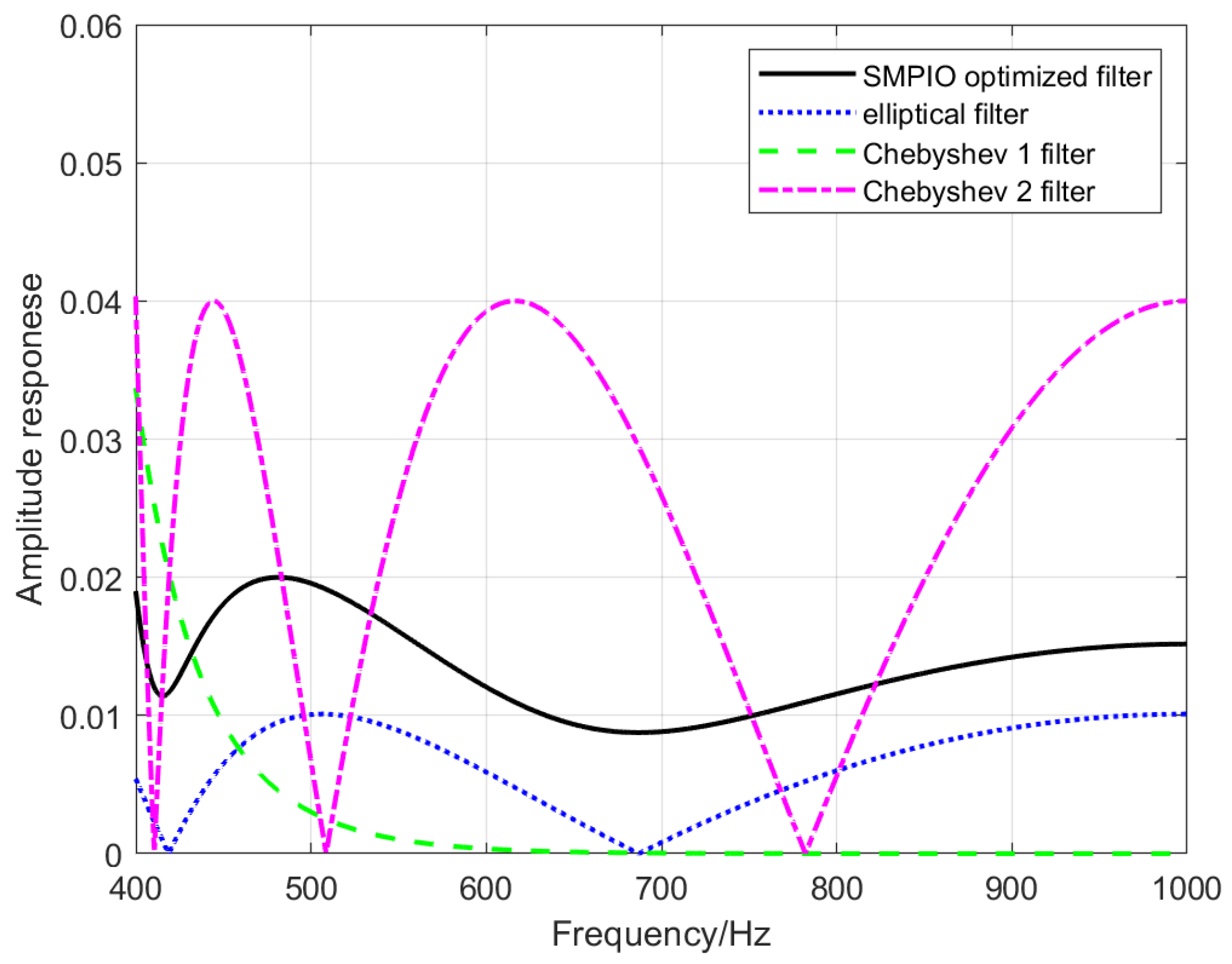
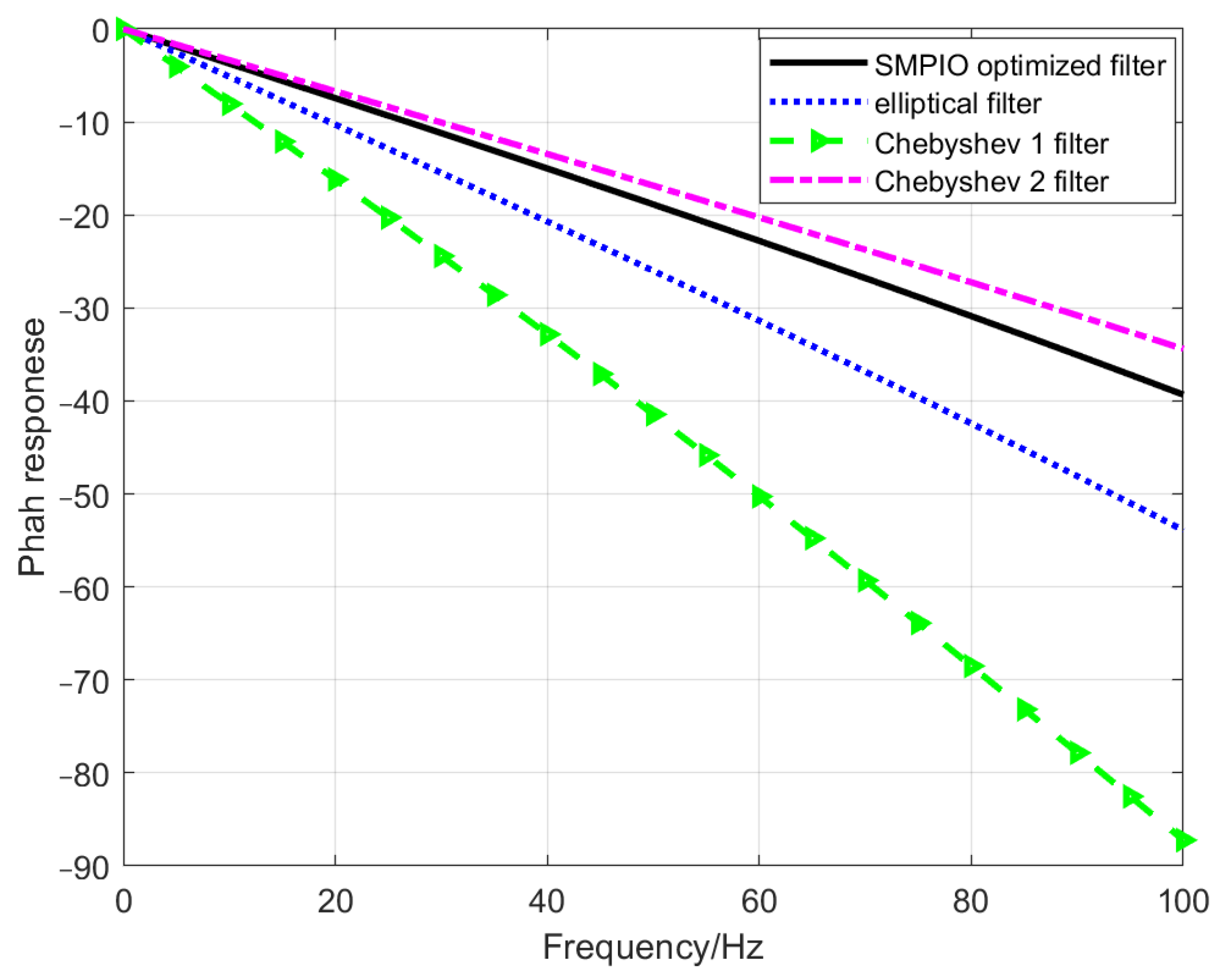
3.1. Filter Design Result of the EA Method
- All 4 kinds of EA methods can be used to design IIR filters;
- The PIO method achieves higher accuracy results and faster convergence than the other 3 methods;
- The SMPIO method has the fastest convergence speed and can achieve the highest accuracy.
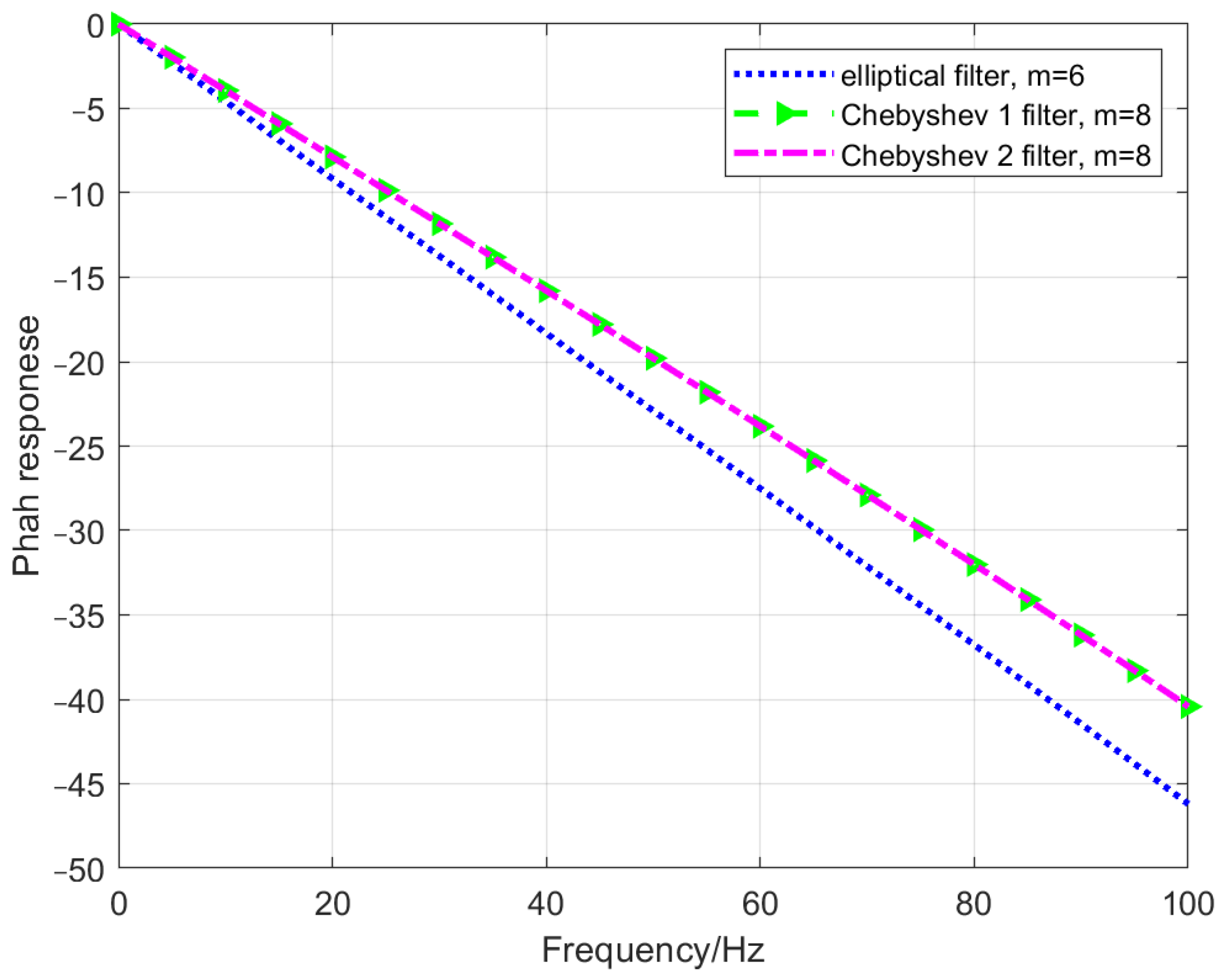
- condition A, , , and ;
- condition B, the order does not exceed 6;
- condition C, the phase of 0 Hz~100 Hz does not exceed −40 degree.
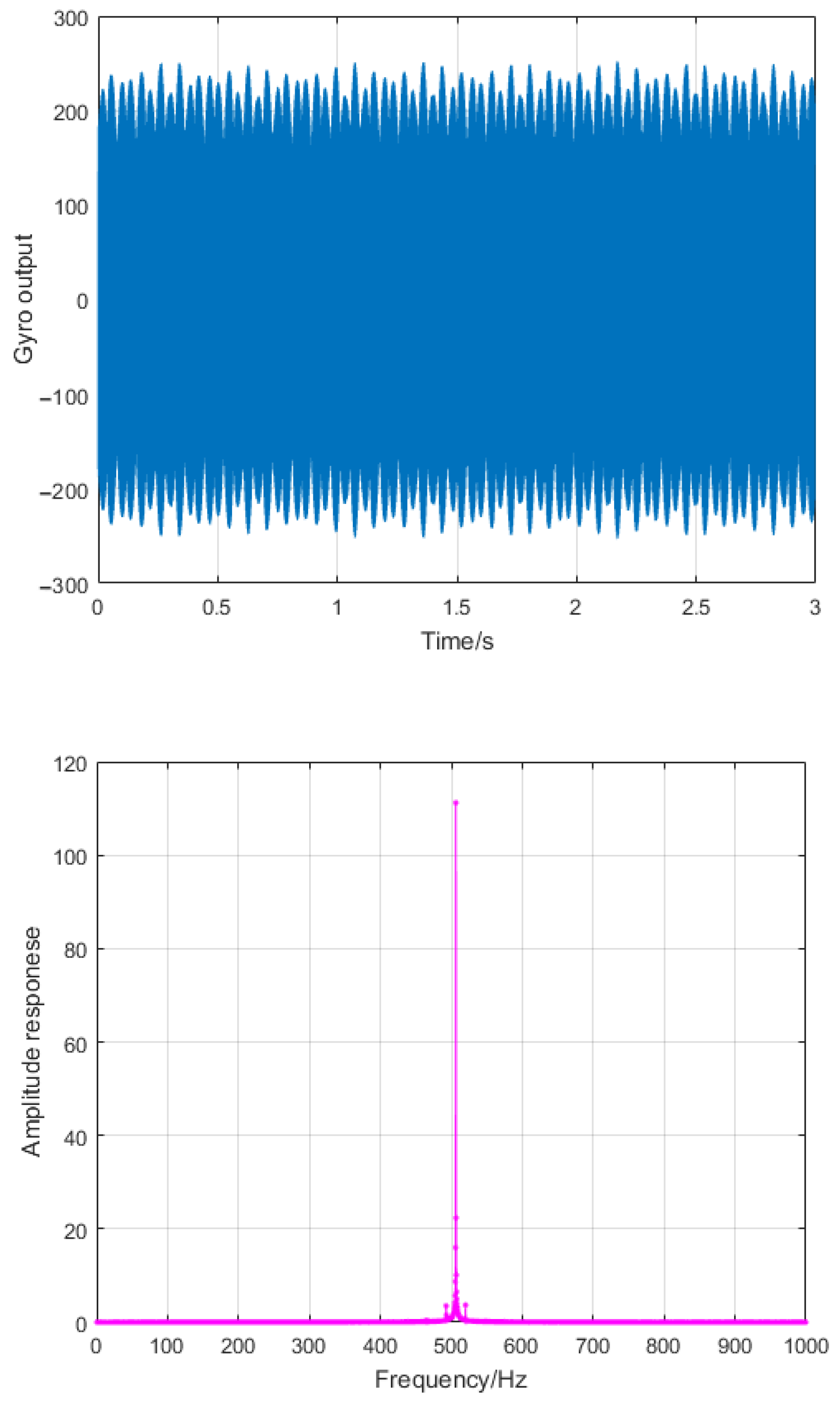
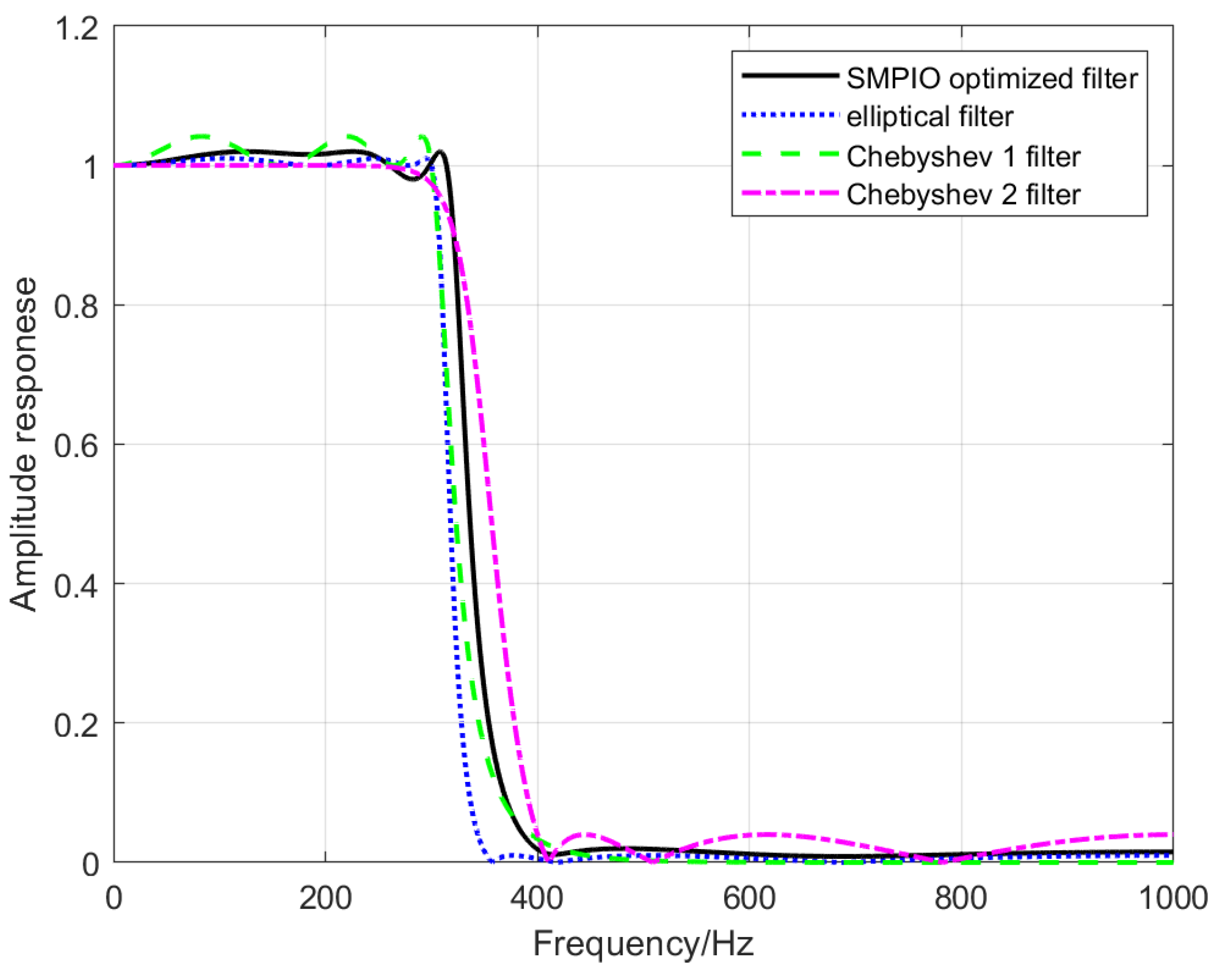
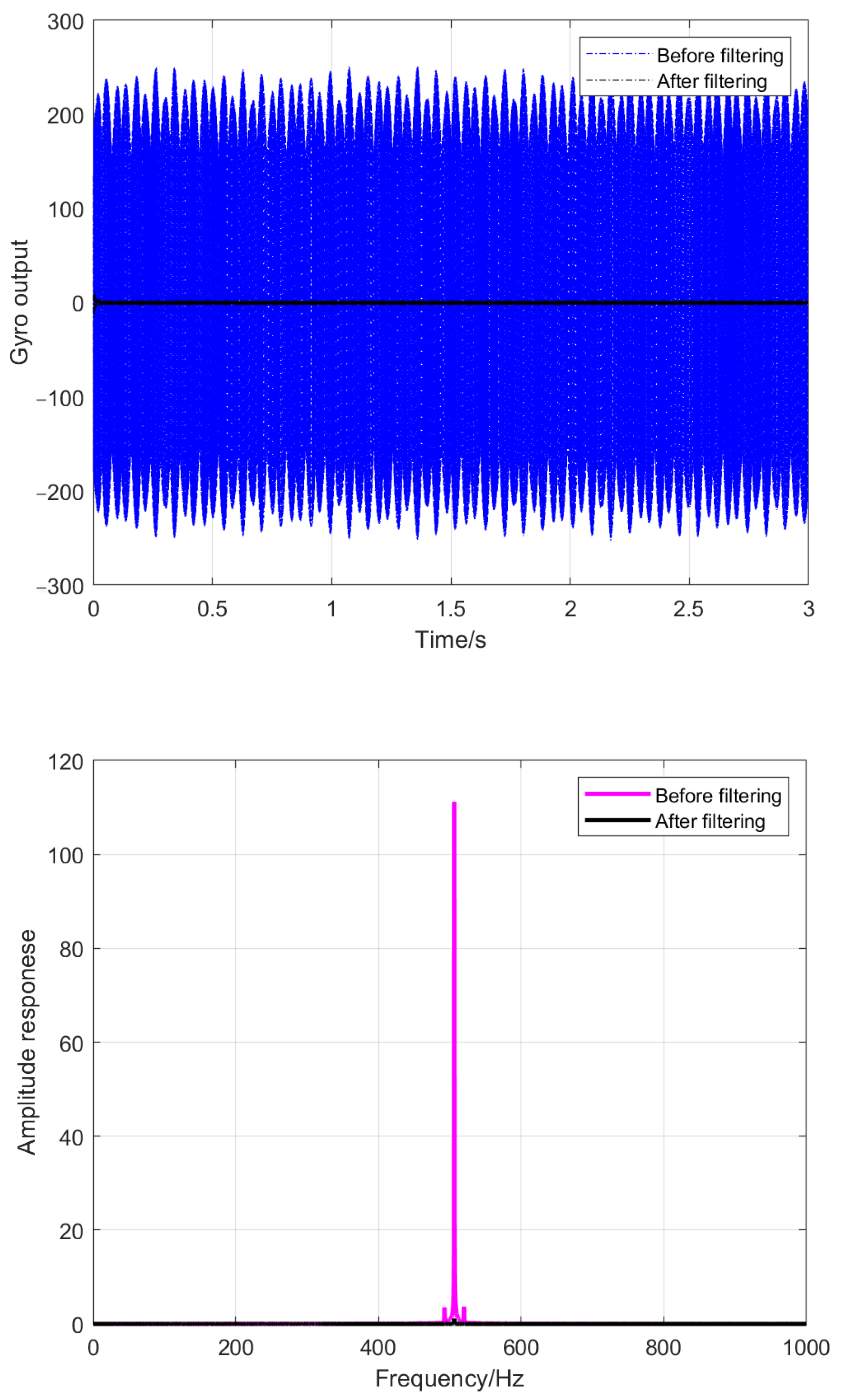
3.2. Effect of LINS Filter
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Al-Radaideh, A.; Al-Jarrah, M.; Jhemi, A. UAV testbed building and development for research purposes at the american universityof sharjah. In Proceedings of the ISMA’10 7th International Symposium on Mechatronics and Its Applications, Sharjah, United Arab Emirates, 20–22 April 2010. [Google Scholar]
- Al-Radaideh, A. Guidance, Control and Trajectory Tracking of Small Fixed Wing Unmanned Aerial Vehicles (UAV’s). Master’s Thesis, American University of Sharjah, Sharjah, United Arab Emirates, 2009. [Google Scholar]
- Yu, X.; Long, X. Parametric design of mechanical dither with bimorph piezoelectric actuator for ring laser gyroscope. Int. J. Appl. Electromagn. Mech. 2015, 47, 305–312. [Google Scholar] [CrossRef]
- Banerjee, K.; Dam, B.; Majumdar, K.; Banerjee, R.; Patranabis, D. An improved dither-stripping scheme for strapdown ring laser gyroscopes. In Proceedings of the 2004 IEEE Region 10 Conference TENCON 2004, Chiang Mai, Thailand, 24–24 November 2004. [Google Scholar]
- Chuang, G.; Jian, W.; Rong, F. Application of the Wavelet Packet Analysis in the RLG Strapdown INS. In Proceedings of the 2006 IEEE International Conference on Information Acquisition, Veihai, China, 20–23 August 2006. [Google Scholar]
- Wu, F.; Cao, Z.; Yang, M. Application of Strapdown Inertial Navigation Technology in Measurement. Int. J. Comput. Appl. 2016, 133, 19–22. [Google Scholar] [CrossRef]
- Kuznetsov, A.G.; Molchanov, A.V.; Chirkin, M.V.; Izmailov, E.A. Precision laser gyro inertial navigation for autonomous. Kvantovaya Elektron. 2015, 45, 78–88. [Google Scholar] [CrossRef]
- Fan, Z.; Luo, H.; Hu, S.; Xiao, G. Research on lock-in correction for mechanical dithered ring laser gyro. Opt. Eng. 2016, 50, 034403. [Google Scholar] [CrossRef]
- Li, G.; Wu, W.; Zhenfang, F.A.; Guangfeng, L.U.; Hu, S.; Luo, H.; Long, X. Research of misalignment between dithered ring laser gyro angle rate input axis and dither axis. Fiber Opt. Sens. 2014, 9297, 428–433. [Google Scholar]
- Mark, J.; Brown, A.; Matthews, T. Quantization reduction for evaluating laser gyro performance using a moving average filter. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP’84), San Diego, CA, USA, 19–21 March 1984. [Google Scholar]
- Regimanu, B.; Das, K.C.; Rao, K.S. Development of multistage digital filters for dither signal removal in ring laser gyro. Frequenz 2019, 73, 123–130. [Google Scholar] [CrossRef]
- Yan, X.J.; Li, J.M.; Li, Z.M.; Yang, Y.J.; Zhai, C.R. Design of Adaptive Filter for Laser Gyro. TELKOMNIKA Indones. J. Electr. Eng. 2014, 12, 7816–7823. [Google Scholar] [CrossRef]
- Chen, A.; Li, J.; Chu, Z. Dither signal removal of ring laser gyro POS based on combined digital filter. In Proceedings of the 2012 8th IEEE International Symposium on Instrumentation and Control Technology (ISICT), London, UK, 11–13 July 2012. [Google Scholar]
- Fan, Z.; Luo, H.; Lu, G.; Hu, S. Direct dither control without external feedback for ring laser gyro. Opt. Laser Technol. 2012, 44, 767–770. [Google Scholar] [CrossRef]
- Regimanu, B.; Das, K.C.; Rao, K.S.; Rao, N.K. Dither signal filtering in ring laser gyroscope using modified Stockwell transform. IEEE Sens. Lett. 2018, 2, 7001104. [Google Scholar] [CrossRef]
- Dash, M.; Panigrahi, T.; Sharma, R. Distributed parameter estimation of IIR system using diffusion particle swarm optimization algorithm. J. King Saud Univ.-Eng. Sci. 2019, 31, 345–354. [Google Scholar] [CrossRef]
- Eswari, P.; Ramalakshmanna, Y.; Prasad, D. An Improved Particle Swarm Optimization-Based System Identification. In Proceedings of the Machine Learning, Deep Learning and Computational Intelligence for Wireless Communication, Online, 29 May 2021; Springer: Singapore, 2021. [Google Scholar]
- Liu, J.; Yu, X.; Li, H. Adaptive inverse control of discrete system using online PSO-IIR filters. J. Comput. Inf. Syst. 2010, 6, 3173–3181. [Google Scholar]
- Sarangi, A.; Kumar Sarangi, S.; Panigrahi, S.P. An approach to identification of unknown IIR systems using crossover cat swarm optimization. Perspect. Sci. 2016, 8, 301–303. [Google Scholar] [CrossRef]
- Panda, G.; Pradhan, P.M.; Majhi, B. IIR system identification using cat swarm optimization. Expert Syst. Appl. 2011, 38, 12671–12683. [Google Scholar] [CrossRef]
- Karaboga, N. A new design method based on artificial bee colony algorithm for digital IIR filters. J. Frankl. Inst. 2009, 346, 328–348. [Google Scholar] [CrossRef]
- Upadhyay, P.; Kar, R.; Mandal, D.; Ghoshal, S.P.; Mukherjee, V. A novel design method for optimal IIR system identification using opposition based harmony search algorithm. J. Frankl. Inst. 2014, 351, 2454–2488. [Google Scholar] [CrossRef]
- Dash, J.; Dam, B.; Swain, R. Improved firefly algorithm based optimal design of special signal blocking IIR filters. Measurement 2020, 149, 106986. [Google Scholar] [CrossRef]
- Upadhyay, P.; Kar, R.; Mandal, D.; Ghoshal, S.P. A new design method based on firefly algorithm for IIR system identification problem. J. King Saud Univ.-Eng. Sci. 2016, 28, 174–198. [Google Scholar] [CrossRef]
- Yadav, S.; Kumar, M.; Yadav, R.; Kumar, A. A Novel method to Design FIR Digital Filter Using Whale Optimization. In Proceedings of the 2021 IEEE Bombay Section Signature Conference (IBSSC), Gwalior, India, 18–20 November 2021. [Google Scholar]
- Barantsev, G.O.; Kozlov, A.V.; Shaimardanov, I.K.; Nekrasov, A.V. Elastic Dynamic Torsion of a Ring Laser Gyroscope Mechanical Dither and its Effect on the Accuracy of Attitude Determination. In Proceedings of the 2021 28th Saint Petersburg International Conference on Integrated Navigation Systems (ICINS), Saint Petersburg, Russia, 31 May–2 June 2021. [Google Scholar]
- Lee, J.C.; Cho, H.J.; Yang, H.S. Zero lock-in implementation by phase wrapping/unwrapping in a ring laser gyroscope. Appl. Opt. 2021, 60, 10529–10538. [Google Scholar] [CrossRef]
- Aviev, A.A. Simulation of the Dither Parameters Measuring Provided by the Optoelectronic System for a Laser Gyro under the Influence of Real Disturbances. In Proceedings of the 2021 28th Saint Petersburg International Conference on Integrated Navigation Systems (ICINS), Saint Petersburg, Russia, 31 May–2 June 2021. [Google Scholar]
- Li, J.; Fang, J.; Ge, S.S. Kinetics and design of a mechanically dithered ring laser gyroscope position and orientation system. IEEE Trans. Instrum. Meas. 2012, 62, 210–220. [Google Scholar] [CrossRef]
- Duan, H.B.; Qiao, P. Pigeon-inspired optimization: A newswarm intelligence optimizer for air robot path planning. Int. J. Int. Comp. Cyber. 2014, 7, 24–37. [Google Scholar] [CrossRef]
- Zhong, Y.; Zhang, Y.; Liao, K.; Zhang, Z. A hybrid pigeon inspired optimization algorithm based on Nelder-Mead simplex operations. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020. [Google Scholar]
- Nath, S.; Bandyopadhyay, R.; Biswas, S.; Sing, J.K.; Sarkar, S.K. A new global routing optimization algorithm based on pigeon inspired optimization. In Proceedings of the 2020 IEEE Calcutta Conference (CALCON), Kolkata, India, 28–29 February 2020. [Google Scholar]
- He, J.; Liu, Y.; Li, S.; Tang, Y. Improved Pigeon-Inspired Optimization Algorithm and Its Application to Minimum-Fuel Ascent Trajectory Optimization. In Proceedings of the 2020 IEEE 16th International Conference on Control & Automation (ICCA), Singapore, 30 November 2020. [Google Scholar]
- Duan, H.; Huo, M.; Shi, Y. Limit-cycle-based mutant multiobjective pigeon-inspired optimization. IEEE Trans. Evol. Comput. 2020, 24, 948–959. [Google Scholar] [CrossRef]
- Cui, Z.; Zhao, L.; Zeng, Y.; Ren, Y.; Zhang, W.; Gao, X.Z. Novel PIO Algorithm with Multiple Selection Strategies for Many-Objective Optimization Problems. Complex Syst. Model. Simul. 2021, 1, 291–307. [Google Scholar] [CrossRef]
- Li, Z.H.; Deng, Y.M.; Liu, W.X. Identification of INS Sensor Errors from Navigation Data Based on Improved Pigeon-Inspired Optimization. Drones 2022, 6, 287. [Google Scholar] [CrossRef]
- Peng, Y.; Duan, H.B.; Deng, Y.M. Reversed Pigeon-Inspired Optimization Algorithm for Unmanned Aerial Vehicle Swarm Cooperative Autonomous Formation Reconfiguration. In Proceedings of the 2022 IEEE 17th International Conference on Control & Automation (ICCA), Naples, Italy, 27–30 June 2022. [Google Scholar]
- Herdianti, W.; Gunawan, A.A.; Komsiyah, S. Distribution cost optimization using pigeon inspired optimization method with reverse learning mechanism. Procedia Comput. Sci. 2021, 179, 920–929. [Google Scholar] [CrossRef]
- Duan, H.B.; Qiu, H.X. Advancements in pigeon-inspired optimization and its variants. Sci. China Inf. Sci. 2019, 62, 70201. [Google Scholar] [CrossRef]

| Acronyms | Full Forms |
|---|---|
| INS | inertial navigation system |
| IMU | inertial measurement unit |
| LINS | laser inertial navigation system |
| IIR filter | infinite impulse response filter |
| FIR filter | finite impulse response filter |
| EA | evolutionary algorithm |
| PIO | pigeon-inspired optimization |
| IPIO | improved pigeon-inspired optimization |
| SMPIO | pigeon-inspired optimization with natural selection and Gaussian mutation |
| GA | genetic algorithm |
| PSO | particle swarm optimization |
| Methods | Parameters |
|---|---|
| GA | particle swarm size: 100, number of generations evolved: 1000, mating probability: 0.5, mutation probability: 0.2 |
| PSO | particle swarm size: 100, number of generations evolved: 1000, inertia weight: w = 0.8, acceleration constants: c1 = 2, c2 = 2 |
| PIO | particle swarm size: 100, number of generations evolved: 1000 R = 0.001 |
| SMPIO | particle swarm size: 100, number of generations evolved: 1000 R = 0.001, , k = 0.0005 |
| Filter Types | IIR Filter Parameters |
|---|---|
| SMPIO optimized filter | a = [1.0000000000, −3.1469411000, 5.1902995000, −5.1231126000, 3.1948383000, −1.1687601000, 0.1983537300] b = [0.0226377066, −0.0004920049, 0.0484860398, 0.0059140339, 0.0457274571, 0.0012101968, 0.0211943007] |
| elliptical filter | a = [1.0000000000, −3.1409901000, 5.1933596000, −5.1225648000 3.1976146000, −1.1680883000, 0.1992300800] b = [0.0300495577, −0.0078353814, 0.0576256820, −0.0011186365, 0.0576256820, −0.0078353814, 0.0300495577] |
| Chebyshev 1 filter | a = [1.0000000000, −3.6736367000, 6.5299764000, −6.8973626000, 4.5129637000, −1.7260817000, 0.3022655200] b = [0.0007519472, 0.0045116830, 0.0112792081, 0.0150389434, 0.0112792081, 0.0045116830, 0.0007519472] |
| Chebyshev 2 filter | a = [1.0000000000, −1.2474697000, 1.5353083000, −0.7027603300, 0.3605929200, −0.0372448440, 0.0134976460] b = [0.0874795614, 0.0917752434, 0.1919701708, 0.1794740408, 0.1919701708, 0.0917752434, 0.0874795614] |
| Filter Types | IIR Filter Parameters |
|---|---|
| SMPIO optimized filter | a = [1.0000000000, −3.1464571000, 5.1854756000, −5.1254502000, 3.2072909000, −1.1781249000, 0.2027716000] b = [0.0636898053, −0.0376032393, 0.0900215835, −0.0220216831, 0.0467710785, −0.0120861956, 0.0167345507] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Zhang, L.; Wu, K. Filter Design for Laser Inertial Navigation System Based on Improved Pigeon-Inspired Optimization. Aerospace 2023, 10, 63. https://doi.org/10.3390/aerospace10010063
Li Z, Zhang L, Wu K. Filter Design for Laser Inertial Navigation System Based on Improved Pigeon-Inspired Optimization. Aerospace. 2023; 10(1):63. https://doi.org/10.3390/aerospace10010063
Chicago/Turabian StyleLi, Zhihua, Lin Zhang, and Kunlun Wu. 2023. "Filter Design for Laser Inertial Navigation System Based on Improved Pigeon-Inspired Optimization" Aerospace 10, no. 1: 63. https://doi.org/10.3390/aerospace10010063
APA StyleLi, Z., Zhang, L., & Wu, K. (2023). Filter Design for Laser Inertial Navigation System Based on Improved Pigeon-Inspired Optimization. Aerospace, 10(1), 63. https://doi.org/10.3390/aerospace10010063




