Abstract
Decision support tools for arrival sequencing and scheduling could assist air traffic controllers in managing the arrival aircraft in terminal areas. However, one critical issue is that the current method for dealing with the arrival sequencing and scheduling problem does not consider the dynamic traffic situation and the human working experience, which results in a deviation between the scheduled and actual landing sequences. This paper develops a data-driven method to address this issue. Firstly, the random forest model is applied to predict the estimated time of arrival (ETA). During the ETA prediction, the trajectory, operation, and airport-related factors that could increase the prediction accuracy are considered. Secondly, the landing sequence is obtained by sorting the predicted ETAs. Thirdly, two optimization methods are proposed to generate the scheduled time of arrival (STA). The former uses the predicted ETAs as inputs and then directly optimizes the landing sequence and the STA. The latter uses both the predicted ETA and the landing sequence as inputs for further optimization. Finally, these proposed methods are evaluated with three sets of historical data on arrival operations at Changsha Huanghua International Airport (ZGHA). The results show that the RF-based ETA prediction method could improve scheduling performance. Moreover, the proposed optimization methods could provide controllers with a more appropriate decision advisory. Such advisories could simultaneously reduce the operation efficiency indicators (average/maximum delay or dwell time) and the operation complexity indicators (Kendall rank correlation or position shift).
1. Introduction
The continuous growth of air traffic has accelerated the development of civil aviation in China. Radar vectoring is undoubtedly the most flexible tactical method for air traffic management (ATM) within the Terminal Maneuvering Area (TMA). However, frequent radar vectoring might lead to flight inefficiency in the high traffic situation and a heavy workload due to growing traffic demand and limited airspace resources. Thereupon, optimizing spatial–temporal resources has always been a hot topic in the ATM research field. In particular, the arrival sequencing and scheduling problem (ASSP) is a typical spatial–temporal resource optimization problem.
To tackle the ASSP, one should allocate the landing runway, determine the landing sequence, and optimize the landing times for arrivals while considering the given objectives and operational constraints [1,2]. During nearly three decades of development, the research on ASSP attracted considerable attention from many researchers. Some research treated the ASSP as a static case [3] and others as a dynamic case [4,5,6,7,8,9,10]; some research tackled the ASSP from a deterministic perspective and others from a stochastic perspective [11,12,13,14]; some research concerned the appeals of one single stakeholder (i.e., single-objective optimization) [15,16,17,18] and others multiple stakeholders (i.e., multiple-objectives optimization) [19,20,21,22,23]; some research solved the ASSP by exact solution methods [3,19,24,25,26,27,28] (e.g., Beasley used solvers such as CPLEX and Briskorn used model language such as GAMS) and others by approximate solution methods [29], including the simulated annealing algorithm [18,30], genetic algorithm [31,32], ant colony optimization algorithm [33], imperialist competitive algorithm [34], local search algorithm [10], and so on; and some research only provided the optimized landing runway, sequence, and time, while others also proposed the advisories for air traffic controllers [22,35,36,37].
As well as the theoretical research, the Air Navigation Service Providers (ANSPs) also developed several decision support tools (DSTs) for the ASSP, for example, the Center-TRACON Automation System (CTAS) [38] in the US and Arrival Manager (AMAN) [39] around Europe. After capturing the arrivals, DSTs first predicted the estimated time of arrival (ETA). Subsequently, these DSTs optimized the landing sequence and provided the scheduled time of arrival (STA) for each arrival aircraft. However, in actual operation, it was highly recommended that “an Arrival Manager should not be over-engineered, nor should it try to replicate to the ultimate degree many of the more complex human tasks or cognitive processes carried out routinely by air traffic controllers” [40]. It meant that, for arrival operations, the utmost concern of air traffic controllers was the landing sequence establishment. Therefore, current studies have focused on building up a sequence and scheduling a time of arrival.
Zhang et al. modeled the ASSP as a machine scheduling problem and proposed a new approach to solve the ASSP [41]. The first stage of such a proposed approach was establishing the landing sequence based on a composite dispatching rule. The second stage was optimizing the landing time using a CPLEX solver or a metaheuristic algorithm. However, this method only focused on the instantaneous situation of the arrival operation to establish the landing sequence. Jung et al. proposed a new classification-based method for predicting the landing sequences to accommodate the cognitive processes of air traffic controllers [42]. Such a data-driven method first learned the pairwise preference functions between two arrivals by logistic regression. Then it induced the entire sequence by comparing the score of each aircraft, which was the sum of pairwise preference probabilities. However, the weakness of this method was the heavy computational burden through pairwise preference learning.
This paper proposes a data-driven method to solve the ASSP concerning the cognitive processes of air traffic controllers. This method works in two stages: the first stage is prediction, and the second is optimization. In the prediction stage, this paper trains machine learning models considering domain knowledge of the ATM field to predict the ETAs [43]. Specifically, tree-based models named random forests (RF) are developed, including three types of features. Then, the landing sequence is obtained by sorting the ETAs of the arrival aircraft. In the optimization stage, two types of optimization models are proposed. The former uses the predicted ETAs as inputs and then directly optimizes STAs [3,23], while the latter sorts the predicted ETAs to obtain landing sequences as inputs for further optimization. The critical difference between the proposed and previous methods is that the traffic situation and controllers’ working experience are considered for ETA prediction, which could guarantee that the optimized landing sequence is consistent with the actual landing sequence. Furthermore, the consistency of the landing sequence between optimization and actual operation could keep the controllers’ working load under an acceptable level.
The main contributions of this paper are as follows: From the theoretical perspective, this paper studies the impact of the accuracy of flight time on the sequencing optimization model. Firstly, this paper develops random forest models to predict the ETAs by considering the domain knowledge in air traffic control, such as trajectory, operation, and airport factors. Then, the landing sequence is obtained based on ETA sorting. Finally, two optimization strategies are proposed to sequence and schedule the arrival aircraft while considering the constraints of operational context and objectives from multi-stakeholders. From the practical perspective, this study also addresses the problem of the scheduled landing sequence deviating from the actual landing sequence. Furthermore, the proposed method can be embedded into the decision support tools to help air traffic controllers schedule arrival aircraft more efficiently. It could also reduce the workloads for controllers and promote operational efficiency around the airport.
This paper is organized as follows: First, the methodology of the proposed data-driven method is provided in Section 2, including data preparation, prediction of ETA, and optimization of arrival schedule. Subsequently, Section 3 details the scenarios of case studies and the results of ETA prediction. Finally, Section 4 presents the validation results and carries out the comparison work before the conclusion in Section 5.
2. Methodology
This paper proposes a data-driven method to provide a landing sequence for the AMAN system. The framework of our proposed method is shown in Figure 1, including three primary steps.

Figure 1.
A framework of data-driven arrival sequencing and scheduling, (A) data preparation; (B) prediction; (C) optimization.
- Prepare and preprocess the historical aircraft trajectories, detailed in Section 2.1.
- Divide the preprocessed data into training and testing subsets, and construct a random-forest-based ETA prediction model. The ETA is predicted using the model for the testing data subset, detailed in Section 2.2.
- After the landing sequence is sorted, an optimization model is proposed in Section 2.3 to obtain the STAs, and another optimization model using only the predicted ETA is constructed for comparison.
Table 1 presents the notations used in this paper.

Table 1.
Notations.
2.1. Data Preparation
In this paper, data preparation contains the following four steps:
- Data decoding: The raw data are aircraft track messages received from Surveillance Data Processing System (SDPS). Based on the Eurocontrol Standard Document (Category 062), aircraft trajectory information could be obtained by decoding the track messages.
- Data partitioning: The aircraft trajectories within the TMA could belong to departure, overflight, or arrival aircraft. Our concern in this paper is the arrival trajectories, which could be partitioned based on the flight plan information.
- Data cleaning: This step eliminates abnormal data, such as the trajectories of testing flights. Accordingly, the remaining data are referred to as the cleaned data.
- Data grouping: After data cleaning, the remaining data are grouped into training and testing sets for further ETA prediction and STA optimization.
2.2. ETA Prediction
ETA prediction can be converted into arrival flight time prediction of the arrival aircraft within the TMA. It is because the ETA equals the actual time of arrival (ATA) at the entry fix, added to the arrival flight time. Furthermore, Trivedi et al. [44] demonstrated that combining clustering and regression could improve the ETA prediction accuracy, compared with only using a single regression model over the whole training set. Therefore, the training datasets are divided into subsets according to different entry fixes. Then, machine learning models are trained to estimate the arrival flight time for each clustered data.
2.2.1. Model of ETA Prediction
In this section, this paper constructs a machine learning model to predict the ETAs. Suppose n features are selected, and the target variable is the flight time of each arrival aircraft, denoted by .
After data preparation (in Section 2.1), several features (trajectory-related features) are available from the data. Heaton [45] pointed out that a suitable feature set can improve the accuracy and interpretability of the machine learning model. Therefore, this paper takes the domain knowledge of the ATM field to extract the affecting factors (airport- and operation-related) that significantly influence the arrival flight time. A detailed description of the features is provided in Table 2, including three categories: trajectory-, airport-, and operation-related features. Among these features, categorical features are encoded using the target encoding method [46]. In addition, the features, hour of the day and day of the week, have been transformed by trigonometric functions to account for periodicity [47]. Furthermore, the TMA is divided into sectors for capturing operation situations according to the ZGHA Aeronautic Information Publication (AIP), as shown in Figure 2. The controllers usually use different strategies in each sector to maintain aircraft separation and establish a landing sequence. Therefore, the prediction of flight time is related not only to the number of aircraft in the whole TMA but also to which sector the arrival aircraft is located in. Therefore, we divide the whole TMA into sectors for constructing the features for further prediction.

Table 2.
Feature Set for Flight Time Estimation.

Figure 2.
Four sectors in TMA of Changsha International Airport (ZGHA).
For a set of training data containing arrivals, the independent variables are denoted by and the corresponding dependent variables are denoted by . Tree-based models have been proven to provide better prediction performance in ETA prediction [48,49]. Specifically, this paper adopts the random forest model (RF) [50] due to several advantages: a small number of tuning parameters, appropriate for nonlinear problems, and robust to outliers. Meanwhile, our previous work also proved that random forest outperforms the other regression models in predicting ETAs when appropriate features are selected [43].
Only a random part of the training set is used when building a forest tree. The model training is performed on the corresponding training subsets to generate the different decision tree models. Thus, each tree becomes a weak learner, while combining such weak learners generates a random forest. Moreover, hyperparameters could significantly impact model performance and generalization ability. Therefore, skillfully selecting the hyperparameters might help to achieve unbiased machine learning models. This work utilizes grid search and K-fold cross-validation for hyperparameters’ tuning.
2.2.2. Evaluation of ETA Prediction
The performance of ETA prediction is evaluated by Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), and Root Mean Squared Error (RMSE). Given a total of m aircraft to predict, the definitions of these three indicators are as follows:
where and are the actual and predicted flight time of jth arrival aircraft within the TMA, respectively, while the predicted ETA of jth arrival is as follows:
where is the actual time of arrival (ATA) at a particular entry fix.
2.3. STA Optimization
The STA optimization aims to find a landing sequence and a set of STAs to assist air traffic controllers in managing the arrival aircraft. In practice, the optimization model is embedded in the AMAN system. This paper considers two optimization strategies. The first one uses the predicted ETAs as inputs and then optimizes STAs directly. In contrast, the second one uses both ETAs and the landing sequence (generated by sorting the predicted ETA) as inputs for further optimization.
2.3.1. Optimization Based on Predicted ETAs
Suppose there are a set of arrivals for the arrival schedule. Optimization based on the predicted ETAs tries to sequence and schedule the arrivals, while the STA () of each aircraft is subject to wake vortex separation and time window constraints. The wake vortex separation, denoted by , ensures the safe separations between the leading aircraft i and following aircraft j. The time window constraints of the STA should be between them. Thus, the earliest and latest arrival times could be defined as: , , where the corresponding percentage of arrival flight time () from the entry fix to the runway could be obtained based on statistical analysis.
In addition to the operational constraints, objective functions should also be concerned from the perspectives of multiple stakeholders (e.g., air traffic controllers, airlines, airports, and governments). This paper selects total delay time and total dwell time as the objective functions to balance the appeals of different stakeholders [23].
Thus, the formulation of the arrival schedule is as follows.
In objective function (7), the weight indicates the trade-off between dwell time and delay. The dwell time in TMA is the time an aircraft spends from entering the TMA to landing on the runway, which is the duration that air traffic controllers need to pay close attention to in order to ensure separation among aircraft to avoid potential collisions. Therefore, the total dwell time is a surrogate of the air traffic controller workload, and minimizing this criterion reduces the air traffic controller workload. Please refer to [23] for a detailed description. Constraint (8) confines the arrival flight time within a defined limit. Constraints (9) and (10) qualify the landing time window constraint of the arrival aircraft: Constraint (11) defines the landing sequence of arrival aircraft. Constraint (12) ensures the wake vortex separations between the leading and following aircraft. Constraints (13)–(14) define the delay of landing aircraft. Finally, Constraint (15) defines the dwell time. For the convenience of the following description, the optimization strategy proposed in this section is referred to as optimization with the predicted ETA, opt-pETA for short.
2.3.2. Optimization Based on Predicted ETA and Landing Sequence
After predicting the ETAs for a set of aircraft J, the landing sequence can be obtained based on:
where means sorting a set of values in non-descending order.
Then, the landing sequence and ETAs are used as inputs to optimize the STAs. Such a strategy could significantly reduce the complexity of the ASSP. Thus, the formulation of the arrival schedule is as follows.
Compared to the strategy using only the predicted ETA, Constraints (11) and (12) are replaced by Constraint (21). With this change, the number of constraints decreases dramatically, which could significantly reduce the computational time. For the convenience of the following description, the optimization strategy proposed in this section will be referred to as optimization with the predicted ETA and landing sequence, opt-seq for short.
2.3.3. Performance of Optimization
In this paper, several indicators of ASSP are adopted to evaluate the performance of optimization, including average delay time (), average dwell time (), maximum delay time (), and maximum dwell time (). As well as these efficiency-related indicators, this paper also considers the deviation between the actual and scheduled landing sequence. Such indicators of sequence deviation could quantify the workload of human controllers since the controllers need to spend extra effort to follow the scheduled landing sequence if they find the recommended sequence is far from the sequence based on their experience.
The Kendall rank correlation is adopted to measure the sequence deviation between the actual and scheduled landing sequence, which is defined as follows.
where and are the number of concordant and discordant pairs between the actual and scheduled landing sequence, respectively, is the number of arrival aircraft. Thus, this coefficient varies between −1 (when the scheduled landing sequence is the inverse of the actual one) and +1 (when the scheduled and actual landing sequences are identical).
The position shift () is another indicator to measure the similarity between the actual and scheduled landing sequence. For example, if the landing sequence of six arrivals shifts from #1 #2 #3 #4 #5 #6 to #3 #2 #1 #4 #5 #6, the value is 2 (since the landing position of aircraft #1 and #3 are changed).
3. Case Studies
This paper takes the actual operation of Changsha International Airport (ZGHA) to evaluate the performance of the proposed opt-pETA and opt-seq scheduling strategies. Figure 3 shows the arrival tracks on December 25, 2019 (238 landing aircraft). It can be seen that there are five entry fixes, including BEMTA, LLC, LIG, OVTAN, and DAPRO. The location of BEMTA is close to LLC, and the inbound traffic shares the same arrival route via these two entry fixes. Therefore, BEMTA and LLC are regarded as the same entry fix and labeled as LLC. In addition, there are two runways in ZGHA airport, which adopts the segregated operating mode, i.e., one is for departure, and the other is for landing.

Figure 3.
Heat map of arrival radar tracks for arrivals within ZGHA TMA.
After data preparation (Section 2.1), 7141 historical radar tracks in December 2019 were obtained. The whole dataset was divided into a training set and a testing set, with the former containing 5711 samples (80%) and the latter containing 1430 samples (20%), respectively. Table 3 presents the number of samples in each dataset. Moreover, this paper selects three real traffic scenarios (group 1, group 2, and group 3) from the testing set to validate the scheduling strategies proposed in this paper. All of those real traffic scenarios correspond to high traffic density.

Table 3.
Dataset splitting.
Four random forest models were constructed based on the corresponding training subsets. The grid search and 5-fold cross-validation techniques were used for hyperparameters’ tuning. The search space for these hyperparameters is shown in Table 4. The result shows that the number of estimators is 500, the max features is 1, the max depth is 3, and the min samples leaf is 1.

Table 4.
Search space for hyperparameters’ tuning.
After determining the optimal hyperparameters, the random forest models for each subset were constructed based on the training set and validated based on the testing set. Table 5 provides the results of ETA prediction performance on the testing sets. In addition, the last row of Table 5 provides the average indicators of ETA prediction while regarding the number of samples used in the testing set.

Table 5.
Results of the ETA prediction.
From Table 5, the best prediction performance for the arrival aircraft is via DAPRO. However, the prediction MAE via DAPRO is not the best due to the longest distance of the arrival route, which could be regarded as the most extended look ahead of time for a prediction. Moreover, Shapley additive explanation (SHAP) values are used to explore which features significantly affect the predicting performance. From the SHAP diagrams, as shown in Figure 4, the number of arrivals within the TMA, the speed when entering the TMA, and the number of arrivals within the corresponding sectors play a crucial role in predicting the arrival flight time.

Figure 4.
SHAP values of different features used for ETA prediction.
The two proposed optimization strategies for arrival scheduling were evaluated using three real traffic scenarios during rush hour. Then, as defined in Section 2.3, those corresponding models were solved by CPLEX (IBM ILOG CPLEX Optimization studio version 12.6) on a PC with a 3.60 GHz Intel Core i7-7700 processor and 16 GB RAM.
The weight in Equation (7) is set as 0.5, and the maximum dwell time is set as 1500. As presented in our previous study [23], when increasing (relaxing the constraints (8) and (18)), the optimum of other criteria can be easily approached; when changing the weight (varying the importance to total delay time or total dwell time in objective function), it is evident that criteria with higher weight will be reduced with the increase in weight. In addition, this paper derives from the quartile map of the flight time via each entry fix of actual operation in December 2019.
Subsequently, the performance of the two proposed scheduling methods, the opt-pETA and the opt-seq, respectively, was compared with the First-Come-First-Served (FCFS) strategy, the widely-used classic scheduling method [3], and the Hybrid Arrival Sequencing method [42]. Finally, all three traffic scenarios in rush hour were evaluated and compared for each strategy.
As mentioned in Section 2.3, the decision variables of the opt-pETA method are the landing sequence and STAs. Therefore, they could be optimized based on the model of Equations (7)–(15), where the random forest models in Section 2.2 predict the ETAs. In contrast, the decision variables of the opt-seq strategy are the STAs only. Therefore, they could be optimized based on the model of Equations (17)–(24), where Equation (16) estimates the landing sequence and the random forest models predict the ETAs.
As for the FCFS scheduling strategy, the ETAs are obtained by using while the landing sequence is obtained by Equation (16). Correspondingly, the STAs for each arrival aircraft are: .
As for the widely-used classic scheduling method [3], the decision variables are the landing sequence and STAs. Therefore, they could be optimized based on the model of Equations (7)–(15), where the ETAs could be obtained by .
As for Jung’s hybrid scheduling method, the landing sequence is obtained using a preference learning approach, which emulates the working experience of controllers [42]. Then, the STAs could be optimized based on the model of Equations (17)–(24), where our proposed random forest models predict the ETAs.
4. Results and Discussion
4.1. Results of Arrival Scheduling
Table 6 compares the indicators between the different scheduling methods. Moreover, Figure 5 provides ATAs on each entry fix (denoted by black circles), ATAs on the runway (denoted by red squares), and STAs on the runway (denoted by blue diamonds) by the three scheduling strategies mentioned above, Beasley’s classic method (the upper part of Figure 5), Jung’s hybrid method (the middle part of Figure 5), and our proposed opt-seq strategy (the bottom part of Figure 5).

Table 6.
Comparison of on arrival scheduling results by different methods.
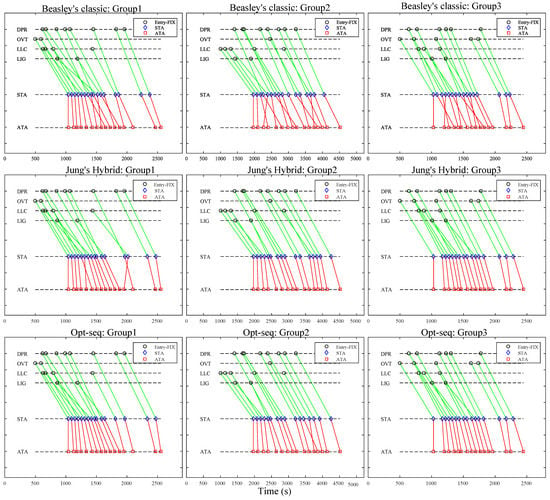
Figure 5.
The schematic diagram for the scheduled and actual time of arrival.
- 1.
- Comparison between the FCFS strategy and our proposed methods. Our proposed methods outperform the FCFS in the operation efficiency indicators (average delay, average dwell time, maximum delay, and maximum dwell time) and the operation complexity indicators (Kendall rank correlation and position shift ).
- 2.
- Comparison between the classic method and the opt-pETA method. These two scheduling methods are both based on the model of Equations (7)–(15). The difference lies in the ETAs since the former ETAs are obtained by statistical analysis, while the latter is by random forest models. The opt-pETA strategy outperforms the classic strategy in most indicators except for the maximum dwell time in Group 2. This result demonstrates the importance of ETA prediction accuracy, indicating that the proposed ETA prediction method could improve scheduling performance. It is all due to the fact that our proposed opt-pETA method could improve the predicting accuracy by considering the dynamic traffic situation and the human working experience.
- 3.
- Comparison between Jung’s hybrid method and the proposed opt-seq method. These two scheduling methods are both based on the model of Equations (17)–(24). The difference lies in the landing sequence since the former landing sequence is obtained by a preference learning approach, while the latter is by sorting the predicted ETAs. The opt-seq method outperforms Jung’s hybrid method in most situations except for the Kendall rank correlation and position shift in group 2.
- 4.
- Comparison between our proposed two methods. These two methods take the same predicted ETAs using random forest models. However, the opt-pETA needs to optimize the landing sequence and STAs simultaneously, while the opt-seq only needs to optimize the STAs based on a given landing sequence (Equation (16)). Therefore, as to the operation efficiency-related indicators, the opt-pETA strategy is a better choice; as to the operation complexity-related indicators, the opt-seq strategy is a better choice. Moreover, in terms of problem-solving efficiency, the opt-seq strategy is undoubtedly more capable of real-time performance.
4.2. Analysis of Opt-pETA Method
This subsection explores the relationship between the accuracy of ETA prediction and the performance of the opt-pETA method.
The accuracy of ETA prediction is first examined by gradually increasing the number of features, as shown in Equations (26)–(28). The MAE and MAPE for ETA prediction are presented in Figure 6 based on different feature sets. In addition, Figure 6 contains the MAE and MAPE of the statistical values ().

Figure 6.
Performance of ETA prediction based on different feature sets.
Figure 6 illustrates the error of the ETA by the classic scheduling method [3] with an MAE of 259.3 s and MAPE of 24.6%. When gradually increasing the number of features, the prediction accuracy could increase up to 77 s of MAE and 6.9% of MAPE, which shows the effectiveness of the features proposed in Section 2.2.
Then take Group 1 as an example to explore the impact of ETA predicting accuracy on the performance of the opt-pETA method. Finally, Table 7 compares the optimization results between the classic method and opt-pETA.

Table 7.
Comparison of arrival scheduling under different accuracies of ETA prediction.
As shown in Table 7, due to the improvement in prediction accuracy, the average delay and dwell time decrease, while the landing sequence gets closer to the actual landing sequence, which indicates that improving the accuracy of ETA prediction could reduce the deviation between the optimized and the actual landing sequence. Therefore, improving the accuracy of ETA prediction could be an alternative method to learning the scheduling strategy of ATCO [42], which could simultaneously improve the operation efficiency and complexity indicators for the ASSP.
It is worth noting that some current studies [51,52] use aircraft performance models to predict ETA and achieve satisfactory results. They usually concern a specific lateral route or predefined optional routes for arrival aircraft. However, in the current operation, aircraft seldom follow the standard arrival route due to radar vectoring. Thus, a regression model may be better for catching the dynamic traffic situation and the human working experience to reduce the deviation between the optimized and the actual landing sequence. Nevertheless, there can be little doubt that the current studies [51,52] are more suitable for the concept of trajectory-based operation.
4.3. Analysis of Opt-seq Method
This subsection explores the relationship between the accuracy of ETA prediction and the performance of the opt-seq method.
The predicted landing sequence, derived from the predicted ETAs, significantly affected the performance of the proposed opt-seq method. In this subsection, the accuracy of the predicted landing sequence is assessed by the indicator of the position shift (# Pshift). As shown in Figure 7, the scheduled landing sequence of the classic method (statistical analysis, MAE: 259.3 s) and the scheduled landing sequence of opt-seq (random forest model F3, MAE: 77 s) are compared to the actual landing sequence.

Figure 7.
The deviation between the predicted and actual landing sequences.
For the landing sequence scheduled by the classic method, the maximum position shift is three, and the total position shift is eight. Thus, while the accuracy of ETA prediction is improved, the total position shift in opt-seq (estimating landing sequence based on ETA prediction by F3) is decreased to two, suggesting that improving ETA prediction could reduce the deviation between the reference and the actual landing sequence. After optimization, according to Equations (17)–(24), the landing positions of AC#9 and AC#11 are exchanged, consistent with the actual landing sequence.
Furthermore, a scenario is selected to estimate the landing sequence based on the ETA prediction by F3 in actual cases. The selected scenario is from Group 3, consisting of three aircraft (AC#4, AC#6, and AC#7), which enter the TMA of ZGHA successively. Table 8 shows detailed information about those aircraft. Figure 8 provides snapshots of the traffic scenario of these three aircraft in the TMA of ZGHA, including three scenes arranged in chronological order.

Table 8.
Information of the arrival aircraft in a selected scenario.

Figure 8.
Traffic scenario about these three aircraft in the TMA of ZGHA, (a) AC #4 entered TMA via DAPRO fix; (b) AC#7 appeared via LIG; (c) a “dog-leg” instruction delivered to AC#7.
As shown in Figure 8a, two aircraft were waiting for landing when AC #4 entered TMA via DAPRO fix. Based on the regression models, the predicted flight time of AC#4 was 1243 s, which was equal to the average flight time via DAPRO (1242 s).
As shown in Figure 8b, when AC#7 appeared via LIG, six aircraft were in the TMA and waiting for landing. Thereupon, the predicted flight time of AC#7 was 1172 s, which was higher than the average flight time via LIG (674 s). Accordingly, the ETAs of AC#4 and AC#7 are 1781 s and 2094 s, respectively. Therefore, based on Equation (16), AC#4 would land before AC#7. Conversely, if the average flight times via LIG were adopted, AC#7 would land before AC#4, as shown in Figure 7.
Figure 8c shows that the controller guided AC#4 to follow the standard arrival route. The actual flight time of AC#4 was close to the average flight time due to no additional vectoring. In contrast, the controller delivered a “dog-leg” instruction to AC#7 for separation maintenance and sequence establishment, which inevitably increased the flight time. Consequently, AC#4 landed on the runway before AC#7. Therefore, the proposed ETA prediction method could better estimate the landing sequence and schedule the arrivals by considering dynamic traffic situations and controllers’ working experiences.
5. Conclusions
The decision support tools aim to assist air traffic controllers in sequencing and scheduling arrival aircraft. However, The ETA estimation method of the current decision support tool does not consider the dynamic traffic situation and controllers’ behavior factors. As a result, the estimated flight time would deviate significantly from the actual flight time, and the corresponding scheduled landing sequence would also deviate from the actual landing sequence.
This paper presents a data-driven method including two stages: prediction and optimization. In the first stage, this paper employs data-driven regression models to predict the ETA for each arrival and then determines the landing sequence for a set of aircraft. In the second stage, this paper develops two optimization methods: opt-pETA and opt-seq, to tackle the ASSP.
This paper also utilizes the actual historical data to examine the accuracy of the ETA prediction and the benefits of the proposed data-driven method. The results indicate that the data-driven ETA prediction method could obtain accurate ETAs, and the estimated sequence is close to the actual sequence since the dynamic traffic situation and the human working experience are considered. Moreover, our proposed methods are compared with the widely-used optimization model in the literature. Finally, the comparison result shows that our proposed opt-pETA and opt-seq methods can perform well in efficiency-related and complexity-related indicators.
This research contributes to the upgrading of conventional decision support tools to provide a suggested sequence that accommodates the traffic condition in TMA. The ETA prediction model proposed in this paper can replace the trajectory prediction module in the support tools to obtain a more accurate ETA. Then the data-driven method can be used as the optimization module in support tools. More specifically, the opt-pETA model is used in scenarios with high operational efficiency requirements, while the opt-seq model is applied when safety is the top priority.
In future work, the authors will extend this method to combined arrival and departure scheduling, multi-runway scheduling, and metroplex scenarios.
Author Contributions
Conceptualization, Z.D. and J.Z.; methodology, Z.D.; data curation, B.K.; writing—original draft preparation, Z.D.; writing—review and editing, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Joint Fund of the National Natural Science Foundation of China and the Civil Aviation Administration of China (Grant No. U1933117), as well as the Postgraduate Research and Practice Innovation Program of NUAA (No. xcxjh20220714).
Data Availability Statement
The data that support the findings of this study are available from Central and Southern Regional ATMB of the CAAC. Restrictions apply to the availability of these data, which were used under license for this study. Data are available from the corresponding author (zhangjunfeng@nuaa.edu.cn) with the permission of Central and Southern Regional ATMB of the CAAC.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bennell, J.A.; Mesgarpour, M.; Potts, C.N. Airport runway scheduling. Ann. Oper. Res. 2013, 204, 249–270. [Google Scholar] [CrossRef]
- Ikli, S.; Mancel, C.; Mongeau, M.; Olive, X.; Rachelson, E. The aircraft runway scheduling problem: A survey. Comput. Oper. Res. 2021, 132, 105336. [Google Scholar] [CrossRef]
- Beasley, J.E.; Krishnamoorthy, M.; Sharaiha, Y.; Abramson, D. Scheduling Aircraft Landings—The Static Case. Transp. Sci. 2000, 34, 180–197. [Google Scholar] [CrossRef]
- Beasley, J.E.; Krishnamoorthy, M.; Sharaiha, Y.; Abramson, D. Displacement problem and dynamically scheduling aircraft landings. J. Oper. Res. Soc. 2004, 55, 54–64. [Google Scholar] [CrossRef]
- Bennell, J.A.; Mesgarpour, M.; Potts, C.N. Dynamic scheduling of aircraft landings. Eur. J. Oper. Res. 2017, 258, 315–327. [Google Scholar] [CrossRef]
- Hong, Y.; Choi, B.; Lee, K.; Kim, Y. Dynamic Robust Sequencing and Scheduling Under Uncertainty for the Point Merge System in Terminal Airspace. IEEE Trans. Intell. Transp. Syst. 2018, 19, 2933–2943. [Google Scholar] [CrossRef]
- Hu, X.-B.; Chen, W.-H. Receding horizon control for aircraft arrival sequencing and scheduling. IEEE Trans. Intell. Transp. Syst. 2005, 6, 189–197. [Google Scholar] [CrossRef]
- Ji, X.-P.; Cao, X.-B.; Du, W.-B.; Tang, K. An evolutionary approach for dynamic single-runway arrival sequencing and scheduling problem. Soft Comput. 2017, 21, 7021–7037. [Google Scholar] [CrossRef]
- Saraf, A.P.; Slater, G.L. Optimal Dynamic Scheduling of Aircraft Arrivals at Congested Airports. J. Guid. Control Dyn. 2008, 31, 53–65. [Google Scholar] [CrossRef]
- Bianco, L.; Dell’Olmo, P.; Giordani, S. Scheduling models for air traffic control in terminal areas. J. Sched. 2006, 9, 223–253. [Google Scholar] [CrossRef]
- Kapolke, M.; Fürstenau, N.; Heidt, A.; Liers, F.; Mittendorf, M.; Weiß, C. Pre-tactical optimization of runway utilization under uncertainty. J. Air Transp. Manag. 2016, 56, 48–56. [Google Scholar] [CrossRef]
- Khassiba, A.; Cafieri, S.; Bastin, F.; Mongeau, M.; Gendron, B. Two-stage stochastic programming models for the extended aircraft arrival management problem with multiple pre-scheduling points. Transp. Res. Part C Emerg. Technol. 2022, 142, 103769. [Google Scholar] [CrossRef]
- Solak, S.; Solveling, G.; Clarke, J.-P.B.; Johnson, E.L. Stochastic Runway Scheduling. Transp. Sci. 2018, 52, 917–940. [Google Scholar] [CrossRef]
- Sölveling, G.; Clarke, J.-P. Scheduling of airport runway operations using stochastic branch and bound methods. Transp. Res. Part C Emerg. Technol. 2014, 45, 119–137. [Google Scholar] [CrossRef]
- Girish, B. An efficient hybrid particle swarm optimization algorithm in a rolling horizon framework for the aircraft landing problem. Appl. Soft Comput. 2016, 44, 200–221. [Google Scholar] [CrossRef]
- Faye, A. Solving the Aircraft Landing Problem with time discretization approach. Eur. J. Oper. Res. 2015, 242, 1028–1038. [Google Scholar] [CrossRef]
- Ji, X.-P.; Cao, X.-B.; Tang, K. Sequence searching and evaluation: A unified approach for aircraft arrival sequencing and scheduling problems. Memetic Comp. 2016, 8, 109–123. [Google Scholar] [CrossRef]
- Salehipour, A.; Modarres, M.; Naeni, L.M. An efficient hybrid meta-heuristic for aircraft landing problem. Comput. Oper. Res. 2013, 40, 207–213. [Google Scholar] [CrossRef]
- Balakrishnan, H.; Chandran, B.G. Algorithms for Scheduling Runway Operations Under Constrained Position Shifting. Oper. Res. 2010, 58, 1650–1665. [Google Scholar] [CrossRef]
- Hong, Y.; Cho, N.; Kim, Y.; Choi, B. Multiobjective Optimization for Aircraft Arrival Sequencing and Scheduling. J. Air Transp. 2017, 25, 115–122. [Google Scholar] [CrossRef]
- Mokhtarimousavi, S.; Rahami, H.; Kaveh, A. Multi-objective mathematical modeling of aircraft landing problem on a runway in static mode, scheduling and sequence determination using NSGA-II. Iran Univ. Sci. Technol. 2015, 5, 21–36. [Google Scholar]
- Samà, M.; D’Ariano, A.; Corman, F.; Pacciarelli, D. Metaheuristics for efficient aircraft scheduling and re-routing at busy terminal control areas. Transp. Res. Part C Emerg. Technol. 2017, 80, 485–511. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, P.; Zhang, Y.; Dai, X.; Sui, D. Criteria selection and multi-objective optimization of aircraft landing problem. J. Air Transp. Manag. 2020, 82, 101734. [Google Scholar] [CrossRef]
- Briskorn, D.; Stolletz, R. Aircraft landing problems with aircraft classes. J. Sched. 2014, 17, 31–45. [Google Scholar] [CrossRef]
- Lieder, A.; Briskorn, D.; Stolletz, R. A dynamic programming approach for the aircraft landing problem with aircraft classes. Eur. J. Oper. Res. 2015, 243, 61–69. [Google Scholar] [CrossRef]
- Veresnikov, G.S.; Egorov, N.; Kulida, E.; Lebedev, V.G. Methods for Solving of the Aircraft Landing Problem. I. Exact Solution Methods. Autom. Remote Control 2019, 80, 1317–1334. [Google Scholar] [CrossRef]
- Artiouchine, K.; Baptiste, P.; Dürr, C. Runway sequencing with holding patterns. Eur. J. Oper. Res. 2008, 189, 1254–1266. [Google Scholar] [CrossRef]
- D’Ariano, A.; D’Urgolo, P.; Pacciarelli, D.; Pranzo, M. Optimal sequencing of aircrafts take-off and landing at a busy airport. In Proceedings of the 13th International IEEE Conference on Intelligent Transportation Systems, Funchal, Portugal, 19–22 September 2010; pp. 1569–1574. [Google Scholar] [CrossRef]
- Veresnikov, G.S.; Egorov, N.; Kulida, E.; Lebedev, V.G. Methods for Solving of the Aircraft Landing Problem. II. Approximate Solution Methods. Autom. Remote Control 2019, 80, 1502–1518. [Google Scholar] [CrossRef]
- Vadlamani, S.; Hosseini, S. A novel heuristic approach for solving aircraft landing problem with single runway. J. Air Transp. Manag. 2014, 40, 144–148. [Google Scholar] [CrossRef]
- Hu, X.-B.; Chen, W.-H. Genetic algorithm based on receding horizon control for arrival sequencing and scheduling. Eng. Appl. Artif. Intell. 2005, 18, 633–642. [Google Scholar] [CrossRef]
- Hu, X.-B.; Paolo, E.A.D. A Ripple-Spreading Genetic Algorithm for the Aircraft Sequencing Problem. Evol. Comput. 2011, 19, 77–106. [Google Scholar] [CrossRef] [PubMed]
- Xu, B. An efficient Ant Colony algorithm based on wake-vortex modeling method for aircraft scheduling problem. J. Comput. Appl. Math. 2017, 317, 157–170. [Google Scholar] [CrossRef]
- Zhang, J.; You, L.; Yang, C. Arrival sequencing and scheduling based on multi-objective imperialist competitive algorithm. Acta Aeronaut. Astronaut. Sin. 2021, 42, 324439. [Google Scholar]
- Eun, Y.; Hwang, I.; Bang, H. Optimal Arrival Flight Sequencing and Scheduling Using Discrete Airborne Delays. IEEE Trans. Intell. Transp. Syst. 2010, 11, 359–373. [Google Scholar] [CrossRef]
- Samà, M.; D’Ariano, A.; Pacciarelli, D. Rolling Horizon Approach for Aircraft Scheduling in the Terminal Control Area of Busy Airports. Procedia Soc. Behav. Sci. 2013, 80, 531–552. [Google Scholar] [CrossRef]
- Samà, M.; D’Ariano, A.; D’Ariano, P.; Pacciarelli, D. Optimal aircraft scheduling and routing at a terminal control area during disturbances. Transp. Res. Part C Emerg. Technol. 2014, 47, 61–85. [Google Scholar] [CrossRef]
- Carr, G.C.; Erzberger, H.; Neuman, F. Fast-Time Study of Airline-Influenced Arrival Sequencing and Scheduling. J. Guid. Control Dyn. 2000, 23, 526–531. [Google Scholar] [CrossRef]
- Hasevoets, N.; Conroy, P. AMAN status review 2010, 1st ed.; Eurocontrol: Brussels, Belgium, 2010. [Google Scholar]
- Hasevoets, N.; Conroy, P. Arrival Manager: Implementation Guidelines and Lessons Learned, 1st ed.; Eurocontrol: Brussels, Belgium, 2010. [Google Scholar]
- Zhang, J.; Zhao, P. A New Meta Heuristic Approach for Aircraft Landing Problem. Trans. Nanjing Univ. Aeronaut. Astronaut. 2020, 37, 197–208. [Google Scholar] [CrossRef]
- Jung, S.; Hong, S.; Lee, K. A Data-Driven Air Traffic Sequencing Model Based on Pairwise Preference Learning. IEEE Trans. Intell. Transp. Syst. 2019, 20, 803–816. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, Z.; Yang, C.; Wang, B. Data-driven flight time prediction for arrival aircraft within the terminal area. IET Intell. Transp. Syst. 2022, 16, 263–275. [Google Scholar] [CrossRef]
- Trivedi, S.; Pardos, Z.; Heffernan, N.T. The Utility of Clustering in Prediction Tasks. arXiv 2015. [Google Scholar] [CrossRef]
- Heaton, J. An empirical analysis of feature engineering for predictive modeling. In Proceedings of the SoutheastCon 2016, Norfolk, VA, USA, 30 March–3 April 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Micci-Barreca, D. A preprocessing scheme for high-cardinality categorical attributes in classification and prediction problems. ACM SIGKDD Explor. Newsl. 2001, 3, 27–32. [Google Scholar] [CrossRef]
- Horiguchi, Y.; Baba, Y.; Kashima, H.; Suzuki, M.; Kayahara, H.; Maeno, J. Predicting fuel consumption and flight delays for low-cost airlines. In Proceedings of the Twenty-Ninth IAAI Conference, San Francisco, CA, USA, 6–9 February 2017. [Google Scholar]
- Wang, Z.; Liang, M.; Delahaye, D. A hybrid machine learning model for short-term estimated time of arrival prediction in terminal manoeuvring area. Transp. Res. Part C Emerg. Technol. 2018, 95, 280–294. [Google Scholar] [CrossRef]
- Wang, Z.; Liang, M.; Delahaye, D. Automated data-driven prediction on aircraft Estimated Time of Arrival. J. Air Transp. Manag. 2020, 88, 101840. [Google Scholar] [CrossRef]
- Probst, P.; Wright, M.; Boulesteix, A.-L. Hyperparameters and tuning strategies for random forest. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2019, 9, e1301. [Google Scholar] [CrossRef]
- Sáez, R.; Prats, X.; Polishchuk, T.; Polishchuk, V. Traffic synchronization in terminal airspace to enable continuous descent operations in trombone sequencing and merging procedures: An implementation study for Frankfurt airport. Transp. Res. Part C Emerg. Technol. 2020, 121, 102875. [Google Scholar] [CrossRef]
- Sáez, R.; Polishchuk, T.; Schmidt, C.; Hardell, H.; Smetanová, L.; Polishchuk, V.; Prats, X. Automated sequencing and merging with dynamic aircraft arrival routes and speed management for continuous descent operations. Transp. Res. Part C Emerg. Technol. 2021, 132, 103402. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).