Abstract
This study aims to determine the impact of the International Civil Aviation Organization’s (ICAO) taxiway system development stages on runway capacity and delays in a single-runway airport that serves mixed operations by using a combined approach integrating the capacity-demand estimation analyses. We proposed a generic and systematic approach to taxiway development alternatives based on the ICAO guidelines rather than case-specific improvements presented in previous studies. The Samsun Çarşamba Airport (LTFH), which has the most basic level of taxiway layout, was chosen as a case study. The development stages were modeled and run in a fast-time simulation environment for different traffic scenarios based on historical data. As a result of modelling, average airborne and gate waiting delay of arrivals, queue delay of departures, taxi times, and runway occupation times were obtained. In addition, gate sensitivity and cost-benefit analyses were carried out. A triple exponential smoothing forecast was performed for different scenarios including normal, runway closures, COVID-19, and recovery from COVID-19. Practical capacities of the stages were revealed using the results of simulation and traffic demand forecasts. In addition, we evaluated the potential operational improvements of the stages by modifying a previously presented mathematical model. The proposed approach can assist airport operators in predicting the airport capacity saturation and selecting the best capacity improvement strategy for unexpected events.
1. Introduction
The global air traffic demand for airports has been growing rapidly for decades until the COVID-19 pandemic. Although the COVID-19 pandemic has significantly reduced flight operations, the industry has already shown signs of recovery within the second half of 2020. EUROCONTROL provided three forecast scenarios for recovery from COVID-19. Even in the worst-case scenario, traffic numbers are predicted to be restored to the levels of 2019 by 2027 [1].
Increasing demand leads to significant capacity problems at airports, such as air traffic congestion and flight delays in the air and on the ground, as well as additional costs, adverse environmental impacts, and customer dissatisfaction associated with these interruptions. Therefore, airport capacity development is one of the main concerns of the global air transportation industry. The capacity development at airports is carried out according to master plans produced by the airport operators that provide guidelines for short, medium, and long-term operational and financial requirements for decision-makers. FAA publishes Advisory Circulars (AC) that provide guidance for the preparation of master plans for airports that range in size and function from small general aviation to large commercial service facilities. These ACs intend to foster a flexible approach for master planning that directs attention and resources to critical issues. The scope of each master plan must be tailored to the individual airport under evaluation. In these ACs, various factors that a master plan should include are introduced in detail. These factors are discussed in many topics such as environmental issues, financial issues, aviation forecasting, airport structure planning, and implementation plans. [2]. Airports prepare their master plans based on these recommendations. For example, in 2012, a master plan was published for Vilnius International Airport considering the increasing environmental impacts on a global and local scale [3]. In another master plan, published in 2014, the existing facilities of Bisbee Douglas International Airport were evaluated in terms of its adequacy for increasing traffic demand, and suggestions about these facilities were presented for the short, medium, and long terms [4]. A master plan has been prepared for Greenlee Country Airport, a relatively small airport compared to the aforementioned ones, considering the regional goals, needs, and plans, as well as increasing traffic demand. Several land-side alternatives are proposed in this plan to enhance the airport’s capacity and safety [5]. In another master plan proposed for Prosser Airport, short-, medium-, and long-term improvements are presented point by point considering environmental and economic goals. Both land-side and air-side improvement alternatives are proposed in the plan [6].
Although master plans have already been prepared for the next 20 years for an airport, they need to be updated regularly according to the latest changes in demand and technology in the industry [7]. Such unexpected global events as COVID-19 can lead to volatility in air traffic demand. Moreover, local events such as urgent maintenance and renovations at airports can decrease the capacity suddenly.
The International Civil Aviation Organization’s (ICAO) taxiway system development stages offer systematic improvements in taxiway geometries [8]. However, the ICAO taxiway system development stages do not provide any quantitative analysis relating to potential capacity improvements and demand growth under nominal conditions as well as demand volatility due to unexpected events, which constitutes the research problem of this study. Therefore, a combined approach is required as a decision support aid that integrates the capacity analysis and demand estimations for airport operators to prepare their development plans efficiently.
The main objective of this study is to evaluate the potential benefits of these capacity developments in terms of throughput and delays and suggest a timeline for the implementation of these improvements under demand volatilities due to pandemics and runway closures. In this context, first the impact of the ICAO’s taxiway system development stages on runway capacity and delays for a single-runway airport serving mixed operations is examined using SIMMOD, a discrete event airport and airspace simulation software. Then, a combined approach is demonstrated by integrating capacity-demand estimations including volatility due to pandemics and runway closures. Thus, it is revealed that while performing capacity analyses for different taxiway development stages whether sudden changes in demand will affect these updates. A gate sensitivity analysis is also performed to estimate the gate capacity improvements required by the taxiway developments under the high traffic demand. In addition, a preliminary cost-benefit analysis is presented to compare the costs of potential fuel savings and building a new taxiway. Finally, potential operational improvements of the stages were revealed by comparing the simulation results with modified mathematical model results. The proposed approach can assist airport operators in predicting the airport capacity saturation and selecting the best capacity improvement strategy in the presence of unexpected events.
The rest of the study is organized as follows: In Section 2, a detailed literature review of capacity studies is presented, and the contribution of the study is emphasized, respectively. In Section 3, the methodology used in the study is introduced. In Section 4, the case study is described. In Section 5, the results of the simulation, mathematical modelling, and forecast analyses are presented. Section 6 and Section 7 consist of the discussion, and the conclusion and future work, respectively.
2. Literature
The capacity of an airport indicates the number of aircraft movements that can be accomplished during a specified period (usually one hour), and it is typically limited by the capacity of its runway system [9]. Runway capacity analysis is a complex process because it involves numerous factors including the geometric layout configuration of the runway system, air traffic control procedures and separation minima, the mix of operation and aircraft types, weather conditions, and environmental restrictions. There are two important measures of runway capacity: ultimate capacity and practical capacity. While the ultimate capacity indicates the maximum number of operations served per hour under continuous demand, practical capacity is the number of flight operations during a given time interval corresponding to an acceptable level of average delay [10]. Researchers generally use analytical models, simulation models, and empirical models to analyze ultimate and practical runway capacities. Analytical models include time-space analysis as well as deterministic and stochastic queueing models [10,11,12]. In analytical models, optimization techniques are used to improve the practical capacity of the runway considering several objectives and constraints. These studies generally consist of two parts: airside and groundside. In the airside, researchers focus on optimizing the traffic flows in the terminal maneuvering area (TMA) [13,14], extended TMA [15,16,17], or enroute operations [18]. On the groundside, operations such as landing, take-off, taxi, pushback, and gate assignment are considered [19,20]. These analytical models are easier to implement and provide good traceability of results, but these models are unable to produce accurate results for complex runway systems. Simulation-based models include Monte Carlo and discrete-event simulation models [21,22]. These simulation models are more difficult to build and execute, but their results are more realistic and detailed. Discrete-event techniques can especially provide a high-level-of detail in dynamic models to track and determine capacity development updates for a wide range of operational scenarios. There are various discrete-event simulation tools including SIMMOD [23], CAST [24], TAAM [25], RAMS [26], and AirTOP [27]. An extensive overview of these tools and techniques is provided in the literature [28,29]. Safrillah and Putra classified runway capacity enhancement studies into five categories: geometry of airside facilities, operations and procedures, aircraft performance, human factors, and external factors. The studies on the first category focus on the expansion of the existing physical facilities including runway systems, taxiway networks, apron areas, and parking stands, and they can provide a significant contribution to the total capacity of airports. The studies in the second category involve the impact of operational improvements on capacity, such as runway operational usage methods, aircraft performance, traffic mixes, separation categories, and arrival sequencing for existing runways. Operational improvements alone provide a limited improvement on capacity; therefore, they are usually used with the improvements in airside geometries [30].
The following studies to be discussed include recent geometric and operational approaches using the abovementioned techniques in runway capacity analysis. Bazargan et al. identified the maximum throughput capacities of proposed expansion alternatives at the Philadelphia International Airport (KPHL) as a sample study, constrained at varying levels, using TAAM [31]. Wang et al. used SIMMOD to calculate the practical capacity of a single runway airport for three different scenarios including parking stand allocation, alternate gate strategy, and high-speed exits [32]. However, in that study, they did not examine any structural development on the runway or taxiways. Bubalo and Daduna modelled an airport having independent parallel runways in a segregated mode using SIMMOD to calculate the capacity utilization and the chosen level of service indicators: practical capacity, minutes of average delay per flight, increasing traffic, and changing traffic mix [33]. Peng et al. in their study applied an agent-based modelling approach to the simulation of a parallel runway system. They evaluated these agent-based models and compared them with the models created in SIMMOD and ARENA [34]. Cetek et al. performed fast and real-time simulations using SIMMOD and the BEST simulator to detect congestion points in the maneuvering areas of a n open-V runway configuration and analyzed the impacts of fast-exit and parallel taxiway alternatives to reduce these congestions for Istanbul Atatürk Airport (LTBA) as a sample case [35]. Aybek Cetek and Cetek used ARENA to analyze the single runway capacity of airports serving training flights under different traffic scenarios [36]. Leege and Janssen presented a system that allows the prediction of runway utilization and capacity at 20-min intervals for the subsequent 30 h. The system serves to predict runway utilization through machine learning based on previous meteorological data and track selections [37]. Tee and Zhong proposed an approach to find out which runway operations could be maximized on parallel runways by simulation modelling [38]. Mirmohammadsadeghi et al. showed how runway capacity was affected by various wake turbulence using simulations [39]. Mirmohammadsadeghi and Trani proposed a simulation model that uses a hybrid approach by combining machine learning techniques and Monte Carlo simulation to predict an accurate value for runway occupancy time and runway exit distance based on historical data [40].
The above-mentioned studies deal with the impacts of specific geometric and operational improvements on capacity and delay analysis for a selected airport under a limited number of traffic scenarios. They do not usually adopt a combined approach that integrates practical capacity estimations and demand forecasts being updated regularly. In contrast, in our study, the combination of the capacity analysis-demand estimations was performed by combining the results of simulations and triple exponential smoothing analysis. It also considered the effect of unusual and unexpected events on traffic estimations. Moreover, a generic and systematic approach to taxiway development alternatives based on the ICAO [8] guidelines are presented, rather than case-specific improvements presented in previous studies. Most previous studies on airport runway capacity have a case-specific approach, as they focus on airports that have already undergone certain improvements. In contrast, our study examined the potential benefits of implementing the ICAO taxiway system development stages at an airport with a basic layout from the beginning. Through this approach, we were able to demonstrate the potential benefits of implementing these development stages in order, starting with the most basic layouts allowing for a more generalizable analysis of the potential benefits of these development stages.
Contribution of the Study
According to the best knowledge of the authors, a simulation study associating the ICAO’s taxiway system development stages with capacity and delays is not yet available in the literature. These development stages are suggested by the ICAO based on historical data and very detailed analyses. These systematic development stages are considered general recommendations for airports, and they can easily be applied on a global scale. In contrast, airport-specific improvements may not apply to other airports or can be difficult to adapt.
The originality of the study can be briefly summarized as follows:
- 1-
- Combines the capacity-demand estimations.
- 2-
- Considers the unusual and unexpected events on demand forecasts.
- 3-
- Proposes a systematic approach to taxiway development alternatives starting with the most basic layout.
- 4-
- Focuses on an ideal sample airport to show the developments and interruptions in the best way.
- 5-
- Considers the cost-benefit analysis of taxiway development stages based on fuel savings and construction costs.
- 6-
- Includes further sensitivity analysis for gate improvement.
- 7-
- Evaluates the potential operational improvements of the stages by using a modified mathematical model.
Our approach can provide two important benefits for versatile, predictive, and proactive runway capacity planning and enhancement. First, it can offer a quick insight to predict potential runway capacity saturations under different traffic scenarios and unexpected events for decision-makers and planners. Second, it can provide an accurate and practical tool to assess what kind of improvements need to be done with the alternatives available under the guidance of the ICAO documentation.
3. Methodology
In this study, first, a discrete-event simulation model was established in SIMMOD, and various generic traffic scenarios were analyzed. In addition, gate sensitivity and cost-benefit analyses were carried out based on simulation outputs. In this analysis, fuel consumption of the aircraft is calculated based on the BADA fuel flow model [41]. After the simulation analysis, traffic estimation was performed using a triple exponential smoothing based on the actual traffic data of the airport. Then, in practical capacity analysis, the triple exponential smoothing analysis results were combined with the simulation analysis results to predict when the capacities would become saturated. At the end of the study, the potential operational improvements of the stages were revealed by using a modified mathematical model. Figure 1 summarizes the methodology of the study.
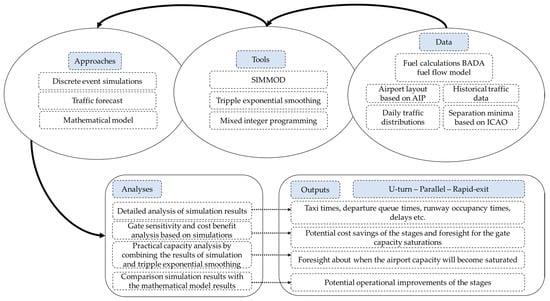
Figure 1.
Methodology.
3.1. Discrete Event Simulations
The discrete event simulation model was developed using SIMMOD. With the novel implementation of a generalized simulation scripting language, SIMMOD provides the flexibility and power of genuine rules-based modeling capabilities. This significantly improves the capacity to model the dynamics, variability, site-specific characteristics, and situation-specific elements in air traffic operations. SIMMOD has been used by users since 1997 to solve their most difficult modeling and simulation problems involving airspace and airport operations [23]. The aircraft models are divided into air and ground groups having common performance characteristics such as airspeeds, runway occupancy times, and so on. Airports can be modeled in detail, or just referenced as a flight’s origin or destination. Modeled airports contain ground nodes and links, runways, parking stands, departure queues, and procedures. The simulation models use the ICAO’s separation minima, airport layout data, and traffic observations as inputs. The models provide flight times and delays on the ground and in the air as outputs for various operational scenarios. Air delay describes the delays imposed upon the arriving flights using vectoring, speed reduction, and holding strategies to ensure safe separation between successive aircraft within the airspace. Ground delay includes gate waiting time for arrivals and queue waiting time for departures. The results also provide predictions for decision-makers on capacity saturation and enhancement alternatives systematically [42].
The following assumptions were used in the simulation analysis:
- More than one aircraft cannot be on the runway at the same time.
- Landing and takeoff operations are performed in one direction. Changes in the direction and magnitude of the wind were disregarded.
- All operations take place under standard atmospheric conditions at the given runway elevation.
- Because the minimum separation between aircraft significantly affects the practical capacity of the airport, wake turbulence separations between two consecutive aircraft, according to aircraft categories, were determined as stated in ICAO Doc. 4444 [43].
- Capacities of other airside elements (i.e., apron) and the aerodrome control zone (i.e., aerodrome traffic circuit) were not accounted for in the models.
- Ten parking stands were modelled based on the airport layout.
- The final approach path (FAP) length and airport layout were determined based on the Aeronautical Information Publication (AIP) [44]. The FAP length was 8.94 nm, and the runway dimension was 3000 m ∗ 45 m.
- The peak hour traffic mix was used as a baseline, which consisted of 80% medium (M) and 20% light (L) category aircrafts based on real traffic observations.
The separation minima, nominal aircraft speeds, flight information in the reference scenario including the expected time of arrivals (ETA) and departures (ETD), and the landing rolls and take-off rolls of aircraft in the simulations are presented in Table 1, Table 2, Table 3 and Table 4, respectively.

Table 1.
Wake turbulence separations (nm) [42].

Table 2.
Nominal aircraft speeds [42].

Table 3.
Flights in the reference scenario [45].

Table 4.
LR and TOR distances (feet) and probabilities [42].
3.2. Traffic Demand Forecast
Several methods can be used for time series forecasting such as the moving averages method, linear regression, exponential smoothing, etc. There are three types of exponential smoothing methods; single, double, and triple. The triple exponential smoothing method, which is called the Holt-Winters (HW) method, is used when the data show trend and seasonality. There are two main HW methods, depending on the type of seasonality: Additive Seasonality and Multiplicative Seasonality. Additive Seasonality is the Triple Exponential Smoothing with a linear seasonality. Multiplicative Seasonality is the Triple Exponential Smoothing with an exponential seasonality. To forecast the traffic demand, we chose the Additive Seasonality method because the traffic data of Samsun Çarşamba Airport had monthly variations while seasonal change was constant throughout the series. Monthly total traffic from 2012 to 2022 (Table 5) is used for the analysis. More information about the triple exponential smoothing and main HW methods can be reached from [46,47].

Table 5.
Total traffic (IFR+VFR) [45].
There are some advantages of the HW additive method compared to other forecast methods. Lesmana et al. (2018) implied that exponential smoothing can perform as well as, if not better than, more complex methods [48]. Petropoulos et al. emphasized that the HW method can give better results compared to moving averages [49]. Dingari et al. compared the HW Additive method and ARIMA technique, which consists of autoregressive and moving average components for domestic air traffic in Air India flights. They concluded that the HW Additive model is best for their data [50]. In the ICAO Manual on Air Traffic Forecasting, it is emphasized that the exponential smoothing method is similar to the moving averages. However, it considers the recent data more than the first data to increase their effect on the forecast [51].
3.3. Mathematical Model
We compared the simulation results with an optimization algorithm proposed by Dönmez [52] to determine the potential operational improvement of the taxiway development stages. We presented a stochastic aircraft sequencing algorithm for a single runway case considering runway occupancy time and runway exit point uncertainties. In this study, we modified this algorithm for our case study in a deterministic way. Therefore, the scenario indices given for the stochastic model were eliminated in the current version. We also integrated our parameters into this model including separation rules, aircraft types, aerodrome, and ground structures (including three type of taxiway configurations) of Çarşamba airport, etc. are the set of aircraft where. represents the start time of the ith aircraft. represents the operating time until the touchdown time of theth aircraft (refers to the final approach duration for arrivals and the taxi durations for departures). Note that these times for each arrival and each departure are considered constant, respectively. describes enough large numbers and corresponds to the separations between the successive aircraft, respectively. is a binary decision variable that takes 1 if the th aircraft is assigned to the touchdown point of the runway before the th aircraft, and 0 otherwise. , , and describe the touchdown time of the th aircraft, airborne delay of th aircraft, and the departure queue delay of the th aircraft, respectively. Operational constraints are derived by using these parameters and variables. Equations (1) and (2) determine the arrival touchdown times and departure times, respectively.
Airborne delays and queue delays are limited with an upper bound, which was determined as 600 s, for both. Equations (3) and (4) ensure that the upper limit of delays will not be exceeded for arrivals and departures, respectively.
Equations (5) and (6) ensure the wake turbulence separations between aircrafts.
Equation (7) describes the objective function to minimize the total delay.
4. Case Study
4.1. Çarşamba Airport
We choose quite an ideal baseline to observe the impacts of these improvements. The Samsun Çarşamba Airport (SZF/LTFH) has been used as the sample study because of its most basic taxiway layout and increasing traffic growth. Moreover, this airport experienced two recent events disturbing the growth in air traffic demand. The first one is the runway closures associated with the runway pavement renovations that resulted in temporary constraints in the existing capacity in 2017. The second one is the COVID-19 pandemic that introduced a sudden decrease in air traffic demand due to travel restrictions in 2020. These interruptions provide an important opportunity to observe the effect of unusual and unexpected events on demand forecasts.
According to AIP data, the airport is located within the borders of the Samsun province in the central black sea region of Turkey at an altitude of 18 ft (6 m) above sea level. The airport has a single (13/31) runway, A-apron, and two taxiways: B and C [44]. Figure 2 shows the location and ground layout of the airport.
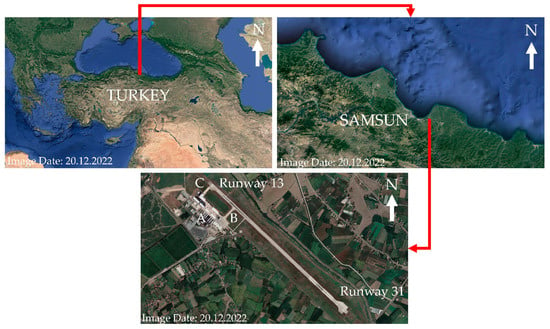
Figure 2.
Location and ground layout of Çarşamba airport, Samsun, Turkey [53].
The Samsun Çarşamba Airport serves both IFR (Instrument Flight Rules) and VFR (Visual Flight Rules) flights. According to the General Directorate of State Airports Authority (GDSAA) data, there is an average of 44 daily commercial flight operations at the airport. In addition to domestic and international commercial passenger flights, training, cargo, and military flight operations are also carried out. Table 5 shows the total number of flight operations that took place at Çarşamba Airport according to the GDSAA data [45].
According to the data, aircraft movements increased annually with an average of 14.4% for the period of 2012–2016. This rapid increase in demand started putting pressure on the existing runway capacity for possible extensions. However, in 2017, the air traffic demand dropped to 76.4% due to the runway closure associated with runway pavement renovation work that took place between August and November 2017. While the traffic levels were recovering with an average increase of 12.8% for the period of 2018–2019, flight restrictions due to the COVID-19 pandemic affected the traffic demand adversely, especially between April and June 2020. Although these restrictions have been relaxed during the summer season in 2020, aircraft movements from January to December are 21.1% less than those of the previous year. The average monthly traffic increased by 9.6% compared to 2020, as a result of the effective vaccination and precautions in 2021. The demand volatility is expected to continue in the following years depending on the course of the pandemic. Table 6 shows the cargo and passenger traffic between 2012 and 2021 based on GDSAA data [45].

Table 6.
Cargo and passenger traffic [45].
As seen in Table 6, similar fluctuations to the total traffic were observed for both cargo traffic and passenger traffic after the renovation work and COVID-19. Table 7 shows the top routes from Çarşamba airport based on flight radar [54] and Figure 3 visualize these routes.

Table 7.
Top routes from SZF/LTFH.
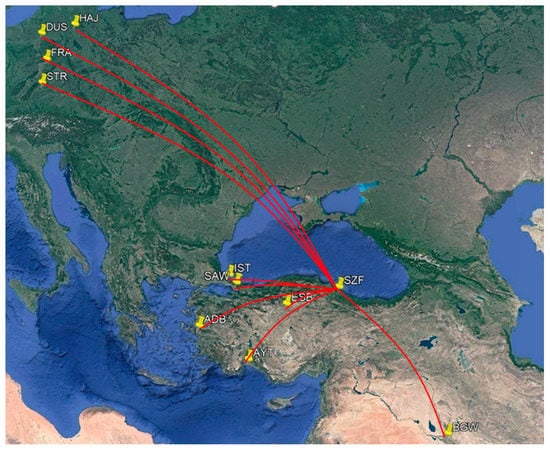
Figure 3.
Visualization of top routes from SZF/LTFH.
4.2. Traffic Scenarios
To generate traffic scenarios, the reference traffic flow level, type of operations, and aircraft type mix were determined based on the actual traffic data obtained from traffic observations and the GDSAA website [45]. The reference day was selected as the peak day of 2015 (28 August). The busiest 3-h period (20:00–23:00) was chosen for the simulation analysis. Within this period, a total of 22 flight operations (11 arrivals and 11 departures) took place at the airport. While 18 of these operations belonged to commercial flights, the remaining 4 operations were general aviation flights. All the commercial aircrafts were of the medium category, with the maximum take-off weight being between 7 and 36 tons. All the general aviation aircrafts were light aircrafts with a maximum take-off weight of less than 7 tons. The peak 3-h period was chosen for the baseline scenario, referred to as 0% in Table 8. The number of operations for the other scenarios was determined by generic traffic increased up to 600% in SIMMOD. The reason of increasing the demand is to observe congestions and saturations under various overcapacity scenarios in the airport. The maximum increase of 600% corresponded to the maximum theoretical capacity of the best taxiway configuration (rapid exit).

Table 8.
Number of operations during the peak 3-h period.
4.3. Taxiway Configurations
Simulation analyses were carried out for three different taxiway configurations. The stages in taxiway system development, published by the ICAO [8], are given in Figure 4a–c. The first configuration, the U-turn taxiway, is the current configuration in use, and therefore, it is selected as the baseline that can be seen in Figure 4a as gray lines including A-apron, and two taxiways: B and C. Flight operations at the Samsun Çarşamba Airport are generally carried out on runway 13, and an arriving flight needs to perform a U-turn (backtrack) at the end of the runway and come back to the parking positions, which leads to very long runway occupancy times. This configuration cannot meet the increasing demand for traffic over time. Therefore, it is important to foresee how far new configurations will increase the capacity of this airport.
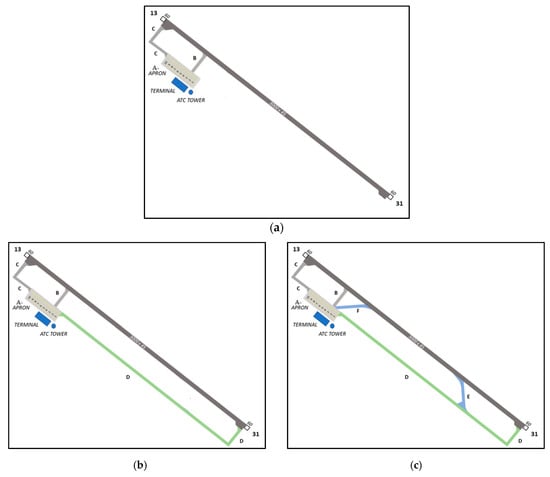
Figure 4.
(a) U-turn, (b) Parallel, (c) Rapid exit.
Considering the development stages of the taxiway system published by the ICAO, the first improvement for the Samsun Çarşamba airport will be the addition of a parallel taxiway D, which is shown as green lines in Figure 4b. The advantage of this taxiway configuration is that arriving flights can leave at the end of runway 13 and go to the parking position by using a parallel taxiway route. This means that the runway becomes available as soon as the aircraft leaves the runway.
When runway capacity becomes saturated again, rapid exit taxiways can be built in addition to the taxiway, which is shown as blue lines in Figure 4c. The rapid exit taxiways are modeled in such a way that 80% of medium category aircrafts can leave the runway at these points, which are added approximately 2150 m from the beginning and end of runway 13 at an angle of about 30 degrees, referring to [8]. The advantage of this configuration is that it allows arriving flights to leave the runway at an earlier point if their speed is appropriate. Thus, the runway is ready for a new operation. Because all operations are assumed to take place on runway 13, the rapid exit taxiway E is modeled to affect only one-way operations. Rapid exit taxiway F can be used for Runway 31, but it is beyond the scope of this study.
According to the ICAO, the complexity level of an airport taxiway system should only be needed to support the runway’s capacity requirements in the near term (to reduce construction costs). Additional taxiway elements should be gradually added to the system to be consistent with airport development and careful planning [8].
5. Results
5.1. Simulation Results
The three configurations were modeled separately in SIMMOD for 11 traffic scenarios. A total of 33 scenarios were run for these three taxiway configurations. SIMMOD produces a wide range of simulation outputs. Runway occupation times and taxi times for arrival, departure queue times for departure flights, and throughputs can be calculated from these outputs. These outputs also allow the calculation of delays for departure and arrival flights.
Runway occupation times of arrivals can be seen in Table 9. In the current U-turn configuration, the average runway occupation time of each aircraft is approximately 3.78 min, which corresponds to 226 s. This is one of the major disadvantages of this layout, which significantly decreases the runway throughput. These results could be verified by comparing the result of a previous study presented by Dönmez 2022 [55]. He handled the same airport and current configuration by observing real ROTs of arrivals at the airport. As a result, it is observed that the highest rate of the operations is in the range of 224–254 s, and this result verifies our current simulation results. The parallel taxiway configuration reduced this time to less than 1 min. In the rapid exit taxiway configuration, average runway occupation times were reduced more than in the parallel taxiway configuration (by approximately 31%). Table 9 shows that the U-turn configuration has less taxi time than other configurations do. This is due to runway backtrack taxi speed being determined as higher than the nominal taxi speed on taxiways [56]. However, after an aircraft lands, making a U-turn at the end of the runway and taxiing back prevents runway use for other aircrafts. Although the average taxi times increased by 1.7 and 0.75 min for parallel and rapid exit taxiway configurations, respectively, runway occupation times decreased significantly and provided runway use for other aircrafts.

Table 9.
Runway occupancy times and taxi times of arrivals (minutes).
Table 10 presents airborne and gate waiting delays of arrivals as well as departure queue delays for departures. Airborne delays of arrivals reduced significantly in parallel and rapid exit taxiway configurations compared to the U-turn configuration. In case of 600% increase in the traffic demand, the average airborne delay per flight is 89.9 min in the U-turn configuration, while it is only 4.7 min for the parallel and rapid exit configurations. As the traffic demand increases, airborne delays increase for all configurations. Departure queue delays were reduced significantly in parallel and rapid exit configurations compared to the U-turn configuration. Departure queue delays increased up to 170 min in the 600% increase in traffic demand for the U-turn configuration, while for the parallel and rapid exits, they are less than 3 min.

Table 10.
Average delays per aircraft.
Although the airborne delays decreased in the parallel and rapid exit configurations, these configurations resulted in higher gate waiting delays for scenarios with 150% and more traffic increase. Gate waiting delay refers to the ground waiting time of arrivals when all available gates are occupied. These results revealed the necessity of increasing the gate capacity in parallel to the airport geometry over 150% traffic increase. Significant gate waiting delays are observed especially in the 600% demand increase scenario. Therefore, a gate sensitivity analysis was performed to find the required number of gates to eliminate the gate waiting delays (Table 11).

Table 11.
Results of gate sensitivity analysis.
According to the analyses when the number of gates is increased to 28, the gate waiting delays are eliminated for all configurations in the 600% demand increase scenario.
We also compared the benefits of potential fuel savings and the cost of building a new taxiway for parallel and rapid exit configurations (Table 12 and Table 13). The fuel consumption of each aircraft is calculated based on BADA 3.7 fuel consumption model [41]. To calculate the fuel consumption of arrivals, we assume that they perform level flights before joining the final approach. Fuel consumptions during the gate waiting delays and departure queue delays are calculated assuming the aircrafts are in idle configuration. To avoid unnecessary lengthening of the study, the whole formulation of fuel calculations is not given here. However, more details and a similar application of fuel calculation can be found from [56]. Current jet fuel prices are obtained from [57]. The cost of building a new taxiway is calculated based on [58], in which more details about the calculation can be reached. Building costs are updated based on the annual inflation rates in the European Area. We assume that a 20 m to 30 m width concrete-based taxiway will be constructed for the airport.

Table 12.
Annual savings compared to U-turn (Million $).

Table 13.
Taxiway construction costs (Million $).
Even according to the results of this preliminary analysis, the cost of building new taxiways can be compensated within a year by the potential fuel savings for the demand increase scenarios of 150% and more. The calculations are performed without considering the operational costs associated with the crew, passenger dissatisfaction, and slot penalties due to delays. This break-even point could be reached much earlier if these factors are included in the analysis.
5.2. Practical Capacity Analysis Results
Practical capacity can be referred to as the total delay tolerance of the airport operator or airline companies; once this is exceeded, the airport capacity is saturated. For example, if the practical capacity is determined as 5 min, this means that companies can tolerate a 5-min delay per aircraft [33]. Horonjeff et al. explains the term of practical capacity and the difference between other capacity definitions as follows: practical capacity is the number of aircraft operations that can be accommodated during a specified time interval, with a tolerable level of average delay. In contrast, ultimate, or throughput capacity, is the maximum number of operations that a service facility can handle over a defined period of time, without considering delay. These two definitions are used because there is no consensus on what level of delay is acceptable at different airports, and because the capabilities of individual airports can vary. Ultimate capacity reflects the ability of an airfield to handle a large number of aircraft during peak periods of activity, while practical capacity takes into account factors such as delay tolerance and other constraints [10]. In the current study, the sum of the departure and arrival delays was considered in the practical capacity analysis. The practical capacity saturations for 5-min and 10-min delays per aircraft are marked in Table 14.

Table 14.
Practical capacity (total delay per AC (minutes)).
According to Table 14, 5-min and 10-min average delays per aircraft are reached at approximately 80% and 150% increase in traffic demand, respectively, in the U-turn configuration. In contrast, for parallel and rapid exit configurations, the 5-min and the 10-min average delays per aircraft are reached at 300% and 400% traffic increase, respectively.
5.3. Traffic Forecasts and Practical Capacity
In Triple Exponential Smoothing analysis, we aim to generate different demand scenarios based on real data. The first scenario is referred to as “normal” based on the traffic data of Samsun Çarşamba Airport between 2012 and 2016. The second scenario is named “renovation work” based on the traffic data between 2012 and 2019. The third scenario is referred to as “COVID-19” scenario, which included traffic data between 2012 and 2020. Finally, the last scenario is named as “recovery from COVID-19”, which included the traffic data between 2012 and October 2021.
The peak 3-h traffic demand forecasts are presented in Table 15. The traffic demand is expected to decrease up to 57%, 64%, and 72% for renovation, recovery from COVID-19, and COVID-19 forecast scenarios, respectively, compared to the normal forecast scenario. The 3-h forecasts were approximately 59, 25, 16, and 21 aircrafts for the normal, renovation work, COVID-19, and recovery from COVID-19 scenarios, respectively, in 2030. By integrating the simulation results and the traffic demand forecasts, it is possible to see when the practical capacity will be reached for each forecast scenario. In the normal forecast scenario, practical capacities with 5-min and 10-min average delay per aircraft would be reached approximately by 2022 and 2029, respectively, for the U-turn configuration. The practical capacity with a 5-min delay cannot be reached even by 2030 for the parallel and rapid exit configurations. The 5-min and 10-min delays per aircraft will not be reached for all stages in the renovation, COVID-19, and recovery from COVID-19 scenarios, even until 2030. It seems that the Çarşamba airport may not need any taxiway development in the short term after renovation work and COVID-19 as well as recovery from COVID-19.

Table 15.
Peak 3-h traffic forecasts scenarios.
It should be noted that triple exponential smoothing only provides a theoretical foresight for a long-term forecast; in practice, some dynamic variables and risks influence this forecast. These variables should be considered to make more realistic estimates. However, this can be considered deeply in another study. In this study, demand scenarios are generated as only theoretical what-if scenarios.
5.4. Evaluating the Operational Improvements Using Mathematical Modeling
We considered the 200% traffic scenario (22 aircrafts for an hour) as a sample scenario for the mathematical model that is the first demand scenario that corresponds to the ultimate capacity saturation of the airport based on the model proposed by [59]. Exact parameters that are used in simulations for this scenario are integrated into the mathematical model including aircraft types, operation mixes, etc. Average ROTs obtained from the simulations are used as constant parameters for each development stage. Then, 10 different expected time of arrival departure (ETA) scenarios were solved for each taxiway development stage by using CPLEX solver in GAMS (the General Algebraic Modeling System), which is a high-level programming language for optimization problems [60]. The model results for each configuration are given in Table 16 in terms of the average delay per aircraft (seconds).

Table 16.
Mathematical model results (sec.).
As seen in Table 16, all three configurations have significant potential operational improvements in terms of delay reduction. These results indicate that the average airborne delay per aircraft can be reduced from 474 s to 142 s for the U-turn configuration by optimizing the sequences, while departure queue delays can be reduced from 1614 s to 66 s. The average airborne and queue delay savings of the operational improvement correspond to approximately 82% for the U-turn configuration, while these percentages correspond to approximately 85% and 88% for the parallel and rapid exits. The average delay per aircraft (both airborne and departure queue) corresponds to 78 s for the parallel and rapid exit taxiway configurations. However, after sequence optimization was applied to both the parallel and rapid exit configurations, it is seen that airborne and queue delays decrease to approximately 10 s per aircraft. These results reveal that significant improvements may be achieved by using structural and operational improvements together. Figure 5 summarizes the delays in one of the reasonable development roadmaps for the Çarşamba airport considering 22 aircraft demand scenarios for an hour.
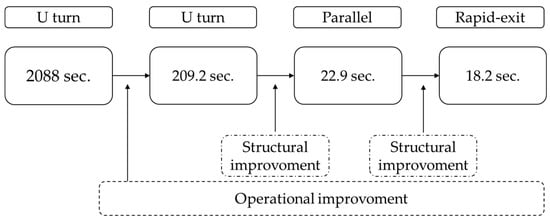
Figure 5.
Optimal road map for sample scenario.
The total of the average airborne and queue delays per aircraft are represented in the boxes in Figure 5. The first operational development will decrease this delay from 2088 s to 209.2 s. Then, structural developments are combined with operational development and the delay decreased to 22.9 s and 18.2 s for the parallel and rapid exit configurations, respectively.
6. Discussion
The analyses showed that the parallel and rapid exit taxiway configurations have important advantages over the U-turn configuration. In simulation results, parallel and rapid exit configurations significantly reduced the average airborne delays of arrivals, departure queue delays, and the runway occupation times of arrival flights. In the cost benefit analysis, we compared the construction cost of the parallel and rapid exit configurations to the fuel cost savings in these configurations. As a result, one interesting finding of the study is that the construction cost of a new taxiway can be compensated within a year if traffic increases by 150% or more. This suggests that investing in a new taxiway can be a worthwhile investment, especially in the long term. Gate waiting delays, however, start occurring when the demand increase reaches 150% for the parallel and rapid exit configurations. Hence, the necessity of building new gates can arise when the demand grows at this rate. Significant gate waiting delays are observed, especially for the 600% demand scenario. Gate sensitivity analysis showed that the gate capacity increase to 28 can solve the gate waiting delay problem of the airport even under high-demand scenarios for all configurations. It should be noted that building new gates will also cause additional costs.
Although the rapid exit configuration significantly reduces the taxi times and runway occupation times compared to the parallel taxiway configuration, these configurations yielded similar results in many respects including airborne, gate waiting, and departure delays. The reason for this is that the rapid exit configuration significantly increased the throughput; however, other facilities of the airport (i.e., number of gates and taxiway capacities) were unable to meet this demand. Therefore, the expected savings could not be obtained from this configuration. In conclusion, the parallel taxiway may be a more reasonable and sufficient alternative at airports with the most basic layouts without enhancing any additional facilities at the first stage. Rapid exit enhancement alternative, therefore, can be considered for higher traffic demand in the medium- to long-term development plans including facility enhancements.
Considering the practical capacity analysis results, another key finding of the study is that parallel and rapid exit configurations can significantly delay the point at which practical capacity is reached. This is important because it means that these configurations can accommodate more traffic before reaching capacity constraints. However, the expected savings from the rapid exit configuration may not be realized if other airport facilities cannot keep up with the increased demand. While the 5-min delay per aircraft is reached with a 60% increase in traffic demand for U-turn, the same practical capacity saturation corresponds to a 300% increase in demand for the parallel and rapid exit taxiway configurations. When the results of the triple exponential smoothing are examined, for the normal traffic forecast, the 5-min and 10-min practical capacities will be saturated in 2022 and 2029, respectively, and therefore, the current taxiway layout will need to be developed in the Samsun Çarşamba Airport. However, when the traffic forecast scenarios are updated for renovation work, COVID-19, and recovery from COVID-19, there is no need for any improvement in the short term.
At the end of the study, potential operational improvements in the stages were also revealed by using mathematical modeling. For the current U-turn configuration, an operational improvement provided approximately 82% delay savings for the 22 aircraft demand per hour. It has been revealed that delay savings of up to 90% can still be achieved with operational improvements after structural improvements. These results revealed the importance of combining structural and operational improvements. These results also indicate that a structural improvement after the operational improvement of the existing configuration would be the more appropriate option for development plans.
7. Conclusions and Future Works
In this study, a discrete-event simulation model in SIMMOD is used to evaluate the potential benefits of the ICAO taxiway system development stages under various generic traffic scenarios at a sample airport. Then, gate sensitivity and cost-benefit analyses are carried out based on the simulation outputs. Triple exponential smoothing on actual traffic data is also performed to estimate future traffic levels, and these estimates are combined with the simulation results to predict when capacity would become saturated. Finally, a modified mathematical model is used to analyze the potential operational improvements of different taxiway stages of the airport.
The key findings of the study can be summarized as follows: parallel and rapid exit taxiway configurations can significantly reduce airborne delays, departure queue delays, and runway occupation times compared to U-turn configurations. The construction cost of a new taxiway can be compensated within a year if traffic increases by 150% or more. Gate waiting delays may occur at this level of demand, indicating the need for additional gates. The rapid exit configuration can further reduce taxi times and runway occupation times but may not fully realize its potential savings if other airport facilities cannot keep up with the increased demand. In addition, the results showed the importance of combining structural and operational improvements for airport development plans.
This study can be considered as a guide to the managers of airports with the most basic taxiway configurations for the implementation of taxiway development stages published by the ICAO. It can provide insight into what increase in traffic level will cause the practical capacity of their airport to become saturated and when this is likely to occur for different forecast scenarios. It is also shown how unexpected events such as COVID-19 and renovation work can affect these development plans.
Events such as COVID-19 and renovation work slowed down the increase curve in traffic forecasts so that more conservative development plans (e.g., operational improvements) could be more economical for the airport in the short term. Thus, the necessity of updating the airport development plans periodically can be emphasized again. Development plans including more than one traffic forecast scenarios, especially in which unexpected events are considered, need to be done more from now on. For decision-makers, the difference between the cost of building a new taxiway and the delay-induced costs will be decisive on whether, how, and when to improve capacity for further plans.
One of the limitations of this study is that it only compares the performance of the parallel and rapid exit taxiway configurations to a U-turn configuration and does not compare them to other potential complex configurations. The development stages can be implemented in future studies by using more complex configurations. Although the study includes the demand volatilities considering COVID-19 and runway closures, it does not consider the potential impact of future developments or changes in the aviation industry, such as the changes in demand due to economic or political events. Additionally, the cost-benefit analysis only considers the cost of building a new taxiway and the fuel savings from using the new configuration but does not account for other potential costs or benefits, such as the cost of building new gates or the potential for increased revenue from improved performance. Finally, the triple exponential smoothing technique used to forecast future traffic levels is a simplification of more complex models and may not accurately predict future demand. A combined forecasting approach that includes more than one forecasting method can be used for more accurate and consistent estimates. Furthermore, different scenarios can be used for the traffic mixes, where heavy aircrafts are included, or the number of light aircrafts is increased more than the numbers included in the current study. To avoid the unnecessary lengthening of this study and to not deviate from its main purpose, only scenarios closest to real operations were modeled.
Author Contributions
Conceptualization, K.D., E.A., C.Ç. and E.E.M.; methodology, K.D. and C.Ç.; software, K.D. and E.A.; validation, K.D.; formal analysis, K.D.; investigation, K.D.; resources, K.D.; writing—original draft preparation, K.D.; writing—review and editing, K.D.; visualization, K.D. and E.E.M.; supervision, C.Ç. and E.E.M.; project administration, K.D., C.Ç. and E.E.M.; funding acquisition, E.E.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No data available.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Eurocontrol. EUROCONTROL Forecast Update 2021–2027 European Flight Movements and Service Units Three Scenarios for Recovery from COVID-19. 2021. Available online: https://www.eurocontrol.int/sites/default/files/2021-10/eurocontrol-7-year-forecast-2021-2027.pdf (accessed on 1 October 2022).
- FAA. Advisory Circular 150/5070-6B. 2015; pp. 1–152. Available online: https://www.faa.gov/regulations_policies/advisory_circulars/ (accessed on 1 November 2022).
- A. T. I. & Logistic. Vilnius International Airport Master Plan; ALG Global: Barcelona, Spain, 2012. [Google Scholar]
- A. C. Inc. Bisbee Douglas International Airport Final Report; Armstrong Consultants, Inc.: Mesa, AZ, USA, 2015. [Google Scholar]
- Coffman Associates, Inc. Greenlee Country Airport Master Plan; Coffman Associates, Inc.: Lee’s Summit, MO, USA, 2010. [Google Scholar]
- Howard, D.; Larson, R.D.; Hagarty, J.F.; Keck, R.D. Airport Master Plan Update—Prosser Airport; JUB engineers, Inc.: Washington, DC, USA, 2019. [Google Scholar]
- Sumathi, N.; Balakrishnan, A.; Venugopal, A. A Study on the Master Planning in Airports. Int. J. Latest Technol. Eng. Manag. Appl. Sci. (IJLTEMAS) 2018, 7. Available online: https://www.ijltemas.in/DigitalLibrary/Vol.7Issue4/157-162.pdf (accessed on 1 November 2022).
- ICAO. Aerodrome Design Manual (Doc 9157) Part 2 Taxiways, Aprons and Holding Bays; International Civil Aviation Organization: Montreal, QC, Canada, 2005. [Google Scholar]
- de Neufville, R.; Odoni, A.R. Airport Systems Planning, Design, and Management, 2nd ed.; McGraw Hill Education: New York, NY, USA, 2013. [Google Scholar]
- Horonjeff, R.; McKelvey, F.; Sproule, W.; Young, S. Planning and Design of Airports; McGraw-Hill Companies, Inc.: New York, NY, USA, 2010. [Google Scholar]
- Janic, M. Air Transport System Analysis and Modelling; CRC Press: Boca Raton, FL, USA, 2000; pp. 9–49. [Google Scholar]
- Wright, P.H.; Ashford, N. Airport Engineering; John Wiley & Sons (S.W.): New York, NY, USA, 1992; pp. 185–229. [Google Scholar]
- Cecen, R.K.; Cetek, C.; Kaya, O. Aircraft sequencing and scheduling in TMAs under wind direction uncertainties. Aeronaut. J. 2020, 124, 1896–1912. [Google Scholar] [CrossRef]
- Dönmez, K.; Çetek, C.; Kaya, O. Aircraft Sequencing and Scheduling in Parallel-Point Merge Systems for Multiple Parallel Runways. Transp. Res. Rec. J. Transp. Res. Board 2022, 2676, 108–124. [Google Scholar] [CrossRef]
- Cecen, R.K. Fuel-Optimal Aircraft Arrival Operations in Extended Terminal Maneuvering Areas. Transp. Res. Rec. 2022, 2676, 330–339. [Google Scholar] [CrossRef]
- Toratani, D.; Delahaye, D.; Ueno, S.; Higuchi, T. Merging Optimization Method with Multiple Entry Points for Extended Terminal Maneuvering Area. In Proceedings of the EIWAC 2015, 4th ENRI International Workshop on ATM/CNS, Tokyo, Japan, 17–19 November 2015; pp. 1–5. [Google Scholar]
- Korn, B.; Helmke, H.; Kuenz, A. 4D trajectory management in the extended TMA: Coupling AMAN and 4D FMS for optimized approach trajectories. In Proceedings of the ICAS-Secretariat—25th International Congress of Aeronautical Sciences, Hamburg, Germany, 3–8 September 2006; Volume 7, pp. 4103–4112. [Google Scholar]
- Chen, D.; Hu, M.; Zhang, H.; Yin, J.; Han, K. A network based dynamic air traffic flow model for en route airspace system traffic flow optimization. Transp. Res. Part E Logist. Transp. Rev. 2017, 106, 1–19. [Google Scholar] [CrossRef]
- Cecen, R.K. Multi-objective optimization model for airport gate assignment problem. Aircr. Eng. Aerosp. Technol. 2021, 93, 311–318. [Google Scholar] [CrossRef]
- Gotteland, J.-B.; Durand, N.; Page, E.; Alliot, J. Aircraft Ground Traffic Optimization. In Proceedings of the 4th USA/Europe Air Traffic Management Research and Development Seminar, Santa Fe, NM, USA, December 2001; Available online: https://www.researchgate.net/publication/2413911_Aircraft_Ground_Traffic_Optimization (accessed on 1 November 2022).
- Law, A.M.; Kelton, W.D. Simulation Modeling and Analysis, 3rd ed.; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar] [CrossRef]
- Odoni, A.R.; Bowman, J.; Delahaye, D.; Deyst, J.; Feron, E.; Hansman, R.; Khan, K.; Kuchar, J.; Pujet, N.; Simpson, R. Existing and Required Modeling Capabilities for Evaluating ATM Systems and Concepts; NASA: Washington, DC, USA, 1997. [Google Scholar]
- SIMMOD PRO. 2022. Available online: https://atac.com/simmod-pro/ (accessed on 1 November 2022).
- CAST. 2022. Available online: https://arc.de/cast-simulation-software/ (accessed on 1 November 2022).
- TAAM (Jeppesen Total Airspace and Airport Modeler). 2022. Available online: https://ww2.jeppesen.com/airspace-solutions/total-airspace-and-airport-modeler/ (accessed on 1 November 2022).
- RAMS Plus. 2022. Available online: https://www.ramsplus.com/ (accessed on 1 November 2022).
- AirTOP. 2022. Available online: https://www.airtop-software.com/ (accessed on 1 November 2022).
- Mumayiz, S.A. Overview of airport terminal simulation models. Transp. Res. Rec. 1990. Available online: https://www.researchgate.net/publication/245360399_An_Overview_of_Airport_Terminal_Simulation_Models (accessed on 1 October 2022).
- Zografos, K.G.; Madas, M.A. Development and demonstration of an integrated decision support system for airport performance analysis. Transp. Res. Part C Emerg. Technol. 2006, 14, 1–17. [Google Scholar] [CrossRef]
- Safrillah; Putra, J.C.P. Review Study on Runway Capacity Parameters and Improvement. Mater. Sci. Eng. 2017, 209, 012108. [Google Scholar] [CrossRef]
- Bazargan, M.; Fleming, K.; Subramanian, P. A simulation study to investigate runway capacity using TAAM. In Proceedings of the the Winter Simulation Conference, San Diego, CA, USA, 8–11 December 2002. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, X.; Xu, X. Simulation study on airfield system capacity analysis using SIMMOD. In Proceedings of the 2008 International Symposium on Computational Intelligence and Design, Wuhan, China, 17–18 October 2008; Volume 1, pp. 87–90. [Google Scholar] [CrossRef]
- Bubalo, B.; Daduna, J.R. Airport capacity and demand calculations by simulation—The case of Berlin-Brandenburg International Airport. NETNOMICS Econ. Res. Electron. Netw. 2011, 12, 161–181. [Google Scholar] [CrossRef]
- Yang, P.; Gao, W.; Sun, J.-Q. Capacity Analysis for Parallel Runway through Agent-Based Simulation. Math. Probl. Eng. 2013, 2013, 1–8. [Google Scholar] [CrossRef]
- Cetek, C.; Cinar, E.; Aybek, F.; Cavcar, A. Capacity and delay analysis for airport manoeuvring areas using simulation. Aircr. Eng. Aerosp. Technol. 2014, 86, 43–55. [Google Scholar] [CrossRef]
- Cetek, F.A.; Cetek, C. Simulation modelling of runway capacity for flight training airports. Aeronaut. J. 2014, 118, 143–154. [Google Scholar] [CrossRef]
- de Leege, A.; Janssen, C. Probabilistic Runway and Capacity Forecasting using Machine Learning to Support Decision Making. In Proceedings of the 6th SESAR Innovation Days, Delft, The Netherlands, 8–10 November 2016. [Google Scholar]
- Tee, Y.Y.; Zhong, Z.W. Modelling and simulation studies of the runway capacity of Changi Airport. Aeronaut. J. 2018, 122, 1022–1037. [Google Scholar] [CrossRef]
- Mirmohammadsadeghi, N.; Hu, J.; Trani, A. Enhancements to the Runway Capacity Simulation Model Using the ASDE-X Data for Estimating Airports Throughput Under Various Wake Separation Systems. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17 June 2019; pp. 1–16. [Google Scholar] [CrossRef]
- Mirmohammadsadeghi, N.; Trani, A. Enhancements to the Runway Exit Design Interactive Model Using a Hybrid Simulation Approach for Estimating Runway Occupancy Times at Airports. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; pp. 1–10. [Google Scholar] [CrossRef]
- Nuic, A. User Manual for the Base of Aircraft Data (Bada) Revision 3.7. 2009. Available online: https://www.eurocontrol.int/sites/default/files/library/003_BADA_3_7_User_manual.pdf (accessed on 1 November 2022).
- FAA. Simmod Manual: How SIMMOD Works. 2022. Available online: http://www.tc.faa.gov/acb300/more_simmod.asp (accessed on 4 December 2022).
- ICAO. Procedures for Air Navigations Services Air Traffic Management (Doc. 4444); ICAO: Montreal, QC, Canada, 2017. [Google Scholar]
- AIP Turkey. Aeronoutical Information Publication. 2022. Available online: https://www.dhmi.gov.tr/Sayfalar/aipturkey.aspx (accessed on 1 March 2022).
- GDSAA. Statistics. 2022. Available online: https://www.dhmi.gov.tr/Sayfalar/Istatistikler.aspx (accessed on 1 November 2022).
- Winters, P.R. Forecasting Sales by Exponentially Weighted Moving Averages. Manag. Sci. 1960, 6, 324–342. [Google Scholar] [CrossRef]
- Kalekar, P. Time series forecasting using Holt-Winters exponential smoothing. Kanwal Rekhi Sch. Inf. Technol. 2004, 1–13. Available online: http://www.it.iitb.ac.in/~praj/acads/seminar/04329008_ExponentialSmoothing.pdf (accessed on 1 November 2022).
- Lesmana, E.; Subartini, B.; Jabar, D.A. Analysis of forecasting and inventory control of raw material supplies in PT INDAC INT’L. IOP Conf. Ser. Mater. Sci. Eng. 2018, 332, 012015. [Google Scholar] [CrossRef]
- Petropoulos, F.; Wang, X.; Disney, S.M. The inventory performance of forecasting methods: Evidence from the M3 competition data. Int. J. Forecast. 2019, 35, 251–265. [Google Scholar] [CrossRef]
- Dingari, M.; Reddy, D.M.; Sumalatha, V. Air Traffic Forecasting using Time Series Models. Int. J. Recent Technol. Eng. 2019, 8, 1061–1065. [Google Scholar] [CrossRef]
- ICAO. Manual on Air Traffic Forecasting; ICAO: Montreal, QC, Canada, 2006; p. 98, DOC 8991 AT172213. [Google Scholar]
- Dönmez, K. A stochastic sequence planning model for the runways with multiple exits. J. Intell. Transp. Syst. Appl. 2022, 5, 89–101. [Google Scholar] [CrossRef]
- Google Earth Pro. Turkey Borders. Microsoft Windows. 2022. Available online: https://www.google.com.tr/intl/tr/earth/. (accessed on 1 November 2022).
- Flightradar. Flight Radar 24. 2022. Available online: https://www.flightradar24.com/ (accessed on 3 November 2022).
- Dönmez, K. Aircraft Sequencing under the Uncertainty of the Runway Occupancy Times of Arrivals during the Backtrack Procedure. Aeronaut. J. 2022. [Google Scholar] [CrossRef]
- Aybek, F.; Antulov-Fantulin, B.; Frost, P.; Dönmez, K.; Kaplan, Z.; Rogosic, T. Project Atcosima: Preliminary Results and Analysis of Simulations, Real-Time Atc and Flight Cockpit Simulations. In Proceedings of the International Scientific Conference “Science and Traffic Development” (ZIRP 2019 ) Topic: Next Generation Transport Industry Innovations, Opatija, Croatia, 10–11 May 2019; pp. 11–22. [Google Scholar]
- Jet Fuel Prices. 2022. Available online: https://jet-a1-fuel.com/ (accessed on 12 March 2022).
- Gibson, G.; Milnes, R.; Morris, M.; Hill, N.; Simbolotti, G.; Tosato, G. Aviation Infrastructure. IEA ETSAP-Technol. Br. 2011, 1–6. Available online: www.etsap.org (accessed on 5 November 2022).
- di Mascio, P.; Rappoli, G.; Moretti, L. Analytical Method for Calculating Sustainable Airport Capacity. Sustainability 2020, 12, 9239. [Google Scholar] [CrossRef]
- Rosenthal, R.E. A GAMS Tutorial; GAMS Development Corporation: Washington, DC, USA, 2007. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).