On the Aeroelasticity of the Active Span and Passive Pitching Polymorphing Wing: Effect of Morphing Rate
Abstract
1. Introduction
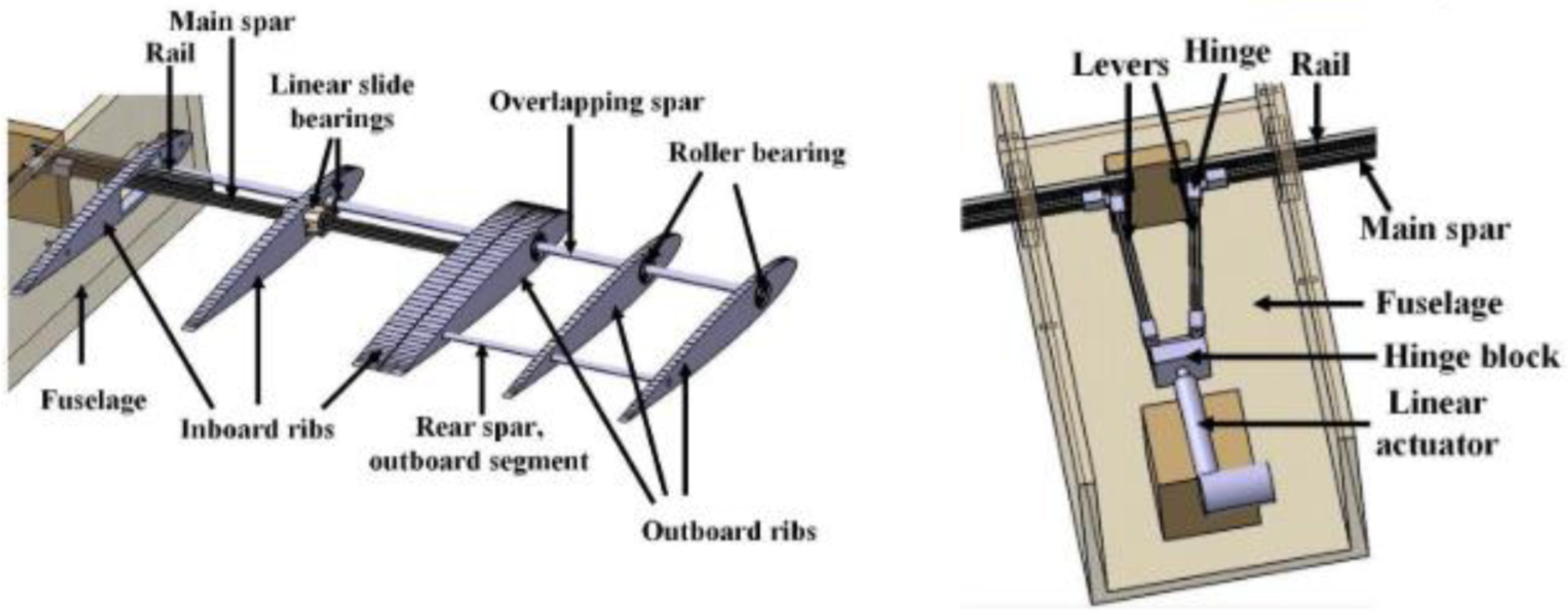
Active Span Extension and Passive Pitching (ASAPP) Wing
2. Modeling and Validation
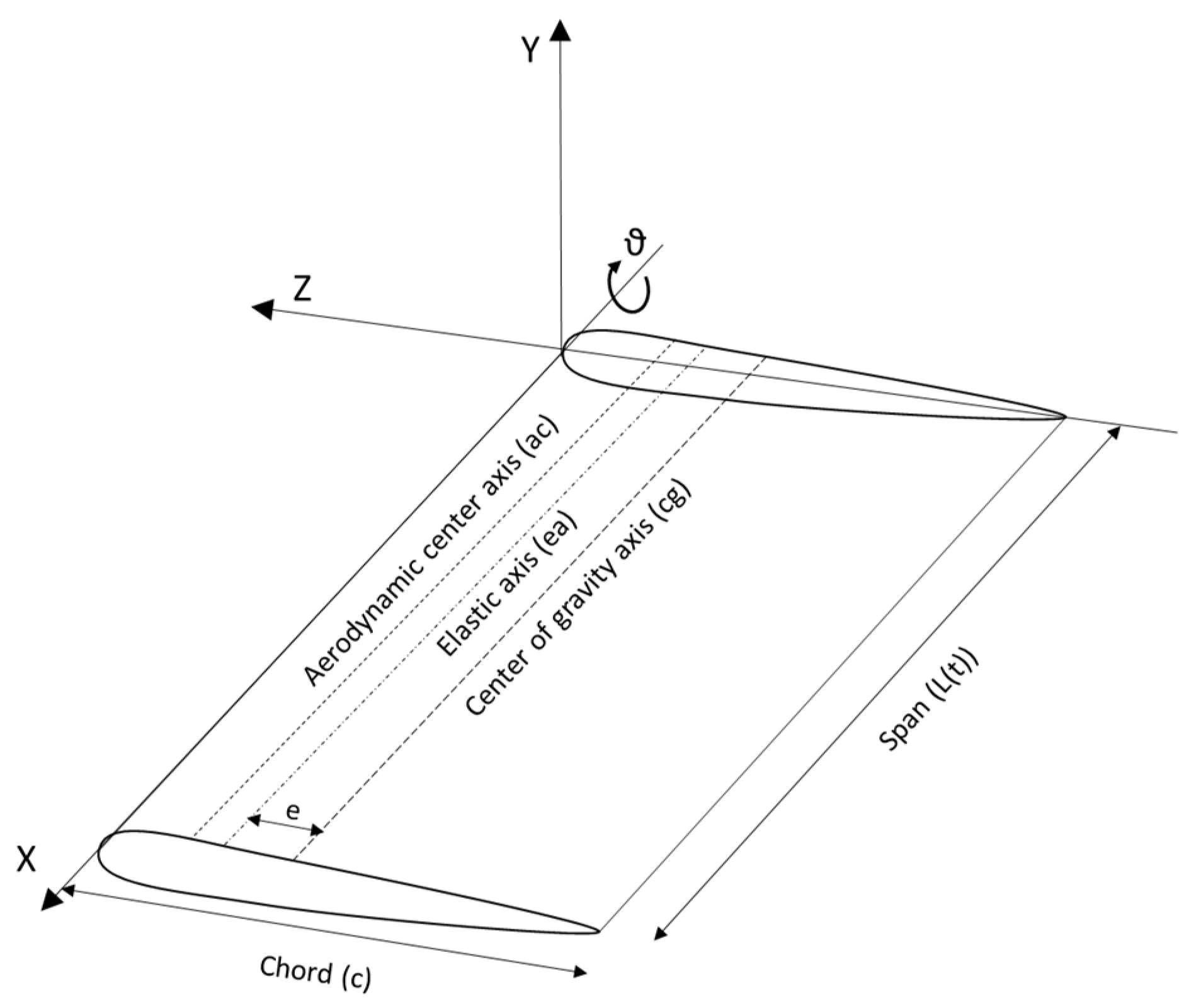
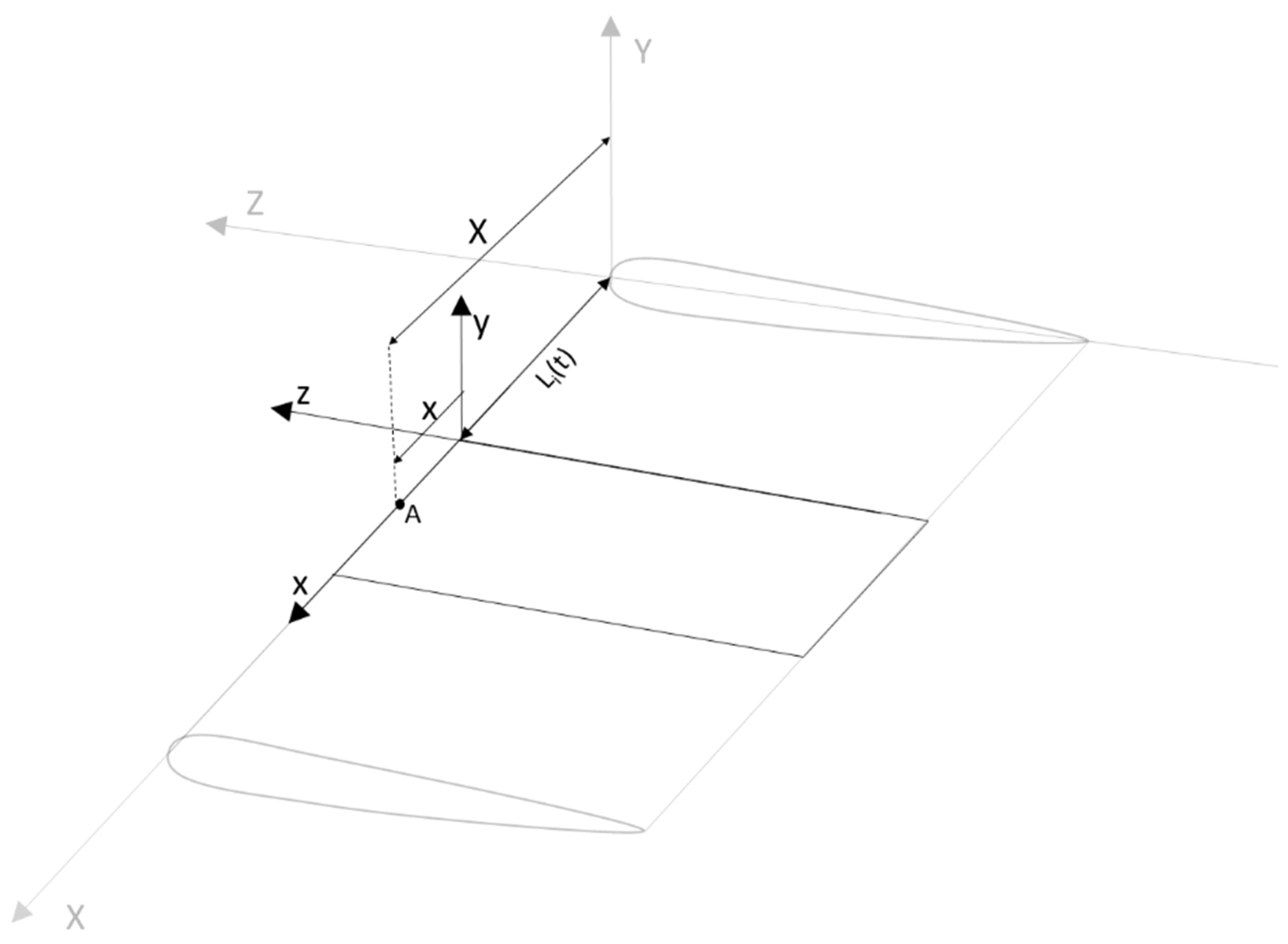
2.1. Structural Dynamics Model
2.2. Aerodynamic Model
2.3. Aeroelastic Model
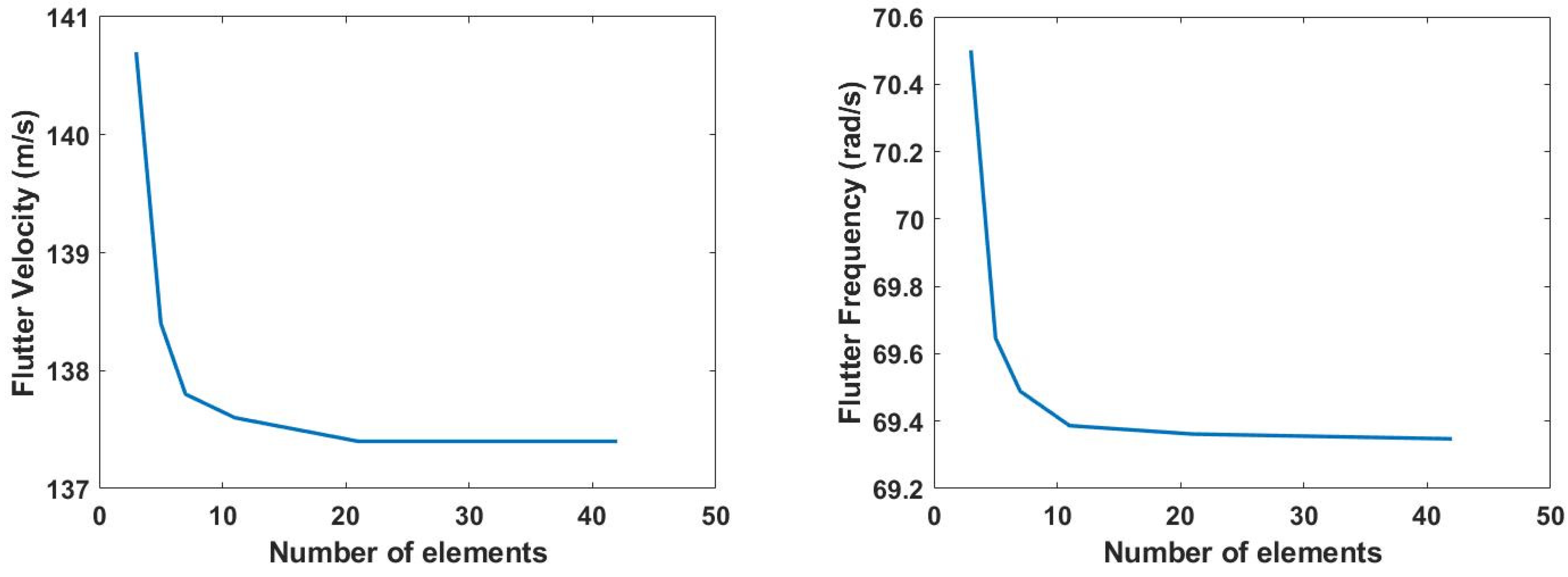
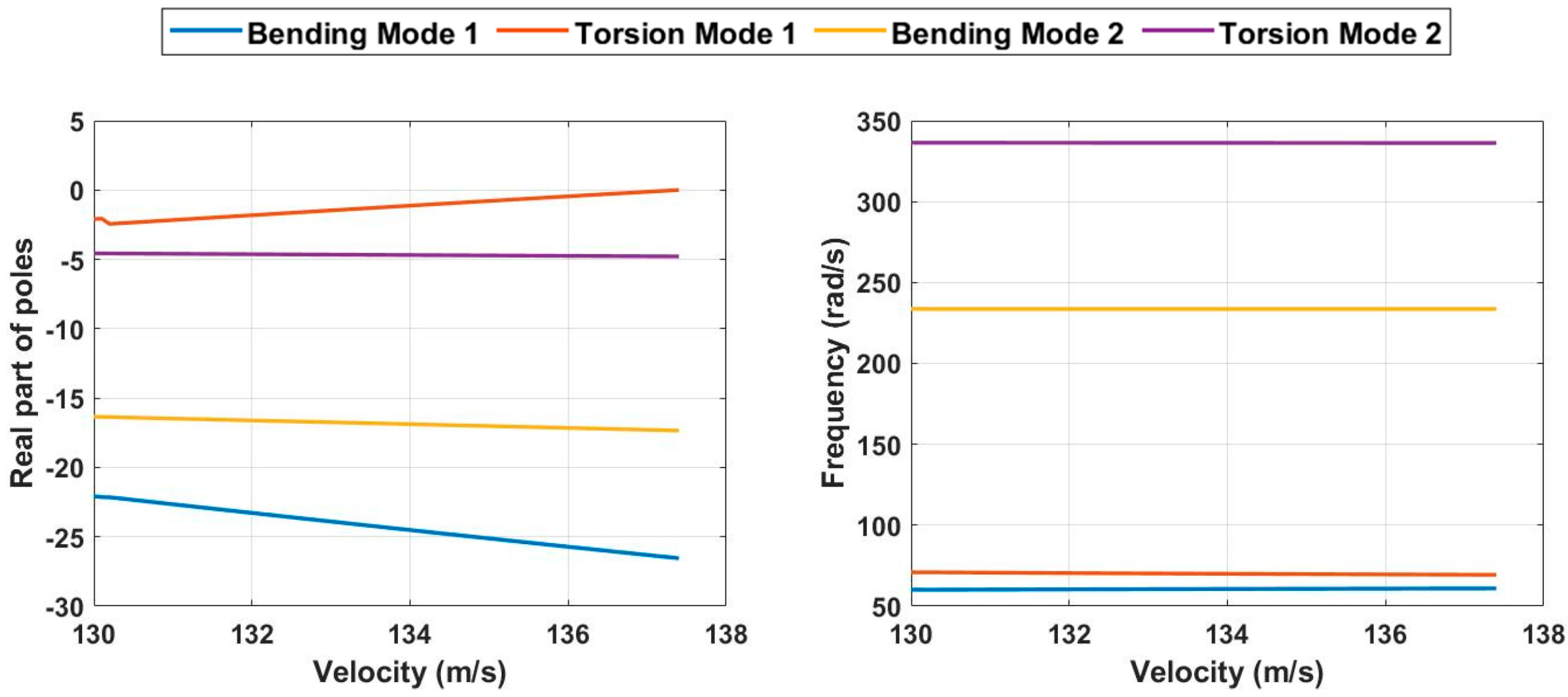
2.4. Model Validation
3. Parametric Analysis
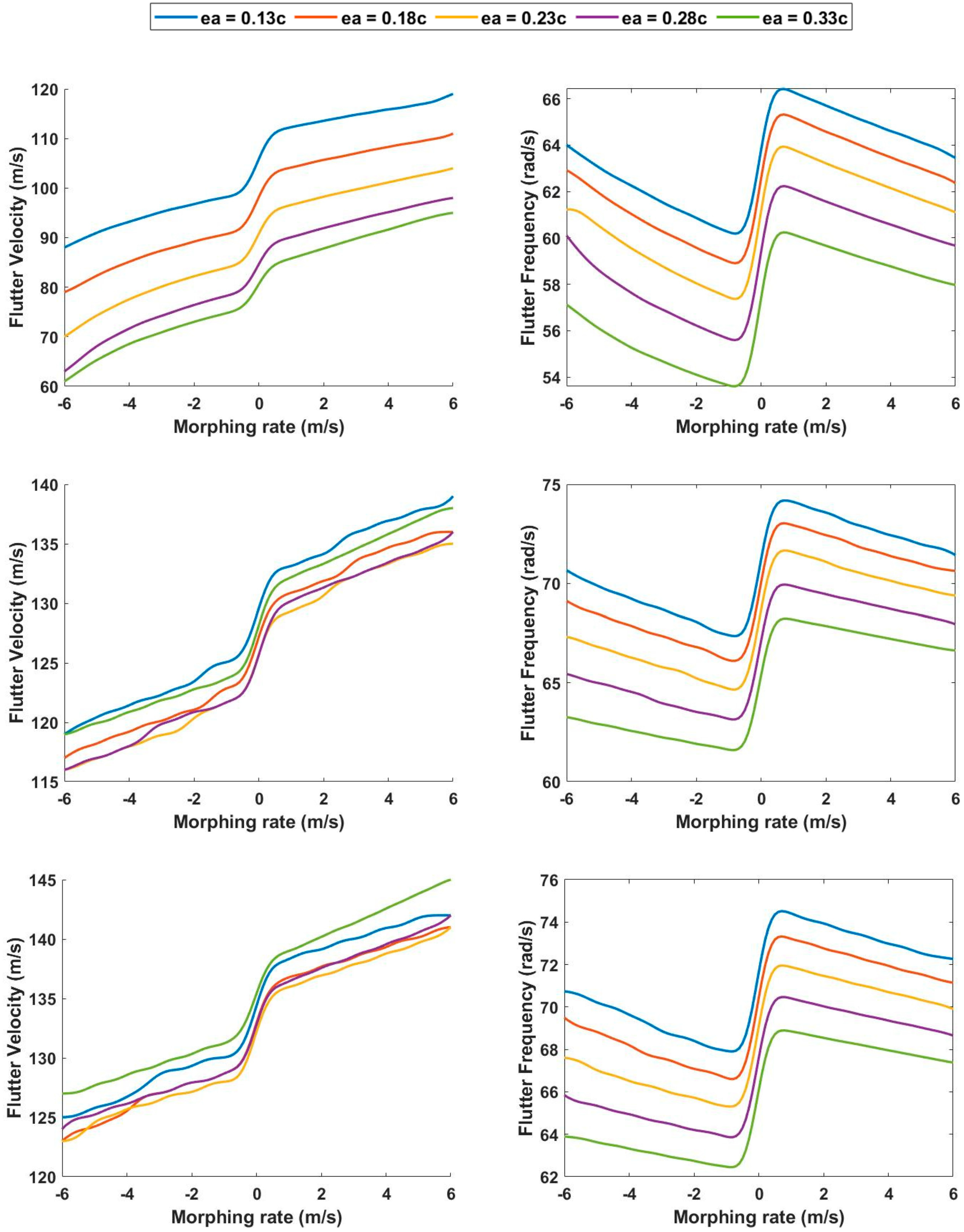
3.1. Morphing Rate Effect on Flutter Behavior at a Half-Span of 6.11 m
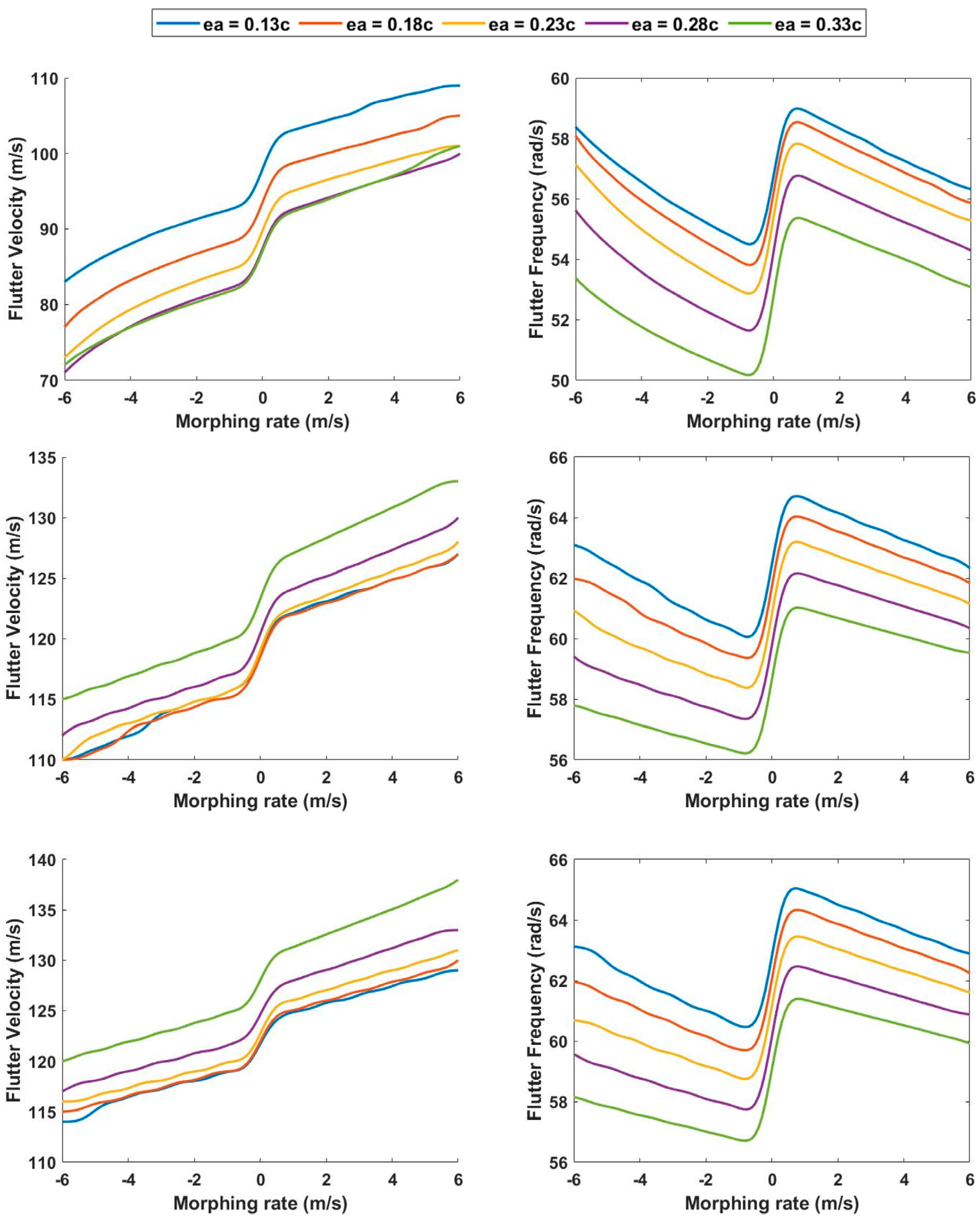
3.2. Morphing Rate Effect on Flutter Behavior at a Half-Span of 6.86 m
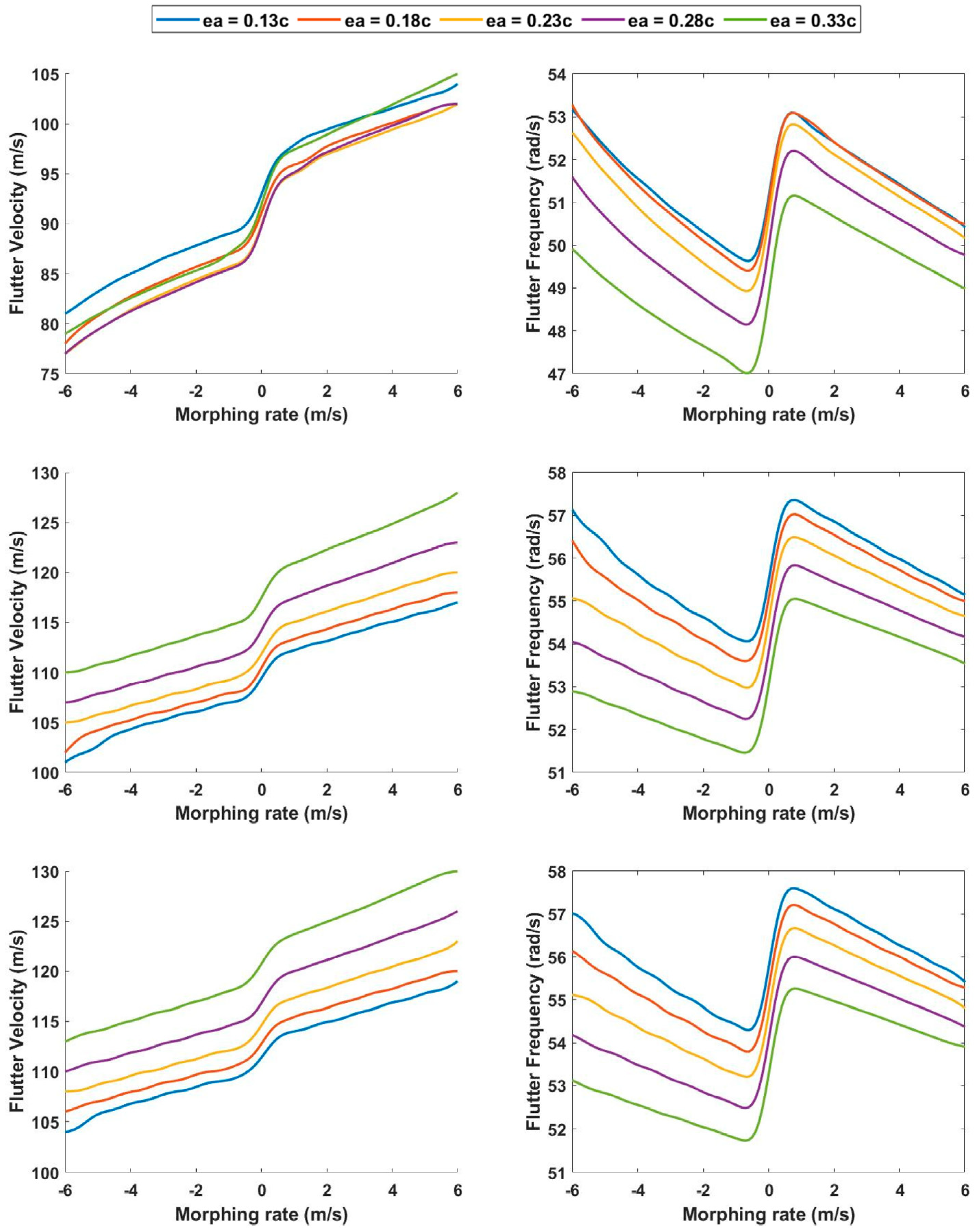
3.3. Morphing Rate Effect on Flutter Behavior at a Half-Span of 7.61 m
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Aerodynamic damping matrix | |
| Aerodynamic damping matrix | |
| Aerodynamic stiffness matrix | |
| Structural damping matrix | |
| Aerodynamic stiffness matrix | |
| Structural stiffness matrix | |
| Rate of change in beam length | |
| Structural inertia matrix | |
| Mass per unit length | |
| C | Damping Matrix |
| C(k) | Theodorsen’s transfer function |
| cg | Center of gravity |
| E | Distance between cg and ea |
| ea | Elastic axis location |
| EI | Bending Rigidity |
| GJ | Torsional Rigidity |
| K | Stiffness Matrix |
| L(t) | Instantaneous length of beam |
| LB | Total length of beam |
| M | Mass Matrix |
| Nb | Hermite’s cubic shape functions |
| Ne | Combined bending-torsion shape functions |
| Nt | Torsional shape functions |
| q | Generalized coordinate |
| rα | Radius of gyration |
| t | Time |
| T | Kinetic Energy |
| U | Potential Energy |
| x | Spanwise position in ECS |
| X | Spanwise position in GCS |
| y | Bending deflection in ECS |
| Y | Bending deflection in GCS |
| Ȳ | Combined bending-torsion displacement vector |
| Bending slope in EXS | |
| Bending slope in GCS | |
| ρ | Density |
| 𝓛 | Lagrangian |
References
- Ajaj, R.M.; Parancheerivilakkathil, M.S.; Amoozgar, M.; Friswell, M.I.; Cantwell, W.J. Recent developments in the aeroelasticity of morphing aircraft. Prog. Aerosp. Sci. 2021, 120, 100682. [Google Scholar] [CrossRef]
- Abdulrahim, M.; Lind, R. Using Avian Morphology to Enhance Aircraft Maneuverability. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006; pp. 1328–1344. [Google Scholar] [CrossRef]
- Weisshaar, T. Morphing aircraft technology-new shapes for aircraft design. Multifunct. Struct. Integr. Sens. Antennas 2006, O1-1–O1-20. Available online: http://oai.dtic.mil/oai/oai?verb=getRecord&metadataPrefix=html&identifier=ADA479821 (accessed on 12 November 2022).
- Schmitt, D. On the Way to ACARE 2020 and Beyond. In Variational Analysis and Aerospace Engineering: Mathematical Challenges for Aerospace Design; Springer: Boston, MA, USA, 2012; pp. 379–394. [Google Scholar]
- Directorate-General for Mobility and Transport and Directorate-General for Research and Innovation. In Flightpath 2050—Publications Office of the EU; EU Publications: Luxembourg, Luxembourg, 2011; pp. 1–32. Available online: https://op.europa.eu/en/publication-detail/-/publication/296a9bd7-fef9-4ae8-82c4-a21ff48be673 (accessed on 2 October 2022).
- Ajaj, R.; Flores, E.S.; Amoozgar, M.; Cooper, J. A Parametric Study on the Aeroelasticity of Flared Hinge Folding Wingtips. Aerospace 2021, 8, 221. [Google Scholar] [CrossRef]
- Cooper, J.E.; Chekkal, I.; Cheung, R.C.M.; Wales, C.; Allen, N.J.; Lawson, S.; Peace, A.J.; Cook, R.; Standen, P.; Hancock, S.D.; et al. Design of a Morphing Wingtip. J. Aircr. 2015, 52, 1394–1403. [Google Scholar] [CrossRef]
- Guo, S.; Li, D.; Sensburg, O. Optimal design of a passive gust alleviation device for a flying wing aircraft. In Proceedings of the 12th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference and 14th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Indianapolis, IN, USA, 17–19 September 2012; pp. 1–12. [Google Scholar] [CrossRef]
- Parancheerivilakkathil, M.S.; Haider, Z.; Ajaj, R.M.; Amoozgar, M. A Polymorphing Wing Capable of Span Extension and Variable Pitch. Aerospace 2022, 9, 205. [Google Scholar] [CrossRef]
- Ajaj, R.M.; Parancheerivilakkathil, M.S.; Amoozgar, M. ASAPP: A polymorphing wing capable of active span extension and passive pitch. In Proceedings of the AIAA Scitech 2021 Forum, Virtual, 11–15 & 19–21 January 2021; pp. 1–19. [Google Scholar]
- Gamboa, P.V.; Santos, P.D.R.; Silva, J.M.A.; Santos, P.M.B. Flutter Analysis of a Composite Variable-span Wing. In Proceedings of the 4th International Conference on Integrity, Reliability and Failure, Funchal, Portugal, 23–27 June 2013; Volume 1, pp. 1–14. [Google Scholar]
- Kidane, B.; Troiani, E. Static Aeroelastic Beam Model Development for Folding Winglet Design. Aerospace 2020, 7, 106. [Google Scholar] [CrossRef]
- Ajaj, R.M.; I Friswell, M. Aeroelasticity of compliant span morphing wings. Smart Mater. Struct. 2018, 27, 105052. [Google Scholar] [CrossRef]
- Andersen, G.; Cowan, D.; Piatak, D. Aeroelastic Modeling, Analysis and Testing of a Morphing Wing Structure. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Honolulu, HI, USA, 23–26 April 2007; Volume 1. [Google Scholar] [CrossRef]
- Zhang, J.; Shaw, A.D.; Wang, C.; Gu, H.; Amoozgar, M.; Friswell, M.I.; Woods, B.K. Aeroelastic model and analysis of an active camber morphing wing. Aerosp. Sci. Technol. 2021, 111, 106534. [Google Scholar] [CrossRef]
- Haider, Z.; Ajaj, R.M.; Seneviratne, L. On the Aeroelasticity of the Active Span and Passive Pitching Polymorphing Wing: A Parametric Study. Aerospace 2022, 9, 483. [Google Scholar] [CrossRef]
- Huang, R.; Qiu, Z. Transient aeroelastic responses and flutter analysis of a variable-span wing during the morphing process. Chin. J. Aeronaut. 2013, 26, 1430–1438. [Google Scholar] [CrossRef]
- Stylianou, M.C. Dynamics of a Flexible Extendible Beam. Ph.D.Thesis, University Microfilms Int./UMI, Ann Arbor, MI, USA, 1993. [Google Scholar]
- Stylianou, M.; Tabarrok, B. Finite Element Analysis Of An Axially Moving Beam, Part I: Time Integration. J. Sound Vib. 1994, 178, 433–453. [Google Scholar] [CrossRef]
- Patil, M.J.; Hodges, D.H.; Cesnik, C.E.S. Nonlinear Aeroelastic Analysis of Complete Aircraft in Subsonic Flow. J. Aircr. 2000, 37, 753–760. [Google Scholar] [CrossRef]
- Raghavan, B.; Patil, M.J. Flight Dynamics of High Aspect-Ratio Flying Wings: Effect of Large Trim Deformation. J. Aircr. 2009, 46, 1808–1812. [Google Scholar] [CrossRef][Green Version]


| Specifications | Goland Wing |
|---|---|
| Half span (m) | 6.096 |
| Chord (m) | 1.8288 |
| Mass per unit length (m’) (kg/m) | 35.71 |
| Air density (ρ) (kg/m3) | 1.225 |
| Moment of inertia per unit length (kgm) around ea | 8.64 |
| Center of gravity (from leading edge) | 43% of chord |
| Elastic axis location (from leading edge) | 33% of chord |
| Flexural rigidity (EI) (Nm2) | 9.77 × 106 |
| Torsional rigidity (GJ) (Nm2) | 9.87 × 105 |
| Method | ||||||
|---|---|---|---|---|---|---|
| Present Work | Ref. [11] | Ref. [6] | Ref. [14] | Ref. [20] | Ref. [21] | |
| Flutter Velocity (m/s) | 137.4 | 137.4 | 136.99 | 137.11 | 135.60 | 136.22 |
| Flutter Frequency (rad/s) | 69.361 | 69.351 | 69.97 | 69.90 | 70.20 | 70.06 |
| Divergence Speed (m/s) | 252.54 | 252.31 | 252.47 | 252.80 | - | 250.82 |
| ASAPP Wing | Inboard Length (m) | Outboard Length (m) | Total Length (m) |
|---|---|---|---|
| Without span extension | 4.267 | 1.8288 | 6.456 |
| 25% span extension | 4.633 | 1.8288 | 6.462 |
| Span at 1% of total morphing time | 4.282 | 1.8288 | 6.111 |
| Span at 50% of total morphing time | 5.029 | 1.8288 | 6.858 |
| Span at 99% of total morphing time | 5.776 | 1.8288 | 7.604 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haider, Z.; Ajaj, R.M.; Seneviratne, L. On the Aeroelasticity of the Active Span and Passive Pitching Polymorphing Wing: Effect of Morphing Rate. Aerospace 2023, 10, 57. https://doi.org/10.3390/aerospace10010057
Haider Z, Ajaj RM, Seneviratne L. On the Aeroelasticity of the Active Span and Passive Pitching Polymorphing Wing: Effect of Morphing Rate. Aerospace. 2023; 10(1):57. https://doi.org/10.3390/aerospace10010057
Chicago/Turabian StyleHaider, Zawar, Rafic M. Ajaj, and Lakmal Seneviratne. 2023. "On the Aeroelasticity of the Active Span and Passive Pitching Polymorphing Wing: Effect of Morphing Rate" Aerospace 10, no. 1: 57. https://doi.org/10.3390/aerospace10010057
APA StyleHaider, Z., Ajaj, R. M., & Seneviratne, L. (2023). On the Aeroelasticity of the Active Span and Passive Pitching Polymorphing Wing: Effect of Morphing Rate. Aerospace, 10(1), 57. https://doi.org/10.3390/aerospace10010057










