Aerodynamic Damping of the Tubed Vortex Reducer in an Axial Compressor Disk Cavity

Abstract

The tubed vortex reducer in the axial compressor can destroy the vortex in the disk cavity, by a thin-walled tube, to reduce the total pressure loss. The tube may suffer from vibration problems, such as flutter and forced vibration, which are closely related to aerodynamic damping. In this paper, the energy method and the influence coefficient method are used to study the aerodynamic damping of the tube. Based on the modal characteristics, steady and unsteady flow characteristics of the tube, the first and second modes with lower frequencies and greater vibration risk are selected as the analysis objects. The energy method is used to calculate the aerodynamic damping of the tube with different amplitudes, which shows that the results approximately meet the linear assumption and are accurate. The results obtained by the influence coefficient method show that the aerodynamic influence between adjacent tubes is very small, and the effect of inter-tube phase angle on the aerodynamic damping can be ignored. Finally, it is found that the effect of structural coupling caused by the support ring on the aerodynamic damping of the tube is mainly reflected in two aspects: frequency reduction and tube mode coupling.

1. Introduction

In the aircraft gas turbine engine, the gas in the main flow of the compressor is extracted to cool the turbine blade and other high-temperature components. The flow in the co-rotating disk cavity of the compressor is very complex. Hide [1] first analyzed the laminar flow in the radial inflow, isothermal, and co-rotating disk cavity, and proposed the source-sink flow model, which consists of the source region, Ekman-type layer, sink region, and core region. Owen and Firouzian further developed the source-sink flow model [2,3] and then verified the model in the co-rotating disk cavity by numerical and experimental methods [4,5,6].

The tubed vortex reducer is a commonly used vortex reducer that reduces the total pressure loss caused by the vortex in the disk cavity [7]. The tubed vortex reducer (hereafter referred to as “vortex reducer”) is composed of a group of thin-walled tubes evenly distributed along the circumferential direction in the disk cavity. So far, researchers have studied the flow in the disk cavity with the vortex reducer comprehensively and in depth using theoretical, experimental, and numerical methods [8,9,10,11,12].

However, there are relatively fewer studies on the vibration of the vortex reducer. The tube of the vortex reducer experienced vibration failure in the actual application process, and the engineers restrained the vibration by installing dampers. In theory, the aerodynamic loads that excite the tube vibration may come from three aspects: (1) pressure fluctuation from the main flow, (2) unsteady vortex in the disk cavity, and (3) pressure fluctuation caused by gas column vibration. At present, there are only studies [13,14,15] on the third aspect in open literature. Luo [13] studied the natural vibration characteristics of the vortex reducer and its internal gas column and further analyzed the forced response of the tube caused by gas column vibration. This paper will qualitatively analyze the possibility of the other aspects. Therefore, there is a risk of high cycle fatigue failure of the tube, due to vibration, when the frequency of the above unsteady aerodynamic load is close to the modal frequency of the tube.

As is known to all, aerodynamic damping is an important part of vibration system damping, which is one of the key factors affecting flow-induced vibration. It determines whether the structure will flutter and directly affects the forced response. However, in the currently published literature, there is no research on the aerodynamic damping of vortex reducers. The aerodynamic damping analysis methods used in the turbomachinery field mainly include the energy method and the influence coefficient method. The energy method proposed by Carta [16] in 1969 has been widely used to calculate the aerodynamic damping of blades and labyrinths. In addition, the influence coefficient method [17] is also a common method to calculate the aerodynamic damping of blades. Bendikson [18,19], Vahdati [20,21,22], Wang [23,24,25], and many other researchers have conducted a lot of research on the mechanism of blade aerodynamic damping. Sayma [26], Phibel [27], and Wang [28] analyzed the aerodynamic damping of the labyrinth and its parameter sensitivity.

This paper aims to verify the applicability of the energy method and the influence coefficient method to the vortex reducer, and then analyze the aerodynamic damping of the tube of the vortex reducer. First, the modal and flow characteristics of the vortex reducer are analyzed by numerical methods. The unsteady aerodynamic loads on the vortex reducer are analyzed to clarify its potential vibration risk. Then, taking the first and second modes as examples, the aerodynamic damping of the tube with different amplitudes is calculated by the energy method. The influence coefficient method is used to analyze the interaction between adjacent tubes and to further obtain the aerodynamic damping of the tube with different inter-tube phase angles. Finally, the effect of the structural coupling caused by the support ring on the aerodynamic damping of the tube is discussed from frequency reduction and tube mode coupling.

2. Numerical Methods

The energy method and the influence coefficient method have been widely used in blade aerodynamic damping analysis. There are two important premises for applying the two methods to the aerodynamic damping analysis of vortex reducers. One is that the flow in the disk cavity with the vortex reducer is little affected by the tube vibration with a small amplitude. The other is that the unsteady aerodynamic force generated by the tube vibration is proportional to the vibration amplitude within the given amplitude range, and the effect of flow nonlinearity can be ignored.

2.1. Energy Method

When the tube vibrates with a certain modal frequency and corresponding modal shape, the unsteady aerodynamic force, $\mathit{F}$, acting on the vortex reducer, can be expressed as:

$$\mathit{F}={\mathit{F}}_0\sin \left(\omega t+\phi \right)$$

(1)

where ${\mathit{F}}_0$ is the unsteady aerodynamic force amplitude vector, $\omega$ is the modal frequency, and $\phi$ is the phase difference between the unsteady aerodynamic force and the vibration. The work done by the unsteady aerodynamic force on the tube in one vibration period is:

$$W={\displaystyle \oint \mathit{F}\cdot \mathrm{d}\mathit{x}=}{\displaystyle \oint \left({\mathit{F}}_{\mathit{x}}\mathrm{d}\mathit{x}+{\mathit{F}}_{\mathit{y}}\mathrm{d}\mathit{y}+{\mathit{F}}_{\mathit{z}}\mathrm{d}\mathit{z}\right)}$$

(2)

where ${\mathit{F}}_{\mathit{x}}$, ${\mathit{F}}_{\mathit{y}}$, ${\mathit{F}}_{\mathit{z}}$, and $\mathrm{d}\mathit{x}$, $\mathrm{d}\mathit{y}$, $\mathrm{d}\mathit{z}$ are the force components and displacement components in $\mathrm{x}$, $\mathrm{y}$, $\mathrm{z}$ directions. Suppose the number of surface nodes is $n_{\mathrm{d}}$ and the number of time steps in one vibration period is $n_{\mathrm{t}}$, then the aerodynamic work can be calculated by:

$$W={\displaystyle \sum _1^{n_{\mathrm{d}}}{\displaystyle \sum _1^{n_{\mathrm{t}}}{W}_i^j}}$$

(3)

where the expression of $W_i^j$ is written as:

$$\begin{array}{ll}{W}_i^j& =\frac{1}{2}\left(F_{\mathrm{x},i}^j+F_{\mathrm{x},i}^{j-1}\right)\left(D_{\mathrm{x},i}^j-D_{\mathrm{x},i}^{j-1}\right)+\frac{1}{2}\left(F_{\mathrm{y},i}^j+F_{\mathrm{y},i}^{j-1}\right)\left(D_{\mathrm{x},i}^j-D_{\mathrm{x},i}^{j-1}\right)\\ & +\frac{1}{2}\left(F_{\mathrm{z},i}^j+F_{\mathrm{z},i}^{j-1}\right)\left(D_{\mathrm{z},i}^j-D_{\mathrm{z},i}^{j-1}\right)\end{array}$$

(4)

The work done by the unsteady aerodynamic force is equal to the energy consumed by the aerodynamic damping in one vibration period. Based on the definition of the vibration system damping ratio, Moffatt and He [29] converted the aerodynamic work into the equivalent aerodynamic modal damping ratio, which can be written as:

$${\zeta }_{\mathrm{a}}=\frac{-W}{2\pi {\omega }^2{q}_{\mathrm{cfd}}{}^2}$$

(5)

where $q_{\mathrm{cfd}}$ is the actual maximum amplitude of the regularized modal shape. $\mathit{F}$ and $\mathrm{d}\mathit{x}$ in Equation (2) are both directly proportional to the vibration amplitude, which means the aerodynamic work is theoretically proportional to the quadratic power of the vibration amplitude. Therefore, the ${\zeta }_{\mathrm{a}}$ is theoretically independent of the vibration amplitude. The following numerical results will verify this theoretical speculation.

2.2. Influence Coefficient Method

The influence coefficient method assumes that the unsteady aerodynamic forces on the tube surface, caused by the tube vibration, can be expressed as the linear superposition of the contribution of each tube. If the phase of the tube vibration is 0, the displacement of the vibrating tube can be expressed as:

$$q=q_0{\mathrm{e}}^{\mathrm{i}\omega t}$$

(6)

where $q_0$ is the vibration amplitude and $\omega$ is the vibration frequency. The real and imaginary parts of the modal aerodynamic force influence coefficient on the $n\mathrm{th}$ tube surface can be written as:

$$a_n^{\mathrm{re}}={\displaystyle \sum _m{\varphi }_t{}^m\frac{F_{\mathrm{a},0}^{m,n}\cos \left({\beta }^{m,n}\right)}{q_0}}$$

(7)

$$a_n^{\mathrm{im}}={\displaystyle \sum _m{\varphi }_t{}^m\frac{F_{\mathrm{a},0}^{m,n}\sin \left({\beta }^{m,n}\right)}{q_0}}$$

(8)

where ${\varphi }_{\mathrm{t}}{}^m$ is the complex modal displacement of the $m\mathrm{th}$ node on the tube surface for a certain mode of the tube, $F_{\mathrm{a},0}^{m,n}$ is the unsteady aerodynamic force amplitude of the $m\mathrm{th}$ node on the $n\mathrm{th}$ tube surface, and ${\beta }^{m,n}$ is the phase difference between unsteady aerodynamic force and tube vibration. For the aeroelastic problem, the modal excitation force is zero. If the unsteady aerodynamic forces caused by tube vibration satisfy the linear superposition hypothesis, the modal aeroelastic force can be written as:

$${\widehat{\mathit{F}}}_{\mathrm{a}}={\mathit{\varphi }}_{\mathrm{t}}{}^{\mathrm{T}}{\mathit{F}}_{\mathrm{a}}=\mathit{A}\mathit{q}$$

(9)

where $\mathit{A}$ is the aerodynamic influence coefficient matrix. Take Equation (9) into the motion equation in the modal coordinate system:

$$\left(\mathit{\Lambda }-{\mathit{\omega }}^2\mathit{I}\right)\mathit{q}={\widehat{\mathit{F}}}_{\mathrm{a}}+{\widehat{\mathit{F}}}_{\mathrm{e}}$$

(10)

to get:

$$\left(\mathit{\Lambda }-\mathit{A}\right)\mathit{q}={\mathit{\omega }}^2\mathit{q}$$

(11)

The complex eigenvalue ${\lambda }_i$ of the matrix $\left(\mathit{\Lambda }-\mathit{A}\right)$ can be solved by numerical method, and the ${\zeta }_{\mathrm{a}}$ of the $i\mathrm{th}$ mode can be obtained by:

$${\zeta }_{\mathrm{a}}^i=\frac{-\mathrm{Im}\left(\sqrt{{\lambda }_i}\right)}{m_0\mathrm{Re}\left(\sqrt{{\lambda }_i}\right)}$$

(12)

where $m_0$ is the modal mass and its value is 1 when the mass normalized modal shapes are used for modal coordinate transformation.

3. Vortex Reducer

3.1. Model

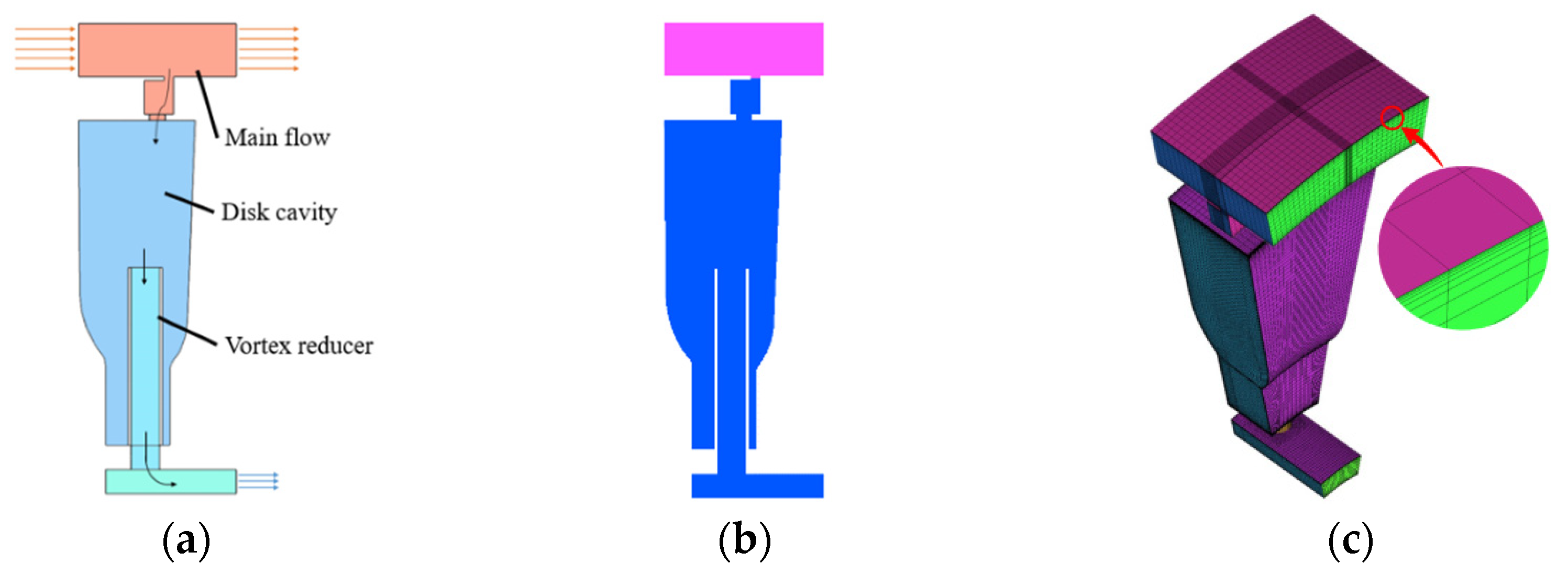
The vortex reducer is in the disk cavity between the 7th and 8th rotors of an axial compressor, and the main geometric parameters of the vortex reducer and disk cavity are described based on the outer diameter of the tube, D, as shown in Figure 1a. The geometric model and grid model of the vortex reducer and the tube are also shown in Figure 1.

The vortex reducer is composed of 18 thin-walled tubes evenly distributed along the circumference of the disk cavity. The tubes are fixed on the support ring by the internal clamping ring. The tube and the support ring are regarded as an integral structure when constructing the full circle grid model of the vortex reducer. The number of elements in the vortex reducer are 380,736, and the number of nodes is 478,494. Different from the geometric model in Figure 1b, the grid model of the tube only includes the part above the support ring, that is, the part with a length of 5.2 D in Figure 1a. The number of elements in the tube is 7050, and the number of nodes is 9600.

3.2. Modal Characteristics

The modal characteristics of the vortex reducer are analyzed by the Finite Element Method (FEM). Assuming that the support ring has strong rigidity, only a single tube is taken as the object of the modal analysis, and the effect of structural coupling caused by the support ring is discussed in Section 4.

Next, the bottom of the tube connected with the support ring is fixed. The tube temperature is between 805 k and 831 k, and the temperature gradient is small, so the tube is given as the uniform temperature, 815 k, in modal analysis. The rotation speed is 12,000 rpm. The material of the vortex reducer is GH4169 and Young’s modulus is 170 GPa, the density is 8200 kg/m³, and the Poisson’s ratio is 0.3 under the above working condition.

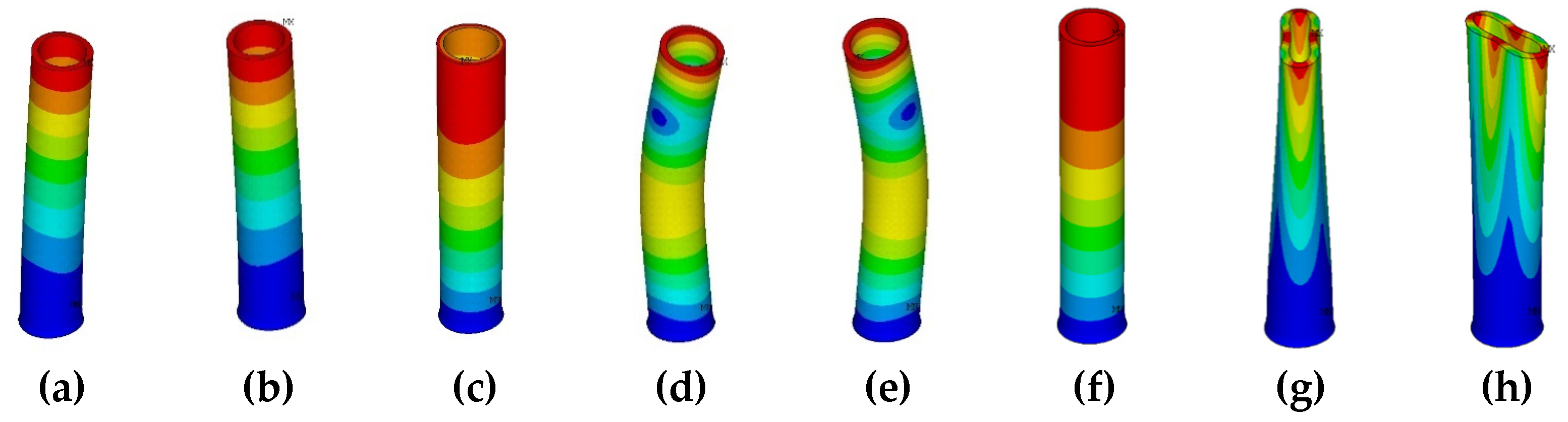
The first eight modal characteristics of the tube are obtained by modal analysis, considering prestress, and shown in

Table 1. Modal frequencies of the first eight modes.

Order	Frequency/Hz	Order	Frequency/Hz
1	1581.2	5	7952.0
2	1594.1	6	11,995.6
3	7300.5	7	16,930.4
4	7893.2	8	16,956.5

, and the modal shapes are shown in Figure 2.

The first, second, fourth, and fifth modes are typical beam modes. The first and second modes are bending modes with one nodal line at the root. The fourth and fifth modes are the bending modes with two nodal lines at the root and the upper part. The first and fourth modes vibrate along the circumferential direction, and the second and fifth modes vibrate along the axial direction. The third and sixth modes are the torsional mode and stretching mode along the axis of the tube, respectively. The seventh and eighth modes are similar to the typical nodal diameter modes of a cylindrical shell. Their modal shapes have two nodal diameters and one nodal line at the root.

3.3. Steady Flow

The three-dimensional Reynolds-averaged Navier-Stokes equations are solved by a CFD solver to obtain the flow characteristics of the vortex reducer in the disk cavity. The finite volume method is used to discretize the equations, and a second-order backward Euler scheme was used for the transient term. The effect of turbulence is simulated by the k-ε two-equation turbulence model with wall function.

Figure 3a shows that the flow field can be divided into three parts: main flow, disk cavity, and vortex reducer. The bleed gap is located at the outlet of the vane where the circumferential velocity of the flow is relatively small. Therefore, taking the bleed gap as the interface, the calculation domain is divided into the station domain (pink) and rotation domain (blue), as shown in Figure 3b. The interface between the station and rotation domains is set to frozen rotor boundary conditions.

Considering that the tubes are evenly distributed along the circumference, the flow characteristics of the whole disk cavity can be simulated by constructing the sector flow field model with only one tube and applying the rotational periodicity boundary conditions on the periodic surfaces on both sides, as shown in Figure 3c.

The total temperature and total pressure at the inlet of the main flow are 796.9 K and 1.8 MPa. The mass flow at the outlet of the main flow and the outlet of the disk cavity is 2 kg/s and 0.04 kg/s for a single sector. The latter accounts for 2% of the former. All walls are set to smooth, no-slip, and adiabatic wall conditions.

The steady flow characteristics of the vortex reducer in the disk cavity are calculated based on the grid models, with different numbers of elements to verify the grid independence of the results. The total pressure at the inlet and outlet of the tube for different grid models is shown in

Table 2. Grid independence verification.

Grid No.	Number of Elements	Inlet Total Pressure/MPa	Outlet Total Pressure/MPa
1	150,000	1.635	1.297
2	300,000	1.612	1.256
3	450,000	1.603	1.250
4	600,000	1.601	1.249
5	750,000	1.601	1.248
6	900,000	1.602	1.248

. The results based on Grid 3, with about 450,000 elements, are accurate enough, and the results change little with the further increase of the number of elements. Therefore, Grid 3 is used in the following analysis.

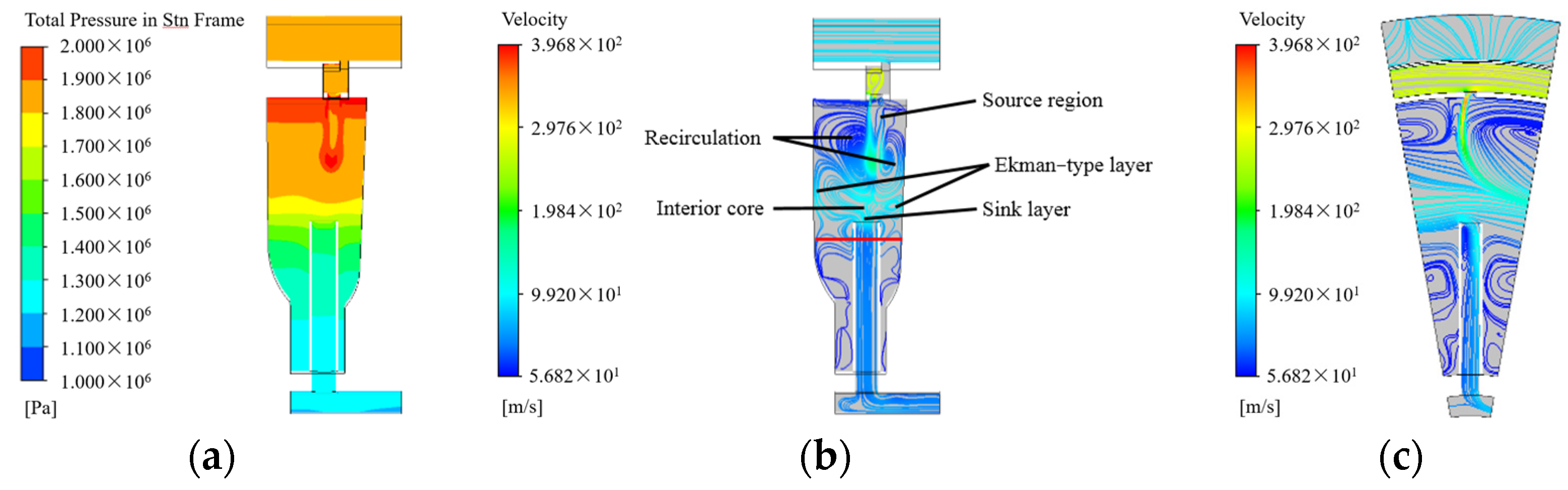
The steady flow characteristics of the vortex reducer in the disk cavity are shown in Figure 4. The total pressure in the disk cavity gradually decreases from the top to the bottom along the radial direction, as shown in Figure 4a. It can be seen from Figure 4b that the flow in the upper part of the disk cavity is similar to the source-sink flow model proposed by Hide [1]. Figure 4c shows that the upper part of the disk cavity is a recirculating region with low velocity, and the middle of the disk cavity is a relatively stable circumferential flow region with relatively high velocity. Some of the gas is diverted into the tube, and there is a small recirculating region at the inlet of the tube. The other gas flows around the outside of the tube, and a small part of the gas forms a recirculating region with low velocity in the lower part of the disk cavity.

In summary, the steady flow characteristics of the vortex reducer in the disk cavity are similar to those in references [10,14]. Therefore, it can be considered that the above numerical simulation is reliable.

3.4. Unsteady Aerodynamic Load

The pressure fluctuation caused by gas column vibration has been discussed in reference [13], which pointed out that the first mode of the tube is more prone to forced vibration under this aerodynamic load. Next, the pressure fluctuation from the main flow is analyzed to clarify the potential vibration risk of the vortex reducer.

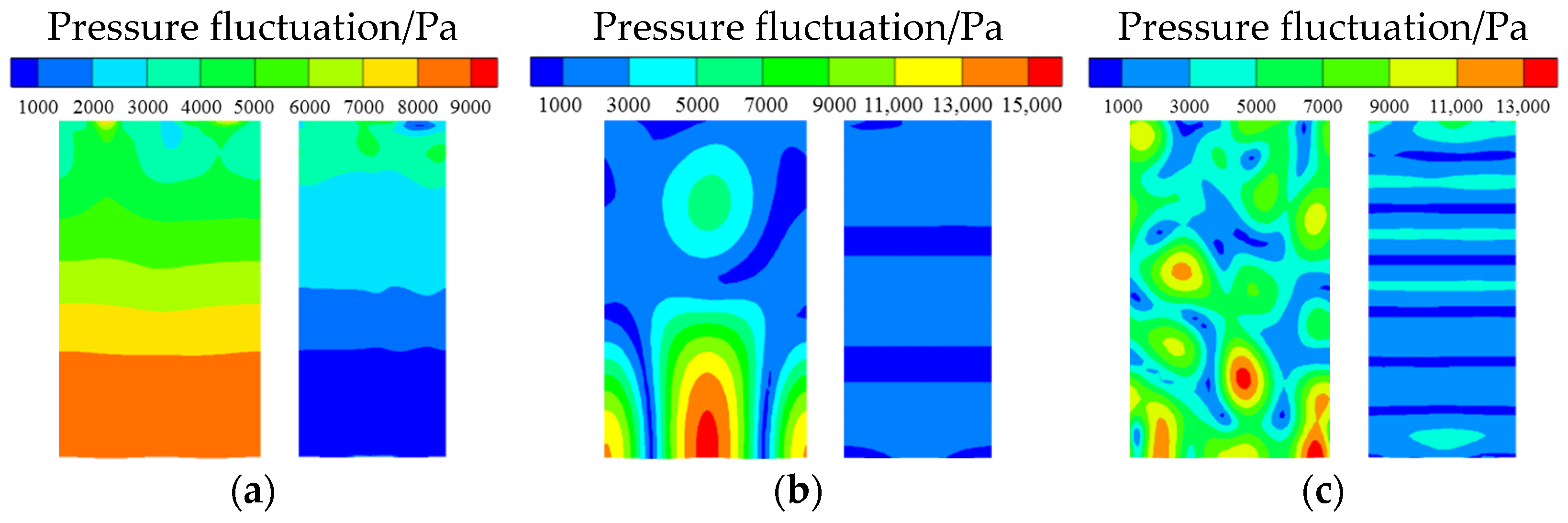
The pressure fluctuation from the main flow is mainly caused by inlet distortion and blade wake, and its frequency is generally an integral multiple of engine rotation frequency. The pressure fluctuation is simulated by directly superimposing a harmonic pressure fluctuation on the original inlet total pressure of the main flow. The amplitude is 1 MPa and the frequency is 1600 Hz, 7200 Hz, or 16,000 Hz, respectively. Other boundary settings are the same as those in Section 3.3. A pressure fluctuation period is divided into 60-time steps. The monitoring points are located on the surface of the tube. The pressure of the surface nodes at each time step in the last period is extracted to calculate the pressure fluctuation after the pressure at the monitoring points fluctuates, with approximately constant amplitude.

As shown in Figure 5, there are large pressure fluctuations on the tube surface under the inlet total pressure fluctuation, with three given frequencies, which may lead to the forced vibration of the tube. The frequency of the pressure fluctuation on the tube surface is independent of the geometry. The forced response of the mode with lower frequency is generally larger when other conditions are the same. Therefore, more attention should be paid to the first and second modes with lower frequency in the subsequent analysis.

4. Aerodynamic Damping

4.1. Results Calculated by the Energy Method

Taking the first and second modes as examples, the aerodynamic work and ${\zeta }_{\mathrm{a}}$ of the tube in the disk cavity, with three different amplitudes, is calculated by the energy method.

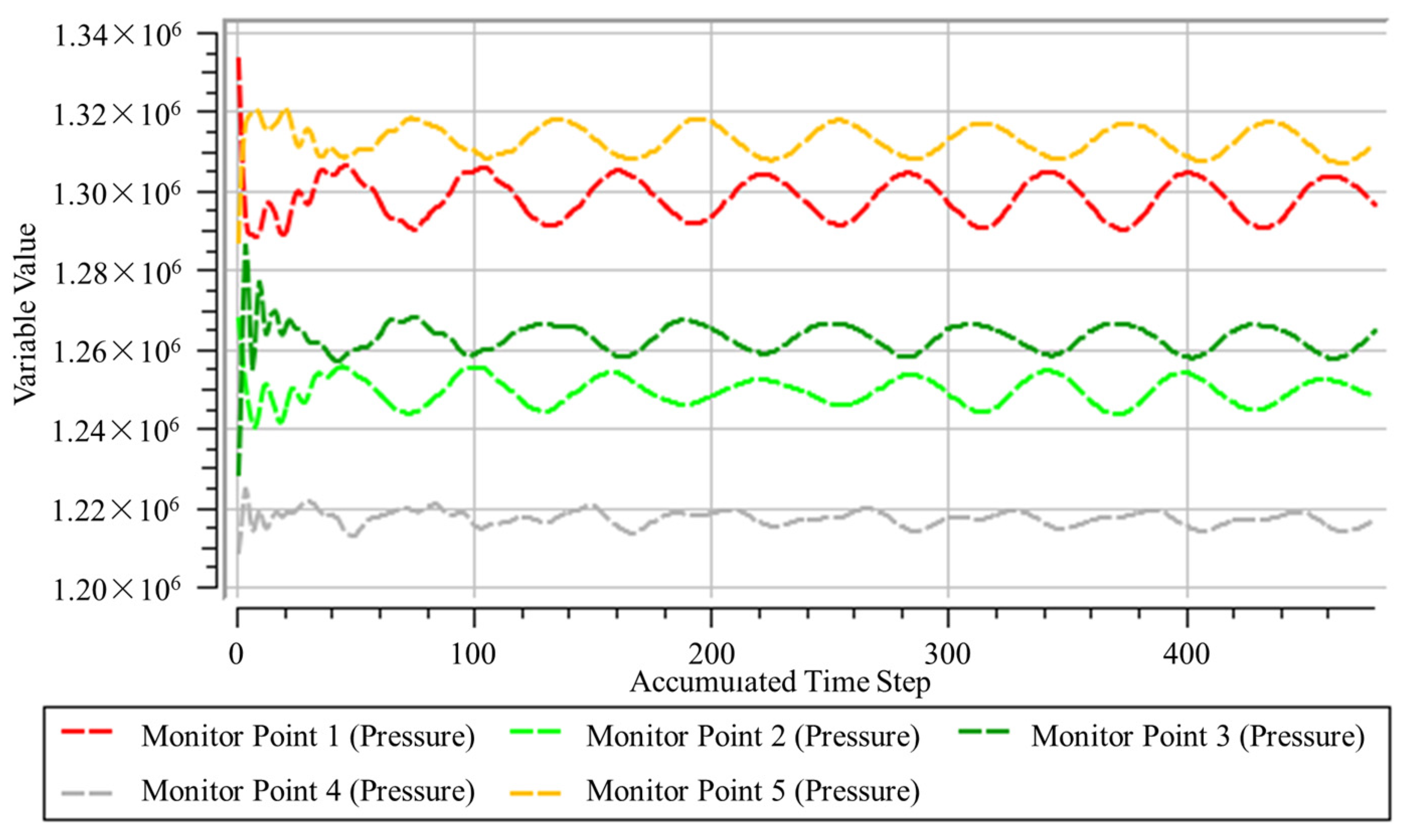
The tube vibrates according to the modal frequency and modal shape of the first or second mode, and the maximum amplitudes of the tube are given as 0.5 mm, 1.0 mm, or 1.5 mm. A vibration period is divided into 60-time steps. As shown in Figure 6, the pressure fluctuation at all monitoring points gradually stabilizes and keeps harmonic fluctuation with approximately constant amplitude.

Finally, the unsteady aerodynamic forces and displacements of the surface nodes at each time step in the last vibration period are extracted to calculate the aerodynamic work and ${\zeta }_{\mathrm{a}}$ of the tube, as shown in

Table 3. Aerodynamic work and ${\zeta }_{\mathrm{a}}$ with different amplitudes.

Mode	Amplitude/mm	Aerodynamic Work/×10−3 J	${\mathit{\zeta }}_{\mathbf{a}}$ × 10−4
First mode	0.5	−0.72	2.87
	1.0	−2.89	2.86
	2.0	−11.38	2.82
Second mode	0.5	−0.65	2.51
	1.0	−2.58	2.50
	2.0	−10.32	2.51

.

The aerodynamic work of the first or second mode is negative and approximately proportional to the quadratic power of the amplitude, and the ${\zeta }_{\mathrm{a}}$ of the first or second mode is positive and the ${\zeta }_{\mathrm{a}}$ with three different amplitudes is almost the same. The results are consistent with the theoretical speculation based on Equation (5) in Section 2.1. The aerodynamic damping is independent of the vibration amplitude within the given amplitude range. It can be considered that the flow in the disk cavity conforms to the linear assumption of the energy method, and the aerodynamic work and ${\zeta }_{\mathrm{a}}$ calculated by the energy method is accurate. According to the results in references [30,31], the aerodynamic damping depends largely on the vibration amplitude for larger amplitude vibrations. However, the maximum von Mises stress corresponding to the maximum amplitude of 1 mm is about 500 MPa, which is very large for vibration stress. Therefore, the larger vibration amplitude is not considered in this paper.

In addition, the positive aerodynamic damping is beneficial for the vibration, which means that the risk of flutter is low, and the forced response will decrease after considering the positive aerodynamic damping. Assuming that the amplitude of modal excitation force is 1 N, and the structural damping ratio is 0.1%, the maximum response of the first mode of the tube before and after considering aerodynamic damping is 0.037 mm and 0.029 mm. The latter is 22.18% smaller than the former.

The aerodynamic work distribution of the first and second modes on the outer (left) and inner (right) surfaces of the tube is shown in Figure 7.

There is a strong correlation between the aerodynamic work distribution and the modal shape. First, the aerodynamic work is mainly concentrated in the upper part of the tube and shows a decreasing trend from top to bottom along the tube axis, which is similar to the distribution of modal displacement. In addition, the circumferential distribution of the aerodynamic work is related to the vibration direction of the mode. The smaller the angle between the normal direction of the surface and the vibration direction, the greater the aerodynamic work is.

4.2. Results Calculated by the Influence Coefficient Method

Taking the first and second modes as examples, the influence coefficient method is used to analyze the aerodynamic influence between adjacent tubes and the aerodynamic damping of the tube, with different nodal diameters.

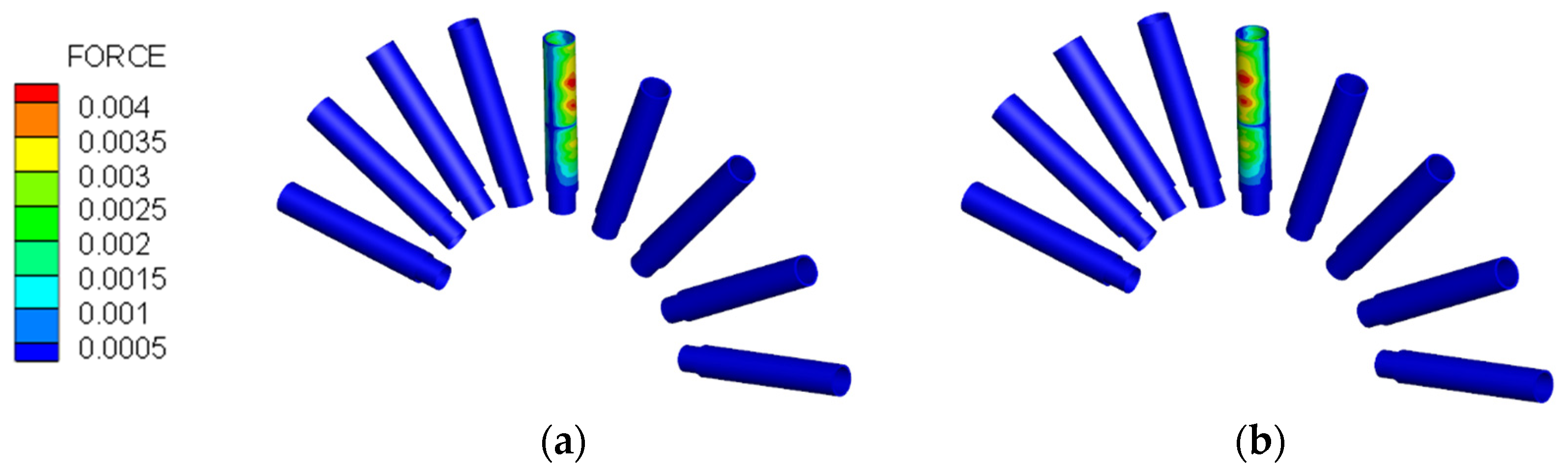
A sector flow field model of the disk cavity with nine tubes is constructed to analyze the unsteady aerodynamic forces caused by tube vibration. The fifth tube vibrates according to the modal frequency and modal shape of the first or second mode, and the maximum vibration amplitude is 1 mm. The other eight tubes remain stationary. A vibration period is divided into 60-time steps. The unsteady aerodynamic forces on all tube surfaces, in each time step of the last vibration period, are extracted to calculate the aerodynamic influence coefficient when the pressure fluctuation at all monitor points is stable. The results are shown in

Table 4. Aerodynamic influence coefficients.

No.	First Mode			Second Mode
	Real Part	Imaginary Part	Amplitude	Real Part	Imaginary Part	Amplitude
−4	809	−1785	1960	−236	212	318
−3	−5339	−1142	5460	−208	231	311
−2	−10,492	2777	10,854	142	−62	155
−1	−4637	4222	6271	4994	−3657	6190
0	237,250	−56,243	243,825	193,584	−42,817	198,263
1	−6875	1417	7020	5937	3519	6902
2	−10,818	−2743	11,160	−447	200	490
3	−2651	−253	2663	−326	181	373
4	−1737	1190	2106	−185	134	228

and Figure 8.

The unsteady aerodynamic force generated by the vibration of the fifth tube is mainly concentrated on its surface, while the unsteady aerodynamic force on the other tube surfaces is relatively small. It can be concluded that the aerodynamic damping of the first and second modes is only related to itself and independent of the adjacent tubes.

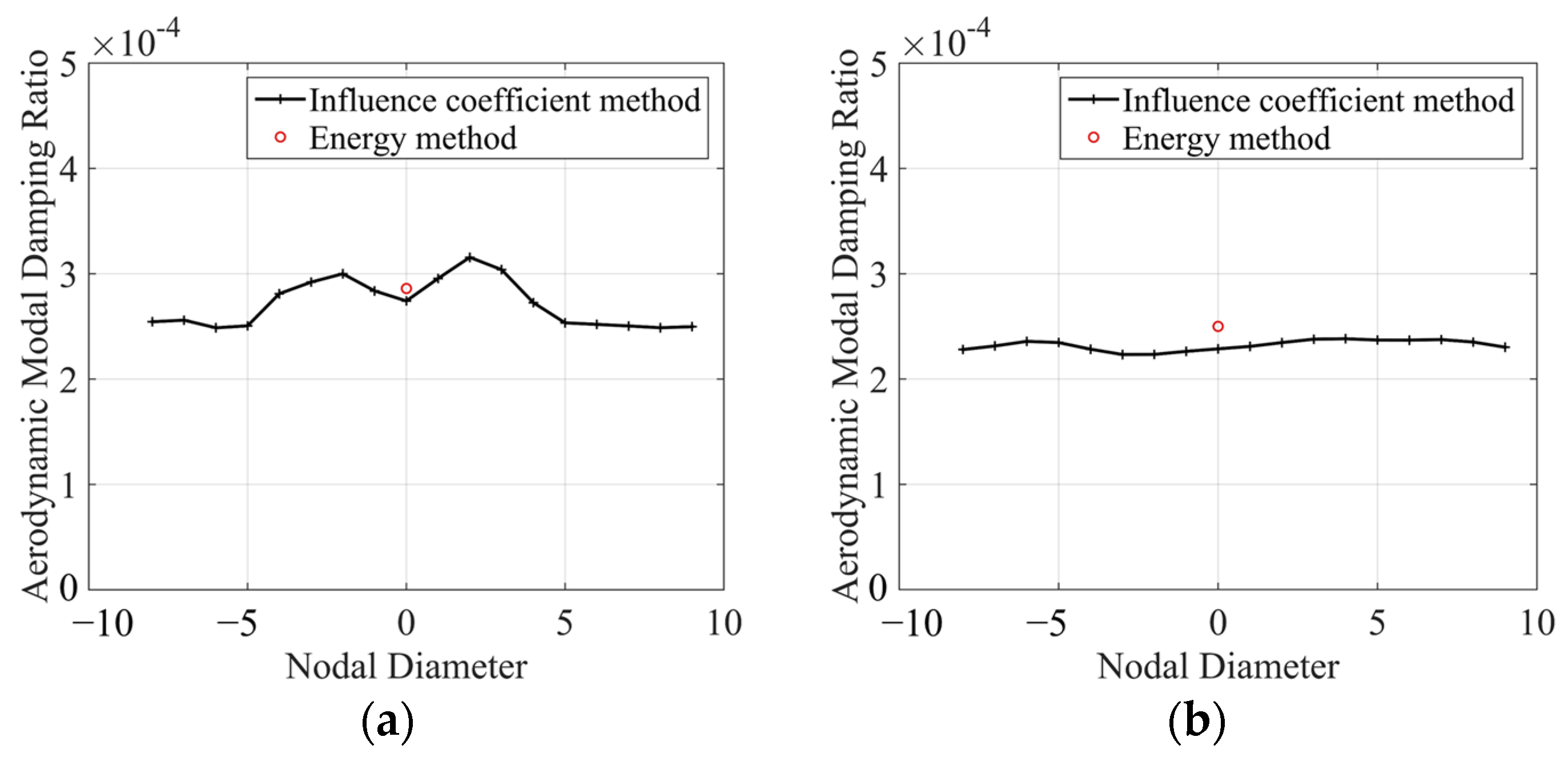
Next, the ${\zeta }_{\mathrm{a}}$ of the first and second modes are calculated by the influence coefficient method and compared with the results of the energy method, as shown in Figure 9.

The ${\zeta }_{\mathrm{a}}$ of the first and second modes with different nodal diameters are almost the same. The maximum relative difference between the ${\zeta }_{\mathrm{a}}$ with zero nodal diameter and the ${\zeta }_{\mathrm{a}}$ with other nodal diameters is less than 10% for the first and second modes. Therefore, it is unnecessary to consider the influence of inter-tube phase angle when analyzing the aerodynamic damping of the first and second modes of the tube. The relative difference between the ${\zeta }_{\mathrm{a}}$ calculated by the influence coefficient method and the ${\zeta }_{\mathrm{a}}$ calculated by the energy method is 4% for the first mode and 9% for the second mode, which further verifies the accuracy of the energy method.

5. Structural Coupling

The support ring of the actual vortex reducer is not completely rigid, and the bottom of the tube is not completely fixed. The structural coupling caused by the support ring can affect the modal characteristics of the tube and further affect the aerodynamic damping.

5.1. Mode of the Vortex Reducer with Support Ring

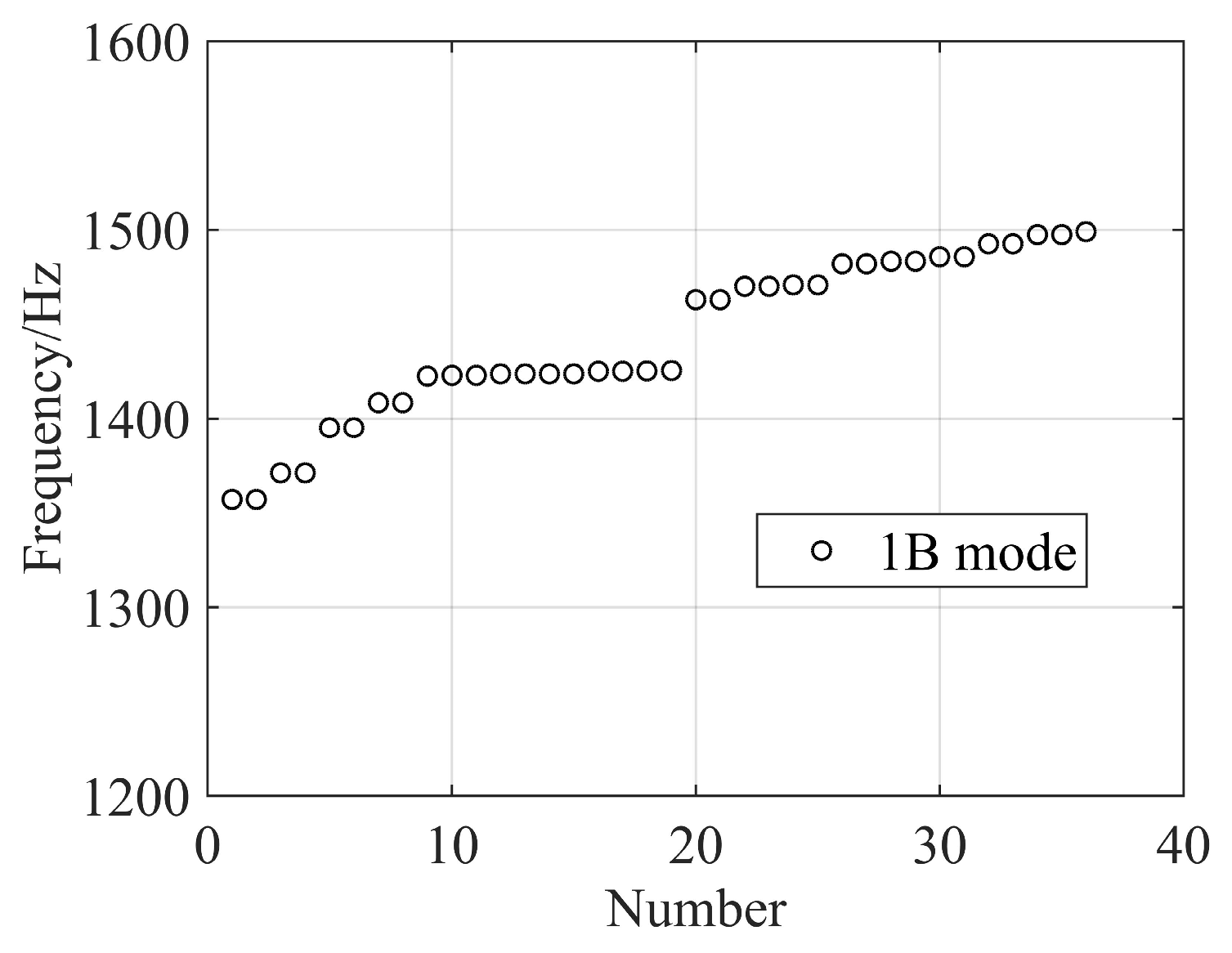
Assuming that the constraint of the clamping ring is very strong, the tube and the support ring can be regarded as an integral structure. The surface of the support ring connected with the disk of the 7th rotor is fixed. The uniform temperature and rotation speed are the same as the single tube model above. Then, the modal frequencies and modal shapes of the first bending mode family are obtained by modal analysis, considering prestress, and shown in Figure 10 and Figure 11.

The modal frequencies of the first bending mode family are different. The maximum and minimum modal frequencies of the first bending mode family are 1357 Hz and 1499 Hz, which are reduced by 14% and 5%, respectively, compared with the first modal frequency of the single tube model, which is 1581 Hz.

It can be seen from Figure 11 that the modal displacements of the support ring in the modal shapes of the first bending mode family are close to zero, and the vibration of the vortex reducer is mainly tube vibration. Some modal shapes of the first bending mode family of the vortex reducer have obvious nodal diameter characteristics, which means that there is an inter-tube phase angle between the vibrations of the tubes.

In addition, the vibration of the tubes in some modal shapes is no longer along the axial or circumferential direction, and there is a certain angle between the vibration direction of the tube and the axial or circumferential direction. These modal shapes are regarded as the coupled modal shapes formed by the weighted summation of the first and second modal shapes.

In summary, the effect of structural coupling on the modal characteristics of the tube is mainly reflected in three aspects: frequency reduction, nodal diameter, and tube mode coupling. However, the aerodynamic influence between adjacent tubes can be ignored when the tube vibrates according to the first or second mode. Therefore, the effect of nodal diameter on the aerodynamic damping of the tube can be ignored. Next, the effect of frequency reduction and tube mode coupling on the aerodynamic damping of the tube is analyzed by the energy method.

5.2. Effect of Frequency Reduction on Aerodynamic Damping

Three typical frequencies, including the minimum and maximum modal frequencies of the first bending mode family of the vortex reducer and the first modal frequency of the tube, are selected to analyze the effect of frequency reduction on the aerodynamic damping of the tube. The three typical frequencies are 1357 Hz, 1499 Hz, and 1581 Hz.

Next, the energy method is used to calculate the aerodynamic damping of the tube when it vibrates, according to the first or second modal shape of the tube and the three typical frequencies. The aerodynamic work and ${\zeta }_{\mathrm{a}}$ are shown in

Table 5. Aerodynamic work and ${\zeta }_{\mathrm{a}}$ of the first and second modes with three typical frequencies.

Frequency/Hz	Aerodynamic Work of the First Mode/×10−3 J	${\mathit{\zeta }}_{\mathbf{a}}$ of the First Mode/×10−4	Aerodynamic Work of the Second Mode/×10−3 J	${\mathit{\zeta }}_{\mathbf{a}}$ of the Second Mode/×10−4
1357	−1.95	2.74	−1.93	2.73
1499	−2.51	2.90	−2.21	2.56
1581	−2.89	2.86	−2.58	2.50

, and the aerodynamic work distribution is shown in Figure 12.

The aerodynamic work of the first or second mode increases with the decrease of vibration frequency. The ${\zeta }_{\mathrm{a}}$ of the second mode increases with the decrease of vibration frequency, while the ${\zeta }_{\mathrm{a}}$ of the first mode first increases and then decreases. However, the maximum relative and absolute difference between the ${\zeta }_{\mathrm{a}}$ with different frequencies are only 6% and 2.3 × 10⁻⁵.

It can be seen from Figure 12 that the aerodynamic work distribution of the first or second modes with different vibration frequencies is very similar, and only the aerodynamic work intensity in some regions changes a little. The change of aerodynamic work is mainly reflected in the decrease of negative work and the increase of positive work with the decrease of vibration frequency. Finally, the absolute value of negative total aerodynamic work decreases.

It is known from Equation (5) that ${\zeta }_{\mathrm{a}}$ is directly proportional to aerodynamic work and inversely proportional to the quadratic power of vibration frequency. Therefore, when the aerodynamic work and frequency decrease simultaneously, the change of the ${\zeta }_{\mathrm{a}}$ depends on which of the two parameters decreases more. The ${\zeta }_{\mathrm{a}}$ increases when the decreasing ratio of the quadratic power of the vibration frequency is larger than that of the aerodynamic work. In summary, the aerodynamic damping of the tube does not fundamentally change within the frequency range caused by structural coupling.

5.3. Effect of Tube Mode Coupling on Aerodynamic Damping

The first and second modes are coupled according to five coupling coefficients to obtain five first bending modes with different vibration directions. The modal frequencies and modal shapes of the coupling modes can be obtained by the following equation:

$$M_{\mathrm{c}}=\left(1-a_{\mathrm{c}}\right)M_1+a_{\mathrm{c}}{M}_2$$

(13)

where $a_{\mathrm{c}}$ is the coupling coefficient, $M_{\mathrm{c}}$, $M_1$, and $M_2$ are modal data of the coupling mode, the first mode, and the second mode, including modal frequencies and modal shapes. The modal frequencies of the coupling are almost the same because the modal frequencies of the first and second modes are very close.

The theoretical aerodynamic work of the coupled modes is obtained by weighted summation of the aerodynamic work of the first and second modes, based on the coupling coefficient. The numerical aerodynamic work of the coupled modes is calculated by the energy method. The above two types of aerodynamic work of the coupled modes are shown in

Table 6. Aerodynamic work of the coupled modes.

${\mathit{a}}_{\mathbf{c}}$	Included Angle between the Vibration Direction and the X-Axis/Degree	Numerical Aerodynamic Work/×10−3 J	Theoretical Aerodynamic Work /×10−3 J
0.00	00.0	2.58	2.59
0.25	22.5	2.63	2.66
0.50	45.0	2.78	2.74
0.75	67.5	2.89	2.81
1.00	90.0	2.89	2.89

.

The results with coupling coefficients of 0 and 1 correspond to the original first and second modes, respectively. With the increase of the coupling coefficient, both types of aerodynamic work gradually increase from the aerodynamic work of the first mode to that of the second mode. The two types of aerodynamic work with the same coupling coefficient are very close. The aerodynamic work distribution of the coupling modes is shown in Figure 13.

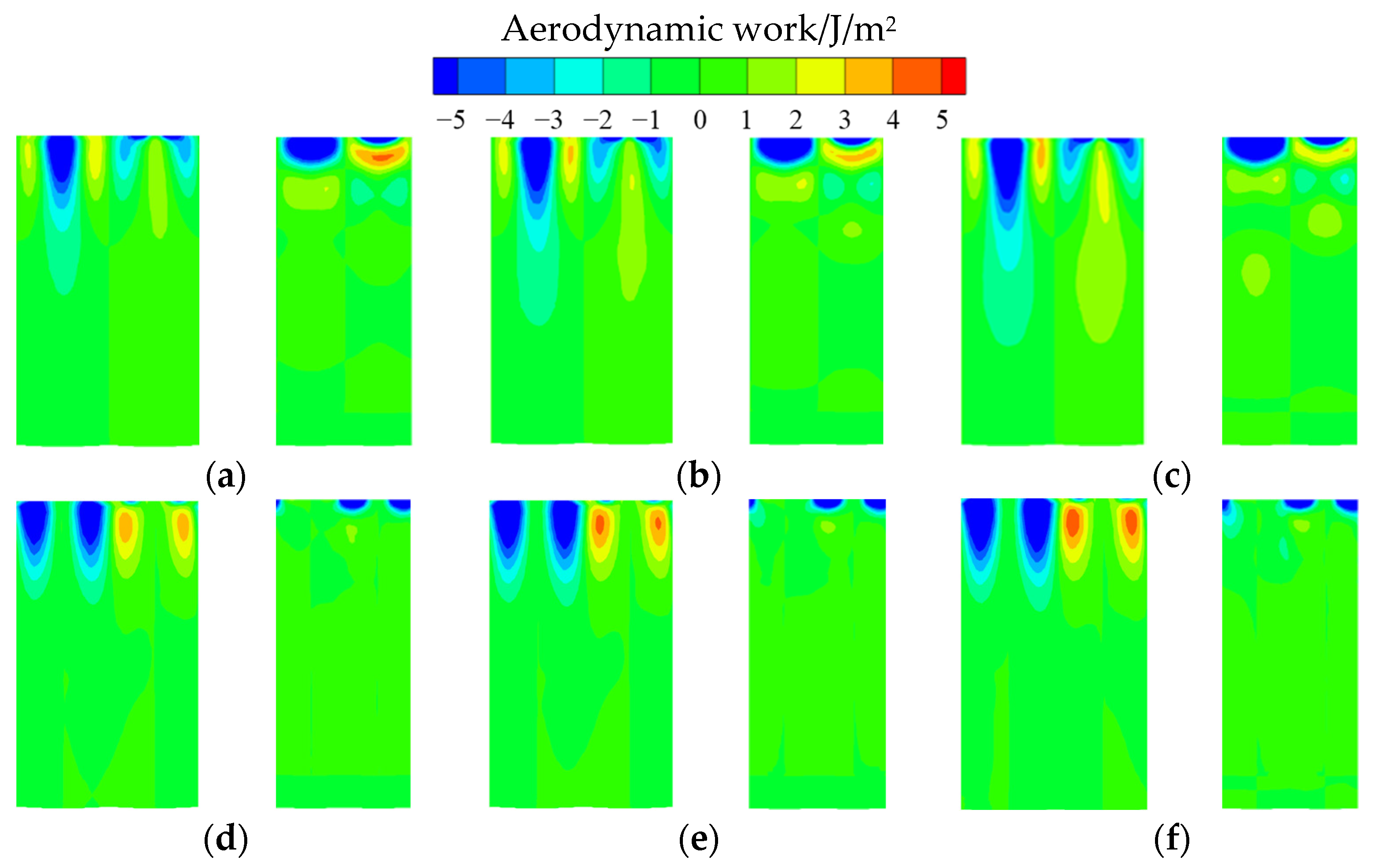
The aerodynamic work distribution on the tube surface gradually changes from the first mode to the second mode, with the coupling coefficient changing from 0 to 1. The variation of aerodynamic work with the coupling coefficient is continuous, and its characteristics are summarized as follows:

When the coupling coefficient increases, all aerodynamic work on the inner and outer walls gradually moves to the left, and the position with large aerodynamic work changes from the transverse quarter and three-quarters to the middle position and the edges on both sides. Meanwhile, the aerodynamic work intensity in some regions changes accordingly in the process of the above position change.

In summary, the results indicate that the effect of tube mode coupling on the aerodynamic work distribution of the first bending mode is obvious. The aerodynamic damping of the coupled modes can be obtained by the weighted summation of the aerodynamic damping of the first and second modes. The results further prove the rationality of using the energy method to calculate the aerodynamic damping of the tube in the disk cavity.

6. Conclusions

Based on the comprehensive analysis of the mode and flow characteristics of the vortex reducer, this paper mainly studies the aerodynamic damping of the vortex reducer by the energy method and the influence coefficient method. Then, the effect of structural coupling on aerodynamic damping is discussed. The main conclusions are as follows:

(1) Based on the modal characteristics, steady flow characteristics, and the unsteady aerodynamic load of the vortex reducer, the first and second modes of the tube have a greater risk of vibration, so they are selected as the object of subsequent aerodynamic damping analysis.

(2) For the first and second modes of the tube, the ${\zeta }_{\mathrm{a}}$ calculated by the energy method are all positive but small, which means that the modes have less risk of flutter but are prone to forced vibration. The ${\zeta }_{\mathrm{a}}$ of the same mode with different amplitudes is almost the same, which indicates that the flow field around the vortex reducer meets the linear assumption of the energy method. The aerodynamic work distribution of the two modes has a strong correlation with their modal shapes.

(3) For the first and second modes of the tube, the distribution of the aerodynamic influence coefficients indicates that the aerodynamic influence between adjacent tubes can be ignored. Therefore, the ${\zeta }_{\mathrm{a}}$ with different nodal diameters are almost the same. Meanwhile, the ${\zeta }_{\mathrm{a}}$ calculated by the influence coefficient method is in good agreement with that calculated by the energy method.

(4) For the first and second modes of the tube, the effect of structural coupling on the aerodynamic damping of the tube is mainly reflected in two aspects: frequency reduction and tube mode coupling. The former leads to the reduction of aerodynamic work. The latter is mainly reflected in that the aerodynamic work of the coupled modes can be approximately expressed as the weighted summation of the aerodynamic work of the original first and second modes, and the weight coefficients depend on the vibration directions of the coupled modes.