Structural Characteristics of a Shock Train Flow Field in a Variable Cross-Section S-Shaped Isolator
Abstract
:1. Introduction
2. Experimental Design and Numerical Calculation
2.1. Numerical Simulation Method
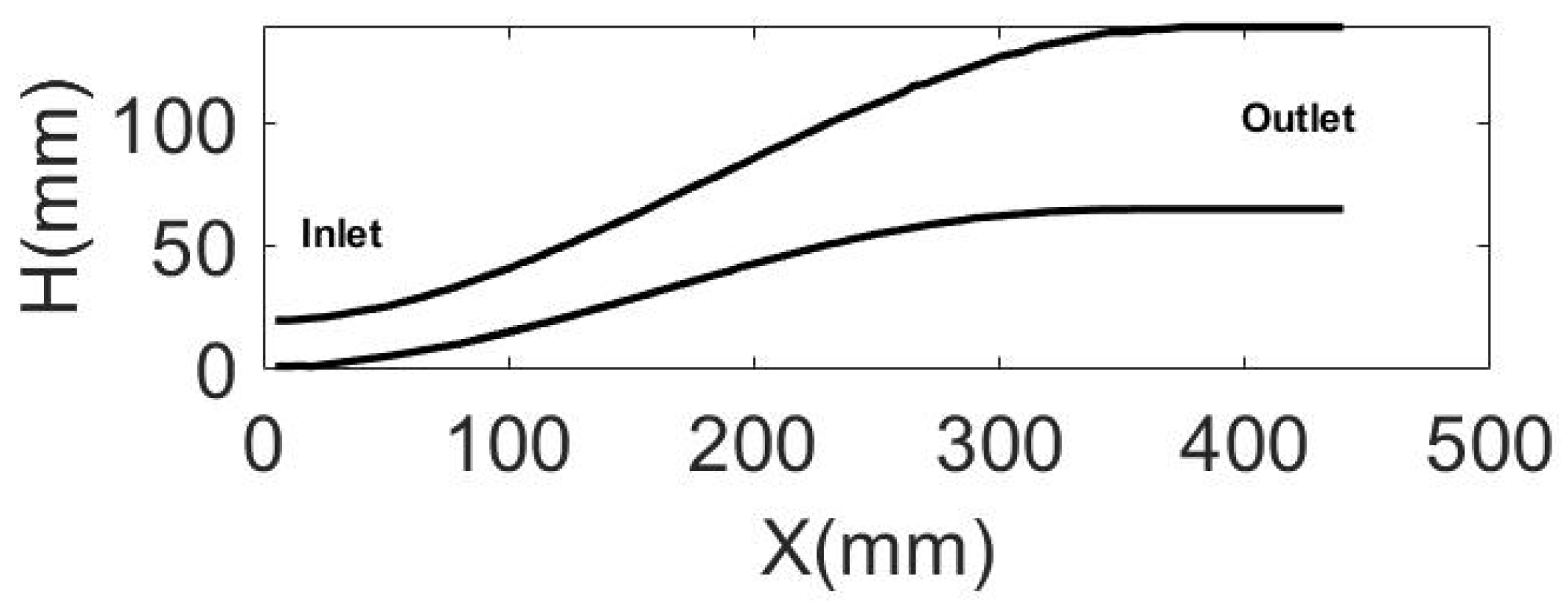
2.2. Experimental Design
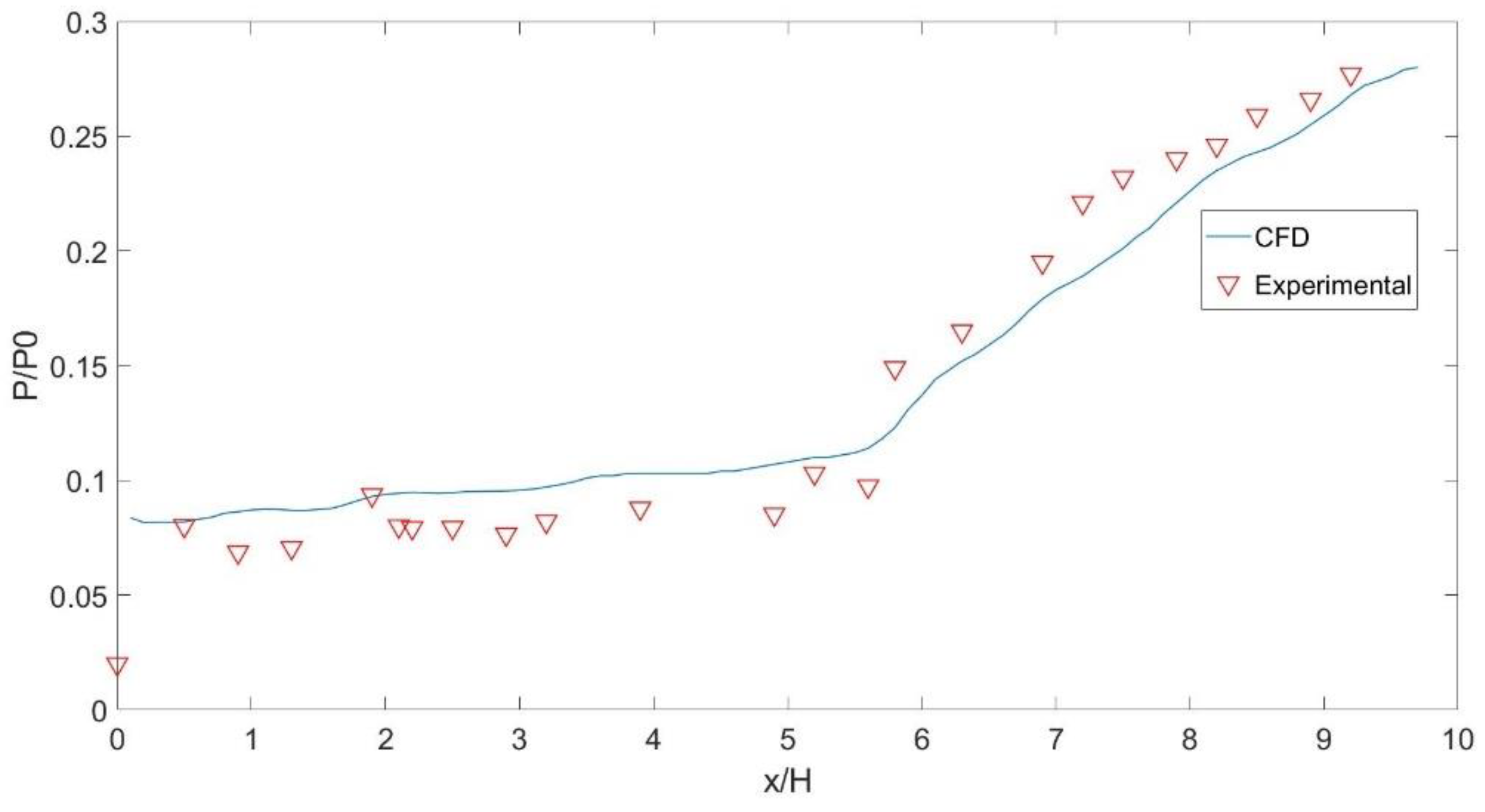
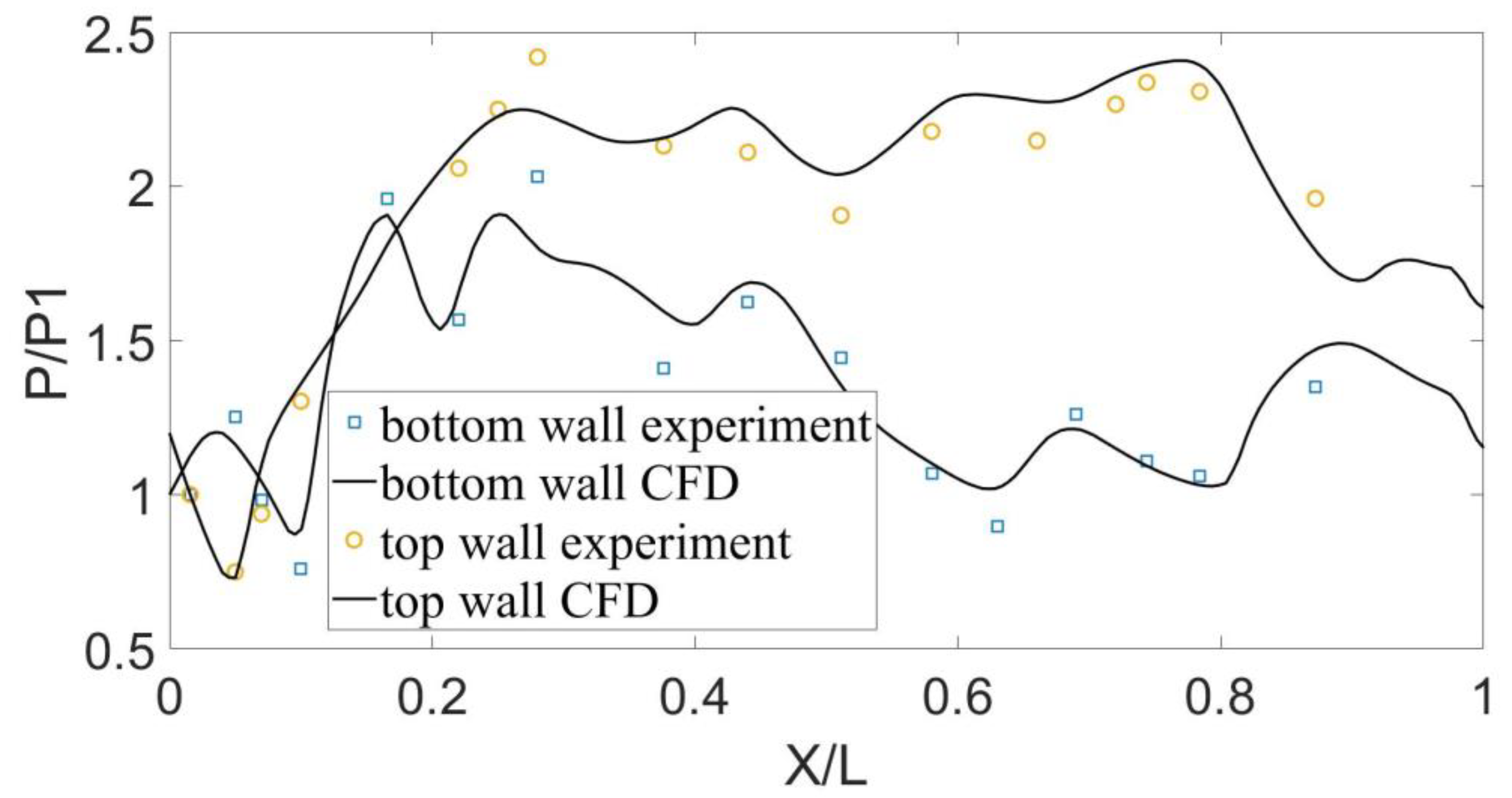
2.3. Experimental Verification of the Numerical Calculations
3. Self-Excited Oscillation Characteristics of a Shock Train in an Isolator
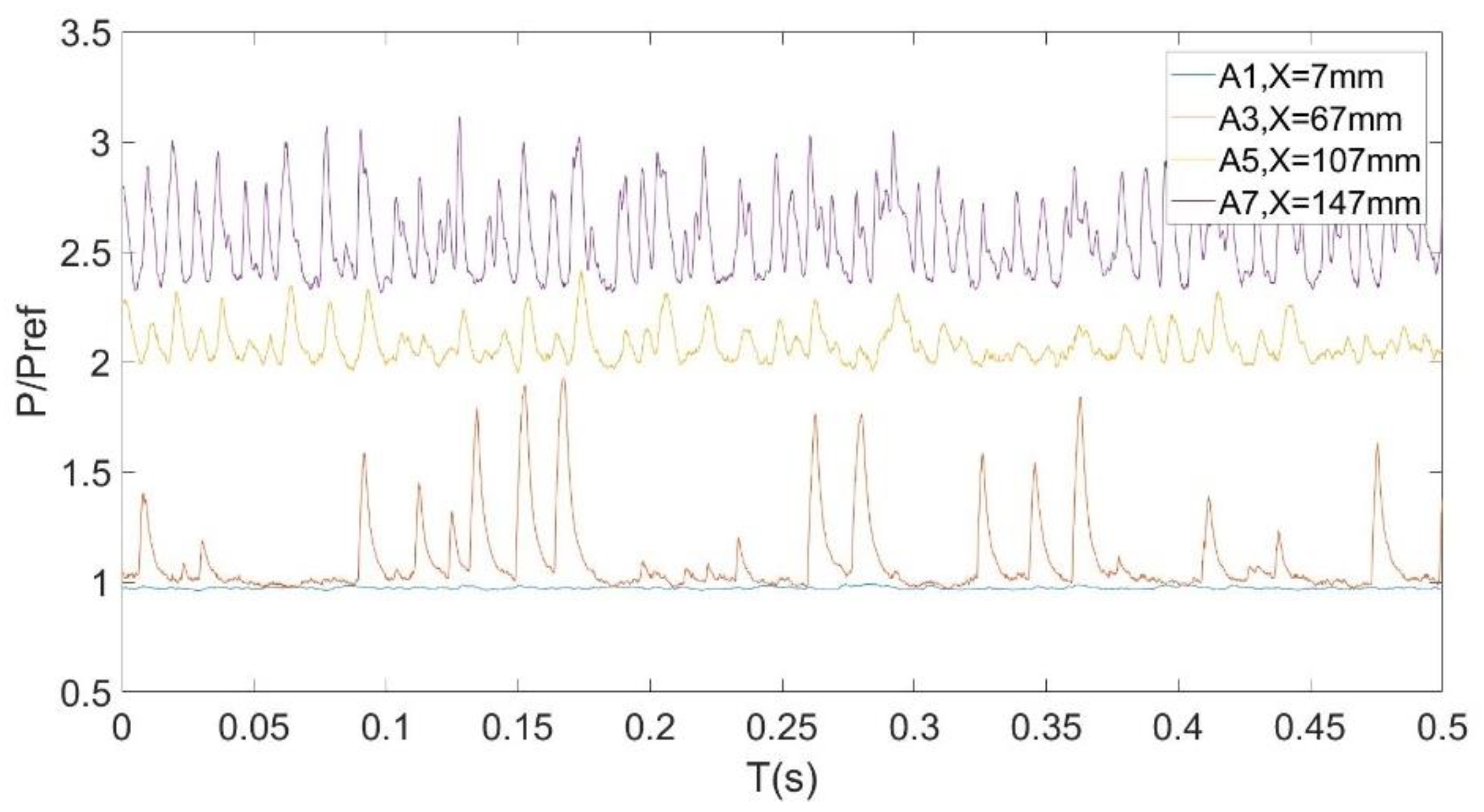
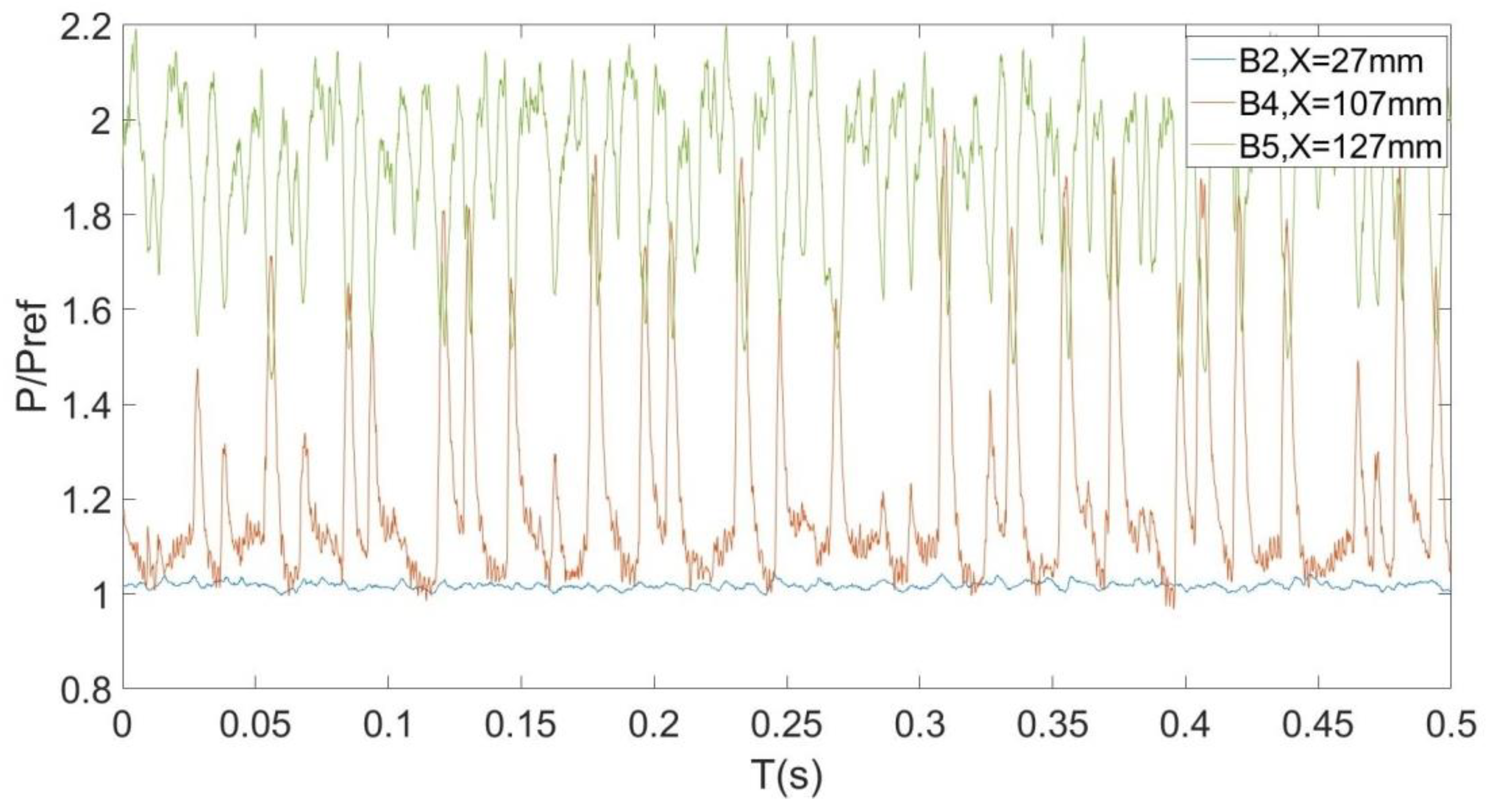
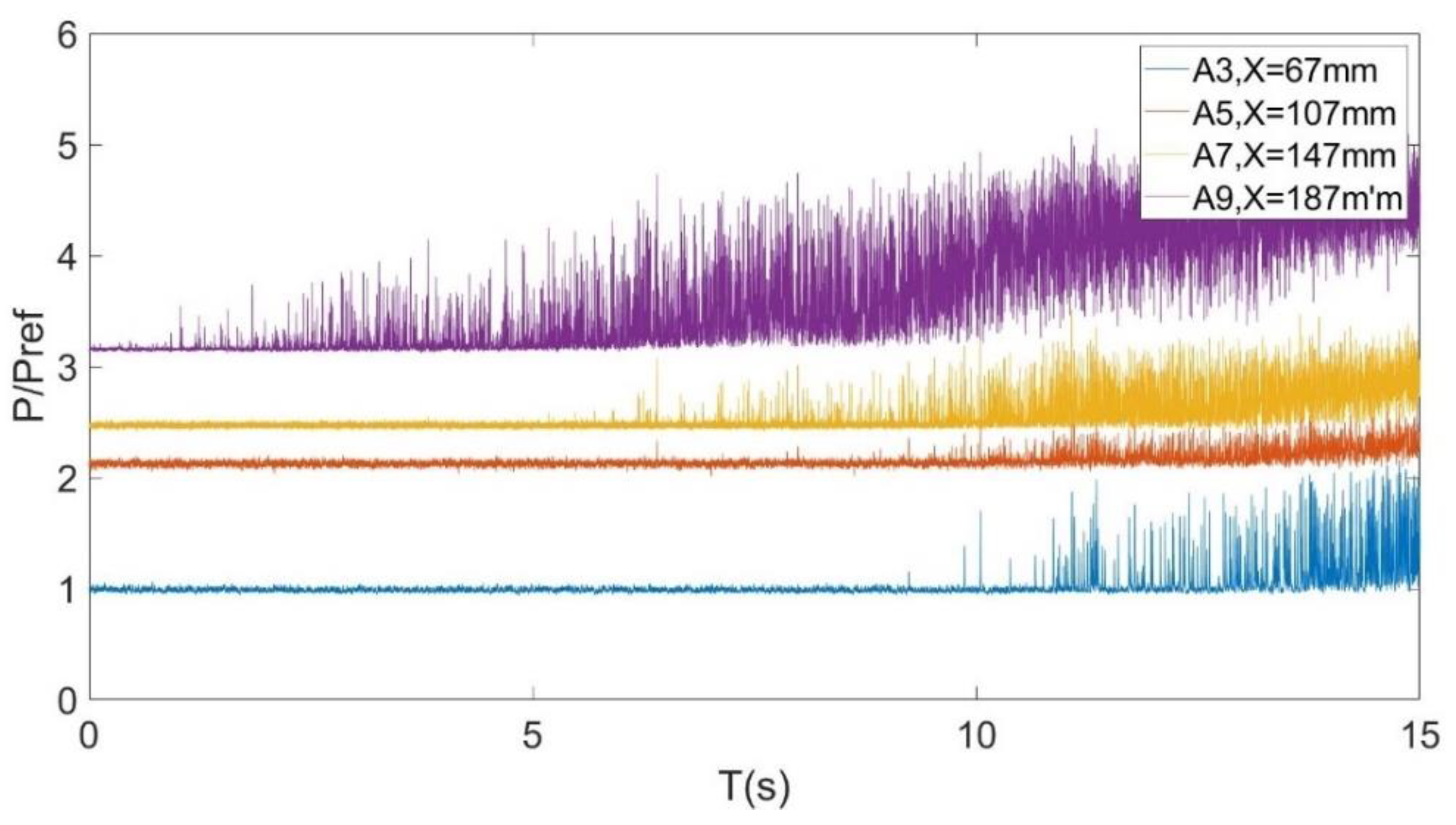
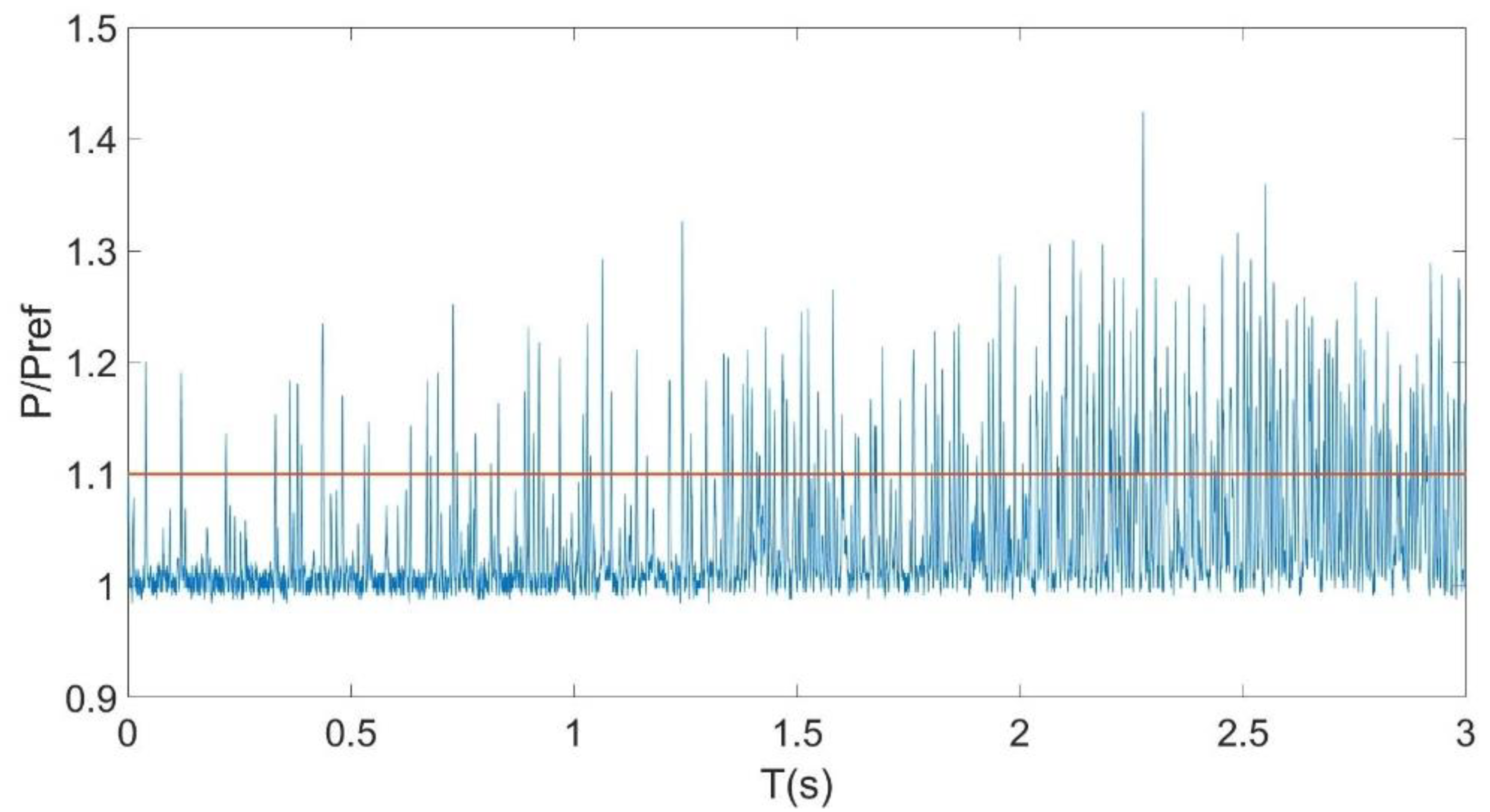
3.1. Pressure Fluctuation Characteristics of a Shock Train
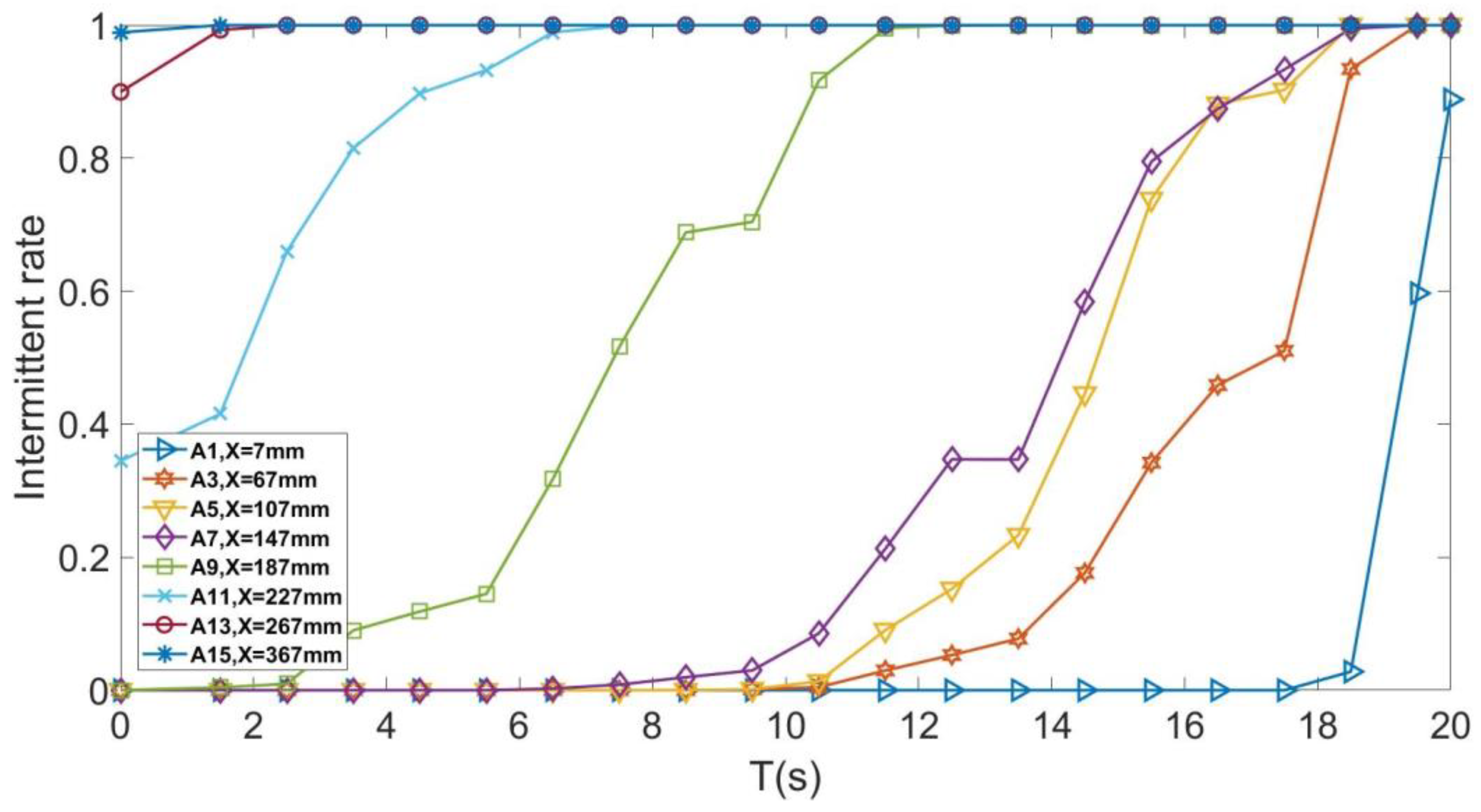
3.2. The Law of Forward Movement of Shock Train Leading Edge under the Back Pressure
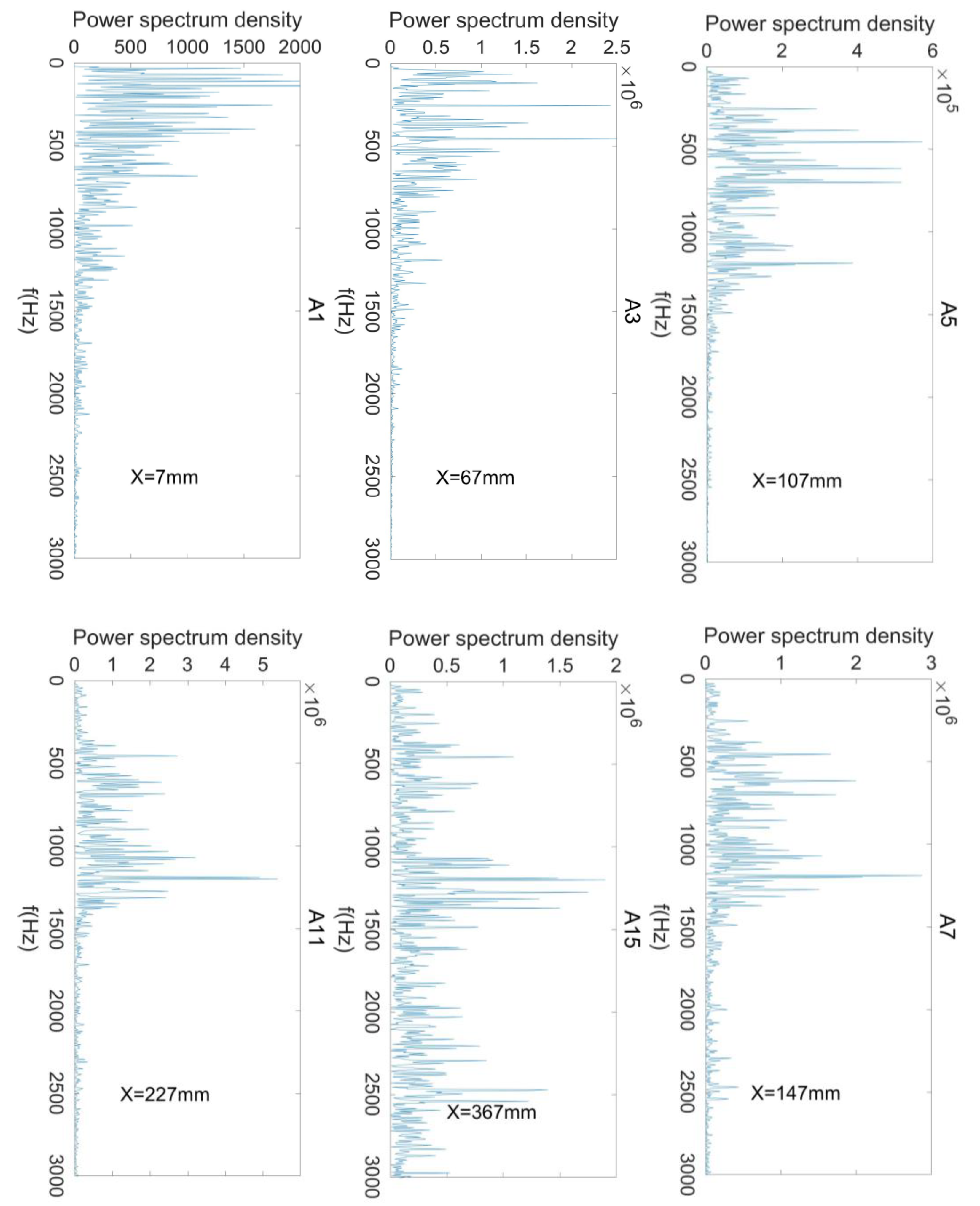
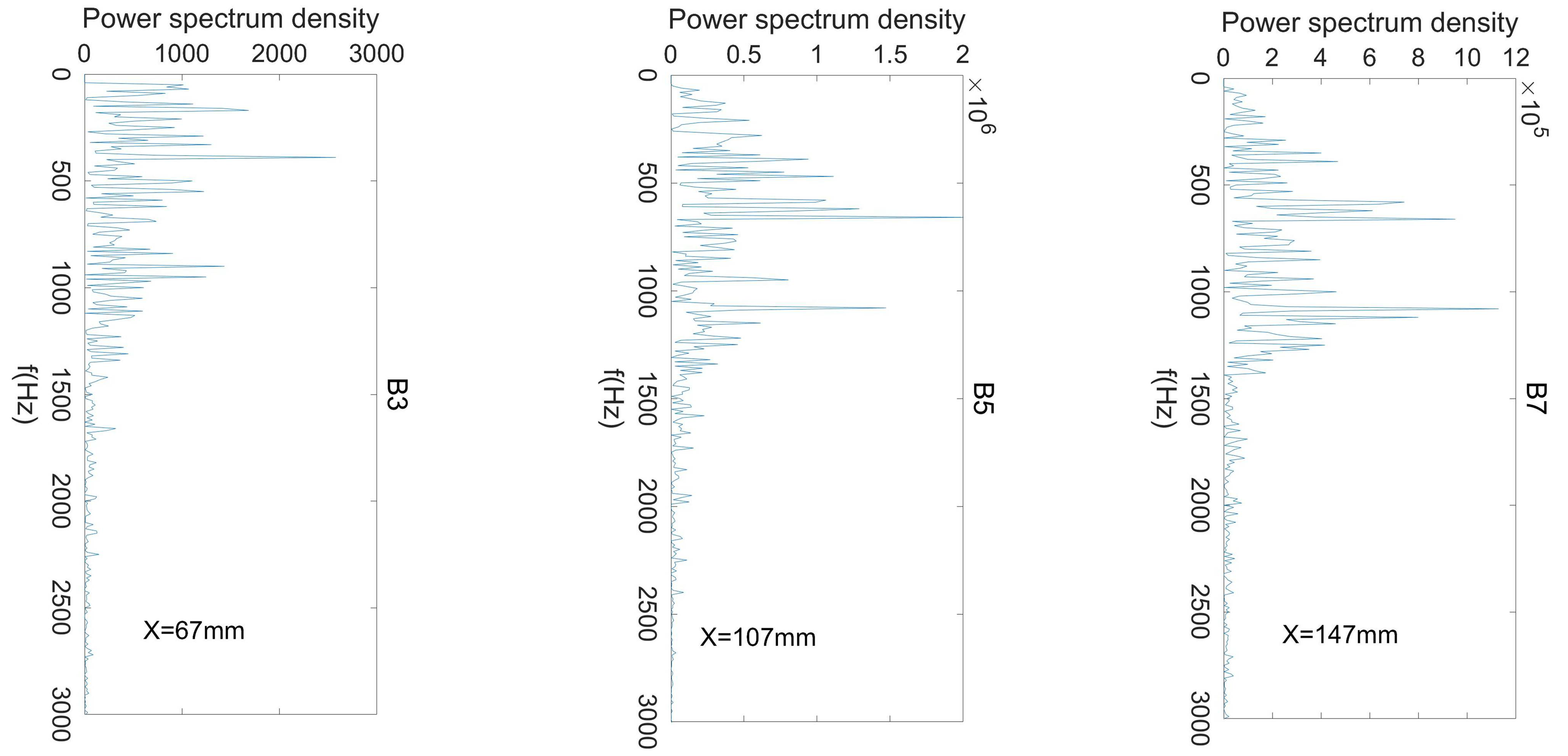
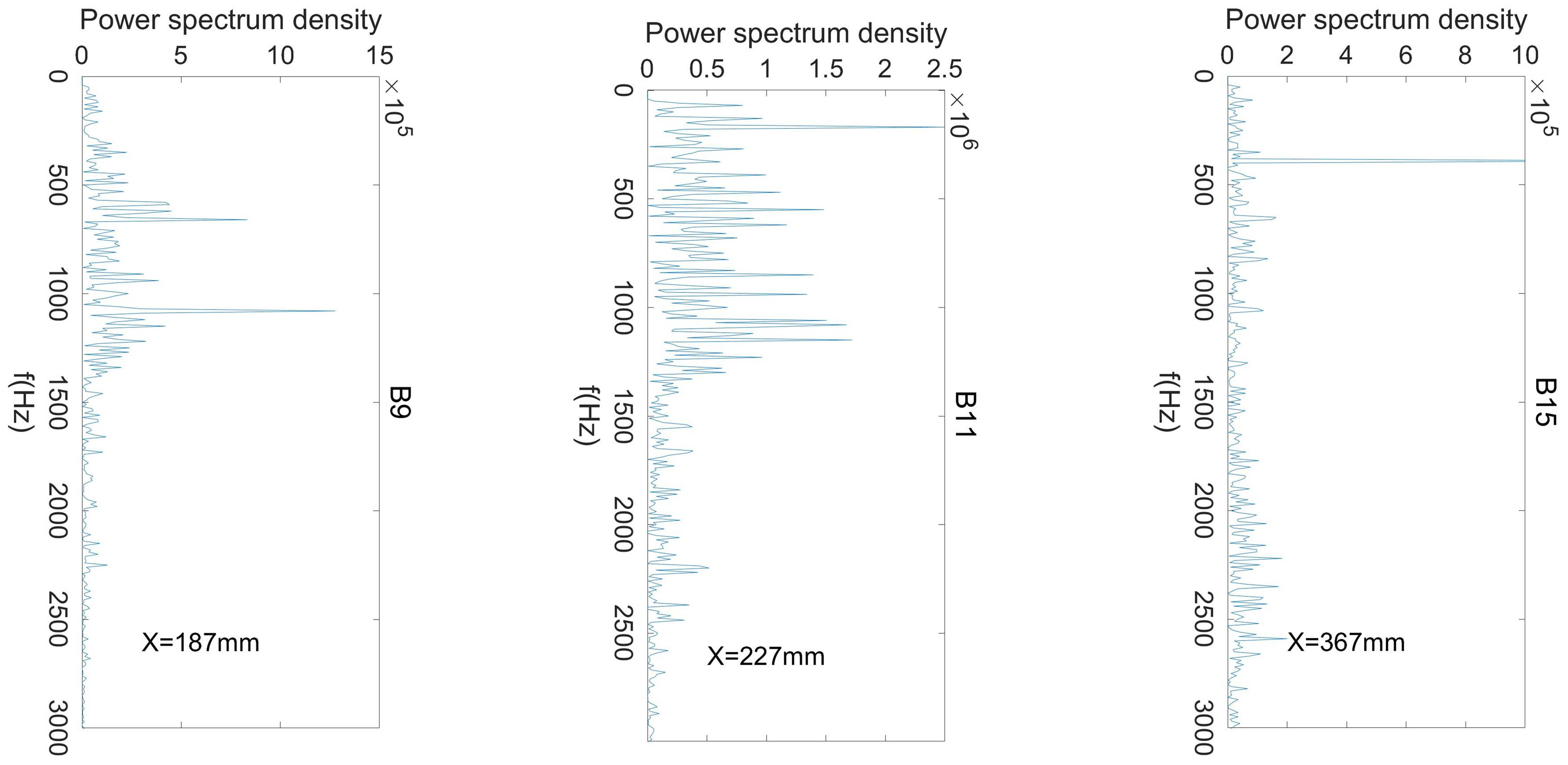
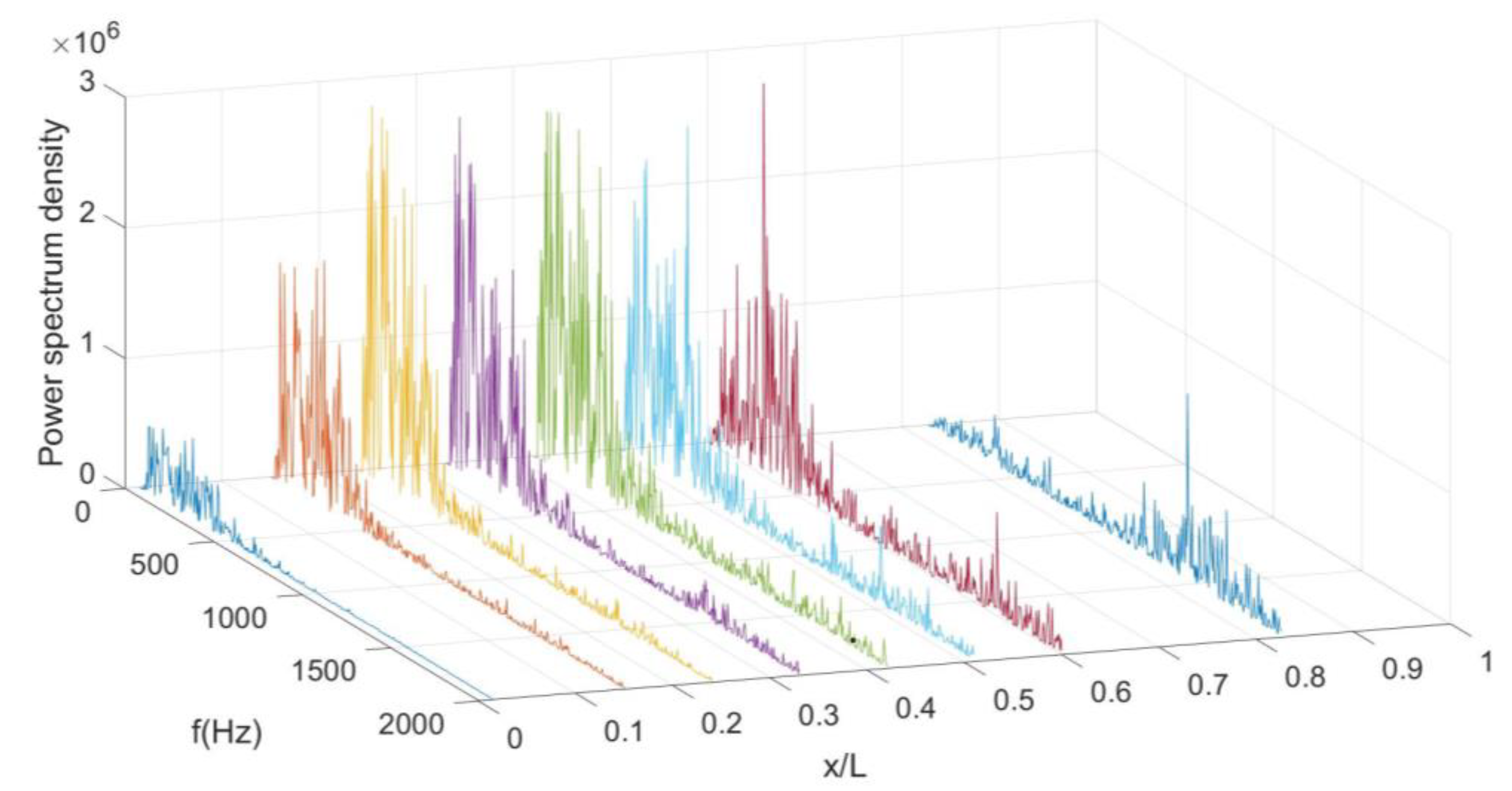
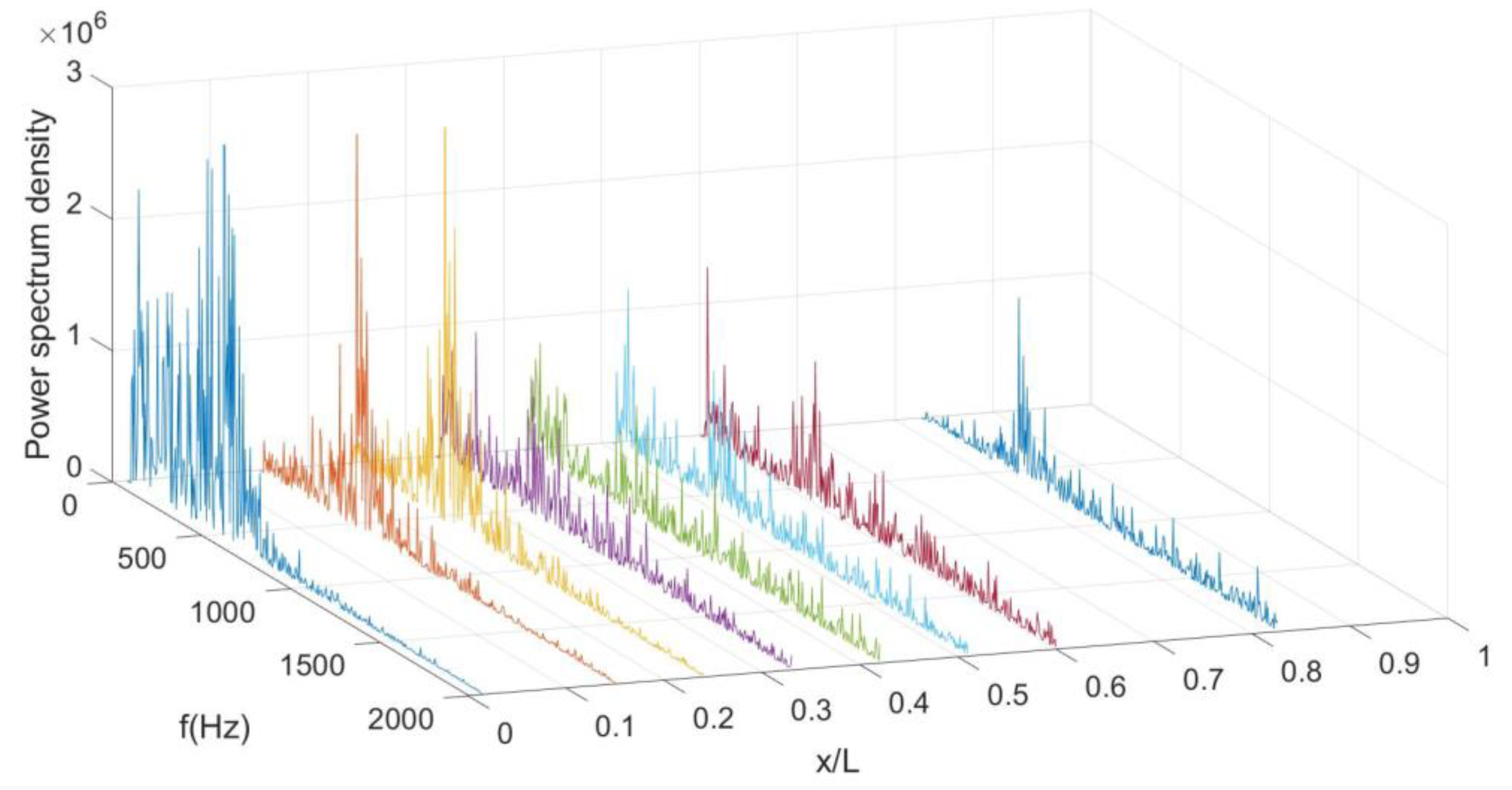
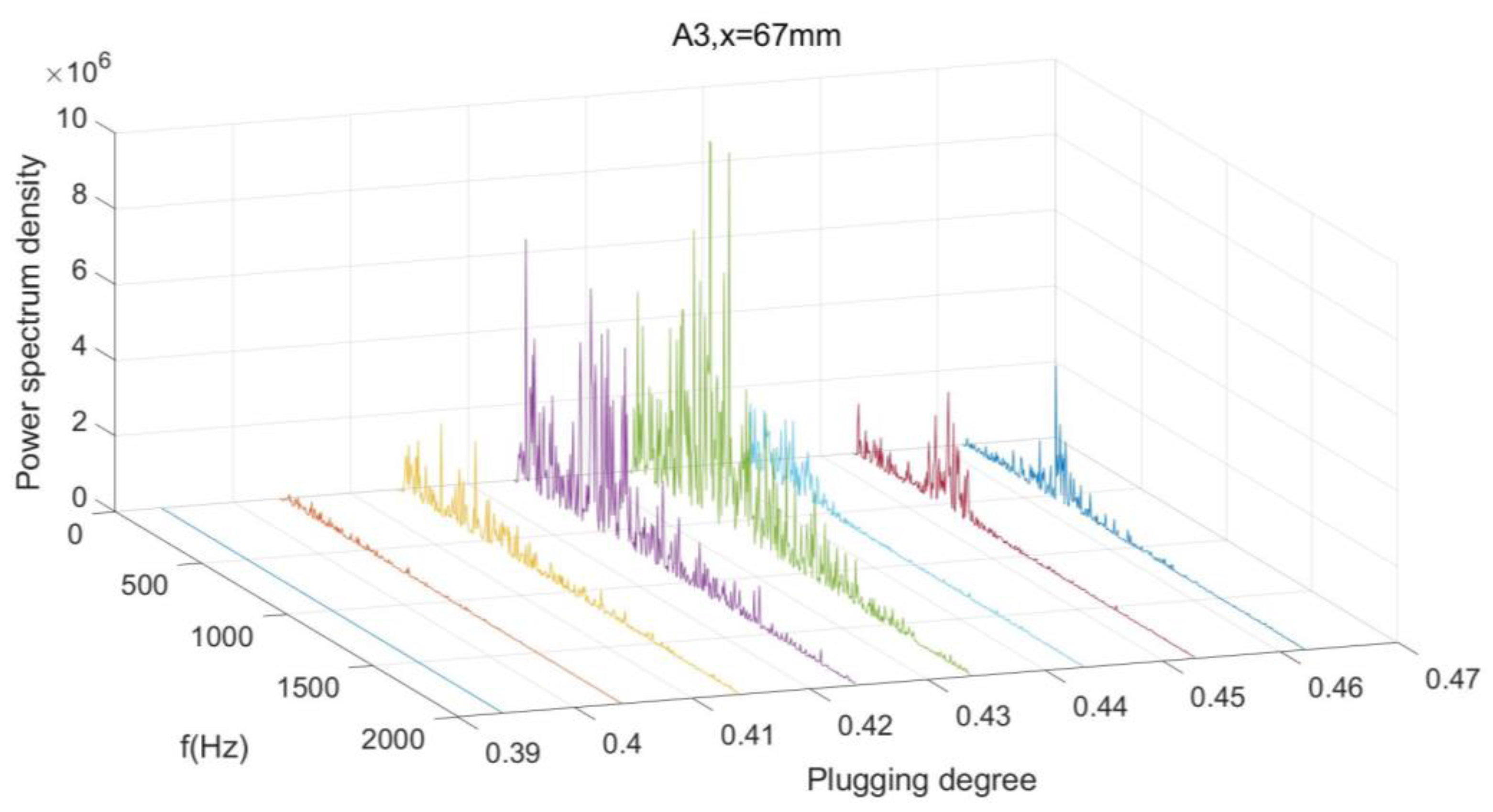
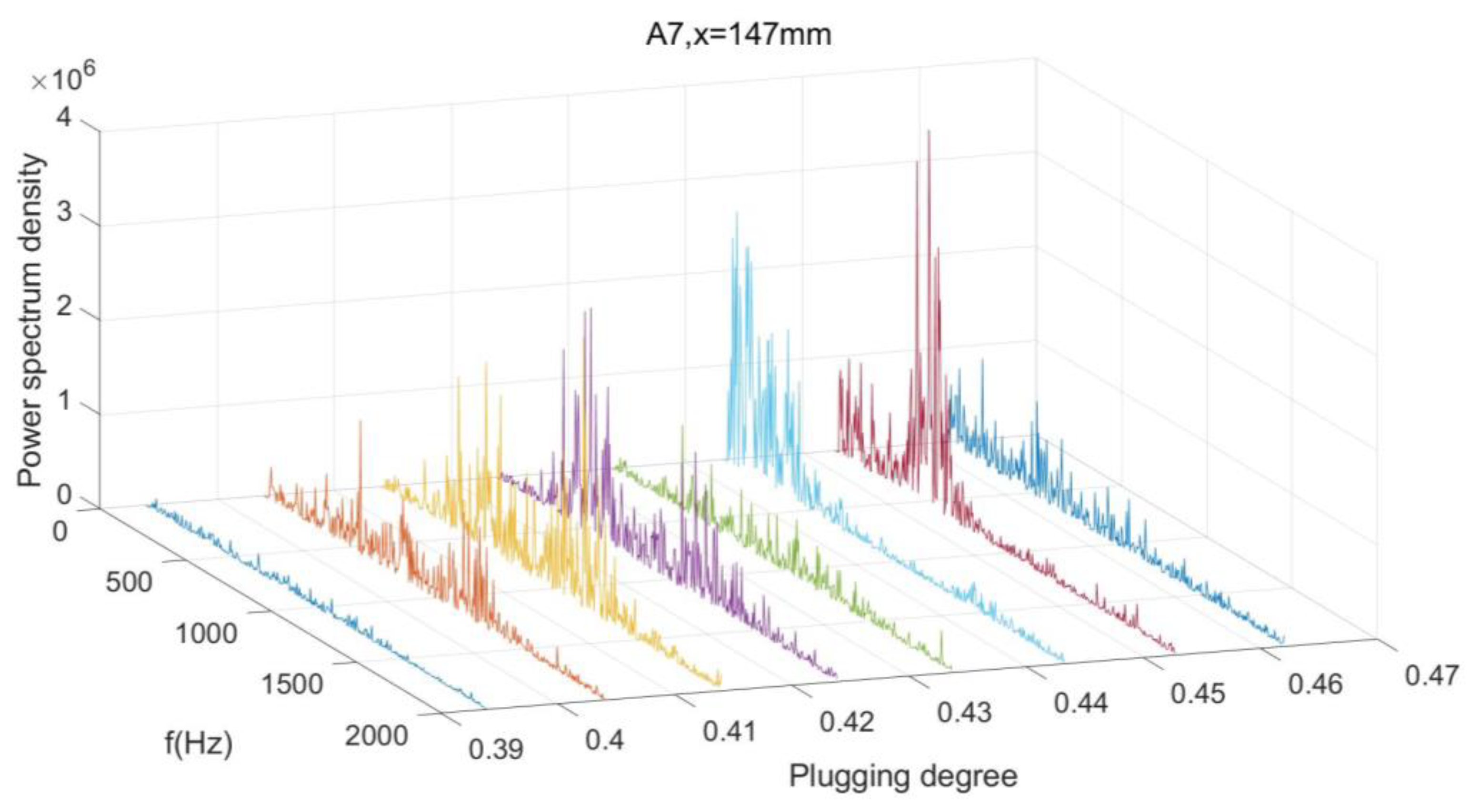
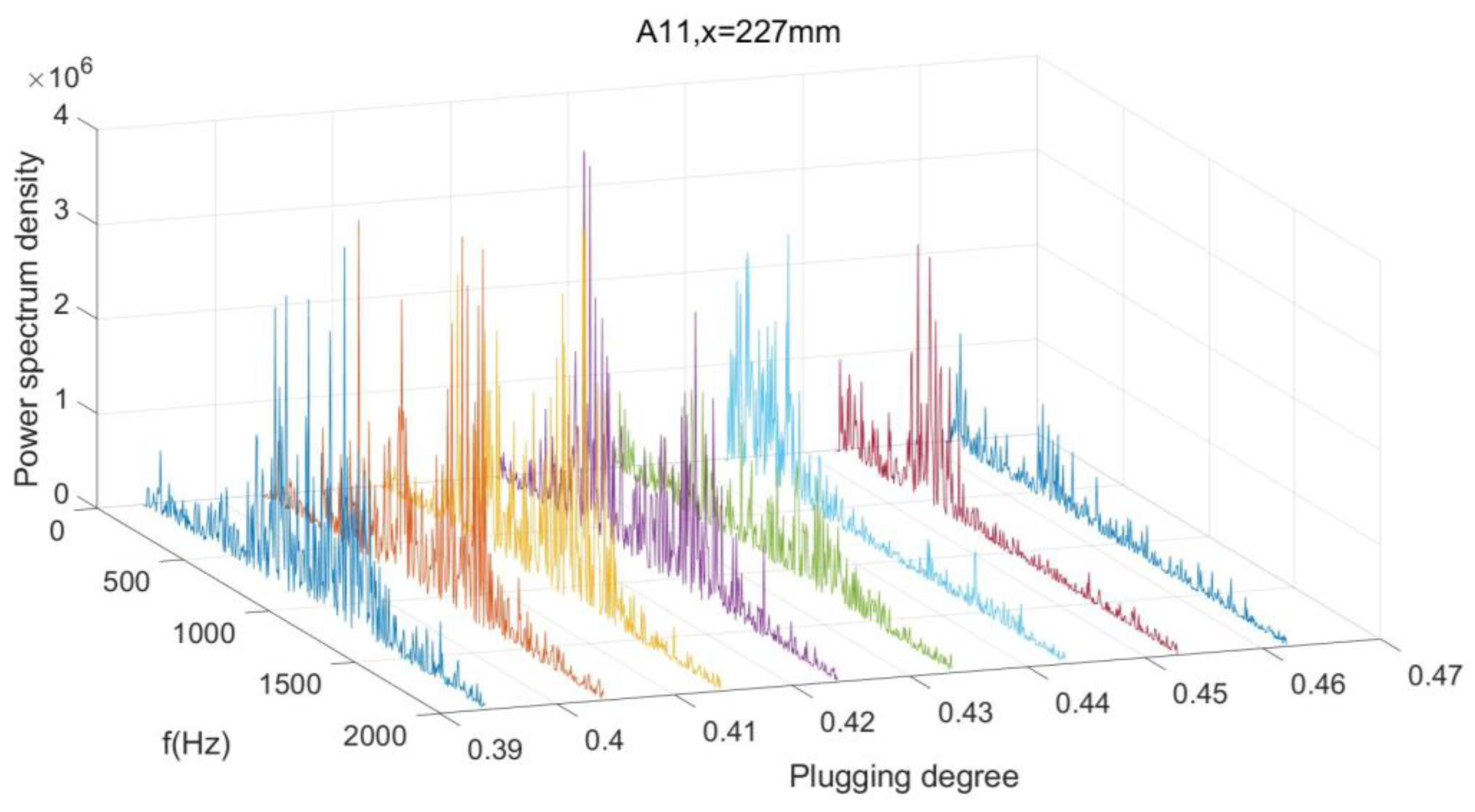
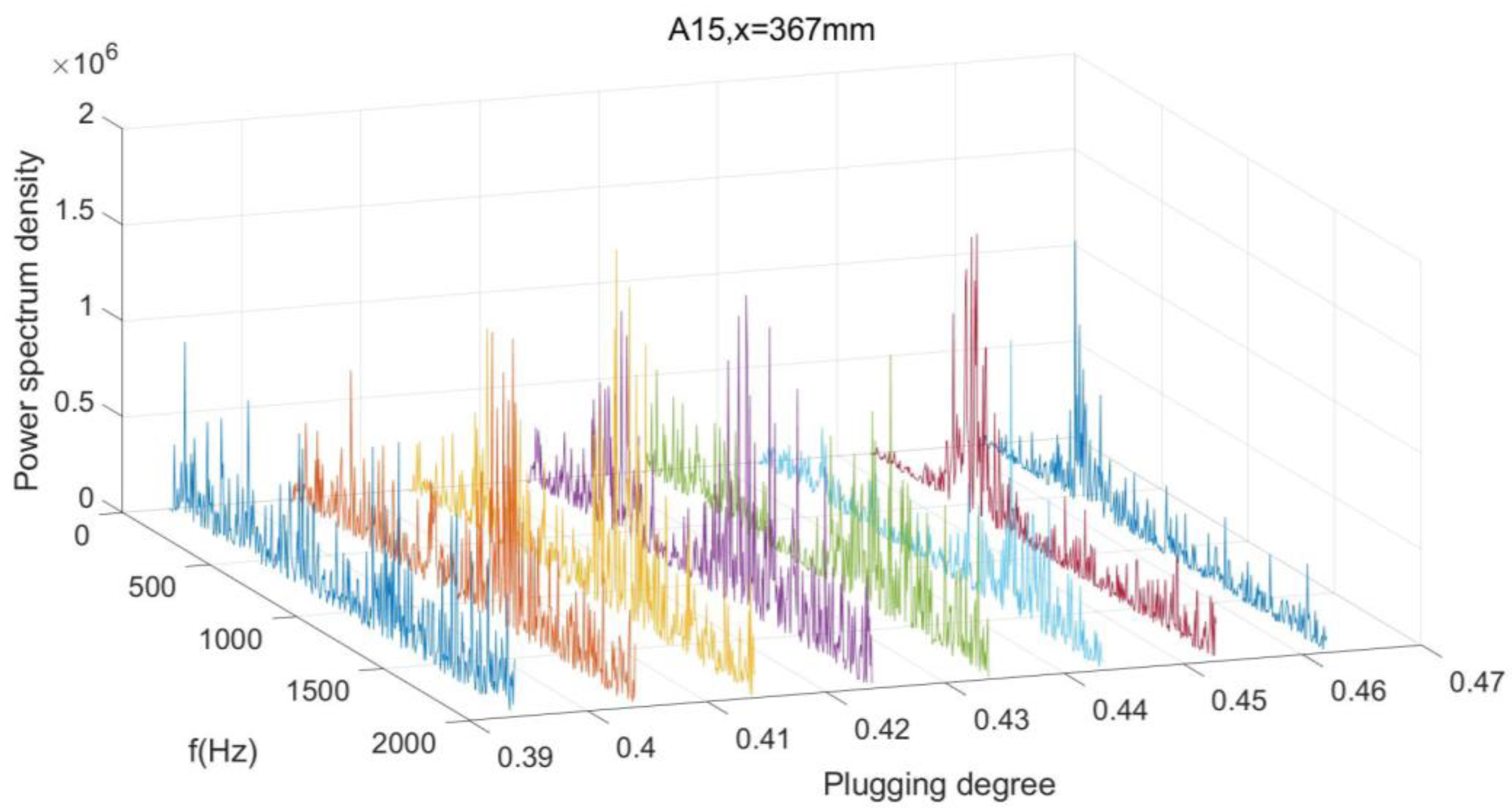
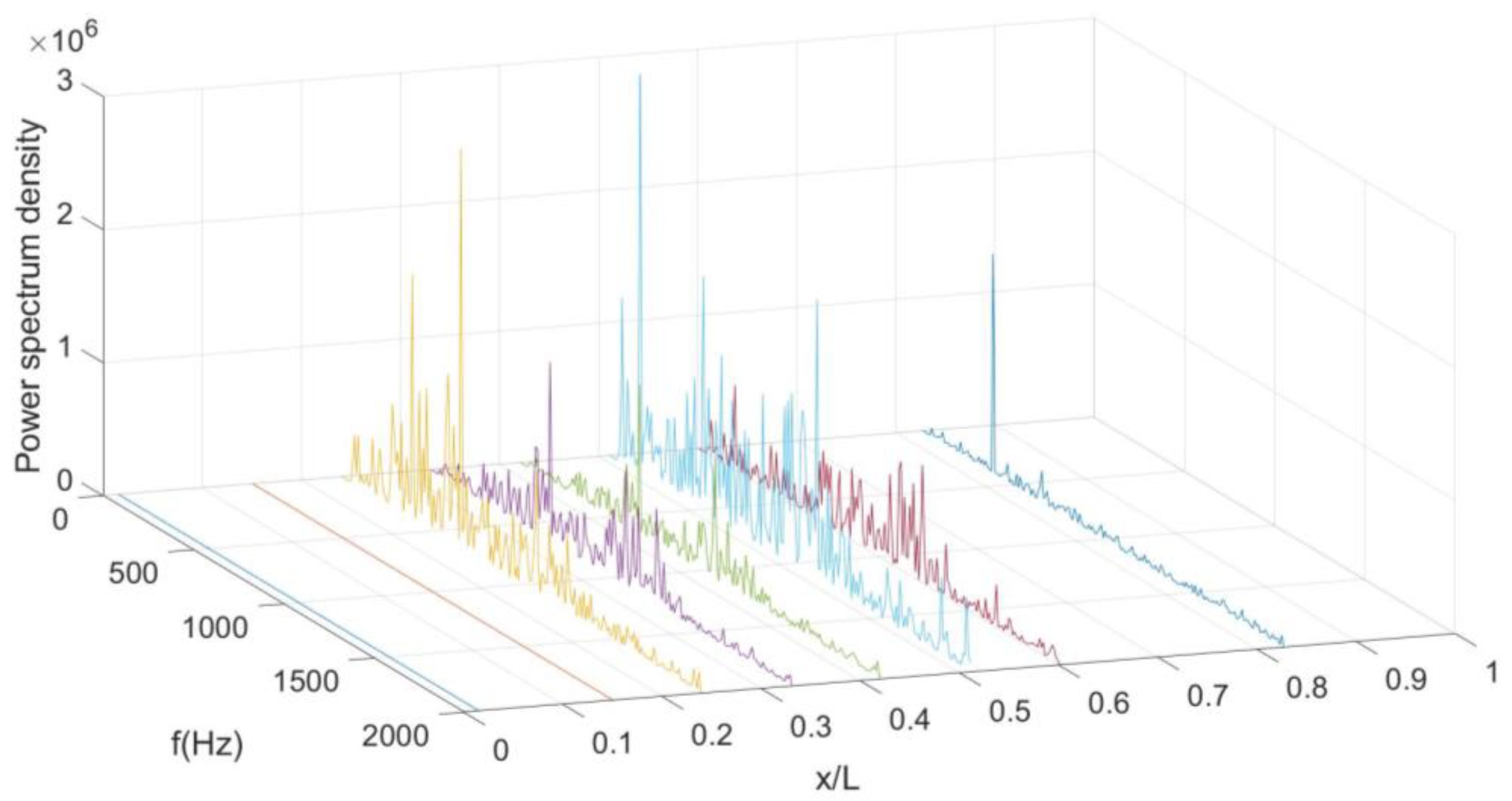
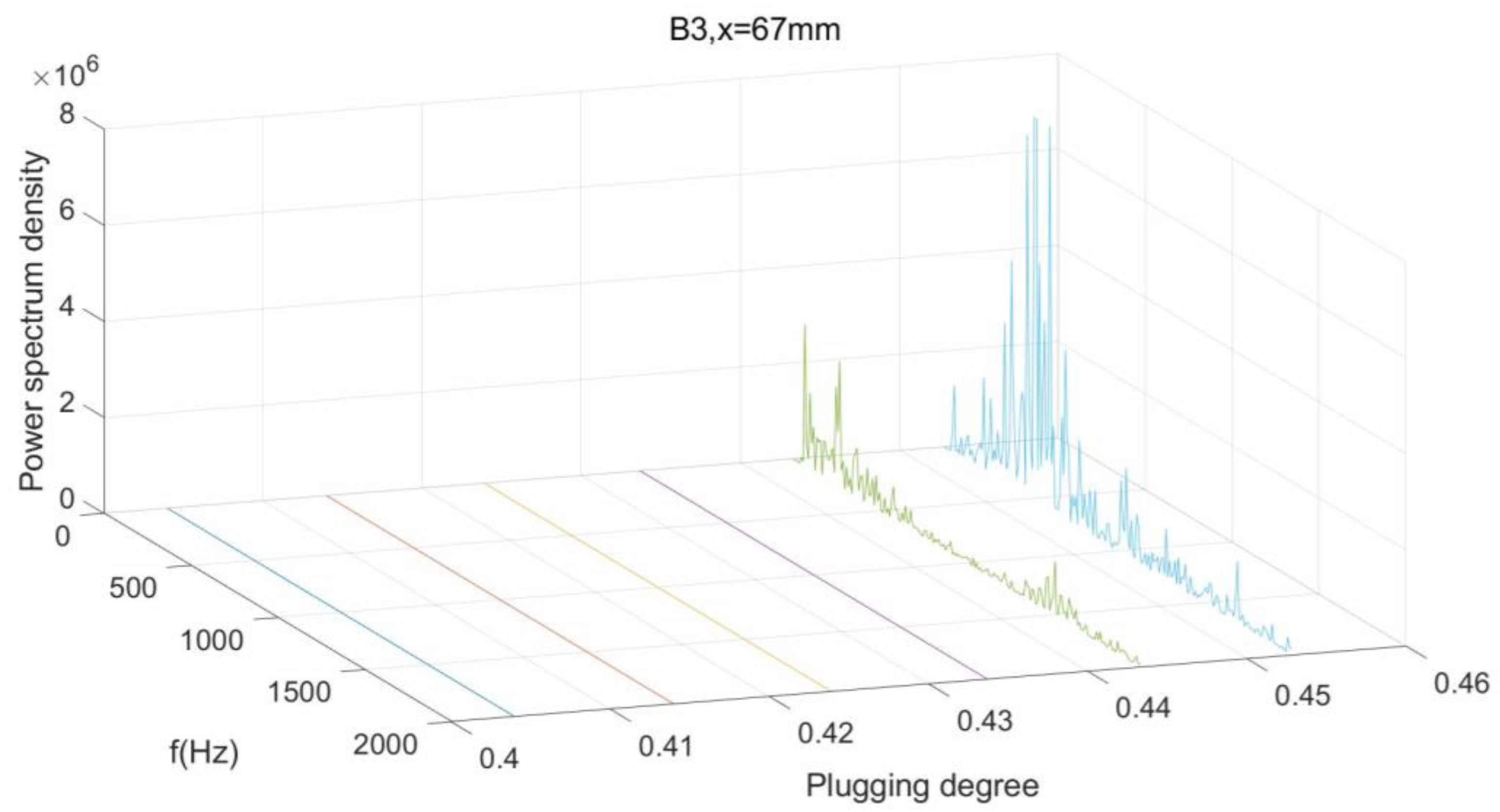
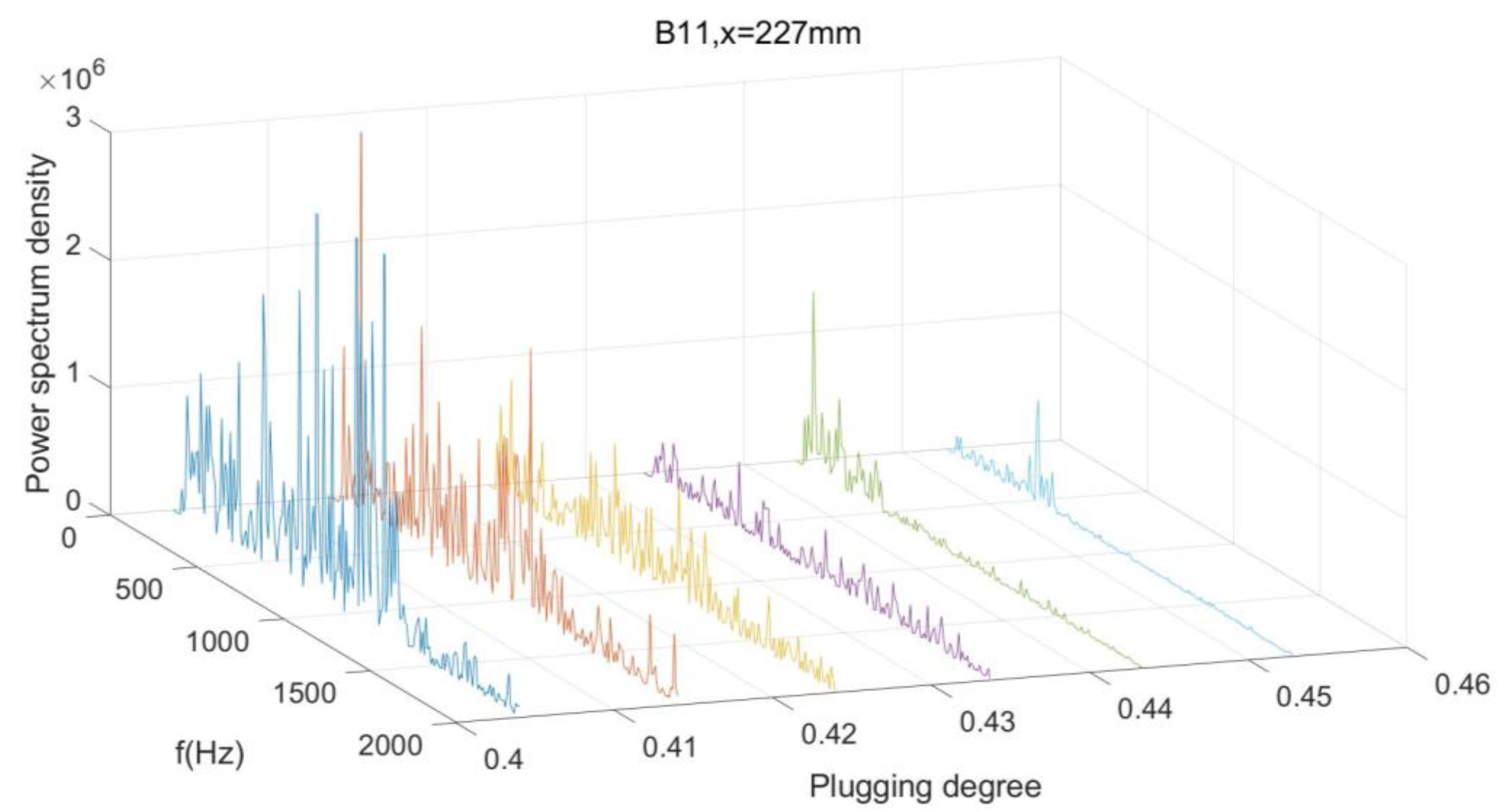
3.3. Power Spectrum Density Analyse of the Wall Pressure Oscillation
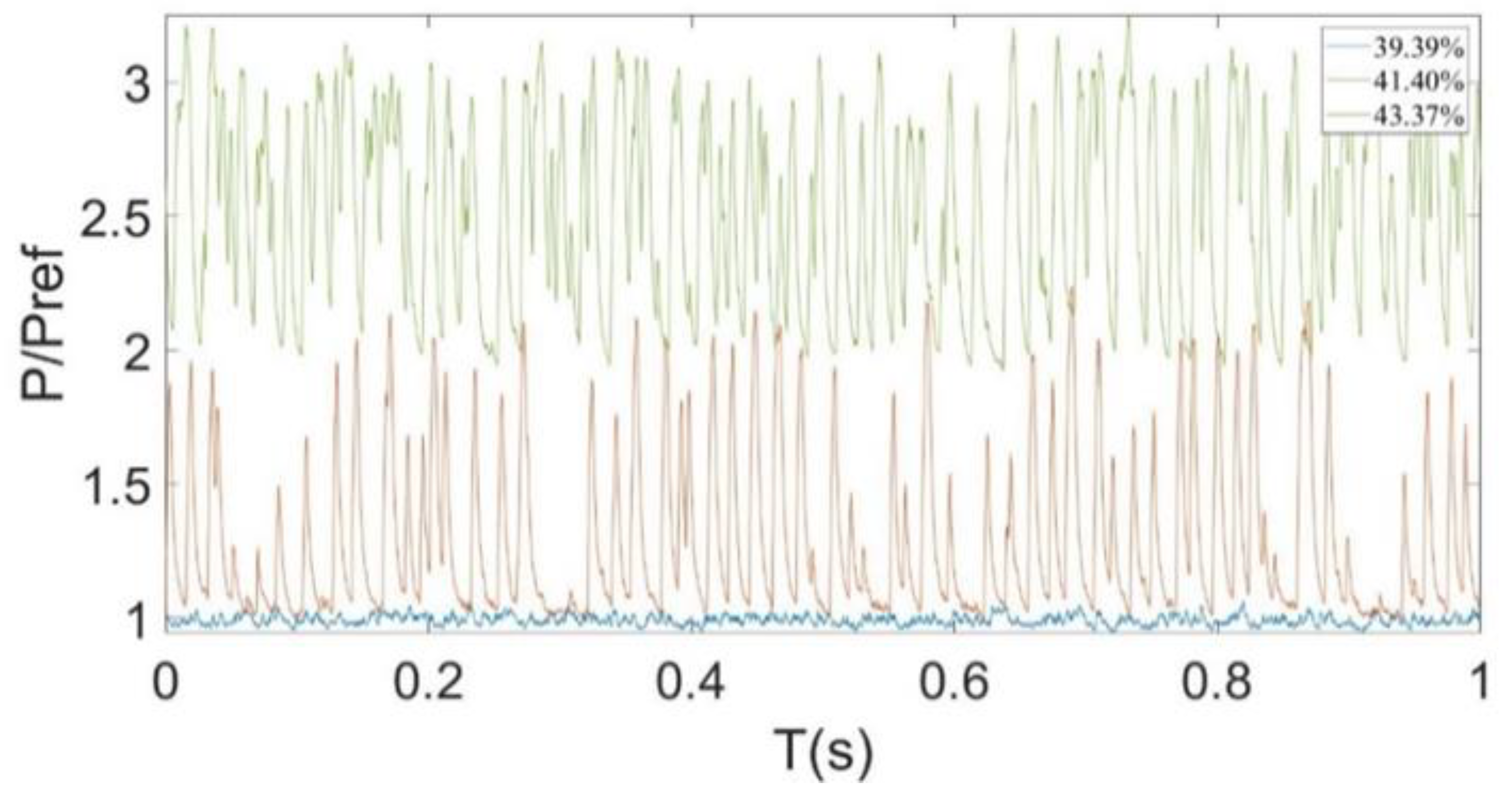
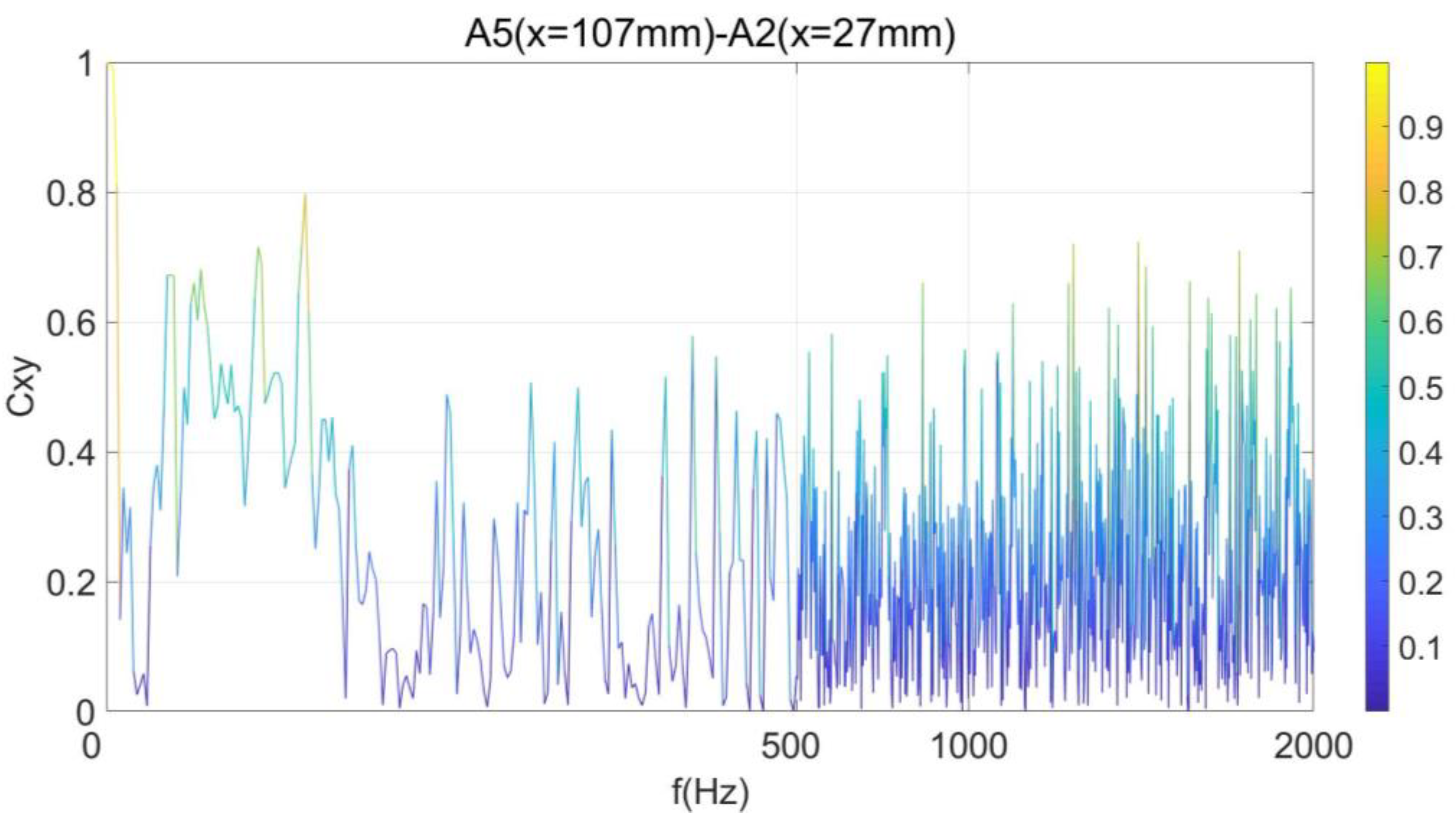
3.4. Analysis of Pressure Oscillation Coherence in the Shock Train Flow Field
4. Conclusions
- The pressure oscillation in the area not affected by the shock train flow field is small and can be ignored. In the shock train flow field, the pressure oscillates most violently near the shock leg. The separation area exhibits low-pressure oscillation energy.
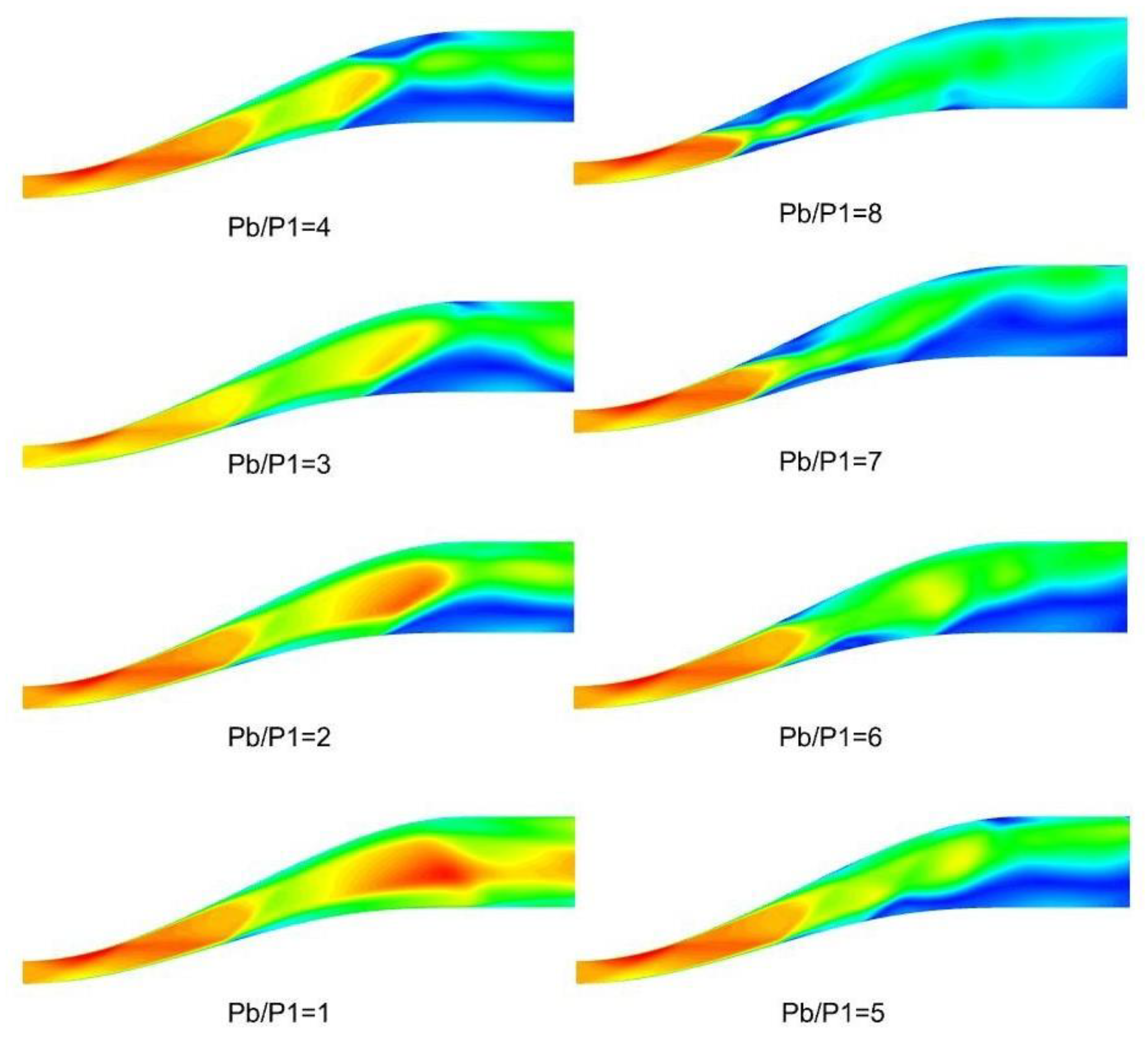
- The shape of the shock waves in the S-shaped isolator of the variable cross-section is asymmetrical, and the positions of shock legs on the upper and lower walls are inconsistent.
- The propagation speed of the shock train in the isolator of the variable section is not constant; however, it propagates slowly in the area involving rapid turning and quickly in the area involving gentle turning.
- It is difficult for the energy of a low-frequency oscillation to propagate from front to back in the shock flow field, while it is easier for the energy of a high-frequency oscillation. The frequency of oscillation is related to the local flow scale. The lower the pressure oscillation energy, the closer the oscillation is to the downstream region of the shock flow field.
- The boundary layer large separation mode of the shock wave flow field in the isolator section switches between the top and bottom walls, and the pressure oscillation frequency is low in the large separation area.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Waltrup, P.J.; Billig, F.S. Structure of shock waves in cylindrical ducts. AIAA J. 1973, 11, 1404–1408. [Google Scholar] [CrossRef]
- Waltrup, P.J.; Dugger, G.L.; Billig, F.S. Direct-connect test of hydrogen-fueled supersonic combustion. Symp. Combust. 1977, 16, 1619–1629. [Google Scholar] [CrossRef]
- Billig, F.S. Research on supersonic combustion. In Proceedings of the AIAA Aerospace Science Meeting, Reno, NV, USA, 6–9 January 1992. [Google Scholar]
- Billig, F.S.; Dugger, G.L. The interaction of shock wave and heat addition in the design of supersonic combustors. Symp. Combust. 1969, 12, 1125–1139. [Google Scholar] [CrossRef]
- Tian, X. Investigation of Flow in a Variable Cross-Section Isolator. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2008. [Google Scholar]
- Gao, L. Research on Isolators with Non-Constant Section and Complicated Condition. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2011. [Google Scholar]
- Tan, H.-J.; Guo, R.-W. Characteristics of Shock Train in Two Dimensional Bends with Constant Area. Acta Aeronaut. Astronaut. Sin. 2006, 27, 1039–1045. [Google Scholar]
- Chen, J.-F.; Fan, X.-Q.; Meng, Z.; Xiong, B.; Wang, Y. Parameterization and Optimization for Variable Cross-Sections Bend Isolator. J. Propuls. Technol. 2020, 41, 1023–1030. [Google Scholar]
- Wang, C.; Zhang, K.; Cheng, K. Effects of Incoming Flow Asymmetry on Shock Train Structures in Constant-Area Isolators. Trans. Nanjing Univ. Aeronaut. Astronaut. 2006, 23, 1–7. [Google Scholar]
- Ding, M.; Li, H.; Fan, X.-Q. Numerical Simulation of Shock Train in a Constant Area Isolator. J. Natl. Univ. Def. Technol. 2001, 23, 15–18. [Google Scholar]
- Wang, D.-P.; Zhao, W.-Z.; Sugiyama, H.; Tojo, A. Numerical and Experimental Investigations of Mach 4 Pseudo-Shock Waves in a Two-dimensional Square Duct. Acta Aeronaut. Astronaut. Sin. 2005, 26, 392–396. [Google Scholar]
- Guo, S.; Wang, Z.; Zhao, Y. The flow hysteresis in the supersonic curved channel. J. Natl. Univ. Def. Technol. 2014, 36, 10–14. [Google Scholar]
- Li, T. Study on Hysteresis Phenomenon Caused by Back Pressure in Curved Isolator. Master’s Thesis, National University of Defense Technology, Changsha, China, 2015. [Google Scholar]
- Zhang, H. Characteristics of Shock-Train at Complicated Geometrical and Incoming Flow Conditions. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2009. [Google Scholar]
- Xiong, B.; Fan, X.-Q.; Wang, Z. Oscillation characteristics of shock train in deflected center-line isolator. J. Aerosp. Power 2016, 30, 1669–1675. [Google Scholar]
- Xiong, B.; Fan, X.-Q.; Tao, Y.; Li, T. Influence of deflected center-line on performance of isolator. J. Rocket Propuls. 2016, 42, 35–41. [Google Scholar]
- Huang, H.; Tan, H.; Sun, S.; Wang, Z. Behavior of shock train in curved isolators with complex background waves. AIAA J. 2018, 56, 329–341. [Google Scholar] [CrossRef]
- An, B.; Fan, X.-Q.; Li, T.; Xiong, B. Numerical investigation on characteristics of shock train in S-shaped isolation section in scramjet engine. J. Rocket Propuls. 2016, 42, 47–52. [Google Scholar]
- Tan, H.; Sun, S. Preliminary Study of Shock Train in a Curved Variable-Section Diffuser. J. Propuls. Power 2008, 24, 245–252. [Google Scholar] [CrossRef]
- Kawatsu, K.; Koike, S.; Kumasaka, T.; Masuya, G.; Takita, K. Pseudo-Shock Wave Produced by Backpressure in Straight and DivergingRectangular Ducts. In Proceedings of the AIAA/CIRA 13th International Space Planes and Hypersonics Systems and Technologies, Sendai, Japan, 20–24 June 2005. [Google Scholar]


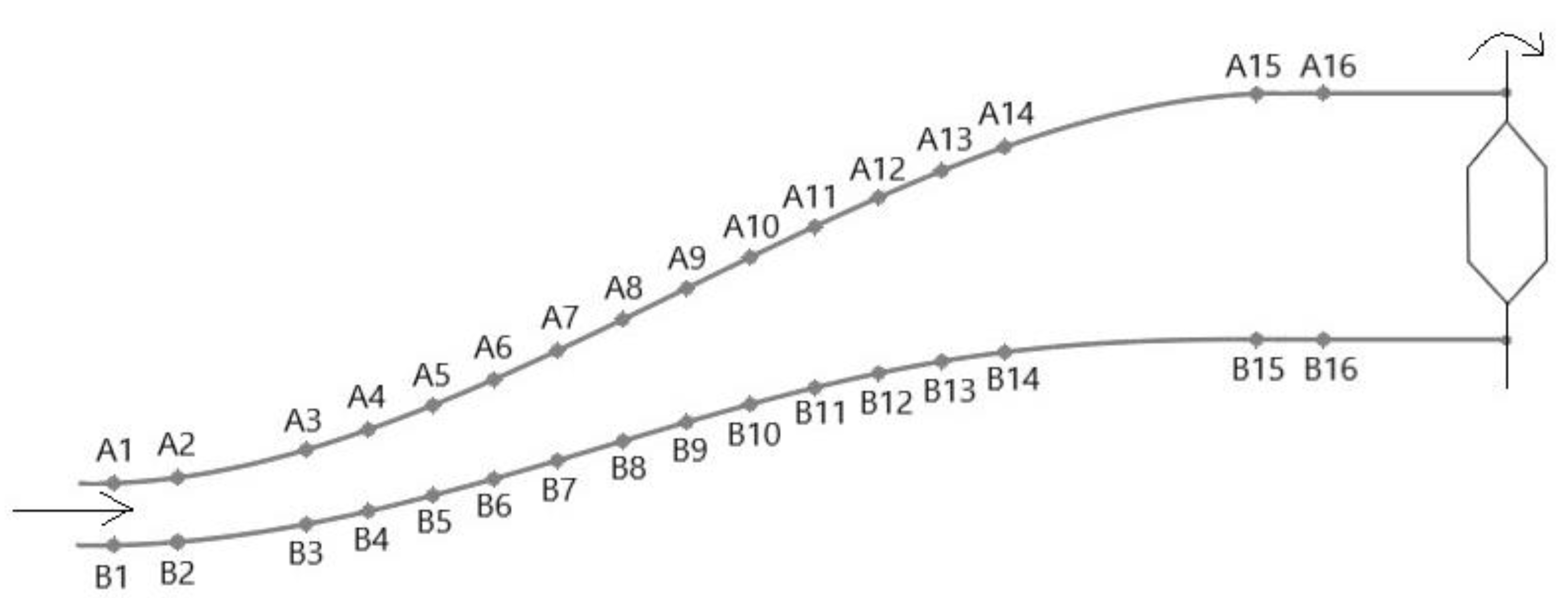

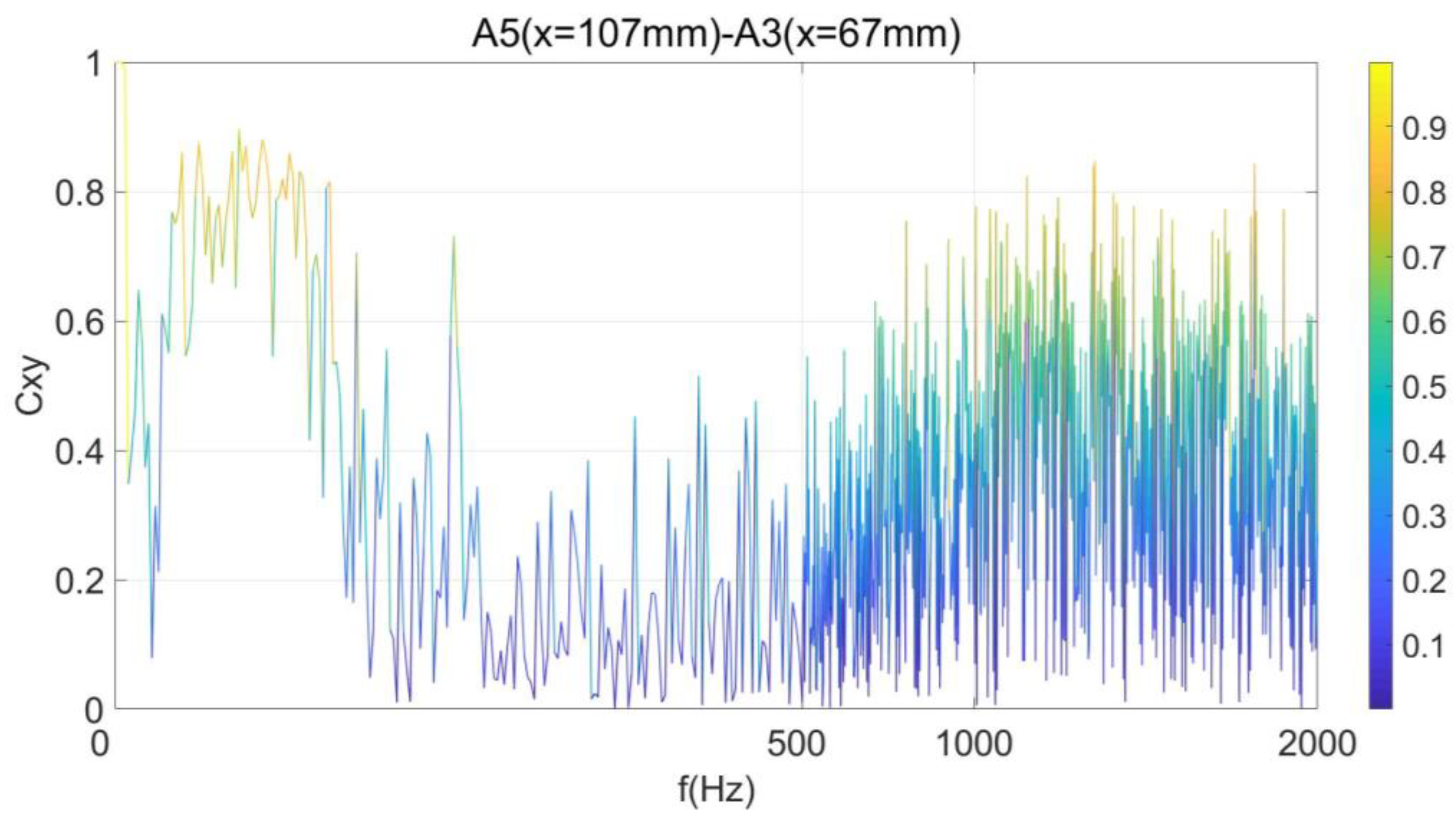

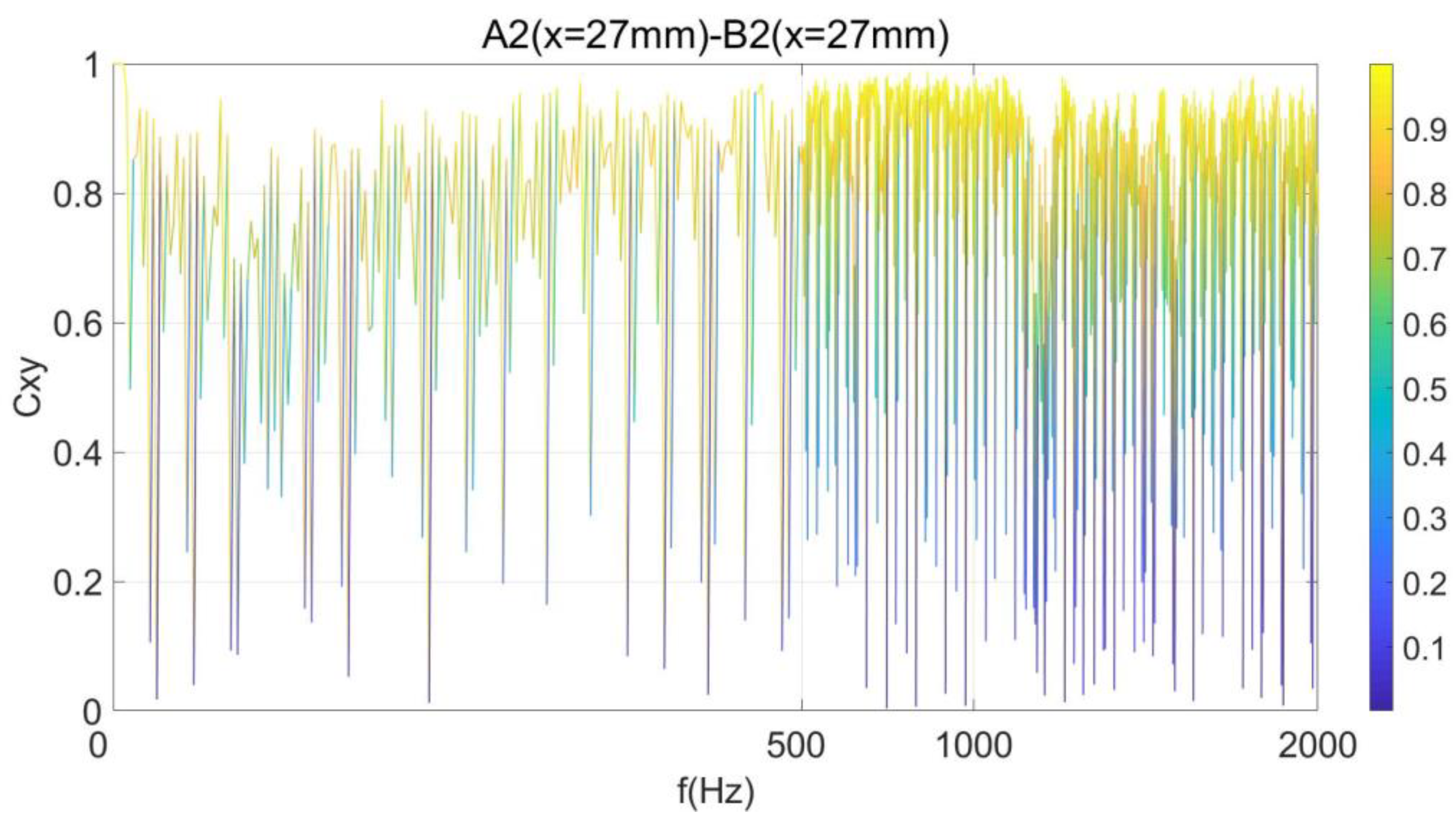
| Sensor | A1, B1 | A2, B2 | A3, B3 | A4, B4 | A5, B5 | A6, B6 | A7, B7 | A8, B8 | A9, B9 | A10, B10 | A11, B11 | A12, B12 | A13, B13 | A14, B14 | A15, B15 | A16, B16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x (mm) | 7 | 27 | 67 | 87 | 107 | 127 | 147 | 167 | 187 | 207 | 227 | 247 | 267 | 287 | 367 | 387 |
| Location | A1–A3 | A3–A5 | A5–A7 | A7–A9 | A9–A11 |
|---|---|---|---|---|---|
| Speed (mm/s) | 12.70 | 23.26 | 71.43 | 5.87 | 6.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Y.; Fan, X.; Xiong, B. Structural Characteristics of a Shock Train Flow Field in a Variable Cross-Section S-Shaped Isolator. Aerospace 2023, 10, 2. https://doi.org/10.3390/aerospace10010002
Yan Y, Fan X, Xiong B. Structural Characteristics of a Shock Train Flow Field in a Variable Cross-Section S-Shaped Isolator. Aerospace. 2023; 10(1):2. https://doi.org/10.3390/aerospace10010002
Chicago/Turabian StyleYan, Yuepeng, Xiaoqiang Fan, and Bing Xiong. 2023. "Structural Characteristics of a Shock Train Flow Field in a Variable Cross-Section S-Shaped Isolator" Aerospace 10, no. 1: 2. https://doi.org/10.3390/aerospace10010002
APA StyleYan, Y., Fan, X., & Xiong, B. (2023). Structural Characteristics of a Shock Train Flow Field in a Variable Cross-Section S-Shaped Isolator. Aerospace, 10(1), 2. https://doi.org/10.3390/aerospace10010002





