Solar and Anthropogenic Influences on Climate: Regression Analysis and Tentative Predictions
Abstract
1. Introduction
2. Double Regression Analysis
2.1. Data
2.1.1. Temperature Data
2.1.2. Geomagnetic aa Index Data
2.1.3. CO Data
2.2. The Most Relevant Data and Their Correlations
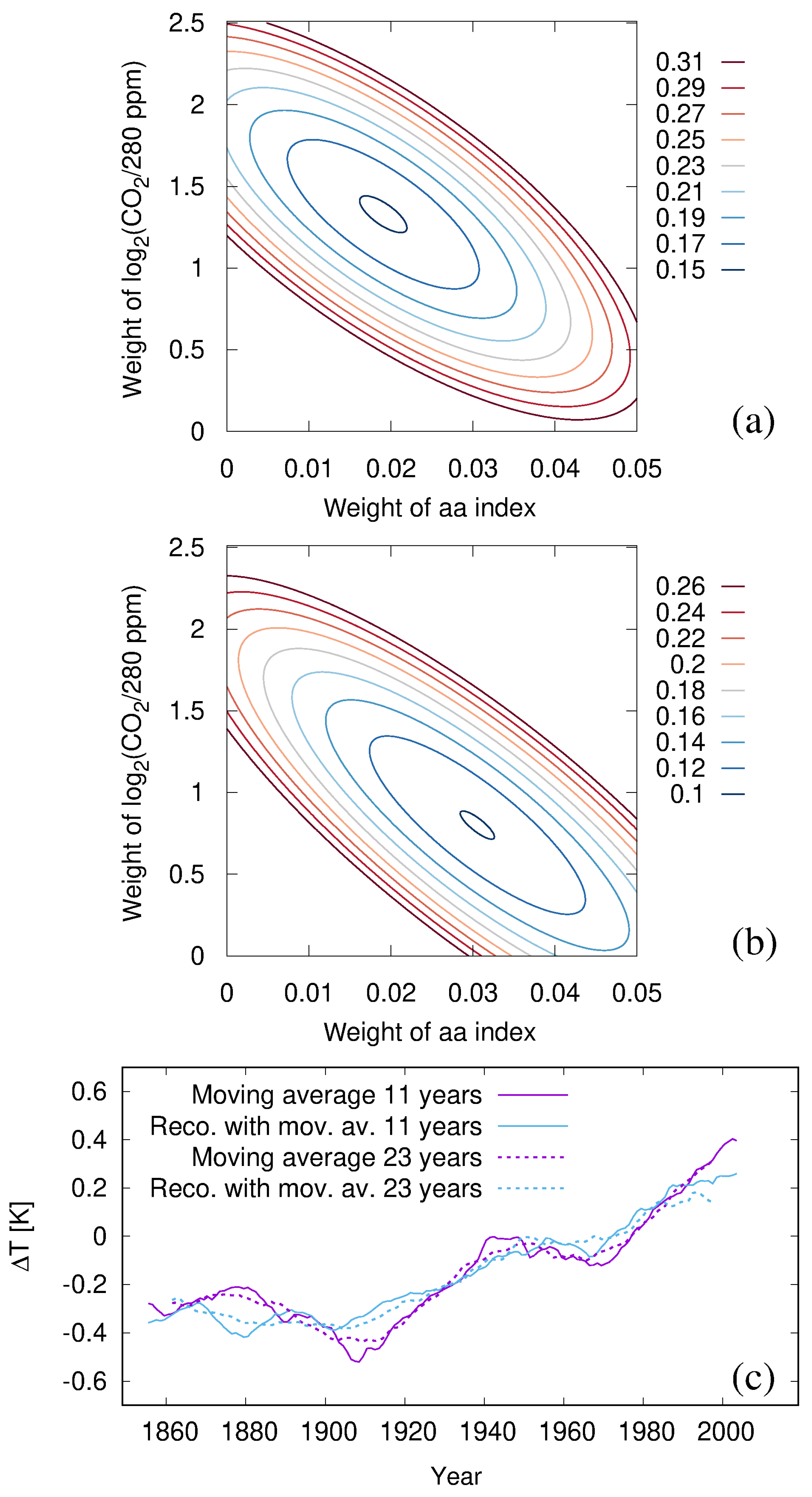
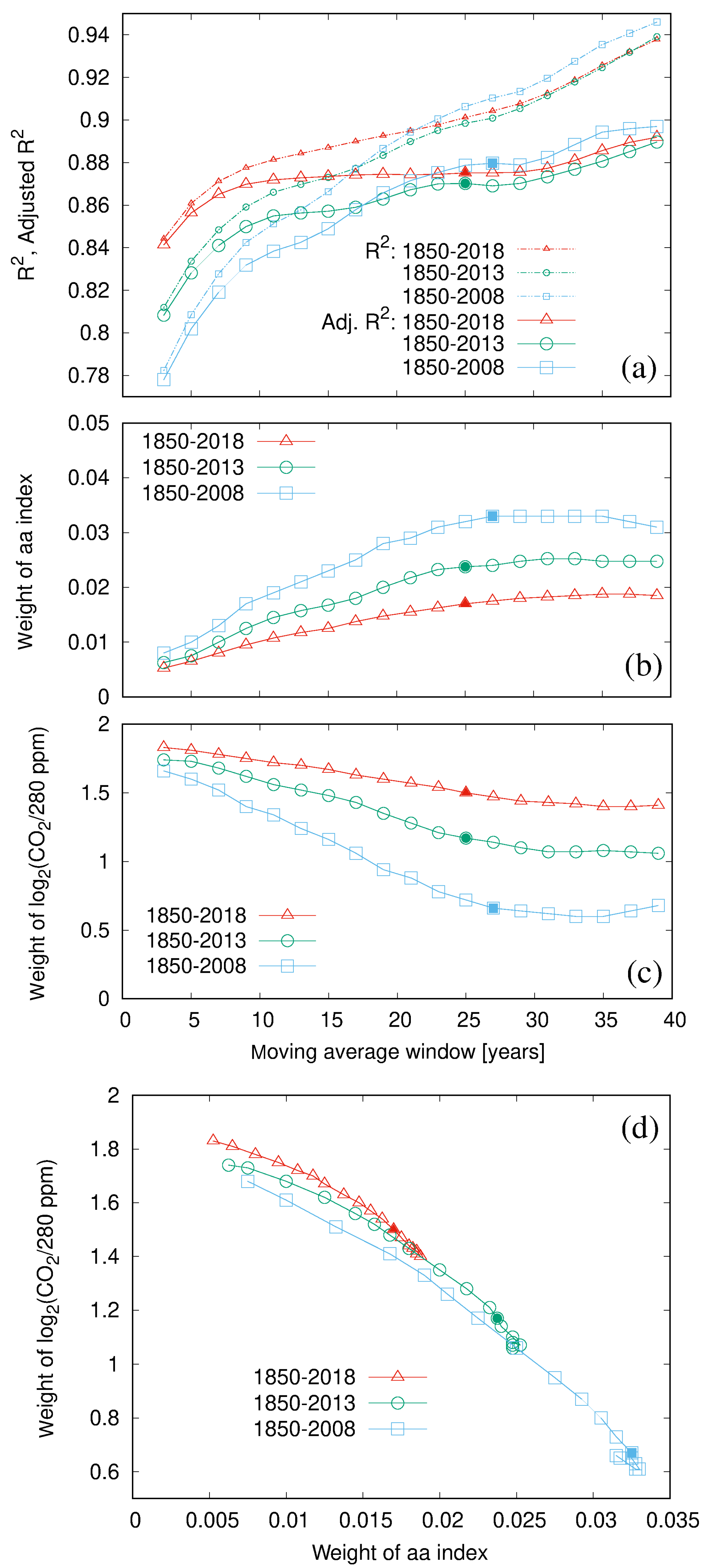
2.3. Regression
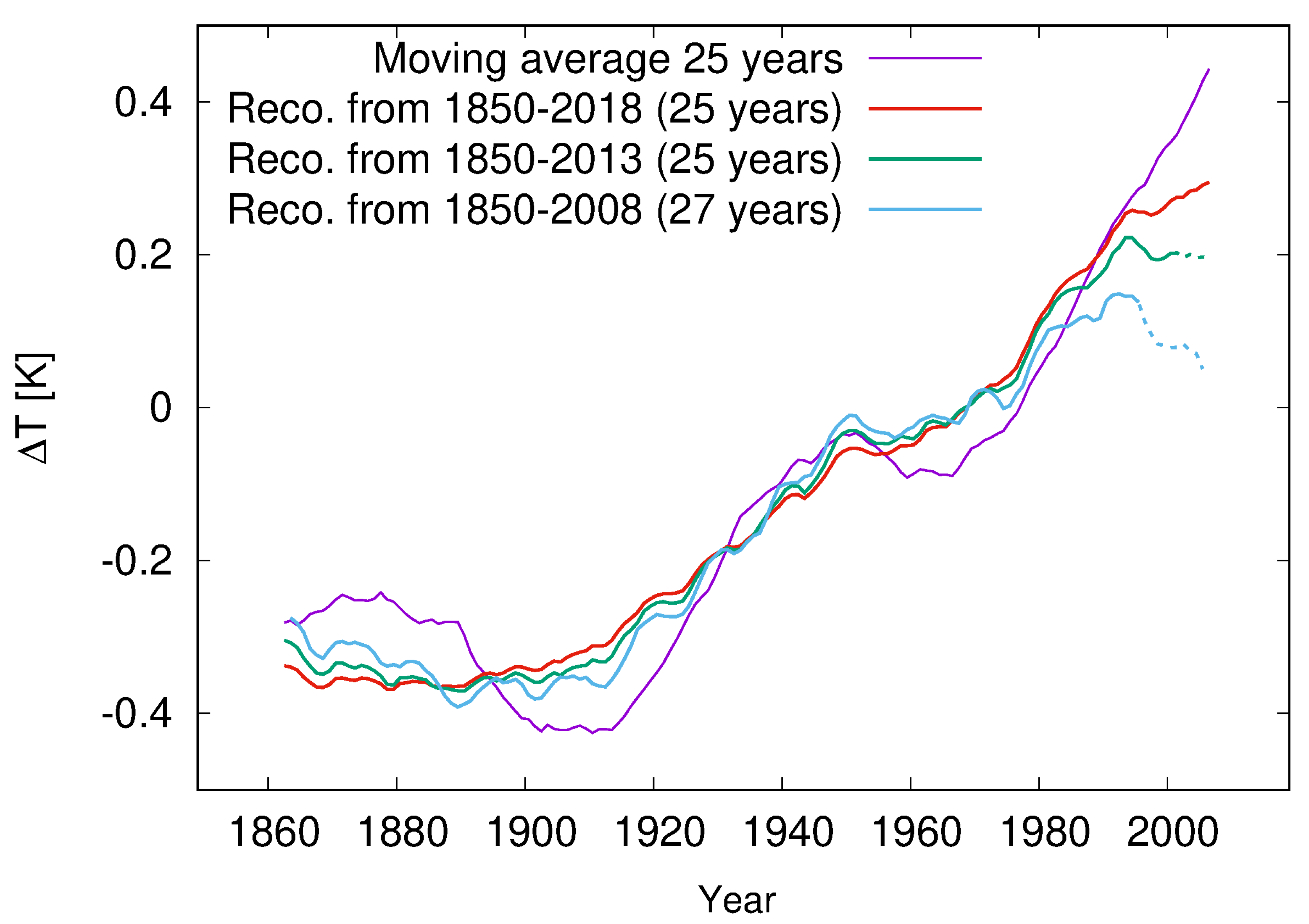
2.4. Some Plausibility Checks and Comparisons
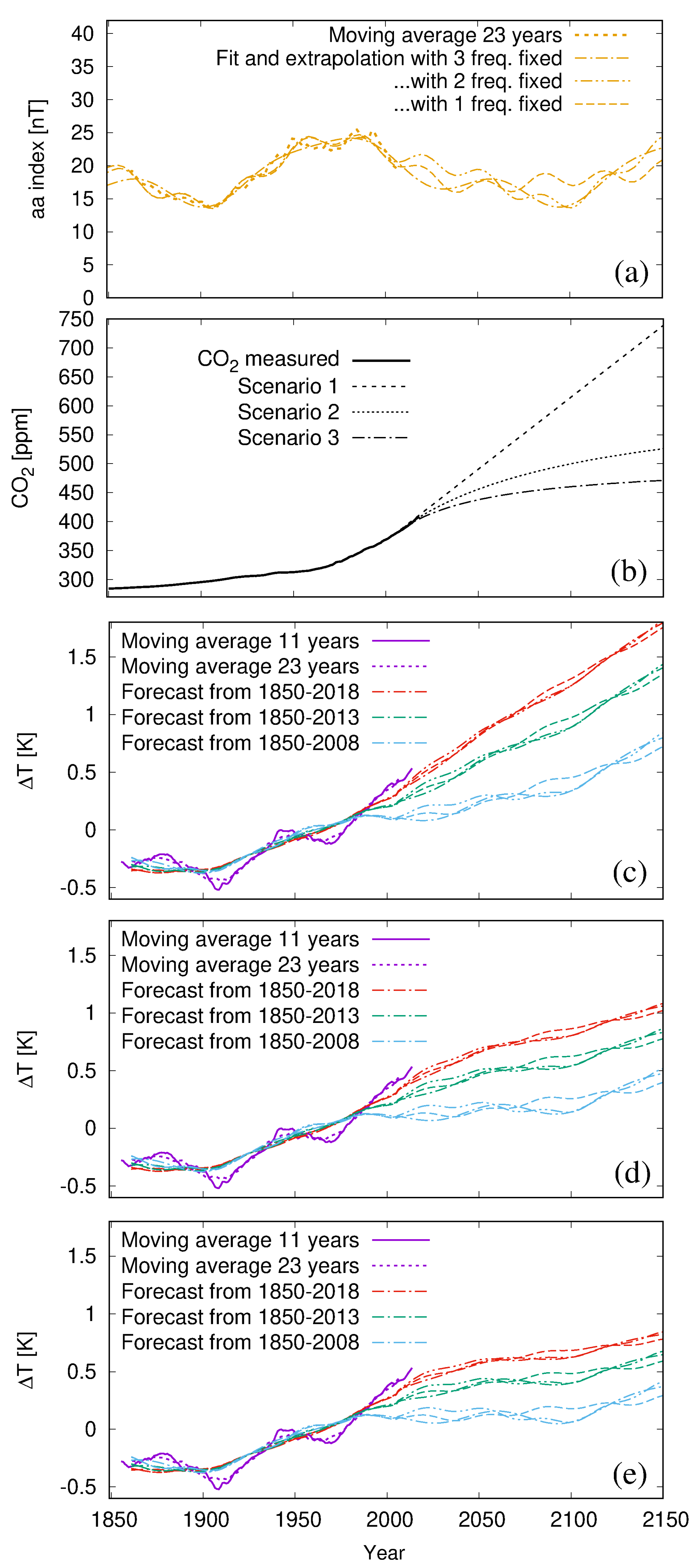
3. Predictions
3.1. Predicting the Solar Dynamo
3.2. Some Scenarios
4. Summary and Discussion
5. Conclusions and Outlook
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arrhenius, S. Die vermutliche Ursache der Klimaschwankungen. Medd. Kungl. Vetenskpasakad. Nobelinst. 1906, 1, 1–10. [Google Scholar]
- Callendar, G.S. The artificial production of carbon dioxide and its influence on temperature. Q. J. R. Meteorol. Soc. 1938, 64, 223–240. [Google Scholar] [CrossRef]
- Knutti, R.; Rugenstein, M.A.A.; Hegerl, G.C. Beyond equilibrium climate sensitivity. Nat. Geosci. 2017, 10, 727–736. [Google Scholar] [CrossRef]
- Charney, J.G.; Arakawa, A.; Baker, D.J.; Bolin, B.; Dickinson, R.E.; Goody, R.M.; Leith, C.E.; Stommel, H.M.; Wunsch, C.I. Carbon Dioxide and Climate: A Scientific Assessment; National Academy of Sciences Press: Washington, DC, USA, 1979. [Google Scholar]
- Lindzen, R.S. An oversimplified picture of the climate behavior based on a single process can lead to distorted conclusions. Eur. Phys. J. Plus 2020, 135, 462. [Google Scholar] [CrossRef]
- Vahrenholt, F.; Lüning, S. Unerwünschte Wahrheiten: Was Sie über den Klimawandel Wissen Sollten; Langen-Müller: Munich, Germany, 2020. [Google Scholar]
- Hoyt, D.V.; Schatten, K.H. A discussion of plausible solar irradiance variations. J. Geophys. Res. 1993, 98, 18895–18906. [Google Scholar] [CrossRef]
- Gray, L.J.; Beer, J.; Geller, M.; Haigh, J.D.; Lockwood, M.; Matthes, K.; Cubasch, U.; Fleitmann, D.; Harrison, G.; Hood, L.; et al. Solar influence on climate. Rev. Geophys. 2010, 48, 1–53. [Google Scholar] [CrossRef]
- Lean, J.L. Cycles and trends in solar irradiance and climate? WIREs Clim. Chang. 2010, 1, 111–121. [Google Scholar] [CrossRef]
- Labitzke, K.; van Loon, H. Associations between the 11-year solar cycle, the QBO and the atmosphere. Part 1: The troposphere and stratosphere in the northern hemisphere in winter. J. Atmos. Terr. Phys. 1988, 50, 197–206. [Google Scholar] [CrossRef]
- Haigh, J.D. The role of stratospheric Ozon in modulating the solar radiative forcing of climate. Nature 1994, 370, 544–546. [Google Scholar] [CrossRef]
- Soon, W.H.; Posmentier, E.S.; Baliunas, S.L. Climate hypersensitivity to solar forcing? Ann. Geophys. 2000, 18, 583–588. [Google Scholar] [CrossRef]
- Georgieva, K.; Kirov, B.; Koucka Knizova, P.; Mosna, Z.; Kouba, D.; Asenovska, Y. Solar influence on atmospheric circulation. J. Atmos. Sol.-Terr. Phys. 2012, 90–91, 15–21. [Google Scholar] [CrossRef]
- Silverman, V.; Harnik, N.; Matthes, K.; Lubis, S.W.; Wahl, S. Radiative effects of ozone waves on the Northern Hemisphere polar vortex and its modulation by the QBO. Atmos. Chem. Phys. 2018, 18, 6637–6659. [Google Scholar] [CrossRef]
- Veretenenko, S.; Ogurtsov, M.G. Influence of Solar-geophysical factors on the state of the stratospheric polar vortex. Geomagn. Aeron. 2020, 60, 974–981. [Google Scholar] [CrossRef]
- Svensmark, H.; Friis-Christensen, E. Variations of cosmic ray flux and global cloud coverage—A missing link in solar-climate relationship. J. Atmos. Sol.-Terr. Phys. 1997, 59, 1225–1232. [Google Scholar] [CrossRef]
- Soon, W.H.; Baliunas, S.L.; Posmentier, E.S.; Okeke, P. Variations of solar coronal hole area and terrestrial lower tropospheric air temperature from 1979 to mid-1998: Astronomical forcings of change in earth’s climate? New Astron. 2000, 4, 563–579. [Google Scholar] [CrossRef]
- Shaviv, N.J.; Veizer, J. Celestial driver of Phanerozoic climate? GSA Today 2003, 13, 4–10. [Google Scholar] [CrossRef]
- Svensmark, H.; Enghoff, M.B.; Shaviv, N.J.; Svensmark, J. Increased ionization supports growth of aerosols into cloud condensation nuclei. Nat. Commun. 2017, 8, 2199. [Google Scholar] [CrossRef]
- Bucha, V.; Bucha, V., Jr. Geomagnetic forcing of changes in climate and in the atmospheric circulation. J. Atmos. Sol.-Terr. Phys. 1998, 60, 145–169. [Google Scholar] [CrossRef]
- Tinsley, B.A. Influence of solar wind on the global electric current, and inferred effects on cloud microphysics, temperature, and dynamics in the troposphere. Space Sci. Rev. 2000, 94, 231–258. [Google Scholar] [CrossRef]
- Tinsley, B.A. The global atmospheric electric circuit and its effects on cloud microphysics. Rep. Prog. Phys. 2008, 71, 66801–66900. [Google Scholar] [CrossRef]
- Vos, H.; Brüchmann, C.; Lücke, A.; Negendank, J.F.W.; Schleser, G.H.; Zolitschka, B. Phase Stability of the Solar Schwabe Cycle in Lake Holzmaar, Germany, and GISP2, Greenland, between 10,000 and 9000 cal. BP. In Climate in Historical Times: Towards a Synthesis of Holocene Proxy Data and Climate Models, GKSS School of Environmental Research; Fischer, H., Kumke, T., Lohmann, G., Floser, G., Miller, H., Storch, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 293–317. [Google Scholar]
- Charlson, R.J.; Lovelock, J.E.; Andreae, M.O.; Warren, S.C. Oceanic phytoplankton, atmospheric sulphur, cloud albedo and climate. Nature 1987, 326, 655–661. [Google Scholar] [CrossRef]
- Scafetta, N.; Willson, R.C. ACRIM total solar irradiance satellite composite validation versus TSI proxy models. Astrophys. Space Sci. 2014, 350, 421–442. [Google Scholar] [CrossRef]
- Egorova, T.; Schmutz, W.; Rozanov, E.; Shapiro, A.I.; Usoskin, I.; Beer, J.; Tagirov, R.V.; Peter, T. Revised historical solar irradiance forcing. Astron. Astrophys. 2018, 615, A85. [Google Scholar] [CrossRef]
- Connolly, R.; Soon, W.; Connolly, M.; Baliunas, S.; Berglund, J.; Butler, C.J.; Cionco, R.G.; Elias, A.G.; Fedorov, V.M.; Harde, H.; et al. How much has the Sun influence Northern hemisphere temperature trends. An ongoing debate. Res. Astron. Astrophys. 2021, 21, 131. [Google Scholar] [CrossRef]
- Wang, Y.-M.; Lean, J.L.; Sheeley, N.R., Jr. Modelling the Sun’s magnetic field and irradiance since 1713. Astrophys. J. 2009, 625, 522–538. [Google Scholar] [CrossRef]
- Steinhilber, F.; Beer, J.; Fröhlich, C. Total solar irradiance during the Holocene. Geophys. Res. Lett. 2009, 36, L19704. [Google Scholar] [CrossRef]
- Krivova, N.A.; Vieira, L.E.A.; Solanki, S. Reconstruction of solar spectral irradiance since the Maunder minimum. J. Geophys. Res. Space Phys. 2010, 115, A12112. [Google Scholar] [CrossRef]
- Solanki, S.K. Solar variability and climate change: Is there a link? Astron. Geophys. 2002, 43, 5.9–5.13. [Google Scholar] [CrossRef]
- Courtillot, V.; Gallet, Y.; Le Mouël, J.-L.; Fluteau, F.; Genevey, A. Are there connections between the Earth’s magnetic field and climate? Earth Planet. Sci. Lett. 2007, 253, 328–339. [Google Scholar] [CrossRef]
- Bindoff, N.L.; Stott, P.A.; Achuta Rao, K.M.; Allen, M.R.; Gillett, N.; Gutzler, D.; Hansingo, K.; Hegerl, G.; Hu, Y.; Jain, S.; et al. Detection and Attribution of Climate Change: From Global to Regional. In IPCC AR5 WG1 Ch10; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Wyatt, M.G.; Peters, J.M. A secularly varying hemispheric climate-signal propagation previously detected in instrumental and proxy data not detected in CMIP3 data base. SpringerPlus 2012, 1, 68. [Google Scholar] [CrossRef]
- Pinault, J.-L. Resonant forcing of the climate system in subharmonic modes. J. Mar. Sci. Eng. 2020, 8, 60. [Google Scholar] [CrossRef]
- Pinault, J.-L. Resonantly forced baroclinic waves in the oceans: A new approach to climate variability. J. Mar. Sci. Eng. 2021, 9, 13. [Google Scholar] [CrossRef]
- Cook, J.; Oreskes, N.; Doran, P.T.; Anderegg, W.R.L.; Verheggen, B.; Maibach, E.W.; Carlton, J.S.; Lewandowsky, S.; Skuce, A.G.; Green, S.E.; et al. Consensus on consensus: A synthesis of consensus estimates on human-caused global warming. Environ. Res. Lett. 2016, 11, 048002. [Google Scholar] [CrossRef]
- Parker, E.N. Sunny side of global warming. Nature 1999, 399, 416–417. [Google Scholar] [CrossRef]
- Laubereau, A.; Iglev, H. On the direct impact of the CO2 concentration rise to the global warming. EPL 2013, 104, 29001. [Google Scholar] [CrossRef]
- Feldman, D.R.; Collins, W.D.; Gero, P.J.; Torn, M.S.; Mlawer, E.J.; Shipper, T.R. Observational determination of surfaced radiative forcing by CO2 from 2000 to 2010. Nature 2015, 519, 339–343. [Google Scholar] [CrossRef]
- Rentsch, C.P. Radiative forcing by CO2 observed at top of atmosphere from 2002 to 2019. arXiv 2019, arXiv:1911.10605. [Google Scholar]
- Reid, G. Influence of solar variability on global sea surface temperatures. Nature 1987, 329, 142–143. [Google Scholar] [CrossRef]
- Friis-Christensen, E.; Lassen, K. Length of the solar cycle: An indicator of solar activity closely associated with climate. Science 1991, 254, 698–700. [Google Scholar] [CrossRef]
- Solheim, J.-E.; Stordahl, K.; Humlum, O. The long sunspot cycle 23 predicts a significant temperature decrease in cycle 24. J. Atmos. Sol.-Terr. Phys. 2012, 80, 267–284. [Google Scholar] [CrossRef][Green Version]
- Cliver, C.W.; Boriakoff, V.; Feynman, J. Solar variability and climate change: Geomagnetic aa index and global surface temperature. Geophys. Res. Lett. 1998, 25, 1035–1038. [Google Scholar] [CrossRef]
- Mufti, S.; Shah, G.N. Solar-geomagnetic activity influence on Earth’s climate. J. Atmos. Sol.-Terr. Phys. 2011, 73, 1607–1615. [Google Scholar] [CrossRef]
- Mayaud, P.-N. The aa indices: A 100-year series characterizing the magnetic activity. J. Geophys. Res. 1972, 77, 6870–6874. [Google Scholar] [CrossRef]
- Love, J.J.; Mursula, K.; Tsai, V.C.; Perkins, D.M. Are secular correlations between sunspots, geomagnetic activity, and global temperature significant? Geophys. Res. Lett. 2012, 38, L21703. [Google Scholar] [CrossRef]
- Pulkkinen, T.I.; Nevanlinna, H.; Pulkkinen, P.J.; Lockwood, M. The Sun-Earth connection in time scales from years to decades and centuries. Space Sci. Rev. 2001, 95, 625–637. [Google Scholar] [CrossRef]
- Zherebtsov, G.A.; Kovalenko, V.A.; Molodykh, S.I.; Kirichenko, K.E. Solar variability manifestations in weather and climate characteristics. J. Atmos. Sol.-Terr. Phys. 2019, 182, 217–222. [Google Scholar] [CrossRef]
- Soon, W.H.; Posmentier, E.S.; Baliunas, S.L. Inference of solar irradiance variability from terrestrial temperature changes, 1880–1993: An astrophysical application of the Sun-climate connection. Astrophys. J. 1996, 472, 891–902. [Google Scholar] [CrossRef]
- Lewis, N.; Curry, J. The Impact of Recent Forcing and Ocean Heat Uptake Data on Estimates of Climate Sensitivity. J. Clim. 2018, 31, 6051–6071. [Google Scholar] [CrossRef]
- Soon, W.; Conolly, R.; Conolly, M. Re-evaluating the role of solar variability on Northern Hemisphere temperature trends since the 19th century. Earth Sci. Rev. 2015, 150, 409–452. [Google Scholar] [CrossRef]
- van Wijngaarden, W.A.; Happer, W. Dependence of Earth’s Thermal Radiation on Five Most Abundant Greenhouse Gases. arXiv 2020, arXiv:2006.03098. [Google Scholar]
- Bond, G.; Kromer, B.; Beer, J.; Muscheler, R.; Evans, M.N.; Showers, W.; Hoffmann, S.; Lotti-Bond, R.; Hajdas, I.; Bonani, G. Persistent solar influence on North Atlantic climate during the Holocene. Science 2001, 294, 2130–2136. [Google Scholar] [CrossRef] [PubMed]
- Stefani, F.; Giesecke, A.; Weber, N.; Weier, T. Synchronized helicity oscillations: A link between planetary tides and the solar cycle? Sol. Phys. 2016, 291, 2197–2212. [Google Scholar] [CrossRef]
- Stefani, F.; Galindo, V.; Giesecke, A.; Weber, N.; Weier, T. The Tayler instability at low magnetic Prandtl numbers: Chiral symmetry breaking and synchronizable helicity oscillations. Magnetohydrodynamics 2017, 53, 169–178. [Google Scholar] [CrossRef]
- Stefani, F.; Giesecke, A.; Weber, N.; Weier, T. On the synchronizability of Tayler-Spruit and Babcock-Leighton type dynamos. Sol. Phys. 2018, 293, 12. [Google Scholar] [CrossRef]
- Stefani, F.; Giesecke, A.; Weier, T. A model of a tidally synchronized solar dynamo. Sol. Phys. 2019, 294, 60. [Google Scholar] [CrossRef]
- Stefani, F.; Giesecke, A.; Seilmayer, M.; Stepanov, R.; Weier, T. Schwabe, Gleissberg, Suess-de Vries: Towards a consistent model of planetary synchronization of solar cycles. Magnetohydrodynamics 2020, 56, 269–280. [Google Scholar]
- Stefani, F.; Beer, J.; Giesecke, A.; Gloaguen, T.; Seilmayer, M.; Stepanov, R.; Weier, T. Phase coherence and phase jumps in the Schwabe cycle. Astron. Nachr. 2020, 341, 600–615. [Google Scholar] [CrossRef]
- Stefani, F.; Stepanov, R.; Weier, T. Shaken and stirred: When Bond meets Suess-de Vries and Gnevyshev-Ohl. Sol. Phys. 2021, 296, 88. [Google Scholar] [CrossRef]
- Weiss, N.O.; Tobias, S.M. Supermodulation of the Sun’s magnetic activity: The effects of symmetry changes. Mon. Not. Roy. Astron. Soc. 2016, 456, 2654–2661. [Google Scholar] [CrossRef]
- Kennedy, J.J.; Rayner, N.A.; Atkinson, C.P.; Killick, R.E. An ensemble data set of sea surface temperature change from 1850: The Met Office Hadley Centre HadSST.4.0.0.0 data set. J. Geophys. Res. Atmos. 2019, 124, 7719–7763. [Google Scholar] [CrossRef]
- Sutton, R.T.; Dong, B.; Gregory, J.M. Land/sea warming ratio in response to climate change: IPCC AR4 model results and comparison with observations. Geophys. Res. Lett. 2007, 34, L02701. [Google Scholar] [CrossRef]
- Scafetta, N. Detection of non-climatic biases in land surface temperature records by comparing climatic data and their model simulations. Clim. Dyn. 2021, 56, 2959–2982. [Google Scholar] [CrossRef]
- Clilverd, M.A.; Clark, T.D.G.; Clarke, E.; Rishbeth, H. Increased magnetic storm activity from 1868 to 1995. J. Atm. Sol.-Terr. Phys. 1998, 60, 1047–1056. [Google Scholar] [CrossRef]
- Cliver, C.W.; Boriakoff, V.; Bounar, K.H. Geomagnetic activity and the solar wind during the Maunder Minimum. Geophys. Res. Lett. 1998, 25, 897–900. [Google Scholar] [CrossRef]
- Nevanlinna, H.; Kataja, E. An extension of the geomagnetic activity index series aa for two solar cycles (1844–1868). Geophys. Res. Lett. 1993, 20, 2703–2706. [Google Scholar] [CrossRef]
- Mantua, N.J.; Hare, S.R. The Pacific Decadal Oscillation. J. Oceanography 2002, 58, 35–44. [Google Scholar] [CrossRef]
- Wyatt, M.G.; Kravtsov, S.; Tsonis, A.A. Atlantic Multidecadal Oscillation and Northern Hemisphere is climate variability. Clim. Dyn. 2012, 38, 929–949. [Google Scholar] [CrossRef]
- Roy, I.; Asikainen, T.; Maliniemi, V.; Mursula, K. Comparing the influence of sunspot activity and geomagnetic activity on winter surface climate. J. Atmos. Sol.-Terr. Phys. 2016, 149, 167–179. [Google Scholar] [CrossRef]
- Lean, J.L.; Rind, D.H. How natural and anthropogenic influences alter global and regional surface temperatures: 1889 to 2006. Geophys. Res. Lett. 2008, 35, L18701. [Google Scholar] [CrossRef]
- Scafetta, N. Reconstruction of the interannual to millennial scale patterns of the global surface temperature. Atmosphere 2021, 12, 147. [Google Scholar] [CrossRef]
- Soden, B.J.; Held, I.M. An assessment of climate feedbacks in coupled ocean-atmosphere models. J. Clim. 2006, 19, 3354–3360. [Google Scholar] [CrossRef]
- Scafetta, N.; West, I.M. Phenomenological reconstructions of the solar signature in the Northern Hemisphere surface temperature records since 1600. J. Geophys. Res. Atmos. 2007, 112, D24S03. [Google Scholar] [CrossRef]
- Scafetta, N.; West, I.M. Is climate sensitive to solar variability. Phys. Today 2008, 61, 50–51. [Google Scholar] [CrossRef]
- Svalgaard, L.; Cliver, E.W.; Kamide, Y. Sunspot cycle 24: Smallest cycle in 100 years? Geophys. Res. Lett. 2005, 32, L01104. [Google Scholar] [CrossRef]
- Petrovay, K. Solar cycle prediction. Liv. Rev. Sol. Phys. 2020, 17, 2. [Google Scholar] [CrossRef]
- Velasco Herrera, V.M.; Soon, W.; Legates, D.R. Does machine learning reconstruct missing sunspots and forecast a new solar minimum? J. Atmos. Sol.-Terr. Phys. 2019, 184, 57–62. [Google Scholar]
- Chattopadhyay, G.; Midya, S.K.; Chattopadhyay, S. MLP based predictive model for surface ozone concentration over an urban area in the Gangetic West Bengal during pre-monsoon season. Adv. Space Res. 2021, 68, 1485–1501. [Google Scholar] [CrossRef]
- Dicke, R.H. Is there a chronometer hidden deep in the Sun? Nature 1978, 276, 676–680. [Google Scholar] [CrossRef]
- Hoyng, P. Is the solar cycle timed by a clock? Solar Phys. 1996, 169, 253–264. [Google Scholar] [CrossRef]
- Hung, C.-C. Apparent relations between solar activity and solar tides caused by the planets. In NASA/TM–2007-214817; Glenn Research Center: Cleveland, OH, USA, 2007. [Google Scholar]
- Wilson, I.R.G.; Carter, B.D.; Waite, I.A. Does a spin–orbit coupling between the Sun and the Jovian planets govern the solar cycle? Publ. Astron. Soc. Austr. 2008, 25, 85–93. [Google Scholar] [CrossRef][Green Version]
- Scafetta, N. Does the Sun work as a nuclear fusion amplifier of planetary tidal forcing? A proposal for a physical mechanism based on the mass-luminosity relation. J. Atmos. Sol.-Terr. Phys. 2012, 81–82, 27–40. [Google Scholar] [CrossRef]
- Wilson, I.R.G. The Venus-Earth-Jupiter spin–orbit coupling model. Pattern Recogn. Phys. 2013, 1, 147–158. [Google Scholar] [CrossRef]
- Okhlopkov, V.P. The gravitational influence of Venus, the Earth, and Jupiter on the 11-year cycle of solar activity. Mosc. Univ. Phys. Bull. 2016, 71, 440–446. [Google Scholar] [CrossRef]
- Weber, N.; Galindo, V.; Stefani, F.; Weier, T. The Tayler instability at low magnetic Prandtl numbers: Between chiral symmetry breaking and helicity oscillations. New J. Phys. 2015, 17, 113013. [Google Scholar] [CrossRef]
- Solheim, J.-E. The sunspot cycle length-modulated by planets? Pattern Recogn. Phys. 2013, 1, 159–164. [Google Scholar] [CrossRef]
- Javaraiah, J. Long-Term Variations in the Solar Differential Rotation. Solar Phys. 2003, 212, 23–49. [Google Scholar] [CrossRef]
- Sharp, G. Are Uranus and Neptune responsible for solar grand minima and solar cycle modulation? Int J. Astron. Astrophys. 2013, 3, 260–273. [Google Scholar] [CrossRef][Green Version]
- Ma, L.; Vaquero, J.M. New evidence of the Suess/de Vries cycle existing in historical naked-eye observations of sunspots. Open Astron. 2020, 29, 28–31. [Google Scholar] [CrossRef]
- Lüdecke, H.-J.; Weiss, C.O.; Hempelmann, A. Paleoclimate forcing by the solar De Vries/Suess cycle. Clim. Past Discuss. 2015, 11, 279–305. [Google Scholar]
- Fredriksen, H.-B.; Berner, J.; Subramanian, A.C.; Capotondi, A. How does El Niño-Southern Oscillation change under global warming—A first look at CMIP6. Geophys. Res. Lett. 2020, 47, e2020GL090640. [Google Scholar] [CrossRef]
- Solanki, S.K.; Usoskin, I.G.; Kromer, B.; Schüssler, M.; Beer, J. Unusual activity of the Sun during recent decades compared to the previous 11,000 years. Nature 2004, 431, 1084–1087. [Google Scholar] [CrossRef] [PubMed]
- Abdussamatov, H. Current long-term negative average annual energy balance of the Earth leads to the new little ice age. Thermal Sci. 2015, 19 (Suppl. S2), 279–288. [Google Scholar] [CrossRef]
- Roe, G. In defense of Milankovitch. Geophys. Res. Lett. 2006, 33, L24703. [Google Scholar] [CrossRef]





| MAW 11 Years: 1855 till | MAW 23 Years: 1867 till | |||||
|---|---|---|---|---|---|---|
| Correlated Data | 2013 | 2008 | 2003 | 2008 | 2003 | 1998 |
| CO with aa | 0.440 | 0.606 | 0.720 | 0.703 | 0.783 | 0.803 |
| (one-sided p) | (0.053) | (0.0099) | (0.0017) | (0.045) | (0.023) | (0.02) |
| CO with | 0.926 | 0.911 | 0.891 | 0.916 | 0.894 | 0.869 |
| (one-sided p) | (0) | (0) | (0) | (0.0017) | (0.0037) | (0.0073) |
| aa with | 0.595 | 0.738 | 0.819 | 0.806 | 0.900 | 0.950 |
| (one-sided p) | (0.010) | (0.001) | (0.0001) | (0.016) | (0.0032) | (0.0005) |
| AMO with | 0.260 | 0.164 | 0.106 | |||
| (one-sided p) | (0.30) | (0.38) | (0.42) | |||
| aa with AMO | −0.015 | −0.013 | −0.028 | |||
| (one-sided p) | (0.49) | (0.40) | (0.48) | |||
| PDO with | −0.131 | −0.001 | 0.126 | |||
| (one-sided p) | (0.40) | (0.50) | (0.41) | |||
| aa with PDO | 0.050 | 0.049 | 0.074 | |||
| (one-sided p) | (0.46) | (0.46) | (0.44) | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stefani, F. Solar and Anthropogenic Influences on Climate: Regression Analysis and Tentative Predictions. Climate 2021, 9, 163. https://doi.org/10.3390/cli9110163
Stefani F. Solar and Anthropogenic Influences on Climate: Regression Analysis and Tentative Predictions. Climate. 2021; 9(11):163. https://doi.org/10.3390/cli9110163
Chicago/Turabian StyleStefani, Frank. 2021. "Solar and Anthropogenic Influences on Climate: Regression Analysis and Tentative Predictions" Climate 9, no. 11: 163. https://doi.org/10.3390/cli9110163
APA StyleStefani, F. (2021). Solar and Anthropogenic Influences on Climate: Regression Analysis and Tentative Predictions. Climate, 9(11), 163. https://doi.org/10.3390/cli9110163






