Increasing Trend on Storm Wave Intensity in the Western Mediterranean
Abstract
1. Introduction
2. Methodology
2.1. Wave Hindcast
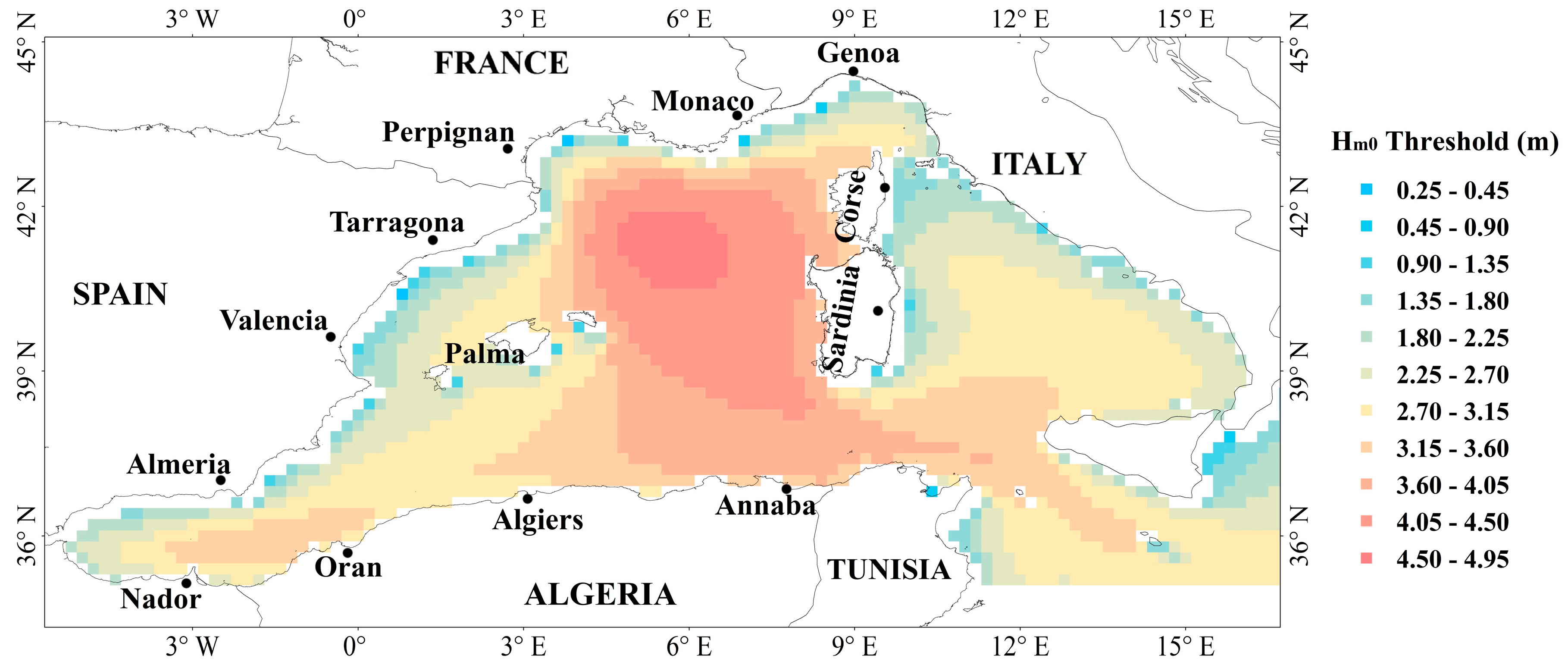
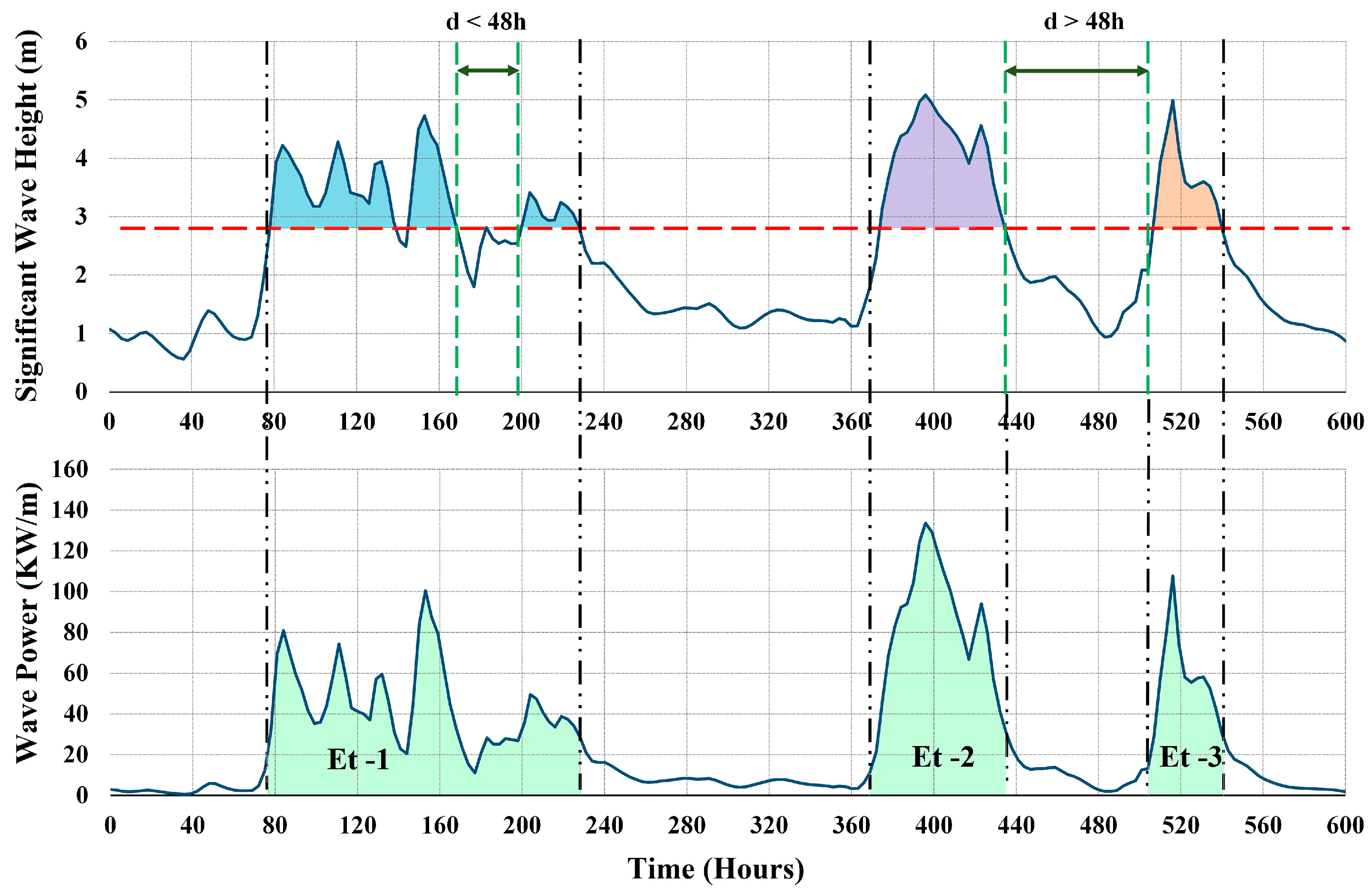
2.2. Storm Wave Characterization
2.3. Trend Aanalysis Method
sgn(Yj − Yk) = 0 if Yj − Yk = 0
sgn(Yj − Yk) = −1 if Yj − Yk < 0
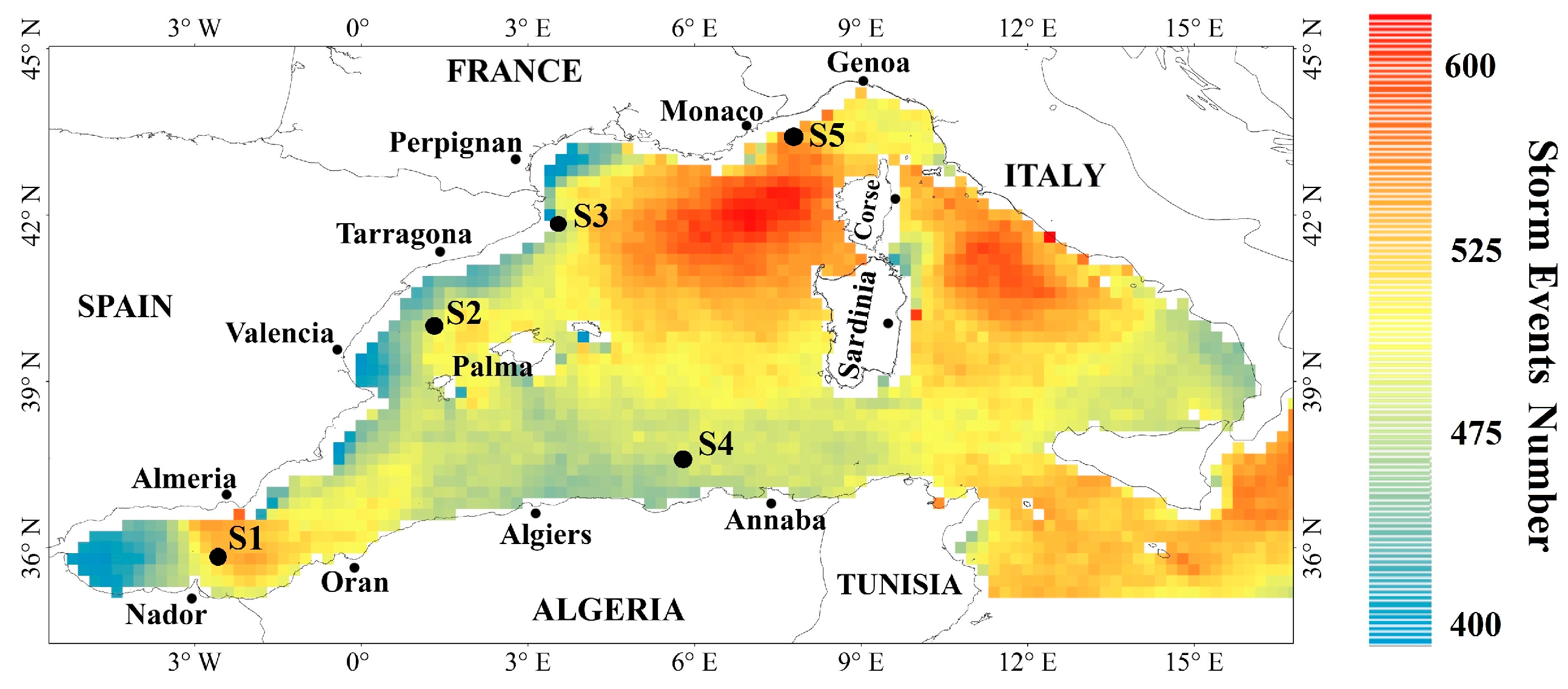
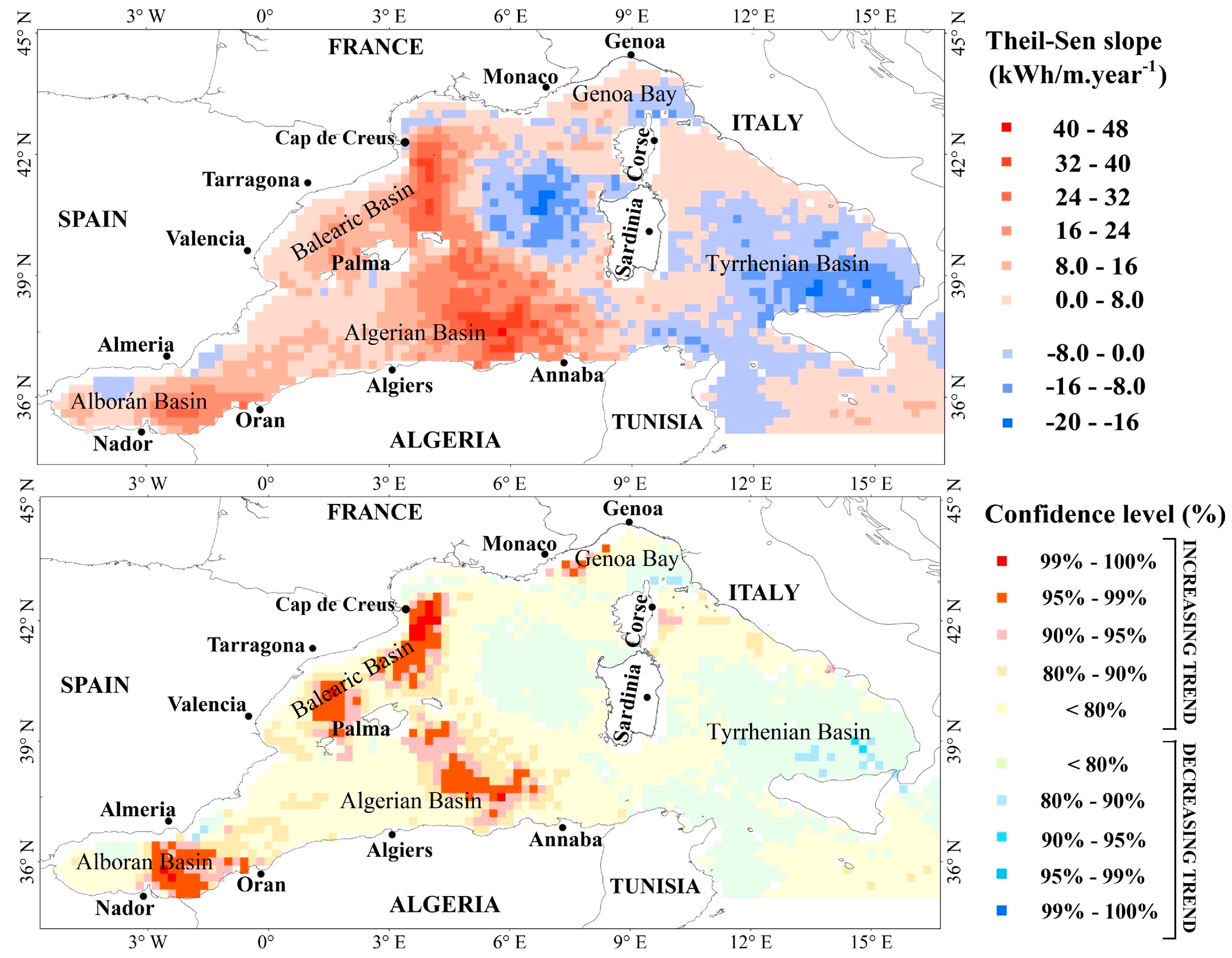
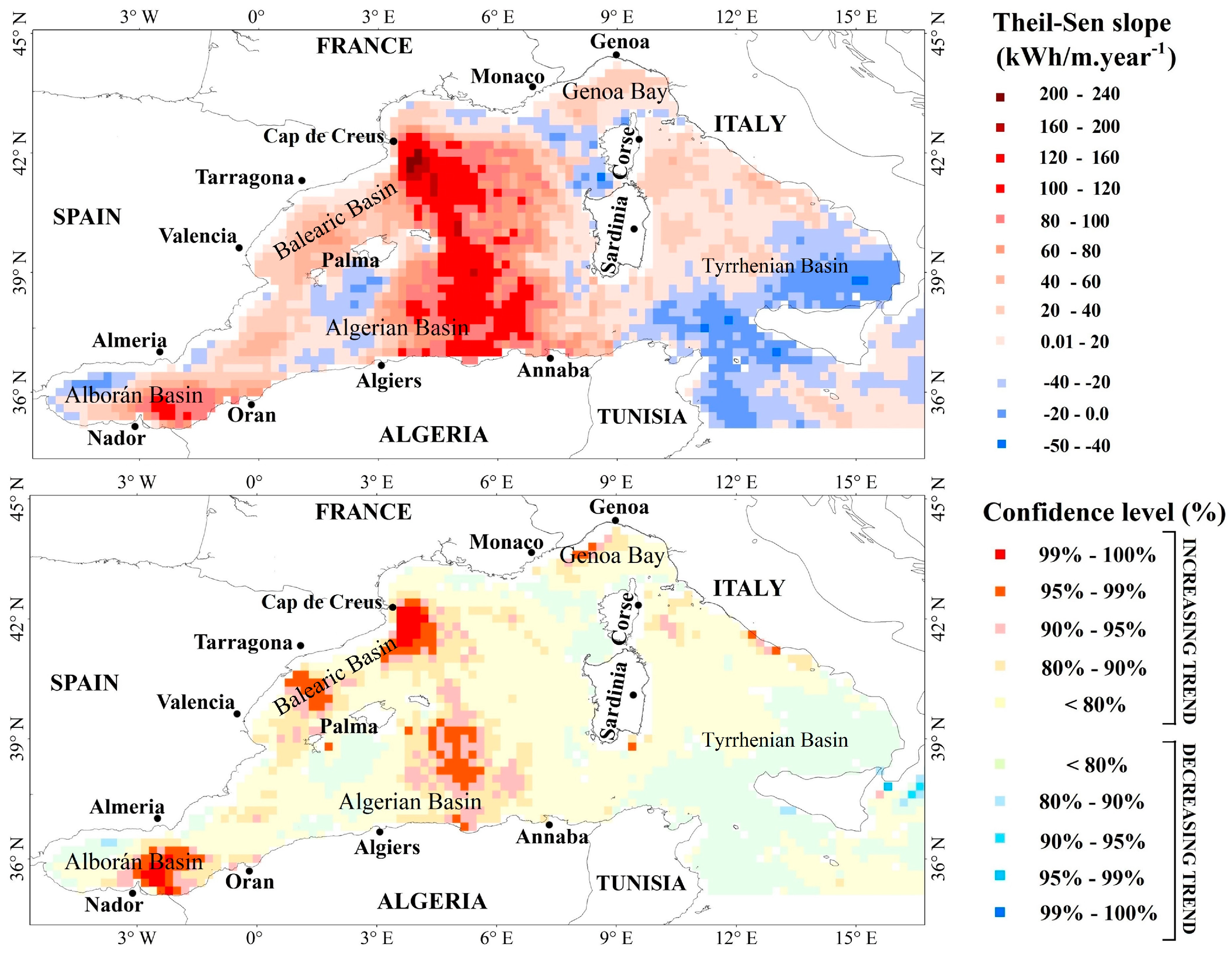
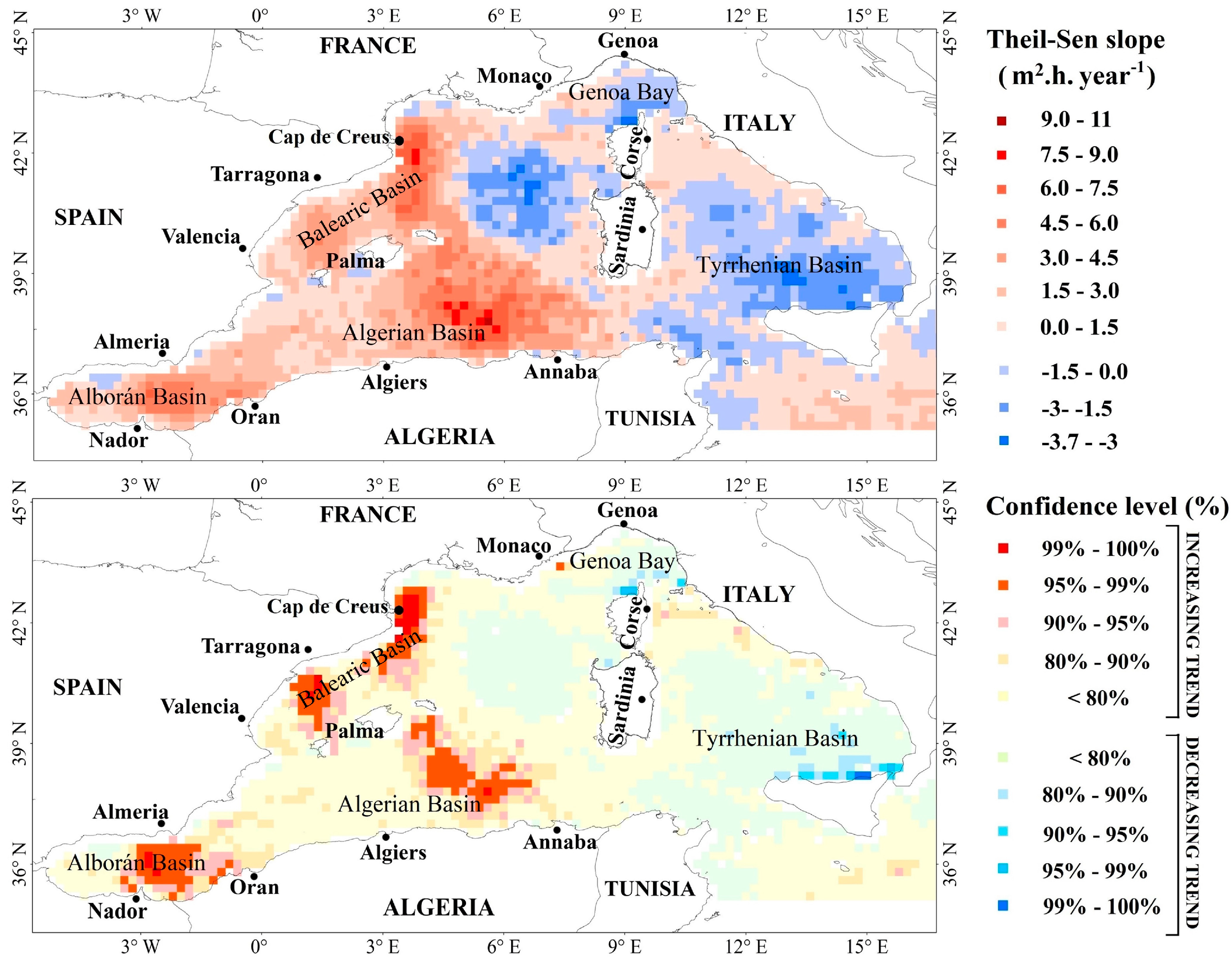
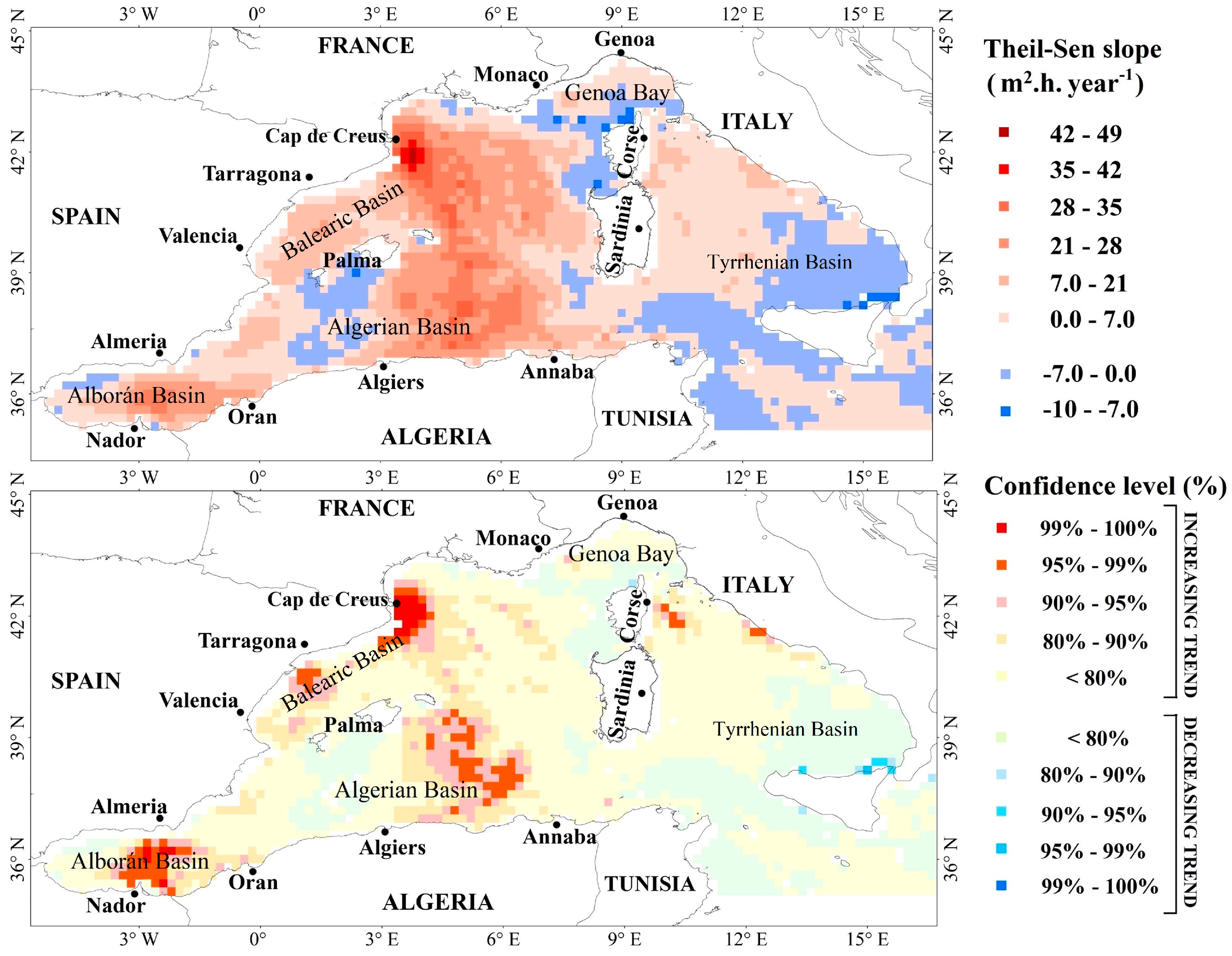
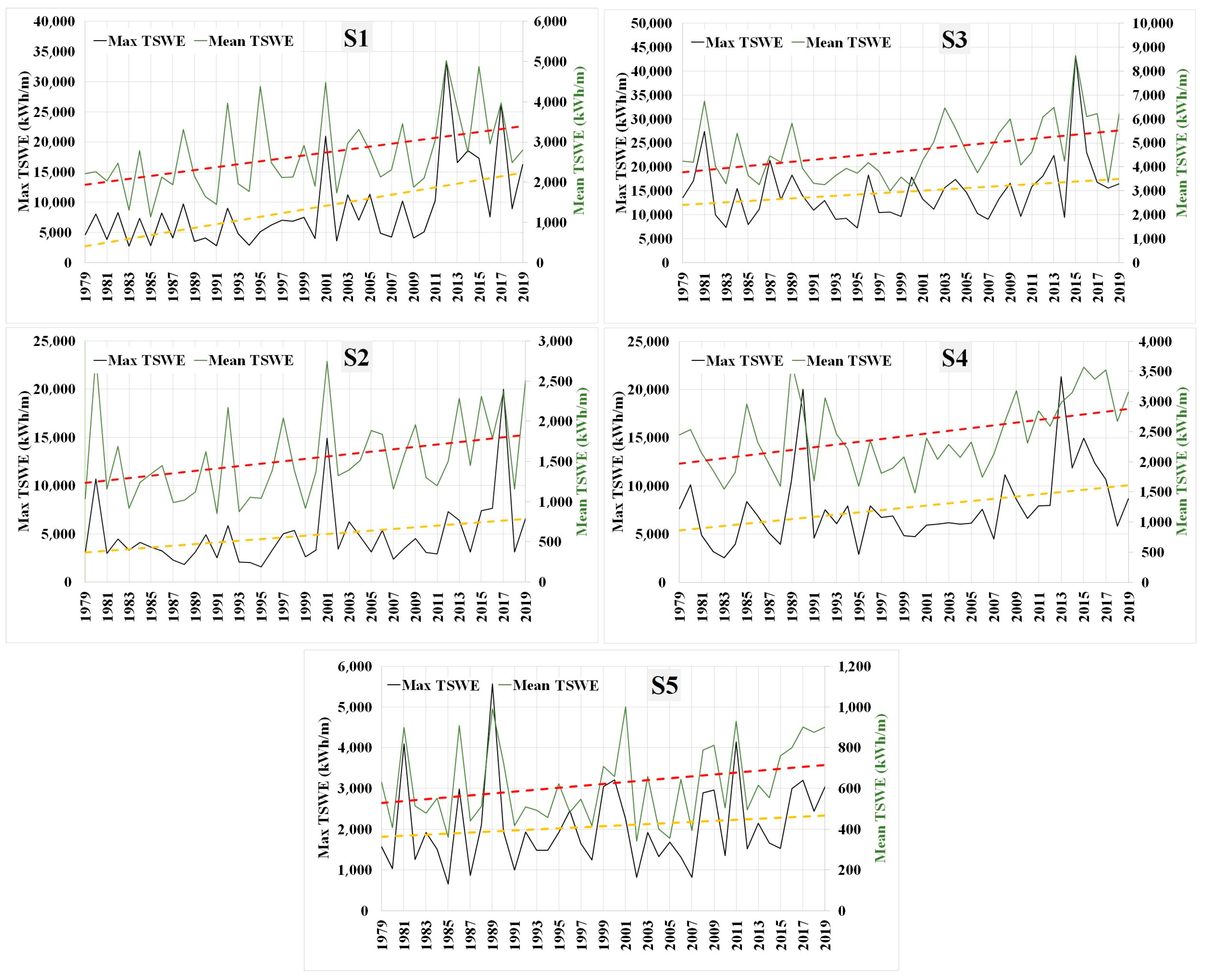
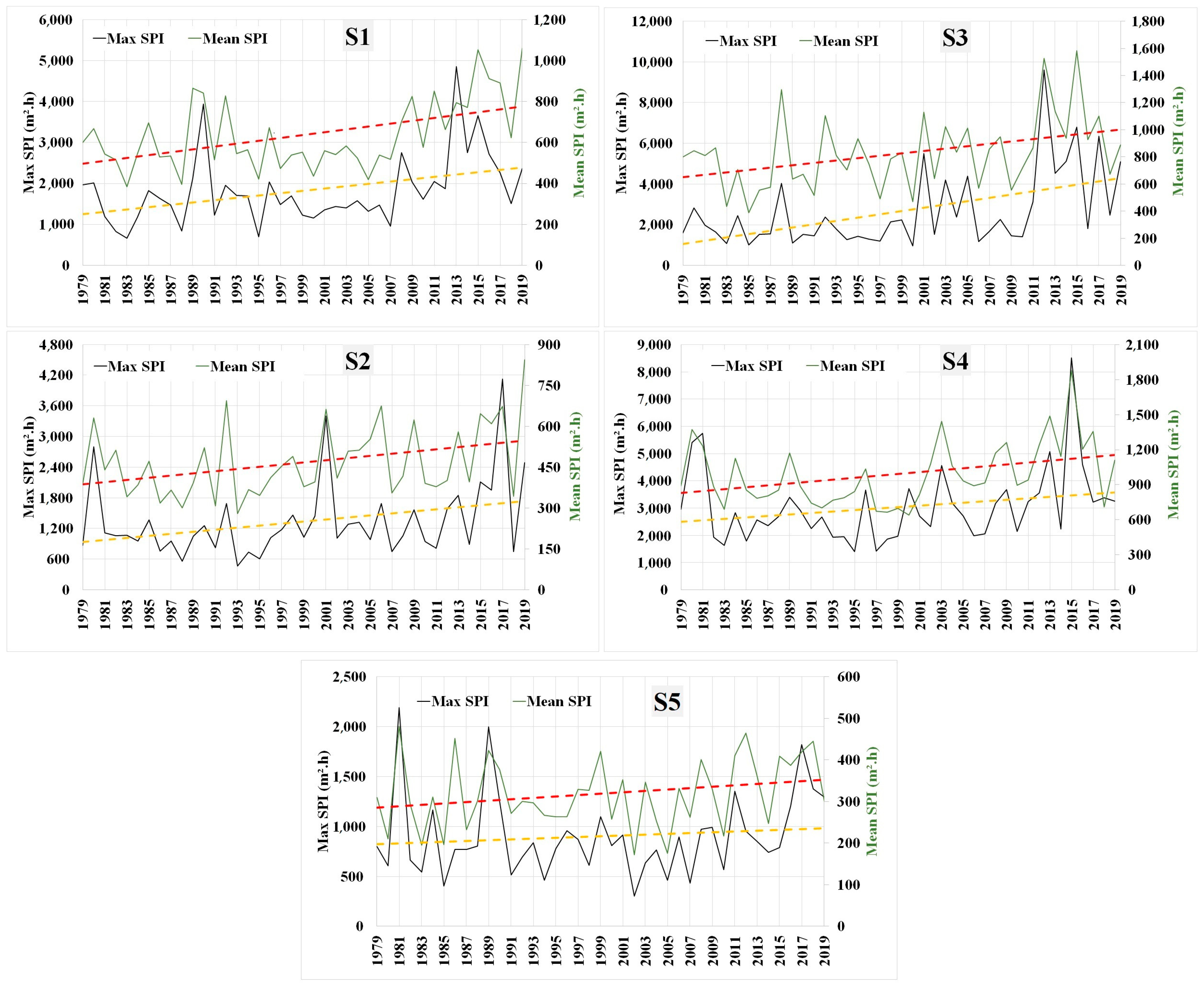
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jackson, D.; Drumm, A.; McEvoy, S.; Jensen, Ø.; Mendiola, D.; Gabiña, G.; Borg, J.A.; Papageorgiou, N.; Karakassis, Y.; Black, K.D. A pan-European valuation of the extent, causes and cost of escape events from sea cage fish farming. Aquaculture 2015, 436, 21–26. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, X.-M. Global ship accidents and ocean swell-related sea states. Hazards Earth Syst. Sci. 2017, 17. [Google Scholar] [CrossRef]
- Xu, S.; Ma, M.; Yin, K.; Tang, S. Risk evaluation system of navigation security based on coupled wind and wave model: A case of study of Qiongzhou strait. IET Intell. Transp. Syst. 2020, 14, 1311–1318. [Google Scholar] [CrossRef]
- Jiménez, J.A.; Sancho-García, A.; Bosom, E.; Valdemoro, H.I.; Guillén, J. Storm-induced damages along the Catalan coast (NW Mediterranean) during the period 1958–2008. Geomorphology 2012, 143–144, 24–33. [Google Scholar] [CrossRef]
- Amarouche, K.; Akpınar, A.; Çakmak, R.E.; Houma, F.; Bachari, N.E.I. Assessment of storm events along the Algiers coast and their potential impacts. Ocean Eng. 2020, 210, 107432. [Google Scholar] [CrossRef]
- Marzeddu, A.; Oliveira, T.C.A.; Sánchez-Arcilla, A.; Gironella, X. Effect of wave storm representation on damage measurements of breakwaters. Ocean Eng. 2020, 200, 107082. [Google Scholar] [CrossRef]
- Casas-Prat, M.; Sierra, J.P. Trend analysis of wave storminess: Wave direction and its impact on harbour agitation. Nat. Hazards Earth Syst. Sci. 2010, 10, 2327–2340. [Google Scholar] [CrossRef]
- Wang, Y.C.; Wang, Y.Z.; Hong, N.N. Dynamic stability analysis of caisson breakwater in lifetime considering the annual frequency of severe storm. China Ocean Eng. 2015, 29, 287–300. [Google Scholar] [CrossRef]
- Sanuy, M.; Jiménez, J.A. Sensitivity of Storm-Induced Hazards in a Highly Curvilinear Coastline to Changing Storm Directions. The Tordera Delta Case (NW Mediterranean). Water 2019, 11, 747. [Google Scholar] [CrossRef]
- Sanuy, M.; Duo, E.; Jäger, W.S.; Ciavola, P.; Jiménez, J.A. Linking source with consequences of coastal storm impacts for climate change and risk reduction scenarios for Mediterranean sandy beaches. Nat. Hazards Earth Syst. Sci. 2018, 18, 1825–1847. [Google Scholar] [CrossRef]
- Lira-Loarca, A.; Cobos, M.; Losada, M.Á.; Baquerizo, A. Storm characterization and simulation for damage evolution models of maritime structures. Coast. Eng. 2020, 156, 103620. [Google Scholar] [CrossRef]
- Amores, A.; Marcos, M.; Carrió, D.S.; Gómez-Pujol, L. Coastal impacts of Storm Gloria (January 2020) over the north-western Mediterranean. Nat. Hazards Earth Syst. Sci. 2020, 20, 1955–1968. [Google Scholar] [CrossRef]
- Cavaleri, L.; Bajo, M.; Barbariol, F.; Bastianini, M.; Benetazzo, A.; Bertotti, L.; Chiggiato, J.; Davolio, S.; Ferrarin, C.; Magnusson, L.; et al. The October 29, 2018 storm in Northern Italy–An exceptional event and its modeling. Prog. Oceanogr. 2019, 178, 102178. [Google Scholar] [CrossRef]
- Sánchez-Arcilla, A.; González-Marco, D.; Doorn, N.; Kortenhaus, A. Extreme values for coastal, estuarine, and riverine environments. J. Hydraul. Res. 2008, 46, 183–190. [Google Scholar] [CrossRef]
- Jiménez, J.A.; Sanuy, M.; Ballesteros, C.; Valdemoro, H.I. The Tordera Delta, a hotspot to storm impacts in the coast northwards of Barcelona (NW Mediterranean). Coast. Eng. 2018, 134, 148–158. [Google Scholar] [CrossRef]
- Cramer, W.; Guiot, J.; Fader, M.; Garrabou, J.; Gattuso, J.-P.; Iglesias, A.; Lange, M.A.; Lionello, P.; Llasat, M.C.; Paz, S.; et al. Climate change and interconnected risks to sustainable development in the Mediterranean. Nat. Clim. Chang. 2018, 8, 972–980. [Google Scholar] [CrossRef]
- Lionello, P.; Scarascia, L. The relation of climate extremes with global warming in the Mediterranean region and its north versus south contrast. Reg. Environ. Chang. 2020, 20. [Google Scholar] [CrossRef]
- Sánchez-Arcilla, A.; González-Marco, D.; Bolaños, R. A review of wave climate and prediction along the Spanish Mediterranean coast. Nat. Hazards Earth Syst. Sci. 2008, 8, 1217–1228. [Google Scholar] [CrossRef]
- Young, I.R.; Ribal, A. Multiplatform evaluation of global trends in wind speed and wave height. Science 2019, 364, 548–552. [Google Scholar] [CrossRef]
- Gulev, S.K. Last century changes in ocean wind wave height from global visual wave data. Geophys. Res. Lett. 2004, 31, L24302. [Google Scholar] [CrossRef]
- Reguero, B.G.; Losada, I.J.; Méndez, F.J. A recent increase in global wave power as a consequence of oceanic warming. Nat. Commun. 2019, 10, 1–14. [Google Scholar] [CrossRef]
- Vieira, F.; Cavalcante, G.; Campos, E. Analysis of wave climate and trends in a semi-enclosed basin (Persian Gulf) using a validated SWAN model. Ocean Eng. 2020, 196, 106821. [Google Scholar] [CrossRef]
- Dobrynin, M.; Murawsky, J.; Yang, S. Evolution of the global wind wave climate in CMIP5 experiments. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Meucci, A.; Young, I.R.; Aarnes, O.J.; Breivik, Ø. Comparison of wind speed and wave height trends from twentieth-century models and satellite altimeters. J. Clim. 2020, 33, 611–624. [Google Scholar] [CrossRef]
- Komar, P.D.; Allan, J.C. Increasing hurricane-generated wave heights along the U.S. East Coast and their climate controls. J. Coast. Res. 2008, 24, 479–488. [Google Scholar] [CrossRef]
- Bromirski, P.D.; Kossin, J.P. Increasing hurricane wave power along the U.S. Atlantic and Gulf coasts. J. Geophys. Res. 2008, 113, C07012. [Google Scholar] [CrossRef]
- Dolan, R.; Davis, E. An intensity scale for Atlantic coast northeast storms. J. Coast. Res. 1992, 8, 840–853. [Google Scholar]
- Molina, R.; Manno, G.; Lo Re, C.; Anfuso, G.; Ciraolo, G. Storm Energy Flux Characterization along the Mediterranean Coast of Andalusia (Spain). Water 2019, 11, 509. [Google Scholar] [CrossRef]
- Martzikos, N.; Afentoulis, V.; Tsoukala, V. Storm clustering and classification for the port of Rethymno in Greece. Water Util. J. 2018, 20, 67–79. [Google Scholar]
- Anfuso, G.; Rangel-Buitrago, N.; Cortés-Useche, C.; Iglesias Castillo, B.; Gracia, F.J. Characterization of storm events along the Gulf of Cadiz (eastern central Atlantic Ocean). Int. J. Climatol. 2016, 36, 3690–3707. [Google Scholar] [CrossRef]
- Rangel-Buitrago, N.; Anfuso, G. Coastal storm characterization and morphological impacts on sandy coasts. Earth Surf. Process. Landforms 2011, 36, 1997–2010. [Google Scholar] [CrossRef]
- Rangel-Buitrago, N.; Anfuso, G. An application of Dolan and Davis (1992) classification to coastal storms in SW Spanish littoral. J. Coast. Res. 2010, 64, 1891–1895. [Google Scholar]
- Ojeda, E.; Appendini, C.M.; Mendoza, E.T. Storm-wave trends in Mexican waters of the Gulf of Mexico and Caribbean Sea. Nat. Hazards Earth Syst. Sci. 2017, 17, 1305–1317. [Google Scholar] [CrossRef]
- Birkemeier, W.; Nicholls, R.; Lee, G. Storms, Storm Groups and Nearshore Morphologic Change, Coastal Sediments’ 99; ASCE Press: Long Island, NY, USA, 1999. [Google Scholar]
- Walker, R.A.; Basco, D.R. Application of coastal storm impulse (COSI) parameter to predict coastal erosion. Coast. Eng. Proc. 2011, 1, 23. [Google Scholar] [CrossRef]
- Mendoza, E.T.; Trejo-Rangel, M.A.; Salles, P.; Appendini, C.M.; Lopez-Gonzalez, J.; Torres-Freyermuth, A. Storm characterization and coastal hazards in the Yucatan Peninsula. J. Coast. Res. 2013, 65, 790–795. [Google Scholar] [CrossRef]
- Satta, A.; Puddu, M.; Venturini, S.; Giupponi, C. Assessment of coastal risks to climate change related impacts at the regional scale: The case of the Mediterranean region. Int. J. Disaster Risk Reduct. 2017, 24, 284–296. [Google Scholar] [CrossRef]
- Han, W.; Stammer, D.; Meehl, G.; Hu, A.; Sienz, F.; Zhang, L. Multi-Decadal Trend and Decadal Variability of the Regional Sea Level over the Indian Ocean since the 1960s: Roles of Climate Modes and External Forcing. Climate 2018, 6, 51. [Google Scholar] [CrossRef]
- Zhang, K.; Douglas, B.C.; Leatherman, S.P. Global warming and coastal erosion. Clim. Change 2004, 64, 41–58. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions: 1. Model description and validation. J. Geophys. Res. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Ris, R.C.; Holthuijsen, L.H.; Booij, N. A third-generation wave model for coastal regions: 2. Verification. J. Geophys. Res. 1999, 104, 7667–7681. [Google Scholar] [CrossRef]
- Amarouche, K.; Akpınar, A.; Bachari, N.E.I.; Çakmak, R.E.; Houma, F. Evaluation of a high-resolution wave hindcast model SWAN for the West Mediterranean basin. Appl. Ocean Res. 2019, 84, 225–241. [Google Scholar] [CrossRef]
- Amarouche, K.; Akpınar, A.; El Islam Bachari, N.; Houma, F. Wave energy resource assessment along the Algerian coast based on 39-year wave hindcast. Renew. Energy 2020. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Pan, H.-L.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D.; et al. The {NCEP} Climate Forecast System Reanalysis. Bull. Am. Meteorol. Soc. 2010, 91, 1015–1058. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.-T.; Chuang, H.; Iredell, M.; et al. The {NCEP} Climate Forecast System Version 2. J. Clim. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- Tiberi-Wadier, A.-L.; Laugel, A.; Benoit, M. Construction of the Numerical Wave Databases Anemoc-2 on the Mediterranean Sea and the Atlantic Ocean Through Hindcast Simulations Over the Period 1979–2010. In Advances in Hydroinformatics; Springer Water; Springer: Singapore, 2016; pp. 127–143. [Google Scholar]
- Campos, R.M.; Guedes Soares, C. Assessment of three wind reanalyses in the North Atlantic Ocean. J. Oper. Oceanogr. 2017, 10, 30–44. [Google Scholar] [CrossRef][Green Version]
- Campos, R.M.; Guedes Soares, C. Comparison and assessment of three wave hindcasts in the North Atlantic Ocean. J. Oper. Oceanogr. 2016, 9, 26–44. [Google Scholar] [CrossRef]
- Stopa, J.E.; Cheung, K.F. Intercomparison of wind and wave data from the ECMWF Reanalysis Interim and the NCEP Climate Forecast System Reanalysis. Ocean Model. 2014, 75, 65–83. [Google Scholar] [CrossRef]
- Carvalho, D. An assessment of NASA’s GMAO MERRA-2 reanalysis surface winds. J. Clim. 2019, 32, 8261–8281. [Google Scholar] [CrossRef]
- Akpinar, A.; Ponce de León, S. An assessment of the wind re-analyses in the modelling of an extreme sea state in the Black Sea. Dyn. Atmos. Ocean. 2016, 73, 61–75. [Google Scholar] [CrossRef]
- Çakmak, R.E.; Akpinar, A.; Van Vledder, G.P. Comparative Performance Analysis of Different Wind Fields in Southern and North-Western Coastal Areas of the Black Sea. Mediterr. Mar. Sci. 2019, 20, 427–452. [Google Scholar] [CrossRef]
- Van Vledder, G.P.; Akpınar, A. Wave model predictions in the Black Sea: Sensitivity to wind fields. Appl. Ocean Res. 2015, 53, 161–178. [Google Scholar] [CrossRef]
- Cavaleri, L.; Rizzoli, P.M. Wind wave prediction in shallow water: Theory and applications. J. Geophys. Res 1981, 86, 10961–10973. [Google Scholar] [CrossRef]
- Komen, G.J.; Hasselmann, K.; Hasselmann, K. On the Existence of a Fully Developed Wind-Sea Spectrum. J. Phys. Oceanogr. 1984, 14, 1271–1285. [Google Scholar] [CrossRef]
- Janssen, P.A.E.M. Quasi-linear Theory of Wind-Wave Generation Applied to Wave Forecasting. J. Phys. Oceanogr. 1991, 21, 1631–1642. [Google Scholar] [CrossRef]
- Janssen, P.A.E.M. Wave-Induced Stress and the Drag of Air Flow over Sea Waves. J. Phys. Oceanogr. 1989, 19, 745–754. [Google Scholar] [CrossRef]
- Hasselmann, S.; Hasselmann, K. Computations and Parameterizations of the Nonlinear Energy Transfer in a Gravity-Wave Spectrum. Part I: A New Method for Efficient Computations of the Exact Nonlinear Transfer Integral. J. Phys. Oceanogr. 1985, 15, 1369–1377. [Google Scholar] [CrossRef]
- Eldeberky, Y. Nonlinear Transformations of Wave Spectra in the Nearshore Zone; Delft University of Technology: Delft, The Netherlands, 1996. [Google Scholar]
- Battjes, J.A.; Janssen, J.P.F.M. Energy Loss and Set-Up Due to Breaking of Random Waves. In Proceedings of the 16th International Conference on Coastal Engineering, Hamburg, Germany, 27 August–3 September 1978; American Society of Civil Engineers: New York, NY, USA, 1978; pp. 569–587. [Google Scholar] [CrossRef]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.A.; Gienapp, H.; Hasselmann, D.E.; Kruseman, P.; et al. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project ({JONSWAP}). Dtsch. Hydrogr. Z 1973, A8, 1–95. [Google Scholar]
- Gusella, V. Estimation of extreme winds from short-term records. J. Struct. Eng. 1991, 117, 375–390. [Google Scholar] [CrossRef]
- Nicholls, R.J.; Hoozemans, F.M.J. The Mediterranean: Vulnerability to coastal implications of climate change. Ocean Coast. Manag. 1996, 31, 105–132. [Google Scholar] [CrossRef]
- Quevauviller, P. (Ed.) Hydrometeorological Hazards; John Wiley & Sons, Ltd.: Chichester, UK, 2014; Volume 1, ISBN 9781118629567. [Google Scholar] [CrossRef]
- Guisado-Pintado, E.; Malvárez, G.; Navas, F.; Carrero, R. Spatial distribution of storm wave energy dissipation for the assessment of beach morphodynamics. J. Coast. Res. 2014, 70, 259–265. [Google Scholar] [CrossRef]
- Karunarathna, H.; Pender, D.; Ranasinghe, R.; Short, A.D.; Reeve, D.E. The effects of storm clustering on beach profile variability. Mar. Geol. 2014, 348, 103–112. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379. [Google Scholar] [CrossRef]
- Theil, H. A rank-invariant method of linear and polynomial regression analysis, Part I. Proc. R. Neth. Acad. Sci. 1950, 53, 387–392. [Google Scholar]
- Kendall, M. Rank Correlation Methods, 4th ed.; Griffin: London, UK, 1975; ISBN 9780852641996. [Google Scholar]
- Mann, H.B. Nonparametric Tests against Trend. Econometrica 1945, 13, 245. [Google Scholar] [CrossRef]
- Cattrell, A.D.; Srokosz, M.; Moat, B.I.; Marsh, R. Seasonal intensification and trends of rogue wave events on the US western seaboard. Sci. Rep. 2019, 9. [Google Scholar] [CrossRef]
- Yang, S.; Oh, J. Long-Term Changes in the Extreme Significant Wave Heights on the Western North Pacific: Impacts of Tropical Cyclone Activity and ENSO. Asia-Pac. J. Atmos. Sci. 2018, 54, 103–109. [Google Scholar] [CrossRef]
- Nchaba, T.; Mpholo, M.; Lennard, C. Long-term austral summer wind speed trends over southern Africa. Int. J. Climatol. 2017, 37, 2850–2862. [Google Scholar] [CrossRef]
- De Leo, F.; De Leo, A.; Besio, G.; Briganti, R. Detection and quantification of trends in time series of significant wave heights: An application in the Mediterranean Sea. Ocean Eng. 2020, 202, 107155. [Google Scholar] [CrossRef]
- De Leo, F.; Besio, G.; Mentaschi, L. Trends and variability of ocean waves under RCP8.5 emission scenario in the Mediterranean Sea. Ocean Dyn. 2020, 1–21. [Google Scholar] [CrossRef]
- Aydoğan, B.; Ayat, B. Spatial variability of long-term trends of significant wave heights in the Black Sea. Appl. Ocean Res. 2018, 79, 20–35. [Google Scholar] [CrossRef]
- Akpınar, A.; Bingölbali, B. Long-term variations of wind and wave conditions in the coastal regions of the Black Sea. Nat. Hazards 2016, 84, 69–92. [Google Scholar] [CrossRef]
- Martzikos, N.T.; Prinos, P.E.; Memos, C.D.; Tsoukala, V.K. Statistical analysis of Mediterranean coastal storms. Oceanologia 2020. [Google Scholar] [CrossRef]
- Cavicchia, L.; von Storch, H.; Gualdi, S. A long-term climatology of medicanes. Clim. Dyn. 2014, 43, 1183–1195. [Google Scholar] [CrossRef]
- Young, I.R.; Zieger, S.; Babanin, A.V. Global trends in wind speed and wave height. Science 2011, 332, 451–455. [Google Scholar] [CrossRef] [PubMed]
- Timmermans, B.W.; Gommenginger, C.P.; Dodet, G.; Bidlot, J.-R. Global Wave Height Trends and Variability from New Multimission Satellite Altimeter Products, Reanalyses, and Wave Buoys. Geophys. Res. Lett. 2020, 47. [Google Scholar] [CrossRef]
- Shanas, P.R.; Kumar, V.S. Trends in surface wind speed and significant wave height as revealed by ERA-Interim wind wave hindcast in the Central Bay of Bengal. Int. J. Climatol. 2015, 35, 2654–2663. [Google Scholar] [CrossRef]
- Wang, X.L.; Swail, V.R. Trends of Atlantic Wave Extremes as Simulated in a 40-Yr Wave Hindcast Using Kinematically Reanalyzed Wind Fields. J. Clim. 2002, 15, 1020–1035. [Google Scholar] [CrossRef]
- Aarnes, O.J.; Abdalla, S.; Bidlot, J.-R.; Breivik, Ø. American Meteorological Society Marine Wind and Wave Height Trends at Different ERA-Interim Forecast Ranges. Source J. Clim. 2015, 28, 819–837. [Google Scholar] [CrossRef]
- Divinsky, B.V.; Kosyan, R.D. Climatic trends in the fluctuations of wind waves power in the Black Sea. Estuar. Coast. Shelf Sci. 2020, 235, 106577. [Google Scholar] [CrossRef]
| Physical Process | Formula References | Parameters |
|---|---|---|
| Linear wind growth | [54] | |
| Exponential wind growth | [55] | |
| Whitecapping | [56,57] | Cds2 = 1.0 & delta = 1 |
| Quadruplets wave–wave interactions | the discrete Interaction approximation (DIA) [58] | ƛ = 0.25 & Cn/4 = 3.0 × 107 |
| Triads wave–wave interactions | [59] | EB = 0.1 |
| Depth-induced breaking | [60] | BJ = 1.0 & γBJ = 0.73 |
| Bottom friction | [61] | CFJON = 0.038 |
| Buoy Name/Positions | Used Period | Nbr of Observation | SI | Bias | R | |||
|---|---|---|---|---|---|---|---|---|
| Hs | Tm02 | Hs | Tm02 | Hs | Tm02 | |||
| Matifou 3.22° E 36.84° N | 1 October 1998 to 31 March 1999 | 1304 | 0.3 | 0.15 | 0.15 | 0.17 | 0.92 | 0.88 |
| Azzefoun 4.39° E 36.917° N | 1 September 2000 to 28 February 2001 | 1196 | 0.31 | 0.21 | 0.09 | −0.03 | 0.92 | 0.78 |
| Kala 8.43° E 36.92° N | 1 January 2002 to 31 December 2002 | 2480 | 0.3 | 0.18 | 0.01 | −0.43 | 0.93 | 0.89 |
| Palos −0.33° E 37.65° N | 1 January 2007 to 31 December 2009 | 25,470 | 0.30 | 0.14 | 0.15 | −0.07 | 0.92 | 0.82 |
| Dragonera 2.1° E 39.55° N | 1 January 2007 to 31 December 2009 | 25,222 | 0.30 | 0.18 | 0.05 | −0.45 | 0.92 | 0.84 |
| Tarragona 1.47° E 40.68° N | 1 January 2008 to 31 December 2008 | 8717 | 0.30 | 0.17 | 0.03 | −0.35 | 0.91 | 0.86 |
| Buger 3.65° E 41.92° N | 1 January 2008 to 31 December 2008 | 6374 | 0.27 | 0.18 | −0.04 | −0.48 | 0.94 | 0.88 |
| Mahon 4.42° E 39.71°N | 1 January 2007 to 31 December 2009 | 23,257 | 0.29 | 0.15 | 0.16 | −0.30 | 0.94 | 0.88 |
| Nice 7.23° E 43.63° N | 1 January 2008 to 31 December 2008 | 8177 | 0.38 | 0.27 | −0.02 | −0.76 | 0.87 | 0.63 |
| Porquerolles 6.20° E 42.97° N | 1 January 2000 to 31 December 2000 | 3129 | 0.25 | 0.17 | −0.03 | −0.4 | 0.94 | 0.88 |
| Marseille 3.66° E 43.33° N | 1 January 2000 to 31 December 2000 | 2095 | 0.28 | 0.29 | −0.06 | −0.92 | 0.96 | 0.84 |
| Stations. | Lon. | Lat. | Depth (m) | Distance from the Coast (km) | Estimated Annual Slope of Mean SPI (m²·h·year−1) | Estimated Annual Slope of Mean TSWE (kWh·m−1·year−1) | Estimated Annual Slope of Max SPI (m²·h·year−1) | Estimated Annual Slope of Max TSWE (kWh·m−1·year−1) |
|---|---|---|---|---|---|---|---|---|
| S1 | 2.6° W | 35.8° N | 750 | 51 | 5.9 | 26.1 | 23.2 | 114.8 |
| S2 | 1.4° E | 40° N | 1439 | 88 | 3.3 | 14.2 | 14.1 | 57.2 |
| S3 | 3.6° E | 41.8° N | 1326 | 35 | 6.4 | 26.5 | 37.4 | 149.7 |
| S4 | 5.8° E | 37.6° N | 2812 | 74 | 5.7 | 40.8 | 21.7 | 98.5 |
| S5 | 7.6° E | 43.4° N | 2418 | 44 | 2.1 | 5.9 | 7.5 | 18.5 |
| Stations: | S1 | S2 | S3 | S4 | S5 |
|---|---|---|---|---|---|
| N | 10 | 107 | 348 | 167 | 1 |
| NE | 187 | 166 | 40 | 7 | 102 |
| E | 0 | 28 | 65 | 20 | 78 |
| SE | 0 | 7 | 10 | 0 | 10 |
| S | 0 | 11 | 6 | 0 | 28 |
| SW | 0 | 70 | 23 | 0 | 347 |
| W | 323 | 34 | 0 | 148 | 4 |
| NW | 11 | 84 | 7 | 148 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amarouche, K.; Akpınar, A. Increasing Trend on Storm Wave Intensity in the Western Mediterranean. Climate 2021, 9, 11. https://doi.org/10.3390/cli9010011
Amarouche K, Akpınar A. Increasing Trend on Storm Wave Intensity in the Western Mediterranean. Climate. 2021; 9(1):11. https://doi.org/10.3390/cli9010011
Chicago/Turabian StyleAmarouche, Khalid, and Adem Akpınar. 2021. "Increasing Trend on Storm Wave Intensity in the Western Mediterranean" Climate 9, no. 1: 11. https://doi.org/10.3390/cli9010011
APA StyleAmarouche, K., & Akpınar, A. (2021). Increasing Trend on Storm Wave Intensity in the Western Mediterranean. Climate, 9(1), 11. https://doi.org/10.3390/cli9010011






