Joint Modeling of Severe Dust Storm Events in Arid and Hyper Arid Regions Based on Copula Theory: A Case Study in the Yazd Province, Iran
Abstract
1. Introduction
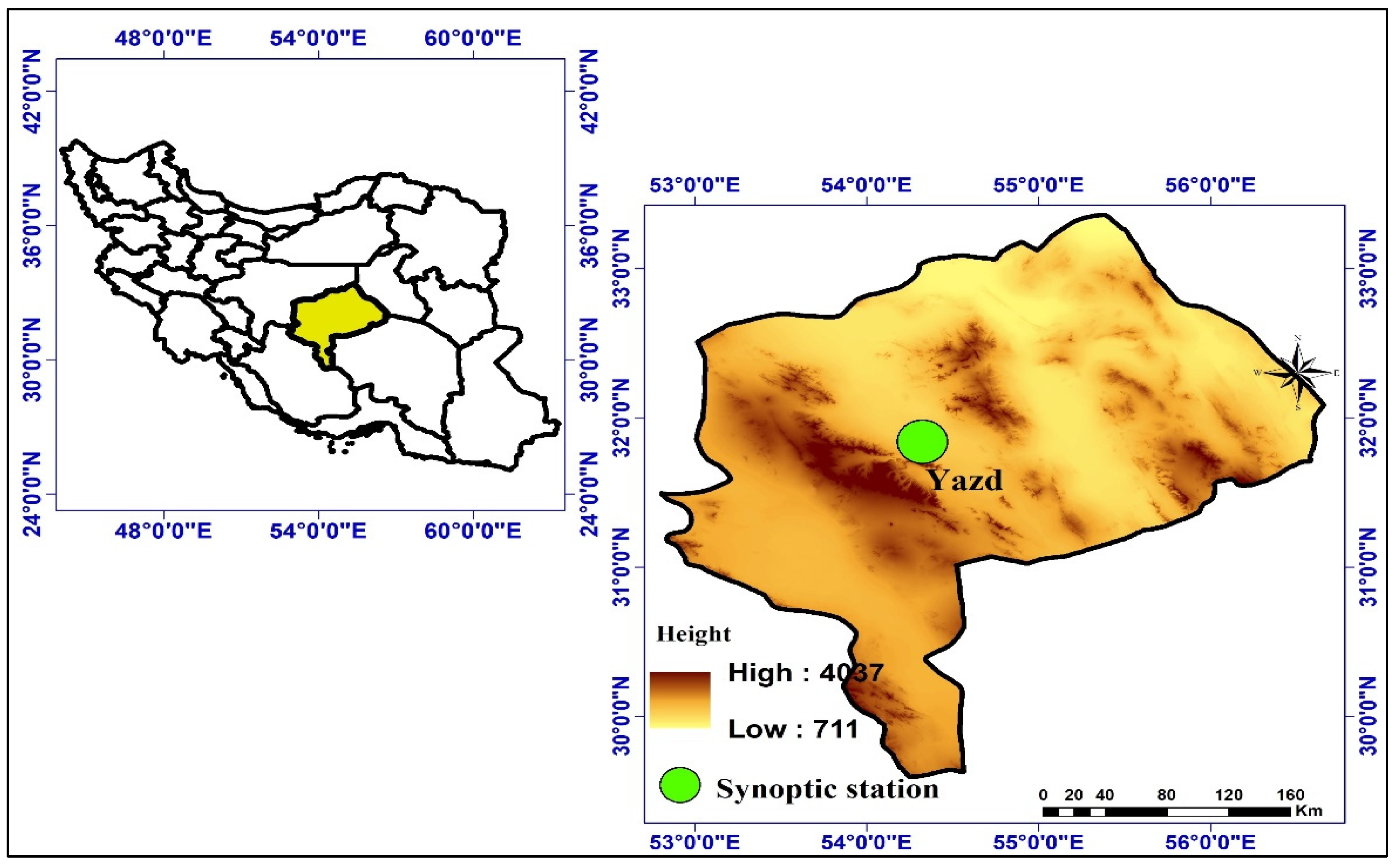
2. Materials and Methods
2.1. Copula Theory
2.1.1. Estimation of the Parameters of the Copula Functions
2.1.2. Selecting the Copula Function
2.1.3. Analysis of Bivariate Dust Storm Return Period
3. Results
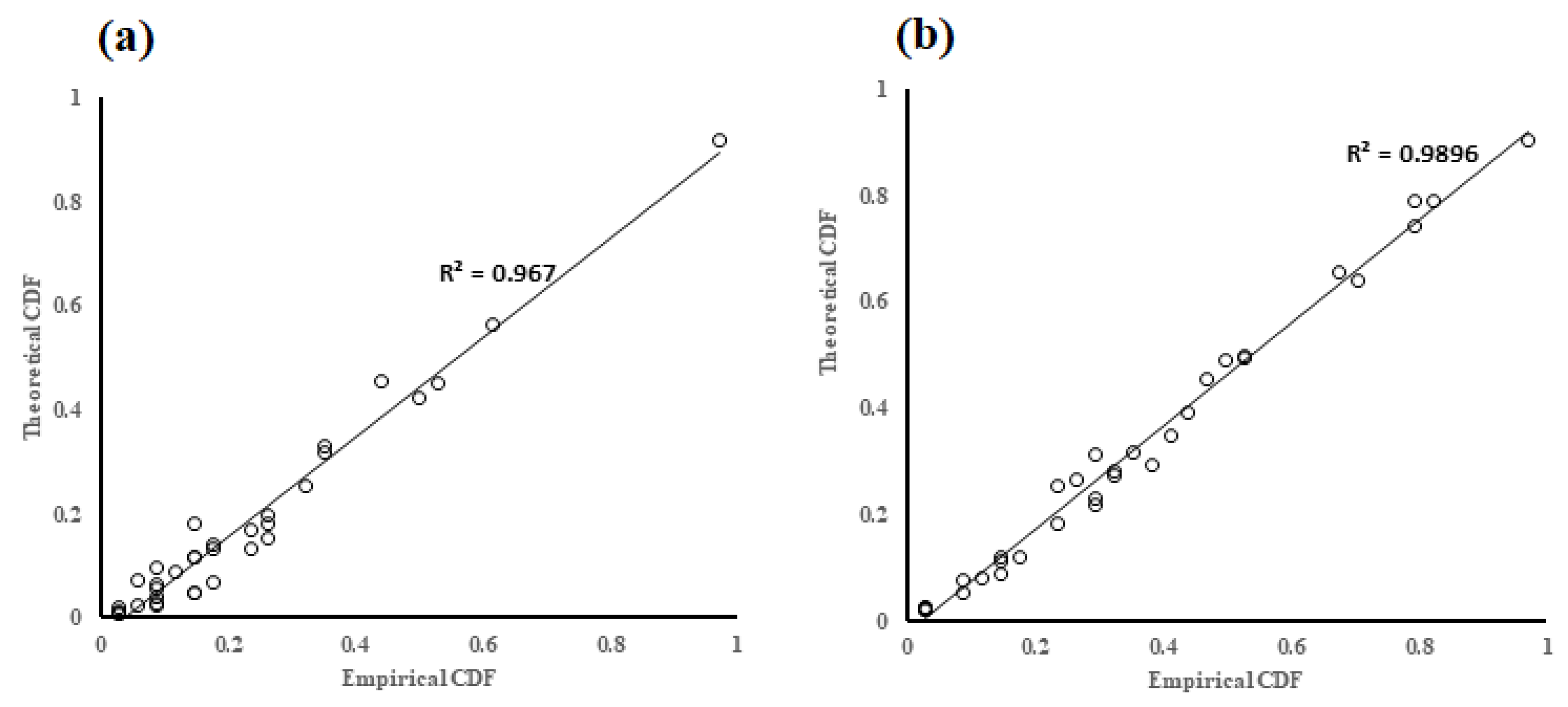
3.1. Determine the Marginal Functions Of’ Dust Storm Variables
3.2. Choosing the Best Copula Function for Bivariate Modeling of Dust Storms
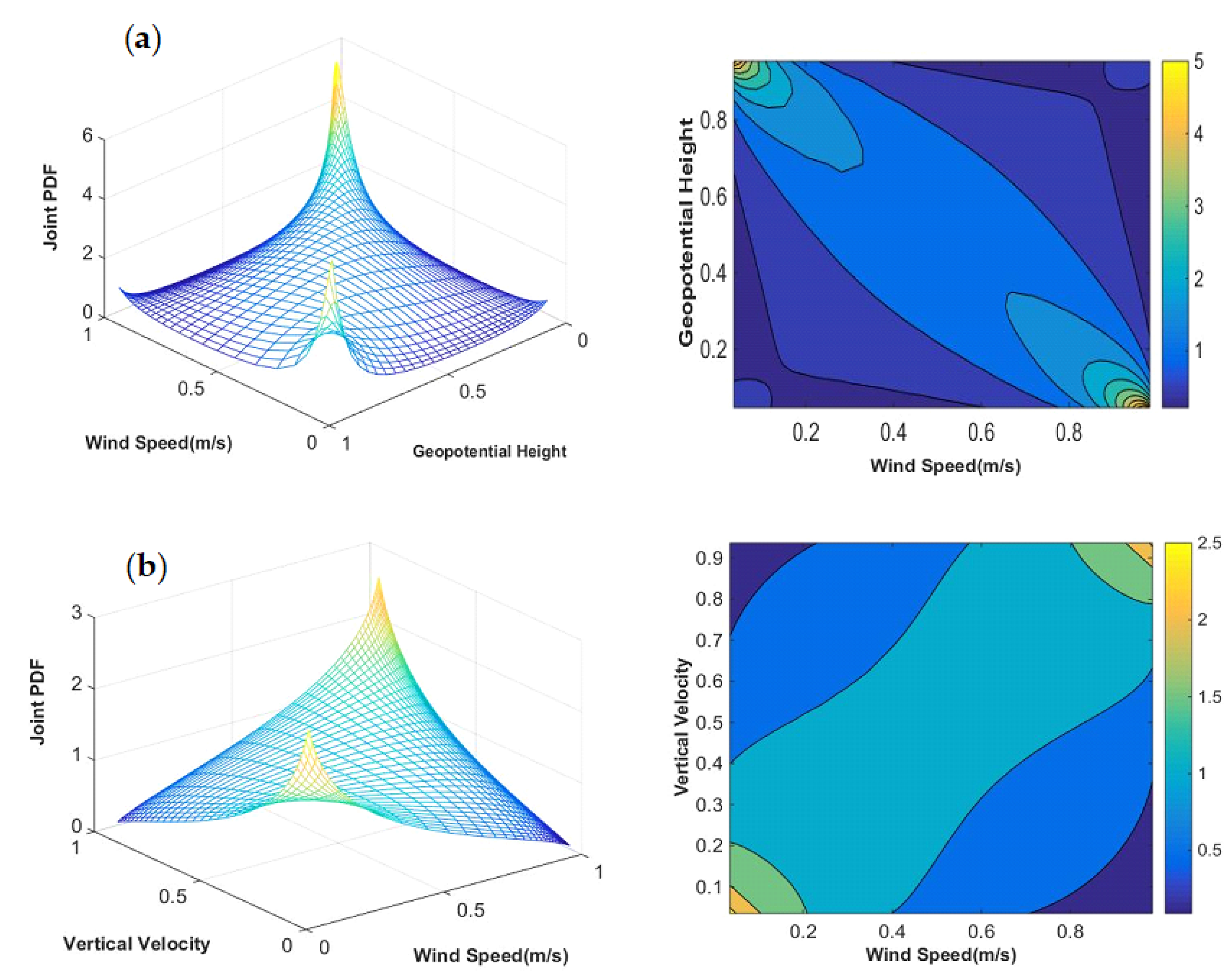
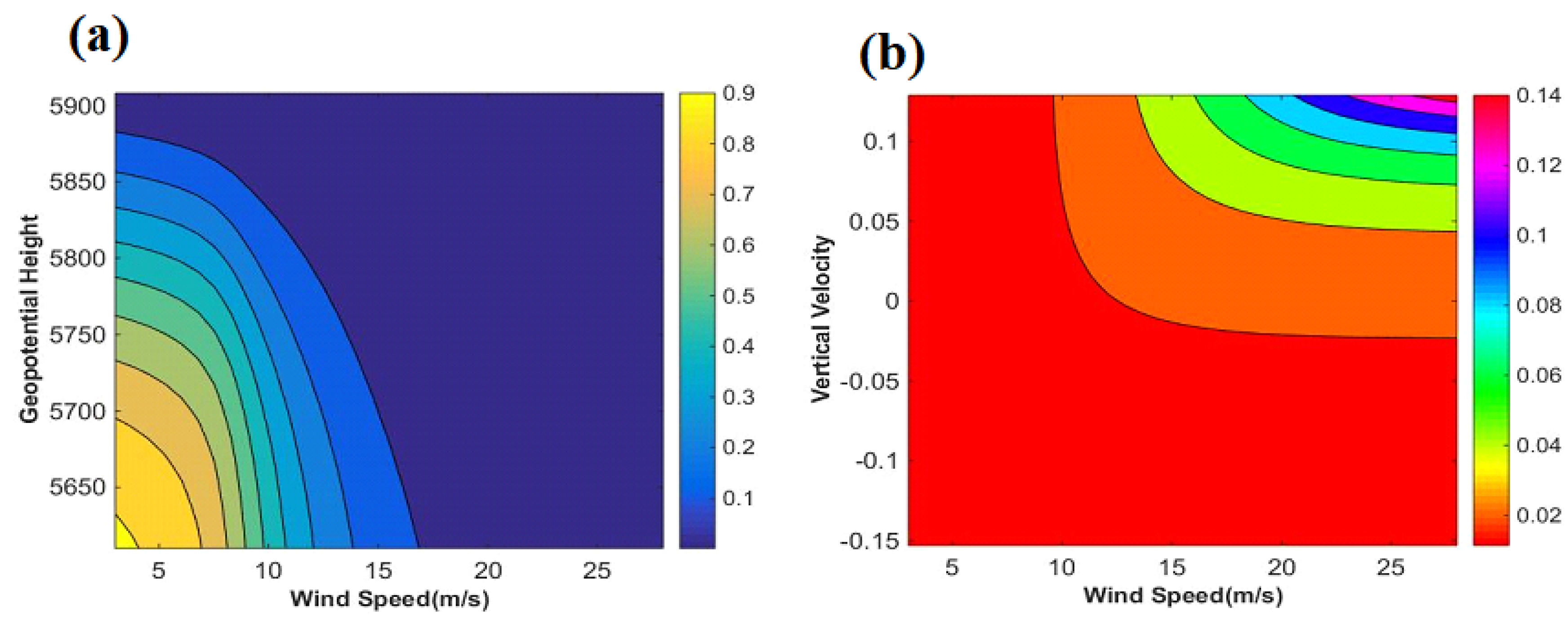
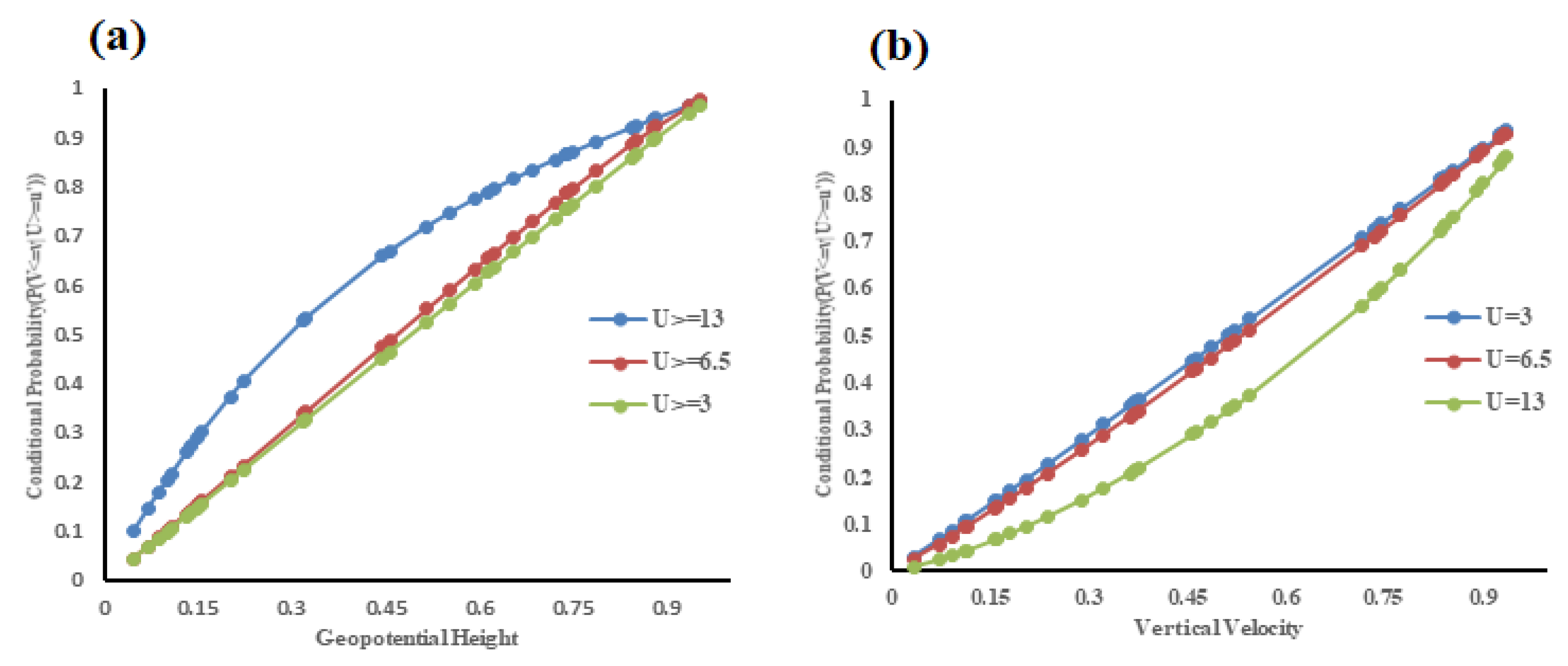
3.3. Joint and Conditional Probability of Dust Storm
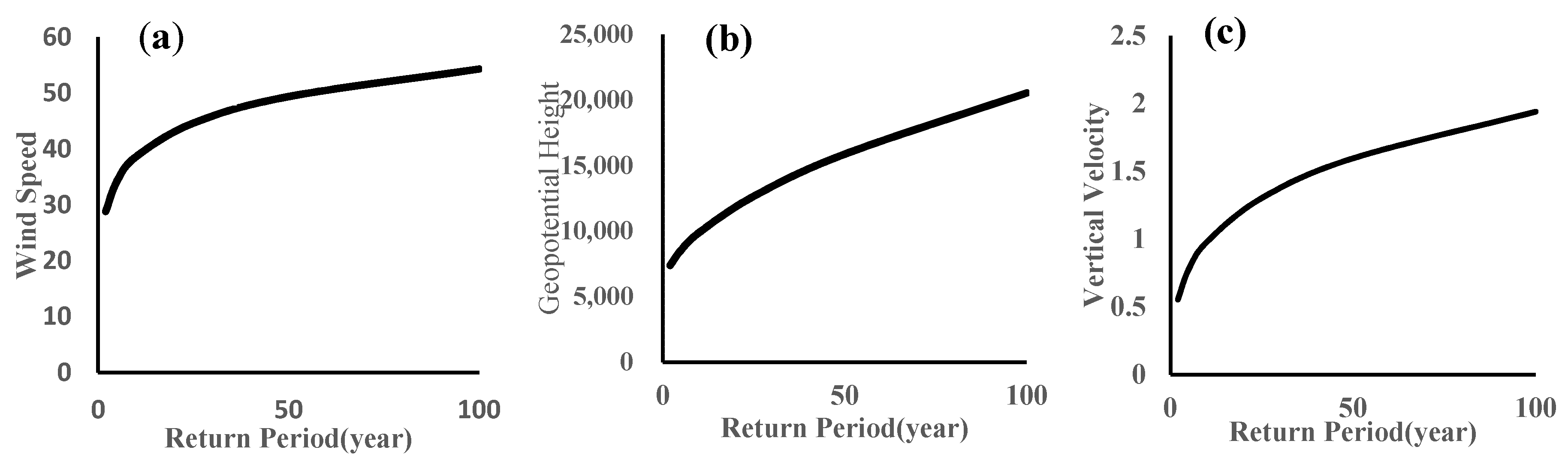
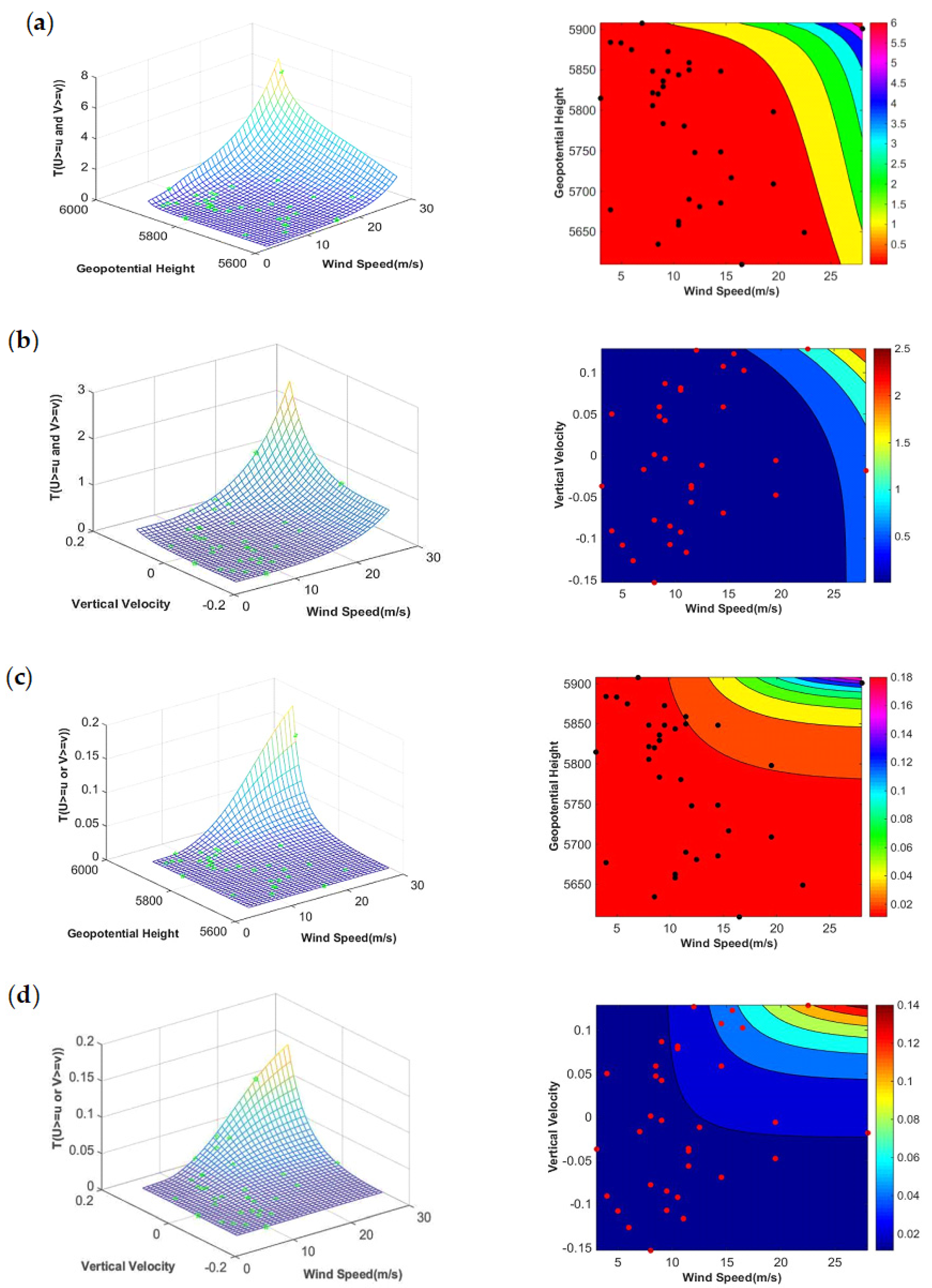
3.4. Bivariate Return Period of Dust Storm
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sivakumar, V.K. Impacts of Sand Storms/Dust Storms on Agriculture. Nat. Disasters Extreme Events Agric. 2005, 7, 160–177. [Google Scholar]
- Wang, X.M.; Dong, Z.B.; Zhang, J.W.; Liu, L.C. Modern dust storms in China: An overview. J. Arid Environ. 2004, 58, 559–574. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, N.; Wu, W.; Wu, J.; Gu, X.; Ji, Z. Exploring the characteristics of major natural disasters in China and their impacts during the past decades. Nat. Hazards. 2013, 69, 829–843. [Google Scholar] [CrossRef]
- Tam, W.W.S.; Wong, T.W.; Wong, A.H.S.; Hui, D.S.C. Effect of dust storm events on daily emergency admissions for respiratory diseases. Respirology 2012, 17, 143–148. [Google Scholar] [CrossRef]
- Hamadneh, H.S.; Ababneh, Z.; Hamasha, K.M.; Ababneh, A.M. The radioactivity of seasonal dust storms in the Middle East: The May 2012 case study in Jordan. Environ. Radioact. 2015, 140, 65–69. [Google Scholar] [CrossRef]
- Kaskaoutis, D.G.; Kosmopoulos, P.; Kambezidis, H.D.; Nastos, P.T. Aerosol climatology and Discrimination of different types over Athens, Greece based on MODIS data. Atmos. Environ. 2007, 41, 7315–7329. [Google Scholar] [CrossRef]
- Liu, X.; Li, N.; Yuan, S.; Xu, N.; Shi, W.; Chen, W. The joint return period analysis of natural disasters based on monitoring and statistical modeling of multidimensional hazard factors. Sci. Total Environ. 2015, 538, 724–732. [Google Scholar] [CrossRef]
- Wang, S.G.; Wang, J.Y.; Zhou, Z.J.; Shang, K.Z. Regional characteristics of three kinds of dust storm events in China. Atmos. Environ. 2005, 39, 509–520. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Gong, S.L.; Zhao, T.L.; Arimoto, R.; Wang, Y.Q.; Zhou, Z.J. Sources of Asian dust and role of climate change versus desertification in Asian dust emission. Geophys. Res. Lett. 2003, 30, 2272–2275. [Google Scholar] [CrossRef]
- Goudie, A.S.; Middleton, N.J. Saharan dust storms: Nature and consequences. Earth Sci. Rev. 2001, 56, 179–204. [Google Scholar] [CrossRef]
- Qian, W.H.; Zhu, Y.F. Climate change in China from 1880 to 1998 and its impact on the environmental condition. Climate Chang. 2001, 50, 419–444. [Google Scholar] [CrossRef]
- Iqbal, M.J.; Ali, M. A probabilistic approach for estimating return period of extreme annual rainfall in different cities of Punjab. Arab. J. Geosci. 2013, 6, 2599–2606. [Google Scholar] [CrossRef]
- Frans, B.; Julia, H.; David, M.G. Learning to adapt: Organizational adaptation to climate change impacts. Climate Chang. 2006, 78, 135–156. [Google Scholar]
- Akbari, S.; Tajar, J. The analysis of the economic damages of dust storms in Iran (the continue of December Paper 2011). Aust. J. Basic Appl. Sci. 2012, 6, 388–395. [Google Scholar]
- Khaniabadi, O.Y.; Daryanoosh, M.; Amrane, A.; Polosa, R.; Hopke Ph, K.; Goudarzi Gh Mohammadi, M.J.; Sicard, P.; Armin, H. Impact of Middle Eastern Dust storms on human health. Atmos. Pollut. Res. 2017, 8, 606–613. [Google Scholar] [CrossRef]
- Kanatani, K.T.; Ito, I.; Al-Delaimy, W.K.; Adachi, Y.; Mathews, W.C.; Ramsdell, J.W. Toyama Asian Desert Dust and Asthma Study Team. Desert dust exposure is associated with increased risk of asthma hospitalization in children. Am. J. Respir. Crit. Care Med. 2010, 182, 1475e1481. [Google Scholar] [CrossRef]
- Chien, L.; Yang, C.; Yu, H.L.E. Estimated effects of Asian Dust Storms on spatiotemporal distributions of clinic visits for respiratory diseases in Taipeichildren (Taiwan). Environ. Health Perspect. 2012, 120, 1215e1220. [Google Scholar] [CrossRef]
- Kang, J.; Liu, T.; Keller, J.; Lin, H. Asian storm events are associated with an acute increase in stroke hospitalisation. J. Epidemiol. Community Health 2013, 67, 125e131. [Google Scholar] [CrossRef]
- Neophytou, A.; Yiallouros, P.; Coull, B.; Kleanthous, S.; Pavlou, P.; Pashiardis, S.; Dockery, D.W.; Koutrakis, P.; Laden, F. Particulate matter concentrations during desert dust outbreaks and daily mortality in Nicosia Cyprus. J. Expo. Sci. Environ. Epidemiol. 2013, 23, 275e280. [Google Scholar] [CrossRef]
- Middleton, N.; Yiallouros, P.; Kleanthous, S.; Kolokotroni, O.; Schwartz, J.; Dockery, D.; Demokritou Ph Koutrakis, P. A 10-year time-series analysis of respiratory and cardiovascular morbidity in Nicosia, Cyprus: The effect of short-term changes in air pollution and dust storms. Environ. Health 2008, 8, 39. [Google Scholar] [CrossRef]
- Duan, H.; Zhao, J.; Li, Y. The frequencies, severities, and driving factors of the sand-dust weather processes occurred in northern China in the spring of 2011. J. Desert Res. 2013, 33, 179–186. [Google Scholar]
- Wang, X.; Ma, Y.; Chen, H.; Wen, G.; Chen, S.J.; Tao, Z.Y.; Chung, Y.S. The relation between sandstorms and strong winds in Xinjiang, China. Water Air Soil Pollut. 2003, 3, 2. [Google Scholar] [CrossRef]
- Salvadori, G. Bivariate return periods via 2- copulas. Stat. Methodol. 2004, 1, 129–144. [Google Scholar] [CrossRef]
- Salvadori, G.; De Michele, C.; Kottegoda, N.T.; Rosso, R. Extremes in Nature. An Approach Using Copulas; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Mirakbari, M.; Ganji, A.; Fallah, S.R. Regional bivariate frequency analysis of meteorological droughts. J. Hydrol. Eng. 2010, 15, 985–1000. [Google Scholar] [CrossRef]
- Li, Y.; Gu, W.; Cui, W.; Chang, Z.; Xu, Y. Exploration of copula function use in crop meteorological drought risk analysis: A case study of winter wheat in Beijing, China. Nat. Hazards. 2015, 77, 1289–1303. [Google Scholar] [CrossRef]
- Li, N.; Guo, L.; Fan, B. A new perspective on understanding the reduced spring dust storm frequency in Inner Mongolia, China. Intern. J. Disaster Risk Sci. 2015, 6, 216–225. [Google Scholar] [CrossRef]
- Dodangeh, E.; Shahedi, K.; Shiau, J.T.; Mirakbari, M. Spatial hydrological drought characteristics in Karkheh River basin, southwest Iran using copulas. J. Earth Syst. Sci. 2017, 126, 1–20. [Google Scholar] [CrossRef]
- Li, N.; Liu, X.; Xie, W.; Wu, J.; Zhang, P. The return period analysis of natural disasters with statistical modeling of bivariate joint probability distribution. Risk Anal. 2013, 33, 134–145. [Google Scholar] [CrossRef]
- Feng, J.; Li, N.; Zhang, Z.; Chen, X. The dual effect of vegetation green-up date and strong wind on the return period of spring dust storms. Sci. Total Environ. 2017, 592, 729–737. [Google Scholar] [CrossRef]
- Fan, Y.D.; Shi, P.J.; Zhou, T.; Li, Y. The impact factor analysis of dust storm disaster in northern China. Adv. Earth Sci. 2007, 22, 350–356. [Google Scholar]
- Kurosaki, Y.; Mikami, M. Recent frequent dust events and their relation to surface wind in East Asia. Geophys. Res. Letter 2003, 30, 1–4. [Google Scholar] [CrossRef]
- Feng, J.; Li, N. The return period analysis of dust storm disaster based on joint distribution of three hazards. In Emerging Economies, Risk and Development, and Intelligent Technology, Proceedings of the 5th International Conference on Risk Analysis and Crisis Response, Tangier, Morocco, 1–3 June 2015; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Shiau, J.T. Fitting drought duration and severity with two-dimensional copulas. Water Resour. Manag. 2006, 20, 795–815. [Google Scholar]
- Wong, G.; Lambert, M.F.; Leonard, M. Drought analysis using bivariate copulas conditional on climatic states. Hydrol. Eng. 2010, 15, 129–141. [Google Scholar] [CrossRef]
- Goda, K.; Ren, J.D. Assessment of seismic loss dependence using copula. Risk Anal. 2010, 30, 1076–1091. [Google Scholar] [CrossRef] [PubMed]
- Xu, K.; Yang, D.; Xu, X.H. Copula based drought frequency analysis considering the spatio-temporal variability in Southwest China. J. Hydrol. 2015, 527, 630–640. [Google Scholar] [CrossRef]
- Fan, L.; Wang, H.; Wang Ch Lai, W.; Zhao, Y. Exploration of Use of Copulas in Analysing the Relationship between Precipitation and Meteorological Drought in Beijing, China. Adv. Meteorol. 2017, 43, 1–12. [Google Scholar] [CrossRef]
- Mirakbari, M.; Mesbah, T.; Mohseni Saravi, M. Bivariate Analysis of Return Period of Dust Storm Based on Copula Theory in Yazd Province. Iran-Watershed Manag. Sci. Eng. 2018, 12, 115–124. [Google Scholar]
- Ekhtesasi, M.R.; Sepehr, A. Investigation of wind erosion process for estimation, prevention, and control of DSS in Yazd–Ardakan plain. Environ. Monit. Assess. 2009, 159, 267–280. [Google Scholar] [CrossRef]
- Omidvar, K. Study and Analysis of Synoptic of Dust and Black Storms in Yazd Province. Geogr. Environ. Plan. 2014, 54, 101–118. [Google Scholar]
- Yu, Y.; Kalashnikova, O.V.; Garay, M.J.; Lee, H.; Notaro, M. Identification and characterization of dust source regions across North Africa and the Middle East using MISR satellite observations. Geophys. Res. Lett. 2018, 45, 6690–6701. [Google Scholar] [CrossRef]
- Sklar, A. Fonctions der´epartition ‘an dimension set leursmarges. Publications de l’Institut de Statistique de l’Universit´e de Paris 1959, 8, 229–231. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas; Springer: New York, NY, USA, 2006. [Google Scholar]
- Genest, C.; Rivest, L.P. Statistical Inference Procedures for Bivariate Archimedean Copula. J. Am. Stat. Assoc. 1993, 8, 1034. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Bozdogan, H. Akaike’s information criterion and recent developments in information complexity. Math. Psychol. 2000, 44, 62–91. [Google Scholar] [CrossRef]
- Sorensen, J.H. Hazard warning systems: Review of 20 years of progress. Nat. Hazards Rev. 2000, 1, 119–125. [Google Scholar] [CrossRef]
- Guharay, S.; Chang, K.; Xu, J. Robust Estimation of Value-at-Risk through Distribution-Free and Parametric Approaches Using the Joint Severity and Frequency Model: Applications in Financial, Actuarial, and Natural Calamities Domains. Risks 2017, 5, 41. [Google Scholar] [CrossRef]
| Archimedean Family | Frank | Joint CDF | Generator Function |
| Gumbel | |||
| Clayton | |||
| Rotated Joe | |||
| Rotated Gumbel | |||
| Rotated Clayton | |||
| Elliptical Family | Student-t | - | |
| Gaussian | - |
| Variables | 500 hPa | 850 hPa | 1000 hPa |
|---|---|---|---|
| Maximum wind speed–geopotential height | −0.29 | −0.26 | −0.19 |
| Maximum wind speed–vertical velocity | 0.14 | 0.27 | 0.3 |
| Variables | CDF | Parameters | |
|---|---|---|---|
| Maximum wind speed | Wakeby | α = 80.89, β = 12.59, γ = 4.56, δ = 0.057, ξ = 0.46 | |
| Geopotential height 500 hPa | GEV | κ = −0.54 σ = 98.19 μ = 5761.7 | |
| Vertical velocity | GEV | κ = −0.23 σ = 0.082 μ = −0.038 | |
| Copula CDF | Parametric Estimation | Nonparametric Estimation | ||||||
|---|---|---|---|---|---|---|---|---|
| AIC | BIC | SOLS | Parameter | AIC | BIC | SOLS | Parameter | |
| Frank | −5.38 | −3.85 | 0.3557 | −2.46 | −5.34 | −2.1 | 0.3557 | −2.3 |
| Gaussian | −2.76 | −0.53 | 0.2533 | −0.46 | −2.31 | −0.88 | 0.3533 | −0.28 |
| Rotated Clayton | −2.66 | −0.34 | 0.256 | −0.77 | −2.02 | −0.201 | 0.3590 | −0.48 |
| Rotated Gumbel | −5.5 | −4.04 | 0.354 | −2.44 | −5.13 | −2.81 | 0.3543 | −1.14 |
| Student t | −7.4 | −4.45 | 0.2312 | −0.57 2 | - | - | - | - |
| Rotated Joe | −5.15 | −3.7 | 0.3451 | −2.68 | −4.2 | −2.6 | 0.3493 | −1.47 |
| Copula CDF | Parametric Estimation | Nonparametric Estimation | ||||||
|---|---|---|---|---|---|---|---|---|
| AIC | BIC | SOLS | Parameter | AIC | BIC | SOLS | Parameter | |
| Frank | −2.82 | −0.489 | 0.036 | 1.85 | −2.24 | −0.0212 | 0.046 | 2.46 |
| Clayton | −2.89 | −0.536 | 0.035 | 0.64 | −2.84 | −0.0157 | 0.047 | 0.643 |
| Gumbel | −3.1 | −0.637 | 0.031 | 1.38 | −1.92 | −0.373 | 0.045 | 1.87 |
| Gaussian | −3.81 | −2.31 | 0.029 | 0.289 | −2.28 | −1.86 | 0.042 | 0.571 |
| Student t | −2.01 | −1.98 | 0.041 | 0.87, 1.58 | - | - | - | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mesbahzadeh, T.; Mirakbari, M.; Mohseni Saravi, M.; Soleimani Sardoo, F.; Krakauer, N.Y. Joint Modeling of Severe Dust Storm Events in Arid and Hyper Arid Regions Based on Copula Theory: A Case Study in the Yazd Province, Iran. Climate 2020, 8, 64. https://doi.org/10.3390/cli8050064
Mesbahzadeh T, Mirakbari M, Mohseni Saravi M, Soleimani Sardoo F, Krakauer NY. Joint Modeling of Severe Dust Storm Events in Arid and Hyper Arid Regions Based on Copula Theory: A Case Study in the Yazd Province, Iran. Climate. 2020; 8(5):64. https://doi.org/10.3390/cli8050064
Chicago/Turabian StyleMesbahzadeh, Tayyebeh, Maryam Mirakbari, Mohsen Mohseni Saravi, Farshad Soleimani Sardoo, and Nir Y. Krakauer. 2020. "Joint Modeling of Severe Dust Storm Events in Arid and Hyper Arid Regions Based on Copula Theory: A Case Study in the Yazd Province, Iran" Climate 8, no. 5: 64. https://doi.org/10.3390/cli8050064
APA StyleMesbahzadeh, T., Mirakbari, M., Mohseni Saravi, M., Soleimani Sardoo, F., & Krakauer, N. Y. (2020). Joint Modeling of Severe Dust Storm Events in Arid and Hyper Arid Regions Based on Copula Theory: A Case Study in the Yazd Province, Iran. Climate, 8(5), 64. https://doi.org/10.3390/cli8050064






