Modeling of Atmospheric Carbon Dioxide (CO2) Concentrations as a Function of Fossil-Fuel and Land-Use Change CO2 Emissions Coupled with Oceanic and Terrestrial Sequestration
Abstract
1. Introduction
2. Materials and Methods
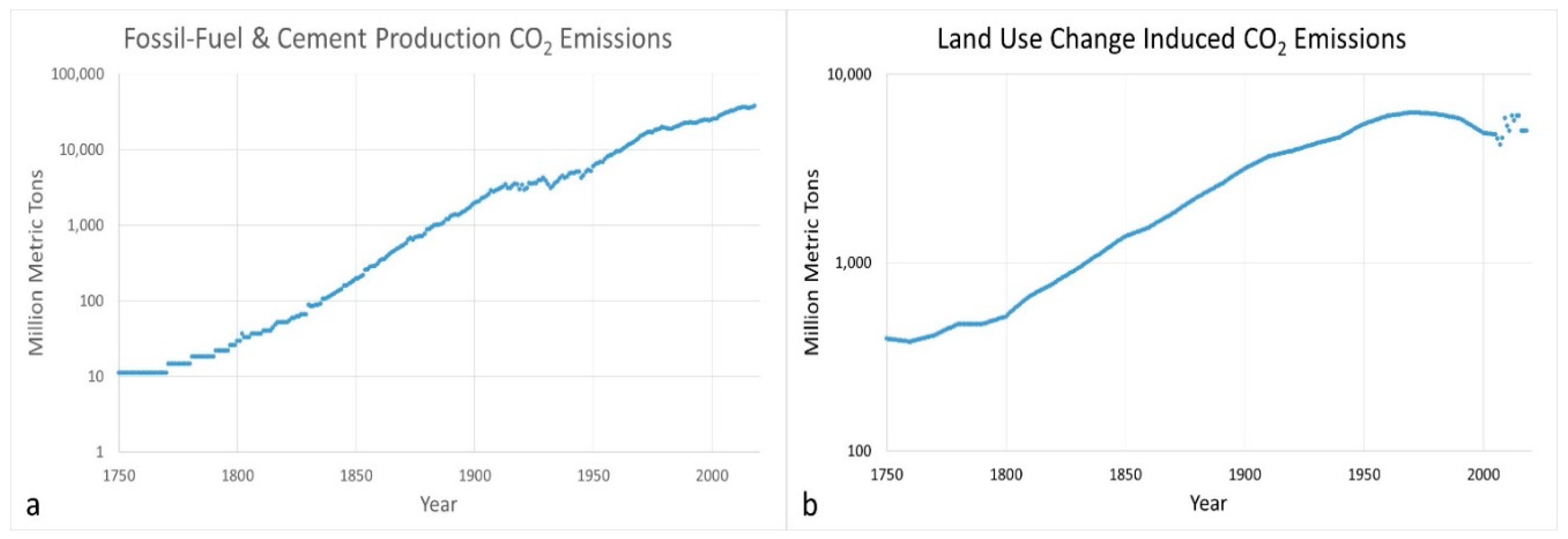
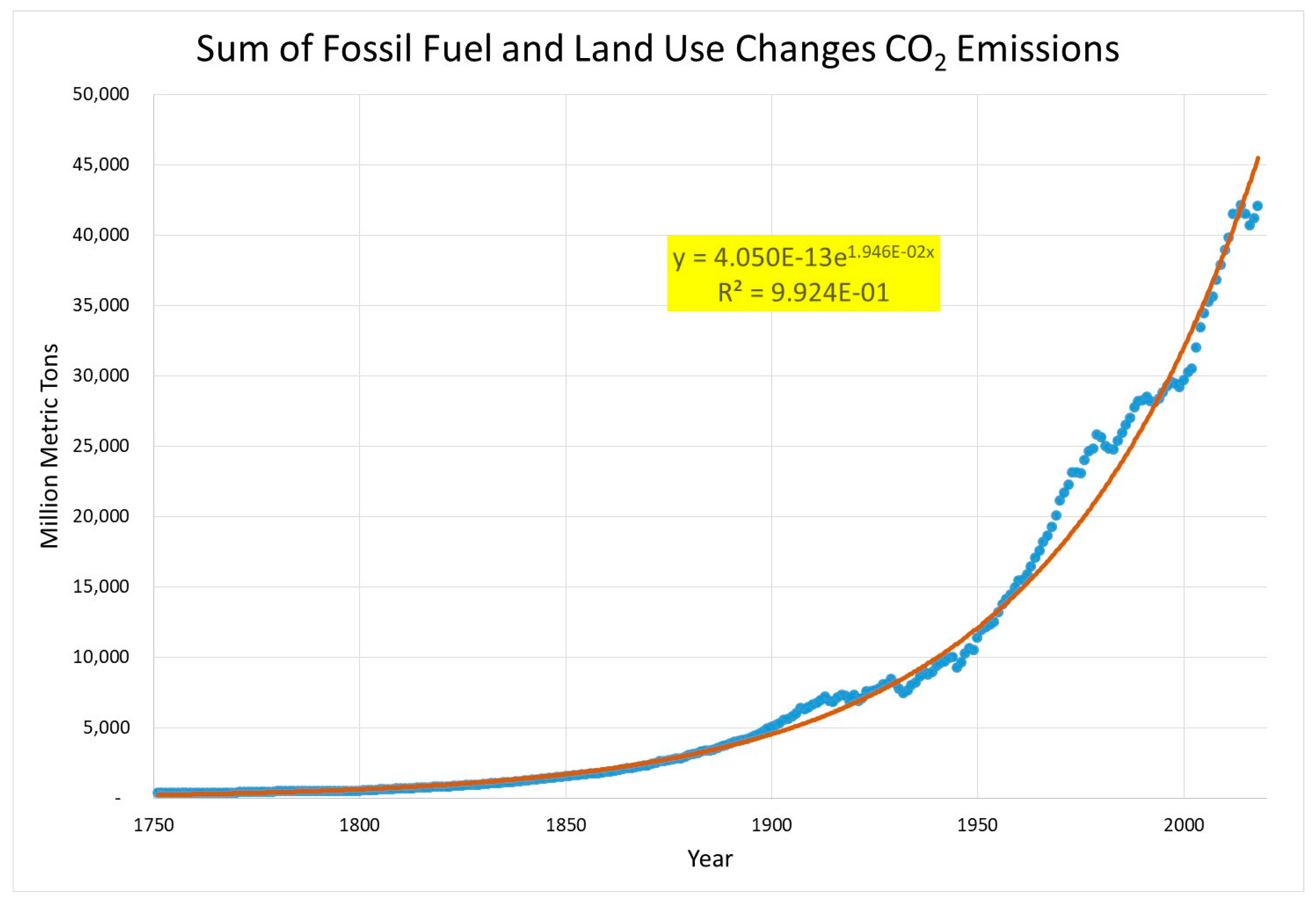
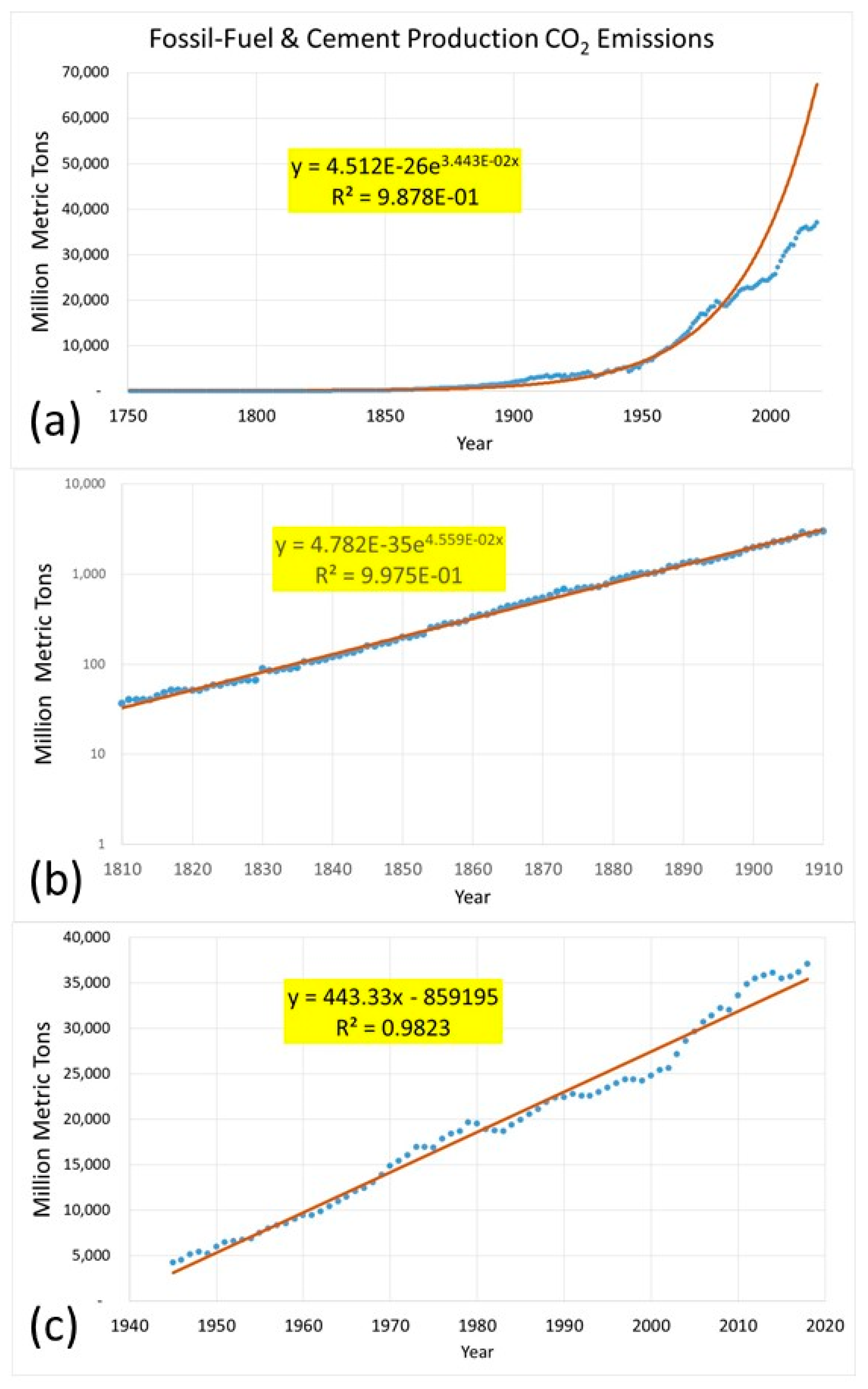
- An evaluation of fossil fuel and land-use change CO2 emissions with determination of best fit exponential or linear trendlines to enable comparison with prior studies, e.g., [31];
- The development of a semi-empirical model to calculate atmospheric CO2 concentrations based on the level of fossil fuel and land-use emissions;
- To compare the model results of CO2 concentration calculations using both
- o
- the traditional atmospheric fraction (AF), and,
- o
- a new approach that employs only AFFF combined with a linear component that addresses the net flux of land-based CO2 emissions combined with a rapidly varying component of the terrestrial sink;
- To determine a value for AFFF for the time period under consideration.
3. Results
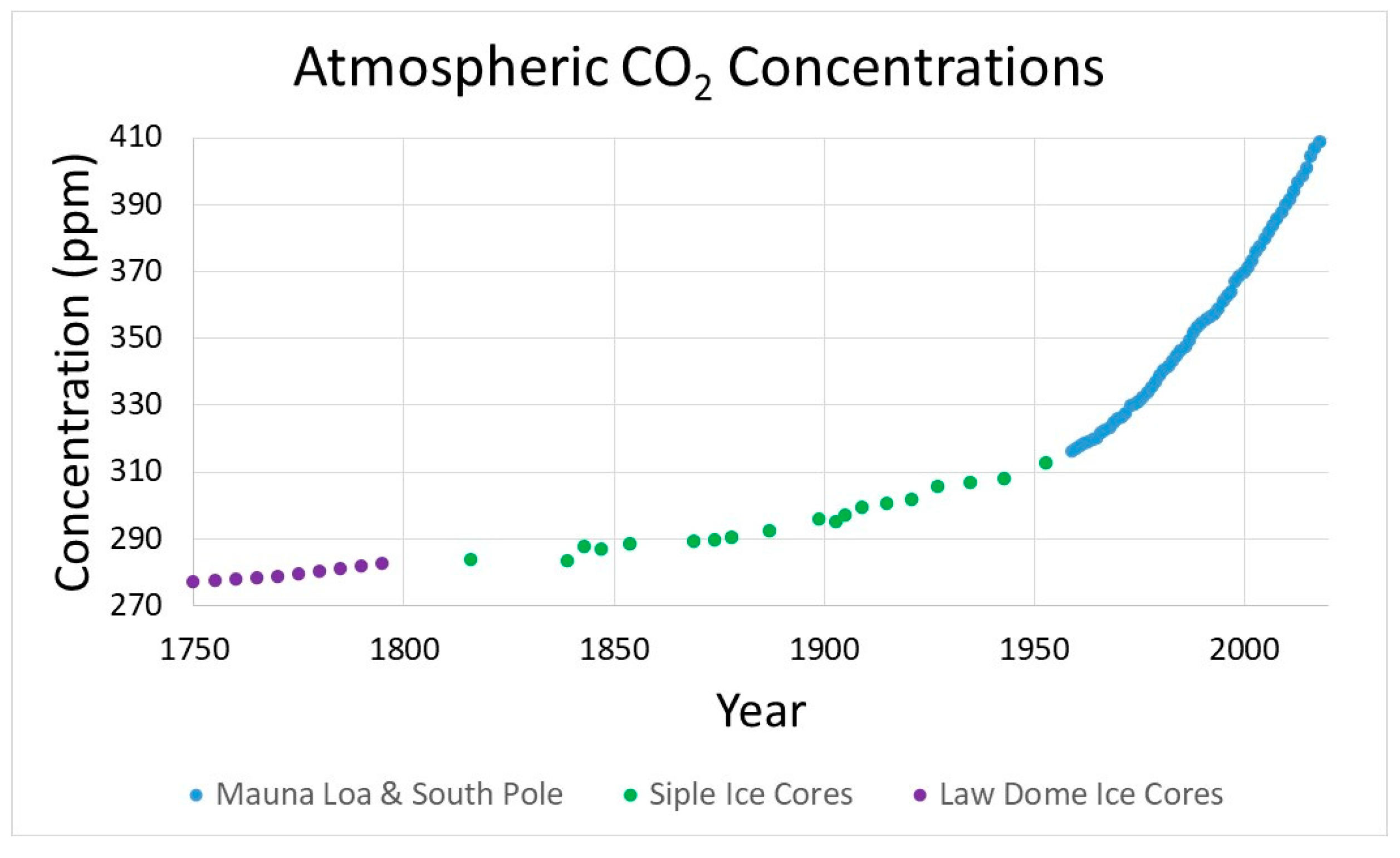
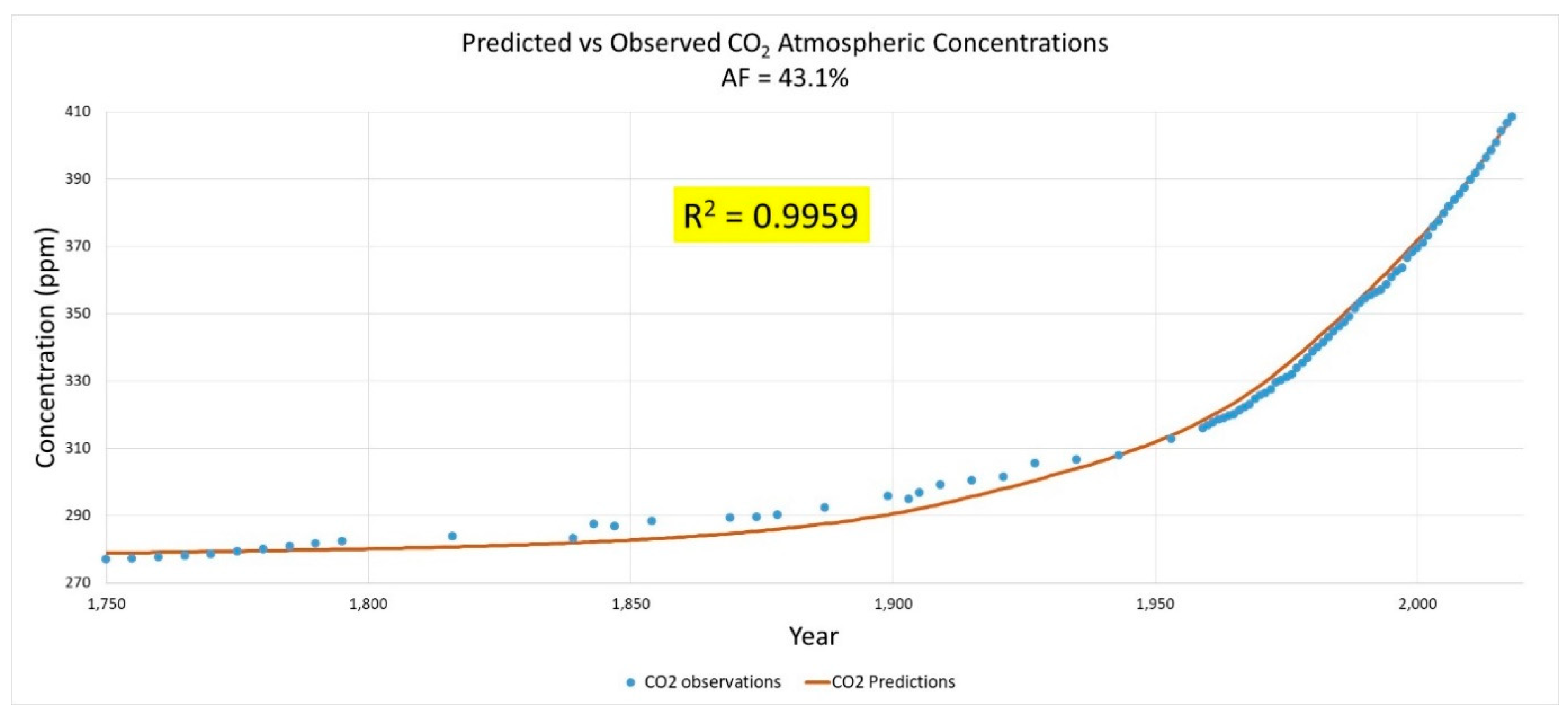
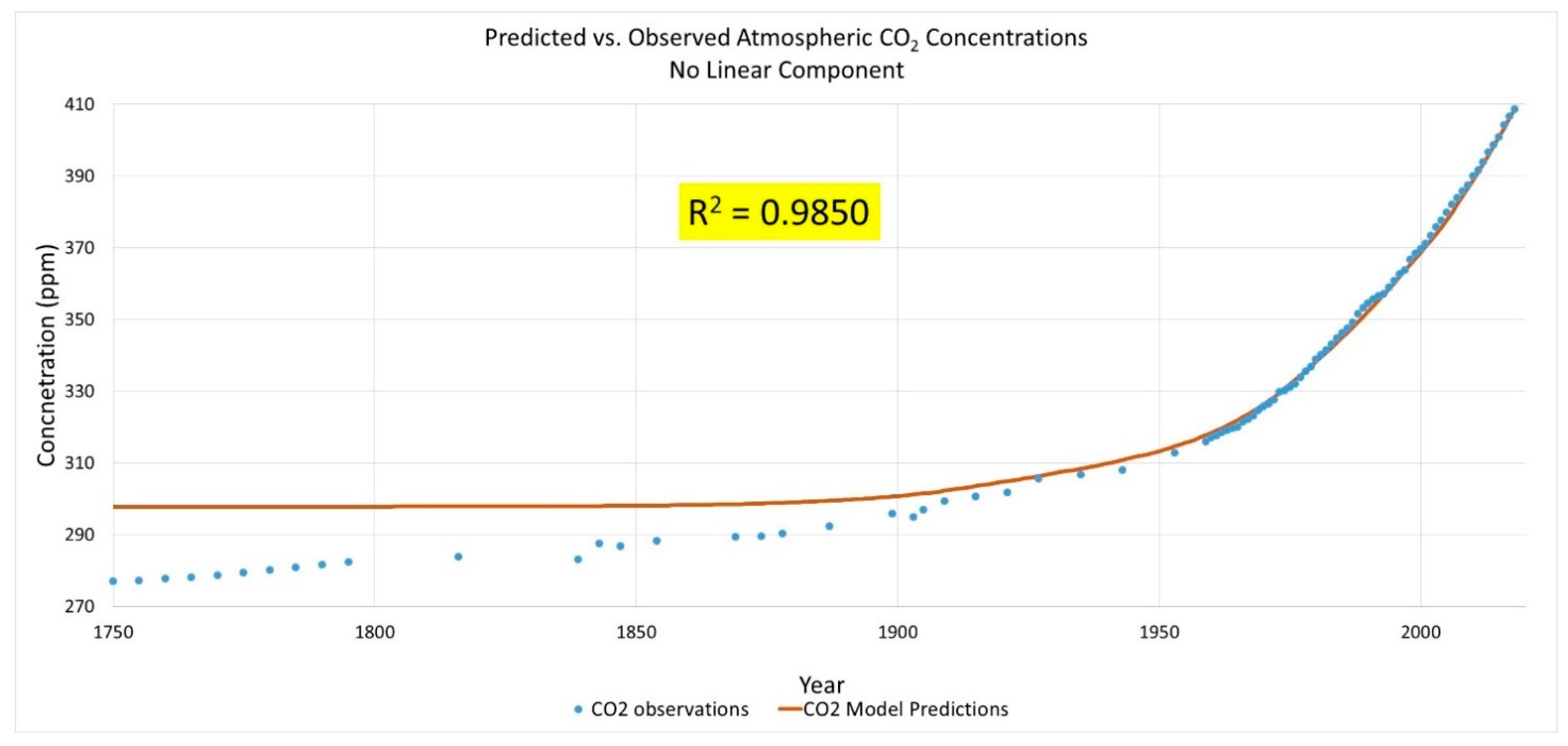
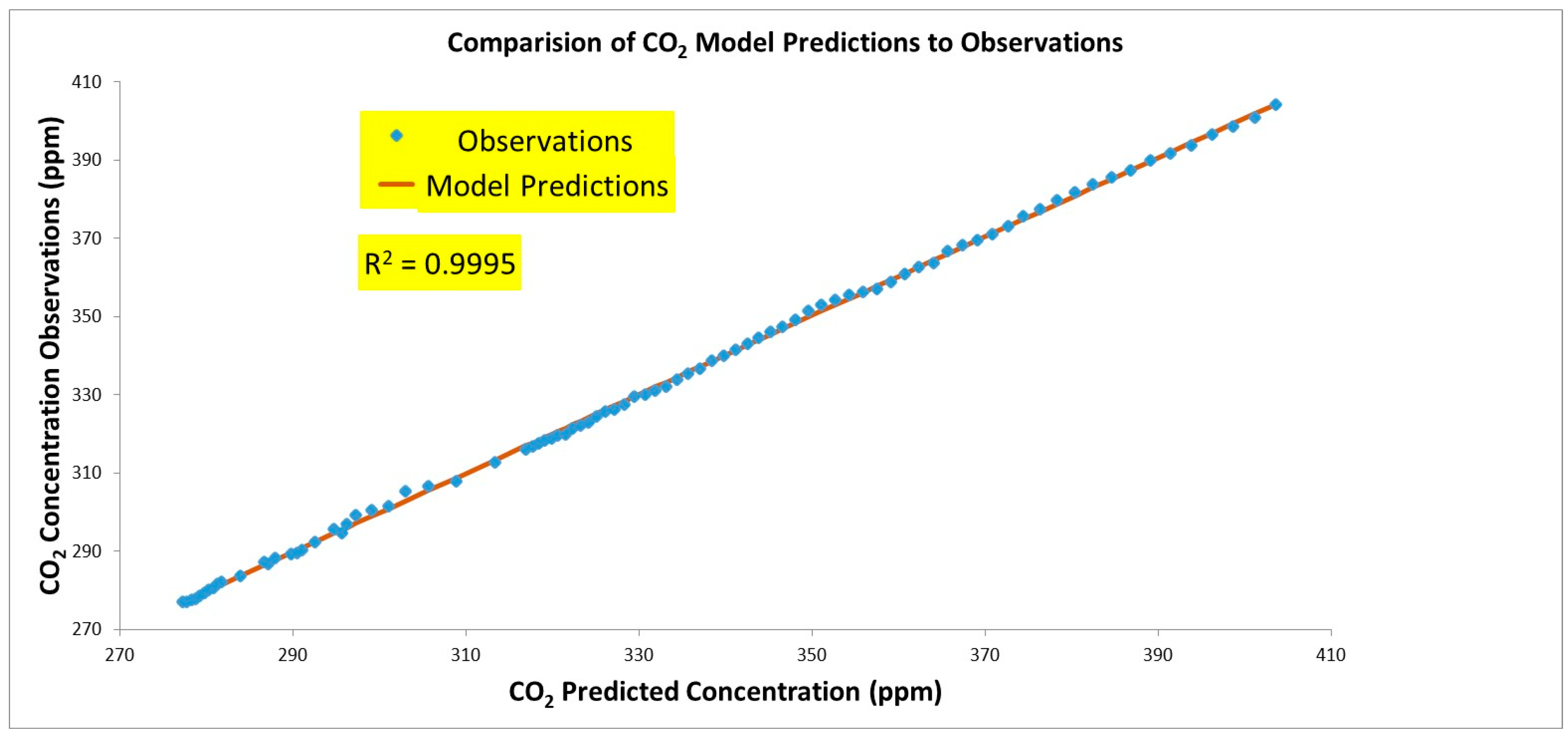
3.1. Correlation of Atmospheric CO2 Concentration with CO2 Emissions
3.1.1. Traditional Approach and Discussion
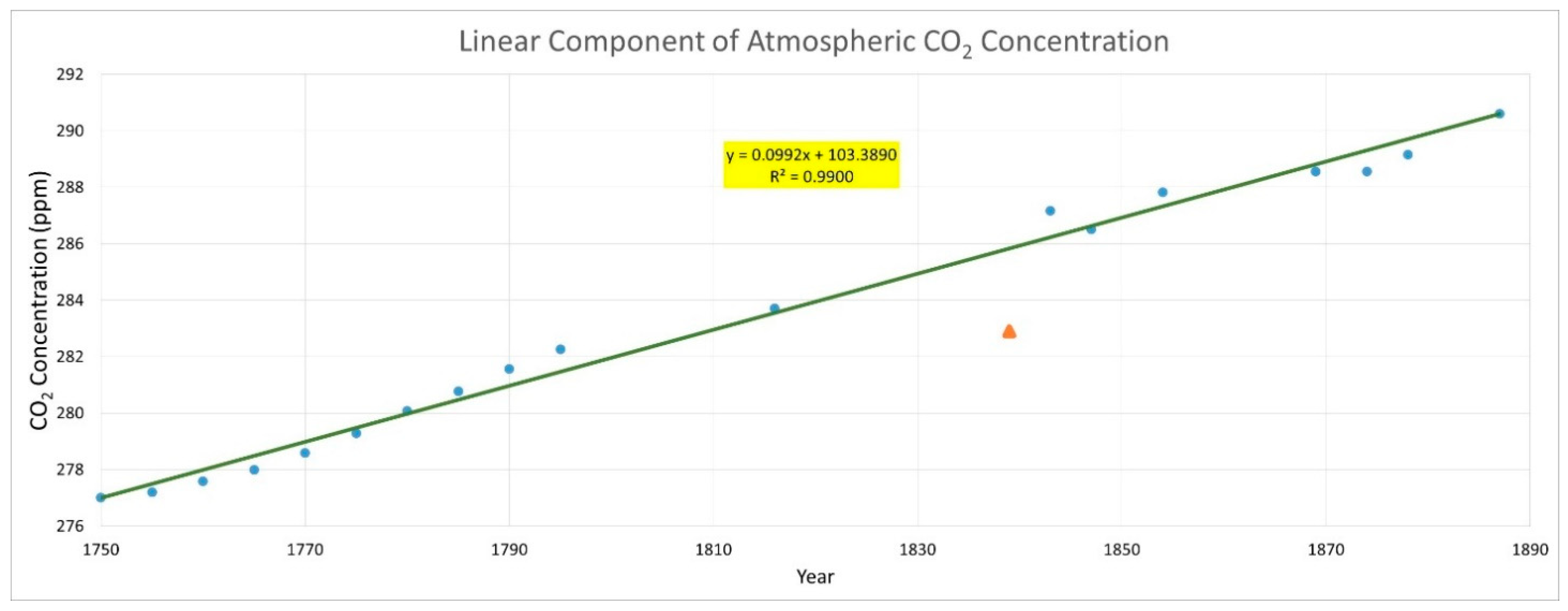
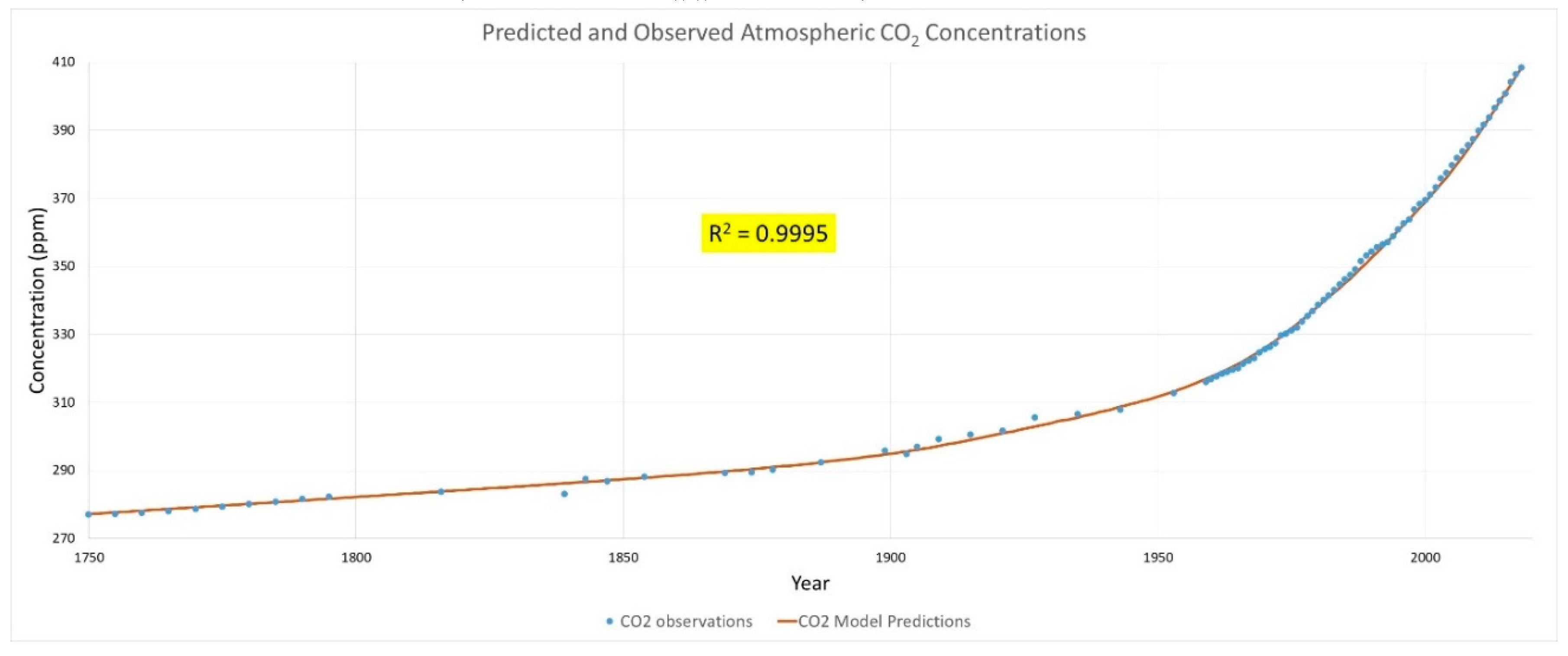
3.1.2. Alternative Correlation Approach
4. Discussion
Uncertainties
5. Conclusions
Supplementary Materials
Funding
Conflicts of Interest
References
- Fleming, J.R. Historical Perspectives on Climate Change; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Tyndall, J. On the Absorption and Radiation of Heat by Gases and Vapours, and on the Physical Connexion of Radiation, Absorption, and Conduction. Phil. Trans. R. Soc. 1861, 151, 1–36. [Google Scholar]
- Oreskes, N. The scientific consensus on global warming. Science 2004, 306, 1686. [Google Scholar] [CrossRef] [PubMed]
- Prentice, I.C.; Farquhar, G.D.; Fasham, M.J.R.; Goulden, M.L.; Heimann, M.; Jaramillo, V.J.; Kheshgi, H.S.; LeQuéré, C.; Scholes, R.J.; Wallace, D.W.R.; et al. Climate Change 2001: The Scientific Basis. Contributions of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2001; pp. 185–237. [Google Scholar]
- Meehl, G.A.; Covey, C.; Delworth, T.; Latif, M.; Mcavaney, B.; Mitchell, J.F.B.; Stouffer, R.J.; Taylor, K.E. THE WCRP CMIP3 MULTIMODEL DATASET A New Era in Climate Change Research. BAMS 2007, 1383–1394. [Google Scholar] [CrossRef]
- Andres, R.J.; Boden, T.A.; Bréon, F.-M.; Ciais, P.; Davis, S.; Erickson, D.; Gregg, J.S.; Jacobson, A.; Marland, G.; Miller, J.; et al. A synthesis of carbon dioxide emissions from fossil-fuel combustion. Biogiosciences 2012, 9, 1845–1871. [Google Scholar] [CrossRef]
- Boden, T.A.; Andres, R.J.; Marland, G. Global, Regional, and National Fossil-Fuel CO2 Emissions; Carbon Dioxide Information Analysis Center, Oak Ridge National Laboratory, U.S. Department of Energy: Oak Ridge, TN, USA, 2013. Available online: http://cdiac.ess-dive.lbl.gov/trends/emis/overview_2010.html (accessed on 20 January 2020).
- Boden, T.A.; Marland, G.; Andres, R.J. Global, Regional, and National Fossil-Fuel CO2 Emissions; Carbon Dioxide Information Analysis Center at Appalachian State University: Boone, NC, USA, 2018; Available online: https://energy.appstate.edu/CDIAC (accessed on 20 January 2020).
- Le Quéré, C.; Robbie, A.M.; Friedlingstein, P.; Sitch, S.; Hauck, J.; Pongratz, J.; Pickers, P.A.; Korsbakken, J.I.; Peters, G.P.; Canadell, J.G.; et al. Global Carbon Budget 2018. Earth Syst. Sci. Data 2018, 10, 2141–2194. [Google Scholar] [CrossRef]
- Stocker, B.D.; Feissli, F.; Strassmann, K.M.; Spahni, R.; Joos, F. Past and future carbon fluxes from land use change, shifting cultivation and wood harvest. Tellus B Chem. Phys. Meteorol. 2014, 66, 23188. [Google Scholar] [CrossRef]
- Andres, R.J.; Fielding, D.J.; Marland, G.; Boden, T.A.; Kumar, N.; Kearney, A.T. Carbon dioxide emissions from fossil-fuel use, 1751–1950. Tellus B 1999, 51, 759–765. [Google Scholar] [CrossRef]
- Andres, R.J.; Boden, T.; Higdon, D. A new evaluation of the uncertainty associated with CDIAC estimates of fossil fuel carbon dioxide emission. Tellus B 2014, 66, 23616. [Google Scholar] [CrossRef]
- Ballantyne, A.P.; Andres, R.; Houghton, R.; Stocker, B.D.; Wanninkhof, R.; Anderegg, W.; Cooper, L.A.; DeGrandpre, M.; Tans, P.P.; Miller, J.B.; et al. Audit of the global carbon budget: Estimate errors and their impact on uptake uncertainty. Biogeosciences 2015, 2015 12, 2565–2584. [Google Scholar] [CrossRef]
- Hurtt, G.C.; Frolking, S.; Fearon, M.G.; Moore, B.; Shevliakova, E.; Malshev, S.; Pacala, S.W.; Houghton, R.A. The underpinnings of land-use history: Three centuries of global gridded land-use transitions, wood harvest activity, and resulting secondary landscapes. Glob. Chan. Biol. 2006, 12, 1208–1229. [Google Scholar] [CrossRef]
- Etheridge, D.M.; Steele, L.P.; Langenfelds, R.L.; Francey, R.J.; Barnola, J.-M.; Morgan, V.I. Historical CO2 Records from the Law Dome DE08, DE08-2, and DSS ice cores In Trends: A Compendium of Data on Global Change; Carbon Dioxide Information Analysis Center, Oak Ridge National Laboratory, U.S. Department of Energy: Oak Ridge, TN, USA, 1998. Available online: http://cdiac.ess-dive.lbl.gov/trends/co2/lawdome.html (accessed on 18 December 2019).
- Neftel, A.; Friedli, H.; Moor, E.; Lötscher, H.; Oeschger, H.; Siegenthaler, U.; Stauffer, B. Historical Carbon Dioxide Record from the Siple Station Ice Core in Trends: A Compendium of Data on Global Change; Carbon Dioxide Information Analysis Center, Oak Ridge National Laboratory, U.S. Department of Energy: Oak Ridge, TN, USA, 1994. Available online: Cdiac.ess-dive.lbl.gov/trends/co2/siple.html (accessed on 18 December 2019).
- Tans, P. 2018. Available online: http://www.esrl.noaa.gov/gmd/ccgg/trends/ (accessed on 18 December 2019).
- Keeling, R.F. 2018. Available online: scrippsco2.ucsd.edu (accessed on 18 December 2019).
- Tans, P.; Thoning, K. “How we measure background CO2 levels on Mauna Loa” NOAA ESRL Global Monitoring Division. 2018. Available online: www.esrl.noaa.gov/gmd/ccgg/about/co2_measurements.html (accessed on 5 January 2020).
- Wanninkhof, R.; Park, G.-H.; Takahasi, T.; Sweeney, C.; Reely, R.; Nojiri, Y.; Gruber, N.; Doney, S.C.; McKinley, G.A.; Lenton, A.; et al. Global ocean carbon uptake: Magnitude, variability and trends. Biogeosciences 2013, 10, 1983–2000. [Google Scholar] [CrossRef]
- Plattner, G.-K.; Joos, F.; Stocker, T.F.; Marchal, O. Feedback mechanisms and sensitivities of ocean carbon uptake under global warming. Tellus B Chem. Phys. Meteorol. 2001, 53, 564–592. [Google Scholar] [CrossRef][Green Version]
- Khatiwala, S.; Primeau, F.; Hall, T. Reconstruction of the history of anthropogenic CO2 concentrations in the ocean. Nature 2009, 462, 346–349. [Google Scholar] [CrossRef] [PubMed]
- Boysen, L.R.; Brovkin, V.; Arora, V.K.; Cadule, P.; de Noblet-Ducoudré, N.; Kato, E.; Pongratz, J.; Gayler, V. Global and regional effects of land-use change on climate in 21st century simulations with interactive carbon cycle. Earth Syst. Dyn. 2014, 5, 309–319. [Google Scholar] [CrossRef]
- Matthews, H.; Weaver, A.; Meissner, K.; Gillett, N.; Eby, M. Natural and anthropogenic climate change: Incorporating historical land cover change, vegetation dynamics and the global carbon cycle. Clim. Dyn. 2004, 22, 461–479. [Google Scholar] [CrossRef]
- Brovkin, V.; Sitch, S.; von Bloh, W.; Claussen, M.; Bauer, E.; Cramer, W. Role of land cover changes for atmospheric CO2 increase and climate change during the last 150 years. Glob. Change. Biol. 2004, 10, 1253–1266. [Google Scholar] [CrossRef]
- Brovkin, V.; Boysen, L.; Arora, V.; Boisier, J.; Cadule, P.; Chini, L.; Claussen, M.; Friedlingstein, P.; Gayler, V.; van den Hurk, B.J.J.M.; et al. Effect of anthropogenic land-use and land cover changes on climate and land carbon storage in CMIP5 projections for the 21st century. J. Clim. 2013, 26, 6859–6881. [Google Scholar] [CrossRef]
- Sitch, S.; Brovkin, V.; von Bloh, W.; van Vuuren, D.; Eickhout, B.; Ganopolski, A. Impacts of future land cover changes on atmospheric CO2 and climate. Glob. Biogeochem. Cycles 2005, 19, GB2013. [Google Scholar] [CrossRef]
- Shevliakova, E.; Stouffer, R.J.; Malyshev, S.; Krasting, J.P.; Hurtt, G.C.; Pacala, S.W. Historical warming reduced due to enhance land carbon uptake. Proc. Natl. Acad. Sci. USA 2013, 110, 16730–16735. [Google Scholar] [CrossRef]
- Pongratz, J.; Reick, C.; Raddatz, T.; Claussen, M. Biogeophysical vs. biogeochemical climate response to historical anthropogenic land cover change. Geophy. Res. Lett. 2010, 37, L08072. [Google Scholar] [CrossRef]
- Bennedsen, M.; Hillebrand, E.; Koopman, S.J. Trend analysis of the airborne fraction and sink rate of anthropogenically released CO2. Biogeosciences 2019, 16, 3651–3663. [Google Scholar] [CrossRef]
- Raupach, M.R.; Canadell, J.G.; LeQuéré, C. Anthropogenic and biophysical contributions to increasing atmospheric CO2 growth rate and airborne fraction. Biogeosciences 2008, 5, 1601–1613. [Google Scholar] [CrossRef]
- Stocker, T.F.; Qin, D.; Plattner, G.-K.; Tignor, M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of IPCC the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Terenzi, F.; Khatiwala, S. Modeling the atmospheric airborne fraction in a simple carbon cycle model. Tellus B 2009, submitted. [Google Scholar]
- Trenberth, K.E.; Smith, L. The Mass of the Atmosphere: A Constraint on Global Analyses. J. Clim. 2005, 18, 864–875. [Google Scholar] [CrossRef]
- Microsoft Corporation. Microsoft Excel. 2018. Available online: https://office.microsoft.com/excel (accessed on 12 February 2020).
- Lawrence, D.M.; Oleson, K.W.; Flanner, M.G.; Thornton, P.E.; Swenson, S.C.; Lawrence, P.J.; Zeng, X.; Yang, Z.-L.; Levis, S.; Sakaguchi, K.; et al. Parameterization improvements and functional and structural advances in version 4 of the Community Land Model. J. Adv. Model. Earth Syst. 2011, 3, M03001. [Google Scholar] [CrossRef]
- Levy, P.E.; Cannell, M.G.R.; Friend, A.D. Modelling the impact of future changes in climate, CO2 concentration and land use on natural ecosystems and the terrestrial carbon sink. Glob. Environ. Chang. 2004, 14, 21–30. [Google Scholar] [CrossRef]
- Clark, D.B.; Mercado, L.M.; Sitch, S.; Jones, C.D.; Gedney, N.; Best, M.J.; Pryor, M.; Rooney, G.G.; Essery, R.L.H.; Blyth, E.; et al. The Joint UK Land Environment Simulator (JULES), model description – Part 2: Carbon fluxes and vegetation dynamics. Geosci. Model Dev. 2011, 4, 701–722. [Google Scholar] [CrossRef]
- Cox, P.M. Description of the “TRIFFID” Dynamic Global Vegetation Model; Hadley Centre: Exeter, UK, 2001. Technical Note 24 2001.
- Sitch, S.; Smith, B.; Prentice, I.C.; Arneth, A.; Bondeau, A.; Cramer, W.; Kaplan, J.O.; Levis, S.; Lucht, W.; Sykes, M.T.; et al. Evaluation of ecosystem dynamics, plant geography and terrestrial carbon cycling in the LPJ dynamic global vegetation model. Glob. Change. Biol. 2003, 9, 161–185. [Google Scholar] [CrossRef]
- Smith, B.; Prentice, I.C.; Sykes, M.T. Representation of vegetation dynamics in the modelling of terrestrial ecosystems: Comparing two contrasting approaches within European climate space. Glob. Ecol. Biogeogr. 2001, 10, 621–637. [Google Scholar] [CrossRef]
- Ahlström, A.; Miller, P.A.; Smith, B. Too early to infer a global NPP decline since 2000. Geophys. Res. Lett. 2012, 39, L15403. [Google Scholar] [CrossRef]
- Zaehle, S.; Ciais, P.; Friend, A.D.; Prieur, V. Carbon benefits of anthropogenic reactive nitrogen offset by nitrous oxide emissions. Nat. Geosci. 2011, 4, 601–605. [Google Scholar] [CrossRef]
- Krinner, G.; Viovy, N.; de Noblet-Ducoudré, N.; Ogee, J.; Polcher, J.; Friedlingstein, P.; Ciais, P.; Sitch, S.; Prentice, I.C. A dynamic global vegetation model for studies of the coupled atmosphere-biosphere system. Glob. Biogeochem. Cycles 2005, 19, Gb1015. [Google Scholar] [CrossRef]
- Woodward, F.I.; Lomas, M.R. Vegetation dynamics—Simulating responses to climatic change. Biol. Rev. 2004, 79, 643–670. [Google Scholar] [CrossRef]
- Zeng, N.; Mariotti, A.; Wetzel, P. Terrestrial mechanisms of interannual CO2 variability. Glob. Biogeochem. Cycles 2005, 19, GB1016. [Google Scholar] [CrossRef]
- Steig, E.J. Sources of Uncertainty in Ice Core Data. In White paper from Workshop on Reducing and Representing Uncertainties in High-Resolution Proxy Data; PAGES/CLIVAR Proxy Uncertainty Workshop: Trieste, Italy, 2008. [Google Scholar]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
O’Connor, J.P. Modeling of Atmospheric Carbon Dioxide (CO2) Concentrations as a Function of Fossil-Fuel and Land-Use Change CO2 Emissions Coupled with Oceanic and Terrestrial Sequestration. Climate 2020, 8, 61. https://doi.org/10.3390/cli8050061
O’Connor JP. Modeling of Atmospheric Carbon Dioxide (CO2) Concentrations as a Function of Fossil-Fuel and Land-Use Change CO2 Emissions Coupled with Oceanic and Terrestrial Sequestration. Climate. 2020; 8(5):61. https://doi.org/10.3390/cli8050061
Chicago/Turabian StyleO’Connor, John P. 2020. "Modeling of Atmospheric Carbon Dioxide (CO2) Concentrations as a Function of Fossil-Fuel and Land-Use Change CO2 Emissions Coupled with Oceanic and Terrestrial Sequestration" Climate 8, no. 5: 61. https://doi.org/10.3390/cli8050061
APA StyleO’Connor, J. P. (2020). Modeling of Atmospheric Carbon Dioxide (CO2) Concentrations as a Function of Fossil-Fuel and Land-Use Change CO2 Emissions Coupled with Oceanic and Terrestrial Sequestration. Climate, 8(5), 61. https://doi.org/10.3390/cli8050061